31 lines
2.6 KiB
Markdown
31 lines
2.6 KiB
Markdown
|
|
---
|
||
|
|
title: Simplifying Square Roots
|
||
|
|
localeTitle: تبسيط الجذور المربعة
|
||
|
|
---
|
||
|
|
### مثال: بسط 
|
||
|
|
|
||
|
|
خطوات الحل:
|
||
|
|
|
||
|
|
* كسر 180 في منتج من العوامل العددية الأولية: 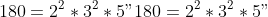
|
||
|
|
* استخدام خاصية المنتج من الجذور 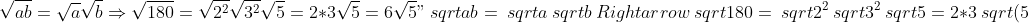} = 6 \ الجذر التربيعي {5}")
|
||
|
|
لا يمكننا تبسيط الجذر التربيعي للرقم الأساسي وبالتالي الإجابة النهائية: 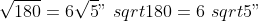
|
||
|
|
|
||
|
|
### مثال: بسط 
|
||
|
|
|
||
|
|
خطوات الحل:
|
||
|
|
|
||
|
|
* كسر 1750 إلى منتج من العوامل العددية الأولية: 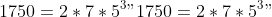
|
||
|
|
* استخدام خاصية المنتج من الجذور والحفاظ على كسر النتائج: 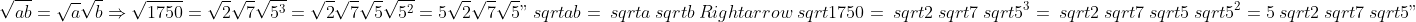
|
||
|
|
الآن استخدم خاصية المنتج مرة أخرى لدمج الجذور التي لا يمكن تبسيطها: 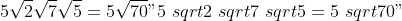
|
||
|
|
|
||
|
|
### المصطلح:
|
||
|
|
|
||
|
|
باستخدام √49 كمثال:
|
||
|
|
|
||
|
|
* "√" يطلق عليها **الرمز الراديكالي** .
|
||
|
|
* يسمى 49 **radicand** .
|
||
|
|
|
||
|
|
#### معلومات اكثر:
|
||
|
|
|
||
|
|
* [Wikihow ، تبسيط الجذر التربيعي](https://www.wikihow.com/Simplify-a-Square-Root)
|
||
|
|
* [أكاديمية خان](https://www.khanacademy.org/math/algebra/rational-exponents-and-radicals/alg1-simplify-square-roots/a/simplifying-square-roots-review)
|