freeCodeCamp/guide/portuguese/algorithms/greatest-common-divisor-euclidean/index.md

---
title: Greatest Common Divisor Euclidean
localeTitle: Maior Divisor Comum Euclidiano
---
## Maior Divisor Comum Euclidiano

Para este tópico, você deve saber sobre o Greatest Common Divisor (GCD) e a operação MOD primeiro.

#### Maior Divisor Comum (GCD)

O GCD de dois ou mais inteiros é o maior número inteiro que divide cada um dos números inteiros, de modo que o restante seja zero.

Exemplo-  
GCD de 20, 30 = 10 _(10 é o maior número que divide 20 e 30 com o restante como 0)_  
GCD de 42, 120, 285 = 3 _(3 é o maior número que divide 42, 120 e 285 com o restante como 0)_

#### Operação "mod"

A operação mod fornece o restante quando dois inteiros positivos são divididos. Nós escrevemos como segue-  
`A mod B = R`

Isto significa que dividir A por B lhe dá o resto R, isto é diferente de sua operação de divisão que lhe dá o quociente.

Exemplo-  
7 mod 2 = 1 _(dividindo 7 por 2 dá o resto 1)_  
42 mod 7 = 0 _(dividindo 42 por 7 dá o resto 0)_

Com os dois conceitos acima compreendidos, você compreenderá facilmente o Algoritmo Euclidiano.

### Algoritmo Euclidiano para o Maior Divisor Comum (GCD)

O Algoritmo Euclidiano encontra o GCD de 2 números.

Você entenderá melhor esse Algoritmo ao vê-lo em ação. Supondo que você queira calcular o GCD de 1220 e 516, vamos aplicar o Algoritmo Euclidiano -

Supondo que você queira calcular o GCD de 1220 e 516, vamos aplicar o Algoritmo Euclidiano - ![Exemplo Euclidiano](https://cdn-media-1.freecodecamp.org/imgr/aa8oGgP.png)

Pseudocódigo do Algoritmo  
Etapa 1: **Seja `a, b` os dois números**  
Etapa 2: **`a mod b = R`**  
Etapa 3: **deixe `a = b` e `b = R`**  
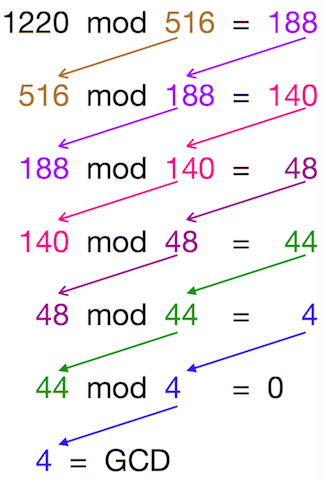
Passo 4: **Repita os passos 2 e 3 até que o `a mod b` seja maior que 0**  
Etapa 5: **GCD = b**  
Etapa 6: finalizar

Código JavaScript para executar o GCD-

```javascript
function gcd(a, b) { 
  var R; 
  while ((a % b) > 0)  { 
    R = a % b; 
    a = b; 
    b = R; 
  } 
  return b; 
 } 
```

Código Javascript para executar o GCD usando Recursion-

```javascript
function gcd(a, b) { 
  if (b == 0) 
    return a; 
  else 
    return gcd(b, (a % b)); 
 } 
```

Você também pode usar o Algoritmo Euclidiano para encontrar o GCD de mais de dois números. Como o GCD é associativo, a seguinte operação é válida - `GCD(a,b,c) == GCD(GCD(a,b), c)`

Calcule o GCD dos dois primeiros números e depois encontre o GCD do resultado e o próximo número. Exemplo - `GCD(203,91,77) == GCD(GCD(203,91),77) == GCD(7, 77) == 7`

Você pode encontrar GCD de `n` números da mesma maneira.