35 lines
1.7 KiB
Markdown
35 lines
1.7 KiB
Markdown
|
|
---
|
||
|
|
title: Polynomial Factorization
|
||
|
|
localeTitle: Fatoração Polinomial
|
||
|
|
---
|
||
|
|
## Fatoração Polinomial
|
||
|
|
|
||
|
|
Polinômios de fatoração é muito parecido com números regulares de fatoração. O objetivo é encontrar números ou polinômios que se dividam uniformemente do polinômio. Em contraste com o factoring, você pode simplificar uma expressão assim:
|
||
|
|
|
||
|
|
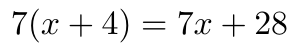
|
||
|
|
|
||
|
|
Você pode pensar em factoring como fazendo o oposto, como neste exemplo em que primeiro encontramos o maior fator comum (GCF) dos termos (9) e depois reescrevemos o polinômio:
|
||
|
|
|
||
|
|
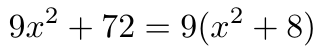
|
||
|
|
|
||
|
|
Vamos fazer mais alguns exemplos.
|
||
|
|
|
||
|
|
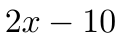
|
||
|
|
|
||
|
|
Você pode fatorar o primeiro termo em (2) (x) e o segundo em (-5) (2). O único fator comum é 2. Mova o fator comum para o início do nosso polinômio reescrito.
|
||
|
|
|
||
|
|

|
||
|
|
|
||
|
|
Quando você divide 2 de 2x você fica com x
|
||
|
|
|
||
|
|
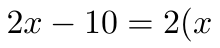
|
||
|
|
|
||
|
|
Quando você divide 2 de 10, você fica com -5.
|
||
|
|
|
||
|
|

|
||
|
|
|
||
|
|
### Erros comuns
|
||
|
|
|
||
|
|
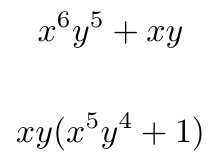
|
||
|
|
|
||
|
|
Quando factoring, muitas vezes você vai acabar com uma divisão que resulta em 1. Certifique-se de incluí-lo em os parênteses.
|