62 lines
5.0 KiB
Markdown
62 lines
5.0 KiB
Markdown
|
|
---
|
|||
|
|
title: Principal Component Analysis
|
|||
|
|
localeTitle: 主成分分析
|
|||
|
|
---
|
|||
|
|
## 主成分分析(PCA)
|
|||
|
|
|
|||
|
|
### 它是什么?
|
|||
|
|
|
|||
|
|
主成分分析(PCA)是一种用于机器学习的算法,用于减少数据集的维数。您可以将包含数百个不同要素的数据集缩减为仅包含两个的新数据集。
|
|||
|
|
|
|||
|
|
例如,假设您想测量飞行员的能力。这涉及许多不同的因素。要考虑的两个相关特征可能是飞行员的技能和飞行员的乐趣。这将是一个二维数据集,因为它包含两个特征。 PCA可以通过将这些功能融合在一起来将这些功能合二为一。您可以将此新功能称为“飞行员资格”。此新功能为您提供了一个更简单的衡量飞行员能力的指标。
|
|||
|
|
|
|||
|
|
如果您将飞行员技能与驾驶员的乐趣相提并论,您可能会得到以下结果:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
直观地说,PCA所做的是找到投影这两个特征的最佳直线(或平面,在更高维度的情况下)。通过在点和线之间绘制垂直线来完成投影。您可以在下面看到以下插图:
|
|||
|
|
|
|||
|
|
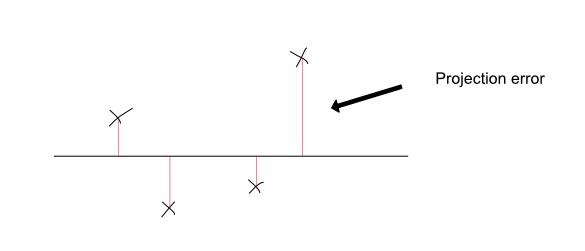
|
|||
|
|
|
|||
|
|
您可以将PCA视为找到数据集的最佳线,以便更好地保留每个点的信息。它通过最小化每个点的平方投影误差的总和来实现这一点。投影误差是将每个点投射到线上的垂直线的长度。通过最小化这些,您可以确保所选择的直线是这两个特征的最佳组合。
|
|||
|
|
|
|||
|
|
下面是一个用于投影数据的良好行的示例,以及一个错误的行。好线的结果预测更能代表原始数据,并且误差较小。坏线的结果预测显然是更糟糕的表现,投影误差要大得多。
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
**重要提示** :值得注意的是,PCA与[线性回归](https://en.wikipedia.org/wiki/Linear_regression)不同。他们的优化目标(他们的目标是最小化)是不同的。
|
|||
|
|
|
|||
|
|
如果您在试用数据集上运行PCA,您可能会得到一个新功能,“pilot aptitude”,看起来像这样:
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
PCA背后的数学有点复杂,但您无需成为专家就可以使用它。即使背后有很多线性代数,使用它也相对容易。这是因为有大量的代码库和现成的PCA实现。一些例子包括:
|
|||
|
|
|
|||
|
|
* [JavaScript PCA实现](https://github.com/mljs/pca) 。
|
|||
|
|
* [Python scikit-learn实现](http://scikit-learn.org/stable/modules/generated/sklearn.decomposition.PCA.html) 。
|
|||
|
|
* [MATLAB实现](https://www.mathworks.com/help/stats/pca.html) 。
|
|||
|
|
|
|||
|
|
### 为什么要用它?
|
|||
|
|
|
|||
|
|
使用PCA算法的原因有很多。一个非常重要的是可视化数据。很容易看到1-D,2-D甚至3-D数据,但除此之外,它变得很难。在机器学习中,在开始处理数据之前可视化数据通常非常有用。但是高维数据集很难想象。通过使用PCA,可以将百维数据集简化为二维数据集。
|
|||
|
|
|
|||
|
|
这在实际情况下尤其有用,其中数据集通常是高维的。例如,您可以将经济绩效指标(如GDP,HDI等)合并为一个功能。这使您可以在国家/地区之间进行更好的比较,还可以使用图表可视化数据。
|
|||
|
|
|
|||
|
|
使用PCA算法的另一个原因是使数据集更小。对于涉及数十万个功能(如图像处理)的问题,机器学习算法可能需要很长时间才能运行。通过减少功能的数量,您可以在不牺牲准确性的情况下提高这些算法的速度。您还可以节省大量磁盘空间,尤其是在使用大型数据集时。
|
|||
|
|
|
|||
|
|
### 限制
|
|||
|
|
|
|||
|
|
由于您在运行PCA时基本上简化了数据集,因此在此过程中可能会丢失一些细节。特别是数据点非常分散并且没有非常强的相关性。
|
|||
|
|
|
|||
|
|
#### 推荐阅读:
|
|||
|
|
|
|||
|
|
* https://www.reddit.com/r/datascience/comments/668pp1
|
|||
|
|
* https://en.wikipedia.org/wiki/Principal _组件_分析
|
|||
|
|
* http://www.cs.otago.ac.nz/cosc453/student _tutorials / principal_ components.pdf
|
|||
|
|
* http://setosa.io/ev/principal-component-analysis/(互动)
|
|||
|
|
|
|||
|
|
维基百科说,“主成分分析(PCA)是一种统计程序,它使用正交变换将可能相关变量的一组观察值转换为一组线性不相关变量的值,称为主成分(或有时,主要变化模式) “。
|
|||
|
|
|
|||
|
|
主成分分析(PCA)是一种统计技术,用于检查一组变量之间的相互关系,以便识别这些变量的基础结构。 PCA通常将特征数量从N维减少到k维,其中k <N
|
|||
|
|
|
|||
|
|
PCA有以下应用: 1)压缩:提高计算速度并减少存储空间 2)可视化:PCA可以将数据减少为二维或三维数据以用于可视化目的
|