61 lines
5.1 KiB
Markdown
61 lines
5.1 KiB
Markdown
|
|
---
|
|||
|
|
title: Logistic Regression
|
|||
|
|
localeTitle: Regressão Logística
|
|||
|
|
---
|
|||
|
|
## Regressão Logística
|
|||
|
|
|
|||
|
|
 A regressão logística é muito semelhante à regressão linear, na medida em que tenta prever uma variável de resposta Y, dado um conjunto de variáveis de entrada X. É uma forma de aprendizado supervisionado, que tenta prever as respostas de dados não-marcados e não vistos, primeiro treinando com dados rotulados, um conjunto de observações de variáveis independentes (X) e dependentes (Y). Mas enquanto a [Regressão Linear](https://guide.freecodecamp.org/machine-learning/linear-regression) assume que a variável de resposta (Y) é quantitativa ou contínua, a Regressão Logística é usada especificamente quando a variável de resposta é qualitativa ou discreta. 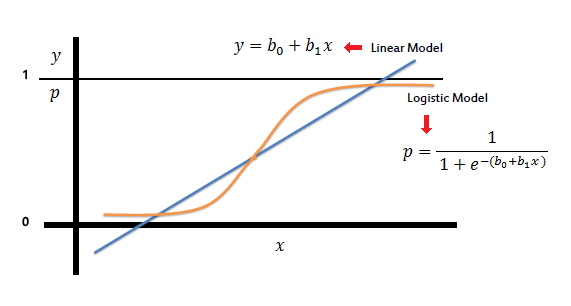
|
|||
|
|
|
|||
|
|
#### Como funciona
|
|||
|
|
|
|||
|
|
A regressão logística modela a probabilidade de que Y, a variável de resposta, pertença a uma determinada categoria. Em muitos casos, a variável de resposta será binária, então a regressão logística desejará modelar uma função y = f (x) que produz um valor normalizado que varia de, digamos, 0 a 1 para todos os valores de X, correspondendo a os dois valores possíveis de Y. Ele faz isso usando a função logística: A regressão logística é a análise de regressão apropriada para conduzir quando a variável dependente é dicotômica (binária). Como todas as análises de regressão, a regressão logística é uma análise preditiva. A regressão logística é usada para descrever dados e para explicar a relação entre uma variável binária dependente e uma ou mais variáveis independentes nominais, ordinais, de intervalo ou de nível de razão.
|
|||
|
|
|
|||
|
|
 A regressão logística é usada para resolver problemas de classificação, onde a saída é da forma y∈ {0,1}. Aqui, 0 é uma classe negativa e 1 é uma classe positiva. Digamos que temos uma hipótese hθ (x), onde x é nosso conjunto de dados (uma matriz) de comprimento m. θ é a matriz paramétrica. Nós temos: 0 <hθ (x) <1
|
|||
|
|
|
|||
|
|
Na regressão logística, hθ (x) é uma função sigmóide, portanto hθ (x) = g (θ'x). g (θ'x) = 1/1 + e ^ (- θ'x)
|
|||
|
|
|
|||
|
|
Nota: θ 'é θ transpose.
|
|||
|
|
|
|||
|
|
#### Função de custo
|
|||
|
|
|
|||
|
|
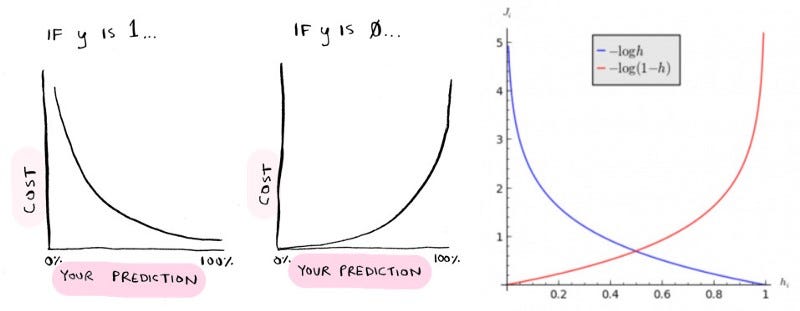
A função de custo usada para a regressão logística é:
|
|||
|
|
|
|||
|
|
J (θ) = (1 / m) ∑ Custo (hθ (x (i)), y (i)), onde a soma é de i = 1 a m.
|
|||
|
|
|
|||
|
|
Custo (h (x), y) = - log (h (x)) se y = 1 Custo (hθ (x), y) = - log (1 − hθ (x)) se y = 0
|
|||
|
|
|
|||
|
|
#### Previsões usando regressão logística:
|
|||
|
|
|
|||
|
|
Modelos de regressão logística a probabilidade da classe padrão (ou seja, a primeira classe). Você pode classificar os resultados dados por:
|
|||
|
|
|
|||
|
|
y = e ^ (b0 + b1 _X) / (1 + e ^ (b0 + b1_ X))
|
|||
|
|
|
|||
|
|
Como a função sigmoide 0,5 é definida como o limite de decisão todo x para o qual y≥0,5 são classificados como classe A e para os quais y <0,5 são classificados como classe B.
|
|||
|
|
|
|||
|
|
#### Regressão logística multi-classe:
|
|||
|
|
|
|||
|
|
Embora você veja a regressão logística geralmente sendo usada no caso de classificação binária, você também pode usá-la em caso de classificação em várias classes por:
|
|||
|
|
|
|||
|
|
##### um contra um método:
|
|||
|
|
|
|||
|
|
Aqui, um classificador para cada classe é criado separadamente e o classificador com a pontuação mais alta é considerado como saída.
|
|||
|
|
|
|||
|
|
##### um vs todo método:
|
|||
|
|
|
|||
|
|
Aqui são feitos múltiplos classificadores binários (N \* N (N-1) / 2, onde N = no. De classes) e, em seguida, comparando as suas pontuações, a saída é obtida.
|
|||
|
|
|
|||
|
|
#### Aplicações de regressão logística:
|
|||
|
|
|
|||
|
|
1) Classificar email como spam ou não spam. 2) Determinar a presença ou ausência de certas doenças, como câncer, com base em sintomas e outros dados médicos. 3) Classifique imagens com base em dados de pixel.
|
|||
|
|
|
|||
|
|
#### Suposições de Regressão Logística
|
|||
|
|
|
|||
|
|
A regressão logística binária exige que a variável dependente seja binária. Para uma regressão binária, o nível de fator 1 da variável dependente deve representar o resultado desejado. Apenas as variáveis significativas devem ser incluídas. As variáveis independentes devem ser independentes umas das outras. Ou seja, o modelo deve ter pouca ou nenhuma multicolinearidade. As variáveis independentes estão linearmente relacionadas com as probabilidades de log. A regressão logística requer tamanhos de amostra bastante grandes.
|
|||
|
|
|
|||
|
|
#### Mais Informações:
|
|||
|
|
|
|||
|
|
Para ler mais, construa a regressão logística passo a passo:
|
|||
|
|
|
|||
|
|
* Clique [aqui](https://medium.com/towards-data-science/building-a-logistic-regression-in-python-step-by-step-becd4d56c9c8) para um artigo sobre como construir uma Regressão Logística em Python.
|
|||
|
|
* Clique [aqui](http://nbviewer.jupyter.org/gist/justmarkham/6d5c061ca5aee67c4316471f8c2ae976) para outro artigo sobre como construir uma Regressão Lógica.
|
|||
|
|
* Clique [aqui](http://nbviewer.jupyter.org/gist/justmarkham/6d5c061ca5aee67c4316471f8c2ae976) para outro artigo sobre matemática e intuição por trás da Regressão Lógica.
|