269 lines
9.1 KiB
Markdown
269 lines
9.1 KiB
Markdown
|
|
---
|
|||
|
|
title: Binary Search Trees
|
|||
|
|
localeTitle: 二叉搜索树
|
|||
|
|
---
|
|||
|
|
## 二叉搜索树
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
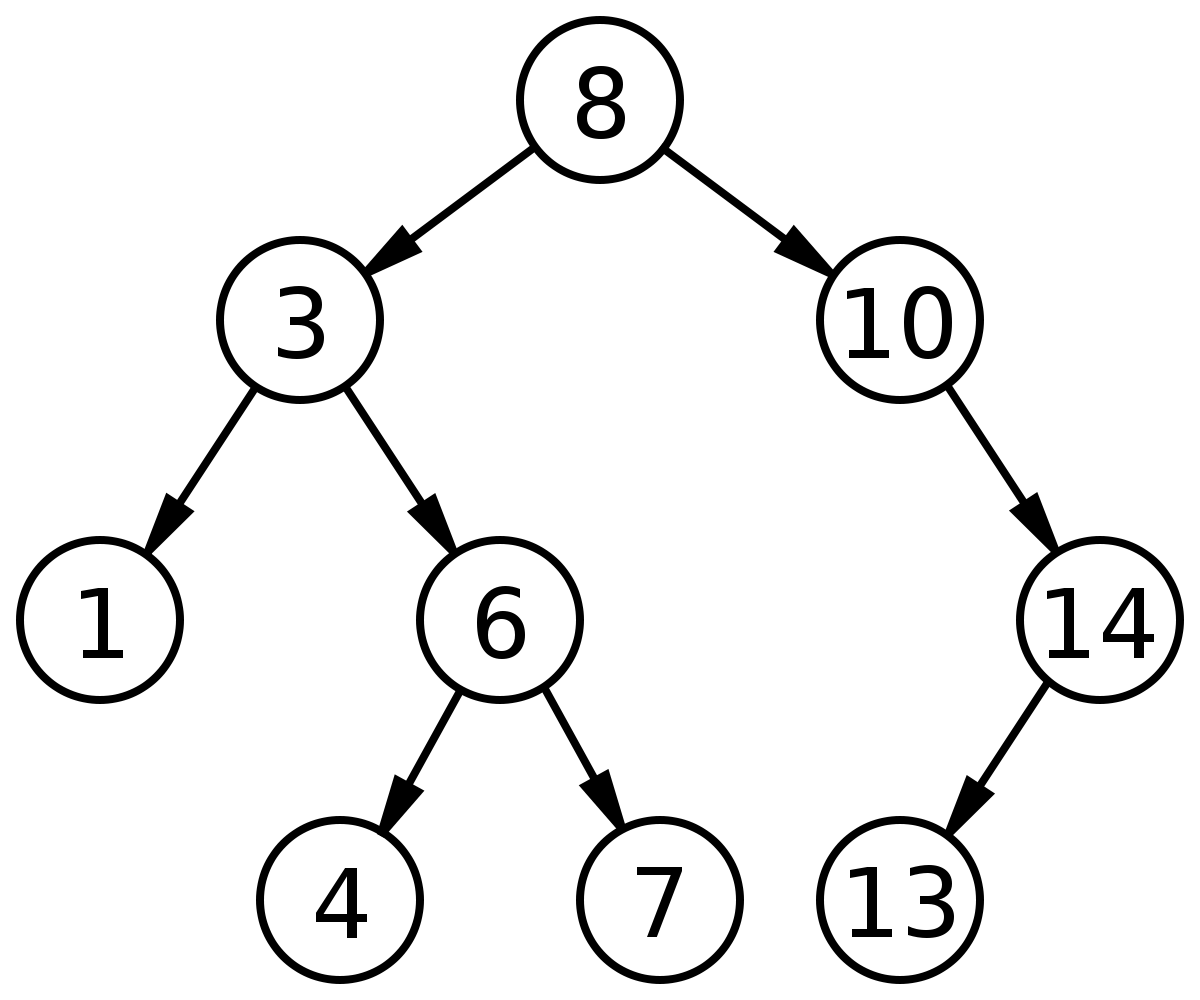
树是由具有以下特征的节点组成的数据结构:
|
|||
|
|
|
|||
|
|
1. 每棵树都有一个根节点(在顶部)有一些值。
|
|||
|
|
2. 根节点具有零个或多个子节点。
|
|||
|
|
3. 每个子节点都有零个或多个子节点,依此类推。这会在树中创建一个子树。每个节点都有自己的子树,由他的孩子和他们的孩子等组成。这意味着每个节点本身都可以是一棵树。
|
|||
|
|
|
|||
|
|
二叉搜索树(BST)添加了以下两个特征:
|
|||
|
|
|
|||
|
|
1. 每个节点最多包含两个子节点。
|
|||
|
|
2. 对于每个节点,其左后代节点的值小于当前节点的值,而当前节点的值小于右后代节点(如果有的话)。
|
|||
|
|
|
|||
|
|
BST建立在[二进制搜索](https://guide.freecodecamp.org/algorithms/search-algorithms/binary-search)算法的基础上,允许快速查找,插入和删除节点。它们的设置方式意味着,平均而言,每次比较都允许操作跳过大约一半的树,因此每次查找,插入或删除都需要与树中存储的项目数的对数成比例的时间, `O(log n)` 。然而,有时候最糟糕的情况可能发生,当树不平衡时,所有这三个函数的时间复杂度都是`O(n)` 。这就是为什么自平衡树(AVL,红黑等)比基本BST更有效的原因。
|
|||
|
|
|
|||
|
|
**最糟糕的情况示例:**当您继续添加_始终_大于节点之前的节点(它的父节点)时会发生这种情况,当您始终添加值低于其父节点的节点时,也会发生同样的情况。
|
|||
|
|
|
|||
|
|
### BST的基本操作
|
|||
|
|
|
|||
|
|
* 创建:创建一个空树。
|
|||
|
|
* 插入:在树中插入一个节点。
|
|||
|
|
* 搜索:在树中搜索节点。
|
|||
|
|
* 删除:从树中删除节点。
|
|||
|
|
|
|||
|
|
#### 创建
|
|||
|
|
|
|||
|
|
最初创建没有任何节点的空树。必须指向根节点的变量/标识符用`NULL`值初始化。
|
|||
|
|
|
|||
|
|
#### 搜索
|
|||
|
|
|
|||
|
|
您总是开始在根节点搜索树并从那里向下移动。您将每个节点中的数据与您要查找的数据进行比较。如果比较的节点不匹配,那么您可以继续使用右子项或左子项,这取决于以下比较的结果:如果您要搜索的节点低于您要比较的节点,你继续前往左边的孩子,否则(如果它更大)你会去找右边的孩子。为什么?因为BST是结构化的(根据其定义),正确的孩子总是比父母大,而左孩子总是较小。
|
|||
|
|
|
|||
|
|
#### 插入
|
|||
|
|
|
|||
|
|
它与搜索功能非常相似。您再次从树的根开始并递归下去,搜索插入新节点的正确位置,方法与搜索功能中说明的相同。如果树中已存在具有相同值的节点,则可以选择是否插入副本。有些树允许重复,有些则不允许。这取决于具体的实施。
|
|||
|
|
|
|||
|
|
#### 删除
|
|||
|
|
|
|||
|
|
当您尝试删除节点时,可能会发生3种情况。如果有,
|
|||
|
|
|
|||
|
|
1. 没有子树(没有孩子):这个是最简单的子树。您只需删除节点,无需任何其他操作。
|
|||
|
|
2. 一个子树(一个子树):您必须确保在删除节点后,其子节点将连接到已删除节点的父节点。
|
|||
|
|
3. 两个子树(两个子节点):您必须找到并替换要删除的节点及其后续节点(右侧子树中最常用的节点)。
|
|||
|
|
|
|||
|
|
创建树的时间复杂度为`O(1)` 。搜索,插入或删除节点的时间复杂度取决于树`h`的高度,因此最坏的情况是`O(h)` 。
|
|||
|
|
|
|||
|
|
#### 节点的前身
|
|||
|
|
|
|||
|
|
前置任务可以被描述为在您当前所在节点之前的节点。要查找当前节点的前一个节点,请查看左子树中最右侧/最大的叶节点。
|
|||
|
|
|
|||
|
|
#### 节点的后继者
|
|||
|
|
|
|||
|
|
后继者可以被描述为在您当前所在节点之后的节点。要查找当前节点的后继节点,请查看右侧子树中最左侧/最小的叶节点。
|
|||
|
|
|
|||
|
|
### 特殊类型的BT
|
|||
|
|
|
|||
|
|
* 堆
|
|||
|
|
* 红黑树
|
|||
|
|
* B树
|
|||
|
|
* Splay树
|
|||
|
|
* N-ary树
|
|||
|
|
* Trie(基数树)
|
|||
|
|
|
|||
|
|
### 运行
|
|||
|
|
|
|||
|
|
**数据结构:数组**
|
|||
|
|
|
|||
|
|
* 最坏情况表现: `O(log n)`
|
|||
|
|
* 最佳表现: `O(1)`
|
|||
|
|
* 平均表现: `O(log n)`
|
|||
|
|
* 最坏情况的空间复杂度: `O(1)`
|
|||
|
|
|
|||
|
|
其中`n`是BST中的节点数。
|
|||
|
|
|
|||
|
|
### BST的实施
|
|||
|
|
|
|||
|
|
这是一个BST节点的定义,它有一些数据,引用它的左右子节点。
|
|||
|
|
|
|||
|
|
```c
|
|||
|
|
struct node {
|
|||
|
|
int data;
|
|||
|
|
struct node *leftChild;
|
|||
|
|
struct node *rightChild;
|
|||
|
|
};
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### 搜索操作
|
|||
|
|
|
|||
|
|
每当要搜索元素时,从根节点开始搜索。然后,如果数据小于键值,则在左子树中搜索元素。否则,搜索右子树中的元素。对每个节点遵循相同的算法。
|
|||
|
|
|
|||
|
|
```c
|
|||
|
|
struct node* search(int data){
|
|||
|
|
struct node *current = root;
|
|||
|
|
printf("Visiting elements: ");
|
|||
|
|
|
|||
|
|
while(current->data != data){
|
|||
|
|
|
|||
|
|
if(current != NULL) {
|
|||
|
|
printf("%d ",current->data);
|
|||
|
|
|
|||
|
|
//go to left tree
|
|||
|
|
if(current->data > data){
|
|||
|
|
current = current->leftChild;
|
|||
|
|
}//else go to right tree
|
|||
|
|
else {
|
|||
|
|
current = current->rightChild;
|
|||
|
|
}
|
|||
|
|
|
|||
|
|
//not found
|
|||
|
|
if(current == NULL){
|
|||
|
|
return NULL;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
return current;
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### 插入操作
|
|||
|
|
|
|||
|
|
无论何时插入元素,首先要找到其正确的位置。从根节点开始搜索,然后如果数据小于键值,则在左子树中搜索空位置并插入数据。否则,在右子树中搜索空位置并插入数据。
|
|||
|
|
|
|||
|
|
```c
|
|||
|
|
void insert(int data) {
|
|||
|
|
struct node *tempNode = (struct node*) malloc(sizeof(struct node));
|
|||
|
|
struct node *current;
|
|||
|
|
struct node *parent;
|
|||
|
|
|
|||
|
|
tempNode->data = data;
|
|||
|
|
tempNode->leftChild = NULL;
|
|||
|
|
tempNode->rightChild = NULL;
|
|||
|
|
|
|||
|
|
//if tree is empty
|
|||
|
|
if(root == NULL) {
|
|||
|
|
root = tempNode;
|
|||
|
|
} else {
|
|||
|
|
current = root;
|
|||
|
|
parent = NULL;
|
|||
|
|
|
|||
|
|
while(1) {
|
|||
|
|
parent = current;
|
|||
|
|
|
|||
|
|
//go to left of the tree
|
|||
|
|
if(data < parent->data) {
|
|||
|
|
current = current->leftChild;
|
|||
|
|
//insert to the left
|
|||
|
|
|
|||
|
|
if(current == NULL) {
|
|||
|
|
parent->leftChild = tempNode;
|
|||
|
|
return;
|
|||
|
|
}
|
|||
|
|
}//go to right of the tree
|
|||
|
|
else {
|
|||
|
|
current = current->rightChild;
|
|||
|
|
|
|||
|
|
//insert to the right
|
|||
|
|
if(current == NULL) {
|
|||
|
|
parent->rightChild = tempNode;
|
|||
|
|
return;
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
二进制搜索树(BST)还使我们能够快速访问前辈和后继者。 前置任务可以被描述为在您当前所在节点之前的节点。
|
|||
|
|
|
|||
|
|
* 要查找当前节点的前任,请查看左子树中最右边/最大的叶节点。 后继者可以被描述为在您当前所在节点之后的节点。
|
|||
|
|
* 要查找当前节点的后继节点,请查看右子树中最左侧/最小的叶节点。
|
|||
|
|
|
|||
|
|
### 让我们看一下在树上运行的几个过程。
|
|||
|
|
|
|||
|
|
由于树是递归定义的,因此编写在树本身上递归的例程是很常见的。
|
|||
|
|
|
|||
|
|
因此,例如,如果我们想要计算树的高度,即根节点的高度,我们可以继续并递归地执行,通过树。所以我们可以说:
|
|||
|
|
|
|||
|
|
* 例如,如果我们有一个nil树,那么它的高度为0。
|
|||
|
|
* 否则,我们是1加上左子树和右子树的最大值。
|
|||
|
|
* 因此,如果我们查看一个叶子,例如,那个高度将是1,因为左子的高度是nil,是0,nil右子的高度也是0.所以最大值是0,然后是1加0。
|
|||
|
|
|
|||
|
|
#### 高度(树)算法
|
|||
|
|
```
|
|||
|
|
if tree = nil:
|
|||
|
|
return 0
|
|||
|
|
return 1 + Max(Height(tree.left),Height(tree.right))
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### 这是C ++中的代码
|
|||
|
|
```
|
|||
|
|
int maxDepth(struct node* node)
|
|||
|
|
{
|
|||
|
|
if (node==NULL)
|
|||
|
|
return 0;
|
|||
|
|
else
|
|||
|
|
{
|
|||
|
|
int rDepth = maxDepth(node->right);
|
|||
|
|
int lDepth = maxDepth(node->left);
|
|||
|
|
|
|||
|
|
if (lDepth > rDepth)
|
|||
|
|
{
|
|||
|
|
return(lDepth+1);
|
|||
|
|
}
|
|||
|
|
else
|
|||
|
|
{
|
|||
|
|
return(rDepth+1);
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
我们还可以考虑计算树的大小,即树的节点数。
|
|||
|
|
|
|||
|
|
* 同样,如果我们有一个零树,我们有零节点。
|
|||
|
|
* 否则,我们有左子节点中的节点数加上我们自己的1节点加上右子节点中的节点数。所以1加上左树的大小加上右树的大小。
|
|||
|
|
|
|||
|
|
#### 大小(树)算法
|
|||
|
|
```
|
|||
|
|
if tree = nil
|
|||
|
|
return 0
|
|||
|
|
return 1 + Size(tree.left) + Size(tree.right)
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### 这是C ++中的代码
|
|||
|
|
```
|
|||
|
|
int treeSize(struct node* node)
|
|||
|
|
{
|
|||
|
|
if (node==NULL)
|
|||
|
|
return 0;
|
|||
|
|
else
|
|||
|
|
return 1+(treeSize(node->left) + treeSize(node->right));
|
|||
|
|
}
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
### 关于freeCodeCamp YouTube频道的相关视频
|
|||
|
|
|
|||
|
|
* [二叉搜索树](https://youtu.be/5cU1ILGy6dM)
|
|||
|
|
* [二叉搜索树:遍历和高度](https://youtu.be/Aagf3RyK3Lw)
|
|||
|
|
|
|||
|
|
### 以下是常见的二叉树类型:
|
|||
|
|
|
|||
|
|
完整二叉树/严格二叉树:如果每个节点只有0或2个子节点,则二叉树已满或严格。
|
|||
|
|
```
|
|||
|
|
18
|
|||
|
|
/ \
|
|||
|
|
15 30
|
|||
|
|
/ \ / \
|
|||
|
|
40 50 100 40
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
在完全二进制树中,叶节点的数量等于内部节点的数量加1。
|
|||
|
|
|
|||
|
|
完整的二进制树:二进制树是完整的二进制树,如果所有级别都被完全填充,除了可能是最后一级,最后一级是尽可能保留所有键
|
|||
|
|
```
|
|||
|
|
18
|
|||
|
|
/ \
|
|||
|
|
15 30
|
|||
|
|
/ \ / \
|
|||
|
|
40 50 100 40
|
|||
|
|
/ \ /
|
|||
|
|
8 7 9
|
|||
|
|
|
|||
|
|
```
|