42 lines
3.4 KiB
Markdown
42 lines
3.4 KiB
Markdown
|
|
---
|
|||
|
|
title: Intro to Logarithms
|
|||
|
|
localeTitle: Введение в логарифмы
|
|||
|
|
---
|
|||
|
|
## Введение в логарифмы
|
|||
|
|
|
|||
|
|
Логарифмы - это математические функции, используемые для определения мощности, на которую создается база, для получения определенного результата.
|
|||
|
|
|
|||
|
|
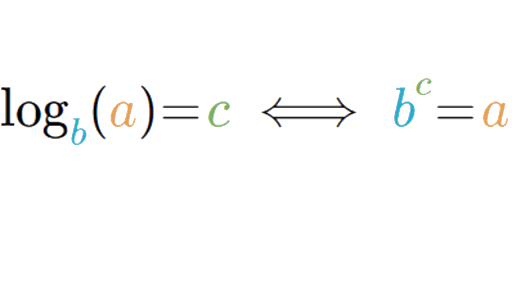
|
|||
|
|
|
|||
|
|
_Здесь в примере переменная b является базой, тогда как переменная a является искомым выходом, а переменная c - показателем._
|
|||
|
|
|
|||
|
|
Журналы используются в разных вещах в реальном мире. Они используются в шкале рН, измерении интенсивности землетрясений (шкале Рихтера) и многих других.
|
|||
|
|
|
|||
|
|
Пример журналов в python:
|
|||
|
|
|
|||
|
|
```python
|
|||
|
|
import math
|
|||
|
|
|
|||
|
|
# math.log(value, base) - outputs exponent
|
|||
|
|
math.log(100, 10) #outputs 2
|
|||
|
|
math.log(2, 2) #outputs 1
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
#### Источники:
|
|||
|
|
|
|||
|
|
* https://betterexplained.com/articles/using-logs-in-the-real-world/
|
|||
|
|
* https://www.khanacademy.org/math/algebra2/exponential-and-logarithmic-functions/introduction-to-logarithms/a/intro-to-logarithms
|
|||
|
|
|
|||
|
|
### Определение логарифма
|
|||
|
|
|
|||
|
|
Логарифм числа **x** , записанный _log ( **x** )_ , обычно означает число, которое вы должны использовать как мощность более 10 для получения **x** . Предположим, вы хотите найти _журнал (10)_ . Это означает, что вы хотите найти номер, который вы должны поднять 10, чтобы получить 10. Это дает нам уравнение: _log (10) = x_ .
|
|||
|
|
|
|||
|
|
Мы можем использовать это и применять его как мощность 10 с обеих сторон. Это изменяет уравнение на: _10 log (10) = 10 x_
|
|||
|
|
|
|||
|
|
_10 log ( **x** )_ , где **x** - любое число, вернет **x** , поскольку _10 log_ отменяет. Это означает, что теперь наше уравнение _10 = 10 х_
|
|||
|
|
|
|||
|
|
Учитывая, что _10 x_ равно 10 раз самому _x_ раз, это означает, что 10 нужно умножить на себя достаточно времени, чтобы быть ровно 10, а _x_ равно 1. Это происходит потому, что _10 1 = 10_
|
|||
|
|
|
|||
|
|
### Определение натурального логарифма
|
|||
|
|
|
|||
|
|
Это строго так же, как определение логарифма, за исключением того, какие числа используются. В нормальном логарифме базовое число обычно равно 10, а в натуральном логарифме, часто написанном _ln_ , используется _e_ , число Эйлера в качестве базы. Это означает, что _ln (e) = 1_ , а не _log (10) = 1_ . Итак, вместо этого мы находим энергию, необходимую для подведения _e_ в _ln ( **x** )_ .
|