freeCodeCamp/guide/english/mathematics/area-of-a-circle/index.md

---
title: Area of a Circle
---
## Area of a Circle

The area of a circle is all the space inside a circle's circumference. 

If 'r' is the radius of circle, its area is calculated with formula πr<sup>2</sup> where π is mathematical constant.

π ≈ 22/7 ≈ 3.141592....

A = π *r<sup>2</sup>, r is the radius of circle

A = π * {d<sup>2</sup>/4}, d is the diameter of circle, d=2* r

![alt](http://areacircle.com/Area_of_a_circle_basics.png)

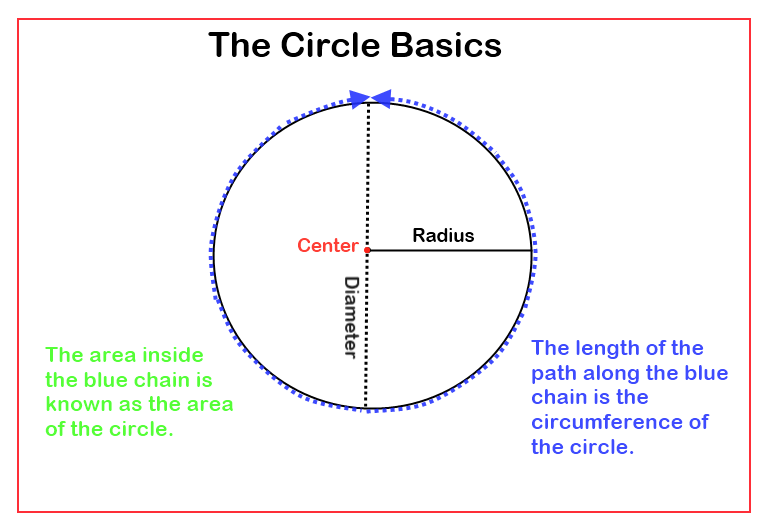
Area of a circle is defined as the space enclosed by the circumference of the circle.

#### Terminology

Circumference (C) - The enclosing boundary of the circle.

Radius (r) - The length of a line from any point on the boundary/cirumference of the circle to the center of the circle.

Diameter (d) - The length of the line that passes across the circle through the center of the circle.

Pi (<span class="texhtml">π</span>) - A mathematical constant which is approximated as 3.14

#### Formula
Area = π × r<sup>2</sup> 

###### Given radius of the circle

Area of circle =  <span class="texhtml"><span class="texhtml">π</span> * <i>radius</i><sup>2</sup></span>

###### Given diameter of the circle

We know that `diameter = 2 * radius`, so you can derive the area of the circle as below,

Area of circle =  <span class="texhtml"><span class="texhtml">π</span> * <i>(diameter/2)</i><sup>2</sup></span>

###### Given circumference of the circle

We know that the circumference of the circle (C), 
<br>`C = 2 * π * (radius)`.
<br><br>From this, you can derive the area of the circle as below,

Area of circle =  <i>C</i><sup>2</sup></span> / 4 * <span class="texhtml"><span class="texhtml">π</span>
  
#### Examples

1. Given radius = 3cm, find area of the circle

     Area = 3.14 * 9 = 28.26 <span>cm<sup>2</sup></span>

2. Given diameter = 8cm, find area of the circle

     Radius = (Diameter/2) = 4cm

     Area = 3.14 * 16 = 50.24 <span>cm<sup>2</sup></span>

3. Given circumference of a circle = 25cm, find the area of the circle

     Area = 625 / (4 * 3.14) = 49.76 <span>cm<sup>2</sup></span>

A "Real World" Example:-

Example: Max is building a house. The first step is to drill holes and fill them with concrete.
The holes are 0.4 m wide and 1 m deep, how much concrete should Max order for each hole?

The holes are circular (in cross section) because they are drilled out using an auger.
The diameter is 0.4m, so the Area is:
A = (π/4) × D2
A = (3.14159.../4) × 0.42
A = 0.7854... × 0.16
A = 0.126 m2 (to 3 decimals)
And the holes are 1 m deep, so:
Volume = 0.126 m2 × 1 m = 0.126 m3
So Max should order 0.126 cubic meters of concrete to fill each hole.
 
Note: Max could have estimated the area by:
1. Calculating a square hole: 0.4 × 0.4 = 0.16 m2
2. Taking 80% of that (estimates a circle): 80% × 0.16 m2 = 0.128 m2
3. And the volume of a 1 m deep hole is: 0.128 m3

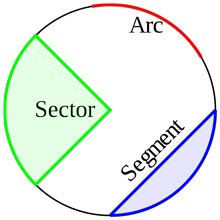
#### Something more about circle
 * ARC- An arc is part of the circumference of a circle.
 * CHORD- Chord is a straight line joining two points on a circle, the diameter is an example of a chord (and the longest possible chord of circle).
 * SEGMENT- A segment is the region between a chord and the arc it joins.
 * SECTOR- A sector is the region between an arc and two radii.

![alt](http://www.kidsmathgamesonline.com/images/facts/circlesector220.jpg)

#### More Information

More information with illustrations can be found [WikiHow](https://www.wikihow.com/Calculate-the-Area-of-a-Circle)