24 lines
1.2 KiB
Markdown
24 lines
1.2 KiB
Markdown
|
|
---
|
|||
|
|
title: Orthogonality
|
|||
|
|
localeTitle: 正交
|
|||
|
|
---
|
|||
|
|
## 正交
|
|||
|
|
|
|||
|
|
在数学和线性代数中,当它们的点积为0时,两个向量u和v被认为是正交的:
|
|||
|
|
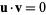
|
|||
|
|
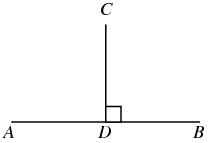
正交性可以被认为是[垂直](http://mathworld.wolfram.com/Perpendicular.html)于较高维向量空间的[垂直](http://mathworld.wolfram.com/Perpendicular.html)度,因为两者是相同的 - 它们意味着直线由线,平面或向量形成。
|
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
|
|
以下是正交性的所有例子:
|
|||
|
|
|
|||
|
|
1. 如果两个矢量是垂直的,即它们以直角(90度)相交或相交,则它们是正交的。
|
|||
|
|
2. 如果两个向量的内积(点积)等于0,则它们是正交的。
|
|||
|
|
3. 如果V中的每个矢量与B中的每个矢量正交,则V中的两个矢量子空间A和B是正交的。
|
|||
|
|
|
|||
|
|
<! - [这种快速风格指南有助于确保您的拉取请求被接受](https://github.com/freecodecamp/guides/blob/master/README.md) 。
|
|||
|
|
|
|||
|
|
#### 更多信息:
|
|||
|
|
|
|||
|
|
1. http://mathworld.wolfram.com/Orthogonal.html
|
|||
|
|
2. http://mathworld.wolfram.com/Perpendicular.html
|