Detailed description for recursion in Fibonacci (#28784)
* Detailed description for recursion in Fibonacci * Removed unnecesasry line breaks
This commit is contained in:
@ -15,34 +15,37 @@ This is the tree to find F(5):
|
|||||||
|
|
||||||
|

|
||||||
|
|
||||||
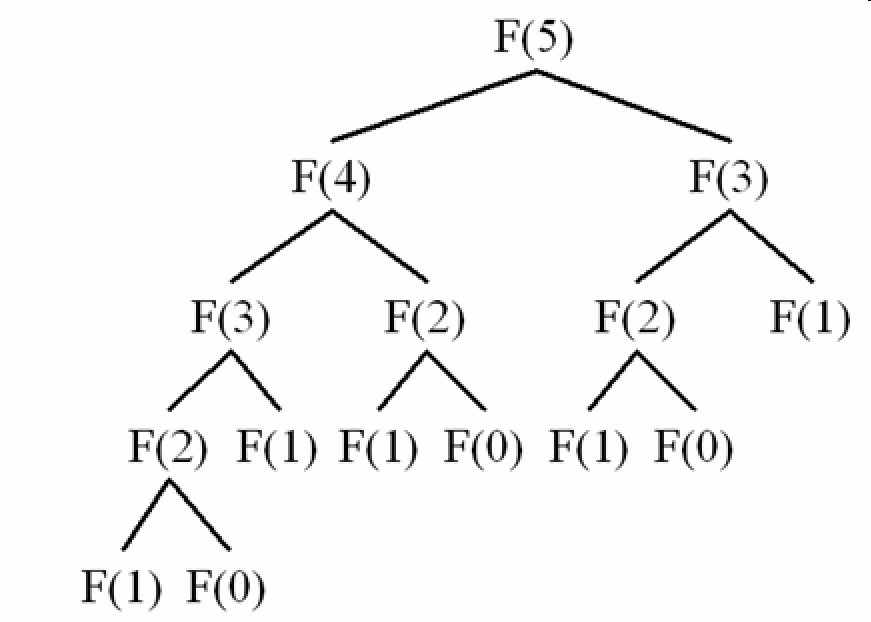
To compute F(5) it will need to compute many times the same F(i). Using recursion:
|
To compute F(5), the recursive method will compute the same value multiple times
|
||||||
|
|
||||||
|
For example:
|
||||||
|
|
||||||
|
F(0) is called 3 times
|
||||||
|
F(1) is called 4 times
|
||||||
|
F(2) is called 3 times
|
||||||
|
F(3) is called 2 times
|
||||||
|
|
||||||
|
Recursive approach:
|
||||||
```python
|
```python
|
||||||
def fib(n)
|
def fib(n):
|
||||||
{
|
|
||||||
if n <= 1:
|
if n <= 1:
|
||||||
return n
|
return n
|
||||||
return fib(n-1) + fib(n-2);
|
return fib(n-1) + fib(n-2)
|
||||||
}
|
|
||||||
```
|
```
|
||||||
|
|
||||||
And below is the optimised solution (using DP)
|
|
||||||
|
|
||||||
For F(5), this solution will generate the calls depicted in the image above, running in O(2^N).
|
For F(5), this solution will generate the calls depicted in the image above, running in O(2^N).
|
||||||
|
|
||||||
|
|
||||||
Here is an optimised solution which uses DP and memoization:
|
Here is an optimised solution which uses DP and memoization:
|
||||||
|
|
||||||
```python
|
```python
|
||||||
lookup = {1 : 1, 2 : 1} # Create a lookup-table (a map) inizialized with the first 2 Fibonacci's numbers
|
lookup = {1 : 1, 2 : 1} # Create a lookup-table (a map) inizialized with the first 2 Fibonacci's numbers
|
||||||
|
|
||||||
def fib(n)
|
def fib(n):
|
||||||
{
|
|
||||||
if n in lookup: # If n is already computed
|
if n in lookup: # If n is already computed
|
||||||
return n # Return the previous computed solution
|
return n # Return the previous computed solution
|
||||||
else
|
else:
|
||||||
lookup[n] = fib(n-1) + fib(n-2) # Else, do the recursion.
|
lookup[n] = fib(n-1) + fib(n-2) # Else, do the recursion.
|
||||||
return lookup[n]
|
return lookup[n]
|
||||||
}
|
|
||||||
```
|
```
|
||||||
Caching computed solutions in a lookup table, and querying it before going for recursion will let the program have a running time of O(N).
|
Caching computed solutions in a lookup table, and querying it before going for recursion will let the program have a running time of O(N).
|
||||||
|
|
||||||
@ -53,5 +56,8 @@ In addition to *memoization* (used in the previous example), there is also *tabu
|
|||||||
#### More Information:
|
#### More Information:
|
||||||
|
|
||||||
[What is dynamic programming on StackOverflow](https://stackoverflow.com/questions/1065433/what-is-dynamic-programming")
|
[What is dynamic programming on StackOverflow](https://stackoverflow.com/questions/1065433/what-is-dynamic-programming")
|
||||||
|
|
||||||
[Difference between memoization and DP on StackOverflow](https://stackoverflow.com/questions/6184869/what-is-the-difference-between-memoization-and-dynamic-programming)
|
[Difference between memoization and DP on StackOverflow](https://stackoverflow.com/questions/6184869/what-is-the-difference-between-memoization-and-dynamic-programming)
|
||||||
|
|
||||||
[Why DP rather than function calling or looping](https://www.quora.com/What-is-the-difference-between-dynamic-programming-and-recursion)
|
[Why DP rather than function calling or looping](https://www.quora.com/What-is-the-difference-between-dynamic-programming-and-recursion)
|
||||||
|
|
||||||
|
|||||||
Reference in New Issue
Block a user