Detailed description for recursion in Fibonacci (#28784)

* Detailed description for recursion in Fibonacci

* Removed unnecesasry line breaks

guide/english/computer-science/dynamic-programming/index.md

@@ -15,34 +15,37 @@ This is the tree to find F(5):
 
 ![Fibonacci serie's tree](https://cdn-media-1.freecodecamp.org/imgr/59Rpw.png)
 
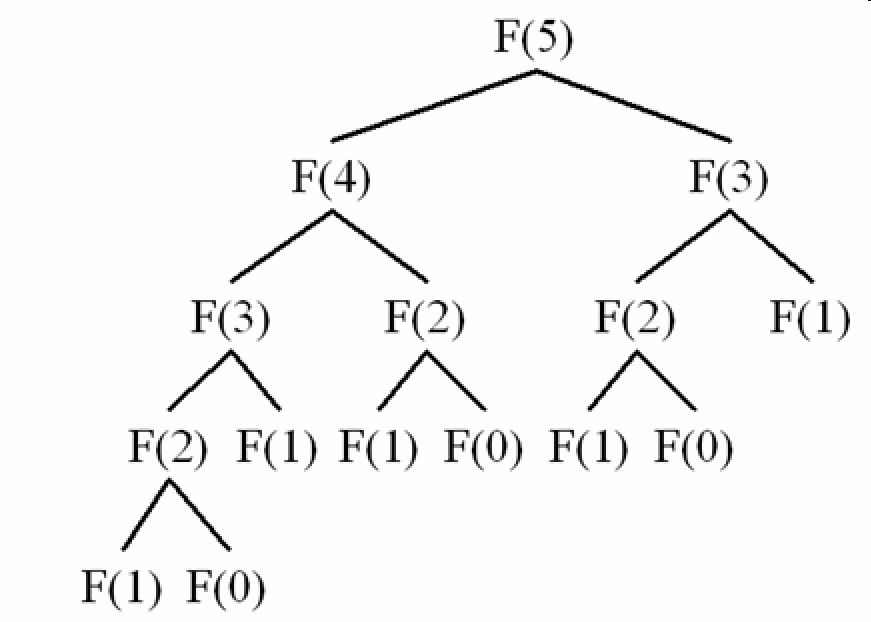
-To compute F(5) it will need to compute many times the same F(i). Using recursion:
+To compute F(5), the recursive method will compute the same value multiple times
 
+For example:
+
+F(0) is called 3 times
+F(1) is called 4 times 
+F(2) is called 3 times
+F(3) is called 2 times
+
+Recursive approach:
 ```python
-def fib(n)
+def fib(n):
-{
     if n <= 1:
         return n
-    return fib(n-1) + fib(n-2);
+    return fib(n-1) + fib(n-2)
-}
 ```
 
-And below is the optimised solution (using DP)
-
 For F(5), this solution will generate the calls depicted in the image above, running in O(2^N).
 
+
 Here is an optimised solution which uses DP and memoization:
 
 ```python
 lookup = {1 : 1, 2 : 1} # Create a lookup-table (a map) inizialized with the first 2 Fibonacci's numbers
 
-def fib(n)
+def fib(n):
-{
     if n in lookup: # If n is already computed
         return n # Return the previous computed solution
-    else 
+    else:
         lookup[n] = fib(n-1) + fib(n-2) # Else, do the recursion.
     return lookup[n]
-}
 ```
 Caching computed solutions in a lookup table, and querying it before going for recursion will let the program have a running time of O(N).
 
@@ -53,5 +56,8 @@ In addition to *memoization* (used in the previous example), there is also *tabu
 #### More Information:
 
 [What is dynamic programming on StackOverflow](https://stackoverflow.com/questions/1065433/what-is-dynamic-programming")
+
 [Difference between memoization and DP on StackOverflow](https://stackoverflow.com/questions/6184869/what-is-the-difference-between-memoization-and-dynamic-programming)
+
 [Why DP rather than function calling or looping](https://www.quora.com/What-is-the-difference-between-dynamic-programming-and-recursion)
+