diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
index 34e52a4dea..d463100407 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
@@ -8,22 +8,28 @@ dashedName: problem-321-swapping-counters
# --description--
-A horizontal row comprising of 2n + 1 squares has n red counters placed at one end and n blue counters at the other end, being separated by a single empty square in the centre. For example, when n = 3.
+A horizontal row comprising of $2n + 1$ squares has $n$ red counters placed at one end and $n$ blue counters at the other end, being separated by a single empty square in the center. For example, when $n = 3$.
+
+ A counter can move from one square to the next (slide) or can jump over another counter (hop) as long as the square next to that counter is unoccupied.
-Let M(n) represent the minimum number of moves/actions to completely reverse the positions of the coloured counters; that is, move all the red counters to the right and all the blue counters to the left. It can be verified M(3) = 15, which also happens to be a triangle number.
+
A counter can move from one square to the next (slide) or can jump over another counter (hop) as long as the square next to that counter is unoccupied.
-Let M(n) represent the minimum number of moves/actions to completely reverse the positions of the coloured counters; that is, move all the red counters to the right and all the blue counters to the left. It can be verified M(3) = 15, which also happens to be a triangle number.
+ -If we create a sequence based on the values of n for which M(n) is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
+Let $M(n)$ represent the minimum number of moves/actions to completely reverse the positions of the colored counters; that is, move all the red counters to the right and all the blue counters to the left.
+
+It can be verified $M(3) = 15$, which also happens to be a triangle number.
+
+If we create a sequence based on the values of n for which $M(n)$ is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
Find the sum of the first forty terms of this sequence.
# --hints--
-`euler321()` should return 2470433131948040.
+`swappingCounters()` should return `2470433131948040`.
```js
-assert.strictEqual(euler321(), 2470433131948040);
+assert.strictEqual(swappingCounters(), 2470433131948040);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler321(), 2470433131948040);
## --seed-contents--
```js
-function euler321() {
+function swappingCounters() {
return true;
}
-euler321();
+swappingCounters();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
index 241c3a74f0..d532a4a95d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
@@ -8,18 +8,18 @@ dashedName: problem-322-binomial-coefficients-divisible-by-10
# --description--
-Let T(m, n) be the number of the binomial coefficients iCn that are divisible by 10 for n ≤ i < m(i, m and n are positive integers).
+Let $T(m, n)$ be the number of the binomial coefficients ${}^iC_n$ that are divisible by 10 for $n ≤ i < m$ ($i$, $m$ and $n$ are positive integers).
-You are given that T(109, 107-10) = 989697000.
+You are given that $T({10}^9, {10}^7 - 10) = 989\\,697\\,000$.
-Find T(1018, 1012-10).
+Find $T({10}^{18}, {10}^{12} - 10)$.
# --hints--
-`euler322()` should return 999998760323314000.
+`binomialCoefficientsDivisibleBy10()` should return `999998760323314000`.
```js
-assert.strictEqual(euler322(), 999998760323314000);
+assert.strictEqual(binomialCoefficientsDivisibleBy10(), 999998760323314000);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler322(), 999998760323314000);
## --seed-contents--
```js
-function euler322() {
+function binomialCoefficientsDivisibleBy10() {
return true;
}
-euler322();
+binomialCoefficientsDivisibleBy10();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
index b336759562..31e36339ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
@@ -8,24 +8,25 @@ dashedName: problem-323-bitwise-or-operations-on-random-integers
# --description--
-Let y0, y1, y2,... be a sequence of random unsigned 32 bit integers
+Let $y_0, y_1, y_2, \ldots$ be a sequence of random unsigned 32 bit integers
-(i.e. 0 ≤ yi < 232, every value equally likely).
+(i.e. $0 ≤ y_i < 2^{32}$, every value equally likely).
-For the sequence xi the following recursion is given:x0 = 0 and
+For the sequence $x_i$ the following recursion is given:
-xi = xi-1| yi-1, for i > 0. ( | is the bitwise-OR operator)
+- $x_0 = 0$ and
+- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$, for $i > 0$. ($\mathbf{|}$ is the bitwise-OR operator)
-It can be seen that eventually there will be an index N such that xi = 232 -1 (a bit-pattern of all ones) for all i ≥ N.
+It can be seen that eventually there will be an index $N$ such that $x_i = 2^{32} - 1$ (a bit-pattern of all ones) for all $i ≥ N$.
-Find the expected value of N. Give your answer rounded to 10 digits after the decimal point.
+Find the expected value of $N$. Give your answer rounded to 10 digits after the decimal point.
# --hints--
-`euler323()` should return 6.3551758451.
+`bitwiseOrOnRandomIntegers()` should return `6.3551758451`.
```js
-assert.strictEqual(euler323(), 6.3551758451);
+assert.strictEqual(bitwiseOrOnRandomIntegers(), 6.3551758451);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler323(), 6.3551758451);
## --seed-contents--
```js
-function euler323() {
+function bitwiseOrOnRandomIntegers() {
return true;
}
-euler323();
+bitwiseOrOnRandomIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
index 66ce491477..b2da2925c4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
@@ -8,18 +8,26 @@ dashedName: problem-324-building-a-tower
# --description--
-Let f(n) represent the number of ways one can fill a 3×3×n tower with blocks of 2×1×1. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
+Let $f(n)$ represent the number of ways one can fill a $3×3×n$ tower with blocks of $2×1×1$. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
-For example (with q = 100000007) :f(2) = 229,f(4) = 117805,f(10) mod q = 96149360,f(103) mod q = 24806056,f(106) mod q = 30808124.
+For example (with $q = 100\\,000\\,007$):
-Find f(1010000) mod 100000007.
+$$\begin{align}
+ & f(2) = 229, \\\\
+ & f(4) = 117\\,805, \\\\
+ & f(10)\bmod q = 96\\,149\\,360, \\\\
+ & f({10}^3)\bmod q = 24\\,806\\,056, \\\\
+ & f({10}^6)\bmod q = 30\\,808\\,124.
+\end{align}$$
+
+Find $f({10}^{10000})\bmod 100\\,000\\,007$.
# --hints--
-`euler324()` should return 96972774.
+`buildingTower()` should return `96972774`.
```js
-assert.strictEqual(euler324(), 96972774);
+assert.strictEqual(buildingTower(), 96972774);
```
# --seed--
@@ -27,12 +35,12 @@ assert.strictEqual(euler324(), 96972774);
## --seed-contents--
```js
-function euler324() {
+function buildingTower() {
return true;
}
-euler324();
+buildingTower();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
index 6d0389b9fa..bc828c87e2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
@@ -8,9 +8,9 @@ dashedName: problem-325-stone-game-ii
# --description--
-A game is played with two piles of stones and two players. At her turn, a player removes a number of stones from the larger pile. The number of stones she removes must be a positive multiple of the number of stones in the smaller pile.
+A game is played with two piles of stones and two players. On each player's turn, the player may remove a number of stones from the larger pile. The number of stones removes must be a positive multiple of the number of stones in the smaller pile.
-E.g., let the ordered pair(6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
+E.g., let the ordered pair (6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
The player taking all the stones from a pile wins the game.
@@ -18,16 +18,16 @@ A winning configuration is one where the first player can force a win. For examp
A losing configuration is one where the second player can force a win, no matter what the first player does. For example, (2,3) and (3,4) are losing configurations: any legal move leaves a winning configuration for the second player.
-Define S(N) as the sum of (xi+yi) for all losing configurations (xi,yi), 0 < xi < yi ≤ N. We can verify that S(10) = 211 and S(104) = 230312207313.
+Define $S(N)$ as the sum of ($x_i + y_i$) for all losing configurations ($x_i$, $y_i$), $0 < x_i < y_i ≤ N$. We can verify that $S(10) = 211$ and $S({10}^4) = 230\\,312\\,207\\,313$.
-Find S(1016) mod 710.
+Find $S({10}^{16})\bmod 7^{10}$.
# --hints--
-`euler325()` should return 54672965.
+`stoneGameTwo()` should return `54672965`.
```js
-assert.strictEqual(euler325(), 54672965);
+assert.strictEqual(stoneGameTwo(), 54672965);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler325(), 54672965);
## --seed-contents--
```js
-function euler325() {
+function stoneGameTwo() {
return true;
}
-euler325();
+stoneGameTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
index 1e6b648d9a..ededd29e91 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
@@ -8,24 +8,26 @@ dashedName: problem-326-modulo-summations
# --description--
-Let an be a sequence recursively defined by: .
+Let an be a sequence recursively defined by: $a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$.
-So the first 10 elements of an are: 1,1,0,3,0,3,5,4,1,9.
+So the first 10 elements of $a_n$ are: 1, 1, 0, 3, 0, 3, 5, 4, 1, 9.
-Let f(N,M) represent the number of pairs (p,q) such that:
+Let $f(N, M)$ represent the number of pairs $(p, q)$ such that:
-It can be seen that f(10,10)=4 with the pairs (3,3), (5,5), (7,9) and (9,10).
+$$ 1 \le p \le q \le N \\; \text{and} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
-You are also given that f(104,103)=97158.
+It can be seen that $f(10, 10) = 4$ with the pairs (3,3), (5,5), (7,9) and (9,10).
-Find f(1012,106).
+You are also given that $f({10}^4, {10}^3) = 97\\,158$.
+
+Find $f({10}^{12}, {10}^6)$.
# --hints--
-`euler326()` should return 1966666166408794400.
+`moduloSummations()` should return `1966666166408794400`.
```js
-assert.strictEqual(euler326(), 1966666166408794400);
+assert.strictEqual(moduloSummations(), 1966666166408794400);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler326(), 1966666166408794400);
## --seed-contents--
```js
-function euler326() {
+function moduloSummations() {
return true;
}
-euler326();
+moduloSummations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
index 354596b1d7..e1714be1e6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
@@ -10,7 +10,9 @@ dashedName: problem-327-rooms-of-doom
A series of three rooms are connected to each other by automatic doors.
-Each door is operated by a security card. Once you enter a room the door automatically closes and that security card cannot be used again. A machine at the start will dispense an unlimited number of cards, but each room (including the starting room) contains scanners and if they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
+
-If we create a sequence based on the values of n for which M(n) is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
+Let $M(n)$ represent the minimum number of moves/actions to completely reverse the positions of the colored counters; that is, move all the red counters to the right and all the blue counters to the left.
+
+It can be verified $M(3) = 15$, which also happens to be a triangle number.
+
+If we create a sequence based on the values of n for which $M(n)$ is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
Find the sum of the first forty terms of this sequence.
# --hints--
-`euler321()` should return 2470433131948040.
+`swappingCounters()` should return `2470433131948040`.
```js
-assert.strictEqual(euler321(), 2470433131948040);
+assert.strictEqual(swappingCounters(), 2470433131948040);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler321(), 2470433131948040);
## --seed-contents--
```js
-function euler321() {
+function swappingCounters() {
return true;
}
-euler321();
+swappingCounters();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
index 241c3a74f0..d532a4a95d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
@@ -8,18 +8,18 @@ dashedName: problem-322-binomial-coefficients-divisible-by-10
# --description--
-Let T(m, n) be the number of the binomial coefficients iCn that are divisible by 10 for n ≤ i < m(i, m and n are positive integers).
+Let $T(m, n)$ be the number of the binomial coefficients ${}^iC_n$ that are divisible by 10 for $n ≤ i < m$ ($i$, $m$ and $n$ are positive integers).
-You are given that T(109, 107-10) = 989697000.
+You are given that $T({10}^9, {10}^7 - 10) = 989\\,697\\,000$.
-Find T(1018, 1012-10).
+Find $T({10}^{18}, {10}^{12} - 10)$.
# --hints--
-`euler322()` should return 999998760323314000.
+`binomialCoefficientsDivisibleBy10()` should return `999998760323314000`.
```js
-assert.strictEqual(euler322(), 999998760323314000);
+assert.strictEqual(binomialCoefficientsDivisibleBy10(), 999998760323314000);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler322(), 999998760323314000);
## --seed-contents--
```js
-function euler322() {
+function binomialCoefficientsDivisibleBy10() {
return true;
}
-euler322();
+binomialCoefficientsDivisibleBy10();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
index b336759562..31e36339ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
@@ -8,24 +8,25 @@ dashedName: problem-323-bitwise-or-operations-on-random-integers
# --description--
-Let y0, y1, y2,... be a sequence of random unsigned 32 bit integers
+Let $y_0, y_1, y_2, \ldots$ be a sequence of random unsigned 32 bit integers
-(i.e. 0 ≤ yi < 232, every value equally likely).
+(i.e. $0 ≤ y_i < 2^{32}$, every value equally likely).
-For the sequence xi the following recursion is given:x0 = 0 and
+For the sequence $x_i$ the following recursion is given:
-xi = xi-1| yi-1, for i > 0. ( | is the bitwise-OR operator)
+- $x_0 = 0$ and
+- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$, for $i > 0$. ($\mathbf{|}$ is the bitwise-OR operator)
-It can be seen that eventually there will be an index N such that xi = 232 -1 (a bit-pattern of all ones) for all i ≥ N.
+It can be seen that eventually there will be an index $N$ such that $x_i = 2^{32} - 1$ (a bit-pattern of all ones) for all $i ≥ N$.
-Find the expected value of N. Give your answer rounded to 10 digits after the decimal point.
+Find the expected value of $N$. Give your answer rounded to 10 digits after the decimal point.
# --hints--
-`euler323()` should return 6.3551758451.
+`bitwiseOrOnRandomIntegers()` should return `6.3551758451`.
```js
-assert.strictEqual(euler323(), 6.3551758451);
+assert.strictEqual(bitwiseOrOnRandomIntegers(), 6.3551758451);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler323(), 6.3551758451);
## --seed-contents--
```js
-function euler323() {
+function bitwiseOrOnRandomIntegers() {
return true;
}
-euler323();
+bitwiseOrOnRandomIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
index 66ce491477..b2da2925c4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
@@ -8,18 +8,26 @@ dashedName: problem-324-building-a-tower
# --description--
-Let f(n) represent the number of ways one can fill a 3×3×n tower with blocks of 2×1×1. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
+Let $f(n)$ represent the number of ways one can fill a $3×3×n$ tower with blocks of $2×1×1$. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
-For example (with q = 100000007) :f(2) = 229,f(4) = 117805,f(10) mod q = 96149360,f(103) mod q = 24806056,f(106) mod q = 30808124.
+For example (with $q = 100\\,000\\,007$):
-Find f(1010000) mod 100000007.
+$$\begin{align}
+ & f(2) = 229, \\\\
+ & f(4) = 117\\,805, \\\\
+ & f(10)\bmod q = 96\\,149\\,360, \\\\
+ & f({10}^3)\bmod q = 24\\,806\\,056, \\\\
+ & f({10}^6)\bmod q = 30\\,808\\,124.
+\end{align}$$
+
+Find $f({10}^{10000})\bmod 100\\,000\\,007$.
# --hints--
-`euler324()` should return 96972774.
+`buildingTower()` should return `96972774`.
```js
-assert.strictEqual(euler324(), 96972774);
+assert.strictEqual(buildingTower(), 96972774);
```
# --seed--
@@ -27,12 +35,12 @@ assert.strictEqual(euler324(), 96972774);
## --seed-contents--
```js
-function euler324() {
+function buildingTower() {
return true;
}
-euler324();
+buildingTower();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
index 6d0389b9fa..bc828c87e2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
@@ -8,9 +8,9 @@ dashedName: problem-325-stone-game-ii
# --description--
-A game is played with two piles of stones and two players. At her turn, a player removes a number of stones from the larger pile. The number of stones she removes must be a positive multiple of the number of stones in the smaller pile.
+A game is played with two piles of stones and two players. On each player's turn, the player may remove a number of stones from the larger pile. The number of stones removes must be a positive multiple of the number of stones in the smaller pile.
-E.g., let the ordered pair(6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
+E.g., let the ordered pair (6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
The player taking all the stones from a pile wins the game.
@@ -18,16 +18,16 @@ A winning configuration is one where the first player can force a win. For examp
A losing configuration is one where the second player can force a win, no matter what the first player does. For example, (2,3) and (3,4) are losing configurations: any legal move leaves a winning configuration for the second player.
-Define S(N) as the sum of (xi+yi) for all losing configurations (xi,yi), 0 < xi < yi ≤ N. We can verify that S(10) = 211 and S(104) = 230312207313.
+Define $S(N)$ as the sum of ($x_i + y_i$) for all losing configurations ($x_i$, $y_i$), $0 < x_i < y_i ≤ N$. We can verify that $S(10) = 211$ and $S({10}^4) = 230\\,312\\,207\\,313$.
-Find S(1016) mod 710.
+Find $S({10}^{16})\bmod 7^{10}$.
# --hints--
-`euler325()` should return 54672965.
+`stoneGameTwo()` should return `54672965`.
```js
-assert.strictEqual(euler325(), 54672965);
+assert.strictEqual(stoneGameTwo(), 54672965);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler325(), 54672965);
## --seed-contents--
```js
-function euler325() {
+function stoneGameTwo() {
return true;
}
-euler325();
+stoneGameTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
index 1e6b648d9a..ededd29e91 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
@@ -8,24 +8,26 @@ dashedName: problem-326-modulo-summations
# --description--
-Let an be a sequence recursively defined by: .
+Let an be a sequence recursively defined by: $a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$.
-So the first 10 elements of an are: 1,1,0,3,0,3,5,4,1,9.
+So the first 10 elements of $a_n$ are: 1, 1, 0, 3, 0, 3, 5, 4, 1, 9.
-Let f(N,M) represent the number of pairs (p,q) such that:
+Let $f(N, M)$ represent the number of pairs $(p, q)$ such that:
-It can be seen that f(10,10)=4 with the pairs (3,3), (5,5), (7,9) and (9,10).
+$$ 1 \le p \le q \le N \\; \text{and} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
-You are also given that f(104,103)=97158.
+It can be seen that $f(10, 10) = 4$ with the pairs (3,3), (5,5), (7,9) and (9,10).
-Find f(1012,106).
+You are also given that $f({10}^4, {10}^3) = 97\\,158$.
+
+Find $f({10}^{12}, {10}^6)$.
# --hints--
-`euler326()` should return 1966666166408794400.
+`moduloSummations()` should return `1966666166408794400`.
```js
-assert.strictEqual(euler326(), 1966666166408794400);
+assert.strictEqual(moduloSummations(), 1966666166408794400);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler326(), 1966666166408794400);
## --seed-contents--
```js
-function euler326() {
+function moduloSummations() {
return true;
}
-euler326();
+moduloSummations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
index 354596b1d7..e1714be1e6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
@@ -10,7 +10,9 @@ dashedName: problem-327-rooms-of-doom
A series of three rooms are connected to each other by automatic doors.
-Each door is operated by a security card. Once you enter a room the door automatically closes and that security card cannot be used again. A machine at the start will dispense an unlimited number of cards, but each room (including the starting room) contains scanners and if they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
+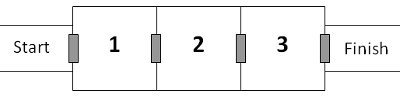 +
+Each door is operated by a security card. Once you enter a room, the door automatically closes, and that security card cannot be used again. A machine will dispense an unlimited number of cards at the start, but each room (including the starting room) contains scanners. If they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
@@ -18,20 +20,26 @@ However, if you make use of the storage boxes, then escape is possible. For exam
It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
-Let C be the maximum number of cards which can be carried at any time. Let R be the number of rooms to travel through. Let M(C,R) be the minimum number of cards required from the dispensing machine to travel through R rooms carrying up to a maximum of C cards at any time.
+Let $C$ be the maximum number of cards which can be carried at any time.
-For example, M(3,6)=123 and M(4,6)=23.And, ΣM(C,6)=146 for 3 ≤ C ≤ 4.
+Let $R$ be the number of rooms to travel through.
-You are given that ΣM(C,10)=10382 for 3 ≤ C ≤ 10.
+Let $M(C, R)$ be the minimum number of cards required from the dispensing machine to travel through $R$ rooms carrying up to a maximum of $C$ cards at any time.
-Find ΣM(C,30) for 3 ≤ C ≤ 40.
+For example, $M(3, 6) = 123$ and $M(4, 6) = 23$.
+
+And, $\sum M(C, 6) = 146$ for $3 ≤ C ≤ 4$.
+
+You are given that $\sum M(C, 10) = 10382$ for $3 ≤ C ≤ 10$.
+
+Find $\sum M(C, 30)$ for $3 ≤ C ≤ 40$.
# --hints--
-`euler327()` should return 34315549139516.
+`roomsOfDoom()` should return `34315549139516`.
```js
-assert.strictEqual(euler327(), 34315549139516);
+assert.strictEqual(roomsOfDoom(), 34315549139516);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler327(), 34315549139516);
## --seed-contents--
```js
-function euler327() {
+function roomsOfDoom() {
return true;
}
-euler327();
+roomsOfDoom();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
index 4a00f455cc..7cb9e0d86e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
@@ -8,32 +8,32 @@ dashedName: problem-328-lowest-cost-search
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., n} by asking questions.
+We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers:
-Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers: "Your guess is lower than the hidden number", or
+- "Your guess is lower than the hidden number", or
+- "Yes, that's it!", or
+- "Your guess is higher than the hidden number".
-"Yes, that's it!", or
+Given the value of $n$, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
-"Your guess is higher than the hidden number".
+If $n = 3$, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
-Given the value of n, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
+If $n = 8$, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be $4 + 6 + 7 = \mathbf{\color{red}{17}}$.
-If n=3, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
+We can improve considerably the worst-case cost for $n = 8$, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of $5 + 7 = \mathbf{\color{blue}{12}}$). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of $5 + 3 + 1 = \mathbf{\color{blue}{9}}$. Since $\mathbf{\color{blue}{12 > 9}}$, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for $n = 8$.
-If n=8, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be 4+6+7=17.
+Let $C(n)$ be the worst-case cost achieved by an optimal strategy for $n$, as described above. Thus $C(1) = 0$, $C(2) = 1$, $C(3) = 2$ and $C(8) = 12$.
-We can improve considerably the worst-case cost for n=8, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of 5+7=12). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of 5+3+1=9. Since 12>9, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for n=8.
+Similarly, $C(100) = 400$ and $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$.
-Let C(n) be the worst-case cost achieved by an optimal strategy for n, as described above. Thus C(1) = 0, C(2) = 1, C(3) = 2 and C(8) = 12. Similarly, C(100) = 400 and C(n) = 17575.
-
-Find C(n).
+Find $\displaystyle\sum_{n = 1}^{200\\,000} C(n)$.
# --hints--
-`euler328()` should return 260511850222.
+`lowestCostSearch()` should return `260511850222`.
```js
-assert.strictEqual(euler328(), 260511850222);
+assert.strictEqual(lowestCostSearch(), 260511850222);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler328(), 260511850222);
## --seed-contents--
```js
-function euler328() {
+function lowestCostSearch() {
return true;
}
-euler328();
+lowestCostSearch();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
index 6b1e185daf..54f72db23f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
@@ -12,20 +12,26 @@ Susan has a prime frog.
Her frog is jumping around over 500 squares numbered 1 to 500.
-He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range \[1;500].(if it lands at either end, it automatically jumps to the only available square on the next move.)
+He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range [1;500]. (if it lands at either end, it automatically jumps to the only available square on the next move.)
-When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability 2/3 or 'N' (NOT PRIME) with probability 1/3 just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability 1/3 or 'N' with probability 2/3 just before jumping to the next square.
+When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability $\frac{2}{3}$ or 'N' (NOT PRIME) with probability $\frac{1}{3}$ just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability $\frac{1}{3}$ or 'N' with probability $\frac{2}{3}$ just before jumping to the next square.
Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
-Give your answer as a fraction p/q in reduced form.
+Give your answer as a string as a fraction `p/q` in reduced form.
# --hints--
-`euler329()` should return 199740353 / 29386561536000.
+`primeFrog()` should return a string.
```js
-assert.strictEqual(euler329(), 199740353 / 29386561536000);
+assert(typeof primeFrog() === 'string');
+```
+
+`primeFrog()` should return the string `199740353/29386561536000`.
+
+```js
+assert.strictEqual(primeFrog(), '199740353/29386561536000');
```
# --seed--
@@ -33,12 +39,12 @@ assert.strictEqual(euler329(), 199740353 / 29386561536000);
## --seed-contents--
```js
-function euler329() {
+function primeFrog() {
return true;
}
-euler329();
+primeFrog();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
index c8a3feab39..d79904dedb 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
@@ -8,30 +8,37 @@ dashedName: problem-330-eulers-number
# --description--
-An infinite sequence of real numbers a(n) is defined for all integers n as follows:
+An infinite sequence of real numbers $a(n)$ is defined for all integers $n$ as follows:
-
+$$ a(n) =
+\begin{cases}
+1 & n < 0 \\\\
+\displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0
+\end{cases}
+$$
-For example,a(0) = 11! + 12! + 13! + ... = e − 1 a(1) = e − 11! + 12! + 13! + ... = 2e − 3 a(2) = 2e − 31! + e − 12! + 13! + ... = 72 e − 6
+For example,
-with e = 2.7182818... being Euler's constant.
+$$\begin{align}
+ & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\
+ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\
+ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6
+\end{align}$$
-It can be shown that a(n) is of the form
+with $e = 2.7182818\ldots$ being Euler's constant.
-A(n) e + B(n)n! for integers A(n) and B(n).
+It can be shown that $a(n)$ is of the form $\displaystyle\frac{A(n)e + B(n)}{n!}$ for integers $A(n)$ and $B(n)$.
-For example a(10) =
+For example $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
-328161643 e − 65269448610!.
-
-Find A(109) + B(109) and give your answer mod 77 777 777.
+Find $A({10}^9)$ + $B({10}^9)$ and give your answer $\bmod 77\\,777\\,777$.
# --hints--
-`euler330()` should return 15955822.
+`eulersNumber()` should return `15955822`.
```js
-assert.strictEqual(euler330(), 15955822);
+assert.strictEqual(eulersNumber(), 15955822);
```
# --seed--
@@ -39,12 +46,12 @@ assert.strictEqual(euler330(), 15955822);
## --seed-contents--
```js
-function euler330() {
+function eulersNumber() {
return true;
}
-euler330();
+eulersNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
index 4d3d330a74..95f5391b7f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
@@ -10,24 +10,26 @@ dashedName: problem-331-cross-flips
N×N disks are placed on a square game board. Each disk has a black side and white side.
-At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus 2×N-1 disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus $2 × N - 1$ disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+
+
+
+Each door is operated by a security card. Once you enter a room, the door automatically closes, and that security card cannot be used again. A machine will dispense an unlimited number of cards at the start, but each room (including the starting room) contains scanners. If they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
@@ -18,20 +20,26 @@ However, if you make use of the storage boxes, then escape is possible. For exam
It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
-Let C be the maximum number of cards which can be carried at any time. Let R be the number of rooms to travel through. Let M(C,R) be the minimum number of cards required from the dispensing machine to travel through R rooms carrying up to a maximum of C cards at any time.
+Let $C$ be the maximum number of cards which can be carried at any time.
-For example, M(3,6)=123 and M(4,6)=23.And, ΣM(C,6)=146 for 3 ≤ C ≤ 4.
+Let $R$ be the number of rooms to travel through.
-You are given that ΣM(C,10)=10382 for 3 ≤ C ≤ 10.
+Let $M(C, R)$ be the minimum number of cards required from the dispensing machine to travel through $R$ rooms carrying up to a maximum of $C$ cards at any time.
-Find ΣM(C,30) for 3 ≤ C ≤ 40.
+For example, $M(3, 6) = 123$ and $M(4, 6) = 23$.
+
+And, $\sum M(C, 6) = 146$ for $3 ≤ C ≤ 4$.
+
+You are given that $\sum M(C, 10) = 10382$ for $3 ≤ C ≤ 10$.
+
+Find $\sum M(C, 30)$ for $3 ≤ C ≤ 40$.
# --hints--
-`euler327()` should return 34315549139516.
+`roomsOfDoom()` should return `34315549139516`.
```js
-assert.strictEqual(euler327(), 34315549139516);
+assert.strictEqual(roomsOfDoom(), 34315549139516);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler327(), 34315549139516);
## --seed-contents--
```js
-function euler327() {
+function roomsOfDoom() {
return true;
}
-euler327();
+roomsOfDoom();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
index 4a00f455cc..7cb9e0d86e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
@@ -8,32 +8,32 @@ dashedName: problem-328-lowest-cost-search
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., n} by asking questions.
+We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers:
-Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers: "Your guess is lower than the hidden number", or
+- "Your guess is lower than the hidden number", or
+- "Yes, that's it!", or
+- "Your guess is higher than the hidden number".
-"Yes, that's it!", or
+Given the value of $n$, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
-"Your guess is higher than the hidden number".
+If $n = 3$, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
-Given the value of n, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
+If $n = 8$, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be $4 + 6 + 7 = \mathbf{\color{red}{17}}$.
-If n=3, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
+We can improve considerably the worst-case cost for $n = 8$, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of $5 + 7 = \mathbf{\color{blue}{12}}$). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of $5 + 3 + 1 = \mathbf{\color{blue}{9}}$. Since $\mathbf{\color{blue}{12 > 9}}$, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for $n = 8$.
-If n=8, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be 4+6+7=17.
+Let $C(n)$ be the worst-case cost achieved by an optimal strategy for $n$, as described above. Thus $C(1) = 0$, $C(2) = 1$, $C(3) = 2$ and $C(8) = 12$.
-We can improve considerably the worst-case cost for n=8, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of 5+7=12). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of 5+3+1=9. Since 12>9, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for n=8.
+Similarly, $C(100) = 400$ and $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$.
-Let C(n) be the worst-case cost achieved by an optimal strategy for n, as described above. Thus C(1) = 0, C(2) = 1, C(3) = 2 and C(8) = 12. Similarly, C(100) = 400 and C(n) = 17575.
-
-Find C(n).
+Find $\displaystyle\sum_{n = 1}^{200\\,000} C(n)$.
# --hints--
-`euler328()` should return 260511850222.
+`lowestCostSearch()` should return `260511850222`.
```js
-assert.strictEqual(euler328(), 260511850222);
+assert.strictEqual(lowestCostSearch(), 260511850222);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler328(), 260511850222);
## --seed-contents--
```js
-function euler328() {
+function lowestCostSearch() {
return true;
}
-euler328();
+lowestCostSearch();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
index 6b1e185daf..54f72db23f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
@@ -12,20 +12,26 @@ Susan has a prime frog.
Her frog is jumping around over 500 squares numbered 1 to 500.
-He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range \[1;500].(if it lands at either end, it automatically jumps to the only available square on the next move.)
+He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range [1;500]. (if it lands at either end, it automatically jumps to the only available square on the next move.)
-When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability 2/3 or 'N' (NOT PRIME) with probability 1/3 just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability 1/3 or 'N' with probability 2/3 just before jumping to the next square.
+When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability $\frac{2}{3}$ or 'N' (NOT PRIME) with probability $\frac{1}{3}$ just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability $\frac{1}{3}$ or 'N' with probability $\frac{2}{3}$ just before jumping to the next square.
Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
-Give your answer as a fraction p/q in reduced form.
+Give your answer as a string as a fraction `p/q` in reduced form.
# --hints--
-`euler329()` should return 199740353 / 29386561536000.
+`primeFrog()` should return a string.
```js
-assert.strictEqual(euler329(), 199740353 / 29386561536000);
+assert(typeof primeFrog() === 'string');
+```
+
+`primeFrog()` should return the string `199740353/29386561536000`.
+
+```js
+assert.strictEqual(primeFrog(), '199740353/29386561536000');
```
# --seed--
@@ -33,12 +39,12 @@ assert.strictEqual(euler329(), 199740353 / 29386561536000);
## --seed-contents--
```js
-function euler329() {
+function primeFrog() {
return true;
}
-euler329();
+primeFrog();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
index c8a3feab39..d79904dedb 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
@@ -8,30 +8,37 @@ dashedName: problem-330-eulers-number
# --description--
-An infinite sequence of real numbers a(n) is defined for all integers n as follows:
+An infinite sequence of real numbers $a(n)$ is defined for all integers $n$ as follows:
-
+$$ a(n) =
+\begin{cases}
+1 & n < 0 \\\\
+\displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0
+\end{cases}
+$$
-For example,a(0) = 11! + 12! + 13! + ... = e − 1 a(1) = e − 11! + 12! + 13! + ... = 2e − 3 a(2) = 2e − 31! + e − 12! + 13! + ... = 72 e − 6
+For example,
-with e = 2.7182818... being Euler's constant.
+$$\begin{align}
+ & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\
+ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\
+ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6
+\end{align}$$
-It can be shown that a(n) is of the form
+with $e = 2.7182818\ldots$ being Euler's constant.
-A(n) e + B(n)n! for integers A(n) and B(n).
+It can be shown that $a(n)$ is of the form $\displaystyle\frac{A(n)e + B(n)}{n!}$ for integers $A(n)$ and $B(n)$.
-For example a(10) =
+For example $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
-328161643 e − 65269448610!.
-
-Find A(109) + B(109) and give your answer mod 77 777 777.
+Find $A({10}^9)$ + $B({10}^9)$ and give your answer $\bmod 77\\,777\\,777$.
# --hints--
-`euler330()` should return 15955822.
+`eulersNumber()` should return `15955822`.
```js
-assert.strictEqual(euler330(), 15955822);
+assert.strictEqual(eulersNumber(), 15955822);
```
# --seed--
@@ -39,12 +46,12 @@ assert.strictEqual(euler330(), 15955822);
## --seed-contents--
```js
-function euler330() {
+function eulersNumber() {
return true;
}
-euler330();
+eulersNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
index 4d3d330a74..95f5391b7f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
@@ -10,24 +10,26 @@ dashedName: problem-331-cross-flips
N×N disks are placed on a square game board. Each disk has a black side and white side.
-At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus 2×N-1 disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus $2 × N - 1$ disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+
+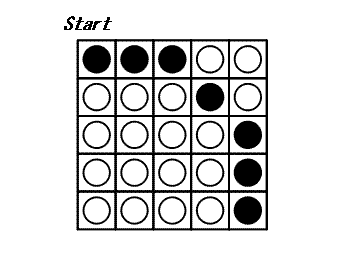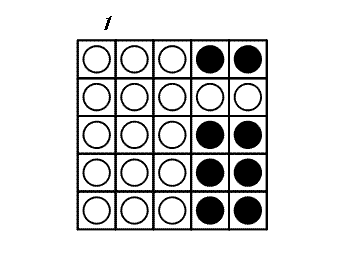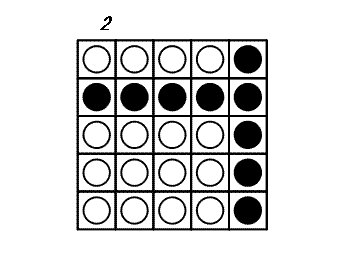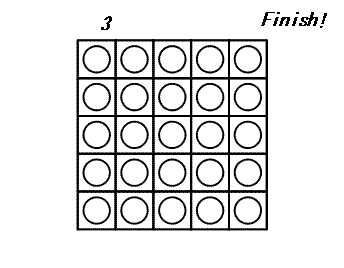 It can be proven that 3 is the minimal number of turns to finish this game.
-The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+The bottom left disk on the $N×N$ board has coordinates (0, 0); the bottom right disk has coordinates ($N - 1$,$0$) and the top left disk has coordinates ($0$,$N - 1$).
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Let $C_N$ be the following configuration of a board with $N × N$disks: A disk at ($x$, $y$) satisfying $N - 1 \le \sqrt{x^2 + y^2} \lt N$, shows its black side; otherwise, it shows its white side. $C_5$ is shown above.
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Let $T(N)$ be the minimal number of turns to finish a game starting from configuration $C_N$ or 0 if configuration $C_N$ is unsolvable. We have shown that $T(5) = 3$. You are also given that $T(10) = 29$ and $T(1\\,000) = 395\\,253$.
-Find .
+Find $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` should return `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..c09640cdef 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -10,18 +10,26 @@ dashedName: problem-332-spherical-triangles
A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+
It can be proven that 3 is the minimal number of turns to finish this game.
-The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+The bottom left disk on the $N×N$ board has coordinates (0, 0); the bottom right disk has coordinates ($N - 1$,$0$) and the top left disk has coordinates ($0$,$N - 1$).
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Let $C_N$ be the following configuration of a board with $N × N$disks: A disk at ($x$, $y$) satisfying $N - 1 \le \sqrt{x^2 + y^2} \lt N$, shows its black side; otherwise, it shows its white side. $C_5$ is shown above.
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Let $T(N)$ be the minimal number of turns to finish a game starting from configuration $C_N$ or 0 if configuration $C_N$ is unsolvable. We have shown that $T(5) = 3$. You are also given that $T(10) = 29$ and $T(1\\,000) = 395\\,253$.
-Find .
+Find $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` should return `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..c09640cdef 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -10,18 +10,26 @@ dashedName: problem-332-spherical-triangles
A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+ -For example A(14) is 3.294040 rounded to six decimal places.
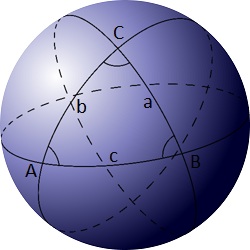
+Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.
+
+Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are not included in $T(r)$.
+
+Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.
+
+For example $A(14)$ is 3.294040 rounded to six decimal places.
+
+Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` should return `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..35023e9837 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -8,26 +8,31 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as $2^i \times 3^j$, where $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ would not be valid since 2 can divide 6. Neither would the partition $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ since 1 can divide 16. The only valid partition of 17 would be $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Many integers have more than one valid partition, the first being 11 having the following two partitions.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align}
+ & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\
+ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1)
+\end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Let's define $P(n)$ as the number of valid partitions of $n$. For example, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Let's consider only the prime integers $q$ which would have a single valid partition such as $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+The sum of the primes $q <100$ such that $P(q) = 1$ equals 233.
+
+Find the sum of the primes $q < 1\\,000\\,000$ such that $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` should return `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +40,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..bc5e4a11e7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -12,20 +12,30 @@ In Plato's heaven, there exist an infinite number of bowls in a straight line. E
For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
-
+
-For example A(14) is 3.294040 rounded to six decimal places.
+Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.
+
+Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are not included in $T(r)$.
+
+Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.
+
+For example $A(14)$ is 3.294040 rounded to six decimal places.
+
+Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` should return `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..35023e9837 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -8,26 +8,31 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as $2^i \times 3^j$, where $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ would not be valid since 2 can divide 6. Neither would the partition $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ since 1 can divide 16. The only valid partition of 17 would be $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Many integers have more than one valid partition, the first being 11 having the following two partitions.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align}
+ & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\
+ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1)
+\end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Let's define $P(n)$ as the number of valid partitions of $n$. For example, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Let's consider only the prime integers $q$ which would have a single valid partition such as $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+The sum of the primes $q <100$ such that $P(q) = 1$ equals 233.
+
+Find the sum of the primes $q < 1\\,000\\,000$ such that $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` should return `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +40,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..bc5e4a11e7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
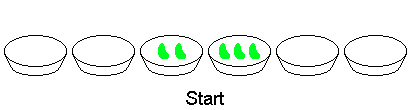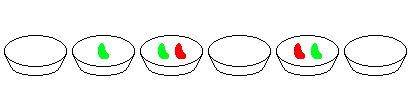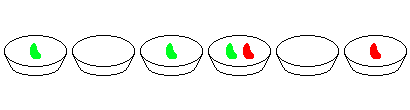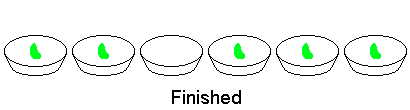
@@ -12,20 +12,30 @@ In Plato's heaven, there exist an infinite number of bowls in a straight line. E
For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
-
+ -You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+You are given the following sequences:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align}
+ & t_0 = 123456, \\\\
+ & t_i = \begin{cases}
+ \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\
+ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd}
+ \end{cases} \\\\
+ & \qquad \text{where $⌊x⌋$ is the floor function and $\oplus$ is the bitwise XOR operator.} \\\\
+ & b_i = (t_i\bmod 2^{11}) + 1.
+\end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+The first two terms of the last sequence are $b_1 = 289$ and $b_2 = 145$. If we start with $b_1$ and $b_2$ beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+
+Consider now 1500 adjacent bowls containing $b_1, b_2, \ldots, b_{1500}$ beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` should return `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +43,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..f20d369ff8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -10,18 +10,20 @@ dashedName: problem-335-gathering-the-beans
Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+
-You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+You are given the following sequences:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align}
+ & t_0 = 123456, \\\\
+ & t_i = \begin{cases}
+ \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\
+ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd}
+ \end{cases} \\\\
+ & \qquad \text{where $⌊x⌋$ is the floor function and $\oplus$ is the bitwise XOR operator.} \\\\
+ & b_i = (t_i\bmod 2^{11}) + 1.
+\end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+The first two terms of the last sequence are $b_1 = 289$ and $b_2 = 145$. If we start with $b_1$ and $b_2$ beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+
+Consider now 1500 adjacent bowls containing $b_1, b_2, \ldots, b_{1500}$ beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` should return `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +43,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..f20d369ff8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -10,18 +10,20 @@ dashedName: problem-335-gathering-the-beans
Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+ +
So with 5 bowls it takes Peter 15 moves to return to the initial situation.
-Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Let $M(x)$ represent the number of moves required to return to the initial situation, starting with $x$ bowls. Thus, $M(5) = 15$. It can also be verified that $M(100) = 10920$.
-Find M(2k+1). Give your answer modulo 79.
+Find $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Give your answer modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` should return `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..e767debe05 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+A train is used to transport four carriages in the order: $ABCD$. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+To rearrange the carriages, they are all shunted onto a large rotating turntable. After the carriages are uncoupled at a specific point, the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180°. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Some arrangements, such as $ADCB$, can be solved easily: the carriages are separated between $A$ and $D$, and after $DCB$ are rotated the correct order has been achieved.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage $A$ in the correct place, then carriage $B$, and so on.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are $DACB$ and $DBAC$; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for $DACB$ is shown below.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+
+
So with 5 bowls it takes Peter 15 moves to return to the initial situation.
-Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Let $M(x)$ represent the number of moves required to return to the initial situation, starting with $x$ bowls. Thus, $M(5) = 15$. It can also be verified that $M(100) = 10920$.
-Find M(2k+1). Give your answer modulo 79.
+Find $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Give your answer modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` should return `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..e767debe05 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+A train is used to transport four carriages in the order: $ABCD$. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+To rearrange the carriages, they are all shunted onto a large rotating turntable. After the carriages are uncoupled at a specific point, the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180°. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Some arrangements, such as $ADCB$, can be solved easily: the carriages are separated between $A$ and $D$, and after $DCB$ are rotated the correct order has been achieved.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage $A$ in the correct place, then carriage $B$, and so on.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are $DACB$ and $DBAC$; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for $DACB$ is shown below.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+ -Find the 2011th lexicographic maximix arrangement for eleven carriages.
+It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is $DFAECB$.
+
+Find the ${2011}^{\text{th}}$ lexicographic maximix arrangement for eleven carriages.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` should return a string.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` should return the string `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..a0298d4170 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Let $\\{a_1, a_2, \ldots, a_n\\}$ be an integer sequence of length $n$ such that:
-a1 = 6
+- $a_1 = 6$
+- for all $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denotes Euler's totient function.
-Let S(N) be the number of such sequences with an ≤ N.
+Let $S(N)$ be the number of such sequences with $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+For example, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+We can verify that $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Find $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` should return `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..7039c9e8af 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+A rectangular sheet of grid paper with integer dimensions $w$ × $h$ is given. Its grid spacing is 1.
When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+For example, from a sheet with dimensions 9 × 4, we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+
-Find the 2011th lexicographic maximix arrangement for eleven carriages.
+It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is $DFAECB$.
+
+Find the ${2011}^{\text{th}}$ lexicographic maximix arrangement for eleven carriages.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` should return a string.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` should return the string `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..a0298d4170 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Let $\\{a_1, a_2, \ldots, a_n\\}$ be an integer sequence of length $n$ such that:
-a1 = 6
+- $a_1 = 6$
+- for all $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denotes Euler's totient function.
-Let S(N) be the number of such sequences with an ≤ N.
+Let $S(N)$ be the number of such sequences with $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+For example, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+We can verify that $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Find $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` should return `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..7039c9e8af 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+A rectangular sheet of grid paper with integer dimensions $w$ × $h$ is given. Its grid spacing is 1.
When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+For example, from a sheet with dimensions 9 × 4, we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+ -For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Similarly, from a sheet with dimensions 9 × 8, we can make rectangles with dimensions 18 × 4 and 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+For a pair $w$ and $h$, let $F(w, h)$ be the number of distinct rectangles that can be made from a sheet with dimensions $w$ × $h$. For example, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ and $F(9, 8) = 2$. Note that rectangles congruent to the initial one are not counted in $F(w, h)$. Note also that rectangles with dimensions $w$ × $h$ and dimensions $h$ × $w$ are not considered distinct.
-Find G(1012). Give your answer modulo 108.
+For an integer $N$, let $G(N)$ be the sum of $F(w, h)$ for all pairs $w$ and $h$ which satisfy $0 < h ≤ w ≤ N$. We can verify that $G(10) = 55$, $G({10}^3) = 971\\,745$ and $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Find $G({10}^{12})$. Give your answer modulo ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` should return `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..c080309b34 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black." - Peredur the Son of Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Initially, each flock consists of $n$ sheep. Each sheep (regardless of color) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let $E(n)$ be the expected final number of black sheep if Peredur uses an optimal strategy.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+You are given that $E(5) = 6.871346$ rounded to 6 places behind the decimal point.
+
+Find $E(10\\,000)$ and give your answer rounded to 6 places behind the decimal point.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` should return `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..64a26640d0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -8,24 +8,25 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+For fixed integers $a$, $b$, $c$, define the crazy function $F(n)$ as follows:
-F(n) = n - c for all n > b
+$$\begin{align}
+ & F(n) = n - c \\;\text{ for all } n > b \\\\
+ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ for all } n ≤ b.
+\end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Also, define $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+For example, if $a = 50$, $b = 2000$ and $c = 40$, then $F(0) = 3240$ and $F(2000) = 2040$. Also, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Find the last 9 digits of $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` should return `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--
-For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Similarly, from a sheet with dimensions 9 × 8, we can make rectangles with dimensions 18 × 4 and 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+For a pair $w$ and $h$, let $F(w, h)$ be the number of distinct rectangles that can be made from a sheet with dimensions $w$ × $h$. For example, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ and $F(9, 8) = 2$. Note that rectangles congruent to the initial one are not counted in $F(w, h)$. Note also that rectangles with dimensions $w$ × $h$ and dimensions $h$ × $w$ are not considered distinct.
-Find G(1012). Give your answer modulo 108.
+For an integer $N$, let $G(N)$ be the sum of $F(w, h)$ for all pairs $w$ and $h$ which satisfy $0 < h ≤ w ≤ N$. We can verify that $G(10) = 55$, $G({10}^3) = 971\\,745$ and $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Find $G({10}^{12})$. Give your answer modulo ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` should return `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..c080309b34 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black." - Peredur the Son of Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Initially, each flock consists of $n$ sheep. Each sheep (regardless of color) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let $E(n)$ be the expected final number of black sheep if Peredur uses an optimal strategy.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+You are given that $E(5) = 6.871346$ rounded to 6 places behind the decimal point.
+
+Find $E(10\\,000)$ and give your answer rounded to 6 places behind the decimal point.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` should return `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..64a26640d0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -8,24 +8,25 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+For fixed integers $a$, $b$, $c$, define the crazy function $F(n)$ as follows:
-F(n) = n - c for all n > b
+$$\begin{align}
+ & F(n) = n - c \\;\text{ for all } n > b \\\\
+ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ for all } n ≤ b.
+\end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Also, define $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+For example, if $a = 50$, $b = 2000$ and $c = 40$, then $F(0) = 3240$ and $F(2000) = 2040$. Also, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Find the last 9 digits of $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` should return `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--
 A counter can move from one square to the next (slide) or can jump over another counter (hop) as long as the square next to that counter is unoccupied.
-Let M(n) represent the minimum number of moves/actions to completely reverse the positions of the coloured counters; that is, move all the red counters to the right and all the blue counters to the left. It can be verified M(3) = 15, which also happens to be a triangle number.
+
A counter can move from one square to the next (slide) or can jump over another counter (hop) as long as the square next to that counter is unoccupied.
-Let M(n) represent the minimum number of moves/actions to completely reverse the positions of the coloured counters; that is, move all the red counters to the right and all the blue counters to the left. It can be verified M(3) = 15, which also happens to be a triangle number.
+ -If we create a sequence based on the values of n for which M(n) is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
+Let $M(n)$ represent the minimum number of moves/actions to completely reverse the positions of the colored counters; that is, move all the red counters to the right and all the blue counters to the left.
+
+It can be verified $M(3) = 15$, which also happens to be a triangle number.
+
+If we create a sequence based on the values of n for which $M(n)$ is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
Find the sum of the first forty terms of this sequence.
# --hints--
-`euler321()` should return 2470433131948040.
+`swappingCounters()` should return `2470433131948040`.
```js
-assert.strictEqual(euler321(), 2470433131948040);
+assert.strictEqual(swappingCounters(), 2470433131948040);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler321(), 2470433131948040);
## --seed-contents--
```js
-function euler321() {
+function swappingCounters() {
return true;
}
-euler321();
+swappingCounters();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
index 241c3a74f0..d532a4a95d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
@@ -8,18 +8,18 @@ dashedName: problem-322-binomial-coefficients-divisible-by-10
# --description--
-Let T(m, n) be the number of the binomial coefficients iCn that are divisible by 10 for n ≤ i < m(i, m and n are positive integers).
+Let $T(m, n)$ be the number of the binomial coefficients ${}^iC_n$ that are divisible by 10 for $n ≤ i < m$ ($i$, $m$ and $n$ are positive integers).
-You are given that T(109, 107-10) = 989697000.
+You are given that $T({10}^9, {10}^7 - 10) = 989\\,697\\,000$.
-Find T(1018, 1012-10).
+Find $T({10}^{18}, {10}^{12} - 10)$.
# --hints--
-`euler322()` should return 999998760323314000.
+`binomialCoefficientsDivisibleBy10()` should return `999998760323314000`.
```js
-assert.strictEqual(euler322(), 999998760323314000);
+assert.strictEqual(binomialCoefficientsDivisibleBy10(), 999998760323314000);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler322(), 999998760323314000);
## --seed-contents--
```js
-function euler322() {
+function binomialCoefficientsDivisibleBy10() {
return true;
}
-euler322();
+binomialCoefficientsDivisibleBy10();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
index b336759562..31e36339ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
@@ -8,24 +8,25 @@ dashedName: problem-323-bitwise-or-operations-on-random-integers
# --description--
-Let y0, y1, y2,... be a sequence of random unsigned 32 bit integers
+Let $y_0, y_1, y_2, \ldots$ be a sequence of random unsigned 32 bit integers
-(i.e. 0 ≤ yi < 232, every value equally likely).
+(i.e. $0 ≤ y_i < 2^{32}$, every value equally likely).
-For the sequence xi the following recursion is given:x0 = 0 and
+For the sequence $x_i$ the following recursion is given:
-xi = xi-1| yi-1, for i > 0. ( | is the bitwise-OR operator)
+- $x_0 = 0$ and
+- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$, for $i > 0$. ($\mathbf{|}$ is the bitwise-OR operator)
-It can be seen that eventually there will be an index N such that xi = 232 -1 (a bit-pattern of all ones) for all i ≥ N.
+It can be seen that eventually there will be an index $N$ such that $x_i = 2^{32} - 1$ (a bit-pattern of all ones) for all $i ≥ N$.
-Find the expected value of N. Give your answer rounded to 10 digits after the decimal point.
+Find the expected value of $N$. Give your answer rounded to 10 digits after the decimal point.
# --hints--
-`euler323()` should return 6.3551758451.
+`bitwiseOrOnRandomIntegers()` should return `6.3551758451`.
```js
-assert.strictEqual(euler323(), 6.3551758451);
+assert.strictEqual(bitwiseOrOnRandomIntegers(), 6.3551758451);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler323(), 6.3551758451);
## --seed-contents--
```js
-function euler323() {
+function bitwiseOrOnRandomIntegers() {
return true;
}
-euler323();
+bitwiseOrOnRandomIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
index 66ce491477..b2da2925c4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
@@ -8,18 +8,26 @@ dashedName: problem-324-building-a-tower
# --description--
-Let f(n) represent the number of ways one can fill a 3×3×n tower with blocks of 2×1×1. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
+Let $f(n)$ represent the number of ways one can fill a $3×3×n$ tower with blocks of $2×1×1$. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
-For example (with q = 100000007) :f(2) = 229,f(4) = 117805,f(10) mod q = 96149360,f(103) mod q = 24806056,f(106) mod q = 30808124.
+For example (with $q = 100\\,000\\,007$):
-Find f(1010000) mod 100000007.
+$$\begin{align}
+ & f(2) = 229, \\\\
+ & f(4) = 117\\,805, \\\\
+ & f(10)\bmod q = 96\\,149\\,360, \\\\
+ & f({10}^3)\bmod q = 24\\,806\\,056, \\\\
+ & f({10}^6)\bmod q = 30\\,808\\,124.
+\end{align}$$
+
+Find $f({10}^{10000})\bmod 100\\,000\\,007$.
# --hints--
-`euler324()` should return 96972774.
+`buildingTower()` should return `96972774`.
```js
-assert.strictEqual(euler324(), 96972774);
+assert.strictEqual(buildingTower(), 96972774);
```
# --seed--
@@ -27,12 +35,12 @@ assert.strictEqual(euler324(), 96972774);
## --seed-contents--
```js
-function euler324() {
+function buildingTower() {
return true;
}
-euler324();
+buildingTower();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
index 6d0389b9fa..bc828c87e2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
@@ -8,9 +8,9 @@ dashedName: problem-325-stone-game-ii
# --description--
-A game is played with two piles of stones and two players. At her turn, a player removes a number of stones from the larger pile. The number of stones she removes must be a positive multiple of the number of stones in the smaller pile.
+A game is played with two piles of stones and two players. On each player's turn, the player may remove a number of stones from the larger pile. The number of stones removes must be a positive multiple of the number of stones in the smaller pile.
-E.g., let the ordered pair(6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
+E.g., let the ordered pair (6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
The player taking all the stones from a pile wins the game.
@@ -18,16 +18,16 @@ A winning configuration is one where the first player can force a win. For examp
A losing configuration is one where the second player can force a win, no matter what the first player does. For example, (2,3) and (3,4) are losing configurations: any legal move leaves a winning configuration for the second player.
-Define S(N) as the sum of (xi+yi) for all losing configurations (xi,yi), 0 < xi < yi ≤ N. We can verify that S(10) = 211 and S(104) = 230312207313.
+Define $S(N)$ as the sum of ($x_i + y_i$) for all losing configurations ($x_i$, $y_i$), $0 < x_i < y_i ≤ N$. We can verify that $S(10) = 211$ and $S({10}^4) = 230\\,312\\,207\\,313$.
-Find S(1016) mod 710.
+Find $S({10}^{16})\bmod 7^{10}$.
# --hints--
-`euler325()` should return 54672965.
+`stoneGameTwo()` should return `54672965`.
```js
-assert.strictEqual(euler325(), 54672965);
+assert.strictEqual(stoneGameTwo(), 54672965);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler325(), 54672965);
## --seed-contents--
```js
-function euler325() {
+function stoneGameTwo() {
return true;
}
-euler325();
+stoneGameTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
index 1e6b648d9a..ededd29e91 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
@@ -8,24 +8,26 @@ dashedName: problem-326-modulo-summations
# --description--
-Let an be a sequence recursively defined by: .
+Let an be a sequence recursively defined by: $a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$.
-So the first 10 elements of an are: 1,1,0,3,0,3,5,4,1,9.
+So the first 10 elements of $a_n$ are: 1, 1, 0, 3, 0, 3, 5, 4, 1, 9.
-Let f(N,M) represent the number of pairs (p,q) such that:
+Let $f(N, M)$ represent the number of pairs $(p, q)$ such that:
-It can be seen that f(10,10)=4 with the pairs (3,3), (5,5), (7,9) and (9,10).
+$$ 1 \le p \le q \le N \\; \text{and} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
-You are also given that f(104,103)=97158.
+It can be seen that $f(10, 10) = 4$ with the pairs (3,3), (5,5), (7,9) and (9,10).
-Find f(1012,106).
+You are also given that $f({10}^4, {10}^3) = 97\\,158$.
+
+Find $f({10}^{12}, {10}^6)$.
# --hints--
-`euler326()` should return 1966666166408794400.
+`moduloSummations()` should return `1966666166408794400`.
```js
-assert.strictEqual(euler326(), 1966666166408794400);
+assert.strictEqual(moduloSummations(), 1966666166408794400);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler326(), 1966666166408794400);
## --seed-contents--
```js
-function euler326() {
+function moduloSummations() {
return true;
}
-euler326();
+moduloSummations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
index 354596b1d7..e1714be1e6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
@@ -10,7 +10,9 @@ dashedName: problem-327-rooms-of-doom
A series of three rooms are connected to each other by automatic doors.
-Each door is operated by a security card. Once you enter a room the door automatically closes and that security card cannot be used again. A machine at the start will dispense an unlimited number of cards, but each room (including the starting room) contains scanners and if they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
+
-If we create a sequence based on the values of n for which M(n) is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
+Let $M(n)$ represent the minimum number of moves/actions to completely reverse the positions of the colored counters; that is, move all the red counters to the right and all the blue counters to the left.
+
+It can be verified $M(3) = 15$, which also happens to be a triangle number.
+
+If we create a sequence based on the values of n for which $M(n)$ is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
Find the sum of the first forty terms of this sequence.
# --hints--
-`euler321()` should return 2470433131948040.
+`swappingCounters()` should return `2470433131948040`.
```js
-assert.strictEqual(euler321(), 2470433131948040);
+assert.strictEqual(swappingCounters(), 2470433131948040);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler321(), 2470433131948040);
## --seed-contents--
```js
-function euler321() {
+function swappingCounters() {
return true;
}
-euler321();
+swappingCounters();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
index 241c3a74f0..d532a4a95d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
@@ -8,18 +8,18 @@ dashedName: problem-322-binomial-coefficients-divisible-by-10
# --description--
-Let T(m, n) be the number of the binomial coefficients iCn that are divisible by 10 for n ≤ i < m(i, m and n are positive integers).
+Let $T(m, n)$ be the number of the binomial coefficients ${}^iC_n$ that are divisible by 10 for $n ≤ i < m$ ($i$, $m$ and $n$ are positive integers).
-You are given that T(109, 107-10) = 989697000.
+You are given that $T({10}^9, {10}^7 - 10) = 989\\,697\\,000$.
-Find T(1018, 1012-10).
+Find $T({10}^{18}, {10}^{12} - 10)$.
# --hints--
-`euler322()` should return 999998760323314000.
+`binomialCoefficientsDivisibleBy10()` should return `999998760323314000`.
```js
-assert.strictEqual(euler322(), 999998760323314000);
+assert.strictEqual(binomialCoefficientsDivisibleBy10(), 999998760323314000);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler322(), 999998760323314000);
## --seed-contents--
```js
-function euler322() {
+function binomialCoefficientsDivisibleBy10() {
return true;
}
-euler322();
+binomialCoefficientsDivisibleBy10();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
index b336759562..31e36339ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
@@ -8,24 +8,25 @@ dashedName: problem-323-bitwise-or-operations-on-random-integers
# --description--
-Let y0, y1, y2,... be a sequence of random unsigned 32 bit integers
+Let $y_0, y_1, y_2, \ldots$ be a sequence of random unsigned 32 bit integers
-(i.e. 0 ≤ yi < 232, every value equally likely).
+(i.e. $0 ≤ y_i < 2^{32}$, every value equally likely).
-For the sequence xi the following recursion is given:x0 = 0 and
+For the sequence $x_i$ the following recursion is given:
-xi = xi-1| yi-1, for i > 0. ( | is the bitwise-OR operator)
+- $x_0 = 0$ and
+- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$, for $i > 0$. ($\mathbf{|}$ is the bitwise-OR operator)
-It can be seen that eventually there will be an index N such that xi = 232 -1 (a bit-pattern of all ones) for all i ≥ N.
+It can be seen that eventually there will be an index $N$ such that $x_i = 2^{32} - 1$ (a bit-pattern of all ones) for all $i ≥ N$.
-Find the expected value of N. Give your answer rounded to 10 digits after the decimal point.
+Find the expected value of $N$. Give your answer rounded to 10 digits after the decimal point.
# --hints--
-`euler323()` should return 6.3551758451.
+`bitwiseOrOnRandomIntegers()` should return `6.3551758451`.
```js
-assert.strictEqual(euler323(), 6.3551758451);
+assert.strictEqual(bitwiseOrOnRandomIntegers(), 6.3551758451);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler323(), 6.3551758451);
## --seed-contents--
```js
-function euler323() {
+function bitwiseOrOnRandomIntegers() {
return true;
}
-euler323();
+bitwiseOrOnRandomIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
index 66ce491477..b2da2925c4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
@@ -8,18 +8,26 @@ dashedName: problem-324-building-a-tower
# --description--
-Let f(n) represent the number of ways one can fill a 3×3×n tower with blocks of 2×1×1. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
+Let $f(n)$ represent the number of ways one can fill a $3×3×n$ tower with blocks of $2×1×1$. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
-For example (with q = 100000007) :f(2) = 229,f(4) = 117805,f(10) mod q = 96149360,f(103) mod q = 24806056,f(106) mod q = 30808124.
+For example (with $q = 100\\,000\\,007$):
-Find f(1010000) mod 100000007.
+$$\begin{align}
+ & f(2) = 229, \\\\
+ & f(4) = 117\\,805, \\\\
+ & f(10)\bmod q = 96\\,149\\,360, \\\\
+ & f({10}^3)\bmod q = 24\\,806\\,056, \\\\
+ & f({10}^6)\bmod q = 30\\,808\\,124.
+\end{align}$$
+
+Find $f({10}^{10000})\bmod 100\\,000\\,007$.
# --hints--
-`euler324()` should return 96972774.
+`buildingTower()` should return `96972774`.
```js
-assert.strictEqual(euler324(), 96972774);
+assert.strictEqual(buildingTower(), 96972774);
```
# --seed--
@@ -27,12 +35,12 @@ assert.strictEqual(euler324(), 96972774);
## --seed-contents--
```js
-function euler324() {
+function buildingTower() {
return true;
}
-euler324();
+buildingTower();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
index 6d0389b9fa..bc828c87e2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
@@ -8,9 +8,9 @@ dashedName: problem-325-stone-game-ii
# --description--
-A game is played with two piles of stones and two players. At her turn, a player removes a number of stones from the larger pile. The number of stones she removes must be a positive multiple of the number of stones in the smaller pile.
+A game is played with two piles of stones and two players. On each player's turn, the player may remove a number of stones from the larger pile. The number of stones removes must be a positive multiple of the number of stones in the smaller pile.
-E.g., let the ordered pair(6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
+E.g., let the ordered pair (6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
The player taking all the stones from a pile wins the game.
@@ -18,16 +18,16 @@ A winning configuration is one where the first player can force a win. For examp
A losing configuration is one where the second player can force a win, no matter what the first player does. For example, (2,3) and (3,4) are losing configurations: any legal move leaves a winning configuration for the second player.
-Define S(N) as the sum of (xi+yi) for all losing configurations (xi,yi), 0 < xi < yi ≤ N. We can verify that S(10) = 211 and S(104) = 230312207313.
+Define $S(N)$ as the sum of ($x_i + y_i$) for all losing configurations ($x_i$, $y_i$), $0 < x_i < y_i ≤ N$. We can verify that $S(10) = 211$ and $S({10}^4) = 230\\,312\\,207\\,313$.
-Find S(1016) mod 710.
+Find $S({10}^{16})\bmod 7^{10}$.
# --hints--
-`euler325()` should return 54672965.
+`stoneGameTwo()` should return `54672965`.
```js
-assert.strictEqual(euler325(), 54672965);
+assert.strictEqual(stoneGameTwo(), 54672965);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler325(), 54672965);
## --seed-contents--
```js
-function euler325() {
+function stoneGameTwo() {
return true;
}
-euler325();
+stoneGameTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
index 1e6b648d9a..ededd29e91 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
@@ -8,24 +8,26 @@ dashedName: problem-326-modulo-summations
# --description--
-Let an be a sequence recursively defined by: .
+Let an be a sequence recursively defined by: $a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$.
-So the first 10 elements of an are: 1,1,0,3,0,3,5,4,1,9.
+So the first 10 elements of $a_n$ are: 1, 1, 0, 3, 0, 3, 5, 4, 1, 9.
-Let f(N,M) represent the number of pairs (p,q) such that:
+Let $f(N, M)$ represent the number of pairs $(p, q)$ such that:
-It can be seen that f(10,10)=4 with the pairs (3,3), (5,5), (7,9) and (9,10).
+$$ 1 \le p \le q \le N \\; \text{and} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
-You are also given that f(104,103)=97158.
+It can be seen that $f(10, 10) = 4$ with the pairs (3,3), (5,5), (7,9) and (9,10).
-Find f(1012,106).
+You are also given that $f({10}^4, {10}^3) = 97\\,158$.
+
+Find $f({10}^{12}, {10}^6)$.
# --hints--
-`euler326()` should return 1966666166408794400.
+`moduloSummations()` should return `1966666166408794400`.
```js
-assert.strictEqual(euler326(), 1966666166408794400);
+assert.strictEqual(moduloSummations(), 1966666166408794400);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler326(), 1966666166408794400);
## --seed-contents--
```js
-function euler326() {
+function moduloSummations() {
return true;
}
-euler326();
+moduloSummations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
index 354596b1d7..e1714be1e6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
@@ -10,7 +10,9 @@ dashedName: problem-327-rooms-of-doom
A series of three rooms are connected to each other by automatic doors.
-Each door is operated by a security card. Once you enter a room the door automatically closes and that security card cannot be used again. A machine at the start will dispense an unlimited number of cards, but each room (including the starting room) contains scanners and if they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
+ +
+Each door is operated by a security card. Once you enter a room, the door automatically closes, and that security card cannot be used again. A machine will dispense an unlimited number of cards at the start, but each room (including the starting room) contains scanners. If they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
@@ -18,20 +20,26 @@ However, if you make use of the storage boxes, then escape is possible. For exam
It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
-Let C be the maximum number of cards which can be carried at any time. Let R be the number of rooms to travel through. Let M(C,R) be the minimum number of cards required from the dispensing machine to travel through R rooms carrying up to a maximum of C cards at any time.
+Let $C$ be the maximum number of cards which can be carried at any time.
-For example, M(3,6)=123 and M(4,6)=23.And, ΣM(C,6)=146 for 3 ≤ C ≤ 4.
+Let $R$ be the number of rooms to travel through.
-You are given that ΣM(C,10)=10382 for 3 ≤ C ≤ 10.
+Let $M(C, R)$ be the minimum number of cards required from the dispensing machine to travel through $R$ rooms carrying up to a maximum of $C$ cards at any time.
-Find ΣM(C,30) for 3 ≤ C ≤ 40.
+For example, $M(3, 6) = 123$ and $M(4, 6) = 23$.
+
+And, $\sum M(C, 6) = 146$ for $3 ≤ C ≤ 4$.
+
+You are given that $\sum M(C, 10) = 10382$ for $3 ≤ C ≤ 10$.
+
+Find $\sum M(C, 30)$ for $3 ≤ C ≤ 40$.
# --hints--
-`euler327()` should return 34315549139516.
+`roomsOfDoom()` should return `34315549139516`.
```js
-assert.strictEqual(euler327(), 34315549139516);
+assert.strictEqual(roomsOfDoom(), 34315549139516);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler327(), 34315549139516);
## --seed-contents--
```js
-function euler327() {
+function roomsOfDoom() {
return true;
}
-euler327();
+roomsOfDoom();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
index 4a00f455cc..7cb9e0d86e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
@@ -8,32 +8,32 @@ dashedName: problem-328-lowest-cost-search
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., n} by asking questions.
+We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers:
-Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers: "Your guess is lower than the hidden number", or
+- "Your guess is lower than the hidden number", or
+- "Yes, that's it!", or
+- "Your guess is higher than the hidden number".
-"Yes, that's it!", or
+Given the value of $n$, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
-"Your guess is higher than the hidden number".
+If $n = 3$, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
-Given the value of n, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
+If $n = 8$, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be $4 + 6 + 7 = \mathbf{\color{red}{17}}$.
-If n=3, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
+We can improve considerably the worst-case cost for $n = 8$, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of $5 + 7 = \mathbf{\color{blue}{12}}$). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of $5 + 3 + 1 = \mathbf{\color{blue}{9}}$. Since $\mathbf{\color{blue}{12 > 9}}$, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for $n = 8$.
-If n=8, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be 4+6+7=17.
+Let $C(n)$ be the worst-case cost achieved by an optimal strategy for $n$, as described above. Thus $C(1) = 0$, $C(2) = 1$, $C(3) = 2$ and $C(8) = 12$.
-We can improve considerably the worst-case cost for n=8, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of 5+7=12). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of 5+3+1=9. Since 12>9, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for n=8.
+Similarly, $C(100) = 400$ and $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$.
-Let C(n) be the worst-case cost achieved by an optimal strategy for n, as described above. Thus C(1) = 0, C(2) = 1, C(3) = 2 and C(8) = 12. Similarly, C(100) = 400 and C(n) = 17575.
-
-Find C(n).
+Find $\displaystyle\sum_{n = 1}^{200\\,000} C(n)$.
# --hints--
-`euler328()` should return 260511850222.
+`lowestCostSearch()` should return `260511850222`.
```js
-assert.strictEqual(euler328(), 260511850222);
+assert.strictEqual(lowestCostSearch(), 260511850222);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler328(), 260511850222);
## --seed-contents--
```js
-function euler328() {
+function lowestCostSearch() {
return true;
}
-euler328();
+lowestCostSearch();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
index 6b1e185daf..54f72db23f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
@@ -12,20 +12,26 @@ Susan has a prime frog.
Her frog is jumping around over 500 squares numbered 1 to 500.
-He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range \[1;500].(if it lands at either end, it automatically jumps to the only available square on the next move.)
+He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range [1;500]. (if it lands at either end, it automatically jumps to the only available square on the next move.)
-When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability 2/3 or 'N' (NOT PRIME) with probability 1/3 just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability 1/3 or 'N' with probability 2/3 just before jumping to the next square.
+When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability $\frac{2}{3}$ or 'N' (NOT PRIME) with probability $\frac{1}{3}$ just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability $\frac{1}{3}$ or 'N' with probability $\frac{2}{3}$ just before jumping to the next square.
Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
-Give your answer as a fraction p/q in reduced form.
+Give your answer as a string as a fraction `p/q` in reduced form.
# --hints--
-`euler329()` should return 199740353 / 29386561536000.
+`primeFrog()` should return a string.
```js
-assert.strictEqual(euler329(), 199740353 / 29386561536000);
+assert(typeof primeFrog() === 'string');
+```
+
+`primeFrog()` should return the string `199740353/29386561536000`.
+
+```js
+assert.strictEqual(primeFrog(), '199740353/29386561536000');
```
# --seed--
@@ -33,12 +39,12 @@ assert.strictEqual(euler329(), 199740353 / 29386561536000);
## --seed-contents--
```js
-function euler329() {
+function primeFrog() {
return true;
}
-euler329();
+primeFrog();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
index c8a3feab39..d79904dedb 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
@@ -8,30 +8,37 @@ dashedName: problem-330-eulers-number
# --description--
-An infinite sequence of real numbers a(n) is defined for all integers n as follows:
+An infinite sequence of real numbers $a(n)$ is defined for all integers $n$ as follows:
-
+$$ a(n) =
+\begin{cases}
+1 & n < 0 \\\\
+\displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0
+\end{cases}
+$$
-For example,a(0) = 11! + 12! + 13! + ... = e − 1 a(1) = e − 11! + 12! + 13! + ... = 2e − 3 a(2) = 2e − 31! + e − 12! + 13! + ... = 72 e − 6
+For example,
-with e = 2.7182818... being Euler's constant.
+$$\begin{align}
+ & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\
+ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\
+ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6
+\end{align}$$
-It can be shown that a(n) is of the form
+with $e = 2.7182818\ldots$ being Euler's constant.
-A(n) e + B(n)n! for integers A(n) and B(n).
+It can be shown that $a(n)$ is of the form $\displaystyle\frac{A(n)e + B(n)}{n!}$ for integers $A(n)$ and $B(n)$.
-For example a(10) =
+For example $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
-328161643 e − 65269448610!.
-
-Find A(109) + B(109) and give your answer mod 77 777 777.
+Find $A({10}^9)$ + $B({10}^9)$ and give your answer $\bmod 77\\,777\\,777$.
# --hints--
-`euler330()` should return 15955822.
+`eulersNumber()` should return `15955822`.
```js
-assert.strictEqual(euler330(), 15955822);
+assert.strictEqual(eulersNumber(), 15955822);
```
# --seed--
@@ -39,12 +46,12 @@ assert.strictEqual(euler330(), 15955822);
## --seed-contents--
```js
-function euler330() {
+function eulersNumber() {
return true;
}
-euler330();
+eulersNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
index 4d3d330a74..95f5391b7f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
@@ -10,24 +10,26 @@ dashedName: problem-331-cross-flips
N×N disks are placed on a square game board. Each disk has a black side and white side.
-At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus 2×N-1 disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus $2 × N - 1$ disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+
+
+
+Each door is operated by a security card. Once you enter a room, the door automatically closes, and that security card cannot be used again. A machine will dispense an unlimited number of cards at the start, but each room (including the starting room) contains scanners. If they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
@@ -18,20 +20,26 @@ However, if you make use of the storage boxes, then escape is possible. For exam
It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
-Let C be the maximum number of cards which can be carried at any time. Let R be the number of rooms to travel through. Let M(C,R) be the minimum number of cards required from the dispensing machine to travel through R rooms carrying up to a maximum of C cards at any time.
+Let $C$ be the maximum number of cards which can be carried at any time.
-For example, M(3,6)=123 and M(4,6)=23.And, ΣM(C,6)=146 for 3 ≤ C ≤ 4.
+Let $R$ be the number of rooms to travel through.
-You are given that ΣM(C,10)=10382 for 3 ≤ C ≤ 10.
+Let $M(C, R)$ be the minimum number of cards required from the dispensing machine to travel through $R$ rooms carrying up to a maximum of $C$ cards at any time.
-Find ΣM(C,30) for 3 ≤ C ≤ 40.
+For example, $M(3, 6) = 123$ and $M(4, 6) = 23$.
+
+And, $\sum M(C, 6) = 146$ for $3 ≤ C ≤ 4$.
+
+You are given that $\sum M(C, 10) = 10382$ for $3 ≤ C ≤ 10$.
+
+Find $\sum M(C, 30)$ for $3 ≤ C ≤ 40$.
# --hints--
-`euler327()` should return 34315549139516.
+`roomsOfDoom()` should return `34315549139516`.
```js
-assert.strictEqual(euler327(), 34315549139516);
+assert.strictEqual(roomsOfDoom(), 34315549139516);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler327(), 34315549139516);
## --seed-contents--
```js
-function euler327() {
+function roomsOfDoom() {
return true;
}
-euler327();
+roomsOfDoom();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
index 4a00f455cc..7cb9e0d86e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
@@ -8,32 +8,32 @@ dashedName: problem-328-lowest-cost-search
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., n} by asking questions.
+We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers:
-Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers: "Your guess is lower than the hidden number", or
+- "Your guess is lower than the hidden number", or
+- "Yes, that's it!", or
+- "Your guess is higher than the hidden number".
-"Yes, that's it!", or
+Given the value of $n$, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
-"Your guess is higher than the hidden number".
+If $n = 3$, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
-Given the value of n, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
+If $n = 8$, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be $4 + 6 + 7 = \mathbf{\color{red}{17}}$.
-If n=3, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
+We can improve considerably the worst-case cost for $n = 8$, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of $5 + 7 = \mathbf{\color{blue}{12}}$). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of $5 + 3 + 1 = \mathbf{\color{blue}{9}}$. Since $\mathbf{\color{blue}{12 > 9}}$, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for $n = 8$.
-If n=8, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be 4+6+7=17.
+Let $C(n)$ be the worst-case cost achieved by an optimal strategy for $n$, as described above. Thus $C(1) = 0$, $C(2) = 1$, $C(3) = 2$ and $C(8) = 12$.
-We can improve considerably the worst-case cost for n=8, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of 5+7=12). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of 5+3+1=9. Since 12>9, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for n=8.
+Similarly, $C(100) = 400$ and $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$.
-Let C(n) be the worst-case cost achieved by an optimal strategy for n, as described above. Thus C(1) = 0, C(2) = 1, C(3) = 2 and C(8) = 12. Similarly, C(100) = 400 and C(n) = 17575.
-
-Find C(n).
+Find $\displaystyle\sum_{n = 1}^{200\\,000} C(n)$.
# --hints--
-`euler328()` should return 260511850222.
+`lowestCostSearch()` should return `260511850222`.
```js
-assert.strictEqual(euler328(), 260511850222);
+assert.strictEqual(lowestCostSearch(), 260511850222);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler328(), 260511850222);
## --seed-contents--
```js
-function euler328() {
+function lowestCostSearch() {
return true;
}
-euler328();
+lowestCostSearch();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
index 6b1e185daf..54f72db23f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
@@ -12,20 +12,26 @@ Susan has a prime frog.
Her frog is jumping around over 500 squares numbered 1 to 500.
-He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range \[1;500].(if it lands at either end, it automatically jumps to the only available square on the next move.)
+He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range [1;500]. (if it lands at either end, it automatically jumps to the only available square on the next move.)
-When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability 2/3 or 'N' (NOT PRIME) with probability 1/3 just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability 1/3 or 'N' with probability 2/3 just before jumping to the next square.
+When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability $\frac{2}{3}$ or 'N' (NOT PRIME) with probability $\frac{1}{3}$ just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability $\frac{1}{3}$ or 'N' with probability $\frac{2}{3}$ just before jumping to the next square.
Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
-Give your answer as a fraction p/q in reduced form.
+Give your answer as a string as a fraction `p/q` in reduced form.
# --hints--
-`euler329()` should return 199740353 / 29386561536000.
+`primeFrog()` should return a string.
```js
-assert.strictEqual(euler329(), 199740353 / 29386561536000);
+assert(typeof primeFrog() === 'string');
+```
+
+`primeFrog()` should return the string `199740353/29386561536000`.
+
+```js
+assert.strictEqual(primeFrog(), '199740353/29386561536000');
```
# --seed--
@@ -33,12 +39,12 @@ assert.strictEqual(euler329(), 199740353 / 29386561536000);
## --seed-contents--
```js
-function euler329() {
+function primeFrog() {
return true;
}
-euler329();
+primeFrog();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
index c8a3feab39..d79904dedb 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
@@ -8,30 +8,37 @@ dashedName: problem-330-eulers-number
# --description--
-An infinite sequence of real numbers a(n) is defined for all integers n as follows:
+An infinite sequence of real numbers $a(n)$ is defined for all integers $n$ as follows:
-
+$$ a(n) =
+\begin{cases}
+1 & n < 0 \\\\
+\displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0
+\end{cases}
+$$
-For example,a(0) = 11! + 12! + 13! + ... = e − 1 a(1) = e − 11! + 12! + 13! + ... = 2e − 3 a(2) = 2e − 31! + e − 12! + 13! + ... = 72 e − 6
+For example,
-with e = 2.7182818... being Euler's constant.
+$$\begin{align}
+ & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\
+ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\
+ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6
+\end{align}$$
-It can be shown that a(n) is of the form
+with $e = 2.7182818\ldots$ being Euler's constant.
-A(n) e + B(n)n! for integers A(n) and B(n).
+It can be shown that $a(n)$ is of the form $\displaystyle\frac{A(n)e + B(n)}{n!}$ for integers $A(n)$ and $B(n)$.
-For example a(10) =
+For example $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
-328161643 e − 65269448610!.
-
-Find A(109) + B(109) and give your answer mod 77 777 777.
+Find $A({10}^9)$ + $B({10}^9)$ and give your answer $\bmod 77\\,777\\,777$.
# --hints--
-`euler330()` should return 15955822.
+`eulersNumber()` should return `15955822`.
```js
-assert.strictEqual(euler330(), 15955822);
+assert.strictEqual(eulersNumber(), 15955822);
```
# --seed--
@@ -39,12 +46,12 @@ assert.strictEqual(euler330(), 15955822);
## --seed-contents--
```js
-function euler330() {
+function eulersNumber() {
return true;
}
-euler330();
+eulersNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
index 4d3d330a74..95f5391b7f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
@@ -10,24 +10,26 @@ dashedName: problem-331-cross-flips
N×N disks are placed on a square game board. Each disk has a black side and white side.
-At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus 2×N-1 disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus $2 × N - 1$ disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+
+ It can be proven that 3 is the minimal number of turns to finish this game.
-The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+The bottom left disk on the $N×N$ board has coordinates (0, 0); the bottom right disk has coordinates ($N - 1$,$0$) and the top left disk has coordinates ($0$,$N - 1$).
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Let $C_N$ be the following configuration of a board with $N × N$disks: A disk at ($x$, $y$) satisfying $N - 1 \le \sqrt{x^2 + y^2} \lt N$, shows its black side; otherwise, it shows its white side. $C_5$ is shown above.
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Let $T(N)$ be the minimal number of turns to finish a game starting from configuration $C_N$ or 0 if configuration $C_N$ is unsolvable. We have shown that $T(5) = 3$. You are also given that $T(10) = 29$ and $T(1\\,000) = 395\\,253$.
-Find .
+Find $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` should return `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..c09640cdef 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -10,18 +10,26 @@ dashedName: problem-332-spherical-triangles
A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+
It can be proven that 3 is the minimal number of turns to finish this game.
-The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+The bottom left disk on the $N×N$ board has coordinates (0, 0); the bottom right disk has coordinates ($N - 1$,$0$) and the top left disk has coordinates ($0$,$N - 1$).
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Let $C_N$ be the following configuration of a board with $N × N$disks: A disk at ($x$, $y$) satisfying $N - 1 \le \sqrt{x^2 + y^2} \lt N$, shows its black side; otherwise, it shows its white side. $C_5$ is shown above.
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Let $T(N)$ be the minimal number of turns to finish a game starting from configuration $C_N$ or 0 if configuration $C_N$ is unsolvable. We have shown that $T(5) = 3$. You are also given that $T(10) = 29$ and $T(1\\,000) = 395\\,253$.
-Find .
+Find $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` should return `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..c09640cdef 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -10,18 +10,26 @@ dashedName: problem-332-spherical-triangles
A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+ -For example A(14) is 3.294040 rounded to six decimal places.
+Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.
+
+Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are not included in $T(r)$.
+
+Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.
+
+For example $A(14)$ is 3.294040 rounded to six decimal places.
+
+Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` should return `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..35023e9837 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -8,26 +8,31 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as $2^i \times 3^j$, where $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ would not be valid since 2 can divide 6. Neither would the partition $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ since 1 can divide 16. The only valid partition of 17 would be $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Many integers have more than one valid partition, the first being 11 having the following two partitions.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align}
+ & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\
+ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1)
+\end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Let's define $P(n)$ as the number of valid partitions of $n$. For example, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Let's consider only the prime integers $q$ which would have a single valid partition such as $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+The sum of the primes $q <100$ such that $P(q) = 1$ equals 233.
+
+Find the sum of the primes $q < 1\\,000\\,000$ such that $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` should return `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +40,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..bc5e4a11e7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -12,20 +12,30 @@ In Plato's heaven, there exist an infinite number of bowls in a straight line. E
For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
-
+
-For example A(14) is 3.294040 rounded to six decimal places.
+Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.
+
+Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are not included in $T(r)$.
+
+Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.
+
+For example $A(14)$ is 3.294040 rounded to six decimal places.
+
+Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` should return `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..35023e9837 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -8,26 +8,31 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as $2^i \times 3^j$, where $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ would not be valid since 2 can divide 6. Neither would the partition $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ since 1 can divide 16. The only valid partition of 17 would be $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Many integers have more than one valid partition, the first being 11 having the following two partitions.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align}
+ & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\
+ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1)
+\end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Let's define $P(n)$ as the number of valid partitions of $n$. For example, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Let's consider only the prime integers $q$ which would have a single valid partition such as $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+The sum of the primes $q <100$ such that $P(q) = 1$ equals 233.
+
+Find the sum of the primes $q < 1\\,000\\,000$ such that $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` should return `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +40,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..bc5e4a11e7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -12,20 +12,30 @@ In Plato's heaven, there exist an infinite number of bowls in a straight line. E
For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
-
+ -You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+You are given the following sequences:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align}
+ & t_0 = 123456, \\\\
+ & t_i = \begin{cases}
+ \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\
+ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd}
+ \end{cases} \\\\
+ & \qquad \text{where $⌊x⌋$ is the floor function and $\oplus$ is the bitwise XOR operator.} \\\\
+ & b_i = (t_i\bmod 2^{11}) + 1.
+\end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+The first two terms of the last sequence are $b_1 = 289$ and $b_2 = 145$. If we start with $b_1$ and $b_2$ beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+
+Consider now 1500 adjacent bowls containing $b_1, b_2, \ldots, b_{1500}$ beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` should return `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +43,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..f20d369ff8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -10,18 +10,20 @@ dashedName: problem-335-gathering-the-beans
Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+
-You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+You are given the following sequences:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align}
+ & t_0 = 123456, \\\\
+ & t_i = \begin{cases}
+ \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\
+ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd}
+ \end{cases} \\\\
+ & \qquad \text{where $⌊x⌋$ is the floor function and $\oplus$ is the bitwise XOR operator.} \\\\
+ & b_i = (t_i\bmod 2^{11}) + 1.
+\end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+The first two terms of the last sequence are $b_1 = 289$ and $b_2 = 145$. If we start with $b_1$ and $b_2$ beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+
+Consider now 1500 adjacent bowls containing $b_1, b_2, \ldots, b_{1500}$ beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` should return `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +43,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..f20d369ff8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -10,18 +10,20 @@ dashedName: problem-335-gathering-the-beans
Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+ +
So with 5 bowls it takes Peter 15 moves to return to the initial situation.
-Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Let $M(x)$ represent the number of moves required to return to the initial situation, starting with $x$ bowls. Thus, $M(5) = 15$. It can also be verified that $M(100) = 10920$.
-Find M(2k+1). Give your answer modulo 79.
+Find $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Give your answer modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` should return `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..e767debe05 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+A train is used to transport four carriages in the order: $ABCD$. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+To rearrange the carriages, they are all shunted onto a large rotating turntable. After the carriages are uncoupled at a specific point, the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180°. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Some arrangements, such as $ADCB$, can be solved easily: the carriages are separated between $A$ and $D$, and after $DCB$ are rotated the correct order has been achieved.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage $A$ in the correct place, then carriage $B$, and so on.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are $DACB$ and $DBAC$; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for $DACB$ is shown below.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+
+
So with 5 bowls it takes Peter 15 moves to return to the initial situation.
-Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Let $M(x)$ represent the number of moves required to return to the initial situation, starting with $x$ bowls. Thus, $M(5) = 15$. It can also be verified that $M(100) = 10920$.
-Find M(2k+1). Give your answer modulo 79.
+Find $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Give your answer modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` should return `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..e767debe05 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+A train is used to transport four carriages in the order: $ABCD$. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+To rearrange the carriages, they are all shunted onto a large rotating turntable. After the carriages are uncoupled at a specific point, the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180°. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Some arrangements, such as $ADCB$, can be solved easily: the carriages are separated between $A$ and $D$, and after $DCB$ are rotated the correct order has been achieved.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage $A$ in the correct place, then carriage $B$, and so on.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are $DACB$ and $DBAC$; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for $DACB$ is shown below.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+ -Find the 2011th lexicographic maximix arrangement for eleven carriages.
+It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is $DFAECB$.
+
+Find the ${2011}^{\text{th}}$ lexicographic maximix arrangement for eleven carriages.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` should return a string.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` should return the string `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..a0298d4170 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Let $\\{a_1, a_2, \ldots, a_n\\}$ be an integer sequence of length $n$ such that:
-a1 = 6
+- $a_1 = 6$
+- for all $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denotes Euler's totient function.
-Let S(N) be the number of such sequences with an ≤ N.
+Let $S(N)$ be the number of such sequences with $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+For example, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+We can verify that $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Find $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` should return `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..7039c9e8af 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+A rectangular sheet of grid paper with integer dimensions $w$ × $h$ is given. Its grid spacing is 1.
When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+For example, from a sheet with dimensions 9 × 4, we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+
-Find the 2011th lexicographic maximix arrangement for eleven carriages.
+It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is $DFAECB$.
+
+Find the ${2011}^{\text{th}}$ lexicographic maximix arrangement for eleven carriages.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` should return a string.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` should return the string `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..a0298d4170 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Let $\\{a_1, a_2, \ldots, a_n\\}$ be an integer sequence of length $n$ such that:
-a1 = 6
+- $a_1 = 6$
+- for all $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denotes Euler's totient function.
-Let S(N) be the number of such sequences with an ≤ N.
+Let $S(N)$ be the number of such sequences with $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+For example, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+We can verify that $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Find $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` should return `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..7039c9e8af 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+A rectangular sheet of grid paper with integer dimensions $w$ × $h$ is given. Its grid spacing is 1.
When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+For example, from a sheet with dimensions 9 × 4, we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+ -For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Similarly, from a sheet with dimensions 9 × 8, we can make rectangles with dimensions 18 × 4 and 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+For a pair $w$ and $h$, let $F(w, h)$ be the number of distinct rectangles that can be made from a sheet with dimensions $w$ × $h$. For example, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ and $F(9, 8) = 2$. Note that rectangles congruent to the initial one are not counted in $F(w, h)$. Note also that rectangles with dimensions $w$ × $h$ and dimensions $h$ × $w$ are not considered distinct.
-Find G(1012). Give your answer modulo 108.
+For an integer $N$, let $G(N)$ be the sum of $F(w, h)$ for all pairs $w$ and $h$ which satisfy $0 < h ≤ w ≤ N$. We can verify that $G(10) = 55$, $G({10}^3) = 971\\,745$ and $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Find $G({10}^{12})$. Give your answer modulo ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` should return `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..c080309b34 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black." - Peredur the Son of Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Initially, each flock consists of $n$ sheep. Each sheep (regardless of color) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let $E(n)$ be the expected final number of black sheep if Peredur uses an optimal strategy.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+You are given that $E(5) = 6.871346$ rounded to 6 places behind the decimal point.
+
+Find $E(10\\,000)$ and give your answer rounded to 6 places behind the decimal point.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` should return `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..64a26640d0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -8,24 +8,25 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+For fixed integers $a$, $b$, $c$, define the crazy function $F(n)$ as follows:
-F(n) = n - c for all n > b
+$$\begin{align}
+ & F(n) = n - c \\;\text{ for all } n > b \\\\
+ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ for all } n ≤ b.
+\end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Also, define $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+For example, if $a = 50$, $b = 2000$ and $c = 40$, then $F(0) = 3240$ and $F(2000) = 2040$. Also, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Find the last 9 digits of $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` should return `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--
-For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Similarly, from a sheet with dimensions 9 × 8, we can make rectangles with dimensions 18 × 4 and 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+For a pair $w$ and $h$, let $F(w, h)$ be the number of distinct rectangles that can be made from a sheet with dimensions $w$ × $h$. For example, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ and $F(9, 8) = 2$. Note that rectangles congruent to the initial one are not counted in $F(w, h)$. Note also that rectangles with dimensions $w$ × $h$ and dimensions $h$ × $w$ are not considered distinct.
-Find G(1012). Give your answer modulo 108.
+For an integer $N$, let $G(N)$ be the sum of $F(w, h)$ for all pairs $w$ and $h$ which satisfy $0 < h ≤ w ≤ N$. We can verify that $G(10) = 55$, $G({10}^3) = 971\\,745$ and $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Find $G({10}^{12})$. Give your answer modulo ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` should return `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..c080309b34 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black." - Peredur the Son of Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Initially, each flock consists of $n$ sheep. Each sheep (regardless of color) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let $E(n)$ be the expected final number of black sheep if Peredur uses an optimal strategy.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+You are given that $E(5) = 6.871346$ rounded to 6 places behind the decimal point.
+
+Find $E(10\\,000)$ and give your answer rounded to 6 places behind the decimal point.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` should return `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..64a26640d0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -8,24 +8,25 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+For fixed integers $a$, $b$, $c$, define the crazy function $F(n)$ as follows:
-F(n) = n - c for all n > b
+$$\begin{align}
+ & F(n) = n - c \\;\text{ for all } n > b \\\\
+ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ for all } n ≤ b.
+\end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Also, define $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+For example, if $a = 50$, $b = 2000$ and $c = 40$, then $F(0) = 3240$ and $F(2000) = 2040$. Also, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Find the last 9 digits of $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` should return `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +34,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--