Design changes and elaborated info on 2D Shapes (#34519)
-Initially, some of the headings were not formatted as headings, so emphasising the headers as strong was suitable -Moreover, it was written that the diagonals of a rectangle is "mutually perpendicular", which is not true for a rectangle, so I removed it to avoid confusion -Changed the mathematical equations through inserting "" and using LaTex Equation Editor to copy the image address of the equation into the round brackets -Added more info about triangles by specifying the types of triangles -Added info on a Trapezium as a 2D Polygon
This commit is contained in:
committed by
 The Coding Aviator
The Coding Aviator
parent
2dac1788be
commit
23dc3cc246
@ -1,58 +1,63 @@
|
|||||||
---
|
---
|
||||||
title: 2d Shapes Polygons and More
|
title: 2D Shapes Polygons and More
|
||||||
---
|
---
|
||||||
|
|
||||||
## 2d Shapes Polygons and More
|
# 2D Shapes Polygons and More
|
||||||
'2D' stands for 2-dimensional. A 2D shape is any shape that has two dimensions. Think about what it means to have two dimensions for a moment. If we had only one dimension to work with, we could only move backwards or forwards in a line. A line is one-dimensional. If we had two dimensions, on the other hand, we could go forwards and backwards in a line and turn in any direction to start a new line. We are essentially able to travel anywhere on a flat surface. In mathematics, a flat surface is called a plane. A plane is one example of a two-dimensional shape. A plane is essentially the largest sheet of paper you will ever find. In fact, it is a sheet of paper so large that it never ends. One way of thinking about 2D shapes is anything that lays flat on a piece of paper.
|
'2D' stands for 2-Dimensional. A 2D shape is any shape that has two dimensions. Think about what it means to have two dimensions for a moment. If we had only one dimension to work with, we could only move backwards or forwards in a line. A line is one-dimensional. If we had two dimensions, on the other hand, we could go forwards and backwards in a line and turn in any direction to start a new line. We are essentially able to travel anywhere on a flat surface. In mathematics, a flat surface is called a plane. A plane is one example of a two-dimensional shape. A plane is essentially the largest sheet of paper you will ever find. In fact, it is a sheet of paper so large that it never ends. One way of thinking about 2D shapes is anything that lays flat on a piece of paper.
|
||||||
|
|
||||||
Any n-sided figure, which can be perfectly and wholly traced on a plane is a 2D figure or polygon. This means any figure having all points on a single plane is a planar figure. Some examples are
|
Any n-sided figure (where n represents the number of sides of a 2D polygon), which can be perfectly and wholly traced on a plane is a 2D figure or polygon. This means any figure having all points on a single plane is a planar figure. Some examples are:
|
||||||
|
|
||||||
### Rectangle
|
## Rectangle
|
||||||
Number of sides - 4
|
**Number of sides-** 4
|
||||||
Special Info-
|
|
||||||
Has four sides, with opposite sides parallel and adjacent sides of same or unequal length(a and b)
|
|
||||||
All internal angles are 90 degrees
|
|
||||||
Sum of all internal angles in 360 degrees
|
|
||||||
Diagonals are mutually perpendicular and bisect one another
|
|
||||||
|
|
||||||
<pre>Area - a * b</pre>
|
**Special Info-** A rectangle is a quadrilateral with four sides, where their opposite sides are parallel and adjacent, but each pair of opposite sides needs to have different lengths. All of their interior angles are 90 degrees and the angle sum of their interior angles is 360 degrees.
|
||||||
<pre>Perimeter - 2(a+b)</pre>
|
|
||||||
|
|
||||||
|
**Area-** 
|
||||||
|
(Where the values of  and 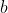 are positive and different numbers)
|
||||||
|
|
||||||
### Square
|
**Perimeter-** 
|
||||||
Number of sides - 4
|
|
||||||
Special Info-
|
|
||||||
Has four sides, with opposite sides parallel and all sides of same length (a)
|
|
||||||
All internal angles are 90 degrees
|
|
||||||
Sum of all internal angles in 360 degrees
|
|
||||||
Diagonals are mutually perpendicular and bisect one another
|
|
||||||
|
|
||||||
<pre>Area - a*a</pre>
|
## Square
|
||||||
<pre>Perimeter - 4*a</pre>
|
**Number of sides-** 4
|
||||||
|
|
||||||
|
**Special Info-** A square has four sides of equal length and parallel opposites sides. All of their interior angles are 90 degrees each and the angle sum of their interior angles is 360 degrees. The diagonals are mutually perpendicular and bisect one another, which also coincidentally proves that a square is a parallelogram through being a 4 sided polygon with 2 pair of equal opposite sides and 2 pairs of equal opposite angles.
|
||||||
|
|
||||||
|
**Area-** 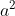 (Where  represents the side length of the square)
|
||||||
|
|
||||||
|
**Perimeter-** 
|
||||||
|
|
||||||
### Triangle
|
### Triangle
|
||||||
Number of sides - 3
|
**Number of sides-** 3
|
||||||
Special Info-
|
|
||||||
Has a height which is the perpendicular distance from a vertex to the opposite side(base), can lie inside or outside the triangle
|
|
||||||
Sum of all angles is 180 degrees
|
|
||||||
|
|
||||||
<pre>Area - 1/2(base * height)</pre>
|
**Special Info-** A triangle is a 3 sided polygon with an angle sum of 180 degrees that can either be:
|
||||||
|
|
||||||
|
* Isosceles- A triangle with 2 equal sides and 1 side with a different length where they also have one pair of equal interior angles. Additionally, the height of the isosceles triangle is perpendicular to the base as well.
|
||||||
|
* Scalene- A triangle where all 3 of their sides are different lengths with 3 completely different interior angles.
|
||||||
|
* Equilateral - A triangle where all 3 of their sides are equal, as well as their interior angles. Coincidentally, this proves that an equilateral triangle can also be an isosceles triangle through having 2 equal sides and 2 equal interior angles.
|
||||||
|
* Right-angled triangle - A triangle with a right angle and two other interior angles that can either be different or equal, but if the two angles are equal, it suggests that the sides opposite to these two equal angles are also equal, which proves that this specific triangle can also become an isosceles triangle.
|
||||||
|
|
||||||
### Circle
|
**Area-** 
|
||||||
Number of sides - Infinite (A polygon with infinite number of sides is a circle)
|
|
||||||
Special Info-
|
|
||||||
Angle through center in 360
|
|
||||||
Always defined from a point known as center of circle
|
|
||||||
Perpendicular distance from the center to a point on periphery is called the radius(r)
|
|
||||||
Any line passing through the circle and touching the periphery at both ends is called a chord
|
|
||||||
Chord passing through the center of the circle is diameter
|
|
||||||
|
|
||||||
<pre>Area - {pi} * r * r</pre>
|
**Perimeter-** Side 1 + Side 2 + Side 3
|
||||||
<pre>Perimeter - 2 * {pi} * r </pre>
|
|
||||||
|
|
||||||
|
## Circle
|
||||||
|
**Number of sides-** Infinite (A polygon with infinite number of sides is a circle)
|
||||||
|
**Special Info-** The angle of the circle through its center is 360 degrees. Some of the features include:
|
||||||
|
|
||||||
|
* Perpendicular distance from the center to a point on periphery is called the radius(r)
|
||||||
|
* Any line passing through the circle and touching the periphery at both ends is called a chord.
|
||||||
|
* Chord passing through the center of the circle is diameter
|
||||||
|
|
||||||
#### More Information:
|
**Area-** 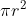
|
||||||
|
|
||||||
|
**Perimeter-** 
|
||||||
|
|
||||||
|
## Trapezium
|
||||||
|
**Number of sides-** 4
|
||||||
|
|
||||||
|
**Special info-** A trapezium is a 4 sided polygon with one pair of parallel sides and one pair of non-parallel sides, where the parallel sides are never equal, but the non-parallel sides can either be equal or not.
|
||||||
|
|
||||||
|
**Area-** 
|
||||||
|
|
||||||
|
**Perimeter-** Side 1 + Side 2 + Side 3 + Side 4
|
||||||
|
|
||||||
|
|||||||
Reference in New Issue
Block a user