diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-329-prime-frog.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
index 6b1e185daf..dbefe0edbd 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
@@ -1,6 +1,6 @@
---
id: 5900f4b51000cf542c50ffc8
-title: 'Problem 329: Prime Frog'
+title: 'Problema 329: Rana prima'
challengeType: 5
forumTopicId: 301986
dashedName: problem-329-prime-frog
@@ -8,24 +8,30 @@ dashedName: problem-329-prime-frog
# --description--
-Susan has a prime frog.
+Susan ha una rana prima.
-Her frog is jumping around over 500 squares numbered 1 to 500.
+La sua rana sta saltando su 500 quadrati numerati da 1 a 500.
-He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range \[1;500].(if it lands at either end, it automatically jumps to the only available square on the next move.)
+Essa può solo saltare di un quadrato a sinistra o a destra, con la stessa probabilità, e non può saltare fuori dall'intervallo [1,500]. (se atterra alle estremità, salta automaticamente all'unico quadrato disponibile alla mossa successiva.)
-When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability 2/3 or 'N' (NOT PRIME) with probability 1/3 just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability 1/3 or 'N' with probability 2/3 just before jumping to the next square.
+Quando è su un quadrato con un numero primo su di esso, gracida 'P' (PRIMO) con probabilità $\frac{2}{3}$ o 'N' (NON PRIMO) con probabilità $\frac{1}{3}$ poco prima di saltare al quadrato successivo. Quando è su un quadrato con un numero su di esso che non è un primo gracida 'P' con probabilità $\frac{1}{3}$ o 'N' con probabilità $\frac{2}{3}$ poco prima di saltare al quadrato successivo.
-Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
+Dato che la posizione di partenza della rana è casuale con la stessa probabilità per ogni quadrato, e dato che sente i suoi primi 15 gracidii, qual è la probabilità di sentire la sequenza PPPPNPPPNPN?
-Give your answer as a fraction p/q in reduced form.
+Dai la tua risposta sotto forma di stringa come una frazione `p/q` in forma semplificata.
# --hints--
-`euler329()` should return 199740353 / 29386561536000.
+`primeFrog()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler329(), 199740353 / 29386561536000);
+assert(typeof primeFrog() === 'string');
+```
+
+`primeFrog()` dovrebbe restiturie la stringa `199740353/29386561536000`.
+
+```js
+assert.strictEqual(primeFrog(), '199740353/29386561536000');
```
# --seed--
@@ -33,12 +39,12 @@ assert.strictEqual(euler329(), 199740353 / 29386561536000);
## --seed-contents--
```js
-function euler329() {
+function primeFrog() {
return true;
}
-euler329();
+primeFrog();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-330-eulers-number.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
index c8a3feab39..3a2f38f5e5 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
@@ -1,6 +1,6 @@
---
id: 5900f4b71000cf542c50ffc9
-title: 'Problem 330: Euler''s Number'
+title: 'Problema 330: Numero di Eulero'
challengeType: 5
forumTopicId: 301988
dashedName: problem-330-eulers-number
@@ -8,30 +8,28 @@ dashedName: problem-330-eulers-number
# --description--
-An infinite sequence of real numbers a(n) is defined for all integers n as follows:
+Una sequenza infinita di numeri reali $a(n)$ è definita per tutti gli interi $n$ come segue:
-
+$$ a(n) = \begin{cases} 1 & n < 0 \\\\ \displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0 \end{cases} $$
-For example,a(0) = 11! + 12! + 13! + ... = e − 1 a(1) = e − 11! + 12! + 13! + ... = 2e − 3 a(2) = 2e − 31! + e − 12! + 13! + ... = 72 e − 6
+Per esempio,
-with e = 2.7182818... being Euler's constant.
+$$\begin{align} & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6 \end{align}$$
-It can be shown that a(n) is of the form
+dove $e = 2.7182818\ldots$ è costante di Euler.
-A(n) e + B(n)n! for integers A(n) and B(n).
+Può essere dimostrato che $a(n)$ è della forma $\displaystyle\frac{A(n)e + B(n)}{n!}$ per i numeri interi $A(n)$ e $B(n)$.
-For example a(10) =
+Per esempio $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
-328161643 e − 65269448610!.
-
-Find A(109) + B(109) and give your answer mod 77 777 777.
+Trova $A({10}^9)$ + $B({10}^9)$ e dai la tua risposta $\bmod 77\\,777\\,777$.
# --hints--
-`euler330()` should return 15955822.
+`eulersNumber()` dovrebbe restituire `15955822`.
```js
-assert.strictEqual(euler330(), 15955822);
+assert.strictEqual(eulersNumber(), 15955822);
```
# --seed--
@@ -39,12 +37,12 @@ assert.strictEqual(euler330(), 15955822);
## --seed-contents--
```js
-function euler330() {
+function eulersNumber() {
return true;
}
-euler330();
+eulersNumber();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-331-cross-flips.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
index 4d3d330a74..f3c471fe60 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
@@ -1,6 +1,6 @@
---
id: 5900f4b71000cf542c50ffca
-title: 'Problem 331: Cross flips'
+title: 'Problema 331: Ribaltamenti a croce'
challengeType: 5
forumTopicId: 301989
dashedName: problem-331-cross-flips
@@ -8,26 +8,28 @@ dashedName: problem-331-cross-flips
# --description--
-N×N disks are placed on a square game board. Each disk has a black side and white side.
+N×N dischi sono posizionati su un tabellone da gioco quadrato. Ogni disco ha un lato nero e un lato bianco.
-At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus 2×N-1 disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+Ad ogni turno, si può scegliere un disco e capovolgere tutti i dischi nella stessa riga e la stessa colonna di questo disco: così $2 × N - 1$ dischi vengono capovolti. Il gioco termina quando tutti i dischi mostrano il loro lato bianco. L'esempio seguente mostra una partita su una griglia 5×5.
-It can be proven that 3 is the minimal number of turns to finish this game.
+ -The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+Si può dimostrare che 3 è il numero minimo di turni per finire questo gioco.
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Il disco in basso a sinistra sulla scheda $N×N$ ha coordinate (0, 0); il disco in basso a destra ha coordinate ($N - 1$,$0$) e il disco in alto a sinistra ha coordinate ($0$,$N - 1$).
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Sia $C_N$ la seguente configurazione di una scheda con $N × N$ dischi: Un disco a ($x$, $y$) soddisfacente $N - 1 \le \sqrt{x^2 + y^2} \lt N$, mostra il suo lato nero; altrimenti, mostra il suo lato bianco. $C_5$ è mostrato sopra.
-Find .
+Sia $T(N)$ il numero minimo di turni per completare una partita che parte dalla configurazione $C_N$ o 0 se la configurazione $C_N$ è irrisolvibile. Abbiamo mostrato che $T(5) = 3$. Ti viene anche dato che $T(10) = 29$ e $T(1\\,000) = 395\\,253$.
+
+Trova $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` dovrebbe restituire `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..9a6be05971 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcb
-title: 'Problem 332: Spherical triangles'
+title: 'Problema 332: Triangoli sferici'
challengeType: 5
forumTopicId: 301990
dashedName: problem-332-spherical-triangles
@@ -8,20 +8,28 @@ dashedName: problem-332-spherical-triangles
# --description--
-A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
+Un triangolo sferico è una figura formata sulla superficie di una sfera da tre grandi archi circolari che intersecano a coppia in tre vertici.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+
-The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+Si può dimostrare che 3 è il numero minimo di turni per finire questo gioco.
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Il disco in basso a sinistra sulla scheda $N×N$ ha coordinate (0, 0); il disco in basso a destra ha coordinate ($N - 1$,$0$) e il disco in alto a sinistra ha coordinate ($0$,$N - 1$).
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Sia $C_N$ la seguente configurazione di una scheda con $N × N$ dischi: Un disco a ($x$, $y$) soddisfacente $N - 1 \le \sqrt{x^2 + y^2} \lt N$, mostra il suo lato nero; altrimenti, mostra il suo lato bianco. $C_5$ è mostrato sopra.
-Find .
+Sia $T(N)$ il numero minimo di turni per completare una partita che parte dalla configurazione $C_N$ o 0 se la configurazione $C_N$ è irrisolvibile. Abbiamo mostrato che $T(5) = 3$. Ti viene anche dato che $T(10) = 29$ e $T(1\\,000) = 395\\,253$.
+
+Trova $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` dovrebbe restituire `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..9a6be05971 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcb
-title: 'Problem 332: Spherical triangles'
+title: 'Problema 332: Triangoli sferici'
challengeType: 5
forumTopicId: 301990
dashedName: problem-332-spherical-triangles
@@ -8,20 +8,28 @@ dashedName: problem-332-spherical-triangles
# --description--
-A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
+Un triangolo sferico è una figura formata sulla superficie di una sfera da tre grandi archi circolari che intersecano a coppia in tre vertici.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+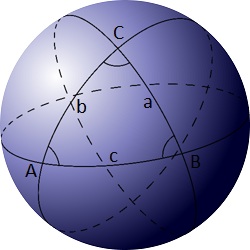 -For example A(14) is 3.294040 rounded to six decimal places.
+Sia $C(r)$ la sfera di centro (0,0,0) e raggio $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Sia $Z(r)$ il set di punti sulla superficie di $C(r)$ con coordinate intere.
+
+Sia $T(r)$ il set di triangoli sferici con vertici in $Z(r)$. Triangoli sferici degeneri, formati da tre punti sullo stesso grande arco, non sono inclusi in $T(r)$.
+
+Sia $A(r)$ l'area del più piccolo triangolo sferico in $T(r)$.
+
+Per esempio, $A(14)$ è 3.294040 arrotondato a sei decimali.
+
+Trova $\displaystyle \sum_{r = 1}^{50} A(r)$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` dovrebbe restituire `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..8b533c9b74 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcc
-title: 'Problem 333: Special partitions'
+title: 'Problema 333: Partizioni speciali'
challengeType: 5
forumTopicId: 301991
dashedName: problem-333-special-partitions
@@ -8,26 +8,28 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+Tutti gli interi positivi possono essere suddivisi in modo tale che ogni termine della partizione possa essere espresso come $2^i \times 3^j$, dove $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Consideriamo solo quelle partizioni dove nessuno dei termini può dividere uno degli altri termini. Ad esempio, la partizione di $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ non sarebbe valida poiché 2 puó dividere 6. Neanche la partizione $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ poiché 1 può dividere 16. L'unica partizione valida di 17 sarebbe $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Molti interi hanno più di una partizione valida, il primo è 11 con le due partizioni seguenti.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align} & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1) \end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Definiamo $P(n)$ come il numero di partizioni valide di $n$. Per esempio, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Consideriamo solo gli interi primi $q$ che avrebbero una singola partizione valida come $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+La somma dei primi $q <100$ tali che $P(q) = 1$ è uguale a 233.
+
+Trova la somma dei primi $q < 1\\,000\\,000$ tali che $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` dovrebbe restituire `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..b2b564d99d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4ba1000cf542c50ffcd
-title: 'Problem 334: Spilling the beans'
+title: 'Problema 334: Versare i fagioli'
challengeType: 5
forumTopicId: 301992
dashedName: problem-334-spilling-the-beans
@@ -8,24 +8,26 @@ dashedName: problem-334-spilling-the-beans
# --description--
-In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.
+Nel paradiso di Platone, esiste un numero infinito di ciotole in linea retta. Ogni ciotola contiene alcuni o nessuno di un numero finito di fagioli. Un bambino gioca un gioco, che permette un solo tipo di mossa: rimuovere due fagioli da qualsiasi ciotola, e metterne uno in ognuna delle due ciotole adiacenti. Il gioco termina quando ogni ciotola contiene uno o nessun fagiolo.
-For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
+Ad esempio, considera due ciotole adiacenti contenenti 2 e 3 fagioli rispettivamente, tutte le altre ciotole sono vuote. Le seguenti otto mosse finiranno il gioco:
-
+
-For example A(14) is 3.294040 rounded to six decimal places.
+Sia $C(r)$ la sfera di centro (0,0,0) e raggio $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Sia $Z(r)$ il set di punti sulla superficie di $C(r)$ con coordinate intere.
+
+Sia $T(r)$ il set di triangoli sferici con vertici in $Z(r)$. Triangoli sferici degeneri, formati da tre punti sullo stesso grande arco, non sono inclusi in $T(r)$.
+
+Sia $A(r)$ l'area del più piccolo triangolo sferico in $T(r)$.
+
+Per esempio, $A(14)$ è 3.294040 arrotondato a sei decimali.
+
+Trova $\displaystyle \sum_{r = 1}^{50} A(r)$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` dovrebbe restituire `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..8b533c9b74 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcc
-title: 'Problem 333: Special partitions'
+title: 'Problema 333: Partizioni speciali'
challengeType: 5
forumTopicId: 301991
dashedName: problem-333-special-partitions
@@ -8,26 +8,28 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+Tutti gli interi positivi possono essere suddivisi in modo tale che ogni termine della partizione possa essere espresso come $2^i \times 3^j$, dove $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Consideriamo solo quelle partizioni dove nessuno dei termini può dividere uno degli altri termini. Ad esempio, la partizione di $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ non sarebbe valida poiché 2 puó dividere 6. Neanche la partizione $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ poiché 1 può dividere 16. L'unica partizione valida di 17 sarebbe $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Molti interi hanno più di una partizione valida, il primo è 11 con le due partizioni seguenti.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align} & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1) \end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Definiamo $P(n)$ come il numero di partizioni valide di $n$. Per esempio, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Consideriamo solo gli interi primi $q$ che avrebbero una singola partizione valida come $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+La somma dei primi $q <100$ tali che $P(q) = 1$ è uguale a 233.
+
+Trova la somma dei primi $q < 1\\,000\\,000$ tali che $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` dovrebbe restituire `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..b2b564d99d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4ba1000cf542c50ffcd
-title: 'Problem 334: Spilling the beans'
+title: 'Problema 334: Versare i fagioli'
challengeType: 5
forumTopicId: 301992
dashedName: problem-334-spilling-the-beans
@@ -8,24 +8,26 @@ dashedName: problem-334-spilling-the-beans
# --description--
-In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.
+Nel paradiso di Platone, esiste un numero infinito di ciotole in linea retta. Ogni ciotola contiene alcuni o nessuno di un numero finito di fagioli. Un bambino gioca un gioco, che permette un solo tipo di mossa: rimuovere due fagioli da qualsiasi ciotola, e metterne uno in ognuna delle due ciotole adiacenti. Il gioco termina quando ogni ciotola contiene uno o nessun fagiolo.
-For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
+Ad esempio, considera due ciotole adiacenti contenenti 2 e 3 fagioli rispettivamente, tutte le altre ciotole sono vuote. Le seguenti otto mosse finiranno il gioco:
-
+ -You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+animazione di una partita con due ciotole adiacenti contenenti rispettivamente 2 e 3 fagioli:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd} \end{cases} \\\\ & \qquad \text{dove$⌊x⌋$ è la funzione arrotonda verso il basso e $\oplus$ è l'operatore bitwise XOR.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+I primi due termini dell'ultima sequenza sono $b_1 = 289$ e $b_2 = 145$. Se iniziamo con $b_1$ e $b_2$ fagioli in due ciotole adiacenti, saranno necessarie 3419100 mosse per finire la partita.
+
+Considera ora 1500 ciotole adiacenti contenenti rispettivamente $b_1, b_2, \ldots, b_{1500}$ fagioli, tutte le altre ciotole sono vuote. Trova quante mosse sono necessarie prima che il gioco finisca.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` dovrebbe restituire `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..47c14f189c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffce
-title: 'Problem 335: Gathering the beans'
+title: 'Problema 335: Raccogliere i fagioli'
challengeType: 5
forumTopicId: 301993
dashedName: problem-335-gathering-the-beans
@@ -8,20 +8,22 @@ dashedName: problem-335-gathering-the-beans
# --description--
-Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+Ogni volta che Peter si sente annoiato, mette alcune ciotole, contenenti un fagiolo ciascuno, in un cerchio. Dopo di che, prende tutti i fagioli da una certa ciotola e li rovescia uno ad uno nelle ciotole andando in senso orario. Lo ripete, a partire dalla ciotola in cui ha lasciato cadere l'ultimo fagiolo, fino a quando la situazione iniziale appare di nuovo. Ad esempio con 5 ciotole agisce come segue:
-So with 5 bowls it takes Peter 15 moves to return to the initial situation.
+
-You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+animazione di una partita con due ciotole adiacenti contenenti rispettivamente 2 e 3 fagioli:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd} \end{cases} \\\\ & \qquad \text{dove$⌊x⌋$ è la funzione arrotonda verso il basso e $\oplus$ è l'operatore bitwise XOR.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+I primi due termini dell'ultima sequenza sono $b_1 = 289$ e $b_2 = 145$. Se iniziamo con $b_1$ e $b_2$ fagioli in due ciotole adiacenti, saranno necessarie 3419100 mosse per finire la partita.
+
+Considera ora 1500 ciotole adiacenti contenenti rispettivamente $b_1, b_2, \ldots, b_{1500}$ fagioli, tutte le altre ciotole sono vuote. Trova quante mosse sono necessarie prima che il gioco finisca.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` dovrebbe restituire `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..47c14f189c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffce
-title: 'Problem 335: Gathering the beans'
+title: 'Problema 335: Raccogliere i fagioli'
challengeType: 5
forumTopicId: 301993
dashedName: problem-335-gathering-the-beans
@@ -8,20 +8,22 @@ dashedName: problem-335-gathering-the-beans
# --description--
-Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+Ogni volta che Peter si sente annoiato, mette alcune ciotole, contenenti un fagiolo ciascuno, in un cerchio. Dopo di che, prende tutti i fagioli da una certa ciotola e li rovescia uno ad uno nelle ciotole andando in senso orario. Lo ripete, a partire dalla ciotola in cui ha lasciato cadere l'ultimo fagiolo, fino a quando la situazione iniziale appare di nuovo. Ad esempio con 5 ciotole agisce come segue:
-So with 5 bowls it takes Peter 15 moves to return to the initial situation.
+ -Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Quindi con 5 ciotole servono a Peter 15 mosse per tornare alla situazione iniziale.
-Find M(2k+1). Give your answer modulo 79.
+Lascia che $M(x)$ rappresenti il numero di mosse necessarie per tornare alla situazione iniziale, a partire da $x$ ciotole. Così, $M(5) = 15$. Può anche essere verificato che $M(100) = 10920$.
+
+Trova $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Dai la tua risposta modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` dovrebbe restituire `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..d538ead789 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffcf
-title: 'Problem 336: Maximix Arrangements'
+title: 'Problema 336: Arrangiamenti Maximix'
challengeType: 5
forumTopicId: 301994
dashedName: problem-336-maximix-arrangements
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+Un treno è utilizzato per trasportare quattro carrozze nell'ordine: $ABCD$. Tuttavia, a volte quando il treno arriva per raccogliere le carrozze, esse non sono nell'ordine corretto.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+Per riorganizzare le carrozze, vengono tutte smistate su un grande disco rotante. Dopo che le carrozze sono disaccoppiate in un punto specifico, il treno si allontana dal disco rotante tirando le carrozze ancora attaccate con esso. Le carrozze rimanenti sono ruotate di 180°. Tutte le carrozze vengono poi ricongiunte e questo processo viene ripetuto tutte le volte necessarie a ottenere il minor numero di utilizzi del disco.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Alcune disposizioni, come $ADCB$, possono essere risolte facilmente: le carrozze sono separate tra $A$ e $D$, e dopo che $DCB$ sono stati ruotati l'ordine corretto è stato raggiunto.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+Tuttavia, Simple Simon, il macchinista del treno, non è noto per la sua efficienza, così risolve sempre il problema ottenendo inizialmente il carrello $A$ nel posto corretto, poi la carrozza $B$, e così via.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Usando quattro carrozze, i peggior possibili arrangiamenti per Simon, che chiamiamo maximix, sono $DACB$ e $DBAC$; ognuno richiedente quattro rotazioni (anche se usando l'approccio più efficiente potrebbero essere risolti usando solo tre rotazioni). Il processo che usa per $DACB$ è mostrato sotto.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+
-Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Quindi con 5 ciotole servono a Peter 15 mosse per tornare alla situazione iniziale.
-Find M(2k+1). Give your answer modulo 79.
+Lascia che $M(x)$ rappresenti il numero di mosse necessarie per tornare alla situazione iniziale, a partire da $x$ ciotole. Così, $M(5) = 15$. Può anche essere verificato che $M(100) = 10920$.
+
+Trova $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Dai la tua risposta modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` dovrebbe restituire `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..d538ead789 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffcf
-title: 'Problem 336: Maximix Arrangements'
+title: 'Problema 336: Arrangiamenti Maximix'
challengeType: 5
forumTopicId: 301994
dashedName: problem-336-maximix-arrangements
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+Un treno è utilizzato per trasportare quattro carrozze nell'ordine: $ABCD$. Tuttavia, a volte quando il treno arriva per raccogliere le carrozze, esse non sono nell'ordine corretto.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+Per riorganizzare le carrozze, vengono tutte smistate su un grande disco rotante. Dopo che le carrozze sono disaccoppiate in un punto specifico, il treno si allontana dal disco rotante tirando le carrozze ancora attaccate con esso. Le carrozze rimanenti sono ruotate di 180°. Tutte le carrozze vengono poi ricongiunte e questo processo viene ripetuto tutte le volte necessarie a ottenere il minor numero di utilizzi del disco.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Alcune disposizioni, come $ADCB$, possono essere risolte facilmente: le carrozze sono separate tra $A$ e $D$, e dopo che $DCB$ sono stati ruotati l'ordine corretto è stato raggiunto.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+Tuttavia, Simple Simon, il macchinista del treno, non è noto per la sua efficienza, così risolve sempre il problema ottenendo inizialmente il carrello $A$ nel posto corretto, poi la carrozza $B$, e così via.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Usando quattro carrozze, i peggior possibili arrangiamenti per Simon, che chiamiamo maximix, sono $DACB$ e $DBAC$; ognuno richiedente quattro rotazioni (anche se usando l'approccio più efficiente potrebbero essere risolti usando solo tre rotazioni). Il processo che usa per $DACB$ è mostrato sotto.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+ -Find the 2011th lexicographic maximix arrangement for eleven carriages.
+Possiamo verificare che ci sono 24 arrangiamenti maximix per sei carrozze, di cui il decimo arrangiamento lessicografico maximix è $DFAECB$.
+
+Trova il ${2011}$-simo arrangiamento maximix lessicografico per undici carrozze.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` dovrebbe restituire la stringa `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..77408eb4ca 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd0
-title: 'Problem 337: Totient Stairstep Sequences'
+title: 'Problema 337: Sequenze tozienti a gradino'
challengeType: 5
forumTopicId: 301995
dashedName: problem-337-totient-stairstep-sequences
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Sia $\\{a_1, a_2, \ldots, a_n\\}$ una sequenza di interi di lunghezza $n$ tale che:
-a1 = 6
+- $a_1 = 6$
+- per ogni $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denota la funzione toziente di Eulero.
-Let S(N) be the number of such sequences with an ≤ N.
+Sia $S(N)$ il numero di tali sequenze con $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+Ad esempio, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} e {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+Possiamo verificare che $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Trova $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` dovrebbe restituire `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..af40fc4d91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd1
-title: 'Problem 338: Cutting Rectangular Grid Paper'
+title: 'Problema 338: Tagliare carta a quadretti rettangolare'
challengeType: 5
forumTopicId: 301996
dashedName: problem-338-cutting-rectangular-grid-paper
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+Viene fornito un foglio rettangolare di carta a quadretti con dimensioni intere $w$ × $h$. La spaziatura della griglia è 1.
-When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
+Quando tagliamo il foglio lungo le linee della griglia in due pezzi e riordiniamo quei pezzi senza sovrapposizioni, possiamo creare nuovi rettangoli con dimensioni diverse.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+Ad esempio, da un foglio con dimensioni 9 × 4, possiamo realizzare rettangoli con dimensioni 18 × 2, 12 × 3 e 6 × 6 mediante taglio e riarrangiamento come segue:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+
-Find the 2011th lexicographic maximix arrangement for eleven carriages.
+Possiamo verificare che ci sono 24 arrangiamenti maximix per sei carrozze, di cui il decimo arrangiamento lessicografico maximix è $DFAECB$.
+
+Trova il ${2011}$-simo arrangiamento maximix lessicografico per undici carrozze.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` dovrebbe restituire la stringa `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..77408eb4ca 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd0
-title: 'Problem 337: Totient Stairstep Sequences'
+title: 'Problema 337: Sequenze tozienti a gradino'
challengeType: 5
forumTopicId: 301995
dashedName: problem-337-totient-stairstep-sequences
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Sia $\\{a_1, a_2, \ldots, a_n\\}$ una sequenza di interi di lunghezza $n$ tale che:
-a1 = 6
+- $a_1 = 6$
+- per ogni $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denota la funzione toziente di Eulero.
-Let S(N) be the number of such sequences with an ≤ N.
+Sia $S(N)$ il numero di tali sequenze con $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+Ad esempio, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} e {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+Possiamo verificare che $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Trova $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` dovrebbe restituire `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..af40fc4d91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd1
-title: 'Problem 338: Cutting Rectangular Grid Paper'
+title: 'Problema 338: Tagliare carta a quadretti rettangolare'
challengeType: 5
forumTopicId: 301996
dashedName: problem-338-cutting-rectangular-grid-paper
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+Viene fornito un foglio rettangolare di carta a quadretti con dimensioni intere $w$ × $h$. La spaziatura della griglia è 1.
-When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
+Quando tagliamo il foglio lungo le linee della griglia in due pezzi e riordiniamo quei pezzi senza sovrapposizioni, possiamo creare nuovi rettangoli con dimensioni diverse.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+Ad esempio, da un foglio con dimensioni 9 × 4, possiamo realizzare rettangoli con dimensioni 18 × 2, 12 × 3 e 6 × 6 mediante taglio e riarrangiamento come segue:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+ -For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Allo stesso modo, da un foglio con dimensioni 9 × 8, possiamo realizzare rettangoli con dimensioni 18 × 4 e 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+Per una coppia $w$ e $h$, sia $F(w, h)$ il numero di rettangoli distinti che possono essere fatti da un foglio con dimensioni $w$ × $h$. Per esempio, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ e $F(9, 8) = 2$. Nota che i rettangoli congruenti a quello iniziale non sono contati in $F(w, h)$. Nota anche che i rettangoli con dimensioni $w$ × $h$ e le dimensioni $h$ × $w$ non sono considerati distinti.
-Find G(1012). Give your answer modulo 108.
+Per un intero $N$, sia $G(N)$ la somma di $F(w, h)$ per tutte le coppie $w$ e $h$ che soddisfano $0 < h ≤ w ≤ N$. Possiamo verificare che $G(10) = 55$, $G({10}^3) = 971\\,745$ e $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Trova $G({10}^{12})$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` dovrebbe restituire `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..602ef1c635 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -1,6 +1,6 @@
---
id: 5900f4c01000cf542c50ffd2
-title: 'Problem 339: Peredur fab Efrawg'
+title: 'Problema 339: Peredur fab Efrawg'
challengeType: 5
forumTopicId: 301997
dashedName: problem-339-peredur-fab-efrawg
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"E venne verso una valle, attraverso la quale correva un fiume; e i confini della valle erano boscosi, e su ogni lato del fiume vi erano prati pianeggianti. Da un lato del fiume vide un gregge di pecore bianche, dall'altro un gregge di pecore nere. E ogni volta che una delle pecore bianche belava, una delle pecore nere attraversava e diventava bianca; e quando una delle pecore nere belava, una delle pecore bianche attraversava e diventava nera." - Peredur Figlio di Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Inizialmente, ogni gregge è costituito da $n$ pecore. Ogni pecora (indipendentemente dal colore) è altrettanto probabile che sia la prossima pecora a belare. Dopo che una pecora ha belato e una pecora dall'altro gregge ha attraversato, Peredur può rimuovere un numero di pecore bianche al fine di massimizzare il numero finale previsto di pecore nere. Sia $E(n)$ il numero aspettato finale di pecore nere se Peredur usa una strategia ottimale.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+Ti è dato che $E(5) = 6.871346$ arrotondato a 6 cifre decimali.
+
+Trova $E(10\\,000)$ e dai la tua risposta arrotondata a 6 cifre decimali.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` dovrebbe restituire `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..c6e17627dc 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4c21000cf542c50ffd4
-title: 'Problem 340: Crazy Function'
+title: 'Problema 340: Funzione Pazza'
challengeType: 5
forumTopicId: 301999
dashedName: problem-340-crazy-function
@@ -8,24 +8,22 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+Per gli interi fissati $a$, $b$, $c$, definire la funzione pazza $F(n)$ come segue:
-F(n) = n - c for all n > b
+$$\begin{align} & F(n) = n - c \\;\text{ per ogni } n > b \\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ per ogni } n ≤ b. \end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Inoltre, definisci $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+Per esempio, se $a = 50$, $b = 2000$ e $c = 40$, allora $F(0) = 3240$ e $F(2000) = 2040$. Inoltre, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Trova le ultime 9 cifre di $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` dovrebbe restituire `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
index 740ef0d751..693beaed83 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4c11000cf542c50ffd3
-title: 'Problem 341: Golomb''s self-describing sequence'
+title: 'Problema 341: Sequenza auto-descrittiva di Golomb'
challengeType: 5
forumTopicId: 302000
dashedName: problem-341-golombs-self-describing-sequence
@@ -8,20 +8,22 @@ dashedName: problem-341-golombs-self-describing-sequence
# --description--
-The Golomb's self-describing sequence {G(n)} is the only nondecreasing sequence of natural numbers such that n appears exactly G(n) times in the sequence. The values of G(n) for the first few n are
+La sequenza di auto-descrizione di Golomb ($G(n)$) è l'unica sequenza non decrescente di numeri naturali tali che $n$ appaia esattamente $G(n)$ volte nella sequenza. I valori di $G(n)$ per i primi $n$ sono
-n123456789101112131415…G(n)122334445556666…
+$$\begin{array}{c} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & \ldots \\\\ G(n) & 1 & 2 & 2 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & \ldots \end{array}$$
-You are given that G(103) = 86, G(106) = 6137. You are also given that ΣG(n3) = 153506976 for 1 ≤ n < 103.
+Ti viene dato che $G({10}^3) = 86$, $G({10}^6) = 6137$.
-Find ΣG(n3) for 1 ≤ n < 106.
+Ti viene anche dato che $\sum G(n^3) = 153\\,506\\,976$ per $1 ≤ n < {10}^3$.
+
+Trova $\sum G(n^3)$ per $1 ≤ n < {10}^6$.
# --hints--
-`euler341()` should return 56098610614277016.
+`golombsSequence()` dovrebbe restituire `56098610614277016`.
```js
-assert.strictEqual(euler341(), 56098610614277016);
+assert.strictEqual(golombsSequence(), 56098610614277016);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler341(), 56098610614277016);
## --seed-contents--
```js
-function euler341() {
+function golombsSequence() {
return true;
}
-euler341();
+golombsSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
index 2253ce390f..cbcc7d8c39 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c31000cf542c50ffd5
-title: 'Problem 342: The totient of a square is a cube'
+title: 'Problema 342: Il toziente di un quadrato è un cubo'
challengeType: 5
forumTopicId: 302001
dashedName: problem-342-the-totient-of-a-square-is-a-cube
@@ -8,22 +8,21 @@ dashedName: problem-342-the-totient-of-a-square-is-a-cube
# --description--
-Consider the number 50.
+Considera il numero 50.
-502 = 2500 = 22 × 54, so φ(2500) = 2 × 4 × 53 = 8 × 53 = 23 × 53. 1
+${50}^2 = 2500 = 2^2 × 5^4$, so $φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$. $φ$ denota la funzione toziente di Eulero.
-So 2500 is a square and φ(2500) is a cube.
+Quindi 2500 è un quadrato e $φ(2500)$ è un cubo.
-Find the sum of all numbers n, 1 < n < 1010 such that φ(n2) is a cube.
+Trova la somma di tutti i numeri $n$, $1 < n < {10}^{10}$ in modo che $φ(n^2)$ sia un cubo.
-1 φ denotes Euler's totient function.
# --hints--
-`euler342()` should return 5943040885644.
+`totientOfSquare()` dovrebbe restituire `5943040885644`.
```js
-assert.strictEqual(euler342(), 5943040885644);
+assert.strictEqual(totientOfSquare(), 5943040885644);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler342(), 5943040885644);
## --seed-contents--
```js
-function euler342() {
+function totientOfSquare() {
return true;
}
-euler342();
+totientOfSquare();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
index 3102009e8c..63e1dab730 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4c41000cf542c50ffd6
-title: 'Problem 343: Fractional Sequences'
+title: 'Problema 343: Sequenze frazionarie'
challengeType: 5
forumTopicId: 302002
dashedName: problem-343-fractional-sequences
@@ -8,32 +8,31 @@ dashedName: problem-343-fractional-sequences
# --description--
-For any positive integer k, a finite sequence ai of fractions xi/yi is defined by:
+Per qualsiasi numero intero positivo $k$, una sequenza finita $a_i$ di frazioni $\frac{x_i}{y_i}$ è definita da:
-a1 = 1/k and
+- $a_1 = \displaystyle\frac{1}{k}$ e
+- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ ridotto ai minimi termini per $i > 1$.
-ai = (xi-1+1)/(yi-1-1) reduced to lowest terms for i>1.
+Quando $a_i$ raggiunge un numero intero $n$, la sequenza si ferma. (cioè, quando $y_i = 1$.)
-When ai reaches some integer n, the sequence stops. (That is, when yi=1.)
+Definisci $f(k) = n$.
-Define f(k) = n.
+Per esempio, per $k = 20$:
-For example, for k = 20:
+$$\frac{1}{20} → \frac{2}{19} → \frac{3}{18} = \frac{1}{6} → \frac{2}{5} → \frac{3}{4} → \frac{4}{3} → \frac{5}{2} → \frac{6}{1} = 6$$
-1/20 → 2/19 → 3/18 = 1/6 → 2/5 → 3/4 → 4/3 → 5/2 → 6/1 = 6
+Quindi $f(20) = 6$.
-So f(20) = 6.
+Anche $f(1) = 1$, $f(2) = 2$, $f(3) = 1$ e $\sum f(k^3) = 118\\,937$ per $1 ≤ k ≤ 100$.
-Also f(1) = 1, f(2) = 2, f(3) = 1 and Σf(k3) = 118937 for 1 ≤ k ≤ 100.
-
-Find Σf(k3) for 1 ≤ k ≤ 2×106.
+Trova $\sum f(k^3)$ per $1 ≤ k ≤ 2 × {10}^6$.
# --hints--
-`euler343()` should return 269533451410884200.
+`fractionalSequences()` dovrebbe restituire `269533451410884200`.
```js
-assert.strictEqual(euler343(), 269533451410884200);
+assert.strictEqual(fractionalSequences(), 269533451410884200);
```
# --seed--
@@ -41,12 +40,12 @@ assert.strictEqual(euler343(), 269533451410884200);
## --seed-contents--
```js
-function euler343() {
+function fractionalSequences() {
return true;
}
-euler343();
+fractionalSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
index 9cb8157d07..a94d255151 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffda
-title: 'Problem 345: Matrix Sum'
+title: 'Problema 345: Somma di matrice'
challengeType: 5
forumTopicId: 302004
dashedName: problem-345-matrix-sum
@@ -8,20 +8,22 @@ dashedName: problem-345-matrix-sum
# --description--
-We define the Matrix Sum of a matrix as the maximum sum of matrix elements with each element being the only one in his row and column. For example, the Matrix Sum of the matrix below equals 3315 ( = 863 + 383 + 343 + 959 + 767):
+Definiamo la Somma di Matrice di una matrice come la somma massima di elementi di matrice dove ogni elemento è l'unico nella sua fila e colonna.
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943767 473 103 699 303
+Ad esempio, la somma di matrice della matrice qui sotto è pari a $3315 ( = 863 + 383 + 343 + 959 + 767)$:
-Find the Matrix Sum of:
+$$\begin{array}{rrrrr} 7 & 53 & 183 & 439 & \color{lime}{863} \\\\ 497 & \color{lime}{383} & 563 & 79 & 973 \\\\ 287 & 63 & \color{lime}{343} & 169 & 583 \\\\ 627 & 343 & 773 & \color{lime}{959} & 943 \\\\ \color{lime}{767} & 473 & 103 & 699 & 303 \end{array}$$
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943 767 473 103 699 303 957 703 583 639 913 447 283 463 29 23 487 463 993 119 883 327 493 423 159 743 217 623 3 399 853 407 103 983 89 463 290 516 212 462 350 960 376 682 962 300 780 486 502 912 800 250 346 172 812 350 870 456 192 162 593 473 915 45 989 873 823 965 425 329 803 973 965 905 919 133 673 665 235 509 613 673 815 165 992 326 322 148 972 962 286 255 941 541 265 323 925 281 601 95 973 445 721 11 525 473 65 511 164 138 672 18 428 154 448 848 414 456 310 312 798 104 566 520 302 248 694 976 430 392 198 184 829 373 181 631 101 969 613 840 740 778 458 284 760 390 821 461 843 513 17 901 711 993 293 157 274 94 192 156 574 34 124 4 878 450 476 712 914 838 669 875 299 823 329 699 815 559 813 459 522 788 168 586 966 232 308 833 251 631 107 813 883 451 509 615 77 281 613 459 205 380 274 302 35 805
+Trova la somma di matrice di:
+
+$$\\begin{array}{r} 7 & 53 & 183 & 439 & 863 & 497 & 383 & 563 & 79 & 973 & 287 & 63 & 343 & 169 & 583 \\\\ 627 & 343 & 773 & 959 & 943 & 767 & 473 & 103 & 699 & 303 & 957 & 703 & 583 & 639 & 913 \\\\ 447 & 283 & 463 & 29 & 23 & 487 & 463 & 993 & 119 & 883 & 327 & 493 & 423 & 159 & 743 \\\\ 217 & 623 & 3 & 399 & 853 & 407 & 103 & 983 & 89 & 463 & 290 & 516 & 212 & 462 & 350 \\\\ 960 & 376 & 682 & 962 & 300 & 780 & 486 & 502 & 912 & 800 & 250 & 346 & 172 & 812 & 350 \\\\ 870 & 456 & 192 & 162 & 593 & 473 & 915 & 45 & 989 & 873 & 823 & 965 & 425 & 329 & 803 \\\\ 973 & 965 & 905 & 919 & 133 & 673 & 665 & 235 & 509 & 613 & 673 & 815 & 165 & 992 & 326 \\\\ 322 & 148 & 972 & 962 & 286 & 255 & 941 & 541 & 265 & 323 & 925 & 281 & 601 & 95 & 973 \\\\ 445 & 721 & 11 & 525 & 473 & 65 & 511 & 164 & 138 & 672 & 18 & 428 & 154 & 448 & 848 \\\\ 414 & 456 & 310 & 312 & 798 & 104 & 566 & 520 & 302 & 248 & 694 & 976 & 430 & 392 & 198 \\\\ 184 & 829 & 373 & 181 & 631 & 101 & 969 & 613 & 840 & 740 & 778 & 458 & 284 & 760 & 390 \\\\ 821 & 461 & 843 & 513 & 17 & 901 & 711 & 993 & 293 & 157 & 274 & 94 & 192 & 156 & 574 \\\\ 34 & 124 & 4 & 878 & 450 & 476 & 712 & 914 & 838 & 669 & 875 & 299 & 823 & 329 & 699 \\\\ 815 & 559 & 813 & 459 & 522 & 788 & 168 & 586 & 966 & 232 & 308 & 833 & 251 & 631 & 107 \\\\ 813 & 883 & 451 & 509 & 615 & 77 & 281 & 613 & 459 & 205 & 380 & 274 & 302 & 35 & 805 \end{array}$$
# --hints--
-`euler345()` should return 13938.
+`matrixSum()` dovrebbe restituire `13938`.
```js
-assert.strictEqual(euler345(), 13938);
+assert.strictEqual(matrixSum(), 13938);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler345(), 13938);
## --seed-contents--
```js
-function euler345() {
+function matrixSum() {
return true;
}
-euler345();
+matrixSum();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
index 49a1f6b2c2..844987961a 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
@@ -1,6 +1,6 @@
---
id: 5900f4c71000cf542c50ffd8
-title: 'Problem 346: Strong Repunits'
+title: 'Problema 346: Repunit Forti'
challengeType: 5
forumTopicId: 302005
dashedName: problem-346-strong-repunits
@@ -8,18 +8,18 @@ dashedName: problem-346-strong-repunits
# --description--
-The number 7 is special, because 7 is 111 written in base 2, and 11 written in base 6 (i.e. 710 = 116 = 1112). In other words, 7 is a repunit in at least two bases b > 1.
+Il numero 7 è speciale, perché 7 è 111 scritto in base 2, e 11 scritto in base 6 (cioè $7_{10} = {11}_6 = {111}_2$). In altre parole, 7 è una repunit in almeno due basi $b > 1$.
-We shall call a positive integer with this property a strong repunit. It can be verified that there are 8 strong repunits below 50: {1,7,13,15,21,31,40,43}. Furthermore, the sum of all strong repunits below 1000 equals 15864.
+Chiameremo un numero intero positivo con questa proprietà una forte repunit. Si può verificare che ci sono 8 forti repunit sotto 50: {1, 7, 13, 15, 21, 31, 40, 43}. Inoltre, la somma di tutti i repunit forti sotto 1000 è pari a 15864.
-Find the sum of all strong repunits below 1012.
+Trova la somma di tutti i repunit forti sotto ${10}^{12}$.
# --hints--
-`euler346()` should return 336108797689259260.
+`strongRepunits()` dovrebbe restituire `336108797689259260`.
```js
-assert.strictEqual(euler346(), 336108797689259260);
+assert.strictEqual(strongRepunits(), 336108797689259260);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler346(), 336108797689259260);
## --seed-contents--
```js
-function euler346() {
+function strongRepunits() {
return true;
}
-euler346();
+strongRepunits();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
index 70845508fa..961ba85720 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffd9
-title: 'Problem 347: Largest integer divisible by two primes'
+title: 'Problema 347: Intero più grande divisibile per due primi'
challengeType: 5
forumTopicId: 302006
dashedName: problem-347-largest-integer-divisible-by-two-primes
@@ -8,24 +8,24 @@ dashedName: problem-347-largest-integer-divisible-by-two-primes
# --description--
-The largest integer ≤ 100 that is only divisible by both the primes 2 and 3 is 96, as 96=32\*3=25\*3.
+Il più grande intero $≤ 100$ che è divisibile solo per entrambe i primi 2 e 3 è 96, poiché $96 = 32 \times 3 = 2^5 \times 3$.
-For two distinct primes p and q let M(p,q,N) be the largest positive integer ≤N only divisible
+Per due primi distinti $p$ e $q$ sia $M(p, q, N)$ il più grande intero positivo $≤ N$ divisibile solo per $p$ e $q$ e $M(p, q, N)=0$ se tale numero intero positivo non esiste.
-by both p and q and M(p,q,N)=0 if such a positive integer does not exist.
+Ad es. $M(2, 3, 100) = 96$.
-E.g. M(2,3,100)=96. M(3,5,100)=75 and not 90 because 90 is divisible by 2 ,3 and 5. Also M(2,73,100)=0 because there does not exist a positive integer ≤ 100 that is divisible by both 2 and 73.
+$M(3, 5, 100) = 75$ e non 90 perché 90 è divisibile per 2, 3 e 5. Anche $M(2, 73, 100) = 0$ perché non esiste un numero intero positivo $≤ 100$ che è divisibile sia per 2 che 73.
-Let S(N) be the sum of all distinct M(p,q,N). S(100)=2262.
+Sia $S(N)$ la somma di tutti gli $M(p, q, N)$ distinti. $S(100)=2262$.
-Find S(10 000 000).
+Trova $S(10\\,000\\,000)$.
# --hints--
-`euler347()` should return 11109800204052.
+`integerDivisibleByTwoPrimes()` dovrebbe restituire `11109800204052`.
```js
-assert.strictEqual(euler347(), 11109800204052);
+assert.strictEqual(integerDivisibleByTwoPrimes(), 11109800204052);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler347(), 11109800204052);
## --seed-contents--
```js
-function euler347() {
+function integerDivisibleByTwoPrimes() {
return true;
}
-euler347();
+integerDivisibleByTwoPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
index 2fe6e2bc13..75d443eac6 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffdb
-title: 'Problem 348: Sum of a square and a cube'
+title: 'Problema 348: Somma di un quadrato e di un cubo'
challengeType: 5
forumTopicId: 302007
dashedName: problem-348-sum-of-a-square-and-a-cube
@@ -8,18 +8,22 @@ dashedName: problem-348-sum-of-a-square-and-a-cube
# --description--
-Many numbers can be expressed as the sum of a square and a cube. Some of them in more than one way.
+Molti numeri possono essere espressi come somma di un quadrato e di un cubo. Alcuni di essi in più in modo.
-Consider the palindromic numbers that can be expressed as the sum of a square and a cube, both greater than 1, in exactly 4 different ways. For example, 5229225 is a palindromic number and it can be expressed in exactly 4 different ways: 22852 + 203 22232 + 663 18102 + 1253 11972 + 1563
+Considera i numeri palindromici che possono essere espressi come la somma di un quadrato e di un cubo, entrambi maggiori di 1, in esattamente 4 modi diversi.
-Find the sum of the five smallest such palindromic numbers.
+Ad esempio, 5229225 è un numero palindromico e può essere espresso esattamente in 4 modi diversi:
+
+$$\begin{align} & {2285}^2 + {20}^3 \\\\ & {2223}^2 + {66}^3 \\\\ & {1810}^2 + {125}^3 \\\\ & {1197}^2 + {156}^3 \end{align}$$
+
+Trova la somma dei cinque numeri palindromi più piccoli.
# --hints--
-`euler348()` should return 1004195061.
+`sumOfSquareAndCube()` dovrebbe restituire `1004195061`.
```js
-assert.strictEqual(euler348(), 1004195061);
+assert.strictEqual(sumOfSquareAndCube(), 1004195061);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler348(), 1004195061);
## --seed-contents--
```js
-function euler348() {
+function sumOfSquareAndCube() {
return true;
}
-euler348();
+sumOfSquareAndCube();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
index 239ba5a6a1..d703403ce9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
@@ -1,6 +1,6 @@
---
id: 5900f4ca1000cf542c50ffdc
-title: 'Problem 349: Langton''s ant'
+title: 'Problema 349: Formica di Langton'
challengeType: 5
forumTopicId: 302008
dashedName: problem-349-langtons-ant
@@ -8,22 +8,21 @@ dashedName: problem-349-langtons-ant
# --description--
-An ant moves on a regular grid of squares that are coloured either black or white.
+Una formica si muove su una griglia regolare di quadrati colorati neri o bianchi.
-The ant is always oriented in one of the cardinal directions (left, right, up or down) and moves from square to adjacent square according to the following rules:
+La formica è sempre orientata in una delle direzioni cardinali (sinistra, destra, su o giù) e si sposta da un quadrato al quadrato adiacente secondo le seguenti regole:
-\- if it is on a black square, it flips the color of the square to white, rotates 90 degrees counterclockwise and moves forward one square.
+- se è su un quadrato nero, capovolge il colore del quadrato a bianco, ruota 90° in senso antiorario e si muove in avanti di un quadrato.
+- se è su un quadrato bianco, capovolge il colore del quadrato a nero, ruota 90° in senso orario e si muove in avanti di un quadrato.
-\- if it is on a white square, it flips the color of the square to black, rotates 90 degrees clockwise and moves forward one square.
-
-Starting with a grid that is entirely white, how many squares are black after 1018 moves of the ant?
+A partire da una griglia completamente bianca, quanti quadrati sono neri dopo ${10}^{18}$ mosse della formica?
# --hints--
-`euler349()` should return 115384615384614940.
+`langtonsAnt()` dovrebbe restituire `115384615384614940`.
```js
-assert.strictEqual(euler349(), 115384615384614940);
+assert.strictEqual(langtonsAnt(), 115384615384614940);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler349(), 115384615384614940);
## --seed-contents--
```js
-function euler349() {
+function langtonsAnt() {
return true;
}
-euler349();
+langtonsAnt();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
index ebc52998b5..3483721e4c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffdd
-title: 'Problem 350: Constraining the least greatest and the greatest least'
+title: 'Problema 350: Mettere limiti al più piccolo più grande e al più grande più piccolo'
challengeType: 5
forumTopicId: 302010
dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
@@ -8,24 +8,24 @@ dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
# --description--
-A list of size n is a sequence of n natural numbers. Examples are (2,4,6), (2,6,4), (10,6,15,6), and (11).
+Una lista di dimensione $n$ è una sequenza di $n$ numeri naturali. Esempi sono (2, 4, 6), (2, 6, 4), (10, 6, 15, 6), e (11).
-The greatest common divisor, or gcd, of a list is the largest natural number that divides all entries of the list. Examples: gcd(2,6,4) = 2, gcd(10,6,15,6) = 1 and gcd(11) = 11.
+Il massimo comun divisore, o $gcd$ (da greatest common divisor in inglese), di una lista è il numero naturale più grande che divide tutti gli elementi della lista. Esempi: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$ e $gcd(11) = 11$.
-The least common multiple, or lcm, of a list is the smallest natural number divisible by each entry of the list. Examples: lcm(2,6,4) = 12, lcm(10,6,15,6) = 30 and lcm(11) = 11.
+Il minimo comun divisore, o $lcm$ (dall'inglese least common multiple), di una lista è il numero naturale più piccolo che è divisibile da ogni numero della lista. Esempi: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$ e $lcm(11) = 11$.
-Let f(G, L, N) be the number of lists of size N with gcd ≥ G and lcm ≤ L. For example:
+Sia $f(G, L, N)$ il numero di liste di dimensione $N$ con $gcd ≥ G$ e $lcm ≤ L$. Ad esempio:
-f(10, 100, 1) = 91. f(10, 100, 2) = 327. f(10, 100, 3) = 1135. f(10, 100, 1000) mod 1014 = 3286053.
+$$\begin{align} & f(10, 100, 1) = 91 \\\\ & f(10, 100, 2) = 327 \\\\ & f(10, 100, 3) = 1135 \\\\ & f(10, 100, 1000)\bmod {101}^4 = 3\\,286\\,053 \end{align}$$
-Find f(106, 1012, 1018) mod 1014.
+Trova $f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$.
# --hints--
-`euler350()` should return 84664213.
+`leastGreatestAndGreatestLeast()` dovrebbe restituire `84664213`.
```js
-assert.strictEqual(euler350(), 84664213);
+assert.strictEqual(leastGreatestAndGreatestLeast(), 84664213);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler350(), 84664213);
## --seed-contents--
```js
-function euler350() {
+function leastGreatestAndGreatestLeast() {
return true;
}
-euler350();
+leastGreatestAndGreatestLeast();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
index 33f0089171..5b57bfdbac 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffde
-title: 'Problem 351: Hexagonal orchards'
+title: 'Problema 351: frutteti esagonali'
challengeType: 5
forumTopicId: 302011
dashedName: problem-351-hexagonal-orchards
@@ -8,22 +8,24 @@ dashedName: problem-351-hexagonal-orchards
# --description--
-A hexagonal orchard of order n is a triangular lattice made up of points within a regular hexagon with side n. The following is an example of a hexagonal orchard of order 5:
+Un frutteto esagonale di ordine $n$ è un reticolo triangolare composto da punti all'interno di un esagono regolare con il lato $n$. Il seguente è un esempio di frutteto esagonale di ordine 5:
-Highlighted in green are the points which are hidden from the center by a point closer to it. It can be seen that for a hexagonal orchard of order 5, 30 points are hidden from the center.
+
-For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Allo stesso modo, da un foglio con dimensioni 9 × 8, possiamo realizzare rettangoli con dimensioni 18 × 4 e 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+Per una coppia $w$ e $h$, sia $F(w, h)$ il numero di rettangoli distinti che possono essere fatti da un foglio con dimensioni $w$ × $h$. Per esempio, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ e $F(9, 8) = 2$. Nota che i rettangoli congruenti a quello iniziale non sono contati in $F(w, h)$. Nota anche che i rettangoli con dimensioni $w$ × $h$ e le dimensioni $h$ × $w$ non sono considerati distinti.
-Find G(1012). Give your answer modulo 108.
+Per un intero $N$, sia $G(N)$ la somma di $F(w, h)$ per tutte le coppie $w$ e $h$ che soddisfano $0 < h ≤ w ≤ N$. Possiamo verificare che $G(10) = 55$, $G({10}^3) = 971\\,745$ e $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Trova $G({10}^{12})$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` dovrebbe restituire `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..602ef1c635 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -1,6 +1,6 @@
---
id: 5900f4c01000cf542c50ffd2
-title: 'Problem 339: Peredur fab Efrawg'
+title: 'Problema 339: Peredur fab Efrawg'
challengeType: 5
forumTopicId: 301997
dashedName: problem-339-peredur-fab-efrawg
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"E venne verso una valle, attraverso la quale correva un fiume; e i confini della valle erano boscosi, e su ogni lato del fiume vi erano prati pianeggianti. Da un lato del fiume vide un gregge di pecore bianche, dall'altro un gregge di pecore nere. E ogni volta che una delle pecore bianche belava, una delle pecore nere attraversava e diventava bianca; e quando una delle pecore nere belava, una delle pecore bianche attraversava e diventava nera." - Peredur Figlio di Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Inizialmente, ogni gregge è costituito da $n$ pecore. Ogni pecora (indipendentemente dal colore) è altrettanto probabile che sia la prossima pecora a belare. Dopo che una pecora ha belato e una pecora dall'altro gregge ha attraversato, Peredur può rimuovere un numero di pecore bianche al fine di massimizzare il numero finale previsto di pecore nere. Sia $E(n)$ il numero aspettato finale di pecore nere se Peredur usa una strategia ottimale.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+Ti è dato che $E(5) = 6.871346$ arrotondato a 6 cifre decimali.
+
+Trova $E(10\\,000)$ e dai la tua risposta arrotondata a 6 cifre decimali.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` dovrebbe restituire `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..c6e17627dc 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4c21000cf542c50ffd4
-title: 'Problem 340: Crazy Function'
+title: 'Problema 340: Funzione Pazza'
challengeType: 5
forumTopicId: 301999
dashedName: problem-340-crazy-function
@@ -8,24 +8,22 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+Per gli interi fissati $a$, $b$, $c$, definire la funzione pazza $F(n)$ come segue:
-F(n) = n - c for all n > b
+$$\begin{align} & F(n) = n - c \\;\text{ per ogni } n > b \\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ per ogni } n ≤ b. \end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Inoltre, definisci $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+Per esempio, se $a = 50$, $b = 2000$ e $c = 40$, allora $F(0) = 3240$ e $F(2000) = 2040$. Inoltre, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Trova le ultime 9 cifre di $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` dovrebbe restituire `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
index 740ef0d751..693beaed83 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4c11000cf542c50ffd3
-title: 'Problem 341: Golomb''s self-describing sequence'
+title: 'Problema 341: Sequenza auto-descrittiva di Golomb'
challengeType: 5
forumTopicId: 302000
dashedName: problem-341-golombs-self-describing-sequence
@@ -8,20 +8,22 @@ dashedName: problem-341-golombs-self-describing-sequence
# --description--
-The Golomb's self-describing sequence {G(n)} is the only nondecreasing sequence of natural numbers such that n appears exactly G(n) times in the sequence. The values of G(n) for the first few n are
+La sequenza di auto-descrizione di Golomb ($G(n)$) è l'unica sequenza non decrescente di numeri naturali tali che $n$ appaia esattamente $G(n)$ volte nella sequenza. I valori di $G(n)$ per i primi $n$ sono
-n123456789101112131415…G(n)122334445556666…
+$$\begin{array}{c} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & \ldots \\\\ G(n) & 1 & 2 & 2 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & \ldots \end{array}$$
-You are given that G(103) = 86, G(106) = 6137. You are also given that ΣG(n3) = 153506976 for 1 ≤ n < 103.
+Ti viene dato che $G({10}^3) = 86$, $G({10}^6) = 6137$.
-Find ΣG(n3) for 1 ≤ n < 106.
+Ti viene anche dato che $\sum G(n^3) = 153\\,506\\,976$ per $1 ≤ n < {10}^3$.
+
+Trova $\sum G(n^3)$ per $1 ≤ n < {10}^6$.
# --hints--
-`euler341()` should return 56098610614277016.
+`golombsSequence()` dovrebbe restituire `56098610614277016`.
```js
-assert.strictEqual(euler341(), 56098610614277016);
+assert.strictEqual(golombsSequence(), 56098610614277016);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler341(), 56098610614277016);
## --seed-contents--
```js
-function euler341() {
+function golombsSequence() {
return true;
}
-euler341();
+golombsSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
index 2253ce390f..cbcc7d8c39 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c31000cf542c50ffd5
-title: 'Problem 342: The totient of a square is a cube'
+title: 'Problema 342: Il toziente di un quadrato è un cubo'
challengeType: 5
forumTopicId: 302001
dashedName: problem-342-the-totient-of-a-square-is-a-cube
@@ -8,22 +8,21 @@ dashedName: problem-342-the-totient-of-a-square-is-a-cube
# --description--
-Consider the number 50.
+Considera il numero 50.
-502 = 2500 = 22 × 54, so φ(2500) = 2 × 4 × 53 = 8 × 53 = 23 × 53. 1
+${50}^2 = 2500 = 2^2 × 5^4$, so $φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$. $φ$ denota la funzione toziente di Eulero.
-So 2500 is a square and φ(2500) is a cube.
+Quindi 2500 è un quadrato e $φ(2500)$ è un cubo.
-Find the sum of all numbers n, 1 < n < 1010 such that φ(n2) is a cube.
+Trova la somma di tutti i numeri $n$, $1 < n < {10}^{10}$ in modo che $φ(n^2)$ sia un cubo.
-1 φ denotes Euler's totient function.
# --hints--
-`euler342()` should return 5943040885644.
+`totientOfSquare()` dovrebbe restituire `5943040885644`.
```js
-assert.strictEqual(euler342(), 5943040885644);
+assert.strictEqual(totientOfSquare(), 5943040885644);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler342(), 5943040885644);
## --seed-contents--
```js
-function euler342() {
+function totientOfSquare() {
return true;
}
-euler342();
+totientOfSquare();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
index 3102009e8c..63e1dab730 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4c41000cf542c50ffd6
-title: 'Problem 343: Fractional Sequences'
+title: 'Problema 343: Sequenze frazionarie'
challengeType: 5
forumTopicId: 302002
dashedName: problem-343-fractional-sequences
@@ -8,32 +8,31 @@ dashedName: problem-343-fractional-sequences
# --description--
-For any positive integer k, a finite sequence ai of fractions xi/yi is defined by:
+Per qualsiasi numero intero positivo $k$, una sequenza finita $a_i$ di frazioni $\frac{x_i}{y_i}$ è definita da:
-a1 = 1/k and
+- $a_1 = \displaystyle\frac{1}{k}$ e
+- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ ridotto ai minimi termini per $i > 1$.
-ai = (xi-1+1)/(yi-1-1) reduced to lowest terms for i>1.
+Quando $a_i$ raggiunge un numero intero $n$, la sequenza si ferma. (cioè, quando $y_i = 1$.)
-When ai reaches some integer n, the sequence stops. (That is, when yi=1.)
+Definisci $f(k) = n$.
-Define f(k) = n.
+Per esempio, per $k = 20$:
-For example, for k = 20:
+$$\frac{1}{20} → \frac{2}{19} → \frac{3}{18} = \frac{1}{6} → \frac{2}{5} → \frac{3}{4} → \frac{4}{3} → \frac{5}{2} → \frac{6}{1} = 6$$
-1/20 → 2/19 → 3/18 = 1/6 → 2/5 → 3/4 → 4/3 → 5/2 → 6/1 = 6
+Quindi $f(20) = 6$.
-So f(20) = 6.
+Anche $f(1) = 1$, $f(2) = 2$, $f(3) = 1$ e $\sum f(k^3) = 118\\,937$ per $1 ≤ k ≤ 100$.
-Also f(1) = 1, f(2) = 2, f(3) = 1 and Σf(k3) = 118937 for 1 ≤ k ≤ 100.
-
-Find Σf(k3) for 1 ≤ k ≤ 2×106.
+Trova $\sum f(k^3)$ per $1 ≤ k ≤ 2 × {10}^6$.
# --hints--
-`euler343()` should return 269533451410884200.
+`fractionalSequences()` dovrebbe restituire `269533451410884200`.
```js
-assert.strictEqual(euler343(), 269533451410884200);
+assert.strictEqual(fractionalSequences(), 269533451410884200);
```
# --seed--
@@ -41,12 +40,12 @@ assert.strictEqual(euler343(), 269533451410884200);
## --seed-contents--
```js
-function euler343() {
+function fractionalSequences() {
return true;
}
-euler343();
+fractionalSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
index 9cb8157d07..a94d255151 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffda
-title: 'Problem 345: Matrix Sum'
+title: 'Problema 345: Somma di matrice'
challengeType: 5
forumTopicId: 302004
dashedName: problem-345-matrix-sum
@@ -8,20 +8,22 @@ dashedName: problem-345-matrix-sum
# --description--
-We define the Matrix Sum of a matrix as the maximum sum of matrix elements with each element being the only one in his row and column. For example, the Matrix Sum of the matrix below equals 3315 ( = 863 + 383 + 343 + 959 + 767):
+Definiamo la Somma di Matrice di una matrice come la somma massima di elementi di matrice dove ogni elemento è l'unico nella sua fila e colonna.
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943767 473 103 699 303
+Ad esempio, la somma di matrice della matrice qui sotto è pari a $3315 ( = 863 + 383 + 343 + 959 + 767)$:
-Find the Matrix Sum of:
+$$\begin{array}{rrrrr} 7 & 53 & 183 & 439 & \color{lime}{863} \\\\ 497 & \color{lime}{383} & 563 & 79 & 973 \\\\ 287 & 63 & \color{lime}{343} & 169 & 583 \\\\ 627 & 343 & 773 & \color{lime}{959} & 943 \\\\ \color{lime}{767} & 473 & 103 & 699 & 303 \end{array}$$
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943 767 473 103 699 303 957 703 583 639 913 447 283 463 29 23 487 463 993 119 883 327 493 423 159 743 217 623 3 399 853 407 103 983 89 463 290 516 212 462 350 960 376 682 962 300 780 486 502 912 800 250 346 172 812 350 870 456 192 162 593 473 915 45 989 873 823 965 425 329 803 973 965 905 919 133 673 665 235 509 613 673 815 165 992 326 322 148 972 962 286 255 941 541 265 323 925 281 601 95 973 445 721 11 525 473 65 511 164 138 672 18 428 154 448 848 414 456 310 312 798 104 566 520 302 248 694 976 430 392 198 184 829 373 181 631 101 969 613 840 740 778 458 284 760 390 821 461 843 513 17 901 711 993 293 157 274 94 192 156 574 34 124 4 878 450 476 712 914 838 669 875 299 823 329 699 815 559 813 459 522 788 168 586 966 232 308 833 251 631 107 813 883 451 509 615 77 281 613 459 205 380 274 302 35 805
+Trova la somma di matrice di:
+
+$$\\begin{array}{r} 7 & 53 & 183 & 439 & 863 & 497 & 383 & 563 & 79 & 973 & 287 & 63 & 343 & 169 & 583 \\\\ 627 & 343 & 773 & 959 & 943 & 767 & 473 & 103 & 699 & 303 & 957 & 703 & 583 & 639 & 913 \\\\ 447 & 283 & 463 & 29 & 23 & 487 & 463 & 993 & 119 & 883 & 327 & 493 & 423 & 159 & 743 \\\\ 217 & 623 & 3 & 399 & 853 & 407 & 103 & 983 & 89 & 463 & 290 & 516 & 212 & 462 & 350 \\\\ 960 & 376 & 682 & 962 & 300 & 780 & 486 & 502 & 912 & 800 & 250 & 346 & 172 & 812 & 350 \\\\ 870 & 456 & 192 & 162 & 593 & 473 & 915 & 45 & 989 & 873 & 823 & 965 & 425 & 329 & 803 \\\\ 973 & 965 & 905 & 919 & 133 & 673 & 665 & 235 & 509 & 613 & 673 & 815 & 165 & 992 & 326 \\\\ 322 & 148 & 972 & 962 & 286 & 255 & 941 & 541 & 265 & 323 & 925 & 281 & 601 & 95 & 973 \\\\ 445 & 721 & 11 & 525 & 473 & 65 & 511 & 164 & 138 & 672 & 18 & 428 & 154 & 448 & 848 \\\\ 414 & 456 & 310 & 312 & 798 & 104 & 566 & 520 & 302 & 248 & 694 & 976 & 430 & 392 & 198 \\\\ 184 & 829 & 373 & 181 & 631 & 101 & 969 & 613 & 840 & 740 & 778 & 458 & 284 & 760 & 390 \\\\ 821 & 461 & 843 & 513 & 17 & 901 & 711 & 993 & 293 & 157 & 274 & 94 & 192 & 156 & 574 \\\\ 34 & 124 & 4 & 878 & 450 & 476 & 712 & 914 & 838 & 669 & 875 & 299 & 823 & 329 & 699 \\\\ 815 & 559 & 813 & 459 & 522 & 788 & 168 & 586 & 966 & 232 & 308 & 833 & 251 & 631 & 107 \\\\ 813 & 883 & 451 & 509 & 615 & 77 & 281 & 613 & 459 & 205 & 380 & 274 & 302 & 35 & 805 \end{array}$$
# --hints--
-`euler345()` should return 13938.
+`matrixSum()` dovrebbe restituire `13938`.
```js
-assert.strictEqual(euler345(), 13938);
+assert.strictEqual(matrixSum(), 13938);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler345(), 13938);
## --seed-contents--
```js
-function euler345() {
+function matrixSum() {
return true;
}
-euler345();
+matrixSum();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
index 49a1f6b2c2..844987961a 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
@@ -1,6 +1,6 @@
---
id: 5900f4c71000cf542c50ffd8
-title: 'Problem 346: Strong Repunits'
+title: 'Problema 346: Repunit Forti'
challengeType: 5
forumTopicId: 302005
dashedName: problem-346-strong-repunits
@@ -8,18 +8,18 @@ dashedName: problem-346-strong-repunits
# --description--
-The number 7 is special, because 7 is 111 written in base 2, and 11 written in base 6 (i.e. 710 = 116 = 1112). In other words, 7 is a repunit in at least two bases b > 1.
+Il numero 7 è speciale, perché 7 è 111 scritto in base 2, e 11 scritto in base 6 (cioè $7_{10} = {11}_6 = {111}_2$). In altre parole, 7 è una repunit in almeno due basi $b > 1$.
-We shall call a positive integer with this property a strong repunit. It can be verified that there are 8 strong repunits below 50: {1,7,13,15,21,31,40,43}. Furthermore, the sum of all strong repunits below 1000 equals 15864.
+Chiameremo un numero intero positivo con questa proprietà una forte repunit. Si può verificare che ci sono 8 forti repunit sotto 50: {1, 7, 13, 15, 21, 31, 40, 43}. Inoltre, la somma di tutti i repunit forti sotto 1000 è pari a 15864.
-Find the sum of all strong repunits below 1012.
+Trova la somma di tutti i repunit forti sotto ${10}^{12}$.
# --hints--
-`euler346()` should return 336108797689259260.
+`strongRepunits()` dovrebbe restituire `336108797689259260`.
```js
-assert.strictEqual(euler346(), 336108797689259260);
+assert.strictEqual(strongRepunits(), 336108797689259260);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler346(), 336108797689259260);
## --seed-contents--
```js
-function euler346() {
+function strongRepunits() {
return true;
}
-euler346();
+strongRepunits();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
index 70845508fa..961ba85720 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffd9
-title: 'Problem 347: Largest integer divisible by two primes'
+title: 'Problema 347: Intero più grande divisibile per due primi'
challengeType: 5
forumTopicId: 302006
dashedName: problem-347-largest-integer-divisible-by-two-primes
@@ -8,24 +8,24 @@ dashedName: problem-347-largest-integer-divisible-by-two-primes
# --description--
-The largest integer ≤ 100 that is only divisible by both the primes 2 and 3 is 96, as 96=32\*3=25\*3.
+Il più grande intero $≤ 100$ che è divisibile solo per entrambe i primi 2 e 3 è 96, poiché $96 = 32 \times 3 = 2^5 \times 3$.
-For two distinct primes p and q let M(p,q,N) be the largest positive integer ≤N only divisible
+Per due primi distinti $p$ e $q$ sia $M(p, q, N)$ il più grande intero positivo $≤ N$ divisibile solo per $p$ e $q$ e $M(p, q, N)=0$ se tale numero intero positivo non esiste.
-by both p and q and M(p,q,N)=0 if such a positive integer does not exist.
+Ad es. $M(2, 3, 100) = 96$.
-E.g. M(2,3,100)=96. M(3,5,100)=75 and not 90 because 90 is divisible by 2 ,3 and 5. Also M(2,73,100)=0 because there does not exist a positive integer ≤ 100 that is divisible by both 2 and 73.
+$M(3, 5, 100) = 75$ e non 90 perché 90 è divisibile per 2, 3 e 5. Anche $M(2, 73, 100) = 0$ perché non esiste un numero intero positivo $≤ 100$ che è divisibile sia per 2 che 73.
-Let S(N) be the sum of all distinct M(p,q,N). S(100)=2262.
+Sia $S(N)$ la somma di tutti gli $M(p, q, N)$ distinti. $S(100)=2262$.
-Find S(10 000 000).
+Trova $S(10\\,000\\,000)$.
# --hints--
-`euler347()` should return 11109800204052.
+`integerDivisibleByTwoPrimes()` dovrebbe restituire `11109800204052`.
```js
-assert.strictEqual(euler347(), 11109800204052);
+assert.strictEqual(integerDivisibleByTwoPrimes(), 11109800204052);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler347(), 11109800204052);
## --seed-contents--
```js
-function euler347() {
+function integerDivisibleByTwoPrimes() {
return true;
}
-euler347();
+integerDivisibleByTwoPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
index 2fe6e2bc13..75d443eac6 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffdb
-title: 'Problem 348: Sum of a square and a cube'
+title: 'Problema 348: Somma di un quadrato e di un cubo'
challengeType: 5
forumTopicId: 302007
dashedName: problem-348-sum-of-a-square-and-a-cube
@@ -8,18 +8,22 @@ dashedName: problem-348-sum-of-a-square-and-a-cube
# --description--
-Many numbers can be expressed as the sum of a square and a cube. Some of them in more than one way.
+Molti numeri possono essere espressi come somma di un quadrato e di un cubo. Alcuni di essi in più in modo.
-Consider the palindromic numbers that can be expressed as the sum of a square and a cube, both greater than 1, in exactly 4 different ways. For example, 5229225 is a palindromic number and it can be expressed in exactly 4 different ways: 22852 + 203 22232 + 663 18102 + 1253 11972 + 1563
+Considera i numeri palindromici che possono essere espressi come la somma di un quadrato e di un cubo, entrambi maggiori di 1, in esattamente 4 modi diversi.
-Find the sum of the five smallest such palindromic numbers.
+Ad esempio, 5229225 è un numero palindromico e può essere espresso esattamente in 4 modi diversi:
+
+$$\begin{align} & {2285}^2 + {20}^3 \\\\ & {2223}^2 + {66}^3 \\\\ & {1810}^2 + {125}^3 \\\\ & {1197}^2 + {156}^3 \end{align}$$
+
+Trova la somma dei cinque numeri palindromi più piccoli.
# --hints--
-`euler348()` should return 1004195061.
+`sumOfSquareAndCube()` dovrebbe restituire `1004195061`.
```js
-assert.strictEqual(euler348(), 1004195061);
+assert.strictEqual(sumOfSquareAndCube(), 1004195061);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler348(), 1004195061);
## --seed-contents--
```js
-function euler348() {
+function sumOfSquareAndCube() {
return true;
}
-euler348();
+sumOfSquareAndCube();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
index 239ba5a6a1..d703403ce9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
@@ -1,6 +1,6 @@
---
id: 5900f4ca1000cf542c50ffdc
-title: 'Problem 349: Langton''s ant'
+title: 'Problema 349: Formica di Langton'
challengeType: 5
forumTopicId: 302008
dashedName: problem-349-langtons-ant
@@ -8,22 +8,21 @@ dashedName: problem-349-langtons-ant
# --description--
-An ant moves on a regular grid of squares that are coloured either black or white.
+Una formica si muove su una griglia regolare di quadrati colorati neri o bianchi.
-The ant is always oriented in one of the cardinal directions (left, right, up or down) and moves from square to adjacent square according to the following rules:
+La formica è sempre orientata in una delle direzioni cardinali (sinistra, destra, su o giù) e si sposta da un quadrato al quadrato adiacente secondo le seguenti regole:
-\- if it is on a black square, it flips the color of the square to white, rotates 90 degrees counterclockwise and moves forward one square.
+- se è su un quadrato nero, capovolge il colore del quadrato a bianco, ruota 90° in senso antiorario e si muove in avanti di un quadrato.
+- se è su un quadrato bianco, capovolge il colore del quadrato a nero, ruota 90° in senso orario e si muove in avanti di un quadrato.
-\- if it is on a white square, it flips the color of the square to black, rotates 90 degrees clockwise and moves forward one square.
-
-Starting with a grid that is entirely white, how many squares are black after 1018 moves of the ant?
+A partire da una griglia completamente bianca, quanti quadrati sono neri dopo ${10}^{18}$ mosse della formica?
# --hints--
-`euler349()` should return 115384615384614940.
+`langtonsAnt()` dovrebbe restituire `115384615384614940`.
```js
-assert.strictEqual(euler349(), 115384615384614940);
+assert.strictEqual(langtonsAnt(), 115384615384614940);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler349(), 115384615384614940);
## --seed-contents--
```js
-function euler349() {
+function langtonsAnt() {
return true;
}
-euler349();
+langtonsAnt();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
index ebc52998b5..3483721e4c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffdd
-title: 'Problem 350: Constraining the least greatest and the greatest least'
+title: 'Problema 350: Mettere limiti al più piccolo più grande e al più grande più piccolo'
challengeType: 5
forumTopicId: 302010
dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
@@ -8,24 +8,24 @@ dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
# --description--
-A list of size n is a sequence of n natural numbers. Examples are (2,4,6), (2,6,4), (10,6,15,6), and (11).
+Una lista di dimensione $n$ è una sequenza di $n$ numeri naturali. Esempi sono (2, 4, 6), (2, 6, 4), (10, 6, 15, 6), e (11).
-The greatest common divisor, or gcd, of a list is the largest natural number that divides all entries of the list. Examples: gcd(2,6,4) = 2, gcd(10,6,15,6) = 1 and gcd(11) = 11.
+Il massimo comun divisore, o $gcd$ (da greatest common divisor in inglese), di una lista è il numero naturale più grande che divide tutti gli elementi della lista. Esempi: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$ e $gcd(11) = 11$.
-The least common multiple, or lcm, of a list is the smallest natural number divisible by each entry of the list. Examples: lcm(2,6,4) = 12, lcm(10,6,15,6) = 30 and lcm(11) = 11.
+Il minimo comun divisore, o $lcm$ (dall'inglese least common multiple), di una lista è il numero naturale più piccolo che è divisibile da ogni numero della lista. Esempi: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$ e $lcm(11) = 11$.
-Let f(G, L, N) be the number of lists of size N with gcd ≥ G and lcm ≤ L. For example:
+Sia $f(G, L, N)$ il numero di liste di dimensione $N$ con $gcd ≥ G$ e $lcm ≤ L$. Ad esempio:
-f(10, 100, 1) = 91. f(10, 100, 2) = 327. f(10, 100, 3) = 1135. f(10, 100, 1000) mod 1014 = 3286053.
+$$\begin{align} & f(10, 100, 1) = 91 \\\\ & f(10, 100, 2) = 327 \\\\ & f(10, 100, 3) = 1135 \\\\ & f(10, 100, 1000)\bmod {101}^4 = 3\\,286\\,053 \end{align}$$
-Find f(106, 1012, 1018) mod 1014.
+Trova $f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$.
# --hints--
-`euler350()` should return 84664213.
+`leastGreatestAndGreatestLeast()` dovrebbe restituire `84664213`.
```js
-assert.strictEqual(euler350(), 84664213);
+assert.strictEqual(leastGreatestAndGreatestLeast(), 84664213);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler350(), 84664213);
## --seed-contents--
```js
-function euler350() {
+function leastGreatestAndGreatestLeast() {
return true;
}
-euler350();
+leastGreatestAndGreatestLeast();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
index 33f0089171..5b57bfdbac 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffde
-title: 'Problem 351: Hexagonal orchards'
+title: 'Problema 351: frutteti esagonali'
challengeType: 5
forumTopicId: 302011
dashedName: problem-351-hexagonal-orchards
@@ -8,22 +8,24 @@ dashedName: problem-351-hexagonal-orchards
# --description--
-A hexagonal orchard of order n is a triangular lattice made up of points within a regular hexagon with side n. The following is an example of a hexagonal orchard of order 5:
+Un frutteto esagonale di ordine $n$ è un reticolo triangolare composto da punti all'interno di un esagono regolare con il lato $n$. Il seguente è un esempio di frutteto esagonale di ordine 5:
-Highlighted in green are the points which are hidden from the center by a point closer to it. It can be seen that for a hexagonal orchard of order 5, 30 points are hidden from the center.
+ -Let H(n) be the number of points hidden from the center in a hexagonal orchard of order n.
+In evidenza in verde si vedono i punti che sono nascosti dal centro da un punto più vicino ad esso. Si può vedere che per un frutteto esagonale di ordine 5, 30 punti sono nascosti dal centro.
-H(5) = 30. H(10) = 138. H(1 000) = 1177848.
+Sia $H(n)$ il numero di punti nascosti al centro in un frutteto esagonale di ordine $n$.
-Find H(100 000 000).
+$H(5) = 30$. $H(10) = 138$. $H(1\\,000)$ = $1\\,177\\,848$.
+
+Trova $H(100\\,000\\,000)$.
# --hints--
-`euler351()` should return 11762187201804552.
+`hexagonalOrchards()` dovrebbe restituire `11762187201804552`.
```js
-assert.strictEqual(euler351(), 11762187201804552);
+assert.strictEqual(hexagonalOrchards(), 11762187201804552);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler351(), 11762187201804552);
## --seed-contents--
```js
-function euler351() {
+function hexagonalOrchards() {
return true;
}
-euler351();
+hexagonalOrchards();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
index 76af2f075c..186af1e8a4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffdf
-title: 'Problem 352: Blood tests'
+title: 'Problema 352: Analisi del sangue'
challengeType: 5
forumTopicId: 302012
dashedName: problem-352-blood-tests
@@ -8,32 +8,46 @@ dashedName: problem-352-blood-tests
# --description--
-Each one of the 25 sheep in a flock must be tested for a rare virus, known to affect 2% of the sheep population.
+Ognuna delle 25 pecore di un gregge deve essere sottoposta a test per individuare un virus raro, noto per colpire il 2% della popolazione ovina.
-An accurate and extremely sensitive PCR test exists for blood samples, producing a clear positive / negative result, but it is very time-consuming and expensive.
+Un test PCR accurato ed estremamente sensibile esiste per i campioni di sangue, producendo un risultato positivo/negativo netto, ma è molto lungo e costoso.
-Because of the high cost, the vet-in-charge suggests that instead of performing 25 separate tests, the following procedure can be used instead: The sheep are split into 5 groups of 5 sheep in each group. For each group, the 5 samples are mixed together and a single test is performed. Then, If the result is negative, all the sheep in that group are deemed to be virus-free. If the result is positive, 5 additional tests will be performed (a separate test for each animal) to determine the affected individual(s).
+A causa del costo elevato, il veterinario suggerisce che invece di eseguire 25 test separati, si può ricorrere alla seguente procedura:
-Since the probability of infection for any specific animal is only 0.02, the first test (on the pooled samples) for each group will be: Negative (and no more tests needed) with probability 0.985 = 0.9039207968. Positive (5 additional tests needed) with probability 1 - 0.9039207968 = 0.0960792032.
+Le pecore sono suddivise in 5 gruppi di 5 pecore in ognuno. Per ciascun gruppo, i 5 campioni sono mescolati insieme e si effettua una singola prova. Poi,
-Thus, the expected number of tests for each group is 1 + 0.0960792032 × 5 = 1.480396016. Consequently, all 5 groups can be screened using an average of only 1.480396016 × 5 = 7.40198008 tests, which represents a huge saving of more than 70% !
+- Se il risultato è negativo, tutte le pecore di quel gruppo sono considerate prive di virus.
+- Se il risultato è positivo, saranno effettuati 5 test supplementari (una prova separata per ciascun animale) per determinare l'individuo/i interessato/i.
-Although the scheme we have just described seems to be very efficient, it can still be improved considerably (always assuming that the test is sufficiently sensitive and that there are no adverse effects caused by mixing different samples). E.g.: We may start by running a test on a mixture of all the 25 samples. It can be verified that in about 60.35% of the cases this test will be negative, thus no more tests will be needed. Further testing will only be required for the remaining 39.65% of the cases. If we know that at least one animal in a group of 5 is infected and the first 4 individual tests come out negative, there is no need to run a test on the fifth animal (we know that it must be infected). We can try a different number of groups / different number of animals in each group, adjusting those numbers at each level so that the total expected number of tests will be minimised.
+Poiché la probabilità di infezione per un animale specifico è solo di 0,02, il primo test (sui campioni aggregati) per ciascun gruppo sarà:
-To simplify the very wide range of possibilities, there is one restriction we place when devising the most cost-efficient testing scheme: whenever we start with a mixed sample, all the sheep contributing to that sample must be fully screened (i.e. a verdict of infected / virus-free must be reached for all of them) before we start examining any other animals.
+- Negativo (e nessun altro test necessario) con probabilità ${0.98}^5 = 0.9039207968$.
+- Positivo (5 ulteriori test necessari) con probabilità $1 - 0.9039207968 = 0.0960792032$.
-For the current example, it turns out that the most cost-efficient testing scheme (we'll call it the optimal strategy) requires an average of just 4.155452 tests!
+Così, il numero previsto di test per ogni gruppo è di $1 + 0.0960792032 × 5 = 1.480396016$.
-Using the optimal strategy, let T(s,p) represent the average number of tests needed to screen a flock of s sheep for a virus having probability p to be present in any individual. Thus, rounded to six decimal places, T(25, 0.02) = 4.155452 and T(25, 0.10) = 12.702124.
+Di conseguenza, tutti i 5 gruppi possono essere controllati utilizzando una media di soli $1.480396016 × 5 = \mathbf{7.40198008}$ test, che rappresenta un enorme risparmio di oltre il 70%!
-Find ΣT(10000, p) for p=0.01, 0.02, 0.03, ... 0.50. Give your answer rounded to six decimal places.
+Anche se lo schema che abbiamo appena descritto sembra essere molto efficiente, può ancora essere migliorato notevolmente (sempre supponendo che il test sia sufficientemente sensibile e che nessun effetto negativo sia causato dalla miscelazione di campioni diversi). Ad es.:
+
+- Possiamo iniziare eseguendo una prova su una miscela di tutti i 25 campioni. Si può verificare che in circa il 60,35% dei casi questo test sarà negativo, quindi non saranno necessari altri test. Saranno necessari ulteriori test solo per il restante 39,65% dei casi.
+- Se sappiamo che almeno un animale in un gruppo di 5 è infetto e i primi 4 test individuali risultano negativi, non è necessario eseguire un test sul quinto animale (sappiamo che deve essere infetto).
+- Possiamo provare un numero diverso di gruppi / numero diverso di animali in ogni gruppo, adeguare tali numeri a ciascun livello in modo da ridurre al minimo il numero totale previsto di prove.
+
+Per semplificare la vasta gamma di possibilità, esiste una restrizione che poniamo quando progettiamo il sistema di test più efficiente in termini di costi: ogni volta che iniziamo con un campione misto, tutti gli ovini che contribuiscono a tale campione devono essere sottoposti a screening completo (cioè prima di iniziare ad esaminare qualsiasi altro animale deve essere raggiunto un verdetto di infezione / non infezione per tutti loro.
+
+Per l'esempio attuale, risulta che lo schema di test più efficiente in termini di costi (lo chiameremo la strategia ottimale) richiede una media di appena 4.155452 test!
+
+Utilizzando la strategia ottimale, lascia che $T(s, p)$ rappresenti il numero medio di test necessari per testare un gregge di $s$ pecore per un virus che ha probabilità $p$ di essere presente in qualsiasi individuo. Così, arrotondato a sei decimali, $T(25, 0.02) = 4.155452$ e $T(25, 0.10) = 12.702124$.
+
+Trova $\sum T(10\\,000, p)$ per $p = 0.01, 0.02, 0.03, \ldots 0.50$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler352()` should return 378563.260589.
+`bloodTests()` dovrebbe restituire `378563.260589`.
```js
-assert.strictEqual(euler352(), 378563.260589);
+assert.strictEqual(bloodTests(), 378563.260589);
```
# --seed--
@@ -41,12 +55,12 @@ assert.strictEqual(euler352(), 378563.260589);
## --seed-contents--
```js
-function euler352() {
+function bloodTests() {
return true;
}
-euler352();
+bloodTests();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
index 74faf24c26..91350909f9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffe0
-title: 'Problem 353: Risky moon'
+title: 'Problema 353: Luna rischiosa'
challengeType: 5
forumTopicId: 302013
dashedName: problem-353-risky-moon
@@ -8,28 +8,30 @@ dashedName: problem-353-risky-moon
# --description--
-A moon could be described by the sphere C(r) with centre (0,0,0) and radius r.
+Una luna potrebbe essere descritta dalla sfera $C(r)$ con centro (0, 0, 0) e raggio $r$.
-There are stations on the moon at the points on the surface of C(r) with integer coordinates. The station at (0,0,r) is called North Pole station, the station at (0,0,-r) is called South Pole station.
+Ci sono stazioni sulla luna nei punti sulla superficie di $C(r)$ con coordinate intere. La stazione a (0, 0, $r$) si chiama Stazione Polo Nord, la stazione a (0, 0, $-r$) si chiama Stazione Polo Sud.
-All stations are connected with each other via the shortest road on the great arc through the stations. A journey between two stations is risky. If d is the length of the road between two stations, (d/(π r))2 is a measure for the risk of the journey (let us call it the risk of the road). If the journey includes more than two stations, the risk of the journey is the sum of risks of the used roads.
+Tutte le stazioni sono collegate tra loro attraverso la strada più breve sul grande arco attraverso le stazioni. Un viaggio tra due stazioni è rischioso. Se $d$ è la lunghezza della strada tra due stazioni, $\{\left(\frac{d}{πr}\right)}^2$ è una misura per il rischio del viaggio (chiamiamolo il rischio della strada). Se il viaggio comprende più di due stazioni, il rischio del viaggio è la somma dei rischi delle strade usate.
-A direct journey from the North Pole station to the South Pole station has the length πr and risk 1. The journey from the North Pole station to the South Pole station via (0,r,0) has the same length, but a smaller risk: (½πr/(πr))2+(½πr/(πr))2=0.5.
+Un viaggio diretto dalla stazione Polo Nord alla stazione Polo Sud ha la lunghezza $πr$ e il rischio 1. Il viaggio dalla stazione Polo Nord alla stazione Polo Sud attraverso (0, $r$, 0) ha la stessa lunghezza, ma un rischio minore:
-The minimal risk of a journey from the North Pole station to the South Pole station on C(r) is M(r).
+$${\left(\frac{\frac{1}{2}πr}{πr}\right)}^2+{\left(\frac{\frac{1}{2}πr}{πr}\right)}^2 = 0.5$$
-You are given that M(7)=0.1784943998 rounded to 10 digits behind the decimal point.
+Il rischio minimo di un viaggio dalla stazione Polo Nord alla stazione Polo Sud su $C(r)$ è $M(r)$.
-Find ∑M(2n-1) for 1≤n≤15.
+Ti viene dato che $M(7) = 0.178\\,494\\,399\\,8$ arrotondato a 10 cifre dietro il punto decimale.
-Give your answer rounded to 10 digits behind the decimal point in the form a.bcdefghijk.
+Trova $\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$.
+
+Dai la tua risposta arrotondata a 10 cifre dietro il punto decimale nella forma a.bcdefghijk.
# --hints--
-`euler353()` should return 1.2759860331.
+`riskyMoon()` dovrebbe restituire `1.2759860331`.
```js
-assert.strictEqual(euler353(), 1.2759860331);
+assert.strictEqual(riskyMoon(), 1.2759860331);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler353(), 1.2759860331);
## --seed-contents--
```js
-function euler353() {
+function riskyMoon() {
return true;
}
-euler353();
+riskyMoon();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
index 346a1af451..9b04b4b5b5 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
@@ -1,6 +1,6 @@
---
id: 5900f4cf1000cf542c50ffe1
-title: 'Problem 354: Distances in a bee''s honeycomb'
+title: 'Problema 354: Distanze in un favo'
challengeType: 5
forumTopicId: 302014
dashedName: problem-354-distances-in-a-bees-honeycomb
@@ -8,18 +8,22 @@ dashedName: problem-354-distances-in-a-bees-honeycomb
# --description--
-Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
+Considera un favo dove ogni cella è un perfetto esagono regolare con lunghezza lato di 1.
-One particular cell is occupied by the queen bee. For a positive real number L, let B(L) count the cells with distance L from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider. For example, B(√3) = 6, B(√21) = 12 and B(111 111 111) = 54.
+
-Let H(n) be the number of points hidden from the center in a hexagonal orchard of order n.
+In evidenza in verde si vedono i punti che sono nascosti dal centro da un punto più vicino ad esso. Si può vedere che per un frutteto esagonale di ordine 5, 30 punti sono nascosti dal centro.
-H(5) = 30. H(10) = 138. H(1 000) = 1177848.
+Sia $H(n)$ il numero di punti nascosti al centro in un frutteto esagonale di ordine $n$.
-Find H(100 000 000).
+$H(5) = 30$. $H(10) = 138$. $H(1\\,000)$ = $1\\,177\\,848$.
+
+Trova $H(100\\,000\\,000)$.
# --hints--
-`euler351()` should return 11762187201804552.
+`hexagonalOrchards()` dovrebbe restituire `11762187201804552`.
```js
-assert.strictEqual(euler351(), 11762187201804552);
+assert.strictEqual(hexagonalOrchards(), 11762187201804552);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler351(), 11762187201804552);
## --seed-contents--
```js
-function euler351() {
+function hexagonalOrchards() {
return true;
}
-euler351();
+hexagonalOrchards();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
index 76af2f075c..186af1e8a4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffdf
-title: 'Problem 352: Blood tests'
+title: 'Problema 352: Analisi del sangue'
challengeType: 5
forumTopicId: 302012
dashedName: problem-352-blood-tests
@@ -8,32 +8,46 @@ dashedName: problem-352-blood-tests
# --description--
-Each one of the 25 sheep in a flock must be tested for a rare virus, known to affect 2% of the sheep population.
+Ognuna delle 25 pecore di un gregge deve essere sottoposta a test per individuare un virus raro, noto per colpire il 2% della popolazione ovina.
-An accurate and extremely sensitive PCR test exists for blood samples, producing a clear positive / negative result, but it is very time-consuming and expensive.
+Un test PCR accurato ed estremamente sensibile esiste per i campioni di sangue, producendo un risultato positivo/negativo netto, ma è molto lungo e costoso.
-Because of the high cost, the vet-in-charge suggests that instead of performing 25 separate tests, the following procedure can be used instead: The sheep are split into 5 groups of 5 sheep in each group. For each group, the 5 samples are mixed together and a single test is performed. Then, If the result is negative, all the sheep in that group are deemed to be virus-free. If the result is positive, 5 additional tests will be performed (a separate test for each animal) to determine the affected individual(s).
+A causa del costo elevato, il veterinario suggerisce che invece di eseguire 25 test separati, si può ricorrere alla seguente procedura:
-Since the probability of infection for any specific animal is only 0.02, the first test (on the pooled samples) for each group will be: Negative (and no more tests needed) with probability 0.985 = 0.9039207968. Positive (5 additional tests needed) with probability 1 - 0.9039207968 = 0.0960792032.
+Le pecore sono suddivise in 5 gruppi di 5 pecore in ognuno. Per ciascun gruppo, i 5 campioni sono mescolati insieme e si effettua una singola prova. Poi,
-Thus, the expected number of tests for each group is 1 + 0.0960792032 × 5 = 1.480396016. Consequently, all 5 groups can be screened using an average of only 1.480396016 × 5 = 7.40198008 tests, which represents a huge saving of more than 70% !
+- Se il risultato è negativo, tutte le pecore di quel gruppo sono considerate prive di virus.
+- Se il risultato è positivo, saranno effettuati 5 test supplementari (una prova separata per ciascun animale) per determinare l'individuo/i interessato/i.
-Although the scheme we have just described seems to be very efficient, it can still be improved considerably (always assuming that the test is sufficiently sensitive and that there are no adverse effects caused by mixing different samples). E.g.: We may start by running a test on a mixture of all the 25 samples. It can be verified that in about 60.35% of the cases this test will be negative, thus no more tests will be needed. Further testing will only be required for the remaining 39.65% of the cases. If we know that at least one animal in a group of 5 is infected and the first 4 individual tests come out negative, there is no need to run a test on the fifth animal (we know that it must be infected). We can try a different number of groups / different number of animals in each group, adjusting those numbers at each level so that the total expected number of tests will be minimised.
+Poiché la probabilità di infezione per un animale specifico è solo di 0,02, il primo test (sui campioni aggregati) per ciascun gruppo sarà:
-To simplify the very wide range of possibilities, there is one restriction we place when devising the most cost-efficient testing scheme: whenever we start with a mixed sample, all the sheep contributing to that sample must be fully screened (i.e. a verdict of infected / virus-free must be reached for all of them) before we start examining any other animals.
+- Negativo (e nessun altro test necessario) con probabilità ${0.98}^5 = 0.9039207968$.
+- Positivo (5 ulteriori test necessari) con probabilità $1 - 0.9039207968 = 0.0960792032$.
-For the current example, it turns out that the most cost-efficient testing scheme (we'll call it the optimal strategy) requires an average of just 4.155452 tests!
+Così, il numero previsto di test per ogni gruppo è di $1 + 0.0960792032 × 5 = 1.480396016$.
-Using the optimal strategy, let T(s,p) represent the average number of tests needed to screen a flock of s sheep for a virus having probability p to be present in any individual. Thus, rounded to six decimal places, T(25, 0.02) = 4.155452 and T(25, 0.10) = 12.702124.
+Di conseguenza, tutti i 5 gruppi possono essere controllati utilizzando una media di soli $1.480396016 × 5 = \mathbf{7.40198008}$ test, che rappresenta un enorme risparmio di oltre il 70%!
-Find ΣT(10000, p) for p=0.01, 0.02, 0.03, ... 0.50. Give your answer rounded to six decimal places.
+Anche se lo schema che abbiamo appena descritto sembra essere molto efficiente, può ancora essere migliorato notevolmente (sempre supponendo che il test sia sufficientemente sensibile e che nessun effetto negativo sia causato dalla miscelazione di campioni diversi). Ad es.:
+
+- Possiamo iniziare eseguendo una prova su una miscela di tutti i 25 campioni. Si può verificare che in circa il 60,35% dei casi questo test sarà negativo, quindi non saranno necessari altri test. Saranno necessari ulteriori test solo per il restante 39,65% dei casi.
+- Se sappiamo che almeno un animale in un gruppo di 5 è infetto e i primi 4 test individuali risultano negativi, non è necessario eseguire un test sul quinto animale (sappiamo che deve essere infetto).
+- Possiamo provare un numero diverso di gruppi / numero diverso di animali in ogni gruppo, adeguare tali numeri a ciascun livello in modo da ridurre al minimo il numero totale previsto di prove.
+
+Per semplificare la vasta gamma di possibilità, esiste una restrizione che poniamo quando progettiamo il sistema di test più efficiente in termini di costi: ogni volta che iniziamo con un campione misto, tutti gli ovini che contribuiscono a tale campione devono essere sottoposti a screening completo (cioè prima di iniziare ad esaminare qualsiasi altro animale deve essere raggiunto un verdetto di infezione / non infezione per tutti loro.
+
+Per l'esempio attuale, risulta che lo schema di test più efficiente in termini di costi (lo chiameremo la strategia ottimale) richiede una media di appena 4.155452 test!
+
+Utilizzando la strategia ottimale, lascia che $T(s, p)$ rappresenti il numero medio di test necessari per testare un gregge di $s$ pecore per un virus che ha probabilità $p$ di essere presente in qualsiasi individuo. Così, arrotondato a sei decimali, $T(25, 0.02) = 4.155452$ e $T(25, 0.10) = 12.702124$.
+
+Trova $\sum T(10\\,000, p)$ per $p = 0.01, 0.02, 0.03, \ldots 0.50$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler352()` should return 378563.260589.
+`bloodTests()` dovrebbe restituire `378563.260589`.
```js
-assert.strictEqual(euler352(), 378563.260589);
+assert.strictEqual(bloodTests(), 378563.260589);
```
# --seed--
@@ -41,12 +55,12 @@ assert.strictEqual(euler352(), 378563.260589);
## --seed-contents--
```js
-function euler352() {
+function bloodTests() {
return true;
}
-euler352();
+bloodTests();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
index 74faf24c26..91350909f9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffe0
-title: 'Problem 353: Risky moon'
+title: 'Problema 353: Luna rischiosa'
challengeType: 5
forumTopicId: 302013
dashedName: problem-353-risky-moon
@@ -8,28 +8,30 @@ dashedName: problem-353-risky-moon
# --description--
-A moon could be described by the sphere C(r) with centre (0,0,0) and radius r.
+Una luna potrebbe essere descritta dalla sfera $C(r)$ con centro (0, 0, 0) e raggio $r$.
-There are stations on the moon at the points on the surface of C(r) with integer coordinates. The station at (0,0,r) is called North Pole station, the station at (0,0,-r) is called South Pole station.
+Ci sono stazioni sulla luna nei punti sulla superficie di $C(r)$ con coordinate intere. La stazione a (0, 0, $r$) si chiama Stazione Polo Nord, la stazione a (0, 0, $-r$) si chiama Stazione Polo Sud.
-All stations are connected with each other via the shortest road on the great arc through the stations. A journey between two stations is risky. If d is the length of the road between two stations, (d/(π r))2 is a measure for the risk of the journey (let us call it the risk of the road). If the journey includes more than two stations, the risk of the journey is the sum of risks of the used roads.
+Tutte le stazioni sono collegate tra loro attraverso la strada più breve sul grande arco attraverso le stazioni. Un viaggio tra due stazioni è rischioso. Se $d$ è la lunghezza della strada tra due stazioni, $\{\left(\frac{d}{πr}\right)}^2$ è una misura per il rischio del viaggio (chiamiamolo il rischio della strada). Se il viaggio comprende più di due stazioni, il rischio del viaggio è la somma dei rischi delle strade usate.
-A direct journey from the North Pole station to the South Pole station has the length πr and risk 1. The journey from the North Pole station to the South Pole station via (0,r,0) has the same length, but a smaller risk: (½πr/(πr))2+(½πr/(πr))2=0.5.
+Un viaggio diretto dalla stazione Polo Nord alla stazione Polo Sud ha la lunghezza $πr$ e il rischio 1. Il viaggio dalla stazione Polo Nord alla stazione Polo Sud attraverso (0, $r$, 0) ha la stessa lunghezza, ma un rischio minore:
-The minimal risk of a journey from the North Pole station to the South Pole station on C(r) is M(r).
+$${\left(\frac{\frac{1}{2}πr}{πr}\right)}^2+{\left(\frac{\frac{1}{2}πr}{πr}\right)}^2 = 0.5$$
-You are given that M(7)=0.1784943998 rounded to 10 digits behind the decimal point.
+Il rischio minimo di un viaggio dalla stazione Polo Nord alla stazione Polo Sud su $C(r)$ è $M(r)$.
-Find ∑M(2n-1) for 1≤n≤15.
+Ti viene dato che $M(7) = 0.178\\,494\\,399\\,8$ arrotondato a 10 cifre dietro il punto decimale.
-Give your answer rounded to 10 digits behind the decimal point in the form a.bcdefghijk.
+Trova $\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$.
+
+Dai la tua risposta arrotondata a 10 cifre dietro il punto decimale nella forma a.bcdefghijk.
# --hints--
-`euler353()` should return 1.2759860331.
+`riskyMoon()` dovrebbe restituire `1.2759860331`.
```js
-assert.strictEqual(euler353(), 1.2759860331);
+assert.strictEqual(riskyMoon(), 1.2759860331);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler353(), 1.2759860331);
## --seed-contents--
```js
-function euler353() {
+function riskyMoon() {
return true;
}
-euler353();
+riskyMoon();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
index 346a1af451..9b04b4b5b5 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
@@ -1,6 +1,6 @@
---
id: 5900f4cf1000cf542c50ffe1
-title: 'Problem 354: Distances in a bee''s honeycomb'
+title: 'Problema 354: Distanze in un favo'
challengeType: 5
forumTopicId: 302014
dashedName: problem-354-distances-in-a-bees-honeycomb
@@ -8,18 +8,22 @@ dashedName: problem-354-distances-in-a-bees-honeycomb
# --description--
-Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
+Considera un favo dove ogni cella è un perfetto esagono regolare con lunghezza lato di 1.
-One particular cell is occupied by the queen bee. For a positive real number L, let B(L) count the cells with distance L from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider. For example, B(√3) = 6, B(√21) = 12 and B(111 111 111) = 54.
+ -Find the number of L ≤ 5·1011 such that B(L) = 450.
+Una particolare cella è occupata dall'ape regina. Per un numero reale positivo $L$, sia $B(L)$ il conteggio delle celle con distanza $L$ dalla cella dell'ape regina (tutte le distanze sono misurate da centro a centro); puoi assumere che il favo è abbastanza grande da accomodare per ogni distanza che vogliamo considerare.
+
+Per esempio, $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$ e $B(111\\,111\\,111) = 54$.
+
+Trova il numero di $L ≤ 5 \times {10}^{11}$ per cui $B(L) = 450$.
# --hints--
-`euler354()` should return 58065134.
+`distancesInHoneycomb()` dovrebbe restituire `58065134`.
```js
-assert.strictEqual(euler354(), 58065134);
+assert.strictEqual(distancesInHoneycomb(), 58065134);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler354(), 58065134);
## --seed-contents--
```js
-function euler354() {
+function distancesInHoneycomb() {
return true;
}
-euler354();
+distancesInHoneycomb();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
index a166a1057a..73bcbb7f10 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe2
-title: 'Problem 355: Maximal coprime subset'
+title: 'Problema 355: Massimo sottoinsieme di coprimi'
challengeType: 5
forumTopicId: 302015
dashedName: problem-355-maximal-coprime-subset
@@ -8,18 +8,18 @@ dashedName: problem-355-maximal-coprime-subset
# --description--
-Define Co(n) to be the maximal possible sum of a set of mutually co-prime elements from {1, 2, ..., n}. For example Co(10) is 30 and hits that maximum on the subset {1, 5, 7, 8, 9}.
+Definisci $Co(n)$ in modo che sia la massima somma possibile di un insieme di elementi reciprocamente co-primi da $\\{1, 2, \ldots, n\\}$. Per esempio $Co(10)$ è di 30 e ha il suo massimo per il sottoinsieme $\\{1, 5, 7, 8, 9\\}$.
-You are given that Co(30) = 193 and Co(100) = 1356.
+Ti viene dato che $Co(30) = 193$ e $Co(100) = 1356$.
-Find Co(200000).
+Trova $Co(200\\,000)$.
# --hints--
-`euler355()` should return 1726545007.
+`maximalCoprimeSubset()` dovrebbe restituire `1726545007`.
```js
-assert.strictEqual(euler355(), 1726545007);
+assert.strictEqual(maximalCoprimeSubset(), 1726545007);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler355(), 1726545007);
## --seed-contents--
```js
-function euler355() {
+function maximalCoprimeSubset() {
return true;
}
-euler355();
+maximalCoprimeSubset();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
index 9027dcecf9..494e59ce91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe3
-title: 'Problem 356: Largest roots of cubic polynomials'
+title: 'Problema 356: Le più grandi radici dei polinomi cubici'
challengeType: 5
forumTopicId: 302016
dashedName: problem-356-largest-roots-of-cubic-polynomials
@@ -8,20 +8,20 @@ dashedName: problem-356-largest-roots-of-cubic-polynomials
# --description--
-Let an be the largest real root of a polynomial g(x) = x3 - 2n·x2 + n.
+Sia $a_n$ la più grande radice reale di un polinomio $g(x) = x^3 - 2^n \times x^2 + n$.
-For example, a2 = 3.86619826...
+Per esempio, $a_2 = 3.86619826\ldots$
-Find the last eight digits of.
+Trova le ultime otto cifre di $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
-Note: represents the floor function.
+**Nota:** $\lfloor a\rfloor$ rappresenta la funzione floor.
# --hints--
-`euler356()` should return 28010159.
+`rootsOfCubicPolynomials()` dovrebbe restituire `28010159`.
```js
-assert.strictEqual(euler356(), 28010159);
+assert.strictEqual(rootsOfCubicPolynomials(), 28010159);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler356(), 28010159);
## --seed-contents--
```js
-function euler356() {
+function rootsOfCubicPolynomials() {
return true;
}
-euler356();
+rootsOfCubicPolynomials();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
index 1bb3f094a2..960124e437 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d11000cf542c50ffe4
-title: 'Problem 357: Prime generating integers'
+title: 'Problema 357: Numeri interi generatori di numeri primi'
challengeType: 5
forumTopicId: 302017
dashedName: problem-357-prime-generating-integers
@@ -8,18 +8,18 @@ dashedName: problem-357-prime-generating-integers
# --description--
-Consider the divisors of 30: 1,2,3,5,6,10,15,30.
+Considera i divisori di 30: 1, 2, 3, 5, 6, 10, 15, 30.
-It can be seen that for every divisor d of 30, d+30/d is prime.
+Si può vedere che per ogni divisore $d$ di 30, $d + \frac{30}{d}$ è primo.
-Find the sum of all positive integers n not exceeding 100 000 000such that for every divisor d of n, d+n/d is prime.
+Trova la somma di tutti gli interi positivi $n$ non superiore a $100\\,000\\, 00$ tale che per ogni divisore $d$ di $n$, $d + \frac{n}{d}$ è primo.
# --hints--
-`euler357()` should return 1739023853137.
+`primeGeneratingIntegers()` dovrebbe restituire `1739023853137`.
```js
-assert.strictEqual(euler357(), 1739023853137);
+assert.strictEqual(primeGeneratingIntegers(), 1739023853137);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler357(), 1739023853137);
## --seed-contents--
```js
-function euler357() {
+function primeGeneratingIntegers() {
return true;
}
-euler357();
+primeGeneratingIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
index fb08a667a8..1e526f8262 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d21000cf542c50ffe5
-title: 'Problem 358: Cyclic numbers'
+title: 'Problema 358: Numeri ciclici'
challengeType: 5
forumTopicId: 302018
dashedName: problem-358-cyclic-numbers
@@ -8,24 +8,28 @@ dashedName: problem-358-cyclic-numbers
# --description--
-A cyclic number with n digits has a very interesting property:
+Un numero ciclico con $n$ cifre ha una proprietà molto interessante:
-When it is multiplied by 1, 2, 3, 4, ... n, all the products have exactly the same digits, in the same order, but rotated in a circular fashion!
+Quando è moltiplicato per 1, 2, 3, 4, ... $n$, tutti i prodotti hanno esattamente le stesse cifre, nello stesso ordine, ma ruotate in modo circolare!
-The smallest cyclic number is the 6-digit number 142857 : 142857 × 1 = 142857 142857 × 2 = 285714 142857 × 3 = 428571 142857 × 4 = 571428 142857 × 5 = 714285 142857 × 6 = 857142
+Il numero ciclico più piccolo è il numero a 6 cifre 142857:
-The next cyclic number is 0588235294117647 with 16 digits : 0588235294117647 × 1 = 0588235294117647 0588235294117647 × 2 = 1176470588235294 0588235294117647 × 3 = 1764705882352941 ... 0588235294117647 × 16 = 9411764705882352
+$$\begin{align} & 142857 × 1 = 142857 \\\\ & 142857 × 2 = 285714 \\\\ & 142857 × 3 = 428571 \\\\ & 142857 × 4 = 571428 \\\\ & 142857 × 5 = 714285 \\\\ & 142857 × 6 = 857142 \end{align}$$
-Note that for cyclic numbers, leading zeros are important.
+Il successivo numero ciclico è 0588235294117647 con 16 cifre:
-There is only one cyclic number for which, the eleven leftmost digits are 00000000137 and the five rightmost digits are 56789 (i.e., it has the form 00000000137...56789 with an unknown number of digits in the middle). Find the sum of all its digits.
+$$\begin{align} & 0588235294117647 × 1 = 0588235294117647 \\\\ & 0588235294117647 × 2 = 1176470588235294 \\\\ & 0588235294117647 × 3 = 1764705882352941 \\\\ & \ldots \\\\ & 0588235294117647 × 16 = 9411764705882352 \end{align}$$
+
+Nota che per i numeri ciclici gli zeri iniziali sono importanti.
+
+C'è solo un numero ciclico per il quale le undici cifre più a sinistra sono 00000000137 e le cinque cifre più a destra sono 56789 (cioè ha la forma $00000000137\ldots56789$ con un numero sconosciuto di cifre nel mezzo). Trova la somma di tutte le sue cifre.
# --hints--
-`euler358()` should return 3284144505.
+`cyclicNumbers()` dovrebbe restituire `3284144505`.
```js
-assert.strictEqual(euler358(), 3284144505);
+assert.strictEqual(cyclicNumbers(), 3284144505);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler358(), 3284144505);
## --seed-contents--
```js
-function euler358() {
+function cyclicNumbers() {
return true;
}
-euler358();
+cyclicNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
index 971ae0f401..2deee5cabb 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
@@ -1,6 +1,6 @@
---
id: 5900f4d31000cf542c50ffe6
-title: 'Problem 359: Hilbert''s New Hotel'
+title: 'Problema 359: Il nuovo Hotel di Hilbert'
challengeType: 5
forumTopicId: 302019
dashedName: problem-359-hilberts-new-hotel
@@ -8,24 +8,35 @@ dashedName: problem-359-hilberts-new-hotel
# --description--
-An infinite number of people (numbered 1, 2, 3, etc.) are lined up to get a room at Hilbert's newest infinite hotel. The hotel contains an infinite number of floors (numbered 1, 2, 3, etc.), and each floor contains an infinite number of rooms (numbered 1, 2, 3, etc.).
+Un numero infinito di persone (numerate 1, 2, 3, ecc.) sono in fila per prendere una stanza al nuovo hotel infinito di Hilbert. L'hotel contienue un numero infinito di piani (numerati 1, 2, 3, ecc) e ogni piano contiene un numero infinito di stanze (numerate 1, 2, 3, ecc.).
-Initially the hotel is empty. Hilbert declares a rule on how the nth person is assigned a room: person n gets the first vacant room in the lowest numbered floor satisfying either of the following: the floor is empty the floor is not empty, and if the latest person taking a room in that floor is person m, then m + n is a perfect square
+All'inizio l'hotel è vuoto. Hilbert dichiara una regola su come la $n$-sima persona è assegnata una stanza: persona $n$ riceve la prima stanza vuota al piano col numero più basso che soddisfa una delle seguenti condizioni:
-Person 1 gets room 1 in floor 1 since floor 1 is empty. Person 2 does not get room 2 in floor 1 since 1 + 2 = 3 is not a perfect square. Person 2 instead gets room 1 in floor 2 since floor 2 is empty. Person 3 gets room 2 in floor 1 since 1 + 3 = 4 is a perfect square.
+- il piano è vuoto
+- il piano non è vuoto, e se l'ultima persona che ha preso una stanza in quel piano è persona $m$ allora $m + n$ è un quadrato perfetto
-Eventually, every person in the line gets a room in the hotel.
+Persona 1 prende stanza 1 in piano 1 visto che piano 1 è vuoto.
-Define P(f, r) to be n if person n occupies room r in floor f, and 0 if no person occupies the room. Here are a few examples: P(1, 1) = 1 P(1, 2) = 3 P(2, 1) = 2 P(10, 20) = 440 P(25, 75) = 4863 P(99, 100) = 19454
+Persona 2 non prende stanza 2 nel piano 1 visto che 1 + 2 = 3 non è un quadrato perfetto.
-Find the sum of all P(f, r) for all positive f and r such that f × r = 71328803586048 and give the last 8 digits as your answer.
+Persona 2 invece prende stanza 1 nel piano 2 visto che piano 2 è vuoto.
+
+Persona 3 prende stanza 2 sul piano 1 visto che 1 + 3 = 4 è un quadrato perfetto.
+
+Alla fine, ogni persona in fila ottiene una stanza nell'hotel.
+
+Sia $P(f, r)$ $n$ se la persona $n$ occupa stanza $r$ al piano $f$, e 0 se nessuna persona occupa la stanza. Ecco alcuni esempi:
+
+$$\begin{align} & P(1, 1) = 1 \\\\ & P(1, 2) = 3 \\\\ & P(2, 1) = 2 \\\\ & P(10, 20) = 440 \\\\ & P(25, 75) = 4863 \\\\ & P(99, 100) = 19454 \end{align}$$
+
+Trova la somma di tutti i $P(f, r)$ per tutti i positivi $f$ e $r$ in modo tale che $f × r = 71\\,328\\,803\\,586\\,048$ e dai le ultime 8 cifre come risposta.
# --hints--
-`euler359()` should return 40632119.
+`hilbertsNewHotel()` dovrebbe restituire `40632119`.
```js
-assert.strictEqual(euler359(), 40632119);
+assert.strictEqual(hilbertsNewHotel(), 40632119);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler359(), 40632119);
## --seed-contents--
```js
-function euler359() {
+function hilbertsNewHotel() {
return true;
}
-euler359();
+hilbertsNewHotel();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
index f028a5d58b..9c9e21541d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
@@ -1,6 +1,6 @@
---
id: 5900f4d41000cf542c50ffe7
-title: 'Problem 360: Scary Sphere'
+title: 'Problema 360: Sfera Spaventosa'
challengeType: 5
forumTopicId: 302021
dashedName: problem-360-scary-sphere
@@ -8,20 +8,24 @@ dashedName: problem-360-scary-sphere
# --description--
-Given two points (x1,y1,z1) and (x2,y2,z2) in three dimensional space, the Manhattan distance between those points is defined as |x1-x2|+|y1-y2|+|z1-z2|.
+Dati due punti ($x_1$, $y_1$, $z_1$) e ($x_2$, $y_2$, $z_2$) nello spazio tridimensionale, la distanza di Manhattan tra questi punti è definita come $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$.
-Let C(r) be a sphere with radius r and center in the origin O(0,0,0). Let I(r) be the set of all points with integer coordinates on the surface of C(r). Let S(r) be the sum of the Manhattan distances of all elements of I(r) to the origin O.
+Sia $C(r)$ una sfera con raggio $r$ e centro nell'origine $O(0, 0, 0)$.
-E.g. S(45)=34518.
+Sia $I(r)$ l'insieme di tutti i punti con coordinate intere sulla superficie di $C(r)$.
-Find S(1010).
+Sia $S(r)$ la somma delle distanze di Manhattan di tutti gli elementi di $I(r)$ dall'origine $O$.
+
+Ad es. $S(45)=34518$.
+
+Trova $S({10}^{10})$.
# --hints--
-`euler360()` should return 878825614395267100.
+`scarySphere()` dovrebbe restituire `878825614395267100`.
```js
-assert.strictEqual(euler360(), 878825614395267100);
+assert.strictEqual(scarySphere(), 878825614395267100);
```
# --seed--
@@ -29,12 +33,12 @@ assert.strictEqual(euler360(), 878825614395267100);
## --seed-contents--
```js
-function euler360() {
+function scarySphere() {
return true;
}
-euler360();
+scarySphere();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
index bc13159789..db80599e17 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4d51000cf542c50ffe8
-title: 'Problem 361: Subsequence of Thue-Morse sequence'
+title: 'Problema 361: sottosequenza della sequenza di Thue-Morse'
challengeType: 5
forumTopicId: 302022
dashedName: problem-361-subsequence-of-thue-morse-sequence
@@ -8,30 +8,30 @@ dashedName: problem-361-subsequence-of-thue-morse-sequence
# --description--
-The Thue-Morse sequence {Tn} is a binary sequence satisfying:
+La sequenza Thue-Morse \\{T_n\\}$ è una sequenza binaria che soddisfa:
-T0 = 0
+- $T_0 = 0$
+- $T_{2n} = T_n$
+- $T_{2n + 1} = 1 - T_n$
-T2n = Tn
+I primi termini di $\\{T_n\\}$ sono dati come segue: $01101001\color{red}{10010}1101001011001101001\ldots$.
-T2n+1 = 1 - Tn
+Definiamo $\\{A_n\\}$ come la sequenza ordinata di interi in modo che l'espressione binaria di ogni elemento appaia come successiva in $\\{T_n\\}$. Ad esempio, il numero decimale 18 è espresso come 10010 in binario. 10010 appare in $\\{T_n\\}$ ($T_8$ a $T_{12}$), quindi 18 è un elemento di $\\{A_n\\}$. Il numero decimale 14 è espresso come 1110 in binario. 1110 non appare mai in $\\{T_n\\}$, quindi 14 non è un elemento di $\\{A_n\\}$.
-The first several terms of {Tn} are given as follows: 01101001100101101001011001101001....
+I primi svariati termini di $A_n$ sono dati come segue:
-We define {An} as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in {Tn}. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in {Tn} (T8 to T12), so 18 is an element of {An}. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in {Tn}, so 14 is not an element of {An}.
+$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
-The first several terms of An are given as follows: n0123456789101112…An012345691011121318…
+Possiamo verificare che $A_{100} = 3251$ e $A_{1000} = 80\\,852\\,364\\,498$.
-We can also verify that A100 = 3251 and A1000 = 80852364498.
-
-Find the last 9 digits of .
+Trova le ultime 9 cifre di \displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
# --hints--
-`euler361()` should return 178476944.
+`subsequenceOfThueMorseSequence()` dovrebbe restituire `178476944`.
```js
-assert.strictEqual(euler361(), 178476944);
+assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler361(), 178476944);
## --seed-contents--
```js
-function euler361() {
+function subsequenceOfThueMorseSequence() {
return true;
}
-euler361();
+subsequenceOfThueMorseSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
index 4d6bc3f4a9..8145f50a49 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
@@ -1,6 +1,6 @@
---
id: 5900f4d61000cf542c50ffe9
-title: 'Problem 362: Squarefree factors'
+title: 'Problema 362: Fattori senza quadrato'
challengeType: 5
forumTopicId: 302023
dashedName: problem-362-squarefree-factors
@@ -8,28 +8,28 @@ dashedName: problem-362-squarefree-factors
# --description--
-Consider the number 54.
+Considera il numero 54.
-54 can be factored in 7 distinct ways into one or more factors larger than 1:
+54 può essere fattorizzato in 7 modi distinti in uno o più fattori superiori a 1:
-54, 2×27, 3×18, 6×9, 3×3×6, 2×3×9 and 2×3×3×3.
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9 \text{ and } 2 × 3 × 3 × 3$$
-If we require that the factors are all squarefree only two ways remain: 3×3×6 and 2×3×3×3.
+Se abbiamo bisogno che i fattori siano tutti privi di quadrati, rimangono solo due modi: $3 × 3 × 6$ e $2 × 3 × 3 × 3$.
-Let's call Fsf(n) the number of ways n can be factored into one or more squarefree factors larger than 1, so Fsf(54)=2.
+Chiamiamo $Fsf(n)$ il numero di modi in cui $n$ può essere fattorizzato senza quadrati più grandi di 1, quindi $Fsf(54) = 2$.
-Let S(n) be ∑Fsf(k) for k=2 to n.
+Sia $S(n)$ $\sum Fsf(k)$ per $k = 2$ a $n$.
-S(100)=193.
+$S(100) = 193$.
-Find S(10 000 000 000).
+Trova $S(10\\,000\\,000\\,000)$.
# --hints--
-`euler362()` should return 457895958010.
+`squarefreeFactors()` dovrebbe restituire `457895958010`.
```js
-assert.strictEqual(euler362(), 457895958010);
+assert.strictEqual(squarefreeFactors(), 457895958010);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler362(), 457895958010);
## --seed-contents--
```js
-function euler362() {
+function squarefreeFactors() {
return true;
}
-euler362();
+squarefreeFactors();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
index 2fde41d1eb..b008e3690e 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffeb
-title: 'Problem 363: Bézier Curves'
+title: 'Problema 363: Curve di Bézier'
challengeType: 5
forumTopicId: 302024
dashedName: problem-363-bzier-curves
@@ -8,24 +8,32 @@ dashedName: problem-363-bzier-curves
# --description--
-A cubic Bézier curve is defined by four points: P0, P1, P2 and P3.
+Una curva cubica di Bézier è definita da quattro punti: $P_0$, $P_1$, $P_2$ e $P_3$.
-The curve is constructed as follows: On the segments P0P1, P1P2 and P2P3 the points Q0,Q1 and Q2 are drawn such that P0Q0 / P0P1 = P1Q1 / P1P2 = P2Q2 / P2P3 = t (t in \[0,1]). On the segments Q0Q1 and Q1Q2 the points R0 and R1 are drawn such that Q0R0 / Q0Q1 = Q1R1 / Q1Q2 = t for the same value of t. On the segment R0R1 the point B is drawn such that R0B / R0R1 = t for the same value of t. The Bézier curve defined by the points P0, P1, P2, P3 is the locus of B as Q0 takes all possible positions on the segment P0P1. (Please note that for all points the value of t is the same.)
+La curva è costruita come segue:
-At this (external) web address you will find an applet that allows you to drag the points P0, P1, P2 and P3 to see what the Bézier curve (green curve) defined by those points looks like. You can also drag the point Q0 along the segment P0P1.
+
-Find the number of L ≤ 5·1011 such that B(L) = 450.
+Una particolare cella è occupata dall'ape regina. Per un numero reale positivo $L$, sia $B(L)$ il conteggio delle celle con distanza $L$ dalla cella dell'ape regina (tutte le distanze sono misurate da centro a centro); puoi assumere che il favo è abbastanza grande da accomodare per ogni distanza che vogliamo considerare.
+
+Per esempio, $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$ e $B(111\\,111\\,111) = 54$.
+
+Trova il numero di $L ≤ 5 \times {10}^{11}$ per cui $B(L) = 450$.
# --hints--
-`euler354()` should return 58065134.
+`distancesInHoneycomb()` dovrebbe restituire `58065134`.
```js
-assert.strictEqual(euler354(), 58065134);
+assert.strictEqual(distancesInHoneycomb(), 58065134);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler354(), 58065134);
## --seed-contents--
```js
-function euler354() {
+function distancesInHoneycomb() {
return true;
}
-euler354();
+distancesInHoneycomb();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
index a166a1057a..73bcbb7f10 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe2
-title: 'Problem 355: Maximal coprime subset'
+title: 'Problema 355: Massimo sottoinsieme di coprimi'
challengeType: 5
forumTopicId: 302015
dashedName: problem-355-maximal-coprime-subset
@@ -8,18 +8,18 @@ dashedName: problem-355-maximal-coprime-subset
# --description--
-Define Co(n) to be the maximal possible sum of a set of mutually co-prime elements from {1, 2, ..., n}. For example Co(10) is 30 and hits that maximum on the subset {1, 5, 7, 8, 9}.
+Definisci $Co(n)$ in modo che sia la massima somma possibile di un insieme di elementi reciprocamente co-primi da $\\{1, 2, \ldots, n\\}$. Per esempio $Co(10)$ è di 30 e ha il suo massimo per il sottoinsieme $\\{1, 5, 7, 8, 9\\}$.
-You are given that Co(30) = 193 and Co(100) = 1356.
+Ti viene dato che $Co(30) = 193$ e $Co(100) = 1356$.
-Find Co(200000).
+Trova $Co(200\\,000)$.
# --hints--
-`euler355()` should return 1726545007.
+`maximalCoprimeSubset()` dovrebbe restituire `1726545007`.
```js
-assert.strictEqual(euler355(), 1726545007);
+assert.strictEqual(maximalCoprimeSubset(), 1726545007);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler355(), 1726545007);
## --seed-contents--
```js
-function euler355() {
+function maximalCoprimeSubset() {
return true;
}
-euler355();
+maximalCoprimeSubset();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
index 9027dcecf9..494e59ce91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe3
-title: 'Problem 356: Largest roots of cubic polynomials'
+title: 'Problema 356: Le più grandi radici dei polinomi cubici'
challengeType: 5
forumTopicId: 302016
dashedName: problem-356-largest-roots-of-cubic-polynomials
@@ -8,20 +8,20 @@ dashedName: problem-356-largest-roots-of-cubic-polynomials
# --description--
-Let an be the largest real root of a polynomial g(x) = x3 - 2n·x2 + n.
+Sia $a_n$ la più grande radice reale di un polinomio $g(x) = x^3 - 2^n \times x^2 + n$.
-For example, a2 = 3.86619826...
+Per esempio, $a_2 = 3.86619826\ldots$
-Find the last eight digits of.
+Trova le ultime otto cifre di $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
-Note: represents the floor function.
+**Nota:** $\lfloor a\rfloor$ rappresenta la funzione floor.
# --hints--
-`euler356()` should return 28010159.
+`rootsOfCubicPolynomials()` dovrebbe restituire `28010159`.
```js
-assert.strictEqual(euler356(), 28010159);
+assert.strictEqual(rootsOfCubicPolynomials(), 28010159);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler356(), 28010159);
## --seed-contents--
```js
-function euler356() {
+function rootsOfCubicPolynomials() {
return true;
}
-euler356();
+rootsOfCubicPolynomials();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
index 1bb3f094a2..960124e437 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d11000cf542c50ffe4
-title: 'Problem 357: Prime generating integers'
+title: 'Problema 357: Numeri interi generatori di numeri primi'
challengeType: 5
forumTopicId: 302017
dashedName: problem-357-prime-generating-integers
@@ -8,18 +8,18 @@ dashedName: problem-357-prime-generating-integers
# --description--
-Consider the divisors of 30: 1,2,3,5,6,10,15,30.
+Considera i divisori di 30: 1, 2, 3, 5, 6, 10, 15, 30.
-It can be seen that for every divisor d of 30, d+30/d is prime.
+Si può vedere che per ogni divisore $d$ di 30, $d + \frac{30}{d}$ è primo.
-Find the sum of all positive integers n not exceeding 100 000 000such that for every divisor d of n, d+n/d is prime.
+Trova la somma di tutti gli interi positivi $n$ non superiore a $100\\,000\\, 00$ tale che per ogni divisore $d$ di $n$, $d + \frac{n}{d}$ è primo.
# --hints--
-`euler357()` should return 1739023853137.
+`primeGeneratingIntegers()` dovrebbe restituire `1739023853137`.
```js
-assert.strictEqual(euler357(), 1739023853137);
+assert.strictEqual(primeGeneratingIntegers(), 1739023853137);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler357(), 1739023853137);
## --seed-contents--
```js
-function euler357() {
+function primeGeneratingIntegers() {
return true;
}
-euler357();
+primeGeneratingIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
index fb08a667a8..1e526f8262 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d21000cf542c50ffe5
-title: 'Problem 358: Cyclic numbers'
+title: 'Problema 358: Numeri ciclici'
challengeType: 5
forumTopicId: 302018
dashedName: problem-358-cyclic-numbers
@@ -8,24 +8,28 @@ dashedName: problem-358-cyclic-numbers
# --description--
-A cyclic number with n digits has a very interesting property:
+Un numero ciclico con $n$ cifre ha una proprietà molto interessante:
-When it is multiplied by 1, 2, 3, 4, ... n, all the products have exactly the same digits, in the same order, but rotated in a circular fashion!
+Quando è moltiplicato per 1, 2, 3, 4, ... $n$, tutti i prodotti hanno esattamente le stesse cifre, nello stesso ordine, ma ruotate in modo circolare!
-The smallest cyclic number is the 6-digit number 142857 : 142857 × 1 = 142857 142857 × 2 = 285714 142857 × 3 = 428571 142857 × 4 = 571428 142857 × 5 = 714285 142857 × 6 = 857142
+Il numero ciclico più piccolo è il numero a 6 cifre 142857:
-The next cyclic number is 0588235294117647 with 16 digits : 0588235294117647 × 1 = 0588235294117647 0588235294117647 × 2 = 1176470588235294 0588235294117647 × 3 = 1764705882352941 ... 0588235294117647 × 16 = 9411764705882352
+$$\begin{align} & 142857 × 1 = 142857 \\\\ & 142857 × 2 = 285714 \\\\ & 142857 × 3 = 428571 \\\\ & 142857 × 4 = 571428 \\\\ & 142857 × 5 = 714285 \\\\ & 142857 × 6 = 857142 \end{align}$$
-Note that for cyclic numbers, leading zeros are important.
+Il successivo numero ciclico è 0588235294117647 con 16 cifre:
-There is only one cyclic number for which, the eleven leftmost digits are 00000000137 and the five rightmost digits are 56789 (i.e., it has the form 00000000137...56789 with an unknown number of digits in the middle). Find the sum of all its digits.
+$$\begin{align} & 0588235294117647 × 1 = 0588235294117647 \\\\ & 0588235294117647 × 2 = 1176470588235294 \\\\ & 0588235294117647 × 3 = 1764705882352941 \\\\ & \ldots \\\\ & 0588235294117647 × 16 = 9411764705882352 \end{align}$$
+
+Nota che per i numeri ciclici gli zeri iniziali sono importanti.
+
+C'è solo un numero ciclico per il quale le undici cifre più a sinistra sono 00000000137 e le cinque cifre più a destra sono 56789 (cioè ha la forma $00000000137\ldots56789$ con un numero sconosciuto di cifre nel mezzo). Trova la somma di tutte le sue cifre.
# --hints--
-`euler358()` should return 3284144505.
+`cyclicNumbers()` dovrebbe restituire `3284144505`.
```js
-assert.strictEqual(euler358(), 3284144505);
+assert.strictEqual(cyclicNumbers(), 3284144505);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler358(), 3284144505);
## --seed-contents--
```js
-function euler358() {
+function cyclicNumbers() {
return true;
}
-euler358();
+cyclicNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
index 971ae0f401..2deee5cabb 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
@@ -1,6 +1,6 @@
---
id: 5900f4d31000cf542c50ffe6
-title: 'Problem 359: Hilbert''s New Hotel'
+title: 'Problema 359: Il nuovo Hotel di Hilbert'
challengeType: 5
forumTopicId: 302019
dashedName: problem-359-hilberts-new-hotel
@@ -8,24 +8,35 @@ dashedName: problem-359-hilberts-new-hotel
# --description--
-An infinite number of people (numbered 1, 2, 3, etc.) are lined up to get a room at Hilbert's newest infinite hotel. The hotel contains an infinite number of floors (numbered 1, 2, 3, etc.), and each floor contains an infinite number of rooms (numbered 1, 2, 3, etc.).
+Un numero infinito di persone (numerate 1, 2, 3, ecc.) sono in fila per prendere una stanza al nuovo hotel infinito di Hilbert. L'hotel contienue un numero infinito di piani (numerati 1, 2, 3, ecc) e ogni piano contiene un numero infinito di stanze (numerate 1, 2, 3, ecc.).
-Initially the hotel is empty. Hilbert declares a rule on how the nth person is assigned a room: person n gets the first vacant room in the lowest numbered floor satisfying either of the following: the floor is empty the floor is not empty, and if the latest person taking a room in that floor is person m, then m + n is a perfect square
+All'inizio l'hotel è vuoto. Hilbert dichiara una regola su come la $n$-sima persona è assegnata una stanza: persona $n$ riceve la prima stanza vuota al piano col numero più basso che soddisfa una delle seguenti condizioni:
-Person 1 gets room 1 in floor 1 since floor 1 is empty. Person 2 does not get room 2 in floor 1 since 1 + 2 = 3 is not a perfect square. Person 2 instead gets room 1 in floor 2 since floor 2 is empty. Person 3 gets room 2 in floor 1 since 1 + 3 = 4 is a perfect square.
+- il piano è vuoto
+- il piano non è vuoto, e se l'ultima persona che ha preso una stanza in quel piano è persona $m$ allora $m + n$ è un quadrato perfetto
-Eventually, every person in the line gets a room in the hotel.
+Persona 1 prende stanza 1 in piano 1 visto che piano 1 è vuoto.
-Define P(f, r) to be n if person n occupies room r in floor f, and 0 if no person occupies the room. Here are a few examples: P(1, 1) = 1 P(1, 2) = 3 P(2, 1) = 2 P(10, 20) = 440 P(25, 75) = 4863 P(99, 100) = 19454
+Persona 2 non prende stanza 2 nel piano 1 visto che 1 + 2 = 3 non è un quadrato perfetto.
-Find the sum of all P(f, r) for all positive f and r such that f × r = 71328803586048 and give the last 8 digits as your answer.
+Persona 2 invece prende stanza 1 nel piano 2 visto che piano 2 è vuoto.
+
+Persona 3 prende stanza 2 sul piano 1 visto che 1 + 3 = 4 è un quadrato perfetto.
+
+Alla fine, ogni persona in fila ottiene una stanza nell'hotel.
+
+Sia $P(f, r)$ $n$ se la persona $n$ occupa stanza $r$ al piano $f$, e 0 se nessuna persona occupa la stanza. Ecco alcuni esempi:
+
+$$\begin{align} & P(1, 1) = 1 \\\\ & P(1, 2) = 3 \\\\ & P(2, 1) = 2 \\\\ & P(10, 20) = 440 \\\\ & P(25, 75) = 4863 \\\\ & P(99, 100) = 19454 \end{align}$$
+
+Trova la somma di tutti i $P(f, r)$ per tutti i positivi $f$ e $r$ in modo tale che $f × r = 71\\,328\\,803\\,586\\,048$ e dai le ultime 8 cifre come risposta.
# --hints--
-`euler359()` should return 40632119.
+`hilbertsNewHotel()` dovrebbe restituire `40632119`.
```js
-assert.strictEqual(euler359(), 40632119);
+assert.strictEqual(hilbertsNewHotel(), 40632119);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler359(), 40632119);
## --seed-contents--
```js
-function euler359() {
+function hilbertsNewHotel() {
return true;
}
-euler359();
+hilbertsNewHotel();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
index f028a5d58b..9c9e21541d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
@@ -1,6 +1,6 @@
---
id: 5900f4d41000cf542c50ffe7
-title: 'Problem 360: Scary Sphere'
+title: 'Problema 360: Sfera Spaventosa'
challengeType: 5
forumTopicId: 302021
dashedName: problem-360-scary-sphere
@@ -8,20 +8,24 @@ dashedName: problem-360-scary-sphere
# --description--
-Given two points (x1,y1,z1) and (x2,y2,z2) in three dimensional space, the Manhattan distance between those points is defined as |x1-x2|+|y1-y2|+|z1-z2|.
+Dati due punti ($x_1$, $y_1$, $z_1$) e ($x_2$, $y_2$, $z_2$) nello spazio tridimensionale, la distanza di Manhattan tra questi punti è definita come $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$.
-Let C(r) be a sphere with radius r and center in the origin O(0,0,0). Let I(r) be the set of all points with integer coordinates on the surface of C(r). Let S(r) be the sum of the Manhattan distances of all elements of I(r) to the origin O.
+Sia $C(r)$ una sfera con raggio $r$ e centro nell'origine $O(0, 0, 0)$.
-E.g. S(45)=34518.
+Sia $I(r)$ l'insieme di tutti i punti con coordinate intere sulla superficie di $C(r)$.
-Find S(1010).
+Sia $S(r)$ la somma delle distanze di Manhattan di tutti gli elementi di $I(r)$ dall'origine $O$.
+
+Ad es. $S(45)=34518$.
+
+Trova $S({10}^{10})$.
# --hints--
-`euler360()` should return 878825614395267100.
+`scarySphere()` dovrebbe restituire `878825614395267100`.
```js
-assert.strictEqual(euler360(), 878825614395267100);
+assert.strictEqual(scarySphere(), 878825614395267100);
```
# --seed--
@@ -29,12 +33,12 @@ assert.strictEqual(euler360(), 878825614395267100);
## --seed-contents--
```js
-function euler360() {
+function scarySphere() {
return true;
}
-euler360();
+scarySphere();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
index bc13159789..db80599e17 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4d51000cf542c50ffe8
-title: 'Problem 361: Subsequence of Thue-Morse sequence'
+title: 'Problema 361: sottosequenza della sequenza di Thue-Morse'
challengeType: 5
forumTopicId: 302022
dashedName: problem-361-subsequence-of-thue-morse-sequence
@@ -8,30 +8,30 @@ dashedName: problem-361-subsequence-of-thue-morse-sequence
# --description--
-The Thue-Morse sequence {Tn} is a binary sequence satisfying:
+La sequenza Thue-Morse \\{T_n\\}$ è una sequenza binaria che soddisfa:
-T0 = 0
+- $T_0 = 0$
+- $T_{2n} = T_n$
+- $T_{2n + 1} = 1 - T_n$
-T2n = Tn
+I primi termini di $\\{T_n\\}$ sono dati come segue: $01101001\color{red}{10010}1101001011001101001\ldots$.
-T2n+1 = 1 - Tn
+Definiamo $\\{A_n\\}$ come la sequenza ordinata di interi in modo che l'espressione binaria di ogni elemento appaia come successiva in $\\{T_n\\}$. Ad esempio, il numero decimale 18 è espresso come 10010 in binario. 10010 appare in $\\{T_n\\}$ ($T_8$ a $T_{12}$), quindi 18 è un elemento di $\\{A_n\\}$. Il numero decimale 14 è espresso come 1110 in binario. 1110 non appare mai in $\\{T_n\\}$, quindi 14 non è un elemento di $\\{A_n\\}$.
-The first several terms of {Tn} are given as follows: 01101001100101101001011001101001....
+I primi svariati termini di $A_n$ sono dati come segue:
-We define {An} as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in {Tn}. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in {Tn} (T8 to T12), so 18 is an element of {An}. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in {Tn}, so 14 is not an element of {An}.
+$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
-The first several terms of An are given as follows: n0123456789101112…An012345691011121318…
+Possiamo verificare che $A_{100} = 3251$ e $A_{1000} = 80\\,852\\,364\\,498$.
-We can also verify that A100 = 3251 and A1000 = 80852364498.
-
-Find the last 9 digits of .
+Trova le ultime 9 cifre di \displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
# --hints--
-`euler361()` should return 178476944.
+`subsequenceOfThueMorseSequence()` dovrebbe restituire `178476944`.
```js
-assert.strictEqual(euler361(), 178476944);
+assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler361(), 178476944);
## --seed-contents--
```js
-function euler361() {
+function subsequenceOfThueMorseSequence() {
return true;
}
-euler361();
+subsequenceOfThueMorseSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
index 4d6bc3f4a9..8145f50a49 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
@@ -1,6 +1,6 @@
---
id: 5900f4d61000cf542c50ffe9
-title: 'Problem 362: Squarefree factors'
+title: 'Problema 362: Fattori senza quadrato'
challengeType: 5
forumTopicId: 302023
dashedName: problem-362-squarefree-factors
@@ -8,28 +8,28 @@ dashedName: problem-362-squarefree-factors
# --description--
-Consider the number 54.
+Considera il numero 54.
-54 can be factored in 7 distinct ways into one or more factors larger than 1:
+54 può essere fattorizzato in 7 modi distinti in uno o più fattori superiori a 1:
-54, 2×27, 3×18, 6×9, 3×3×6, 2×3×9 and 2×3×3×3.
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9 \text{ and } 2 × 3 × 3 × 3$$
-If we require that the factors are all squarefree only two ways remain: 3×3×6 and 2×3×3×3.
+Se abbiamo bisogno che i fattori siano tutti privi di quadrati, rimangono solo due modi: $3 × 3 × 6$ e $2 × 3 × 3 × 3$.
-Let's call Fsf(n) the number of ways n can be factored into one or more squarefree factors larger than 1, so Fsf(54)=2.
+Chiamiamo $Fsf(n)$ il numero di modi in cui $n$ può essere fattorizzato senza quadrati più grandi di 1, quindi $Fsf(54) = 2$.
-Let S(n) be ∑Fsf(k) for k=2 to n.
+Sia $S(n)$ $\sum Fsf(k)$ per $k = 2$ a $n$.
-S(100)=193.
+$S(100) = 193$.
-Find S(10 000 000 000).
+Trova $S(10\\,000\\,000\\,000)$.
# --hints--
-`euler362()` should return 457895958010.
+`squarefreeFactors()` dovrebbe restituire `457895958010`.
```js
-assert.strictEqual(euler362(), 457895958010);
+assert.strictEqual(squarefreeFactors(), 457895958010);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler362(), 457895958010);
## --seed-contents--
```js
-function euler362() {
+function squarefreeFactors() {
return true;
}
-euler362();
+squarefreeFactors();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
index 2fde41d1eb..b008e3690e 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffeb
-title: 'Problem 363: Bézier Curves'
+title: 'Problema 363: Curve di Bézier'
challengeType: 5
forumTopicId: 302024
dashedName: problem-363-bzier-curves
@@ -8,24 +8,32 @@ dashedName: problem-363-bzier-curves
# --description--
-A cubic Bézier curve is defined by four points: P0, P1, P2 and P3.
+Una curva cubica di Bézier è definita da quattro punti: $P_0$, $P_1$, $P_2$ e $P_3$.
-The curve is constructed as follows: On the segments P0P1, P1P2 and P2P3 the points Q0,Q1 and Q2 are drawn such that P0Q0 / P0P1 = P1Q1 / P1P2 = P2Q2 / P2P3 = t (t in \[0,1]). On the segments Q0Q1 and Q1Q2 the points R0 and R1 are drawn such that Q0R0 / Q0Q1 = Q1R1 / Q1Q2 = t for the same value of t. On the segment R0R1 the point B is drawn such that R0B / R0R1 = t for the same value of t. The Bézier curve defined by the points P0, P1, P2, P3 is the locus of B as Q0 takes all possible positions on the segment P0P1. (Please note that for all points the value of t is the same.)
+La curva è costruita come segue:
-At this (external) web address you will find an applet that allows you to drag the points P0, P1, P2 and P3 to see what the Bézier curve (green curve) defined by those points looks like. You can also drag the point Q0 along the segment P0P1.
+ -From the construction it is clear that the Bézier curve will be tangent to the segments P0P1 in P0 and P2P3 in P3.
+Sui segmenti $P_0P_1$, $P_1P_2$ e $P_2P_3$ i punti $Q_0$,$Q_1$ e $Q_2$ sono disegnati in modo tale che $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, con $t$ in [0,1].
-A cubic Bézier curve with P0=(1,0), P1=(1,v), P2=(v,1) and P3=(0,1) is used to approximate a quarter circle. The value v > 0 is chosen such that the area enclosed by the lines OP0, OP3 and the curve is equal to π/4 (the area of the quarter circle).
+Sui segmenti $Q_0Q_1$ e $Q_1Q_2$ i punti $R_0$ e $R_1$ sono disegnati in modo tale che $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ per lo stesso valore di $t$.
-By how many percent does the length of the curve differ from the length of the quarter circle? That is, if L is the length of the curve, calculate 100 × L − π/2π/2Give your answer rounded to 10 digits behind the decimal point.
+Sul segmento $R_0R_1$ il punto $B$ è disegnato in modo tale che $\frac{R_0B}{R_0R_1} = t$ per lo stesso valore di $t$.
+
+La curva di Bézier definita dai punti $P_0$, $P_1$, $P_2$, $P_3$ è il luogo di $B$ tale che $Q_0$ prende tutte le posizioni possibili sul segmento $P_0P_1$. (Si noti che per tutti i punti il valore di $t$ è lo stesso.)
+
+Dalla costruzione è chiaro che la curva di Bézier sarà tangente ai segmenti $P_0P_1$ in $P_0$ e $P_2P_3$ in $P_3$.
+
+Una curva cubica di Bézier con $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ e $P_3 = (0, 1)$ viene utilizzata per approssimare un quarto di cerchio. Il valore $v > 0$ è scelto in modo tale che l'area racchiusa tra le linee $OP_0$, $OP_3$ e la curva sia pari a $\frac{π}{4}$ (l'area del quarto di circonferenza).
+
+Di quanti punti percentuali la lunghezza della curva differisce dalla lunghezza del quarto di circonferenza? Cioè, se $L$ è la lunghezza della curva, calcolare $100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler363()` should return 0.0000372091.
+`bezierCurves()` dovrebbe restituire `0.0000372091`.
```js
-assert.strictEqual(euler363(), 0.0000372091);
+assert.strictEqual(bezierCurves(), 0.0000372091);
```
# --seed--
@@ -33,12 +41,12 @@ assert.strictEqual(euler363(), 0.0000372091);
## --seed-contents--
```js
-function euler363() {
+function bezierCurves() {
return true;
}
-euler363();
+bezierCurves();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
index 84637798b8..f5ce69e0a1 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffea
-title: 'Problem 364: Comfortable distance'
+title: 'Problema 364: Distanza confortevole'
challengeType: 5
forumTopicId: 302025
dashedName: problem-364-comfortable-distance
@@ -8,24 +8,26 @@ dashedName: problem-364-comfortable-distance
# --description--
-There are N seats in a row. N people come after each other to fill the seats according to the following rules:
+Ci sono $N$ posti in fila. $N$ persone vengono una dopo l'altra per riempire i posti secondo le seguenti regole:
-If there is any seat whose adjacent seat(s) are not occupied take such a seat.
+1. Se esiste un sedile i cui sedili adiacenti non sono occupati prendono tale sedile.
+2. Se questo posto è occupato e c'è un posto per il quale solo un posto adiacente è occupato si prende tale posto.
+3. Altrimenti si prende uno dei posti disponibili rimanenti.
-If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
+Sia $T(N)$ il numero di possibilità che $N$ posti siano occupati da $N$ persone con le regole date. La seguente figura mostra $T(4) = 8$.
-Otherwise take one of the remaining available seats.
+
-From the construction it is clear that the Bézier curve will be tangent to the segments P0P1 in P0 and P2P3 in P3.
+Sui segmenti $P_0P_1$, $P_1P_2$ e $P_2P_3$ i punti $Q_0$,$Q_1$ e $Q_2$ sono disegnati in modo tale che $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, con $t$ in [0,1].
-A cubic Bézier curve with P0=(1,0), P1=(1,v), P2=(v,1) and P3=(0,1) is used to approximate a quarter circle. The value v > 0 is chosen such that the area enclosed by the lines OP0, OP3 and the curve is equal to π/4 (the area of the quarter circle).
+Sui segmenti $Q_0Q_1$ e $Q_1Q_2$ i punti $R_0$ e $R_1$ sono disegnati in modo tale che $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ per lo stesso valore di $t$.
-By how many percent does the length of the curve differ from the length of the quarter circle? That is, if L is the length of the curve, calculate 100 × L − π/2π/2Give your answer rounded to 10 digits behind the decimal point.
+Sul segmento $R_0R_1$ il punto $B$ è disegnato in modo tale che $\frac{R_0B}{R_0R_1} = t$ per lo stesso valore di $t$.
+
+La curva di Bézier definita dai punti $P_0$, $P_1$, $P_2$, $P_3$ è il luogo di $B$ tale che $Q_0$ prende tutte le posizioni possibili sul segmento $P_0P_1$. (Si noti che per tutti i punti il valore di $t$ è lo stesso.)
+
+Dalla costruzione è chiaro che la curva di Bézier sarà tangente ai segmenti $P_0P_1$ in $P_0$ e $P_2P_3$ in $P_3$.
+
+Una curva cubica di Bézier con $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ e $P_3 = (0, 1)$ viene utilizzata per approssimare un quarto di cerchio. Il valore $v > 0$ è scelto in modo tale che l'area racchiusa tra le linee $OP_0$, $OP_3$ e la curva sia pari a $\frac{π}{4}$ (l'area del quarto di circonferenza).
+
+Di quanti punti percentuali la lunghezza della curva differisce dalla lunghezza del quarto di circonferenza? Cioè, se $L$ è la lunghezza della curva, calcolare $100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler363()` should return 0.0000372091.
+`bezierCurves()` dovrebbe restituire `0.0000372091`.
```js
-assert.strictEqual(euler363(), 0.0000372091);
+assert.strictEqual(bezierCurves(), 0.0000372091);
```
# --seed--
@@ -33,12 +41,12 @@ assert.strictEqual(euler363(), 0.0000372091);
## --seed-contents--
```js
-function euler363() {
+function bezierCurves() {
return true;
}
-euler363();
+bezierCurves();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
index 84637798b8..f5ce69e0a1 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffea
-title: 'Problem 364: Comfortable distance'
+title: 'Problema 364: Distanza confortevole'
challengeType: 5
forumTopicId: 302025
dashedName: problem-364-comfortable-distance
@@ -8,24 +8,26 @@ dashedName: problem-364-comfortable-distance
# --description--
-There are N seats in a row. N people come after each other to fill the seats according to the following rules:
+Ci sono $N$ posti in fila. $N$ persone vengono una dopo l'altra per riempire i posti secondo le seguenti regole:
-If there is any seat whose adjacent seat(s) are not occupied take such a seat.
+1. Se esiste un sedile i cui sedili adiacenti non sono occupati prendono tale sedile.
+2. Se questo posto è occupato e c'è un posto per il quale solo un posto adiacente è occupato si prende tale posto.
+3. Altrimenti si prende uno dei posti disponibili rimanenti.
-If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
+Sia $T(N)$ il numero di possibilità che $N$ posti siano occupati da $N$ persone con le regole date. La seguente figura mostra $T(4) = 8$.
-Otherwise take one of the remaining available seats.
+ -Let T(N) be the number of possibilities that N seats are occupied by N people with the given rules. The following figure shows T(4)=8.
+Possiamo verificare che $T(10) = 61\\,632$ e $T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094$.
-We can verify that T(10) = 61632 and T(1 000) mod 100 000 007 = 47255094. Find T(1 000 000) mod 100 000 007.
+Trova $T(1\\,000\\,000)\bmod 100\\,000\\,007$.
# --hints--
-`euler364()` should return 44855254.
+`comfortableDistance()` dovrebbe restituire `44855254`.
```js
-assert.strictEqual(euler364(), 44855254);
+assert.strictEqual(comfortableDistance(), 44855254);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler364(), 44855254);
## --seed-contents--
```js
-function euler364() {
+function comfortableDistance() {
return true;
}
-euler364();
+comfortableDistance();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
index 1647ff46ea..90911f54a8 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffec
-title: 'Problem 365: A huge binomial coefficient'
+title: 'Problema 365: Un grande coefficiente binomiale'
challengeType: 5
forumTopicId: 302026
dashedName: problem-365-a-huge-binomial-coefficient
@@ -8,18 +8,18 @@ dashedName: problem-365-a-huge-binomial-coefficient
# --description--
-The binomial coefficient C(1018,109) is a number with more than 9 billion (9×109) digits.
+Il coefficiente binomiale $\displaystyle\binom{{10}^{18}}{{10}^9}$ è un numero con più di 9 miliardi ($9 × {10}^9$) di cifre.
-Let M(n,k,m) denote the binomial coefficient C(n,k) modulo m.
+Sia $M(n, k, m)$ il coefficiente binomiale $\displaystyle\binom{n}{k}$ modulo $m$.
-Calculate ∑M(1018,109,p*q*r) for 1000<p<q<r<5000 and p,q,r prime.
+Calcola $\sum M({10}^{18}, {10}^9, p \times q \times r)$ per $1000 < p < q < r < 5000$ e $p$, $q$, $r$ numeri primi.
# --hints--
-`euler365()` should return 162619462356610300.
+`hugeBinomialCoefficient()` dovrebbe restituire `162619462356610300`.
```js
-assert.strictEqual(euler365(), 162619462356610300);
+assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler365(), 162619462356610300);
## --seed-contents--
```js
-function euler365() {
+function hugeBinomialCoefficient() {
return true;
}
-euler365();
+hugeBinomialCoefficient();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
index b7f832ebf4..bf6252b74c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffed
-title: 'Problem 366: Stone Game III'
+title: 'Problema 366: Gioco delle pietre III'
challengeType: 5
forumTopicId: 302027
dashedName: problem-366-stone-game-iii
@@ -8,30 +8,44 @@ dashedName: problem-366-stone-game-iii
# --description--
-Two players, Anton and Bernhard, are playing the following game.
+Due giocatori, Anton e Bernhard, stanno giocando il seguente gioco.
-There is one pile of n stones.
+C'è una pila di $n$ pietre.
-The first player may remove any positive number of stones, but not the whole pile.
+Il primo giocatore può rimuovere qualsiasi numero positivo di pietre, ma non l'intera pila.
-Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+Successivamente, ogni giocatore può rimuovere al massimo il doppio del numero di pietre che il suo avversario ha preso nella mossa precedente.
-The player who removes the last stone wins.
+Il giocatore che rimuove l'ultima pietra vince.
-E.g. n=5 If the first player takes anything more than one stone the next player will be able to take all remaining stones. If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones. The first player cannot take all three because he may take at most 2x1=2 stones. So let's say he takes also one stone, leaving 2. The second player can take the two remaining stones and wins. So 5 is a losing position for the first player. For some winning positions there is more than one possible move for the first player. E.g. when n=17 the first player can remove one or four stones.
+Ad es. $n = 5$
-Let M(n) be the maximum number of stones the first player can take from a winning position at his first turn and M(n)=0 for any other position.
+Se il primo giocatore prende più di una pietra il giocatore successivo sarà in grado di prendere tutte le pietre rimaste.
-∑M(n) for n≤100 is 728.
+Se il primo giocatore prende una pietra, lasciandone quattro, anche il suo avversario prenderà una pietra, lasciando tre pietre.
-Find ∑M(n) for n≤1018. Give your answer modulo 108.
+Il primo giocatore non può prenderle tutte e tre perché può prendere al massimo $2 \times 1 = 2$ pietre. Quindi diciamo che anche lui prende una pietra, lasciandone 2.
+
+Il secondo giocatore può prendere le due pietre rimanenti e vince.
+
+Quindi 5 è una posizione perdente per il primo giocatore.
+
+Per alcune posizioni vincenti c'è più di una possibile mossa per il primo giocatore.
+
+Ad es. quando $n = 17$ il primo giocatore può rimuovere una o quattro pietre.
+
+Sia $M(n)$ il numero massimo di pietre che il primo giocatore può prendere da una posizione vincente al suo primo turno e $M(n) = 0$ per qualsiasi altra posizione.
+
+$\sum M(n)$ per $n ≤ 100$ è 728.
+
+Trova $\sum M(n)$ per $n ≤ {10}^{18}$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler366()` should return 88351299.
+`stoneGameThree()` dovrebbe restituire `88351299`.
```js
-assert.strictEqual(euler366(), 88351299);
+assert.strictEqual(stoneGameThree(), 88351299);
```
# --seed--
@@ -39,12 +53,12 @@ assert.strictEqual(euler366(), 88351299);
## --seed-contents--
```js
-function euler366() {
+function stoneGameThree() {
return true;
}
-euler366();
+stoneGameThree();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
index 979702592a..a34132973d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
@@ -1,6 +1,6 @@
---
id: 5900f4db1000cf542c50ffee
-title: 'Problem 367: Bozo sort'
+title: 'Problema 367: Bozo sort'
challengeType: 5
forumTopicId: 302028
dashedName: problem-367-bozo-sort
@@ -8,20 +8,32 @@ dashedName: problem-367-bozo-sort
# --description--
-Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+Bozo sort, da non confondersi con il'algoritmo leggermente meno efficiente bogo sort, consiste nel controllare se la sequenza di input è ordinata, e se non lo è scambiare a caso due elementi. Questo viene ripetuto fino a che la sequenza non è eventualmente in ordine.
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all 4! input sequences is 24.75. The already sorted sequence takes 0 steps.
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di scambi, mediato su tutte le $4!$ sequenze di input è $24.75$.
-In this problem we consider the following variant on bozo sort. If the sequence is not in order we pick three elements at random and shuffle these three elements randomly. All 3!=6 permutations of those three elements are equally likely. The already sorted sequence will take 0 steps. If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all 4! input sequences is 27.5. Consider as input sequences the permutations of the first 11 natural numbers. Averaged over all 11! input sequences, what is the expected number of shuffles this sorting algorithm will perform?
+La sequenza già ordinata ha bisogno di 0 step.
-Give your answer rounded to the nearest integer.
+In questo problema consideriamo le seguenti varianti nel bozo sort.
+
+Se la sequenza non è in ordine, scegliamo 3 elementi a caso e mescoliamo questi tre elementi casualmente.
+
+Tutte le $3! = 6$ permutazioni di questi tre elementi sono altrettanto probabili.
+
+La sequenza già ordinata ha bisogno di 0 step.
+
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di mescolamenti, mediato su tutte le $4!$ sequenze di input è $27.5$.
+
+Considera come sequenze di input le permutazioni dei primi 11 numeri naturali.
+
+Mediato su tutte le $11!$ sequenze di input, qual è il numero medio di mescolamenti che questo algoritmo performerà? Dai la tua risposta arrotondata al numero intero più vicino.
# --hints--
-`euler367()` should return 48271207.
+`bozoSort()` dovrebbe restituire `48271207`.
```js
-assert.strictEqual(euler367(), 48271207);
+assert.strictEqual(bozoSort(), 48271207);
```
# --seed--
@@ -29,12 +41,12 @@ assert.strictEqual(euler367(), 48271207);
## --seed-contents--
```js
-function euler367() {
+function bozoSort() {
return true;
}
-euler367();
+bozoSort();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
index dc9cf2f919..e262f93378 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
@@ -1,6 +1,6 @@
---
id: 5900f4dd1000cf542c50ffef
-title: 'Problem 368: A Kempner-like series'
+title: 'Problema 368: Una serie di Kempner'
challengeType: 5
forumTopicId: 302029
dashedName: problem-368-a-kempner-like-series
@@ -8,22 +8,26 @@ dashedName: problem-368-a-kempner-like-series
# --description--
-The harmonic series $1 + \\dfrac{1}{2} + \\dfrac{1}{3} + \\dfrac{1}{4} + ...$ is well known to be divergent.
+La serie armonica $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ è nota per essere divergente.
-If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+Se comunque si omette da questa serie ogni termine in cui il denominatore ha un 9 in esso, la serie converge abbastanza notevolmente a circa 22.9206766193. Questa serie armonica modificata è chiamata serie Kempner.
-Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted. These 20 omitted terms are: $$\\dfrac{1}{111}, \\dfrac{1}{222}, \\dfrac{1}{333}, \\dfrac{1}{444}, \\dfrac{1}{555}, \\dfrac{1}{666}, \\dfrac{1}{777}, \\dfrac{1}{888}, \\dfrac{1}{999}, \\dfrac{1}{1000}, \\dfrac{1}{1110}, \\\\ \\dfrac{1}{1111}, \\dfrac{1}{1112}, \\dfrac{1}{1113}, \\dfrac{1}{1114}, \\dfrac{1}{1115}, \\dfrac{1}{1116}, \\dfrac{1}{1117}, \\dfrac{1}{1118}, \\dfrac{1}{1119}$$
+Consideriamo ora un'altra serie armonica modificata omettendo dalla serie armonica ogni termine in cui il denominatore ha 3 o più cifre consecutive uguali. Si può verificare che sui primi 1200 termini della serie armonica, solo 20 termini saranno omessi.
-This series converges as well.
+Questi 20 termini omessi sono:
-Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\ \dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
+
+Anche questa serie converge.
+
+Trova il valore a cui converge la serie. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler368()` should return 253.6135092068.
+`kempnerLikeSeries()` dovrebbe restituire `253.6135092068`.
```js
-assert.strictEqual(euler368(), 253.6135092068);
+assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
```
# --seed--
@@ -31,12 +35,12 @@ assert.strictEqual(euler368(), 253.6135092068);
## --seed-contents--
```js
-function euler368() {
+function kempnerLikeSeries() {
return true;
}
-euler368();
+kempnerLikeSeries();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
index abdcb4c810..953a36e727 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff0
-title: 'Problem 369: Badugi'
+title: 'Problema 369: Badugi'
challengeType: 5
forumTopicId: 302030
dashedName: problem-369-badugi
@@ -8,18 +8,18 @@ dashedName: problem-369-badugi
# --description--
-In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+In un mazzo standard di 52 carte da gioco, un set di 4 carte è un Badugi se contiene 4 carte senza coppie e nessuna due carte dello stesso seme.
-Let f(n) be the number of ways to choose n cards with a 4 card subset that is a Badugi. For example, there are 2598960 ways to choose five cards from a standard 52 card deck, of which 514800 contain a 4 card subset that is a Badugi, so f(5) = 514800.
+Lascia che $f(n)$ sia il numero di modi per scegliere $n$ carte con un sottoinsieme di 4 carte che è un Badugi. Ad esempio, ci sono $2\\,598\\,960$ modi per scegliere cinque carte da un mazzo standard di 52 carte, di cui $514\\,800$ contengono un sottoinsieme di 4 carte che è un Badugi, quindi $f(5) = 514800$.
-Find ∑f(n) for 4 ≤ n ≤ 13.
+Trova $\sum f(n)$ per $4 ≤ n ≤ 13$.
# --hints--
-`euler369()` should return 862400558448.
+`badugi()` dovrebbe restituire `862400558448`.
```js
-assert.strictEqual(euler369(), 862400558448);
+assert.strictEqual(badugi(), 862400558448);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler369(), 862400558448);
## --seed-contents--
```js
-function euler369() {
+function badugi() {
return true;
}
-euler369();
+badugi();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
index 469f9151e0..4b5b6947ea 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff1
-title: 'Problem 370: Geometric triangles'
+title: 'Problema 370: Triangoli geometrici'
challengeType: 5
forumTopicId: 302032
dashedName: problem-370-geometric-triangles
@@ -8,20 +8,20 @@ dashedName: problem-370-geometric-triangles
# --description--
-Let us define a geometric triangle as an integer sided triangle with sides a ≤ b ≤ c so that its sides form a geometric progression, i.e. b2 = a · c .
+Sia un triangolo geometrico un triangolo con lati interi con lati $a ≤ b ≤ c$ cossìcché i suoi lati formino una progressione geometrica, cioè $b^2 = a \times c$.
-An example of such a geometric triangle is the triangle with sides a = 144, b = 156 and c = 169.
+Un esempio di tale triangolo è il triangolo con lati $a = 144$, $b = 156$ e $c = 169$.
-There are 861805 geometric triangles with perimeter ≤ 106 .
+Ci sono $861\\,805$ triangoli geometrici con $\text{perimetro} ≤ {10}^6$.
-How many geometric triangles exist with perimeter ≤ 2.5·1013 ?
+Quanti triangoli geometrici esistono con $\text{perimetro} ≤ 2.5 \times {10}^{13}$?
# --hints--
-`euler370()` should return 41791929448408.
+`geometricTriangles()` dovrebbe restituire `41791929448408`.
```js
-assert.strictEqual(euler370(), 41791929448408);
+assert.strictEqual(geometricTriangles(), 41791929448408);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler370(), 41791929448408);
## --seed-contents--
```js
-function euler370() {
+function geometricTriangles() {
return true;
}
-euler370();
+geometricTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
index 005b5aaf07..cc2e62c6fd 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
@@ -1,6 +1,6 @@
---
id: 5900f4e01000cf542c50fff2
-title: 'Problem 371: Licence plates'
+title: 'Problema 371: Targhe'
challengeType: 5
forumTopicId: 302033
dashedName: problem-371-licence-plates
@@ -8,24 +8,24 @@ dashedName: problem-371-licence-plates
# --description--
-Oregon licence plates consist of three letters followed by a three digit number (each digit can be from \[0..9]).
+Le targhe dell'Oregon sono composte da tre lettere seguite da un numero a tre cifre (ciascuna cifra può essere in [0...9]).
-While driving to work Seth plays the following game:
+Mentre guida per andare a lavoro Seth gioca il seguente gioco:
-Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+Ogni volta che i numeri di due targhe visti nel suo viaggio si sommano a 1000, vince.
-E.g. MIC-012 and HAN-988 is a win and RYU-500 and SET-500 too. (as long as he sees them in the same trip).
+Ad es. `MIC-012` e `HAN-988` è una vittoria e `RYU-500` e `SET-500` anche. (finché li vede nello stesso viaggio).
-Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+Trova il numero previsto di targhe che ha bisogno di vedere per una vittoria. Dai la tua risposta approssimata a 8 cifre dopo il punto decimale.
-Note: We assume that each licence plate seen is equally likely to have any three digit number on it.
+**Nota:** Assumiamo che ogni targa vista ha la stessa probabilità di avere un qualsiasi numero di tre cifre su di essa.
# --hints--
-`euler371()` should return 40.66368097.
+`licensePlates()` dovrebbe restituire `40.66368097`.
```js
-assert.strictEqual(euler371(), 40.66368097);
+assert.strictEqual(licensePlates(), 40.66368097);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler371(), 40.66368097);
## --seed-contents--
```js
-function euler371() {
+function licensePlates() {
return true;
}
-euler371();
+licensePlates();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
index 1a04cacb71..1a21a55186 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff3
-title: 'Problem 372: Pencils of rays'
+title: 'Problema 372: Raggi di matite'
challengeType: 5
forumTopicId: 302034
dashedName: problem-372-pencils-of-rays
@@ -8,16 +8,20 @@ dashedName: problem-372-pencils-of-rays
# --description--
-Let R(M, N) be the number of lattice points (x, y) which satisfy M
+Sia $R(M, N)$ il numero di punti di reticolo ($x$, $y$) che soddisfa $M \lt x \le N$, $M \lt y \le N$ e $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ è dispari.
-Note: represents the floor function.
+Possiamo verificare che $R(0, 100) = 3\\,019$ e $R(100, 10\\,000) = 29\\,750\\,422$.
+
+Trova $R(2 \times {10}^6, {10}^9)$.
+
+**Nota:** $\lfloor x\rfloor$ è la funzione che arrotonda verso il basso.
# --hints--
-`euler372()` should return 301450082318807040.
+`pencilsOfRays()` dovrebbe restituire `301450082318807040`.
```js
-assert.strictEqual(euler372(), 301450082318807040);
+assert.strictEqual(pencilsOfRays(), 301450082318807040);
```
# --seed--
@@ -25,12 +29,12 @@ assert.strictEqual(euler372(), 301450082318807040);
## --seed-contents--
```js
-function euler372() {
+function pencilsOfRays() {
return true;
}
-euler372();
+pencilsOfRays();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
index 534c32ea25..fd6f508ef4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff4
-title: 'Problem 373: Circumscribed Circles'
+title: 'Problema 373: Cerchi circoscritti'
challengeType: 5
forumTopicId: 302035
dashedName: problem-373-circumscribed-circles
@@ -8,22 +8,20 @@ dashedName: problem-373-circumscribed-circles
# --description--
-Every triangle has a circumscribed circle that goes through the three vertices.
+Ogni triangolo ha un cerchio circoscritto che attraversa i tre vertici. Considera tutti i triangoli a lati interi per i quali è intero anche il raggio del cerchio circoscritto.
-Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+Sia $S(n)$ la somma dei raggi dei cerchi circoscritti di tutti questi triangoli per i quali il raggio non supera $n$.
-Let S(n) be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed n.
+$S(100) = 4\\,950$ and $S(1\\,200) = 1\\,653\\,605$.
-S(100)=4950 and S(1200)=1653605.
-
-Find S(107).
+Trova $S({10}^7)$.
# --hints--
-`euler373()` should return 727227472448913.
+`circumscribedCircles()` dovrebbe restituire `727227472448913`.
```js
-assert.strictEqual(euler373(), 727227472448913);
+assert.strictEqual(circumscribedCircles(), 727227472448913);
```
# --seed--
@@ -31,12 +29,12 @@ assert.strictEqual(euler373(), 727227472448913);
## --seed-contents--
```js
-function euler373() {
+function circumscribedCircles() {
return true;
}
-euler373();
+circumscribedCircles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
index 10fe621891..70ed56fae7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff6
-title: 'Problem 374: Maximum Integer Partition Product'
+title: 'Problema 374: Massimo prodotto di partizione di un numero intero'
challengeType: 5
forumTopicId: 302036
dashedName: problem-374-maximum-integer-partition-product
@@ -8,28 +8,30 @@ dashedName: problem-374-maximum-integer-partition-product
# --description--
-An integer partition of a number n is a way of writing n as a sum of positive integers.
+Una partizione intera di un numero $n$ è un modo di scrivere $n$ come una somma di numeri interi positivi.
-Partitions that differ only in the order of their summands are considered the same. A partition of n into distinct parts is a partition of n in which every part occurs at most once.
+Le partizioni che differiscono solo nell'ordine dei loro addendi sono considerate le stesse. Una partizione di $n$ in parti distinte è una partizione di $n$ in cui ogni parte si verifica al massimo una volta.
-The partitions of 5 into distinct parts are: 5, 4+1 and 3+2.
+Le partizioni in parti distinte di 5 sono:
-Let f(n) be the maximum product of the parts of any such partition of n into distinct parts and let m(n) be the number of elements of any such partition of n with that product.
+5, 4 + 1 e 3 + 2.
-So f(5)=6 and m(5)=2.
+Sia $f(n)$ il prodotto massimo delle parti di una tale partizione di $n$ in parti distinte e sia $m(n)$ il numero di elementi di una tale partizione di $n$ con quel prodotto.
-For n=10 the partition with the largest product is 10=2+3+5, which gives f(10)=30 and m(10)=3. And their product, f(10)·m(10) = 30·3 = 90
+Quindi $f(5) = 6$ e $m(5) = 2$.
-It can be verified that ∑f(n)·m(n) for 1 ≤ n ≤ 100 = 1683550844462.
+Per $n = 10$ la partizione con il prodotto più grande è $10 = 2 + 3 + 5$, che dà $f(10) = 30$ e $m(10) = 3$. E il loro prodotto, $f(10) \times m(10) = 30 \times 3 = 90$
-Find ∑f(n)·m(n) for 1 ≤ n ≤ 1014. Give your answer modulo 982451653, the 50 millionth prime.
+Si può verificare che $\sum f(n) \times m(n)$ for $1 ≤ n ≤ 100 = 1\\,683\\,550\\,844\\,462$.
+
+Trova $\sum f(n) \times m(n)$ for $1 ≤ n ≤ {10}^{14}$. Dai la tua risposta modulo $982\\,451\\,653$, il 50 millionesimo primo.
# --hints--
-`euler374()` should return 334420941.
+`maximumIntegerPartitionProduct()` dovrebbe restituire `334420941`.
```js
-assert.strictEqual(euler374(), 334420941);
+assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler374(), 334420941);
## --seed-contents--
```js
-function euler374() {
+function maximumIntegerPartitionProduct() {
return true;
}
-euler374();
+maximumIntegerPartitionProduct();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
index 684613a235..d02d316962 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4e41000cf542c50fff5
-title: 'Problem 375: Minimum of subsequences'
+title: 'Problema 375: Minimo delle sottosequenze'
challengeType: 5
forumTopicId: 302037
dashedName: problem-375-minimum-of-subsequences
@@ -8,30 +8,22 @@ dashedName: problem-375-minimum-of-subsequences
# --description--
-Let Sn be an integer sequence produced with the following pseudo-random number generator:
+Lascia che $S_n$ sia una sequenza intera prodotta con il seguente generatore di numeri pseudo-casuali:
-S0
+$$\begin{align} S_0 & = 290\\,797 \\\\ S_{n + 1} & = {S_n}^2\bmod 50\\,515\\,093 \end{align}$$
-=
+Sia $A(i, j)$ il minimo dei numeri $S_i, S_{i + 1}, \ldots, S_j$ per $i ≤ j$. Sia $M(N) = \sum A(i, j)$ per $1 ≤ i ≤ j ≤ N$.
-290797
+Possiamo verificare che $M(10) = 432\\,256\\,955$ e $M(10\\,000) = 3\\,264\\,567\\,774\\,119$.
-Sn+1
-
-=
-
-Sn2 mod 50515093
-
-Let A(i, j) be the minimum of the numbers Si, Si+1, ... , Sj for i ≤ j. Let M(N) = ΣA(i, j) for 1 ≤ i ≤ j ≤ N. We can verify that M(10) = 432256955 and M(10 000) = 3264567774119.
-
-Find M(2 000 000 000).
+Trova $M(2\\,000\\,000\\,000)$.
# --hints--
-`euler375()` should return 7435327983715286000.
+`minimumOfSubsequences()` dovrebbe restituire `7435327983715286000`.
```js
-assert.strictEqual(euler375(), 7435327983715286000);
+assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
```
# --seed--
@@ -39,12 +31,12 @@ assert.strictEqual(euler375(), 7435327983715286000);
## --seed-contents--
```js
-function euler375() {
+function minimumOfSubsequences() {
return true;
}
-euler375();
+minimumOfSubsequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
index b76c4d26e8..49d34bd6da 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff7
-title: 'Problem 376: Nontransitive sets of dice'
+title: 'Problema 376: Set di dadi non transitivo'
challengeType: 5
forumTopicId: 302038
dashedName: problem-376-nontransitive-sets-of-dice
@@ -8,30 +8,43 @@ dashedName: problem-376-nontransitive-sets-of-dice
# --description--
-Consider the following set of dice with nonstandard pips:
+Considera la seguente serie di dadi con pallini non standard:
-Die A: 1 4 4 4 4 4 Die B: 2 2 2 5 5 5 Die C: 3 3 3 3 3 6
+$$$\begin{array}{} \text{Dado A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{Dado B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Dado C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
-A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+Un gioco è giocato da due giocatori scegliendo un dado a turno e lanciandolo. Il giocatore che lancia il valore più alto vince.
-If the first player picks die A and the second player picks die B we get P(second player wins) = 7/12 > 1/2
+Se il primo giocatore sceglie dado $A$ e il secondo giocatore sceglie dado $B$ otteniamo
-If the first player picks die B and the second player picks die C we get P(second player wins) = 7/12 > 1/2
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die C and the second player picks die A we get P(second player wins) = 25/36 > 1/2
+Se il primo giocatore sceglie dado $B$ e il secondo giocatore sceglie dado $C$ otteniamo
-So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:There are three six-sided dice with each side having between 1 and N pips, inclusive. Dice with the same set of pips are equal, regardless of which side on the die the pips are located. The same pip value may appear on multiple dice; if both players roll the same value neither player wins. The sets of dice {A,B,C}, {B,C,A} and {C,A,B} are the same set.
+Se il primo giocatore sceglie dado $C$ e il secondo giocatore sceglie dado $A$ otteniamo
-For N = 7 we find there are 9780 such sets. How many are there for N = 30 ?
+$P(\text{secondo giocatore vince}) = \frac{25}{36} > \frac{1}{2}$
+
+Quindi, qualunque scelta faccia il primo giocatore, il secondo giocatore può scegliere un altro dado e avere una probabilità maggiore del 50% di vittoria. Un set di dadi che hanno questa proprietà è chiamato un set di dadi non transitivi.
+
+Vogliamo indagare quanti insiemi di dadi non transitivi esistono. Assumeremo le seguenti condizioni:
+
+- Ci sono tre dadi a sei facce con ogni faccia che ha tra 1 e $N$ pallini, inclusi.
+- I dadi con lo stesso set di pallini sono uguali, indipendentemente dalla faccia del dado su cui i pallini sono situati.
+- Lo stesso valore di pallini può apparire su più dadi; se entrambi i giocatori lanciano lo stesso valore nessuno vince.
+- I set di dadi $\\{A, B, C\\}$, $\\{B, C, A\\}$ e $\\{C, A, B\\}$ sono lo stesso set.
+
+Per $N = 7$ troviamo 9780 set di questo tipo.
+
+Quanti ce ne sono per $N = 30$?
# --hints--
-`euler376()` should return 973059630185670.
+`nontransitiveSetsOfDice()` dovrebbe restituire `973059630185670`.
```js
-assert.strictEqual(euler376(), 973059630185670);
+assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
```
# --seed--
@@ -39,12 +52,12 @@ assert.strictEqual(euler376(), 973059630185670);
## --seed-contents--
```js
-function euler376() {
+function nontransitiveSetsOfDice() {
return true;
}
-euler376();
+nontransitiveSetsOfDice();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
index 660508c234..0b674e8a71 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff8
-title: 'Problem 377: Sum of digits, experience 13'
+title: 'Problema 377: Somma delle cifre, esperienza 13'
challengeType: 5
forumTopicId: 302039
dashedName: problem-377-sum-of-digits-experience-13
@@ -8,22 +8,22 @@ dashedName: problem-377-sum-of-digits-experience-13
# --description--
-There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+Ci sono 16 numeri interi positivi che non hanno uno 0 tra le loro cifre e che hanno una somma delle cifre uguale a 5:
-5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 e 11111.
-Their sum is 17891.
+La loro somma è 17891.
-Let f(n) be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to n.
+Sia $f(n)$ la somma di tutti i numeri interi positivi che non hanno uno zero tra le loro cifre e che hanno una somma delle cifre pari a $n$.
-Find $\\displaystyle \\sum\_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+Trova $\displaystyle\sum_{i=1}^{17} f(13^i)$. Dai le ultime 9 cifre della tua risposta.
# --hints--
-`euler377()` should return 732385277.
+`experience13()` dovrebbe restituire `732385277`.
```js
-assert.strictEqual(euler377(), 732385277);
+assert.strictEqual(experience13(), 732385277);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler377(), 732385277);
## --seed-contents--
```js
-function euler377() {
+function experience13() {
return true;
}
-euler377();
+experience13();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
index 22589747fe..0c8d5d5b65 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f4e61000cf542c50fff9
-title: 'Problem 378: Triangle Triples'
+title: 'Problema 378: tripli triangoli'
challengeType: 5
forumTopicId: 302040
dashedName: problem-378-triangle-triples
@@ -8,24 +8,20 @@ dashedName: problem-378-triangle-triples
# --description--
-Let T(n) be the nth triangle number, so T(n) =
+Sia $T(n)$ l'$n$-simo numero triangolare, quindi $T(n) = \frac{n(n + 1)}{2}$.
-n (n+1)2
+Sia $dT(n)$ il numero di divisori di $T(n)$. Esempio: $T(7) = 28$ e $dT(7) = 6$.
-.
+Sia $Tr(n)$ il numero di triplette ($i$, $j$, $k$) per cui $1 ≤ i < j < k ≤ n$ e $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5\\,772$ e $Tr(1000) = 11\\,174\\,776$.
-Let dT(n) be the number of divisors of T(n). E.g.: T(7) = 28 and dT(7) = 6.
-
-Let Tr(n) be the number of triples (i, j, k) such that 1 ≤ i < j < k ≤ n and dT(i) > dT(j) > dT(k). Tr(20) = 14, Tr(100) = 5772 and Tr(1000) = 11174776.
-
-Find Tr(60 000 000). Give the last 18 digits of your answer.
+Trova $Tr(60\\,000\\,000)$. Dai le ultime 18 cifre della tua risposta.
# --hints--
-`euler378()` should return 147534623725724700.
+`triangleTriples()` dovrebbe restituire `147534623725724700`.
```js
-assert.strictEqual(euler378(), 147534623725724700);
+assert.strictEqual(triangleTriples(), 147534623725724700);
```
# --seed--
@@ -33,12 +29,12 @@ assert.strictEqual(euler378(), 147534623725724700);
## --seed-contents--
```js
-function euler378() {
+function triangleTriples() {
return true;
}
-euler378();
+triangleTriples();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
index 3933d82ea2..7798debf82 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffa
-title: 'Problem 379: Least common multiple count'
+title: 'Problema 379: conteggio del minimo comune multiplo'
challengeType: 5
forumTopicId: 302041
dashedName: problem-379-least-common-multiple-count
@@ -8,20 +8,20 @@ dashedName: problem-379-least-common-multiple-count
# --description--
-Let f(n) be the number of couples (x,y) with x and y positive integers, x ≤ y and the least common multiple of x and y equal to n.
+Sia $f(n)$ il numero di coppie ($x$, $y$) con $x$ e $y$ numeri interi positivi, per cui $x ≤ y$ e il minimo comune multiplo di $x$ e $y$ è uguale a $n$.
-Let g be the summatory function of f, i.e.: g(n) = ∑ f(i) for 1 ≤ i ≤ n.
+Sia $g$ la funzione sommatoria di $f$, cioè $g(n) = \sum f(i)$ per $1 ≤ i ≤ n$.
-You are given that g(106) = 37429395.
+Ti è dato che $g({10}^6) = 37\\,429\\,395$.
-Find g(1012).
+Trova $g({10}^{12})$.
# --hints--
-`euler379()` should return 132314136838185.
+`leastCommonMultipleCount()` dovrebbe restituire `132314136838185`.
```js
-assert.strictEqual(euler379(), 132314136838185);
+assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler379(), 132314136838185);
## --seed-contents--
```js
-function euler379() {
+function leastCommonMultipleCount() {
return true;
}
-euler379();
+leastCommonMultipleCount();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
index 8596f52fa7..2fa9c3c7b7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffb
-title: 'Problem 380: Amazing Mazes!'
+title: 'Problema 380: fantastici labirinti!'
challengeType: 5
forumTopicId: 302044
dashedName: problem-380-amazing-mazes
@@ -8,20 +8,30 @@ dashedName: problem-380-amazing-mazes
# --description--
-An m×n maze is an m×n rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+Un labirinto $m×n$ è una griglia rettangolare $m×n$ con muri piazzati tra celle della griglia in modo tale che c'è un unico percorso dal quadrato in alto a sinistra a qualsiasi altro quadrato. I seguenti sono esempi di labirinti 9×12 e 15×20:
-Let C(m,n) be the number of distinct m×n mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+
-Let T(N) be the number of possibilities that N seats are occupied by N people with the given rules. The following figure shows T(4)=8.
+Possiamo verificare che $T(10) = 61\\,632$ e $T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094$.
-We can verify that T(10) = 61632 and T(1 000) mod 100 000 007 = 47255094. Find T(1 000 000) mod 100 000 007.
+Trova $T(1\\,000\\,000)\bmod 100\\,000\\,007$.
# --hints--
-`euler364()` should return 44855254.
+`comfortableDistance()` dovrebbe restituire `44855254`.
```js
-assert.strictEqual(euler364(), 44855254);
+assert.strictEqual(comfortableDistance(), 44855254);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler364(), 44855254);
## --seed-contents--
```js
-function euler364() {
+function comfortableDistance() {
return true;
}
-euler364();
+comfortableDistance();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
index 1647ff46ea..90911f54a8 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffec
-title: 'Problem 365: A huge binomial coefficient'
+title: 'Problema 365: Un grande coefficiente binomiale'
challengeType: 5
forumTopicId: 302026
dashedName: problem-365-a-huge-binomial-coefficient
@@ -8,18 +8,18 @@ dashedName: problem-365-a-huge-binomial-coefficient
# --description--
-The binomial coefficient C(1018,109) is a number with more than 9 billion (9×109) digits.
+Il coefficiente binomiale $\displaystyle\binom{{10}^{18}}{{10}^9}$ è un numero con più di 9 miliardi ($9 × {10}^9$) di cifre.
-Let M(n,k,m) denote the binomial coefficient C(n,k) modulo m.
+Sia $M(n, k, m)$ il coefficiente binomiale $\displaystyle\binom{n}{k}$ modulo $m$.
-Calculate ∑M(1018,109,p*q*r) for 1000<p<q<r<5000 and p,q,r prime.
+Calcola $\sum M({10}^{18}, {10}^9, p \times q \times r)$ per $1000 < p < q < r < 5000$ e $p$, $q$, $r$ numeri primi.
# --hints--
-`euler365()` should return 162619462356610300.
+`hugeBinomialCoefficient()` dovrebbe restituire `162619462356610300`.
```js
-assert.strictEqual(euler365(), 162619462356610300);
+assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler365(), 162619462356610300);
## --seed-contents--
```js
-function euler365() {
+function hugeBinomialCoefficient() {
return true;
}
-euler365();
+hugeBinomialCoefficient();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
index b7f832ebf4..bf6252b74c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffed
-title: 'Problem 366: Stone Game III'
+title: 'Problema 366: Gioco delle pietre III'
challengeType: 5
forumTopicId: 302027
dashedName: problem-366-stone-game-iii
@@ -8,30 +8,44 @@ dashedName: problem-366-stone-game-iii
# --description--
-Two players, Anton and Bernhard, are playing the following game.
+Due giocatori, Anton e Bernhard, stanno giocando il seguente gioco.
-There is one pile of n stones.
+C'è una pila di $n$ pietre.
-The first player may remove any positive number of stones, but not the whole pile.
+Il primo giocatore può rimuovere qualsiasi numero positivo di pietre, ma non l'intera pila.
-Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+Successivamente, ogni giocatore può rimuovere al massimo il doppio del numero di pietre che il suo avversario ha preso nella mossa precedente.
-The player who removes the last stone wins.
+Il giocatore che rimuove l'ultima pietra vince.
-E.g. n=5 If the first player takes anything more than one stone the next player will be able to take all remaining stones. If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones. The first player cannot take all three because he may take at most 2x1=2 stones. So let's say he takes also one stone, leaving 2. The second player can take the two remaining stones and wins. So 5 is a losing position for the first player. For some winning positions there is more than one possible move for the first player. E.g. when n=17 the first player can remove one or four stones.
+Ad es. $n = 5$
-Let M(n) be the maximum number of stones the first player can take from a winning position at his first turn and M(n)=0 for any other position.
+Se il primo giocatore prende più di una pietra il giocatore successivo sarà in grado di prendere tutte le pietre rimaste.
-∑M(n) for n≤100 is 728.
+Se il primo giocatore prende una pietra, lasciandone quattro, anche il suo avversario prenderà una pietra, lasciando tre pietre.
-Find ∑M(n) for n≤1018. Give your answer modulo 108.
+Il primo giocatore non può prenderle tutte e tre perché può prendere al massimo $2 \times 1 = 2$ pietre. Quindi diciamo che anche lui prende una pietra, lasciandone 2.
+
+Il secondo giocatore può prendere le due pietre rimanenti e vince.
+
+Quindi 5 è una posizione perdente per il primo giocatore.
+
+Per alcune posizioni vincenti c'è più di una possibile mossa per il primo giocatore.
+
+Ad es. quando $n = 17$ il primo giocatore può rimuovere una o quattro pietre.
+
+Sia $M(n)$ il numero massimo di pietre che il primo giocatore può prendere da una posizione vincente al suo primo turno e $M(n) = 0$ per qualsiasi altra posizione.
+
+$\sum M(n)$ per $n ≤ 100$ è 728.
+
+Trova $\sum M(n)$ per $n ≤ {10}^{18}$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler366()` should return 88351299.
+`stoneGameThree()` dovrebbe restituire `88351299`.
```js
-assert.strictEqual(euler366(), 88351299);
+assert.strictEqual(stoneGameThree(), 88351299);
```
# --seed--
@@ -39,12 +53,12 @@ assert.strictEqual(euler366(), 88351299);
## --seed-contents--
```js
-function euler366() {
+function stoneGameThree() {
return true;
}
-euler366();
+stoneGameThree();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
index 979702592a..a34132973d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
@@ -1,6 +1,6 @@
---
id: 5900f4db1000cf542c50ffee
-title: 'Problem 367: Bozo sort'
+title: 'Problema 367: Bozo sort'
challengeType: 5
forumTopicId: 302028
dashedName: problem-367-bozo-sort
@@ -8,20 +8,32 @@ dashedName: problem-367-bozo-sort
# --description--
-Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+Bozo sort, da non confondersi con il'algoritmo leggermente meno efficiente bogo sort, consiste nel controllare se la sequenza di input è ordinata, e se non lo è scambiare a caso due elementi. Questo viene ripetuto fino a che la sequenza non è eventualmente in ordine.
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all 4! input sequences is 24.75. The already sorted sequence takes 0 steps.
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di scambi, mediato su tutte le $4!$ sequenze di input è $24.75$.
-In this problem we consider the following variant on bozo sort. If the sequence is not in order we pick three elements at random and shuffle these three elements randomly. All 3!=6 permutations of those three elements are equally likely. The already sorted sequence will take 0 steps. If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all 4! input sequences is 27.5. Consider as input sequences the permutations of the first 11 natural numbers. Averaged over all 11! input sequences, what is the expected number of shuffles this sorting algorithm will perform?
+La sequenza già ordinata ha bisogno di 0 step.
-Give your answer rounded to the nearest integer.
+In questo problema consideriamo le seguenti varianti nel bozo sort.
+
+Se la sequenza non è in ordine, scegliamo 3 elementi a caso e mescoliamo questi tre elementi casualmente.
+
+Tutte le $3! = 6$ permutazioni di questi tre elementi sono altrettanto probabili.
+
+La sequenza già ordinata ha bisogno di 0 step.
+
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di mescolamenti, mediato su tutte le $4!$ sequenze di input è $27.5$.
+
+Considera come sequenze di input le permutazioni dei primi 11 numeri naturali.
+
+Mediato su tutte le $11!$ sequenze di input, qual è il numero medio di mescolamenti che questo algoritmo performerà? Dai la tua risposta arrotondata al numero intero più vicino.
# --hints--
-`euler367()` should return 48271207.
+`bozoSort()` dovrebbe restituire `48271207`.
```js
-assert.strictEqual(euler367(), 48271207);
+assert.strictEqual(bozoSort(), 48271207);
```
# --seed--
@@ -29,12 +41,12 @@ assert.strictEqual(euler367(), 48271207);
## --seed-contents--
```js
-function euler367() {
+function bozoSort() {
return true;
}
-euler367();
+bozoSort();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
index dc9cf2f919..e262f93378 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
@@ -1,6 +1,6 @@
---
id: 5900f4dd1000cf542c50ffef
-title: 'Problem 368: A Kempner-like series'
+title: 'Problema 368: Una serie di Kempner'
challengeType: 5
forumTopicId: 302029
dashedName: problem-368-a-kempner-like-series
@@ -8,22 +8,26 @@ dashedName: problem-368-a-kempner-like-series
# --description--
-The harmonic series $1 + \\dfrac{1}{2} + \\dfrac{1}{3} + \\dfrac{1}{4} + ...$ is well known to be divergent.
+La serie armonica $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ è nota per essere divergente.
-If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+Se comunque si omette da questa serie ogni termine in cui il denominatore ha un 9 in esso, la serie converge abbastanza notevolmente a circa 22.9206766193. Questa serie armonica modificata è chiamata serie Kempner.
-Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted. These 20 omitted terms are: $$\\dfrac{1}{111}, \\dfrac{1}{222}, \\dfrac{1}{333}, \\dfrac{1}{444}, \\dfrac{1}{555}, \\dfrac{1}{666}, \\dfrac{1}{777}, \\dfrac{1}{888}, \\dfrac{1}{999}, \\dfrac{1}{1000}, \\dfrac{1}{1110}, \\\\ \\dfrac{1}{1111}, \\dfrac{1}{1112}, \\dfrac{1}{1113}, \\dfrac{1}{1114}, \\dfrac{1}{1115}, \\dfrac{1}{1116}, \\dfrac{1}{1117}, \\dfrac{1}{1118}, \\dfrac{1}{1119}$$
+Consideriamo ora un'altra serie armonica modificata omettendo dalla serie armonica ogni termine in cui il denominatore ha 3 o più cifre consecutive uguali. Si può verificare che sui primi 1200 termini della serie armonica, solo 20 termini saranno omessi.
-This series converges as well.
+Questi 20 termini omessi sono:
-Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\ \dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
+
+Anche questa serie converge.
+
+Trova il valore a cui converge la serie. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler368()` should return 253.6135092068.
+`kempnerLikeSeries()` dovrebbe restituire `253.6135092068`.
```js
-assert.strictEqual(euler368(), 253.6135092068);
+assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
```
# --seed--
@@ -31,12 +35,12 @@ assert.strictEqual(euler368(), 253.6135092068);
## --seed-contents--
```js
-function euler368() {
+function kempnerLikeSeries() {
return true;
}
-euler368();
+kempnerLikeSeries();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
index abdcb4c810..953a36e727 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff0
-title: 'Problem 369: Badugi'
+title: 'Problema 369: Badugi'
challengeType: 5
forumTopicId: 302030
dashedName: problem-369-badugi
@@ -8,18 +8,18 @@ dashedName: problem-369-badugi
# --description--
-In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+In un mazzo standard di 52 carte da gioco, un set di 4 carte è un Badugi se contiene 4 carte senza coppie e nessuna due carte dello stesso seme.
-Let f(n) be the number of ways to choose n cards with a 4 card subset that is a Badugi. For example, there are 2598960 ways to choose five cards from a standard 52 card deck, of which 514800 contain a 4 card subset that is a Badugi, so f(5) = 514800.
+Lascia che $f(n)$ sia il numero di modi per scegliere $n$ carte con un sottoinsieme di 4 carte che è un Badugi. Ad esempio, ci sono $2\\,598\\,960$ modi per scegliere cinque carte da un mazzo standard di 52 carte, di cui $514\\,800$ contengono un sottoinsieme di 4 carte che è un Badugi, quindi $f(5) = 514800$.
-Find ∑f(n) for 4 ≤ n ≤ 13.
+Trova $\sum f(n)$ per $4 ≤ n ≤ 13$.
# --hints--
-`euler369()` should return 862400558448.
+`badugi()` dovrebbe restituire `862400558448`.
```js
-assert.strictEqual(euler369(), 862400558448);
+assert.strictEqual(badugi(), 862400558448);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler369(), 862400558448);
## --seed-contents--
```js
-function euler369() {
+function badugi() {
return true;
}
-euler369();
+badugi();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
index 469f9151e0..4b5b6947ea 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff1
-title: 'Problem 370: Geometric triangles'
+title: 'Problema 370: Triangoli geometrici'
challengeType: 5
forumTopicId: 302032
dashedName: problem-370-geometric-triangles
@@ -8,20 +8,20 @@ dashedName: problem-370-geometric-triangles
# --description--
-Let us define a geometric triangle as an integer sided triangle with sides a ≤ b ≤ c so that its sides form a geometric progression, i.e. b2 = a · c .
+Sia un triangolo geometrico un triangolo con lati interi con lati $a ≤ b ≤ c$ cossìcché i suoi lati formino una progressione geometrica, cioè $b^2 = a \times c$.
-An example of such a geometric triangle is the triangle with sides a = 144, b = 156 and c = 169.
+Un esempio di tale triangolo è il triangolo con lati $a = 144$, $b = 156$ e $c = 169$.
-There are 861805 geometric triangles with perimeter ≤ 106 .
+Ci sono $861\\,805$ triangoli geometrici con $\text{perimetro} ≤ {10}^6$.
-How many geometric triangles exist with perimeter ≤ 2.5·1013 ?
+Quanti triangoli geometrici esistono con $\text{perimetro} ≤ 2.5 \times {10}^{13}$?
# --hints--
-`euler370()` should return 41791929448408.
+`geometricTriangles()` dovrebbe restituire `41791929448408`.
```js
-assert.strictEqual(euler370(), 41791929448408);
+assert.strictEqual(geometricTriangles(), 41791929448408);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler370(), 41791929448408);
## --seed-contents--
```js
-function euler370() {
+function geometricTriangles() {
return true;
}
-euler370();
+geometricTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
index 005b5aaf07..cc2e62c6fd 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
@@ -1,6 +1,6 @@
---
id: 5900f4e01000cf542c50fff2
-title: 'Problem 371: Licence plates'
+title: 'Problema 371: Targhe'
challengeType: 5
forumTopicId: 302033
dashedName: problem-371-licence-plates
@@ -8,24 +8,24 @@ dashedName: problem-371-licence-plates
# --description--
-Oregon licence plates consist of three letters followed by a three digit number (each digit can be from \[0..9]).
+Le targhe dell'Oregon sono composte da tre lettere seguite da un numero a tre cifre (ciascuna cifra può essere in [0...9]).
-While driving to work Seth plays the following game:
+Mentre guida per andare a lavoro Seth gioca il seguente gioco:
-Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+Ogni volta che i numeri di due targhe visti nel suo viaggio si sommano a 1000, vince.
-E.g. MIC-012 and HAN-988 is a win and RYU-500 and SET-500 too. (as long as he sees them in the same trip).
+Ad es. `MIC-012` e `HAN-988` è una vittoria e `RYU-500` e `SET-500` anche. (finché li vede nello stesso viaggio).
-Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+Trova il numero previsto di targhe che ha bisogno di vedere per una vittoria. Dai la tua risposta approssimata a 8 cifre dopo il punto decimale.
-Note: We assume that each licence plate seen is equally likely to have any three digit number on it.
+**Nota:** Assumiamo che ogni targa vista ha la stessa probabilità di avere un qualsiasi numero di tre cifre su di essa.
# --hints--
-`euler371()` should return 40.66368097.
+`licensePlates()` dovrebbe restituire `40.66368097`.
```js
-assert.strictEqual(euler371(), 40.66368097);
+assert.strictEqual(licensePlates(), 40.66368097);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler371(), 40.66368097);
## --seed-contents--
```js
-function euler371() {
+function licensePlates() {
return true;
}
-euler371();
+licensePlates();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
index 1a04cacb71..1a21a55186 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff3
-title: 'Problem 372: Pencils of rays'
+title: 'Problema 372: Raggi di matite'
challengeType: 5
forumTopicId: 302034
dashedName: problem-372-pencils-of-rays
@@ -8,16 +8,20 @@ dashedName: problem-372-pencils-of-rays
# --description--
-Let R(M, N) be the number of lattice points (x, y) which satisfy M
+Sia $R(M, N)$ il numero di punti di reticolo ($x$, $y$) che soddisfa $M \lt x \le N$, $M \lt y \le N$ e $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ è dispari.
-Note: represents the floor function.
+Possiamo verificare che $R(0, 100) = 3\\,019$ e $R(100, 10\\,000) = 29\\,750\\,422$.
+
+Trova $R(2 \times {10}^6, {10}^9)$.
+
+**Nota:** $\lfloor x\rfloor$ è la funzione che arrotonda verso il basso.
# --hints--
-`euler372()` should return 301450082318807040.
+`pencilsOfRays()` dovrebbe restituire `301450082318807040`.
```js
-assert.strictEqual(euler372(), 301450082318807040);
+assert.strictEqual(pencilsOfRays(), 301450082318807040);
```
# --seed--
@@ -25,12 +29,12 @@ assert.strictEqual(euler372(), 301450082318807040);
## --seed-contents--
```js
-function euler372() {
+function pencilsOfRays() {
return true;
}
-euler372();
+pencilsOfRays();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
index 534c32ea25..fd6f508ef4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff4
-title: 'Problem 373: Circumscribed Circles'
+title: 'Problema 373: Cerchi circoscritti'
challengeType: 5
forumTopicId: 302035
dashedName: problem-373-circumscribed-circles
@@ -8,22 +8,20 @@ dashedName: problem-373-circumscribed-circles
# --description--
-Every triangle has a circumscribed circle that goes through the three vertices.
+Ogni triangolo ha un cerchio circoscritto che attraversa i tre vertici. Considera tutti i triangoli a lati interi per i quali è intero anche il raggio del cerchio circoscritto.
-Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+Sia $S(n)$ la somma dei raggi dei cerchi circoscritti di tutti questi triangoli per i quali il raggio non supera $n$.
-Let S(n) be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed n.
+$S(100) = 4\\,950$ and $S(1\\,200) = 1\\,653\\,605$.
-S(100)=4950 and S(1200)=1653605.
-
-Find S(107).
+Trova $S({10}^7)$.
# --hints--
-`euler373()` should return 727227472448913.
+`circumscribedCircles()` dovrebbe restituire `727227472448913`.
```js
-assert.strictEqual(euler373(), 727227472448913);
+assert.strictEqual(circumscribedCircles(), 727227472448913);
```
# --seed--
@@ -31,12 +29,12 @@ assert.strictEqual(euler373(), 727227472448913);
## --seed-contents--
```js
-function euler373() {
+function circumscribedCircles() {
return true;
}
-euler373();
+circumscribedCircles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
index 10fe621891..70ed56fae7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff6
-title: 'Problem 374: Maximum Integer Partition Product'
+title: 'Problema 374: Massimo prodotto di partizione di un numero intero'
challengeType: 5
forumTopicId: 302036
dashedName: problem-374-maximum-integer-partition-product
@@ -8,28 +8,30 @@ dashedName: problem-374-maximum-integer-partition-product
# --description--
-An integer partition of a number n is a way of writing n as a sum of positive integers.
+Una partizione intera di un numero $n$ è un modo di scrivere $n$ come una somma di numeri interi positivi.
-Partitions that differ only in the order of their summands are considered the same. A partition of n into distinct parts is a partition of n in which every part occurs at most once.
+Le partizioni che differiscono solo nell'ordine dei loro addendi sono considerate le stesse. Una partizione di $n$ in parti distinte è una partizione di $n$ in cui ogni parte si verifica al massimo una volta.
-The partitions of 5 into distinct parts are: 5, 4+1 and 3+2.
+Le partizioni in parti distinte di 5 sono:
-Let f(n) be the maximum product of the parts of any such partition of n into distinct parts and let m(n) be the number of elements of any such partition of n with that product.
+5, 4 + 1 e 3 + 2.
-So f(5)=6 and m(5)=2.
+Sia $f(n)$ il prodotto massimo delle parti di una tale partizione di $n$ in parti distinte e sia $m(n)$ il numero di elementi di una tale partizione di $n$ con quel prodotto.
-For n=10 the partition with the largest product is 10=2+3+5, which gives f(10)=30 and m(10)=3. And their product, f(10)·m(10) = 30·3 = 90
+Quindi $f(5) = 6$ e $m(5) = 2$.
-It can be verified that ∑f(n)·m(n) for 1 ≤ n ≤ 100 = 1683550844462.
+Per $n = 10$ la partizione con il prodotto più grande è $10 = 2 + 3 + 5$, che dà $f(10) = 30$ e $m(10) = 3$. E il loro prodotto, $f(10) \times m(10) = 30 \times 3 = 90$
-Find ∑f(n)·m(n) for 1 ≤ n ≤ 1014. Give your answer modulo 982451653, the 50 millionth prime.
+Si può verificare che $\sum f(n) \times m(n)$ for $1 ≤ n ≤ 100 = 1\\,683\\,550\\,844\\,462$.
+
+Trova $\sum f(n) \times m(n)$ for $1 ≤ n ≤ {10}^{14}$. Dai la tua risposta modulo $982\\,451\\,653$, il 50 millionesimo primo.
# --hints--
-`euler374()` should return 334420941.
+`maximumIntegerPartitionProduct()` dovrebbe restituire `334420941`.
```js
-assert.strictEqual(euler374(), 334420941);
+assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler374(), 334420941);
## --seed-contents--
```js
-function euler374() {
+function maximumIntegerPartitionProduct() {
return true;
}
-euler374();
+maximumIntegerPartitionProduct();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
index 684613a235..d02d316962 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4e41000cf542c50fff5
-title: 'Problem 375: Minimum of subsequences'
+title: 'Problema 375: Minimo delle sottosequenze'
challengeType: 5
forumTopicId: 302037
dashedName: problem-375-minimum-of-subsequences
@@ -8,30 +8,22 @@ dashedName: problem-375-minimum-of-subsequences
# --description--
-Let Sn be an integer sequence produced with the following pseudo-random number generator:
+Lascia che $S_n$ sia una sequenza intera prodotta con il seguente generatore di numeri pseudo-casuali:
-S0
+$$\begin{align} S_0 & = 290\\,797 \\\\ S_{n + 1} & = {S_n}^2\bmod 50\\,515\\,093 \end{align}$$
-=
+Sia $A(i, j)$ il minimo dei numeri $S_i, S_{i + 1}, \ldots, S_j$ per $i ≤ j$. Sia $M(N) = \sum A(i, j)$ per $1 ≤ i ≤ j ≤ N$.
-290797
+Possiamo verificare che $M(10) = 432\\,256\\,955$ e $M(10\\,000) = 3\\,264\\,567\\,774\\,119$.
-Sn+1
-
-=
-
-Sn2 mod 50515093
-
-Let A(i, j) be the minimum of the numbers Si, Si+1, ... , Sj for i ≤ j. Let M(N) = ΣA(i, j) for 1 ≤ i ≤ j ≤ N. We can verify that M(10) = 432256955 and M(10 000) = 3264567774119.
-
-Find M(2 000 000 000).
+Trova $M(2\\,000\\,000\\,000)$.
# --hints--
-`euler375()` should return 7435327983715286000.
+`minimumOfSubsequences()` dovrebbe restituire `7435327983715286000`.
```js
-assert.strictEqual(euler375(), 7435327983715286000);
+assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
```
# --seed--
@@ -39,12 +31,12 @@ assert.strictEqual(euler375(), 7435327983715286000);
## --seed-contents--
```js
-function euler375() {
+function minimumOfSubsequences() {
return true;
}
-euler375();
+minimumOfSubsequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
index b76c4d26e8..49d34bd6da 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff7
-title: 'Problem 376: Nontransitive sets of dice'
+title: 'Problema 376: Set di dadi non transitivo'
challengeType: 5
forumTopicId: 302038
dashedName: problem-376-nontransitive-sets-of-dice
@@ -8,30 +8,43 @@ dashedName: problem-376-nontransitive-sets-of-dice
# --description--
-Consider the following set of dice with nonstandard pips:
+Considera la seguente serie di dadi con pallini non standard:
-Die A: 1 4 4 4 4 4 Die B: 2 2 2 5 5 5 Die C: 3 3 3 3 3 6
+$$$\begin{array}{} \text{Dado A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{Dado B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Dado C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
-A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+Un gioco è giocato da due giocatori scegliendo un dado a turno e lanciandolo. Il giocatore che lancia il valore più alto vince.
-If the first player picks die A and the second player picks die B we get P(second player wins) = 7/12 > 1/2
+Se il primo giocatore sceglie dado $A$ e il secondo giocatore sceglie dado $B$ otteniamo
-If the first player picks die B and the second player picks die C we get P(second player wins) = 7/12 > 1/2
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die C and the second player picks die A we get P(second player wins) = 25/36 > 1/2
+Se il primo giocatore sceglie dado $B$ e il secondo giocatore sceglie dado $C$ otteniamo
-So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:There are three six-sided dice with each side having between 1 and N pips, inclusive. Dice with the same set of pips are equal, regardless of which side on the die the pips are located. The same pip value may appear on multiple dice; if both players roll the same value neither player wins. The sets of dice {A,B,C}, {B,C,A} and {C,A,B} are the same set.
+Se il primo giocatore sceglie dado $C$ e il secondo giocatore sceglie dado $A$ otteniamo
-For N = 7 we find there are 9780 such sets. How many are there for N = 30 ?
+$P(\text{secondo giocatore vince}) = \frac{25}{36} > \frac{1}{2}$
+
+Quindi, qualunque scelta faccia il primo giocatore, il secondo giocatore può scegliere un altro dado e avere una probabilità maggiore del 50% di vittoria. Un set di dadi che hanno questa proprietà è chiamato un set di dadi non transitivi.
+
+Vogliamo indagare quanti insiemi di dadi non transitivi esistono. Assumeremo le seguenti condizioni:
+
+- Ci sono tre dadi a sei facce con ogni faccia che ha tra 1 e $N$ pallini, inclusi.
+- I dadi con lo stesso set di pallini sono uguali, indipendentemente dalla faccia del dado su cui i pallini sono situati.
+- Lo stesso valore di pallini può apparire su più dadi; se entrambi i giocatori lanciano lo stesso valore nessuno vince.
+- I set di dadi $\\{A, B, C\\}$, $\\{B, C, A\\}$ e $\\{C, A, B\\}$ sono lo stesso set.
+
+Per $N = 7$ troviamo 9780 set di questo tipo.
+
+Quanti ce ne sono per $N = 30$?
# --hints--
-`euler376()` should return 973059630185670.
+`nontransitiveSetsOfDice()` dovrebbe restituire `973059630185670`.
```js
-assert.strictEqual(euler376(), 973059630185670);
+assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
```
# --seed--
@@ -39,12 +52,12 @@ assert.strictEqual(euler376(), 973059630185670);
## --seed-contents--
```js
-function euler376() {
+function nontransitiveSetsOfDice() {
return true;
}
-euler376();
+nontransitiveSetsOfDice();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
index 660508c234..0b674e8a71 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff8
-title: 'Problem 377: Sum of digits, experience 13'
+title: 'Problema 377: Somma delle cifre, esperienza 13'
challengeType: 5
forumTopicId: 302039
dashedName: problem-377-sum-of-digits-experience-13
@@ -8,22 +8,22 @@ dashedName: problem-377-sum-of-digits-experience-13
# --description--
-There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+Ci sono 16 numeri interi positivi che non hanno uno 0 tra le loro cifre e che hanno una somma delle cifre uguale a 5:
-5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 e 11111.
-Their sum is 17891.
+La loro somma è 17891.
-Let f(n) be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to n.
+Sia $f(n)$ la somma di tutti i numeri interi positivi che non hanno uno zero tra le loro cifre e che hanno una somma delle cifre pari a $n$.
-Find $\\displaystyle \\sum\_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+Trova $\displaystyle\sum_{i=1}^{17} f(13^i)$. Dai le ultime 9 cifre della tua risposta.
# --hints--
-`euler377()` should return 732385277.
+`experience13()` dovrebbe restituire `732385277`.
```js
-assert.strictEqual(euler377(), 732385277);
+assert.strictEqual(experience13(), 732385277);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler377(), 732385277);
## --seed-contents--
```js
-function euler377() {
+function experience13() {
return true;
}
-euler377();
+experience13();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
index 22589747fe..0c8d5d5b65 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f4e61000cf542c50fff9
-title: 'Problem 378: Triangle Triples'
+title: 'Problema 378: tripli triangoli'
challengeType: 5
forumTopicId: 302040
dashedName: problem-378-triangle-triples
@@ -8,24 +8,20 @@ dashedName: problem-378-triangle-triples
# --description--
-Let T(n) be the nth triangle number, so T(n) =
+Sia $T(n)$ l'$n$-simo numero triangolare, quindi $T(n) = \frac{n(n + 1)}{2}$.
-n (n+1)2
+Sia $dT(n)$ il numero di divisori di $T(n)$. Esempio: $T(7) = 28$ e $dT(7) = 6$.
-.
+Sia $Tr(n)$ il numero di triplette ($i$, $j$, $k$) per cui $1 ≤ i < j < k ≤ n$ e $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5\\,772$ e $Tr(1000) = 11\\,174\\,776$.
-Let dT(n) be the number of divisors of T(n). E.g.: T(7) = 28 and dT(7) = 6.
-
-Let Tr(n) be the number of triples (i, j, k) such that 1 ≤ i < j < k ≤ n and dT(i) > dT(j) > dT(k). Tr(20) = 14, Tr(100) = 5772 and Tr(1000) = 11174776.
-
-Find Tr(60 000 000). Give the last 18 digits of your answer.
+Trova $Tr(60\\,000\\,000)$. Dai le ultime 18 cifre della tua risposta.
# --hints--
-`euler378()` should return 147534623725724700.
+`triangleTriples()` dovrebbe restituire `147534623725724700`.
```js
-assert.strictEqual(euler378(), 147534623725724700);
+assert.strictEqual(triangleTriples(), 147534623725724700);
```
# --seed--
@@ -33,12 +29,12 @@ assert.strictEqual(euler378(), 147534623725724700);
## --seed-contents--
```js
-function euler378() {
+function triangleTriples() {
return true;
}
-euler378();
+triangleTriples();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
index 3933d82ea2..7798debf82 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffa
-title: 'Problem 379: Least common multiple count'
+title: 'Problema 379: conteggio del minimo comune multiplo'
challengeType: 5
forumTopicId: 302041
dashedName: problem-379-least-common-multiple-count
@@ -8,20 +8,20 @@ dashedName: problem-379-least-common-multiple-count
# --description--
-Let f(n) be the number of couples (x,y) with x and y positive integers, x ≤ y and the least common multiple of x and y equal to n.
+Sia $f(n)$ il numero di coppie ($x$, $y$) con $x$ e $y$ numeri interi positivi, per cui $x ≤ y$ e il minimo comune multiplo di $x$ e $y$ è uguale a $n$.
-Let g be the summatory function of f, i.e.: g(n) = ∑ f(i) for 1 ≤ i ≤ n.
+Sia $g$ la funzione sommatoria di $f$, cioè $g(n) = \sum f(i)$ per $1 ≤ i ≤ n$.
-You are given that g(106) = 37429395.
+Ti è dato che $g({10}^6) = 37\\,429\\,395$.
-Find g(1012).
+Trova $g({10}^{12})$.
# --hints--
-`euler379()` should return 132314136838185.
+`leastCommonMultipleCount()` dovrebbe restituire `132314136838185`.
```js
-assert.strictEqual(euler379(), 132314136838185);
+assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler379(), 132314136838185);
## --seed-contents--
```js
-function euler379() {
+function leastCommonMultipleCount() {
return true;
}
-euler379();
+leastCommonMultipleCount();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
index 8596f52fa7..2fa9c3c7b7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffb
-title: 'Problem 380: Amazing Mazes!'
+title: 'Problema 380: fantastici labirinti!'
challengeType: 5
forumTopicId: 302044
dashedName: problem-380-amazing-mazes
@@ -8,20 +8,30 @@ dashedName: problem-380-amazing-mazes
# --description--
-An m×n maze is an m×n rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+Un labirinto $m×n$ è una griglia rettangolare $m×n$ con muri piazzati tra celle della griglia in modo tale che c'è un unico percorso dal quadrato in alto a sinistra a qualsiasi altro quadrato. I seguenti sono esempi di labirinti 9×12 e 15×20:
-Let C(m,n) be the number of distinct m×n mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+ -It can be verified that C(1,1) = 1, C(2,2) = 4, C(3,4) = 2415, and C(9,12) = 2.5720e46 (in scientific notation rounded to 5 significant digits). Find C(100,500) and write your answer in scientific notation rounded to 5 significant digits.
+Sia $C(m, n)$ il numero di labirinti distinti $m×n$. Labirinti che possono essere formati per rotazione e riflessione da un altro labirinto sono considerati distinti.
-When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be 1.2346e12.
+Si può verificare che $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, e $C(9, 12) = 2.5720\mathrm{e}\\,46$ (in notazione scientifica arrotondato a 5 cifre significative).
+
+Trova $C(100, 500)$ e scrivi la tua risposta come una stringa in notazione scientifica arrotondato a 5 cifre significative.
+
+Quando dai la tua risposta, usa una e minuscola per separare la mantissa e l'esponente. Ad es. se la risposta è 1234567891011 allora la risposta formattata sarebbe la stringa `1.2346e12`.
# --hints--
-`euler380()` should return Infinity.
+`amazingMazes()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler380(), Infinity);
+assert(typeof amazingMazes() === 'string');
+```
+
+`amazingMazes()` dovrebbe restituire la stringa `6.3202e25093`.
+
+```js
+assert.strictEqual(amazingMazes(), '6.3202e25093');
```
# --seed--
@@ -29,12 +39,12 @@ assert.strictEqual(euler380(), Infinity);
## --seed-contents--
```js
-function euler380() {
+function amazingMazes() {
return true;
}
-euler380();
+amazingMazes();
```
# --solutions--
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
index 21c6460649..a1b1526ba9 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
@@ -10,14 +10,9 @@ dashedName: arithmetic-formatter
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-arithmetic-formatter)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-小学校の算数では計算問題を解きやすくるために縦書きにすることが多くあります。 たとえば「235 + 52」を次のように記述します。
+Students in primary school often arrange arithmetic problems vertically to make them easier to solve. For example, "235 + 52" becomes:
```py
235
@@ -25,17 +20,17 @@ Python カリキュラムの対話式教育コンテンツを引き続き開発
-----
```
-計算問題を表す文字列のリストを受け取り、問題を縦書きに整形して返す関数を作成してください。 この関数はオプションで第 2 引数を受け取る必要があります。 第 2 引数が `True` に設定されている場合は、解答を表示する必要があります。
+Create a function that receives a list of strings that are arithmetic problems and returns the problems arranged vertically and side-by-side. The function should optionally take a second argument. When the second argument is set to `True`, the answers should be displayed.
## 例
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
```
-出力:
+Output:
```py
32 3801 45 123
@@ -43,13 +38,13 @@ arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
----- ------ ---- -----
```
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
```
-出力:
+Output:
```py
32 1 9999 523
@@ -60,35 +55,35 @@ arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
## ルール
-入力された問題が正しく整形されている場合、この関数は正しい変換結果を返します。それ以外の場合は、**ユーザーにとって意味のあるエラーを記述した****文字列**を返します。
+The function will return the correct conversion if the supplied problems are properly formatted, otherwise, it will **return** a **string** that describes an error that is meaningful to the user.
-- エラーを返す場合:
- - 関数に入力した**問題の数が多すぎる**場合。 上限を **5** つとし、それを超える場合は `Error: Too many problems.` (エラー: 問題が多すぎます) を返します。
- - 関数が受け取ることのできる適切な演算子は**足し算**と**引き算**です。 掛け算と割り算はエラーを返します。 この箇条書きで指示していない他の演算子についてはテストする必要はありません。 次のようなエラーを返します: `Error: Operator must be '+' or '-'.` (エラー: '+' または '-' の演算子を使用してください)。
- - 数値 (オペランド) にはそれぞれ数字のみを含める必要があります。 数値以外の場合、関数は次のエラーを返します: `Error: Numbers must only contain digits.` (エラー: 数値には数字のみを含める必要があります)。
- - それぞれのオペランド (演算子の両側の数値) の幅は最大 4 桁です。 それ以外の場合は、次のようなエラー文字列を返します: `Error: Numbers cannot be more than four digits.` (エラー: 数値は 4 桁以内にする必要があります)。
-- ユーザーが問題を正しい形式で入力した場合は、次のルールに従って変換結果を返します。
- - 演算子と、2 つのオペランドのうち最も長いオペランドとの間に、スペースを 1 つ含めます。演算子は 2 つ目のオペランドと同じ行に表示し、両方のオペランドは入力されたとおりの順序で表示します (1 つ目のオペランドを上側に、2 つ目のオペランドを下側に表示します)。
- - 数値は右揃えにする必要があります。
- - それぞれの問題の間に 4 つのスペースが必要です。
- - それぞれの問題の一番下にダッシュが必要です。 ダッシュは、各問題の全体の長さに沿った長さにする必要があります (上の表示例を参考にしてください)
+- Situations that will return an error:
+ - If there are **too many problems** supplied to the function. The limit is **five**, anything more will return: `Error: Too many problems.`
+ - The appropriate operators the function will accept are **addition** and **subtraction**. Multiplication and division will return an error. Other operators not mentioned in this bullet point will not need to be tested. The error returned will be: `Error: Operator must be '+' or '-'.`
+ - Each number (operand) should only contain digits. Otherwise, the function will return: `Error: Numbers must only contain digits.`
+ - Each operand (aka number on each side of the operator) has a max of four digits in width. Otherwise, the error string returned will be: `Error: Numbers cannot be more than four digits.`
+- If the user supplied the correct format of problems, the conversion you return will follow these rules:
+ - There should be a single space between the operator and the longest of the two operands, the operator will be on the same line as the second operand, both operands will be in the same order as provided (the first will be the top one and the second will be the bottom.
+ - Numbers should be right-aligned.
+ - There should be four spaces between each problem.
+ - There should be dashes at the bottom of each problem. The dashes should run along the entire length of each problem individually. (The example above shows what this should look like.)
## 開発
-`arithmetic_arranger.py` でコードを記述してください。 開発には `main.py` を使用して `arithmetic_arranger()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `arithmetic_arranger.py`. For development, you can use `main.py` to test your `arithmetic_arranger()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 `test_module.py` のテストを `main.py` で実行できるようになっています。 「実行」ボタンを押すと自動的にテストが実行されます。 または、コンソールに `pytest` と入力してテストを実行することもできます。
+The unit tests for this project are in `test_module.py`. We are running the tests from `test_module.py` in `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button. Alternatively you may run the tests by inputting `pytest` in the console.
## 提出
-プロジェクトの URL をコピーし、下記に提出してください。
+Copy your project's URL and submit it below.
# --hints--
-計算問題を正しく整形し、すべてのテストに合格する必要があります。
+It should correctly format an arithmetic problem and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
index 71548845e3..85c5ccb811 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
@@ -10,29 +10,23 @@ dashedName: budget-app
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-budget-app)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-`budget.py` の `Category` クラスを完成させてください。 *食費*、*服飾費*、*娯楽費*など、さまざまな予算のカテゴリに応じてオブジェクトをインスタンス化できるようにする必要があります。 オブジェクトを作成したら、カテゴリの名前をオブジェクトに渡します。 クラスには、リスト形式の帳簿となる `ledger` というインスタンス変数が必要です。 クラスには次のメソッドも含める必要があります。
+Complete the `Category` class in `budget.py`. It should be able to instantiate objects based on different budget categories like *food*, *clothing*, and *entertainment*. When objects are created, they are passed in the name of the category. The class should have an instance variable called `ledger` that is a list. The class should also contain the following methods:
-- `deposit` (預け入れ) メソッド。金額と説明を受け取ります。 説明がない場合は、デフォルトで空の文字列にします。 このメソッドでは、`{"amount": amount, "description": description}` という形式で帳簿リストの末尾にオブジェクトを追加する必要があります。
-- `withdraw` (引き出し) メソッド。`deposit` メソッドに似ていますが、渡された金額を負数として帳簿に保存する必要があります。 十分な資金がない場合は、帳簿に何も追加しないでください。 このメソッドは、引き出しが行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `get_balance` (残高確認) メソッド。発生した入出金に基づいて予算カテゴリの現在の残高を返します。
-- `transfer` (送金) メソッド。引数として金額と別の予算カテゴリを受け取ります。 このメソッドでは、金額と "Transfer to [Destination Budget Category]" ([送金先の予算カテゴリ] への送金) という記述からなる出金を追加する必要があります。 このメソッドによって、金額と "Transfer to [Destination Budget Category]" という記述からなる入金額が他の予算カテゴリに追加されます。 十分な資金がない場合は、どちらの帳簿にも何も追加しないでください。 このメソッドは、送金が行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `check_funds` (資金確認) メソッド。引数として金額を受け取ります。 金額が予算カテゴリの残高よりも大きい場合は `False` を返し、それ以外の場合は `True` を返します。 このメソッドは `withdraw` メソッドと `transfer` メソッドの両方で使用する必要があります。
+- A `deposit` method that accepts an amount and description. If no description is given, it should default to an empty string. The method should append an object to the ledger list in the form of `{"amount": amount, "description": description}`.
+- A `withdraw` method that is similar to the `deposit` method, but the amount passed in should be stored in the ledger as a negative number. If there are not enough funds, nothing should be added to the ledger. This method should return `True` if the withdrawal took place, and `False` otherwise.
+- A `get_balance` method that returns the current balance of the budget category based on the deposits and withdrawals that have occurred.
+- A `transfer` method that accepts an amount and another budget category as arguments. The method should add a withdrawal with the amount and the description "Transfer to [Destination Budget Category]". The method should then add a deposit to the other budget category with the amount and the description "Transfer from [Source Budget Category]". If there are not enough funds, nothing should be added to either ledgers. This method should return `True` if the transfer took place, and `False` otherwise.
+- A `check_funds` method that accepts an amount as an argument. It returns `False` if the amount is greater than the balance of the budget category and returns `True` otherwise. This method should be used by both the `withdraw` method and `transfer` method.
-予算オブジェクトを出力するときは次のように表示する必要があります。
+When the budget object is printed it should display:
-- 30 文字のタイトル行。`*` 文字を並べて 1 行とし、中央にカテゴリの名前を置きます。
-- 帳簿にある品目のリスト。 各行に説明と金額を表示します。 説明の最初の 23 文字を表示し、その後に金額を表示します。 金額は右揃えで、小数点以下 2 桁までを含み、最大 7 文字まで表示します。
-- カテゴリの合計を表示する行。
+- A title line of 30 characters where the name of the category is centered in a line of `*` characters.
+- A list of the items in the ledger. Each line should show the description and amount. The first 23 characters of the description should be displayed, then the amount. The amount should be right aligned, contain two decimal places, and display a maximum of 7 characters.
+- A line displaying the category total.
-出力の例を次に示します。
+Here is an example of the output:
```bash
*************Food*************
@@ -43,13 +37,13 @@ Transfer to Clothing -50.00
Total: 923.96
```
-`Category` クラスの他に、カテゴリのリストを引数に取る `create_spend_chart` という関数を (クラスの外で) 作成してください。 この関数は棒グラフとなる文字列を返す必要があります。
+Besides the `Category` class, create a function (outside of the class) called `create_spend_chart` that takes a list of categories as an argument. It should return a string that is a bar chart.
-グラフでは、関数に渡された各カテゴリについて、その出費の割合を表示する必要があります。 出費の割合は、引き出し額でのみ計算する必要があり、預け入れ額では計算しません。 グラフの左下には 0 ~ 100 のラベルを付ける必要があります。 棒グラフの「棒」は文字 "o" を使用して作成する必要があります。 各棒の高さは最も近い 10 に切り下げる必要があります。 グラフの下の水平線は最後の棒からスペース 2 つ分だけ離す必要があります。 各カテゴリ名は棒の下に垂直に記述する必要があります。 一番上には "Percentage spent by category" (カテゴリ別の出費の割合) というタイトルを付ける必要があります。
+The chart should show the percentage spent in each category passed in to the function. The percentage spent should be calculated only with withdrawals and not with deposits. Down the left side of the chart should be labels 0 - 100. The "bars" in the bar chart should be made out of the "o" character. The height of each bar should be rounded down to the nearest 10. The horizontal line below the bars should go two spaces past the final bar. Each category name should be written vertically below the bar. There should be a title at the top that says "Percentage spent by category".
-この関数は最大 4 つのカテゴリでテストされます。
+This function will be tested with up to four categories.
-次の出力例を参考にして、出力の間隔を例と正確に合わせてください。
+Look at the example output below very closely and make sure the spacing of the output matches the example exactly.
```bash
Percentage spent by category
@@ -75,23 +69,23 @@ Percentage spent by category
g
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`budget.py` でコードを記述してください。 開発には `main.py` を使用して `Category` クラスをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `budget.py`. For development, you can use `main.py` to test your `Category` class. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Category クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Category class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
index 6719641228..5d230fc031 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
@@ -10,37 +10,31 @@ dashedName: polygon-area-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-polygon-area-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-このプロジェクトでは、オブジェクト指向プログラミングを使用して、Rectangle クラスと Square クラスを作成します。 Square クラスは Rectangle のサブクラスであり、メソッドと属性を継承する必要があります。
+In this project you will use object oriented programming to create a Rectangle class and a Square class. The Square class should be a subclass of Rectangle and inherit methods and attributes.
## Rectangle クラス
-Rectangle オブジェクトが作成されるときは、`width` 属性と `height` 属性で初期化する必要があります。 クラスには、次のメソッドも含める必要があります。
+When a Rectangle object is created, it should be initialized with `width` and `height` attributes. The class should also contain the following methods:
- `set_width`
- `set_height`
-- `get_area`: 面積を返します (`width * height`)
-- `get_perimeter`: 外周を返します (`2 * width + 2 * height`)
-- `get_diagonal`: 対角線を返します(`(width ** 2 + height ** 2) ** .5`)
-- `get_picture`: "\*" の行を使用して図形を表す文字列を返します。 行数は高さと等しく、各行の"\*"の数は幅と等しくする必要があります。 各行の末尾に改行 (`\n`) が必要です。 幅または高さが 50 より大きい場合は、文字列 "Too big for picture." を返す必要があります。
-- `get_amount_inside`: 引数として別の図形 (正方形または長方形) を受け取ります。 渡された図形が、その図形の中に何個収まるかを返します (回転はしません)。 たとえば、幅が 4 で高さが 8 の長方形には、一辺が 4 の正方形が 2つ収まります。
+- `get_area`: Returns area (`width * height`)
+- `get_perimeter`: Returns perimeter (`2 * width + 2 * height`)
+- `get_diagonal`: Returns diagonal (`(width ** 2 + height ** 2) ** .5`)
+- `get_picture`: Returns a string that represents the shape using lines of "\*". The number of lines should be equal to the height and the number of "\*" in each line should be equal to the width. There should be a new line (`\n`) at the end of each line. If the width or height is larger than 50, this should return the string: "Too big for picture.".
+- `get_amount_inside`: Takes another shape (square or rectangle) as an argument. Returns the number of times the passed in shape could fit inside the shape (with no rotations). For instance, a rectangle with a width of 4 and a height of 8 could fit in two squares with sides of 4.
-また、Rectangle のインスタンスを文字列として表現する場合は、`Rectangle(width=5, height=10)` のようにする必要があります。
+Additionally, if an instance of a Rectangle is represented as a string, it should look like: `Rectangle(width=5, height=10)`
## Square クラス
-Square クラスは Rectangle のサブクラスである必要があります。 Square オブジェクトが生成されるときは、一辺の長さを渡します。 `__init__` メソッドでは、一辺の長さを Rectangle クラスの `width` 属性と `height` 属性の両方に格納する必要があります。
+The Square class should be a subclass of Rectangle. When a Square object is created, a single side length is passed in. The `__init__` method should store the side length in both the `width` and `height` attributes from the Rectangle class.
-Square クラスは、Rectangle クラスのメソッドにアクセスできる必要があり、加えて `set_side` メソッドも含める必要があります。 Square のインスタンスを文字列として表現する場合は、`Square(side=9)` のようにする必要があります。
+The Square class should be able to access the Rectangle class methods but should also contain a `set_side` method. If an instance of a Square is represented as a string, it should look like: `Square(side=9)`
-また、Square クラスの `set_width` と `set_height` メソッドでは、幅と高さの両方を設定する必要があります。
+Additionally, the `set_width` and `set_height` methods on the Square class should set both the width and height.
## 使用例
@@ -64,7 +58,7 @@ rect.set_width(16)
print(rect.get_amount_inside(sq))
```
-上記のコードは次を返す必要があります。
+That code should return:
```bash
50
@@ -85,23 +79,23 @@ Square(side=4)
8
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`shape_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `shape_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `shape_calculator.py`. For development, you can use `main.py` to test your `shape_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Rectangle クラスと Square クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Rectangle class and Square class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
index a4f59e83b4..923413b43f 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
@@ -10,19 +10,13 @@ dashedName: probability-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-probability-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-帽子があり、その中に青いボールが 5 個、赤いボールが 4 個、緑のボールが 2 個入っているとします。 4 個のボールを無作為に取り出す場合、赤のボールが 1 個以上、緑のボールが 2 個含まれる確率は、いくらになりますか? 高度な数学を駆使して確率を計算することも可能ですが、多数の実験を実行しておおよその確率を推定するプログラムを記述する方が簡単です。
+Suppose there is a hat containing 5 blue balls, 4 red balls, and 2 green balls. What is the probability that a random draw of 4 balls will contain at least 1 red ball and 2 green balls? While it would be possible to calculate the probability using advanced mathematics, an easier way is to write a program to perform a large number of experiments to estimate an approximate probability.
-このプロジェクトでは、特定のボールを帽子から無作為に取り出す場合のおおよその確率を調べるプログラムを作成します。
+For this project, you will write a program to determine the approximate probability of drawing certain balls randomly from a hat.
-まず、`prob_calculator.py` で `Hat` クラスを作成してください。 このクラスは、帽子に入っている各色のボールの数を指定する可変個の引数を受け取る必要があります。 たとえば、次のどの方法でもクラスオブジェクトを作成することができます。
+First, create a `Hat` class in `prob_calculator.py`. The class should take a variable number of arguments that specify the number of balls of each color that are in the hat. For example, a class object could be created in any of these ways:
```py
hat1 = Hat(yellow=3, blue=2, green=6)
@@ -30,22 +24,22 @@ hat2 = Hat(red=5, orange=4)
hat3 = Hat(red=5, orange=4, black=1, blue=0, pink=2, striped=9)
```
-帽子は常に、少なくとも 1 個のボールが入った状態で作成されます。 作成時に帽子オブジェクトに渡された引数を、`contents` インスタンス変数に変換する必要があります。 `contents` は、帽子に入っているボールごとにアイテムを 1 つずつ含む文字列のリストである必要があります。 リスト内の各アイテムは、その色のボール 1 個分を表す色の名前である必要があります。 たとえば、帽子が `{"red": 2, "blue": 1}` の場合、`contents` は `["red", "red", "blue"]` になる必要があります。
+A hat will always be created with at least one ball. The arguments passed into the hat object upon creation should be converted to a `contents` instance variable. `contents` should be a list of strings containing one item for each ball in the hat. Each item in the list should be a color name representing a single ball of that color. For example, if your hat is `{"red": 2, "blue": 1}`, `contents` should be `["red", "red", "blue"]`.
-`Hat` クラスには `draw` メソッドが必要です。このメソッドは、帽子から取り出すボールの個数を示す引数を受け取ります。 draw メソッドは、`contents` からボールを無作為に取り除き、それらのボールを文字列のリストとして返す必要があります。 交換のできない壺の実験と同様に、取り出したボールは帽子に戻さないものとします。 取り出すボールの数が利用可能な数を超える場合は、すべてのボールを返してください。
+The `Hat` class should have a `draw` method that accepts an argument indicating the number of balls to draw from the hat. This method should remove balls at random from `contents` and return those balls as a list of strings. The balls should not go back into the hat during the draw, similar to an urn experiment without replacement. If the number of balls to draw exceeds the available quantity, return all the balls.
-次に、(`Hat` クラスの中ではなく) `prob_calculator.py` で `experiment` 関数を作成してください。 この関数は次の引数を受け取る必要があります。
+Next, create an `experiment` function in `prob_calculator.py` (not inside the `Hat` class). This function should accept the following arguments:
-- `hat`: 関数内でコピーする必要のあるボールを含む帽子オブジェクト。
-- `expected_balls`: 実験で帽子から取り出そうとするボールの正確なグループを示すオブジェクト。 たとえば、青のボール 2 個と赤のボール 1 個を帽子から取り出す確率を調べるには、`expected_balls` を `{"blue":2, "red":1}` に設定します。
-- `num_balls_drawn`: 各実験で帽子から取り出すボールの数。
-- `num_experiments`: 実行する実験の回数 (実験の回数が多いほど、おおよその確率の正確性が高まります)。
+- `hat`: A hat object containing balls that should be copied inside the function.
+- `expected_balls`: An object indicating the exact group of balls to attempt to draw from the hat for the experiment. For example, to determine the probability of drawing 2 blue balls and 1 red ball from the hat, set `expected_balls` to `{"blue":2, "red":1}`.
+- `num_balls_drawn`: The number of balls to draw out of the hat in each experiment.
+- `num_experiments`: The number of experiments to perform. (The more experiments performed, the more accurate the approximate probability will be.)
-`experiment` 関数は、確率を返す必要があります。
+The `experiment` function should return a probability.
-たとえば、黒を 6 個、赤を 4 個、緑を 3 個含む帽子から 5 個のボールを取り出す場合に、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個含まれる確率を求めたいとしましょう。 それには、`N` 回の実験を行い、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個になった回数 `M` を数え、確率を `M/N` として推定します。 実験ではそれぞれ、指定されたボールの入った帽子の状態から始め、いくつかのボールを取り出し、期待されるボールを取り出したかどうかを確認します。
+For example, let's say that you want to determine the probability of getting at least 2 red balls and 1 green ball when you draw 5 balls from a hat containing 6 black, 4 red, and 3 green. To do this, we perform `N` experiments, count how many times `M` we get at least 2 red balls and 1 green ball, and estimate the probability as `M/N`. Each experiment consists of starting with a hat containing the specified balls, drawing a number of balls, and checking if we got the balls we were attempting to draw.
-上記の例で 2000 回の実験を行う場合は、`experiment` 関数を次のように呼び出します。
+Here is how you would call the `experiment` function based on the example above with 2000 experiments:
```py
hat = Hat(black=6, red=4, green=3)
@@ -55,27 +49,27 @@ probability = experiment(hat=hat,
num_experiments=2000)
```
-この方法は無作為抽出に基づいているため、コードが実行されるたびに確率が多少変わります。
+Since this is based on random draws, the probability will be slightly different each time the code is run.
-*ヒント: `prob_calculator.py` の先頭ですでにインポートされているモジュールを使用することを検討してください。 `prob_calculator.py` の中で乱数シードを初期化しないでください。*
+*Hint: Consider using the modules that are already imported at the top of `prob_calculator.py`. Do not initialize random seed within `prob_calculator.py`.*
## 開発
-`prob_calculator.py` でコードを記述してください。 開発には `main.py` を使用してコードをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `prob_calculator.py`. For development, you can use `main.py` to test your code. Click the "run" button and `main.py` will run.
-ボイラープレートには `copy` モジュールと `random` モジュール用の `import` ステートメントが含まれています。 これらをプロジェクトで使用することを検討してください。
+The boilerplate includes `import` statements for the `copy` and `random` modules. Consider using those in your project.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-確率を正しく計算し、すべてのテストに合格する必要があります。
+It should correctly calculate probabilities and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
index 1b8344540a..7b7bcfcad1 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
@@ -10,27 +10,21 @@ dashedName: time-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-time-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-下記に示す 2 つの必須パラメーターと 1 つのオプションパラメーターを受け取る関数 `add_time` を記述してください。
+Write a function named `add_time` that takes in two required parameters and one optional parameter:
-- 12 時制形式の開始時刻 (末尾に AM または PM)
-- 時数と分数で示される経過時間
-- (オプション) 開始の曜日 (大文字小文字の記述は自由)
+- a start time in the 12-hour clock format (ending in AM or PM)
+- a duration time that indicates the number of hours and minutes
+- (optional) a starting day of the week, case insensitive
-関数は、経過時間を開始時刻に追加し、その結果を返す必要があります。
+The function should add the duration time to the start time and return the result.
-結果が翌日になる場合は、時刻の後に `(next day)` (翌日) を表示する必要があります。 結果が翌日以降になる場合は、時刻の後に `(n days later)` (n 日後) を表示する必要があります。ここで "n" は何日後かを示します。
+If the result will be the next day, it should show `(next day)` after the time. If the result will be more than one day later, it should show `(n days later)` after the time, where "n" is the number of days later.
-関数にオプションの開始曜日パラメーターが与えられた場合は、結果の曜日を出力に表示する必要があります。 出力する曜日は、時刻の後、「n 日後」の前に表示する必要があります。
+If the function is given the optional starting day of the week parameter, then the output should display the day of the week of the result. The day of the week in the output should appear after the time and before the number of days later.
-関数が扱うさまざまなケースの例を次に示します。 結果のスペースと句読点の表示に特に注意を払ってください。
+Below are some examples of different cases the function should handle. Pay close attention to the spacing and punctuation of the results.
```py
add_time("3:00 PM", "3:10")
@@ -52,23 +46,23 @@ add_time("6:30 PM", "205:12")
# Returns: 7:42 AM (9 days later)
```
-Python ライブラリをインポートしないでください。 開始時刻は有効な時刻であると仮定します。 経過時間の分数は 60 未満の整数になりますが、時数は任意の整数になります。
+Do not import any Python libraries. Assume that the start times are valid times. The minutes in the duration time will be a whole number less than 60, but the hour can be any whole number.
## 開発
-`time_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `time_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `time_calculator.py`. For development, you can use `main.py` to test your `time_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-正確に時間を追加し、すべてのテストに合格する必要があります。
+It should correctly add times and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
index 3bbff2c99e..9be6dd072f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
@@ -8,7 +8,7 @@ dashedName: problem-344-silver-dollar-game
# --description--
-ニコラース・ホーヴァート・ ド・ブラウンの銀貨ゲームにはいくつかバリエーションがあり、その一つは次のように説明されます。
+One variant of N.G. de Bruijn's silver dollar game can be described as follows:
マスが並ぶ細長い盤上に硬貨が何枚か置かれています (1 マスにたかだか 1 枚)。 銀貨 (1 ドル硬貨) と呼ばれる 1 枚しかない硬貨に、任意の価値があります。 2 人のプレイヤーが交互にプレイします。 各ターンで、プレイヤーは通常の移動または特別な移動を行う必要があります。
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
index 81a2c58f4a..0468ec26fd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
@@ -8,7 +8,7 @@ dashedName: problem-250-250250
# --description--
-Encontre o número de subconjuntos não vazios de $\\{11, 22, 33, \ldots, {250250}^{250250}\\}$, cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
+Encontre o número de subconjuntos não vazios de $\\{{1}^{1}, {2}^{2}, {3}^{3}, \ldots, {250250}^{250250}\\}$ cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
# --hints--
-It can be verified that C(1,1) = 1, C(2,2) = 4, C(3,4) = 2415, and C(9,12) = 2.5720e46 (in scientific notation rounded to 5 significant digits). Find C(100,500) and write your answer in scientific notation rounded to 5 significant digits.
+Sia $C(m, n)$ il numero di labirinti distinti $m×n$. Labirinti che possono essere formati per rotazione e riflessione da un altro labirinto sono considerati distinti.
-When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be 1.2346e12.
+Si può verificare che $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, e $C(9, 12) = 2.5720\mathrm{e}\\,46$ (in notazione scientifica arrotondato a 5 cifre significative).
+
+Trova $C(100, 500)$ e scrivi la tua risposta come una stringa in notazione scientifica arrotondato a 5 cifre significative.
+
+Quando dai la tua risposta, usa una e minuscola per separare la mantissa e l'esponente. Ad es. se la risposta è 1234567891011 allora la risposta formattata sarebbe la stringa `1.2346e12`.
# --hints--
-`euler380()` should return Infinity.
+`amazingMazes()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler380(), Infinity);
+assert(typeof amazingMazes() === 'string');
+```
+
+`amazingMazes()` dovrebbe restituire la stringa `6.3202e25093`.
+
+```js
+assert.strictEqual(amazingMazes(), '6.3202e25093');
```
# --seed--
@@ -29,12 +39,12 @@ assert.strictEqual(euler380(), Infinity);
## --seed-contents--
```js
-function euler380() {
+function amazingMazes() {
return true;
}
-euler380();
+amazingMazes();
```
# --solutions--
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
index 21c6460649..a1b1526ba9 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
@@ -10,14 +10,9 @@ dashedName: arithmetic-formatter
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-arithmetic-formatter)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-小学校の算数では計算問題を解きやすくるために縦書きにすることが多くあります。 たとえば「235 + 52」を次のように記述します。
+Students in primary school often arrange arithmetic problems vertically to make them easier to solve. For example, "235 + 52" becomes:
```py
235
@@ -25,17 +20,17 @@ Python カリキュラムの対話式教育コンテンツを引き続き開発
-----
```
-計算問題を表す文字列のリストを受け取り、問題を縦書きに整形して返す関数を作成してください。 この関数はオプションで第 2 引数を受け取る必要があります。 第 2 引数が `True` に設定されている場合は、解答を表示する必要があります。
+Create a function that receives a list of strings that are arithmetic problems and returns the problems arranged vertically and side-by-side. The function should optionally take a second argument. When the second argument is set to `True`, the answers should be displayed.
## 例
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
```
-出力:
+Output:
```py
32 3801 45 123
@@ -43,13 +38,13 @@ arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
----- ------ ---- -----
```
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
```
-出力:
+Output:
```py
32 1 9999 523
@@ -60,35 +55,35 @@ arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
## ルール
-入力された問題が正しく整形されている場合、この関数は正しい変換結果を返します。それ以外の場合は、**ユーザーにとって意味のあるエラーを記述した****文字列**を返します。
+The function will return the correct conversion if the supplied problems are properly formatted, otherwise, it will **return** a **string** that describes an error that is meaningful to the user.
-- エラーを返す場合:
- - 関数に入力した**問題の数が多すぎる**場合。 上限を **5** つとし、それを超える場合は `Error: Too many problems.` (エラー: 問題が多すぎます) を返します。
- - 関数が受け取ることのできる適切な演算子は**足し算**と**引き算**です。 掛け算と割り算はエラーを返します。 この箇条書きで指示していない他の演算子についてはテストする必要はありません。 次のようなエラーを返します: `Error: Operator must be '+' or '-'.` (エラー: '+' または '-' の演算子を使用してください)。
- - 数値 (オペランド) にはそれぞれ数字のみを含める必要があります。 数値以外の場合、関数は次のエラーを返します: `Error: Numbers must only contain digits.` (エラー: 数値には数字のみを含める必要があります)。
- - それぞれのオペランド (演算子の両側の数値) の幅は最大 4 桁です。 それ以外の場合は、次のようなエラー文字列を返します: `Error: Numbers cannot be more than four digits.` (エラー: 数値は 4 桁以内にする必要があります)。
-- ユーザーが問題を正しい形式で入力した場合は、次のルールに従って変換結果を返します。
- - 演算子と、2 つのオペランドのうち最も長いオペランドとの間に、スペースを 1 つ含めます。演算子は 2 つ目のオペランドと同じ行に表示し、両方のオペランドは入力されたとおりの順序で表示します (1 つ目のオペランドを上側に、2 つ目のオペランドを下側に表示します)。
- - 数値は右揃えにする必要があります。
- - それぞれの問題の間に 4 つのスペースが必要です。
- - それぞれの問題の一番下にダッシュが必要です。 ダッシュは、各問題の全体の長さに沿った長さにする必要があります (上の表示例を参考にしてください)
+- Situations that will return an error:
+ - If there are **too many problems** supplied to the function. The limit is **five**, anything more will return: `Error: Too many problems.`
+ - The appropriate operators the function will accept are **addition** and **subtraction**. Multiplication and division will return an error. Other operators not mentioned in this bullet point will not need to be tested. The error returned will be: `Error: Operator must be '+' or '-'.`
+ - Each number (operand) should only contain digits. Otherwise, the function will return: `Error: Numbers must only contain digits.`
+ - Each operand (aka number on each side of the operator) has a max of four digits in width. Otherwise, the error string returned will be: `Error: Numbers cannot be more than four digits.`
+- If the user supplied the correct format of problems, the conversion you return will follow these rules:
+ - There should be a single space between the operator and the longest of the two operands, the operator will be on the same line as the second operand, both operands will be in the same order as provided (the first will be the top one and the second will be the bottom.
+ - Numbers should be right-aligned.
+ - There should be four spaces between each problem.
+ - There should be dashes at the bottom of each problem. The dashes should run along the entire length of each problem individually. (The example above shows what this should look like.)
## 開発
-`arithmetic_arranger.py` でコードを記述してください。 開発には `main.py` を使用して `arithmetic_arranger()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `arithmetic_arranger.py`. For development, you can use `main.py` to test your `arithmetic_arranger()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 `test_module.py` のテストを `main.py` で実行できるようになっています。 「実行」ボタンを押すと自動的にテストが実行されます。 または、コンソールに `pytest` と入力してテストを実行することもできます。
+The unit tests for this project are in `test_module.py`. We are running the tests from `test_module.py` in `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button. Alternatively you may run the tests by inputting `pytest` in the console.
## 提出
-プロジェクトの URL をコピーし、下記に提出してください。
+Copy your project's URL and submit it below.
# --hints--
-計算問題を正しく整形し、すべてのテストに合格する必要があります。
+It should correctly format an arithmetic problem and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
index 71548845e3..85c5ccb811 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
@@ -10,29 +10,23 @@ dashedName: budget-app
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-budget-app)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-`budget.py` の `Category` クラスを完成させてください。 *食費*、*服飾費*、*娯楽費*など、さまざまな予算のカテゴリに応じてオブジェクトをインスタンス化できるようにする必要があります。 オブジェクトを作成したら、カテゴリの名前をオブジェクトに渡します。 クラスには、リスト形式の帳簿となる `ledger` というインスタンス変数が必要です。 クラスには次のメソッドも含める必要があります。
+Complete the `Category` class in `budget.py`. It should be able to instantiate objects based on different budget categories like *food*, *clothing*, and *entertainment*. When objects are created, they are passed in the name of the category. The class should have an instance variable called `ledger` that is a list. The class should also contain the following methods:
-- `deposit` (預け入れ) メソッド。金額と説明を受け取ります。 説明がない場合は、デフォルトで空の文字列にします。 このメソッドでは、`{"amount": amount, "description": description}` という形式で帳簿リストの末尾にオブジェクトを追加する必要があります。
-- `withdraw` (引き出し) メソッド。`deposit` メソッドに似ていますが、渡された金額を負数として帳簿に保存する必要があります。 十分な資金がない場合は、帳簿に何も追加しないでください。 このメソッドは、引き出しが行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `get_balance` (残高確認) メソッド。発生した入出金に基づいて予算カテゴリの現在の残高を返します。
-- `transfer` (送金) メソッド。引数として金額と別の予算カテゴリを受け取ります。 このメソッドでは、金額と "Transfer to [Destination Budget Category]" ([送金先の予算カテゴリ] への送金) という記述からなる出金を追加する必要があります。 このメソッドによって、金額と "Transfer to [Destination Budget Category]" という記述からなる入金額が他の予算カテゴリに追加されます。 十分な資金がない場合は、どちらの帳簿にも何も追加しないでください。 このメソッドは、送金が行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `check_funds` (資金確認) メソッド。引数として金額を受け取ります。 金額が予算カテゴリの残高よりも大きい場合は `False` を返し、それ以外の場合は `True` を返します。 このメソッドは `withdraw` メソッドと `transfer` メソッドの両方で使用する必要があります。
+- A `deposit` method that accepts an amount and description. If no description is given, it should default to an empty string. The method should append an object to the ledger list in the form of `{"amount": amount, "description": description}`.
+- A `withdraw` method that is similar to the `deposit` method, but the amount passed in should be stored in the ledger as a negative number. If there are not enough funds, nothing should be added to the ledger. This method should return `True` if the withdrawal took place, and `False` otherwise.
+- A `get_balance` method that returns the current balance of the budget category based on the deposits and withdrawals that have occurred.
+- A `transfer` method that accepts an amount and another budget category as arguments. The method should add a withdrawal with the amount and the description "Transfer to [Destination Budget Category]". The method should then add a deposit to the other budget category with the amount and the description "Transfer from [Source Budget Category]". If there are not enough funds, nothing should be added to either ledgers. This method should return `True` if the transfer took place, and `False` otherwise.
+- A `check_funds` method that accepts an amount as an argument. It returns `False` if the amount is greater than the balance of the budget category and returns `True` otherwise. This method should be used by both the `withdraw` method and `transfer` method.
-予算オブジェクトを出力するときは次のように表示する必要があります。
+When the budget object is printed it should display:
-- 30 文字のタイトル行。`*` 文字を並べて 1 行とし、中央にカテゴリの名前を置きます。
-- 帳簿にある品目のリスト。 各行に説明と金額を表示します。 説明の最初の 23 文字を表示し、その後に金額を表示します。 金額は右揃えで、小数点以下 2 桁までを含み、最大 7 文字まで表示します。
-- カテゴリの合計を表示する行。
+- A title line of 30 characters where the name of the category is centered in a line of `*` characters.
+- A list of the items in the ledger. Each line should show the description and amount. The first 23 characters of the description should be displayed, then the amount. The amount should be right aligned, contain two decimal places, and display a maximum of 7 characters.
+- A line displaying the category total.
-出力の例を次に示します。
+Here is an example of the output:
```bash
*************Food*************
@@ -43,13 +37,13 @@ Transfer to Clothing -50.00
Total: 923.96
```
-`Category` クラスの他に、カテゴリのリストを引数に取る `create_spend_chart` という関数を (クラスの外で) 作成してください。 この関数は棒グラフとなる文字列を返す必要があります。
+Besides the `Category` class, create a function (outside of the class) called `create_spend_chart` that takes a list of categories as an argument. It should return a string that is a bar chart.
-グラフでは、関数に渡された各カテゴリについて、その出費の割合を表示する必要があります。 出費の割合は、引き出し額でのみ計算する必要があり、預け入れ額では計算しません。 グラフの左下には 0 ~ 100 のラベルを付ける必要があります。 棒グラフの「棒」は文字 "o" を使用して作成する必要があります。 各棒の高さは最も近い 10 に切り下げる必要があります。 グラフの下の水平線は最後の棒からスペース 2 つ分だけ離す必要があります。 各カテゴリ名は棒の下に垂直に記述する必要があります。 一番上には "Percentage spent by category" (カテゴリ別の出費の割合) というタイトルを付ける必要があります。
+The chart should show the percentage spent in each category passed in to the function. The percentage spent should be calculated only with withdrawals and not with deposits. Down the left side of the chart should be labels 0 - 100. The "bars" in the bar chart should be made out of the "o" character. The height of each bar should be rounded down to the nearest 10. The horizontal line below the bars should go two spaces past the final bar. Each category name should be written vertically below the bar. There should be a title at the top that says "Percentage spent by category".
-この関数は最大 4 つのカテゴリでテストされます。
+This function will be tested with up to four categories.
-次の出力例を参考にして、出力の間隔を例と正確に合わせてください。
+Look at the example output below very closely and make sure the spacing of the output matches the example exactly.
```bash
Percentage spent by category
@@ -75,23 +69,23 @@ Percentage spent by category
g
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`budget.py` でコードを記述してください。 開発には `main.py` を使用して `Category` クラスをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `budget.py`. For development, you can use `main.py` to test your `Category` class. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Category クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Category class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
index 6719641228..5d230fc031 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
@@ -10,37 +10,31 @@ dashedName: polygon-area-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-polygon-area-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-このプロジェクトでは、オブジェクト指向プログラミングを使用して、Rectangle クラスと Square クラスを作成します。 Square クラスは Rectangle のサブクラスであり、メソッドと属性を継承する必要があります。
+In this project you will use object oriented programming to create a Rectangle class and a Square class. The Square class should be a subclass of Rectangle and inherit methods and attributes.
## Rectangle クラス
-Rectangle オブジェクトが作成されるときは、`width` 属性と `height` 属性で初期化する必要があります。 クラスには、次のメソッドも含める必要があります。
+When a Rectangle object is created, it should be initialized with `width` and `height` attributes. The class should also contain the following methods:
- `set_width`
- `set_height`
-- `get_area`: 面積を返します (`width * height`)
-- `get_perimeter`: 外周を返します (`2 * width + 2 * height`)
-- `get_diagonal`: 対角線を返します(`(width ** 2 + height ** 2) ** .5`)
-- `get_picture`: "\*" の行を使用して図形を表す文字列を返します。 行数は高さと等しく、各行の"\*"の数は幅と等しくする必要があります。 各行の末尾に改行 (`\n`) が必要です。 幅または高さが 50 より大きい場合は、文字列 "Too big for picture." を返す必要があります。
-- `get_amount_inside`: 引数として別の図形 (正方形または長方形) を受け取ります。 渡された図形が、その図形の中に何個収まるかを返します (回転はしません)。 たとえば、幅が 4 で高さが 8 の長方形には、一辺が 4 の正方形が 2つ収まります。
+- `get_area`: Returns area (`width * height`)
+- `get_perimeter`: Returns perimeter (`2 * width + 2 * height`)
+- `get_diagonal`: Returns diagonal (`(width ** 2 + height ** 2) ** .5`)
+- `get_picture`: Returns a string that represents the shape using lines of "\*". The number of lines should be equal to the height and the number of "\*" in each line should be equal to the width. There should be a new line (`\n`) at the end of each line. If the width or height is larger than 50, this should return the string: "Too big for picture.".
+- `get_amount_inside`: Takes another shape (square or rectangle) as an argument. Returns the number of times the passed in shape could fit inside the shape (with no rotations). For instance, a rectangle with a width of 4 and a height of 8 could fit in two squares with sides of 4.
-また、Rectangle のインスタンスを文字列として表現する場合は、`Rectangle(width=5, height=10)` のようにする必要があります。
+Additionally, if an instance of a Rectangle is represented as a string, it should look like: `Rectangle(width=5, height=10)`
## Square クラス
-Square クラスは Rectangle のサブクラスである必要があります。 Square オブジェクトが生成されるときは、一辺の長さを渡します。 `__init__` メソッドでは、一辺の長さを Rectangle クラスの `width` 属性と `height` 属性の両方に格納する必要があります。
+The Square class should be a subclass of Rectangle. When a Square object is created, a single side length is passed in. The `__init__` method should store the side length in both the `width` and `height` attributes from the Rectangle class.
-Square クラスは、Rectangle クラスのメソッドにアクセスできる必要があり、加えて `set_side` メソッドも含める必要があります。 Square のインスタンスを文字列として表現する場合は、`Square(side=9)` のようにする必要があります。
+The Square class should be able to access the Rectangle class methods but should also contain a `set_side` method. If an instance of a Square is represented as a string, it should look like: `Square(side=9)`
-また、Square クラスの `set_width` と `set_height` メソッドでは、幅と高さの両方を設定する必要があります。
+Additionally, the `set_width` and `set_height` methods on the Square class should set both the width and height.
## 使用例
@@ -64,7 +58,7 @@ rect.set_width(16)
print(rect.get_amount_inside(sq))
```
-上記のコードは次を返す必要があります。
+That code should return:
```bash
50
@@ -85,23 +79,23 @@ Square(side=4)
8
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`shape_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `shape_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `shape_calculator.py`. For development, you can use `main.py` to test your `shape_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Rectangle クラスと Square クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Rectangle class and Square class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
index a4f59e83b4..923413b43f 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
@@ -10,19 +10,13 @@ dashedName: probability-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-probability-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-帽子があり、その中に青いボールが 5 個、赤いボールが 4 個、緑のボールが 2 個入っているとします。 4 個のボールを無作為に取り出す場合、赤のボールが 1 個以上、緑のボールが 2 個含まれる確率は、いくらになりますか? 高度な数学を駆使して確率を計算することも可能ですが、多数の実験を実行しておおよその確率を推定するプログラムを記述する方が簡単です。
+Suppose there is a hat containing 5 blue balls, 4 red balls, and 2 green balls. What is the probability that a random draw of 4 balls will contain at least 1 red ball and 2 green balls? While it would be possible to calculate the probability using advanced mathematics, an easier way is to write a program to perform a large number of experiments to estimate an approximate probability.
-このプロジェクトでは、特定のボールを帽子から無作為に取り出す場合のおおよその確率を調べるプログラムを作成します。
+For this project, you will write a program to determine the approximate probability of drawing certain balls randomly from a hat.
-まず、`prob_calculator.py` で `Hat` クラスを作成してください。 このクラスは、帽子に入っている各色のボールの数を指定する可変個の引数を受け取る必要があります。 たとえば、次のどの方法でもクラスオブジェクトを作成することができます。
+First, create a `Hat` class in `prob_calculator.py`. The class should take a variable number of arguments that specify the number of balls of each color that are in the hat. For example, a class object could be created in any of these ways:
```py
hat1 = Hat(yellow=3, blue=2, green=6)
@@ -30,22 +24,22 @@ hat2 = Hat(red=5, orange=4)
hat3 = Hat(red=5, orange=4, black=1, blue=0, pink=2, striped=9)
```
-帽子は常に、少なくとも 1 個のボールが入った状態で作成されます。 作成時に帽子オブジェクトに渡された引数を、`contents` インスタンス変数に変換する必要があります。 `contents` は、帽子に入っているボールごとにアイテムを 1 つずつ含む文字列のリストである必要があります。 リスト内の各アイテムは、その色のボール 1 個分を表す色の名前である必要があります。 たとえば、帽子が `{"red": 2, "blue": 1}` の場合、`contents` は `["red", "red", "blue"]` になる必要があります。
+A hat will always be created with at least one ball. The arguments passed into the hat object upon creation should be converted to a `contents` instance variable. `contents` should be a list of strings containing one item for each ball in the hat. Each item in the list should be a color name representing a single ball of that color. For example, if your hat is `{"red": 2, "blue": 1}`, `contents` should be `["red", "red", "blue"]`.
-`Hat` クラスには `draw` メソッドが必要です。このメソッドは、帽子から取り出すボールの個数を示す引数を受け取ります。 draw メソッドは、`contents` からボールを無作為に取り除き、それらのボールを文字列のリストとして返す必要があります。 交換のできない壺の実験と同様に、取り出したボールは帽子に戻さないものとします。 取り出すボールの数が利用可能な数を超える場合は、すべてのボールを返してください。
+The `Hat` class should have a `draw` method that accepts an argument indicating the number of balls to draw from the hat. This method should remove balls at random from `contents` and return those balls as a list of strings. The balls should not go back into the hat during the draw, similar to an urn experiment without replacement. If the number of balls to draw exceeds the available quantity, return all the balls.
-次に、(`Hat` クラスの中ではなく) `prob_calculator.py` で `experiment` 関数を作成してください。 この関数は次の引数を受け取る必要があります。
+Next, create an `experiment` function in `prob_calculator.py` (not inside the `Hat` class). This function should accept the following arguments:
-- `hat`: 関数内でコピーする必要のあるボールを含む帽子オブジェクト。
-- `expected_balls`: 実験で帽子から取り出そうとするボールの正確なグループを示すオブジェクト。 たとえば、青のボール 2 個と赤のボール 1 個を帽子から取り出す確率を調べるには、`expected_balls` を `{"blue":2, "red":1}` に設定します。
-- `num_balls_drawn`: 各実験で帽子から取り出すボールの数。
-- `num_experiments`: 実行する実験の回数 (実験の回数が多いほど、おおよその確率の正確性が高まります)。
+- `hat`: A hat object containing balls that should be copied inside the function.
+- `expected_balls`: An object indicating the exact group of balls to attempt to draw from the hat for the experiment. For example, to determine the probability of drawing 2 blue balls and 1 red ball from the hat, set `expected_balls` to `{"blue":2, "red":1}`.
+- `num_balls_drawn`: The number of balls to draw out of the hat in each experiment.
+- `num_experiments`: The number of experiments to perform. (The more experiments performed, the more accurate the approximate probability will be.)
-`experiment` 関数は、確率を返す必要があります。
+The `experiment` function should return a probability.
-たとえば、黒を 6 個、赤を 4 個、緑を 3 個含む帽子から 5 個のボールを取り出す場合に、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個含まれる確率を求めたいとしましょう。 それには、`N` 回の実験を行い、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個になった回数 `M` を数え、確率を `M/N` として推定します。 実験ではそれぞれ、指定されたボールの入った帽子の状態から始め、いくつかのボールを取り出し、期待されるボールを取り出したかどうかを確認します。
+For example, let's say that you want to determine the probability of getting at least 2 red balls and 1 green ball when you draw 5 balls from a hat containing 6 black, 4 red, and 3 green. To do this, we perform `N` experiments, count how many times `M` we get at least 2 red balls and 1 green ball, and estimate the probability as `M/N`. Each experiment consists of starting with a hat containing the specified balls, drawing a number of balls, and checking if we got the balls we were attempting to draw.
-上記の例で 2000 回の実験を行う場合は、`experiment` 関数を次のように呼び出します。
+Here is how you would call the `experiment` function based on the example above with 2000 experiments:
```py
hat = Hat(black=6, red=4, green=3)
@@ -55,27 +49,27 @@ probability = experiment(hat=hat,
num_experiments=2000)
```
-この方法は無作為抽出に基づいているため、コードが実行されるたびに確率が多少変わります。
+Since this is based on random draws, the probability will be slightly different each time the code is run.
-*ヒント: `prob_calculator.py` の先頭ですでにインポートされているモジュールを使用することを検討してください。 `prob_calculator.py` の中で乱数シードを初期化しないでください。*
+*Hint: Consider using the modules that are already imported at the top of `prob_calculator.py`. Do not initialize random seed within `prob_calculator.py`.*
## 開発
-`prob_calculator.py` でコードを記述してください。 開発には `main.py` を使用してコードをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `prob_calculator.py`. For development, you can use `main.py` to test your code. Click the "run" button and `main.py` will run.
-ボイラープレートには `copy` モジュールと `random` モジュール用の `import` ステートメントが含まれています。 これらをプロジェクトで使用することを検討してください。
+The boilerplate includes `import` statements for the `copy` and `random` modules. Consider using those in your project.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-確率を正しく計算し、すべてのテストに合格する必要があります。
+It should correctly calculate probabilities and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
index 1b8344540a..7b7bcfcad1 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
@@ -10,27 +10,21 @@ dashedName: time-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-time-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-下記に示す 2 つの必須パラメーターと 1 つのオプションパラメーターを受け取る関数 `add_time` を記述してください。
+Write a function named `add_time` that takes in two required parameters and one optional parameter:
-- 12 時制形式の開始時刻 (末尾に AM または PM)
-- 時数と分数で示される経過時間
-- (オプション) 開始の曜日 (大文字小文字の記述は自由)
+- a start time in the 12-hour clock format (ending in AM or PM)
+- a duration time that indicates the number of hours and minutes
+- (optional) a starting day of the week, case insensitive
-関数は、経過時間を開始時刻に追加し、その結果を返す必要があります。
+The function should add the duration time to the start time and return the result.
-結果が翌日になる場合は、時刻の後に `(next day)` (翌日) を表示する必要があります。 結果が翌日以降になる場合は、時刻の後に `(n days later)` (n 日後) を表示する必要があります。ここで "n" は何日後かを示します。
+If the result will be the next day, it should show `(next day)` after the time. If the result will be more than one day later, it should show `(n days later)` after the time, where "n" is the number of days later.
-関数にオプションの開始曜日パラメーターが与えられた場合は、結果の曜日を出力に表示する必要があります。 出力する曜日は、時刻の後、「n 日後」の前に表示する必要があります。
+If the function is given the optional starting day of the week parameter, then the output should display the day of the week of the result. The day of the week in the output should appear after the time and before the number of days later.
-関数が扱うさまざまなケースの例を次に示します。 結果のスペースと句読点の表示に特に注意を払ってください。
+Below are some examples of different cases the function should handle. Pay close attention to the spacing and punctuation of the results.
```py
add_time("3:00 PM", "3:10")
@@ -52,23 +46,23 @@ add_time("6:30 PM", "205:12")
# Returns: 7:42 AM (9 days later)
```
-Python ライブラリをインポートしないでください。 開始時刻は有効な時刻であると仮定します。 経過時間の分数は 60 未満の整数になりますが、時数は任意の整数になります。
+Do not import any Python libraries. Assume that the start times are valid times. The minutes in the duration time will be a whole number less than 60, but the hour can be any whole number.
## 開発
-`time_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `time_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `time_calculator.py`. For development, you can use `main.py` to test your `time_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-正確に時間を追加し、すべてのテストに合格する必要があります。
+It should correctly add times and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
index 3bbff2c99e..9be6dd072f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
@@ -8,7 +8,7 @@ dashedName: problem-344-silver-dollar-game
# --description--
-ニコラース・ホーヴァート・ ド・ブラウンの銀貨ゲームにはいくつかバリエーションがあり、その一つは次のように説明されます。
+One variant of N.G. de Bruijn's silver dollar game can be described as follows:
マスが並ぶ細長い盤上に硬貨が何枚か置かれています (1 マスにたかだか 1 枚)。 銀貨 (1 ドル硬貨) と呼ばれる 1 枚しかない硬貨に、任意の価値があります。 2 人のプレイヤーが交互にプレイします。 各ターンで、プレイヤーは通常の移動または特別な移動を行う必要があります。
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
index 81a2c58f4a..0468ec26fd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
@@ -8,7 +8,7 @@ dashedName: problem-250-250250
# --description--
-Encontre o número de subconjuntos não vazios de $\\{11, 22, 33, \ldots, {250250}^{250250}\\}$, cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
+Encontre o número de subconjuntos não vazios de $\\{{1}^{1}, {2}^{2}, {3}^{3}, \ldots, {250250}^{250250}\\}$ cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
# --hints--
 -The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+Si può dimostrare che 3 è il numero minimo di turni per finire questo gioco.
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Il disco in basso a sinistra sulla scheda $N×N$ ha coordinate (0, 0); il disco in basso a destra ha coordinate ($N - 1$,$0$) e il disco in alto a sinistra ha coordinate ($0$,$N - 1$).
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Sia $C_N$ la seguente configurazione di una scheda con $N × N$ dischi: Un disco a ($x$, $y$) soddisfacente $N - 1 \le \sqrt{x^2 + y^2} \lt N$, mostra il suo lato nero; altrimenti, mostra il suo lato bianco. $C_5$ è mostrato sopra.
-Find .
+Sia $T(N)$ il numero minimo di turni per completare una partita che parte dalla configurazione $C_N$ o 0 se la configurazione $C_N$ è irrisolvibile. Abbiamo mostrato che $T(5) = 3$. Ti viene anche dato che $T(10) = 29$ e $T(1\\,000) = 395\\,253$.
+
+Trova $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` dovrebbe restituire `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..9a6be05971 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcb
-title: 'Problem 332: Spherical triangles'
+title: 'Problema 332: Triangoli sferici'
challengeType: 5
forumTopicId: 301990
dashedName: problem-332-spherical-triangles
@@ -8,20 +8,28 @@ dashedName: problem-332-spherical-triangles
# --description--
-A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
+Un triangolo sferico è una figura formata sulla superficie di una sfera da tre grandi archi circolari che intersecano a coppia in tre vertici.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+
-The bottom left disk on the N×N board has coordinates (0,0); the bottom right disk has coordinates (N-1,0) and the top left disk has coordinates (0,N-1).
+Si può dimostrare che 3 è il numero minimo di turni per finire questo gioco.
-Let CN be the following configuration of a board with N×N disks: A disk at (x,y) satisfying , shows its black side; otherwise, it shows its white side. C5 is shown above.
+Il disco in basso a sinistra sulla scheda $N×N$ ha coordinate (0, 0); il disco in basso a destra ha coordinate ($N - 1$,$0$) e il disco in alto a sinistra ha coordinate ($0$,$N - 1$).
-Let T(N) be the minimal number of turns to finish a game starting from configuration CN or 0 if configuration CN is unsolvable. We have shown that T(5)=3. You are also given that T(10)=29 and T(1 000)=395253.
+Sia $C_N$ la seguente configurazione di una scheda con $N × N$ dischi: Un disco a ($x$, $y$) soddisfacente $N - 1 \le \sqrt{x^2 + y^2} \lt N$, mostra il suo lato nero; altrimenti, mostra il suo lato bianco. $C_5$ è mostrato sopra.
-Find .
+Sia $T(N)$ il numero minimo di turni per completare una partita che parte dalla configurazione $C_N$ o 0 se la configurazione $C_N$ è irrisolvibile. Abbiamo mostrato che $T(5) = 3$. Ti viene anche dato che $T(10) = 29$ e $T(1\\,000) = 395\\,253$.
+
+Trova $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
# --hints--
-`euler331()` should return 467178235146843500.
+`crossFlips()` dovrebbe restituire `467178235146843500`.
```js
-assert.strictEqual(euler331(), 467178235146843500);
+assert.strictEqual(crossFlips(), 467178235146843500);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler331(), 467178235146843500);
## --seed-contents--
```js
-function euler331() {
+function crossFlips() {
return true;
}
-euler331();
+crossFlips();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index ea3a4d0c43..9a6be05971 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcb
-title: 'Problem 332: Spherical triangles'
+title: 'Problema 332: Triangoli sferici'
challengeType: 5
forumTopicId: 301990
dashedName: problem-332-spherical-triangles
@@ -8,20 +8,28 @@ dashedName: problem-332-spherical-triangles
# --description--
-A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
+Un triangolo sferico è una figura formata sulla superficie di una sfera da tre grandi archi circolari che intersecano a coppia in tre vertici.
-Let C(r) be the sphere with the centre (0,0,0) and radius r. Let Z(r) be the set of points on the surface of C(r) with integer coordinates. Let T(r) be the set of spherical triangles with vertices in Z(r). Degenerate spherical triangles, formed by three points on the same great arc, are not included in T(r). Let A(r) be the area of the smallest spherical triangle in T(r).
+ -For example A(14) is 3.294040 rounded to six decimal places.
+Sia $C(r)$ la sfera di centro (0,0,0) e raggio $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Sia $Z(r)$ il set di punti sulla superficie di $C(r)$ con coordinate intere.
+
+Sia $T(r)$ il set di triangoli sferici con vertici in $Z(r)$. Triangoli sferici degeneri, formati da tre punti sullo stesso grande arco, non sono inclusi in $T(r)$.
+
+Sia $A(r)$ l'area del più piccolo triangolo sferico in $T(r)$.
+
+Per esempio, $A(14)$ è 3.294040 arrotondato a sei decimali.
+
+Trova $\displaystyle \sum_{r = 1}^{50} A(r)$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` dovrebbe restituire `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..8b533c9b74 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcc
-title: 'Problem 333: Special partitions'
+title: 'Problema 333: Partizioni speciali'
challengeType: 5
forumTopicId: 301991
dashedName: problem-333-special-partitions
@@ -8,26 +8,28 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+Tutti gli interi positivi possono essere suddivisi in modo tale che ogni termine della partizione possa essere espresso come $2^i \times 3^j$, dove $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Consideriamo solo quelle partizioni dove nessuno dei termini può dividere uno degli altri termini. Ad esempio, la partizione di $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ non sarebbe valida poiché 2 puó dividere 6. Neanche la partizione $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ poiché 1 può dividere 16. L'unica partizione valida di 17 sarebbe $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Molti interi hanno più di una partizione valida, il primo è 11 con le due partizioni seguenti.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align} & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1) \end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Definiamo $P(n)$ come il numero di partizioni valide di $n$. Per esempio, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Consideriamo solo gli interi primi $q$ che avrebbero una singola partizione valida come $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+La somma dei primi $q <100$ tali che $P(q) = 1$ è uguale a 233.
+
+Trova la somma dei primi $q < 1\\,000\\,000$ tali che $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` dovrebbe restituire `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..b2b564d99d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4ba1000cf542c50ffcd
-title: 'Problem 334: Spilling the beans'
+title: 'Problema 334: Versare i fagioli'
challengeType: 5
forumTopicId: 301992
dashedName: problem-334-spilling-the-beans
@@ -8,24 +8,26 @@ dashedName: problem-334-spilling-the-beans
# --description--
-In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.
+Nel paradiso di Platone, esiste un numero infinito di ciotole in linea retta. Ogni ciotola contiene alcuni o nessuno di un numero finito di fagioli. Un bambino gioca un gioco, che permette un solo tipo di mossa: rimuovere due fagioli da qualsiasi ciotola, e metterne uno in ognuna delle due ciotole adiacenti. Il gioco termina quando ogni ciotola contiene uno o nessun fagiolo.
-For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
+Ad esempio, considera due ciotole adiacenti contenenti 2 e 3 fagioli rispettivamente, tutte le altre ciotole sono vuote. Le seguenti otto mosse finiranno il gioco:
-
+
-For example A(14) is 3.294040 rounded to six decimal places.
+Sia $C(r)$ la sfera di centro (0,0,0) e raggio $r$.
-Find A(r). Give your answer rounded to six decimal places.
+Sia $Z(r)$ il set di punti sulla superficie di $C(r)$ con coordinate intere.
+
+Sia $T(r)$ il set di triangoli sferici con vertici in $Z(r)$. Triangoli sferici degeneri, formati da tre punti sullo stesso grande arco, non sono inclusi in $T(r)$.
+
+Sia $A(r)$ l'area del più piccolo triangolo sferico in $T(r)$.
+
+Per esempio, $A(14)$ è 3.294040 arrotondato a sei decimali.
+
+Trova $\displaystyle \sum_{r = 1}^{50} A(r)$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler332()` should return 2717.751525.
+`sphericalTriangles()` dovrebbe restituire `2717.751525`.
```js
-assert.strictEqual(euler332(), 2717.751525);
+assert.strictEqual(sphericalTriangles(), 2717.751525);
```
# --seed--
@@ -29,12 +37,12 @@ assert.strictEqual(euler332(), 2717.751525);
## --seed-contents--
```js
-function euler332() {
+function sphericalTriangles() {
return true;
}
-euler332();
+sphericalTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 5af490eb7e..8b533c9b74 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcc
-title: 'Problem 333: Special partitions'
+title: 'Problema 333: Partizioni speciali'
challengeType: 5
forumTopicId: 301991
dashedName: problem-333-special-partitions
@@ -8,26 +8,28 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as 2ix3j, where i,j ≥ 0.
+Tutti gli interi positivi possono essere suddivisi in modo tale che ogni termine della partizione possa essere espresso come $2^i \times 3^j$, dove $i, j ≥ 0$.
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of 17 = 2 + 6 + 9 = (21x30 + 21x31 + 20x32) would not be valid since 2 can divide 6. Neither would the partition 17 = 16 + 1 = (24x30 + 20x30) since 1 can divide 16. The only valid partition of 17 would be 8 + 9 = (23x30 + 20x32).
+Consideriamo solo quelle partizioni dove nessuno dei termini può dividere uno degli altri termini. Ad esempio, la partizione di $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ non sarebbe valida poiché 2 puó dividere 6. Neanche la partizione $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ poiché 1 può dividere 16. L'unica partizione valida di 17 sarebbe $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
-Many integers have more than one valid partition, the first being 11 having the following two partitions. 11 = 2 + 9 = (21x30 + 20x32) 11 = 8 + 3 = (23x30 + 20x31)
+Molti interi hanno più di una partizione valida, il primo è 11 con le due partizioni seguenti.
-Let's define P(n) as the number of valid partitions of n. For example, P(11) = 2.
+$$\begin{align} & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1) \end{align}$$
-Let's consider only the prime integers q which would have a single valid partition such as P(17).
+Definiamo $P(n)$ come il numero di partizioni valide di $n$. Per esempio, $P(11) = 2$.
-The sum of the primes q <100 such that P(q)=1 equals 233.
+Consideriamo solo gli interi primi $q$ che avrebbero una singola partizione valida come $P(17)$.
-Find the sum of the primes q <1000000 such that P(q)=1.
+La somma dei primi $q <100$ tali che $P(q) = 1$ è uguale a 233.
+
+Trova la somma dei primi $q < 1\\,000\\,000$ tali che $P(q) = 1$.
# --hints--
-`euler333()` should return 3053105.
+`specialPartitions()` dovrebbe restituire `3053105`.
```js
-assert.strictEqual(euler333(), 3053105);
+assert.strictEqual(specialPartitions(), 3053105);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler333(), 3053105);
## --seed-contents--
```js
-function euler333() {
+function specialPartitions() {
return true;
}
-euler333();
+specialPartitions();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index fe354cec8a..b2b564d99d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4ba1000cf542c50ffcd
-title: 'Problem 334: Spilling the beans'
+title: 'Problema 334: Versare i fagioli'
challengeType: 5
forumTopicId: 301992
dashedName: problem-334-spilling-the-beans
@@ -8,24 +8,26 @@ dashedName: problem-334-spilling-the-beans
# --description--
-In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.
+Nel paradiso di Platone, esiste un numero infinito di ciotole in linea retta. Ogni ciotola contiene alcuni o nessuno di un numero finito di fagioli. Un bambino gioca un gioco, che permette un solo tipo di mossa: rimuovere due fagioli da qualsiasi ciotola, e metterne uno in ognuna delle due ciotole adiacenti. Il gioco termina quando ogni ciotola contiene uno o nessun fagiolo.
-For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
+Ad esempio, considera due ciotole adiacenti contenenti 2 e 3 fagioli rispettivamente, tutte le altre ciotole sono vuote. Le seguenti otto mosse finiranno il gioco:
-
+ -You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+animazione di una partita con due ciotole adiacenti contenenti rispettivamente 2 e 3 fagioli:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd} \end{cases} \\\\ & \qquad \text{dove$⌊x⌋$ è la funzione arrotonda verso il basso e $\oplus$ è l'operatore bitwise XOR.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+I primi due termini dell'ultima sequenza sono $b_1 = 289$ e $b_2 = 145$. Se iniziamo con $b_1$ e $b_2$ fagioli in due ciotole adiacenti, saranno necessarie 3419100 mosse per finire la partita.
+
+Considera ora 1500 ciotole adiacenti contenenti rispettivamente $b_1, b_2, \ldots, b_{1500}$ fagioli, tutte le altre ciotole sono vuote. Trova quante mosse sono necessarie prima che il gioco finisca.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` dovrebbe restituire `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..47c14f189c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffce
-title: 'Problem 335: Gathering the beans'
+title: 'Problema 335: Raccogliere i fagioli'
challengeType: 5
forumTopicId: 301993
dashedName: problem-335-gathering-the-beans
@@ -8,20 +8,22 @@ dashedName: problem-335-gathering-the-beans
# --description--
-Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+Ogni volta che Peter si sente annoiato, mette alcune ciotole, contenenti un fagiolo ciascuno, in un cerchio. Dopo di che, prende tutti i fagioli da una certa ciotola e li rovescia uno ad uno nelle ciotole andando in senso orario. Lo ripete, a partire dalla ciotola in cui ha lasciato cadere l'ultimo fagiolo, fino a quando la situazione iniziale appare di nuovo. Ad esempio con 5 ciotole agisce come segue:
-So with 5 bowls it takes Peter 15 moves to return to the initial situation.
+
-You are given the following sequences: t0 = 123456. ti = ti-12, if ti-1 is even ti-12 926252, if ti-1 is odd where ⌊x⌋ is the floor function and is the bitwise XOR operator. bi = ( ti mod 211) + 1.
+animazione di una partita con due ciotole adiacenti contenenti rispettivamente 2 e 3 fagioli:
-The first two terms of the last sequence are b1 = 289 and b2 = 145. If we start with b1 and b2 beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd} \end{cases} \\\\ & \qquad \text{dove$⌊x⌋$ è la funzione arrotonda verso il basso e $\oplus$ è l'operatore bitwise XOR.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
-Consider now 1500 adjacent bowls containing b1, b2,..., b1500 beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+I primi due termini dell'ultima sequenza sono $b_1 = 289$ e $b_2 = 145$. Se iniziamo con $b_1$ e $b_2$ fagioli in due ciotole adiacenti, saranno necessarie 3419100 mosse per finire la partita.
+
+Considera ora 1500 ciotole adiacenti contenenti rispettivamente $b_1, b_2, \ldots, b_{1500}$ fagioli, tutte le altre ciotole sono vuote. Trova quante mosse sono necessarie prima che il gioco finisca.
# --hints--
-`euler334()` should return 150320021261690850.
+`spillingTheBeans()` dovrebbe restituire `150320021261690850`.
```js
-assert.strictEqual(euler334(), 150320021261690850);
+assert.strictEqual(spillingTheBeans(), 150320021261690850);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler334(), 150320021261690850);
## --seed-contents--
```js
-function euler334() {
+function spillingTheBeans() {
return true;
}
-euler334();
+spillingTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index 0605e0d053..47c14f189c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffce
-title: 'Problem 335: Gathering the beans'
+title: 'Problema 335: Raccogliere i fagioli'
challengeType: 5
forumTopicId: 301993
dashedName: problem-335-gathering-the-beans
@@ -8,20 +8,22 @@ dashedName: problem-335-gathering-the-beans
# --description--
-Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+Ogni volta che Peter si sente annoiato, mette alcune ciotole, contenenti un fagiolo ciascuno, in un cerchio. Dopo di che, prende tutti i fagioli da una certa ciotola e li rovescia uno ad uno nelle ciotole andando in senso orario. Lo ripete, a partire dalla ciotola in cui ha lasciato cadere l'ultimo fagiolo, fino a quando la situazione iniziale appare di nuovo. Ad esempio con 5 ciotole agisce come segue:
-So with 5 bowls it takes Peter 15 moves to return to the initial situation.
+ -Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Quindi con 5 ciotole servono a Peter 15 mosse per tornare alla situazione iniziale.
-Find M(2k+1). Give your answer modulo 79.
+Lascia che $M(x)$ rappresenti il numero di mosse necessarie per tornare alla situazione iniziale, a partire da $x$ ciotole. Così, $M(5) = 15$. Può anche essere verificato che $M(100) = 10920$.
+
+Trova $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Dai la tua risposta modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` dovrebbe restituire `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..d538ead789 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffcf
-title: 'Problem 336: Maximix Arrangements'
+title: 'Problema 336: Arrangiamenti Maximix'
challengeType: 5
forumTopicId: 301994
dashedName: problem-336-maximix-arrangements
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+Un treno è utilizzato per trasportare quattro carrozze nell'ordine: $ABCD$. Tuttavia, a volte quando il treno arriva per raccogliere le carrozze, esse non sono nell'ordine corretto.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+Per riorganizzare le carrozze, vengono tutte smistate su un grande disco rotante. Dopo che le carrozze sono disaccoppiate in un punto specifico, il treno si allontana dal disco rotante tirando le carrozze ancora attaccate con esso. Le carrozze rimanenti sono ruotate di 180°. Tutte le carrozze vengono poi ricongiunte e questo processo viene ripetuto tutte le volte necessarie a ottenere il minor numero di utilizzi del disco.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Alcune disposizioni, come $ADCB$, possono essere risolte facilmente: le carrozze sono separate tra $A$ e $D$, e dopo che $DCB$ sono stati ruotati l'ordine corretto è stato raggiunto.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+Tuttavia, Simple Simon, il macchinista del treno, non è noto per la sua efficienza, così risolve sempre il problema ottenendo inizialmente il carrello $A$ nel posto corretto, poi la carrozza $B$, e così via.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Usando quattro carrozze, i peggior possibili arrangiamenti per Simon, che chiamiamo maximix, sono $DACB$ e $DBAC$; ognuno richiedente quattro rotazioni (anche se usando l'approccio più efficiente potrebbero essere risolti usando solo tre rotazioni). Il processo che usa per $DACB$ è mostrato sotto.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+
-Let M(x) represent the number of moves required to return to the initial situation, starting with x bowls. Thus, M(5) = 15. It can also be verified that M(100) = 10920.
+Quindi con 5 ciotole servono a Peter 15 mosse per tornare alla situazione iniziale.
-Find M(2k+1). Give your answer modulo 79.
+Lascia che $M(x)$ rappresenti il numero di mosse necessarie per tornare alla situazione iniziale, a partire da $x$ ciotole. Così, $M(5) = 15$. Può anche essere verificato che $M(100) = 10920$.
+
+Trova $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Dai la tua risposta modulo $7^9$.
# --hints--
-`euler335()` should return 5032316.
+`gatheringTheBeans()` dovrebbe restituire `5032316`.
```js
-assert.strictEqual(euler335(), 5032316);
+assert.strictEqual(gatheringTheBeans(), 5032316);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler335(), 5032316);
## --seed-contents--
```js
-function euler335() {
+function gatheringTheBeans() {
return true;
}
-euler335();
+gatheringTheBeans();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index 3dbf18111c..d538ead789 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffcf
-title: 'Problem 336: Maximix Arrangements'
+title: 'Problema 336: Arrangiamenti Maximix'
challengeType: 5
forumTopicId: 301994
dashedName: problem-336-maximix-arrangements
@@ -8,26 +8,34 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: ABCD. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+Un treno è utilizzato per trasportare quattro carrozze nell'ordine: $ABCD$. Tuttavia, a volte quando il treno arriva per raccogliere le carrozze, esse non sono nell'ordine corretto.
-To rearrange the carriages they are all shunted on to a large rotating turntable. After the carriages are uncoupled at a specific point the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180 degrees. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+Per riorganizzare le carrozze, vengono tutte smistate su un grande disco rotante. Dopo che le carrozze sono disaccoppiate in un punto specifico, il treno si allontana dal disco rotante tirando le carrozze ancora attaccate con esso. Le carrozze rimanenti sono ruotate di 180°. Tutte le carrozze vengono poi ricongiunte e questo processo viene ripetuto tutte le volte necessarie a ottenere il minor numero di utilizzi del disco.
-Some arrangements, such as ADCB, can be solved easily: the carriages are separated between A and D, and after DCB are rotated the correct order has been achieved.
+Alcune disposizioni, come $ADCB$, possono essere risolte facilmente: le carrozze sono separate tra $A$ e $D$, e dopo che $DCB$ sono stati ruotati l'ordine corretto è stato raggiunto.
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage A in the correct place, then carriage B, and so on.
+Tuttavia, Simple Simon, il macchinista del treno, non è noto per la sua efficienza, così risolve sempre il problema ottenendo inizialmente il carrello $A$ nel posto corretto, poi la carrozza $B$, e così via.
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are DACB and DBAC; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for DACB is shown below.
+Usando quattro carrozze, i peggior possibili arrangiamenti per Simon, che chiamiamo maximix, sono $DACB$ e $DBAC$; ognuno richiedente quattro rotazioni (anche se usando l'approccio più efficiente potrebbero essere risolti usando solo tre rotazioni). Il processo che usa per $DACB$ è mostrato sotto.
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is DFAECB.
+ -Find the 2011th lexicographic maximix arrangement for eleven carriages.
+Possiamo verificare che ci sono 24 arrangiamenti maximix per sei carrozze, di cui il decimo arrangiamento lessicografico maximix è $DFAECB$.
+
+Trova il ${2011}$-simo arrangiamento maximix lessicografico per undici carrozze.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` dovrebbe restituire la stringa `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..77408eb4ca 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd0
-title: 'Problem 337: Totient Stairstep Sequences'
+title: 'Problema 337: Sequenze tozienti a gradino'
challengeType: 5
forumTopicId: 301995
dashedName: problem-337-totient-stairstep-sequences
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Sia $\\{a_1, a_2, \ldots, a_n\\}$ una sequenza di interi di lunghezza $n$ tale che:
-a1 = 6
+- $a_1 = 6$
+- per ogni $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denota la funzione toziente di Eulero.
-Let S(N) be the number of such sequences with an ≤ N.
+Sia $S(N)$ il numero di tali sequenze con $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+Ad esempio, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} e {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+Possiamo verificare che $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Trova $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` dovrebbe restituire `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..af40fc4d91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd1
-title: 'Problem 338: Cutting Rectangular Grid Paper'
+title: 'Problema 338: Tagliare carta a quadretti rettangolare'
challengeType: 5
forumTopicId: 301996
dashedName: problem-338-cutting-rectangular-grid-paper
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+Viene fornito un foglio rettangolare di carta a quadretti con dimensioni intere $w$ × $h$. La spaziatura della griglia è 1.
-When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
+Quando tagliamo il foglio lungo le linee della griglia in due pezzi e riordiniamo quei pezzi senza sovrapposizioni, possiamo creare nuovi rettangoli con dimensioni diverse.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+Ad esempio, da un foglio con dimensioni 9 × 4, possiamo realizzare rettangoli con dimensioni 18 × 2, 12 × 3 e 6 × 6 mediante taglio e riarrangiamento come segue:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+
-Find the 2011th lexicographic maximix arrangement for eleven carriages.
+Possiamo verificare che ci sono 24 arrangiamenti maximix per sei carrozze, di cui il decimo arrangiamento lessicografico maximix è $DFAECB$.
+
+Trova il ${2011}$-simo arrangiamento maximix lessicografico per undici carrozze.
# --hints--
-`euler336()` should return CAGBIHEFJDK.
+`maximixArrangements()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler336(), CAGBIHEFJDK);
+assert(typeof maximixArrangements() === 'string');
+```
+
+`maximixArrangements()` dovrebbe restituire la stringa `CAGBIHEFJDK`.
+
+```js
+assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
```
# --seed--
@@ -35,12 +43,12 @@ assert.strictEqual(euler336(), CAGBIHEFJDK);
## --seed-contents--
```js
-function euler336() {
+function maximixArrangements() {
return true;
}
-euler336();
+maximixArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index 677c918f05..77408eb4ca 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd0
-title: 'Problem 337: Totient Stairstep Sequences'
+title: 'Problema 337: Sequenze tozienti a gradino'
challengeType: 5
forumTopicId: 301995
dashedName: problem-337-totient-stairstep-sequences
@@ -8,28 +8,28 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let {a1, a2,..., an} be an integer sequence of length n such that:
+Sia $\\{a_1, a_2, \ldots, a_n\\}$ una sequenza di interi di lunghezza $n$ tale che:
-a1 = 6
+- $a_1 = 6$
+- per ogni $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-for all 1 ≤ i < n : φ(ai) < φ(ai+1) < ai < ai+11
+$φ$ denota la funzione toziente di Eulero.
-Let S(N) be the number of such sequences with an ≤ N.
+Sia $S(N)$ il numero di tali sequenze con $a_n ≤ N$.
-For example, S(10) = 4: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+Ad esempio, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} e {6, 10}.
-We can verify that S(100) = 482073668 and S(10 000) mod 108 = 73808307.
+Possiamo verificare che $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
-Find S(20 000 000) mod 108.
+Trova $S(20\\,000\\,000)\bmod {10}^8$.
-1 φ denotes Euler's totient function.
# --hints--
-`euler337()` should return 85068035.
+`totientStairstepSequences()` dovrebbe restituire `85068035`.
```js
-assert.strictEqual(euler337(), 85068035);
+assert.strictEqual(totientStairstepSequences(), 85068035);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler337(), 85068035);
## --seed-contents--
```js
-function euler337() {
+function totientStairstepSequences() {
return true;
}
-euler337();
+totientStairstepSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index 514dc560b0..af40fc4d91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd1
-title: 'Problem 338: Cutting Rectangular Grid Paper'
+title: 'Problema 338: Tagliare carta a quadretti rettangolare'
challengeType: 5
forumTopicId: 301996
dashedName: problem-338-cutting-rectangular-grid-paper
@@ -8,26 +8,28 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions w × h is given. Its grid spacing is 1.
+Viene fornito un foglio rettangolare di carta a quadretti con dimensioni intere $w$ × $h$. La spaziatura della griglia è 1.
-When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
+Quando tagliamo il foglio lungo le linee della griglia in due pezzi e riordiniamo quei pezzi senza sovrapposizioni, possiamo creare nuovi rettangoli con dimensioni diverse.
-For example, from a sheet with dimensions 9 × 4 , we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+Ad esempio, da un foglio con dimensioni 9 × 4, possiamo realizzare rettangoli con dimensioni 18 × 2, 12 × 3 e 6 × 6 mediante taglio e riarrangiamento come segue:
-Similarly, from a sheet with dimensions 9 × 8 , we can make rectangles with dimensions 18 × 4 and 12 × 6 .
+ -For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Allo stesso modo, da un foglio con dimensioni 9 × 8, possiamo realizzare rettangoli con dimensioni 18 × 4 e 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+Per una coppia $w$ e $h$, sia $F(w, h)$ il numero di rettangoli distinti che possono essere fatti da un foglio con dimensioni $w$ × $h$. Per esempio, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ e $F(9, 8) = 2$. Nota che i rettangoli congruenti a quello iniziale non sono contati in $F(w, h)$. Nota anche che i rettangoli con dimensioni $w$ × $h$ e le dimensioni $h$ × $w$ non sono considerati distinti.
-Find G(1012). Give your answer modulo 108.
+Per un intero $N$, sia $G(N)$ la somma di $F(w, h)$ per tutte le coppie $w$ e $h$ che soddisfano $0 < h ≤ w ≤ N$. Possiamo verificare che $G(10) = 55$, $G({10}^3) = 971\\,745$ e $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Trova $G({10}^{12})$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` dovrebbe restituire `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..602ef1c635 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -1,6 +1,6 @@
---
id: 5900f4c01000cf542c50ffd2
-title: 'Problem 339: Peredur fab Efrawg'
+title: 'Problema 339: Peredur fab Efrawg'
challengeType: 5
forumTopicId: 301997
dashedName: problem-339-peredur-fab-efrawg
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"E venne verso una valle, attraverso la quale correva un fiume; e i confini della valle erano boscosi, e su ogni lato del fiume vi erano prati pianeggianti. Da un lato del fiume vide un gregge di pecore bianche, dall'altro un gregge di pecore nere. E ogni volta che una delle pecore bianche belava, una delle pecore nere attraversava e diventava bianca; e quando una delle pecore nere belava, una delle pecore bianche attraversava e diventava nera." - Peredur Figlio di Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Inizialmente, ogni gregge è costituito da $n$ pecore. Ogni pecora (indipendentemente dal colore) è altrettanto probabile che sia la prossima pecora a belare. Dopo che una pecora ha belato e una pecora dall'altro gregge ha attraversato, Peredur può rimuovere un numero di pecore bianche al fine di massimizzare il numero finale previsto di pecore nere. Sia $E(n)$ il numero aspettato finale di pecore nere se Peredur usa una strategia ottimale.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+Ti è dato che $E(5) = 6.871346$ arrotondato a 6 cifre decimali.
+
+Trova $E(10\\,000)$ e dai la tua risposta arrotondata a 6 cifre decimali.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` dovrebbe restituire `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..c6e17627dc 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4c21000cf542c50ffd4
-title: 'Problem 340: Crazy Function'
+title: 'Problema 340: Funzione Pazza'
challengeType: 5
forumTopicId: 301999
dashedName: problem-340-crazy-function
@@ -8,24 +8,22 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+Per gli interi fissati $a$, $b$, $c$, definire la funzione pazza $F(n)$ come segue:
-F(n) = n - c for all n > b
+$$\begin{align} & F(n) = n - c \\;\text{ per ogni } n > b \\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ per ogni } n ≤ b. \end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Inoltre, definisci $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+Per esempio, se $a = 50$, $b = 2000$ e $c = 40$, allora $F(0) = 3240$ e $F(2000) = 2040$. Inoltre, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Trova le ultime 9 cifre di $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` dovrebbe restituire `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
index 740ef0d751..693beaed83 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4c11000cf542c50ffd3
-title: 'Problem 341: Golomb''s self-describing sequence'
+title: 'Problema 341: Sequenza auto-descrittiva di Golomb'
challengeType: 5
forumTopicId: 302000
dashedName: problem-341-golombs-self-describing-sequence
@@ -8,20 +8,22 @@ dashedName: problem-341-golombs-self-describing-sequence
# --description--
-The Golomb's self-describing sequence {G(n)} is the only nondecreasing sequence of natural numbers such that n appears exactly G(n) times in the sequence. The values of G(n) for the first few n are
+La sequenza di auto-descrizione di Golomb ($G(n)$) è l'unica sequenza non decrescente di numeri naturali tali che $n$ appaia esattamente $G(n)$ volte nella sequenza. I valori di $G(n)$ per i primi $n$ sono
-n123456789101112131415…G(n)122334445556666…
+$$\begin{array}{c} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & \ldots \\\\ G(n) & 1 & 2 & 2 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & \ldots \end{array}$$
-You are given that G(103) = 86, G(106) = 6137. You are also given that ΣG(n3) = 153506976 for 1 ≤ n < 103.
+Ti viene dato che $G({10}^3) = 86$, $G({10}^6) = 6137$.
-Find ΣG(n3) for 1 ≤ n < 106.
+Ti viene anche dato che $\sum G(n^3) = 153\\,506\\,976$ per $1 ≤ n < {10}^3$.
+
+Trova $\sum G(n^3)$ per $1 ≤ n < {10}^6$.
# --hints--
-`euler341()` should return 56098610614277016.
+`golombsSequence()` dovrebbe restituire `56098610614277016`.
```js
-assert.strictEqual(euler341(), 56098610614277016);
+assert.strictEqual(golombsSequence(), 56098610614277016);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler341(), 56098610614277016);
## --seed-contents--
```js
-function euler341() {
+function golombsSequence() {
return true;
}
-euler341();
+golombsSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
index 2253ce390f..cbcc7d8c39 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c31000cf542c50ffd5
-title: 'Problem 342: The totient of a square is a cube'
+title: 'Problema 342: Il toziente di un quadrato è un cubo'
challengeType: 5
forumTopicId: 302001
dashedName: problem-342-the-totient-of-a-square-is-a-cube
@@ -8,22 +8,21 @@ dashedName: problem-342-the-totient-of-a-square-is-a-cube
# --description--
-Consider the number 50.
+Considera il numero 50.
-502 = 2500 = 22 × 54, so φ(2500) = 2 × 4 × 53 = 8 × 53 = 23 × 53. 1
+${50}^2 = 2500 = 2^2 × 5^4$, so $φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$. $φ$ denota la funzione toziente di Eulero.
-So 2500 is a square and φ(2500) is a cube.
+Quindi 2500 è un quadrato e $φ(2500)$ è un cubo.
-Find the sum of all numbers n, 1 < n < 1010 such that φ(n2) is a cube.
+Trova la somma di tutti i numeri $n$, $1 < n < {10}^{10}$ in modo che $φ(n^2)$ sia un cubo.
-1 φ denotes Euler's totient function.
# --hints--
-`euler342()` should return 5943040885644.
+`totientOfSquare()` dovrebbe restituire `5943040885644`.
```js
-assert.strictEqual(euler342(), 5943040885644);
+assert.strictEqual(totientOfSquare(), 5943040885644);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler342(), 5943040885644);
## --seed-contents--
```js
-function euler342() {
+function totientOfSquare() {
return true;
}
-euler342();
+totientOfSquare();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
index 3102009e8c..63e1dab730 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4c41000cf542c50ffd6
-title: 'Problem 343: Fractional Sequences'
+title: 'Problema 343: Sequenze frazionarie'
challengeType: 5
forumTopicId: 302002
dashedName: problem-343-fractional-sequences
@@ -8,32 +8,31 @@ dashedName: problem-343-fractional-sequences
# --description--
-For any positive integer k, a finite sequence ai of fractions xi/yi is defined by:
+Per qualsiasi numero intero positivo $k$, una sequenza finita $a_i$ di frazioni $\frac{x_i}{y_i}$ è definita da:
-a1 = 1/k and
+- $a_1 = \displaystyle\frac{1}{k}$ e
+- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ ridotto ai minimi termini per $i > 1$.
-ai = (xi-1+1)/(yi-1-1) reduced to lowest terms for i>1.
+Quando $a_i$ raggiunge un numero intero $n$, la sequenza si ferma. (cioè, quando $y_i = 1$.)
-When ai reaches some integer n, the sequence stops. (That is, when yi=1.)
+Definisci $f(k) = n$.
-Define f(k) = n.
+Per esempio, per $k = 20$:
-For example, for k = 20:
+$$\frac{1}{20} → \frac{2}{19} → \frac{3}{18} = \frac{1}{6} → \frac{2}{5} → \frac{3}{4} → \frac{4}{3} → \frac{5}{2} → \frac{6}{1} = 6$$
-1/20 → 2/19 → 3/18 = 1/6 → 2/5 → 3/4 → 4/3 → 5/2 → 6/1 = 6
+Quindi $f(20) = 6$.
-So f(20) = 6.
+Anche $f(1) = 1$, $f(2) = 2$, $f(3) = 1$ e $\sum f(k^3) = 118\\,937$ per $1 ≤ k ≤ 100$.
-Also f(1) = 1, f(2) = 2, f(3) = 1 and Σf(k3) = 118937 for 1 ≤ k ≤ 100.
-
-Find Σf(k3) for 1 ≤ k ≤ 2×106.
+Trova $\sum f(k^3)$ per $1 ≤ k ≤ 2 × {10}^6$.
# --hints--
-`euler343()` should return 269533451410884200.
+`fractionalSequences()` dovrebbe restituire `269533451410884200`.
```js
-assert.strictEqual(euler343(), 269533451410884200);
+assert.strictEqual(fractionalSequences(), 269533451410884200);
```
# --seed--
@@ -41,12 +40,12 @@ assert.strictEqual(euler343(), 269533451410884200);
## --seed-contents--
```js
-function euler343() {
+function fractionalSequences() {
return true;
}
-euler343();
+fractionalSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
index 9cb8157d07..a94d255151 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffda
-title: 'Problem 345: Matrix Sum'
+title: 'Problema 345: Somma di matrice'
challengeType: 5
forumTopicId: 302004
dashedName: problem-345-matrix-sum
@@ -8,20 +8,22 @@ dashedName: problem-345-matrix-sum
# --description--
-We define the Matrix Sum of a matrix as the maximum sum of matrix elements with each element being the only one in his row and column. For example, the Matrix Sum of the matrix below equals 3315 ( = 863 + 383 + 343 + 959 + 767):
+Definiamo la Somma di Matrice di una matrice come la somma massima di elementi di matrice dove ogni elemento è l'unico nella sua fila e colonna.
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943767 473 103 699 303
+Ad esempio, la somma di matrice della matrice qui sotto è pari a $3315 ( = 863 + 383 + 343 + 959 + 767)$:
-Find the Matrix Sum of:
+$$\begin{array}{rrrrr} 7 & 53 & 183 & 439 & \color{lime}{863} \\\\ 497 & \color{lime}{383} & 563 & 79 & 973 \\\\ 287 & 63 & \color{lime}{343} & 169 & 583 \\\\ 627 & 343 & 773 & \color{lime}{959} & 943 \\\\ \color{lime}{767} & 473 & 103 & 699 & 303 \end{array}$$
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943 767 473 103 699 303 957 703 583 639 913 447 283 463 29 23 487 463 993 119 883 327 493 423 159 743 217 623 3 399 853 407 103 983 89 463 290 516 212 462 350 960 376 682 962 300 780 486 502 912 800 250 346 172 812 350 870 456 192 162 593 473 915 45 989 873 823 965 425 329 803 973 965 905 919 133 673 665 235 509 613 673 815 165 992 326 322 148 972 962 286 255 941 541 265 323 925 281 601 95 973 445 721 11 525 473 65 511 164 138 672 18 428 154 448 848 414 456 310 312 798 104 566 520 302 248 694 976 430 392 198 184 829 373 181 631 101 969 613 840 740 778 458 284 760 390 821 461 843 513 17 901 711 993 293 157 274 94 192 156 574 34 124 4 878 450 476 712 914 838 669 875 299 823 329 699 815 559 813 459 522 788 168 586 966 232 308 833 251 631 107 813 883 451 509 615 77 281 613 459 205 380 274 302 35 805
+Trova la somma di matrice di:
+
+$$\\begin{array}{r} 7 & 53 & 183 & 439 & 863 & 497 & 383 & 563 & 79 & 973 & 287 & 63 & 343 & 169 & 583 \\\\ 627 & 343 & 773 & 959 & 943 & 767 & 473 & 103 & 699 & 303 & 957 & 703 & 583 & 639 & 913 \\\\ 447 & 283 & 463 & 29 & 23 & 487 & 463 & 993 & 119 & 883 & 327 & 493 & 423 & 159 & 743 \\\\ 217 & 623 & 3 & 399 & 853 & 407 & 103 & 983 & 89 & 463 & 290 & 516 & 212 & 462 & 350 \\\\ 960 & 376 & 682 & 962 & 300 & 780 & 486 & 502 & 912 & 800 & 250 & 346 & 172 & 812 & 350 \\\\ 870 & 456 & 192 & 162 & 593 & 473 & 915 & 45 & 989 & 873 & 823 & 965 & 425 & 329 & 803 \\\\ 973 & 965 & 905 & 919 & 133 & 673 & 665 & 235 & 509 & 613 & 673 & 815 & 165 & 992 & 326 \\\\ 322 & 148 & 972 & 962 & 286 & 255 & 941 & 541 & 265 & 323 & 925 & 281 & 601 & 95 & 973 \\\\ 445 & 721 & 11 & 525 & 473 & 65 & 511 & 164 & 138 & 672 & 18 & 428 & 154 & 448 & 848 \\\\ 414 & 456 & 310 & 312 & 798 & 104 & 566 & 520 & 302 & 248 & 694 & 976 & 430 & 392 & 198 \\\\ 184 & 829 & 373 & 181 & 631 & 101 & 969 & 613 & 840 & 740 & 778 & 458 & 284 & 760 & 390 \\\\ 821 & 461 & 843 & 513 & 17 & 901 & 711 & 993 & 293 & 157 & 274 & 94 & 192 & 156 & 574 \\\\ 34 & 124 & 4 & 878 & 450 & 476 & 712 & 914 & 838 & 669 & 875 & 299 & 823 & 329 & 699 \\\\ 815 & 559 & 813 & 459 & 522 & 788 & 168 & 586 & 966 & 232 & 308 & 833 & 251 & 631 & 107 \\\\ 813 & 883 & 451 & 509 & 615 & 77 & 281 & 613 & 459 & 205 & 380 & 274 & 302 & 35 & 805 \end{array}$$
# --hints--
-`euler345()` should return 13938.
+`matrixSum()` dovrebbe restituire `13938`.
```js
-assert.strictEqual(euler345(), 13938);
+assert.strictEqual(matrixSum(), 13938);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler345(), 13938);
## --seed-contents--
```js
-function euler345() {
+function matrixSum() {
return true;
}
-euler345();
+matrixSum();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
index 49a1f6b2c2..844987961a 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
@@ -1,6 +1,6 @@
---
id: 5900f4c71000cf542c50ffd8
-title: 'Problem 346: Strong Repunits'
+title: 'Problema 346: Repunit Forti'
challengeType: 5
forumTopicId: 302005
dashedName: problem-346-strong-repunits
@@ -8,18 +8,18 @@ dashedName: problem-346-strong-repunits
# --description--
-The number 7 is special, because 7 is 111 written in base 2, and 11 written in base 6 (i.e. 710 = 116 = 1112). In other words, 7 is a repunit in at least two bases b > 1.
+Il numero 7 è speciale, perché 7 è 111 scritto in base 2, e 11 scritto in base 6 (cioè $7_{10} = {11}_6 = {111}_2$). In altre parole, 7 è una repunit in almeno due basi $b > 1$.
-We shall call a positive integer with this property a strong repunit. It can be verified that there are 8 strong repunits below 50: {1,7,13,15,21,31,40,43}. Furthermore, the sum of all strong repunits below 1000 equals 15864.
+Chiameremo un numero intero positivo con questa proprietà una forte repunit. Si può verificare che ci sono 8 forti repunit sotto 50: {1, 7, 13, 15, 21, 31, 40, 43}. Inoltre, la somma di tutti i repunit forti sotto 1000 è pari a 15864.
-Find the sum of all strong repunits below 1012.
+Trova la somma di tutti i repunit forti sotto ${10}^{12}$.
# --hints--
-`euler346()` should return 336108797689259260.
+`strongRepunits()` dovrebbe restituire `336108797689259260`.
```js
-assert.strictEqual(euler346(), 336108797689259260);
+assert.strictEqual(strongRepunits(), 336108797689259260);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler346(), 336108797689259260);
## --seed-contents--
```js
-function euler346() {
+function strongRepunits() {
return true;
}
-euler346();
+strongRepunits();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
index 70845508fa..961ba85720 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffd9
-title: 'Problem 347: Largest integer divisible by two primes'
+title: 'Problema 347: Intero più grande divisibile per due primi'
challengeType: 5
forumTopicId: 302006
dashedName: problem-347-largest-integer-divisible-by-two-primes
@@ -8,24 +8,24 @@ dashedName: problem-347-largest-integer-divisible-by-two-primes
# --description--
-The largest integer ≤ 100 that is only divisible by both the primes 2 and 3 is 96, as 96=32\*3=25\*3.
+Il più grande intero $≤ 100$ che è divisibile solo per entrambe i primi 2 e 3 è 96, poiché $96 = 32 \times 3 = 2^5 \times 3$.
-For two distinct primes p and q let M(p,q,N) be the largest positive integer ≤N only divisible
+Per due primi distinti $p$ e $q$ sia $M(p, q, N)$ il più grande intero positivo $≤ N$ divisibile solo per $p$ e $q$ e $M(p, q, N)=0$ se tale numero intero positivo non esiste.
-by both p and q and M(p,q,N)=0 if such a positive integer does not exist.
+Ad es. $M(2, 3, 100) = 96$.
-E.g. M(2,3,100)=96. M(3,5,100)=75 and not 90 because 90 is divisible by 2 ,3 and 5. Also M(2,73,100)=0 because there does not exist a positive integer ≤ 100 that is divisible by both 2 and 73.
+$M(3, 5, 100) = 75$ e non 90 perché 90 è divisibile per 2, 3 e 5. Anche $M(2, 73, 100) = 0$ perché non esiste un numero intero positivo $≤ 100$ che è divisibile sia per 2 che 73.
-Let S(N) be the sum of all distinct M(p,q,N). S(100)=2262.
+Sia $S(N)$ la somma di tutti gli $M(p, q, N)$ distinti. $S(100)=2262$.
-Find S(10 000 000).
+Trova $S(10\\,000\\,000)$.
# --hints--
-`euler347()` should return 11109800204052.
+`integerDivisibleByTwoPrimes()` dovrebbe restituire `11109800204052`.
```js
-assert.strictEqual(euler347(), 11109800204052);
+assert.strictEqual(integerDivisibleByTwoPrimes(), 11109800204052);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler347(), 11109800204052);
## --seed-contents--
```js
-function euler347() {
+function integerDivisibleByTwoPrimes() {
return true;
}
-euler347();
+integerDivisibleByTwoPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
index 2fe6e2bc13..75d443eac6 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffdb
-title: 'Problem 348: Sum of a square and a cube'
+title: 'Problema 348: Somma di un quadrato e di un cubo'
challengeType: 5
forumTopicId: 302007
dashedName: problem-348-sum-of-a-square-and-a-cube
@@ -8,18 +8,22 @@ dashedName: problem-348-sum-of-a-square-and-a-cube
# --description--
-Many numbers can be expressed as the sum of a square and a cube. Some of them in more than one way.
+Molti numeri possono essere espressi come somma di un quadrato e di un cubo. Alcuni di essi in più in modo.
-Consider the palindromic numbers that can be expressed as the sum of a square and a cube, both greater than 1, in exactly 4 different ways. For example, 5229225 is a palindromic number and it can be expressed in exactly 4 different ways: 22852 + 203 22232 + 663 18102 + 1253 11972 + 1563
+Considera i numeri palindromici che possono essere espressi come la somma di un quadrato e di un cubo, entrambi maggiori di 1, in esattamente 4 modi diversi.
-Find the sum of the five smallest such palindromic numbers.
+Ad esempio, 5229225 è un numero palindromico e può essere espresso esattamente in 4 modi diversi:
+
+$$\begin{align} & {2285}^2 + {20}^3 \\\\ & {2223}^2 + {66}^3 \\\\ & {1810}^2 + {125}^3 \\\\ & {1197}^2 + {156}^3 \end{align}$$
+
+Trova la somma dei cinque numeri palindromi più piccoli.
# --hints--
-`euler348()` should return 1004195061.
+`sumOfSquareAndCube()` dovrebbe restituire `1004195061`.
```js
-assert.strictEqual(euler348(), 1004195061);
+assert.strictEqual(sumOfSquareAndCube(), 1004195061);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler348(), 1004195061);
## --seed-contents--
```js
-function euler348() {
+function sumOfSquareAndCube() {
return true;
}
-euler348();
+sumOfSquareAndCube();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
index 239ba5a6a1..d703403ce9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
@@ -1,6 +1,6 @@
---
id: 5900f4ca1000cf542c50ffdc
-title: 'Problem 349: Langton''s ant'
+title: 'Problema 349: Formica di Langton'
challengeType: 5
forumTopicId: 302008
dashedName: problem-349-langtons-ant
@@ -8,22 +8,21 @@ dashedName: problem-349-langtons-ant
# --description--
-An ant moves on a regular grid of squares that are coloured either black or white.
+Una formica si muove su una griglia regolare di quadrati colorati neri o bianchi.
-The ant is always oriented in one of the cardinal directions (left, right, up or down) and moves from square to adjacent square according to the following rules:
+La formica è sempre orientata in una delle direzioni cardinali (sinistra, destra, su o giù) e si sposta da un quadrato al quadrato adiacente secondo le seguenti regole:
-\- if it is on a black square, it flips the color of the square to white, rotates 90 degrees counterclockwise and moves forward one square.
+- se è su un quadrato nero, capovolge il colore del quadrato a bianco, ruota 90° in senso antiorario e si muove in avanti di un quadrato.
+- se è su un quadrato bianco, capovolge il colore del quadrato a nero, ruota 90° in senso orario e si muove in avanti di un quadrato.
-\- if it is on a white square, it flips the color of the square to black, rotates 90 degrees clockwise and moves forward one square.
-
-Starting with a grid that is entirely white, how many squares are black after 1018 moves of the ant?
+A partire da una griglia completamente bianca, quanti quadrati sono neri dopo ${10}^{18}$ mosse della formica?
# --hints--
-`euler349()` should return 115384615384614940.
+`langtonsAnt()` dovrebbe restituire `115384615384614940`.
```js
-assert.strictEqual(euler349(), 115384615384614940);
+assert.strictEqual(langtonsAnt(), 115384615384614940);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler349(), 115384615384614940);
## --seed-contents--
```js
-function euler349() {
+function langtonsAnt() {
return true;
}
-euler349();
+langtonsAnt();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
index ebc52998b5..3483721e4c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffdd
-title: 'Problem 350: Constraining the least greatest and the greatest least'
+title: 'Problema 350: Mettere limiti al più piccolo più grande e al più grande più piccolo'
challengeType: 5
forumTopicId: 302010
dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
@@ -8,24 +8,24 @@ dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
# --description--
-A list of size n is a sequence of n natural numbers. Examples are (2,4,6), (2,6,4), (10,6,15,6), and (11).
+Una lista di dimensione $n$ è una sequenza di $n$ numeri naturali. Esempi sono (2, 4, 6), (2, 6, 4), (10, 6, 15, 6), e (11).
-The greatest common divisor, or gcd, of a list is the largest natural number that divides all entries of the list. Examples: gcd(2,6,4) = 2, gcd(10,6,15,6) = 1 and gcd(11) = 11.
+Il massimo comun divisore, o $gcd$ (da greatest common divisor in inglese), di una lista è il numero naturale più grande che divide tutti gli elementi della lista. Esempi: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$ e $gcd(11) = 11$.
-The least common multiple, or lcm, of a list is the smallest natural number divisible by each entry of the list. Examples: lcm(2,6,4) = 12, lcm(10,6,15,6) = 30 and lcm(11) = 11.
+Il minimo comun divisore, o $lcm$ (dall'inglese least common multiple), di una lista è il numero naturale più piccolo che è divisibile da ogni numero della lista. Esempi: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$ e $lcm(11) = 11$.
-Let f(G, L, N) be the number of lists of size N with gcd ≥ G and lcm ≤ L. For example:
+Sia $f(G, L, N)$ il numero di liste di dimensione $N$ con $gcd ≥ G$ e $lcm ≤ L$. Ad esempio:
-f(10, 100, 1) = 91. f(10, 100, 2) = 327. f(10, 100, 3) = 1135. f(10, 100, 1000) mod 1014 = 3286053.
+$$\begin{align} & f(10, 100, 1) = 91 \\\\ & f(10, 100, 2) = 327 \\\\ & f(10, 100, 3) = 1135 \\\\ & f(10, 100, 1000)\bmod {101}^4 = 3\\,286\\,053 \end{align}$$
-Find f(106, 1012, 1018) mod 1014.
+Trova $f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$.
# --hints--
-`euler350()` should return 84664213.
+`leastGreatestAndGreatestLeast()` dovrebbe restituire `84664213`.
```js
-assert.strictEqual(euler350(), 84664213);
+assert.strictEqual(leastGreatestAndGreatestLeast(), 84664213);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler350(), 84664213);
## --seed-contents--
```js
-function euler350() {
+function leastGreatestAndGreatestLeast() {
return true;
}
-euler350();
+leastGreatestAndGreatestLeast();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
index 33f0089171..5b57bfdbac 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffde
-title: 'Problem 351: Hexagonal orchards'
+title: 'Problema 351: frutteti esagonali'
challengeType: 5
forumTopicId: 302011
dashedName: problem-351-hexagonal-orchards
@@ -8,22 +8,24 @@ dashedName: problem-351-hexagonal-orchards
# --description--
-A hexagonal orchard of order n is a triangular lattice made up of points within a regular hexagon with side n. The following is an example of a hexagonal orchard of order 5:
+Un frutteto esagonale di ordine $n$ è un reticolo triangolare composto da punti all'interno di un esagono regolare con il lato $n$. Il seguente è un esempio di frutteto esagonale di ordine 5:
-Highlighted in green are the points which are hidden from the center by a point closer to it. It can be seen that for a hexagonal orchard of order 5, 30 points are hidden from the center.
+
-For a pair w and h, let F(w,h) be the number of distinct rectangles that can be made from a sheet with dimensions w × h . For example, F(2,1) = 0, F(2,2) = 1, F(9,4) = 3 and F(9,8) = 2. Note that rectangles congruent to the initial one are not counted in F(w,h). Note also that rectangles with dimensions w × h and dimensions h × w are not considered distinct.
+Allo stesso modo, da un foglio con dimensioni 9 × 8, possiamo realizzare rettangoli con dimensioni 18 × 4 e 12 × 6.
-For an integer N, let G(N) be the sum of F(w,h) for all pairs w and h which satisfy 0 < h ≤ w ≤ N. We can verify that G(10) = 55, G(103) = 971745 and G(105) = 9992617687.
+Per una coppia $w$ e $h$, sia $F(w, h)$ il numero di rettangoli distinti che possono essere fatti da un foglio con dimensioni $w$ × $h$. Per esempio, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ e $F(9, 8) = 2$. Nota che i rettangoli congruenti a quello iniziale non sono contati in $F(w, h)$. Nota anche che i rettangoli con dimensioni $w$ × $h$ e le dimensioni $h$ × $w$ non sono considerati distinti.
-Find G(1012). Give your answer modulo 108.
+Per un intero $N$, sia $G(N)$ la somma di $F(w, h)$ per tutte le coppie $w$ e $h$ che soddisfano $0 < h ≤ w ≤ N$. Possiamo verificare che $G(10) = 55$, $G({10}^3) = 971\\,745$ e $G({10}^5) = 9\\,992\\,617\\,687$.
+
+Trova $G({10}^{12})$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler338()` should return 15614292.
+`cuttingRectangularGridPaper()` dovrebbe restituire `15614292`.
```js
-assert.strictEqual(euler338(), 15614292);
+assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler338(), 15614292);
## --seed-contents--
```js
-function euler338() {
+function cuttingRectangularGridPaper() {
return true;
}
-euler338();
+cuttingRectangularGridPaper();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index 6844c7e65c..602ef1c635 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -1,6 +1,6 @@
---
id: 5900f4c01000cf542c50ffd2
-title: 'Problem 339: Peredur fab Efrawg'
+title: 'Problema 339: Peredur fab Efrawg'
challengeType: 5
forumTopicId: 301997
dashedName: problem-339-peredur-fab-efrawg
@@ -8,18 +8,20 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black."en.wikisource.org
+"E venne verso una valle, attraverso la quale correva un fiume; e i confini della valle erano boscosi, e su ogni lato del fiume vi erano prati pianeggianti. Da un lato del fiume vide un gregge di pecore bianche, dall'altro un gregge di pecore nere. E ogni volta che una delle pecore bianche belava, una delle pecore nere attraversava e diventava bianca; e quando una delle pecore nere belava, una delle pecore bianche attraversava e diventava nera." - Peredur Figlio di Evrawc
-Initially each flock consists of n sheep. Each sheep (regardless of colour) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let E(n) be the expected final number of black sheep if Peredur uses an optimal strategy.
+Inizialmente, ogni gregge è costituito da $n$ pecore. Ogni pecora (indipendentemente dal colore) è altrettanto probabile che sia la prossima pecora a belare. Dopo che una pecora ha belato e una pecora dall'altro gregge ha attraversato, Peredur può rimuovere un numero di pecore bianche al fine di massimizzare il numero finale previsto di pecore nere. Sia $E(n)$ il numero aspettato finale di pecore nere se Peredur usa una strategia ottimale.
-You are given that E(5) = 6.871346 rounded to 6 places behind the decimal point. Find E(10 000) and give your answer rounded to 6 places behind the decimal point.
+Ti è dato che $E(5) = 6.871346$ arrotondato a 6 cifre decimali.
+
+Trova $E(10\\,000)$ e dai la tua risposta arrotondata a 6 cifre decimali.
# --hints--
-`euler339()` should return 19823.542204.
+`peredurFabEfrawg()` dovrebbe restituire `19823.542204`.
```js
-assert.strictEqual(euler339(), 19823.542204);
+assert.strictEqual(peredurFabEfrawg(), 19823.542204);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler339(), 19823.542204);
## --seed-contents--
```js
-function euler339() {
+function peredurFabEfrawg() {
return true;
}
-euler339();
+peredurFabEfrawg();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 86b29f061e..c6e17627dc 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4c21000cf542c50ffd4
-title: 'Problem 340: Crazy Function'
+title: 'Problema 340: Funzione Pazza'
challengeType: 5
forumTopicId: 301999
dashedName: problem-340-crazy-function
@@ -8,24 +8,22 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers a, b, c, define the crazy function F(n) as follows:
+Per gli interi fissati $a$, $b$, $c$, definire la funzione pazza $F(n)$ come segue:
-F(n) = n - c for all n > b
+$$\begin{align} & F(n) = n - c \\;\text{ per ogni } n > b \\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ per ogni } n ≤ b. \end{align}$$
-F(n) = F(a + F(a + F(a + F(a + n)))) for all n ≤ b.
+Inoltre, definisci $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
-Also, define S(a, b, c) = .
+Per esempio, se $a = 50$, $b = 2000$ e $c = 40$, allora $F(0) = 3240$ e $F(2000) = 2040$. Inoltre, $S(50, 2000, 40) = 5\\,204\\,240$.
-For example, if a = 50, b = 2000 and c = 40, then F(0) = 3240 and F(2000) = 2040. Also, S(50, 2000, 40) = 5204240.
-
-Find the last 9 digits of S(217, 721, 127).
+Trova le ultime 9 cifre di $S({21}^7, 7^{21}, {12}^7)$.
# --hints--
-`euler340()` should return 291504964.
+`crazyFunction()` dovrebbe restituire `291504964`.
```js
-assert.strictEqual(euler340(), 291504964);
+assert.strictEqual(crazyFunction(), 291504964);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler340(), 291504964);
## --seed-contents--
```js
-function euler340() {
+function crazyFunction() {
return true;
}
-euler340();
+crazyFunction();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
index 740ef0d751..693beaed83 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4c11000cf542c50ffd3
-title: 'Problem 341: Golomb''s self-describing sequence'
+title: 'Problema 341: Sequenza auto-descrittiva di Golomb'
challengeType: 5
forumTopicId: 302000
dashedName: problem-341-golombs-self-describing-sequence
@@ -8,20 +8,22 @@ dashedName: problem-341-golombs-self-describing-sequence
# --description--
-The Golomb's self-describing sequence {G(n)} is the only nondecreasing sequence of natural numbers such that n appears exactly G(n) times in the sequence. The values of G(n) for the first few n are
+La sequenza di auto-descrizione di Golomb ($G(n)$) è l'unica sequenza non decrescente di numeri naturali tali che $n$ appaia esattamente $G(n)$ volte nella sequenza. I valori di $G(n)$ per i primi $n$ sono
-n123456789101112131415…G(n)122334445556666…
+$$\begin{array}{c} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & \ldots \\\\ G(n) & 1 & 2 & 2 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & \ldots \end{array}$$
-You are given that G(103) = 86, G(106) = 6137. You are also given that ΣG(n3) = 153506976 for 1 ≤ n < 103.
+Ti viene dato che $G({10}^3) = 86$, $G({10}^6) = 6137$.
-Find ΣG(n3) for 1 ≤ n < 106.
+Ti viene anche dato che $\sum G(n^3) = 153\\,506\\,976$ per $1 ≤ n < {10}^3$.
+
+Trova $\sum G(n^3)$ per $1 ≤ n < {10}^6$.
# --hints--
-`euler341()` should return 56098610614277016.
+`golombsSequence()` dovrebbe restituire `56098610614277016`.
```js
-assert.strictEqual(euler341(), 56098610614277016);
+assert.strictEqual(golombsSequence(), 56098610614277016);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler341(), 56098610614277016);
## --seed-contents--
```js
-function euler341() {
+function golombsSequence() {
return true;
}
-euler341();
+golombsSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
index 2253ce390f..cbcc7d8c39 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c31000cf542c50ffd5
-title: 'Problem 342: The totient of a square is a cube'
+title: 'Problema 342: Il toziente di un quadrato è un cubo'
challengeType: 5
forumTopicId: 302001
dashedName: problem-342-the-totient-of-a-square-is-a-cube
@@ -8,22 +8,21 @@ dashedName: problem-342-the-totient-of-a-square-is-a-cube
# --description--
-Consider the number 50.
+Considera il numero 50.
-502 = 2500 = 22 × 54, so φ(2500) = 2 × 4 × 53 = 8 × 53 = 23 × 53. 1
+${50}^2 = 2500 = 2^2 × 5^4$, so $φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$. $φ$ denota la funzione toziente di Eulero.
-So 2500 is a square and φ(2500) is a cube.
+Quindi 2500 è un quadrato e $φ(2500)$ è un cubo.
-Find the sum of all numbers n, 1 < n < 1010 such that φ(n2) is a cube.
+Trova la somma di tutti i numeri $n$, $1 < n < {10}^{10}$ in modo che $φ(n^2)$ sia un cubo.
-1 φ denotes Euler's totient function.
# --hints--
-`euler342()` should return 5943040885644.
+`totientOfSquare()` dovrebbe restituire `5943040885644`.
```js
-assert.strictEqual(euler342(), 5943040885644);
+assert.strictEqual(totientOfSquare(), 5943040885644);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler342(), 5943040885644);
## --seed-contents--
```js
-function euler342() {
+function totientOfSquare() {
return true;
}
-euler342();
+totientOfSquare();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
index 3102009e8c..63e1dab730 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4c41000cf542c50ffd6
-title: 'Problem 343: Fractional Sequences'
+title: 'Problema 343: Sequenze frazionarie'
challengeType: 5
forumTopicId: 302002
dashedName: problem-343-fractional-sequences
@@ -8,32 +8,31 @@ dashedName: problem-343-fractional-sequences
# --description--
-For any positive integer k, a finite sequence ai of fractions xi/yi is defined by:
+Per qualsiasi numero intero positivo $k$, una sequenza finita $a_i$ di frazioni $\frac{x_i}{y_i}$ è definita da:
-a1 = 1/k and
+- $a_1 = \displaystyle\frac{1}{k}$ e
+- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ ridotto ai minimi termini per $i > 1$.
-ai = (xi-1+1)/(yi-1-1) reduced to lowest terms for i>1.
+Quando $a_i$ raggiunge un numero intero $n$, la sequenza si ferma. (cioè, quando $y_i = 1$.)
-When ai reaches some integer n, the sequence stops. (That is, when yi=1.)
+Definisci $f(k) = n$.
-Define f(k) = n.
+Per esempio, per $k = 20$:
-For example, for k = 20:
+$$\frac{1}{20} → \frac{2}{19} → \frac{3}{18} = \frac{1}{6} → \frac{2}{5} → \frac{3}{4} → \frac{4}{3} → \frac{5}{2} → \frac{6}{1} = 6$$
-1/20 → 2/19 → 3/18 = 1/6 → 2/5 → 3/4 → 4/3 → 5/2 → 6/1 = 6
+Quindi $f(20) = 6$.
-So f(20) = 6.
+Anche $f(1) = 1$, $f(2) = 2$, $f(3) = 1$ e $\sum f(k^3) = 118\\,937$ per $1 ≤ k ≤ 100$.
-Also f(1) = 1, f(2) = 2, f(3) = 1 and Σf(k3) = 118937 for 1 ≤ k ≤ 100.
-
-Find Σf(k3) for 1 ≤ k ≤ 2×106.
+Trova $\sum f(k^3)$ per $1 ≤ k ≤ 2 × {10}^6$.
# --hints--
-`euler343()` should return 269533451410884200.
+`fractionalSequences()` dovrebbe restituire `269533451410884200`.
```js
-assert.strictEqual(euler343(), 269533451410884200);
+assert.strictEqual(fractionalSequences(), 269533451410884200);
```
# --seed--
@@ -41,12 +40,12 @@ assert.strictEqual(euler343(), 269533451410884200);
## --seed-contents--
```js
-function euler343() {
+function fractionalSequences() {
return true;
}
-euler343();
+fractionalSequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
index 9cb8157d07..a94d255151 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffda
-title: 'Problem 345: Matrix Sum'
+title: 'Problema 345: Somma di matrice'
challengeType: 5
forumTopicId: 302004
dashedName: problem-345-matrix-sum
@@ -8,20 +8,22 @@ dashedName: problem-345-matrix-sum
# --description--
-We define the Matrix Sum of a matrix as the maximum sum of matrix elements with each element being the only one in his row and column. For example, the Matrix Sum of the matrix below equals 3315 ( = 863 + 383 + 343 + 959 + 767):
+Definiamo la Somma di Matrice di una matrice come la somma massima di elementi di matrice dove ogni elemento è l'unico nella sua fila e colonna.
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943767 473 103 699 303
+Ad esempio, la somma di matrice della matrice qui sotto è pari a $3315 ( = 863 + 383 + 343 + 959 + 767)$:
-Find the Matrix Sum of:
+$$\begin{array}{rrrrr} 7 & 53 & 183 & 439 & \color{lime}{863} \\\\ 497 & \color{lime}{383} & 563 & 79 & 973 \\\\ 287 & 63 & \color{lime}{343} & 169 & 583 \\\\ 627 & 343 & 773 & \color{lime}{959} & 943 \\\\ \color{lime}{767} & 473 & 103 & 699 & 303 \end{array}$$
-7 53 183 439 863 497 383 563 79 973 287 63 343 169 583 627 343 773 959 943 767 473 103 699 303 957 703 583 639 913 447 283 463 29 23 487 463 993 119 883 327 493 423 159 743 217 623 3 399 853 407 103 983 89 463 290 516 212 462 350 960 376 682 962 300 780 486 502 912 800 250 346 172 812 350 870 456 192 162 593 473 915 45 989 873 823 965 425 329 803 973 965 905 919 133 673 665 235 509 613 673 815 165 992 326 322 148 972 962 286 255 941 541 265 323 925 281 601 95 973 445 721 11 525 473 65 511 164 138 672 18 428 154 448 848 414 456 310 312 798 104 566 520 302 248 694 976 430 392 198 184 829 373 181 631 101 969 613 840 740 778 458 284 760 390 821 461 843 513 17 901 711 993 293 157 274 94 192 156 574 34 124 4 878 450 476 712 914 838 669 875 299 823 329 699 815 559 813 459 522 788 168 586 966 232 308 833 251 631 107 813 883 451 509 615 77 281 613 459 205 380 274 302 35 805
+Trova la somma di matrice di:
+
+$$\\begin{array}{r} 7 & 53 & 183 & 439 & 863 & 497 & 383 & 563 & 79 & 973 & 287 & 63 & 343 & 169 & 583 \\\\ 627 & 343 & 773 & 959 & 943 & 767 & 473 & 103 & 699 & 303 & 957 & 703 & 583 & 639 & 913 \\\\ 447 & 283 & 463 & 29 & 23 & 487 & 463 & 993 & 119 & 883 & 327 & 493 & 423 & 159 & 743 \\\\ 217 & 623 & 3 & 399 & 853 & 407 & 103 & 983 & 89 & 463 & 290 & 516 & 212 & 462 & 350 \\\\ 960 & 376 & 682 & 962 & 300 & 780 & 486 & 502 & 912 & 800 & 250 & 346 & 172 & 812 & 350 \\\\ 870 & 456 & 192 & 162 & 593 & 473 & 915 & 45 & 989 & 873 & 823 & 965 & 425 & 329 & 803 \\\\ 973 & 965 & 905 & 919 & 133 & 673 & 665 & 235 & 509 & 613 & 673 & 815 & 165 & 992 & 326 \\\\ 322 & 148 & 972 & 962 & 286 & 255 & 941 & 541 & 265 & 323 & 925 & 281 & 601 & 95 & 973 \\\\ 445 & 721 & 11 & 525 & 473 & 65 & 511 & 164 & 138 & 672 & 18 & 428 & 154 & 448 & 848 \\\\ 414 & 456 & 310 & 312 & 798 & 104 & 566 & 520 & 302 & 248 & 694 & 976 & 430 & 392 & 198 \\\\ 184 & 829 & 373 & 181 & 631 & 101 & 969 & 613 & 840 & 740 & 778 & 458 & 284 & 760 & 390 \\\\ 821 & 461 & 843 & 513 & 17 & 901 & 711 & 993 & 293 & 157 & 274 & 94 & 192 & 156 & 574 \\\\ 34 & 124 & 4 & 878 & 450 & 476 & 712 & 914 & 838 & 669 & 875 & 299 & 823 & 329 & 699 \\\\ 815 & 559 & 813 & 459 & 522 & 788 & 168 & 586 & 966 & 232 & 308 & 833 & 251 & 631 & 107 \\\\ 813 & 883 & 451 & 509 & 615 & 77 & 281 & 613 & 459 & 205 & 380 & 274 & 302 & 35 & 805 \end{array}$$
# --hints--
-`euler345()` should return 13938.
+`matrixSum()` dovrebbe restituire `13938`.
```js
-assert.strictEqual(euler345(), 13938);
+assert.strictEqual(matrixSum(), 13938);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler345(), 13938);
## --seed-contents--
```js
-function euler345() {
+function matrixSum() {
return true;
}
-euler345();
+matrixSum();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
index 49a1f6b2c2..844987961a 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
@@ -1,6 +1,6 @@
---
id: 5900f4c71000cf542c50ffd8
-title: 'Problem 346: Strong Repunits'
+title: 'Problema 346: Repunit Forti'
challengeType: 5
forumTopicId: 302005
dashedName: problem-346-strong-repunits
@@ -8,18 +8,18 @@ dashedName: problem-346-strong-repunits
# --description--
-The number 7 is special, because 7 is 111 written in base 2, and 11 written in base 6 (i.e. 710 = 116 = 1112). In other words, 7 is a repunit in at least two bases b > 1.
+Il numero 7 è speciale, perché 7 è 111 scritto in base 2, e 11 scritto in base 6 (cioè $7_{10} = {11}_6 = {111}_2$). In altre parole, 7 è una repunit in almeno due basi $b > 1$.
-We shall call a positive integer with this property a strong repunit. It can be verified that there are 8 strong repunits below 50: {1,7,13,15,21,31,40,43}. Furthermore, the sum of all strong repunits below 1000 equals 15864.
+Chiameremo un numero intero positivo con questa proprietà una forte repunit. Si può verificare che ci sono 8 forti repunit sotto 50: {1, 7, 13, 15, 21, 31, 40, 43}. Inoltre, la somma di tutti i repunit forti sotto 1000 è pari a 15864.
-Find the sum of all strong repunits below 1012.
+Trova la somma di tutti i repunit forti sotto ${10}^{12}$.
# --hints--
-`euler346()` should return 336108797689259260.
+`strongRepunits()` dovrebbe restituire `336108797689259260`.
```js
-assert.strictEqual(euler346(), 336108797689259260);
+assert.strictEqual(strongRepunits(), 336108797689259260);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler346(), 336108797689259260);
## --seed-contents--
```js
-function euler346() {
+function strongRepunits() {
return true;
}
-euler346();
+strongRepunits();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
index 70845508fa..961ba85720 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffd9
-title: 'Problem 347: Largest integer divisible by two primes'
+title: 'Problema 347: Intero più grande divisibile per due primi'
challengeType: 5
forumTopicId: 302006
dashedName: problem-347-largest-integer-divisible-by-two-primes
@@ -8,24 +8,24 @@ dashedName: problem-347-largest-integer-divisible-by-two-primes
# --description--
-The largest integer ≤ 100 that is only divisible by both the primes 2 and 3 is 96, as 96=32\*3=25\*3.
+Il più grande intero $≤ 100$ che è divisibile solo per entrambe i primi 2 e 3 è 96, poiché $96 = 32 \times 3 = 2^5 \times 3$.
-For two distinct primes p and q let M(p,q,N) be the largest positive integer ≤N only divisible
+Per due primi distinti $p$ e $q$ sia $M(p, q, N)$ il più grande intero positivo $≤ N$ divisibile solo per $p$ e $q$ e $M(p, q, N)=0$ se tale numero intero positivo non esiste.
-by both p and q and M(p,q,N)=0 if such a positive integer does not exist.
+Ad es. $M(2, 3, 100) = 96$.
-E.g. M(2,3,100)=96. M(3,5,100)=75 and not 90 because 90 is divisible by 2 ,3 and 5. Also M(2,73,100)=0 because there does not exist a positive integer ≤ 100 that is divisible by both 2 and 73.
+$M(3, 5, 100) = 75$ e non 90 perché 90 è divisibile per 2, 3 e 5. Anche $M(2, 73, 100) = 0$ perché non esiste un numero intero positivo $≤ 100$ che è divisibile sia per 2 che 73.
-Let S(N) be the sum of all distinct M(p,q,N). S(100)=2262.
+Sia $S(N)$ la somma di tutti gli $M(p, q, N)$ distinti. $S(100)=2262$.
-Find S(10 000 000).
+Trova $S(10\\,000\\,000)$.
# --hints--
-`euler347()` should return 11109800204052.
+`integerDivisibleByTwoPrimes()` dovrebbe restituire `11109800204052`.
```js
-assert.strictEqual(euler347(), 11109800204052);
+assert.strictEqual(integerDivisibleByTwoPrimes(), 11109800204052);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler347(), 11109800204052);
## --seed-contents--
```js
-function euler347() {
+function integerDivisibleByTwoPrimes() {
return true;
}
-euler347();
+integerDivisibleByTwoPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
index 2fe6e2bc13..75d443eac6 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffdb
-title: 'Problem 348: Sum of a square and a cube'
+title: 'Problema 348: Somma di un quadrato e di un cubo'
challengeType: 5
forumTopicId: 302007
dashedName: problem-348-sum-of-a-square-and-a-cube
@@ -8,18 +8,22 @@ dashedName: problem-348-sum-of-a-square-and-a-cube
# --description--
-Many numbers can be expressed as the sum of a square and a cube. Some of them in more than one way.
+Molti numeri possono essere espressi come somma di un quadrato e di un cubo. Alcuni di essi in più in modo.
-Consider the palindromic numbers that can be expressed as the sum of a square and a cube, both greater than 1, in exactly 4 different ways. For example, 5229225 is a palindromic number and it can be expressed in exactly 4 different ways: 22852 + 203 22232 + 663 18102 + 1253 11972 + 1563
+Considera i numeri palindromici che possono essere espressi come la somma di un quadrato e di un cubo, entrambi maggiori di 1, in esattamente 4 modi diversi.
-Find the sum of the five smallest such palindromic numbers.
+Ad esempio, 5229225 è un numero palindromico e può essere espresso esattamente in 4 modi diversi:
+
+$$\begin{align} & {2285}^2 + {20}^3 \\\\ & {2223}^2 + {66}^3 \\\\ & {1810}^2 + {125}^3 \\\\ & {1197}^2 + {156}^3 \end{align}$$
+
+Trova la somma dei cinque numeri palindromi più piccoli.
# --hints--
-`euler348()` should return 1004195061.
+`sumOfSquareAndCube()` dovrebbe restituire `1004195061`.
```js
-assert.strictEqual(euler348(), 1004195061);
+assert.strictEqual(sumOfSquareAndCube(), 1004195061);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler348(), 1004195061);
## --seed-contents--
```js
-function euler348() {
+function sumOfSquareAndCube() {
return true;
}
-euler348();
+sumOfSquareAndCube();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
index 239ba5a6a1..d703403ce9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
@@ -1,6 +1,6 @@
---
id: 5900f4ca1000cf542c50ffdc
-title: 'Problem 349: Langton''s ant'
+title: 'Problema 349: Formica di Langton'
challengeType: 5
forumTopicId: 302008
dashedName: problem-349-langtons-ant
@@ -8,22 +8,21 @@ dashedName: problem-349-langtons-ant
# --description--
-An ant moves on a regular grid of squares that are coloured either black or white.
+Una formica si muove su una griglia regolare di quadrati colorati neri o bianchi.
-The ant is always oriented in one of the cardinal directions (left, right, up or down) and moves from square to adjacent square according to the following rules:
+La formica è sempre orientata in una delle direzioni cardinali (sinistra, destra, su o giù) e si sposta da un quadrato al quadrato adiacente secondo le seguenti regole:
-\- if it is on a black square, it flips the color of the square to white, rotates 90 degrees counterclockwise and moves forward one square.
+- se è su un quadrato nero, capovolge il colore del quadrato a bianco, ruota 90° in senso antiorario e si muove in avanti di un quadrato.
+- se è su un quadrato bianco, capovolge il colore del quadrato a nero, ruota 90° in senso orario e si muove in avanti di un quadrato.
-\- if it is on a white square, it flips the color of the square to black, rotates 90 degrees clockwise and moves forward one square.
-
-Starting with a grid that is entirely white, how many squares are black after 1018 moves of the ant?
+A partire da una griglia completamente bianca, quanti quadrati sono neri dopo ${10}^{18}$ mosse della formica?
# --hints--
-`euler349()` should return 115384615384614940.
+`langtonsAnt()` dovrebbe restituire `115384615384614940`.
```js
-assert.strictEqual(euler349(), 115384615384614940);
+assert.strictEqual(langtonsAnt(), 115384615384614940);
```
# --seed--
@@ -31,12 +30,12 @@ assert.strictEqual(euler349(), 115384615384614940);
## --seed-contents--
```js
-function euler349() {
+function langtonsAnt() {
return true;
}
-euler349();
+langtonsAnt();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
index ebc52998b5..3483721e4c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffdd
-title: 'Problem 350: Constraining the least greatest and the greatest least'
+title: 'Problema 350: Mettere limiti al più piccolo più grande e al più grande più piccolo'
challengeType: 5
forumTopicId: 302010
dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
@@ -8,24 +8,24 @@ dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
# --description--
-A list of size n is a sequence of n natural numbers. Examples are (2,4,6), (2,6,4), (10,6,15,6), and (11).
+Una lista di dimensione $n$ è una sequenza di $n$ numeri naturali. Esempi sono (2, 4, 6), (2, 6, 4), (10, 6, 15, 6), e (11).
-The greatest common divisor, or gcd, of a list is the largest natural number that divides all entries of the list. Examples: gcd(2,6,4) = 2, gcd(10,6,15,6) = 1 and gcd(11) = 11.
+Il massimo comun divisore, o $gcd$ (da greatest common divisor in inglese), di una lista è il numero naturale più grande che divide tutti gli elementi della lista. Esempi: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$ e $gcd(11) = 11$.
-The least common multiple, or lcm, of a list is the smallest natural number divisible by each entry of the list. Examples: lcm(2,6,4) = 12, lcm(10,6,15,6) = 30 and lcm(11) = 11.
+Il minimo comun divisore, o $lcm$ (dall'inglese least common multiple), di una lista è il numero naturale più piccolo che è divisibile da ogni numero della lista. Esempi: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$ e $lcm(11) = 11$.
-Let f(G, L, N) be the number of lists of size N with gcd ≥ G and lcm ≤ L. For example:
+Sia $f(G, L, N)$ il numero di liste di dimensione $N$ con $gcd ≥ G$ e $lcm ≤ L$. Ad esempio:
-f(10, 100, 1) = 91. f(10, 100, 2) = 327. f(10, 100, 3) = 1135. f(10, 100, 1000) mod 1014 = 3286053.
+$$\begin{align} & f(10, 100, 1) = 91 \\\\ & f(10, 100, 2) = 327 \\\\ & f(10, 100, 3) = 1135 \\\\ & f(10, 100, 1000)\bmod {101}^4 = 3\\,286\\,053 \end{align}$$
-Find f(106, 1012, 1018) mod 1014.
+Trova $f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$.
# --hints--
-`euler350()` should return 84664213.
+`leastGreatestAndGreatestLeast()` dovrebbe restituire `84664213`.
```js
-assert.strictEqual(euler350(), 84664213);
+assert.strictEqual(leastGreatestAndGreatestLeast(), 84664213);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler350(), 84664213);
## --seed-contents--
```js
-function euler350() {
+function leastGreatestAndGreatestLeast() {
return true;
}
-euler350();
+leastGreatestAndGreatestLeast();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
index 33f0089171..5b57bfdbac 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffde
-title: 'Problem 351: Hexagonal orchards'
+title: 'Problema 351: frutteti esagonali'
challengeType: 5
forumTopicId: 302011
dashedName: problem-351-hexagonal-orchards
@@ -8,22 +8,24 @@ dashedName: problem-351-hexagonal-orchards
# --description--
-A hexagonal orchard of order n is a triangular lattice made up of points within a regular hexagon with side n. The following is an example of a hexagonal orchard of order 5:
+Un frutteto esagonale di ordine $n$ è un reticolo triangolare composto da punti all'interno di un esagono regolare con il lato $n$. Il seguente è un esempio di frutteto esagonale di ordine 5:
-Highlighted in green are the points which are hidden from the center by a point closer to it. It can be seen that for a hexagonal orchard of order 5, 30 points are hidden from the center.
+ -Let H(n) be the number of points hidden from the center in a hexagonal orchard of order n.
+In evidenza in verde si vedono i punti che sono nascosti dal centro da un punto più vicino ad esso. Si può vedere che per un frutteto esagonale di ordine 5, 30 punti sono nascosti dal centro.
-H(5) = 30. H(10) = 138. H(1 000) = 1177848.
+Sia $H(n)$ il numero di punti nascosti al centro in un frutteto esagonale di ordine $n$.
-Find H(100 000 000).
+$H(5) = 30$. $H(10) = 138$. $H(1\\,000)$ = $1\\,177\\,848$.
+
+Trova $H(100\\,000\\,000)$.
# --hints--
-`euler351()` should return 11762187201804552.
+`hexagonalOrchards()` dovrebbe restituire `11762187201804552`.
```js
-assert.strictEqual(euler351(), 11762187201804552);
+assert.strictEqual(hexagonalOrchards(), 11762187201804552);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler351(), 11762187201804552);
## --seed-contents--
```js
-function euler351() {
+function hexagonalOrchards() {
return true;
}
-euler351();
+hexagonalOrchards();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
index 76af2f075c..186af1e8a4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffdf
-title: 'Problem 352: Blood tests'
+title: 'Problema 352: Analisi del sangue'
challengeType: 5
forumTopicId: 302012
dashedName: problem-352-blood-tests
@@ -8,32 +8,46 @@ dashedName: problem-352-blood-tests
# --description--
-Each one of the 25 sheep in a flock must be tested for a rare virus, known to affect 2% of the sheep population.
+Ognuna delle 25 pecore di un gregge deve essere sottoposta a test per individuare un virus raro, noto per colpire il 2% della popolazione ovina.
-An accurate and extremely sensitive PCR test exists for blood samples, producing a clear positive / negative result, but it is very time-consuming and expensive.
+Un test PCR accurato ed estremamente sensibile esiste per i campioni di sangue, producendo un risultato positivo/negativo netto, ma è molto lungo e costoso.
-Because of the high cost, the vet-in-charge suggests that instead of performing 25 separate tests, the following procedure can be used instead: The sheep are split into 5 groups of 5 sheep in each group. For each group, the 5 samples are mixed together and a single test is performed. Then, If the result is negative, all the sheep in that group are deemed to be virus-free. If the result is positive, 5 additional tests will be performed (a separate test for each animal) to determine the affected individual(s).
+A causa del costo elevato, il veterinario suggerisce che invece di eseguire 25 test separati, si può ricorrere alla seguente procedura:
-Since the probability of infection for any specific animal is only 0.02, the first test (on the pooled samples) for each group will be: Negative (and no more tests needed) with probability 0.985 = 0.9039207968. Positive (5 additional tests needed) with probability 1 - 0.9039207968 = 0.0960792032.
+Le pecore sono suddivise in 5 gruppi di 5 pecore in ognuno. Per ciascun gruppo, i 5 campioni sono mescolati insieme e si effettua una singola prova. Poi,
-Thus, the expected number of tests for each group is 1 + 0.0960792032 × 5 = 1.480396016. Consequently, all 5 groups can be screened using an average of only 1.480396016 × 5 = 7.40198008 tests, which represents a huge saving of more than 70% !
+- Se il risultato è negativo, tutte le pecore di quel gruppo sono considerate prive di virus.
+- Se il risultato è positivo, saranno effettuati 5 test supplementari (una prova separata per ciascun animale) per determinare l'individuo/i interessato/i.
-Although the scheme we have just described seems to be very efficient, it can still be improved considerably (always assuming that the test is sufficiently sensitive and that there are no adverse effects caused by mixing different samples). E.g.: We may start by running a test on a mixture of all the 25 samples. It can be verified that in about 60.35% of the cases this test will be negative, thus no more tests will be needed. Further testing will only be required for the remaining 39.65% of the cases. If we know that at least one animal in a group of 5 is infected and the first 4 individual tests come out negative, there is no need to run a test on the fifth animal (we know that it must be infected). We can try a different number of groups / different number of animals in each group, adjusting those numbers at each level so that the total expected number of tests will be minimised.
+Poiché la probabilità di infezione per un animale specifico è solo di 0,02, il primo test (sui campioni aggregati) per ciascun gruppo sarà:
-To simplify the very wide range of possibilities, there is one restriction we place when devising the most cost-efficient testing scheme: whenever we start with a mixed sample, all the sheep contributing to that sample must be fully screened (i.e. a verdict of infected / virus-free must be reached for all of them) before we start examining any other animals.
+- Negativo (e nessun altro test necessario) con probabilità ${0.98}^5 = 0.9039207968$.
+- Positivo (5 ulteriori test necessari) con probabilità $1 - 0.9039207968 = 0.0960792032$.
-For the current example, it turns out that the most cost-efficient testing scheme (we'll call it the optimal strategy) requires an average of just 4.155452 tests!
+Così, il numero previsto di test per ogni gruppo è di $1 + 0.0960792032 × 5 = 1.480396016$.
-Using the optimal strategy, let T(s,p) represent the average number of tests needed to screen a flock of s sheep for a virus having probability p to be present in any individual. Thus, rounded to six decimal places, T(25, 0.02) = 4.155452 and T(25, 0.10) = 12.702124.
+Di conseguenza, tutti i 5 gruppi possono essere controllati utilizzando una media di soli $1.480396016 × 5 = \mathbf{7.40198008}$ test, che rappresenta un enorme risparmio di oltre il 70%!
-Find ΣT(10000, p) for p=0.01, 0.02, 0.03, ... 0.50. Give your answer rounded to six decimal places.
+Anche se lo schema che abbiamo appena descritto sembra essere molto efficiente, può ancora essere migliorato notevolmente (sempre supponendo che il test sia sufficientemente sensibile e che nessun effetto negativo sia causato dalla miscelazione di campioni diversi). Ad es.:
+
+- Possiamo iniziare eseguendo una prova su una miscela di tutti i 25 campioni. Si può verificare che in circa il 60,35% dei casi questo test sarà negativo, quindi non saranno necessari altri test. Saranno necessari ulteriori test solo per il restante 39,65% dei casi.
+- Se sappiamo che almeno un animale in un gruppo di 5 è infetto e i primi 4 test individuali risultano negativi, non è necessario eseguire un test sul quinto animale (sappiamo che deve essere infetto).
+- Possiamo provare un numero diverso di gruppi / numero diverso di animali in ogni gruppo, adeguare tali numeri a ciascun livello in modo da ridurre al minimo il numero totale previsto di prove.
+
+Per semplificare la vasta gamma di possibilità, esiste una restrizione che poniamo quando progettiamo il sistema di test più efficiente in termini di costi: ogni volta che iniziamo con un campione misto, tutti gli ovini che contribuiscono a tale campione devono essere sottoposti a screening completo (cioè prima di iniziare ad esaminare qualsiasi altro animale deve essere raggiunto un verdetto di infezione / non infezione per tutti loro.
+
+Per l'esempio attuale, risulta che lo schema di test più efficiente in termini di costi (lo chiameremo la strategia ottimale) richiede una media di appena 4.155452 test!
+
+Utilizzando la strategia ottimale, lascia che $T(s, p)$ rappresenti il numero medio di test necessari per testare un gregge di $s$ pecore per un virus che ha probabilità $p$ di essere presente in qualsiasi individuo. Così, arrotondato a sei decimali, $T(25, 0.02) = 4.155452$ e $T(25, 0.10) = 12.702124$.
+
+Trova $\sum T(10\\,000, p)$ per $p = 0.01, 0.02, 0.03, \ldots 0.50$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler352()` should return 378563.260589.
+`bloodTests()` dovrebbe restituire `378563.260589`.
```js
-assert.strictEqual(euler352(), 378563.260589);
+assert.strictEqual(bloodTests(), 378563.260589);
```
# --seed--
@@ -41,12 +55,12 @@ assert.strictEqual(euler352(), 378563.260589);
## --seed-contents--
```js
-function euler352() {
+function bloodTests() {
return true;
}
-euler352();
+bloodTests();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
index 74faf24c26..91350909f9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffe0
-title: 'Problem 353: Risky moon'
+title: 'Problema 353: Luna rischiosa'
challengeType: 5
forumTopicId: 302013
dashedName: problem-353-risky-moon
@@ -8,28 +8,30 @@ dashedName: problem-353-risky-moon
# --description--
-A moon could be described by the sphere C(r) with centre (0,0,0) and radius r.
+Una luna potrebbe essere descritta dalla sfera $C(r)$ con centro (0, 0, 0) e raggio $r$.
-There are stations on the moon at the points on the surface of C(r) with integer coordinates. The station at (0,0,r) is called North Pole station, the station at (0,0,-r) is called South Pole station.
+Ci sono stazioni sulla luna nei punti sulla superficie di $C(r)$ con coordinate intere. La stazione a (0, 0, $r$) si chiama Stazione Polo Nord, la stazione a (0, 0, $-r$) si chiama Stazione Polo Sud.
-All stations are connected with each other via the shortest road on the great arc through the stations. A journey between two stations is risky. If d is the length of the road between two stations, (d/(π r))2 is a measure for the risk of the journey (let us call it the risk of the road). If the journey includes more than two stations, the risk of the journey is the sum of risks of the used roads.
+Tutte le stazioni sono collegate tra loro attraverso la strada più breve sul grande arco attraverso le stazioni. Un viaggio tra due stazioni è rischioso. Se $d$ è la lunghezza della strada tra due stazioni, $\{\left(\frac{d}{πr}\right)}^2$ è una misura per il rischio del viaggio (chiamiamolo il rischio della strada). Se il viaggio comprende più di due stazioni, il rischio del viaggio è la somma dei rischi delle strade usate.
-A direct journey from the North Pole station to the South Pole station has the length πr and risk 1. The journey from the North Pole station to the South Pole station via (0,r,0) has the same length, but a smaller risk: (½πr/(πr))2+(½πr/(πr))2=0.5.
+Un viaggio diretto dalla stazione Polo Nord alla stazione Polo Sud ha la lunghezza $πr$ e il rischio 1. Il viaggio dalla stazione Polo Nord alla stazione Polo Sud attraverso (0, $r$, 0) ha la stessa lunghezza, ma un rischio minore:
-The minimal risk of a journey from the North Pole station to the South Pole station on C(r) is M(r).
+$${\left(\frac{\frac{1}{2}πr}{πr}\right)}^2+{\left(\frac{\frac{1}{2}πr}{πr}\right)}^2 = 0.5$$
-You are given that M(7)=0.1784943998 rounded to 10 digits behind the decimal point.
+Il rischio minimo di un viaggio dalla stazione Polo Nord alla stazione Polo Sud su $C(r)$ è $M(r)$.
-Find ∑M(2n-1) for 1≤n≤15.
+Ti viene dato che $M(7) = 0.178\\,494\\,399\\,8$ arrotondato a 10 cifre dietro il punto decimale.
-Give your answer rounded to 10 digits behind the decimal point in the form a.bcdefghijk.
+Trova $\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$.
+
+Dai la tua risposta arrotondata a 10 cifre dietro il punto decimale nella forma a.bcdefghijk.
# --hints--
-`euler353()` should return 1.2759860331.
+`riskyMoon()` dovrebbe restituire `1.2759860331`.
```js
-assert.strictEqual(euler353(), 1.2759860331);
+assert.strictEqual(riskyMoon(), 1.2759860331);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler353(), 1.2759860331);
## --seed-contents--
```js
-function euler353() {
+function riskyMoon() {
return true;
}
-euler353();
+riskyMoon();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
index 346a1af451..9b04b4b5b5 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
@@ -1,6 +1,6 @@
---
id: 5900f4cf1000cf542c50ffe1
-title: 'Problem 354: Distances in a bee''s honeycomb'
+title: 'Problema 354: Distanze in un favo'
challengeType: 5
forumTopicId: 302014
dashedName: problem-354-distances-in-a-bees-honeycomb
@@ -8,18 +8,22 @@ dashedName: problem-354-distances-in-a-bees-honeycomb
# --description--
-Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
+Considera un favo dove ogni cella è un perfetto esagono regolare con lunghezza lato di 1.
-One particular cell is occupied by the queen bee. For a positive real number L, let B(L) count the cells with distance L from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider. For example, B(√3) = 6, B(√21) = 12 and B(111 111 111) = 54.
+
-Let H(n) be the number of points hidden from the center in a hexagonal orchard of order n.
+In evidenza in verde si vedono i punti che sono nascosti dal centro da un punto più vicino ad esso. Si può vedere che per un frutteto esagonale di ordine 5, 30 punti sono nascosti dal centro.
-H(5) = 30. H(10) = 138. H(1 000) = 1177848.
+Sia $H(n)$ il numero di punti nascosti al centro in un frutteto esagonale di ordine $n$.
-Find H(100 000 000).
+$H(5) = 30$. $H(10) = 138$. $H(1\\,000)$ = $1\\,177\\,848$.
+
+Trova $H(100\\,000\\,000)$.
# --hints--
-`euler351()` should return 11762187201804552.
+`hexagonalOrchards()` dovrebbe restituire `11762187201804552`.
```js
-assert.strictEqual(euler351(), 11762187201804552);
+assert.strictEqual(hexagonalOrchards(), 11762187201804552);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler351(), 11762187201804552);
## --seed-contents--
```js
-function euler351() {
+function hexagonalOrchards() {
return true;
}
-euler351();
+hexagonalOrchards();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
index 76af2f075c..186af1e8a4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffdf
-title: 'Problem 352: Blood tests'
+title: 'Problema 352: Analisi del sangue'
challengeType: 5
forumTopicId: 302012
dashedName: problem-352-blood-tests
@@ -8,32 +8,46 @@ dashedName: problem-352-blood-tests
# --description--
-Each one of the 25 sheep in a flock must be tested for a rare virus, known to affect 2% of the sheep population.
+Ognuna delle 25 pecore di un gregge deve essere sottoposta a test per individuare un virus raro, noto per colpire il 2% della popolazione ovina.
-An accurate and extremely sensitive PCR test exists for blood samples, producing a clear positive / negative result, but it is very time-consuming and expensive.
+Un test PCR accurato ed estremamente sensibile esiste per i campioni di sangue, producendo un risultato positivo/negativo netto, ma è molto lungo e costoso.
-Because of the high cost, the vet-in-charge suggests that instead of performing 25 separate tests, the following procedure can be used instead: The sheep are split into 5 groups of 5 sheep in each group. For each group, the 5 samples are mixed together and a single test is performed. Then, If the result is negative, all the sheep in that group are deemed to be virus-free. If the result is positive, 5 additional tests will be performed (a separate test for each animal) to determine the affected individual(s).
+A causa del costo elevato, il veterinario suggerisce che invece di eseguire 25 test separati, si può ricorrere alla seguente procedura:
-Since the probability of infection for any specific animal is only 0.02, the first test (on the pooled samples) for each group will be: Negative (and no more tests needed) with probability 0.985 = 0.9039207968. Positive (5 additional tests needed) with probability 1 - 0.9039207968 = 0.0960792032.
+Le pecore sono suddivise in 5 gruppi di 5 pecore in ognuno. Per ciascun gruppo, i 5 campioni sono mescolati insieme e si effettua una singola prova. Poi,
-Thus, the expected number of tests for each group is 1 + 0.0960792032 × 5 = 1.480396016. Consequently, all 5 groups can be screened using an average of only 1.480396016 × 5 = 7.40198008 tests, which represents a huge saving of more than 70% !
+- Se il risultato è negativo, tutte le pecore di quel gruppo sono considerate prive di virus.
+- Se il risultato è positivo, saranno effettuati 5 test supplementari (una prova separata per ciascun animale) per determinare l'individuo/i interessato/i.
-Although the scheme we have just described seems to be very efficient, it can still be improved considerably (always assuming that the test is sufficiently sensitive and that there are no adverse effects caused by mixing different samples). E.g.: We may start by running a test on a mixture of all the 25 samples. It can be verified that in about 60.35% of the cases this test will be negative, thus no more tests will be needed. Further testing will only be required for the remaining 39.65% of the cases. If we know that at least one animal in a group of 5 is infected and the first 4 individual tests come out negative, there is no need to run a test on the fifth animal (we know that it must be infected). We can try a different number of groups / different number of animals in each group, adjusting those numbers at each level so that the total expected number of tests will be minimised.
+Poiché la probabilità di infezione per un animale specifico è solo di 0,02, il primo test (sui campioni aggregati) per ciascun gruppo sarà:
-To simplify the very wide range of possibilities, there is one restriction we place when devising the most cost-efficient testing scheme: whenever we start with a mixed sample, all the sheep contributing to that sample must be fully screened (i.e. a verdict of infected / virus-free must be reached for all of them) before we start examining any other animals.
+- Negativo (e nessun altro test necessario) con probabilità ${0.98}^5 = 0.9039207968$.
+- Positivo (5 ulteriori test necessari) con probabilità $1 - 0.9039207968 = 0.0960792032$.
-For the current example, it turns out that the most cost-efficient testing scheme (we'll call it the optimal strategy) requires an average of just 4.155452 tests!
+Così, il numero previsto di test per ogni gruppo è di $1 + 0.0960792032 × 5 = 1.480396016$.
-Using the optimal strategy, let T(s,p) represent the average number of tests needed to screen a flock of s sheep for a virus having probability p to be present in any individual. Thus, rounded to six decimal places, T(25, 0.02) = 4.155452 and T(25, 0.10) = 12.702124.
+Di conseguenza, tutti i 5 gruppi possono essere controllati utilizzando una media di soli $1.480396016 × 5 = \mathbf{7.40198008}$ test, che rappresenta un enorme risparmio di oltre il 70%!
-Find ΣT(10000, p) for p=0.01, 0.02, 0.03, ... 0.50. Give your answer rounded to six decimal places.
+Anche se lo schema che abbiamo appena descritto sembra essere molto efficiente, può ancora essere migliorato notevolmente (sempre supponendo che il test sia sufficientemente sensibile e che nessun effetto negativo sia causato dalla miscelazione di campioni diversi). Ad es.:
+
+- Possiamo iniziare eseguendo una prova su una miscela di tutti i 25 campioni. Si può verificare che in circa il 60,35% dei casi questo test sarà negativo, quindi non saranno necessari altri test. Saranno necessari ulteriori test solo per il restante 39,65% dei casi.
+- Se sappiamo che almeno un animale in un gruppo di 5 è infetto e i primi 4 test individuali risultano negativi, non è necessario eseguire un test sul quinto animale (sappiamo che deve essere infetto).
+- Possiamo provare un numero diverso di gruppi / numero diverso di animali in ogni gruppo, adeguare tali numeri a ciascun livello in modo da ridurre al minimo il numero totale previsto di prove.
+
+Per semplificare la vasta gamma di possibilità, esiste una restrizione che poniamo quando progettiamo il sistema di test più efficiente in termini di costi: ogni volta che iniziamo con un campione misto, tutti gli ovini che contribuiscono a tale campione devono essere sottoposti a screening completo (cioè prima di iniziare ad esaminare qualsiasi altro animale deve essere raggiunto un verdetto di infezione / non infezione per tutti loro.
+
+Per l'esempio attuale, risulta che lo schema di test più efficiente in termini di costi (lo chiameremo la strategia ottimale) richiede una media di appena 4.155452 test!
+
+Utilizzando la strategia ottimale, lascia che $T(s, p)$ rappresenti il numero medio di test necessari per testare un gregge di $s$ pecore per un virus che ha probabilità $p$ di essere presente in qualsiasi individuo. Così, arrotondato a sei decimali, $T(25, 0.02) = 4.155452$ e $T(25, 0.10) = 12.702124$.
+
+Trova $\sum T(10\\,000, p)$ per $p = 0.01, 0.02, 0.03, \ldots 0.50$. Dai la risposta arrotondata a sei decimali.
# --hints--
-`euler352()` should return 378563.260589.
+`bloodTests()` dovrebbe restituire `378563.260589`.
```js
-assert.strictEqual(euler352(), 378563.260589);
+assert.strictEqual(bloodTests(), 378563.260589);
```
# --seed--
@@ -41,12 +55,12 @@ assert.strictEqual(euler352(), 378563.260589);
## --seed-contents--
```js
-function euler352() {
+function bloodTests() {
return true;
}
-euler352();
+bloodTests();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
index 74faf24c26..91350909f9 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffe0
-title: 'Problem 353: Risky moon'
+title: 'Problema 353: Luna rischiosa'
challengeType: 5
forumTopicId: 302013
dashedName: problem-353-risky-moon
@@ -8,28 +8,30 @@ dashedName: problem-353-risky-moon
# --description--
-A moon could be described by the sphere C(r) with centre (0,0,0) and radius r.
+Una luna potrebbe essere descritta dalla sfera $C(r)$ con centro (0, 0, 0) e raggio $r$.
-There are stations on the moon at the points on the surface of C(r) with integer coordinates. The station at (0,0,r) is called North Pole station, the station at (0,0,-r) is called South Pole station.
+Ci sono stazioni sulla luna nei punti sulla superficie di $C(r)$ con coordinate intere. La stazione a (0, 0, $r$) si chiama Stazione Polo Nord, la stazione a (0, 0, $-r$) si chiama Stazione Polo Sud.
-All stations are connected with each other via the shortest road on the great arc through the stations. A journey between two stations is risky. If d is the length of the road between two stations, (d/(π r))2 is a measure for the risk of the journey (let us call it the risk of the road). If the journey includes more than two stations, the risk of the journey is the sum of risks of the used roads.
+Tutte le stazioni sono collegate tra loro attraverso la strada più breve sul grande arco attraverso le stazioni. Un viaggio tra due stazioni è rischioso. Se $d$ è la lunghezza della strada tra due stazioni, $\{\left(\frac{d}{πr}\right)}^2$ è una misura per il rischio del viaggio (chiamiamolo il rischio della strada). Se il viaggio comprende più di due stazioni, il rischio del viaggio è la somma dei rischi delle strade usate.
-A direct journey from the North Pole station to the South Pole station has the length πr and risk 1. The journey from the North Pole station to the South Pole station via (0,r,0) has the same length, but a smaller risk: (½πr/(πr))2+(½πr/(πr))2=0.5.
+Un viaggio diretto dalla stazione Polo Nord alla stazione Polo Sud ha la lunghezza $πr$ e il rischio 1. Il viaggio dalla stazione Polo Nord alla stazione Polo Sud attraverso (0, $r$, 0) ha la stessa lunghezza, ma un rischio minore:
-The minimal risk of a journey from the North Pole station to the South Pole station on C(r) is M(r).
+$${\left(\frac{\frac{1}{2}πr}{πr}\right)}^2+{\left(\frac{\frac{1}{2}πr}{πr}\right)}^2 = 0.5$$
-You are given that M(7)=0.1784943998 rounded to 10 digits behind the decimal point.
+Il rischio minimo di un viaggio dalla stazione Polo Nord alla stazione Polo Sud su $C(r)$ è $M(r)$.
-Find ∑M(2n-1) for 1≤n≤15.
+Ti viene dato che $M(7) = 0.178\\,494\\,399\\,8$ arrotondato a 10 cifre dietro il punto decimale.
-Give your answer rounded to 10 digits behind the decimal point in the form a.bcdefghijk.
+Trova $\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$.
+
+Dai la tua risposta arrotondata a 10 cifre dietro il punto decimale nella forma a.bcdefghijk.
# --hints--
-`euler353()` should return 1.2759860331.
+`riskyMoon()` dovrebbe restituire `1.2759860331`.
```js
-assert.strictEqual(euler353(), 1.2759860331);
+assert.strictEqual(riskyMoon(), 1.2759860331);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler353(), 1.2759860331);
## --seed-contents--
```js
-function euler353() {
+function riskyMoon() {
return true;
}
-euler353();
+riskyMoon();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
index 346a1af451..9b04b4b5b5 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
@@ -1,6 +1,6 @@
---
id: 5900f4cf1000cf542c50ffe1
-title: 'Problem 354: Distances in a bee''s honeycomb'
+title: 'Problema 354: Distanze in un favo'
challengeType: 5
forumTopicId: 302014
dashedName: problem-354-distances-in-a-bees-honeycomb
@@ -8,18 +8,22 @@ dashedName: problem-354-distances-in-a-bees-honeycomb
# --description--
-Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
+Considera un favo dove ogni cella è un perfetto esagono regolare con lunghezza lato di 1.
-One particular cell is occupied by the queen bee. For a positive real number L, let B(L) count the cells with distance L from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider. For example, B(√3) = 6, B(√21) = 12 and B(111 111 111) = 54.
+ -Find the number of L ≤ 5·1011 such that B(L) = 450.
+Una particolare cella è occupata dall'ape regina. Per un numero reale positivo $L$, sia $B(L)$ il conteggio delle celle con distanza $L$ dalla cella dell'ape regina (tutte le distanze sono misurate da centro a centro); puoi assumere che il favo è abbastanza grande da accomodare per ogni distanza che vogliamo considerare.
+
+Per esempio, $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$ e $B(111\\,111\\,111) = 54$.
+
+Trova il numero di $L ≤ 5 \times {10}^{11}$ per cui $B(L) = 450$.
# --hints--
-`euler354()` should return 58065134.
+`distancesInHoneycomb()` dovrebbe restituire `58065134`.
```js
-assert.strictEqual(euler354(), 58065134);
+assert.strictEqual(distancesInHoneycomb(), 58065134);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler354(), 58065134);
## --seed-contents--
```js
-function euler354() {
+function distancesInHoneycomb() {
return true;
}
-euler354();
+distancesInHoneycomb();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
index a166a1057a..73bcbb7f10 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe2
-title: 'Problem 355: Maximal coprime subset'
+title: 'Problema 355: Massimo sottoinsieme di coprimi'
challengeType: 5
forumTopicId: 302015
dashedName: problem-355-maximal-coprime-subset
@@ -8,18 +8,18 @@ dashedName: problem-355-maximal-coprime-subset
# --description--
-Define Co(n) to be the maximal possible sum of a set of mutually co-prime elements from {1, 2, ..., n}. For example Co(10) is 30 and hits that maximum on the subset {1, 5, 7, 8, 9}.
+Definisci $Co(n)$ in modo che sia la massima somma possibile di un insieme di elementi reciprocamente co-primi da $\\{1, 2, \ldots, n\\}$. Per esempio $Co(10)$ è di 30 e ha il suo massimo per il sottoinsieme $\\{1, 5, 7, 8, 9\\}$.
-You are given that Co(30) = 193 and Co(100) = 1356.
+Ti viene dato che $Co(30) = 193$ e $Co(100) = 1356$.
-Find Co(200000).
+Trova $Co(200\\,000)$.
# --hints--
-`euler355()` should return 1726545007.
+`maximalCoprimeSubset()` dovrebbe restituire `1726545007`.
```js
-assert.strictEqual(euler355(), 1726545007);
+assert.strictEqual(maximalCoprimeSubset(), 1726545007);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler355(), 1726545007);
## --seed-contents--
```js
-function euler355() {
+function maximalCoprimeSubset() {
return true;
}
-euler355();
+maximalCoprimeSubset();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
index 9027dcecf9..494e59ce91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe3
-title: 'Problem 356: Largest roots of cubic polynomials'
+title: 'Problema 356: Le più grandi radici dei polinomi cubici'
challengeType: 5
forumTopicId: 302016
dashedName: problem-356-largest-roots-of-cubic-polynomials
@@ -8,20 +8,20 @@ dashedName: problem-356-largest-roots-of-cubic-polynomials
# --description--
-Let an be the largest real root of a polynomial g(x) = x3 - 2n·x2 + n.
+Sia $a_n$ la più grande radice reale di un polinomio $g(x) = x^3 - 2^n \times x^2 + n$.
-For example, a2 = 3.86619826...
+Per esempio, $a_2 = 3.86619826\ldots$
-Find the last eight digits of.
+Trova le ultime otto cifre di $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
-Note: represents the floor function.
+**Nota:** $\lfloor a\rfloor$ rappresenta la funzione floor.
# --hints--
-`euler356()` should return 28010159.
+`rootsOfCubicPolynomials()` dovrebbe restituire `28010159`.
```js
-assert.strictEqual(euler356(), 28010159);
+assert.strictEqual(rootsOfCubicPolynomials(), 28010159);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler356(), 28010159);
## --seed-contents--
```js
-function euler356() {
+function rootsOfCubicPolynomials() {
return true;
}
-euler356();
+rootsOfCubicPolynomials();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
index 1bb3f094a2..960124e437 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d11000cf542c50ffe4
-title: 'Problem 357: Prime generating integers'
+title: 'Problema 357: Numeri interi generatori di numeri primi'
challengeType: 5
forumTopicId: 302017
dashedName: problem-357-prime-generating-integers
@@ -8,18 +8,18 @@ dashedName: problem-357-prime-generating-integers
# --description--
-Consider the divisors of 30: 1,2,3,5,6,10,15,30.
+Considera i divisori di 30: 1, 2, 3, 5, 6, 10, 15, 30.
-It can be seen that for every divisor d of 30, d+30/d is prime.
+Si può vedere che per ogni divisore $d$ di 30, $d + \frac{30}{d}$ è primo.
-Find the sum of all positive integers n not exceeding 100 000 000such that for every divisor d of n, d+n/d is prime.
+Trova la somma di tutti gli interi positivi $n$ non superiore a $100\\,000\\, 00$ tale che per ogni divisore $d$ di $n$, $d + \frac{n}{d}$ è primo.
# --hints--
-`euler357()` should return 1739023853137.
+`primeGeneratingIntegers()` dovrebbe restituire `1739023853137`.
```js
-assert.strictEqual(euler357(), 1739023853137);
+assert.strictEqual(primeGeneratingIntegers(), 1739023853137);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler357(), 1739023853137);
## --seed-contents--
```js
-function euler357() {
+function primeGeneratingIntegers() {
return true;
}
-euler357();
+primeGeneratingIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
index fb08a667a8..1e526f8262 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d21000cf542c50ffe5
-title: 'Problem 358: Cyclic numbers'
+title: 'Problema 358: Numeri ciclici'
challengeType: 5
forumTopicId: 302018
dashedName: problem-358-cyclic-numbers
@@ -8,24 +8,28 @@ dashedName: problem-358-cyclic-numbers
# --description--
-A cyclic number with n digits has a very interesting property:
+Un numero ciclico con $n$ cifre ha una proprietà molto interessante:
-When it is multiplied by 1, 2, 3, 4, ... n, all the products have exactly the same digits, in the same order, but rotated in a circular fashion!
+Quando è moltiplicato per 1, 2, 3, 4, ... $n$, tutti i prodotti hanno esattamente le stesse cifre, nello stesso ordine, ma ruotate in modo circolare!
-The smallest cyclic number is the 6-digit number 142857 : 142857 × 1 = 142857 142857 × 2 = 285714 142857 × 3 = 428571 142857 × 4 = 571428 142857 × 5 = 714285 142857 × 6 = 857142
+Il numero ciclico più piccolo è il numero a 6 cifre 142857:
-The next cyclic number is 0588235294117647 with 16 digits : 0588235294117647 × 1 = 0588235294117647 0588235294117647 × 2 = 1176470588235294 0588235294117647 × 3 = 1764705882352941 ... 0588235294117647 × 16 = 9411764705882352
+$$\begin{align} & 142857 × 1 = 142857 \\\\ & 142857 × 2 = 285714 \\\\ & 142857 × 3 = 428571 \\\\ & 142857 × 4 = 571428 \\\\ & 142857 × 5 = 714285 \\\\ & 142857 × 6 = 857142 \end{align}$$
-Note that for cyclic numbers, leading zeros are important.
+Il successivo numero ciclico è 0588235294117647 con 16 cifre:
-There is only one cyclic number for which, the eleven leftmost digits are 00000000137 and the five rightmost digits are 56789 (i.e., it has the form 00000000137...56789 with an unknown number of digits in the middle). Find the sum of all its digits.
+$$\begin{align} & 0588235294117647 × 1 = 0588235294117647 \\\\ & 0588235294117647 × 2 = 1176470588235294 \\\\ & 0588235294117647 × 3 = 1764705882352941 \\\\ & \ldots \\\\ & 0588235294117647 × 16 = 9411764705882352 \end{align}$$
+
+Nota che per i numeri ciclici gli zeri iniziali sono importanti.
+
+C'è solo un numero ciclico per il quale le undici cifre più a sinistra sono 00000000137 e le cinque cifre più a destra sono 56789 (cioè ha la forma $00000000137\ldots56789$ con un numero sconosciuto di cifre nel mezzo). Trova la somma di tutte le sue cifre.
# --hints--
-`euler358()` should return 3284144505.
+`cyclicNumbers()` dovrebbe restituire `3284144505`.
```js
-assert.strictEqual(euler358(), 3284144505);
+assert.strictEqual(cyclicNumbers(), 3284144505);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler358(), 3284144505);
## --seed-contents--
```js
-function euler358() {
+function cyclicNumbers() {
return true;
}
-euler358();
+cyclicNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
index 971ae0f401..2deee5cabb 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
@@ -1,6 +1,6 @@
---
id: 5900f4d31000cf542c50ffe6
-title: 'Problem 359: Hilbert''s New Hotel'
+title: 'Problema 359: Il nuovo Hotel di Hilbert'
challengeType: 5
forumTopicId: 302019
dashedName: problem-359-hilberts-new-hotel
@@ -8,24 +8,35 @@ dashedName: problem-359-hilberts-new-hotel
# --description--
-An infinite number of people (numbered 1, 2, 3, etc.) are lined up to get a room at Hilbert's newest infinite hotel. The hotel contains an infinite number of floors (numbered 1, 2, 3, etc.), and each floor contains an infinite number of rooms (numbered 1, 2, 3, etc.).
+Un numero infinito di persone (numerate 1, 2, 3, ecc.) sono in fila per prendere una stanza al nuovo hotel infinito di Hilbert. L'hotel contienue un numero infinito di piani (numerati 1, 2, 3, ecc) e ogni piano contiene un numero infinito di stanze (numerate 1, 2, 3, ecc.).
-Initially the hotel is empty. Hilbert declares a rule on how the nth person is assigned a room: person n gets the first vacant room in the lowest numbered floor satisfying either of the following: the floor is empty the floor is not empty, and if the latest person taking a room in that floor is person m, then m + n is a perfect square
+All'inizio l'hotel è vuoto. Hilbert dichiara una regola su come la $n$-sima persona è assegnata una stanza: persona $n$ riceve la prima stanza vuota al piano col numero più basso che soddisfa una delle seguenti condizioni:
-Person 1 gets room 1 in floor 1 since floor 1 is empty. Person 2 does not get room 2 in floor 1 since 1 + 2 = 3 is not a perfect square. Person 2 instead gets room 1 in floor 2 since floor 2 is empty. Person 3 gets room 2 in floor 1 since 1 + 3 = 4 is a perfect square.
+- il piano è vuoto
+- il piano non è vuoto, e se l'ultima persona che ha preso una stanza in quel piano è persona $m$ allora $m + n$ è un quadrato perfetto
-Eventually, every person in the line gets a room in the hotel.
+Persona 1 prende stanza 1 in piano 1 visto che piano 1 è vuoto.
-Define P(f, r) to be n if person n occupies room r in floor f, and 0 if no person occupies the room. Here are a few examples: P(1, 1) = 1 P(1, 2) = 3 P(2, 1) = 2 P(10, 20) = 440 P(25, 75) = 4863 P(99, 100) = 19454
+Persona 2 non prende stanza 2 nel piano 1 visto che 1 + 2 = 3 non è un quadrato perfetto.
-Find the sum of all P(f, r) for all positive f and r such that f × r = 71328803586048 and give the last 8 digits as your answer.
+Persona 2 invece prende stanza 1 nel piano 2 visto che piano 2 è vuoto.
+
+Persona 3 prende stanza 2 sul piano 1 visto che 1 + 3 = 4 è un quadrato perfetto.
+
+Alla fine, ogni persona in fila ottiene una stanza nell'hotel.
+
+Sia $P(f, r)$ $n$ se la persona $n$ occupa stanza $r$ al piano $f$, e 0 se nessuna persona occupa la stanza. Ecco alcuni esempi:
+
+$$\begin{align} & P(1, 1) = 1 \\\\ & P(1, 2) = 3 \\\\ & P(2, 1) = 2 \\\\ & P(10, 20) = 440 \\\\ & P(25, 75) = 4863 \\\\ & P(99, 100) = 19454 \end{align}$$
+
+Trova la somma di tutti i $P(f, r)$ per tutti i positivi $f$ e $r$ in modo tale che $f × r = 71\\,328\\,803\\,586\\,048$ e dai le ultime 8 cifre come risposta.
# --hints--
-`euler359()` should return 40632119.
+`hilbertsNewHotel()` dovrebbe restituire `40632119`.
```js
-assert.strictEqual(euler359(), 40632119);
+assert.strictEqual(hilbertsNewHotel(), 40632119);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler359(), 40632119);
## --seed-contents--
```js
-function euler359() {
+function hilbertsNewHotel() {
return true;
}
-euler359();
+hilbertsNewHotel();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
index f028a5d58b..9c9e21541d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
@@ -1,6 +1,6 @@
---
id: 5900f4d41000cf542c50ffe7
-title: 'Problem 360: Scary Sphere'
+title: 'Problema 360: Sfera Spaventosa'
challengeType: 5
forumTopicId: 302021
dashedName: problem-360-scary-sphere
@@ -8,20 +8,24 @@ dashedName: problem-360-scary-sphere
# --description--
-Given two points (x1,y1,z1) and (x2,y2,z2) in three dimensional space, the Manhattan distance between those points is defined as |x1-x2|+|y1-y2|+|z1-z2|.
+Dati due punti ($x_1$, $y_1$, $z_1$) e ($x_2$, $y_2$, $z_2$) nello spazio tridimensionale, la distanza di Manhattan tra questi punti è definita come $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$.
-Let C(r) be a sphere with radius r and center in the origin O(0,0,0). Let I(r) be the set of all points with integer coordinates on the surface of C(r). Let S(r) be the sum of the Manhattan distances of all elements of I(r) to the origin O.
+Sia $C(r)$ una sfera con raggio $r$ e centro nell'origine $O(0, 0, 0)$.
-E.g. S(45)=34518.
+Sia $I(r)$ l'insieme di tutti i punti con coordinate intere sulla superficie di $C(r)$.
-Find S(1010).
+Sia $S(r)$ la somma delle distanze di Manhattan di tutti gli elementi di $I(r)$ dall'origine $O$.
+
+Ad es. $S(45)=34518$.
+
+Trova $S({10}^{10})$.
# --hints--
-`euler360()` should return 878825614395267100.
+`scarySphere()` dovrebbe restituire `878825614395267100`.
```js
-assert.strictEqual(euler360(), 878825614395267100);
+assert.strictEqual(scarySphere(), 878825614395267100);
```
# --seed--
@@ -29,12 +33,12 @@ assert.strictEqual(euler360(), 878825614395267100);
## --seed-contents--
```js
-function euler360() {
+function scarySphere() {
return true;
}
-euler360();
+scarySphere();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
index bc13159789..db80599e17 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4d51000cf542c50ffe8
-title: 'Problem 361: Subsequence of Thue-Morse sequence'
+title: 'Problema 361: sottosequenza della sequenza di Thue-Morse'
challengeType: 5
forumTopicId: 302022
dashedName: problem-361-subsequence-of-thue-morse-sequence
@@ -8,30 +8,30 @@ dashedName: problem-361-subsequence-of-thue-morse-sequence
# --description--
-The Thue-Morse sequence {Tn} is a binary sequence satisfying:
+La sequenza Thue-Morse \\{T_n\\}$ è una sequenza binaria che soddisfa:
-T0 = 0
+- $T_0 = 0$
+- $T_{2n} = T_n$
+- $T_{2n + 1} = 1 - T_n$
-T2n = Tn
+I primi termini di $\\{T_n\\}$ sono dati come segue: $01101001\color{red}{10010}1101001011001101001\ldots$.
-T2n+1 = 1 - Tn
+Definiamo $\\{A_n\\}$ come la sequenza ordinata di interi in modo che l'espressione binaria di ogni elemento appaia come successiva in $\\{T_n\\}$. Ad esempio, il numero decimale 18 è espresso come 10010 in binario. 10010 appare in $\\{T_n\\}$ ($T_8$ a $T_{12}$), quindi 18 è un elemento di $\\{A_n\\}$. Il numero decimale 14 è espresso come 1110 in binario. 1110 non appare mai in $\\{T_n\\}$, quindi 14 non è un elemento di $\\{A_n\\}$.
-The first several terms of {Tn} are given as follows: 01101001100101101001011001101001....
+I primi svariati termini di $A_n$ sono dati come segue:
-We define {An} as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in {Tn}. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in {Tn} (T8 to T12), so 18 is an element of {An}. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in {Tn}, so 14 is not an element of {An}.
+$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
-The first several terms of An are given as follows: n0123456789101112…An012345691011121318…
+Possiamo verificare che $A_{100} = 3251$ e $A_{1000} = 80\\,852\\,364\\,498$.
-We can also verify that A100 = 3251 and A1000 = 80852364498.
-
-Find the last 9 digits of .
+Trova le ultime 9 cifre di \displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
# --hints--
-`euler361()` should return 178476944.
+`subsequenceOfThueMorseSequence()` dovrebbe restituire `178476944`.
```js
-assert.strictEqual(euler361(), 178476944);
+assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler361(), 178476944);
## --seed-contents--
```js
-function euler361() {
+function subsequenceOfThueMorseSequence() {
return true;
}
-euler361();
+subsequenceOfThueMorseSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
index 4d6bc3f4a9..8145f50a49 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
@@ -1,6 +1,6 @@
---
id: 5900f4d61000cf542c50ffe9
-title: 'Problem 362: Squarefree factors'
+title: 'Problema 362: Fattori senza quadrato'
challengeType: 5
forumTopicId: 302023
dashedName: problem-362-squarefree-factors
@@ -8,28 +8,28 @@ dashedName: problem-362-squarefree-factors
# --description--
-Consider the number 54.
+Considera il numero 54.
-54 can be factored in 7 distinct ways into one or more factors larger than 1:
+54 può essere fattorizzato in 7 modi distinti in uno o più fattori superiori a 1:
-54, 2×27, 3×18, 6×9, 3×3×6, 2×3×9 and 2×3×3×3.
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9 \text{ and } 2 × 3 × 3 × 3$$
-If we require that the factors are all squarefree only two ways remain: 3×3×6 and 2×3×3×3.
+Se abbiamo bisogno che i fattori siano tutti privi di quadrati, rimangono solo due modi: $3 × 3 × 6$ e $2 × 3 × 3 × 3$.
-Let's call Fsf(n) the number of ways n can be factored into one or more squarefree factors larger than 1, so Fsf(54)=2.
+Chiamiamo $Fsf(n)$ il numero di modi in cui $n$ può essere fattorizzato senza quadrati più grandi di 1, quindi $Fsf(54) = 2$.
-Let S(n) be ∑Fsf(k) for k=2 to n.
+Sia $S(n)$ $\sum Fsf(k)$ per $k = 2$ a $n$.
-S(100)=193.
+$S(100) = 193$.
-Find S(10 000 000 000).
+Trova $S(10\\,000\\,000\\,000)$.
# --hints--
-`euler362()` should return 457895958010.
+`squarefreeFactors()` dovrebbe restituire `457895958010`.
```js
-assert.strictEqual(euler362(), 457895958010);
+assert.strictEqual(squarefreeFactors(), 457895958010);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler362(), 457895958010);
## --seed-contents--
```js
-function euler362() {
+function squarefreeFactors() {
return true;
}
-euler362();
+squarefreeFactors();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
index 2fde41d1eb..b008e3690e 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffeb
-title: 'Problem 363: Bézier Curves'
+title: 'Problema 363: Curve di Bézier'
challengeType: 5
forumTopicId: 302024
dashedName: problem-363-bzier-curves
@@ -8,24 +8,32 @@ dashedName: problem-363-bzier-curves
# --description--
-A cubic Bézier curve is defined by four points: P0, P1, P2 and P3.
+Una curva cubica di Bézier è definita da quattro punti: $P_0$, $P_1$, $P_2$ e $P_3$.
-The curve is constructed as follows: On the segments P0P1, P1P2 and P2P3 the points Q0,Q1 and Q2 are drawn such that P0Q0 / P0P1 = P1Q1 / P1P2 = P2Q2 / P2P3 = t (t in \[0,1]). On the segments Q0Q1 and Q1Q2 the points R0 and R1 are drawn such that Q0R0 / Q0Q1 = Q1R1 / Q1Q2 = t for the same value of t. On the segment R0R1 the point B is drawn such that R0B / R0R1 = t for the same value of t. The Bézier curve defined by the points P0, P1, P2, P3 is the locus of B as Q0 takes all possible positions on the segment P0P1. (Please note that for all points the value of t is the same.)
+La curva è costruita come segue:
-At this (external) web address you will find an applet that allows you to drag the points P0, P1, P2 and P3 to see what the Bézier curve (green curve) defined by those points looks like. You can also drag the point Q0 along the segment P0P1.
+
-Find the number of L ≤ 5·1011 such that B(L) = 450.
+Una particolare cella è occupata dall'ape regina. Per un numero reale positivo $L$, sia $B(L)$ il conteggio delle celle con distanza $L$ dalla cella dell'ape regina (tutte le distanze sono misurate da centro a centro); puoi assumere che il favo è abbastanza grande da accomodare per ogni distanza che vogliamo considerare.
+
+Per esempio, $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$ e $B(111\\,111\\,111) = 54$.
+
+Trova il numero di $L ≤ 5 \times {10}^{11}$ per cui $B(L) = 450$.
# --hints--
-`euler354()` should return 58065134.
+`distancesInHoneycomb()` dovrebbe restituire `58065134`.
```js
-assert.strictEqual(euler354(), 58065134);
+assert.strictEqual(distancesInHoneycomb(), 58065134);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler354(), 58065134);
## --seed-contents--
```js
-function euler354() {
+function distancesInHoneycomb() {
return true;
}
-euler354();
+distancesInHoneycomb();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
index a166a1057a..73bcbb7f10 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe2
-title: 'Problem 355: Maximal coprime subset'
+title: 'Problema 355: Massimo sottoinsieme di coprimi'
challengeType: 5
forumTopicId: 302015
dashedName: problem-355-maximal-coprime-subset
@@ -8,18 +8,18 @@ dashedName: problem-355-maximal-coprime-subset
# --description--
-Define Co(n) to be the maximal possible sum of a set of mutually co-prime elements from {1, 2, ..., n}. For example Co(10) is 30 and hits that maximum on the subset {1, 5, 7, 8, 9}.
+Definisci $Co(n)$ in modo che sia la massima somma possibile di un insieme di elementi reciprocamente co-primi da $\\{1, 2, \ldots, n\\}$. Per esempio $Co(10)$ è di 30 e ha il suo massimo per il sottoinsieme $\\{1, 5, 7, 8, 9\\}$.
-You are given that Co(30) = 193 and Co(100) = 1356.
+Ti viene dato che $Co(30) = 193$ e $Co(100) = 1356$.
-Find Co(200000).
+Trova $Co(200\\,000)$.
# --hints--
-`euler355()` should return 1726545007.
+`maximalCoprimeSubset()` dovrebbe restituire `1726545007`.
```js
-assert.strictEqual(euler355(), 1726545007);
+assert.strictEqual(maximalCoprimeSubset(), 1726545007);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler355(), 1726545007);
## --seed-contents--
```js
-function euler355() {
+function maximalCoprimeSubset() {
return true;
}
-euler355();
+maximalCoprimeSubset();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
index 9027dcecf9..494e59ce91 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe3
-title: 'Problem 356: Largest roots of cubic polynomials'
+title: 'Problema 356: Le più grandi radici dei polinomi cubici'
challengeType: 5
forumTopicId: 302016
dashedName: problem-356-largest-roots-of-cubic-polynomials
@@ -8,20 +8,20 @@ dashedName: problem-356-largest-roots-of-cubic-polynomials
# --description--
-Let an be the largest real root of a polynomial g(x) = x3 - 2n·x2 + n.
+Sia $a_n$ la più grande radice reale di un polinomio $g(x) = x^3 - 2^n \times x^2 + n$.
-For example, a2 = 3.86619826...
+Per esempio, $a_2 = 3.86619826\ldots$
-Find the last eight digits of.
+Trova le ultime otto cifre di $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
-Note: represents the floor function.
+**Nota:** $\lfloor a\rfloor$ rappresenta la funzione floor.
# --hints--
-`euler356()` should return 28010159.
+`rootsOfCubicPolynomials()` dovrebbe restituire `28010159`.
```js
-assert.strictEqual(euler356(), 28010159);
+assert.strictEqual(rootsOfCubicPolynomials(), 28010159);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler356(), 28010159);
## --seed-contents--
```js
-function euler356() {
+function rootsOfCubicPolynomials() {
return true;
}
-euler356();
+rootsOfCubicPolynomials();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
index 1bb3f094a2..960124e437 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d11000cf542c50ffe4
-title: 'Problem 357: Prime generating integers'
+title: 'Problema 357: Numeri interi generatori di numeri primi'
challengeType: 5
forumTopicId: 302017
dashedName: problem-357-prime-generating-integers
@@ -8,18 +8,18 @@ dashedName: problem-357-prime-generating-integers
# --description--
-Consider the divisors of 30: 1,2,3,5,6,10,15,30.
+Considera i divisori di 30: 1, 2, 3, 5, 6, 10, 15, 30.
-It can be seen that for every divisor d of 30, d+30/d is prime.
+Si può vedere che per ogni divisore $d$ di 30, $d + \frac{30}{d}$ è primo.
-Find the sum of all positive integers n not exceeding 100 000 000such that for every divisor d of n, d+n/d is prime.
+Trova la somma di tutti gli interi positivi $n$ non superiore a $100\\,000\\, 00$ tale che per ogni divisore $d$ di $n$, $d + \frac{n}{d}$ è primo.
# --hints--
-`euler357()` should return 1739023853137.
+`primeGeneratingIntegers()` dovrebbe restituire `1739023853137`.
```js
-assert.strictEqual(euler357(), 1739023853137);
+assert.strictEqual(primeGeneratingIntegers(), 1739023853137);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler357(), 1739023853137);
## --seed-contents--
```js
-function euler357() {
+function primeGeneratingIntegers() {
return true;
}
-euler357();
+primeGeneratingIntegers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
index fb08a667a8..1e526f8262 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d21000cf542c50ffe5
-title: 'Problem 358: Cyclic numbers'
+title: 'Problema 358: Numeri ciclici'
challengeType: 5
forumTopicId: 302018
dashedName: problem-358-cyclic-numbers
@@ -8,24 +8,28 @@ dashedName: problem-358-cyclic-numbers
# --description--
-A cyclic number with n digits has a very interesting property:
+Un numero ciclico con $n$ cifre ha una proprietà molto interessante:
-When it is multiplied by 1, 2, 3, 4, ... n, all the products have exactly the same digits, in the same order, but rotated in a circular fashion!
+Quando è moltiplicato per 1, 2, 3, 4, ... $n$, tutti i prodotti hanno esattamente le stesse cifre, nello stesso ordine, ma ruotate in modo circolare!
-The smallest cyclic number is the 6-digit number 142857 : 142857 × 1 = 142857 142857 × 2 = 285714 142857 × 3 = 428571 142857 × 4 = 571428 142857 × 5 = 714285 142857 × 6 = 857142
+Il numero ciclico più piccolo è il numero a 6 cifre 142857:
-The next cyclic number is 0588235294117647 with 16 digits : 0588235294117647 × 1 = 0588235294117647 0588235294117647 × 2 = 1176470588235294 0588235294117647 × 3 = 1764705882352941 ... 0588235294117647 × 16 = 9411764705882352
+$$\begin{align} & 142857 × 1 = 142857 \\\\ & 142857 × 2 = 285714 \\\\ & 142857 × 3 = 428571 \\\\ & 142857 × 4 = 571428 \\\\ & 142857 × 5 = 714285 \\\\ & 142857 × 6 = 857142 \end{align}$$
-Note that for cyclic numbers, leading zeros are important.
+Il successivo numero ciclico è 0588235294117647 con 16 cifre:
-There is only one cyclic number for which, the eleven leftmost digits are 00000000137 and the five rightmost digits are 56789 (i.e., it has the form 00000000137...56789 with an unknown number of digits in the middle). Find the sum of all its digits.
+$$\begin{align} & 0588235294117647 × 1 = 0588235294117647 \\\\ & 0588235294117647 × 2 = 1176470588235294 \\\\ & 0588235294117647 × 3 = 1764705882352941 \\\\ & \ldots \\\\ & 0588235294117647 × 16 = 9411764705882352 \end{align}$$
+
+Nota che per i numeri ciclici gli zeri iniziali sono importanti.
+
+C'è solo un numero ciclico per il quale le undici cifre più a sinistra sono 00000000137 e le cinque cifre più a destra sono 56789 (cioè ha la forma $00000000137\ldots56789$ con un numero sconosciuto di cifre nel mezzo). Trova la somma di tutte le sue cifre.
# --hints--
-`euler358()` should return 3284144505.
+`cyclicNumbers()` dovrebbe restituire `3284144505`.
```js
-assert.strictEqual(euler358(), 3284144505);
+assert.strictEqual(cyclicNumbers(), 3284144505);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler358(), 3284144505);
## --seed-contents--
```js
-function euler358() {
+function cyclicNumbers() {
return true;
}
-euler358();
+cyclicNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
index 971ae0f401..2deee5cabb 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
@@ -1,6 +1,6 @@
---
id: 5900f4d31000cf542c50ffe6
-title: 'Problem 359: Hilbert''s New Hotel'
+title: 'Problema 359: Il nuovo Hotel di Hilbert'
challengeType: 5
forumTopicId: 302019
dashedName: problem-359-hilberts-new-hotel
@@ -8,24 +8,35 @@ dashedName: problem-359-hilberts-new-hotel
# --description--
-An infinite number of people (numbered 1, 2, 3, etc.) are lined up to get a room at Hilbert's newest infinite hotel. The hotel contains an infinite number of floors (numbered 1, 2, 3, etc.), and each floor contains an infinite number of rooms (numbered 1, 2, 3, etc.).
+Un numero infinito di persone (numerate 1, 2, 3, ecc.) sono in fila per prendere una stanza al nuovo hotel infinito di Hilbert. L'hotel contienue un numero infinito di piani (numerati 1, 2, 3, ecc) e ogni piano contiene un numero infinito di stanze (numerate 1, 2, 3, ecc.).
-Initially the hotel is empty. Hilbert declares a rule on how the nth person is assigned a room: person n gets the first vacant room in the lowest numbered floor satisfying either of the following: the floor is empty the floor is not empty, and if the latest person taking a room in that floor is person m, then m + n is a perfect square
+All'inizio l'hotel è vuoto. Hilbert dichiara una regola su come la $n$-sima persona è assegnata una stanza: persona $n$ riceve la prima stanza vuota al piano col numero più basso che soddisfa una delle seguenti condizioni:
-Person 1 gets room 1 in floor 1 since floor 1 is empty. Person 2 does not get room 2 in floor 1 since 1 + 2 = 3 is not a perfect square. Person 2 instead gets room 1 in floor 2 since floor 2 is empty. Person 3 gets room 2 in floor 1 since 1 + 3 = 4 is a perfect square.
+- il piano è vuoto
+- il piano non è vuoto, e se l'ultima persona che ha preso una stanza in quel piano è persona $m$ allora $m + n$ è un quadrato perfetto
-Eventually, every person in the line gets a room in the hotel.
+Persona 1 prende stanza 1 in piano 1 visto che piano 1 è vuoto.
-Define P(f, r) to be n if person n occupies room r in floor f, and 0 if no person occupies the room. Here are a few examples: P(1, 1) = 1 P(1, 2) = 3 P(2, 1) = 2 P(10, 20) = 440 P(25, 75) = 4863 P(99, 100) = 19454
+Persona 2 non prende stanza 2 nel piano 1 visto che 1 + 2 = 3 non è un quadrato perfetto.
-Find the sum of all P(f, r) for all positive f and r such that f × r = 71328803586048 and give the last 8 digits as your answer.
+Persona 2 invece prende stanza 1 nel piano 2 visto che piano 2 è vuoto.
+
+Persona 3 prende stanza 2 sul piano 1 visto che 1 + 3 = 4 è un quadrato perfetto.
+
+Alla fine, ogni persona in fila ottiene una stanza nell'hotel.
+
+Sia $P(f, r)$ $n$ se la persona $n$ occupa stanza $r$ al piano $f$, e 0 se nessuna persona occupa la stanza. Ecco alcuni esempi:
+
+$$\begin{align} & P(1, 1) = 1 \\\\ & P(1, 2) = 3 \\\\ & P(2, 1) = 2 \\\\ & P(10, 20) = 440 \\\\ & P(25, 75) = 4863 \\\\ & P(99, 100) = 19454 \end{align}$$
+
+Trova la somma di tutti i $P(f, r)$ per tutti i positivi $f$ e $r$ in modo tale che $f × r = 71\\,328\\,803\\,586\\,048$ e dai le ultime 8 cifre come risposta.
# --hints--
-`euler359()` should return 40632119.
+`hilbertsNewHotel()` dovrebbe restituire `40632119`.
```js
-assert.strictEqual(euler359(), 40632119);
+assert.strictEqual(hilbertsNewHotel(), 40632119);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler359(), 40632119);
## --seed-contents--
```js
-function euler359() {
+function hilbertsNewHotel() {
return true;
}
-euler359();
+hilbertsNewHotel();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
index f028a5d58b..9c9e21541d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
@@ -1,6 +1,6 @@
---
id: 5900f4d41000cf542c50ffe7
-title: 'Problem 360: Scary Sphere'
+title: 'Problema 360: Sfera Spaventosa'
challengeType: 5
forumTopicId: 302021
dashedName: problem-360-scary-sphere
@@ -8,20 +8,24 @@ dashedName: problem-360-scary-sphere
# --description--
-Given two points (x1,y1,z1) and (x2,y2,z2) in three dimensional space, the Manhattan distance between those points is defined as |x1-x2|+|y1-y2|+|z1-z2|.
+Dati due punti ($x_1$, $y_1$, $z_1$) e ($x_2$, $y_2$, $z_2$) nello spazio tridimensionale, la distanza di Manhattan tra questi punti è definita come $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$.
-Let C(r) be a sphere with radius r and center in the origin O(0,0,0). Let I(r) be the set of all points with integer coordinates on the surface of C(r). Let S(r) be the sum of the Manhattan distances of all elements of I(r) to the origin O.
+Sia $C(r)$ una sfera con raggio $r$ e centro nell'origine $O(0, 0, 0)$.
-E.g. S(45)=34518.
+Sia $I(r)$ l'insieme di tutti i punti con coordinate intere sulla superficie di $C(r)$.
-Find S(1010).
+Sia $S(r)$ la somma delle distanze di Manhattan di tutti gli elementi di $I(r)$ dall'origine $O$.
+
+Ad es. $S(45)=34518$.
+
+Trova $S({10}^{10})$.
# --hints--
-`euler360()` should return 878825614395267100.
+`scarySphere()` dovrebbe restituire `878825614395267100`.
```js
-assert.strictEqual(euler360(), 878825614395267100);
+assert.strictEqual(scarySphere(), 878825614395267100);
```
# --seed--
@@ -29,12 +33,12 @@ assert.strictEqual(euler360(), 878825614395267100);
## --seed-contents--
```js
-function euler360() {
+function scarySphere() {
return true;
}
-euler360();
+scarySphere();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
index bc13159789..db80599e17 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4d51000cf542c50ffe8
-title: 'Problem 361: Subsequence of Thue-Morse sequence'
+title: 'Problema 361: sottosequenza della sequenza di Thue-Morse'
challengeType: 5
forumTopicId: 302022
dashedName: problem-361-subsequence-of-thue-morse-sequence
@@ -8,30 +8,30 @@ dashedName: problem-361-subsequence-of-thue-morse-sequence
# --description--
-The Thue-Morse sequence {Tn} is a binary sequence satisfying:
+La sequenza Thue-Morse \\{T_n\\}$ è una sequenza binaria che soddisfa:
-T0 = 0
+- $T_0 = 0$
+- $T_{2n} = T_n$
+- $T_{2n + 1} = 1 - T_n$
-T2n = Tn
+I primi termini di $\\{T_n\\}$ sono dati come segue: $01101001\color{red}{10010}1101001011001101001\ldots$.
-T2n+1 = 1 - Tn
+Definiamo $\\{A_n\\}$ come la sequenza ordinata di interi in modo che l'espressione binaria di ogni elemento appaia come successiva in $\\{T_n\\}$. Ad esempio, il numero decimale 18 è espresso come 10010 in binario. 10010 appare in $\\{T_n\\}$ ($T_8$ a $T_{12}$), quindi 18 è un elemento di $\\{A_n\\}$. Il numero decimale 14 è espresso come 1110 in binario. 1110 non appare mai in $\\{T_n\\}$, quindi 14 non è un elemento di $\\{A_n\\}$.
-The first several terms of {Tn} are given as follows: 01101001100101101001011001101001....
+I primi svariati termini di $A_n$ sono dati come segue:
-We define {An} as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in {Tn}. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in {Tn} (T8 to T12), so 18 is an element of {An}. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in {Tn}, so 14 is not an element of {An}.
+$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
-The first several terms of An are given as follows: n0123456789101112…An012345691011121318…
+Possiamo verificare che $A_{100} = 3251$ e $A_{1000} = 80\\,852\\,364\\,498$.
-We can also verify that A100 = 3251 and A1000 = 80852364498.
-
-Find the last 9 digits of .
+Trova le ultime 9 cifre di \displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
# --hints--
-`euler361()` should return 178476944.
+`subsequenceOfThueMorseSequence()` dovrebbe restituire `178476944`.
```js
-assert.strictEqual(euler361(), 178476944);
+assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler361(), 178476944);
## --seed-contents--
```js
-function euler361() {
+function subsequenceOfThueMorseSequence() {
return true;
}
-euler361();
+subsequenceOfThueMorseSequence();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
index 4d6bc3f4a9..8145f50a49 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
@@ -1,6 +1,6 @@
---
id: 5900f4d61000cf542c50ffe9
-title: 'Problem 362: Squarefree factors'
+title: 'Problema 362: Fattori senza quadrato'
challengeType: 5
forumTopicId: 302023
dashedName: problem-362-squarefree-factors
@@ -8,28 +8,28 @@ dashedName: problem-362-squarefree-factors
# --description--
-Consider the number 54.
+Considera il numero 54.
-54 can be factored in 7 distinct ways into one or more factors larger than 1:
+54 può essere fattorizzato in 7 modi distinti in uno o più fattori superiori a 1:
-54, 2×27, 3×18, 6×9, 3×3×6, 2×3×9 and 2×3×3×3.
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9 \text{ and } 2 × 3 × 3 × 3$$
-If we require that the factors are all squarefree only two ways remain: 3×3×6 and 2×3×3×3.
+Se abbiamo bisogno che i fattori siano tutti privi di quadrati, rimangono solo due modi: $3 × 3 × 6$ e $2 × 3 × 3 × 3$.
-Let's call Fsf(n) the number of ways n can be factored into one or more squarefree factors larger than 1, so Fsf(54)=2.
+Chiamiamo $Fsf(n)$ il numero di modi in cui $n$ può essere fattorizzato senza quadrati più grandi di 1, quindi $Fsf(54) = 2$.
-Let S(n) be ∑Fsf(k) for k=2 to n.
+Sia $S(n)$ $\sum Fsf(k)$ per $k = 2$ a $n$.
-S(100)=193.
+$S(100) = 193$.
-Find S(10 000 000 000).
+Trova $S(10\\,000\\,000\\,000)$.
# --hints--
-`euler362()` should return 457895958010.
+`squarefreeFactors()` dovrebbe restituire `457895958010`.
```js
-assert.strictEqual(euler362(), 457895958010);
+assert.strictEqual(squarefreeFactors(), 457895958010);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler362(), 457895958010);
## --seed-contents--
```js
-function euler362() {
+function squarefreeFactors() {
return true;
}
-euler362();
+squarefreeFactors();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
index 2fde41d1eb..b008e3690e 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffeb
-title: 'Problem 363: Bézier Curves'
+title: 'Problema 363: Curve di Bézier'
challengeType: 5
forumTopicId: 302024
dashedName: problem-363-bzier-curves
@@ -8,24 +8,32 @@ dashedName: problem-363-bzier-curves
# --description--
-A cubic Bézier curve is defined by four points: P0, P1, P2 and P3.
+Una curva cubica di Bézier è definita da quattro punti: $P_0$, $P_1$, $P_2$ e $P_3$.
-The curve is constructed as follows: On the segments P0P1, P1P2 and P2P3 the points Q0,Q1 and Q2 are drawn such that P0Q0 / P0P1 = P1Q1 / P1P2 = P2Q2 / P2P3 = t (t in \[0,1]). On the segments Q0Q1 and Q1Q2 the points R0 and R1 are drawn such that Q0R0 / Q0Q1 = Q1R1 / Q1Q2 = t for the same value of t. On the segment R0R1 the point B is drawn such that R0B / R0R1 = t for the same value of t. The Bézier curve defined by the points P0, P1, P2, P3 is the locus of B as Q0 takes all possible positions on the segment P0P1. (Please note that for all points the value of t is the same.)
+La curva è costruita come segue:
-At this (external) web address you will find an applet that allows you to drag the points P0, P1, P2 and P3 to see what the Bézier curve (green curve) defined by those points looks like. You can also drag the point Q0 along the segment P0P1.
+ -From the construction it is clear that the Bézier curve will be tangent to the segments P0P1 in P0 and P2P3 in P3.
+Sui segmenti $P_0P_1$, $P_1P_2$ e $P_2P_3$ i punti $Q_0$,$Q_1$ e $Q_2$ sono disegnati in modo tale che $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, con $t$ in [0,1].
-A cubic Bézier curve with P0=(1,0), P1=(1,v), P2=(v,1) and P3=(0,1) is used to approximate a quarter circle. The value v > 0 is chosen such that the area enclosed by the lines OP0, OP3 and the curve is equal to π/4 (the area of the quarter circle).
+Sui segmenti $Q_0Q_1$ e $Q_1Q_2$ i punti $R_0$ e $R_1$ sono disegnati in modo tale che $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ per lo stesso valore di $t$.
-By how many percent does the length of the curve differ from the length of the quarter circle? That is, if L is the length of the curve, calculate 100 × L − π/2π/2Give your answer rounded to 10 digits behind the decimal point.
+Sul segmento $R_0R_1$ il punto $B$ è disegnato in modo tale che $\frac{R_0B}{R_0R_1} = t$ per lo stesso valore di $t$.
+
+La curva di Bézier definita dai punti $P_0$, $P_1$, $P_2$, $P_3$ è il luogo di $B$ tale che $Q_0$ prende tutte le posizioni possibili sul segmento $P_0P_1$. (Si noti che per tutti i punti il valore di $t$ è lo stesso.)
+
+Dalla costruzione è chiaro che la curva di Bézier sarà tangente ai segmenti $P_0P_1$ in $P_0$ e $P_2P_3$ in $P_3$.
+
+Una curva cubica di Bézier con $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ e $P_3 = (0, 1)$ viene utilizzata per approssimare un quarto di cerchio. Il valore $v > 0$ è scelto in modo tale che l'area racchiusa tra le linee $OP_0$, $OP_3$ e la curva sia pari a $\frac{π}{4}$ (l'area del quarto di circonferenza).
+
+Di quanti punti percentuali la lunghezza della curva differisce dalla lunghezza del quarto di circonferenza? Cioè, se $L$ è la lunghezza della curva, calcolare $100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler363()` should return 0.0000372091.
+`bezierCurves()` dovrebbe restituire `0.0000372091`.
```js
-assert.strictEqual(euler363(), 0.0000372091);
+assert.strictEqual(bezierCurves(), 0.0000372091);
```
# --seed--
@@ -33,12 +41,12 @@ assert.strictEqual(euler363(), 0.0000372091);
## --seed-contents--
```js
-function euler363() {
+function bezierCurves() {
return true;
}
-euler363();
+bezierCurves();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
index 84637798b8..f5ce69e0a1 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffea
-title: 'Problem 364: Comfortable distance'
+title: 'Problema 364: Distanza confortevole'
challengeType: 5
forumTopicId: 302025
dashedName: problem-364-comfortable-distance
@@ -8,24 +8,26 @@ dashedName: problem-364-comfortable-distance
# --description--
-There are N seats in a row. N people come after each other to fill the seats according to the following rules:
+Ci sono $N$ posti in fila. $N$ persone vengono una dopo l'altra per riempire i posti secondo le seguenti regole:
-If there is any seat whose adjacent seat(s) are not occupied take such a seat.
+1. Se esiste un sedile i cui sedili adiacenti non sono occupati prendono tale sedile.
+2. Se questo posto è occupato e c'è un posto per il quale solo un posto adiacente è occupato si prende tale posto.
+3. Altrimenti si prende uno dei posti disponibili rimanenti.
-If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
+Sia $T(N)$ il numero di possibilità che $N$ posti siano occupati da $N$ persone con le regole date. La seguente figura mostra $T(4) = 8$.
-Otherwise take one of the remaining available seats.
+
-From the construction it is clear that the Bézier curve will be tangent to the segments P0P1 in P0 and P2P3 in P3.
+Sui segmenti $P_0P_1$, $P_1P_2$ e $P_2P_3$ i punti $Q_0$,$Q_1$ e $Q_2$ sono disegnati in modo tale che $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, con $t$ in [0,1].
-A cubic Bézier curve with P0=(1,0), P1=(1,v), P2=(v,1) and P3=(0,1) is used to approximate a quarter circle. The value v > 0 is chosen such that the area enclosed by the lines OP0, OP3 and the curve is equal to π/4 (the area of the quarter circle).
+Sui segmenti $Q_0Q_1$ e $Q_1Q_2$ i punti $R_0$ e $R_1$ sono disegnati in modo tale che $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ per lo stesso valore di $t$.
-By how many percent does the length of the curve differ from the length of the quarter circle? That is, if L is the length of the curve, calculate 100 × L − π/2π/2Give your answer rounded to 10 digits behind the decimal point.
+Sul segmento $R_0R_1$ il punto $B$ è disegnato in modo tale che $\frac{R_0B}{R_0R_1} = t$ per lo stesso valore di $t$.
+
+La curva di Bézier definita dai punti $P_0$, $P_1$, $P_2$, $P_3$ è il luogo di $B$ tale che $Q_0$ prende tutte le posizioni possibili sul segmento $P_0P_1$. (Si noti che per tutti i punti il valore di $t$ è lo stesso.)
+
+Dalla costruzione è chiaro che la curva di Bézier sarà tangente ai segmenti $P_0P_1$ in $P_0$ e $P_2P_3$ in $P_3$.
+
+Una curva cubica di Bézier con $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ e $P_3 = (0, 1)$ viene utilizzata per approssimare un quarto di cerchio. Il valore $v > 0$ è scelto in modo tale che l'area racchiusa tra le linee $OP_0$, $OP_3$ e la curva sia pari a $\frac{π}{4}$ (l'area del quarto di circonferenza).
+
+Di quanti punti percentuali la lunghezza della curva differisce dalla lunghezza del quarto di circonferenza? Cioè, se $L$ è la lunghezza della curva, calcolare $100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler363()` should return 0.0000372091.
+`bezierCurves()` dovrebbe restituire `0.0000372091`.
```js
-assert.strictEqual(euler363(), 0.0000372091);
+assert.strictEqual(bezierCurves(), 0.0000372091);
```
# --seed--
@@ -33,12 +41,12 @@ assert.strictEqual(euler363(), 0.0000372091);
## --seed-contents--
```js
-function euler363() {
+function bezierCurves() {
return true;
}
-euler363();
+bezierCurves();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
index 84637798b8..f5ce69e0a1 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffea
-title: 'Problem 364: Comfortable distance'
+title: 'Problema 364: Distanza confortevole'
challengeType: 5
forumTopicId: 302025
dashedName: problem-364-comfortable-distance
@@ -8,24 +8,26 @@ dashedName: problem-364-comfortable-distance
# --description--
-There are N seats in a row. N people come after each other to fill the seats according to the following rules:
+Ci sono $N$ posti in fila. $N$ persone vengono una dopo l'altra per riempire i posti secondo le seguenti regole:
-If there is any seat whose adjacent seat(s) are not occupied take such a seat.
+1. Se esiste un sedile i cui sedili adiacenti non sono occupati prendono tale sedile.
+2. Se questo posto è occupato e c'è un posto per il quale solo un posto adiacente è occupato si prende tale posto.
+3. Altrimenti si prende uno dei posti disponibili rimanenti.
-If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
+Sia $T(N)$ il numero di possibilità che $N$ posti siano occupati da $N$ persone con le regole date. La seguente figura mostra $T(4) = 8$.
-Otherwise take one of the remaining available seats.
+ -Let T(N) be the number of possibilities that N seats are occupied by N people with the given rules. The following figure shows T(4)=8.
+Possiamo verificare che $T(10) = 61\\,632$ e $T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094$.
-We can verify that T(10) = 61632 and T(1 000) mod 100 000 007 = 47255094. Find T(1 000 000) mod 100 000 007.
+Trova $T(1\\,000\\,000)\bmod 100\\,000\\,007$.
# --hints--
-`euler364()` should return 44855254.
+`comfortableDistance()` dovrebbe restituire `44855254`.
```js
-assert.strictEqual(euler364(), 44855254);
+assert.strictEqual(comfortableDistance(), 44855254);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler364(), 44855254);
## --seed-contents--
```js
-function euler364() {
+function comfortableDistance() {
return true;
}
-euler364();
+comfortableDistance();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
index 1647ff46ea..90911f54a8 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffec
-title: 'Problem 365: A huge binomial coefficient'
+title: 'Problema 365: Un grande coefficiente binomiale'
challengeType: 5
forumTopicId: 302026
dashedName: problem-365-a-huge-binomial-coefficient
@@ -8,18 +8,18 @@ dashedName: problem-365-a-huge-binomial-coefficient
# --description--
-The binomial coefficient C(1018,109) is a number with more than 9 billion (9×109) digits.
+Il coefficiente binomiale $\displaystyle\binom{{10}^{18}}{{10}^9}$ è un numero con più di 9 miliardi ($9 × {10}^9$) di cifre.
-Let M(n,k,m) denote the binomial coefficient C(n,k) modulo m.
+Sia $M(n, k, m)$ il coefficiente binomiale $\displaystyle\binom{n}{k}$ modulo $m$.
-Calculate ∑M(1018,109,p*q*r) for 1000<p<q<r<5000 and p,q,r prime.
+Calcola $\sum M({10}^{18}, {10}^9, p \times q \times r)$ per $1000 < p < q < r < 5000$ e $p$, $q$, $r$ numeri primi.
# --hints--
-`euler365()` should return 162619462356610300.
+`hugeBinomialCoefficient()` dovrebbe restituire `162619462356610300`.
```js
-assert.strictEqual(euler365(), 162619462356610300);
+assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler365(), 162619462356610300);
## --seed-contents--
```js
-function euler365() {
+function hugeBinomialCoefficient() {
return true;
}
-euler365();
+hugeBinomialCoefficient();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
index b7f832ebf4..bf6252b74c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffed
-title: 'Problem 366: Stone Game III'
+title: 'Problema 366: Gioco delle pietre III'
challengeType: 5
forumTopicId: 302027
dashedName: problem-366-stone-game-iii
@@ -8,30 +8,44 @@ dashedName: problem-366-stone-game-iii
# --description--
-Two players, Anton and Bernhard, are playing the following game.
+Due giocatori, Anton e Bernhard, stanno giocando il seguente gioco.
-There is one pile of n stones.
+C'è una pila di $n$ pietre.
-The first player may remove any positive number of stones, but not the whole pile.
+Il primo giocatore può rimuovere qualsiasi numero positivo di pietre, ma non l'intera pila.
-Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+Successivamente, ogni giocatore può rimuovere al massimo il doppio del numero di pietre che il suo avversario ha preso nella mossa precedente.
-The player who removes the last stone wins.
+Il giocatore che rimuove l'ultima pietra vince.
-E.g. n=5 If the first player takes anything more than one stone the next player will be able to take all remaining stones. If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones. The first player cannot take all three because he may take at most 2x1=2 stones. So let's say he takes also one stone, leaving 2. The second player can take the two remaining stones and wins. So 5 is a losing position for the first player. For some winning positions there is more than one possible move for the first player. E.g. when n=17 the first player can remove one or four stones.
+Ad es. $n = 5$
-Let M(n) be the maximum number of stones the first player can take from a winning position at his first turn and M(n)=0 for any other position.
+Se il primo giocatore prende più di una pietra il giocatore successivo sarà in grado di prendere tutte le pietre rimaste.
-∑M(n) for n≤100 is 728.
+Se il primo giocatore prende una pietra, lasciandone quattro, anche il suo avversario prenderà una pietra, lasciando tre pietre.
-Find ∑M(n) for n≤1018. Give your answer modulo 108.
+Il primo giocatore non può prenderle tutte e tre perché può prendere al massimo $2 \times 1 = 2$ pietre. Quindi diciamo che anche lui prende una pietra, lasciandone 2.
+
+Il secondo giocatore può prendere le due pietre rimanenti e vince.
+
+Quindi 5 è una posizione perdente per il primo giocatore.
+
+Per alcune posizioni vincenti c'è più di una possibile mossa per il primo giocatore.
+
+Ad es. quando $n = 17$ il primo giocatore può rimuovere una o quattro pietre.
+
+Sia $M(n)$ il numero massimo di pietre che il primo giocatore può prendere da una posizione vincente al suo primo turno e $M(n) = 0$ per qualsiasi altra posizione.
+
+$\sum M(n)$ per $n ≤ 100$ è 728.
+
+Trova $\sum M(n)$ per $n ≤ {10}^{18}$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler366()` should return 88351299.
+`stoneGameThree()` dovrebbe restituire `88351299`.
```js
-assert.strictEqual(euler366(), 88351299);
+assert.strictEqual(stoneGameThree(), 88351299);
```
# --seed--
@@ -39,12 +53,12 @@ assert.strictEqual(euler366(), 88351299);
## --seed-contents--
```js
-function euler366() {
+function stoneGameThree() {
return true;
}
-euler366();
+stoneGameThree();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
index 979702592a..a34132973d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
@@ -1,6 +1,6 @@
---
id: 5900f4db1000cf542c50ffee
-title: 'Problem 367: Bozo sort'
+title: 'Problema 367: Bozo sort'
challengeType: 5
forumTopicId: 302028
dashedName: problem-367-bozo-sort
@@ -8,20 +8,32 @@ dashedName: problem-367-bozo-sort
# --description--
-Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+Bozo sort, da non confondersi con il'algoritmo leggermente meno efficiente bogo sort, consiste nel controllare se la sequenza di input è ordinata, e se non lo è scambiare a caso due elementi. Questo viene ripetuto fino a che la sequenza non è eventualmente in ordine.
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all 4! input sequences is 24.75. The already sorted sequence takes 0 steps.
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di scambi, mediato su tutte le $4!$ sequenze di input è $24.75$.
-In this problem we consider the following variant on bozo sort. If the sequence is not in order we pick three elements at random and shuffle these three elements randomly. All 3!=6 permutations of those three elements are equally likely. The already sorted sequence will take 0 steps. If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all 4! input sequences is 27.5. Consider as input sequences the permutations of the first 11 natural numbers. Averaged over all 11! input sequences, what is the expected number of shuffles this sorting algorithm will perform?
+La sequenza già ordinata ha bisogno di 0 step.
-Give your answer rounded to the nearest integer.
+In questo problema consideriamo le seguenti varianti nel bozo sort.
+
+Se la sequenza non è in ordine, scegliamo 3 elementi a caso e mescoliamo questi tre elementi casualmente.
+
+Tutte le $3! = 6$ permutazioni di questi tre elementi sono altrettanto probabili.
+
+La sequenza già ordinata ha bisogno di 0 step.
+
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di mescolamenti, mediato su tutte le $4!$ sequenze di input è $27.5$.
+
+Considera come sequenze di input le permutazioni dei primi 11 numeri naturali.
+
+Mediato su tutte le $11!$ sequenze di input, qual è il numero medio di mescolamenti che questo algoritmo performerà? Dai la tua risposta arrotondata al numero intero più vicino.
# --hints--
-`euler367()` should return 48271207.
+`bozoSort()` dovrebbe restituire `48271207`.
```js
-assert.strictEqual(euler367(), 48271207);
+assert.strictEqual(bozoSort(), 48271207);
```
# --seed--
@@ -29,12 +41,12 @@ assert.strictEqual(euler367(), 48271207);
## --seed-contents--
```js
-function euler367() {
+function bozoSort() {
return true;
}
-euler367();
+bozoSort();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
index dc9cf2f919..e262f93378 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
@@ -1,6 +1,6 @@
---
id: 5900f4dd1000cf542c50ffef
-title: 'Problem 368: A Kempner-like series'
+title: 'Problema 368: Una serie di Kempner'
challengeType: 5
forumTopicId: 302029
dashedName: problem-368-a-kempner-like-series
@@ -8,22 +8,26 @@ dashedName: problem-368-a-kempner-like-series
# --description--
-The harmonic series $1 + \\dfrac{1}{2} + \\dfrac{1}{3} + \\dfrac{1}{4} + ...$ is well known to be divergent.
+La serie armonica $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ è nota per essere divergente.
-If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+Se comunque si omette da questa serie ogni termine in cui il denominatore ha un 9 in esso, la serie converge abbastanza notevolmente a circa 22.9206766193. Questa serie armonica modificata è chiamata serie Kempner.
-Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted. These 20 omitted terms are: $$\\dfrac{1}{111}, \\dfrac{1}{222}, \\dfrac{1}{333}, \\dfrac{1}{444}, \\dfrac{1}{555}, \\dfrac{1}{666}, \\dfrac{1}{777}, \\dfrac{1}{888}, \\dfrac{1}{999}, \\dfrac{1}{1000}, \\dfrac{1}{1110}, \\\\ \\dfrac{1}{1111}, \\dfrac{1}{1112}, \\dfrac{1}{1113}, \\dfrac{1}{1114}, \\dfrac{1}{1115}, \\dfrac{1}{1116}, \\dfrac{1}{1117}, \\dfrac{1}{1118}, \\dfrac{1}{1119}$$
+Consideriamo ora un'altra serie armonica modificata omettendo dalla serie armonica ogni termine in cui il denominatore ha 3 o più cifre consecutive uguali. Si può verificare che sui primi 1200 termini della serie armonica, solo 20 termini saranno omessi.
-This series converges as well.
+Questi 20 termini omessi sono:
-Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\ \dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
+
+Anche questa serie converge.
+
+Trova il valore a cui converge la serie. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler368()` should return 253.6135092068.
+`kempnerLikeSeries()` dovrebbe restituire `253.6135092068`.
```js
-assert.strictEqual(euler368(), 253.6135092068);
+assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
```
# --seed--
@@ -31,12 +35,12 @@ assert.strictEqual(euler368(), 253.6135092068);
## --seed-contents--
```js
-function euler368() {
+function kempnerLikeSeries() {
return true;
}
-euler368();
+kempnerLikeSeries();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
index abdcb4c810..953a36e727 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff0
-title: 'Problem 369: Badugi'
+title: 'Problema 369: Badugi'
challengeType: 5
forumTopicId: 302030
dashedName: problem-369-badugi
@@ -8,18 +8,18 @@ dashedName: problem-369-badugi
# --description--
-In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+In un mazzo standard di 52 carte da gioco, un set di 4 carte è un Badugi se contiene 4 carte senza coppie e nessuna due carte dello stesso seme.
-Let f(n) be the number of ways to choose n cards with a 4 card subset that is a Badugi. For example, there are 2598960 ways to choose five cards from a standard 52 card deck, of which 514800 contain a 4 card subset that is a Badugi, so f(5) = 514800.
+Lascia che $f(n)$ sia il numero di modi per scegliere $n$ carte con un sottoinsieme di 4 carte che è un Badugi. Ad esempio, ci sono $2\\,598\\,960$ modi per scegliere cinque carte da un mazzo standard di 52 carte, di cui $514\\,800$ contengono un sottoinsieme di 4 carte che è un Badugi, quindi $f(5) = 514800$.
-Find ∑f(n) for 4 ≤ n ≤ 13.
+Trova $\sum f(n)$ per $4 ≤ n ≤ 13$.
# --hints--
-`euler369()` should return 862400558448.
+`badugi()` dovrebbe restituire `862400558448`.
```js
-assert.strictEqual(euler369(), 862400558448);
+assert.strictEqual(badugi(), 862400558448);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler369(), 862400558448);
## --seed-contents--
```js
-function euler369() {
+function badugi() {
return true;
}
-euler369();
+badugi();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
index 469f9151e0..4b5b6947ea 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff1
-title: 'Problem 370: Geometric triangles'
+title: 'Problema 370: Triangoli geometrici'
challengeType: 5
forumTopicId: 302032
dashedName: problem-370-geometric-triangles
@@ -8,20 +8,20 @@ dashedName: problem-370-geometric-triangles
# --description--
-Let us define a geometric triangle as an integer sided triangle with sides a ≤ b ≤ c so that its sides form a geometric progression, i.e. b2 = a · c .
+Sia un triangolo geometrico un triangolo con lati interi con lati $a ≤ b ≤ c$ cossìcché i suoi lati formino una progressione geometrica, cioè $b^2 = a \times c$.
-An example of such a geometric triangle is the triangle with sides a = 144, b = 156 and c = 169.
+Un esempio di tale triangolo è il triangolo con lati $a = 144$, $b = 156$ e $c = 169$.
-There are 861805 geometric triangles with perimeter ≤ 106 .
+Ci sono $861\\,805$ triangoli geometrici con $\text{perimetro} ≤ {10}^6$.
-How many geometric triangles exist with perimeter ≤ 2.5·1013 ?
+Quanti triangoli geometrici esistono con $\text{perimetro} ≤ 2.5 \times {10}^{13}$?
# --hints--
-`euler370()` should return 41791929448408.
+`geometricTriangles()` dovrebbe restituire `41791929448408`.
```js
-assert.strictEqual(euler370(), 41791929448408);
+assert.strictEqual(geometricTriangles(), 41791929448408);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler370(), 41791929448408);
## --seed-contents--
```js
-function euler370() {
+function geometricTriangles() {
return true;
}
-euler370();
+geometricTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
index 005b5aaf07..cc2e62c6fd 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
@@ -1,6 +1,6 @@
---
id: 5900f4e01000cf542c50fff2
-title: 'Problem 371: Licence plates'
+title: 'Problema 371: Targhe'
challengeType: 5
forumTopicId: 302033
dashedName: problem-371-licence-plates
@@ -8,24 +8,24 @@ dashedName: problem-371-licence-plates
# --description--
-Oregon licence plates consist of three letters followed by a three digit number (each digit can be from \[0..9]).
+Le targhe dell'Oregon sono composte da tre lettere seguite da un numero a tre cifre (ciascuna cifra può essere in [0...9]).
-While driving to work Seth plays the following game:
+Mentre guida per andare a lavoro Seth gioca il seguente gioco:
-Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+Ogni volta che i numeri di due targhe visti nel suo viaggio si sommano a 1000, vince.
-E.g. MIC-012 and HAN-988 is a win and RYU-500 and SET-500 too. (as long as he sees them in the same trip).
+Ad es. `MIC-012` e `HAN-988` è una vittoria e `RYU-500` e `SET-500` anche. (finché li vede nello stesso viaggio).
-Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+Trova il numero previsto di targhe che ha bisogno di vedere per una vittoria. Dai la tua risposta approssimata a 8 cifre dopo il punto decimale.
-Note: We assume that each licence plate seen is equally likely to have any three digit number on it.
+**Nota:** Assumiamo che ogni targa vista ha la stessa probabilità di avere un qualsiasi numero di tre cifre su di essa.
# --hints--
-`euler371()` should return 40.66368097.
+`licensePlates()` dovrebbe restituire `40.66368097`.
```js
-assert.strictEqual(euler371(), 40.66368097);
+assert.strictEqual(licensePlates(), 40.66368097);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler371(), 40.66368097);
## --seed-contents--
```js
-function euler371() {
+function licensePlates() {
return true;
}
-euler371();
+licensePlates();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
index 1a04cacb71..1a21a55186 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff3
-title: 'Problem 372: Pencils of rays'
+title: 'Problema 372: Raggi di matite'
challengeType: 5
forumTopicId: 302034
dashedName: problem-372-pencils-of-rays
@@ -8,16 +8,20 @@ dashedName: problem-372-pencils-of-rays
# --description--
-Let R(M, N) be the number of lattice points (x, y) which satisfy M
+Sia $R(M, N)$ il numero di punti di reticolo ($x$, $y$) che soddisfa $M \lt x \le N$, $M \lt y \le N$ e $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ è dispari.
-Note: represents the floor function.
+Possiamo verificare che $R(0, 100) = 3\\,019$ e $R(100, 10\\,000) = 29\\,750\\,422$.
+
+Trova $R(2 \times {10}^6, {10}^9)$.
+
+**Nota:** $\lfloor x\rfloor$ è la funzione che arrotonda verso il basso.
# --hints--
-`euler372()` should return 301450082318807040.
+`pencilsOfRays()` dovrebbe restituire `301450082318807040`.
```js
-assert.strictEqual(euler372(), 301450082318807040);
+assert.strictEqual(pencilsOfRays(), 301450082318807040);
```
# --seed--
@@ -25,12 +29,12 @@ assert.strictEqual(euler372(), 301450082318807040);
## --seed-contents--
```js
-function euler372() {
+function pencilsOfRays() {
return true;
}
-euler372();
+pencilsOfRays();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
index 534c32ea25..fd6f508ef4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff4
-title: 'Problem 373: Circumscribed Circles'
+title: 'Problema 373: Cerchi circoscritti'
challengeType: 5
forumTopicId: 302035
dashedName: problem-373-circumscribed-circles
@@ -8,22 +8,20 @@ dashedName: problem-373-circumscribed-circles
# --description--
-Every triangle has a circumscribed circle that goes through the three vertices.
+Ogni triangolo ha un cerchio circoscritto che attraversa i tre vertici. Considera tutti i triangoli a lati interi per i quali è intero anche il raggio del cerchio circoscritto.
-Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+Sia $S(n)$ la somma dei raggi dei cerchi circoscritti di tutti questi triangoli per i quali il raggio non supera $n$.
-Let S(n) be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed n.
+$S(100) = 4\\,950$ and $S(1\\,200) = 1\\,653\\,605$.
-S(100)=4950 and S(1200)=1653605.
-
-Find S(107).
+Trova $S({10}^7)$.
# --hints--
-`euler373()` should return 727227472448913.
+`circumscribedCircles()` dovrebbe restituire `727227472448913`.
```js
-assert.strictEqual(euler373(), 727227472448913);
+assert.strictEqual(circumscribedCircles(), 727227472448913);
```
# --seed--
@@ -31,12 +29,12 @@ assert.strictEqual(euler373(), 727227472448913);
## --seed-contents--
```js
-function euler373() {
+function circumscribedCircles() {
return true;
}
-euler373();
+circumscribedCircles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
index 10fe621891..70ed56fae7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff6
-title: 'Problem 374: Maximum Integer Partition Product'
+title: 'Problema 374: Massimo prodotto di partizione di un numero intero'
challengeType: 5
forumTopicId: 302036
dashedName: problem-374-maximum-integer-partition-product
@@ -8,28 +8,30 @@ dashedName: problem-374-maximum-integer-partition-product
# --description--
-An integer partition of a number n is a way of writing n as a sum of positive integers.
+Una partizione intera di un numero $n$ è un modo di scrivere $n$ come una somma di numeri interi positivi.
-Partitions that differ only in the order of their summands are considered the same. A partition of n into distinct parts is a partition of n in which every part occurs at most once.
+Le partizioni che differiscono solo nell'ordine dei loro addendi sono considerate le stesse. Una partizione di $n$ in parti distinte è una partizione di $n$ in cui ogni parte si verifica al massimo una volta.
-The partitions of 5 into distinct parts are: 5, 4+1 and 3+2.
+Le partizioni in parti distinte di 5 sono:
-Let f(n) be the maximum product of the parts of any such partition of n into distinct parts and let m(n) be the number of elements of any such partition of n with that product.
+5, 4 + 1 e 3 + 2.
-So f(5)=6 and m(5)=2.
+Sia $f(n)$ il prodotto massimo delle parti di una tale partizione di $n$ in parti distinte e sia $m(n)$ il numero di elementi di una tale partizione di $n$ con quel prodotto.
-For n=10 the partition with the largest product is 10=2+3+5, which gives f(10)=30 and m(10)=3. And their product, f(10)·m(10) = 30·3 = 90
+Quindi $f(5) = 6$ e $m(5) = 2$.
-It can be verified that ∑f(n)·m(n) for 1 ≤ n ≤ 100 = 1683550844462.
+Per $n = 10$ la partizione con il prodotto più grande è $10 = 2 + 3 + 5$, che dà $f(10) = 30$ e $m(10) = 3$. E il loro prodotto, $f(10) \times m(10) = 30 \times 3 = 90$
-Find ∑f(n)·m(n) for 1 ≤ n ≤ 1014. Give your answer modulo 982451653, the 50 millionth prime.
+Si può verificare che $\sum f(n) \times m(n)$ for $1 ≤ n ≤ 100 = 1\\,683\\,550\\,844\\,462$.
+
+Trova $\sum f(n) \times m(n)$ for $1 ≤ n ≤ {10}^{14}$. Dai la tua risposta modulo $982\\,451\\,653$, il 50 millionesimo primo.
# --hints--
-`euler374()` should return 334420941.
+`maximumIntegerPartitionProduct()` dovrebbe restituire `334420941`.
```js
-assert.strictEqual(euler374(), 334420941);
+assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler374(), 334420941);
## --seed-contents--
```js
-function euler374() {
+function maximumIntegerPartitionProduct() {
return true;
}
-euler374();
+maximumIntegerPartitionProduct();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
index 684613a235..d02d316962 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4e41000cf542c50fff5
-title: 'Problem 375: Minimum of subsequences'
+title: 'Problema 375: Minimo delle sottosequenze'
challengeType: 5
forumTopicId: 302037
dashedName: problem-375-minimum-of-subsequences
@@ -8,30 +8,22 @@ dashedName: problem-375-minimum-of-subsequences
# --description--
-Let Sn be an integer sequence produced with the following pseudo-random number generator:
+Lascia che $S_n$ sia una sequenza intera prodotta con il seguente generatore di numeri pseudo-casuali:
-S0
+$$\begin{align} S_0 & = 290\\,797 \\\\ S_{n + 1} & = {S_n}^2\bmod 50\\,515\\,093 \end{align}$$
-=
+Sia $A(i, j)$ il minimo dei numeri $S_i, S_{i + 1}, \ldots, S_j$ per $i ≤ j$. Sia $M(N) = \sum A(i, j)$ per $1 ≤ i ≤ j ≤ N$.
-290797
+Possiamo verificare che $M(10) = 432\\,256\\,955$ e $M(10\\,000) = 3\\,264\\,567\\,774\\,119$.
-Sn+1
-
-=
-
-Sn2 mod 50515093
-
-Let A(i, j) be the minimum of the numbers Si, Si+1, ... , Sj for i ≤ j. Let M(N) = ΣA(i, j) for 1 ≤ i ≤ j ≤ N. We can verify that M(10) = 432256955 and M(10 000) = 3264567774119.
-
-Find M(2 000 000 000).
+Trova $M(2\\,000\\,000\\,000)$.
# --hints--
-`euler375()` should return 7435327983715286000.
+`minimumOfSubsequences()` dovrebbe restituire `7435327983715286000`.
```js
-assert.strictEqual(euler375(), 7435327983715286000);
+assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
```
# --seed--
@@ -39,12 +31,12 @@ assert.strictEqual(euler375(), 7435327983715286000);
## --seed-contents--
```js
-function euler375() {
+function minimumOfSubsequences() {
return true;
}
-euler375();
+minimumOfSubsequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
index b76c4d26e8..49d34bd6da 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff7
-title: 'Problem 376: Nontransitive sets of dice'
+title: 'Problema 376: Set di dadi non transitivo'
challengeType: 5
forumTopicId: 302038
dashedName: problem-376-nontransitive-sets-of-dice
@@ -8,30 +8,43 @@ dashedName: problem-376-nontransitive-sets-of-dice
# --description--
-Consider the following set of dice with nonstandard pips:
+Considera la seguente serie di dadi con pallini non standard:
-Die A: 1 4 4 4 4 4 Die B: 2 2 2 5 5 5 Die C: 3 3 3 3 3 6
+$$$\begin{array}{} \text{Dado A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{Dado B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Dado C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
-A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+Un gioco è giocato da due giocatori scegliendo un dado a turno e lanciandolo. Il giocatore che lancia il valore più alto vince.
-If the first player picks die A and the second player picks die B we get P(second player wins) = 7/12 > 1/2
+Se il primo giocatore sceglie dado $A$ e il secondo giocatore sceglie dado $B$ otteniamo
-If the first player picks die B and the second player picks die C we get P(second player wins) = 7/12 > 1/2
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die C and the second player picks die A we get P(second player wins) = 25/36 > 1/2
+Se il primo giocatore sceglie dado $B$ e il secondo giocatore sceglie dado $C$ otteniamo
-So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:There are three six-sided dice with each side having between 1 and N pips, inclusive. Dice with the same set of pips are equal, regardless of which side on the die the pips are located. The same pip value may appear on multiple dice; if both players roll the same value neither player wins. The sets of dice {A,B,C}, {B,C,A} and {C,A,B} are the same set.
+Se il primo giocatore sceglie dado $C$ e il secondo giocatore sceglie dado $A$ otteniamo
-For N = 7 we find there are 9780 such sets. How many are there for N = 30 ?
+$P(\text{secondo giocatore vince}) = \frac{25}{36} > \frac{1}{2}$
+
+Quindi, qualunque scelta faccia il primo giocatore, il secondo giocatore può scegliere un altro dado e avere una probabilità maggiore del 50% di vittoria. Un set di dadi che hanno questa proprietà è chiamato un set di dadi non transitivi.
+
+Vogliamo indagare quanti insiemi di dadi non transitivi esistono. Assumeremo le seguenti condizioni:
+
+- Ci sono tre dadi a sei facce con ogni faccia che ha tra 1 e $N$ pallini, inclusi.
+- I dadi con lo stesso set di pallini sono uguali, indipendentemente dalla faccia del dado su cui i pallini sono situati.
+- Lo stesso valore di pallini può apparire su più dadi; se entrambi i giocatori lanciano lo stesso valore nessuno vince.
+- I set di dadi $\\{A, B, C\\}$, $\\{B, C, A\\}$ e $\\{C, A, B\\}$ sono lo stesso set.
+
+Per $N = 7$ troviamo 9780 set di questo tipo.
+
+Quanti ce ne sono per $N = 30$?
# --hints--
-`euler376()` should return 973059630185670.
+`nontransitiveSetsOfDice()` dovrebbe restituire `973059630185670`.
```js
-assert.strictEqual(euler376(), 973059630185670);
+assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
```
# --seed--
@@ -39,12 +52,12 @@ assert.strictEqual(euler376(), 973059630185670);
## --seed-contents--
```js
-function euler376() {
+function nontransitiveSetsOfDice() {
return true;
}
-euler376();
+nontransitiveSetsOfDice();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
index 660508c234..0b674e8a71 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff8
-title: 'Problem 377: Sum of digits, experience 13'
+title: 'Problema 377: Somma delle cifre, esperienza 13'
challengeType: 5
forumTopicId: 302039
dashedName: problem-377-sum-of-digits-experience-13
@@ -8,22 +8,22 @@ dashedName: problem-377-sum-of-digits-experience-13
# --description--
-There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+Ci sono 16 numeri interi positivi che non hanno uno 0 tra le loro cifre e che hanno una somma delle cifre uguale a 5:
-5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 e 11111.
-Their sum is 17891.
+La loro somma è 17891.
-Let f(n) be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to n.
+Sia $f(n)$ la somma di tutti i numeri interi positivi che non hanno uno zero tra le loro cifre e che hanno una somma delle cifre pari a $n$.
-Find $\\displaystyle \\sum\_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+Trova $\displaystyle\sum_{i=1}^{17} f(13^i)$. Dai le ultime 9 cifre della tua risposta.
# --hints--
-`euler377()` should return 732385277.
+`experience13()` dovrebbe restituire `732385277`.
```js
-assert.strictEqual(euler377(), 732385277);
+assert.strictEqual(experience13(), 732385277);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler377(), 732385277);
## --seed-contents--
```js
-function euler377() {
+function experience13() {
return true;
}
-euler377();
+experience13();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
index 22589747fe..0c8d5d5b65 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f4e61000cf542c50fff9
-title: 'Problem 378: Triangle Triples'
+title: 'Problema 378: tripli triangoli'
challengeType: 5
forumTopicId: 302040
dashedName: problem-378-triangle-triples
@@ -8,24 +8,20 @@ dashedName: problem-378-triangle-triples
# --description--
-Let T(n) be the nth triangle number, so T(n) =
+Sia $T(n)$ l'$n$-simo numero triangolare, quindi $T(n) = \frac{n(n + 1)}{2}$.
-n (n+1)2
+Sia $dT(n)$ il numero di divisori di $T(n)$. Esempio: $T(7) = 28$ e $dT(7) = 6$.
-.
+Sia $Tr(n)$ il numero di triplette ($i$, $j$, $k$) per cui $1 ≤ i < j < k ≤ n$ e $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5\\,772$ e $Tr(1000) = 11\\,174\\,776$.
-Let dT(n) be the number of divisors of T(n). E.g.: T(7) = 28 and dT(7) = 6.
-
-Let Tr(n) be the number of triples (i, j, k) such that 1 ≤ i < j < k ≤ n and dT(i) > dT(j) > dT(k). Tr(20) = 14, Tr(100) = 5772 and Tr(1000) = 11174776.
-
-Find Tr(60 000 000). Give the last 18 digits of your answer.
+Trova $Tr(60\\,000\\,000)$. Dai le ultime 18 cifre della tua risposta.
# --hints--
-`euler378()` should return 147534623725724700.
+`triangleTriples()` dovrebbe restituire `147534623725724700`.
```js
-assert.strictEqual(euler378(), 147534623725724700);
+assert.strictEqual(triangleTriples(), 147534623725724700);
```
# --seed--
@@ -33,12 +29,12 @@ assert.strictEqual(euler378(), 147534623725724700);
## --seed-contents--
```js
-function euler378() {
+function triangleTriples() {
return true;
}
-euler378();
+triangleTriples();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
index 3933d82ea2..7798debf82 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffa
-title: 'Problem 379: Least common multiple count'
+title: 'Problema 379: conteggio del minimo comune multiplo'
challengeType: 5
forumTopicId: 302041
dashedName: problem-379-least-common-multiple-count
@@ -8,20 +8,20 @@ dashedName: problem-379-least-common-multiple-count
# --description--
-Let f(n) be the number of couples (x,y) with x and y positive integers, x ≤ y and the least common multiple of x and y equal to n.
+Sia $f(n)$ il numero di coppie ($x$, $y$) con $x$ e $y$ numeri interi positivi, per cui $x ≤ y$ e il minimo comune multiplo di $x$ e $y$ è uguale a $n$.
-Let g be the summatory function of f, i.e.: g(n) = ∑ f(i) for 1 ≤ i ≤ n.
+Sia $g$ la funzione sommatoria di $f$, cioè $g(n) = \sum f(i)$ per $1 ≤ i ≤ n$.
-You are given that g(106) = 37429395.
+Ti è dato che $g({10}^6) = 37\\,429\\,395$.
-Find g(1012).
+Trova $g({10}^{12})$.
# --hints--
-`euler379()` should return 132314136838185.
+`leastCommonMultipleCount()` dovrebbe restituire `132314136838185`.
```js
-assert.strictEqual(euler379(), 132314136838185);
+assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler379(), 132314136838185);
## --seed-contents--
```js
-function euler379() {
+function leastCommonMultipleCount() {
return true;
}
-euler379();
+leastCommonMultipleCount();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
index 8596f52fa7..2fa9c3c7b7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffb
-title: 'Problem 380: Amazing Mazes!'
+title: 'Problema 380: fantastici labirinti!'
challengeType: 5
forumTopicId: 302044
dashedName: problem-380-amazing-mazes
@@ -8,20 +8,30 @@ dashedName: problem-380-amazing-mazes
# --description--
-An m×n maze is an m×n rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+Un labirinto $m×n$ è una griglia rettangolare $m×n$ con muri piazzati tra celle della griglia in modo tale che c'è un unico percorso dal quadrato in alto a sinistra a qualsiasi altro quadrato. I seguenti sono esempi di labirinti 9×12 e 15×20:
-Let C(m,n) be the number of distinct m×n mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+
-Let T(N) be the number of possibilities that N seats are occupied by N people with the given rules. The following figure shows T(4)=8.
+Possiamo verificare che $T(10) = 61\\,632$ e $T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094$.
-We can verify that T(10) = 61632 and T(1 000) mod 100 000 007 = 47255094. Find T(1 000 000) mod 100 000 007.
+Trova $T(1\\,000\\,000)\bmod 100\\,000\\,007$.
# --hints--
-`euler364()` should return 44855254.
+`comfortableDistance()` dovrebbe restituire `44855254`.
```js
-assert.strictEqual(euler364(), 44855254);
+assert.strictEqual(comfortableDistance(), 44855254);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler364(), 44855254);
## --seed-contents--
```js
-function euler364() {
+function comfortableDistance() {
return true;
}
-euler364();
+comfortableDistance();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
index 1647ff46ea..90911f54a8 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffec
-title: 'Problem 365: A huge binomial coefficient'
+title: 'Problema 365: Un grande coefficiente binomiale'
challengeType: 5
forumTopicId: 302026
dashedName: problem-365-a-huge-binomial-coefficient
@@ -8,18 +8,18 @@ dashedName: problem-365-a-huge-binomial-coefficient
# --description--
-The binomial coefficient C(1018,109) is a number with more than 9 billion (9×109) digits.
+Il coefficiente binomiale $\displaystyle\binom{{10}^{18}}{{10}^9}$ è un numero con più di 9 miliardi ($9 × {10}^9$) di cifre.
-Let M(n,k,m) denote the binomial coefficient C(n,k) modulo m.
+Sia $M(n, k, m)$ il coefficiente binomiale $\displaystyle\binom{n}{k}$ modulo $m$.
-Calculate ∑M(1018,109,p*q*r) for 1000<p<q<r<5000 and p,q,r prime.
+Calcola $\sum M({10}^{18}, {10}^9, p \times q \times r)$ per $1000 < p < q < r < 5000$ e $p$, $q$, $r$ numeri primi.
# --hints--
-`euler365()` should return 162619462356610300.
+`hugeBinomialCoefficient()` dovrebbe restituire `162619462356610300`.
```js
-assert.strictEqual(euler365(), 162619462356610300);
+assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler365(), 162619462356610300);
## --seed-contents--
```js
-function euler365() {
+function hugeBinomialCoefficient() {
return true;
}
-euler365();
+hugeBinomialCoefficient();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
index b7f832ebf4..bf6252b74c 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffed
-title: 'Problem 366: Stone Game III'
+title: 'Problema 366: Gioco delle pietre III'
challengeType: 5
forumTopicId: 302027
dashedName: problem-366-stone-game-iii
@@ -8,30 +8,44 @@ dashedName: problem-366-stone-game-iii
# --description--
-Two players, Anton and Bernhard, are playing the following game.
+Due giocatori, Anton e Bernhard, stanno giocando il seguente gioco.
-There is one pile of n stones.
+C'è una pila di $n$ pietre.
-The first player may remove any positive number of stones, but not the whole pile.
+Il primo giocatore può rimuovere qualsiasi numero positivo di pietre, ma non l'intera pila.
-Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+Successivamente, ogni giocatore può rimuovere al massimo il doppio del numero di pietre che il suo avversario ha preso nella mossa precedente.
-The player who removes the last stone wins.
+Il giocatore che rimuove l'ultima pietra vince.
-E.g. n=5 If the first player takes anything more than one stone the next player will be able to take all remaining stones. If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones. The first player cannot take all three because he may take at most 2x1=2 stones. So let's say he takes also one stone, leaving 2. The second player can take the two remaining stones and wins. So 5 is a losing position for the first player. For some winning positions there is more than one possible move for the first player. E.g. when n=17 the first player can remove one or four stones.
+Ad es. $n = 5$
-Let M(n) be the maximum number of stones the first player can take from a winning position at his first turn and M(n)=0 for any other position.
+Se il primo giocatore prende più di una pietra il giocatore successivo sarà in grado di prendere tutte le pietre rimaste.
-∑M(n) for n≤100 is 728.
+Se il primo giocatore prende una pietra, lasciandone quattro, anche il suo avversario prenderà una pietra, lasciando tre pietre.
-Find ∑M(n) for n≤1018. Give your answer modulo 108.
+Il primo giocatore non può prenderle tutte e tre perché può prendere al massimo $2 \times 1 = 2$ pietre. Quindi diciamo che anche lui prende una pietra, lasciandone 2.
+
+Il secondo giocatore può prendere le due pietre rimanenti e vince.
+
+Quindi 5 è una posizione perdente per il primo giocatore.
+
+Per alcune posizioni vincenti c'è più di una possibile mossa per il primo giocatore.
+
+Ad es. quando $n = 17$ il primo giocatore può rimuovere una o quattro pietre.
+
+Sia $M(n)$ il numero massimo di pietre che il primo giocatore può prendere da una posizione vincente al suo primo turno e $M(n) = 0$ per qualsiasi altra posizione.
+
+$\sum M(n)$ per $n ≤ 100$ è 728.
+
+Trova $\sum M(n)$ per $n ≤ {10}^{18}$. Dai la tua risposta nel formato ${10}^8$.
# --hints--
-`euler366()` should return 88351299.
+`stoneGameThree()` dovrebbe restituire `88351299`.
```js
-assert.strictEqual(euler366(), 88351299);
+assert.strictEqual(stoneGameThree(), 88351299);
```
# --seed--
@@ -39,12 +53,12 @@ assert.strictEqual(euler366(), 88351299);
## --seed-contents--
```js
-function euler366() {
+function stoneGameThree() {
return true;
}
-euler366();
+stoneGameThree();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
index 979702592a..a34132973d 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
@@ -1,6 +1,6 @@
---
id: 5900f4db1000cf542c50ffee
-title: 'Problem 367: Bozo sort'
+title: 'Problema 367: Bozo sort'
challengeType: 5
forumTopicId: 302028
dashedName: problem-367-bozo-sort
@@ -8,20 +8,32 @@ dashedName: problem-367-bozo-sort
# --description--
-Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+Bozo sort, da non confondersi con il'algoritmo leggermente meno efficiente bogo sort, consiste nel controllare se la sequenza di input è ordinata, e se non lo è scambiare a caso due elementi. Questo viene ripetuto fino a che la sequenza non è eventualmente in ordine.
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all 4! input sequences is 24.75. The already sorted sequence takes 0 steps.
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di scambi, mediato su tutte le $4!$ sequenze di input è $24.75$.
-In this problem we consider the following variant on bozo sort. If the sequence is not in order we pick three elements at random and shuffle these three elements randomly. All 3!=6 permutations of those three elements are equally likely. The already sorted sequence will take 0 steps. If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all 4! input sequences is 27.5. Consider as input sequences the permutations of the first 11 natural numbers. Averaged over all 11! input sequences, what is the expected number of shuffles this sorting algorithm will perform?
+La sequenza già ordinata ha bisogno di 0 step.
-Give your answer rounded to the nearest integer.
+In questo problema consideriamo le seguenti varianti nel bozo sort.
+
+Se la sequenza non è in ordine, scegliamo 3 elementi a caso e mescoliamo questi tre elementi casualmente.
+
+Tutte le $3! = 6$ permutazioni di questi tre elementi sono altrettanto probabili.
+
+La sequenza già ordinata ha bisogno di 0 step.
+
+Se consideriamo tutte le permutazioni dei primi 4 numeri naturali come input, il valore di aspettazione del numero di mescolamenti, mediato su tutte le $4!$ sequenze di input è $27.5$.
+
+Considera come sequenze di input le permutazioni dei primi 11 numeri naturali.
+
+Mediato su tutte le $11!$ sequenze di input, qual è il numero medio di mescolamenti che questo algoritmo performerà? Dai la tua risposta arrotondata al numero intero più vicino.
# --hints--
-`euler367()` should return 48271207.
+`bozoSort()` dovrebbe restituire `48271207`.
```js
-assert.strictEqual(euler367(), 48271207);
+assert.strictEqual(bozoSort(), 48271207);
```
# --seed--
@@ -29,12 +41,12 @@ assert.strictEqual(euler367(), 48271207);
## --seed-contents--
```js
-function euler367() {
+function bozoSort() {
return true;
}
-euler367();
+bozoSort();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
index dc9cf2f919..e262f93378 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
@@ -1,6 +1,6 @@
---
id: 5900f4dd1000cf542c50ffef
-title: 'Problem 368: A Kempner-like series'
+title: 'Problema 368: Una serie di Kempner'
challengeType: 5
forumTopicId: 302029
dashedName: problem-368-a-kempner-like-series
@@ -8,22 +8,26 @@ dashedName: problem-368-a-kempner-like-series
# --description--
-The harmonic series $1 + \\dfrac{1}{2} + \\dfrac{1}{3} + \\dfrac{1}{4} + ...$ is well known to be divergent.
+La serie armonica $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ è nota per essere divergente.
-If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+Se comunque si omette da questa serie ogni termine in cui il denominatore ha un 9 in esso, la serie converge abbastanza notevolmente a circa 22.9206766193. Questa serie armonica modificata è chiamata serie Kempner.
-Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted. These 20 omitted terms are: $$\\dfrac{1}{111}, \\dfrac{1}{222}, \\dfrac{1}{333}, \\dfrac{1}{444}, \\dfrac{1}{555}, \\dfrac{1}{666}, \\dfrac{1}{777}, \\dfrac{1}{888}, \\dfrac{1}{999}, \\dfrac{1}{1000}, \\dfrac{1}{1110}, \\\\ \\dfrac{1}{1111}, \\dfrac{1}{1112}, \\dfrac{1}{1113}, \\dfrac{1}{1114}, \\dfrac{1}{1115}, \\dfrac{1}{1116}, \\dfrac{1}{1117}, \\dfrac{1}{1118}, \\dfrac{1}{1119}$$
+Consideriamo ora un'altra serie armonica modificata omettendo dalla serie armonica ogni termine in cui il denominatore ha 3 o più cifre consecutive uguali. Si può verificare che sui primi 1200 termini della serie armonica, solo 20 termini saranno omessi.
-This series converges as well.
+Questi 20 termini omessi sono:
-Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\ \dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
+
+Anche questa serie converge.
+
+Trova il valore a cui converge la serie. Dai la tua risposta approssimata a 10 cifre dopo il punto decimale.
# --hints--
-`euler368()` should return 253.6135092068.
+`kempnerLikeSeries()` dovrebbe restituire `253.6135092068`.
```js
-assert.strictEqual(euler368(), 253.6135092068);
+assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
```
# --seed--
@@ -31,12 +35,12 @@ assert.strictEqual(euler368(), 253.6135092068);
## --seed-contents--
```js
-function euler368() {
+function kempnerLikeSeries() {
return true;
}
-euler368();
+kempnerLikeSeries();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
index abdcb4c810..953a36e727 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-369-badugi.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff0
-title: 'Problem 369: Badugi'
+title: 'Problema 369: Badugi'
challengeType: 5
forumTopicId: 302030
dashedName: problem-369-badugi
@@ -8,18 +8,18 @@ dashedName: problem-369-badugi
# --description--
-In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+In un mazzo standard di 52 carte da gioco, un set di 4 carte è un Badugi se contiene 4 carte senza coppie e nessuna due carte dello stesso seme.
-Let f(n) be the number of ways to choose n cards with a 4 card subset that is a Badugi. For example, there are 2598960 ways to choose five cards from a standard 52 card deck, of which 514800 contain a 4 card subset that is a Badugi, so f(5) = 514800.
+Lascia che $f(n)$ sia il numero di modi per scegliere $n$ carte con un sottoinsieme di 4 carte che è un Badugi. Ad esempio, ci sono $2\\,598\\,960$ modi per scegliere cinque carte da un mazzo standard di 52 carte, di cui $514\\,800$ contengono un sottoinsieme di 4 carte che è un Badugi, quindi $f(5) = 514800$.
-Find ∑f(n) for 4 ≤ n ≤ 13.
+Trova $\sum f(n)$ per $4 ≤ n ≤ 13$.
# --hints--
-`euler369()` should return 862400558448.
+`badugi()` dovrebbe restituire `862400558448`.
```js
-assert.strictEqual(euler369(), 862400558448);
+assert.strictEqual(badugi(), 862400558448);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler369(), 862400558448);
## --seed-contents--
```js
-function euler369() {
+function badugi() {
return true;
}
-euler369();
+badugi();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
index 469f9151e0..4b5b6947ea 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff1
-title: 'Problem 370: Geometric triangles'
+title: 'Problema 370: Triangoli geometrici'
challengeType: 5
forumTopicId: 302032
dashedName: problem-370-geometric-triangles
@@ -8,20 +8,20 @@ dashedName: problem-370-geometric-triangles
# --description--
-Let us define a geometric triangle as an integer sided triangle with sides a ≤ b ≤ c so that its sides form a geometric progression, i.e. b2 = a · c .
+Sia un triangolo geometrico un triangolo con lati interi con lati $a ≤ b ≤ c$ cossìcché i suoi lati formino una progressione geometrica, cioè $b^2 = a \times c$.
-An example of such a geometric triangle is the triangle with sides a = 144, b = 156 and c = 169.
+Un esempio di tale triangolo è il triangolo con lati $a = 144$, $b = 156$ e $c = 169$.
-There are 861805 geometric triangles with perimeter ≤ 106 .
+Ci sono $861\\,805$ triangoli geometrici con $\text{perimetro} ≤ {10}^6$.
-How many geometric triangles exist with perimeter ≤ 2.5·1013 ?
+Quanti triangoli geometrici esistono con $\text{perimetro} ≤ 2.5 \times {10}^{13}$?
# --hints--
-`euler370()` should return 41791929448408.
+`geometricTriangles()` dovrebbe restituire `41791929448408`.
```js
-assert.strictEqual(euler370(), 41791929448408);
+assert.strictEqual(geometricTriangles(), 41791929448408);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler370(), 41791929448408);
## --seed-contents--
```js
-function euler370() {
+function geometricTriangles() {
return true;
}
-euler370();
+geometricTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
index 005b5aaf07..cc2e62c6fd 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
@@ -1,6 +1,6 @@
---
id: 5900f4e01000cf542c50fff2
-title: 'Problem 371: Licence plates'
+title: 'Problema 371: Targhe'
challengeType: 5
forumTopicId: 302033
dashedName: problem-371-licence-plates
@@ -8,24 +8,24 @@ dashedName: problem-371-licence-plates
# --description--
-Oregon licence plates consist of three letters followed by a three digit number (each digit can be from \[0..9]).
+Le targhe dell'Oregon sono composte da tre lettere seguite da un numero a tre cifre (ciascuna cifra può essere in [0...9]).
-While driving to work Seth plays the following game:
+Mentre guida per andare a lavoro Seth gioca il seguente gioco:
-Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+Ogni volta che i numeri di due targhe visti nel suo viaggio si sommano a 1000, vince.
-E.g. MIC-012 and HAN-988 is a win and RYU-500 and SET-500 too. (as long as he sees them in the same trip).
+Ad es. `MIC-012` e `HAN-988` è una vittoria e `RYU-500` e `SET-500` anche. (finché li vede nello stesso viaggio).
-Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+Trova il numero previsto di targhe che ha bisogno di vedere per una vittoria. Dai la tua risposta approssimata a 8 cifre dopo il punto decimale.
-Note: We assume that each licence plate seen is equally likely to have any three digit number on it.
+**Nota:** Assumiamo che ogni targa vista ha la stessa probabilità di avere un qualsiasi numero di tre cifre su di essa.
# --hints--
-`euler371()` should return 40.66368097.
+`licensePlates()` dovrebbe restituire `40.66368097`.
```js
-assert.strictEqual(euler371(), 40.66368097);
+assert.strictEqual(licensePlates(), 40.66368097);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler371(), 40.66368097);
## --seed-contents--
```js
-function euler371() {
+function licensePlates() {
return true;
}
-euler371();
+licensePlates();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
index 1a04cacb71..1a21a55186 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff3
-title: 'Problem 372: Pencils of rays'
+title: 'Problema 372: Raggi di matite'
challengeType: 5
forumTopicId: 302034
dashedName: problem-372-pencils-of-rays
@@ -8,16 +8,20 @@ dashedName: problem-372-pencils-of-rays
# --description--
-Let R(M, N) be the number of lattice points (x, y) which satisfy M
+Sia $R(M, N)$ il numero di punti di reticolo ($x$, $y$) che soddisfa $M \lt x \le N$, $M \lt y \le N$ e $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ è dispari.
-Note: represents the floor function.
+Possiamo verificare che $R(0, 100) = 3\\,019$ e $R(100, 10\\,000) = 29\\,750\\,422$.
+
+Trova $R(2 \times {10}^6, {10}^9)$.
+
+**Nota:** $\lfloor x\rfloor$ è la funzione che arrotonda verso il basso.
# --hints--
-`euler372()` should return 301450082318807040.
+`pencilsOfRays()` dovrebbe restituire `301450082318807040`.
```js
-assert.strictEqual(euler372(), 301450082318807040);
+assert.strictEqual(pencilsOfRays(), 301450082318807040);
```
# --seed--
@@ -25,12 +29,12 @@ assert.strictEqual(euler372(), 301450082318807040);
## --seed-contents--
```js
-function euler372() {
+function pencilsOfRays() {
return true;
}
-euler372();
+pencilsOfRays();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
index 534c32ea25..fd6f508ef4 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff4
-title: 'Problem 373: Circumscribed Circles'
+title: 'Problema 373: Cerchi circoscritti'
challengeType: 5
forumTopicId: 302035
dashedName: problem-373-circumscribed-circles
@@ -8,22 +8,20 @@ dashedName: problem-373-circumscribed-circles
# --description--
-Every triangle has a circumscribed circle that goes through the three vertices.
+Ogni triangolo ha un cerchio circoscritto che attraversa i tre vertici. Considera tutti i triangoli a lati interi per i quali è intero anche il raggio del cerchio circoscritto.
-Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+Sia $S(n)$ la somma dei raggi dei cerchi circoscritti di tutti questi triangoli per i quali il raggio non supera $n$.
-Let S(n) be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed n.
+$S(100) = 4\\,950$ and $S(1\\,200) = 1\\,653\\,605$.
-S(100)=4950 and S(1200)=1653605.
-
-Find S(107).
+Trova $S({10}^7)$.
# --hints--
-`euler373()` should return 727227472448913.
+`circumscribedCircles()` dovrebbe restituire `727227472448913`.
```js
-assert.strictEqual(euler373(), 727227472448913);
+assert.strictEqual(circumscribedCircles(), 727227472448913);
```
# --seed--
@@ -31,12 +29,12 @@ assert.strictEqual(euler373(), 727227472448913);
## --seed-contents--
```js
-function euler373() {
+function circumscribedCircles() {
return true;
}
-euler373();
+circumscribedCircles();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
index 10fe621891..70ed56fae7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff6
-title: 'Problem 374: Maximum Integer Partition Product'
+title: 'Problema 374: Massimo prodotto di partizione di un numero intero'
challengeType: 5
forumTopicId: 302036
dashedName: problem-374-maximum-integer-partition-product
@@ -8,28 +8,30 @@ dashedName: problem-374-maximum-integer-partition-product
# --description--
-An integer partition of a number n is a way of writing n as a sum of positive integers.
+Una partizione intera di un numero $n$ è un modo di scrivere $n$ come una somma di numeri interi positivi.
-Partitions that differ only in the order of their summands are considered the same. A partition of n into distinct parts is a partition of n in which every part occurs at most once.
+Le partizioni che differiscono solo nell'ordine dei loro addendi sono considerate le stesse. Una partizione di $n$ in parti distinte è una partizione di $n$ in cui ogni parte si verifica al massimo una volta.
-The partitions of 5 into distinct parts are: 5, 4+1 and 3+2.
+Le partizioni in parti distinte di 5 sono:
-Let f(n) be the maximum product of the parts of any such partition of n into distinct parts and let m(n) be the number of elements of any such partition of n with that product.
+5, 4 + 1 e 3 + 2.
-So f(5)=6 and m(5)=2.
+Sia $f(n)$ il prodotto massimo delle parti di una tale partizione di $n$ in parti distinte e sia $m(n)$ il numero di elementi di una tale partizione di $n$ con quel prodotto.
-For n=10 the partition with the largest product is 10=2+3+5, which gives f(10)=30 and m(10)=3. And their product, f(10)·m(10) = 30·3 = 90
+Quindi $f(5) = 6$ e $m(5) = 2$.
-It can be verified that ∑f(n)·m(n) for 1 ≤ n ≤ 100 = 1683550844462.
+Per $n = 10$ la partizione con il prodotto più grande è $10 = 2 + 3 + 5$, che dà $f(10) = 30$ e $m(10) = 3$. E il loro prodotto, $f(10) \times m(10) = 30 \times 3 = 90$
-Find ∑f(n)·m(n) for 1 ≤ n ≤ 1014. Give your answer modulo 982451653, the 50 millionth prime.
+Si può verificare che $\sum f(n) \times m(n)$ for $1 ≤ n ≤ 100 = 1\\,683\\,550\\,844\\,462$.
+
+Trova $\sum f(n) \times m(n)$ for $1 ≤ n ≤ {10}^{14}$. Dai la tua risposta modulo $982\\,451\\,653$, il 50 millionesimo primo.
# --hints--
-`euler374()` should return 334420941.
+`maximumIntegerPartitionProduct()` dovrebbe restituire `334420941`.
```js
-assert.strictEqual(euler374(), 334420941);
+assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler374(), 334420941);
## --seed-contents--
```js
-function euler374() {
+function maximumIntegerPartitionProduct() {
return true;
}
-euler374();
+maximumIntegerPartitionProduct();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
index 684613a235..d02d316962 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4e41000cf542c50fff5
-title: 'Problem 375: Minimum of subsequences'
+title: 'Problema 375: Minimo delle sottosequenze'
challengeType: 5
forumTopicId: 302037
dashedName: problem-375-minimum-of-subsequences
@@ -8,30 +8,22 @@ dashedName: problem-375-minimum-of-subsequences
# --description--
-Let Sn be an integer sequence produced with the following pseudo-random number generator:
+Lascia che $S_n$ sia una sequenza intera prodotta con il seguente generatore di numeri pseudo-casuali:
-S0
+$$\begin{align} S_0 & = 290\\,797 \\\\ S_{n + 1} & = {S_n}^2\bmod 50\\,515\\,093 \end{align}$$
-=
+Sia $A(i, j)$ il minimo dei numeri $S_i, S_{i + 1}, \ldots, S_j$ per $i ≤ j$. Sia $M(N) = \sum A(i, j)$ per $1 ≤ i ≤ j ≤ N$.
-290797
+Possiamo verificare che $M(10) = 432\\,256\\,955$ e $M(10\\,000) = 3\\,264\\,567\\,774\\,119$.
-Sn+1
-
-=
-
-Sn2 mod 50515093
-
-Let A(i, j) be the minimum of the numbers Si, Si+1, ... , Sj for i ≤ j. Let M(N) = ΣA(i, j) for 1 ≤ i ≤ j ≤ N. We can verify that M(10) = 432256955 and M(10 000) = 3264567774119.
-
-Find M(2 000 000 000).
+Trova $M(2\\,000\\,000\\,000)$.
# --hints--
-`euler375()` should return 7435327983715286000.
+`minimumOfSubsequences()` dovrebbe restituire `7435327983715286000`.
```js
-assert.strictEqual(euler375(), 7435327983715286000);
+assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
```
# --seed--
@@ -39,12 +31,12 @@ assert.strictEqual(euler375(), 7435327983715286000);
## --seed-contents--
```js
-function euler375() {
+function minimumOfSubsequences() {
return true;
}
-euler375();
+minimumOfSubsequences();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
index b76c4d26e8..49d34bd6da 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff7
-title: 'Problem 376: Nontransitive sets of dice'
+title: 'Problema 376: Set di dadi non transitivo'
challengeType: 5
forumTopicId: 302038
dashedName: problem-376-nontransitive-sets-of-dice
@@ -8,30 +8,43 @@ dashedName: problem-376-nontransitive-sets-of-dice
# --description--
-Consider the following set of dice with nonstandard pips:
+Considera la seguente serie di dadi con pallini non standard:
-Die A: 1 4 4 4 4 4 Die B: 2 2 2 5 5 5 Die C: 3 3 3 3 3 6
+$$$\begin{array}{} \text{Dado A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{Dado B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Dado C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
-A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+Un gioco è giocato da due giocatori scegliendo un dado a turno e lanciandolo. Il giocatore che lancia il valore più alto vince.
-If the first player picks die A and the second player picks die B we get P(second player wins) = 7/12 > 1/2
+Se il primo giocatore sceglie dado $A$ e il secondo giocatore sceglie dado $B$ otteniamo
-If the first player picks die B and the second player picks die C we get P(second player wins) = 7/12 > 1/2
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die C and the second player picks die A we get P(second player wins) = 25/36 > 1/2
+Se il primo giocatore sceglie dado $B$ e il secondo giocatore sceglie dado $C$ otteniamo
-So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+$P(\text{secondo giocatore vince}) = \frac{7}{12} > \frac{1}{2}$
-We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:There are three six-sided dice with each side having between 1 and N pips, inclusive. Dice with the same set of pips are equal, regardless of which side on the die the pips are located. The same pip value may appear on multiple dice; if both players roll the same value neither player wins. The sets of dice {A,B,C}, {B,C,A} and {C,A,B} are the same set.
+Se il primo giocatore sceglie dado $C$ e il secondo giocatore sceglie dado $A$ otteniamo
-For N = 7 we find there are 9780 such sets. How many are there for N = 30 ?
+$P(\text{secondo giocatore vince}) = \frac{25}{36} > \frac{1}{2}$
+
+Quindi, qualunque scelta faccia il primo giocatore, il secondo giocatore può scegliere un altro dado e avere una probabilità maggiore del 50% di vittoria. Un set di dadi che hanno questa proprietà è chiamato un set di dadi non transitivi.
+
+Vogliamo indagare quanti insiemi di dadi non transitivi esistono. Assumeremo le seguenti condizioni:
+
+- Ci sono tre dadi a sei facce con ogni faccia che ha tra 1 e $N$ pallini, inclusi.
+- I dadi con lo stesso set di pallini sono uguali, indipendentemente dalla faccia del dado su cui i pallini sono situati.
+- Lo stesso valore di pallini può apparire su più dadi; se entrambi i giocatori lanciano lo stesso valore nessuno vince.
+- I set di dadi $\\{A, B, C\\}$, $\\{B, C, A\\}$ e $\\{C, A, B\\}$ sono lo stesso set.
+
+Per $N = 7$ troviamo 9780 set di questo tipo.
+
+Quanti ce ne sono per $N = 30$?
# --hints--
-`euler376()` should return 973059630185670.
+`nontransitiveSetsOfDice()` dovrebbe restituire `973059630185670`.
```js
-assert.strictEqual(euler376(), 973059630185670);
+assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
```
# --seed--
@@ -39,12 +52,12 @@ assert.strictEqual(euler376(), 973059630185670);
## --seed-contents--
```js
-function euler376() {
+function nontransitiveSetsOfDice() {
return true;
}
-euler376();
+nontransitiveSetsOfDice();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
index 660508c234..0b674e8a71 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff8
-title: 'Problem 377: Sum of digits, experience 13'
+title: 'Problema 377: Somma delle cifre, esperienza 13'
challengeType: 5
forumTopicId: 302039
dashedName: problem-377-sum-of-digits-experience-13
@@ -8,22 +8,22 @@ dashedName: problem-377-sum-of-digits-experience-13
# --description--
-There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+Ci sono 16 numeri interi positivi che non hanno uno 0 tra le loro cifre e che hanno una somma delle cifre uguale a 5:
-5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 e 11111.
-Their sum is 17891.
+La loro somma è 17891.
-Let f(n) be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to n.
+Sia $f(n)$ la somma di tutti i numeri interi positivi che non hanno uno zero tra le loro cifre e che hanno una somma delle cifre pari a $n$.
-Find $\\displaystyle \\sum\_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+Trova $\displaystyle\sum_{i=1}^{17} f(13^i)$. Dai le ultime 9 cifre della tua risposta.
# --hints--
-`euler377()` should return 732385277.
+`experience13()` dovrebbe restituire `732385277`.
```js
-assert.strictEqual(euler377(), 732385277);
+assert.strictEqual(experience13(), 732385277);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler377(), 732385277);
## --seed-contents--
```js
-function euler377() {
+function experience13() {
return true;
}
-euler377();
+experience13();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
index 22589747fe..0c8d5d5b65 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f4e61000cf542c50fff9
-title: 'Problem 378: Triangle Triples'
+title: 'Problema 378: tripli triangoli'
challengeType: 5
forumTopicId: 302040
dashedName: problem-378-triangle-triples
@@ -8,24 +8,20 @@ dashedName: problem-378-triangle-triples
# --description--
-Let T(n) be the nth triangle number, so T(n) =
+Sia $T(n)$ l'$n$-simo numero triangolare, quindi $T(n) = \frac{n(n + 1)}{2}$.
-n (n+1)2
+Sia $dT(n)$ il numero di divisori di $T(n)$. Esempio: $T(7) = 28$ e $dT(7) = 6$.
-.
+Sia $Tr(n)$ il numero di triplette ($i$, $j$, $k$) per cui $1 ≤ i < j < k ≤ n$ e $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5\\,772$ e $Tr(1000) = 11\\,174\\,776$.
-Let dT(n) be the number of divisors of T(n). E.g.: T(7) = 28 and dT(7) = 6.
-
-Let Tr(n) be the number of triples (i, j, k) such that 1 ≤ i < j < k ≤ n and dT(i) > dT(j) > dT(k). Tr(20) = 14, Tr(100) = 5772 and Tr(1000) = 11174776.
-
-Find Tr(60 000 000). Give the last 18 digits of your answer.
+Trova $Tr(60\\,000\\,000)$. Dai le ultime 18 cifre della tua risposta.
# --hints--
-`euler378()` should return 147534623725724700.
+`triangleTriples()` dovrebbe restituire `147534623725724700`.
```js
-assert.strictEqual(euler378(), 147534623725724700);
+assert.strictEqual(triangleTriples(), 147534623725724700);
```
# --seed--
@@ -33,12 +29,12 @@ assert.strictEqual(euler378(), 147534623725724700);
## --seed-contents--
```js
-function euler378() {
+function triangleTriples() {
return true;
}
-euler378();
+triangleTriples();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
index 3933d82ea2..7798debf82 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffa
-title: 'Problem 379: Least common multiple count'
+title: 'Problema 379: conteggio del minimo comune multiplo'
challengeType: 5
forumTopicId: 302041
dashedName: problem-379-least-common-multiple-count
@@ -8,20 +8,20 @@ dashedName: problem-379-least-common-multiple-count
# --description--
-Let f(n) be the number of couples (x,y) with x and y positive integers, x ≤ y and the least common multiple of x and y equal to n.
+Sia $f(n)$ il numero di coppie ($x$, $y$) con $x$ e $y$ numeri interi positivi, per cui $x ≤ y$ e il minimo comune multiplo di $x$ e $y$ è uguale a $n$.
-Let g be the summatory function of f, i.e.: g(n) = ∑ f(i) for 1 ≤ i ≤ n.
+Sia $g$ la funzione sommatoria di $f$, cioè $g(n) = \sum f(i)$ per $1 ≤ i ≤ n$.
-You are given that g(106) = 37429395.
+Ti è dato che $g({10}^6) = 37\\,429\\,395$.
-Find g(1012).
+Trova $g({10}^{12})$.
# --hints--
-`euler379()` should return 132314136838185.
+`leastCommonMultipleCount()` dovrebbe restituire `132314136838185`.
```js
-assert.strictEqual(euler379(), 132314136838185);
+assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler379(), 132314136838185);
## --seed-contents--
```js
-function euler379() {
+function leastCommonMultipleCount() {
return true;
}
-euler379();
+leastCommonMultipleCount();
```
# --solutions--
diff --git a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
index 8596f52fa7..2fa9c3c7b7 100644
--- a/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
+++ b/curriculum/challenges/italian/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffb
-title: 'Problem 380: Amazing Mazes!'
+title: 'Problema 380: fantastici labirinti!'
challengeType: 5
forumTopicId: 302044
dashedName: problem-380-amazing-mazes
@@ -8,20 +8,30 @@ dashedName: problem-380-amazing-mazes
# --description--
-An m×n maze is an m×n rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+Un labirinto $m×n$ è una griglia rettangolare $m×n$ con muri piazzati tra celle della griglia in modo tale che c'è un unico percorso dal quadrato in alto a sinistra a qualsiasi altro quadrato. I seguenti sono esempi di labirinti 9×12 e 15×20:
-Let C(m,n) be the number of distinct m×n mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+ -It can be verified that C(1,1) = 1, C(2,2) = 4, C(3,4) = 2415, and C(9,12) = 2.5720e46 (in scientific notation rounded to 5 significant digits). Find C(100,500) and write your answer in scientific notation rounded to 5 significant digits.
+Sia $C(m, n)$ il numero di labirinti distinti $m×n$. Labirinti che possono essere formati per rotazione e riflessione da un altro labirinto sono considerati distinti.
-When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be 1.2346e12.
+Si può verificare che $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, e $C(9, 12) = 2.5720\mathrm{e}\\,46$ (in notazione scientifica arrotondato a 5 cifre significative).
+
+Trova $C(100, 500)$ e scrivi la tua risposta come una stringa in notazione scientifica arrotondato a 5 cifre significative.
+
+Quando dai la tua risposta, usa una e minuscola per separare la mantissa e l'esponente. Ad es. se la risposta è 1234567891011 allora la risposta formattata sarebbe la stringa `1.2346e12`.
# --hints--
-`euler380()` should return Infinity.
+`amazingMazes()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler380(), Infinity);
+assert(typeof amazingMazes() === 'string');
+```
+
+`amazingMazes()` dovrebbe restituire la stringa `6.3202e25093`.
+
+```js
+assert.strictEqual(amazingMazes(), '6.3202e25093');
```
# --seed--
@@ -29,12 +39,12 @@ assert.strictEqual(euler380(), Infinity);
## --seed-contents--
```js
-function euler380() {
+function amazingMazes() {
return true;
}
-euler380();
+amazingMazes();
```
# --solutions--
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
index 21c6460649..a1b1526ba9 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
@@ -10,14 +10,9 @@ dashedName: arithmetic-formatter
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-arithmetic-formatter)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-小学校の算数では計算問題を解きやすくるために縦書きにすることが多くあります。 たとえば「235 + 52」を次のように記述します。
+Students in primary school often arrange arithmetic problems vertically to make them easier to solve. For example, "235 + 52" becomes:
```py
235
@@ -25,17 +20,17 @@ Python カリキュラムの対話式教育コンテンツを引き続き開発
-----
```
-計算問題を表す文字列のリストを受け取り、問題を縦書きに整形して返す関数を作成してください。 この関数はオプションで第 2 引数を受け取る必要があります。 第 2 引数が `True` に設定されている場合は、解答を表示する必要があります。
+Create a function that receives a list of strings that are arithmetic problems and returns the problems arranged vertically and side-by-side. The function should optionally take a second argument. When the second argument is set to `True`, the answers should be displayed.
## 例
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
```
-出力:
+Output:
```py
32 3801 45 123
@@ -43,13 +38,13 @@ arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
----- ------ ---- -----
```
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
```
-出力:
+Output:
```py
32 1 9999 523
@@ -60,35 +55,35 @@ arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
## ルール
-入力された問題が正しく整形されている場合、この関数は正しい変換結果を返します。それ以外の場合は、**ユーザーにとって意味のあるエラーを記述した****文字列**を返します。
+The function will return the correct conversion if the supplied problems are properly formatted, otherwise, it will **return** a **string** that describes an error that is meaningful to the user.
-- エラーを返す場合:
- - 関数に入力した**問題の数が多すぎる**場合。 上限を **5** つとし、それを超える場合は `Error: Too many problems.` (エラー: 問題が多すぎます) を返します。
- - 関数が受け取ることのできる適切な演算子は**足し算**と**引き算**です。 掛け算と割り算はエラーを返します。 この箇条書きで指示していない他の演算子についてはテストする必要はありません。 次のようなエラーを返します: `Error: Operator must be '+' or '-'.` (エラー: '+' または '-' の演算子を使用してください)。
- - 数値 (オペランド) にはそれぞれ数字のみを含める必要があります。 数値以外の場合、関数は次のエラーを返します: `Error: Numbers must only contain digits.` (エラー: 数値には数字のみを含める必要があります)。
- - それぞれのオペランド (演算子の両側の数値) の幅は最大 4 桁です。 それ以外の場合は、次のようなエラー文字列を返します: `Error: Numbers cannot be more than four digits.` (エラー: 数値は 4 桁以内にする必要があります)。
-- ユーザーが問題を正しい形式で入力した場合は、次のルールに従って変換結果を返します。
- - 演算子と、2 つのオペランドのうち最も長いオペランドとの間に、スペースを 1 つ含めます。演算子は 2 つ目のオペランドと同じ行に表示し、両方のオペランドは入力されたとおりの順序で表示します (1 つ目のオペランドを上側に、2 つ目のオペランドを下側に表示します)。
- - 数値は右揃えにする必要があります。
- - それぞれの問題の間に 4 つのスペースが必要です。
- - それぞれの問題の一番下にダッシュが必要です。 ダッシュは、各問題の全体の長さに沿った長さにする必要があります (上の表示例を参考にしてください)
+- Situations that will return an error:
+ - If there are **too many problems** supplied to the function. The limit is **five**, anything more will return: `Error: Too many problems.`
+ - The appropriate operators the function will accept are **addition** and **subtraction**. Multiplication and division will return an error. Other operators not mentioned in this bullet point will not need to be tested. The error returned will be: `Error: Operator must be '+' or '-'.`
+ - Each number (operand) should only contain digits. Otherwise, the function will return: `Error: Numbers must only contain digits.`
+ - Each operand (aka number on each side of the operator) has a max of four digits in width. Otherwise, the error string returned will be: `Error: Numbers cannot be more than four digits.`
+- If the user supplied the correct format of problems, the conversion you return will follow these rules:
+ - There should be a single space between the operator and the longest of the two operands, the operator will be on the same line as the second operand, both operands will be in the same order as provided (the first will be the top one and the second will be the bottom.
+ - Numbers should be right-aligned.
+ - There should be four spaces between each problem.
+ - There should be dashes at the bottom of each problem. The dashes should run along the entire length of each problem individually. (The example above shows what this should look like.)
## 開発
-`arithmetic_arranger.py` でコードを記述してください。 開発には `main.py` を使用して `arithmetic_arranger()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `arithmetic_arranger.py`. For development, you can use `main.py` to test your `arithmetic_arranger()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 `test_module.py` のテストを `main.py` で実行できるようになっています。 「実行」ボタンを押すと自動的にテストが実行されます。 または、コンソールに `pytest` と入力してテストを実行することもできます。
+The unit tests for this project are in `test_module.py`. We are running the tests from `test_module.py` in `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button. Alternatively you may run the tests by inputting `pytest` in the console.
## 提出
-プロジェクトの URL をコピーし、下記に提出してください。
+Copy your project's URL and submit it below.
# --hints--
-計算問題を正しく整形し、すべてのテストに合格する必要があります。
+It should correctly format an arithmetic problem and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
index 71548845e3..85c5ccb811 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
@@ -10,29 +10,23 @@ dashedName: budget-app
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-budget-app)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-`budget.py` の `Category` クラスを完成させてください。 *食費*、*服飾費*、*娯楽費*など、さまざまな予算のカテゴリに応じてオブジェクトをインスタンス化できるようにする必要があります。 オブジェクトを作成したら、カテゴリの名前をオブジェクトに渡します。 クラスには、リスト形式の帳簿となる `ledger` というインスタンス変数が必要です。 クラスには次のメソッドも含める必要があります。
+Complete the `Category` class in `budget.py`. It should be able to instantiate objects based on different budget categories like *food*, *clothing*, and *entertainment*. When objects are created, they are passed in the name of the category. The class should have an instance variable called `ledger` that is a list. The class should also contain the following methods:
-- `deposit` (預け入れ) メソッド。金額と説明を受け取ります。 説明がない場合は、デフォルトで空の文字列にします。 このメソッドでは、`{"amount": amount, "description": description}` という形式で帳簿リストの末尾にオブジェクトを追加する必要があります。
-- `withdraw` (引き出し) メソッド。`deposit` メソッドに似ていますが、渡された金額を負数として帳簿に保存する必要があります。 十分な資金がない場合は、帳簿に何も追加しないでください。 このメソッドは、引き出しが行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `get_balance` (残高確認) メソッド。発生した入出金に基づいて予算カテゴリの現在の残高を返します。
-- `transfer` (送金) メソッド。引数として金額と別の予算カテゴリを受け取ります。 このメソッドでは、金額と "Transfer to [Destination Budget Category]" ([送金先の予算カテゴリ] への送金) という記述からなる出金を追加する必要があります。 このメソッドによって、金額と "Transfer to [Destination Budget Category]" という記述からなる入金額が他の予算カテゴリに追加されます。 十分な資金がない場合は、どちらの帳簿にも何も追加しないでください。 このメソッドは、送金が行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `check_funds` (資金確認) メソッド。引数として金額を受け取ります。 金額が予算カテゴリの残高よりも大きい場合は `False` を返し、それ以外の場合は `True` を返します。 このメソッドは `withdraw` メソッドと `transfer` メソッドの両方で使用する必要があります。
+- A `deposit` method that accepts an amount and description. If no description is given, it should default to an empty string. The method should append an object to the ledger list in the form of `{"amount": amount, "description": description}`.
+- A `withdraw` method that is similar to the `deposit` method, but the amount passed in should be stored in the ledger as a negative number. If there are not enough funds, nothing should be added to the ledger. This method should return `True` if the withdrawal took place, and `False` otherwise.
+- A `get_balance` method that returns the current balance of the budget category based on the deposits and withdrawals that have occurred.
+- A `transfer` method that accepts an amount and another budget category as arguments. The method should add a withdrawal with the amount and the description "Transfer to [Destination Budget Category]". The method should then add a deposit to the other budget category with the amount and the description "Transfer from [Source Budget Category]". If there are not enough funds, nothing should be added to either ledgers. This method should return `True` if the transfer took place, and `False` otherwise.
+- A `check_funds` method that accepts an amount as an argument. It returns `False` if the amount is greater than the balance of the budget category and returns `True` otherwise. This method should be used by both the `withdraw` method and `transfer` method.
-予算オブジェクトを出力するときは次のように表示する必要があります。
+When the budget object is printed it should display:
-- 30 文字のタイトル行。`*` 文字を並べて 1 行とし、中央にカテゴリの名前を置きます。
-- 帳簿にある品目のリスト。 各行に説明と金額を表示します。 説明の最初の 23 文字を表示し、その後に金額を表示します。 金額は右揃えで、小数点以下 2 桁までを含み、最大 7 文字まで表示します。
-- カテゴリの合計を表示する行。
+- A title line of 30 characters where the name of the category is centered in a line of `*` characters.
+- A list of the items in the ledger. Each line should show the description and amount. The first 23 characters of the description should be displayed, then the amount. The amount should be right aligned, contain two decimal places, and display a maximum of 7 characters.
+- A line displaying the category total.
-出力の例を次に示します。
+Here is an example of the output:
```bash
*************Food*************
@@ -43,13 +37,13 @@ Transfer to Clothing -50.00
Total: 923.96
```
-`Category` クラスの他に、カテゴリのリストを引数に取る `create_spend_chart` という関数を (クラスの外で) 作成してください。 この関数は棒グラフとなる文字列を返す必要があります。
+Besides the `Category` class, create a function (outside of the class) called `create_spend_chart` that takes a list of categories as an argument. It should return a string that is a bar chart.
-グラフでは、関数に渡された各カテゴリについて、その出費の割合を表示する必要があります。 出費の割合は、引き出し額でのみ計算する必要があり、預け入れ額では計算しません。 グラフの左下には 0 ~ 100 のラベルを付ける必要があります。 棒グラフの「棒」は文字 "o" を使用して作成する必要があります。 各棒の高さは最も近い 10 に切り下げる必要があります。 グラフの下の水平線は最後の棒からスペース 2 つ分だけ離す必要があります。 各カテゴリ名は棒の下に垂直に記述する必要があります。 一番上には "Percentage spent by category" (カテゴリ別の出費の割合) というタイトルを付ける必要があります。
+The chart should show the percentage spent in each category passed in to the function. The percentage spent should be calculated only with withdrawals and not with deposits. Down the left side of the chart should be labels 0 - 100. The "bars" in the bar chart should be made out of the "o" character. The height of each bar should be rounded down to the nearest 10. The horizontal line below the bars should go two spaces past the final bar. Each category name should be written vertically below the bar. There should be a title at the top that says "Percentage spent by category".
-この関数は最大 4 つのカテゴリでテストされます。
+This function will be tested with up to four categories.
-次の出力例を参考にして、出力の間隔を例と正確に合わせてください。
+Look at the example output below very closely and make sure the spacing of the output matches the example exactly.
```bash
Percentage spent by category
@@ -75,23 +69,23 @@ Percentage spent by category
g
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`budget.py` でコードを記述してください。 開発には `main.py` を使用して `Category` クラスをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `budget.py`. For development, you can use `main.py` to test your `Category` class. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Category クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Category class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
index 6719641228..5d230fc031 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
@@ -10,37 +10,31 @@ dashedName: polygon-area-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-polygon-area-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-このプロジェクトでは、オブジェクト指向プログラミングを使用して、Rectangle クラスと Square クラスを作成します。 Square クラスは Rectangle のサブクラスであり、メソッドと属性を継承する必要があります。
+In this project you will use object oriented programming to create a Rectangle class and a Square class. The Square class should be a subclass of Rectangle and inherit methods and attributes.
## Rectangle クラス
-Rectangle オブジェクトが作成されるときは、`width` 属性と `height` 属性で初期化する必要があります。 クラスには、次のメソッドも含める必要があります。
+When a Rectangle object is created, it should be initialized with `width` and `height` attributes. The class should also contain the following methods:
- `set_width`
- `set_height`
-- `get_area`: 面積を返します (`width * height`)
-- `get_perimeter`: 外周を返します (`2 * width + 2 * height`)
-- `get_diagonal`: 対角線を返します(`(width ** 2 + height ** 2) ** .5`)
-- `get_picture`: "\*" の行を使用して図形を表す文字列を返します。 行数は高さと等しく、各行の"\*"の数は幅と等しくする必要があります。 各行の末尾に改行 (`\n`) が必要です。 幅または高さが 50 より大きい場合は、文字列 "Too big for picture." を返す必要があります。
-- `get_amount_inside`: 引数として別の図形 (正方形または長方形) を受け取ります。 渡された図形が、その図形の中に何個収まるかを返します (回転はしません)。 たとえば、幅が 4 で高さが 8 の長方形には、一辺が 4 の正方形が 2つ収まります。
+- `get_area`: Returns area (`width * height`)
+- `get_perimeter`: Returns perimeter (`2 * width + 2 * height`)
+- `get_diagonal`: Returns diagonal (`(width ** 2 + height ** 2) ** .5`)
+- `get_picture`: Returns a string that represents the shape using lines of "\*". The number of lines should be equal to the height and the number of "\*" in each line should be equal to the width. There should be a new line (`\n`) at the end of each line. If the width or height is larger than 50, this should return the string: "Too big for picture.".
+- `get_amount_inside`: Takes another shape (square or rectangle) as an argument. Returns the number of times the passed in shape could fit inside the shape (with no rotations). For instance, a rectangle with a width of 4 and a height of 8 could fit in two squares with sides of 4.
-また、Rectangle のインスタンスを文字列として表現する場合は、`Rectangle(width=5, height=10)` のようにする必要があります。
+Additionally, if an instance of a Rectangle is represented as a string, it should look like: `Rectangle(width=5, height=10)`
## Square クラス
-Square クラスは Rectangle のサブクラスである必要があります。 Square オブジェクトが生成されるときは、一辺の長さを渡します。 `__init__` メソッドでは、一辺の長さを Rectangle クラスの `width` 属性と `height` 属性の両方に格納する必要があります。
+The Square class should be a subclass of Rectangle. When a Square object is created, a single side length is passed in. The `__init__` method should store the side length in both the `width` and `height` attributes from the Rectangle class.
-Square クラスは、Rectangle クラスのメソッドにアクセスできる必要があり、加えて `set_side` メソッドも含める必要があります。 Square のインスタンスを文字列として表現する場合は、`Square(side=9)` のようにする必要があります。
+The Square class should be able to access the Rectangle class methods but should also contain a `set_side` method. If an instance of a Square is represented as a string, it should look like: `Square(side=9)`
-また、Square クラスの `set_width` と `set_height` メソッドでは、幅と高さの両方を設定する必要があります。
+Additionally, the `set_width` and `set_height` methods on the Square class should set both the width and height.
## 使用例
@@ -64,7 +58,7 @@ rect.set_width(16)
print(rect.get_amount_inside(sq))
```
-上記のコードは次を返す必要があります。
+That code should return:
```bash
50
@@ -85,23 +79,23 @@ Square(side=4)
8
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`shape_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `shape_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `shape_calculator.py`. For development, you can use `main.py` to test your `shape_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Rectangle クラスと Square クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Rectangle class and Square class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
index a4f59e83b4..923413b43f 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
@@ -10,19 +10,13 @@ dashedName: probability-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-probability-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-帽子があり、その中に青いボールが 5 個、赤いボールが 4 個、緑のボールが 2 個入っているとします。 4 個のボールを無作為に取り出す場合、赤のボールが 1 個以上、緑のボールが 2 個含まれる確率は、いくらになりますか? 高度な数学を駆使して確率を計算することも可能ですが、多数の実験を実行しておおよその確率を推定するプログラムを記述する方が簡単です。
+Suppose there is a hat containing 5 blue balls, 4 red balls, and 2 green balls. What is the probability that a random draw of 4 balls will contain at least 1 red ball and 2 green balls? While it would be possible to calculate the probability using advanced mathematics, an easier way is to write a program to perform a large number of experiments to estimate an approximate probability.
-このプロジェクトでは、特定のボールを帽子から無作為に取り出す場合のおおよその確率を調べるプログラムを作成します。
+For this project, you will write a program to determine the approximate probability of drawing certain balls randomly from a hat.
-まず、`prob_calculator.py` で `Hat` クラスを作成してください。 このクラスは、帽子に入っている各色のボールの数を指定する可変個の引数を受け取る必要があります。 たとえば、次のどの方法でもクラスオブジェクトを作成することができます。
+First, create a `Hat` class in `prob_calculator.py`. The class should take a variable number of arguments that specify the number of balls of each color that are in the hat. For example, a class object could be created in any of these ways:
```py
hat1 = Hat(yellow=3, blue=2, green=6)
@@ -30,22 +24,22 @@ hat2 = Hat(red=5, orange=4)
hat3 = Hat(red=5, orange=4, black=1, blue=0, pink=2, striped=9)
```
-帽子は常に、少なくとも 1 個のボールが入った状態で作成されます。 作成時に帽子オブジェクトに渡された引数を、`contents` インスタンス変数に変換する必要があります。 `contents` は、帽子に入っているボールごとにアイテムを 1 つずつ含む文字列のリストである必要があります。 リスト内の各アイテムは、その色のボール 1 個分を表す色の名前である必要があります。 たとえば、帽子が `{"red": 2, "blue": 1}` の場合、`contents` は `["red", "red", "blue"]` になる必要があります。
+A hat will always be created with at least one ball. The arguments passed into the hat object upon creation should be converted to a `contents` instance variable. `contents` should be a list of strings containing one item for each ball in the hat. Each item in the list should be a color name representing a single ball of that color. For example, if your hat is `{"red": 2, "blue": 1}`, `contents` should be `["red", "red", "blue"]`.
-`Hat` クラスには `draw` メソッドが必要です。このメソッドは、帽子から取り出すボールの個数を示す引数を受け取ります。 draw メソッドは、`contents` からボールを無作為に取り除き、それらのボールを文字列のリストとして返す必要があります。 交換のできない壺の実験と同様に、取り出したボールは帽子に戻さないものとします。 取り出すボールの数が利用可能な数を超える場合は、すべてのボールを返してください。
+The `Hat` class should have a `draw` method that accepts an argument indicating the number of balls to draw from the hat. This method should remove balls at random from `contents` and return those balls as a list of strings. The balls should not go back into the hat during the draw, similar to an urn experiment without replacement. If the number of balls to draw exceeds the available quantity, return all the balls.
-次に、(`Hat` クラスの中ではなく) `prob_calculator.py` で `experiment` 関数を作成してください。 この関数は次の引数を受け取る必要があります。
+Next, create an `experiment` function in `prob_calculator.py` (not inside the `Hat` class). This function should accept the following arguments:
-- `hat`: 関数内でコピーする必要のあるボールを含む帽子オブジェクト。
-- `expected_balls`: 実験で帽子から取り出そうとするボールの正確なグループを示すオブジェクト。 たとえば、青のボール 2 個と赤のボール 1 個を帽子から取り出す確率を調べるには、`expected_balls` を `{"blue":2, "red":1}` に設定します。
-- `num_balls_drawn`: 各実験で帽子から取り出すボールの数。
-- `num_experiments`: 実行する実験の回数 (実験の回数が多いほど、おおよその確率の正確性が高まります)。
+- `hat`: A hat object containing balls that should be copied inside the function.
+- `expected_balls`: An object indicating the exact group of balls to attempt to draw from the hat for the experiment. For example, to determine the probability of drawing 2 blue balls and 1 red ball from the hat, set `expected_balls` to `{"blue":2, "red":1}`.
+- `num_balls_drawn`: The number of balls to draw out of the hat in each experiment.
+- `num_experiments`: The number of experiments to perform. (The more experiments performed, the more accurate the approximate probability will be.)
-`experiment` 関数は、確率を返す必要があります。
+The `experiment` function should return a probability.
-たとえば、黒を 6 個、赤を 4 個、緑を 3 個含む帽子から 5 個のボールを取り出す場合に、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個含まれる確率を求めたいとしましょう。 それには、`N` 回の実験を行い、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個になった回数 `M` を数え、確率を `M/N` として推定します。 実験ではそれぞれ、指定されたボールの入った帽子の状態から始め、いくつかのボールを取り出し、期待されるボールを取り出したかどうかを確認します。
+For example, let's say that you want to determine the probability of getting at least 2 red balls and 1 green ball when you draw 5 balls from a hat containing 6 black, 4 red, and 3 green. To do this, we perform `N` experiments, count how many times `M` we get at least 2 red balls and 1 green ball, and estimate the probability as `M/N`. Each experiment consists of starting with a hat containing the specified balls, drawing a number of balls, and checking if we got the balls we were attempting to draw.
-上記の例で 2000 回の実験を行う場合は、`experiment` 関数を次のように呼び出します。
+Here is how you would call the `experiment` function based on the example above with 2000 experiments:
```py
hat = Hat(black=6, red=4, green=3)
@@ -55,27 +49,27 @@ probability = experiment(hat=hat,
num_experiments=2000)
```
-この方法は無作為抽出に基づいているため、コードが実行されるたびに確率が多少変わります。
+Since this is based on random draws, the probability will be slightly different each time the code is run.
-*ヒント: `prob_calculator.py` の先頭ですでにインポートされているモジュールを使用することを検討してください。 `prob_calculator.py` の中で乱数シードを初期化しないでください。*
+*Hint: Consider using the modules that are already imported at the top of `prob_calculator.py`. Do not initialize random seed within `prob_calculator.py`.*
## 開発
-`prob_calculator.py` でコードを記述してください。 開発には `main.py` を使用してコードをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `prob_calculator.py`. For development, you can use `main.py` to test your code. Click the "run" button and `main.py` will run.
-ボイラープレートには `copy` モジュールと `random` モジュール用の `import` ステートメントが含まれています。 これらをプロジェクトで使用することを検討してください。
+The boilerplate includes `import` statements for the `copy` and `random` modules. Consider using those in your project.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-確率を正しく計算し、すべてのテストに合格する必要があります。
+It should correctly calculate probabilities and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
index 1b8344540a..7b7bcfcad1 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
@@ -10,27 +10,21 @@ dashedName: time-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-time-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-下記に示す 2 つの必須パラメーターと 1 つのオプションパラメーターを受け取る関数 `add_time` を記述してください。
+Write a function named `add_time` that takes in two required parameters and one optional parameter:
-- 12 時制形式の開始時刻 (末尾に AM または PM)
-- 時数と分数で示される経過時間
-- (オプション) 開始の曜日 (大文字小文字の記述は自由)
+- a start time in the 12-hour clock format (ending in AM or PM)
+- a duration time that indicates the number of hours and minutes
+- (optional) a starting day of the week, case insensitive
-関数は、経過時間を開始時刻に追加し、その結果を返す必要があります。
+The function should add the duration time to the start time and return the result.
-結果が翌日になる場合は、時刻の後に `(next day)` (翌日) を表示する必要があります。 結果が翌日以降になる場合は、時刻の後に `(n days later)` (n 日後) を表示する必要があります。ここで "n" は何日後かを示します。
+If the result will be the next day, it should show `(next day)` after the time. If the result will be more than one day later, it should show `(n days later)` after the time, where "n" is the number of days later.
-関数にオプションの開始曜日パラメーターが与えられた場合は、結果の曜日を出力に表示する必要があります。 出力する曜日は、時刻の後、「n 日後」の前に表示する必要があります。
+If the function is given the optional starting day of the week parameter, then the output should display the day of the week of the result. The day of the week in the output should appear after the time and before the number of days later.
-関数が扱うさまざまなケースの例を次に示します。 結果のスペースと句読点の表示に特に注意を払ってください。
+Below are some examples of different cases the function should handle. Pay close attention to the spacing and punctuation of the results.
```py
add_time("3:00 PM", "3:10")
@@ -52,23 +46,23 @@ add_time("6:30 PM", "205:12")
# Returns: 7:42 AM (9 days later)
```
-Python ライブラリをインポートしないでください。 開始時刻は有効な時刻であると仮定します。 経過時間の分数は 60 未満の整数になりますが、時数は任意の整数になります。
+Do not import any Python libraries. Assume that the start times are valid times. The minutes in the duration time will be a whole number less than 60, but the hour can be any whole number.
## 開発
-`time_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `time_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `time_calculator.py`. For development, you can use `main.py` to test your `time_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-正確に時間を追加し、すべてのテストに合格する必要があります。
+It should correctly add times and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
index 3bbff2c99e..9be6dd072f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
@@ -8,7 +8,7 @@ dashedName: problem-344-silver-dollar-game
# --description--
-ニコラース・ホーヴァート・ ド・ブラウンの銀貨ゲームにはいくつかバリエーションがあり、その一つは次のように説明されます。
+One variant of N.G. de Bruijn's silver dollar game can be described as follows:
マスが並ぶ細長い盤上に硬貨が何枚か置かれています (1 マスにたかだか 1 枚)。 銀貨 (1 ドル硬貨) と呼ばれる 1 枚しかない硬貨に、任意の価値があります。 2 人のプレイヤーが交互にプレイします。 各ターンで、プレイヤーは通常の移動または特別な移動を行う必要があります。
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
index 81a2c58f4a..0468ec26fd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
@@ -8,7 +8,7 @@ dashedName: problem-250-250250
# --description--
-Encontre o número de subconjuntos não vazios de $\\{11, 22, 33, \ldots, {250250}^{250250}\\}$, cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
+Encontre o número de subconjuntos não vazios de $\\{{1}^{1}, {2}^{2}, {3}^{3}, \ldots, {250250}^{250250}\\}$ cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
# --hints--
-It can be verified that C(1,1) = 1, C(2,2) = 4, C(3,4) = 2415, and C(9,12) = 2.5720e46 (in scientific notation rounded to 5 significant digits). Find C(100,500) and write your answer in scientific notation rounded to 5 significant digits.
+Sia $C(m, n)$ il numero di labirinti distinti $m×n$. Labirinti che possono essere formati per rotazione e riflessione da un altro labirinto sono considerati distinti.
-When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be 1.2346e12.
+Si può verificare che $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, e $C(9, 12) = 2.5720\mathrm{e}\\,46$ (in notazione scientifica arrotondato a 5 cifre significative).
+
+Trova $C(100, 500)$ e scrivi la tua risposta come una stringa in notazione scientifica arrotondato a 5 cifre significative.
+
+Quando dai la tua risposta, usa una e minuscola per separare la mantissa e l'esponente. Ad es. se la risposta è 1234567891011 allora la risposta formattata sarebbe la stringa `1.2346e12`.
# --hints--
-`euler380()` should return Infinity.
+`amazingMazes()` dovrebbe restituire una stringa.
```js
-assert.strictEqual(euler380(), Infinity);
+assert(typeof amazingMazes() === 'string');
+```
+
+`amazingMazes()` dovrebbe restituire la stringa `6.3202e25093`.
+
+```js
+assert.strictEqual(amazingMazes(), '6.3202e25093');
```
# --seed--
@@ -29,12 +39,12 @@ assert.strictEqual(euler380(), Infinity);
## --seed-contents--
```js
-function euler380() {
+function amazingMazes() {
return true;
}
-euler380();
+amazingMazes();
```
# --solutions--
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
index 21c6460649..a1b1526ba9 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/arithmetic-formatter.md
@@ -10,14 +10,9 @@ dashedName: arithmetic-formatter
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-arithmetic-formatter)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-小学校の算数では計算問題を解きやすくるために縦書きにすることが多くあります。 たとえば「235 + 52」を次のように記述します。
+Students in primary school often arrange arithmetic problems vertically to make them easier to solve. For example, "235 + 52" becomes:
```py
235
@@ -25,17 +20,17 @@ Python カリキュラムの対話式教育コンテンツを引き続き開発
-----
```
-計算問題を表す文字列のリストを受け取り、問題を縦書きに整形して返す関数を作成してください。 この関数はオプションで第 2 引数を受け取る必要があります。 第 2 引数が `True` に設定されている場合は、解答を表示する必要があります。
+Create a function that receives a list of strings that are arithmetic problems and returns the problems arranged vertically and side-by-side. The function should optionally take a second argument. When the second argument is set to `True`, the answers should be displayed.
## 例
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
```
-出力:
+Output:
```py
32 3801 45 123
@@ -43,13 +38,13 @@ arithmetic_arranger(["32 + 698", "3801 - 2", "45 + 43", "123 + 49"])
----- ------ ---- -----
```
-関数呼び出し:
+Function Call:
```py
arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
```
-出力:
+Output:
```py
32 1 9999 523
@@ -60,35 +55,35 @@ arithmetic_arranger(["32 + 8", "1 - 3801", "9999 + 9999", "523 - 49"], True)
## ルール
-入力された問題が正しく整形されている場合、この関数は正しい変換結果を返します。それ以外の場合は、**ユーザーにとって意味のあるエラーを記述した****文字列**を返します。
+The function will return the correct conversion if the supplied problems are properly formatted, otherwise, it will **return** a **string** that describes an error that is meaningful to the user.
-- エラーを返す場合:
- - 関数に入力した**問題の数が多すぎる**場合。 上限を **5** つとし、それを超える場合は `Error: Too many problems.` (エラー: 問題が多すぎます) を返します。
- - 関数が受け取ることのできる適切な演算子は**足し算**と**引き算**です。 掛け算と割り算はエラーを返します。 この箇条書きで指示していない他の演算子についてはテストする必要はありません。 次のようなエラーを返します: `Error: Operator must be '+' or '-'.` (エラー: '+' または '-' の演算子を使用してください)。
- - 数値 (オペランド) にはそれぞれ数字のみを含める必要があります。 数値以外の場合、関数は次のエラーを返します: `Error: Numbers must only contain digits.` (エラー: 数値には数字のみを含める必要があります)。
- - それぞれのオペランド (演算子の両側の数値) の幅は最大 4 桁です。 それ以外の場合は、次のようなエラー文字列を返します: `Error: Numbers cannot be more than four digits.` (エラー: 数値は 4 桁以内にする必要があります)。
-- ユーザーが問題を正しい形式で入力した場合は、次のルールに従って変換結果を返します。
- - 演算子と、2 つのオペランドのうち最も長いオペランドとの間に、スペースを 1 つ含めます。演算子は 2 つ目のオペランドと同じ行に表示し、両方のオペランドは入力されたとおりの順序で表示します (1 つ目のオペランドを上側に、2 つ目のオペランドを下側に表示します)。
- - 数値は右揃えにする必要があります。
- - それぞれの問題の間に 4 つのスペースが必要です。
- - それぞれの問題の一番下にダッシュが必要です。 ダッシュは、各問題の全体の長さに沿った長さにする必要があります (上の表示例を参考にしてください)
+- Situations that will return an error:
+ - If there are **too many problems** supplied to the function. The limit is **five**, anything more will return: `Error: Too many problems.`
+ - The appropriate operators the function will accept are **addition** and **subtraction**. Multiplication and division will return an error. Other operators not mentioned in this bullet point will not need to be tested. The error returned will be: `Error: Operator must be '+' or '-'.`
+ - Each number (operand) should only contain digits. Otherwise, the function will return: `Error: Numbers must only contain digits.`
+ - Each operand (aka number on each side of the operator) has a max of four digits in width. Otherwise, the error string returned will be: `Error: Numbers cannot be more than four digits.`
+- If the user supplied the correct format of problems, the conversion you return will follow these rules:
+ - There should be a single space between the operator and the longest of the two operands, the operator will be on the same line as the second operand, both operands will be in the same order as provided (the first will be the top one and the second will be the bottom.
+ - Numbers should be right-aligned.
+ - There should be four spaces between each problem.
+ - There should be dashes at the bottom of each problem. The dashes should run along the entire length of each problem individually. (The example above shows what this should look like.)
## 開発
-`arithmetic_arranger.py` でコードを記述してください。 開発には `main.py` を使用して `arithmetic_arranger()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `arithmetic_arranger.py`. For development, you can use `main.py` to test your `arithmetic_arranger()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 `test_module.py` のテストを `main.py` で実行できるようになっています。 「実行」ボタンを押すと自動的にテストが実行されます。 または、コンソールに `pytest` と入力してテストを実行することもできます。
+The unit tests for this project are in `test_module.py`. We are running the tests from `test_module.py` in `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button. Alternatively you may run the tests by inputting `pytest` in the console.
## 提出
-プロジェクトの URL をコピーし、下記に提出してください。
+Copy your project's URL and submit it below.
# --hints--
-計算問題を正しく整形し、すべてのテストに合格する必要があります。
+It should correctly format an arithmetic problem and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
index 71548845e3..85c5ccb811 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/budget-app.md
@@ -10,29 +10,23 @@ dashedName: budget-app
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-budget-app)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-`budget.py` の `Category` クラスを完成させてください。 *食費*、*服飾費*、*娯楽費*など、さまざまな予算のカテゴリに応じてオブジェクトをインスタンス化できるようにする必要があります。 オブジェクトを作成したら、カテゴリの名前をオブジェクトに渡します。 クラスには、リスト形式の帳簿となる `ledger` というインスタンス変数が必要です。 クラスには次のメソッドも含める必要があります。
+Complete the `Category` class in `budget.py`. It should be able to instantiate objects based on different budget categories like *food*, *clothing*, and *entertainment*. When objects are created, they are passed in the name of the category. The class should have an instance variable called `ledger` that is a list. The class should also contain the following methods:
-- `deposit` (預け入れ) メソッド。金額と説明を受け取ります。 説明がない場合は、デフォルトで空の文字列にします。 このメソッドでは、`{"amount": amount, "description": description}` という形式で帳簿リストの末尾にオブジェクトを追加する必要があります。
-- `withdraw` (引き出し) メソッド。`deposit` メソッドに似ていますが、渡された金額を負数として帳簿に保存する必要があります。 十分な資金がない場合は、帳簿に何も追加しないでください。 このメソッドは、引き出しが行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `get_balance` (残高確認) メソッド。発生した入出金に基づいて予算カテゴリの現在の残高を返します。
-- `transfer` (送金) メソッド。引数として金額と別の予算カテゴリを受け取ります。 このメソッドでは、金額と "Transfer to [Destination Budget Category]" ([送金先の予算カテゴリ] への送金) という記述からなる出金を追加する必要があります。 このメソッドによって、金額と "Transfer to [Destination Budget Category]" という記述からなる入金額が他の予算カテゴリに追加されます。 十分な資金がない場合は、どちらの帳簿にも何も追加しないでください。 このメソッドは、送金が行われた場合は `True` を返し、それ以外の場合は `False` を返す必要があります。
-- `check_funds` (資金確認) メソッド。引数として金額を受け取ります。 金額が予算カテゴリの残高よりも大きい場合は `False` を返し、それ以外の場合は `True` を返します。 このメソッドは `withdraw` メソッドと `transfer` メソッドの両方で使用する必要があります。
+- A `deposit` method that accepts an amount and description. If no description is given, it should default to an empty string. The method should append an object to the ledger list in the form of `{"amount": amount, "description": description}`.
+- A `withdraw` method that is similar to the `deposit` method, but the amount passed in should be stored in the ledger as a negative number. If there are not enough funds, nothing should be added to the ledger. This method should return `True` if the withdrawal took place, and `False` otherwise.
+- A `get_balance` method that returns the current balance of the budget category based on the deposits and withdrawals that have occurred.
+- A `transfer` method that accepts an amount and another budget category as arguments. The method should add a withdrawal with the amount and the description "Transfer to [Destination Budget Category]". The method should then add a deposit to the other budget category with the amount and the description "Transfer from [Source Budget Category]". If there are not enough funds, nothing should be added to either ledgers. This method should return `True` if the transfer took place, and `False` otherwise.
+- A `check_funds` method that accepts an amount as an argument. It returns `False` if the amount is greater than the balance of the budget category and returns `True` otherwise. This method should be used by both the `withdraw` method and `transfer` method.
-予算オブジェクトを出力するときは次のように表示する必要があります。
+When the budget object is printed it should display:
-- 30 文字のタイトル行。`*` 文字を並べて 1 行とし、中央にカテゴリの名前を置きます。
-- 帳簿にある品目のリスト。 各行に説明と金額を表示します。 説明の最初の 23 文字を表示し、その後に金額を表示します。 金額は右揃えで、小数点以下 2 桁までを含み、最大 7 文字まで表示します。
-- カテゴリの合計を表示する行。
+- A title line of 30 characters where the name of the category is centered in a line of `*` characters.
+- A list of the items in the ledger. Each line should show the description and amount. The first 23 characters of the description should be displayed, then the amount. The amount should be right aligned, contain two decimal places, and display a maximum of 7 characters.
+- A line displaying the category total.
-出力の例を次に示します。
+Here is an example of the output:
```bash
*************Food*************
@@ -43,13 +37,13 @@ Transfer to Clothing -50.00
Total: 923.96
```
-`Category` クラスの他に、カテゴリのリストを引数に取る `create_spend_chart` という関数を (クラスの外で) 作成してください。 この関数は棒グラフとなる文字列を返す必要があります。
+Besides the `Category` class, create a function (outside of the class) called `create_spend_chart` that takes a list of categories as an argument. It should return a string that is a bar chart.
-グラフでは、関数に渡された各カテゴリについて、その出費の割合を表示する必要があります。 出費の割合は、引き出し額でのみ計算する必要があり、預け入れ額では計算しません。 グラフの左下には 0 ~ 100 のラベルを付ける必要があります。 棒グラフの「棒」は文字 "o" を使用して作成する必要があります。 各棒の高さは最も近い 10 に切り下げる必要があります。 グラフの下の水平線は最後の棒からスペース 2 つ分だけ離す必要があります。 各カテゴリ名は棒の下に垂直に記述する必要があります。 一番上には "Percentage spent by category" (カテゴリ別の出費の割合) というタイトルを付ける必要があります。
+The chart should show the percentage spent in each category passed in to the function. The percentage spent should be calculated only with withdrawals and not with deposits. Down the left side of the chart should be labels 0 - 100. The "bars" in the bar chart should be made out of the "o" character. The height of each bar should be rounded down to the nearest 10. The horizontal line below the bars should go two spaces past the final bar. Each category name should be written vertically below the bar. There should be a title at the top that says "Percentage spent by category".
-この関数は最大 4 つのカテゴリでテストされます。
+This function will be tested with up to four categories.
-次の出力例を参考にして、出力の間隔を例と正確に合わせてください。
+Look at the example output below very closely and make sure the spacing of the output matches the example exactly.
```bash
Percentage spent by category
@@ -75,23 +69,23 @@ Percentage spent by category
g
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`budget.py` でコードを記述してください。 開発には `main.py` を使用して `Category` クラスをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `budget.py`. For development, you can use `main.py` to test your `Category` class. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Category クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Category class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
index 6719641228..5d230fc031 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
@@ -10,37 +10,31 @@ dashedName: polygon-area-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-polygon-area-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-このプロジェクトでは、オブジェクト指向プログラミングを使用して、Rectangle クラスと Square クラスを作成します。 Square クラスは Rectangle のサブクラスであり、メソッドと属性を継承する必要があります。
+In this project you will use object oriented programming to create a Rectangle class and a Square class. The Square class should be a subclass of Rectangle and inherit methods and attributes.
## Rectangle クラス
-Rectangle オブジェクトが作成されるときは、`width` 属性と `height` 属性で初期化する必要があります。 クラスには、次のメソッドも含める必要があります。
+When a Rectangle object is created, it should be initialized with `width` and `height` attributes. The class should also contain the following methods:
- `set_width`
- `set_height`
-- `get_area`: 面積を返します (`width * height`)
-- `get_perimeter`: 外周を返します (`2 * width + 2 * height`)
-- `get_diagonal`: 対角線を返します(`(width ** 2 + height ** 2) ** .5`)
-- `get_picture`: "\*" の行を使用して図形を表す文字列を返します。 行数は高さと等しく、各行の"\*"の数は幅と等しくする必要があります。 各行の末尾に改行 (`\n`) が必要です。 幅または高さが 50 より大きい場合は、文字列 "Too big for picture." を返す必要があります。
-- `get_amount_inside`: 引数として別の図形 (正方形または長方形) を受け取ります。 渡された図形が、その図形の中に何個収まるかを返します (回転はしません)。 たとえば、幅が 4 で高さが 8 の長方形には、一辺が 4 の正方形が 2つ収まります。
+- `get_area`: Returns area (`width * height`)
+- `get_perimeter`: Returns perimeter (`2 * width + 2 * height`)
+- `get_diagonal`: Returns diagonal (`(width ** 2 + height ** 2) ** .5`)
+- `get_picture`: Returns a string that represents the shape using lines of "\*". The number of lines should be equal to the height and the number of "\*" in each line should be equal to the width. There should be a new line (`\n`) at the end of each line. If the width or height is larger than 50, this should return the string: "Too big for picture.".
+- `get_amount_inside`: Takes another shape (square or rectangle) as an argument. Returns the number of times the passed in shape could fit inside the shape (with no rotations). For instance, a rectangle with a width of 4 and a height of 8 could fit in two squares with sides of 4.
-また、Rectangle のインスタンスを文字列として表現する場合は、`Rectangle(width=5, height=10)` のようにする必要があります。
+Additionally, if an instance of a Rectangle is represented as a string, it should look like: `Rectangle(width=5, height=10)`
## Square クラス
-Square クラスは Rectangle のサブクラスである必要があります。 Square オブジェクトが生成されるときは、一辺の長さを渡します。 `__init__` メソッドでは、一辺の長さを Rectangle クラスの `width` 属性と `height` 属性の両方に格納する必要があります。
+The Square class should be a subclass of Rectangle. When a Square object is created, a single side length is passed in. The `__init__` method should store the side length in both the `width` and `height` attributes from the Rectangle class.
-Square クラスは、Rectangle クラスのメソッドにアクセスできる必要があり、加えて `set_side` メソッドも含める必要があります。 Square のインスタンスを文字列として表現する場合は、`Square(side=9)` のようにする必要があります。
+The Square class should be able to access the Rectangle class methods but should also contain a `set_side` method. If an instance of a Square is represented as a string, it should look like: `Square(side=9)`
-また、Square クラスの `set_width` と `set_height` メソッドでは、幅と高さの両方を設定する必要があります。
+Additionally, the `set_width` and `set_height` methods on the Square class should set both the width and height.
## 使用例
@@ -64,7 +58,7 @@ rect.set_width(16)
print(rect.get_amount_inside(sq))
```
-上記のコードは次を返す必要があります。
+That code should return:
```bash
50
@@ -85,23 +79,23 @@ Square(side=4)
8
```
-このプロジェクトの単体テストは `test_module.py` にあります。
+The unit tests for this project are in `test_module.py`.
## 開発
-`shape_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `shape_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `shape_calculator.py`. For development, you can use `main.py` to test your `shape_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-Rectangle クラスと Square クラスを作成し、すべてのテストに合格する必要があります。
+It should create a Rectangle class and Square class and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
index a4f59e83b4..923413b43f 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
@@ -10,19 +10,13 @@ dashedName: probability-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-probability-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-帽子があり、その中に青いボールが 5 個、赤いボールが 4 個、緑のボールが 2 個入っているとします。 4 個のボールを無作為に取り出す場合、赤のボールが 1 個以上、緑のボールが 2 個含まれる確率は、いくらになりますか? 高度な数学を駆使して確率を計算することも可能ですが、多数の実験を実行しておおよその確率を推定するプログラムを記述する方が簡単です。
+Suppose there is a hat containing 5 blue balls, 4 red balls, and 2 green balls. What is the probability that a random draw of 4 balls will contain at least 1 red ball and 2 green balls? While it would be possible to calculate the probability using advanced mathematics, an easier way is to write a program to perform a large number of experiments to estimate an approximate probability.
-このプロジェクトでは、特定のボールを帽子から無作為に取り出す場合のおおよその確率を調べるプログラムを作成します。
+For this project, you will write a program to determine the approximate probability of drawing certain balls randomly from a hat.
-まず、`prob_calculator.py` で `Hat` クラスを作成してください。 このクラスは、帽子に入っている各色のボールの数を指定する可変個の引数を受け取る必要があります。 たとえば、次のどの方法でもクラスオブジェクトを作成することができます。
+First, create a `Hat` class in `prob_calculator.py`. The class should take a variable number of arguments that specify the number of balls of each color that are in the hat. For example, a class object could be created in any of these ways:
```py
hat1 = Hat(yellow=3, blue=2, green=6)
@@ -30,22 +24,22 @@ hat2 = Hat(red=5, orange=4)
hat3 = Hat(red=5, orange=4, black=1, blue=0, pink=2, striped=9)
```
-帽子は常に、少なくとも 1 個のボールが入った状態で作成されます。 作成時に帽子オブジェクトに渡された引数を、`contents` インスタンス変数に変換する必要があります。 `contents` は、帽子に入っているボールごとにアイテムを 1 つずつ含む文字列のリストである必要があります。 リスト内の各アイテムは、その色のボール 1 個分を表す色の名前である必要があります。 たとえば、帽子が `{"red": 2, "blue": 1}` の場合、`contents` は `["red", "red", "blue"]` になる必要があります。
+A hat will always be created with at least one ball. The arguments passed into the hat object upon creation should be converted to a `contents` instance variable. `contents` should be a list of strings containing one item for each ball in the hat. Each item in the list should be a color name representing a single ball of that color. For example, if your hat is `{"red": 2, "blue": 1}`, `contents` should be `["red", "red", "blue"]`.
-`Hat` クラスには `draw` メソッドが必要です。このメソッドは、帽子から取り出すボールの個数を示す引数を受け取ります。 draw メソッドは、`contents` からボールを無作為に取り除き、それらのボールを文字列のリストとして返す必要があります。 交換のできない壺の実験と同様に、取り出したボールは帽子に戻さないものとします。 取り出すボールの数が利用可能な数を超える場合は、すべてのボールを返してください。
+The `Hat` class should have a `draw` method that accepts an argument indicating the number of balls to draw from the hat. This method should remove balls at random from `contents` and return those balls as a list of strings. The balls should not go back into the hat during the draw, similar to an urn experiment without replacement. If the number of balls to draw exceeds the available quantity, return all the balls.
-次に、(`Hat` クラスの中ではなく) `prob_calculator.py` で `experiment` 関数を作成してください。 この関数は次の引数を受け取る必要があります。
+Next, create an `experiment` function in `prob_calculator.py` (not inside the `Hat` class). This function should accept the following arguments:
-- `hat`: 関数内でコピーする必要のあるボールを含む帽子オブジェクト。
-- `expected_balls`: 実験で帽子から取り出そうとするボールの正確なグループを示すオブジェクト。 たとえば、青のボール 2 個と赤のボール 1 個を帽子から取り出す確率を調べるには、`expected_balls` を `{"blue":2, "red":1}` に設定します。
-- `num_balls_drawn`: 各実験で帽子から取り出すボールの数。
-- `num_experiments`: 実行する実験の回数 (実験の回数が多いほど、おおよその確率の正確性が高まります)。
+- `hat`: A hat object containing balls that should be copied inside the function.
+- `expected_balls`: An object indicating the exact group of balls to attempt to draw from the hat for the experiment. For example, to determine the probability of drawing 2 blue balls and 1 red ball from the hat, set `expected_balls` to `{"blue":2, "red":1}`.
+- `num_balls_drawn`: The number of balls to draw out of the hat in each experiment.
+- `num_experiments`: The number of experiments to perform. (The more experiments performed, the more accurate the approximate probability will be.)
-`experiment` 関数は、確率を返す必要があります。
+The `experiment` function should return a probability.
-たとえば、黒を 6 個、赤を 4 個、緑を 3 個含む帽子から 5 個のボールを取り出す場合に、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個含まれる確率を求めたいとしましょう。 それには、`N` 回の実験を行い、赤のボールが少なくとも 2 個、緑のボールが少なくとも 1 個になった回数 `M` を数え、確率を `M/N` として推定します。 実験ではそれぞれ、指定されたボールの入った帽子の状態から始め、いくつかのボールを取り出し、期待されるボールを取り出したかどうかを確認します。
+For example, let's say that you want to determine the probability of getting at least 2 red balls and 1 green ball when you draw 5 balls from a hat containing 6 black, 4 red, and 3 green. To do this, we perform `N` experiments, count how many times `M` we get at least 2 red balls and 1 green ball, and estimate the probability as `M/N`. Each experiment consists of starting with a hat containing the specified balls, drawing a number of balls, and checking if we got the balls we were attempting to draw.
-上記の例で 2000 回の実験を行う場合は、`experiment` 関数を次のように呼び出します。
+Here is how you would call the `experiment` function based on the example above with 2000 experiments:
```py
hat = Hat(black=6, red=4, green=3)
@@ -55,27 +49,27 @@ probability = experiment(hat=hat,
num_experiments=2000)
```
-この方法は無作為抽出に基づいているため、コードが実行されるたびに確率が多少変わります。
+Since this is based on random draws, the probability will be slightly different each time the code is run.
-*ヒント: `prob_calculator.py` の先頭ですでにインポートされているモジュールを使用することを検討してください。 `prob_calculator.py` の中で乱数シードを初期化しないでください。*
+*Hint: Consider using the modules that are already imported at the top of `prob_calculator.py`. Do not initialize random seed within `prob_calculator.py`.*
## 開発
-`prob_calculator.py` でコードを記述してください。 開発には `main.py` を使用してコードをテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `prob_calculator.py`. For development, you can use `main.py` to test your code. Click the "run" button and `main.py` will run.
-ボイラープレートには `copy` モジュールと `random` モジュール用の `import` ステートメントが含まれています。 これらをプロジェクトで使用することを検討してください。
+The boilerplate includes `import` statements for the `copy` and `random` modules. Consider using those in your project.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-確率を正しく計算し、すべてのテストに合格する必要があります。
+It should correctly calculate probabilities and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
index 1b8344540a..7b7bcfcad1 100644
--- a/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
+++ b/curriculum/challenges/japanese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
@@ -10,27 +10,21 @@ dashedName: time-calculator
このプロジェクトは [Replit スターターコード](https://replit.com/github/freeCodeCamp/boilerplate-time-calculator)を使用して作業を行います。
-Python カリキュラムの対話式教育コンテンツを引き続き開発中です。 現在、下記の freeCodeCamp.org YouTube チャンネルで、このプロジェクトの完了に必要なすべての知識について説明する動画をいくつか公開しています。
-
-- [「みんなで Python」ビデオコース](https://www.freecodecamp.org/news/python-for-everybody/) (14 時間)
-
-- [「Python を学ぶ」ビデオコース](https://www.freecodecamp.org/news/learn-python-video-course/) (10 時間)
-
# --instructions--
-下記に示す 2 つの必須パラメーターと 1 つのオプションパラメーターを受け取る関数 `add_time` を記述してください。
+Write a function named `add_time` that takes in two required parameters and one optional parameter:
-- 12 時制形式の開始時刻 (末尾に AM または PM)
-- 時数と分数で示される経過時間
-- (オプション) 開始の曜日 (大文字小文字の記述は自由)
+- a start time in the 12-hour clock format (ending in AM or PM)
+- a duration time that indicates the number of hours and minutes
+- (optional) a starting day of the week, case insensitive
-関数は、経過時間を開始時刻に追加し、その結果を返す必要があります。
+The function should add the duration time to the start time and return the result.
-結果が翌日になる場合は、時刻の後に `(next day)` (翌日) を表示する必要があります。 結果が翌日以降になる場合は、時刻の後に `(n days later)` (n 日後) を表示する必要があります。ここで "n" は何日後かを示します。
+If the result will be the next day, it should show `(next day)` after the time. If the result will be more than one day later, it should show `(n days later)` after the time, where "n" is the number of days later.
-関数にオプションの開始曜日パラメーターが与えられた場合は、結果の曜日を出力に表示する必要があります。 出力する曜日は、時刻の後、「n 日後」の前に表示する必要があります。
+If the function is given the optional starting day of the week parameter, then the output should display the day of the week of the result. The day of the week in the output should appear after the time and before the number of days later.
-関数が扱うさまざまなケースの例を次に示します。 結果のスペースと句読点の表示に特に注意を払ってください。
+Below are some examples of different cases the function should handle. Pay close attention to the spacing and punctuation of the results.
```py
add_time("3:00 PM", "3:10")
@@ -52,23 +46,23 @@ add_time("6:30 PM", "205:12")
# Returns: 7:42 AM (9 days later)
```
-Python ライブラリをインポートしないでください。 開始時刻は有効な時刻であると仮定します。 経過時間の分数は 60 未満の整数になりますが、時数は任意の整数になります。
+Do not import any Python libraries. Assume that the start times are valid times. The minutes in the duration time will be a whole number less than 60, but the hour can be any whole number.
## 開発
-`time_calculator.py` でコードを記述してください。 開発には `main.py` を使用して `time_calculator()` 関数をテストすることができます。 「実行」ボタンをクリックすると `main.py` が実行されます。
+Write your code in `time_calculator.py`. For development, you can use `main.py` to test your `time_calculator()` function. Click the "run" button and `main.py` will run.
## テスト
-このプロジェクトの単体テストは `test_module.py` にあります。 すでに `test_module.py` から `main.py` にテストをインポートしてあります。 「実行」ボタンを押すと自動的にテストが実行されます。
+The unit tests for this project are in `test_module.py`. We imported the tests from `test_module.py` to `main.py` for your convenience. The tests will run automatically whenever you hit the "run" button.
## 提出
-プロジェクトの URL をコピーし、freeCodeCamp に提出してください。
+Copy your project's URL and submit it to freeCodeCamp.
# --hints--
-正確に時間を追加し、すべてのテストに合格する必要があります。
+It should correctly add times and pass all tests.
```js
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
index 3bbff2c99e..9be6dd072f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
@@ -8,7 +8,7 @@ dashedName: problem-344-silver-dollar-game
# --description--
-ニコラース・ホーヴァート・ ド・ブラウンの銀貨ゲームにはいくつかバリエーションがあり、その一つは次のように説明されます。
+One variant of N.G. de Bruijn's silver dollar game can be described as follows:
マスが並ぶ細長い盤上に硬貨が何枚か置かれています (1 マスにたかだか 1 枚)。 銀貨 (1 ドル硬貨) と呼ばれる 1 枚しかない硬貨に、任意の価値があります。 2 人のプレイヤーが交互にプレイします。 各ターンで、プレイヤーは通常の移動または特別な移動を行う必要があります。
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
index 81a2c58f4a..0468ec26fd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-250-250250.md
@@ -8,7 +8,7 @@ dashedName: problem-250-250250
# --description--
-Encontre o número de subconjuntos não vazios de $\\{11, 22, 33, \ldots, {250250}^{250250}\\}$, cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
+Encontre o número de subconjuntos não vazios de $\\{{1}^{1}, {2}^{2}, {3}^{3}, \ldots, {250250}^{250250}\\}$ cuja soma de elementos é divisível por 250. Insira os 16 algarismos mais à direita para sua resposta.
# --hints--