From 2b1d0cdaf8e39afbd1399e2fa91a899a17d6b867 Mon Sep 17 00:00:00 2001
From: gikf <60067306+gikf@users.noreply.github.com>
Date: Thu, 27 May 2021 19:27:16 +0200
Subject: [PATCH] fix(curriculum): rework Project Euler 91 (#42224)
* fix: rework challenge to use argument in function
* fix: add solution
* fix: use MathJax to improve math notation
---
...ight-triangles-with-integer-coordinates.md | 87 ++++++++++++++++---
1 file changed, 77 insertions(+), 10 deletions(-)
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-91-right-triangles-with-integer-coordinates.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-91-right-triangles-with-integer-coordinates.md
index 5d454f2754..b38a0eb1bc 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-91-right-triangles-with-integer-coordinates.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-91-right-triangles-with-integer-coordinates.md
@@ -8,28 +8,46 @@ dashedName: problem-91-right-triangles-with-integer-coordinates
# --description--
-The points P (`x`1, `y`1) and Q (`x`2, `y`2) are plotted at integer co-ordinates and are joined to the origin, O(0,0), to form ΔOPQ.
+The points ${P}(x_1, y_1)$ and ${Q}(x_2, y_2)$ are plotted at integer co-ordinates and are joined to the origin, ${O}(0, 0)$, to form ${\Delta}OPQ$.
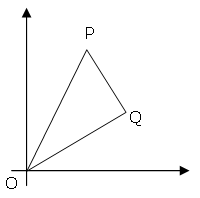 -There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 2.
+There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, $0 ≤ x_1, y_1, x_2, y_2 ≤ 2$.
-There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 2.
+There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, $0 ≤ x_1, y_1, x_2, y_2 ≤ 2$.
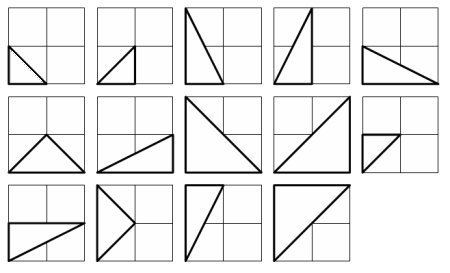 -Given that 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 50, how many right triangles can be formed?
+Given that $0 ≤ x_1, y_1, x_2, y_2 ≤ limit$, how many right triangles can be formed?
# --hints--
-`rightTrianglesIntCoords()` should return a number.
+`rightTrianglesIntCoords(2)` should return a number.
```js
-assert(typeof rightTrianglesIntCoords() === 'number');
+assert(typeof rightTrianglesIntCoords(2) === 'number');
```
-`rightTrianglesIntCoords()` should return 14234.
+`rightTrianglesIntCoords(2)` should return `14`.
```js
-assert.strictEqual(rightTrianglesIntCoords(), 14234);
+assert.strictEqual(rightTrianglesIntCoords(2), 14);
+```
+
+`rightTrianglesIntCoords(10)` should return `448`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(10), 448);
+```
+
+`rightTrianglesIntCoords(25)` should return `3207`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(25), 3207);
+```
+
+`rightTrianglesIntCoords(50)` should return `14234`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(50), 14234);
```
# --seed--
@@ -37,16 +55,65 @@ assert.strictEqual(rightTrianglesIntCoords(), 14234);
## --seed-contents--
```js
-function rightTrianglesIntCoords() {
+function rightTrianglesIntCoords(limit) {
return true;
}
-rightTrianglesIntCoords();
+rightTrianglesIntCoords(2);
```
# --solutions--
```js
-// solution required
+function rightTrianglesIntCoords(limit) {
+ function isRightTriangle(points) {
+ for (let i = 0; i < points.length; i++) {
+ const pointA = points[i];
+ const pointB = points[(i + 1) % 3];
+ const pointC = points[(i + 2) % 3];
+ const vectorAB = [pointB[0] - pointA[0], pointB[1] - pointA[1]];
+ const vectorAC = [pointC[0] - pointA[0], pointC[1] - pointA[1]];
+
+ if (isRightAngleBetween(vectorAB, vectorAC)) {
+ return true;
+ }
+ }
+ return false;
+ }
+
+ function isRightAngleBetween(vector1, vector2) {
+ return vector1[0] * vector2[0] + vector1[1] * vector2[1] === 0;
+ }
+
+ function getSetKey(points) {
+ return (
+ '0.0,' +
+ points
+ .sort((a, b) => a[0] - b[0])
+ .map(point => point.join('.'))
+ .join(',')
+ );
+ }
+
+ const pointO = [0, 0];
+ const rightTriangles = new Set();
+ for (let x1 = 1; x1 <= limit; x1++) {
+ for (let y1 = 0; y1 <= limit; y1++) {
+ const pointP = [x1, y1];
+ for (let x2 = 0; x2 <= limit; x2++) {
+ for (let y2 = 1; y2 <= limit; y2++) {
+ const pointQ = [x2, y2];
+ if (pointP[0] === pointQ[0] && pointP[1] === pointQ[1]) {
+ continue;
+ }
+ if (isRightTriangle([pointO, pointP, pointQ])) {
+ rightTriangles.add(getSetKey([pointP, pointQ]));
+ }
+ }
+ }
+ }
+ }
+ return rightTriangles.size;
+}
```
-Given that 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 50, how many right triangles can be formed?
+Given that $0 ≤ x_1, y_1, x_2, y_2 ≤ limit$, how many right triangles can be formed?
# --hints--
-`rightTrianglesIntCoords()` should return a number.
+`rightTrianglesIntCoords(2)` should return a number.
```js
-assert(typeof rightTrianglesIntCoords() === 'number');
+assert(typeof rightTrianglesIntCoords(2) === 'number');
```
-`rightTrianglesIntCoords()` should return 14234.
+`rightTrianglesIntCoords(2)` should return `14`.
```js
-assert.strictEqual(rightTrianglesIntCoords(), 14234);
+assert.strictEqual(rightTrianglesIntCoords(2), 14);
+```
+
+`rightTrianglesIntCoords(10)` should return `448`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(10), 448);
+```
+
+`rightTrianglesIntCoords(25)` should return `3207`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(25), 3207);
+```
+
+`rightTrianglesIntCoords(50)` should return `14234`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(50), 14234);
```
# --seed--
@@ -37,16 +55,65 @@ assert.strictEqual(rightTrianglesIntCoords(), 14234);
## --seed-contents--
```js
-function rightTrianglesIntCoords() {
+function rightTrianglesIntCoords(limit) {
return true;
}
-rightTrianglesIntCoords();
+rightTrianglesIntCoords(2);
```
# --solutions--
```js
-// solution required
+function rightTrianglesIntCoords(limit) {
+ function isRightTriangle(points) {
+ for (let i = 0; i < points.length; i++) {
+ const pointA = points[i];
+ const pointB = points[(i + 1) % 3];
+ const pointC = points[(i + 2) % 3];
+ const vectorAB = [pointB[0] - pointA[0], pointB[1] - pointA[1]];
+ const vectorAC = [pointC[0] - pointA[0], pointC[1] - pointA[1]];
+
+ if (isRightAngleBetween(vectorAB, vectorAC)) {
+ return true;
+ }
+ }
+ return false;
+ }
+
+ function isRightAngleBetween(vector1, vector2) {
+ return vector1[0] * vector2[0] + vector1[1] * vector2[1] === 0;
+ }
+
+ function getSetKey(points) {
+ return (
+ '0.0,' +
+ points
+ .sort((a, b) => a[0] - b[0])
+ .map(point => point.join('.'))
+ .join(',')
+ );
+ }
+
+ const pointO = [0, 0];
+ const rightTriangles = new Set();
+ for (let x1 = 1; x1 <= limit; x1++) {
+ for (let y1 = 0; y1 <= limit; y1++) {
+ const pointP = [x1, y1];
+ for (let x2 = 0; x2 <= limit; x2++) {
+ for (let y2 = 1; y2 <= limit; y2++) {
+ const pointQ = [x2, y2];
+ if (pointP[0] === pointQ[0] && pointP[1] === pointQ[1]) {
+ continue;
+ }
+ if (isRightTriangle([pointO, pointP, pointQ])) {
+ rightTriangles.add(getSetKey([pointP, pointQ]));
+ }
+ }
+ }
+ }
+ }
+ return rightTriangles.size;
+}
```
 -There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 2.
+There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, $0 ≤ x_1, y_1, x_2, y_2 ≤ 2$.
-There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 2.
+There are exactly fourteen triangles containing a right angle that can be formed when each co-ordinate lies between 0 and 2 inclusive; that is, $0 ≤ x_1, y_1, x_2, y_2 ≤ 2$.
 -Given that 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 50, how many right triangles can be formed?
+Given that $0 ≤ x_1, y_1, x_2, y_2 ≤ limit$, how many right triangles can be formed?
# --hints--
-`rightTrianglesIntCoords()` should return a number.
+`rightTrianglesIntCoords(2)` should return a number.
```js
-assert(typeof rightTrianglesIntCoords() === 'number');
+assert(typeof rightTrianglesIntCoords(2) === 'number');
```
-`rightTrianglesIntCoords()` should return 14234.
+`rightTrianglesIntCoords(2)` should return `14`.
```js
-assert.strictEqual(rightTrianglesIntCoords(), 14234);
+assert.strictEqual(rightTrianglesIntCoords(2), 14);
+```
+
+`rightTrianglesIntCoords(10)` should return `448`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(10), 448);
+```
+
+`rightTrianglesIntCoords(25)` should return `3207`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(25), 3207);
+```
+
+`rightTrianglesIntCoords(50)` should return `14234`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(50), 14234);
```
# --seed--
@@ -37,16 +55,65 @@ assert.strictEqual(rightTrianglesIntCoords(), 14234);
## --seed-contents--
```js
-function rightTrianglesIntCoords() {
+function rightTrianglesIntCoords(limit) {
return true;
}
-rightTrianglesIntCoords();
+rightTrianglesIntCoords(2);
```
# --solutions--
```js
-// solution required
+function rightTrianglesIntCoords(limit) {
+ function isRightTriangle(points) {
+ for (let i = 0; i < points.length; i++) {
+ const pointA = points[i];
+ const pointB = points[(i + 1) % 3];
+ const pointC = points[(i + 2) % 3];
+ const vectorAB = [pointB[0] - pointA[0], pointB[1] - pointA[1]];
+ const vectorAC = [pointC[0] - pointA[0], pointC[1] - pointA[1]];
+
+ if (isRightAngleBetween(vectorAB, vectorAC)) {
+ return true;
+ }
+ }
+ return false;
+ }
+
+ function isRightAngleBetween(vector1, vector2) {
+ return vector1[0] * vector2[0] + vector1[1] * vector2[1] === 0;
+ }
+
+ function getSetKey(points) {
+ return (
+ '0.0,' +
+ points
+ .sort((a, b) => a[0] - b[0])
+ .map(point => point.join('.'))
+ .join(',')
+ );
+ }
+
+ const pointO = [0, 0];
+ const rightTriangles = new Set();
+ for (let x1 = 1; x1 <= limit; x1++) {
+ for (let y1 = 0; y1 <= limit; y1++) {
+ const pointP = [x1, y1];
+ for (let x2 = 0; x2 <= limit; x2++) {
+ for (let y2 = 1; y2 <= limit; y2++) {
+ const pointQ = [x2, y2];
+ if (pointP[0] === pointQ[0] && pointP[1] === pointQ[1]) {
+ continue;
+ }
+ if (isRightTriangle([pointO, pointP, pointQ])) {
+ rightTriangles.add(getSetKey([pointP, pointQ]));
+ }
+ }
+ }
+ }
+ }
+ return rightTriangles.size;
+}
```
-Given that 0 ≤ `x`1, `y`1, `x`2, `y`2 ≤ 50, how many right triangles can be formed?
+Given that $0 ≤ x_1, y_1, x_2, y_2 ≤ limit$, how many right triangles can be formed?
# --hints--
-`rightTrianglesIntCoords()` should return a number.
+`rightTrianglesIntCoords(2)` should return a number.
```js
-assert(typeof rightTrianglesIntCoords() === 'number');
+assert(typeof rightTrianglesIntCoords(2) === 'number');
```
-`rightTrianglesIntCoords()` should return 14234.
+`rightTrianglesIntCoords(2)` should return `14`.
```js
-assert.strictEqual(rightTrianglesIntCoords(), 14234);
+assert.strictEqual(rightTrianglesIntCoords(2), 14);
+```
+
+`rightTrianglesIntCoords(10)` should return `448`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(10), 448);
+```
+
+`rightTrianglesIntCoords(25)` should return `3207`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(25), 3207);
+```
+
+`rightTrianglesIntCoords(50)` should return `14234`.
+
+```js
+assert.strictEqual(rightTrianglesIntCoords(50), 14234);
```
# --seed--
@@ -37,16 +55,65 @@ assert.strictEqual(rightTrianglesIntCoords(), 14234);
## --seed-contents--
```js
-function rightTrianglesIntCoords() {
+function rightTrianglesIntCoords(limit) {
return true;
}
-rightTrianglesIntCoords();
+rightTrianglesIntCoords(2);
```
# --solutions--
```js
-// solution required
+function rightTrianglesIntCoords(limit) {
+ function isRightTriangle(points) {
+ for (let i = 0; i < points.length; i++) {
+ const pointA = points[i];
+ const pointB = points[(i + 1) % 3];
+ const pointC = points[(i + 2) % 3];
+ const vectorAB = [pointB[0] - pointA[0], pointB[1] - pointA[1]];
+ const vectorAC = [pointC[0] - pointA[0], pointC[1] - pointA[1]];
+
+ if (isRightAngleBetween(vectorAB, vectorAC)) {
+ return true;
+ }
+ }
+ return false;
+ }
+
+ function isRightAngleBetween(vector1, vector2) {
+ return vector1[0] * vector2[0] + vector1[1] * vector2[1] === 0;
+ }
+
+ function getSetKey(points) {
+ return (
+ '0.0,' +
+ points
+ .sort((a, b) => a[0] - b[0])
+ .map(point => point.join('.'))
+ .join(',')
+ );
+ }
+
+ const pointO = [0, 0];
+ const rightTriangles = new Set();
+ for (let x1 = 1; x1 <= limit; x1++) {
+ for (let y1 = 0; y1 <= limit; y1++) {
+ const pointP = [x1, y1];
+ for (let x2 = 0; x2 <= limit; x2++) {
+ for (let y2 = 1; y2 <= limit; y2++) {
+ const pointQ = [x2, y2];
+ if (pointP[0] === pointQ[0] && pointP[1] === pointQ[1]) {
+ continue;
+ }
+ if (isRightTriangle([pointO, pointP, pointQ])) {
+ rightTriangles.add(getSetKey([pointP, pointQ]));
+ }
+ }
+ }
+ }
+ }
+ return rightTriangles.size;
+}
```