gaspersic/freeCodeCamp
1
0
Fork 0
Code Issues Pull Requests Projects Releases Wiki Activity

Added definitions of different types of matrices (#30128)

Browse Source
This commit is contained in:
Ankush Soni
2019-06-25 22:45:51 +05:30
committed by Randell Dawson
parent 2f8d009133
commit 2ff2b82d51
1 changed files with 16 additions and 3 deletions
Download Patch File Download Diff File Expand all files Collapse all files

19
guide/english/mathematics/intro-to-matrices/index.md
View File

@ -19,14 +19,27 @@ Transpose is the operations of inver the rows and columns of a matrix.
You can also think of it as the column num of matrix A needs to be the same as the row size of matrix B. The size of the new array is the row num of matrix A and the column num of matrix B. You can also think of it as the column num of matrix A needs to be the same as the row size of matrix B. The size of the new array is the row num of matrix A and the column num of matrix B.
#### Types of Matrices
1. Square Matrix- A matrix with equal no. of rows and columns is called a square matrix.
2. Diagonal Matrix- A square matrix with only diagonal elements as non-zero elements. For example:
![alt text](https://encrypted-tbn0.gstatic.com/images?q=tbn:ANd9GcQQgGANz1Dgr3d4tzSkJjS4LMIeM3MGsC2LO6wcKMQXHHCg10ax)
3. Scalar Matrix- A diagonal matrix is said to be scalar if all of its diagonal elements are the same.
![alt text](https://qph.fs.quoracdn.net/main-qimg-1cbbbaac2443a2725acedfe63b95f2e5)
4. Identity Matrix- A diagonal matrix is said to be identity if all of its diagonal elements are equal to one, denoted by I.
![alt text](https://qph.fs.quoracdn.net/main-qimg-6f2d174e18b8a327973289af2eca72ec)
5. Triangular Matrix: A square matrix is said to be triangular if all of its elements above the principal diagonal are zero (lower triangular matrix) or all of its elements below the principal diagonal are zero (upper triangular matrix).
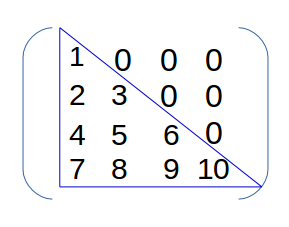
![alt text](https://3.bp.blogspot.com/-vR6xL2kgNIw/WK18Gw-xzwI/AAAAAAAAALA/g0ihK15Juug152JBZeZ31rb8Rx5tUsuQQCLcB/s1600/ltm.png)
#### Addition and Subraction of Matrices #### Addition and Subraction of Matrices
To add or subtract matrices, they must be the same size. For example, if I had a 3x3 matrix, I can only add with another 3x3 martrix. To add or subtract, get the first position of the first matrix, and add or subtract to the first position on the second matrix. Do this for all of the positions. You will end up with a new matrix with the addition or subtraction. To add or subtract matrices, they must be the same size. For example, if I had a 3x3 matrix, I can only add with another 3x3 martrix. To add or subtract, get the first position of the first matrix, and add or subtract to the first position on the second matrix. Do this for all of the positions. You will end up with a new matrix with the addition or subtraction.
![alt text](https://mathpullzone-8231.kxcdn.com/wp-content/uploads/add-two-matrices.jpg) ![alt text](https://mathpullzone-8231.kxcdn.com/wp-content/uploads/add-two-matrices.jpg)
![alt text](https://mathpullzone-8231.kxcdn.com/wp-content/uploads/subtracting-matrices.jpg) ![alt text](https://mathpullzone-8231.kxcdn.com/wp-content/uploads/subtracting-matrices.jpg)
#### More Information: #### More Information:
[Wikipedia](https://en.wikipedia.org/wiki/Matrix_(mathematics)) [Wikipedia](https://en.wikipedia.org/wiki/Matrix_(mathematics))