From 32fac23a2da945104ec3109159e4728be6128fe9 Mon Sep 17 00:00:00 2001
From: gikf <60067306+gikf@users.noreply.github.com>
Date: Mon, 12 Jul 2021 16:19:03 +0200
Subject: [PATCH] fix(curriculum): clean-up Project Euler 161-180 (#42782)
* fix: clean-up Project Euler 161-180
* fix: corrections from review
Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
---
.../project-euler/problem-161-triominoes.md | 14 +++++--
.../problem-162-hexadecimal-numbers.md | 22 ++++++----
.../problem-163-cross-hatched-triangles.md | 23 ++++++++---
...s-have-a-sum-greater-than-a-given-value.md | 10 ++---
.../problem-165-intersections.md | 40 ++++++++++++++-----
.../project-euler/problem-166-criss-cross.md | 19 +++++----
...roblem-167-investigating-ulam-sequences.md | 20 +++++-----
.../problem-168-number-rotations.md | 12 +++---
...an-be-expressed-as-a-sum-of-powers-of-2.md | 28 ++++++-------
...can-be-formed-by-concatenating-products.md | 15 ++++---
...f-the-squares-of-the-digits-is-a-square.md | 22 +++++-----
...gating-numbers-with-few-repeated-digits.md | 10 ++---
...ent-hollow-square-laminae-can-be-formed.md | 10 +++--
...one-two-three-...-distinct-arrangements.md | 16 +++++---
...an-be-expressed-as-a-sum-of-powers-of-2.md | 32 +++++++++++----
...-angled-triangles-that-share-a-cathetus.md | 8 ++--
...oblem-177-integer-angled-quadrilaterals.md | 18 ++++++---
.../project-euler/problem-178-step-numbers.md | 10 ++---
...oblem-179-consecutive-positive-divisors.md | 10 ++---
...-zeros-of-a-function-of-three-variables.md | 30 ++++++++------
20 files changed, 230 insertions(+), 139 deletions(-)
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-161-triominoes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-161-triominoes.md
index ea369bae60..3c645846a9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-161-triominoes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-161-triominoes.md
@@ -12,18 +12,24 @@ A triomino is a shape consisting of three squares joined via the edges.
There are two basic forms:
+ +
If all possible orientations are taken into account there are six:
+
+
If all possible orientations are taken into account there are six:
+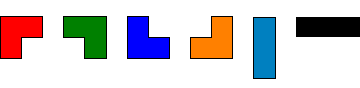 +
Any n by m grid for which nxm is divisible by 3 can be tiled with triominoes. If we consider tilings that can be obtained by reflection or rotation from another tiling as different there are 41 ways a 2 by 9 grid can be tiled with triominoes:
+
+
Any n by m grid for which nxm is divisible by 3 can be tiled with triominoes. If we consider tilings that can be obtained by reflection or rotation from another tiling as different there are 41 ways a 2 by 9 grid can be tiled with triominoes:
+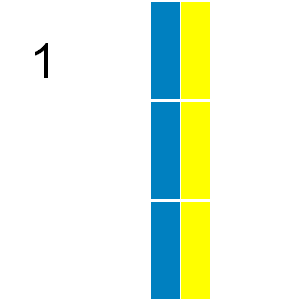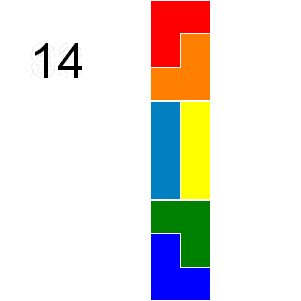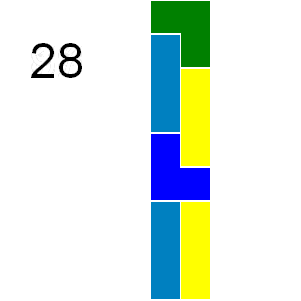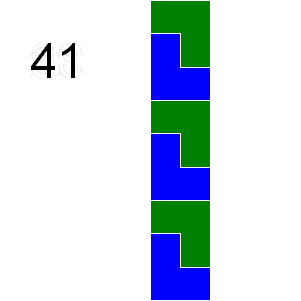 +
In how many ways can a 9 by 12 grid be tiled in this way by triominoes?
# --hints--
-`euler161()` should return 20574308184277972.
+`triominoes()` should return `20574308184277972`.
```js
-assert.strictEqual(euler161(), 20574308184277972);
+assert.strictEqual(triominoes(), 20574308184277972);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler161(), 20574308184277972);
## --seed-contents--
```js
-function euler161() {
+function triominoes() {
return true;
}
-euler161();
+triominoes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
index 53a6bcd772..8b63fdc2ab 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
@@ -10,9 +10,9 @@ dashedName: problem-162-hexadecimal-numbers
In the hexadecimal number system numbers are represented using 16 different digits:
-0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
+$$0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F$$
-The hexadecimal number AF when written in the decimal number system equals 10x16+15=175.
+The hexadecimal number AF when written in the decimal number system equals $10 \times 16 + 15 = 175$.
In the 3-digit hexadecimal numbers 10A, 1A0, A10, and A01 the digits 0,1 and A are all present.
@@ -20,16 +20,22 @@ Like numbers written in base ten we write hexadecimal numbers without leading ze
How many hexadecimal numbers containing at most sixteen hexadecimal digits exist with all of the digits 0,1, and A present at least once?
-Give your answer as a hexadecimal number.
+Give your answer with hexadecimal number as a string.
-(A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
+**Note:** (A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
# --hints--
-`euler162()` should return 3D58725572C62302.
+`hexadecimalNumbers()` should return a string.
```js
-assert.strictEqual(euler162(), '3D58725572C62302');
+assert(typeof hexadecimalNumbers() === 'string');
+```
+
+`hexadecimalNumbers()` should return the string `3D58725572C62302`.
+
+```js
+assert.strictEqual(hexadecimalNumbers(), '3D58725572C62302');
```
# --seed--
@@ -37,12 +43,12 @@ assert.strictEqual(euler162(), '3D58725572C62302');
## --seed-contents--
```js
-function euler162() {
+function hexadecimalNumbers() {
return true;
}
-euler162();
+hexadecimalNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
index 72ed1158b1..1bd17c7351 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
@@ -10,14 +10,27 @@ dashedName: problem-163-cross-hatched-triangles
Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
-Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle. It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size n triangle would thus contain n2 size 1 triangle building blocks. If we denote T(n) as the number of triangles present in a triangle of size n, then T(1) = 16 T(2) = 104 Find T(36).
+
+
In how many ways can a 9 by 12 grid be tiled in this way by triominoes?
# --hints--
-`euler161()` should return 20574308184277972.
+`triominoes()` should return `20574308184277972`.
```js
-assert.strictEqual(euler161(), 20574308184277972);
+assert.strictEqual(triominoes(), 20574308184277972);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler161(), 20574308184277972);
## --seed-contents--
```js
-function euler161() {
+function triominoes() {
return true;
}
-euler161();
+triominoes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
index 53a6bcd772..8b63fdc2ab 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
@@ -10,9 +10,9 @@ dashedName: problem-162-hexadecimal-numbers
In the hexadecimal number system numbers are represented using 16 different digits:
-0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
+$$0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F$$
-The hexadecimal number AF when written in the decimal number system equals 10x16+15=175.
+The hexadecimal number AF when written in the decimal number system equals $10 \times 16 + 15 = 175$.
In the 3-digit hexadecimal numbers 10A, 1A0, A10, and A01 the digits 0,1 and A are all present.
@@ -20,16 +20,22 @@ Like numbers written in base ten we write hexadecimal numbers without leading ze
How many hexadecimal numbers containing at most sixteen hexadecimal digits exist with all of the digits 0,1, and A present at least once?
-Give your answer as a hexadecimal number.
+Give your answer with hexadecimal number as a string.
-(A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
+**Note:** (A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
# --hints--
-`euler162()` should return 3D58725572C62302.
+`hexadecimalNumbers()` should return a string.
```js
-assert.strictEqual(euler162(), '3D58725572C62302');
+assert(typeof hexadecimalNumbers() === 'string');
+```
+
+`hexadecimalNumbers()` should return the string `3D58725572C62302`.
+
+```js
+assert.strictEqual(hexadecimalNumbers(), '3D58725572C62302');
```
# --seed--
@@ -37,12 +43,12 @@ assert.strictEqual(euler162(), '3D58725572C62302');
## --seed-contents--
```js
-function euler162() {
+function hexadecimalNumbers() {
return true;
}
-euler162();
+hexadecimalNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
index 72ed1158b1..1bd17c7351 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
@@ -10,14 +10,27 @@ dashedName: problem-163-cross-hatched-triangles
Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
-Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle. It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size n triangle would thus contain n2 size 1 triangle building blocks. If we denote T(n) as the number of triangles present in a triangle of size n, then T(1) = 16 T(2) = 104 Find T(36).
+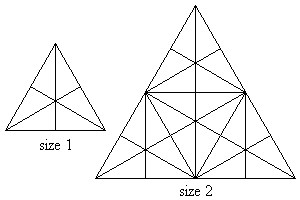 +
+Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
+
+It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size $n$ triangle would thus contain $n^2$ size 1 triangle building blocks.
+
+If we denote $T(n)$ as the number of triangles present in a triangle of size $n$, then
+
+$$\begin{align}
+ & T(1) = 16 \\\\
+ & T(2) = 104
+\end{align}$$
+
+Find $T(36)$.
# --hints--
-`euler163()` should return 343047.
+`crossHatchedTriangles()` should return `343047`.
```js
-assert.strictEqual(euler163(), 343047);
+assert.strictEqual(crossHatchedTriangles(), 343047);
```
# --seed--
@@ -25,12 +38,12 @@ assert.strictEqual(euler163(), 343047);
## --seed-contents--
```js
-function euler163() {
+function crossHatchedTriangles() {
return true;
}
-euler163();
+crossHatchedTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
index e511646823..18a4bc8bad 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
@@ -11,14 +11,14 @@ dashedName: >-
# --description--
-How many 20 digit numbers n (without any leading zero) exist such that no three consecutive digits of n have a sum greater than 9?
+How many 20 digit numbers $n$ (without any leading zero) exist such that no three consecutive digits of $n$ have a sum greater than 9?
# --hints--
-`euler164()` should return 378158756814587.
+`consecutiveDigitsSum()` should return `378158756814587`.
```js
-assert.strictEqual(euler164(), 378158756814587);
+assert.strictEqual(consecutiveDigitsSum(), 378158756814587);
```
# --seed--
@@ -26,12 +26,12 @@ assert.strictEqual(euler164(), 378158756814587);
## --seed-contents--
```js
-function euler164() {
+function consecutiveDigitsSum() {
return true;
}
-euler164();
+consecutiveDigitsSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
index a98373c338..9a25a1588c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
@@ -8,22 +8,44 @@ dashedName: problem-165-intersections
# --description--
-A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities:
-
-the segments have zero points, one point, or infinitely many points in common.
+A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities: the segments have zero points, one point, or infinitely many points in common.
Moreover when two segments have exactly one point in common it might be the case that that common point is an endpoint of either one of the segments or of both. If a common point of two segments is not an endpoint of either of the segments it is an interior point of both segments.
-We will call a common point T of two segments L1 and L2 a true intersection point of L1 and L2 if T is the only common point of L1 and L2 and T is an interior point of both segments.
+We will call a common point $T$ of two segments $L_1$ and $L_2$ a true intersection point of $L_1$ and $L_2$ if $T$ is the only common point of $L_1$ and $L_2$ and $T$ is an interior point of both segments.
-Consider the three segments L1, L2, and L3: L1: (27, 44) to (12, 32) L2: (46, 53) to (17, 62) L3: (46, 70) to (22, 40) It can be verified that line segments L2 and L3 have a true intersection point. We note that as the one of the end points of L3: (22,40) lies on L1 this is not considered to be a true point of intersection. L1 and L2 have no common point. So among the three line segments, we find one true intersection point. Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator. s0 = 290797 sn+1 = sn×sn (modulo 50515093) tn = sn (modulo 500) To create each line segment, we use four consecutive numbers tn. That is, the first line segment is given by: (t1, t2) to (t3, t4) The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27,144) to (12,232). How many distinct true intersection points are found among the 5000 line segments?
+Consider the three segments $L_1$, $L_2$, and $L_3$:
+
+$$\begin{align}
+ & L_1: (27, 44) \\;\text{to}\\; (12, 32) \\\\
+ & L_2: (46, 53) \\;\text{to}\\; (17, 62) \\\\
+ & L_3: (46, 70) \\;\text{to}\\; (22, 40) \\\\
+\end{align}$$
+
+It can be verified that line segments $L_2$ and $L_3$ have a true intersection point. We note that as the one of the end points of $L_3$: (22, 40) lies on $L_1$ this is not considered to be a true point of intersection. $L_1$ and $L_2$ have no common point. So among the three line segments, we find one true intersection point.
+
+Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator.
+
+$$\begin{align}
+ & s_0 = 290797 \\\\
+ & s_{n + 1} = s_n × s_n (\text{modulo}\\; 50515093) \\\\
+ & t_n = s_n (\text{modulo}\\; 500) \\\\
+\end{align}$$
+
+To create each line segment, we use four consecutive numbers $t_n$. That is, the first line segment is given by:
+
+($_t$1, $t_2$) to ($t_3$, $t_4$)
+
+The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27, 144) to (12, 232).
+
+How many distinct true intersection points are found among the 5000 line segments?
# --hints--
-`euler165()` should return 2868868.
+`distinctIntersections()` should return `2868868`.
```js
-assert.strictEqual(euler165(), 2868868);
+assert.strictEqual(distinctIntersections(), 2868868);
```
# --seed--
@@ -31,12 +53,12 @@ assert.strictEqual(euler165(), 2868868);
## --seed-contents--
```js
-function euler165() {
+function distinctIntersections() {
return true;
}
-euler165();
+distinctIntersections();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
index 9f1db5cea4..dfb3821789 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
@@ -8,22 +8,27 @@ dashedName: problem-166-criss-cross
# --description--
-A 4x4 grid is filled with digits d, 0 ≤ d ≤ 9.
+A 4x4 grid is filled with digits $d$, $0 ≤ d ≤ 9$.
It can be seen that in the grid
-6 3 3 0 5 0 4 3 0 7 1 4 1 2 4 5
+$$\begin{array}{}
+ 6 & 3 & 3 & 0 \\\\
+ 5 & 0 & 4 & 3 \\\\
+ 0 & 7 & 1 & 4 \\\\
+ 1 & 2 & 4 & 5
+\end{array}$$
the sum of each row and each column has the value 12. Moreover the sum of each diagonal is also 12.
-In how many ways can you fill a 4x4 grid with the digits d, 0 ≤ d ≤ 9 so that each row, each column, and both diagonals have the same sum?
+In how many ways can you fill a 4x4 grid with the digits $d$, $0 ≤ d ≤ 9$ so that each row, each column, and both diagonals have the same sum?
# --hints--
-`euler166()` should return 7130034.
+`crissCross()` should return `7130034`.
```js
-assert.strictEqual(euler166(), 7130034);
+assert.strictEqual(crissCross(), 7130034);
```
# --seed--
@@ -31,12 +36,12 @@ assert.strictEqual(euler166(), 7130034);
## --seed-contents--
```js
-function euler166() {
+function crissCross() {
return true;
}
-euler166();
+crissCross();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
index 6f30b4b272..6e2b3c1b4d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
@@ -8,24 +8,22 @@ dashedName: problem-167-investigating-ulam-sequences
# --description--
-For two positive integers a and b, the Ulam sequence U(a,b) is defined by U(a,b)1 = a, U(a,b)2 = b and for k > 2,
+For two positive integers $a$ and $b$, the Ulam sequence $U(a,b)$ is defined by ${U{(a,b)}\_1} = a$, ${U{(a,b)}\_2} = b$ and for $k > 2$, ${U{(a,b)}\_k}$ is the smallest integer greater than ${U{(a,b)}\_{(k-1)}}$ which can be written in exactly one way as the sum of two distinct previous members of $U(a,b)$.
-U(a,b)k is the smallest integer greater than U(a,b)(k-1) which can be written in exactly one way as the sum of two distinct previous members of U(a,b).
+For example, the sequence $U(1,2)$ begins with
-For example, the sequence U(1,2) begins with
+$$1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8$$
-1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8;
+5 does not belong to it because $5 = 1 + 4 = 2 + 3$ has two representations as the sum of two previous members, likewise $7 = 1 + 6 = 3 + 4$.
-5 does not belong to it because 5 = 1 + 4 = 2 + 3 has two representations as the sum of two previous members, likewise 7 = 1 + 6 = 3 + 4.
-
-Find ∑U(2,2n+1)k for 2 ≤ n ≤10, where k = 1011.
+Find $\sum {U(2, 2n + 1)_k}$ for $2 ≤ n ≤ 10$, where $k = {10}^{11}$.
# --hints--
-`euler167()` should return 3916160068885.
+`ulamSequences()` should return `3916160068885`.
```js
-assert.strictEqual(euler167(), 3916160068885);
+assert.strictEqual(ulamSequences(), 3916160068885);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler167(), 3916160068885);
## --seed-contents--
```js
-function euler167() {
+function ulamSequences() {
return true;
}
-euler167();
+ulamSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
index 9ad5f78e64..6f5c679ed3 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
@@ -10,18 +10,18 @@ dashedName: problem-168-number-rotations
Consider the number 142857. We can right-rotate this number by moving the last digit (7) to the front of it, giving us 714285.
-It can be verified that 714285=5×142857.
+It can be verified that $714285 = 5 × 142857$.
This demonstrates an unusual property of 142857: it is a divisor of its right-rotation.
-Find the last 5 digits of the sum of all integers n, 10 < n < 10100, that have this property.
+Find the last 5 digits of the sum of all integers $n$, $10 < n < 10100$, that have this property.
# --hints--
-`euler168()` should return 59206.
+`numberRotations()` should return `59206`.
```js
-assert.strictEqual(euler168(), 59206);
+assert.strictEqual(numberRotations(), 59206);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler168(), 59206);
## --seed-contents--
```js
-function euler168() {
+function numberRotations() {
return true;
}
-euler168();
+numberRotations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 0cfb0034f4..78f6895092 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,26 +11,26 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of different ways n can be expressed as a sum of integer powers of 2 using each power no more than twice.
+Define $f(0)=1$ and $f(n)$ to be the number of different ways $n$ can be expressed as a sum of integer powers of 2 using each power no more than twice.
-For example, f(10)=5 since there are five different ways to express 10:
+For example, $f(10)=5$ since there are five different ways to express 10:
-1 + 1 + 8
+$$\begin{align}
+ & 1 + 1 + 8 \\\\
+ & 1 + 1 + 4 + 4 \\\\
+ & 1 + 1 + 2 + 2 + 4 \\\\
+ & 2 + 4 + 4 \\\\
+ & 2 + 8
+\end{align}$$
-1 + 1 + 4 + 41 + 1 + 2 + 2 + 4
-
-2 + 4 + 4
-
-2 + 8
-
-What is f(1025)?
+What is $f({10}^{25})$?
# --hints--
-`euler169()` should return 178653872807.
+`numberOfWaysToExpress()` should return `178653872807`.
```js
-assert.strictEqual(euler169(), 178653872807);
+assert.strictEqual(numberOfWaysToExpress(), 178653872807);
```
# --seed--
@@ -38,12 +38,12 @@ assert.strictEqual(euler169(), 178653872807);
## --seed-contents--
```js
-function euler169() {
+function numberOfWaysToExpress() {
return true;
}
-euler169();
+numberOfWaysToExpress();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
index f12d0490f2..6cce571bac 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
@@ -13,9 +13,12 @@ dashedName: >-
Take the number 6 and multiply it by each of 1273 and 9854:
-6 × 1273 = 7638 6 × 9854 = 59124
+$$\begin{align}
+ & 6 × 1273 = 7638 \\\\
+ & 6 × 9854 = 59124 \\\\
+\end{align}$$
-By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273,9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
+By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273, 9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
The same can be done for 0 to 9 pandigital numbers.
@@ -23,10 +26,10 @@ What is the largest 0 to 9 pandigital 10-digit concatenated product of an intege
# --hints--
-`euler170()` should return 9857164023.
+`largestPandigital()` should return `9857164023`.
```js
-assert.strictEqual(euler170(), 9857164023);
+assert.strictEqual(largestPandigital(), 9857164023);
```
# --seed--
@@ -34,12 +37,12 @@ assert.strictEqual(euler170(), 9857164023);
## --seed-contents--
```js
-function euler170() {
+function largestPandigital() {
return true;
}
-euler170();
+largestPandigital();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
index d03ddf909b..e4658cd2b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
@@ -11,22 +11,22 @@ dashedName: >-
# --description--
-For a positive integer n, let f(n) be the sum of the squares of the digits (in base 10) of n, e.g.
+For a positive integer $n$, let $f(n)$ be the sum of the squares of the digits (in base 10) of $n$, e.g.
-f(3) = 32 = 9,
+$$\begin{align}
+ & f(3) = 3^2 = 9 \\\\
+ & f(25) = 2^2 + 5^2 = 4 + 25 = 29 \\\\
+ & f(442) = 4^2 + 4^2 + 2^2 = 16 + 16 + 4 = 36 \\\\
+\end{align}$$
-f(25) = 22 + 52 = 4 + 25 = 29,
-
-f(442) = 42 + 42 + 22 = 16 + 16 + 4 = 36
-
-Find the last nine digits of the sum of all n, 0 < n < 1020, such that f(n) is a perfect square.
+Find the last nine digits of the sum of all $n$, $0 < n < {10}^{20}$, such that $f(n)$ is a perfect square.
# --hints--
-`euler171()` should return 142989277.
+`lastDigitsSumOfPerfectSquare()` should return `142989277`.
```js
-assert.strictEqual(euler171(), 142989277);
+assert.strictEqual(lastDigitsSumOfPerfectSquare(), 142989277);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler171(), 142989277);
## --seed-contents--
```js
-function euler171() {
+function lastDigitsSumOfPerfectSquare() {
return true;
}
-euler171();
+lastDigitsSumOfPerfectSquare();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
index a25ab3224f..0ad7b86f36 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
@@ -8,14 +8,14 @@ dashedName: problem-172-investigating-numbers-with-few-repeated-digits
# --description--
-How many 18-digit numbers n (without leading zeros) are there such that no digit occurs more than three times in n?
+How many 18-digit numbers $n$ (without leading zeros) are there such that no digit occurs more than three times in $n$?
# --hints--
-`euler172()` should return 227485267000992000.
+`numbersWithRepeatedDigits()` should return `227485267000992000`.
```js
-assert.strictEqual(euler172(), 227485267000992000);
+assert.strictEqual(numbersWithRepeatedDigits(), 227485267000992000);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler172(), 227485267000992000);
## --seed-contents--
```js
-function euler172() {
+function numbersWithRepeatedDigits() {
return true;
}
-euler172();
+numbersWithRepeatedDigits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
index a07789fd1d..5d49c3b9fa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
@@ -13,14 +13,16 @@ dashedName: >-
We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:
+
+
+Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
+
+It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size $n$ triangle would thus contain $n^2$ size 1 triangle building blocks.
+
+If we denote $T(n)$ as the number of triangles present in a triangle of size $n$, then
+
+$$\begin{align}
+ & T(1) = 16 \\\\
+ & T(2) = 104
+\end{align}$$
+
+Find $T(36)$.
# --hints--
-`euler163()` should return 343047.
+`crossHatchedTriangles()` should return `343047`.
```js
-assert.strictEqual(euler163(), 343047);
+assert.strictEqual(crossHatchedTriangles(), 343047);
```
# --seed--
@@ -25,12 +38,12 @@ assert.strictEqual(euler163(), 343047);
## --seed-contents--
```js
-function euler163() {
+function crossHatchedTriangles() {
return true;
}
-euler163();
+crossHatchedTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
index e511646823..18a4bc8bad 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
@@ -11,14 +11,14 @@ dashedName: >-
# --description--
-How many 20 digit numbers n (without any leading zero) exist such that no three consecutive digits of n have a sum greater than 9?
+How many 20 digit numbers $n$ (without any leading zero) exist such that no three consecutive digits of $n$ have a sum greater than 9?
# --hints--
-`euler164()` should return 378158756814587.
+`consecutiveDigitsSum()` should return `378158756814587`.
```js
-assert.strictEqual(euler164(), 378158756814587);
+assert.strictEqual(consecutiveDigitsSum(), 378158756814587);
```
# --seed--
@@ -26,12 +26,12 @@ assert.strictEqual(euler164(), 378158756814587);
## --seed-contents--
```js
-function euler164() {
+function consecutiveDigitsSum() {
return true;
}
-euler164();
+consecutiveDigitsSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
index a98373c338..9a25a1588c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
@@ -8,22 +8,44 @@ dashedName: problem-165-intersections
# --description--
-A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities:
-
-the segments have zero points, one point, or infinitely many points in common.
+A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities: the segments have zero points, one point, or infinitely many points in common.
Moreover when two segments have exactly one point in common it might be the case that that common point is an endpoint of either one of the segments or of both. If a common point of two segments is not an endpoint of either of the segments it is an interior point of both segments.
-We will call a common point T of two segments L1 and L2 a true intersection point of L1 and L2 if T is the only common point of L1 and L2 and T is an interior point of both segments.
+We will call a common point $T$ of two segments $L_1$ and $L_2$ a true intersection point of $L_1$ and $L_2$ if $T$ is the only common point of $L_1$ and $L_2$ and $T$ is an interior point of both segments.
-Consider the three segments L1, L2, and L3: L1: (27, 44) to (12, 32) L2: (46, 53) to (17, 62) L3: (46, 70) to (22, 40) It can be verified that line segments L2 and L3 have a true intersection point. We note that as the one of the end points of L3: (22,40) lies on L1 this is not considered to be a true point of intersection. L1 and L2 have no common point. So among the three line segments, we find one true intersection point. Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator. s0 = 290797 sn+1 = sn×sn (modulo 50515093) tn = sn (modulo 500) To create each line segment, we use four consecutive numbers tn. That is, the first line segment is given by: (t1, t2) to (t3, t4) The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27,144) to (12,232). How many distinct true intersection points are found among the 5000 line segments?
+Consider the three segments $L_1$, $L_2$, and $L_3$:
+
+$$\begin{align}
+ & L_1: (27, 44) \\;\text{to}\\; (12, 32) \\\\
+ & L_2: (46, 53) \\;\text{to}\\; (17, 62) \\\\
+ & L_3: (46, 70) \\;\text{to}\\; (22, 40) \\\\
+\end{align}$$
+
+It can be verified that line segments $L_2$ and $L_3$ have a true intersection point. We note that as the one of the end points of $L_3$: (22, 40) lies on $L_1$ this is not considered to be a true point of intersection. $L_1$ and $L_2$ have no common point. So among the three line segments, we find one true intersection point.
+
+Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator.
+
+$$\begin{align}
+ & s_0 = 290797 \\\\
+ & s_{n + 1} = s_n × s_n (\text{modulo}\\; 50515093) \\\\
+ & t_n = s_n (\text{modulo}\\; 500) \\\\
+\end{align}$$
+
+To create each line segment, we use four consecutive numbers $t_n$. That is, the first line segment is given by:
+
+($_t$1, $t_2$) to ($t_3$, $t_4$)
+
+The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27, 144) to (12, 232).
+
+How many distinct true intersection points are found among the 5000 line segments?
# --hints--
-`euler165()` should return 2868868.
+`distinctIntersections()` should return `2868868`.
```js
-assert.strictEqual(euler165(), 2868868);
+assert.strictEqual(distinctIntersections(), 2868868);
```
# --seed--
@@ -31,12 +53,12 @@ assert.strictEqual(euler165(), 2868868);
## --seed-contents--
```js
-function euler165() {
+function distinctIntersections() {
return true;
}
-euler165();
+distinctIntersections();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
index 9f1db5cea4..dfb3821789 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
@@ -8,22 +8,27 @@ dashedName: problem-166-criss-cross
# --description--
-A 4x4 grid is filled with digits d, 0 ≤ d ≤ 9.
+A 4x4 grid is filled with digits $d$, $0 ≤ d ≤ 9$.
It can be seen that in the grid
-6 3 3 0 5 0 4 3 0 7 1 4 1 2 4 5
+$$\begin{array}{}
+ 6 & 3 & 3 & 0 \\\\
+ 5 & 0 & 4 & 3 \\\\
+ 0 & 7 & 1 & 4 \\\\
+ 1 & 2 & 4 & 5
+\end{array}$$
the sum of each row and each column has the value 12. Moreover the sum of each diagonal is also 12.
-In how many ways can you fill a 4x4 grid with the digits d, 0 ≤ d ≤ 9 so that each row, each column, and both diagonals have the same sum?
+In how many ways can you fill a 4x4 grid with the digits $d$, $0 ≤ d ≤ 9$ so that each row, each column, and both diagonals have the same sum?
# --hints--
-`euler166()` should return 7130034.
+`crissCross()` should return `7130034`.
```js
-assert.strictEqual(euler166(), 7130034);
+assert.strictEqual(crissCross(), 7130034);
```
# --seed--
@@ -31,12 +36,12 @@ assert.strictEqual(euler166(), 7130034);
## --seed-contents--
```js
-function euler166() {
+function crissCross() {
return true;
}
-euler166();
+crissCross();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
index 6f30b4b272..6e2b3c1b4d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
@@ -8,24 +8,22 @@ dashedName: problem-167-investigating-ulam-sequences
# --description--
-For two positive integers a and b, the Ulam sequence U(a,b) is defined by U(a,b)1 = a, U(a,b)2 = b and for k > 2,
+For two positive integers $a$ and $b$, the Ulam sequence $U(a,b)$ is defined by ${U{(a,b)}\_1} = a$, ${U{(a,b)}\_2} = b$ and for $k > 2$, ${U{(a,b)}\_k}$ is the smallest integer greater than ${U{(a,b)}\_{(k-1)}}$ which can be written in exactly one way as the sum of two distinct previous members of $U(a,b)$.
-U(a,b)k is the smallest integer greater than U(a,b)(k-1) which can be written in exactly one way as the sum of two distinct previous members of U(a,b).
+For example, the sequence $U(1,2)$ begins with
-For example, the sequence U(1,2) begins with
+$$1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8$$
-1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8;
+5 does not belong to it because $5 = 1 + 4 = 2 + 3$ has two representations as the sum of two previous members, likewise $7 = 1 + 6 = 3 + 4$.
-5 does not belong to it because 5 = 1 + 4 = 2 + 3 has two representations as the sum of two previous members, likewise 7 = 1 + 6 = 3 + 4.
-
-Find ∑U(2,2n+1)k for 2 ≤ n ≤10, where k = 1011.
+Find $\sum {U(2, 2n + 1)_k}$ for $2 ≤ n ≤ 10$, where $k = {10}^{11}$.
# --hints--
-`euler167()` should return 3916160068885.
+`ulamSequences()` should return `3916160068885`.
```js
-assert.strictEqual(euler167(), 3916160068885);
+assert.strictEqual(ulamSequences(), 3916160068885);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler167(), 3916160068885);
## --seed-contents--
```js
-function euler167() {
+function ulamSequences() {
return true;
}
-euler167();
+ulamSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
index 9ad5f78e64..6f5c679ed3 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
@@ -10,18 +10,18 @@ dashedName: problem-168-number-rotations
Consider the number 142857. We can right-rotate this number by moving the last digit (7) to the front of it, giving us 714285.
-It can be verified that 714285=5×142857.
+It can be verified that $714285 = 5 × 142857$.
This demonstrates an unusual property of 142857: it is a divisor of its right-rotation.
-Find the last 5 digits of the sum of all integers n, 10 < n < 10100, that have this property.
+Find the last 5 digits of the sum of all integers $n$, $10 < n < 10100$, that have this property.
# --hints--
-`euler168()` should return 59206.
+`numberRotations()` should return `59206`.
```js
-assert.strictEqual(euler168(), 59206);
+assert.strictEqual(numberRotations(), 59206);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler168(), 59206);
## --seed-contents--
```js
-function euler168() {
+function numberRotations() {
return true;
}
-euler168();
+numberRotations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 0cfb0034f4..78f6895092 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,26 +11,26 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of different ways n can be expressed as a sum of integer powers of 2 using each power no more than twice.
+Define $f(0)=1$ and $f(n)$ to be the number of different ways $n$ can be expressed as a sum of integer powers of 2 using each power no more than twice.
-For example, f(10)=5 since there are five different ways to express 10:
+For example, $f(10)=5$ since there are five different ways to express 10:
-1 + 1 + 8
+$$\begin{align}
+ & 1 + 1 + 8 \\\\
+ & 1 + 1 + 4 + 4 \\\\
+ & 1 + 1 + 2 + 2 + 4 \\\\
+ & 2 + 4 + 4 \\\\
+ & 2 + 8
+\end{align}$$
-1 + 1 + 4 + 41 + 1 + 2 + 2 + 4
-
-2 + 4 + 4
-
-2 + 8
-
-What is f(1025)?
+What is $f({10}^{25})$?
# --hints--
-`euler169()` should return 178653872807.
+`numberOfWaysToExpress()` should return `178653872807`.
```js
-assert.strictEqual(euler169(), 178653872807);
+assert.strictEqual(numberOfWaysToExpress(), 178653872807);
```
# --seed--
@@ -38,12 +38,12 @@ assert.strictEqual(euler169(), 178653872807);
## --seed-contents--
```js
-function euler169() {
+function numberOfWaysToExpress() {
return true;
}
-euler169();
+numberOfWaysToExpress();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
index f12d0490f2..6cce571bac 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
@@ -13,9 +13,12 @@ dashedName: >-
Take the number 6 and multiply it by each of 1273 and 9854:
-6 × 1273 = 7638 6 × 9854 = 59124
+$$\begin{align}
+ & 6 × 1273 = 7638 \\\\
+ & 6 × 9854 = 59124 \\\\
+\end{align}$$
-By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273,9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
+By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273, 9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
The same can be done for 0 to 9 pandigital numbers.
@@ -23,10 +26,10 @@ What is the largest 0 to 9 pandigital 10-digit concatenated product of an intege
# --hints--
-`euler170()` should return 9857164023.
+`largestPandigital()` should return `9857164023`.
```js
-assert.strictEqual(euler170(), 9857164023);
+assert.strictEqual(largestPandigital(), 9857164023);
```
# --seed--
@@ -34,12 +37,12 @@ assert.strictEqual(euler170(), 9857164023);
## --seed-contents--
```js
-function euler170() {
+function largestPandigital() {
return true;
}
-euler170();
+largestPandigital();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
index d03ddf909b..e4658cd2b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
@@ -11,22 +11,22 @@ dashedName: >-
# --description--
-For a positive integer n, let f(n) be the sum of the squares of the digits (in base 10) of n, e.g.
+For a positive integer $n$, let $f(n)$ be the sum of the squares of the digits (in base 10) of $n$, e.g.
-f(3) = 32 = 9,
+$$\begin{align}
+ & f(3) = 3^2 = 9 \\\\
+ & f(25) = 2^2 + 5^2 = 4 + 25 = 29 \\\\
+ & f(442) = 4^2 + 4^2 + 2^2 = 16 + 16 + 4 = 36 \\\\
+\end{align}$$
-f(25) = 22 + 52 = 4 + 25 = 29,
-
-f(442) = 42 + 42 + 22 = 16 + 16 + 4 = 36
-
-Find the last nine digits of the sum of all n, 0 < n < 1020, such that f(n) is a perfect square.
+Find the last nine digits of the sum of all $n$, $0 < n < {10}^{20}$, such that $f(n)$ is a perfect square.
# --hints--
-`euler171()` should return 142989277.
+`lastDigitsSumOfPerfectSquare()` should return `142989277`.
```js
-assert.strictEqual(euler171(), 142989277);
+assert.strictEqual(lastDigitsSumOfPerfectSquare(), 142989277);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler171(), 142989277);
## --seed-contents--
```js
-function euler171() {
+function lastDigitsSumOfPerfectSquare() {
return true;
}
-euler171();
+lastDigitsSumOfPerfectSquare();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
index a25ab3224f..0ad7b86f36 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
@@ -8,14 +8,14 @@ dashedName: problem-172-investigating-numbers-with-few-repeated-digits
# --description--
-How many 18-digit numbers n (without leading zeros) are there such that no digit occurs more than three times in n?
+How many 18-digit numbers $n$ (without leading zeros) are there such that no digit occurs more than three times in $n$?
# --hints--
-`euler172()` should return 227485267000992000.
+`numbersWithRepeatedDigits()` should return `227485267000992000`.
```js
-assert.strictEqual(euler172(), 227485267000992000);
+assert.strictEqual(numbersWithRepeatedDigits(), 227485267000992000);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler172(), 227485267000992000);
## --seed-contents--
```js
-function euler172() {
+function numbersWithRepeatedDigits() {
return true;
}
-euler172();
+numbersWithRepeatedDigits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
index a07789fd1d..5d49c3b9fa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
@@ -13,14 +13,16 @@ dashedName: >-
We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:
+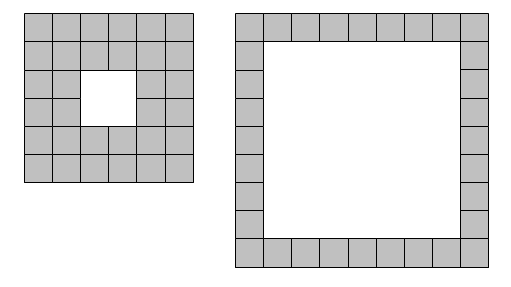 +
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae. Using up to one million tiles how many different square laminae can be formed?
# --hints--
-`euler173()` should return 1572729.
+`differentHollowSquareLaminae()` should return `1572729`.
```js
-assert.strictEqual(euler173(), 1572729);
+assert.strictEqual(differentHollowSquareLaminae(), 1572729);
```
# --seed--
@@ -28,12 +30,12 @@ assert.strictEqual(euler173(), 1572729);
## --seed-contents--
```js
-function euler173() {
+function differentHollowSquareLaminae() {
return true;
}
-euler173();
+differentHollowSquareLaminae();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
index e7183612d5..ff7276377f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
@@ -15,14 +15,20 @@ We shall define a square lamina to be a square outline with a square "hole" so t
Given eight tiles it is possible to form a lamina in only one way: 3x3 square with a 1x1 hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.
-If t represents the number of tiles used, we shall say that t = 8 is type L(1) and t = 32 is type L(2). Let N(n) be the number of t ≤ 1000000 such that t is type L(n); for example, N(15) = 832. What is ∑ N(n) for 1 ≤ n ≤ 10?
+
+
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae. Using up to one million tiles how many different square laminae can be formed?
# --hints--
-`euler173()` should return 1572729.
+`differentHollowSquareLaminae()` should return `1572729`.
```js
-assert.strictEqual(euler173(), 1572729);
+assert.strictEqual(differentHollowSquareLaminae(), 1572729);
```
# --seed--
@@ -28,12 +30,12 @@ assert.strictEqual(euler173(), 1572729);
## --seed-contents--
```js
-function euler173() {
+function differentHollowSquareLaminae() {
return true;
}
-euler173();
+differentHollowSquareLaminae();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
index e7183612d5..ff7276377f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
@@ -15,14 +15,20 @@ We shall define a square lamina to be a square outline with a square "hole" so t
Given eight tiles it is possible to form a lamina in only one way: 3x3 square with a 1x1 hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.
-If t represents the number of tiles used, we shall say that t = 8 is type L(1) and t = 32 is type L(2). Let N(n) be the number of t ≤ 1000000 such that t is type L(n); for example, N(15) = 832. What is ∑ N(n) for 1 ≤ n ≤ 10?
+ +
+If $t$ represents the number of tiles used, we shall say that $t = 8$ is type $L(1)$ and $t = 32$ is type $L(2)$.
+
+Let $N(n)$ be the number of $t ≤ 1000000$ such that $t$ is type $L(n)$; for example, $N(15) = 832$.
+
+What is $\sum N(n)$ for $1 ≤ n ≤ 10$?
# --hints--
-`euler174()` should return 209566.
+`hollowSquareLaminaeDistinctArrangements()` should return `209566`.
```js
-assert.strictEqual(euler174(), 209566);
+assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);
```
# --seed--
@@ -30,12 +36,12 @@ assert.strictEqual(euler174(), 209566);
## --seed-contents--
```js
-function euler174() {
+function hollowSquareLaminaeDistinctArrangements() {
return true;
}
-euler174();
+hollowSquareLaminaeDistinctArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 8f32fcb4bd..20907644d9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,18 +11,36 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of ways to write n as a sum of powers of 2 where no power occurs more than twice.
+Define $f(0) = 1$ and $f(n)$ to be the number of ways to write $n$ as a sum of powers of 2 where no power occurs more than twice.
-For example, f(10)=5 since there are five different ways to express 10:10 = 8+2 = 8+1+1 = 4+4+2 = 4+2+2+1+1 = 4+4+1+1
+For example, $f(10) = 5$ since there are five different ways to express 10:
-It can be shown that for every fraction p/q (p>0, q>0) there exists at least one integer n such that f(n)/f(n-1)=p/q. For instance, the smallest n for which f(n)/f(n-1)=13/17 is 241. The binary expansion of 241 is 11110001. Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241. Find the Shortened Binary Expansion of the smallest n for which f(n)/f(n-1)=123456789/987654321. Give your answer as comma separated integers, without any whitespaces.
+$$10 = 8 + 2 = 8 + 1 + 1 = 4 + 4 + 2 = 4 + 2 + 2 + 1 + 1 = 4 + 4 + 1 + 1$$
+
+It can be shown that for every fraction $\frac{p}{q}\\; (p>0, q>0)$ there exists at least one integer $n$ such that $\frac{f(n)}{f(n - 1)} = \frac{p}{q}$.
+
+For instance, the smallest $n$ for which $\frac{f(n)}{f(n - 1)} = \frac{13}{17}$ is 241. The binary expansion of 241 is 11110001.
+
+Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241.
+
+Find the Shortened Binary Expansion of the smallest $n$ for which
+
+$$\frac{f(n)}{f(n - 1)} = \frac{123456789}{987654321}$$
+
+Give your answer as a string with comma separated integers, without any whitespaces.
# --hints--
-`euler175()` should return 1, 13717420, 8.
+`shortenedBinaryExpansionOfNumber()` should return a string.
```js
-assert.strictEqual(euler175(), 1, 13717420, 8);
+assert(typeof shortenedBinaryExpansionOfNumber() === 'string');
+```
+
+`shortenedBinaryExpansionOfNumber()` should return the string `1,13717420,8`.
+
+```js
+assert.strictEqual(shortenedBinaryExpansionOfNumber(), '1,13717420,8');
```
# --seed--
@@ -30,12 +48,12 @@ assert.strictEqual(euler175(), 1, 13717420, 8);
## --seed-contents--
```js
-function euler175() {
+function shortenedBinaryExpansionOfNumber() {
return true;
}
-euler175();
+shortenedBinaryExpansionOfNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
index c3b6c090fe..d5e7b34ad6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
@@ -14,10 +14,10 @@ Find the smallest integer that can be the length of a cathetus of exactly 47547
# --hints--
-`euler176()` should return 96818198400000.
+`trianglesSharingCathetus()` should return `96818198400000`.
```js
-assert.strictEqual(euler176(), 96818198400000);
+assert.strictEqual(trianglesSharingCathetus(), 96818198400000);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler176(), 96818198400000);
## --seed-contents--
```js
-function euler176() {
+function trianglesSharingCathetus() {
return true;
}
-euler176();
+trianglesSharingCathetus();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
index 2e39114654..686ddad5cd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
@@ -10,14 +10,22 @@ dashedName: problem-177-integer-angled-quadrilaterals
Let ABCD be a convex quadrilateral, with diagonals AC and BD. At each vertex the diagonal makes an angle with each of the two sides, creating eight corner angles.
-For example, at vertex A, the two angles are CAD, CAB. We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°. What is the total number of non-similar integer angled quadrilaterals? Note: In your calculations you may assume that a calculated angle is integral if it is within a tolerance of 10-9 of an integer value.
+
+
+If $t$ represents the number of tiles used, we shall say that $t = 8$ is type $L(1)$ and $t = 32$ is type $L(2)$.
+
+Let $N(n)$ be the number of $t ≤ 1000000$ such that $t$ is type $L(n)$; for example, $N(15) = 832$.
+
+What is $\sum N(n)$ for $1 ≤ n ≤ 10$?
# --hints--
-`euler174()` should return 209566.
+`hollowSquareLaminaeDistinctArrangements()` should return `209566`.
```js
-assert.strictEqual(euler174(), 209566);
+assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);
```
# --seed--
@@ -30,12 +36,12 @@ assert.strictEqual(euler174(), 209566);
## --seed-contents--
```js
-function euler174() {
+function hollowSquareLaminaeDistinctArrangements() {
return true;
}
-euler174();
+hollowSquareLaminaeDistinctArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 8f32fcb4bd..20907644d9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,18 +11,36 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of ways to write n as a sum of powers of 2 where no power occurs more than twice.
+Define $f(0) = 1$ and $f(n)$ to be the number of ways to write $n$ as a sum of powers of 2 where no power occurs more than twice.
-For example, f(10)=5 since there are five different ways to express 10:10 = 8+2 = 8+1+1 = 4+4+2 = 4+2+2+1+1 = 4+4+1+1
+For example, $f(10) = 5$ since there are five different ways to express 10:
-It can be shown that for every fraction p/q (p>0, q>0) there exists at least one integer n such that f(n)/f(n-1)=p/q. For instance, the smallest n for which f(n)/f(n-1)=13/17 is 241. The binary expansion of 241 is 11110001. Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241. Find the Shortened Binary Expansion of the smallest n for which f(n)/f(n-1)=123456789/987654321. Give your answer as comma separated integers, without any whitespaces.
+$$10 = 8 + 2 = 8 + 1 + 1 = 4 + 4 + 2 = 4 + 2 + 2 + 1 + 1 = 4 + 4 + 1 + 1$$
+
+It can be shown that for every fraction $\frac{p}{q}\\; (p>0, q>0)$ there exists at least one integer $n$ such that $\frac{f(n)}{f(n - 1)} = \frac{p}{q}$.
+
+For instance, the smallest $n$ for which $\frac{f(n)}{f(n - 1)} = \frac{13}{17}$ is 241. The binary expansion of 241 is 11110001.
+
+Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241.
+
+Find the Shortened Binary Expansion of the smallest $n$ for which
+
+$$\frac{f(n)}{f(n - 1)} = \frac{123456789}{987654321}$$
+
+Give your answer as a string with comma separated integers, without any whitespaces.
# --hints--
-`euler175()` should return 1, 13717420, 8.
+`shortenedBinaryExpansionOfNumber()` should return a string.
```js
-assert.strictEqual(euler175(), 1, 13717420, 8);
+assert(typeof shortenedBinaryExpansionOfNumber() === 'string');
+```
+
+`shortenedBinaryExpansionOfNumber()` should return the string `1,13717420,8`.
+
+```js
+assert.strictEqual(shortenedBinaryExpansionOfNumber(), '1,13717420,8');
```
# --seed--
@@ -30,12 +48,12 @@ assert.strictEqual(euler175(), 1, 13717420, 8);
## --seed-contents--
```js
-function euler175() {
+function shortenedBinaryExpansionOfNumber() {
return true;
}
-euler175();
+shortenedBinaryExpansionOfNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
index c3b6c090fe..d5e7b34ad6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
@@ -14,10 +14,10 @@ Find the smallest integer that can be the length of a cathetus of exactly 47547
# --hints--
-`euler176()` should return 96818198400000.
+`trianglesSharingCathetus()` should return `96818198400000`.
```js
-assert.strictEqual(euler176(), 96818198400000);
+assert.strictEqual(trianglesSharingCathetus(), 96818198400000);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler176(), 96818198400000);
## --seed-contents--
```js
-function euler176() {
+function trianglesSharingCathetus() {
return true;
}
-euler176();
+trianglesSharingCathetus();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
index 2e39114654..686ddad5cd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
@@ -10,14 +10,22 @@ dashedName: problem-177-integer-angled-quadrilaterals
Let ABCD be a convex quadrilateral, with diagonals AC and BD. At each vertex the diagonal makes an angle with each of the two sides, creating eight corner angles.
-For example, at vertex A, the two angles are CAD, CAB. We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°. What is the total number of non-similar integer angled quadrilaterals? Note: In your calculations you may assume that a calculated angle is integral if it is within a tolerance of 10-9 of an integer value.
+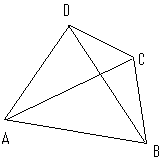 +
+For example, at vertex A, the two angles are CAD, CAB.
+
+We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°.
+
+What is the total number of non-similar integer angled quadrilaterals?
+
+**Note:** In your calculations you may assume that a calculated angle is integral if it is within a tolerance of ${10}^{-9}$ of an integer value.
# --hints--
-`euler177()` should return 129325.
+`integerAngledQuadrilaterals()` should return `129325`.
```js
-assert.strictEqual(euler177(), 129325);
+assert.strictEqual(integerAngledQuadrilaterals(), 129325);
```
# --seed--
@@ -25,12 +33,12 @@ assert.strictEqual(euler177(), 129325);
## --seed-contents--
```js
-function euler177() {
+function integerAngledQuadrilaterals() {
return true;
}
-euler177();
+integerAngledQuadrilaterals();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
index 12bad9c5ad..e9ea0adc66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
@@ -16,14 +16,14 @@ A number for which every pair of consecutive digits has a difference of one is c
A pandigital number contains every decimal digit from 0 to 9 at least once.
-How many pandigital step numbers less than 1040 are there?
+How many pandigital step numbers less than ${10}^{40}$ are there?
# --hints--
-`euler178()` should return 126461847755.
+`stepNumbers()` should return `126461847755`.
```js
-assert.strictEqual(euler178(), 126461847755);
+assert.strictEqual(stepNumbers(), 126461847755);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler178(), 126461847755);
## --seed-contents--
```js
-function euler178() {
+function stepNumbers() {
return true;
}
-euler178();
+stepNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
index 1811def962..9245393058 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
@@ -8,14 +8,14 @@ dashedName: problem-179-consecutive-positive-divisors
# --description--
-Find the number of integers 1 < n < 107, for which n and n + 1 have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
+Find the number of integers $1 < n < {10}^7$, for which $n$ and $n + 1$ have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
# --hints--
-`euler179()` should return 986262.
+`consecutivePositiveDivisors()` should return `986262`.
```js
-assert.strictEqual(euler179(), 986262);
+assert.strictEqual(consecutivePositiveDivisors(), 986262);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler179(), 986262);
## --seed-contents--
```js
-function euler179() {
+function consecutivePositiveDivisors() {
return true;
}
-euler179();
+consecutivePositiveDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
index 3b46677319..e1b5202106 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
@@ -8,30 +8,34 @@ dashedName: problem-180-rational-zeros-of-a-function-of-three-variables
# --description--
-For any integer n, consider the three functions
+For any integer $n$, consider the three functions
-f1,n(x,y,z) = xn+1 + yn+1 − zn+1f2,n(x,y,z) = (xy + yz + zx)\*(xn-1 + yn-1 − zn-1)f3,n(x,y,z) = xyz\*(xn-2 + yn-2 − zn-2)
+$$\begin{align}
+ & f_{1,n}(x,y,z) = x^{n + 1} + y^{n + 1} − z^{n + 1}\\\\
+ & f_{2,n}(x,y,z) = (xy + yz + zx) \times (x^{n - 1} + y^{n - 1} − z^{n - 1})\\\\
+ & f_{3,n}(x,y,z) = xyz \times (x^{n - 2} + y^{n - 2} − z^{n - 2})
+\end{align}$$
and their combination
-fn(x,y,z) = f1,n(x,y,z) + f2,n(x,y,z) − f3,n(x,y,z)
+$$\begin{align}
+ & f_n(x,y,z) = f_{1,n}(x,y,z) + f_{2,n}(x,y,z) − f_{3,n}(x,y,z)
+\end{align}$$
-We call (x,y,z) a golden triple of order k if x, y, and z are all rational numbers of the form a / b with
+We call $(x,y,z)$ a golden triple of order $k$ if $x$, $y$, and $z$ are all rational numbers of the form $\frac{a}{b}$ with $0 < a < b ≤ k$ and there is (at least) one integer $n$, so that $f_n(x,y,z) = 0$.
-0 < a < b ≤ k and there is (at least) one integer n, so that fn(x,y,z) = 0.
+Let $s(x,y,z) = x + y + z$.
-Let s(x,y,z) = x + y + z.
+Let $t = \frac{u}{v}$ be the sum of all distinct $s(x,y,z)$ for all golden triples $(x,y,z)$ of order 35. All the $s(x,y,z)$ and $t$ must be in reduced form.
-Let t = u / v be the sum of all distinct s(x,y,z) for all golden triples (x,y,z) of order 35. All the s(x,y,z) and t must be in reduced form.
-
-Find u + v.
+Find $u + v$.
# --hints--
-`euler180()` should return 285196020571078980.
+`rationalZeros()` should return `285196020571078980`.
```js
-assert.strictEqual(euler180(), 285196020571078980);
+assert.strictEqual(rationalZeros(), 285196020571078980);
```
# --seed--
@@ -39,12 +43,12 @@ assert.strictEqual(euler180(), 285196020571078980);
## --seed-contents--
```js
-function euler180() {
+function rationalZeros() {
return true;
}
-euler180();
+rationalZeros();
```
# --solutions--
+
+For example, at vertex A, the two angles are CAD, CAB.
+
+We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°.
+
+What is the total number of non-similar integer angled quadrilaterals?
+
+**Note:** In your calculations you may assume that a calculated angle is integral if it is within a tolerance of ${10}^{-9}$ of an integer value.
# --hints--
-`euler177()` should return 129325.
+`integerAngledQuadrilaterals()` should return `129325`.
```js
-assert.strictEqual(euler177(), 129325);
+assert.strictEqual(integerAngledQuadrilaterals(), 129325);
```
# --seed--
@@ -25,12 +33,12 @@ assert.strictEqual(euler177(), 129325);
## --seed-contents--
```js
-function euler177() {
+function integerAngledQuadrilaterals() {
return true;
}
-euler177();
+integerAngledQuadrilaterals();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
index 12bad9c5ad..e9ea0adc66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
@@ -16,14 +16,14 @@ A number for which every pair of consecutive digits has a difference of one is c
A pandigital number contains every decimal digit from 0 to 9 at least once.
-How many pandigital step numbers less than 1040 are there?
+How many pandigital step numbers less than ${10}^{40}$ are there?
# --hints--
-`euler178()` should return 126461847755.
+`stepNumbers()` should return `126461847755`.
```js
-assert.strictEqual(euler178(), 126461847755);
+assert.strictEqual(stepNumbers(), 126461847755);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler178(), 126461847755);
## --seed-contents--
```js
-function euler178() {
+function stepNumbers() {
return true;
}
-euler178();
+stepNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
index 1811def962..9245393058 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
@@ -8,14 +8,14 @@ dashedName: problem-179-consecutive-positive-divisors
# --description--
-Find the number of integers 1 < n < 107, for which n and n + 1 have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
+Find the number of integers $1 < n < {10}^7$, for which $n$ and $n + 1$ have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
# --hints--
-`euler179()` should return 986262.
+`consecutivePositiveDivisors()` should return `986262`.
```js
-assert.strictEqual(euler179(), 986262);
+assert.strictEqual(consecutivePositiveDivisors(), 986262);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler179(), 986262);
## --seed-contents--
```js
-function euler179() {
+function consecutivePositiveDivisors() {
return true;
}
-euler179();
+consecutivePositiveDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
index 3b46677319..e1b5202106 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
@@ -8,30 +8,34 @@ dashedName: problem-180-rational-zeros-of-a-function-of-three-variables
# --description--
-For any integer n, consider the three functions
+For any integer $n$, consider the three functions
-f1,n(x,y,z) = xn+1 + yn+1 − zn+1f2,n(x,y,z) = (xy + yz + zx)\*(xn-1 + yn-1 − zn-1)f3,n(x,y,z) = xyz\*(xn-2 + yn-2 − zn-2)
+$$\begin{align}
+ & f_{1,n}(x,y,z) = x^{n + 1} + y^{n + 1} − z^{n + 1}\\\\
+ & f_{2,n}(x,y,z) = (xy + yz + zx) \times (x^{n - 1} + y^{n - 1} − z^{n - 1})\\\\
+ & f_{3,n}(x,y,z) = xyz \times (x^{n - 2} + y^{n - 2} − z^{n - 2})
+\end{align}$$
and their combination
-fn(x,y,z) = f1,n(x,y,z) + f2,n(x,y,z) − f3,n(x,y,z)
+$$\begin{align}
+ & f_n(x,y,z) = f_{1,n}(x,y,z) + f_{2,n}(x,y,z) − f_{3,n}(x,y,z)
+\end{align}$$
-We call (x,y,z) a golden triple of order k if x, y, and z are all rational numbers of the form a / b with
+We call $(x,y,z)$ a golden triple of order $k$ if $x$, $y$, and $z$ are all rational numbers of the form $\frac{a}{b}$ with $0 < a < b ≤ k$ and there is (at least) one integer $n$, so that $f_n(x,y,z) = 0$.
-0 < a < b ≤ k and there is (at least) one integer n, so that fn(x,y,z) = 0.
+Let $s(x,y,z) = x + y + z$.
-Let s(x,y,z) = x + y + z.
+Let $t = \frac{u}{v}$ be the sum of all distinct $s(x,y,z)$ for all golden triples $(x,y,z)$ of order 35. All the $s(x,y,z)$ and $t$ must be in reduced form.
-Let t = u / v be the sum of all distinct s(x,y,z) for all golden triples (x,y,z) of order 35. All the s(x,y,z) and t must be in reduced form.
-
-Find u + v.
+Find $u + v$.
# --hints--
-`euler180()` should return 285196020571078980.
+`rationalZeros()` should return `285196020571078980`.
```js
-assert.strictEqual(euler180(), 285196020571078980);
+assert.strictEqual(rationalZeros(), 285196020571078980);
```
# --seed--
@@ -39,12 +43,12 @@ assert.strictEqual(euler180(), 285196020571078980);
## --seed-contents--
```js
-function euler180() {
+function rationalZeros() {
return true;
}
-euler180();
+rationalZeros();
```
# --solutions--
 +
If all possible orientations are taken into account there are six:
+
+
If all possible orientations are taken into account there are six:
+ +
Any n by m grid for which nxm is divisible by 3 can be tiled with triominoes. If we consider tilings that can be obtained by reflection or rotation from another tiling as different there are 41 ways a 2 by 9 grid can be tiled with triominoes:
+
+
Any n by m grid for which nxm is divisible by 3 can be tiled with triominoes. If we consider tilings that can be obtained by reflection or rotation from another tiling as different there are 41 ways a 2 by 9 grid can be tiled with triominoes:
+ +
In how many ways can a 9 by 12 grid be tiled in this way by triominoes?
# --hints--
-`euler161()` should return 20574308184277972.
+`triominoes()` should return `20574308184277972`.
```js
-assert.strictEqual(euler161(), 20574308184277972);
+assert.strictEqual(triominoes(), 20574308184277972);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler161(), 20574308184277972);
## --seed-contents--
```js
-function euler161() {
+function triominoes() {
return true;
}
-euler161();
+triominoes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
index 53a6bcd772..8b63fdc2ab 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
@@ -10,9 +10,9 @@ dashedName: problem-162-hexadecimal-numbers
In the hexadecimal number system numbers are represented using 16 different digits:
-0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
+$$0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F$$
-The hexadecimal number AF when written in the decimal number system equals 10x16+15=175.
+The hexadecimal number AF when written in the decimal number system equals $10 \times 16 + 15 = 175$.
In the 3-digit hexadecimal numbers 10A, 1A0, A10, and A01 the digits 0,1 and A are all present.
@@ -20,16 +20,22 @@ Like numbers written in base ten we write hexadecimal numbers without leading ze
How many hexadecimal numbers containing at most sixteen hexadecimal digits exist with all of the digits 0,1, and A present at least once?
-Give your answer as a hexadecimal number.
+Give your answer with hexadecimal number as a string.
-(A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
+**Note:** (A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
# --hints--
-`euler162()` should return 3D58725572C62302.
+`hexadecimalNumbers()` should return a string.
```js
-assert.strictEqual(euler162(), '3D58725572C62302');
+assert(typeof hexadecimalNumbers() === 'string');
+```
+
+`hexadecimalNumbers()` should return the string `3D58725572C62302`.
+
+```js
+assert.strictEqual(hexadecimalNumbers(), '3D58725572C62302');
```
# --seed--
@@ -37,12 +43,12 @@ assert.strictEqual(euler162(), '3D58725572C62302');
## --seed-contents--
```js
-function euler162() {
+function hexadecimalNumbers() {
return true;
}
-euler162();
+hexadecimalNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
index 72ed1158b1..1bd17c7351 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
@@ -10,14 +10,27 @@ dashedName: problem-163-cross-hatched-triangles
Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
-Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle. It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size n triangle would thus contain n2 size 1 triangle building blocks. If we denote T(n) as the number of triangles present in a triangle of size n, then T(1) = 16 T(2) = 104 Find T(36).
+
+
In how many ways can a 9 by 12 grid be tiled in this way by triominoes?
# --hints--
-`euler161()` should return 20574308184277972.
+`triominoes()` should return `20574308184277972`.
```js
-assert.strictEqual(euler161(), 20574308184277972);
+assert.strictEqual(triominoes(), 20574308184277972);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler161(), 20574308184277972);
## --seed-contents--
```js
-function euler161() {
+function triominoes() {
return true;
}
-euler161();
+triominoes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
index 53a6bcd772..8b63fdc2ab 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-162-hexadecimal-numbers.md
@@ -10,9 +10,9 @@ dashedName: problem-162-hexadecimal-numbers
In the hexadecimal number system numbers are represented using 16 different digits:
-0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F
+$$0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F$$
-The hexadecimal number AF when written in the decimal number system equals 10x16+15=175.
+The hexadecimal number AF when written in the decimal number system equals $10 \times 16 + 15 = 175$.
In the 3-digit hexadecimal numbers 10A, 1A0, A10, and A01 the digits 0,1 and A are all present.
@@ -20,16 +20,22 @@ Like numbers written in base ten we write hexadecimal numbers without leading ze
How many hexadecimal numbers containing at most sixteen hexadecimal digits exist with all of the digits 0,1, and A present at least once?
-Give your answer as a hexadecimal number.
+Give your answer with hexadecimal number as a string.
-(A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
+**Note:** (A,B,C,D,E and F in upper case, without any leading or trailing code that marks the number as hexadecimal and without leading zeroes , e.g. 1A3F and not: 1a3f and not 0x1a3f and not $1A3F and not #1A3F and not 0000001A3F)
# --hints--
-`euler162()` should return 3D58725572C62302.
+`hexadecimalNumbers()` should return a string.
```js
-assert.strictEqual(euler162(), '3D58725572C62302');
+assert(typeof hexadecimalNumbers() === 'string');
+```
+
+`hexadecimalNumbers()` should return the string `3D58725572C62302`.
+
+```js
+assert.strictEqual(hexadecimalNumbers(), '3D58725572C62302');
```
# --seed--
@@ -37,12 +43,12 @@ assert.strictEqual(euler162(), '3D58725572C62302');
## --seed-contents--
```js
-function euler162() {
+function hexadecimalNumbers() {
return true;
}
-euler162();
+hexadecimalNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
index 72ed1158b1..1bd17c7351 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-163-cross-hatched-triangles.md
@@ -10,14 +10,27 @@ dashedName: problem-163-cross-hatched-triangles
Consider an equilateral triangle in which straight lines are drawn from each vertex to the middle of the opposite side, such as in the size 1 triangle in the sketch below.
-Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle. It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size n triangle would thus contain n2 size 1 triangle building blocks. If we denote T(n) as the number of triangles present in a triangle of size n, then T(1) = 16 T(2) = 104 Find T(36).
+ +
+Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
+
+It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size $n$ triangle would thus contain $n^2$ size 1 triangle building blocks.
+
+If we denote $T(n)$ as the number of triangles present in a triangle of size $n$, then
+
+$$\begin{align}
+ & T(1) = 16 \\\\
+ & T(2) = 104
+\end{align}$$
+
+Find $T(36)$.
# --hints--
-`euler163()` should return 343047.
+`crossHatchedTriangles()` should return `343047`.
```js
-assert.strictEqual(euler163(), 343047);
+assert.strictEqual(crossHatchedTriangles(), 343047);
```
# --seed--
@@ -25,12 +38,12 @@ assert.strictEqual(euler163(), 343047);
## --seed-contents--
```js
-function euler163() {
+function crossHatchedTriangles() {
return true;
}
-euler163();
+crossHatchedTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
index e511646823..18a4bc8bad 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
@@ -11,14 +11,14 @@ dashedName: >-
# --description--
-How many 20 digit numbers n (without any leading zero) exist such that no three consecutive digits of n have a sum greater than 9?
+How many 20 digit numbers $n$ (without any leading zero) exist such that no three consecutive digits of $n$ have a sum greater than 9?
# --hints--
-`euler164()` should return 378158756814587.
+`consecutiveDigitsSum()` should return `378158756814587`.
```js
-assert.strictEqual(euler164(), 378158756814587);
+assert.strictEqual(consecutiveDigitsSum(), 378158756814587);
```
# --seed--
@@ -26,12 +26,12 @@ assert.strictEqual(euler164(), 378158756814587);
## --seed-contents--
```js
-function euler164() {
+function consecutiveDigitsSum() {
return true;
}
-euler164();
+consecutiveDigitsSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
index a98373c338..9a25a1588c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
@@ -8,22 +8,44 @@ dashedName: problem-165-intersections
# --description--
-A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities:
-
-the segments have zero points, one point, or infinitely many points in common.
+A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities: the segments have zero points, one point, or infinitely many points in common.
Moreover when two segments have exactly one point in common it might be the case that that common point is an endpoint of either one of the segments or of both. If a common point of two segments is not an endpoint of either of the segments it is an interior point of both segments.
-We will call a common point T of two segments L1 and L2 a true intersection point of L1 and L2 if T is the only common point of L1 and L2 and T is an interior point of both segments.
+We will call a common point $T$ of two segments $L_1$ and $L_2$ a true intersection point of $L_1$ and $L_2$ if $T$ is the only common point of $L_1$ and $L_2$ and $T$ is an interior point of both segments.
-Consider the three segments L1, L2, and L3: L1: (27, 44) to (12, 32) L2: (46, 53) to (17, 62) L3: (46, 70) to (22, 40) It can be verified that line segments L2 and L3 have a true intersection point. We note that as the one of the end points of L3: (22,40) lies on L1 this is not considered to be a true point of intersection. L1 and L2 have no common point. So among the three line segments, we find one true intersection point. Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator. s0 = 290797 sn+1 = sn×sn (modulo 50515093) tn = sn (modulo 500) To create each line segment, we use four consecutive numbers tn. That is, the first line segment is given by: (t1, t2) to (t3, t4) The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27,144) to (12,232). How many distinct true intersection points are found among the 5000 line segments?
+Consider the three segments $L_1$, $L_2$, and $L_3$:
+
+$$\begin{align}
+ & L_1: (27, 44) \\;\text{to}\\; (12, 32) \\\\
+ & L_2: (46, 53) \\;\text{to}\\; (17, 62) \\\\
+ & L_3: (46, 70) \\;\text{to}\\; (22, 40) \\\\
+\end{align}$$
+
+It can be verified that line segments $L_2$ and $L_3$ have a true intersection point. We note that as the one of the end points of $L_3$: (22, 40) lies on $L_1$ this is not considered to be a true point of intersection. $L_1$ and $L_2$ have no common point. So among the three line segments, we find one true intersection point.
+
+Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator.
+
+$$\begin{align}
+ & s_0 = 290797 \\\\
+ & s_{n + 1} = s_n × s_n (\text{modulo}\\; 50515093) \\\\
+ & t_n = s_n (\text{modulo}\\; 500) \\\\
+\end{align}$$
+
+To create each line segment, we use four consecutive numbers $t_n$. That is, the first line segment is given by:
+
+($_t$1, $t_2$) to ($t_3$, $t_4$)
+
+The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27, 144) to (12, 232).
+
+How many distinct true intersection points are found among the 5000 line segments?
# --hints--
-`euler165()` should return 2868868.
+`distinctIntersections()` should return `2868868`.
```js
-assert.strictEqual(euler165(), 2868868);
+assert.strictEqual(distinctIntersections(), 2868868);
```
# --seed--
@@ -31,12 +53,12 @@ assert.strictEqual(euler165(), 2868868);
## --seed-contents--
```js
-function euler165() {
+function distinctIntersections() {
return true;
}
-euler165();
+distinctIntersections();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
index 9f1db5cea4..dfb3821789 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
@@ -8,22 +8,27 @@ dashedName: problem-166-criss-cross
# --description--
-A 4x4 grid is filled with digits d, 0 ≤ d ≤ 9.
+A 4x4 grid is filled with digits $d$, $0 ≤ d ≤ 9$.
It can be seen that in the grid
-6 3 3 0 5 0 4 3 0 7 1 4 1 2 4 5
+$$\begin{array}{}
+ 6 & 3 & 3 & 0 \\\\
+ 5 & 0 & 4 & 3 \\\\
+ 0 & 7 & 1 & 4 \\\\
+ 1 & 2 & 4 & 5
+\end{array}$$
the sum of each row and each column has the value 12. Moreover the sum of each diagonal is also 12.
-In how many ways can you fill a 4x4 grid with the digits d, 0 ≤ d ≤ 9 so that each row, each column, and both diagonals have the same sum?
+In how many ways can you fill a 4x4 grid with the digits $d$, $0 ≤ d ≤ 9$ so that each row, each column, and both diagonals have the same sum?
# --hints--
-`euler166()` should return 7130034.
+`crissCross()` should return `7130034`.
```js
-assert.strictEqual(euler166(), 7130034);
+assert.strictEqual(crissCross(), 7130034);
```
# --seed--
@@ -31,12 +36,12 @@ assert.strictEqual(euler166(), 7130034);
## --seed-contents--
```js
-function euler166() {
+function crissCross() {
return true;
}
-euler166();
+crissCross();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
index 6f30b4b272..6e2b3c1b4d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
@@ -8,24 +8,22 @@ dashedName: problem-167-investigating-ulam-sequences
# --description--
-For two positive integers a and b, the Ulam sequence U(a,b) is defined by U(a,b)1 = a, U(a,b)2 = b and for k > 2,
+For two positive integers $a$ and $b$, the Ulam sequence $U(a,b)$ is defined by ${U{(a,b)}\_1} = a$, ${U{(a,b)}\_2} = b$ and for $k > 2$, ${U{(a,b)}\_k}$ is the smallest integer greater than ${U{(a,b)}\_{(k-1)}}$ which can be written in exactly one way as the sum of two distinct previous members of $U(a,b)$.
-U(a,b)k is the smallest integer greater than U(a,b)(k-1) which can be written in exactly one way as the sum of two distinct previous members of U(a,b).
+For example, the sequence $U(1,2)$ begins with
-For example, the sequence U(1,2) begins with
+$$1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8$$
-1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8;
+5 does not belong to it because $5 = 1 + 4 = 2 + 3$ has two representations as the sum of two previous members, likewise $7 = 1 + 6 = 3 + 4$.
-5 does not belong to it because 5 = 1 + 4 = 2 + 3 has two representations as the sum of two previous members, likewise 7 = 1 + 6 = 3 + 4.
-
-Find ∑U(2,2n+1)k for 2 ≤ n ≤10, where k = 1011.
+Find $\sum {U(2, 2n + 1)_k}$ for $2 ≤ n ≤ 10$, where $k = {10}^{11}$.
# --hints--
-`euler167()` should return 3916160068885.
+`ulamSequences()` should return `3916160068885`.
```js
-assert.strictEqual(euler167(), 3916160068885);
+assert.strictEqual(ulamSequences(), 3916160068885);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler167(), 3916160068885);
## --seed-contents--
```js
-function euler167() {
+function ulamSequences() {
return true;
}
-euler167();
+ulamSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
index 9ad5f78e64..6f5c679ed3 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
@@ -10,18 +10,18 @@ dashedName: problem-168-number-rotations
Consider the number 142857. We can right-rotate this number by moving the last digit (7) to the front of it, giving us 714285.
-It can be verified that 714285=5×142857.
+It can be verified that $714285 = 5 × 142857$.
This demonstrates an unusual property of 142857: it is a divisor of its right-rotation.
-Find the last 5 digits of the sum of all integers n, 10 < n < 10100, that have this property.
+Find the last 5 digits of the sum of all integers $n$, $10 < n < 10100$, that have this property.
# --hints--
-`euler168()` should return 59206.
+`numberRotations()` should return `59206`.
```js
-assert.strictEqual(euler168(), 59206);
+assert.strictEqual(numberRotations(), 59206);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler168(), 59206);
## --seed-contents--
```js
-function euler168() {
+function numberRotations() {
return true;
}
-euler168();
+numberRotations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 0cfb0034f4..78f6895092 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,26 +11,26 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of different ways n can be expressed as a sum of integer powers of 2 using each power no more than twice.
+Define $f(0)=1$ and $f(n)$ to be the number of different ways $n$ can be expressed as a sum of integer powers of 2 using each power no more than twice.
-For example, f(10)=5 since there are five different ways to express 10:
+For example, $f(10)=5$ since there are five different ways to express 10:
-1 + 1 + 8
+$$\begin{align}
+ & 1 + 1 + 8 \\\\
+ & 1 + 1 + 4 + 4 \\\\
+ & 1 + 1 + 2 + 2 + 4 \\\\
+ & 2 + 4 + 4 \\\\
+ & 2 + 8
+\end{align}$$
-1 + 1 + 4 + 41 + 1 + 2 + 2 + 4
-
-2 + 4 + 4
-
-2 + 8
-
-What is f(1025)?
+What is $f({10}^{25})$?
# --hints--
-`euler169()` should return 178653872807.
+`numberOfWaysToExpress()` should return `178653872807`.
```js
-assert.strictEqual(euler169(), 178653872807);
+assert.strictEqual(numberOfWaysToExpress(), 178653872807);
```
# --seed--
@@ -38,12 +38,12 @@ assert.strictEqual(euler169(), 178653872807);
## --seed-contents--
```js
-function euler169() {
+function numberOfWaysToExpress() {
return true;
}
-euler169();
+numberOfWaysToExpress();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
index f12d0490f2..6cce571bac 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
@@ -13,9 +13,12 @@ dashedName: >-
Take the number 6 and multiply it by each of 1273 and 9854:
-6 × 1273 = 7638 6 × 9854 = 59124
+$$\begin{align}
+ & 6 × 1273 = 7638 \\\\
+ & 6 × 9854 = 59124 \\\\
+\end{align}$$
-By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273,9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
+By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273, 9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
The same can be done for 0 to 9 pandigital numbers.
@@ -23,10 +26,10 @@ What is the largest 0 to 9 pandigital 10-digit concatenated product of an intege
# --hints--
-`euler170()` should return 9857164023.
+`largestPandigital()` should return `9857164023`.
```js
-assert.strictEqual(euler170(), 9857164023);
+assert.strictEqual(largestPandigital(), 9857164023);
```
# --seed--
@@ -34,12 +37,12 @@ assert.strictEqual(euler170(), 9857164023);
## --seed-contents--
```js
-function euler170() {
+function largestPandigital() {
return true;
}
-euler170();
+largestPandigital();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
index d03ddf909b..e4658cd2b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
@@ -11,22 +11,22 @@ dashedName: >-
# --description--
-For a positive integer n, let f(n) be the sum of the squares of the digits (in base 10) of n, e.g.
+For a positive integer $n$, let $f(n)$ be the sum of the squares of the digits (in base 10) of $n$, e.g.
-f(3) = 32 = 9,
+$$\begin{align}
+ & f(3) = 3^2 = 9 \\\\
+ & f(25) = 2^2 + 5^2 = 4 + 25 = 29 \\\\
+ & f(442) = 4^2 + 4^2 + 2^2 = 16 + 16 + 4 = 36 \\\\
+\end{align}$$
-f(25) = 22 + 52 = 4 + 25 = 29,
-
-f(442) = 42 + 42 + 22 = 16 + 16 + 4 = 36
-
-Find the last nine digits of the sum of all n, 0 < n < 1020, such that f(n) is a perfect square.
+Find the last nine digits of the sum of all $n$, $0 < n < {10}^{20}$, such that $f(n)$ is a perfect square.
# --hints--
-`euler171()` should return 142989277.
+`lastDigitsSumOfPerfectSquare()` should return `142989277`.
```js
-assert.strictEqual(euler171(), 142989277);
+assert.strictEqual(lastDigitsSumOfPerfectSquare(), 142989277);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler171(), 142989277);
## --seed-contents--
```js
-function euler171() {
+function lastDigitsSumOfPerfectSquare() {
return true;
}
-euler171();
+lastDigitsSumOfPerfectSquare();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
index a25ab3224f..0ad7b86f36 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
@@ -8,14 +8,14 @@ dashedName: problem-172-investigating-numbers-with-few-repeated-digits
# --description--
-How many 18-digit numbers n (without leading zeros) are there such that no digit occurs more than three times in n?
+How many 18-digit numbers $n$ (without leading zeros) are there such that no digit occurs more than three times in $n$?
# --hints--
-`euler172()` should return 227485267000992000.
+`numbersWithRepeatedDigits()` should return `227485267000992000`.
```js
-assert.strictEqual(euler172(), 227485267000992000);
+assert.strictEqual(numbersWithRepeatedDigits(), 227485267000992000);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler172(), 227485267000992000);
## --seed-contents--
```js
-function euler172() {
+function numbersWithRepeatedDigits() {
return true;
}
-euler172();
+numbersWithRepeatedDigits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
index a07789fd1d..5d49c3b9fa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
@@ -13,14 +13,16 @@ dashedName: >-
We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:
+
+
+Sixteen triangles of either different shape or size or orientation or location can now be observed in that triangle. Using size 1 triangles as building blocks, larger triangles can be formed, such as the size 2 triangle in the above sketch. One-hundred and four triangles of either different shape or size or orientation or location can now be observed in that size 2 triangle.
+
+It can be observed that the size 2 triangle contains 4 size 1 triangle building blocks. A size 3 triangle would contain 9 size 1 triangle building blocks and a size $n$ triangle would thus contain $n^2$ size 1 triangle building blocks.
+
+If we denote $T(n)$ as the number of triangles present in a triangle of size $n$, then
+
+$$\begin{align}
+ & T(1) = 16 \\\\
+ & T(2) = 104
+\end{align}$$
+
+Find $T(36)$.
# --hints--
-`euler163()` should return 343047.
+`crossHatchedTriangles()` should return `343047`.
```js
-assert.strictEqual(euler163(), 343047);
+assert.strictEqual(crossHatchedTriangles(), 343047);
```
# --seed--
@@ -25,12 +38,12 @@ assert.strictEqual(euler163(), 343047);
## --seed-contents--
```js
-function euler163() {
+function crossHatchedTriangles() {
return true;
}
-euler163();
+crossHatchedTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
index e511646823..18a4bc8bad 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-164-numbers-for-which-no-three-consecutive-digits-have-a-sum-greater-than-a-given-value.md
@@ -11,14 +11,14 @@ dashedName: >-
# --description--
-How many 20 digit numbers n (without any leading zero) exist such that no three consecutive digits of n have a sum greater than 9?
+How many 20 digit numbers $n$ (without any leading zero) exist such that no three consecutive digits of $n$ have a sum greater than 9?
# --hints--
-`euler164()` should return 378158756814587.
+`consecutiveDigitsSum()` should return `378158756814587`.
```js
-assert.strictEqual(euler164(), 378158756814587);
+assert.strictEqual(consecutiveDigitsSum(), 378158756814587);
```
# --seed--
@@ -26,12 +26,12 @@ assert.strictEqual(euler164(), 378158756814587);
## --seed-contents--
```js
-function euler164() {
+function consecutiveDigitsSum() {
return true;
}
-euler164();
+consecutiveDigitsSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
index a98373c338..9a25a1588c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-165-intersections.md
@@ -8,22 +8,44 @@ dashedName: problem-165-intersections
# --description--
-A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities:
-
-the segments have zero points, one point, or infinitely many points in common.
+A segment is uniquely defined by its two endpoints. By considering two line segments in plane geometry there are three possibilities: the segments have zero points, one point, or infinitely many points in common.
Moreover when two segments have exactly one point in common it might be the case that that common point is an endpoint of either one of the segments or of both. If a common point of two segments is not an endpoint of either of the segments it is an interior point of both segments.
-We will call a common point T of two segments L1 and L2 a true intersection point of L1 and L2 if T is the only common point of L1 and L2 and T is an interior point of both segments.
+We will call a common point $T$ of two segments $L_1$ and $L_2$ a true intersection point of $L_1$ and $L_2$ if $T$ is the only common point of $L_1$ and $L_2$ and $T$ is an interior point of both segments.
-Consider the three segments L1, L2, and L3: L1: (27, 44) to (12, 32) L2: (46, 53) to (17, 62) L3: (46, 70) to (22, 40) It can be verified that line segments L2 and L3 have a true intersection point. We note that as the one of the end points of L3: (22,40) lies on L1 this is not considered to be a true point of intersection. L1 and L2 have no common point. So among the three line segments, we find one true intersection point. Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator. s0 = 290797 sn+1 = sn×sn (modulo 50515093) tn = sn (modulo 500) To create each line segment, we use four consecutive numbers tn. That is, the first line segment is given by: (t1, t2) to (t3, t4) The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27,144) to (12,232). How many distinct true intersection points are found among the 5000 line segments?
+Consider the three segments $L_1$, $L_2$, and $L_3$:
+
+$$\begin{align}
+ & L_1: (27, 44) \\;\text{to}\\; (12, 32) \\\\
+ & L_2: (46, 53) \\;\text{to}\\; (17, 62) \\\\
+ & L_3: (46, 70) \\;\text{to}\\; (22, 40) \\\\
+\end{align}$$
+
+It can be verified that line segments $L_2$ and $L_3$ have a true intersection point. We note that as the one of the end points of $L_3$: (22, 40) lies on $L_1$ this is not considered to be a true point of intersection. $L_1$ and $L_2$ have no common point. So among the three line segments, we find one true intersection point.
+
+Now let us do the same for 5000 line segments. To this end, we generate 20000 numbers using the so-called "Blum Blum Shub" pseudo-random number generator.
+
+$$\begin{align}
+ & s_0 = 290797 \\\\
+ & s_{n + 1} = s_n × s_n (\text{modulo}\\; 50515093) \\\\
+ & t_n = s_n (\text{modulo}\\; 500) \\\\
+\end{align}$$
+
+To create each line segment, we use four consecutive numbers $t_n$. That is, the first line segment is given by:
+
+($_t$1, $t_2$) to ($t_3$, $t_4$)
+
+The first four numbers computed according to the above generator should be: 27, 144, 12 and 232. The first segment would thus be (27, 144) to (12, 232).
+
+How many distinct true intersection points are found among the 5000 line segments?
# --hints--
-`euler165()` should return 2868868.
+`distinctIntersections()` should return `2868868`.
```js
-assert.strictEqual(euler165(), 2868868);
+assert.strictEqual(distinctIntersections(), 2868868);
```
# --seed--
@@ -31,12 +53,12 @@ assert.strictEqual(euler165(), 2868868);
## --seed-contents--
```js
-function euler165() {
+function distinctIntersections() {
return true;
}
-euler165();
+distinctIntersections();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
index 9f1db5cea4..dfb3821789 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-166-criss-cross.md
@@ -8,22 +8,27 @@ dashedName: problem-166-criss-cross
# --description--
-A 4x4 grid is filled with digits d, 0 ≤ d ≤ 9.
+A 4x4 grid is filled with digits $d$, $0 ≤ d ≤ 9$.
It can be seen that in the grid
-6 3 3 0 5 0 4 3 0 7 1 4 1 2 4 5
+$$\begin{array}{}
+ 6 & 3 & 3 & 0 \\\\
+ 5 & 0 & 4 & 3 \\\\
+ 0 & 7 & 1 & 4 \\\\
+ 1 & 2 & 4 & 5
+\end{array}$$
the sum of each row and each column has the value 12. Moreover the sum of each diagonal is also 12.
-In how many ways can you fill a 4x4 grid with the digits d, 0 ≤ d ≤ 9 so that each row, each column, and both diagonals have the same sum?
+In how many ways can you fill a 4x4 grid with the digits $d$, $0 ≤ d ≤ 9$ so that each row, each column, and both diagonals have the same sum?
# --hints--
-`euler166()` should return 7130034.
+`crissCross()` should return `7130034`.
```js
-assert.strictEqual(euler166(), 7130034);
+assert.strictEqual(crissCross(), 7130034);
```
# --seed--
@@ -31,12 +36,12 @@ assert.strictEqual(euler166(), 7130034);
## --seed-contents--
```js
-function euler166() {
+function crissCross() {
return true;
}
-euler166();
+crissCross();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
index 6f30b4b272..6e2b3c1b4d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-167-investigating-ulam-sequences.md
@@ -8,24 +8,22 @@ dashedName: problem-167-investigating-ulam-sequences
# --description--
-For two positive integers a and b, the Ulam sequence U(a,b) is defined by U(a,b)1 = a, U(a,b)2 = b and for k > 2,
+For two positive integers $a$ and $b$, the Ulam sequence $U(a,b)$ is defined by ${U{(a,b)}\_1} = a$, ${U{(a,b)}\_2} = b$ and for $k > 2$, ${U{(a,b)}\_k}$ is the smallest integer greater than ${U{(a,b)}\_{(k-1)}}$ which can be written in exactly one way as the sum of two distinct previous members of $U(a,b)$.
-U(a,b)k is the smallest integer greater than U(a,b)(k-1) which can be written in exactly one way as the sum of two distinct previous members of U(a,b).
+For example, the sequence $U(1,2)$ begins with
-For example, the sequence U(1,2) begins with
+$$1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8$$
-1, 2, 3 = 1 + 2, 4 = 1 + 3, 6 = 2 + 4, 8 = 2 + 6, 11 = 3 + 8;
+5 does not belong to it because $5 = 1 + 4 = 2 + 3$ has two representations as the sum of two previous members, likewise $7 = 1 + 6 = 3 + 4$.
-5 does not belong to it because 5 = 1 + 4 = 2 + 3 has two representations as the sum of two previous members, likewise 7 = 1 + 6 = 3 + 4.
-
-Find ∑U(2,2n+1)k for 2 ≤ n ≤10, where k = 1011.
+Find $\sum {U(2, 2n + 1)_k}$ for $2 ≤ n ≤ 10$, where $k = {10}^{11}$.
# --hints--
-`euler167()` should return 3916160068885.
+`ulamSequences()` should return `3916160068885`.
```js
-assert.strictEqual(euler167(), 3916160068885);
+assert.strictEqual(ulamSequences(), 3916160068885);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler167(), 3916160068885);
## --seed-contents--
```js
-function euler167() {
+function ulamSequences() {
return true;
}
-euler167();
+ulamSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
index 9ad5f78e64..6f5c679ed3 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-168-number-rotations.md
@@ -10,18 +10,18 @@ dashedName: problem-168-number-rotations
Consider the number 142857. We can right-rotate this number by moving the last digit (7) to the front of it, giving us 714285.
-It can be verified that 714285=5×142857.
+It can be verified that $714285 = 5 × 142857$.
This demonstrates an unusual property of 142857: it is a divisor of its right-rotation.
-Find the last 5 digits of the sum of all integers n, 10 < n < 10100, that have this property.
+Find the last 5 digits of the sum of all integers $n$, $10 < n < 10100$, that have this property.
# --hints--
-`euler168()` should return 59206.
+`numberRotations()` should return `59206`.
```js
-assert.strictEqual(euler168(), 59206);
+assert.strictEqual(numberRotations(), 59206);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler168(), 59206);
## --seed-contents--
```js
-function euler168() {
+function numberRotations() {
return true;
}
-euler168();
+numberRotations();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 0cfb0034f4..78f6895092 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-169-exploring-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,26 +11,26 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of different ways n can be expressed as a sum of integer powers of 2 using each power no more than twice.
+Define $f(0)=1$ and $f(n)$ to be the number of different ways $n$ can be expressed as a sum of integer powers of 2 using each power no more than twice.
-For example, f(10)=5 since there are five different ways to express 10:
+For example, $f(10)=5$ since there are five different ways to express 10:
-1 + 1 + 8
+$$\begin{align}
+ & 1 + 1 + 8 \\\\
+ & 1 + 1 + 4 + 4 \\\\
+ & 1 + 1 + 2 + 2 + 4 \\\\
+ & 2 + 4 + 4 \\\\
+ & 2 + 8
+\end{align}$$
-1 + 1 + 4 + 41 + 1 + 2 + 2 + 4
-
-2 + 4 + 4
-
-2 + 8
-
-What is f(1025)?
+What is $f({10}^{25})$?
# --hints--
-`euler169()` should return 178653872807.
+`numberOfWaysToExpress()` should return `178653872807`.
```js
-assert.strictEqual(euler169(), 178653872807);
+assert.strictEqual(numberOfWaysToExpress(), 178653872807);
```
# --seed--
@@ -38,12 +38,12 @@ assert.strictEqual(euler169(), 178653872807);
## --seed-contents--
```js
-function euler169() {
+function numberOfWaysToExpress() {
return true;
}
-euler169();
+numberOfWaysToExpress();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
index f12d0490f2..6cce571bac 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-170-find-the-largest-0-to-9-pandigital-that-can-be-formed-by-concatenating-products.md
@@ -13,9 +13,12 @@ dashedName: >-
Take the number 6 and multiply it by each of 1273 and 9854:
-6 × 1273 = 7638 6 × 9854 = 59124
+$$\begin{align}
+ & 6 × 1273 = 7638 \\\\
+ & 6 × 9854 = 59124 \\\\
+\end{align}$$
-By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273,9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
+By concatenating these products we get the 1 to 9 pandigital 763859124. We will call 763859124 the "concatenated product of 6 and (1273, 9854)". Notice too, that the concatenation of the input numbers, 612739854, is also 1 to 9 pandigital.
The same can be done for 0 to 9 pandigital numbers.
@@ -23,10 +26,10 @@ What is the largest 0 to 9 pandigital 10-digit concatenated product of an intege
# --hints--
-`euler170()` should return 9857164023.
+`largestPandigital()` should return `9857164023`.
```js
-assert.strictEqual(euler170(), 9857164023);
+assert.strictEqual(largestPandigital(), 9857164023);
```
# --seed--
@@ -34,12 +37,12 @@ assert.strictEqual(euler170(), 9857164023);
## --seed-contents--
```js
-function euler170() {
+function largestPandigital() {
return true;
}
-euler170();
+largestPandigital();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
index d03ddf909b..e4658cd2b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-171-finding-numbers-for-which-the-sum-of-the-squares-of-the-digits-is-a-square.md
@@ -11,22 +11,22 @@ dashedName: >-
# --description--
-For a positive integer n, let f(n) be the sum of the squares of the digits (in base 10) of n, e.g.
+For a positive integer $n$, let $f(n)$ be the sum of the squares of the digits (in base 10) of $n$, e.g.
-f(3) = 32 = 9,
+$$\begin{align}
+ & f(3) = 3^2 = 9 \\\\
+ & f(25) = 2^2 + 5^2 = 4 + 25 = 29 \\\\
+ & f(442) = 4^2 + 4^2 + 2^2 = 16 + 16 + 4 = 36 \\\\
+\end{align}$$
-f(25) = 22 + 52 = 4 + 25 = 29,
-
-f(442) = 42 + 42 + 22 = 16 + 16 + 4 = 36
-
-Find the last nine digits of the sum of all n, 0 < n < 1020, such that f(n) is a perfect square.
+Find the last nine digits of the sum of all $n$, $0 < n < {10}^{20}$, such that $f(n)$ is a perfect square.
# --hints--
-`euler171()` should return 142989277.
+`lastDigitsSumOfPerfectSquare()` should return `142989277`.
```js
-assert.strictEqual(euler171(), 142989277);
+assert.strictEqual(lastDigitsSumOfPerfectSquare(), 142989277);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler171(), 142989277);
## --seed-contents--
```js
-function euler171() {
+function lastDigitsSumOfPerfectSquare() {
return true;
}
-euler171();
+lastDigitsSumOfPerfectSquare();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
index a25ab3224f..0ad7b86f36 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-172-investigating-numbers-with-few-repeated-digits.md
@@ -8,14 +8,14 @@ dashedName: problem-172-investigating-numbers-with-few-repeated-digits
# --description--
-How many 18-digit numbers n (without leading zeros) are there such that no digit occurs more than three times in n?
+How many 18-digit numbers $n$ (without leading zeros) are there such that no digit occurs more than three times in $n$?
# --hints--
-`euler172()` should return 227485267000992000.
+`numbersWithRepeatedDigits()` should return `227485267000992000`.
```js
-assert.strictEqual(euler172(), 227485267000992000);
+assert.strictEqual(numbersWithRepeatedDigits(), 227485267000992000);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler172(), 227485267000992000);
## --seed-contents--
```js
-function euler172() {
+function numbersWithRepeatedDigits() {
return true;
}
-euler172();
+numbersWithRepeatedDigits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
index a07789fd1d..5d49c3b9fa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-173-using-up-to-one-million-tiles-how-many-different-hollow-square-laminae-can-be-formed.md
@@ -13,14 +13,16 @@ dashedName: >-
We shall define a square lamina to be a square outline with a square "hole" so that the shape possesses vertical and horizontal symmetry. For example, using exactly thirty-two square tiles we can form two different square laminae:
+ +
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae. Using up to one million tiles how many different square laminae can be formed?
# --hints--
-`euler173()` should return 1572729.
+`differentHollowSquareLaminae()` should return `1572729`.
```js
-assert.strictEqual(euler173(), 1572729);
+assert.strictEqual(differentHollowSquareLaminae(), 1572729);
```
# --seed--
@@ -28,12 +30,12 @@ assert.strictEqual(euler173(), 1572729);
## --seed-contents--
```js
-function euler173() {
+function differentHollowSquareLaminae() {
return true;
}
-euler173();
+differentHollowSquareLaminae();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
index e7183612d5..ff7276377f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
@@ -15,14 +15,20 @@ We shall define a square lamina to be a square outline with a square "hole" so t
Given eight tiles it is possible to form a lamina in only one way: 3x3 square with a 1x1 hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.
-If t represents the number of tiles used, we shall say that t = 8 is type L(1) and t = 32 is type L(2). Let N(n) be the number of t ≤ 1000000 such that t is type L(n); for example, N(15) = 832. What is ∑ N(n) for 1 ≤ n ≤ 10?
+
+
With one-hundred tiles, and not necessarily using all of the tiles at one time, it is possible to form forty-one different square laminae. Using up to one million tiles how many different square laminae can be formed?
# --hints--
-`euler173()` should return 1572729.
+`differentHollowSquareLaminae()` should return `1572729`.
```js
-assert.strictEqual(euler173(), 1572729);
+assert.strictEqual(differentHollowSquareLaminae(), 1572729);
```
# --seed--
@@ -28,12 +30,12 @@ assert.strictEqual(euler173(), 1572729);
## --seed-contents--
```js
-function euler173() {
+function differentHollowSquareLaminae() {
return true;
}
-euler173();
+differentHollowSquareLaminae();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
index e7183612d5..ff7276377f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-174-counting-the-number-of-hollow-square-laminae-that-can-form-one-two-three-...-distinct-arrangements.md
@@ -15,14 +15,20 @@ We shall define a square lamina to be a square outline with a square "hole" so t
Given eight tiles it is possible to form a lamina in only one way: 3x3 square with a 1x1 hole in the middle. However, using thirty-two tiles it is possible to form two distinct laminae.
-If t represents the number of tiles used, we shall say that t = 8 is type L(1) and t = 32 is type L(2). Let N(n) be the number of t ≤ 1000000 such that t is type L(n); for example, N(15) = 832. What is ∑ N(n) for 1 ≤ n ≤ 10?
+ +
+If $t$ represents the number of tiles used, we shall say that $t = 8$ is type $L(1)$ and $t = 32$ is type $L(2)$.
+
+Let $N(n)$ be the number of $t ≤ 1000000$ such that $t$ is type $L(n)$; for example, $N(15) = 832$.
+
+What is $\sum N(n)$ for $1 ≤ n ≤ 10$?
# --hints--
-`euler174()` should return 209566.
+`hollowSquareLaminaeDistinctArrangements()` should return `209566`.
```js
-assert.strictEqual(euler174(), 209566);
+assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);
```
# --seed--
@@ -30,12 +36,12 @@ assert.strictEqual(euler174(), 209566);
## --seed-contents--
```js
-function euler174() {
+function hollowSquareLaminaeDistinctArrangements() {
return true;
}
-euler174();
+hollowSquareLaminaeDistinctArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 8f32fcb4bd..20907644d9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,18 +11,36 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of ways to write n as a sum of powers of 2 where no power occurs more than twice.
+Define $f(0) = 1$ and $f(n)$ to be the number of ways to write $n$ as a sum of powers of 2 where no power occurs more than twice.
-For example, f(10)=5 since there are five different ways to express 10:10 = 8+2 = 8+1+1 = 4+4+2 = 4+2+2+1+1 = 4+4+1+1
+For example, $f(10) = 5$ since there are five different ways to express 10:
-It can be shown that for every fraction p/q (p>0, q>0) there exists at least one integer n such that f(n)/f(n-1)=p/q. For instance, the smallest n for which f(n)/f(n-1)=13/17 is 241. The binary expansion of 241 is 11110001. Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241. Find the Shortened Binary Expansion of the smallest n for which f(n)/f(n-1)=123456789/987654321. Give your answer as comma separated integers, without any whitespaces.
+$$10 = 8 + 2 = 8 + 1 + 1 = 4 + 4 + 2 = 4 + 2 + 2 + 1 + 1 = 4 + 4 + 1 + 1$$
+
+It can be shown that for every fraction $\frac{p}{q}\\; (p>0, q>0)$ there exists at least one integer $n$ such that $\frac{f(n)}{f(n - 1)} = \frac{p}{q}$.
+
+For instance, the smallest $n$ for which $\frac{f(n)}{f(n - 1)} = \frac{13}{17}$ is 241. The binary expansion of 241 is 11110001.
+
+Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241.
+
+Find the Shortened Binary Expansion of the smallest $n$ for which
+
+$$\frac{f(n)}{f(n - 1)} = \frac{123456789}{987654321}$$
+
+Give your answer as a string with comma separated integers, without any whitespaces.
# --hints--
-`euler175()` should return 1, 13717420, 8.
+`shortenedBinaryExpansionOfNumber()` should return a string.
```js
-assert.strictEqual(euler175(), 1, 13717420, 8);
+assert(typeof shortenedBinaryExpansionOfNumber() === 'string');
+```
+
+`shortenedBinaryExpansionOfNumber()` should return the string `1,13717420,8`.
+
+```js
+assert.strictEqual(shortenedBinaryExpansionOfNumber(), '1,13717420,8');
```
# --seed--
@@ -30,12 +48,12 @@ assert.strictEqual(euler175(), 1, 13717420, 8);
## --seed-contents--
```js
-function euler175() {
+function shortenedBinaryExpansionOfNumber() {
return true;
}
-euler175();
+shortenedBinaryExpansionOfNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
index c3b6c090fe..d5e7b34ad6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
@@ -14,10 +14,10 @@ Find the smallest integer that can be the length of a cathetus of exactly 47547
# --hints--
-`euler176()` should return 96818198400000.
+`trianglesSharingCathetus()` should return `96818198400000`.
```js
-assert.strictEqual(euler176(), 96818198400000);
+assert.strictEqual(trianglesSharingCathetus(), 96818198400000);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler176(), 96818198400000);
## --seed-contents--
```js
-function euler176() {
+function trianglesSharingCathetus() {
return true;
}
-euler176();
+trianglesSharingCathetus();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
index 2e39114654..686ddad5cd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
@@ -10,14 +10,22 @@ dashedName: problem-177-integer-angled-quadrilaterals
Let ABCD be a convex quadrilateral, with diagonals AC and BD. At each vertex the diagonal makes an angle with each of the two sides, creating eight corner angles.
-For example, at vertex A, the two angles are CAD, CAB. We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°. What is the total number of non-similar integer angled quadrilaterals? Note: In your calculations you may assume that a calculated angle is integral if it is within a tolerance of 10-9 of an integer value.
+
+
+If $t$ represents the number of tiles used, we shall say that $t = 8$ is type $L(1)$ and $t = 32$ is type $L(2)$.
+
+Let $N(n)$ be the number of $t ≤ 1000000$ such that $t$ is type $L(n)$; for example, $N(15) = 832$.
+
+What is $\sum N(n)$ for $1 ≤ n ≤ 10$?
# --hints--
-`euler174()` should return 209566.
+`hollowSquareLaminaeDistinctArrangements()` should return `209566`.
```js
-assert.strictEqual(euler174(), 209566);
+assert.strictEqual(hollowSquareLaminaeDistinctArrangements(), 209566);
```
# --seed--
@@ -30,12 +36,12 @@ assert.strictEqual(euler174(), 209566);
## --seed-contents--
```js
-function euler174() {
+function hollowSquareLaminaeDistinctArrangements() {
return true;
}
-euler174();
+hollowSquareLaminaeDistinctArrangements();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
index 8f32fcb4bd..20907644d9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-175-fractions-involving-the-number-of-different-ways-a-number-can-be-expressed-as-a-sum-of-powers-of-2.md
@@ -11,18 +11,36 @@ dashedName: >-
# --description--
-Define f(0)=1 and f(n) to be the number of ways to write n as a sum of powers of 2 where no power occurs more than twice.
+Define $f(0) = 1$ and $f(n)$ to be the number of ways to write $n$ as a sum of powers of 2 where no power occurs more than twice.
-For example, f(10)=5 since there are five different ways to express 10:10 = 8+2 = 8+1+1 = 4+4+2 = 4+2+2+1+1 = 4+4+1+1
+For example, $f(10) = 5$ since there are five different ways to express 10:
-It can be shown that for every fraction p/q (p>0, q>0) there exists at least one integer n such that f(n)/f(n-1)=p/q. For instance, the smallest n for which f(n)/f(n-1)=13/17 is 241. The binary expansion of 241 is 11110001. Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241. Find the Shortened Binary Expansion of the smallest n for which f(n)/f(n-1)=123456789/987654321. Give your answer as comma separated integers, without any whitespaces.
+$$10 = 8 + 2 = 8 + 1 + 1 = 4 + 4 + 2 = 4 + 2 + 2 + 1 + 1 = 4 + 4 + 1 + 1$$
+
+It can be shown that for every fraction $\frac{p}{q}\\; (p>0, q>0)$ there exists at least one integer $n$ such that $\frac{f(n)}{f(n - 1)} = \frac{p}{q}$.
+
+For instance, the smallest $n$ for which $\frac{f(n)}{f(n - 1)} = \frac{13}{17}$ is 241. The binary expansion of 241 is 11110001.
+
+Reading this binary number from the most significant bit to the least significant bit there are 4 one's, 3 zeroes and 1 one. We shall call the string 4,3,1 the Shortened Binary Expansion of 241.
+
+Find the Shortened Binary Expansion of the smallest $n$ for which
+
+$$\frac{f(n)}{f(n - 1)} = \frac{123456789}{987654321}$$
+
+Give your answer as a string with comma separated integers, without any whitespaces.
# --hints--
-`euler175()` should return 1, 13717420, 8.
+`shortenedBinaryExpansionOfNumber()` should return a string.
```js
-assert.strictEqual(euler175(), 1, 13717420, 8);
+assert(typeof shortenedBinaryExpansionOfNumber() === 'string');
+```
+
+`shortenedBinaryExpansionOfNumber()` should return the string `1,13717420,8`.
+
+```js
+assert.strictEqual(shortenedBinaryExpansionOfNumber(), '1,13717420,8');
```
# --seed--
@@ -30,12 +48,12 @@ assert.strictEqual(euler175(), 1, 13717420, 8);
## --seed-contents--
```js
-function euler175() {
+function shortenedBinaryExpansionOfNumber() {
return true;
}
-euler175();
+shortenedBinaryExpansionOfNumber();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
index c3b6c090fe..d5e7b34ad6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-176-right-angled-triangles-that-share-a-cathetus.md
@@ -14,10 +14,10 @@ Find the smallest integer that can be the length of a cathetus of exactly 47547
# --hints--
-`euler176()` should return 96818198400000.
+`trianglesSharingCathetus()` should return `96818198400000`.
```js
-assert.strictEqual(euler176(), 96818198400000);
+assert.strictEqual(trianglesSharingCathetus(), 96818198400000);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler176(), 96818198400000);
## --seed-contents--
```js
-function euler176() {
+function trianglesSharingCathetus() {
return true;
}
-euler176();
+trianglesSharingCathetus();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
index 2e39114654..686ddad5cd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-177-integer-angled-quadrilaterals.md
@@ -10,14 +10,22 @@ dashedName: problem-177-integer-angled-quadrilaterals
Let ABCD be a convex quadrilateral, with diagonals AC and BD. At each vertex the diagonal makes an angle with each of the two sides, creating eight corner angles.
-For example, at vertex A, the two angles are CAD, CAB. We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°. What is the total number of non-similar integer angled quadrilaterals? Note: In your calculations you may assume that a calculated angle is integral if it is within a tolerance of 10-9 of an integer value.
+ +
+For example, at vertex A, the two angles are CAD, CAB.
+
+We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°.
+
+What is the total number of non-similar integer angled quadrilaterals?
+
+**Note:** In your calculations you may assume that a calculated angle is integral if it is within a tolerance of ${10}^{-9}$ of an integer value.
# --hints--
-`euler177()` should return 129325.
+`integerAngledQuadrilaterals()` should return `129325`.
```js
-assert.strictEqual(euler177(), 129325);
+assert.strictEqual(integerAngledQuadrilaterals(), 129325);
```
# --seed--
@@ -25,12 +33,12 @@ assert.strictEqual(euler177(), 129325);
## --seed-contents--
```js
-function euler177() {
+function integerAngledQuadrilaterals() {
return true;
}
-euler177();
+integerAngledQuadrilaterals();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
index 12bad9c5ad..e9ea0adc66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
@@ -16,14 +16,14 @@ A number for which every pair of consecutive digits has a difference of one is c
A pandigital number contains every decimal digit from 0 to 9 at least once.
-How many pandigital step numbers less than 1040 are there?
+How many pandigital step numbers less than ${10}^{40}$ are there?
# --hints--
-`euler178()` should return 126461847755.
+`stepNumbers()` should return `126461847755`.
```js
-assert.strictEqual(euler178(), 126461847755);
+assert.strictEqual(stepNumbers(), 126461847755);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler178(), 126461847755);
## --seed-contents--
```js
-function euler178() {
+function stepNumbers() {
return true;
}
-euler178();
+stepNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
index 1811def962..9245393058 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
@@ -8,14 +8,14 @@ dashedName: problem-179-consecutive-positive-divisors
# --description--
-Find the number of integers 1 < n < 107, for which n and n + 1 have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
+Find the number of integers $1 < n < {10}^7$, for which $n$ and $n + 1$ have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
# --hints--
-`euler179()` should return 986262.
+`consecutivePositiveDivisors()` should return `986262`.
```js
-assert.strictEqual(euler179(), 986262);
+assert.strictEqual(consecutivePositiveDivisors(), 986262);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler179(), 986262);
## --seed-contents--
```js
-function euler179() {
+function consecutivePositiveDivisors() {
return true;
}
-euler179();
+consecutivePositiveDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
index 3b46677319..e1b5202106 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
@@ -8,30 +8,34 @@ dashedName: problem-180-rational-zeros-of-a-function-of-three-variables
# --description--
-For any integer n, consider the three functions
+For any integer $n$, consider the three functions
-f1,n(x,y,z) = xn+1 + yn+1 − zn+1f2,n(x,y,z) = (xy + yz + zx)\*(xn-1 + yn-1 − zn-1)f3,n(x,y,z) = xyz\*(xn-2 + yn-2 − zn-2)
+$$\begin{align}
+ & f_{1,n}(x,y,z) = x^{n + 1} + y^{n + 1} − z^{n + 1}\\\\
+ & f_{2,n}(x,y,z) = (xy + yz + zx) \times (x^{n - 1} + y^{n - 1} − z^{n - 1})\\\\
+ & f_{3,n}(x,y,z) = xyz \times (x^{n - 2} + y^{n - 2} − z^{n - 2})
+\end{align}$$
and their combination
-fn(x,y,z) = f1,n(x,y,z) + f2,n(x,y,z) − f3,n(x,y,z)
+$$\begin{align}
+ & f_n(x,y,z) = f_{1,n}(x,y,z) + f_{2,n}(x,y,z) − f_{3,n}(x,y,z)
+\end{align}$$
-We call (x,y,z) a golden triple of order k if x, y, and z are all rational numbers of the form a / b with
+We call $(x,y,z)$ a golden triple of order $k$ if $x$, $y$, and $z$ are all rational numbers of the form $\frac{a}{b}$ with $0 < a < b ≤ k$ and there is (at least) one integer $n$, so that $f_n(x,y,z) = 0$.
-0 < a < b ≤ k and there is (at least) one integer n, so that fn(x,y,z) = 0.
+Let $s(x,y,z) = x + y + z$.
-Let s(x,y,z) = x + y + z.
+Let $t = \frac{u}{v}$ be the sum of all distinct $s(x,y,z)$ for all golden triples $(x,y,z)$ of order 35. All the $s(x,y,z)$ and $t$ must be in reduced form.
-Let t = u / v be the sum of all distinct s(x,y,z) for all golden triples (x,y,z) of order 35. All the s(x,y,z) and t must be in reduced form.
-
-Find u + v.
+Find $u + v$.
# --hints--
-`euler180()` should return 285196020571078980.
+`rationalZeros()` should return `285196020571078980`.
```js
-assert.strictEqual(euler180(), 285196020571078980);
+assert.strictEqual(rationalZeros(), 285196020571078980);
```
# --seed--
@@ -39,12 +43,12 @@ assert.strictEqual(euler180(), 285196020571078980);
## --seed-contents--
```js
-function euler180() {
+function rationalZeros() {
return true;
}
-euler180();
+rationalZeros();
```
# --solutions--
+
+For example, at vertex A, the two angles are CAD, CAB.
+
+We call such a quadrilateral for which all eight corner angles have integer values when measured in degrees an "integer angled quadrilateral". An example of an integer angled quadrilateral is a square, where all eight corner angles are 45°. Another example is given by DAC = 20°, BAC = 60°, ABD = 50°, CBD = 30°, BCA = 40°, DCA = 30°, CDB = 80°, ADB = 50°.
+
+What is the total number of non-similar integer angled quadrilaterals?
+
+**Note:** In your calculations you may assume that a calculated angle is integral if it is within a tolerance of ${10}^{-9}$ of an integer value.
# --hints--
-`euler177()` should return 129325.
+`integerAngledQuadrilaterals()` should return `129325`.
```js
-assert.strictEqual(euler177(), 129325);
+assert.strictEqual(integerAngledQuadrilaterals(), 129325);
```
# --seed--
@@ -25,12 +33,12 @@ assert.strictEqual(euler177(), 129325);
## --seed-contents--
```js
-function euler177() {
+function integerAngledQuadrilaterals() {
return true;
}
-euler177();
+integerAngledQuadrilaterals();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
index 12bad9c5ad..e9ea0adc66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-178-step-numbers.md
@@ -16,14 +16,14 @@ A number for which every pair of consecutive digits has a difference of one is c
A pandigital number contains every decimal digit from 0 to 9 at least once.
-How many pandigital step numbers less than 1040 are there?
+How many pandigital step numbers less than ${10}^{40}$ are there?
# --hints--
-`euler178()` should return 126461847755.
+`stepNumbers()` should return `126461847755`.
```js
-assert.strictEqual(euler178(), 126461847755);
+assert.strictEqual(stepNumbers(), 126461847755);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler178(), 126461847755);
## --seed-contents--
```js
-function euler178() {
+function stepNumbers() {
return true;
}
-euler178();
+stepNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
index 1811def962..9245393058 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-179-consecutive-positive-divisors.md
@@ -8,14 +8,14 @@ dashedName: problem-179-consecutive-positive-divisors
# --description--
-Find the number of integers 1 < n < 107, for which n and n + 1 have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
+Find the number of integers $1 < n < {10}^7$, for which $n$ and $n + 1$ have the same number of positive divisors. For example, 14 has the positive divisors 1, 2, 7, 14 while 15 has 1, 3, 5, 15.
# --hints--
-`euler179()` should return 986262.
+`consecutivePositiveDivisors()` should return `986262`.
```js
-assert.strictEqual(euler179(), 986262);
+assert.strictEqual(consecutivePositiveDivisors(), 986262);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler179(), 986262);
## --seed-contents--
```js
-function euler179() {
+function consecutivePositiveDivisors() {
return true;
}
-euler179();
+consecutivePositiveDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
index 3b46677319..e1b5202106 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-180-rational-zeros-of-a-function-of-three-variables.md
@@ -8,30 +8,34 @@ dashedName: problem-180-rational-zeros-of-a-function-of-three-variables
# --description--
-For any integer n, consider the three functions
+For any integer $n$, consider the three functions
-f1,n(x,y,z) = xn+1 + yn+1 − zn+1f2,n(x,y,z) = (xy + yz + zx)\*(xn-1 + yn-1 − zn-1)f3,n(x,y,z) = xyz\*(xn-2 + yn-2 − zn-2)
+$$\begin{align}
+ & f_{1,n}(x,y,z) = x^{n + 1} + y^{n + 1} − z^{n + 1}\\\\
+ & f_{2,n}(x,y,z) = (xy + yz + zx) \times (x^{n - 1} + y^{n - 1} − z^{n - 1})\\\\
+ & f_{3,n}(x,y,z) = xyz \times (x^{n - 2} + y^{n - 2} − z^{n - 2})
+\end{align}$$
and their combination
-fn(x,y,z) = f1,n(x,y,z) + f2,n(x,y,z) − f3,n(x,y,z)
+$$\begin{align}
+ & f_n(x,y,z) = f_{1,n}(x,y,z) + f_{2,n}(x,y,z) − f_{3,n}(x,y,z)
+\end{align}$$
-We call (x,y,z) a golden triple of order k if x, y, and z are all rational numbers of the form a / b with
+We call $(x,y,z)$ a golden triple of order $k$ if $x$, $y$, and $z$ are all rational numbers of the form $\frac{a}{b}$ with $0 < a < b ≤ k$ and there is (at least) one integer $n$, so that $f_n(x,y,z) = 0$.
-0 < a < b ≤ k and there is (at least) one integer n, so that fn(x,y,z) = 0.
+Let $s(x,y,z) = x + y + z$.
-Let s(x,y,z) = x + y + z.
+Let $t = \frac{u}{v}$ be the sum of all distinct $s(x,y,z)$ for all golden triples $(x,y,z)$ of order 35. All the $s(x,y,z)$ and $t$ must be in reduced form.
-Let t = u / v be the sum of all distinct s(x,y,z) for all golden triples (x,y,z) of order 35. All the s(x,y,z) and t must be in reduced form.
-
-Find u + v.
+Find $u + v$.
# --hints--
-`euler180()` should return 285196020571078980.
+`rationalZeros()` should return `285196020571078980`.
```js
-assert.strictEqual(euler180(), 285196020571078980);
+assert.strictEqual(rationalZeros(), 285196020571078980);
```
# --seed--
@@ -39,12 +43,12 @@ assert.strictEqual(euler180(), 285196020571078980);
## --seed-contents--
```js
-function euler180() {
+function rationalZeros() {
return true;
}
-euler180();
+rationalZeros();
```
# --solutions--