From 397a9f0c3e5e9ab58bc408df90ee80837fcdafbe Mon Sep 17 00:00:00 2001
From: gikf <60067306+gikf@users.noreply.github.com>
Date: Fri, 30 Jul 2021 17:32:21 +0200
Subject: [PATCH] fix(curriculum): clean-up Project Euler 462-480 (#43069)
* fix: clean-up Project Euler 462-480
* fix: missing image extension
* fix: corrections from review
Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
---
...lem-462-permutation-of-3-smooth-numbers.md | 26 ++--
...problem-463-a-weird-recurrence-relation.md | 26 ++--
...roblem-464-mbius-function-and-intervals.md | 29 +++--
.../problem-465-polar-polygons.md | 18 +--
...istinct-terms-in-a-multiplication-table.md | 29 +++--
.../project-euler/problem-467-superinteger.md | 35 ++++--
...mooth-divisors-of-binomial-coefficients.md | 32 +++--
.../project-euler/problem-469-empty-chairs.md | 16 +--
.../project-euler/problem-470-super-ramvok.md | 16 +--
...oblem-471-triangle-inscribed-in-ellipse.md | 32 +++--
.../problem-472-comfortable-distance-ii.md | 28 ++---
.../problem-473-phigital-number-base.md | 18 +--
.../problem-474-last-digits-of-divisors.md | 16 +--
.../problem-475-music-festival.md | 18 +--
.../problem-476-circle-packing-ii.md | 16 +--
.../problem-477-number-sequence-game.md | 38 +++---
.../project-euler/problem-478-mixtures.md | 26 ++--
.../problem-479-roots-on-the-rise.md | 18 +--
.../problem-480-the-last-question.md | 112 ++++++++----------
19 files changed, 309 insertions(+), 240 deletions(-)
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
index 6eb9550e45..550715f701 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
@@ -8,13 +8,11 @@ dashedName: problem-462-permutation-of-3-smooth-numbers
# --description--
-
+A 3-smooth number is an integer which has no prime factor larger than 3. For an integer $N$, we define $S(N)$ as the set of 3-smooth numbers less than or equal to $N$. For example, $S(20) = \\{1, 2, 3, 4, 6, 8, 9, 12, 16, 18\\}$.
-A 3-smooth number is an integer which has no prime factor larger than 3. For an integer N, we define S(N) as the set of 3-smooth numbers less than or equal to N . For example, S(20) = { 1, 2, 3, 4, 6, 8, 9, 12, 16, 18 }.
+We define $F(N)$ as the number of permutations of $S(N)$ in which each element comes after all of its proper divisors.
-We define F(N) as the number of permutations of S(N) in which each element comes after all of its proper divisors.
-
-This is one of the possible permutations for N = 20.
+This is one of the possible permutations for $N = 20$.
- 1, 2, 4, 3, 9, 8, 16, 6, 18, 12.
@@ -22,14 +20,22 @@ This is not a valid permutation because 12 comes before its divisor 6.
- 1, 2, 4, 3, 9, 8, 12, 16, 6, 18.
-We can verify that F(6) = 5, F(8) = 9, F(20) = 450 and F(1000) ≈ 8.8521816557e21. Find F(1018). Give as your answer its scientific notation rounded to ten digits after the decimal point. When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 112,233,445,566,778,899 then the answer format would be 1.1223344557e17.
+We can verify that $F(6) = 5$, $F(8) = 9$, $F(20) = 450$ and $F(1000) ≈ 8.8521816557e\\,21$.
+
+Find $F({10}^{18})$. Give as your answer as a string in its scientific notation rounded to ten digits after the decimal point. When giving your answer, use a lowercase `e` to separate mantissa and exponent. E.g. if the answer is $112\\,233\\,445\\,566\\,778\\,899$ then the answer format would be `1.1223344557e17`.
# --hints--
-`euler462()` should return Infinity.
+`permutationOf3SmoothNumbers()` should return a string.
```js
-assert.strictEqual(euler462(), Infinity);
+assert.strictEqual(typeof permutationOf3SmoothNumbers() === 'string');
+```
+
+`permutationOf3SmoothNumbers()` should return the string `5.5350769703e1512`.
+
+```js
+assert.strictEqual(permutationOf3SmoothNumbers(), '5.5350769703e1512');
```
# --seed--
@@ -37,12 +43,12 @@ assert.strictEqual(euler462(), Infinity);
## --seed-contents--
```js
-function euler462() {
+function permutationOf3SmoothNumbers() {
return true;
}
-euler462();
+permutationOf3SmoothNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
index 014935108f..2d1236555f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
@@ -10,24 +10,26 @@ dashedName: problem-463-a-weird-recurrence-relation
The function $f$ is defined for all positive integers as follows:
-$f(1)=1$
+$$\begin{align}
+ & f(1) = 1 \\\\
+ & f(3) = 3 \\\\
+ & f(2n) = f(n) \\\\
+ & f(4n + 1) = 2f(2n + 1) - f(n) \\\\
+ & f(4n + 3) = 3f(2n + 1) - 2f(n)
+\end{align}$$
-$f(3)=3$
+The function $S(n)$ is defined as $\sum_{i=1}^{n} f(i)$.
-$f(2n)=f(n)$
+$S(8) = 22$ and $S(100) = 3604$.
-$f(4n + 1)=2f(2n + 1) - f(n)$
-
-$f(4n + 3)=3f(2n + 1) - 2f(n)$
-
-The function $S(n)$ is defined as $\\sum\_{i=1}^{n}f(i)$. $S(8)=22$ and $S(100)=3604$. Find $S(3^{37})$. Give the last 9 digits of your answer.
+Find $S(3^{37})$. Give the last 9 digits of your answer.
# --hints--
-`euler463()` should return 808981553.
+`weirdRecurrenceRelation()` should return `808981553`.
```js
-assert.strictEqual(euler463(), 808981553);
+assert.strictEqual(weirdRecurrenceRelation(), 808981553);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler463(), 808981553);
## --seed-contents--
```js
-function euler463() {
+function weirdRecurrenceRelation() {
return true;
}
-euler463();
+weirdRecurrenceRelation();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
index 5b209dd1d7..2e12caa276 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
@@ -8,26 +8,33 @@ dashedName: problem-464-mbius-function-and-intervals
# --description--
-The Möbius function, denoted μ(n), is defined as:
+The Möbius function, denoted $μ(n)$, is defined as:
-μ(n) = (-1)ω(n) if n is squarefree (where ω(n) is the number of distinct prime factors of n)
+- $μ(n) = (-1)^{ω(n)}$ if $n$ is squarefree (where $ω(n)$ is the number of distinct prime factors of $n$)
+- $μ(n) = 0$ if $n$ is not squarefree.
-μ(n) = 0 if n is not squarefree.
+Let $P(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = 1$.
-Let P(a,b) be the number of integers n in the interval \[a,b] such that μ(n) = 1. Let N(a,b) be the number of integers n in the interval \[a,b] such that μ(n) = -1. For example, P(2,10) = 2 and N(2,10) = 4.
+Let $N(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = -1$.
-Let C(n) be the number of integer pairs (a,b) such that: 1 ≤ a ≤ b ≤ n, 99·N(a,b) ≤ 100·P(a,b), and 99·P(a,b) ≤ 100·N(a,b).
+For example, $P(2, 10) = 2$ and $N(2, 10) = 4$.
-For example, C(10) = 13, C(500) = 16676 and C(10 000) = 20155319.
+Let $C(n)$ be the number of integer pairs $(a, b)$ such that:
-Find C(20 000 000).
+- $1 ≤ a ≤ b ≤ n$,
+- $99 \times N(a, b) ≤ 100 \times P(a, b)$, and
+- $99 \times P(a, b) ≤ 100 \times N(a, b)$.
+
+For example, $C(10) = 13$, $C(500) = 16\\,676$ and $C(10\\,000) = 20\\,155\\,319$.
+
+Find $C(20\\,000\\,000)$.
# --hints--
-`euler464()` should return 198775297232878.
+`mobiusFunctionAndIntervals()` should return `198775297232878`.
```js
-assert.strictEqual(euler464(), 198775297232878);
+assert.strictEqual(mobiusFunctionAndIntervals(), 198775297232878);
```
# --seed--
@@ -35,12 +42,12 @@ assert.strictEqual(euler464(), 198775297232878);
## --seed-contents--
```js
-function euler464() {
+function mobiusFunctionAndIntervals() {
return true;
}
-euler464();
+mobiusFunctionAndIntervals();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
index 2baaf0d775..ac58e07e80 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
@@ -14,22 +14,24 @@ For this problem, a polygon can have collinear consecutive vertices. However, a
For example, only the first of the following is a polar polygon (the kernels of the second, third, and fourth do not strictly contain the origin, and the fifth does not have a kernel at all):
+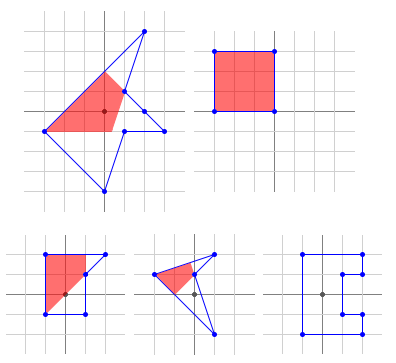 +
Notice that the first polygon has three consecutive collinear vertices.
-Let P(n) be the number of polar polygons such that the vertices (x, y) have integer coordinates whose absolute values are not greater than n.
+Let $P(n)$ be the number of polar polygons such that the vertices $(x, y)$ have integer coordinates whose absolute values are not greater than $n$.
-Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices \[(0,0),(0,3),(1,1),(3,0)] is distinct from the polygon with vertices \[(0,0),(0,3),(1,1),(3,0),(1,0)].
+Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices [(0,0), (0,3), (1,1), (3,0)] is distinct from the polygon with vertices [(0,0), (0,3), (1,1), (3,0), (1,0)].
-For example, P(1) = 131, P(2) = 1648531, P(3) = 1099461296175 and P(343) mod 1 000 000 007 = 937293740.
+For example, $P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$ and $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$.
-Find P(713) mod 1 000 000 007.
+Find $P(7^{13})\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler465()` should return 585965659.
+`polarPolygons()` should return `585965659`.
```js
-assert.strictEqual(euler465(), 585965659);
+assert.strictEqual(polarPolygons(), 585965659);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler465(), 585965659);
## --seed-contents--
```js
-function euler465() {
+function polarPolygons() {
return true;
}
-euler465();
+polarPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
index 3050ea410b..f578dd0bb0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
@@ -8,24 +8,35 @@ dashedName: problem-466-distinct-terms-in-a-multiplication-table
# --description--
-Let P(m,n) be the number of distinct terms in an m×n multiplication table.
+Let $P(m,n)$ be the number of distinct terms in an $m×n$ multiplication table.
For example, a 3×4 multiplication table looks like this:
-× 12341 12342 24683 36912
+$$\begin{array}{c}
+ × & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} \\\\
+ \mathbf{1} & 1 & 2 & 3 & 4 \\\\
+ \mathbf{2} & 2 & 4 & 6 & 8 \\\\
+ \mathbf{3} & 3 & 6 & 9 & 12
+\end{array}$$
-There are 8 distinct terms {1,2,3,4,6,8,9,12}, therefore P(3,4) = 8.
+There are 8 distinct terms {1, 2, 3, 4, 6, 8, 9, 12}, therefore $P(3, 4) = 8$.
-You are given that: P(64,64) = 1263, P(12,345) = 1998, and P(32,1015) = 13826382602124302.
+You are given that:
-Find P(64,1016).
+$$\begin{align}
+ & P(64, 64) = 1\\,263, \\\\
+ & P(12, 345) = 1\\,998, \text{ and} \\\\
+ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302. \\\\
+\end{align}$$
+
+Find $P(64, {10}^{16})$.
# --hints--
-`euler466()` should return 258381958195474750.
+`multiplicationTable()` should return `258381958195474750`.
```js
-assert.strictEqual(euler466(), 258381958195474750);
+assert.strictEqual(multiplicationTable(), 258381958195474750);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler466(), 258381958195474750);
## --seed-contents--
```js
-function euler466() {
+function multiplicationTable() {
return true;
}
-euler466();
+multiplicationTable();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
index 8cfd9dc16a..d237fc953c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
@@ -8,26 +8,41 @@ dashedName: problem-467-superinteger
# --description--
-An integer s is called a superinteger of another integer n if the digits of n form a subsequence of the digits of s.
+An integer $s$ is called a superinteger of another integer $n$ if the digits of $n$ form a subsequence of the digits of $s$.
For example, 2718281828 is a superinteger of 18828, while 314159 is not a superinteger of 151.
-Let p(n) be the nth prime number, and let c(n) be the nth composite number. For example, p(1) = 2, p(10) = 29, c(1) = 4 and c(10) = 18. {p(i) : i ≥ 1} = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...} {c(i) : i ≥ 1} = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, ...}
+Let $p(n)$ be the $n$th prime number, and let $c(n)$ be the $n$th composite number. For example, $p(1) = 2$, $p(10) = 29$, $c(1) = 4$ and $c(10) = 18$.
-Let PD the sequence of the digital roots of {p(i)} (CD is defined similarly for {c(i)}): PD = {2, 3, 5, 7, 2, 4, 8, 1, 5, 2, ...} CD = {4, 6, 8, 9, 1, 3, 5, 6, 7, 9, ...}
+$$\begin{align}
+ & \\{p(i) : i ≥ 1\\} = \\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots \\} \\\\
+ & \\{c(i) : i ≥ 1\\} = \\{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, \ldots \\}
+\end{align}$$
-Let Pn be the integer formed by concatenating the first n elements of PD (Cn is defined similarly for CD). P10 = 2357248152 C10 = 4689135679
+Let $P^D$ the sequence of the digital roots of $\\{p(i)\\}$ ($C^D$ is defined similarly for $\\{c(i)\\}$):
-Let f(n) be the smallest positive integer that is a common superinteger of Pn and Cn. For example, f(10) = 2357246891352679, and f(100) mod 1 000 000 007 = 771661825.
+$$\begin{align}
+ & P^D = \\{2, 3, 5, 7, 2, 4, 8, 1, 5, 2, \ldots \\} \\\\
+ & C^D = \\{4, 6, 8, 9, 1, 3, 5, 6, 7, 9, \ldots \\}
+\end{align}$$
-Find f(10 000) mod 1 000 000 007.
+Let $P_n$ be the integer formed by concatenating the first $n$ elements of $P^D$ ($C_n$ is defined similarly for $C^D$).
+
+$$\begin{align}
+ & P_{10} = 2\\,357\\,248\\,152 \\\\
+ & C_{10} = 4\\,689\\,135\\,679
+\end{align}$$
+
+Let $f(n)$ be the smallest positive integer that is a common superinteger of $P_n$ and $C_n$. For example, $f(10) = 2\\,357\\,246\\,891\\,352\\,679$, and $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$.
+
+Find $f(10\\,000)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler467()` should return 775181359.
+`superinteger()` should return `775181359`.
```js
-assert.strictEqual(euler467(), 775181359);
+assert.strictEqual(superinteger(), 775181359);
```
# --seed--
@@ -35,12 +50,12 @@ assert.strictEqual(euler467(), 775181359);
## --seed-contents--
```js
-function euler467() {
+function superinteger() {
return true;
}
-euler467();
+superinteger();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
index 239d2cf56d..369c04b06e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
@@ -8,20 +8,36 @@ dashedName: problem-468-smooth-divisors-of-binomial-coefficients
# --description--
-An integer is called B-smooth if none of its prime factors is greater than B.
+An integer is called B-smooth if none of its prime factors is greater than $B$.
-Let SB(n) be the largest B-smooth divisor of n. Examples: S1(10) = 1 S4(2100) = 12 S17(2496144) = 5712
+Let $SB(n)$ be the largest B-smooth divisor of $n$.
-Define F(n) = ∑1≤B≤n ∑0≤r≤n SB(C(n,r)). Here, C(n,r) denotes the binomial coefficient. Examples: F(11) = 3132 F(1 111) mod 1 000 000 993 = 706036312 F(111 111) mod 1 000 000 993 = 22156169
+Examples:
-Find F(11 111 111) mod 1 000 000 993.
+$$\begin{align}
+ & S_1(10) = 1 \\\\
+ & S_4(2\\,100) = 12 \\\\
+ & S_{17}(2\\,496\\,144) = 5\\,712
+\end{align}$$
+
+Define $F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$. Here, $\displaystyle\binom{n}{r}$ denotes the binomial coefficient.
+
+Examples:
+
+$$\begin{align}
+ & F(11) = 3132 \\\\
+ & F(1\\,111)\bmod 1\\,000\\,000\\,993 = 706\\,036\\,312 \\\\
+ & F(111\\,111)\bmod 1\\,000\\,000\\,993 = 22\\,156\\,169
+\end{align}$$
+
+Find $F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$.
# --hints--
-`euler468()` should return 852950321.
+`smoothDivisorsOfBinomialCoefficients()` should return `852950321`.
```js
-assert.strictEqual(euler468(), 852950321);
+assert.strictEqual(smoothDivisorsOfBinomialCoefficients(), 852950321);
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler468(), 852950321);
## --seed-contents--
```js
-function euler468() {
+function smoothDivisorsOfBinomialCoefficients() {
return true;
}
-euler468();
+smoothDivisorsOfBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
index 4e8be025a2..d1db21f4f4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
@@ -8,22 +8,24 @@ dashedName: problem-469-empty-chairs
# --description--
-In a room N chairs are placed around a round table.
+In a room $N$ chairs are placed around a round table.
Knights enter the room one by one and choose at random an available empty chair.
To have enough elbow room the knights always leave at least one empty chair between each other.
-When there aren't any suitable chairs left, the fraction C of empty chairs is determined. We also define E(N) as the expected value of C. We can verify that E(4) = 1/2 and E(6) = 5/9.
+When there aren't any suitable chairs left, the fraction $C$ of empty chairs is determined. We also define $E(N)$ as the expected value of $C$.
-Find E(1018). Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
+We can verify that $E(4) = \frac{1}{2}$ and $E(6) = \frac{5}{9}$.
+
+Find $E({10}^{18})$. Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
# --hints--
-`euler469()` should return 0.56766764161831.
+`emptyChairs()` should return `0.56766764161831`.
```js
-assert.strictEqual(euler469(), 0.56766764161831);
+assert.strictEqual(emptyChairs(), 0.56766764161831);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler469(), 0.56766764161831);
## --seed-contents--
```js
-function euler469() {
+function emptyChairs() {
return true;
}
-euler469();
+emptyChairs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
index 10ee6d95d8..a8f59ece37 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
@@ -10,24 +10,24 @@ dashedName: problem-470-super-ramvok
Consider a single game of Ramvok:
-Let t represent the maximum number of turns the game lasts. If t = 0, then the game ends immediately. Otherwise, on each turn i, the player rolls a die. After rolling, if i < t the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If i = t, then the roll cannot be discarded and the prize must be accepted. Before the game begins, t is chosen by the player, who must then pay an up-front cost ct for some constant c. For c = 0, t can be chosen to be infinite (with an up-front cost of 0). Let R(d, c) be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair d-sided die and cost constant c. For example, R(4, 0.2) = 2.65. Assume that the player has sufficient funds for paying any/all up-front costs.
+Let $t$ represent the maximum number of turns the game lasts. If $t = 0$, then the game ends immediately. Otherwise, on each turn $i$, the player rolls a die. After rolling, if $i < t$ the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If $i = t$, then the roll cannot be discarded and the prize must be accepted. Before the game begins, $t$ is chosen by the player, who must then pay an up-front cost $ct$ for some constant $c$. For $c = 0$, $t$ can be chosen to be infinite (with an up-front cost of 0). Let $R(d, c)$ be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair $d$-sided die and cost constant $c$. For example, $R(4, 0.2) = 2.65$. Assume that the player has sufficient funds for paying any/all up-front costs.
Now consider a game of Super Ramvok:
In Super Ramvok, the game of Ramvok is played repeatedly, but with a slight modification. After each game, the die is altered. The alteration process is as follows: The die is rolled once, and if the resulting face has its pips visible, then that face is altered to be blank instead. If the face is already blank, then it is changed back to its original value. After the alteration is made, another game of Ramvok can begin (and during such a game, at each turn, the die is rolled until a face with a value on it appears). The player knows which faces are blank and which are not at all times. The game of Super Ramvok ends once all faces of the die are blank.
-Let S(d, c) be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair d-sided die to start (with all sides visible), and cost constant c. For example, S(6, 1) = 208.3.
+Let $S(d, c)$ be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair $d$-sided die to start (with all sides visible), and cost constant $c$. For example, $S(6, 1) = 208.3$.
-Let F(n) = ∑4≤d≤n ∑0≤c≤n S(d, c).
+Let $F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$.
-Calculate F(20), rounded to the nearest integer.
+Calculate $F(20)$, rounded to the nearest integer.
# --hints--
-`euler470()` should return 147668794.
+`superRamvok()` should return `147668794`.
```js
-assert.strictEqual(euler470(), 147668794);
+assert.strictEqual(superRamvok(), 147668794);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler470(), 147668794);
## --seed-contents--
```js
-function euler470() {
+function superRamvok() {
return true;
}
-euler470();
+superRamvok();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
index 95385ddec9..7970b9d11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
@@ -8,20 +8,36 @@ dashedName: problem-471-triangle-inscribed-in-ellipse
# --description--
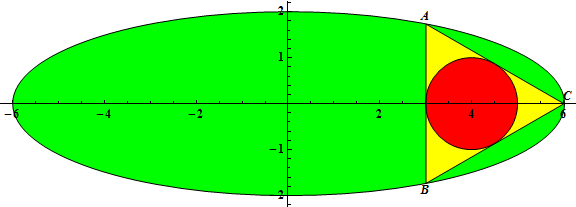
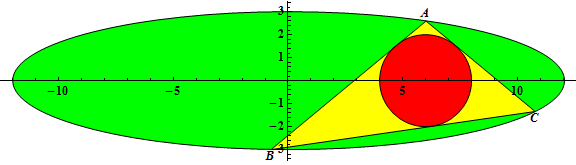
-The triangle ΔABC is inscribed in an ellipse with equation $\\frac {x^2} {a^2} + \\frac {y^2} {b^2} = 1$, 0 < 2b < a, a and b integers.
+The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
-Let r(a,b) be the radius of the incircle of ΔABC when the incircle has center (2b, 0) and A has coordinates $\\left( \\frac a 2, \\frac {\\sqrt 3} 2 b\\right)$.
+Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
-For example, r(3,1) = ½, r(6,2) = 1, r(12,3) = 2.
+For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
-Let $G(n) = \\sum*{a=3}^n \\sum*{b=1}^{\\lfloor \\frac {a - 1} 2 \\rfloor} r(a, b)$ You are given G(10) = 20.59722222, G(100) = 19223.60980 (rounded to 10 significant digits). Find G(1011). Give your answer in scientific notation rounded to 10 significant digits. Use a lowercase e to separate mantissa and exponent. For G(10) the answer would have been 2.059722222e1.
+
+
Notice that the first polygon has three consecutive collinear vertices.
-Let P(n) be the number of polar polygons such that the vertices (x, y) have integer coordinates whose absolute values are not greater than n.
+Let $P(n)$ be the number of polar polygons such that the vertices $(x, y)$ have integer coordinates whose absolute values are not greater than $n$.
-Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices \[(0,0),(0,3),(1,1),(3,0)] is distinct from the polygon with vertices \[(0,0),(0,3),(1,1),(3,0),(1,0)].
+Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices [(0,0), (0,3), (1,1), (3,0)] is distinct from the polygon with vertices [(0,0), (0,3), (1,1), (3,0), (1,0)].
-For example, P(1) = 131, P(2) = 1648531, P(3) = 1099461296175 and P(343) mod 1 000 000 007 = 937293740.
+For example, $P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$ and $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$.
-Find P(713) mod 1 000 000 007.
+Find $P(7^{13})\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler465()` should return 585965659.
+`polarPolygons()` should return `585965659`.
```js
-assert.strictEqual(euler465(), 585965659);
+assert.strictEqual(polarPolygons(), 585965659);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler465(), 585965659);
## --seed-contents--
```js
-function euler465() {
+function polarPolygons() {
return true;
}
-euler465();
+polarPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
index 3050ea410b..f578dd0bb0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
@@ -8,24 +8,35 @@ dashedName: problem-466-distinct-terms-in-a-multiplication-table
# --description--
-Let P(m,n) be the number of distinct terms in an m×n multiplication table.
+Let $P(m,n)$ be the number of distinct terms in an $m×n$ multiplication table.
For example, a 3×4 multiplication table looks like this:
-× 12341 12342 24683 36912
+$$\begin{array}{c}
+ × & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} \\\\
+ \mathbf{1} & 1 & 2 & 3 & 4 \\\\
+ \mathbf{2} & 2 & 4 & 6 & 8 \\\\
+ \mathbf{3} & 3 & 6 & 9 & 12
+\end{array}$$
-There are 8 distinct terms {1,2,3,4,6,8,9,12}, therefore P(3,4) = 8.
+There are 8 distinct terms {1, 2, 3, 4, 6, 8, 9, 12}, therefore $P(3, 4) = 8$.
-You are given that: P(64,64) = 1263, P(12,345) = 1998, and P(32,1015) = 13826382602124302.
+You are given that:
-Find P(64,1016).
+$$\begin{align}
+ & P(64, 64) = 1\\,263, \\\\
+ & P(12, 345) = 1\\,998, \text{ and} \\\\
+ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302. \\\\
+\end{align}$$
+
+Find $P(64, {10}^{16})$.
# --hints--
-`euler466()` should return 258381958195474750.
+`multiplicationTable()` should return `258381958195474750`.
```js
-assert.strictEqual(euler466(), 258381958195474750);
+assert.strictEqual(multiplicationTable(), 258381958195474750);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler466(), 258381958195474750);
## --seed-contents--
```js
-function euler466() {
+function multiplicationTable() {
return true;
}
-euler466();
+multiplicationTable();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
index 8cfd9dc16a..d237fc953c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
@@ -8,26 +8,41 @@ dashedName: problem-467-superinteger
# --description--
-An integer s is called a superinteger of another integer n if the digits of n form a subsequence of the digits of s.
+An integer $s$ is called a superinteger of another integer $n$ if the digits of $n$ form a subsequence of the digits of $s$.
For example, 2718281828 is a superinteger of 18828, while 314159 is not a superinteger of 151.
-Let p(n) be the nth prime number, and let c(n) be the nth composite number. For example, p(1) = 2, p(10) = 29, c(1) = 4 and c(10) = 18. {p(i) : i ≥ 1} = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...} {c(i) : i ≥ 1} = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, ...}
+Let $p(n)$ be the $n$th prime number, and let $c(n)$ be the $n$th composite number. For example, $p(1) = 2$, $p(10) = 29$, $c(1) = 4$ and $c(10) = 18$.
-Let PD the sequence of the digital roots of {p(i)} (CD is defined similarly for {c(i)}): PD = {2, 3, 5, 7, 2, 4, 8, 1, 5, 2, ...} CD = {4, 6, 8, 9, 1, 3, 5, 6, 7, 9, ...}
+$$\begin{align}
+ & \\{p(i) : i ≥ 1\\} = \\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots \\} \\\\
+ & \\{c(i) : i ≥ 1\\} = \\{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, \ldots \\}
+\end{align}$$
-Let Pn be the integer formed by concatenating the first n elements of PD (Cn is defined similarly for CD). P10 = 2357248152 C10 = 4689135679
+Let $P^D$ the sequence of the digital roots of $\\{p(i)\\}$ ($C^D$ is defined similarly for $\\{c(i)\\}$):
-Let f(n) be the smallest positive integer that is a common superinteger of Pn and Cn. For example, f(10) = 2357246891352679, and f(100) mod 1 000 000 007 = 771661825.
+$$\begin{align}
+ & P^D = \\{2, 3, 5, 7, 2, 4, 8, 1, 5, 2, \ldots \\} \\\\
+ & C^D = \\{4, 6, 8, 9, 1, 3, 5, 6, 7, 9, \ldots \\}
+\end{align}$$
-Find f(10 000) mod 1 000 000 007.
+Let $P_n$ be the integer formed by concatenating the first $n$ elements of $P^D$ ($C_n$ is defined similarly for $C^D$).
+
+$$\begin{align}
+ & P_{10} = 2\\,357\\,248\\,152 \\\\
+ & C_{10} = 4\\,689\\,135\\,679
+\end{align}$$
+
+Let $f(n)$ be the smallest positive integer that is a common superinteger of $P_n$ and $C_n$. For example, $f(10) = 2\\,357\\,246\\,891\\,352\\,679$, and $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$.
+
+Find $f(10\\,000)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler467()` should return 775181359.
+`superinteger()` should return `775181359`.
```js
-assert.strictEqual(euler467(), 775181359);
+assert.strictEqual(superinteger(), 775181359);
```
# --seed--
@@ -35,12 +50,12 @@ assert.strictEqual(euler467(), 775181359);
## --seed-contents--
```js
-function euler467() {
+function superinteger() {
return true;
}
-euler467();
+superinteger();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
index 239d2cf56d..369c04b06e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
@@ -8,20 +8,36 @@ dashedName: problem-468-smooth-divisors-of-binomial-coefficients
# --description--
-An integer is called B-smooth if none of its prime factors is greater than B.
+An integer is called B-smooth if none of its prime factors is greater than $B$.
-Let SB(n) be the largest B-smooth divisor of n. Examples: S1(10) = 1 S4(2100) = 12 S17(2496144) = 5712
+Let $SB(n)$ be the largest B-smooth divisor of $n$.
-Define F(n) = ∑1≤B≤n ∑0≤r≤n SB(C(n,r)). Here, C(n,r) denotes the binomial coefficient. Examples: F(11) = 3132 F(1 111) mod 1 000 000 993 = 706036312 F(111 111) mod 1 000 000 993 = 22156169
+Examples:
-Find F(11 111 111) mod 1 000 000 993.
+$$\begin{align}
+ & S_1(10) = 1 \\\\
+ & S_4(2\\,100) = 12 \\\\
+ & S_{17}(2\\,496\\,144) = 5\\,712
+\end{align}$$
+
+Define $F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$. Here, $\displaystyle\binom{n}{r}$ denotes the binomial coefficient.
+
+Examples:
+
+$$\begin{align}
+ & F(11) = 3132 \\\\
+ & F(1\\,111)\bmod 1\\,000\\,000\\,993 = 706\\,036\\,312 \\\\
+ & F(111\\,111)\bmod 1\\,000\\,000\\,993 = 22\\,156\\,169
+\end{align}$$
+
+Find $F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$.
# --hints--
-`euler468()` should return 852950321.
+`smoothDivisorsOfBinomialCoefficients()` should return `852950321`.
```js
-assert.strictEqual(euler468(), 852950321);
+assert.strictEqual(smoothDivisorsOfBinomialCoefficients(), 852950321);
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler468(), 852950321);
## --seed-contents--
```js
-function euler468() {
+function smoothDivisorsOfBinomialCoefficients() {
return true;
}
-euler468();
+smoothDivisorsOfBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
index 4e8be025a2..d1db21f4f4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
@@ -8,22 +8,24 @@ dashedName: problem-469-empty-chairs
# --description--
-In a room N chairs are placed around a round table.
+In a room $N$ chairs are placed around a round table.
Knights enter the room one by one and choose at random an available empty chair.
To have enough elbow room the knights always leave at least one empty chair between each other.
-When there aren't any suitable chairs left, the fraction C of empty chairs is determined. We also define E(N) as the expected value of C. We can verify that E(4) = 1/2 and E(6) = 5/9.
+When there aren't any suitable chairs left, the fraction $C$ of empty chairs is determined. We also define $E(N)$ as the expected value of $C$.
-Find E(1018). Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
+We can verify that $E(4) = \frac{1}{2}$ and $E(6) = \frac{5}{9}$.
+
+Find $E({10}^{18})$. Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
# --hints--
-`euler469()` should return 0.56766764161831.
+`emptyChairs()` should return `0.56766764161831`.
```js
-assert.strictEqual(euler469(), 0.56766764161831);
+assert.strictEqual(emptyChairs(), 0.56766764161831);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler469(), 0.56766764161831);
## --seed-contents--
```js
-function euler469() {
+function emptyChairs() {
return true;
}
-euler469();
+emptyChairs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
index 10ee6d95d8..a8f59ece37 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
@@ -10,24 +10,24 @@ dashedName: problem-470-super-ramvok
Consider a single game of Ramvok:
-Let t represent the maximum number of turns the game lasts. If t = 0, then the game ends immediately. Otherwise, on each turn i, the player rolls a die. After rolling, if i < t the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If i = t, then the roll cannot be discarded and the prize must be accepted. Before the game begins, t is chosen by the player, who must then pay an up-front cost ct for some constant c. For c = 0, t can be chosen to be infinite (with an up-front cost of 0). Let R(d, c) be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair d-sided die and cost constant c. For example, R(4, 0.2) = 2.65. Assume that the player has sufficient funds for paying any/all up-front costs.
+Let $t$ represent the maximum number of turns the game lasts. If $t = 0$, then the game ends immediately. Otherwise, on each turn $i$, the player rolls a die. After rolling, if $i < t$ the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If $i = t$, then the roll cannot be discarded and the prize must be accepted. Before the game begins, $t$ is chosen by the player, who must then pay an up-front cost $ct$ for some constant $c$. For $c = 0$, $t$ can be chosen to be infinite (with an up-front cost of 0). Let $R(d, c)$ be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair $d$-sided die and cost constant $c$. For example, $R(4, 0.2) = 2.65$. Assume that the player has sufficient funds for paying any/all up-front costs.
Now consider a game of Super Ramvok:
In Super Ramvok, the game of Ramvok is played repeatedly, but with a slight modification. After each game, the die is altered. The alteration process is as follows: The die is rolled once, and if the resulting face has its pips visible, then that face is altered to be blank instead. If the face is already blank, then it is changed back to its original value. After the alteration is made, another game of Ramvok can begin (and during such a game, at each turn, the die is rolled until a face with a value on it appears). The player knows which faces are blank and which are not at all times. The game of Super Ramvok ends once all faces of the die are blank.
-Let S(d, c) be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair d-sided die to start (with all sides visible), and cost constant c. For example, S(6, 1) = 208.3.
+Let $S(d, c)$ be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair $d$-sided die to start (with all sides visible), and cost constant $c$. For example, $S(6, 1) = 208.3$.
-Let F(n) = ∑4≤d≤n ∑0≤c≤n S(d, c).
+Let $F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$.
-Calculate F(20), rounded to the nearest integer.
+Calculate $F(20)$, rounded to the nearest integer.
# --hints--
-`euler470()` should return 147668794.
+`superRamvok()` should return `147668794`.
```js
-assert.strictEqual(euler470(), 147668794);
+assert.strictEqual(superRamvok(), 147668794);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler470(), 147668794);
## --seed-contents--
```js
-function euler470() {
+function superRamvok() {
return true;
}
-euler470();
+superRamvok();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
index 95385ddec9..7970b9d11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
@@ -8,20 +8,36 @@ dashedName: problem-471-triangle-inscribed-in-ellipse
# --description--
-The triangle ΔABC is inscribed in an ellipse with equation $\\frac {x^2} {a^2} + \\frac {y^2} {b^2} = 1$, 0 < 2b < a, a and b integers.
+The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
-Let r(a,b) be the radius of the incircle of ΔABC when the incircle has center (2b, 0) and A has coordinates $\\left( \\frac a 2, \\frac {\\sqrt 3} 2 b\\right)$.
+Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
-For example, r(3,1) = ½, r(6,2) = 1, r(12,3) = 2.
+For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
-Let $G(n) = \\sum*{a=3}^n \\sum*{b=1}^{\\lfloor \\frac {a - 1} 2 \\rfloor} r(a, b)$ You are given G(10) = 20.59722222, G(100) = 19223.60980 (rounded to 10 significant digits). Find G(1011). Give your answer in scientific notation rounded to 10 significant digits. Use a lowercase e to separate mantissa and exponent. For G(10) the answer would have been 2.059722222e1.
+ +
+
+
+ +
+Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
+
+You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
+
+Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
+
+For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
-`euler471()` should return 1.895093981e+31.
+`triangleInscribedInEllipse()` should return a string.
```js
-assert.strictEqual(euler471(), 1.895093981e31);
+assert(typeof triangleInscribedInEllipse() === 'string');
+```
+
+`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
+
+```js
+assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler471(), 1.895093981e31);
## --seed-contents--
```js
-function euler471() {
+function triangleInscribedInEllipse() {
return true;
}
-euler471();
+triangleInscribedInEllipse();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
index f4e9015549..0d4c54d635 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
@@ -8,32 +8,32 @@ dashedName: problem-472-comfortable-distance-ii
# --description--
-There are N seats in a row. N people come one after another to fill the seats according to the following rules:
+There are $N$ seats in a row. $N$ people come one after another to fill the seats according to the following rules:
-No person sits beside another.
+1. No person sits beside another.
+1. The first person chooses any seat.
+1. Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
-The first person chooses any seat.
+Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than $N$ (for $N > 1$).
-Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
+Here are the possible seating arrangements for $N = 15$:
-Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than N (for N > 1).
-
-Here are the possible seating arrangements for N = 15:
+
+
+Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
+
+You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
+
+Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
+
+For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
-`euler471()` should return 1.895093981e+31.
+`triangleInscribedInEllipse()` should return a string.
```js
-assert.strictEqual(euler471(), 1.895093981e31);
+assert(typeof triangleInscribedInEllipse() === 'string');
+```
+
+`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
+
+```js
+assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler471(), 1.895093981e31);
## --seed-contents--
```js
-function euler471() {
+function triangleInscribedInEllipse() {
return true;
}
-euler471();
+triangleInscribedInEllipse();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
index f4e9015549..0d4c54d635 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
@@ -8,32 +8,32 @@ dashedName: problem-472-comfortable-distance-ii
# --description--
-There are N seats in a row. N people come one after another to fill the seats according to the following rules:
+There are $N$ seats in a row. $N$ people come one after another to fill the seats according to the following rules:
-No person sits beside another.
+1. No person sits beside another.
+1. The first person chooses any seat.
+1. Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
-The first person chooses any seat.
+Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than $N$ (for $N > 1$).
-Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
+Here are the possible seating arrangements for $N = 15$:
-Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than N (for N > 1).
-
-Here are the possible seating arrangements for N = 15:
+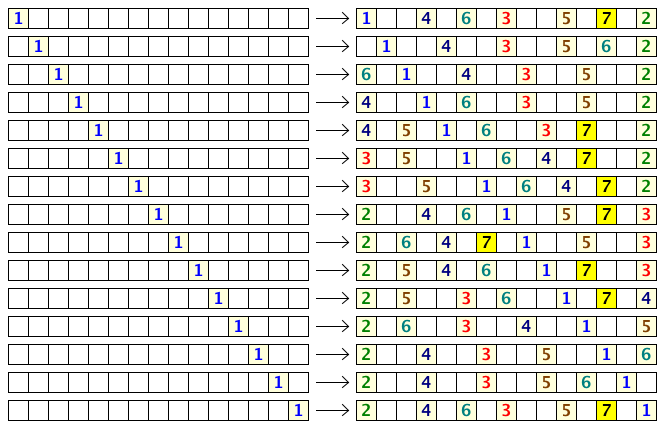 We see that if the first person chooses correctly, the 15 seats can seat up to 7 people. We can also see that the first person has 9 choices to maximize the number of people that may be seated.
-Let f(N) be the number of choices the first person has to maximize the number of occupants for N seats in a row. Thus, f(1) = 1, f(15) = 9, f(20) = 6, and f(500) = 16.
+Let $f(N)$ be the number of choices the first person has to maximize the number of occupants for $N$ seats in a row. Thus, $f(1) = 1$, $f(15) = 9$, $f(20) = 6$, and $f(500) = 16$.
-Also, ∑f(N) = 83 for 1 ≤ N ≤ 20 and ∑f(N) = 13343 for 1 ≤ N ≤ 500.
+Also, $\sum f(N) = 83$ for $1 ≤ N ≤ 20$ and $\sum f(N) = 13\\,343$ for $1 ≤ N ≤ 500$.
-Find ∑f(N) for 1 ≤ N ≤ 1012. Give the last 8 digits of your answer.
+Find $\sum f(N)$ for $1 ≤ N ≤ {10}^{12}$. Give the last 8 digits of your answer.
# --hints--
-`euler472()` should return 73811586.
+`comfortableDistanceTwo()` should return `73811586`.
```js
-assert.strictEqual(euler472(), 73811586);
+assert.strictEqual(comfortableDistanceTwo(), 73811586);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler472(), 73811586);
## --seed-contents--
```js
-function euler472() {
+function comfortableDistanceTwo() {
return true;
}
-euler472();
+comfortableDistanceTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
index 505c8a757b..0936140110 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
@@ -8,9 +8,9 @@ dashedName: problem-473-phigital-number-base
# --description--
-Let $\\varphi$ be the golden ratio: $\\varphi=\\frac{1+\\sqrt{5}}{2}.$
+Let $\varphi$ be the golden ratio: $\varphi = \frac{1+\sqrt{5}}{2}.$
-Remarkably it is possible to write every positive integer as a sum of powers of $\\varphi$ even if we require that every power of $\\varphi$ is used at most once in this sum.
+Remarkably it is possible to write every positive integer as a sum of powers of $\varphi$ even if we require that every power of $\varphi$ is used at most once in this sum.
Even then this representation is not unique.
@@ -18,9 +18,11 @@ We can make it unique by requiring that no powers with consecutive exponents are
E.g:
-$2=\\varphi+\\varphi^{-2}$ and $3=\\varphi^{2}+\\varphi^{-2}$
+$2 = \varphi + \varphi^{-2}$ and $3 = \varphi^{2} + \varphi^{-2}$
-To represent this sum of powers of $\\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase. So $1=1*{\\varphi}$, $2=10.01*{\\varphi}$, $3=100.01*{\\varphi}$ and $14=100100.001001*{\\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
+To represent this sum of powers of $\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase.
+
+So $1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$ and $14 = 100100.001001_{\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
The sum of the positive integers not exceeding 1000 whose phigital representation is palindromic is 4345.
@@ -28,10 +30,10 @@ Find the sum of the positive integers not exceeding $10^{10}$ whose phigital rep
# --hints--
-`euler473()` should return 35856681704365.
+`phigitalNumberBase()` should return `35856681704365`.
```js
-assert.strictEqual(euler473(), 35856681704365);
+assert.strictEqual(phigitalNumberBase(), 35856681704365);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler473(), 35856681704365);
## --seed-contents--
```js
-function euler473() {
+function phigitalNumberBase() {
return true;
}
-euler473();
+phigitalNumberBase();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
index 5c77726bd2..04123a2b35 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
@@ -8,20 +8,20 @@ dashedName: problem-474-last-digits-of-divisors
# --description--
-For a positive integer n and digits d, we define F(n, d) as the number of the divisors of n whose last digits equal d.
+For a positive integer $n$ and digits $d$, we define $F(n, d)$ as the number of the divisors of $n$ whose last digits equal $d$.
-For example, F(84, 4) = 3. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
+For example, $F(84, 4) = 3$. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
-We can also verify that F(12!, 12) = 11 and F(50!, 123) = 17888.
+We can also verify that $F(12!, 12) = 11$ and $F(50!, 123) = 17\\,888$.
-Find F(106!, 65432) modulo (1016 + 61).
+Find $F({10}^6!, 65\\,432) \text{ modulo } ({10}^{16} + 61)$.
# --hints--
-`euler474()` should return 9690646731515010.
+`lastDigitsOfDivisors()` should return `9690646731515010`.
```js
-assert.strictEqual(euler474(), 9690646731515010);
+assert.strictEqual(lastDigitsOfDivisors(), 9690646731515010);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler474(), 9690646731515010);
## --seed-contents--
```js
-function euler474() {
+function lastDigitsOfDivisors() {
return true;
}
-euler474();
+lastDigitsOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
index dd8cf3538b..4ab0b69b3a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
@@ -8,22 +8,24 @@ dashedName: problem-475-music-festival
# --description--
-12n musicians participate at a music festival. On the first day, they form 3n quartets and practice all day.
+$12n$ musicians participate at a music festival. On the first day, they form $3n$ quartets and practice all day.
It is a disaster. At the end of the day, all musicians decide they will never again agree to play with any member of their quartet.
-On the second day, they form 4n trios, each musician avoiding his previous quartet partners.
+On the second day, they form $4n$ trios, each musician avoiding his previous quartet partners.
-Let f(12n) be the number of ways to organize the trios amongst the 12n musicians. You are given f(12) = 576 and f(24) mod 1 000 000 007 = 509089824.
+Let $f(12n)$ be the number of ways to organize the trios amongst the $12n$ musicians.
-Find f(600) mod 1 000 000 007.
+You are given $f(12) = 576$ and $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$.
+
+Find $f(600)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler475()` should return 75780067.
+`musicFestival()` should return `75780067`.
```js
-assert.strictEqual(euler475(), 75780067);
+assert.strictEqual(musicFestival(), 75780067);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler475(), 75780067);
## --seed-contents--
```js
-function euler475() {
+function musicFestival() {
return true;
}
-euler475();
+musicFestival();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
index a5a8bf868b..b87eca74b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
@@ -8,20 +8,20 @@ dashedName: problem-476-circle-packing-ii
# --description--
-Let R(a, b, c) be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths a, b and c.
+Let $R(a, b, c)$ be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths $a$, $b$ and $c$.
-Let S(n) be the average value of R(a, b, c) over all integer triplets (a, b, c) such that 1 ≤ a ≤ b ≤ c < a + b ≤ n
+Let $S(n)$ be the average value of $R(a, b, c)$ over all integer triplets $(a, b, c)$ such that $1 ≤ a ≤ b ≤ c < a + b ≤ n$.
-You are given S(2) = R(1, 1, 1) ≈ 0.31998, S(5) ≈ 1.25899.
+You are given $S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$.
-Find S(1803) rounded to 5 decimal places behind the decimal point.
+Find $S(1803)$ rounded to 5 decimal places behind the decimal point.
# --hints--
-`euler476()` should return 110242.87794.
+`circlePackingTwo()` should return `110242.87794`.
```js
-assert.strictEqual(euler476(), 110242.87794);
+assert.strictEqual(circlePackingTwo(), 110242.87794);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler476(), 110242.87794);
## --seed-contents--
```js
-function euler476() {
+function circlePackingTwo() {
return true;
}
-euler476();
+circlePackingTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
index f4c95faba7..24fa79f131 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
@@ -8,42 +8,38 @@ dashedName: problem-477-number-sequence-game
# --description--
-The number sequence game starts with a sequence S of N numbers written on a line.
+The number sequence game starts with a sequence $S$ of $N$ numbers written on a line.
Two players alternate turns. At his turn, a player must select and remove either the first or the last number remaining in the sequence.
The player score is the sum of all the numbers he has taken. Each player attempts to maximize his own sum.
-If N = 4 and S = {1, 2, 10, 3}, then each player maximizes his score as follows:
+If $N = 4$ and $S = \\{1, 2, 10, 3\\}$, then each player maximizes his score as follows:
-Player 1: removes the first number (1)
+- Player 1: removes the first number (1)
+- Player 2: removes the last number from the remaining sequence (3)
+- Player 1: removes the last number from the remaining sequence (10)
+- Player 2: removes the remaining number (2)
-Player 2: removes the last number from the remaining sequence (3)
+Player 1 score is $1 + 10 = 11$.
-Player 1: removes the last number from the remaining sequence (10)
+Let $F(N)$ be the score of player 1 if both players follow the optimal strategy for the sequence $S = \\{s_1, s_2, \ldots, s_N\\}$ defined as:
-Player 2: removes the remaining number (2)
+- $s_1 = 0$
+- $s_{i + 1} = ({s_i}^2 + 45)$ modulo $1\\,000\\,000\\,007$
-Player 1 score is 1 + 10 = 11.
+The sequence begins with $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,107\\,844, 894\\,218\\,625, \ldots\\}$.
-Let F(N) be the score of player 1 if both players follow the optimal strategy for the sequence S = {s1, s2, ..., sN} defined as:
+You are given $F(2) = 45$, $F(4) = 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$.
-s1 = 0
-
-si+1 = (si2 + 45) modulo 1 000 000 007
-
-The sequence begins with S = {0, 45, 2070, 4284945, 753524550, 478107844, 894218625, ...}.
-
-You are given F(2) = 45, F(4) = 4284990, F(100) = 26365463243, F(104) = 2495838522951.
-
-Find F(108).
+Find $F({10}^8)$.
# --hints--
-`euler477()` should return 25044905874565164.
+`numberSequenceGame()` should return `25044905874565164`.
```js
-assert.strictEqual(euler477(), 25044905874565164);
+assert.strictEqual(numberSequenceGame(), 25044905874565164);
```
# --seed--
@@ -51,12 +47,12 @@ assert.strictEqual(euler477(), 25044905874565164);
## --seed-contents--
```js
-function euler477() {
+function numberSequenceGame() {
return true;
}
-euler477();
+numberSequenceGame();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
index 37e7681ecf..745aefc824 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
@@ -8,26 +8,32 @@ dashedName: problem-478-mixtures
# --description--
-Let us consider mixtures of three substances: A, B and C. A mixture can be described by a ratio of the amounts of A, B, and C in it, i.e., (a : b : c). For example, a mixture described by the ratio (2 : 3 : 5) contains 20% A, 30% B and 50% C.
+Let us consider mixtures of three substances: $A$, $B$ and $C$. A mixture can be described by a ratio of the amounts of $A$, $B$, and $C$ in it, i.e., $(a : b : c)$. For example, a mixture described by the ratio (2 : 3 : 5) contains 20% $A$, 30% $B$ and 50% $C$.
For the purposes of this problem, we cannot separate the individual components from a mixture. However, we can combine different amounts of different mixtures to form mixtures with new ratios.
-For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: (10·3/5 + 20·3/20 + 30·3/10 : 10·0/5 + 20·6/20 + 30·3/10 : 10·2/5 + 20·11/20 + 30·4/10) = (18 : 15 : 27) = (6 : 5 : 9)
+For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: ($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9)
-However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of B is always less than the amount of C.
+However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of $B$ is always less than the amount of $C$.
-Let n be a positive integer. Suppose that for every triple of integers (a, b, c) with 0 ≤ a, b, c ≤ n and gcd(a, b, c) = 1, we have a mixture with ratio (a : b : c). Let M(n) be the set of all such mixtures.
+Let $n$ be a positive integer. Suppose that for every triple of integers $(a, b, c)$ with $0 ≤ a, b, c ≤ n$ and $gcd(a, b, c) = 1$, we have a mixture with ratio $(a : b : c)$. Let $M(n)$ be the set of all such mixtures.
-For example, M(2) contains the 19 mixtures with the following ratios: {(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+For example, $M(2)$ contains the 19 mixtures with the following ratios:
-Let E(n) be the number of subsets of M(n) which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts A, B and C. We can verify that E(1) = 103, E(2) = 520447, E(10) mod 118 = 82608406 and E(500) mod 118 = 13801403. Find E(10 000 000) mod 118.
+{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+
+Let $E(n)$ be the number of subsets of $M(n)$ which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts $A$, $B$ and $C$.
+
+We can verify that $E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$ and $E(500)\bmod {11}^8 = 13\\,801\\,403$.
+
+Find $E(10\\,000\\,000)\bmod {11}^8$.
# --hints--
-`euler478()` should return 59510340.
+`mixtures()` should return `59510340`.
```js
-assert.strictEqual(euler478(), 59510340);
+assert.strictEqual(mixtures(), 59510340);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler478(), 59510340);
## --seed-contents--
```js
-function euler478() {
+function mixtures() {
return true;
}
-euler478();
+mixtures();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
index 202e7e04be..f2114e53c2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
@@ -8,22 +8,22 @@ dashedName: problem-479-roots-on-the-rise
# --description--
-Let ak, bk, and ck represent the three solutions (real or complex numbers) to the expression 1/x = (k/x)2(k+x2) - kx.
+Let $a_k$, $b_k$, and $c_k$ represent the three solutions (real or complex numbers) to the expression $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$.
-For instance, for k = 5, we see that {a5, b5, c5} is approximately {5.727244, -0.363622+2.057397i, -0.363622-2.057397i}.
+For instance, for $k = 5$, we see that $\\{a_5, b_5, c_5\\}$ is approximately $\\{5.727244, -0.363622 + 2.057397i, -0.363622 - 2.057397i\\}$.
-Let S(n) = Σ (ak+bk)p(bk+ck)p(ck+ak)p for all integers p, k such that 1 ≤ p, k ≤ n.
+Let $S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ for all integers $p$, $k$ such that $1 ≤ p, k ≤ n$.
-Interestingly, S(n) is always an integer. For example, S(4) = 51160.
+Interestingly, $S(n)$ is always an integer. For example, $S(4) = 51\\,160$.
-Find S(106) modulo 1 000 000 007.
+Find $S({10}^6) \text{ modulo } 1\\,000\\,000\\,007$.
# --hints--
-`euler479()` should return 191541795.
+`rootsOnTheRise()` should return `191541795`.
```js
-assert.strictEqual(euler479(), 191541795);
+assert.strictEqual(rootsOnTheRise(), 191541795);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler479(), 191541795);
## --seed-contents--
```js
-function euler479() {
+function rootsOnTheRise() {
return true;
}
-euler479();
+rootsOnTheRise();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
index 9e2ac8d96d..56ac54b858 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
@@ -10,88 +10,74 @@ dashedName: problem-480-the-last-question
Consider all the words which can be formed by selecting letters, in any order, from the phrase:
-thereisasyetinsufficientdataforameaningfulanswer
+$$\mathbf{\text{thereisasyetinsufficientdataforameaningfulanswer}}$$
Suppose those with 15 letters or less are listed in alphabetical order and numbered sequentially starting at 1.
The list would include:
-1 : a
+$$\begin{align}
+ & 1: \text{a} \\\\
+ & 2: \text{aa} \\\\
+ & 3: \text{aaa} \\\\
+ & 4: \text{aaaa} \\\\
+ & 5: \text{aaaaa} \\\\
+ & 6: \text{aaaaaa} \\\\
+ & 7: \text{aaaaaac} \\\\
+ & 8: \text{aaaaaacd} \\\\
+ & 9: \text{aaaaaacde} \\\\
+ & 10: \text{aaaaaacdee} \\\\
+ & 11: \text{aaaaaacdeee} \\\\
+ & 12: \text{aaaaaacdeeee} \\\\
+ & 13: \text{aaaaaacdeeeee} \\\\
+ & 14: \text{aaaaaacdeeeeee} \\\\
+ & 15: \text{aaaaaacdeeeeeef} \\\\
+ & 16: \text{aaaaaacdeeeeeeg} \\\\
+ & 17: \text{aaaaaacdeeeeeeh} \\\\
+ & \ldots \\\\
+ & 28: \text{aaaaaacdeeeeeey} \\\\
+ & 29: \text{aaaaaacdeeeeef} \\\\
+ & 30: \text{aaaaaacdeeeeefe} \\\\
+ & \ldots \\\\
+ & 115246685191495242: \text{euleoywuttttsss} \\\\
+ & 115246685191495243: \text{euler} \\\\
+ & 115246685191495244: \text{eulera} \\\\
+ & ... \\\\
+ & 525069350231428029: \text{ywuuttttssssrrr} \\\\
+\end{align}$$
-2 : aa
+Define $P(w)$ as the position of the word $w$.
-3 : aaa
+Define $W(p)$ as the word in position $p$.
-4 : aaaa
-
-5 : aaaaa
-
-6 : aaaaaa
-
-7 : aaaaaac
-
-8 : aaaaaacd
-
-9 : aaaaaacde
-
-10 : aaaaaacdee
-
-11 : aaaaaacdeee
-
-12 : aaaaaacdeeee
-
-13 : aaaaaacdeeeee
-
-14 : aaaaaacdeeeeee
-
-15 : aaaaaacdeeeeeef
-
-16 : aaaaaacdeeeeeeg
-
-17 : aaaaaacdeeeeeeh
-
-...
-
-28 : aaaaaacdeeeeeey
-
-29 : aaaaaacdeeeeef
-
-30 : aaaaaacdeeeeefe
-
-...
-
-115246685191495242: euleoywuttttsss
-
-115246685191495243: euler
-
-115246685191495244: eulera
-
-...
-
-525069350231428029: ywuuttttssssrrrDefine P(w) as the position of the word w.
-
-Define W(p) as the word in position p.
-
-We can see that P(w) and W(p) are inverses: P(W(p)) = p and W(P(w)) = w.
+We can see that $P(w)$ and $W(p)$ are inverses: $P(W(p)) = p$ and $W(P(w)) = w$.
Examples:
-W(10) = aaaaaacdee
+$$\begin{align}
+ & W(10) = \text{ aaaaaacdee} \\\\
+ & P(\text{aaaaaacdee}) = 10 \\\\
+ & W(115246685191495243) = \text{ euler} \\\\
+ & P(\text{euler}) = 115246685191495243 \\\\
+\end{align}$$
-P(aaaaaacdee) = 10
-
-W(115246685191495243) = euler
-
-P(euler) = 115246685191495243Find W(P(legionary) + P(calorimeters) - P(annihilate) + P(orchestrated) - P(fluttering)).
+Find
+$$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering})).$$
Give your answer using lowercase characters (no punctuation or space).
# --hints--
-`euler480()` should return turnthestarson.
+`euler480()` should return a string.
```js
-assert.strictEqual(euler480(), turnthestarson);
+assert(typeof euler480() === 'string');
+```
+
+`euler480()` should return the string `turnthestarson`.
+
+```js
+assert.strictEqual(euler480(), 'turnthestarson');
```
# --seed--
We see that if the first person chooses correctly, the 15 seats can seat up to 7 people. We can also see that the first person has 9 choices to maximize the number of people that may be seated.
-Let f(N) be the number of choices the first person has to maximize the number of occupants for N seats in a row. Thus, f(1) = 1, f(15) = 9, f(20) = 6, and f(500) = 16.
+Let $f(N)$ be the number of choices the first person has to maximize the number of occupants for $N$ seats in a row. Thus, $f(1) = 1$, $f(15) = 9$, $f(20) = 6$, and $f(500) = 16$.
-Also, ∑f(N) = 83 for 1 ≤ N ≤ 20 and ∑f(N) = 13343 for 1 ≤ N ≤ 500.
+Also, $\sum f(N) = 83$ for $1 ≤ N ≤ 20$ and $\sum f(N) = 13\\,343$ for $1 ≤ N ≤ 500$.
-Find ∑f(N) for 1 ≤ N ≤ 1012. Give the last 8 digits of your answer.
+Find $\sum f(N)$ for $1 ≤ N ≤ {10}^{12}$. Give the last 8 digits of your answer.
# --hints--
-`euler472()` should return 73811586.
+`comfortableDistanceTwo()` should return `73811586`.
```js
-assert.strictEqual(euler472(), 73811586);
+assert.strictEqual(comfortableDistanceTwo(), 73811586);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler472(), 73811586);
## --seed-contents--
```js
-function euler472() {
+function comfortableDistanceTwo() {
return true;
}
-euler472();
+comfortableDistanceTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
index 505c8a757b..0936140110 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
@@ -8,9 +8,9 @@ dashedName: problem-473-phigital-number-base
# --description--
-Let $\\varphi$ be the golden ratio: $\\varphi=\\frac{1+\\sqrt{5}}{2}.$
+Let $\varphi$ be the golden ratio: $\varphi = \frac{1+\sqrt{5}}{2}.$
-Remarkably it is possible to write every positive integer as a sum of powers of $\\varphi$ even if we require that every power of $\\varphi$ is used at most once in this sum.
+Remarkably it is possible to write every positive integer as a sum of powers of $\varphi$ even if we require that every power of $\varphi$ is used at most once in this sum.
Even then this representation is not unique.
@@ -18,9 +18,11 @@ We can make it unique by requiring that no powers with consecutive exponents are
E.g:
-$2=\\varphi+\\varphi^{-2}$ and $3=\\varphi^{2}+\\varphi^{-2}$
+$2 = \varphi + \varphi^{-2}$ and $3 = \varphi^{2} + \varphi^{-2}$
-To represent this sum of powers of $\\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase. So $1=1*{\\varphi}$, $2=10.01*{\\varphi}$, $3=100.01*{\\varphi}$ and $14=100100.001001*{\\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
+To represent this sum of powers of $\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase.
+
+So $1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$ and $14 = 100100.001001_{\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
The sum of the positive integers not exceeding 1000 whose phigital representation is palindromic is 4345.
@@ -28,10 +30,10 @@ Find the sum of the positive integers not exceeding $10^{10}$ whose phigital rep
# --hints--
-`euler473()` should return 35856681704365.
+`phigitalNumberBase()` should return `35856681704365`.
```js
-assert.strictEqual(euler473(), 35856681704365);
+assert.strictEqual(phigitalNumberBase(), 35856681704365);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler473(), 35856681704365);
## --seed-contents--
```js
-function euler473() {
+function phigitalNumberBase() {
return true;
}
-euler473();
+phigitalNumberBase();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
index 5c77726bd2..04123a2b35 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
@@ -8,20 +8,20 @@ dashedName: problem-474-last-digits-of-divisors
# --description--
-For a positive integer n and digits d, we define F(n, d) as the number of the divisors of n whose last digits equal d.
+For a positive integer $n$ and digits $d$, we define $F(n, d)$ as the number of the divisors of $n$ whose last digits equal $d$.
-For example, F(84, 4) = 3. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
+For example, $F(84, 4) = 3$. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
-We can also verify that F(12!, 12) = 11 and F(50!, 123) = 17888.
+We can also verify that $F(12!, 12) = 11$ and $F(50!, 123) = 17\\,888$.
-Find F(106!, 65432) modulo (1016 + 61).
+Find $F({10}^6!, 65\\,432) \text{ modulo } ({10}^{16} + 61)$.
# --hints--
-`euler474()` should return 9690646731515010.
+`lastDigitsOfDivisors()` should return `9690646731515010`.
```js
-assert.strictEqual(euler474(), 9690646731515010);
+assert.strictEqual(lastDigitsOfDivisors(), 9690646731515010);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler474(), 9690646731515010);
## --seed-contents--
```js
-function euler474() {
+function lastDigitsOfDivisors() {
return true;
}
-euler474();
+lastDigitsOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
index dd8cf3538b..4ab0b69b3a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
@@ -8,22 +8,24 @@ dashedName: problem-475-music-festival
# --description--
-12n musicians participate at a music festival. On the first day, they form 3n quartets and practice all day.
+$12n$ musicians participate at a music festival. On the first day, they form $3n$ quartets and practice all day.
It is a disaster. At the end of the day, all musicians decide they will never again agree to play with any member of their quartet.
-On the second day, they form 4n trios, each musician avoiding his previous quartet partners.
+On the second day, they form $4n$ trios, each musician avoiding his previous quartet partners.
-Let f(12n) be the number of ways to organize the trios amongst the 12n musicians. You are given f(12) = 576 and f(24) mod 1 000 000 007 = 509089824.
+Let $f(12n)$ be the number of ways to organize the trios amongst the $12n$ musicians.
-Find f(600) mod 1 000 000 007.
+You are given $f(12) = 576$ and $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$.
+
+Find $f(600)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler475()` should return 75780067.
+`musicFestival()` should return `75780067`.
```js
-assert.strictEqual(euler475(), 75780067);
+assert.strictEqual(musicFestival(), 75780067);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler475(), 75780067);
## --seed-contents--
```js
-function euler475() {
+function musicFestival() {
return true;
}
-euler475();
+musicFestival();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
index a5a8bf868b..b87eca74b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
@@ -8,20 +8,20 @@ dashedName: problem-476-circle-packing-ii
# --description--
-Let R(a, b, c) be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths a, b and c.
+Let $R(a, b, c)$ be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths $a$, $b$ and $c$.
-Let S(n) be the average value of R(a, b, c) over all integer triplets (a, b, c) such that 1 ≤ a ≤ b ≤ c < a + b ≤ n
+Let $S(n)$ be the average value of $R(a, b, c)$ over all integer triplets $(a, b, c)$ such that $1 ≤ a ≤ b ≤ c < a + b ≤ n$.
-You are given S(2) = R(1, 1, 1) ≈ 0.31998, S(5) ≈ 1.25899.
+You are given $S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$.
-Find S(1803) rounded to 5 decimal places behind the decimal point.
+Find $S(1803)$ rounded to 5 decimal places behind the decimal point.
# --hints--
-`euler476()` should return 110242.87794.
+`circlePackingTwo()` should return `110242.87794`.
```js
-assert.strictEqual(euler476(), 110242.87794);
+assert.strictEqual(circlePackingTwo(), 110242.87794);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler476(), 110242.87794);
## --seed-contents--
```js
-function euler476() {
+function circlePackingTwo() {
return true;
}
-euler476();
+circlePackingTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
index f4c95faba7..24fa79f131 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
@@ -8,42 +8,38 @@ dashedName: problem-477-number-sequence-game
# --description--
-The number sequence game starts with a sequence S of N numbers written on a line.
+The number sequence game starts with a sequence $S$ of $N$ numbers written on a line.
Two players alternate turns. At his turn, a player must select and remove either the first or the last number remaining in the sequence.
The player score is the sum of all the numbers he has taken. Each player attempts to maximize his own sum.
-If N = 4 and S = {1, 2, 10, 3}, then each player maximizes his score as follows:
+If $N = 4$ and $S = \\{1, 2, 10, 3\\}$, then each player maximizes his score as follows:
-Player 1: removes the first number (1)
+- Player 1: removes the first number (1)
+- Player 2: removes the last number from the remaining sequence (3)
+- Player 1: removes the last number from the remaining sequence (10)
+- Player 2: removes the remaining number (2)
-Player 2: removes the last number from the remaining sequence (3)
+Player 1 score is $1 + 10 = 11$.
-Player 1: removes the last number from the remaining sequence (10)
+Let $F(N)$ be the score of player 1 if both players follow the optimal strategy for the sequence $S = \\{s_1, s_2, \ldots, s_N\\}$ defined as:
-Player 2: removes the remaining number (2)
+- $s_1 = 0$
+- $s_{i + 1} = ({s_i}^2 + 45)$ modulo $1\\,000\\,000\\,007$
-Player 1 score is 1 + 10 = 11.
+The sequence begins with $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,107\\,844, 894\\,218\\,625, \ldots\\}$.
-Let F(N) be the score of player 1 if both players follow the optimal strategy for the sequence S = {s1, s2, ..., sN} defined as:
+You are given $F(2) = 45$, $F(4) = 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$.
-s1 = 0
-
-si+1 = (si2 + 45) modulo 1 000 000 007
-
-The sequence begins with S = {0, 45, 2070, 4284945, 753524550, 478107844, 894218625, ...}.
-
-You are given F(2) = 45, F(4) = 4284990, F(100) = 26365463243, F(104) = 2495838522951.
-
-Find F(108).
+Find $F({10}^8)$.
# --hints--
-`euler477()` should return 25044905874565164.
+`numberSequenceGame()` should return `25044905874565164`.
```js
-assert.strictEqual(euler477(), 25044905874565164);
+assert.strictEqual(numberSequenceGame(), 25044905874565164);
```
# --seed--
@@ -51,12 +47,12 @@ assert.strictEqual(euler477(), 25044905874565164);
## --seed-contents--
```js
-function euler477() {
+function numberSequenceGame() {
return true;
}
-euler477();
+numberSequenceGame();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
index 37e7681ecf..745aefc824 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
@@ -8,26 +8,32 @@ dashedName: problem-478-mixtures
# --description--
-Let us consider mixtures of three substances: A, B and C. A mixture can be described by a ratio of the amounts of A, B, and C in it, i.e., (a : b : c). For example, a mixture described by the ratio (2 : 3 : 5) contains 20% A, 30% B and 50% C.
+Let us consider mixtures of three substances: $A$, $B$ and $C$. A mixture can be described by a ratio of the amounts of $A$, $B$, and $C$ in it, i.e., $(a : b : c)$. For example, a mixture described by the ratio (2 : 3 : 5) contains 20% $A$, 30% $B$ and 50% $C$.
For the purposes of this problem, we cannot separate the individual components from a mixture. However, we can combine different amounts of different mixtures to form mixtures with new ratios.
-For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: (10·3/5 + 20·3/20 + 30·3/10 : 10·0/5 + 20·6/20 + 30·3/10 : 10·2/5 + 20·11/20 + 30·4/10) = (18 : 15 : 27) = (6 : 5 : 9)
+For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: ($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9)
-However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of B is always less than the amount of C.
+However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of $B$ is always less than the amount of $C$.
-Let n be a positive integer. Suppose that for every triple of integers (a, b, c) with 0 ≤ a, b, c ≤ n and gcd(a, b, c) = 1, we have a mixture with ratio (a : b : c). Let M(n) be the set of all such mixtures.
+Let $n$ be a positive integer. Suppose that for every triple of integers $(a, b, c)$ with $0 ≤ a, b, c ≤ n$ and $gcd(a, b, c) = 1$, we have a mixture with ratio $(a : b : c)$. Let $M(n)$ be the set of all such mixtures.
-For example, M(2) contains the 19 mixtures with the following ratios: {(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+For example, $M(2)$ contains the 19 mixtures with the following ratios:
-Let E(n) be the number of subsets of M(n) which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts A, B and C. We can verify that E(1) = 103, E(2) = 520447, E(10) mod 118 = 82608406 and E(500) mod 118 = 13801403. Find E(10 000 000) mod 118.
+{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+
+Let $E(n)$ be the number of subsets of $M(n)$ which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts $A$, $B$ and $C$.
+
+We can verify that $E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$ and $E(500)\bmod {11}^8 = 13\\,801\\,403$.
+
+Find $E(10\\,000\\,000)\bmod {11}^8$.
# --hints--
-`euler478()` should return 59510340.
+`mixtures()` should return `59510340`.
```js
-assert.strictEqual(euler478(), 59510340);
+assert.strictEqual(mixtures(), 59510340);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler478(), 59510340);
## --seed-contents--
```js
-function euler478() {
+function mixtures() {
return true;
}
-euler478();
+mixtures();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
index 202e7e04be..f2114e53c2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
@@ -8,22 +8,22 @@ dashedName: problem-479-roots-on-the-rise
# --description--
-Let ak, bk, and ck represent the three solutions (real or complex numbers) to the expression 1/x = (k/x)2(k+x2) - kx.
+Let $a_k$, $b_k$, and $c_k$ represent the three solutions (real or complex numbers) to the expression $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$.
-For instance, for k = 5, we see that {a5, b5, c5} is approximately {5.727244, -0.363622+2.057397i, -0.363622-2.057397i}.
+For instance, for $k = 5$, we see that $\\{a_5, b_5, c_5\\}$ is approximately $\\{5.727244, -0.363622 + 2.057397i, -0.363622 - 2.057397i\\}$.
-Let S(n) = Σ (ak+bk)p(bk+ck)p(ck+ak)p for all integers p, k such that 1 ≤ p, k ≤ n.
+Let $S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ for all integers $p$, $k$ such that $1 ≤ p, k ≤ n$.
-Interestingly, S(n) is always an integer. For example, S(4) = 51160.
+Interestingly, $S(n)$ is always an integer. For example, $S(4) = 51\\,160$.
-Find S(106) modulo 1 000 000 007.
+Find $S({10}^6) \text{ modulo } 1\\,000\\,000\\,007$.
# --hints--
-`euler479()` should return 191541795.
+`rootsOnTheRise()` should return `191541795`.
```js
-assert.strictEqual(euler479(), 191541795);
+assert.strictEqual(rootsOnTheRise(), 191541795);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler479(), 191541795);
## --seed-contents--
```js
-function euler479() {
+function rootsOnTheRise() {
return true;
}
-euler479();
+rootsOnTheRise();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
index 9e2ac8d96d..56ac54b858 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
@@ -10,88 +10,74 @@ dashedName: problem-480-the-last-question
Consider all the words which can be formed by selecting letters, in any order, from the phrase:
-thereisasyetinsufficientdataforameaningfulanswer
+$$\mathbf{\text{thereisasyetinsufficientdataforameaningfulanswer}}$$
Suppose those with 15 letters or less are listed in alphabetical order and numbered sequentially starting at 1.
The list would include:
-1 : a
+$$\begin{align}
+ & 1: \text{a} \\\\
+ & 2: \text{aa} \\\\
+ & 3: \text{aaa} \\\\
+ & 4: \text{aaaa} \\\\
+ & 5: \text{aaaaa} \\\\
+ & 6: \text{aaaaaa} \\\\
+ & 7: \text{aaaaaac} \\\\
+ & 8: \text{aaaaaacd} \\\\
+ & 9: \text{aaaaaacde} \\\\
+ & 10: \text{aaaaaacdee} \\\\
+ & 11: \text{aaaaaacdeee} \\\\
+ & 12: \text{aaaaaacdeeee} \\\\
+ & 13: \text{aaaaaacdeeeee} \\\\
+ & 14: \text{aaaaaacdeeeeee} \\\\
+ & 15: \text{aaaaaacdeeeeeef} \\\\
+ & 16: \text{aaaaaacdeeeeeeg} \\\\
+ & 17: \text{aaaaaacdeeeeeeh} \\\\
+ & \ldots \\\\
+ & 28: \text{aaaaaacdeeeeeey} \\\\
+ & 29: \text{aaaaaacdeeeeef} \\\\
+ & 30: \text{aaaaaacdeeeeefe} \\\\
+ & \ldots \\\\
+ & 115246685191495242: \text{euleoywuttttsss} \\\\
+ & 115246685191495243: \text{euler} \\\\
+ & 115246685191495244: \text{eulera} \\\\
+ & ... \\\\
+ & 525069350231428029: \text{ywuuttttssssrrr} \\\\
+\end{align}$$
-2 : aa
+Define $P(w)$ as the position of the word $w$.
-3 : aaa
+Define $W(p)$ as the word in position $p$.
-4 : aaaa
-
-5 : aaaaa
-
-6 : aaaaaa
-
-7 : aaaaaac
-
-8 : aaaaaacd
-
-9 : aaaaaacde
-
-10 : aaaaaacdee
-
-11 : aaaaaacdeee
-
-12 : aaaaaacdeeee
-
-13 : aaaaaacdeeeee
-
-14 : aaaaaacdeeeeee
-
-15 : aaaaaacdeeeeeef
-
-16 : aaaaaacdeeeeeeg
-
-17 : aaaaaacdeeeeeeh
-
-...
-
-28 : aaaaaacdeeeeeey
-
-29 : aaaaaacdeeeeef
-
-30 : aaaaaacdeeeeefe
-
-...
-
-115246685191495242: euleoywuttttsss
-
-115246685191495243: euler
-
-115246685191495244: eulera
-
-...
-
-525069350231428029: ywuuttttssssrrrDefine P(w) as the position of the word w.
-
-Define W(p) as the word in position p.
-
-We can see that P(w) and W(p) are inverses: P(W(p)) = p and W(P(w)) = w.
+We can see that $P(w)$ and $W(p)$ are inverses: $P(W(p)) = p$ and $W(P(w)) = w$.
Examples:
-W(10) = aaaaaacdee
+$$\begin{align}
+ & W(10) = \text{ aaaaaacdee} \\\\
+ & P(\text{aaaaaacdee}) = 10 \\\\
+ & W(115246685191495243) = \text{ euler} \\\\
+ & P(\text{euler}) = 115246685191495243 \\\\
+\end{align}$$
-P(aaaaaacdee) = 10
-
-W(115246685191495243) = euler
-
-P(euler) = 115246685191495243Find W(P(legionary) + P(calorimeters) - P(annihilate) + P(orchestrated) - P(fluttering)).
+Find
+$$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering})).$$
Give your answer using lowercase characters (no punctuation or space).
# --hints--
-`euler480()` should return turnthestarson.
+`euler480()` should return a string.
```js
-assert.strictEqual(euler480(), turnthestarson);
+assert(typeof euler480() === 'string');
+```
+
+`euler480()` should return the string `turnthestarson`.
+
+```js
+assert.strictEqual(euler480(), 'turnthestarson');
```
# --seed--
 +
Notice that the first polygon has three consecutive collinear vertices.
-Let P(n) be the number of polar polygons such that the vertices (x, y) have integer coordinates whose absolute values are not greater than n.
+Let $P(n)$ be the number of polar polygons such that the vertices $(x, y)$ have integer coordinates whose absolute values are not greater than $n$.
-Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices \[(0,0),(0,3),(1,1),(3,0)] is distinct from the polygon with vertices \[(0,0),(0,3),(1,1),(3,0),(1,0)].
+Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices [(0,0), (0,3), (1,1), (3,0)] is distinct from the polygon with vertices [(0,0), (0,3), (1,1), (3,0), (1,0)].
-For example, P(1) = 131, P(2) = 1648531, P(3) = 1099461296175 and P(343) mod 1 000 000 007 = 937293740.
+For example, $P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$ and $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$.
-Find P(713) mod 1 000 000 007.
+Find $P(7^{13})\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler465()` should return 585965659.
+`polarPolygons()` should return `585965659`.
```js
-assert.strictEqual(euler465(), 585965659);
+assert.strictEqual(polarPolygons(), 585965659);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler465(), 585965659);
## --seed-contents--
```js
-function euler465() {
+function polarPolygons() {
return true;
}
-euler465();
+polarPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
index 3050ea410b..f578dd0bb0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
@@ -8,24 +8,35 @@ dashedName: problem-466-distinct-terms-in-a-multiplication-table
# --description--
-Let P(m,n) be the number of distinct terms in an m×n multiplication table.
+Let $P(m,n)$ be the number of distinct terms in an $m×n$ multiplication table.
For example, a 3×4 multiplication table looks like this:
-× 12341 12342 24683 36912
+$$\begin{array}{c}
+ × & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} \\\\
+ \mathbf{1} & 1 & 2 & 3 & 4 \\\\
+ \mathbf{2} & 2 & 4 & 6 & 8 \\\\
+ \mathbf{3} & 3 & 6 & 9 & 12
+\end{array}$$
-There are 8 distinct terms {1,2,3,4,6,8,9,12}, therefore P(3,4) = 8.
+There are 8 distinct terms {1, 2, 3, 4, 6, 8, 9, 12}, therefore $P(3, 4) = 8$.
-You are given that: P(64,64) = 1263, P(12,345) = 1998, and P(32,1015) = 13826382602124302.
+You are given that:
-Find P(64,1016).
+$$\begin{align}
+ & P(64, 64) = 1\\,263, \\\\
+ & P(12, 345) = 1\\,998, \text{ and} \\\\
+ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302. \\\\
+\end{align}$$
+
+Find $P(64, {10}^{16})$.
# --hints--
-`euler466()` should return 258381958195474750.
+`multiplicationTable()` should return `258381958195474750`.
```js
-assert.strictEqual(euler466(), 258381958195474750);
+assert.strictEqual(multiplicationTable(), 258381958195474750);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler466(), 258381958195474750);
## --seed-contents--
```js
-function euler466() {
+function multiplicationTable() {
return true;
}
-euler466();
+multiplicationTable();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
index 8cfd9dc16a..d237fc953c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
@@ -8,26 +8,41 @@ dashedName: problem-467-superinteger
# --description--
-An integer s is called a superinteger of another integer n if the digits of n form a subsequence of the digits of s.
+An integer $s$ is called a superinteger of another integer $n$ if the digits of $n$ form a subsequence of the digits of $s$.
For example, 2718281828 is a superinteger of 18828, while 314159 is not a superinteger of 151.
-Let p(n) be the nth prime number, and let c(n) be the nth composite number. For example, p(1) = 2, p(10) = 29, c(1) = 4 and c(10) = 18. {p(i) : i ≥ 1} = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...} {c(i) : i ≥ 1} = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, ...}
+Let $p(n)$ be the $n$th prime number, and let $c(n)$ be the $n$th composite number. For example, $p(1) = 2$, $p(10) = 29$, $c(1) = 4$ and $c(10) = 18$.
-Let PD the sequence of the digital roots of {p(i)} (CD is defined similarly for {c(i)}): PD = {2, 3, 5, 7, 2, 4, 8, 1, 5, 2, ...} CD = {4, 6, 8, 9, 1, 3, 5, 6, 7, 9, ...}
+$$\begin{align}
+ & \\{p(i) : i ≥ 1\\} = \\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots \\} \\\\
+ & \\{c(i) : i ≥ 1\\} = \\{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, \ldots \\}
+\end{align}$$
-Let Pn be the integer formed by concatenating the first n elements of PD (Cn is defined similarly for CD). P10 = 2357248152 C10 = 4689135679
+Let $P^D$ the sequence of the digital roots of $\\{p(i)\\}$ ($C^D$ is defined similarly for $\\{c(i)\\}$):
-Let f(n) be the smallest positive integer that is a common superinteger of Pn and Cn. For example, f(10) = 2357246891352679, and f(100) mod 1 000 000 007 = 771661825.
+$$\begin{align}
+ & P^D = \\{2, 3, 5, 7, 2, 4, 8, 1, 5, 2, \ldots \\} \\\\
+ & C^D = \\{4, 6, 8, 9, 1, 3, 5, 6, 7, 9, \ldots \\}
+\end{align}$$
-Find f(10 000) mod 1 000 000 007.
+Let $P_n$ be the integer formed by concatenating the first $n$ elements of $P^D$ ($C_n$ is defined similarly for $C^D$).
+
+$$\begin{align}
+ & P_{10} = 2\\,357\\,248\\,152 \\\\
+ & C_{10} = 4\\,689\\,135\\,679
+\end{align}$$
+
+Let $f(n)$ be the smallest positive integer that is a common superinteger of $P_n$ and $C_n$. For example, $f(10) = 2\\,357\\,246\\,891\\,352\\,679$, and $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$.
+
+Find $f(10\\,000)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler467()` should return 775181359.
+`superinteger()` should return `775181359`.
```js
-assert.strictEqual(euler467(), 775181359);
+assert.strictEqual(superinteger(), 775181359);
```
# --seed--
@@ -35,12 +50,12 @@ assert.strictEqual(euler467(), 775181359);
## --seed-contents--
```js
-function euler467() {
+function superinteger() {
return true;
}
-euler467();
+superinteger();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
index 239d2cf56d..369c04b06e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
@@ -8,20 +8,36 @@ dashedName: problem-468-smooth-divisors-of-binomial-coefficients
# --description--
-An integer is called B-smooth if none of its prime factors is greater than B.
+An integer is called B-smooth if none of its prime factors is greater than $B$.
-Let SB(n) be the largest B-smooth divisor of n. Examples: S1(10) = 1 S4(2100) = 12 S17(2496144) = 5712
+Let $SB(n)$ be the largest B-smooth divisor of $n$.
-Define F(n) = ∑1≤B≤n ∑0≤r≤n SB(C(n,r)). Here, C(n,r) denotes the binomial coefficient. Examples: F(11) = 3132 F(1 111) mod 1 000 000 993 = 706036312 F(111 111) mod 1 000 000 993 = 22156169
+Examples:
-Find F(11 111 111) mod 1 000 000 993.
+$$\begin{align}
+ & S_1(10) = 1 \\\\
+ & S_4(2\\,100) = 12 \\\\
+ & S_{17}(2\\,496\\,144) = 5\\,712
+\end{align}$$
+
+Define $F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$. Here, $\displaystyle\binom{n}{r}$ denotes the binomial coefficient.
+
+Examples:
+
+$$\begin{align}
+ & F(11) = 3132 \\\\
+ & F(1\\,111)\bmod 1\\,000\\,000\\,993 = 706\\,036\\,312 \\\\
+ & F(111\\,111)\bmod 1\\,000\\,000\\,993 = 22\\,156\\,169
+\end{align}$$
+
+Find $F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$.
# --hints--
-`euler468()` should return 852950321.
+`smoothDivisorsOfBinomialCoefficients()` should return `852950321`.
```js
-assert.strictEqual(euler468(), 852950321);
+assert.strictEqual(smoothDivisorsOfBinomialCoefficients(), 852950321);
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler468(), 852950321);
## --seed-contents--
```js
-function euler468() {
+function smoothDivisorsOfBinomialCoefficients() {
return true;
}
-euler468();
+smoothDivisorsOfBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
index 4e8be025a2..d1db21f4f4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
@@ -8,22 +8,24 @@ dashedName: problem-469-empty-chairs
# --description--
-In a room N chairs are placed around a round table.
+In a room $N$ chairs are placed around a round table.
Knights enter the room one by one and choose at random an available empty chair.
To have enough elbow room the knights always leave at least one empty chair between each other.
-When there aren't any suitable chairs left, the fraction C of empty chairs is determined. We also define E(N) as the expected value of C. We can verify that E(4) = 1/2 and E(6) = 5/9.
+When there aren't any suitable chairs left, the fraction $C$ of empty chairs is determined. We also define $E(N)$ as the expected value of $C$.
-Find E(1018). Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
+We can verify that $E(4) = \frac{1}{2}$ and $E(6) = \frac{5}{9}$.
+
+Find $E({10}^{18})$. Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
# --hints--
-`euler469()` should return 0.56766764161831.
+`emptyChairs()` should return `0.56766764161831`.
```js
-assert.strictEqual(euler469(), 0.56766764161831);
+assert.strictEqual(emptyChairs(), 0.56766764161831);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler469(), 0.56766764161831);
## --seed-contents--
```js
-function euler469() {
+function emptyChairs() {
return true;
}
-euler469();
+emptyChairs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
index 10ee6d95d8..a8f59ece37 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
@@ -10,24 +10,24 @@ dashedName: problem-470-super-ramvok
Consider a single game of Ramvok:
-Let t represent the maximum number of turns the game lasts. If t = 0, then the game ends immediately. Otherwise, on each turn i, the player rolls a die. After rolling, if i < t the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If i = t, then the roll cannot be discarded and the prize must be accepted. Before the game begins, t is chosen by the player, who must then pay an up-front cost ct for some constant c. For c = 0, t can be chosen to be infinite (with an up-front cost of 0). Let R(d, c) be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair d-sided die and cost constant c. For example, R(4, 0.2) = 2.65. Assume that the player has sufficient funds for paying any/all up-front costs.
+Let $t$ represent the maximum number of turns the game lasts. If $t = 0$, then the game ends immediately. Otherwise, on each turn $i$, the player rolls a die. After rolling, if $i < t$ the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If $i = t$, then the roll cannot be discarded and the prize must be accepted. Before the game begins, $t$ is chosen by the player, who must then pay an up-front cost $ct$ for some constant $c$. For $c = 0$, $t$ can be chosen to be infinite (with an up-front cost of 0). Let $R(d, c)$ be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair $d$-sided die and cost constant $c$. For example, $R(4, 0.2) = 2.65$. Assume that the player has sufficient funds for paying any/all up-front costs.
Now consider a game of Super Ramvok:
In Super Ramvok, the game of Ramvok is played repeatedly, but with a slight modification. After each game, the die is altered. The alteration process is as follows: The die is rolled once, and if the resulting face has its pips visible, then that face is altered to be blank instead. If the face is already blank, then it is changed back to its original value. After the alteration is made, another game of Ramvok can begin (and during such a game, at each turn, the die is rolled until a face with a value on it appears). The player knows which faces are blank and which are not at all times. The game of Super Ramvok ends once all faces of the die are blank.
-Let S(d, c) be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair d-sided die to start (with all sides visible), and cost constant c. For example, S(6, 1) = 208.3.
+Let $S(d, c)$ be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair $d$-sided die to start (with all sides visible), and cost constant $c$. For example, $S(6, 1) = 208.3$.
-Let F(n) = ∑4≤d≤n ∑0≤c≤n S(d, c).
+Let $F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$.
-Calculate F(20), rounded to the nearest integer.
+Calculate $F(20)$, rounded to the nearest integer.
# --hints--
-`euler470()` should return 147668794.
+`superRamvok()` should return `147668794`.
```js
-assert.strictEqual(euler470(), 147668794);
+assert.strictEqual(superRamvok(), 147668794);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler470(), 147668794);
## --seed-contents--
```js
-function euler470() {
+function superRamvok() {
return true;
}
-euler470();
+superRamvok();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
index 95385ddec9..7970b9d11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
@@ -8,20 +8,36 @@ dashedName: problem-471-triangle-inscribed-in-ellipse
# --description--
-The triangle ΔABC is inscribed in an ellipse with equation $\\frac {x^2} {a^2} + \\frac {y^2} {b^2} = 1$, 0 < 2b < a, a and b integers.
+The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
-Let r(a,b) be the radius of the incircle of ΔABC when the incircle has center (2b, 0) and A has coordinates $\\left( \\frac a 2, \\frac {\\sqrt 3} 2 b\\right)$.
+Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
-For example, r(3,1) = ½, r(6,2) = 1, r(12,3) = 2.
+For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
-Let $G(n) = \\sum*{a=3}^n \\sum*{b=1}^{\\lfloor \\frac {a - 1} 2 \\rfloor} r(a, b)$ You are given G(10) = 20.59722222, G(100) = 19223.60980 (rounded to 10 significant digits). Find G(1011). Give your answer in scientific notation rounded to 10 significant digits. Use a lowercase e to separate mantissa and exponent. For G(10) the answer would have been 2.059722222e1.
+
+
Notice that the first polygon has three consecutive collinear vertices.
-Let P(n) be the number of polar polygons such that the vertices (x, y) have integer coordinates whose absolute values are not greater than n.
+Let $P(n)$ be the number of polar polygons such that the vertices $(x, y)$ have integer coordinates whose absolute values are not greater than $n$.
-Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices \[(0,0),(0,3),(1,1),(3,0)] is distinct from the polygon with vertices \[(0,0),(0,3),(1,1),(3,0),(1,0)].
+Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices [(0,0), (0,3), (1,1), (3,0)] is distinct from the polygon with vertices [(0,0), (0,3), (1,1), (3,0), (1,0)].
-For example, P(1) = 131, P(2) = 1648531, P(3) = 1099461296175 and P(343) mod 1 000 000 007 = 937293740.
+For example, $P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$ and $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$.
-Find P(713) mod 1 000 000 007.
+Find $P(7^{13})\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler465()` should return 585965659.
+`polarPolygons()` should return `585965659`.
```js
-assert.strictEqual(euler465(), 585965659);
+assert.strictEqual(polarPolygons(), 585965659);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler465(), 585965659);
## --seed-contents--
```js
-function euler465() {
+function polarPolygons() {
return true;
}
-euler465();
+polarPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
index 3050ea410b..f578dd0bb0 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
@@ -8,24 +8,35 @@ dashedName: problem-466-distinct-terms-in-a-multiplication-table
# --description--
-Let P(m,n) be the number of distinct terms in an m×n multiplication table.
+Let $P(m,n)$ be the number of distinct terms in an $m×n$ multiplication table.
For example, a 3×4 multiplication table looks like this:
-× 12341 12342 24683 36912
+$$\begin{array}{c}
+ × & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} \\\\
+ \mathbf{1} & 1 & 2 & 3 & 4 \\\\
+ \mathbf{2} & 2 & 4 & 6 & 8 \\\\
+ \mathbf{3} & 3 & 6 & 9 & 12
+\end{array}$$
-There are 8 distinct terms {1,2,3,4,6,8,9,12}, therefore P(3,4) = 8.
+There are 8 distinct terms {1, 2, 3, 4, 6, 8, 9, 12}, therefore $P(3, 4) = 8$.
-You are given that: P(64,64) = 1263, P(12,345) = 1998, and P(32,1015) = 13826382602124302.
+You are given that:
-Find P(64,1016).
+$$\begin{align}
+ & P(64, 64) = 1\\,263, \\\\
+ & P(12, 345) = 1\\,998, \text{ and} \\\\
+ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302. \\\\
+\end{align}$$
+
+Find $P(64, {10}^{16})$.
# --hints--
-`euler466()` should return 258381958195474750.
+`multiplicationTable()` should return `258381958195474750`.
```js
-assert.strictEqual(euler466(), 258381958195474750);
+assert.strictEqual(multiplicationTable(), 258381958195474750);
```
# --seed--
@@ -33,12 +44,12 @@ assert.strictEqual(euler466(), 258381958195474750);
## --seed-contents--
```js
-function euler466() {
+function multiplicationTable() {
return true;
}
-euler466();
+multiplicationTable();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
index 8cfd9dc16a..d237fc953c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-467-superinteger.md
@@ -8,26 +8,41 @@ dashedName: problem-467-superinteger
# --description--
-An integer s is called a superinteger of another integer n if the digits of n form a subsequence of the digits of s.
+An integer $s$ is called a superinteger of another integer $n$ if the digits of $n$ form a subsequence of the digits of $s$.
For example, 2718281828 is a superinteger of 18828, while 314159 is not a superinteger of 151.
-Let p(n) be the nth prime number, and let c(n) be the nth composite number. For example, p(1) = 2, p(10) = 29, c(1) = 4 and c(10) = 18. {p(i) : i ≥ 1} = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, ...} {c(i) : i ≥ 1} = {4, 6, 8, 9, 10, 12, 14, 15, 16, 18, ...}
+Let $p(n)$ be the $n$th prime number, and let $c(n)$ be the $n$th composite number. For example, $p(1) = 2$, $p(10) = 29$, $c(1) = 4$ and $c(10) = 18$.
-Let PD the sequence of the digital roots of {p(i)} (CD is defined similarly for {c(i)}): PD = {2, 3, 5, 7, 2, 4, 8, 1, 5, 2, ...} CD = {4, 6, 8, 9, 1, 3, 5, 6, 7, 9, ...}
+$$\begin{align}
+ & \\{p(i) : i ≥ 1\\} = \\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots \\} \\\\
+ & \\{c(i) : i ≥ 1\\} = \\{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, \ldots \\}
+\end{align}$$
-Let Pn be the integer formed by concatenating the first n elements of PD (Cn is defined similarly for CD). P10 = 2357248152 C10 = 4689135679
+Let $P^D$ the sequence of the digital roots of $\\{p(i)\\}$ ($C^D$ is defined similarly for $\\{c(i)\\}$):
-Let f(n) be the smallest positive integer that is a common superinteger of Pn and Cn. For example, f(10) = 2357246891352679, and f(100) mod 1 000 000 007 = 771661825.
+$$\begin{align}
+ & P^D = \\{2, 3, 5, 7, 2, 4, 8, 1, 5, 2, \ldots \\} \\\\
+ & C^D = \\{4, 6, 8, 9, 1, 3, 5, 6, 7, 9, \ldots \\}
+\end{align}$$
-Find f(10 000) mod 1 000 000 007.
+Let $P_n$ be the integer formed by concatenating the first $n$ elements of $P^D$ ($C_n$ is defined similarly for $C^D$).
+
+$$\begin{align}
+ & P_{10} = 2\\,357\\,248\\,152 \\\\
+ & C_{10} = 4\\,689\\,135\\,679
+\end{align}$$
+
+Let $f(n)$ be the smallest positive integer that is a common superinteger of $P_n$ and $C_n$. For example, $f(10) = 2\\,357\\,246\\,891\\,352\\,679$, and $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$.
+
+Find $f(10\\,000)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler467()` should return 775181359.
+`superinteger()` should return `775181359`.
```js
-assert.strictEqual(euler467(), 775181359);
+assert.strictEqual(superinteger(), 775181359);
```
# --seed--
@@ -35,12 +50,12 @@ assert.strictEqual(euler467(), 775181359);
## --seed-contents--
```js
-function euler467() {
+function superinteger() {
return true;
}
-euler467();
+superinteger();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
index 239d2cf56d..369c04b06e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
@@ -8,20 +8,36 @@ dashedName: problem-468-smooth-divisors-of-binomial-coefficients
# --description--
-An integer is called B-smooth if none of its prime factors is greater than B.
+An integer is called B-smooth if none of its prime factors is greater than $B$.
-Let SB(n) be the largest B-smooth divisor of n. Examples: S1(10) = 1 S4(2100) = 12 S17(2496144) = 5712
+Let $SB(n)$ be the largest B-smooth divisor of $n$.
-Define F(n) = ∑1≤B≤n ∑0≤r≤n SB(C(n,r)). Here, C(n,r) denotes the binomial coefficient. Examples: F(11) = 3132 F(1 111) mod 1 000 000 993 = 706036312 F(111 111) mod 1 000 000 993 = 22156169
+Examples:
-Find F(11 111 111) mod 1 000 000 993.
+$$\begin{align}
+ & S_1(10) = 1 \\\\
+ & S_4(2\\,100) = 12 \\\\
+ & S_{17}(2\\,496\\,144) = 5\\,712
+\end{align}$$
+
+Define $F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$. Here, $\displaystyle\binom{n}{r}$ denotes the binomial coefficient.
+
+Examples:
+
+$$\begin{align}
+ & F(11) = 3132 \\\\
+ & F(1\\,111)\bmod 1\\,000\\,000\\,993 = 706\\,036\\,312 \\\\
+ & F(111\\,111)\bmod 1\\,000\\,000\\,993 = 22\\,156\\,169
+\end{align}$$
+
+Find $F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$.
# --hints--
-`euler468()` should return 852950321.
+`smoothDivisorsOfBinomialCoefficients()` should return `852950321`.
```js
-assert.strictEqual(euler468(), 852950321);
+assert.strictEqual(smoothDivisorsOfBinomialCoefficients(), 852950321);
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler468(), 852950321);
## --seed-contents--
```js
-function euler468() {
+function smoothDivisorsOfBinomialCoefficients() {
return true;
}
-euler468();
+smoothDivisorsOfBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
index 4e8be025a2..d1db21f4f4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
@@ -8,22 +8,24 @@ dashedName: problem-469-empty-chairs
# --description--
-In a room N chairs are placed around a round table.
+In a room $N$ chairs are placed around a round table.
Knights enter the room one by one and choose at random an available empty chair.
To have enough elbow room the knights always leave at least one empty chair between each other.
-When there aren't any suitable chairs left, the fraction C of empty chairs is determined. We also define E(N) as the expected value of C. We can verify that E(4) = 1/2 and E(6) = 5/9.
+When there aren't any suitable chairs left, the fraction $C$ of empty chairs is determined. We also define $E(N)$ as the expected value of $C$.
-Find E(1018). Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
+We can verify that $E(4) = \frac{1}{2}$ and $E(6) = \frac{5}{9}$.
+
+Find $E({10}^{18})$. Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
# --hints--
-`euler469()` should return 0.56766764161831.
+`emptyChairs()` should return `0.56766764161831`.
```js
-assert.strictEqual(euler469(), 0.56766764161831);
+assert.strictEqual(emptyChairs(), 0.56766764161831);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler469(), 0.56766764161831);
## --seed-contents--
```js
-function euler469() {
+function emptyChairs() {
return true;
}
-euler469();
+emptyChairs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
index 10ee6d95d8..a8f59ece37 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
@@ -10,24 +10,24 @@ dashedName: problem-470-super-ramvok
Consider a single game of Ramvok:
-Let t represent the maximum number of turns the game lasts. If t = 0, then the game ends immediately. Otherwise, on each turn i, the player rolls a die. After rolling, if i < t the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If i = t, then the roll cannot be discarded and the prize must be accepted. Before the game begins, t is chosen by the player, who must then pay an up-front cost ct for some constant c. For c = 0, t can be chosen to be infinite (with an up-front cost of 0). Let R(d, c) be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair d-sided die and cost constant c. For example, R(4, 0.2) = 2.65. Assume that the player has sufficient funds for paying any/all up-front costs.
+Let $t$ represent the maximum number of turns the game lasts. If $t = 0$, then the game ends immediately. Otherwise, on each turn $i$, the player rolls a die. After rolling, if $i < t$ the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If $i = t$, then the roll cannot be discarded and the prize must be accepted. Before the game begins, $t$ is chosen by the player, who must then pay an up-front cost $ct$ for some constant $c$. For $c = 0$, $t$ can be chosen to be infinite (with an up-front cost of 0). Let $R(d, c)$ be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair $d$-sided die and cost constant $c$. For example, $R(4, 0.2) = 2.65$. Assume that the player has sufficient funds for paying any/all up-front costs.
Now consider a game of Super Ramvok:
In Super Ramvok, the game of Ramvok is played repeatedly, but with a slight modification. After each game, the die is altered. The alteration process is as follows: The die is rolled once, and if the resulting face has its pips visible, then that face is altered to be blank instead. If the face is already blank, then it is changed back to its original value. After the alteration is made, another game of Ramvok can begin (and during such a game, at each turn, the die is rolled until a face with a value on it appears). The player knows which faces are blank and which are not at all times. The game of Super Ramvok ends once all faces of the die are blank.
-Let S(d, c) be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair d-sided die to start (with all sides visible), and cost constant c. For example, S(6, 1) = 208.3.
+Let $S(d, c)$ be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair $d$-sided die to start (with all sides visible), and cost constant $c$. For example, $S(6, 1) = 208.3$.
-Let F(n) = ∑4≤d≤n ∑0≤c≤n S(d, c).
+Let $F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$.
-Calculate F(20), rounded to the nearest integer.
+Calculate $F(20)$, rounded to the nearest integer.
# --hints--
-`euler470()` should return 147668794.
+`superRamvok()` should return `147668794`.
```js
-assert.strictEqual(euler470(), 147668794);
+assert.strictEqual(superRamvok(), 147668794);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler470(), 147668794);
## --seed-contents--
```js
-function euler470() {
+function superRamvok() {
return true;
}
-euler470();
+superRamvok();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
index 95385ddec9..7970b9d11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
@@ -8,20 +8,36 @@ dashedName: problem-471-triangle-inscribed-in-ellipse
# --description--
-The triangle ΔABC is inscribed in an ellipse with equation $\\frac {x^2} {a^2} + \\frac {y^2} {b^2} = 1$, 0 < 2b < a, a and b integers.
+The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
-Let r(a,b) be the radius of the incircle of ΔABC when the incircle has center (2b, 0) and A has coordinates $\\left( \\frac a 2, \\frac {\\sqrt 3} 2 b\\right)$.
+Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
-For example, r(3,1) = ½, r(6,2) = 1, r(12,3) = 2.
+For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
-Let $G(n) = \\sum*{a=3}^n \\sum*{b=1}^{\\lfloor \\frac {a - 1} 2 \\rfloor} r(a, b)$ You are given G(10) = 20.59722222, G(100) = 19223.60980 (rounded to 10 significant digits). Find G(1011). Give your answer in scientific notation rounded to 10 significant digits. Use a lowercase e to separate mantissa and exponent. For G(10) the answer would have been 2.059722222e1.
+ +
+
+
+ +
+Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
+
+You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
+
+Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
+
+For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
-`euler471()` should return 1.895093981e+31.
+`triangleInscribedInEllipse()` should return a string.
```js
-assert.strictEqual(euler471(), 1.895093981e31);
+assert(typeof triangleInscribedInEllipse() === 'string');
+```
+
+`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
+
+```js
+assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler471(), 1.895093981e31);
## --seed-contents--
```js
-function euler471() {
+function triangleInscribedInEllipse() {
return true;
}
-euler471();
+triangleInscribedInEllipse();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
index f4e9015549..0d4c54d635 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
@@ -8,32 +8,32 @@ dashedName: problem-472-comfortable-distance-ii
# --description--
-There are N seats in a row. N people come one after another to fill the seats according to the following rules:
+There are $N$ seats in a row. $N$ people come one after another to fill the seats according to the following rules:
-No person sits beside another.
+1. No person sits beside another.
+1. The first person chooses any seat.
+1. Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
-The first person chooses any seat.
+Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than $N$ (for $N > 1$).
-Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
+Here are the possible seating arrangements for $N = 15$:
-Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than N (for N > 1).
-
-Here are the possible seating arrangements for N = 15:
+
+
+Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
+
+You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
+
+Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
+
+For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
-`euler471()` should return 1.895093981e+31.
+`triangleInscribedInEllipse()` should return a string.
```js
-assert.strictEqual(euler471(), 1.895093981e31);
+assert(typeof triangleInscribedInEllipse() === 'string');
+```
+
+`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
+
+```js
+assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
@@ -29,12 +45,12 @@ assert.strictEqual(euler471(), 1.895093981e31);
## --seed-contents--
```js
-function euler471() {
+function triangleInscribedInEllipse() {
return true;
}
-euler471();
+triangleInscribedInEllipse();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
index f4e9015549..0d4c54d635 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
@@ -8,32 +8,32 @@ dashedName: problem-472-comfortable-distance-ii
# --description--
-There are N seats in a row. N people come one after another to fill the seats according to the following rules:
+There are $N$ seats in a row. $N$ people come one after another to fill the seats according to the following rules:
-No person sits beside another.
+1. No person sits beside another.
+1. The first person chooses any seat.
+1. Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
-The first person chooses any seat.
+Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than $N$ (for $N > 1$).
-Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
+Here are the possible seating arrangements for $N = 15$:
-Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than N (for N > 1).
-
-Here are the possible seating arrangements for N = 15:
+ We see that if the first person chooses correctly, the 15 seats can seat up to 7 people. We can also see that the first person has 9 choices to maximize the number of people that may be seated.
-Let f(N) be the number of choices the first person has to maximize the number of occupants for N seats in a row. Thus, f(1) = 1, f(15) = 9, f(20) = 6, and f(500) = 16.
+Let $f(N)$ be the number of choices the first person has to maximize the number of occupants for $N$ seats in a row. Thus, $f(1) = 1$, $f(15) = 9$, $f(20) = 6$, and $f(500) = 16$.
-Also, ∑f(N) = 83 for 1 ≤ N ≤ 20 and ∑f(N) = 13343 for 1 ≤ N ≤ 500.
+Also, $\sum f(N) = 83$ for $1 ≤ N ≤ 20$ and $\sum f(N) = 13\\,343$ for $1 ≤ N ≤ 500$.
-Find ∑f(N) for 1 ≤ N ≤ 1012. Give the last 8 digits of your answer.
+Find $\sum f(N)$ for $1 ≤ N ≤ {10}^{12}$. Give the last 8 digits of your answer.
# --hints--
-`euler472()` should return 73811586.
+`comfortableDistanceTwo()` should return `73811586`.
```js
-assert.strictEqual(euler472(), 73811586);
+assert.strictEqual(comfortableDistanceTwo(), 73811586);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler472(), 73811586);
## --seed-contents--
```js
-function euler472() {
+function comfortableDistanceTwo() {
return true;
}
-euler472();
+comfortableDistanceTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
index 505c8a757b..0936140110 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
@@ -8,9 +8,9 @@ dashedName: problem-473-phigital-number-base
# --description--
-Let $\\varphi$ be the golden ratio: $\\varphi=\\frac{1+\\sqrt{5}}{2}.$
+Let $\varphi$ be the golden ratio: $\varphi = \frac{1+\sqrt{5}}{2}.$
-Remarkably it is possible to write every positive integer as a sum of powers of $\\varphi$ even if we require that every power of $\\varphi$ is used at most once in this sum.
+Remarkably it is possible to write every positive integer as a sum of powers of $\varphi$ even if we require that every power of $\varphi$ is used at most once in this sum.
Even then this representation is not unique.
@@ -18,9 +18,11 @@ We can make it unique by requiring that no powers with consecutive exponents are
E.g:
-$2=\\varphi+\\varphi^{-2}$ and $3=\\varphi^{2}+\\varphi^{-2}$
+$2 = \varphi + \varphi^{-2}$ and $3 = \varphi^{2} + \varphi^{-2}$
-To represent this sum of powers of $\\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase. So $1=1*{\\varphi}$, $2=10.01*{\\varphi}$, $3=100.01*{\\varphi}$ and $14=100100.001001*{\\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
+To represent this sum of powers of $\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase.
+
+So $1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$ and $14 = 100100.001001_{\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
The sum of the positive integers not exceeding 1000 whose phigital representation is palindromic is 4345.
@@ -28,10 +30,10 @@ Find the sum of the positive integers not exceeding $10^{10}$ whose phigital rep
# --hints--
-`euler473()` should return 35856681704365.
+`phigitalNumberBase()` should return `35856681704365`.
```js
-assert.strictEqual(euler473(), 35856681704365);
+assert.strictEqual(phigitalNumberBase(), 35856681704365);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler473(), 35856681704365);
## --seed-contents--
```js
-function euler473() {
+function phigitalNumberBase() {
return true;
}
-euler473();
+phigitalNumberBase();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
index 5c77726bd2..04123a2b35 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
@@ -8,20 +8,20 @@ dashedName: problem-474-last-digits-of-divisors
# --description--
-For a positive integer n and digits d, we define F(n, d) as the number of the divisors of n whose last digits equal d.
+For a positive integer $n$ and digits $d$, we define $F(n, d)$ as the number of the divisors of $n$ whose last digits equal $d$.
-For example, F(84, 4) = 3. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
+For example, $F(84, 4) = 3$. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
-We can also verify that F(12!, 12) = 11 and F(50!, 123) = 17888.
+We can also verify that $F(12!, 12) = 11$ and $F(50!, 123) = 17\\,888$.
-Find F(106!, 65432) modulo (1016 + 61).
+Find $F({10}^6!, 65\\,432) \text{ modulo } ({10}^{16} + 61)$.
# --hints--
-`euler474()` should return 9690646731515010.
+`lastDigitsOfDivisors()` should return `9690646731515010`.
```js
-assert.strictEqual(euler474(), 9690646731515010);
+assert.strictEqual(lastDigitsOfDivisors(), 9690646731515010);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler474(), 9690646731515010);
## --seed-contents--
```js
-function euler474() {
+function lastDigitsOfDivisors() {
return true;
}
-euler474();
+lastDigitsOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
index dd8cf3538b..4ab0b69b3a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
@@ -8,22 +8,24 @@ dashedName: problem-475-music-festival
# --description--
-12n musicians participate at a music festival. On the first day, they form 3n quartets and practice all day.
+$12n$ musicians participate at a music festival. On the first day, they form $3n$ quartets and practice all day.
It is a disaster. At the end of the day, all musicians decide they will never again agree to play with any member of their quartet.
-On the second day, they form 4n trios, each musician avoiding his previous quartet partners.
+On the second day, they form $4n$ trios, each musician avoiding his previous quartet partners.
-Let f(12n) be the number of ways to organize the trios amongst the 12n musicians. You are given f(12) = 576 and f(24) mod 1 000 000 007 = 509089824.
+Let $f(12n)$ be the number of ways to organize the trios amongst the $12n$ musicians.
-Find f(600) mod 1 000 000 007.
+You are given $f(12) = 576$ and $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$.
+
+Find $f(600)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler475()` should return 75780067.
+`musicFestival()` should return `75780067`.
```js
-assert.strictEqual(euler475(), 75780067);
+assert.strictEqual(musicFestival(), 75780067);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler475(), 75780067);
## --seed-contents--
```js
-function euler475() {
+function musicFestival() {
return true;
}
-euler475();
+musicFestival();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
index a5a8bf868b..b87eca74b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
@@ -8,20 +8,20 @@ dashedName: problem-476-circle-packing-ii
# --description--
-Let R(a, b, c) be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths a, b and c.
+Let $R(a, b, c)$ be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths $a$, $b$ and $c$.
-Let S(n) be the average value of R(a, b, c) over all integer triplets (a, b, c) such that 1 ≤ a ≤ b ≤ c < a + b ≤ n
+Let $S(n)$ be the average value of $R(a, b, c)$ over all integer triplets $(a, b, c)$ such that $1 ≤ a ≤ b ≤ c < a + b ≤ n$.
-You are given S(2) = R(1, 1, 1) ≈ 0.31998, S(5) ≈ 1.25899.
+You are given $S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$.
-Find S(1803) rounded to 5 decimal places behind the decimal point.
+Find $S(1803)$ rounded to 5 decimal places behind the decimal point.
# --hints--
-`euler476()` should return 110242.87794.
+`circlePackingTwo()` should return `110242.87794`.
```js
-assert.strictEqual(euler476(), 110242.87794);
+assert.strictEqual(circlePackingTwo(), 110242.87794);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler476(), 110242.87794);
## --seed-contents--
```js
-function euler476() {
+function circlePackingTwo() {
return true;
}
-euler476();
+circlePackingTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
index f4c95faba7..24fa79f131 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
@@ -8,42 +8,38 @@ dashedName: problem-477-number-sequence-game
# --description--
-The number sequence game starts with a sequence S of N numbers written on a line.
+The number sequence game starts with a sequence $S$ of $N$ numbers written on a line.
Two players alternate turns. At his turn, a player must select and remove either the first or the last number remaining in the sequence.
The player score is the sum of all the numbers he has taken. Each player attempts to maximize his own sum.
-If N = 4 and S = {1, 2, 10, 3}, then each player maximizes his score as follows:
+If $N = 4$ and $S = \\{1, 2, 10, 3\\}$, then each player maximizes his score as follows:
-Player 1: removes the first number (1)
+- Player 1: removes the first number (1)
+- Player 2: removes the last number from the remaining sequence (3)
+- Player 1: removes the last number from the remaining sequence (10)
+- Player 2: removes the remaining number (2)
-Player 2: removes the last number from the remaining sequence (3)
+Player 1 score is $1 + 10 = 11$.
-Player 1: removes the last number from the remaining sequence (10)
+Let $F(N)$ be the score of player 1 if both players follow the optimal strategy for the sequence $S = \\{s_1, s_2, \ldots, s_N\\}$ defined as:
-Player 2: removes the remaining number (2)
+- $s_1 = 0$
+- $s_{i + 1} = ({s_i}^2 + 45)$ modulo $1\\,000\\,000\\,007$
-Player 1 score is 1 + 10 = 11.
+The sequence begins with $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,107\\,844, 894\\,218\\,625, \ldots\\}$.
-Let F(N) be the score of player 1 if both players follow the optimal strategy for the sequence S = {s1, s2, ..., sN} defined as:
+You are given $F(2) = 45$, $F(4) = 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$.
-s1 = 0
-
-si+1 = (si2 + 45) modulo 1 000 000 007
-
-The sequence begins with S = {0, 45, 2070, 4284945, 753524550, 478107844, 894218625, ...}.
-
-You are given F(2) = 45, F(4) = 4284990, F(100) = 26365463243, F(104) = 2495838522951.
-
-Find F(108).
+Find $F({10}^8)$.
# --hints--
-`euler477()` should return 25044905874565164.
+`numberSequenceGame()` should return `25044905874565164`.
```js
-assert.strictEqual(euler477(), 25044905874565164);
+assert.strictEqual(numberSequenceGame(), 25044905874565164);
```
# --seed--
@@ -51,12 +47,12 @@ assert.strictEqual(euler477(), 25044905874565164);
## --seed-contents--
```js
-function euler477() {
+function numberSequenceGame() {
return true;
}
-euler477();
+numberSequenceGame();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
index 37e7681ecf..745aefc824 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
@@ -8,26 +8,32 @@ dashedName: problem-478-mixtures
# --description--
-Let us consider mixtures of three substances: A, B and C. A mixture can be described by a ratio of the amounts of A, B, and C in it, i.e., (a : b : c). For example, a mixture described by the ratio (2 : 3 : 5) contains 20% A, 30% B and 50% C.
+Let us consider mixtures of three substances: $A$, $B$ and $C$. A mixture can be described by a ratio of the amounts of $A$, $B$, and $C$ in it, i.e., $(a : b : c)$. For example, a mixture described by the ratio (2 : 3 : 5) contains 20% $A$, 30% $B$ and 50% $C$.
For the purposes of this problem, we cannot separate the individual components from a mixture. However, we can combine different amounts of different mixtures to form mixtures with new ratios.
-For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: (10·3/5 + 20·3/20 + 30·3/10 : 10·0/5 + 20·6/20 + 30·3/10 : 10·2/5 + 20·11/20 + 30·4/10) = (18 : 15 : 27) = (6 : 5 : 9)
+For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: ($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9)
-However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of B is always less than the amount of C.
+However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of $B$ is always less than the amount of $C$.
-Let n be a positive integer. Suppose that for every triple of integers (a, b, c) with 0 ≤ a, b, c ≤ n and gcd(a, b, c) = 1, we have a mixture with ratio (a : b : c). Let M(n) be the set of all such mixtures.
+Let $n$ be a positive integer. Suppose that for every triple of integers $(a, b, c)$ with $0 ≤ a, b, c ≤ n$ and $gcd(a, b, c) = 1$, we have a mixture with ratio $(a : b : c)$. Let $M(n)$ be the set of all such mixtures.
-For example, M(2) contains the 19 mixtures with the following ratios: {(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+For example, $M(2)$ contains the 19 mixtures with the following ratios:
-Let E(n) be the number of subsets of M(n) which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts A, B and C. We can verify that E(1) = 103, E(2) = 520447, E(10) mod 118 = 82608406 and E(500) mod 118 = 13801403. Find E(10 000 000) mod 118.
+{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+
+Let $E(n)$ be the number of subsets of $M(n)$ which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts $A$, $B$ and $C$.
+
+We can verify that $E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$ and $E(500)\bmod {11}^8 = 13\\,801\\,403$.
+
+Find $E(10\\,000\\,000)\bmod {11}^8$.
# --hints--
-`euler478()` should return 59510340.
+`mixtures()` should return `59510340`.
```js
-assert.strictEqual(euler478(), 59510340);
+assert.strictEqual(mixtures(), 59510340);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler478(), 59510340);
## --seed-contents--
```js
-function euler478() {
+function mixtures() {
return true;
}
-euler478();
+mixtures();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
index 202e7e04be..f2114e53c2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
@@ -8,22 +8,22 @@ dashedName: problem-479-roots-on-the-rise
# --description--
-Let ak, bk, and ck represent the three solutions (real or complex numbers) to the expression 1/x = (k/x)2(k+x2) - kx.
+Let $a_k$, $b_k$, and $c_k$ represent the three solutions (real or complex numbers) to the expression $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$.
-For instance, for k = 5, we see that {a5, b5, c5} is approximately {5.727244, -0.363622+2.057397i, -0.363622-2.057397i}.
+For instance, for $k = 5$, we see that $\\{a_5, b_5, c_5\\}$ is approximately $\\{5.727244, -0.363622 + 2.057397i, -0.363622 - 2.057397i\\}$.
-Let S(n) = Σ (ak+bk)p(bk+ck)p(ck+ak)p for all integers p, k such that 1 ≤ p, k ≤ n.
+Let $S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ for all integers $p$, $k$ such that $1 ≤ p, k ≤ n$.
-Interestingly, S(n) is always an integer. For example, S(4) = 51160.
+Interestingly, $S(n)$ is always an integer. For example, $S(4) = 51\\,160$.
-Find S(106) modulo 1 000 000 007.
+Find $S({10}^6) \text{ modulo } 1\\,000\\,000\\,007$.
# --hints--
-`euler479()` should return 191541795.
+`rootsOnTheRise()` should return `191541795`.
```js
-assert.strictEqual(euler479(), 191541795);
+assert.strictEqual(rootsOnTheRise(), 191541795);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler479(), 191541795);
## --seed-contents--
```js
-function euler479() {
+function rootsOnTheRise() {
return true;
}
-euler479();
+rootsOnTheRise();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
index 9e2ac8d96d..56ac54b858 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
@@ -10,88 +10,74 @@ dashedName: problem-480-the-last-question
Consider all the words which can be formed by selecting letters, in any order, from the phrase:
-thereisasyetinsufficientdataforameaningfulanswer
+$$\mathbf{\text{thereisasyetinsufficientdataforameaningfulanswer}}$$
Suppose those with 15 letters or less are listed in alphabetical order and numbered sequentially starting at 1.
The list would include:
-1 : a
+$$\begin{align}
+ & 1: \text{a} \\\\
+ & 2: \text{aa} \\\\
+ & 3: \text{aaa} \\\\
+ & 4: \text{aaaa} \\\\
+ & 5: \text{aaaaa} \\\\
+ & 6: \text{aaaaaa} \\\\
+ & 7: \text{aaaaaac} \\\\
+ & 8: \text{aaaaaacd} \\\\
+ & 9: \text{aaaaaacde} \\\\
+ & 10: \text{aaaaaacdee} \\\\
+ & 11: \text{aaaaaacdeee} \\\\
+ & 12: \text{aaaaaacdeeee} \\\\
+ & 13: \text{aaaaaacdeeeee} \\\\
+ & 14: \text{aaaaaacdeeeeee} \\\\
+ & 15: \text{aaaaaacdeeeeeef} \\\\
+ & 16: \text{aaaaaacdeeeeeeg} \\\\
+ & 17: \text{aaaaaacdeeeeeeh} \\\\
+ & \ldots \\\\
+ & 28: \text{aaaaaacdeeeeeey} \\\\
+ & 29: \text{aaaaaacdeeeeef} \\\\
+ & 30: \text{aaaaaacdeeeeefe} \\\\
+ & \ldots \\\\
+ & 115246685191495242: \text{euleoywuttttsss} \\\\
+ & 115246685191495243: \text{euler} \\\\
+ & 115246685191495244: \text{eulera} \\\\
+ & ... \\\\
+ & 525069350231428029: \text{ywuuttttssssrrr} \\\\
+\end{align}$$
-2 : aa
+Define $P(w)$ as the position of the word $w$.
-3 : aaa
+Define $W(p)$ as the word in position $p$.
-4 : aaaa
-
-5 : aaaaa
-
-6 : aaaaaa
-
-7 : aaaaaac
-
-8 : aaaaaacd
-
-9 : aaaaaacde
-
-10 : aaaaaacdee
-
-11 : aaaaaacdeee
-
-12 : aaaaaacdeeee
-
-13 : aaaaaacdeeeee
-
-14 : aaaaaacdeeeeee
-
-15 : aaaaaacdeeeeeef
-
-16 : aaaaaacdeeeeeeg
-
-17 : aaaaaacdeeeeeeh
-
-...
-
-28 : aaaaaacdeeeeeey
-
-29 : aaaaaacdeeeeef
-
-30 : aaaaaacdeeeeefe
-
-...
-
-115246685191495242: euleoywuttttsss
-
-115246685191495243: euler
-
-115246685191495244: eulera
-
-...
-
-525069350231428029: ywuuttttssssrrrDefine P(w) as the position of the word w.
-
-Define W(p) as the word in position p.
-
-We can see that P(w) and W(p) are inverses: P(W(p)) = p and W(P(w)) = w.
+We can see that $P(w)$ and $W(p)$ are inverses: $P(W(p)) = p$ and $W(P(w)) = w$.
Examples:
-W(10) = aaaaaacdee
+$$\begin{align}
+ & W(10) = \text{ aaaaaacdee} \\\\
+ & P(\text{aaaaaacdee}) = 10 \\\\
+ & W(115246685191495243) = \text{ euler} \\\\
+ & P(\text{euler}) = 115246685191495243 \\\\
+\end{align}$$
-P(aaaaaacdee) = 10
-
-W(115246685191495243) = euler
-
-P(euler) = 115246685191495243Find W(P(legionary) + P(calorimeters) - P(annihilate) + P(orchestrated) - P(fluttering)).
+Find
+$$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering})).$$
Give your answer using lowercase characters (no punctuation or space).
# --hints--
-`euler480()` should return turnthestarson.
+`euler480()` should return a string.
```js
-assert.strictEqual(euler480(), turnthestarson);
+assert(typeof euler480() === 'string');
+```
+
+`euler480()` should return the string `turnthestarson`.
+
+```js
+assert.strictEqual(euler480(), 'turnthestarson');
```
# --seed--
We see that if the first person chooses correctly, the 15 seats can seat up to 7 people. We can also see that the first person has 9 choices to maximize the number of people that may be seated.
-Let f(N) be the number of choices the first person has to maximize the number of occupants for N seats in a row. Thus, f(1) = 1, f(15) = 9, f(20) = 6, and f(500) = 16.
+Let $f(N)$ be the number of choices the first person has to maximize the number of occupants for $N$ seats in a row. Thus, $f(1) = 1$, $f(15) = 9$, $f(20) = 6$, and $f(500) = 16$.
-Also, ∑f(N) = 83 for 1 ≤ N ≤ 20 and ∑f(N) = 13343 for 1 ≤ N ≤ 500.
+Also, $\sum f(N) = 83$ for $1 ≤ N ≤ 20$ and $\sum f(N) = 13\\,343$ for $1 ≤ N ≤ 500$.
-Find ∑f(N) for 1 ≤ N ≤ 1012. Give the last 8 digits of your answer.
+Find $\sum f(N)$ for $1 ≤ N ≤ {10}^{12}$. Give the last 8 digits of your answer.
# --hints--
-`euler472()` should return 73811586.
+`comfortableDistanceTwo()` should return `73811586`.
```js
-assert.strictEqual(euler472(), 73811586);
+assert.strictEqual(comfortableDistanceTwo(), 73811586);
```
# --seed--
@@ -41,12 +41,12 @@ assert.strictEqual(euler472(), 73811586);
## --seed-contents--
```js
-function euler472() {
+function comfortableDistanceTwo() {
return true;
}
-euler472();
+comfortableDistanceTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
index 505c8a757b..0936140110 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
@@ -8,9 +8,9 @@ dashedName: problem-473-phigital-number-base
# --description--
-Let $\\varphi$ be the golden ratio: $\\varphi=\\frac{1+\\sqrt{5}}{2}.$
+Let $\varphi$ be the golden ratio: $\varphi = \frac{1+\sqrt{5}}{2}.$
-Remarkably it is possible to write every positive integer as a sum of powers of $\\varphi$ even if we require that every power of $\\varphi$ is used at most once in this sum.
+Remarkably it is possible to write every positive integer as a sum of powers of $\varphi$ even if we require that every power of $\varphi$ is used at most once in this sum.
Even then this representation is not unique.
@@ -18,9 +18,11 @@ We can make it unique by requiring that no powers with consecutive exponents are
E.g:
-$2=\\varphi+\\varphi^{-2}$ and $3=\\varphi^{2}+\\varphi^{-2}$
+$2 = \varphi + \varphi^{-2}$ and $3 = \varphi^{2} + \varphi^{-2}$
-To represent this sum of powers of $\\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase. So $1=1*{\\varphi}$, $2=10.01*{\\varphi}$, $3=100.01*{\\varphi}$ and $14=100100.001001*{\\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
+To represent this sum of powers of $\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase.
+
+So $1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$ and $14 = 100100.001001_{\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
The sum of the positive integers not exceeding 1000 whose phigital representation is palindromic is 4345.
@@ -28,10 +30,10 @@ Find the sum of the positive integers not exceeding $10^{10}$ whose phigital rep
# --hints--
-`euler473()` should return 35856681704365.
+`phigitalNumberBase()` should return `35856681704365`.
```js
-assert.strictEqual(euler473(), 35856681704365);
+assert.strictEqual(phigitalNumberBase(), 35856681704365);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler473(), 35856681704365);
## --seed-contents--
```js
-function euler473() {
+function phigitalNumberBase() {
return true;
}
-euler473();
+phigitalNumberBase();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
index 5c77726bd2..04123a2b35 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
@@ -8,20 +8,20 @@ dashedName: problem-474-last-digits-of-divisors
# --description--
-For a positive integer n and digits d, we define F(n, d) as the number of the divisors of n whose last digits equal d.
+For a positive integer $n$ and digits $d$, we define $F(n, d)$ as the number of the divisors of $n$ whose last digits equal $d$.
-For example, F(84, 4) = 3. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
+For example, $F(84, 4) = 3$. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
-We can also verify that F(12!, 12) = 11 and F(50!, 123) = 17888.
+We can also verify that $F(12!, 12) = 11$ and $F(50!, 123) = 17\\,888$.
-Find F(106!, 65432) modulo (1016 + 61).
+Find $F({10}^6!, 65\\,432) \text{ modulo } ({10}^{16} + 61)$.
# --hints--
-`euler474()` should return 9690646731515010.
+`lastDigitsOfDivisors()` should return `9690646731515010`.
```js
-assert.strictEqual(euler474(), 9690646731515010);
+assert.strictEqual(lastDigitsOfDivisors(), 9690646731515010);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler474(), 9690646731515010);
## --seed-contents--
```js
-function euler474() {
+function lastDigitsOfDivisors() {
return true;
}
-euler474();
+lastDigitsOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
index dd8cf3538b..4ab0b69b3a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-475-music-festival.md
@@ -8,22 +8,24 @@ dashedName: problem-475-music-festival
# --description--
-12n musicians participate at a music festival. On the first day, they form 3n quartets and practice all day.
+$12n$ musicians participate at a music festival. On the first day, they form $3n$ quartets and practice all day.
It is a disaster. At the end of the day, all musicians decide they will never again agree to play with any member of their quartet.
-On the second day, they form 4n trios, each musician avoiding his previous quartet partners.
+On the second day, they form $4n$ trios, each musician avoiding his previous quartet partners.
-Let f(12n) be the number of ways to organize the trios amongst the 12n musicians. You are given f(12) = 576 and f(24) mod 1 000 000 007 = 509089824.
+Let $f(12n)$ be the number of ways to organize the trios amongst the $12n$ musicians.
-Find f(600) mod 1 000 000 007.
+You are given $f(12) = 576$ and $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$.
+
+Find $f(600)\bmod 1\\,000\\,000\\,007$.
# --hints--
-`euler475()` should return 75780067.
+`musicFestival()` should return `75780067`.
```js
-assert.strictEqual(euler475(), 75780067);
+assert.strictEqual(musicFestival(), 75780067);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler475(), 75780067);
## --seed-contents--
```js
-function euler475() {
+function musicFestival() {
return true;
}
-euler475();
+musicFestival();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
index a5a8bf868b..b87eca74b7 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
@@ -8,20 +8,20 @@ dashedName: problem-476-circle-packing-ii
# --description--
-Let R(a, b, c) be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths a, b and c.
+Let $R(a, b, c)$ be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths $a$, $b$ and $c$.
-Let S(n) be the average value of R(a, b, c) over all integer triplets (a, b, c) such that 1 ≤ a ≤ b ≤ c < a + b ≤ n
+Let $S(n)$ be the average value of $R(a, b, c)$ over all integer triplets $(a, b, c)$ such that $1 ≤ a ≤ b ≤ c < a + b ≤ n$.
-You are given S(2) = R(1, 1, 1) ≈ 0.31998, S(5) ≈ 1.25899.
+You are given $S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$.
-Find S(1803) rounded to 5 decimal places behind the decimal point.
+Find $S(1803)$ rounded to 5 decimal places behind the decimal point.
# --hints--
-`euler476()` should return 110242.87794.
+`circlePackingTwo()` should return `110242.87794`.
```js
-assert.strictEqual(euler476(), 110242.87794);
+assert.strictEqual(circlePackingTwo(), 110242.87794);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler476(), 110242.87794);
## --seed-contents--
```js
-function euler476() {
+function circlePackingTwo() {
return true;
}
-euler476();
+circlePackingTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
index f4c95faba7..24fa79f131 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
@@ -8,42 +8,38 @@ dashedName: problem-477-number-sequence-game
# --description--
-The number sequence game starts with a sequence S of N numbers written on a line.
+The number sequence game starts with a sequence $S$ of $N$ numbers written on a line.
Two players alternate turns. At his turn, a player must select and remove either the first or the last number remaining in the sequence.
The player score is the sum of all the numbers he has taken. Each player attempts to maximize his own sum.
-If N = 4 and S = {1, 2, 10, 3}, then each player maximizes his score as follows:
+If $N = 4$ and $S = \\{1, 2, 10, 3\\}$, then each player maximizes his score as follows:
-Player 1: removes the first number (1)
+- Player 1: removes the first number (1)
+- Player 2: removes the last number from the remaining sequence (3)
+- Player 1: removes the last number from the remaining sequence (10)
+- Player 2: removes the remaining number (2)
-Player 2: removes the last number from the remaining sequence (3)
+Player 1 score is $1 + 10 = 11$.
-Player 1: removes the last number from the remaining sequence (10)
+Let $F(N)$ be the score of player 1 if both players follow the optimal strategy for the sequence $S = \\{s_1, s_2, \ldots, s_N\\}$ defined as:
-Player 2: removes the remaining number (2)
+- $s_1 = 0$
+- $s_{i + 1} = ({s_i}^2 + 45)$ modulo $1\\,000\\,000\\,007$
-Player 1 score is 1 + 10 = 11.
+The sequence begins with $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,107\\,844, 894\\,218\\,625, \ldots\\}$.
-Let F(N) be the score of player 1 if both players follow the optimal strategy for the sequence S = {s1, s2, ..., sN} defined as:
+You are given $F(2) = 45$, $F(4) = 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$.
-s1 = 0
-
-si+1 = (si2 + 45) modulo 1 000 000 007
-
-The sequence begins with S = {0, 45, 2070, 4284945, 753524550, 478107844, 894218625, ...}.
-
-You are given F(2) = 45, F(4) = 4284990, F(100) = 26365463243, F(104) = 2495838522951.
-
-Find F(108).
+Find $F({10}^8)$.
# --hints--
-`euler477()` should return 25044905874565164.
+`numberSequenceGame()` should return `25044905874565164`.
```js
-assert.strictEqual(euler477(), 25044905874565164);
+assert.strictEqual(numberSequenceGame(), 25044905874565164);
```
# --seed--
@@ -51,12 +47,12 @@ assert.strictEqual(euler477(), 25044905874565164);
## --seed-contents--
```js
-function euler477() {
+function numberSequenceGame() {
return true;
}
-euler477();
+numberSequenceGame();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
index 37e7681ecf..745aefc824 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-478-mixtures.md
@@ -8,26 +8,32 @@ dashedName: problem-478-mixtures
# --description--
-Let us consider mixtures of three substances: A, B and C. A mixture can be described by a ratio of the amounts of A, B, and C in it, i.e., (a : b : c). For example, a mixture described by the ratio (2 : 3 : 5) contains 20% A, 30% B and 50% C.
+Let us consider mixtures of three substances: $A$, $B$ and $C$. A mixture can be described by a ratio of the amounts of $A$, $B$, and $C$ in it, i.e., $(a : b : c)$. For example, a mixture described by the ratio (2 : 3 : 5) contains 20% $A$, 30% $B$ and 50% $C$.
For the purposes of this problem, we cannot separate the individual components from a mixture. However, we can combine different amounts of different mixtures to form mixtures with new ratios.
-For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: (10·3/5 + 20·3/20 + 30·3/10 : 10·0/5 + 20·6/20 + 30·3/10 : 10·2/5 + 20·11/20 + 30·4/10) = (18 : 15 : 27) = (6 : 5 : 9)
+For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: ($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9)
-However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of B is always less than the amount of C.
+However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of $B$ is always less than the amount of $C$.
-Let n be a positive integer. Suppose that for every triple of integers (a, b, c) with 0 ≤ a, b, c ≤ n and gcd(a, b, c) = 1, we have a mixture with ratio (a : b : c). Let M(n) be the set of all such mixtures.
+Let $n$ be a positive integer. Suppose that for every triple of integers $(a, b, c)$ with $0 ≤ a, b, c ≤ n$ and $gcd(a, b, c) = 1$, we have a mixture with ratio $(a : b : c)$. Let $M(n)$ be the set of all such mixtures.
-For example, M(2) contains the 19 mixtures with the following ratios: {(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+For example, $M(2)$ contains the 19 mixtures with the following ratios:
-Let E(n) be the number of subsets of M(n) which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts A, B and C. We can verify that E(1) = 103, E(2) = 520447, E(10) mod 118 = 82608406 and E(500) mod 118 = 13801403. Find E(10 000 000) mod 118.
+{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+
+Let $E(n)$ be the number of subsets of $M(n)$ which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts $A$, $B$ and $C$.
+
+We can verify that $E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$ and $E(500)\bmod {11}^8 = 13\\,801\\,403$.
+
+Find $E(10\\,000\\,000)\bmod {11}^8$.
# --hints--
-`euler478()` should return 59510340.
+`mixtures()` should return `59510340`.
```js
-assert.strictEqual(euler478(), 59510340);
+assert.strictEqual(mixtures(), 59510340);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler478(), 59510340);
## --seed-contents--
```js
-function euler478() {
+function mixtures() {
return true;
}
-euler478();
+mixtures();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
index 202e7e04be..f2114e53c2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
@@ -8,22 +8,22 @@ dashedName: problem-479-roots-on-the-rise
# --description--
-Let ak, bk, and ck represent the three solutions (real or complex numbers) to the expression 1/x = (k/x)2(k+x2) - kx.
+Let $a_k$, $b_k$, and $c_k$ represent the three solutions (real or complex numbers) to the expression $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$.
-For instance, for k = 5, we see that {a5, b5, c5} is approximately {5.727244, -0.363622+2.057397i, -0.363622-2.057397i}.
+For instance, for $k = 5$, we see that $\\{a_5, b_5, c_5\\}$ is approximately $\\{5.727244, -0.363622 + 2.057397i, -0.363622 - 2.057397i\\}$.
-Let S(n) = Σ (ak+bk)p(bk+ck)p(ck+ak)p for all integers p, k such that 1 ≤ p, k ≤ n.
+Let $S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ for all integers $p$, $k$ such that $1 ≤ p, k ≤ n$.
-Interestingly, S(n) is always an integer. For example, S(4) = 51160.
+Interestingly, $S(n)$ is always an integer. For example, $S(4) = 51\\,160$.
-Find S(106) modulo 1 000 000 007.
+Find $S({10}^6) \text{ modulo } 1\\,000\\,000\\,007$.
# --hints--
-`euler479()` should return 191541795.
+`rootsOnTheRise()` should return `191541795`.
```js
-assert.strictEqual(euler479(), 191541795);
+assert.strictEqual(rootsOnTheRise(), 191541795);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler479(), 191541795);
## --seed-contents--
```js
-function euler479() {
+function rootsOnTheRise() {
return true;
}
-euler479();
+rootsOnTheRise();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
index 9e2ac8d96d..56ac54b858 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
@@ -10,88 +10,74 @@ dashedName: problem-480-the-last-question
Consider all the words which can be formed by selecting letters, in any order, from the phrase:
-thereisasyetinsufficientdataforameaningfulanswer
+$$\mathbf{\text{thereisasyetinsufficientdataforameaningfulanswer}}$$
Suppose those with 15 letters or less are listed in alphabetical order and numbered sequentially starting at 1.
The list would include:
-1 : a
+$$\begin{align}
+ & 1: \text{a} \\\\
+ & 2: \text{aa} \\\\
+ & 3: \text{aaa} \\\\
+ & 4: \text{aaaa} \\\\
+ & 5: \text{aaaaa} \\\\
+ & 6: \text{aaaaaa} \\\\
+ & 7: \text{aaaaaac} \\\\
+ & 8: \text{aaaaaacd} \\\\
+ & 9: \text{aaaaaacde} \\\\
+ & 10: \text{aaaaaacdee} \\\\
+ & 11: \text{aaaaaacdeee} \\\\
+ & 12: \text{aaaaaacdeeee} \\\\
+ & 13: \text{aaaaaacdeeeee} \\\\
+ & 14: \text{aaaaaacdeeeeee} \\\\
+ & 15: \text{aaaaaacdeeeeeef} \\\\
+ & 16: \text{aaaaaacdeeeeeeg} \\\\
+ & 17: \text{aaaaaacdeeeeeeh} \\\\
+ & \ldots \\\\
+ & 28: \text{aaaaaacdeeeeeey} \\\\
+ & 29: \text{aaaaaacdeeeeef} \\\\
+ & 30: \text{aaaaaacdeeeeefe} \\\\
+ & \ldots \\\\
+ & 115246685191495242: \text{euleoywuttttsss} \\\\
+ & 115246685191495243: \text{euler} \\\\
+ & 115246685191495244: \text{eulera} \\\\
+ & ... \\\\
+ & 525069350231428029: \text{ywuuttttssssrrr} \\\\
+\end{align}$$
-2 : aa
+Define $P(w)$ as the position of the word $w$.
-3 : aaa
+Define $W(p)$ as the word in position $p$.
-4 : aaaa
-
-5 : aaaaa
-
-6 : aaaaaa
-
-7 : aaaaaac
-
-8 : aaaaaacd
-
-9 : aaaaaacde
-
-10 : aaaaaacdee
-
-11 : aaaaaacdeee
-
-12 : aaaaaacdeeee
-
-13 : aaaaaacdeeeee
-
-14 : aaaaaacdeeeeee
-
-15 : aaaaaacdeeeeeef
-
-16 : aaaaaacdeeeeeeg
-
-17 : aaaaaacdeeeeeeh
-
-...
-
-28 : aaaaaacdeeeeeey
-
-29 : aaaaaacdeeeeef
-
-30 : aaaaaacdeeeeefe
-
-...
-
-115246685191495242: euleoywuttttsss
-
-115246685191495243: euler
-
-115246685191495244: eulera
-
-...
-
-525069350231428029: ywuuttttssssrrrDefine P(w) as the position of the word w.
-
-Define W(p) as the word in position p.
-
-We can see that P(w) and W(p) are inverses: P(W(p)) = p and W(P(w)) = w.
+We can see that $P(w)$ and $W(p)$ are inverses: $P(W(p)) = p$ and $W(P(w)) = w$.
Examples:
-W(10) = aaaaaacdee
+$$\begin{align}
+ & W(10) = \text{ aaaaaacdee} \\\\
+ & P(\text{aaaaaacdee}) = 10 \\\\
+ & W(115246685191495243) = \text{ euler} \\\\
+ & P(\text{euler}) = 115246685191495243 \\\\
+\end{align}$$
-P(aaaaaacdee) = 10
-
-W(115246685191495243) = euler
-
-P(euler) = 115246685191495243Find W(P(legionary) + P(calorimeters) - P(annihilate) + P(orchestrated) - P(fluttering)).
+Find
+$$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering})).$$
Give your answer using lowercase characters (no punctuation or space).
# --hints--
-`euler480()` should return turnthestarson.
+`euler480()` should return a string.
```js
-assert.strictEqual(euler480(), turnthestarson);
+assert(typeof euler480() === 'string');
+```
+
+`euler480()` should return the string `turnthestarson`.
+
+```js
+assert.strictEqual(euler480(), 'turnthestarson');
```
# --seed--