A(2, 9), B(9, -2), C(-6, -7)
A(9, 2), B(2, -9), C(-6, 7)
-

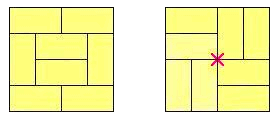 +
+ -The arrangement on the left is acceptable, whereas the one on the right is not: a red "X" in the middle, marks the point where four tatami meet.
+左側の配置は問題ありませんが、右側の配置はルールに反しています。中央の赤い印 "X" は、4 枚の畳の角が集まっている個所を示しています。
-Because of this rule, certain even-sized rooms cannot be covered with tatami: we call them tatami-free rooms. Further, we define $T(s)$ as the number of tatami-free rooms of size $s$.
+このルールにより、ある偶数サイズの部屋は畳を敷き詰めることができません。そのような部屋を「畳を敷けない部屋」と呼ぶことにします。 さらに、サイズが $s$ である「畳を敷けない部屋」の数を $T(s)$ とします。
-The smallest tatami-free room has size $s = 70$ and dimensions 7×10. All the other rooms of size $s = 70$ can be covered with tatami; they are: 1×70, 2×35 and 5×14. Hence, $T(70) = 1$.
+最小の「畳を敷けない部屋」はサイズが $s = 70$、寸法が 7x10 です。 サイズ $s = 70$ である他のすべての部屋 (1×70, 2×35, 5×14) には畳を敷き詰めることができます。 したがって、$T(70) = 1$ です。
-Similarly, we can verify that $T(1320) = 5$ because there are exactly 5 tatami-free rooms of size $s = 1320$: 20×66, 22×60, 24×55, 30×44 and 33×40. In fact, $s = 1320$ is the smallest room-size $s$ for which $T(s) = 5$.
+同様に、サイズが $s = 1320$ である「畳を敷けない部屋」はちょうど 5 つあるので (20×66, 22×60, 24×55, 30×44, 33x40)、$T(1320) = 5$ であることを確認できます。 実は $s = 1320$ は、$T(s) = 5$ である最小の部屋のサイズ $s$ です。
-Find the smallest room-size $s$ for which $T(s) = 200$.
+$T(s) = 200$ である最小の部屋のサイズ $s$ を求めなさい。
# --hints--
-`tatamiFreeRooms()` should return `85765680`.
+`tatamiFreeRooms()` は `85765680` を返す必要があります。
```js
assert.strictEqual(tatamiFreeRooms(), 85765680);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md
index d3ae38a1b9..75c66c2b7e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md
@@ -1,6 +1,6 @@
---
id: 5900f46e1000cf542c50ff80
-title: 'Problem 257: Angular Bisectors'
+title: '問題 257: 角の二等分線'
challengeType: 5
forumTopicId: 301905
dashedName: problem-257-angular-bisectors
@@ -8,19 +8,19 @@ dashedName: problem-257-angular-bisectors
# --description--
-Given is an integer sided triangle $ABC$ with sides $a ≤ b ≤ c$. ($AB = c$, $BC = a$ and $AC = b$).
+整数の辺長を持つ三角形 $ABC$ が与えられ、辺は $a ≤ b ≤ c$ です ($AB = c$, $BC = a$, $AC = b$)。
-The angular bisectors of the triangle intersect the sides at points $E$, $F$ and $G$ (see picture below).
+三角形の角の二等分線は、点 $E$, $F$, $G$ で辺と交わります (下図参照)。
-
-The arrangement on the left is acceptable, whereas the one on the right is not: a red "X" in the middle, marks the point where four tatami meet.
+左側の配置は問題ありませんが、右側の配置はルールに反しています。中央の赤い印 "X" は、4 枚の畳の角が集まっている個所を示しています。
-Because of this rule, certain even-sized rooms cannot be covered with tatami: we call them tatami-free rooms. Further, we define $T(s)$ as the number of tatami-free rooms of size $s$.
+このルールにより、ある偶数サイズの部屋は畳を敷き詰めることができません。そのような部屋を「畳を敷けない部屋」と呼ぶことにします。 さらに、サイズが $s$ である「畳を敷けない部屋」の数を $T(s)$ とします。
-The smallest tatami-free room has size $s = 70$ and dimensions 7×10. All the other rooms of size $s = 70$ can be covered with tatami; they are: 1×70, 2×35 and 5×14. Hence, $T(70) = 1$.
+最小の「畳を敷けない部屋」はサイズが $s = 70$、寸法が 7x10 です。 サイズ $s = 70$ である他のすべての部屋 (1×70, 2×35, 5×14) には畳を敷き詰めることができます。 したがって、$T(70) = 1$ です。
-Similarly, we can verify that $T(1320) = 5$ because there are exactly 5 tatami-free rooms of size $s = 1320$: 20×66, 22×60, 24×55, 30×44 and 33×40. In fact, $s = 1320$ is the smallest room-size $s$ for which $T(s) = 5$.
+同様に、サイズが $s = 1320$ である「畳を敷けない部屋」はちょうど 5 つあるので (20×66, 22×60, 24×55, 30×44, 33x40)、$T(1320) = 5$ であることを確認できます。 実は $s = 1320$ は、$T(s) = 5$ である最小の部屋のサイズ $s$ です。
-Find the smallest room-size $s$ for which $T(s) = 200$.
+$T(s) = 200$ である最小の部屋のサイズ $s$ を求めなさい。
# --hints--
-`tatamiFreeRooms()` should return `85765680`.
+`tatamiFreeRooms()` は `85765680` を返す必要があります。
```js
assert.strictEqual(tatamiFreeRooms(), 85765680);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md
index d3ae38a1b9..75c66c2b7e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-257-angular-bisectors.md
@@ -1,6 +1,6 @@
---
id: 5900f46e1000cf542c50ff80
-title: 'Problem 257: Angular Bisectors'
+title: '問題 257: 角の二等分線'
challengeType: 5
forumTopicId: 301905
dashedName: problem-257-angular-bisectors
@@ -8,19 +8,19 @@ dashedName: problem-257-angular-bisectors
# --description--
-Given is an integer sided triangle $ABC$ with sides $a ≤ b ≤ c$. ($AB = c$, $BC = a$ and $AC = b$).
+整数の辺長を持つ三角形 $ABC$ が与えられ、辺は $a ≤ b ≤ c$ です ($AB = c$, $BC = a$, $AC = b$)。
-The angular bisectors of the triangle intersect the sides at points $E$, $F$ and $G$ (see picture below).
+三角形の角の二等分線は、点 $E$, $F$, $G$ で辺と交わります (下図参照)。
-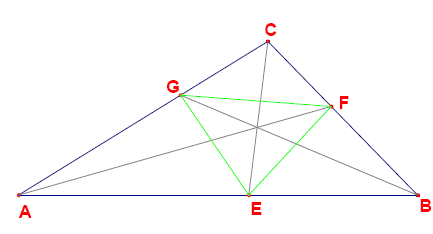 +
+ -The segments $EF$, $EG$ and $FG$ partition the triangle $ABC$ into four smaller triangles: $AEG$, $BFE$, $CGF$ and $EFG$. It can be proven that for each of these four triangles the ratio $\frac{\text{area}(ABC)}{\text{area}(\text{subtriangle})}$ is rational. However, there exist triangles for which some or all of these ratios are integral.
+線分 $EF$, $EG$, $FG$ は、$ABC$ を 4 つの小さな三角形 $AEG$, $BFE$, $CGF$, $EFG$ に分割します。 この 4 つの三角形のそれぞれについて、比率 $\frac{\text{面積}(ABC)}{\text{面積}(\text{部分三角形})}$ が有理数であることを証明できます。 しかし、これらの比率の一部またはすべてが整数である三角形が存在します。
-How many triangles $ABC$ with perimeter $≤ 100\\,000\\,000$ exist so that the ratio $\frac{\text{area}(ABC)}{\text{area}(AEG)}$ is integral?
+周長が $100\\,000\\,000$ 以下で、比率 $\frac{\text{面積}(ABC)}{\text{面積}(AEG)}$ が整数である三角形 $ABC$ はいくつ存在しますか。
# --hints--
-`angularBisectors()` should return `139012411`.
+`angularBisectors()` は `139012411` を返す必要があります。
```js
assert.strictEqual(angularBisectors(), 139012411);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md
index a8c17db8bb..99e643e02c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f46e1000cf542c50ff81
-title: 'Problem 258: A lagged Fibonacci sequence'
+title: '問題 258: ラグ付きフィボナッチ数列'
challengeType: 5
forumTopicId: 301906
dashedName: problem-258-a-lagged-fibonacci-sequence
@@ -8,16 +8,16 @@ dashedName: problem-258-a-lagged-fibonacci-sequence
# --description--
-A sequence is defined as:
+数列を次のように定義します。
-- $g_k = 1$, for $0 ≤ k ≤ 1999$
-- $g_k = g_{k - 2000} + g_{k - 1999}$, for $k ≥ 2000$.
+- $0 ≤ k ≤ 1999$ のとき、$g_k = 1$
+- $k ≥ 2000$ のとき、$g_k = g_{k - 2000} + g_{k - 1999}$
-Find $g_k$ mod 20092010 for $k = {10}^{18}$.
+$k = {10}^{18} $ のとき、$g_k$ mod 20092010 を求めなさい。
# --hints--
-`laggedFibonacciSequence()` should return `12747994`.
+`laggedFibonacciSequence()` は `12747994` を返す必要があります。
```js
assert.strictEqual(laggedFibonacciSequence(), 12747994);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md
index fb73482aba..651cf39f90 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4701000cf542c50ff82
-title: 'Problem 259: Reachable Numbers'
+title: 'Problem 259: 到達可能な数'
challengeType: 5
forumTopicId: 301907
dashedName: problem-259-reachable-numbers
@@ -8,22 +8,22 @@ dashedName: problem-259-reachable-numbers
# --description--
-A positive integer will be called reachable if it can result from an arithmetic expression obeying the following rules:
+次の規則に沿った算術式によって得られる正の整数を、「到達可能な数」と呼ぶことにします。
-- Uses the digits 1 through 9, in that order and exactly once each.
-- Any successive digits can be concatenated (for example, using the digits 2, 3 and 4 we obtain the number 234).
-- Only the four usual binary arithmetic operations (addition, subtraction, multiplication and division) are allowed.
-- Each operation can be used any number of times, or not at all.
-- Unary minus is not allowed.
-- Any number of (possibly nested) parentheses may be used to define the order of operations.
+- 1 から 9 の数字を、この順番でちょうど 1 回ずつ使用する。
+- 任意の連続した数字を連結できる (例: 2, 3, 4 を使って 234 を得る)。
+- 一般的な 2 項の四則演算 (加算、減算、乗算、除算) のみが許される。
+- 各演算は何回でも使用でき、全く使用しなくても良い。
+- 単項マイナスは使用できない。
+- 演算の順序を指定するために括弧を何個でも使用できる (入れ子も可)。
-For example, 42 is reachable, since $\frac{1}{23} \times ((4 \times 5) - 6) \times (78 - 9) = 42$.
+例えば、$\frac{1}{23} \times ((4 \times 5) - 6) \times (78 - 9) = 42$ なので、42 は到達可能な数です。
-What is the sum of all positive reachable integers?
+到達可能な正の整数の総和を求めなさい。
# --hints--
-`reachableNumbers()` should return `20101196798`.
+`reachableNumbers()` は `20101196798` を返す必要があります。
```js
assert.strictEqual(reachableNumbers(), 20101196798);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md
index 717d3bfcb3..2a3851db61 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4701000cf542c50ff83
-title: 'Problem 260: Stone Game'
+title: '問題 260: 石取りゲーム'
challengeType: 5
forumTopicId: 301909
dashedName: problem-260-stone-game
@@ -8,33 +8,33 @@ dashedName: problem-260-stone-game
# --description--
-A game is played with three piles of stones and two players.
+石を積み上げた 3 つの山と 2 人のプレイヤーでゲームをします。
-On each player's turn, the player removes one or more stones from the piles. However, if the player takes stones from more than one pile, the same number of stones must be removed from each of the selected piles.
+各プレイヤーは自分のターンで、石の山から 1 つ以上の石を取ります。 ただし、複数の山から石を取る場合は、選んだ山のそれぞれから同じ数の石を取らなければなりません。
-In other words, the player chooses some $N > 0$ and removes:
+つまり、プレイヤーは次のいずれかのパターンで個数 $N > 0$ を選び、山から取ります。
-- $N$ stones from any single pile; or
-- $N$ stones from each of any two piles ($2N$ total); or
-- $N$ stones from each of the three piles ($3N$ total).
+- 1 つの山から $N$ 個の石を取る。
+- 2 つの山から $N$ 個ずつ石を取る (計: $2N$ 個)。
+- 3 つの山から $N$ 個ずつ石を取る (計: $3N$ 個)。
-The player taking the last stone(s) wins the game.
+最後の石を取ったプレイヤーの勝ちです。
-A winning configuration is one where the first player can force a win.
+勝利構成とは、先手が必ず勝てる構成です。
-For example, (0,0,13), (0,11,11) and (5,5,5) are winning configurations because the first player can immediately remove all stones.
+例えば、(0,0,13), (0,11,11), (5,5,5) は、先手が即座にすべての石を取れるので、勝利構成です。
-A losing configuration is one where the second player can force a win, no matter what the first player does.
+敗北構成とは、先手が何をしようと 後手が必ず勝てる構成です。
-For example, (0,1,2) and (1,3,3) are losing configurations: any legal move leaves a winning configuration for the second player.
+例えば、(0,1,2) と (1,3,3) は敗北構成です。ルールに従う限り、何をしても 後手の勝利構成になります。
-Consider all losing configurations ($x_i$,$y_i$,$z_i$) where $x_i ≤ y_i ≤ z_i ≤ 100$. We can verify that $\sum (x_i + y_i + z_i) = 173\\,895$ for these.
+$x_i ≤ y_i ≤ z_i ≤ 100$ として、すべての敗北構成 ($x_i$,$y_i$,$z_i$) について考えます。 それらの構成について $\sum (x_i + y_i + z_i) = 173\\,895$ であることを確認できます。
-Find $\sum (x_i + y_i + z_i)$ where ($x_i$,$y_i$,$z_i$) ranges over the losing configurations with $x_i ≤ y_i ≤ z_i ≤ 1000$.
+$x_i ≤ y_i ≤ z_i ≤ 1000$ として、($x_i$,$y_i$,$z_i$) が敗北構成の全範囲を表すとき、$\sum (x_i + y_i + z_i)$ を求めなさい。
# --hints--
-`stoneGame()` should return `167542057`.
+`stoneGame()` は `167542057` を返す必要があります。
```js
assert.strictEqual(stoneGame(), 167542057);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md
index aa00d603ec..91bcc145e0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md
@@ -1,6 +1,6 @@
---
id: 5900f4711000cf542c50ff84
-title: 'Problem 261: Pivotal Square Sums'
+title: '問題 261: 平方ピボットの和'
challengeType: 5
forumTopicId: 301910
dashedName: problem-261-pivotal-square-sums
@@ -8,19 +8,19 @@ dashedName: problem-261-pivotal-square-sums
# --description--
-Let us call a positive integer $k$ a square-pivot, if there is a pair of integers $m > 0$ and $n ≥ k$, such that the sum of the ($m + 1$) consecutive squares up to $k$ equals the sum of the $m$ consecutive squares from ($n + 1$) on:
+正の整数 $k$ まで連続する ($m + 1$) 個の平方数の和が、($n + 1$) から連続する $m$ 個の平方数の和に等しくなるような、整数 $m > 0$ と 整数 $n ≥ k$ の対がある場合、すなわち次の式が成り立つ場合、$k$ を「平方ピボット」と呼ぶことにします。
$${(k - m)}^2 + \ldots + k^2 = {(n + 1)}^2 + \ldots + {(n + m)}^2$$
-Some small square-pivots are
+小さい平方ピボットをいくつか下に示します。
$$\begin{align} & \mathbf{4}: 3^2 + \mathbf{4}^2 = 5^2 \\\\ & \mathbf{21}: {20}^2 + \mathbf{21}^2 = {29}^2 \\\\ & \mathbf{24}: {21}^2 + {22}^2 + {23}^2 + \mathbf{24}^2 = {25}^2 + {26}^2 + {27}^2 \\\\ & \mathbf{110}: {108}^2 + {109}^2 + \mathbf{110}^2 = {133}^2 + {134}^2 \\\\ \end{align}$$
-Find the sum of all distinct square-pivots $≤ {10}^{10}$.
+${10}^{10}$ 以下の相異なる平方ピボットの総和を求めなさい。
# --hints--
-`pivotalSquareSums()` should return `238890850232021`.
+`pivotalSquareSums()` は `238890850232021` を返す必要があります。
```js
assert.strictEqual(pivotalSquareSums(), 238890850232021);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md
index 310064738e..d3a71eb465 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md
@@ -1,6 +1,6 @@
---
id: 5900f4731000cf542c50ff85
-title: 'Problem 262: Mountain Range'
+title: '問題 262: 山脈'
challengeType: 5
forumTopicId: 301911
dashedName: problem-262-mountain-range
@@ -8,23 +8,23 @@ dashedName: problem-262-mountain-range
# --description--
-The following equation represents the continuous topography of a mountainous region, giving the elevation $h$ at any point ($x$,$y$):
+下の式は山岳地帯の連続した地形図を表し、任意の地点 ($x$,$y$) の標高 $h$ を示しています。
$$h = \left(5000 - \frac{x^2 + y^2 + xy}{200} + \frac{25(x + y)}{2}\right) \times e^{-\left|\frac{x^2 + y^2}{1\\,000\\,000} - \frac{3(x + y)}{2000} + \frac{7}{10}\right|}$$
-A mosquito intends to fly from A(200,200) to B(1400,1400), without leaving the area given by $0 ≤ x$, $y ≤ 1600$.
+1 匹の蚊が、$0 ≤ x$, $y ≤ 1600$ で表される領域を離れることなく、A(200,200) から B(1400,1400) まで飛んで行こうとしています。
-Because of the intervening mountains, it first rises straight up to a point A', having elevation $f$. Then, while remaining at the same elevation $f$, it flies around any obstacles until it arrives at a point B' directly above B.
+山に遮られるので、蚊はまず標高 $f$ の地点 A' まで真上に飛びます。 次に、同じ標高 $f$ を保ったまま障害物を避けながら飛び、B の真上にある地点 B' まで飛びます。
-First, determine $f_{min}$ which is the minimum constant elevation allowing such a trip from A to B, while remaining in the specified area. Then, find the length of the shortest path between A' and B', while flying at that constant elevation $f_{min}$.
+まず、指定された領域内にとどまりながら上述のとおりに A から B へ移動できる、最小の一定の標高 $f_{min}$ を決定しなさい。 次に、その一定の標高 $f_{min}$ で飛びながら A' から B' へ移動するための最短経路の長さを求めなさい。
-Give that length as your answer, rounded to three decimal places.
+回答は、経路の長さを四捨五入して小数第 3 位まで示すこと。
-**Note:** For convenience, the elevation function shown above is repeated below, in a form suitable for most programming languages: `h=( 5000-0.005*(x*x+y*y+x*y)+12.5*(x+y) )* exp( -abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7) )`.
+**注:** 参考として、多くのプログラム言語に適した形で上述の標高関数を次に再掲します。`h=( 5000-0.005*(x*x+y*y+x*y)+12.5*(x+y) )* exp( -abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7) )`
# --hints--
-`mountainRange()` should return `2531.205`.
+`mountainRange()` は `2531.205` を返す必要があります。
```js
assert.strictEqual(mountainRange(), 2531.205);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md
index a5677f364d..ba64e8e5b0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md
@@ -1,6 +1,6 @@
---
id: 5900f4741000cf542c50ff86
-title: 'Problem 263: An engineers'' dream come true'
+title: '問題 263: エンジニアの夢がかなう'
challengeType: 5
forumTopicId: 301912
dashedName: problem-263-an-engineers-dream-come-true
@@ -8,30 +8,30 @@ dashedName: problem-263-an-engineers-dream-come-true
# --description--
-Consider the number 6. The divisors of 6 are: 1,2,3 and 6.
+6 という数について考えます。 6 の約数は 1, 2, 3, 6 です。
-Every number from 1 up to and including 6 can be written as a sum of distinct divisors of 6:
+1 から 6 までのすべての数は、次のように 6 の相異なる約数の和として表せます。
-$1 = 1$, $2 = 2$, $3 = 1 + 2$, $4 = 1 + 3$, $5 = 2 + 3$, $6 = 6$.
+$1 = 1$, $2 = 2$, $3 = 1 + 2$, $4 = 1 + 3$, $5 = 2 + 3$, $6 = 6$
-A number $n$ is called a practical number if every number from 1 up to and including $n$ can be expressed as a sum of distinct divisors of $n$.
+1 から $n$ までのすべての数が $n$ の相異なる約数の和として表すことができる場合、 $n$ はプラクティカル数と呼ばれます。
-A pair of consecutive prime numbers with a difference of six is called a sexy pair (since "sex" is the Latin word for "six"). The first sexy pair is (23, 29).
+差が 6 である連続した素数のペアは、セクシーペアと呼ばれます ("six" はラテン語で "sex" なので) 。 最初のセクシーペアは (23, 29) です。
-We may occasionally find a triple-pair, which means three consecutive sexy prime pairs, such that the second member of each pair is the first member of the next pair.
+トリプルペアが見つかることがあります。トリプルペアとは、各ペアの 2 つ目の要素が次のペアの 1 つ目の要素になるような、3 つの連続したセクシーペアのことです。
-We shall call a number $n$ such that:
+次のような数 $n$ を考えます。
-- ($n - 9$, $n - 3$), ($n - 3$, $n + 3$), ($n + 3$, $n + 9$) form a triple-pair, and
-- the numbers $n - 8$, $n - 4$, $n$, $n + 4$ and $n + 8$ are all practical,
+- ($n - 9$, $n - 3$), ($n - 3$, $n + 3$), ($n + 3$, $n + 9$) がトリプルペアになっている。かつ、
+- 数 $n - 8$, $n - 4$, $n$, $n + 4$, $n + 8$ がすべてプラクティカル数である。
-an engineers’ paradise.
+このような数を「エンジニアの楽園」と呼ぶことにします。
-Find the sum of the first four engineers’ paradises.
+エンジニアの楽園のうち最初の 4 つの和を求めなさい。
# --hints--
-`engineersDreamComeTrue()` should return `2039506520`.
+`engineersDreamComeTrue()` は `2039506520` を返す必要があります。
```js
assert.strictEqual(engineersDreamComeTrue(), 2039506520);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md
index 1414627fa5..9e9cac582e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md
@@ -1,6 +1,6 @@
---
id: 5900f4751000cf542c50ff87
-title: 'Problem 264: Triangle Centres'
+title: '問題 264: 三角形の中心'
challengeType: 5
forumTopicId: 301913
dashedName: problem-264-triangle-centres
@@ -8,15 +8,15 @@ dashedName: problem-264-triangle-centres
# --description--
-Consider all the triangles having:
+以下が当てはまるすべての三角形について考えてます。
-- All their vertices on lattice points.
-- Circumcentre at the origin O.
-- Orthocentre at the point H(5, 0).
+- すべての頂点が格子点上にある。
+- 外心が原点 O にある。
+- 垂心が点 H (5, 0) にある。
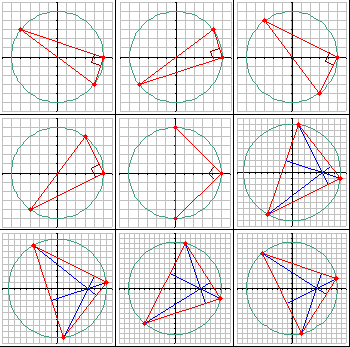
-There are nine such triangles having a $\text{perimeter} ≤ 50$.
+$\text{周長} ≤ 50$ に対してこのような三角形は 9 つあります。
-Listed and shown in ascending order of their perimeter, they are:
+それらを下表に周長の昇順で示します。
-The segments $EF$, $EG$ and $FG$ partition the triangle $ABC$ into four smaller triangles: $AEG$, $BFE$, $CGF$ and $EFG$. It can be proven that for each of these four triangles the ratio $\frac{\text{area}(ABC)}{\text{area}(\text{subtriangle})}$ is rational. However, there exist triangles for which some or all of these ratios are integral.
+線分 $EF$, $EG$, $FG$ は、$ABC$ を 4 つの小さな三角形 $AEG$, $BFE$, $CGF$, $EFG$ に分割します。 この 4 つの三角形のそれぞれについて、比率 $\frac{\text{面積}(ABC)}{\text{面積}(\text{部分三角形})}$ が有理数であることを証明できます。 しかし、これらの比率の一部またはすべてが整数である三角形が存在します。
-How many triangles $ABC$ with perimeter $≤ 100\\,000\\,000$ exist so that the ratio $\frac{\text{area}(ABC)}{\text{area}(AEG)}$ is integral?
+周長が $100\\,000\\,000$ 以下で、比率 $\frac{\text{面積}(ABC)}{\text{面積}(AEG)}$ が整数である三角形 $ABC$ はいくつ存在しますか。
# --hints--
-`angularBisectors()` should return `139012411`.
+`angularBisectors()` は `139012411` を返す必要があります。
```js
assert.strictEqual(angularBisectors(), 139012411);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md
index a8c17db8bb..99e643e02c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-258-a-lagged-fibonacci-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f46e1000cf542c50ff81
-title: 'Problem 258: A lagged Fibonacci sequence'
+title: '問題 258: ラグ付きフィボナッチ数列'
challengeType: 5
forumTopicId: 301906
dashedName: problem-258-a-lagged-fibonacci-sequence
@@ -8,16 +8,16 @@ dashedName: problem-258-a-lagged-fibonacci-sequence
# --description--
-A sequence is defined as:
+数列を次のように定義します。
-- $g_k = 1$, for $0 ≤ k ≤ 1999$
-- $g_k = g_{k - 2000} + g_{k - 1999}$, for $k ≥ 2000$.
+- $0 ≤ k ≤ 1999$ のとき、$g_k = 1$
+- $k ≥ 2000$ のとき、$g_k = g_{k - 2000} + g_{k - 1999}$
-Find $g_k$ mod 20092010 for $k = {10}^{18}$.
+$k = {10}^{18} $ のとき、$g_k$ mod 20092010 を求めなさい。
# --hints--
-`laggedFibonacciSequence()` should return `12747994`.
+`laggedFibonacciSequence()` は `12747994` を返す必要があります。
```js
assert.strictEqual(laggedFibonacciSequence(), 12747994);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md
index fb73482aba..651cf39f90 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-259-reachable-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4701000cf542c50ff82
-title: 'Problem 259: Reachable Numbers'
+title: 'Problem 259: 到達可能な数'
challengeType: 5
forumTopicId: 301907
dashedName: problem-259-reachable-numbers
@@ -8,22 +8,22 @@ dashedName: problem-259-reachable-numbers
# --description--
-A positive integer will be called reachable if it can result from an arithmetic expression obeying the following rules:
+次の規則に沿った算術式によって得られる正の整数を、「到達可能な数」と呼ぶことにします。
-- Uses the digits 1 through 9, in that order and exactly once each.
-- Any successive digits can be concatenated (for example, using the digits 2, 3 and 4 we obtain the number 234).
-- Only the four usual binary arithmetic operations (addition, subtraction, multiplication and division) are allowed.
-- Each operation can be used any number of times, or not at all.
-- Unary minus is not allowed.
-- Any number of (possibly nested) parentheses may be used to define the order of operations.
+- 1 から 9 の数字を、この順番でちょうど 1 回ずつ使用する。
+- 任意の連続した数字を連結できる (例: 2, 3, 4 を使って 234 を得る)。
+- 一般的な 2 項の四則演算 (加算、減算、乗算、除算) のみが許される。
+- 各演算は何回でも使用でき、全く使用しなくても良い。
+- 単項マイナスは使用できない。
+- 演算の順序を指定するために括弧を何個でも使用できる (入れ子も可)。
-For example, 42 is reachable, since $\frac{1}{23} \times ((4 \times 5) - 6) \times (78 - 9) = 42$.
+例えば、$\frac{1}{23} \times ((4 \times 5) - 6) \times (78 - 9) = 42$ なので、42 は到達可能な数です。
-What is the sum of all positive reachable integers?
+到達可能な正の整数の総和を求めなさい。
# --hints--
-`reachableNumbers()` should return `20101196798`.
+`reachableNumbers()` は `20101196798` を返す必要があります。
```js
assert.strictEqual(reachableNumbers(), 20101196798);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md
index 717d3bfcb3..2a3851db61 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-260-stone-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4701000cf542c50ff83
-title: 'Problem 260: Stone Game'
+title: '問題 260: 石取りゲーム'
challengeType: 5
forumTopicId: 301909
dashedName: problem-260-stone-game
@@ -8,33 +8,33 @@ dashedName: problem-260-stone-game
# --description--
-A game is played with three piles of stones and two players.
+石を積み上げた 3 つの山と 2 人のプレイヤーでゲームをします。
-On each player's turn, the player removes one or more stones from the piles. However, if the player takes stones from more than one pile, the same number of stones must be removed from each of the selected piles.
+各プレイヤーは自分のターンで、石の山から 1 つ以上の石を取ります。 ただし、複数の山から石を取る場合は、選んだ山のそれぞれから同じ数の石を取らなければなりません。
-In other words, the player chooses some $N > 0$ and removes:
+つまり、プレイヤーは次のいずれかのパターンで個数 $N > 0$ を選び、山から取ります。
-- $N$ stones from any single pile; or
-- $N$ stones from each of any two piles ($2N$ total); or
-- $N$ stones from each of the three piles ($3N$ total).
+- 1 つの山から $N$ 個の石を取る。
+- 2 つの山から $N$ 個ずつ石を取る (計: $2N$ 個)。
+- 3 つの山から $N$ 個ずつ石を取る (計: $3N$ 個)。
-The player taking the last stone(s) wins the game.
+最後の石を取ったプレイヤーの勝ちです。
-A winning configuration is one where the first player can force a win.
+勝利構成とは、先手が必ず勝てる構成です。
-For example, (0,0,13), (0,11,11) and (5,5,5) are winning configurations because the first player can immediately remove all stones.
+例えば、(0,0,13), (0,11,11), (5,5,5) は、先手が即座にすべての石を取れるので、勝利構成です。
-A losing configuration is one where the second player can force a win, no matter what the first player does.
+敗北構成とは、先手が何をしようと 後手が必ず勝てる構成です。
-For example, (0,1,2) and (1,3,3) are losing configurations: any legal move leaves a winning configuration for the second player.
+例えば、(0,1,2) と (1,3,3) は敗北構成です。ルールに従う限り、何をしても 後手の勝利構成になります。
-Consider all losing configurations ($x_i$,$y_i$,$z_i$) where $x_i ≤ y_i ≤ z_i ≤ 100$. We can verify that $\sum (x_i + y_i + z_i) = 173\\,895$ for these.
+$x_i ≤ y_i ≤ z_i ≤ 100$ として、すべての敗北構成 ($x_i$,$y_i$,$z_i$) について考えます。 それらの構成について $\sum (x_i + y_i + z_i) = 173\\,895$ であることを確認できます。
-Find $\sum (x_i + y_i + z_i)$ where ($x_i$,$y_i$,$z_i$) ranges over the losing configurations with $x_i ≤ y_i ≤ z_i ≤ 1000$.
+$x_i ≤ y_i ≤ z_i ≤ 1000$ として、($x_i$,$y_i$,$z_i$) が敗北構成の全範囲を表すとき、$\sum (x_i + y_i + z_i)$ を求めなさい。
# --hints--
-`stoneGame()` should return `167542057`.
+`stoneGame()` は `167542057` を返す必要があります。
```js
assert.strictEqual(stoneGame(), 167542057);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md
index aa00d603ec..91bcc145e0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-261-pivotal-square-sums.md
@@ -1,6 +1,6 @@
---
id: 5900f4711000cf542c50ff84
-title: 'Problem 261: Pivotal Square Sums'
+title: '問題 261: 平方ピボットの和'
challengeType: 5
forumTopicId: 301910
dashedName: problem-261-pivotal-square-sums
@@ -8,19 +8,19 @@ dashedName: problem-261-pivotal-square-sums
# --description--
-Let us call a positive integer $k$ a square-pivot, if there is a pair of integers $m > 0$ and $n ≥ k$, such that the sum of the ($m + 1$) consecutive squares up to $k$ equals the sum of the $m$ consecutive squares from ($n + 1$) on:
+正の整数 $k$ まで連続する ($m + 1$) 個の平方数の和が、($n + 1$) から連続する $m$ 個の平方数の和に等しくなるような、整数 $m > 0$ と 整数 $n ≥ k$ の対がある場合、すなわち次の式が成り立つ場合、$k$ を「平方ピボット」と呼ぶことにします。
$${(k - m)}^2 + \ldots + k^2 = {(n + 1)}^2 + \ldots + {(n + m)}^2$$
-Some small square-pivots are
+小さい平方ピボットをいくつか下に示します。
$$\begin{align} & \mathbf{4}: 3^2 + \mathbf{4}^2 = 5^2 \\\\ & \mathbf{21}: {20}^2 + \mathbf{21}^2 = {29}^2 \\\\ & \mathbf{24}: {21}^2 + {22}^2 + {23}^2 + \mathbf{24}^2 = {25}^2 + {26}^2 + {27}^2 \\\\ & \mathbf{110}: {108}^2 + {109}^2 + \mathbf{110}^2 = {133}^2 + {134}^2 \\\\ \end{align}$$
-Find the sum of all distinct square-pivots $≤ {10}^{10}$.
+${10}^{10}$ 以下の相異なる平方ピボットの総和を求めなさい。
# --hints--
-`pivotalSquareSums()` should return `238890850232021`.
+`pivotalSquareSums()` は `238890850232021` を返す必要があります。
```js
assert.strictEqual(pivotalSquareSums(), 238890850232021);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md
index 310064738e..d3a71eb465 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-262-mountain-range.md
@@ -1,6 +1,6 @@
---
id: 5900f4731000cf542c50ff85
-title: 'Problem 262: Mountain Range'
+title: '問題 262: 山脈'
challengeType: 5
forumTopicId: 301911
dashedName: problem-262-mountain-range
@@ -8,23 +8,23 @@ dashedName: problem-262-mountain-range
# --description--
-The following equation represents the continuous topography of a mountainous region, giving the elevation $h$ at any point ($x$,$y$):
+下の式は山岳地帯の連続した地形図を表し、任意の地点 ($x$,$y$) の標高 $h$ を示しています。
$$h = \left(5000 - \frac{x^2 + y^2 + xy}{200} + \frac{25(x + y)}{2}\right) \times e^{-\left|\frac{x^2 + y^2}{1\\,000\\,000} - \frac{3(x + y)}{2000} + \frac{7}{10}\right|}$$
-A mosquito intends to fly from A(200,200) to B(1400,1400), without leaving the area given by $0 ≤ x$, $y ≤ 1600$.
+1 匹の蚊が、$0 ≤ x$, $y ≤ 1600$ で表される領域を離れることなく、A(200,200) から B(1400,1400) まで飛んで行こうとしています。
-Because of the intervening mountains, it first rises straight up to a point A', having elevation $f$. Then, while remaining at the same elevation $f$, it flies around any obstacles until it arrives at a point B' directly above B.
+山に遮られるので、蚊はまず標高 $f$ の地点 A' まで真上に飛びます。 次に、同じ標高 $f$ を保ったまま障害物を避けながら飛び、B の真上にある地点 B' まで飛びます。
-First, determine $f_{min}$ which is the minimum constant elevation allowing such a trip from A to B, while remaining in the specified area. Then, find the length of the shortest path between A' and B', while flying at that constant elevation $f_{min}$.
+まず、指定された領域内にとどまりながら上述のとおりに A から B へ移動できる、最小の一定の標高 $f_{min}$ を決定しなさい。 次に、その一定の標高 $f_{min}$ で飛びながら A' から B' へ移動するための最短経路の長さを求めなさい。
-Give that length as your answer, rounded to three decimal places.
+回答は、経路の長さを四捨五入して小数第 3 位まで示すこと。
-**Note:** For convenience, the elevation function shown above is repeated below, in a form suitable for most programming languages: `h=( 5000-0.005*(x*x+y*y+x*y)+12.5*(x+y) )* exp( -abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7) )`.
+**注:** 参考として、多くのプログラム言語に適した形で上述の標高関数を次に再掲します。`h=( 5000-0.005*(x*x+y*y+x*y)+12.5*(x+y) )* exp( -abs(0.000001*(x*x+y*y)-0.0015*(x+y)+0.7) )`
# --hints--
-`mountainRange()` should return `2531.205`.
+`mountainRange()` は `2531.205` を返す必要があります。
```js
assert.strictEqual(mountainRange(), 2531.205);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md
index a5677f364d..ba64e8e5b0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-263-an-engineers-dream-come-true.md
@@ -1,6 +1,6 @@
---
id: 5900f4741000cf542c50ff86
-title: 'Problem 263: An engineers'' dream come true'
+title: '問題 263: エンジニアの夢がかなう'
challengeType: 5
forumTopicId: 301912
dashedName: problem-263-an-engineers-dream-come-true
@@ -8,30 +8,30 @@ dashedName: problem-263-an-engineers-dream-come-true
# --description--
-Consider the number 6. The divisors of 6 are: 1,2,3 and 6.
+6 という数について考えます。 6 の約数は 1, 2, 3, 6 です。
-Every number from 1 up to and including 6 can be written as a sum of distinct divisors of 6:
+1 から 6 までのすべての数は、次のように 6 の相異なる約数の和として表せます。
-$1 = 1$, $2 = 2$, $3 = 1 + 2$, $4 = 1 + 3$, $5 = 2 + 3$, $6 = 6$.
+$1 = 1$, $2 = 2$, $3 = 1 + 2$, $4 = 1 + 3$, $5 = 2 + 3$, $6 = 6$
-A number $n$ is called a practical number if every number from 1 up to and including $n$ can be expressed as a sum of distinct divisors of $n$.
+1 から $n$ までのすべての数が $n$ の相異なる約数の和として表すことができる場合、 $n$ はプラクティカル数と呼ばれます。
-A pair of consecutive prime numbers with a difference of six is called a sexy pair (since "sex" is the Latin word for "six"). The first sexy pair is (23, 29).
+差が 6 である連続した素数のペアは、セクシーペアと呼ばれます ("six" はラテン語で "sex" なので) 。 最初のセクシーペアは (23, 29) です。
-We may occasionally find a triple-pair, which means three consecutive sexy prime pairs, such that the second member of each pair is the first member of the next pair.
+トリプルペアが見つかることがあります。トリプルペアとは、各ペアの 2 つ目の要素が次のペアの 1 つ目の要素になるような、3 つの連続したセクシーペアのことです。
-We shall call a number $n$ such that:
+次のような数 $n$ を考えます。
-- ($n - 9$, $n - 3$), ($n - 3$, $n + 3$), ($n + 3$, $n + 9$) form a triple-pair, and
-- the numbers $n - 8$, $n - 4$, $n$, $n + 4$ and $n + 8$ are all practical,
+- ($n - 9$, $n - 3$), ($n - 3$, $n + 3$), ($n + 3$, $n + 9$) がトリプルペアになっている。かつ、
+- 数 $n - 8$, $n - 4$, $n$, $n + 4$, $n + 8$ がすべてプラクティカル数である。
-an engineers’ paradise.
+このような数を「エンジニアの楽園」と呼ぶことにします。
-Find the sum of the first four engineers’ paradises.
+エンジニアの楽園のうち最初の 4 つの和を求めなさい。
# --hints--
-`engineersDreamComeTrue()` should return `2039506520`.
+`engineersDreamComeTrue()` は `2039506520` を返す必要があります。
```js
assert.strictEqual(engineersDreamComeTrue(), 2039506520);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md
index 1414627fa5..9e9cac582e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-264-triangle-centres.md
@@ -1,6 +1,6 @@
---
id: 5900f4751000cf542c50ff87
-title: 'Problem 264: Triangle Centres'
+title: '問題 264: 三角形の中心'
challengeType: 5
forumTopicId: 301913
dashedName: problem-264-triangle-centres
@@ -8,15 +8,15 @@ dashedName: problem-264-triangle-centres
# --description--
-Consider all the triangles having:
+以下が当てはまるすべての三角形について考えてます。
-- All their vertices on lattice points.
-- Circumcentre at the origin O.
-- Orthocentre at the point H(5, 0).
+- すべての頂点が格子点上にある。
+- 外心が原点 O にある。
+- 垂心が点 H (5, 0) にある。
-There are nine such triangles having a $\text{perimeter} ≤ 50$.
+$\text{周長} ≤ 50$ に対してこのような三角形は 9 つあります。
-Listed and shown in ascending order of their perimeter, they are:
+それらを下表に周長の昇順で示します。
 |
+  |
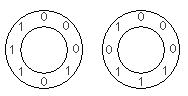 +
+ -For the first arrangement, the 3-digit subsequences, in clockwise order, are: 000, 001, 010, 101, 011, 111, 110 and 100.
+1 つ目の配置では、3 桁の部分列は時計回りに 000, 001, 010, 101, 011, 111, 110, 100 です。
-Each circular arrangement can be encoded as a number by concatenating the binary digits starting with the subsequence of all zeros as the most significant bits and proceeding clockwise. The two arrangements for $N = 3$ are thus represented as 23 and 29:
+0 のみからなる部分列を最上位の数字としてそこから開始し、時計回りに 2 進法の数字をつなげていくと、それぞれの円形配置を 1 つの数に変換できます。 したがって、$N = 3$ のとき、上の 2 つの配置は次のように 23 および 29 として表されます。
$${00010111}_2 = 23\\\\
{00011101}_2 = 29$$
-Calling $S(N)$ the sum of the unique numeric representations, we can see that $S(3) = 23 + 29 = 52$.
+一意の数値表現の和を $S(N)$ とすると、$S(3) = 23 + 29 = 52$ であることが分かります。
-Find $S(5)$.
+$S(5)$ を求めなさい。
# --hints--
-`binaryCircles()` should return `209110240768`.
+`binaryCircles()` は `209110240768` を返す必要があります。
```js
assert.strictEqual(binaryCircles(), 209110240768);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
index 8b188974a5..9bb53af9d1 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
@@ -1,6 +1,6 @@
---
id: 5900f4771000cf542c50ff89
-title: 'Problem 266: Pseudo Square Root'
+title: '問題 266: 擬似平方根'
challengeType: 5
forumTopicId: 301915
dashedName: problem-266-pseudo-square-root
@@ -8,19 +8,19 @@ dashedName: problem-266-pseudo-square-root
# --description--
-The divisors of 12 are: 1,2,3,4,6 and 12.
+12 の約数は 1, 2, 3, 4, 6, 12 です。
-The largest divisor of 12 that does not exceed the square root of 12 is 3.
+12 の平方根を超えない 12 の最大の約数は 3 です。
-We shall call the largest divisor of an integer $n$ that does not exceed the square root of $n$ the pseudo square root ($PSR$) of $n$.
+$n$ の平方根を超えないような整数 $n$ の最大の約数を、$n$ の「擬似平方根」 ($PSR$) と呼ぶことにします。
-It can be seen that $PSR(3102) = 47$.
+$PSR(3102) = 47$ であることが分かります。
-Let $p$ be the product of the primes below 190. Find $PSR(p)\bmod {10}^{16}$.
+$p$ を 190 未満の素数の積とします。 $PSR(p)\bmod {10}^{16} $ を求めなさい。
# --hints--
-`pseudoSquareRoot()` should return `1096883702440585`.
+`pseudoSquareRoot()` は `1096883702440585` を返す必要があります。
```js
assert.strictEqual(pseudoSquareRoot(), 1096883702440585);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md
index 2330fc805b..7ae8e4b7dd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md
@@ -1,6 +1,6 @@
---
id: 5900f4771000cf542c50ff8a
-title: 'Problem 267: Billionaire'
+title: 'Problem 267: 億万長者'
challengeType: 5
forumTopicId: 301916
dashedName: problem-267-billionaire
@@ -8,21 +8,21 @@ dashedName: problem-267-billionaire
# --description--
-You are given a unique investment opportunity.
+一風変わった投資機会が与えられます。
-Starting with £1 of capital, you can choose a fixed proportion, $f$, of your capital to bet on a fair coin toss repeatedly for 1000 tosses.
+1 ポンドの資金で始め、1000 回の公正なコイントスに対して繰り返し賭ける資金の固定比率 $f$ を選択します。
-Your return is double your bet for heads and you lose your bet for tails.
+表が出たら賭け金の倍額を稼ぎ、裏が出たら賭け金を失います。
-For example, if $f = \frac{1}{4}$, for the first toss you bet £0.25, and if heads comes up you win £0.5 and so then have £1.5. You then bet £0.375 and if the second toss is tails, you have £1.125.
+例えば、$f = \frac{1}{4}$の場合、最初のコイントスで 0.25 ポンドを賭け、表が出たら 0.5 ポンドを獲得するので、資金は 1.5 ポンドになります。 その後、0.375 ポンドを賭け、2 回目のトスが裏であれば資金は 1.125 ポンドになります。
-Choosing $f$ to maximize your chances of having at least £1,000,000,000 after 1,000 flips, what is the chance that you become a billionaire?
+1,000 回後に資金が少なくとも 1,000,000,000 ポンドになっている確率が最大になるような $f$ を選んだ場合に、資金が 1,000,000,000 ポンドになっている確率を求めなさい。
-All computations are assumed to be exact (no rounding), but give your answer rounded to 12 digits behind the decimal point in the form 0.abcdefghijkl.
+計算はすべて (四捨五入なしで) 厳密に行われることが想定されています。ただし回答は、四捨五入して小数第 12 位まで求め、0.abcdefghijkl の形式にすること。
# --hints--
-`billionaire()` should return `0.999992836187`.
+`billionaire()` は `0.999992836187` を返す必要があります。
```js
assert.strictEqual(billionaire(), 0.999992836187);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
index d793c013e2..7291471c0c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
@@ -1,7 +1,7 @@
---
id: 5900f4791000cf542c50ff8b
title: >-
- Problem 268: Counting numbers with at least four distinct prime factors less than 100
+ 問題 268: 相異なる 100 未満の素因数を少なくとも 4 つ持つ数を数え上げる
challengeType: 5
forumTopicId: 301917
dashedName: >-
@@ -10,13 +10,13 @@ dashedName: >-
# --description--
-It can be verified that there are 23 positive integers less than 1000 that are divisible by at least four distinct primes less than 100.
+少なくとも 4 つの 100 未満の相異なる素数で割り切れる、1000 未満の正の整数が 23 個あることを確認できます。
-Find how many positive integers less than ${10}^{16}$ are divisible by at least four distinct primes less than 100.
+少なくとも 4 つの 100 未満の相異なる素数で割り切れる、${10}^{16}$ 未満の正の整数はいくつありますか。
# --hints--
-`fourDistinctPrimeFactors()` should return `785478606870985`.
+`fourDistinctPrimeFactors()` は `785478606870985` を返す必要があります。
```js
assert.strictEqual(fourDistinctPrimeFactors(), 785478606870985);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
index da8ed3eaf3..13b66acf35 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
@@ -1,6 +1,6 @@
---
id: 5900f4791000cf542c50ff8c
-title: 'Problem 269: Polynomials with at least one integer root'
+title: '問題 269: 少なくとも 1 つの整数根を持つ多項式'
challengeType: 5
forumTopicId: 301918
dashedName: problem-269-polynomials-with-at-least-one-integer-root
@@ -8,27 +8,27 @@ dashedName: problem-269-polynomials-with-at-least-one-integer-root
# --description--
-A root or zero of a polynomial $P(x)$ is a solution to the equation $P(x) = 0$.
+多項式 $P(x)$ の根すなわち零点とは、式 $P(x) = 0$ の解です。
-Define $P_n$ as the polynomial whose coefficients are the digits of $n$.
+$P_n$ を多項式として定義し、その係数を $n$ の各位とします。
-For example, $P_{5703}(x) = 5x^3 + 7x^2 + 3$.
+例えば、$P_{5703}(x) = 5x^3 + 7x^2 + 3$ です。
-We can see that:
+次のことが分かります。
-- $P_n(0)$ is the last digit of $n$,
-- $P_n(1)$ is the sum of the digits of $n$,
-- $Pn(10)$ is $n$ itself.
+- $P_n(0)$ は $n$ の最下位の数字である。
+- $P_n(1)$ は $n$ の各位の和である。
+- $Pn(10)$ は $n$ そのものである。
-Define $Z(k)$ as the number of positive integers, $n$, not exceeding $k$ for which the polynomial $P_n$ has at least one integer root.
+多項式 $P_n$ が少なくとも 1 つの整数根 (integer root) を持つような $k$ 以下の正の整数 $n$ の個数を、$Z(k)$とします。
-It can be verified that $Z(100\\,000)$ is 14696.
+$Z(100\\,000)$ が 14696 であることを確認できます。
-What is $Z({10}^{16})$?
+$Z({10}^{16})$ を求めなさい。
# --hints--
-`polynomialsWithOneIntegerRoot()` should return `1311109198529286`.
+`polynomialsWithOneIntegerRoot()` は `1311109198529286` を返す必要があります。
```js
assert.strictEqual(polynomialsWithOneIntegerRoot(), 1311109198529286);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
index 96a732ef77..6618d574eb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
@@ -1,6 +1,6 @@
---
id: 5900f47c1000cf542c50ff8e
-title: 'Problem 270: Cutting Squares'
+title: '問題 270: 正方形を切る'
challengeType: 5
forumTopicId: 301920
dashedName: problem-270-cutting-squares
@@ -8,21 +8,21 @@ dashedName: problem-270-cutting-squares
# --description--
-A square piece of paper with integer dimensions $N×N$ is placed with a corner at the origin and two of its sides along the $x$- and $y$-axes. Then, we cut it up respecting the following rules:
+整数寸法 $N×N$ を持つ正方形の紙片が座標上に置かれています。角は原点にあり、辺は $x$ 軸と $y$ 軸に沿っています。 次に、以下のルールに従って紙を切ります。
-- We only make straight cuts between two points lying on different sides of the square, and having integer coordinates.
-- Two cuts cannot cross, but several cuts can meet at the same border point.
-- Proceed until no more legal cuts can be made.
+- 正方形の異なる辺上にあり整数座標を持つ 2 つの点の間のみを、まっすぐ切る。
+- 2 本の切断線が交差してはいけないが、複数の切断線の端点が同じでも良い。
+- ルールに従った切り方がそれ以上できなくなるまで続ける。
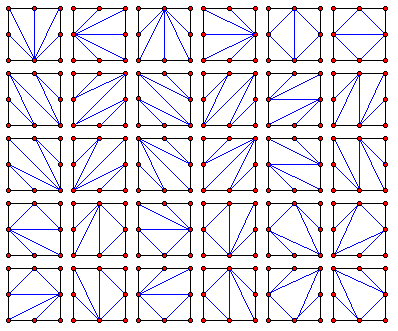
-Counting any reflections or rotations as distinct, we call $C(N)$ the number of ways to cut an $N×N$ square. For example, $C(1) = 2$ and $C(2) = 30$ (shown below).
+反転または回転した図もすべて相異なる切り方として数え、$N×N$ の正方形の切り方の数を $C(N)$ とします。 例えば、$C(1) = 2$ であり、$C(2) = 30$ です (下図参照)。
-
-For the first arrangement, the 3-digit subsequences, in clockwise order, are: 000, 001, 010, 101, 011, 111, 110 and 100.
+1 つ目の配置では、3 桁の部分列は時計回りに 000, 001, 010, 101, 011, 111, 110, 100 です。
-Each circular arrangement can be encoded as a number by concatenating the binary digits starting with the subsequence of all zeros as the most significant bits and proceeding clockwise. The two arrangements for $N = 3$ are thus represented as 23 and 29:
+0 のみからなる部分列を最上位の数字としてそこから開始し、時計回りに 2 進法の数字をつなげていくと、それぞれの円形配置を 1 つの数に変換できます。 したがって、$N = 3$ のとき、上の 2 つの配置は次のように 23 および 29 として表されます。
$${00010111}_2 = 23\\\\
{00011101}_2 = 29$$
-Calling $S(N)$ the sum of the unique numeric representations, we can see that $S(3) = 23 + 29 = 52$.
+一意の数値表現の和を $S(N)$ とすると、$S(3) = 23 + 29 = 52$ であることが分かります。
-Find $S(5)$.
+$S(5)$ を求めなさい。
# --hints--
-`binaryCircles()` should return `209110240768`.
+`binaryCircles()` は `209110240768` を返す必要があります。
```js
assert.strictEqual(binaryCircles(), 209110240768);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
index 8b188974a5..9bb53af9d1 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
@@ -1,6 +1,6 @@
---
id: 5900f4771000cf542c50ff89
-title: 'Problem 266: Pseudo Square Root'
+title: '問題 266: 擬似平方根'
challengeType: 5
forumTopicId: 301915
dashedName: problem-266-pseudo-square-root
@@ -8,19 +8,19 @@ dashedName: problem-266-pseudo-square-root
# --description--
-The divisors of 12 are: 1,2,3,4,6 and 12.
+12 の約数は 1, 2, 3, 4, 6, 12 です。
-The largest divisor of 12 that does not exceed the square root of 12 is 3.
+12 の平方根を超えない 12 の最大の約数は 3 です。
-We shall call the largest divisor of an integer $n$ that does not exceed the square root of $n$ the pseudo square root ($PSR$) of $n$.
+$n$ の平方根を超えないような整数 $n$ の最大の約数を、$n$ の「擬似平方根」 ($PSR$) と呼ぶことにします。
-It can be seen that $PSR(3102) = 47$.
+$PSR(3102) = 47$ であることが分かります。
-Let $p$ be the product of the primes below 190. Find $PSR(p)\bmod {10}^{16}$.
+$p$ を 190 未満の素数の積とします。 $PSR(p)\bmod {10}^{16} $ を求めなさい。
# --hints--
-`pseudoSquareRoot()` should return `1096883702440585`.
+`pseudoSquareRoot()` は `1096883702440585` を返す必要があります。
```js
assert.strictEqual(pseudoSquareRoot(), 1096883702440585);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md
index 2330fc805b..7ae8e4b7dd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-267-billionaire.md
@@ -1,6 +1,6 @@
---
id: 5900f4771000cf542c50ff8a
-title: 'Problem 267: Billionaire'
+title: 'Problem 267: 億万長者'
challengeType: 5
forumTopicId: 301916
dashedName: problem-267-billionaire
@@ -8,21 +8,21 @@ dashedName: problem-267-billionaire
# --description--
-You are given a unique investment opportunity.
+一風変わった投資機会が与えられます。
-Starting with £1 of capital, you can choose a fixed proportion, $f$, of your capital to bet on a fair coin toss repeatedly for 1000 tosses.
+1 ポンドの資金で始め、1000 回の公正なコイントスに対して繰り返し賭ける資金の固定比率 $f$ を選択します。
-Your return is double your bet for heads and you lose your bet for tails.
+表が出たら賭け金の倍額を稼ぎ、裏が出たら賭け金を失います。
-For example, if $f = \frac{1}{4}$, for the first toss you bet £0.25, and if heads comes up you win £0.5 and so then have £1.5. You then bet £0.375 and if the second toss is tails, you have £1.125.
+例えば、$f = \frac{1}{4}$の場合、最初のコイントスで 0.25 ポンドを賭け、表が出たら 0.5 ポンドを獲得するので、資金は 1.5 ポンドになります。 その後、0.375 ポンドを賭け、2 回目のトスが裏であれば資金は 1.125 ポンドになります。
-Choosing $f$ to maximize your chances of having at least £1,000,000,000 after 1,000 flips, what is the chance that you become a billionaire?
+1,000 回後に資金が少なくとも 1,000,000,000 ポンドになっている確率が最大になるような $f$ を選んだ場合に、資金が 1,000,000,000 ポンドになっている確率を求めなさい。
-All computations are assumed to be exact (no rounding), but give your answer rounded to 12 digits behind the decimal point in the form 0.abcdefghijkl.
+計算はすべて (四捨五入なしで) 厳密に行われることが想定されています。ただし回答は、四捨五入して小数第 12 位まで求め、0.abcdefghijkl の形式にすること。
# --hints--
-`billionaire()` should return `0.999992836187`.
+`billionaire()` は `0.999992836187` を返す必要があります。
```js
assert.strictEqual(billionaire(), 0.999992836187);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
index d793c013e2..7291471c0c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
@@ -1,7 +1,7 @@
---
id: 5900f4791000cf542c50ff8b
title: >-
- Problem 268: Counting numbers with at least four distinct prime factors less than 100
+ 問題 268: 相異なる 100 未満の素因数を少なくとも 4 つ持つ数を数え上げる
challengeType: 5
forumTopicId: 301917
dashedName: >-
@@ -10,13 +10,13 @@ dashedName: >-
# --description--
-It can be verified that there are 23 positive integers less than 1000 that are divisible by at least four distinct primes less than 100.
+少なくとも 4 つの 100 未満の相異なる素数で割り切れる、1000 未満の正の整数が 23 個あることを確認できます。
-Find how many positive integers less than ${10}^{16}$ are divisible by at least four distinct primes less than 100.
+少なくとも 4 つの 100 未満の相異なる素数で割り切れる、${10}^{16}$ 未満の正の整数はいくつありますか。
# --hints--
-`fourDistinctPrimeFactors()` should return `785478606870985`.
+`fourDistinctPrimeFactors()` は `785478606870985` を返す必要があります。
```js
assert.strictEqual(fourDistinctPrimeFactors(), 785478606870985);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
index da8ed3eaf3..13b66acf35 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
@@ -1,6 +1,6 @@
---
id: 5900f4791000cf542c50ff8c
-title: 'Problem 269: Polynomials with at least one integer root'
+title: '問題 269: 少なくとも 1 つの整数根を持つ多項式'
challengeType: 5
forumTopicId: 301918
dashedName: problem-269-polynomials-with-at-least-one-integer-root
@@ -8,27 +8,27 @@ dashedName: problem-269-polynomials-with-at-least-one-integer-root
# --description--
-A root or zero of a polynomial $P(x)$ is a solution to the equation $P(x) = 0$.
+多項式 $P(x)$ の根すなわち零点とは、式 $P(x) = 0$ の解です。
-Define $P_n$ as the polynomial whose coefficients are the digits of $n$.
+$P_n$ を多項式として定義し、その係数を $n$ の各位とします。
-For example, $P_{5703}(x) = 5x^3 + 7x^2 + 3$.
+例えば、$P_{5703}(x) = 5x^3 + 7x^2 + 3$ です。
-We can see that:
+次のことが分かります。
-- $P_n(0)$ is the last digit of $n$,
-- $P_n(1)$ is the sum of the digits of $n$,
-- $Pn(10)$ is $n$ itself.
+- $P_n(0)$ は $n$ の最下位の数字である。
+- $P_n(1)$ は $n$ の各位の和である。
+- $Pn(10)$ は $n$ そのものである。
-Define $Z(k)$ as the number of positive integers, $n$, not exceeding $k$ for which the polynomial $P_n$ has at least one integer root.
+多項式 $P_n$ が少なくとも 1 つの整数根 (integer root) を持つような $k$ 以下の正の整数 $n$ の個数を、$Z(k)$とします。
-It can be verified that $Z(100\\,000)$ is 14696.
+$Z(100\\,000)$ が 14696 であることを確認できます。
-What is $Z({10}^{16})$?
+$Z({10}^{16})$ を求めなさい。
# --hints--
-`polynomialsWithOneIntegerRoot()` should return `1311109198529286`.
+`polynomialsWithOneIntegerRoot()` は `1311109198529286` を返す必要があります。
```js
assert.strictEqual(polynomialsWithOneIntegerRoot(), 1311109198529286);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
index 96a732ef77..6618d574eb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
@@ -1,6 +1,6 @@
---
id: 5900f47c1000cf542c50ff8e
-title: 'Problem 270: Cutting Squares'
+title: '問題 270: 正方形を切る'
challengeType: 5
forumTopicId: 301920
dashedName: problem-270-cutting-squares
@@ -8,21 +8,21 @@ dashedName: problem-270-cutting-squares
# --description--
-A square piece of paper with integer dimensions $N×N$ is placed with a corner at the origin and two of its sides along the $x$- and $y$-axes. Then, we cut it up respecting the following rules:
+整数寸法 $N×N$ を持つ正方形の紙片が座標上に置かれています。角は原点にあり、辺は $x$ 軸と $y$ 軸に沿っています。 次に、以下のルールに従って紙を切ります。
-- We only make straight cuts between two points lying on different sides of the square, and having integer coordinates.
-- Two cuts cannot cross, but several cuts can meet at the same border point.
-- Proceed until no more legal cuts can be made.
+- 正方形の異なる辺上にあり整数座標を持つ 2 つの点の間のみを、まっすぐ切る。
+- 2 本の切断線が交差してはいけないが、複数の切断線の端点が同じでも良い。
+- ルールに従った切り方がそれ以上できなくなるまで続ける。
-Counting any reflections or rotations as distinct, we call $C(N)$ the number of ways to cut an $N×N$ square. For example, $C(1) = 2$ and $C(2) = 30$ (shown below).
+反転または回転した図もすべて相異なる切り方として数え、$N×N$ の正方形の切り方の数を $C(N)$ とします。 例えば、$C(1) = 2$ であり、$C(2) = 30$ です (下図参照)。
- +
+ -What is $C(30)\bmod {10}^8$ ?
+$C(30)\bmod {10}^8$ を求めなさい。
# --hints--
-`cuttingSquares()` should return `82282080`.
+`cuttingSquares()` は `82282080` を返す必要があります。
```js
assert.strictEqual(cuttingSquares(), 82282080);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
index 1566254c63..7324517aeb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
@@ -1,6 +1,6 @@
---
id: 5900f47b1000cf542c50ff8d
-title: 'Problem 271: Modular Cubes, part 1'
+title: '問題 272: モジュラー立方数 (1)'
challengeType: 5
forumTopicId: 301921
dashedName: problem-271-modular-cubes-part-1
@@ -8,15 +8,15 @@ dashedName: problem-271-modular-cubes-part-1
# --description--
-For a positive number $n$, define $S(n)$ as the sum of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
+正の整数 $n$ について、$1 < x < n$ かつ $x^3 \equiv 1\bmod n$ であるような整数 $x$ の和を $S(n)$ とします。
-When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $S(91) = 9 + 16 + 22 + 29 + 53 + 74 + 79 + 81 = 363$.
+$n = 91$ のとき、考えられる $x$ の値は 9, 16, 22, 29, 53, 74, 79, 81 の 8 つです。 したがって、$S(91) = 9 + 16 + 22 + 29 + 53 + 74 + 79 + 81 = 363$ です。
-Find $S(13\\,082\\,761\\,331\\,670\\,030)$.
+$S(13\\,082\\,761\\,331\\,670\\,030)$ を求めなさい。
# --hints--
-`modularCubesOne()` should return `4617456485273130000`.
+`modularCubesOne()` は `4617456485273130000` を返す必要があります。
```js
assert.strictEqual(modularCubesOne(), 4617456485273130000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
index 136646718c..02bb672061 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
@@ -1,6 +1,6 @@
---
id: 5900f47d1000cf542c50ff8f
-title: 'Problem 272: Modular Cubes, part 2'
+title: '問題 272: モジュラー立方数 (2)'
challengeType: 5
forumTopicId: 301922
dashedName: problem-272-modular-cubes-part-2
@@ -8,15 +8,15 @@ dashedName: problem-272-modular-cubes-part-2
# --description--
-For a positive number $n$, define $C(n)$ as the number of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
+正の整数 $n$ について、$1 < x < n$ かつ $x^3 \equiv 1\bmod n$ であるような整数 $x$ の個数を $C(n)$ とします。
-When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $C(91) = 8$.
+$n = 91$ のとき、考えられる $x$ の値は 9, 16, 22, 29, 53, 74, 79, 81 の 8 つです。 したがって、$C(91) = 8$ です。
-Find the sum of the positive numbers $n ≤ {10}^{11}$ for which $C(n)=242$.
+$C(n)=242$ となる正の整数 $n ≤ {10}^{11}$ の和を求めなさい。
# --hints--
-`modularCubesTwo()` should return `8495585919506151000`.
+`modularCubesTwo()` は `8495585919506151000` を返す必要があります。
```js
assert.strictEqual(modularCubesTwo(), 8495585919506151000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
index f53c8f36ee..7353cd88e4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
@@ -1,6 +1,6 @@
---
id: 5900f47e1000cf542c50ff90
-title: 'Problem 273: Sum of Squares'
+title: '問題 273: 平方数の和'
challengeType: 5
forumTopicId: 301923
dashedName: problem-273-sum-of-squares
@@ -8,21 +8,21 @@ dashedName: problem-273-sum-of-squares
# --description--
-Consider equations of the form: $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
+式 $a^2 + b^2 = N$, $0 ≤ a ≤ b$ ($a$, $b$, $N$ は整数) について考えます。
-For $N = 65$ there are two solutions:
+$N = 65$ のとき、解は 2 つあります。
-$a = 1, b = 8$ and $a = 4, b = 7$.
+$a = 1, b = 8$ と、$a = 4, b = 7$ です。
-We call $S(N)$ the sum of the values of $a$ of all solutions of $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
+$a^2 + b^2 = N$, $0 ≤ a ≤ b$ ($a$, $b$, $N$ は整数) のすべての解の $a$ 値の和を $S(N)$ とします。
-Thus $S(65) = 1 + 4 = 5$.
+したがって、$S(65) = 1 + 4 = 5$ です。
-Find $\sum S(N)$, for all squarefree $N$ only divisible by primes of the form $4k + 1$ with $4k + 1 < 150$.
+$4k + 1 < 150$ のとき、$4k + 1$ で表される素数でのみ割り切れるすべての無平方数 $N$ について $\sum S(N)$ を求めなさい。
# --hints--
-`sumOfSquares()` should return `2032447591196869000`.
+`sumOfSquares()` は `2032447591196869000` を返す必要があります。
```js
assert.strictEqual(sumOfSquares(), 2032447591196869000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
index 8534028bc1..1a3cdd0873 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
@@ -1,6 +1,6 @@
---
id: 5900f47f1000cf542c50ff91
-title: 'Problem 274: Divisibility Multipliers'
+title: '問題 274: 整除乗数'
challengeType: 5
forumTopicId: 301924
dashedName: problem-274-divisibility-multipliers
@@ -8,25 +8,25 @@ dashedName: problem-274-divisibility-multipliers
# --description--
-For each integer $p > 1$ coprime to 10 there is a positive divisibility multiplier $m < p$ which preserves divisibility by $p$ for the following function on any positive integer, $n$:
+10 と互いに素な整数 $p > 1$ のそれぞれについて、任意の正の整数 $n$ の $p$ での整除性が次の関数に対しても維持されるような、正の整除乗数 (divisibility multiplier) $m < p$ が存在します。
-$f(n) = (\text{all but the last digit of} \\; n) + (\text{the last digit of} \\; n) \times m$
+$f(n) = (\\; n {\text{の最下位の桁以外すべて}) + (\\; n \text{の最下位の桁}) \times m$
-That is, if $m$ is the divisibility multiplier for $p$, then $f(n)$ is divisible by $p$ if and only if $n$ is divisible by $p$.
+つまり、$m$ が $p$ の整除乗数である場合、$f(n) が $p$ で整除できるための必要十分条件は $n$ が $p$ で整除できることです。
-(When $n$ is much larger than $p$, $f(n)$ will be less than $n$ and repeated application of $f$ provides a multiplicative divisibility test for $p$.)
+($n$ が $p$よりもはるかに大きい場合、$f(n)$ は $n$ よりも小さくなり、$f$ を繰り返し適用することで $p$ の乗法整除性を検証できます。)
-For example, the divisibility multiplier for 113 is 34.
+例えば、113 の 整除乗数は 34 です。
-$f(76275) = 7627 + 5 \times 34 = 7797$: 76275 and 7797 are both divisible by 113
+$f(76275) = 7627 + 5 \times 34 = 7797$: 76275 と 77977 はいずれも 113 で割り切れます。
-$f(12345) = 1234 + 5 \times 34 = 1404$: 12345 and 1404 are both not divisible by 113
+$f(12345) = 1234 + 5 \times 34 = 1404$: 12345 と 14047 はいずれも 113 で割り切れません。
-The sum of the divisibility multipliers for the primes that are coprime to 10 and less than 1000 is 39517. What is the sum of the divisibility multipliers for the primes that are coprime to 10 and less than ${10}^7$?
+10 と互いに素な 1000 未満の素数の、整除乗数の和は 39517 です。 10 と互いに素な ${10}^7$ 未満の素数の、整除乗数の和を求めなさい。
# --hints--
-`divisibilityMultipliers()` should return `1601912348822`.
+`divisibilityMultipliers()` は `1601912348822` を返す必要があります。
```js
assert.strictEqual(divisibilityMultipliers(), 1601912348822);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
index d195e25c2a..22e7cd40c2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
@@ -1,6 +1,6 @@
---
id: 5900f4801000cf542c50ff92
-title: 'Problem 275: Balanced Sculptures'
+title: '問題 275: 平衡な彫像'
challengeType: 5
forumTopicId: 301925
dashedName: problem-275-balanced-sculptures
@@ -8,24 +8,24 @@ dashedName: problem-275-balanced-sculptures
# --description--
-Let us define a balanced sculpture of order $n$ as follows:
+位数 $n$ の平衡な彫像を次のように定義します。
-- A polyomino made up of $n + 1$ tiles known as the blocks ($n$ tiles) and the plinth (remaining tile);
-- the plinth has its centre at position ($x = 0$, $y = 0$);
-- the blocks have $y$-coordinates greater than zero (so the plinth is the unique lowest tile);
-- the centre of mass of all the blocks, combined, has $x$-coordinate equal to zero.
+- ブロック ($n$ 枚のタイル) と台座 (残りのタイル) として知られる $n + 1$ 枚のタイルで構成されたポリオミノである。
+- 台座の中心は ($x = 0$, $y = 0$) に位置する。
+- ブロックの $y$ 座標は 0 より大きい (したがって台座は唯一の一番下のタイル)。
+- すべてのブロックを合わせたときの重心の $x$ 座標は 0 に等しい。
-When counting the sculptures, any arrangements which are simply reflections about the $y$-axis, are not counted as distinct. For example, the 18 balanced sculptures of order 6 are shown below; note that each pair of mirror images (about the $y$-axis) is counted as one sculpture:
+彫像を数えるとき、単に $y$ 軸で反転させた配置は区別されません。 例えば、位数 6 の平衡な彫像 18 個を下に示します。($y$ 軸で反転して) 鏡像となる各ペアが 1 つの彫像としてカウントされることに注意してください。
-
-What is $C(30)\bmod {10}^8$ ?
+$C(30)\bmod {10}^8$ を求めなさい。
# --hints--
-`cuttingSquares()` should return `82282080`.
+`cuttingSquares()` は `82282080` を返す必要があります。
```js
assert.strictEqual(cuttingSquares(), 82282080);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
index 1566254c63..7324517aeb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
@@ -1,6 +1,6 @@
---
id: 5900f47b1000cf542c50ff8d
-title: 'Problem 271: Modular Cubes, part 1'
+title: '問題 272: モジュラー立方数 (1)'
challengeType: 5
forumTopicId: 301921
dashedName: problem-271-modular-cubes-part-1
@@ -8,15 +8,15 @@ dashedName: problem-271-modular-cubes-part-1
# --description--
-For a positive number $n$, define $S(n)$ as the sum of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
+正の整数 $n$ について、$1 < x < n$ かつ $x^3 \equiv 1\bmod n$ であるような整数 $x$ の和を $S(n)$ とします。
-When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $S(91) = 9 + 16 + 22 + 29 + 53 + 74 + 79 + 81 = 363$.
+$n = 91$ のとき、考えられる $x$ の値は 9, 16, 22, 29, 53, 74, 79, 81 の 8 つです。 したがって、$S(91) = 9 + 16 + 22 + 29 + 53 + 74 + 79 + 81 = 363$ です。
-Find $S(13\\,082\\,761\\,331\\,670\\,030)$.
+$S(13\\,082\\,761\\,331\\,670\\,030)$ を求めなさい。
# --hints--
-`modularCubesOne()` should return `4617456485273130000`.
+`modularCubesOne()` は `4617456485273130000` を返す必要があります。
```js
assert.strictEqual(modularCubesOne(), 4617456485273130000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
index 136646718c..02bb672061 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
@@ -1,6 +1,6 @@
---
id: 5900f47d1000cf542c50ff8f
-title: 'Problem 272: Modular Cubes, part 2'
+title: '問題 272: モジュラー立方数 (2)'
challengeType: 5
forumTopicId: 301922
dashedName: problem-272-modular-cubes-part-2
@@ -8,15 +8,15 @@ dashedName: problem-272-modular-cubes-part-2
# --description--
-For a positive number $n$, define $C(n)$ as the number of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
+正の整数 $n$ について、$1 < x < n$ かつ $x^3 \equiv 1\bmod n$ であるような整数 $x$ の個数を $C(n)$ とします。
-When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $C(91) = 8$.
+$n = 91$ のとき、考えられる $x$ の値は 9, 16, 22, 29, 53, 74, 79, 81 の 8 つです。 したがって、$C(91) = 8$ です。
-Find the sum of the positive numbers $n ≤ {10}^{11}$ for which $C(n)=242$.
+$C(n)=242$ となる正の整数 $n ≤ {10}^{11}$ の和を求めなさい。
# --hints--
-`modularCubesTwo()` should return `8495585919506151000`.
+`modularCubesTwo()` は `8495585919506151000` を返す必要があります。
```js
assert.strictEqual(modularCubesTwo(), 8495585919506151000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
index f53c8f36ee..7353cd88e4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
@@ -1,6 +1,6 @@
---
id: 5900f47e1000cf542c50ff90
-title: 'Problem 273: Sum of Squares'
+title: '問題 273: 平方数の和'
challengeType: 5
forumTopicId: 301923
dashedName: problem-273-sum-of-squares
@@ -8,21 +8,21 @@ dashedName: problem-273-sum-of-squares
# --description--
-Consider equations of the form: $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
+式 $a^2 + b^2 = N$, $0 ≤ a ≤ b$ ($a$, $b$, $N$ は整数) について考えます。
-For $N = 65$ there are two solutions:
+$N = 65$ のとき、解は 2 つあります。
-$a = 1, b = 8$ and $a = 4, b = 7$.
+$a = 1, b = 8$ と、$a = 4, b = 7$ です。
-We call $S(N)$ the sum of the values of $a$ of all solutions of $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
+$a^2 + b^2 = N$, $0 ≤ a ≤ b$ ($a$, $b$, $N$ は整数) のすべての解の $a$ 値の和を $S(N)$ とします。
-Thus $S(65) = 1 + 4 = 5$.
+したがって、$S(65) = 1 + 4 = 5$ です。
-Find $\sum S(N)$, for all squarefree $N$ only divisible by primes of the form $4k + 1$ with $4k + 1 < 150$.
+$4k + 1 < 150$ のとき、$4k + 1$ で表される素数でのみ割り切れるすべての無平方数 $N$ について $\sum S(N)$ を求めなさい。
# --hints--
-`sumOfSquares()` should return `2032447591196869000`.
+`sumOfSquares()` は `2032447591196869000` を返す必要があります。
```js
assert.strictEqual(sumOfSquares(), 2032447591196869000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
index 8534028bc1..1a3cdd0873 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
@@ -1,6 +1,6 @@
---
id: 5900f47f1000cf542c50ff91
-title: 'Problem 274: Divisibility Multipliers'
+title: '問題 274: 整除乗数'
challengeType: 5
forumTopicId: 301924
dashedName: problem-274-divisibility-multipliers
@@ -8,25 +8,25 @@ dashedName: problem-274-divisibility-multipliers
# --description--
-For each integer $p > 1$ coprime to 10 there is a positive divisibility multiplier $m < p$ which preserves divisibility by $p$ for the following function on any positive integer, $n$:
+10 と互いに素な整数 $p > 1$ のそれぞれについて、任意の正の整数 $n$ の $p$ での整除性が次の関数に対しても維持されるような、正の整除乗数 (divisibility multiplier) $m < p$ が存在します。
-$f(n) = (\text{all but the last digit of} \\; n) + (\text{the last digit of} \\; n) \times m$
+$f(n) = (\\; n {\text{の最下位の桁以外すべて}) + (\\; n \text{の最下位の桁}) \times m$
-That is, if $m$ is the divisibility multiplier for $p$, then $f(n)$ is divisible by $p$ if and only if $n$ is divisible by $p$.
+つまり、$m$ が $p$ の整除乗数である場合、$f(n) が $p$ で整除できるための必要十分条件は $n$ が $p$ で整除できることです。
-(When $n$ is much larger than $p$, $f(n)$ will be less than $n$ and repeated application of $f$ provides a multiplicative divisibility test for $p$.)
+($n$ が $p$よりもはるかに大きい場合、$f(n)$ は $n$ よりも小さくなり、$f$ を繰り返し適用することで $p$ の乗法整除性を検証できます。)
-For example, the divisibility multiplier for 113 is 34.
+例えば、113 の 整除乗数は 34 です。
-$f(76275) = 7627 + 5 \times 34 = 7797$: 76275 and 7797 are both divisible by 113
+$f(76275) = 7627 + 5 \times 34 = 7797$: 76275 と 77977 はいずれも 113 で割り切れます。
-$f(12345) = 1234 + 5 \times 34 = 1404$: 12345 and 1404 are both not divisible by 113
+$f(12345) = 1234 + 5 \times 34 = 1404$: 12345 と 14047 はいずれも 113 で割り切れません。
-The sum of the divisibility multipliers for the primes that are coprime to 10 and less than 1000 is 39517. What is the sum of the divisibility multipliers for the primes that are coprime to 10 and less than ${10}^7$?
+10 と互いに素な 1000 未満の素数の、整除乗数の和は 39517 です。 10 と互いに素な ${10}^7$ 未満の素数の、整除乗数の和を求めなさい。
# --hints--
-`divisibilityMultipliers()` should return `1601912348822`.
+`divisibilityMultipliers()` は `1601912348822` を返す必要があります。
```js
assert.strictEqual(divisibilityMultipliers(), 1601912348822);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
index d195e25c2a..22e7cd40c2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
@@ -1,6 +1,6 @@
---
id: 5900f4801000cf542c50ff92
-title: 'Problem 275: Balanced Sculptures'
+title: '問題 275: 平衡な彫像'
challengeType: 5
forumTopicId: 301925
dashedName: problem-275-balanced-sculptures
@@ -8,24 +8,24 @@ dashedName: problem-275-balanced-sculptures
# --description--
-Let us define a balanced sculpture of order $n$ as follows:
+位数 $n$ の平衡な彫像を次のように定義します。
-- A polyomino made up of $n + 1$ tiles known as the blocks ($n$ tiles) and the plinth (remaining tile);
-- the plinth has its centre at position ($x = 0$, $y = 0$);
-- the blocks have $y$-coordinates greater than zero (so the plinth is the unique lowest tile);
-- the centre of mass of all the blocks, combined, has $x$-coordinate equal to zero.
+- ブロック ($n$ 枚のタイル) と台座 (残りのタイル) として知られる $n + 1$ 枚のタイルで構成されたポリオミノである。
+- 台座の中心は ($x = 0$, $y = 0$) に位置する。
+- ブロックの $y$ 座標は 0 より大きい (したがって台座は唯一の一番下のタイル)。
+- すべてのブロックを合わせたときの重心の $x$ 座標は 0 に等しい。
-When counting the sculptures, any arrangements which are simply reflections about the $y$-axis, are not counted as distinct. For example, the 18 balanced sculptures of order 6 are shown below; note that each pair of mirror images (about the $y$-axis) is counted as one sculpture:
+彫像を数えるとき、単に $y$ 軸で反転させた配置は区別されません。 例えば、位数 6 の平衡な彫像 18 個を下に示します。($y$ 軸で反転して) 鏡像となる各ペアが 1 つの彫像としてカウントされることに注意してください。
-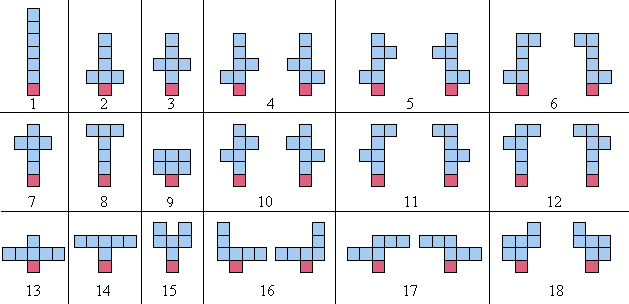 +
+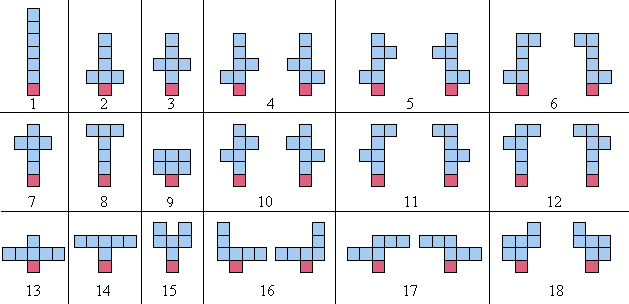 -There are 964 balanced sculptures of order 10 and 360505 of order 15.
+位数 10 の平衡な彫像は 964 個、位数 15 の平衡な彫像は 360505 個あります。
-How many balanced sculptures are there of order 18?
+位数 18 の平衡な彫像はいくつありますか。
# --hints--
-`balancedSculptures()` should return `15030564`.
+`balancedSculptures()` は `15030564` を返す必要があります。
```js
assert.strictEqual(balancedSculptures(), 15030564);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
index b5e187731b..d16a0b0fd3 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4801000cf542c50ff93
-title: 'Problem 276: Primitive Triangles'
+title: '問題 276: 原始的な三角形'
challengeType: 5
forumTopicId: 301926
dashedName: problem-276-primitive-triangles
@@ -8,15 +8,15 @@ dashedName: problem-276-primitive-triangles
# --description--
-Consider the triangles with integer sides $a$, $b$ and $c$ with $a ≤ b ≤ c$.
+整数辺 $a$, $b$, $c$ ($a ≤ b ≤ c$) を持つ三角形を考えます。
-An integer sided triangle $(a,b,c)$ is called primitive if $gcd(a,b,c) = 1$.
+$gcd(a,b,c) = 1$ が成り立つとき、整数辺を持つ三角形 $(a,b,c)$ は「原始的」(primitive) であると呼ばれます。
-How many primitive integer sided triangles exist with a perimeter not exceeding $10\\,000\\,000$?
+周長が $10\\,000\\,000$ 以下、辺長が整数、かつ原始的である三角形はいくつありますか。
# --hints--
-`primitiveTriangles()` should return `5777137137739633000`.
+`primitiveTriangles()` は `5777137137739633000` を返す必要があります。
```js
assert.strictEqual(primitiveTriangles(), 5777137137739633000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
index 108215479e..d9fbf6f559 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4811000cf542c50ff94
-title: 'Problem 277: A Modified Collatz sequence'
+title: '問題 277: 変形コラッツ数列'
challengeType: 5
forumTopicId: 301927
dashedName: problem-277-a-modified-collatz-sequence
@@ -8,29 +8,29 @@ dashedName: problem-277-a-modified-collatz-sequence
# --description--
-A modified Collatz sequence of integers is obtained from a starting value $a_1$ in the following way:
+整数の変形コラッツ列は、開始値 $a_1$ から次のようにして得られます。
-$a_{n + 1} = \frac{a_n}{3}$ if $a_n$ is divisible by 3. We shall denote this as a large downward step, "D".
+$a_n$ が 3 で割り切れる場合、$a_{n + 1} = \frac{a_n}{3}$ です。 これを、大きな下向きのステップ "D"と表すことにします。
-$a_{n + 1} = \frac{4a_n + 2}{3}$ if $a_n$ divided by 3 gives a remainder of 1. We shall denote this as an upward step, "U".
+$a_n$ を 3 で割ると 1 余る場合、$a_{n + 1} = \frac{4a_n + 2}{3}$ です。 これを、大きな上向きのステップ "U" と表すことにします。
-$a_{n + 1} = \frac{2a_n - 1}{3}$ if $a_n$ divided by 3 gives a remainder of 2. We shall denote this as a small downward step, "d".
+$a_n$ を 3 で割ると 2 余る場合、$a_{n + 1} = \frac{2a_n - 1}{3}$ です。 これを、小さな下向きのステップ "d" と表すことにします。
-The sequence terminates when some $a_n = 1$.
+この数列は $a_n = 1$ のときに終了します。
-Given any integer, we can list out the sequence of steps. For instance if $a_1 = 231$, then the sequence $\\{a_n\\} = \\{231, 77, 51, 17, 11, 7, 10, 14, 9, 3, 1\\}$ corresponds to the steps "DdDddUUdDD".
+任意の整数について、ステップの数列を列挙できます。 例えば $a_1 = 231$ の場合、数列 $\\{a_n\\} = \\{231, 77, 51, 17, 11, 7, 10, 14, 9, 3, 1\\}$ は "DdDddUUdDD" に相当します。
-Of course, there are other sequences that begin with that same sequence "DdDddUUdDD....".
+もちろん、同じ数列 "DdDddUUdDD...." で始まる数列は他にもあります。
-For instance, if $a_1 = 1004064$, then the sequence is DdDddUUdDDDdUDUUUdDdUUDDDUdDD.
+例えば、$a_1 = 1004064$ の場合、数列は DdDddUUdDDDdUDUUUdDdUUDDDUdDD です。
-In fact, 1004064 is the smallest possible $a_1 > {10}^6$ that begins with the sequence DdDddUUdDD.
+実は、1004064 は数列 DdDddUUdDD から始まる最小の $a_1 > {10}^6$ です。
-What is the smallest $a_1 > {10}^{15}$ that begins with the sequence "UDDDUdddDDUDDddDdDddDDUDDdUUDd"?
+"UDDDUdddDDUDDddDdDddDDUDDdUUDd" で始まる最小の $a_1 > {10}^{15}$を求めなさい。
# --hints--
-`modifiedCollatzSequence()` should return `1125977393124310`.
+`modifiedCollatzSequence()` は `1125977393124310` を返す必要があります。
```js
assert.strictEqual(modifiedCollatzSequence(), 1125977393124310);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
index 19e3042fdb..df977450ff 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
@@ -1,6 +1,6 @@
---
id: 5900f4831000cf542c50ff95
-title: 'Problem 278: Linear Combinations of Semiprimes'
+title: '問題 278: 半素数の線型結合'
challengeType: 5
forumTopicId: 301928
dashedName: problem-278-linear-combinations-of-semiprimes
@@ -8,17 +8,17 @@ dashedName: problem-278-linear-combinations-of-semiprimes
# --description--
-Given the values of integers $1 < a_1 < a_2 < \ldots < a_n$, consider the linear combination $q_1a_1 + q_2a_2 + \ldots + q_na_n = b$, using only integer values $q_k ≥ 0$.
+整数 $1 < a_1 < a_2 < \ldots < a_n$ について、整数値 $q_k ≥ 0$ のみを使った線形結合 $q_1a_1 + q_2a_2 + \ldots + q_na_n = b$ を考えます。
-Note that for a given set of $a_k$, it may be that not all values of $b$ are possible. For instance, if $a_1 = 5$ and $a_2 = 7$, there are no $q_1 ≥ 0$ and $q_2 ≥ 0$ such that $b$ could be 1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18 or 23.
+なお、与えられた $a_k$ の組に対し、すべての $b$ 値が可能とは限りません。 例えば、$a_1 = 5$ かつ $a_2 = 7$ の場合、$b$ が 1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18, 23 のいずれかになり得るような $q_1 ≥ 0$ と $q_2 ≥ 0$ は存在しません。
-In fact, 23 is the largest impossible value of $b$ for $a_1 = 5$ and $a_2 = 7$. We therefore call $f(5, 7) = 23$. Similarly, it can be shown that $f(6, 10, 15)=29$ and $f(14, 22, 77) = 195$.
+実際、$a_1 = 5$ かつ $a_2 = 7$ に対して $b$ 値になり得ない最大の数は 23 です。 これを $f(5, 7) = 23$ と定義します。 同様に、$f(6, 10, 15) = 29$ および $f(14, 22, 77) = 195$ であることを示せます。
-Find $\sum f(pq,pr,qr)$, where $p$, $q$ and $r$ are prime numbers and $p < q < r < 5000$.
+$p$, $q$, $r$ が素数であり $p < q < r < 5000$ のとき、$\sum f(pq,pr,qr)$ を求めなさい。
# --hints--
-`linearCombinationOfSemiprimes()` should return `1228215747273908500`.
+`linearCombinationOfSemiprimes()` は `1228215747273908500` を返す必要があります。
```js
assert.strictEqual(linearCombinationOfSemiprimes(), 1228215747273908500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
index c83c6736f4..d4af2ebf71 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
@@ -1,6 +1,6 @@
---
id: 5900f4841000cf542c50ff96
-title: 'Problem 279: Triangles with integral sides and an integral angle'
+title: '問題 279: 辺と角度が整数である三角形'
challengeType: 5
forumTopicId: 301929
dashedName: problem-279-triangles-with-integral-sides-and-an-integral-angle
@@ -8,11 +8,11 @@ dashedName: problem-279-triangles-with-integral-sides-and-an-integral-angle
# --description--
-How many triangles are there with integral sides, at least one integral angle (measured in degrees), and a perimeter that does not exceed ${10}^8$?
+3 辺の長さが整数であり、少なくとも 1 つの角度 (度単位で測定) が整数であり、かつ、周長が ${10}^8$ を超えない三角形はいくつありますか。
# --hints--
-`trianglesWithIntegralSidesAndAngle()` should return `416577688`.
+`trianglesWithIntegralSidesAndAngle()` は `416577688` を返す必要があります。
```js
assert.strictEqual(trianglesWithIntegralSidesAndAngle(), 416577688);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
index 7aec32e7cc..57462446da 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
@@ -1,6 +1,6 @@
---
id: 5900f4841000cf542c50ff97
-title: 'Problem 280: Ant and seeds'
+title: '問題 280: アリと種'
challengeType: 5
forumTopicId: 301931
dashedName: problem-280-ant-and-seeds
@@ -8,15 +8,15 @@ dashedName: problem-280-ant-and-seeds
# --description--
-A laborious ant walks randomly on a 5x5 grid. The walk starts from the central square. At each step, the ant moves to an adjacent square at random, without leaving the grid; thus there are 2, 3 or 4 possible moves at each step depending on the ant's position.
+働き者のアリが 5x5 の格子上を不規則に歩きます。 中央のマスから出発します。 各ステップで、アリは格子を離れることなく、不規則に隣のマスに移動します。したがって、アリの位置に応じて各ステップで 2 通り、3 通り、または 4 通りの動き方があります。
-At the start of the walk, a seed is placed on each square of the lower row. When the ant isn't carrying a seed and reaches a square of the lower row containing a seed, it will start to carry the seed. The ant will drop the seed on the first empty square of the upper row it eventually reaches.
+アリが歩き始めると、より下の列の各マスに種が置かれます。 種の運搬中でないアリは、より下の列の、種のあるマスに達すると種を運び始めます。 そして、最終的に到達する、より上の列にある最初の空のマスに種を下ろします。
-What's the expected number of steps until all seeds have been dropped in the top row? Give your answer rounded to 6 decimal places.
+すべての種が最上列に下ろされるまでの期待ステップ数を求めなさい。 回答は、四捨五入して小数第 6 位まで示すこと。
# --hints--
-`antAndSeeds()` should return `430.088247`.
+`antAndSeeds()` は `430.088247` を返す必要があります。
```js
assert.strictEqual(antAndSeeds(), 430.088247);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
index 0db2a589c3..c1f0edf36a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
@@ -1,6 +1,6 @@
---
id: 5900f4861000cf542c50ff98
-title: 'Problem 281: Pizza Toppings'
+title: '問題 281: ピザのトッピング'
challengeType: 5
forumTopicId: 301932
dashedName: problem-281-pizza-toppings
@@ -8,19 +8,19 @@ dashedName: problem-281-pizza-toppings
# --description--
-You are given a pizza (perfect circle) that has been cut into $m·n$ equal pieces and you want to have exactly one topping on each slice.
+ピザ (完全な円) を $m·n$ 枚のスライスに等分し、各スライスにちょうど 1 つずつトッピングを載せます。
-Let $f(m,n)$ denote the number of ways you can have toppings on the pizza with $m$ different toppings ($m ≥ 2$), using each topping on exactly $n$ slices ($n ≥ 1$). Reflections are considered distinct, rotations are not.
+ちょうど $n$ 枚のスライス ($n ≥ 1$) にそれぞれのトッピングを使って、$m$ 種類のトッピング ($m ≥ 2$) でピザにトッピングを載せる方法が何通りあるかを、$f(m,n)$ で表します。 反転させたものは相異なるとみなされますが、回転させたものは同一とみなされます。
-Thus, for instance, $f(2,1) = 1$, $f(2,2) = f(3,1) = 2$ and $f(3,2) = 16$. $f(3,2)$ is shown below:
+例えば、$f(2,1) = 1$, $f(2,2) = f(3,1) = 2$, $f(3,2) = 16$ です。 $f(3,2)$ を下に示します。
-
-There are 964 balanced sculptures of order 10 and 360505 of order 15.
+位数 10 の平衡な彫像は 964 個、位数 15 の平衡な彫像は 360505 個あります。
-How many balanced sculptures are there of order 18?
+位数 18 の平衡な彫像はいくつありますか。
# --hints--
-`balancedSculptures()` should return `15030564`.
+`balancedSculptures()` は `15030564` を返す必要があります。
```js
assert.strictEqual(balancedSculptures(), 15030564);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
index b5e187731b..d16a0b0fd3 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4801000cf542c50ff93
-title: 'Problem 276: Primitive Triangles'
+title: '問題 276: 原始的な三角形'
challengeType: 5
forumTopicId: 301926
dashedName: problem-276-primitive-triangles
@@ -8,15 +8,15 @@ dashedName: problem-276-primitive-triangles
# --description--
-Consider the triangles with integer sides $a$, $b$ and $c$ with $a ≤ b ≤ c$.
+整数辺 $a$, $b$, $c$ ($a ≤ b ≤ c$) を持つ三角形を考えます。
-An integer sided triangle $(a,b,c)$ is called primitive if $gcd(a,b,c) = 1$.
+$gcd(a,b,c) = 1$ が成り立つとき、整数辺を持つ三角形 $(a,b,c)$ は「原始的」(primitive) であると呼ばれます。
-How many primitive integer sided triangles exist with a perimeter not exceeding $10\\,000\\,000$?
+周長が $10\\,000\\,000$ 以下、辺長が整数、かつ原始的である三角形はいくつありますか。
# --hints--
-`primitiveTriangles()` should return `5777137137739633000`.
+`primitiveTriangles()` は `5777137137739633000` を返す必要があります。
```js
assert.strictEqual(primitiveTriangles(), 5777137137739633000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
index 108215479e..d9fbf6f559 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4811000cf542c50ff94
-title: 'Problem 277: A Modified Collatz sequence'
+title: '問題 277: 変形コラッツ数列'
challengeType: 5
forumTopicId: 301927
dashedName: problem-277-a-modified-collatz-sequence
@@ -8,29 +8,29 @@ dashedName: problem-277-a-modified-collatz-sequence
# --description--
-A modified Collatz sequence of integers is obtained from a starting value $a_1$ in the following way:
+整数の変形コラッツ列は、開始値 $a_1$ から次のようにして得られます。
-$a_{n + 1} = \frac{a_n}{3}$ if $a_n$ is divisible by 3. We shall denote this as a large downward step, "D".
+$a_n$ が 3 で割り切れる場合、$a_{n + 1} = \frac{a_n}{3}$ です。 これを、大きな下向きのステップ "D"と表すことにします。
-$a_{n + 1} = \frac{4a_n + 2}{3}$ if $a_n$ divided by 3 gives a remainder of 1. We shall denote this as an upward step, "U".
+$a_n$ を 3 で割ると 1 余る場合、$a_{n + 1} = \frac{4a_n + 2}{3}$ です。 これを、大きな上向きのステップ "U" と表すことにします。
-$a_{n + 1} = \frac{2a_n - 1}{3}$ if $a_n$ divided by 3 gives a remainder of 2. We shall denote this as a small downward step, "d".
+$a_n$ を 3 で割ると 2 余る場合、$a_{n + 1} = \frac{2a_n - 1}{3}$ です。 これを、小さな下向きのステップ "d" と表すことにします。
-The sequence terminates when some $a_n = 1$.
+この数列は $a_n = 1$ のときに終了します。
-Given any integer, we can list out the sequence of steps. For instance if $a_1 = 231$, then the sequence $\\{a_n\\} = \\{231, 77, 51, 17, 11, 7, 10, 14, 9, 3, 1\\}$ corresponds to the steps "DdDddUUdDD".
+任意の整数について、ステップの数列を列挙できます。 例えば $a_1 = 231$ の場合、数列 $\\{a_n\\} = \\{231, 77, 51, 17, 11, 7, 10, 14, 9, 3, 1\\}$ は "DdDddUUdDD" に相当します。
-Of course, there are other sequences that begin with that same sequence "DdDddUUdDD....".
+もちろん、同じ数列 "DdDddUUdDD...." で始まる数列は他にもあります。
-For instance, if $a_1 = 1004064$, then the sequence is DdDddUUdDDDdUDUUUdDdUUDDDUdDD.
+例えば、$a_1 = 1004064$ の場合、数列は DdDddUUdDDDdUDUUUdDdUUDDDUdDD です。
-In fact, 1004064 is the smallest possible $a_1 > {10}^6$ that begins with the sequence DdDddUUdDD.
+実は、1004064 は数列 DdDddUUdDD から始まる最小の $a_1 > {10}^6$ です。
-What is the smallest $a_1 > {10}^{15}$ that begins with the sequence "UDDDUdddDDUDDddDdDddDDUDDdUUDd"?
+"UDDDUdddDDUDDddDdDddDDUDDdUUDd" で始まる最小の $a_1 > {10}^{15}$を求めなさい。
# --hints--
-`modifiedCollatzSequence()` should return `1125977393124310`.
+`modifiedCollatzSequence()` は `1125977393124310` を返す必要があります。
```js
assert.strictEqual(modifiedCollatzSequence(), 1125977393124310);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
index 19e3042fdb..df977450ff 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
@@ -1,6 +1,6 @@
---
id: 5900f4831000cf542c50ff95
-title: 'Problem 278: Linear Combinations of Semiprimes'
+title: '問題 278: 半素数の線型結合'
challengeType: 5
forumTopicId: 301928
dashedName: problem-278-linear-combinations-of-semiprimes
@@ -8,17 +8,17 @@ dashedName: problem-278-linear-combinations-of-semiprimes
# --description--
-Given the values of integers $1 < a_1 < a_2 < \ldots < a_n$, consider the linear combination $q_1a_1 + q_2a_2 + \ldots + q_na_n = b$, using only integer values $q_k ≥ 0$.
+整数 $1 < a_1 < a_2 < \ldots < a_n$ について、整数値 $q_k ≥ 0$ のみを使った線形結合 $q_1a_1 + q_2a_2 + \ldots + q_na_n = b$ を考えます。
-Note that for a given set of $a_k$, it may be that not all values of $b$ are possible. For instance, if $a_1 = 5$ and $a_2 = 7$, there are no $q_1 ≥ 0$ and $q_2 ≥ 0$ such that $b$ could be 1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18 or 23.
+なお、与えられた $a_k$ の組に対し、すべての $b$ 値が可能とは限りません。 例えば、$a_1 = 5$ かつ $a_2 = 7$ の場合、$b$ が 1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18, 23 のいずれかになり得るような $q_1 ≥ 0$ と $q_2 ≥ 0$ は存在しません。
-In fact, 23 is the largest impossible value of $b$ for $a_1 = 5$ and $a_2 = 7$. We therefore call $f(5, 7) = 23$. Similarly, it can be shown that $f(6, 10, 15)=29$ and $f(14, 22, 77) = 195$.
+実際、$a_1 = 5$ かつ $a_2 = 7$ に対して $b$ 値になり得ない最大の数は 23 です。 これを $f(5, 7) = 23$ と定義します。 同様に、$f(6, 10, 15) = 29$ および $f(14, 22, 77) = 195$ であることを示せます。
-Find $\sum f(pq,pr,qr)$, where $p$, $q$ and $r$ are prime numbers and $p < q < r < 5000$.
+$p$, $q$, $r$ が素数であり $p < q < r < 5000$ のとき、$\sum f(pq,pr,qr)$ を求めなさい。
# --hints--
-`linearCombinationOfSemiprimes()` should return `1228215747273908500`.
+`linearCombinationOfSemiprimes()` は `1228215747273908500` を返す必要があります。
```js
assert.strictEqual(linearCombinationOfSemiprimes(), 1228215747273908500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
index c83c6736f4..d4af2ebf71 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
@@ -1,6 +1,6 @@
---
id: 5900f4841000cf542c50ff96
-title: 'Problem 279: Triangles with integral sides and an integral angle'
+title: '問題 279: 辺と角度が整数である三角形'
challengeType: 5
forumTopicId: 301929
dashedName: problem-279-triangles-with-integral-sides-and-an-integral-angle
@@ -8,11 +8,11 @@ dashedName: problem-279-triangles-with-integral-sides-and-an-integral-angle
# --description--
-How many triangles are there with integral sides, at least one integral angle (measured in degrees), and a perimeter that does not exceed ${10}^8$?
+3 辺の長さが整数であり、少なくとも 1 つの角度 (度単位で測定) が整数であり、かつ、周長が ${10}^8$ を超えない三角形はいくつありますか。
# --hints--
-`trianglesWithIntegralSidesAndAngle()` should return `416577688`.
+`trianglesWithIntegralSidesAndAngle()` は `416577688` を返す必要があります。
```js
assert.strictEqual(trianglesWithIntegralSidesAndAngle(), 416577688);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
index 7aec32e7cc..57462446da 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
@@ -1,6 +1,6 @@
---
id: 5900f4841000cf542c50ff97
-title: 'Problem 280: Ant and seeds'
+title: '問題 280: アリと種'
challengeType: 5
forumTopicId: 301931
dashedName: problem-280-ant-and-seeds
@@ -8,15 +8,15 @@ dashedName: problem-280-ant-and-seeds
# --description--
-A laborious ant walks randomly on a 5x5 grid. The walk starts from the central square. At each step, the ant moves to an adjacent square at random, without leaving the grid; thus there are 2, 3 or 4 possible moves at each step depending on the ant's position.
+働き者のアリが 5x5 の格子上を不規則に歩きます。 中央のマスから出発します。 各ステップで、アリは格子を離れることなく、不規則に隣のマスに移動します。したがって、アリの位置に応じて各ステップで 2 通り、3 通り、または 4 通りの動き方があります。
-At the start of the walk, a seed is placed on each square of the lower row. When the ant isn't carrying a seed and reaches a square of the lower row containing a seed, it will start to carry the seed. The ant will drop the seed on the first empty square of the upper row it eventually reaches.
+アリが歩き始めると、より下の列の各マスに種が置かれます。 種の運搬中でないアリは、より下の列の、種のあるマスに達すると種を運び始めます。 そして、最終的に到達する、より上の列にある最初の空のマスに種を下ろします。
-What's the expected number of steps until all seeds have been dropped in the top row? Give your answer rounded to 6 decimal places.
+すべての種が最上列に下ろされるまでの期待ステップ数を求めなさい。 回答は、四捨五入して小数第 6 位まで示すこと。
# --hints--
-`antAndSeeds()` should return `430.088247`.
+`antAndSeeds()` は `430.088247` を返す必要があります。
```js
assert.strictEqual(antAndSeeds(), 430.088247);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
index 0db2a589c3..c1f0edf36a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
@@ -1,6 +1,6 @@
---
id: 5900f4861000cf542c50ff98
-title: 'Problem 281: Pizza Toppings'
+title: '問題 281: ピザのトッピング'
challengeType: 5
forumTopicId: 301932
dashedName: problem-281-pizza-toppings
@@ -8,19 +8,19 @@ dashedName: problem-281-pizza-toppings
# --description--
-You are given a pizza (perfect circle) that has been cut into $m·n$ equal pieces and you want to have exactly one topping on each slice.
+ピザ (完全な円) を $m·n$ 枚のスライスに等分し、各スライスにちょうど 1 つずつトッピングを載せます。
-Let $f(m,n)$ denote the number of ways you can have toppings on the pizza with $m$ different toppings ($m ≥ 2$), using each topping on exactly $n$ slices ($n ≥ 1$). Reflections are considered distinct, rotations are not.
+ちょうど $n$ 枚のスライス ($n ≥ 1$) にそれぞれのトッピングを使って、$m$ 種類のトッピング ($m ≥ 2$) でピザにトッピングを載せる方法が何通りあるかを、$f(m,n)$ で表します。 反転させたものは相異なるとみなされますが、回転させたものは同一とみなされます。
-Thus, for instance, $f(2,1) = 1$, $f(2,2) = f(3,1) = 2$ and $f(3,2) = 16$. $f(3,2)$ is shown below:
+例えば、$f(2,1) = 1$, $f(2,2) = f(3,1) = 2$, $f(3,2) = 16$ です。 $f(3,2)$ を下に示します。
-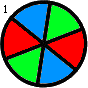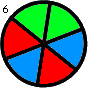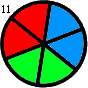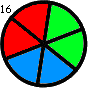 +
+ -Find the sum of all $f(m,n)$ such that $f(m,n) ≤ {10}^{15}$.
+$f(m,n) ≤ {10}^{15}$ となる $f(m,n)$ の総和を求めなさい。
# --hints--
-`pizzaToppings()` should return `1485776387445623`.
+`pizzaToppings()` は `1485776387445623` を返す必要があります。
```js
assert.strictEqual(pizzaToppings(), 1485776387445623);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
index af033cdcf7..882a20ba3a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4861000cf542c50ff99
-title: 'Problem 282: The Ackermann function'
+title: '問題 282: アッカーマン関数'
challengeType: 5
forumTopicId: 301933
dashedName: problem-282-the-ackermann-function
@@ -8,17 +8,17 @@ dashedName: problem-282-the-ackermann-function
# --description--
-For non-negative integers $m$, $n$, the Ackermann function $A(m, n)$ is defined as follows:
+負でない整数 $m$, $n$ に対して、アッカーマン関数 $A(m, n)$ は次のように定義されます。
-$$A(m, n) = \begin{cases} n + 1 & \text{if $m = 0$} \\\\ A(m - 1, 1) & \text{if $m > 0$ and $n = 0$} \\\\ A(m - 1, A(m, n - 1)) & \text{if $m > 0$ and $n > 0$} \end{cases}$$
+$$A(m, n) = \begin{cases} n + 1 & \text{$m = 0$ の場合} \\\\ A(m - 1, 1) & \text{$m > 0$ かつ $n = 0$ の場合} \\\\ A(m - 1, A(m, n - 1)) & \text{$m > 0$ かつ $n > 0$ の場合} \end{cases}$$
-For example $A(1, 0) = 2$, $A(2, 2) = 7$ and $A(3, 4) = 125$.
+例えば、$A(1, 0) = 2$, $A(2, 2) = 7$, $A(3, 4) = 125$ です。
-Find $\displaystyle\sum_{n = 0}^6 A(n, n)$ and give your answer mod ${14}^8$.
+$\displaystyle\sum_{n = 0}^6 A(n, n)$ を求め、mod ${14}^8$ で答えなさい。
# --hints--
-`ackermanFunction()` should return `1098988351`.
+`ackermanFunction()` は `1098988351` を返す必要があります。
```js
assert.strictEqual(ackermanFunction(), 1098988351);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
index d88415d481..419c29163e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
@@ -1,7 +1,7 @@
---
id: 5900f4881000cf542c50ff9a
title: >-
- Problem 283: Integer sided triangles for which the area / perimeter ratio is integral
+ 問題 283: 面積 / 周長の比率が整数である整数辺三角形
challengeType: 5
forumTopicId: 301934
dashedName: >-
@@ -10,19 +10,19 @@ dashedName: >-
# --description--
-Consider the triangle with sides 6, 8 and 10. It can be seen that the perimeter and the area are both equal to 24.
+辺の長さが 6, 8, 10 である三角形について考えます。 周長と面積がともに 24 に等しいことが分かります。
-So the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 1.
+したがって、$\frac{\text{面積}}{\text{周長}}$ の比率は 1 です。
-Consider also the triangle with sides 13, 14 and 15. The perimeter equals 42 while the area is equal to 84.
+辺 13, 14, 15 の三角形についても考えます。 周長は 42、面積は 84 です。
-So for this triangle the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 2.
+したがって、この三角形の $\frac{\text{面積}}{\text{周長}}$ の比率は 2 です。
-Find the sum of the perimeters of all integer sided triangles for which the area/perimeter ratios are equal to positive integers not exceeding 1000.
+面積 / 周長の比率が 1000 以下の正の整数に等しくなるようなすべての整数三角形について、それらの周長の和を求めなさい。
# --hints--
-`integralAreaPerimeterRatio()` should return `28038042525570324`.
+`integralAreaPerimeterRatio()` は `28038042525570324` を返す必要があります。
```js
assert.strictEqual(integralAreaPerimeterRatio(), 28038042525570324);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
index 417ddd2948..9b47aa1ddb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
@@ -1,6 +1,6 @@
---
id: 5900f4891000cf542c50ff9b
-title: 'Problem 284: Steady Squares'
+title: '問題 284: 安定平方数'
challengeType: 5
forumTopicId: 301935
dashedName: problem-284-steady-squares
@@ -8,23 +8,23 @@ dashedName: problem-284-steady-squares
# --description--
-The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: ${376}^2 = 141376$. Let's call a number with this property a steady square.
+3 桁の 10 進数 376 は、その平方数の下位桁がそれ自体と同じである (${376}^2 = 141376$) という、特殊な性質を持つ数の一例です。 この性質を持つ数を「安定平方数」と呼ぶことにします。
-Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number $c37$ is also a steady square: $c37^2 = aa0c37$, and the sum of its digits is $c+3+7=18$ in the same numbering system. The letters $a$, $b$, $c$ and $d$ are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
+安定平方数は他の進数でも現れます。 3 桁の14 進数 $c37$ も安定平方数であり、$c37^2 = aa0c37$ となります。また、その各位の和は 14 進数で $c+3+7=18$ です。 文字 $a$, $b$, $c$, $d$ はそれぞれ 10, 11, 12, 13 を表すのに使われます。これは 16 進数と同様の方法です。
-For $1 ≤ n ≤ 9$, the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system is $2d8$ (582 decimal). Steady squares with leading 0's are not allowed.
+$1 ≤ n ≤ 9$ のとき、すべての $n$ 桁の 14 進数の安定平方数の各位の和は $2d8$ (10 進数で 582) です。 先行ゼロを持つ安定平方数は許容されません。
-Find the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system for $1 ≤ n ≤ 10000$ (decimal) and give your answer as a string in the base 14 system using lower case letters where necessary.
+$1 ≤ n ≤ 10000$ (10進数) のとき、$n$ 桁の安定平方数 (14 進数) のすべてについて各位の和を求め、適宜、小文字の文字を使用して 14 進数の文字列で答えなさい。
# --hints--
-`steadySquares()` should return a string.
+`steadySquares()` は文字列を返す必要があります。
```js
assert(typeof steadySquares() === 'string');
```
-`steadySquares()` should return the string `5a411d7b`.
+`steadySquares()` は文字列 `5a411d7b` を返す必要があります。
```js
assert.strictEqual(steadySquares(), '5a411d7b');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
index ad75e381a1..935dd194d2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
@@ -1,6 +1,6 @@
---
id: 5900f48a1000cf542c50ff9c
-title: 'Problem 285: Pythagorean odds'
+title: '問題 285: ピタゴラスオッズ'
challengeType: 5
forumTopicId: 301936
dashedName: problem-285-pythagorean-odds
@@ -8,19 +8,19 @@ dashedName: problem-285-pythagorean-odds
# --description--
-Albert chooses a positive integer $k$, then two real numbers $a$, $b$ are randomly chosen in the interval [0,1] with uniform distribution.
+アルバートが正の整数 $k$ を 1 つ選ぶと、一様分布の区間 [0,1] から 2 つの実数 $a$, $b$ が無作為に選ばれます。
-The square root of the sum ${(ka + 1)}^2 + {(kb + 1)}^2$ is then computed and rounded to the nearest integer. If the result is equal to $k$, he scores $k$ points; otherwise he scores nothing.
+次に、和 ${(ka + 1)}^2 + {(kb + 1)}^2$ の平方根が計算され、最も近い整数に丸められます。 結果が $k$ に等しければ $k$ 点を獲得し、それ以外は 0 点です。
-For example, if $k = 6$, $a = 0.2$ and $b = 0.85$, then ${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to $k$, so he scores 6 points.
+例えば、$k = 6$, $a = 0.2$, $b = 0.85$ の場合、${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$ です。 42.05 の平方根は 6.484... で、最も近い整数に四捨五入すると 6 になります。 これは $k$ に等しいので、6 点を獲得します。
-It can be shown that if he plays 10 turns with $k = 1, k = 2, \ldots, k = 10$, the expected value of his total score, rounded to five decimal places, is 10.20914.
+$k = 1, k = 2, \ldots, k = 10$ として 10 回プレイした場合の合計点の期待値は 10.20914 (小数第 5 位に四捨五入) である、ということを示せます。
-If he plays ${10}^5$ turns with $k = 1, k = 2, k = 3, \ldots, k = {10}^5$, what is the expected value of his total score, rounded to five decimal places?
+$k = 1, k = 2, k = 3, \ldots, k = {10}^5$ として ${10}^5$ 回プレイした場合の合計点の期待値を、四捨五入して小数第 5 位まで求めなさい。
# --hints--
-`pythagoreanOdds()` should return `157055.80999`.
+`pythagoreanOdds()` は `157055.80999` を返す必要があります。
```js
assert.strictEqual(pythagoreanOdds(), 157055.80999);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
index 1e5a4445df..0a4329ab28 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
@@ -1,6 +1,6 @@
---
id: 5900f48a1000cf542c50ff9d
-title: 'Problem 286: Scoring probabilities'
+title: '問題 286: 得点の確率'
challengeType: 5
forumTopicId: 301937
dashedName: problem-286-scoring-probabilities
@@ -8,15 +8,15 @@ dashedName: problem-286-scoring-probabilities
# --description--
-Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance $x$ is exactly ($1 - \frac{x}{q}$), where $q$ is a real constant greater than 50.
+バーバラは数学者で、バスケットボール選手でもあります。 彼女は、距離 $x$ からシュートしたときに 1 点取れる確率がちょうど ($1 - \frac{x}{q}$) であること気付きました。ここで、$q$ は 50 よりも大きい実数定数です。
-During each practice run, she takes shots from distances $x = 1, x = 2, \ldots, x = 50$ and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
+1 回の練習ごとにそれぞれ距離 $x = 1, x = 2, \ldots, x = 50$ からシュートし、記録によると、合計がちょうど 20 点になる確率はちょうど 2% です。
-Find $q$ and give your answer rounded to 10 decimal places.
+$q$ を求め、四捨五入して小数点以下 10 桁まで示しなさい。
# --hints--
-`scoringProbabilities()` should return `52.6494571953`.
+`scoringProbabilities()` は `52.6494571953` を返す必要があります。
```js
assert.strictEqual(scoringProbabilities(), 52.6494571953);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
index c495184e4a..c41333ebd8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
@@ -1,6 +1,6 @@
---
id: 5900f48b1000cf542c50ff9e
-title: 'Problem 287: Quadtree encoding (a simple compression algorithm)'
+title: '問題 287: 四分木符号化 (単純な圧縮アルゴリズム)'
challengeType: 5
forumTopicId: 301938
dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
@@ -8,32 +8,32 @@ dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
# --description--
-The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
+四分木符号化により、$2^N×2^N$ の白黒画像をビット (0, 1) 列で表すことができます。 このビット列は、左から右へ次のように解釈されます。
-- the first bit deals with the complete $2^N×2^N$ region;
-- "0" denotes a split:
- - the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
- - the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
-- "10" indicates that the current region contains only black pixels;
-- "11" indicates that the current region contains only white pixels.
+- 最初のビットは $2^N×2^N$ の領域全体を表します。
+- "0" は分割を意味します。
+ - 現在の $2^n×2^n$ の領域は、寸法 $2^{n - 1}×2^{n - 1}$ の 4 つの部分領域に分割されます。
+ - 次のビットには、左上、右上、左下、右下の部分領域の説明がこの順序で含まれています。
+- "10" は、現在の領域が黒いピクセルのみを含んでいることを示します。
+- "11" は、現在の領域が白いピクセルのみを含んでいることを示します。
-Consider the following 4×4 image (colored marks denote places where a split can occur):
+次の 4×4 の画像について考えます (色付きのマークは分割可能な場所を示します)。
-
-Find the sum of all $f(m,n)$ such that $f(m,n) ≤ {10}^{15}$.
+$f(m,n) ≤ {10}^{15}$ となる $f(m,n)$ の総和を求めなさい。
# --hints--
-`pizzaToppings()` should return `1485776387445623`.
+`pizzaToppings()` は `1485776387445623` を返す必要があります。
```js
assert.strictEqual(pizzaToppings(), 1485776387445623);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
index af033cdcf7..882a20ba3a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4861000cf542c50ff99
-title: 'Problem 282: The Ackermann function'
+title: '問題 282: アッカーマン関数'
challengeType: 5
forumTopicId: 301933
dashedName: problem-282-the-ackermann-function
@@ -8,17 +8,17 @@ dashedName: problem-282-the-ackermann-function
# --description--
-For non-negative integers $m$, $n$, the Ackermann function $A(m, n)$ is defined as follows:
+負でない整数 $m$, $n$ に対して、アッカーマン関数 $A(m, n)$ は次のように定義されます。
-$$A(m, n) = \begin{cases} n + 1 & \text{if $m = 0$} \\\\ A(m - 1, 1) & \text{if $m > 0$ and $n = 0$} \\\\ A(m - 1, A(m, n - 1)) & \text{if $m > 0$ and $n > 0$} \end{cases}$$
+$$A(m, n) = \begin{cases} n + 1 & \text{$m = 0$ の場合} \\\\ A(m - 1, 1) & \text{$m > 0$ かつ $n = 0$ の場合} \\\\ A(m - 1, A(m, n - 1)) & \text{$m > 0$ かつ $n > 0$ の場合} \end{cases}$$
-For example $A(1, 0) = 2$, $A(2, 2) = 7$ and $A(3, 4) = 125$.
+例えば、$A(1, 0) = 2$, $A(2, 2) = 7$, $A(3, 4) = 125$ です。
-Find $\displaystyle\sum_{n = 0}^6 A(n, n)$ and give your answer mod ${14}^8$.
+$\displaystyle\sum_{n = 0}^6 A(n, n)$ を求め、mod ${14}^8$ で答えなさい。
# --hints--
-`ackermanFunction()` should return `1098988351`.
+`ackermanFunction()` は `1098988351` を返す必要があります。
```js
assert.strictEqual(ackermanFunction(), 1098988351);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
index d88415d481..419c29163e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
@@ -1,7 +1,7 @@
---
id: 5900f4881000cf542c50ff9a
title: >-
- Problem 283: Integer sided triangles for which the area / perimeter ratio is integral
+ 問題 283: 面積 / 周長の比率が整数である整数辺三角形
challengeType: 5
forumTopicId: 301934
dashedName: >-
@@ -10,19 +10,19 @@ dashedName: >-
# --description--
-Consider the triangle with sides 6, 8 and 10. It can be seen that the perimeter and the area are both equal to 24.
+辺の長さが 6, 8, 10 である三角形について考えます。 周長と面積がともに 24 に等しいことが分かります。
-So the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 1.
+したがって、$\frac{\text{面積}}{\text{周長}}$ の比率は 1 です。
-Consider also the triangle with sides 13, 14 and 15. The perimeter equals 42 while the area is equal to 84.
+辺 13, 14, 15 の三角形についても考えます。 周長は 42、面積は 84 です。
-So for this triangle the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 2.
+したがって、この三角形の $\frac{\text{面積}}{\text{周長}}$ の比率は 2 です。
-Find the sum of the perimeters of all integer sided triangles for which the area/perimeter ratios are equal to positive integers not exceeding 1000.
+面積 / 周長の比率が 1000 以下の正の整数に等しくなるようなすべての整数三角形について、それらの周長の和を求めなさい。
# --hints--
-`integralAreaPerimeterRatio()` should return `28038042525570324`.
+`integralAreaPerimeterRatio()` は `28038042525570324` を返す必要があります。
```js
assert.strictEqual(integralAreaPerimeterRatio(), 28038042525570324);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
index 417ddd2948..9b47aa1ddb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
@@ -1,6 +1,6 @@
---
id: 5900f4891000cf542c50ff9b
-title: 'Problem 284: Steady Squares'
+title: '問題 284: 安定平方数'
challengeType: 5
forumTopicId: 301935
dashedName: problem-284-steady-squares
@@ -8,23 +8,23 @@ dashedName: problem-284-steady-squares
# --description--
-The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: ${376}^2 = 141376$. Let's call a number with this property a steady square.
+3 桁の 10 進数 376 は、その平方数の下位桁がそれ自体と同じである (${376}^2 = 141376$) という、特殊な性質を持つ数の一例です。 この性質を持つ数を「安定平方数」と呼ぶことにします。
-Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number $c37$ is also a steady square: $c37^2 = aa0c37$, and the sum of its digits is $c+3+7=18$ in the same numbering system. The letters $a$, $b$, $c$ and $d$ are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
+安定平方数は他の進数でも現れます。 3 桁の14 進数 $c37$ も安定平方数であり、$c37^2 = aa0c37$ となります。また、その各位の和は 14 進数で $c+3+7=18$ です。 文字 $a$, $b$, $c$, $d$ はそれぞれ 10, 11, 12, 13 を表すのに使われます。これは 16 進数と同様の方法です。
-For $1 ≤ n ≤ 9$, the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system is $2d8$ (582 decimal). Steady squares with leading 0's are not allowed.
+$1 ≤ n ≤ 9$ のとき、すべての $n$ 桁の 14 進数の安定平方数の各位の和は $2d8$ (10 進数で 582) です。 先行ゼロを持つ安定平方数は許容されません。
-Find the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system for $1 ≤ n ≤ 10000$ (decimal) and give your answer as a string in the base 14 system using lower case letters where necessary.
+$1 ≤ n ≤ 10000$ (10進数) のとき、$n$ 桁の安定平方数 (14 進数) のすべてについて各位の和を求め、適宜、小文字の文字を使用して 14 進数の文字列で答えなさい。
# --hints--
-`steadySquares()` should return a string.
+`steadySquares()` は文字列を返す必要があります。
```js
assert(typeof steadySquares() === 'string');
```
-`steadySquares()` should return the string `5a411d7b`.
+`steadySquares()` は文字列 `5a411d7b` を返す必要があります。
```js
assert.strictEqual(steadySquares(), '5a411d7b');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
index ad75e381a1..935dd194d2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
@@ -1,6 +1,6 @@
---
id: 5900f48a1000cf542c50ff9c
-title: 'Problem 285: Pythagorean odds'
+title: '問題 285: ピタゴラスオッズ'
challengeType: 5
forumTopicId: 301936
dashedName: problem-285-pythagorean-odds
@@ -8,19 +8,19 @@ dashedName: problem-285-pythagorean-odds
# --description--
-Albert chooses a positive integer $k$, then two real numbers $a$, $b$ are randomly chosen in the interval [0,1] with uniform distribution.
+アルバートが正の整数 $k$ を 1 つ選ぶと、一様分布の区間 [0,1] から 2 つの実数 $a$, $b$ が無作為に選ばれます。
-The square root of the sum ${(ka + 1)}^2 + {(kb + 1)}^2$ is then computed and rounded to the nearest integer. If the result is equal to $k$, he scores $k$ points; otherwise he scores nothing.
+次に、和 ${(ka + 1)}^2 + {(kb + 1)}^2$ の平方根が計算され、最も近い整数に丸められます。 結果が $k$ に等しければ $k$ 点を獲得し、それ以外は 0 点です。
-For example, if $k = 6$, $a = 0.2$ and $b = 0.85$, then ${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to $k$, so he scores 6 points.
+例えば、$k = 6$, $a = 0.2$, $b = 0.85$ の場合、${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$ です。 42.05 の平方根は 6.484... で、最も近い整数に四捨五入すると 6 になります。 これは $k$ に等しいので、6 点を獲得します。
-It can be shown that if he plays 10 turns with $k = 1, k = 2, \ldots, k = 10$, the expected value of his total score, rounded to five decimal places, is 10.20914.
+$k = 1, k = 2, \ldots, k = 10$ として 10 回プレイした場合の合計点の期待値は 10.20914 (小数第 5 位に四捨五入) である、ということを示せます。
-If he plays ${10}^5$ turns with $k = 1, k = 2, k = 3, \ldots, k = {10}^5$, what is the expected value of his total score, rounded to five decimal places?
+$k = 1, k = 2, k = 3, \ldots, k = {10}^5$ として ${10}^5$ 回プレイした場合の合計点の期待値を、四捨五入して小数第 5 位まで求めなさい。
# --hints--
-`pythagoreanOdds()` should return `157055.80999`.
+`pythagoreanOdds()` は `157055.80999` を返す必要があります。
```js
assert.strictEqual(pythagoreanOdds(), 157055.80999);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
index 1e5a4445df..0a4329ab28 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
@@ -1,6 +1,6 @@
---
id: 5900f48a1000cf542c50ff9d
-title: 'Problem 286: Scoring probabilities'
+title: '問題 286: 得点の確率'
challengeType: 5
forumTopicId: 301937
dashedName: problem-286-scoring-probabilities
@@ -8,15 +8,15 @@ dashedName: problem-286-scoring-probabilities
# --description--
-Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance $x$ is exactly ($1 - \frac{x}{q}$), where $q$ is a real constant greater than 50.
+バーバラは数学者で、バスケットボール選手でもあります。 彼女は、距離 $x$ からシュートしたときに 1 点取れる確率がちょうど ($1 - \frac{x}{q}$) であること気付きました。ここで、$q$ は 50 よりも大きい実数定数です。
-During each practice run, she takes shots from distances $x = 1, x = 2, \ldots, x = 50$ and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
+1 回の練習ごとにそれぞれ距離 $x = 1, x = 2, \ldots, x = 50$ からシュートし、記録によると、合計がちょうど 20 点になる確率はちょうど 2% です。
-Find $q$ and give your answer rounded to 10 decimal places.
+$q$ を求め、四捨五入して小数点以下 10 桁まで示しなさい。
# --hints--
-`scoringProbabilities()` should return `52.6494571953`.
+`scoringProbabilities()` は `52.6494571953` を返す必要があります。
```js
assert.strictEqual(scoringProbabilities(), 52.6494571953);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
index c495184e4a..c41333ebd8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
@@ -1,6 +1,6 @@
---
id: 5900f48b1000cf542c50ff9e
-title: 'Problem 287: Quadtree encoding (a simple compression algorithm)'
+title: '問題 287: 四分木符号化 (単純な圧縮アルゴリズム)'
challengeType: 5
forumTopicId: 301938
dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
@@ -8,32 +8,32 @@ dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
# --description--
-The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
+四分木符号化により、$2^N×2^N$ の白黒画像をビット (0, 1) 列で表すことができます。 このビット列は、左から右へ次のように解釈されます。
-- the first bit deals with the complete $2^N×2^N$ region;
-- "0" denotes a split:
- - the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
- - the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
-- "10" indicates that the current region contains only black pixels;
-- "11" indicates that the current region contains only white pixels.
+- 最初のビットは $2^N×2^N$ の領域全体を表します。
+- "0" は分割を意味します。
+ - 現在の $2^n×2^n$ の領域は、寸法 $2^{n - 1}×2^{n - 1}$ の 4 つの部分領域に分割されます。
+ - 次のビットには、左上、右上、左下、右下の部分領域の説明がこの順序で含まれています。
+- "10" は、現在の領域が黒いピクセルのみを含んでいることを示します。
+- "11" は、現在の領域が白いピクセルのみを含んでいることを示します。
-Consider the following 4×4 image (colored marks denote places where a split can occur):
+次の 4×4 の画像について考えます (色付きのマークは分割可能な場所を示します)。
-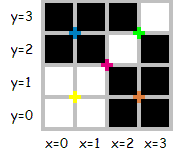 +
+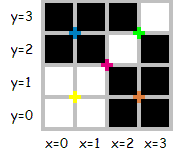 -This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
+この画像は、例えば次のようにいくつかの数列で表すことができます。"001010101001011111011010101010" (長さ 30)、または "0100101111101110" (長さ 16、この画像での最小数列)
-For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
+正の整数 $N$ に対し、次のように色が付く $2^N×2^N$ の画像を$D_N$ とします。
-- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
-- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
-- otherwise the pixel is white.
+- 座標 $x = 0$, $y = 0$ のピクセルは左下のピクセルに対応します。
+- ${(x - 2^{N - 1})}^2 + {(y - 2 ^{N - 1})}^2 = 2^{2N - 2}$ の場合、ピクセルは黒です。
+- それ以外の場合、ピクセルは白です。
-What is the length of the minimal sequence describing $D_{24}$?
+$D_{24} $ を表す最小の数列の長さを求めなさい。
# --hints--
-`quadtreeEncoding()` should return `313135496`.
+`quadtreeEncoding()` は `313135496` を返す必要があります。
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
index 49ce39b3e7..85f3b00051 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
@@ -1,6 +1,6 @@
---
id: 5900f48d1000cf542c50ff9f
-title: 'Problem 288: An enormous factorial'
+title: '問題 288: 巨大な階乗'
challengeType: 5
forumTopicId: 301939
dashedName: problem-288-an-enormous-factorial
@@ -8,21 +8,21 @@ dashedName: problem-288-an-enormous-factorial
# --description--
-For any prime $p$ the number $N(p,q)$ is defined by $N(p,q) = \sum_{n=0}^q T_n \times p^n$ with $T_n$ generated by the following random number generator:
+任意の素数 $p$ に対し、数 $N(p,q)$ は $N(p,q) = \sum_{n=0}^q T_n \times p^n$ と定義されます。$T_n$ は下の乱数生成法で生成されます。
$$\begin{align} & S_0 = 290797 \\\\ & S_{n + 1} = {S_n}^2\bmod 50\\,515\\,093 \\\\ & T_n = S_n\bmod p \end{align}$$
-Let $Nfac(p,q)$ be the factorial of $N(p,q)$.
+$Nfac(p,q)$ を、$N(p,q)$ の階乗と定義します。
-Let $NF(p,q)$ be the number of factors $p$ in $Nfac(p,q)$.
+$NF(p,q)$ を、$Nfac(p,q)$ 内の因数 $p$ の数と定義します。
-You are given that $NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$.
+$NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$ が与えられます。
-Find $NF(61,{10}^7)\bmod {61}^{10}$.
+$NF(61,{10}^7)\bmod {61}^{10}$ を求めなさい。
# --hints--
-`enormousFactorial()` should return `605857431263982000`.
+`enormousFactorial()` は `605857431263982000` を返す必要があります。
```js
assert.strictEqual(enormousFactorial(), 605857431263982000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
index d07af291c4..cd45bc5405 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
@@ -1,6 +1,6 @@
---
id: 5900f48d1000cf542c50ffa0
-title: 'Problem 289: Eulerian Cycles'
+title: '問題 289: オイラー閉路'
challengeType: 5
forumTopicId: 301940
dashedName: problem-289-eulerian-cycles
@@ -8,23 +8,23 @@ dashedName: problem-289-eulerian-cycles
# --description--
-Let $C(x,y)$ be a circle passing through the points ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$) and ($x + 1$, $y + 1$).
+点 ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$), ($x + 1$, $y + 1$) を通過する円を $C(x,y)$ とします。
-For positive integers $m$ and $n$, let $E(m,n)$ be a configuration which consists of the $m·n$ circles: { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ and $y$ are integers }
+正の整数 $m$, $n$ に対し、$m·n$ の円 { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ と $y$ は整数 } からなる図形を $E (m,n) とします。
-An Eulerian cycle on $E(m,n)$ is a closed path that passes through each arc exactly once. Many such paths are possible on $E(m,n)$, but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
+$E(m,n)$ 上のオイラー閉路は、各弧をちょうど 1 回ずつ通る閉路です。 $E(m,n)$ 上にはそのような経路が数多くありますが、ここではそれ自体と交差しないもののみに注目します。交差しない経路とは、格子点でそれ自体に触れるだけであり、それ自体と決して交わらない経路です。
-The image below shows $E(3,3)$ and an example of an Eulerian non-crossing path.
+下の画像は、$E(3,3)$ と、交差しないオイラー経路の例です。
-
-This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
+この画像は、例えば次のようにいくつかの数列で表すことができます。"001010101001011111011010101010" (長さ 30)、または "0100101111101110" (長さ 16、この画像での最小数列)
-For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
+正の整数 $N$ に対し、次のように色が付く $2^N×2^N$ の画像を$D_N$ とします。
-- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
-- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
-- otherwise the pixel is white.
+- 座標 $x = 0$, $y = 0$ のピクセルは左下のピクセルに対応します。
+- ${(x - 2^{N - 1})}^2 + {(y - 2 ^{N - 1})}^2 = 2^{2N - 2}$ の場合、ピクセルは黒です。
+- それ以外の場合、ピクセルは白です。
-What is the length of the minimal sequence describing $D_{24}$?
+$D_{24} $ を表す最小の数列の長さを求めなさい。
# --hints--
-`quadtreeEncoding()` should return `313135496`.
+`quadtreeEncoding()` は `313135496` を返す必要があります。
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
index 49ce39b3e7..85f3b00051 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
@@ -1,6 +1,6 @@
---
id: 5900f48d1000cf542c50ff9f
-title: 'Problem 288: An enormous factorial'
+title: '問題 288: 巨大な階乗'
challengeType: 5
forumTopicId: 301939
dashedName: problem-288-an-enormous-factorial
@@ -8,21 +8,21 @@ dashedName: problem-288-an-enormous-factorial
# --description--
-For any prime $p$ the number $N(p,q)$ is defined by $N(p,q) = \sum_{n=0}^q T_n \times p^n$ with $T_n$ generated by the following random number generator:
+任意の素数 $p$ に対し、数 $N(p,q)$ は $N(p,q) = \sum_{n=0}^q T_n \times p^n$ と定義されます。$T_n$ は下の乱数生成法で生成されます。
$$\begin{align} & S_0 = 290797 \\\\ & S_{n + 1} = {S_n}^2\bmod 50\\,515\\,093 \\\\ & T_n = S_n\bmod p \end{align}$$
-Let $Nfac(p,q)$ be the factorial of $N(p,q)$.
+$Nfac(p,q)$ を、$N(p,q)$ の階乗と定義します。
-Let $NF(p,q)$ be the number of factors $p$ in $Nfac(p,q)$.
+$NF(p,q)$ を、$Nfac(p,q)$ 内の因数 $p$ の数と定義します。
-You are given that $NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$.
+$NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$ が与えられます。
-Find $NF(61,{10}^7)\bmod {61}^{10}$.
+$NF(61,{10}^7)\bmod {61}^{10}$ を求めなさい。
# --hints--
-`enormousFactorial()` should return `605857431263982000`.
+`enormousFactorial()` は `605857431263982000` を返す必要があります。
```js
assert.strictEqual(enormousFactorial(), 605857431263982000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
index d07af291c4..cd45bc5405 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
@@ -1,6 +1,6 @@
---
id: 5900f48d1000cf542c50ffa0
-title: 'Problem 289: Eulerian Cycles'
+title: '問題 289: オイラー閉路'
challengeType: 5
forumTopicId: 301940
dashedName: problem-289-eulerian-cycles
@@ -8,23 +8,23 @@ dashedName: problem-289-eulerian-cycles
# --description--
-Let $C(x,y)$ be a circle passing through the points ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$) and ($x + 1$, $y + 1$).
+点 ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$), ($x + 1$, $y + 1$) を通過する円を $C(x,y)$ とします。
-For positive integers $m$ and $n$, let $E(m,n)$ be a configuration which consists of the $m·n$ circles: { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ and $y$ are integers }
+正の整数 $m$, $n$ に対し、$m·n$ の円 { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ と $y$ は整数 } からなる図形を $E (m,n) とします。
-An Eulerian cycle on $E(m,n)$ is a closed path that passes through each arc exactly once. Many such paths are possible on $E(m,n)$, but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
+$E(m,n)$ 上のオイラー閉路は、各弧をちょうど 1 回ずつ通る閉路です。 $E(m,n)$ 上にはそのような経路が数多くありますが、ここではそれ自体と交差しないもののみに注目します。交差しない経路とは、格子点でそれ自体に触れるだけであり、それ自体と決して交わらない経路です。
-The image below shows $E(3,3)$ and an example of an Eulerian non-crossing path.
+下の画像は、$E(3,3)$ と、交差しないオイラー経路の例です。
-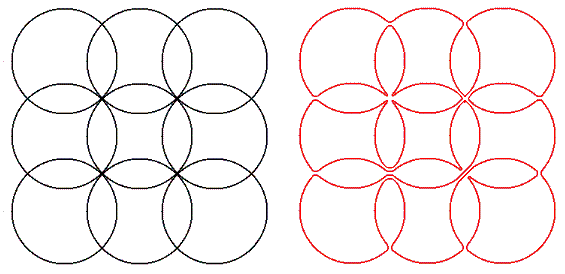 +
+ -Let $L(m,n)$ be the number of Eulerian non-crossing paths on $E(m,n)$. For example, $L(1,2) = 2$, $L(2,2) = 37$ and $L(3,3) = 104290$.
+$E(m,n)$ 上の交差しないオイラー経路の数を $L(m,n)$ とします。 例えば、$L(1,2) = 2$, $L(2,2) = 37$, $L(3,3) = 104290$ です。
-Find $L(6,10)\bmod {10}^{10}$.
+$L(6,10)\bmod {10}^{10}$ を求めなさい。
# --hints--
-`eulerianCycles()` should return `6567944538`.
+`eulerianCycles()` は `6567944538` を返す必要があります。
```js
assert.strictEqual(eulerianCycles(), 6567944538);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
index 9439010175..7af55f1bbd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
@@ -1,6 +1,6 @@
---
id: 5900f48f1000cf542c50ffa1
-title: 'Problem 290: Digital Signature'
+title: '問題 290: 数字の性質'
challengeType: 5
forumTopicId: 301942
dashedName: problem-290-digital-signature
@@ -8,11 +8,11 @@ dashedName: problem-290-digital-signature
# --description--
-How many integers $0 ≤ n < {10}^{18}$ have the property that the sum of the digits of $n$ equals the sum of digits of $137n$?
+$0 ≤ n < {10}^{18}$ のとき、$n$ の各位の和が $137n$ の各位の和と等しくなるという性質を持つ整数 $n$ はいくつありますか。
# --hints--
-`digitalSignature()` should return `20444710234716470`.
+`digitalSignature()` は `20444710234716470` を返す必要があります。
```js
assert.strictEqual(digitalSignature(), 20444710234716470);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
index 2922bdcbe5..75bfb66e70 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f48f1000cf542c50ffa2
-title: 'Problem 291: Panaitopol Primes'
+title: '問題 291: Panaitopol 素数'
challengeType: 5
forumTopicId: 301943
dashedName: problem-291-panaitopol-primes
@@ -8,13 +8,13 @@ dashedName: problem-291-panaitopol-primes
# --description--
-A prime number $p$ is called a Panaitopol prime if $p = \frac{x^4 - y^4}{x^3 + y^3}$ for some positive integers $x$ and $y$.
+正の整数 $x$ と $y$ に対して素数 $p = \frac{x^4 - y^4}{x^3 + y^3}$ が成り立つとき、$p$ は Panaitopol 素数と呼ばれます。
-Find how many Panaitopol primes are less than $5 × {10}^{15}$.
+$5 × {10}^{15}$ 未満の Panaitopol 素数はいくつありますか。
# --hints--
-`panaitopolPrimes()` should return `4037526`.
+`panaitopolPrimes()` は `4037526` を返す必要があります。
```js
assert.strictEqual(panaitopolPrimes(), 4037526);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
index 7f4ae44273..e6b65cafff 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
@@ -1,6 +1,6 @@
---
id: 5900f4911000cf542c50ffa3
-title: 'Problem 292: Pythagorean Polygons'
+title: '問題 292: ピタゴラス多角形'
challengeType: 5
forumTopicId: 301944
dashedName: problem-292-pythagorean-polygons
@@ -8,24 +8,24 @@ dashedName: problem-292-pythagorean-polygons
# --description--
-We shall define a pythagorean polygon to be a convex polygon with the following properties:
+次の性質をすべて備える凸多角形を「ピタゴラス多角形」と定義します。
-- there are at least three vertices,
-- no three vertices are aligned,
-- each vertex has integer coordinates,
-- each edge has integer length.
+- 少なくとも 3 つの頂点がある。
+- どの 3 頂点も一直線上に並んでいない。
+- 各頂点の座標が整数である。
+- 各辺の長さが整数である。
-For a given integer $n$, define $P(n)$ as the number of distinct pythagorean polygons for which the perimeter is $≤ n$.
+与えられた整数 $n$ について、周長が $n$ 以下の相異なるピタゴラス多角形の個数を $P(n)$ とします。
-Pythagorean polygons should be considered distinct as long as none is a translation of another.
+ピタゴラス多角形は、平行移動で同一にならない限り相異なるものとみなされます。
-You are given that $P(4) = 1$, $P(30) = 3655$ and $P(60) = 891045$.
+$P(4) = 1$, $P(30) = 3655$, $P(60) = 891045$ が与えられます。
-Find $P(120)$.
+$P(120)$ を求めなさい。
# --hints--
-`pythagoreanPolygons()` should return `3600060866`.
+`pythagoreanPolygons()` は `3600060866` を返す必要があります。
```js
assert.strictEqual(pythagoreanPolygons(), 3600060866);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
index 2da024c967..a4eacafe0d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4931000cf542c50ffa4
-title: 'Problem 293: Pseudo-Fortunate Numbers'
+title: '問題 293: 疑似フォーチュン数'
challengeType: 5
forumTopicId: 301945
dashedName: problem-293-pseudo-fortunate-numbers
@@ -8,19 +8,19 @@ dashedName: problem-293-pseudo-fortunate-numbers
# --description--
-An even positive integer $N$ will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
+偶数の正整数 $N$ は、2 の累乗であるか、またはその相異なる素因数が連続した素数である場合、「許容的」であるとされます。
-The first twelve admissible numbers are 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48.
+許容的な数を最小のものから 12 個挙げると 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48 となります。
-If $N$ is admissible, the smallest integer $M > 1$ such that $N + M$ is prime, will be called the pseudo-Fortunate number for $N$.
+$N$ が許容的である場合、$N + M$ が素数になるような最小の整数 $M > 1$ を、$N$ に対する「擬似フォーチュン数」と呼ぶことにします。
-For example, $N = 630$ is admissible since it is even and its distinct prime factors are the consecutive primes 2, 3, 5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is $M = 11$. It can also be seen that the pseudo-Fortunate number for 16 is 3.
+例えば、$N = 630$ は許容的です。偶数であり、その相異なる素因子は連続する素数 2, 3, 5, 7 だからです。 631 の次の 素数は 641 なので、630 に対する疑似フォーチュン数は $M = 11$ です。 また、16 の擬似フォーチュン数が 3 であることが分かります。
-Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers $N$ less than ${10}^9$.
+${10}^9$ 未満の許容的な数 $N$ に対する相異なる疑似フォーチュン数の総和を求めなさい。
# --hints--
-`pseudoFortunateNumbers()` should return `2209`.
+`pseudoFortunateNumbers()` は `2209` を返す必要があります。
```js
assert.strictEqual(pseudoFortunateNumbers(), 2209);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
index 20216ace66..c84df5043c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
@@ -1,6 +1,6 @@
---
id: 5900f4931000cf542c50ffa5
-title: 'Problem 294: Sum of digits - experience #23'
+title: '問題 294: 各位の和 - 23 に注目'
challengeType: 5
forumTopicId: 301946
dashedName: problem-294-sum-of-digits---experience-23
@@ -8,20 +8,20 @@ dashedName: problem-294-sum-of-digits---experience-23
# --description--
-For a positive integer $k$, define $d(k)$ as the sum of the digits of $k$ in its usual decimal representation. Thus $d(42) = 4 + 2 = 6$.
+正の整数 $k$ について、通常の 10 進数で表された $k$ の各位の和を $d(k)$ とします。 したがって、$d(42) = 4 + 2 = 6$ です。
-For a positive integer $n$, define $S(n)$ as the number of positive integers $k < {10}^n$ with the following properties:
+正の整数 $n$ について、次の性質を持つ整数 $k < {10}^n$ の個数を $S(n)$ とします。
-- $k$ is divisible by 23 and,
-- $d(k) = 23$.
+- $k$ が 23 で割り切れる。かつ、
+- $d(k) = 23$ である。
-You are given that $S(9) = 263\\,626$ and $S(42) = 6\\,377\\,168\\,878\\,570\\,056$.
+$S(9) = 263\\,626$, $S(42) = 6\\,377\\,168\\,878\\,570\\,056$ が与えられます。
-Find $S({11}^{12})$ and give your answer $\bmod {10}^9$.
+$S({11}^{12})$ を求め、$\bmod {10}^9$ で答えなさい。
# --hints--
-`experience23()` should return `789184709`.
+`experience23()` は `789184709` を返す必要があります。
```js
assert.strictEqual(experience23(), 789184709);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
index e494b5e770..bd067607a0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
@@ -1,6 +1,6 @@
---
id: 5900f4931000cf542c50ffa6
-title: 'Problem 295: Lenticular holes'
+title: '問題 295: レンズ状の穴'
challengeType: 5
forumTopicId: 301947
dashedName: problem-295-lenticular-holes
@@ -8,31 +8,31 @@ dashedName: problem-295-lenticular-holes
# --description--
-We call the convex area enclosed by two circles a lenticular hole if:
+2 つの円に囲まれた凸状の領域が次の条件を満たす場合、その領域を「レンズ状の穴」と呼びます。
-- The centres of both circles are on lattice points.
-- The two circles intersect at two distinct lattice points.
-- The interior of the convex area enclosed by both circles does not contain any lattice points.
+- 両方の円心が格子点上にある。
+- 2 つの円が 2 つの相異なる格子点で交差する
+- 両方の円に囲まれた凸状の領域が格子点を内包しない。
-Consider the circles:
+次のような円を考えます。
$$\begin{align} & C_0: x^2 + y^2 = 25 \\\\ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65 \end{align}$$
-The circles $C_0$, $C_1$ and $C_2$ are drawn in the picture below.
+円 $C_0$, $C_1$, $C_2$ を下図に示します。
-
-Let $L(m,n)$ be the number of Eulerian non-crossing paths on $E(m,n)$. For example, $L(1,2) = 2$, $L(2,2) = 37$ and $L(3,3) = 104290$.
+$E(m,n)$ 上の交差しないオイラー経路の数を $L(m,n)$ とします。 例えば、$L(1,2) = 2$, $L(2,2) = 37$, $L(3,3) = 104290$ です。
-Find $L(6,10)\bmod {10}^{10}$.
+$L(6,10)\bmod {10}^{10}$ を求めなさい。
# --hints--
-`eulerianCycles()` should return `6567944538`.
+`eulerianCycles()` は `6567944538` を返す必要があります。
```js
assert.strictEqual(eulerianCycles(), 6567944538);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
index 9439010175..7af55f1bbd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
@@ -1,6 +1,6 @@
---
id: 5900f48f1000cf542c50ffa1
-title: 'Problem 290: Digital Signature'
+title: '問題 290: 数字の性質'
challengeType: 5
forumTopicId: 301942
dashedName: problem-290-digital-signature
@@ -8,11 +8,11 @@ dashedName: problem-290-digital-signature
# --description--
-How many integers $0 ≤ n < {10}^{18}$ have the property that the sum of the digits of $n$ equals the sum of digits of $137n$?
+$0 ≤ n < {10}^{18}$ のとき、$n$ の各位の和が $137n$ の各位の和と等しくなるという性質を持つ整数 $n$ はいくつありますか。
# --hints--
-`digitalSignature()` should return `20444710234716470`.
+`digitalSignature()` は `20444710234716470` を返す必要があります。
```js
assert.strictEqual(digitalSignature(), 20444710234716470);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
index 2922bdcbe5..75bfb66e70 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f48f1000cf542c50ffa2
-title: 'Problem 291: Panaitopol Primes'
+title: '問題 291: Panaitopol 素数'
challengeType: 5
forumTopicId: 301943
dashedName: problem-291-panaitopol-primes
@@ -8,13 +8,13 @@ dashedName: problem-291-panaitopol-primes
# --description--
-A prime number $p$ is called a Panaitopol prime if $p = \frac{x^4 - y^4}{x^3 + y^3}$ for some positive integers $x$ and $y$.
+正の整数 $x$ と $y$ に対して素数 $p = \frac{x^4 - y^4}{x^3 + y^3}$ が成り立つとき、$p$ は Panaitopol 素数と呼ばれます。
-Find how many Panaitopol primes are less than $5 × {10}^{15}$.
+$5 × {10}^{15}$ 未満の Panaitopol 素数はいくつありますか。
# --hints--
-`panaitopolPrimes()` should return `4037526`.
+`panaitopolPrimes()` は `4037526` を返す必要があります。
```js
assert.strictEqual(panaitopolPrimes(), 4037526);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
index 7f4ae44273..e6b65cafff 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
@@ -1,6 +1,6 @@
---
id: 5900f4911000cf542c50ffa3
-title: 'Problem 292: Pythagorean Polygons'
+title: '問題 292: ピタゴラス多角形'
challengeType: 5
forumTopicId: 301944
dashedName: problem-292-pythagorean-polygons
@@ -8,24 +8,24 @@ dashedName: problem-292-pythagorean-polygons
# --description--
-We shall define a pythagorean polygon to be a convex polygon with the following properties:
+次の性質をすべて備える凸多角形を「ピタゴラス多角形」と定義します。
-- there are at least three vertices,
-- no three vertices are aligned,
-- each vertex has integer coordinates,
-- each edge has integer length.
+- 少なくとも 3 つの頂点がある。
+- どの 3 頂点も一直線上に並んでいない。
+- 各頂点の座標が整数である。
+- 各辺の長さが整数である。
-For a given integer $n$, define $P(n)$ as the number of distinct pythagorean polygons for which the perimeter is $≤ n$.
+与えられた整数 $n$ について、周長が $n$ 以下の相異なるピタゴラス多角形の個数を $P(n)$ とします。
-Pythagorean polygons should be considered distinct as long as none is a translation of another.
+ピタゴラス多角形は、平行移動で同一にならない限り相異なるものとみなされます。
-You are given that $P(4) = 1$, $P(30) = 3655$ and $P(60) = 891045$.
+$P(4) = 1$, $P(30) = 3655$, $P(60) = 891045$ が与えられます。
-Find $P(120)$.
+$P(120)$ を求めなさい。
# --hints--
-`pythagoreanPolygons()` should return `3600060866`.
+`pythagoreanPolygons()` は `3600060866` を返す必要があります。
```js
assert.strictEqual(pythagoreanPolygons(), 3600060866);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
index 2da024c967..a4eacafe0d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4931000cf542c50ffa4
-title: 'Problem 293: Pseudo-Fortunate Numbers'
+title: '問題 293: 疑似フォーチュン数'
challengeType: 5
forumTopicId: 301945
dashedName: problem-293-pseudo-fortunate-numbers
@@ -8,19 +8,19 @@ dashedName: problem-293-pseudo-fortunate-numbers
# --description--
-An even positive integer $N$ will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
+偶数の正整数 $N$ は、2 の累乗であるか、またはその相異なる素因数が連続した素数である場合、「許容的」であるとされます。
-The first twelve admissible numbers are 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48.
+許容的な数を最小のものから 12 個挙げると 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48 となります。
-If $N$ is admissible, the smallest integer $M > 1$ such that $N + M$ is prime, will be called the pseudo-Fortunate number for $N$.
+$N$ が許容的である場合、$N + M$ が素数になるような最小の整数 $M > 1$ を、$N$ に対する「擬似フォーチュン数」と呼ぶことにします。
-For example, $N = 630$ is admissible since it is even and its distinct prime factors are the consecutive primes 2, 3, 5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is $M = 11$. It can also be seen that the pseudo-Fortunate number for 16 is 3.
+例えば、$N = 630$ は許容的です。偶数であり、その相異なる素因子は連続する素数 2, 3, 5, 7 だからです。 631 の次の 素数は 641 なので、630 に対する疑似フォーチュン数は $M = 11$ です。 また、16 の擬似フォーチュン数が 3 であることが分かります。
-Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers $N$ less than ${10}^9$.
+${10}^9$ 未満の許容的な数 $N$ に対する相異なる疑似フォーチュン数の総和を求めなさい。
# --hints--
-`pseudoFortunateNumbers()` should return `2209`.
+`pseudoFortunateNumbers()` は `2209` を返す必要があります。
```js
assert.strictEqual(pseudoFortunateNumbers(), 2209);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
index 20216ace66..c84df5043c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
@@ -1,6 +1,6 @@
---
id: 5900f4931000cf542c50ffa5
-title: 'Problem 294: Sum of digits - experience #23'
+title: '問題 294: 各位の和 - 23 に注目'
challengeType: 5
forumTopicId: 301946
dashedName: problem-294-sum-of-digits---experience-23
@@ -8,20 +8,20 @@ dashedName: problem-294-sum-of-digits---experience-23
# --description--
-For a positive integer $k$, define $d(k)$ as the sum of the digits of $k$ in its usual decimal representation. Thus $d(42) = 4 + 2 = 6$.
+正の整数 $k$ について、通常の 10 進数で表された $k$ の各位の和を $d(k)$ とします。 したがって、$d(42) = 4 + 2 = 6$ です。
-For a positive integer $n$, define $S(n)$ as the number of positive integers $k < {10}^n$ with the following properties:
+正の整数 $n$ について、次の性質を持つ整数 $k < {10}^n$ の個数を $S(n)$ とします。
-- $k$ is divisible by 23 and,
-- $d(k) = 23$.
+- $k$ が 23 で割り切れる。かつ、
+- $d(k) = 23$ である。
-You are given that $S(9) = 263\\,626$ and $S(42) = 6\\,377\\,168\\,878\\,570\\,056$.
+$S(9) = 263\\,626$, $S(42) = 6\\,377\\,168\\,878\\,570\\,056$ が与えられます。
-Find $S({11}^{12})$ and give your answer $\bmod {10}^9$.
+$S({11}^{12})$ を求め、$\bmod {10}^9$ で答えなさい。
# --hints--
-`experience23()` should return `789184709`.
+`experience23()` は `789184709` を返す必要があります。
```js
assert.strictEqual(experience23(), 789184709);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
index e494b5e770..bd067607a0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
@@ -1,6 +1,6 @@
---
id: 5900f4931000cf542c50ffa6
-title: 'Problem 295: Lenticular holes'
+title: '問題 295: レンズ状の穴'
challengeType: 5
forumTopicId: 301947
dashedName: problem-295-lenticular-holes
@@ -8,31 +8,31 @@ dashedName: problem-295-lenticular-holes
# --description--
-We call the convex area enclosed by two circles a lenticular hole if:
+2 つの円に囲まれた凸状の領域が次の条件を満たす場合、その領域を「レンズ状の穴」と呼びます。
-- The centres of both circles are on lattice points.
-- The two circles intersect at two distinct lattice points.
-- The interior of the convex area enclosed by both circles does not contain any lattice points.
+- 両方の円心が格子点上にある。
+- 2 つの円が 2 つの相異なる格子点で交差する
+- 両方の円に囲まれた凸状の領域が格子点を内包しない。
-Consider the circles:
+次のような円を考えます。
$$\begin{align} & C_0: x^2 + y^2 = 25 \\\\ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65 \end{align}$$
-The circles $C_0$, $C_1$ and $C_2$ are drawn in the picture below.
+円 $C_0$, $C_1$, $C_2$ を下図に示します。
-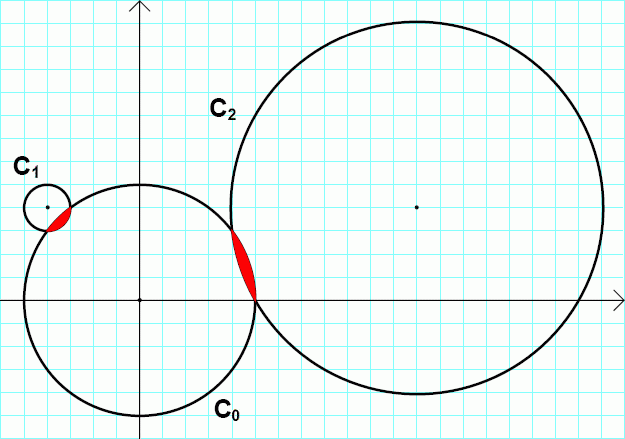 +
+ -$C_0$ and $C_1$ form a lenticular hole, as well as $C_0$ and $C_2$.
+$C_0$ と $C_1$ はレンズ状の穴を形成し、$C_0$ と $C_2$ も同様です。
-We call an ordered pair of positive real numbers ($r_1$, $r_2$) a lenticular pair if there exist two circles with radii $r_1$ and $r_2$ that form a lenticular hole. We can verify that ($1$, $5$) and ($5$, $\sqrt{65}$) are the lenticular pairs of the example above.
+レンズ状の穴を形成する半径 $r_1$, $r_2$ の 2 つの円が存在する場合、正の実数の順序対 ($r_1$, $r_2$) を「レンズペア」と呼びます。 上の例では、($1$, $5$) と ($5$, $\sqrt{65}$) が共にレンズペアであることを確認できます。
-Let $L(N)$ be the number of distinct lenticular pairs ($r_1$, $r_2$) for which $0 < r_1 ≤ r_2 ≤ N$. We can verify that $L(10) = 30$ and $L(100) = 3442$.
+$0 < r_1 ≤ r_2 ≤ N$ となるような相異なるレンズペア ($r_1$, $r_2$) の個数を $L(N)$ とします。 $L(10) = 30$, $L(100) = 3442$ であることを確認できます。
-Find $L(100\\,000)$.
+$L(100\\,000)$ を求めなさい。
# --hints--
-`lenticularHoles()` should return `4884650818`.
+`lenticularHoles()` は `4884650818` を返す必要があります。
```js
assert.strictEqual(lenticularHoles(), 4884650818);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
index 997f033fee..d444def0d5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
@@ -1,6 +1,6 @@
---
id: 5900f4941000cf542c50ffa7
-title: 'Problem 296: Angular Bisector and Tangent'
+title: '問題 296: 角の二等分線と接線'
challengeType: 5
forumTopicId: 301948
dashedName: problem-296-angular-bisector-and-tangent
@@ -8,17 +8,17 @@ dashedName: problem-296-angular-bisector-and-tangent
# --description--
-Given is an integer sided triangle $ABC$ with $BC ≤ AC ≤ AB$. $k$ is the angular bisector of angle $ACB$. $m$ is the tangent at $C$ to the circumscribed circle of $ABC$. $n$ is a line parallel to $m$ through $B$.
+辺の長さが整数である三角形 $ABC$ ($BC ≤ AC ≤ AB$) が与えられます。 $k$ は角 $ACB$ の二等分線です。 $m$ は、$ABC$ の外接円の $C$ における接線です。 $n$は、$B$ を通り $m$ に平行な線です。
-The intersection of $n$ and $k$ is called $E$.
+$n$ と $k$ の交点を $E$ とします。
-
-$C_0$ and $C_1$ form a lenticular hole, as well as $C_0$ and $C_2$.
+$C_0$ と $C_1$ はレンズ状の穴を形成し、$C_0$ と $C_2$ も同様です。
-We call an ordered pair of positive real numbers ($r_1$, $r_2$) a lenticular pair if there exist two circles with radii $r_1$ and $r_2$ that form a lenticular hole. We can verify that ($1$, $5$) and ($5$, $\sqrt{65}$) are the lenticular pairs of the example above.
+レンズ状の穴を形成する半径 $r_1$, $r_2$ の 2 つの円が存在する場合、正の実数の順序対 ($r_1$, $r_2$) を「レンズペア」と呼びます。 上の例では、($1$, $5$) と ($5$, $\sqrt{65}$) が共にレンズペアであることを確認できます。
-Let $L(N)$ be the number of distinct lenticular pairs ($r_1$, $r_2$) for which $0 < r_1 ≤ r_2 ≤ N$. We can verify that $L(10) = 30$ and $L(100) = 3442$.
+$0 < r_1 ≤ r_2 ≤ N$ となるような相異なるレンズペア ($r_1$, $r_2$) の個数を $L(N)$ とします。 $L(10) = 30$, $L(100) = 3442$ であることを確認できます。
-Find $L(100\\,000)$.
+$L(100\\,000)$ を求めなさい。
# --hints--
-`lenticularHoles()` should return `4884650818`.
+`lenticularHoles()` は `4884650818` を返す必要があります。
```js
assert.strictEqual(lenticularHoles(), 4884650818);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
index 997f033fee..d444def0d5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
@@ -1,6 +1,6 @@
---
id: 5900f4941000cf542c50ffa7
-title: 'Problem 296: Angular Bisector and Tangent'
+title: '問題 296: 角の二等分線と接線'
challengeType: 5
forumTopicId: 301948
dashedName: problem-296-angular-bisector-and-tangent
@@ -8,17 +8,17 @@ dashedName: problem-296-angular-bisector-and-tangent
# --description--
-Given is an integer sided triangle $ABC$ with $BC ≤ AC ≤ AB$. $k$ is the angular bisector of angle $ACB$. $m$ is the tangent at $C$ to the circumscribed circle of $ABC$. $n$ is a line parallel to $m$ through $B$.
+辺の長さが整数である三角形 $ABC$ ($BC ≤ AC ≤ AB$) が与えられます。 $k$ は角 $ACB$ の二等分線です。 $m$ は、$ABC$ の外接円の $C$ における接線です。 $n$は、$B$ を通り $m$ に平行な線です。
-The intersection of $n$ and $k$ is called $E$.
+$n$ と $k$ の交点を $E$ とします。
-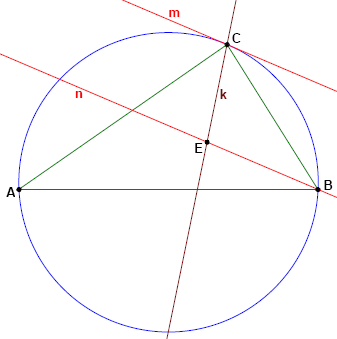 +
+ -How many triangles $ABC$ with a perimeter not exceeding $100\\,000$ exist such that $BE$ has integral length?
+$BE$ の長さが整数であり周長が $100\\,000$ を超えない三角形 $ABC$ はいくつありますか。
# --hints--
-`angularBisectorAndTangent()` should return `1137208419`.
+`angularBisectorAndTangent()` は `1137208419` を返す必要があります。
```js
assert.strictEqual(angularBisectorAndTangent(), 1137208419);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
index 8178fce31e..b5ec3bb19e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
@@ -1,6 +1,6 @@
---
id: 5900f4951000cf542c50ffa8
-title: 'Problem 297: Zeckendorf Representation'
+title: '問題 297: ゼッケンドルフ表現'
challengeType: 5
forumTopicId: 301949
dashedName: problem-297-zeckendorf-representation
@@ -8,25 +8,25 @@ dashedName: problem-297-zeckendorf-representation
# --description--
-Each new term in the Fibonacci sequence is generated by adding the previous two terms.
+フィボナッチ数列の新しい項はそれぞれ、前の 2 項を足すことによって得られます。
-Starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
+1 と 2 から始まる最初の 10 項は 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 です。
-Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89.
+すべての正の整数は、フィボナッチ数列の非連続項の和として一意に表すことができます。 例えば、100 = 3 + 8 + 89です。
-Such a sum is called the Zeckendorf representation of the number.
+このような和は、数のゼッケンドルフ表現と呼ばれます。
-For any integer $n>0$, let $z(n)$ be the number of terms in the Zeckendorf representation of $n$.
+任意の整数 $n>0$ について、$n$ のゼッケンドルフ表現における項数を $z(n)$ とします。
-Thus, $z(5) = 1$, $z(14) = 2$, $z(100) = 3$ etc.
+すなわち、$z(5) = 1$, $z(14) = 2$, $z(100) = 3$ などです。
-Also, for $0 < n < {10}^6$, $\sum z(n) = 7\\,894\\,453$.
+また、$0 < < {10}^6$ のとき、$\sum z(n) = 7\\,894\\,453$ です。
-Find $\sum z(n)$ for $0 < n < {10}^{17}$.
+$0 < n < {10}^{17}$ のとき、$\sum z(n)$ を求めなさい。
# --hints--
-`zeckendorfRepresentation()` should return `2252639041804718000`.
+`zeckendorfRepresentation()` は `2252639041804718000` を返す必要があります。
```js
assert.strictEqual(zeckendorfRepresentation(), 2252639041804718000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
index cfa8aa205b..7338217576 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
@@ -1,6 +1,6 @@
---
id: 5900f4971000cf542c50ffa9
-title: 'Problem 298: Selective Amnesia'
+title: '問題 298: 選択的健忘'
challengeType: 5
forumTopicId: 301950
dashedName: problem-298-selective-amnesia
@@ -8,30 +8,30 @@ dashedName: problem-298-selective-amnesia
# --description--
-Larry and Robin play a memory game involving of a sequence of random numbers between 1 and 10, inclusive, that are called out one at a time. Each player can remember up to 5 previous numbers. When the called number is in a player's memory, that player is awarded a point. If it's not, the player adds the called number to his memory, removing another number if his memory is full.
+ラリーとロビンが記憶ゲームをします。1 から 10 のうち無作為に選ばれた数が一度に 1 つずつ呼び出されます。 各プレイヤーは、以前の数を最大 5 つ記憶できます。 呼び出された数がプレイヤーの記憶にあれば、1 点が与えられます。 記憶になければ、プレイヤーは呼び出された数を自分の記憶に加え、もし記憶が一杯であれば他の数を 1 つ記憶から消します。
-Both players start with empty memories. Both players always add new missed numbers to their memory but use a different strategy in deciding which number to remove: Larry's strategy is to remove the number that hasn't been called in the longest time. Robin's strategy is to remove the number that's been in the memory the longest time.
+開始時、2 人のプレイヤーの記憶は空です。 両プレイヤーは、記憶になかった新しい数を必ず記憶に加えますが、どの数を消すかを決めるための戦略が異なります。ラリーの戦略は、最も長い間呼び出されなかった数を消すことです。 ロビンの戦略は、最も長く記憶にとどまっていた数を消すことです。
-Example game:
+ゲームの例:
-| Turn | Called number | Larry's memory | Larry's score | Robin's memory | Robin's score |
-| ---- | ------------- | --------------:| ------------- | -------------- | ------------- |
-| 1 | 1 | 1 | 0 | 1 | 0 |
-| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
-| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
-| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
-| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
-| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
-| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
-| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
-| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
-| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
+| ターン | 呼び出された番号 | ラリーの記憶 | ラリーのスコア | ロビンの記憶 | ロビンのスコア |
+| --- | -------- | ----------:| ------- | ---------- | ------- |
+| 1 | 1 | 1 | 0 | 1 | 0 |
+| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
+| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
+| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
+| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
+| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
+| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
+| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
+| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
+| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
-Denoting Larry's score by $L$ and Robin's score by $R$, what is the expected value of $|L - R|$ after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+ラリーのスコアを $L$、ロビンのスコアを $R$ で表すものとし、50 ターン後の $|L-R|$ の期待値を求めなさい。 回答は、四捨五入して小数第 8 位まで求め、x.xxxxxxxx の形式にすること。
# --hints--
-`selectiveAmnesia()` should return `1.76882294`.
+`selectiveAmnesia()` は `1.76882294` を返す必要があります。
```js
assert.strictEqual(selectiveAmnesia(), 1.76882294);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
index 19cdc14e04..4d77f4dace 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4971000cf542c50ffaa
-title: 'Problem 299: Three similar triangles'
+title: '問題 299: 3 つの相似三角形'
challengeType: 5
forumTopicId: 301951
dashedName: problem-299-three-similar-triangles
@@ -8,29 +8,29 @@ dashedName: problem-299-three-similar-triangles
# --description--
-Four points with integer coordinates are selected:
+整数座標を持つ、次の 4 つの点が選択されます。
-$A(a, 0)$, $B(b, 0)$, $C(0, c)$ and $D(0, d)$, with $0 < a < b$ and $0 < c < d$.
+$A(a, 0)$, $B(b, 0)$, $C(0, c)$, $D(0, d)$ ($0 < a < b$ かつ $0 < c < d$)
-Point $P$, also with integer coordinates, is chosen on the line $AC$ so that the three triangles $ABP$, $CDP$ and $BDP$ are all similar.
+3 つの三角形 $ABP$, $CDP$, $BDP$ がすべて相似形になるように、同じく整数座標を持つ点 $P$ を線 $AC$ 上で選びます。
-
-How many triangles $ABC$ with a perimeter not exceeding $100\\,000$ exist such that $BE$ has integral length?
+$BE$ の長さが整数であり周長が $100\\,000$ を超えない三角形 $ABC$ はいくつありますか。
# --hints--
-`angularBisectorAndTangent()` should return `1137208419`.
+`angularBisectorAndTangent()` は `1137208419` を返す必要があります。
```js
assert.strictEqual(angularBisectorAndTangent(), 1137208419);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
index 8178fce31e..b5ec3bb19e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
@@ -1,6 +1,6 @@
---
id: 5900f4951000cf542c50ffa8
-title: 'Problem 297: Zeckendorf Representation'
+title: '問題 297: ゼッケンドルフ表現'
challengeType: 5
forumTopicId: 301949
dashedName: problem-297-zeckendorf-representation
@@ -8,25 +8,25 @@ dashedName: problem-297-zeckendorf-representation
# --description--
-Each new term in the Fibonacci sequence is generated by adding the previous two terms.
+フィボナッチ数列の新しい項はそれぞれ、前の 2 項を足すことによって得られます。
-Starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
+1 と 2 から始まる最初の 10 項は 1, 2, 3, 5, 8, 13, 21, 34, 55, 89 です。
-Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89.
+すべての正の整数は、フィボナッチ数列の非連続項の和として一意に表すことができます。 例えば、100 = 3 + 8 + 89です。
-Such a sum is called the Zeckendorf representation of the number.
+このような和は、数のゼッケンドルフ表現と呼ばれます。
-For any integer $n>0$, let $z(n)$ be the number of terms in the Zeckendorf representation of $n$.
+任意の整数 $n>0$ について、$n$ のゼッケンドルフ表現における項数を $z(n)$ とします。
-Thus, $z(5) = 1$, $z(14) = 2$, $z(100) = 3$ etc.
+すなわち、$z(5) = 1$, $z(14) = 2$, $z(100) = 3$ などです。
-Also, for $0 < n < {10}^6$, $\sum z(n) = 7\\,894\\,453$.
+また、$0 < < {10}^6$ のとき、$\sum z(n) = 7\\,894\\,453$ です。
-Find $\sum z(n)$ for $0 < n < {10}^{17}$.
+$0 < n < {10}^{17}$ のとき、$\sum z(n)$ を求めなさい。
# --hints--
-`zeckendorfRepresentation()` should return `2252639041804718000`.
+`zeckendorfRepresentation()` は `2252639041804718000` を返す必要があります。
```js
assert.strictEqual(zeckendorfRepresentation(), 2252639041804718000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
index cfa8aa205b..7338217576 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
@@ -1,6 +1,6 @@
---
id: 5900f4971000cf542c50ffa9
-title: 'Problem 298: Selective Amnesia'
+title: '問題 298: 選択的健忘'
challengeType: 5
forumTopicId: 301950
dashedName: problem-298-selective-amnesia
@@ -8,30 +8,30 @@ dashedName: problem-298-selective-amnesia
# --description--
-Larry and Robin play a memory game involving of a sequence of random numbers between 1 and 10, inclusive, that are called out one at a time. Each player can remember up to 5 previous numbers. When the called number is in a player's memory, that player is awarded a point. If it's not, the player adds the called number to his memory, removing another number if his memory is full.
+ラリーとロビンが記憶ゲームをします。1 から 10 のうち無作為に選ばれた数が一度に 1 つずつ呼び出されます。 各プレイヤーは、以前の数を最大 5 つ記憶できます。 呼び出された数がプレイヤーの記憶にあれば、1 点が与えられます。 記憶になければ、プレイヤーは呼び出された数を自分の記憶に加え、もし記憶が一杯であれば他の数を 1 つ記憶から消します。
-Both players start with empty memories. Both players always add new missed numbers to their memory but use a different strategy in deciding which number to remove: Larry's strategy is to remove the number that hasn't been called in the longest time. Robin's strategy is to remove the number that's been in the memory the longest time.
+開始時、2 人のプレイヤーの記憶は空です。 両プレイヤーは、記憶になかった新しい数を必ず記憶に加えますが、どの数を消すかを決めるための戦略が異なります。ラリーの戦略は、最も長い間呼び出されなかった数を消すことです。 ロビンの戦略は、最も長く記憶にとどまっていた数を消すことです。
-Example game:
+ゲームの例:
-| Turn | Called number | Larry's memory | Larry's score | Robin's memory | Robin's score |
-| ---- | ------------- | --------------:| ------------- | -------------- | ------------- |
-| 1 | 1 | 1 | 0 | 1 | 0 |
-| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
-| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
-| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
-| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
-| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
-| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
-| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
-| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
-| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
+| ターン | 呼び出された番号 | ラリーの記憶 | ラリーのスコア | ロビンの記憶 | ロビンのスコア |
+| --- | -------- | ----------:| ------- | ---------- | ------- |
+| 1 | 1 | 1 | 0 | 1 | 0 |
+| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
+| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
+| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
+| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
+| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
+| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
+| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
+| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
+| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
-Denoting Larry's score by $L$ and Robin's score by $R$, what is the expected value of $|L - R|$ after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+ラリーのスコアを $L$、ロビンのスコアを $R$ で表すものとし、50 ターン後の $|L-R|$ の期待値を求めなさい。 回答は、四捨五入して小数第 8 位まで求め、x.xxxxxxxx の形式にすること。
# --hints--
-`selectiveAmnesia()` should return `1.76882294`.
+`selectiveAmnesia()` は `1.76882294` を返す必要があります。
```js
assert.strictEqual(selectiveAmnesia(), 1.76882294);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
index 19cdc14e04..4d77f4dace 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4971000cf542c50ffaa
-title: 'Problem 299: Three similar triangles'
+title: '問題 299: 3 つの相似三角形'
challengeType: 5
forumTopicId: 301951
dashedName: problem-299-three-similar-triangles
@@ -8,29 +8,29 @@ dashedName: problem-299-three-similar-triangles
# --description--
-Four points with integer coordinates are selected:
+整数座標を持つ、次の 4 つの点が選択されます。
-$A(a, 0)$, $B(b, 0)$, $C(0, c)$ and $D(0, d)$, with $0 < a < b$ and $0 < c < d$.
+$A(a, 0)$, $B(b, 0)$, $C(0, c)$, $D(0, d)$ ($0 < a < b$ かつ $0 < c < d$)
-Point $P$, also with integer coordinates, is chosen on the line $AC$ so that the three triangles $ABP$, $CDP$ and $BDP$ are all similar.
+3 つの三角形 $ABP$, $CDP$, $BDP$ がすべて相似形になるように、同じく整数座標を持つ点 $P$ を線 $AC$ 上で選びます。
-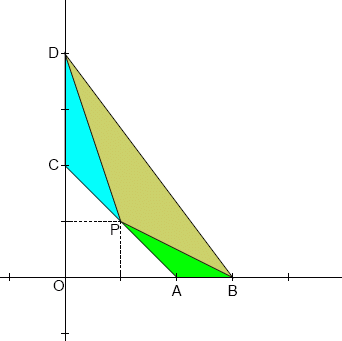 +
+ -It is easy to prove that the three triangles can be similar, only if $a = c$.
+$a = c$ のときのみ 3 つの三角形が相似形になり得るということは、容易に証明できます。
-So, given that $a = c$, we are looking for triplets ($a$, $b$, $d$) such that at least one point $P$ (with integer coordinates) exists on $AC$, making the three triangles $ABP$, $CDP$ and $BDP$ all similar.
+つまり、$a=c$ とすると、(整数座標を持つ) 点 $P$ が $AC$ 上に少なくとも 1 つ存在して 3 つの三角形 $ABP$, $CDP$, $BDP$ がすべて相似形になるような、三つ組数 ($a$, $b$, $d$) を探します。
-For example, if $(a, b, d) = (2, 3, 4)$, it can be easily verified that point $P(1, 1)$ satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point $P(1, 1)$ is common for both.
+例えば、$(a, b, d) = (2, 3, 4)$ の場合、点 $P(1, 1)$ が上の条件を満たすことを容易に確認できます。 注意点として、三つ組数 (2,3,4) と (2,4,3) は点 $P(1, 1)$ を共有しますが相異なる組とみなされます。
-If $b + d < 100$, there are 92 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+$b + d < 100$ の場合、点 $P$ が存在するような相異なる三つ組数 ($a$, $b$, $d$) は 92 個存在します。
-If $b + d < 100\\,000$, there are 320471 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+$b + d < 100\\,000$ の場合、点 $P$ が存在するような相異なる三つ組数 ($a$, $b$, $d$) は 320471 個存在します。
-If $b + d < 100\\,000\\,000$, how many distinct triplets ($a$, $b$, $d$) are there such that point $P$ exists?
+$b + d < 100\\,000\\,000$ の場合、点 $P$ が存在するような相異なる三つ組数 ($a$, $b$, $d$) はいくつ存在しますか。
# --hints--
-`threeSimilarTriangles()` should return `549936643`.
+`threeSimilarTriangles()` は `549936643` を返す必要があります。
```js
assert.strictEqual(threeSimilarTriangles(), 549936643);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
index 26526c4497..7ecb6fd9ab 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
@@ -1,6 +1,6 @@
---
id: 5900f49a1000cf542c50ffac
-title: 'Problem 300: Protein folding'
+title: '問題 300: タンパク質の折り畳み'
challengeType: 5
forumTopicId: 301954
dashedName: problem-300-protein-folding
@@ -8,29 +8,29 @@ dashedName: problem-300-protein-folding
# --description--
-In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
+非常に単純化すれば、タンパク質は疎水性要素 (H) と極性要素 (P) で構成される文字列と考えることができます。例えば、HHPPHHHPHHPH です。
-For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are $2^n$ distinct proteins consisting of $n$ elements.
+この問題ではタンパク質の方向が重要であり、例えば HPP は PPH と区別されます。 したがって、$n$ 個の要素で構成される相異なるタンパク質は $2^n$ 種類存在します。
-When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
+自然界では、これらの文字列は常に H-H 接点の数ができるだけ多くなるように折り畳まれています。その方がエネルギー面で有利だからです。
-As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
+その結果、H 要素は内側に蓄積し、P 要素は外側に蓄積する傾向があります。
-Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
+自然のタンパク質はもちろん三次元で折り畳まれていますが、ここでは二次元で折り畳まれるタンパク質のみを考えます。
-The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
+下図は、上の例のタンパク質を折り畳む 2 通りの方法を示しています (赤い点は H-H 接点)。
-
-It is easy to prove that the three triangles can be similar, only if $a = c$.
+$a = c$ のときのみ 3 つの三角形が相似形になり得るということは、容易に証明できます。
-So, given that $a = c$, we are looking for triplets ($a$, $b$, $d$) such that at least one point $P$ (with integer coordinates) exists on $AC$, making the three triangles $ABP$, $CDP$ and $BDP$ all similar.
+つまり、$a=c$ とすると、(整数座標を持つ) 点 $P$ が $AC$ 上に少なくとも 1 つ存在して 3 つの三角形 $ABP$, $CDP$, $BDP$ がすべて相似形になるような、三つ組数 ($a$, $b$, $d$) を探します。
-For example, if $(a, b, d) = (2, 3, 4)$, it can be easily verified that point $P(1, 1)$ satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point $P(1, 1)$ is common for both.
+例えば、$(a, b, d) = (2, 3, 4)$ の場合、点 $P(1, 1)$ が上の条件を満たすことを容易に確認できます。 注意点として、三つ組数 (2,3,4) と (2,4,3) は点 $P(1, 1)$ を共有しますが相異なる組とみなされます。
-If $b + d < 100$, there are 92 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+$b + d < 100$ の場合、点 $P$ が存在するような相異なる三つ組数 ($a$, $b$, $d$) は 92 個存在します。
-If $b + d < 100\\,000$, there are 320471 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+$b + d < 100\\,000$ の場合、点 $P$ が存在するような相異なる三つ組数 ($a$, $b$, $d$) は 320471 個存在します。
-If $b + d < 100\\,000\\,000$, how many distinct triplets ($a$, $b$, $d$) are there such that point $P$ exists?
+$b + d < 100\\,000\\,000$ の場合、点 $P$ が存在するような相異なる三つ組数 ($a$, $b$, $d$) はいくつ存在しますか。
# --hints--
-`threeSimilarTriangles()` should return `549936643`.
+`threeSimilarTriangles()` は `549936643` を返す必要があります。
```js
assert.strictEqual(threeSimilarTriangles(), 549936643);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
index 26526c4497..7ecb6fd9ab 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
@@ -1,6 +1,6 @@
---
id: 5900f49a1000cf542c50ffac
-title: 'Problem 300: Protein folding'
+title: '問題 300: タンパク質の折り畳み'
challengeType: 5
forumTopicId: 301954
dashedName: problem-300-protein-folding
@@ -8,29 +8,29 @@ dashedName: problem-300-protein-folding
# --description--
-In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
+非常に単純化すれば、タンパク質は疎水性要素 (H) と極性要素 (P) で構成される文字列と考えることができます。例えば、HHPPHHHPHHPH です。
-For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are $2^n$ distinct proteins consisting of $n$ elements.
+この問題ではタンパク質の方向が重要であり、例えば HPP は PPH と区別されます。 したがって、$n$ 個の要素で構成される相異なるタンパク質は $2^n$ 種類存在します。
-When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
+自然界では、これらの文字列は常に H-H 接点の数ができるだけ多くなるように折り畳まれています。その方がエネルギー面で有利だからです。
-As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
+その結果、H 要素は内側に蓄積し、P 要素は外側に蓄積する傾向があります。
-Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
+自然のタンパク質はもちろん三次元で折り畳まれていますが、ここでは二次元で折り畳まれるタンパク質のみを考えます。
-The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
+下図は、上の例のタンパク質を折り畳む 2 通りの方法を示しています (赤い点は H-H 接点)。
-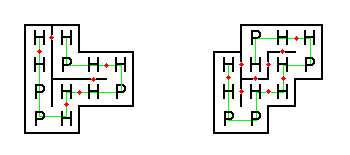 +
+ -The folding on the left has only six H-H contact points, thus it would never occur naturally. On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
+左側の折り畳みは H-H 接点が 6つしかないため、自然にこの形になることはあり得ないでしょう。 一方、右側の折り畳みは H-H 接点が 9 つあり、この文字列には最適です。
-Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be $\frac{850}{2^8} = 3.3203125$.
+文字列のいずれの位置にも H 要素と P 要素が同じ確率で存在すると仮定すると、長さ 8 の無作為なタンパク質文字列の最適な折り畳みにおいて、H-H 接点の平均数は $\frac{850}{2^8} = 3.3203125$ になります。
-What is the average number of H-H contact points in an optimal folding of a random protein string of length 15? Give your answer using as many decimal places as necessary for an exact result.
+長さ 15 の無作為なタンパク質文字列の最適な折り畳みにおいて、H-H 接点の平均数はいくつですか。 回答は、厳密な結果に対して適宜小数位を使用すること。
# --hints--
-`proteinFolding()` should return `8.0540771484375`.
+`proteinFolding()` は `8.0540771484375` を返す必要があります。
```js
assert.strictEqual(proteinFolding(), 8.0540771484375);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md
index 064b907f8c..a15adb4e36 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md
@@ -1,6 +1,6 @@
---
id: 5900f4991000cf542c50ffab
-title: 'Problem 301: Nim'
+title: '問題 301: ニム (石取りゲーム)'
challengeType: 5
forumTopicId: 301955
dashedName: problem-301-nim
@@ -8,31 +8,31 @@ dashedName: problem-301-nim
# --description--
-Nim is a game played with heaps of stones, where two players take it in turn to remove any number of stones from any heap until no stones remain.
+ニムは石が積まれた山で遊ぶゲームです。2 人のプレイヤーが交互に任意の山から任意の数の石を取り、石がなくなったら終了です。
-We'll consider the three-heap normal-play version of Nim, which works as follows:
+ここでは、3 つの山を使う一般的なニムの遊び方を考えます。ルールは次のとおりです。
-- At the start of the game there are three heaps of stones.
-- On his turn the player removes any positive number of stones from any single heap.
-- The first player unable to move (because no stones remain) loses.
+- 開始時、石の山が 3 つあります。
+- プレイヤーは自分のターンで、任意の 1 つの山から任意の正の整数個の石を取ります。
+- 先に (もう石がないために) 石を取れなくなったプレイヤーの負けです。
-If ($n_1$, $n_2$, $n_3$) indicates a Nim position consisting of heaps of size $n_1$, $n_2$ and $n_3$ then there is a simple function $X(n_1,n_2,n_3)$ — that you may look up or attempt to deduce for yourself — that returns:
+サイズ $n_1$, $n_2$, $n_3$ の山がある場合のニムのポジションを ($n_1$, $n_2$, $n_3$) で表すとします。次の結果を返す単純な関数 $X(n_1,n_2,n_3)$ があります (この関数については自ら調べるか導出すること)。
-- zero if, with perfect strategy, the player about to move will eventually lose; or
-- non-zero if, with perfect strategy, the player about to move will eventually win.
+- 0: 完璧な戦略に基づけば、現在のプレイヤー(今、自分の番を迎えている人) が最終的に負ける。
+- 0 以外: 完璧な戦略に基づけば、現在のプレイヤー(今、自分の番を迎えている人) が最終的に勝つ。
-For example $X(1, 2, 3) = 0$ because, no matter what the current player does, his opponent can respond with a move that leaves two heaps of equal size, at which point every move by the current player can be mirrored by his opponent until no stones remain; so the current player loses. To illustrate:
+例えば、$X(1, 2, 3) = 0$ です。なぜなら現在のプレイヤーが何をしても、対戦相手は同じサイズの山を 2 つ残すように石を取れるからです。その時点で、以降に現在のプレイヤーがどのように石を取っても対戦相手が同じように取れることが確定し、現在のプレーヤーは負けます。 下に具体例を示します。
-- current player moves to (1,2,1)
-- opponent moves to (1,0,1)
-- current player moves to (0,0,1)
-- opponent moves to (0,0,0), and so wins.
+- 現在のプレイヤーがポジションを (1,2,1) にする
+- 対戦相手がポジションを (1,0,1) にする
+- 現在のプレイヤーがポジションを (0,0,1) にする
+- 対戦相手がポジションを (0,0,0) にし、勝つ。
-For how many positive integers $n ≤ 2^{30}$ does $X(n, 2n, 3n) = 0$?
+$X(n, 2n, 3n) = 0$ となる正の整数 $n ≤ 2^{30}$ はいくつありますか。
# --hints--
-`nim()` should return `2178309`.
+`nim()` は `2178309` を返す必要があります。
```js
assert.strictEqual(nim(), 2178309);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md
index a6a7c46645..a2d82a1031 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f49b1000cf542c50ffad
-title: 'Problem 302: Strong Achilles Numbers'
+title: '問題 302: 強力なアキレス数'
challengeType: 5
forumTopicId: 301956
dashedName: problem-302-strong-achilles-numbers
@@ -8,23 +8,23 @@ dashedName: problem-302-strong-achilles-numbers
# --description--
-A positive integer $n$ is powerful if $p^2$ is a divisor of $n$ for every prime factor $p$ in $n$.
+正の整数 $n$ のすべての素因数 $p$ について $p^2$ が $n$ の約数である場合、$n$ は多冪数です。
-A positive integer $n$ is a perfect power if $n$ can be expressed as a power of another positive integer.
+正の整数 $n$ を別の正の整数の累乗で表せる場合、$n$ は累乗数です。
-A positive integer $n$ is an Achilles number if $n$ is powerful but not a perfect power. For example, 864 and 1800 are Achilles numbers: $864 = 2^5 \times 3^3$ and $1800 = 2^3 \times 3^2 \times 5^2$.
+正の整数 $n$ が多冪数であるが累乗数ではない場合、$n$ はアキレス数です。 例えば、864 と 1800 はアキレス数です。それぞれ、$864 = 2^5 \times 3^3$ と $1800 = 2^3 \times 3^2 \times 5^2$ です。
-We shall call a positive integer $S$ a Strong Achilles number if both $S$ and $φ(S)$ are Achilles numbers. $φ$ denotes Euler's totient function.
+正の整数 $S$ と φ(S)$ の両方がアキレス数の場合、$S$ を「強力なアキレス数」と呼ぶことにします。 $φ$ はオイラーのトーティエント関数を表します。
-For example, 864 is a Strong Achilles number: $φ(864) = 288 = 2^5 \times 3^2$. However, 1800 isn't a Strong Achilles number because: $φ(1800) = 480 = 2^5 \times 3^1 \times 5^1$.
+例えば、864 は強力なアキレス数です。$φ(864) = 288 = 2^5 \times 3^2$ となるからです。 しかし、1800 は強力なアキレス数ではありません。$φ(1800) = 480 = 2^5 \times 3^1 \times 5^1$ となるからです。
-There are 7 Strong Achilles numbers below ${10}^4$ and 656 below ${10}^8$.
+強力なアキレス数は ${10}^4$ 未満に 7 つ、${10}^8$ 未満に 656 個あります。
-How many Strong Achilles numbers are there below ${10}^{18}$?
+${10}^{18}$ 未満の強力なアキレス数はいくつありますか。
# --hints--
-`strongAchillesNumbers()` should return `1170060`.
+`strongAchillesNumbers()` は `1170060` を返す必要があります。
```js
assert.strictEqual(strongAchillesNumbers(), 1170060);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md
index 75fca87cd5..f3aef7bf39 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md
@@ -1,6 +1,6 @@
---
id: 5900f49b1000cf542c50ffae
-title: 'Problem 303: Multiples with small digits'
+title: '問題 303: 小さい数字からなる倍数'
challengeType: 5
forumTopicId: 301957
dashedName: problem-303-multiples-with-small-digits
@@ -8,17 +8,17 @@ dashedName: problem-303-multiples-with-small-digits
# --description--
-For a positive integer $n$, define $f(n)$ as the least positive multiple of $n$ that, written in base 10, uses only digits $≤ 2$.
+正の整数 $n$ について、$n$ の最小の正の倍数であり 10 進数表記で 2 以下の数字のみを使用する数を、$f(n)$ とします。
-Thus $f(2) = 2$, $f(3) = 12$, $f(7) = 21$, $f(42) = 210$, $f(89) = 1\\,121\\,222$.
+したがって、$f(2) = 2$, $f(3) = 12$, $f(7) = 21$, $f(42) = 210$, $f(89) = 1\\,121\\,222$ です。
-Also, $\displaystyle\sum_{n = 1}^{100} \frac{f(n)}{n} = 11\\,363\\,107$.
+また、$\displaystyle\sum_{n = 1}^{100} \frac{f(n)}{n} = 11\\,363\\,107$ です。
-Find $\displaystyle\sum_{n = 1}^{10\\,000} \frac{f(n)}{n}$.
+$\displaystyle\sum_{n = 1}^{10\\000} \frac{f(n)}{n} $ を求めなさい。
# --hints--
-`multiplesWithSmallDigits()` should return `1111981904675169`.
+`multiplesWithSmallDigits()` は `1111981904675169` を返す必要があります。
```js
assert.strictEqual(multiplesWithSmallDigits(), 1111981904675169);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md
index add0b83c8b..08d604c715 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md
@@ -1,6 +1,6 @@
---
id: 5900f49d1000cf542c50ffaf
-title: 'Problem 304: Primonacci'
+title: '問題 304: 素数フィボナッチ数列 (Primonacci)'
challengeType: 5
forumTopicId: 301958
dashedName: problem-304-primonacci
@@ -8,19 +8,19 @@ dashedName: problem-304-primonacci
# --description--
-For any positive integer $n$ the function $\text{next_prime}(n)$ returns the smallest prime $p$ such that $p > n$.
+任意の正の整数 $n$ について、関数 $\text{next_prime}(n)$ は、$p > n$ を満たす最小の素数 $p$ を返します。
-The sequence $a(n)$ is defined by: $a(1) = \text{next_prime}({10}^{14})$ and $a(n) = \text{next_prime}(a(n - 1))$ for $n > 1$.
+数列 $a(n)$ は次のように定義されます: $n > 1$ のとき、$a(1) = \text{next_prime}({10}^{14})$, $a(n) = \text{next_prime}(a(n - 1))$
-The fibonacci sequence $f(n)$ is defined by: $f(0) = 0$, $f(1) = 1$ and $f(n) = f(n - 1) + f(n - 2)$ for $n > 1$.
+フィボナッチ数列 $f(n)$ は次のように定義されます: $n > 1$ のとき、$f(0) = 0$, $f(1) = 1$, $f(n) = f(n - 1) + f(n - 2)$
-The sequence $b(n)$ is defined as $f(a(n))$.
+数列 $b(n)$ は $f(a(n))$ と定義されます。
-Find $\sum b(n)$ for $1≤n≤100\\,000$. Give your answer $\bmod 1\\,234\\,567\\,891\\,011$.
+$1 ≤ n ≤ 100\\,000$ のとき、$\sum b(n)$ を求めなさい。 $\bmod 1\\,234\\,567\\,891\\,011$ で答えること。
# --hints--
-`primonacci()` should return `283988410192`.
+`primonacci()` は `283988410192` を返す必要があります。
```js
assert.strictEqual(primonacci(), 283988410192);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md
index eff1a148a8..6a7128bd4b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md
@@ -1,6 +1,6 @@
---
id: 5900f49d1000cf542c50ffb0
-title: 'Problem 305: Reflexive Position'
+title: '問題 305: 再帰位置'
challengeType: 5
forumTopicId: 301959
dashedName: problem-305-reflexive-position
@@ -8,19 +8,19 @@ dashedName: problem-305-reflexive-position
# --description--
-Let's call $S$ the (infinite) string that is made by concatenating the consecutive positive integers (starting from 1) written down in base 10.
+10 進数表記の (1から始まる) 連続する正の整数を連結した (無限の) 文字列を、$S$ とします。
-Thus, $S = 1234567891011121314151617181920212223242\ldots$
+したがって、$S = 1234567891011121314151617181920212223242\ldots$ です。
-It's easy to see that any number will show up an infinite number of times in $S$.
+一見して分かるとおり、$S$ にはどの数字も無限に現れます。
-Let's call $f(n)$ the starting position of the $n^{\text{th}}$ occurrence of $n$ in $S$. For example, $f(1) = 1$, $f(5) = 81$, $f(12) = 271$ and $f(7780) = 111\\,111\\,365$.
+$S$ 内で $n$ が $n$ 回目に現れた開始位置を、$f(n)$ と定義します。 例えば、$f(1) = 1$, $f(5) = 81$, $f(12) = 271$, $f(7780) = 111\\,111\\,365$ です。
-Find $\sum f(3^k) for 1 ≤ k ≤ 13$.
+$1 ≤ k ≤ 13$ のとき、$\sum f(3^k) を求めなさい。
# --hints--
-`reflexivePosition()` should return `18174995535140`.
+`reflexivePosition()` は `18174995535140` を返す必要があります。
```js
assert.strictEqual(reflexivePosition(), 18174995535140);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md
index ac028b63fb..16494b4fee 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md
@@ -1,6 +1,6 @@
---
id: 5900f49f1000cf542c50ffb1
-title: 'Problem 306: Paper-strip Game'
+title: '問題 306: 短冊ゲーム'
challengeType: 5
forumTopicId: 301960
dashedName: problem-306-paper-strip-game
@@ -8,27 +8,27 @@ dashedName: problem-306-paper-strip-game
# --description--
-The following game is a classic example of Combinatorial Game Theory:
+次のゲームは、組み合わせゲーム理論の古典的な例です。
-Two players start with a strip of $n$ white squares and they take alternate turns. On each turn, a player picks two contiguous white squares and paints them black. The first player who cannot make a move loses.
+一列に並べた $n$ 個の白いマスが最初にあり、2 人のプレイヤーが交互にプレイしていきます。 それぞれのターンで、プレイヤーは連続する白いマスを 2 つ選び、それらを黒く塗ります。 先にどこも塗れなくなったプレイヤーの負けです。
-- $n = 1$: No valid moves, so the first player loses automatically.
-- $n = 2$: Only one valid move, after which the second player loses.
-- $n = 3$: Two valid moves, but both leave a situation where the second player loses.
-- $n = 4$: There are three valid moves for the first player; who is able to win the game by painting the two middle squares.
-- $n = 5$: Four valid moves for the first player (shown below in red); but no matter what the player does, the second player (blue) wins.
+- $n = 1$: 有効な塗り方がないため、先手が自動的に負けます。
+- $n = 2$: 有効な塗り方は 1 通りのみです。その後、後手が負けます。
+- $n = 3$: 有効な塗り方が 2 通りありますが、いずれでも後手が負けます。
+- $n = 4$: 先手には 3 通りの有効な塗り方があります。中央の 2 マスを塗れば勝てます。
+- $n = 5$: 先手には有効な塗り方が 4 通りありますが (下図の赤色)、いずれでも後手 (青) が勝ちます。
-
-The folding on the left has only six H-H contact points, thus it would never occur naturally. On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
+左側の折り畳みは H-H 接点が 6つしかないため、自然にこの形になることはあり得ないでしょう。 一方、右側の折り畳みは H-H 接点が 9 つあり、この文字列には最適です。
-Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be $\frac{850}{2^8} = 3.3203125$.
+文字列のいずれの位置にも H 要素と P 要素が同じ確率で存在すると仮定すると、長さ 8 の無作為なタンパク質文字列の最適な折り畳みにおいて、H-H 接点の平均数は $\frac{850}{2^8} = 3.3203125$ になります。
-What is the average number of H-H contact points in an optimal folding of a random protein string of length 15? Give your answer using as many decimal places as necessary for an exact result.
+長さ 15 の無作為なタンパク質文字列の最適な折り畳みにおいて、H-H 接点の平均数はいくつですか。 回答は、厳密な結果に対して適宜小数位を使用すること。
# --hints--
-`proteinFolding()` should return `8.0540771484375`.
+`proteinFolding()` は `8.0540771484375` を返す必要があります。
```js
assert.strictEqual(proteinFolding(), 8.0540771484375);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md
index 064b907f8c..a15adb4e36 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-301-nim.md
@@ -1,6 +1,6 @@
---
id: 5900f4991000cf542c50ffab
-title: 'Problem 301: Nim'
+title: '問題 301: ニム (石取りゲーム)'
challengeType: 5
forumTopicId: 301955
dashedName: problem-301-nim
@@ -8,31 +8,31 @@ dashedName: problem-301-nim
# --description--
-Nim is a game played with heaps of stones, where two players take it in turn to remove any number of stones from any heap until no stones remain.
+ニムは石が積まれた山で遊ぶゲームです。2 人のプレイヤーが交互に任意の山から任意の数の石を取り、石がなくなったら終了です。
-We'll consider the three-heap normal-play version of Nim, which works as follows:
+ここでは、3 つの山を使う一般的なニムの遊び方を考えます。ルールは次のとおりです。
-- At the start of the game there are three heaps of stones.
-- On his turn the player removes any positive number of stones from any single heap.
-- The first player unable to move (because no stones remain) loses.
+- 開始時、石の山が 3 つあります。
+- プレイヤーは自分のターンで、任意の 1 つの山から任意の正の整数個の石を取ります。
+- 先に (もう石がないために) 石を取れなくなったプレイヤーの負けです。
-If ($n_1$, $n_2$, $n_3$) indicates a Nim position consisting of heaps of size $n_1$, $n_2$ and $n_3$ then there is a simple function $X(n_1,n_2,n_3)$ — that you may look up or attempt to deduce for yourself — that returns:
+サイズ $n_1$, $n_2$, $n_3$ の山がある場合のニムのポジションを ($n_1$, $n_2$, $n_3$) で表すとします。次の結果を返す単純な関数 $X(n_1,n_2,n_3)$ があります (この関数については自ら調べるか導出すること)。
-- zero if, with perfect strategy, the player about to move will eventually lose; or
-- non-zero if, with perfect strategy, the player about to move will eventually win.
+- 0: 完璧な戦略に基づけば、現在のプレイヤー(今、自分の番を迎えている人) が最終的に負ける。
+- 0 以外: 完璧な戦略に基づけば、現在のプレイヤー(今、自分の番を迎えている人) が最終的に勝つ。
-For example $X(1, 2, 3) = 0$ because, no matter what the current player does, his opponent can respond with a move that leaves two heaps of equal size, at which point every move by the current player can be mirrored by his opponent until no stones remain; so the current player loses. To illustrate:
+例えば、$X(1, 2, 3) = 0$ です。なぜなら現在のプレイヤーが何をしても、対戦相手は同じサイズの山を 2 つ残すように石を取れるからです。その時点で、以降に現在のプレイヤーがどのように石を取っても対戦相手が同じように取れることが確定し、現在のプレーヤーは負けます。 下に具体例を示します。
-- current player moves to (1,2,1)
-- opponent moves to (1,0,1)
-- current player moves to (0,0,1)
-- opponent moves to (0,0,0), and so wins.
+- 現在のプレイヤーがポジションを (1,2,1) にする
+- 対戦相手がポジションを (1,0,1) にする
+- 現在のプレイヤーがポジションを (0,0,1) にする
+- 対戦相手がポジションを (0,0,0) にし、勝つ。
-For how many positive integers $n ≤ 2^{30}$ does $X(n, 2n, 3n) = 0$?
+$X(n, 2n, 3n) = 0$ となる正の整数 $n ≤ 2^{30}$ はいくつありますか。
# --hints--
-`nim()` should return `2178309`.
+`nim()` は `2178309` を返す必要があります。
```js
assert.strictEqual(nim(), 2178309);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md
index a6a7c46645..a2d82a1031 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-302-strong-achilles-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f49b1000cf542c50ffad
-title: 'Problem 302: Strong Achilles Numbers'
+title: '問題 302: 強力なアキレス数'
challengeType: 5
forumTopicId: 301956
dashedName: problem-302-strong-achilles-numbers
@@ -8,23 +8,23 @@ dashedName: problem-302-strong-achilles-numbers
# --description--
-A positive integer $n$ is powerful if $p^2$ is a divisor of $n$ for every prime factor $p$ in $n$.
+正の整数 $n$ のすべての素因数 $p$ について $p^2$ が $n$ の約数である場合、$n$ は多冪数です。
-A positive integer $n$ is a perfect power if $n$ can be expressed as a power of another positive integer.
+正の整数 $n$ を別の正の整数の累乗で表せる場合、$n$ は累乗数です。
-A positive integer $n$ is an Achilles number if $n$ is powerful but not a perfect power. For example, 864 and 1800 are Achilles numbers: $864 = 2^5 \times 3^3$ and $1800 = 2^3 \times 3^2 \times 5^2$.
+正の整数 $n$ が多冪数であるが累乗数ではない場合、$n$ はアキレス数です。 例えば、864 と 1800 はアキレス数です。それぞれ、$864 = 2^5 \times 3^3$ と $1800 = 2^3 \times 3^2 \times 5^2$ です。
-We shall call a positive integer $S$ a Strong Achilles number if both $S$ and $φ(S)$ are Achilles numbers. $φ$ denotes Euler's totient function.
+正の整数 $S$ と φ(S)$ の両方がアキレス数の場合、$S$ を「強力なアキレス数」と呼ぶことにします。 $φ$ はオイラーのトーティエント関数を表します。
-For example, 864 is a Strong Achilles number: $φ(864) = 288 = 2^5 \times 3^2$. However, 1800 isn't a Strong Achilles number because: $φ(1800) = 480 = 2^5 \times 3^1 \times 5^1$.
+例えば、864 は強力なアキレス数です。$φ(864) = 288 = 2^5 \times 3^2$ となるからです。 しかし、1800 は強力なアキレス数ではありません。$φ(1800) = 480 = 2^5 \times 3^1 \times 5^1$ となるからです。
-There are 7 Strong Achilles numbers below ${10}^4$ and 656 below ${10}^8$.
+強力なアキレス数は ${10}^4$ 未満に 7 つ、${10}^8$ 未満に 656 個あります。
-How many Strong Achilles numbers are there below ${10}^{18}$?
+${10}^{18}$ 未満の強力なアキレス数はいくつありますか。
# --hints--
-`strongAchillesNumbers()` should return `1170060`.
+`strongAchillesNumbers()` は `1170060` を返す必要があります。
```js
assert.strictEqual(strongAchillesNumbers(), 1170060);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md
index 75fca87cd5..f3aef7bf39 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-303-multiples-with-small-digits.md
@@ -1,6 +1,6 @@
---
id: 5900f49b1000cf542c50ffae
-title: 'Problem 303: Multiples with small digits'
+title: '問題 303: 小さい数字からなる倍数'
challengeType: 5
forumTopicId: 301957
dashedName: problem-303-multiples-with-small-digits
@@ -8,17 +8,17 @@ dashedName: problem-303-multiples-with-small-digits
# --description--
-For a positive integer $n$, define $f(n)$ as the least positive multiple of $n$ that, written in base 10, uses only digits $≤ 2$.
+正の整数 $n$ について、$n$ の最小の正の倍数であり 10 進数表記で 2 以下の数字のみを使用する数を、$f(n)$ とします。
-Thus $f(2) = 2$, $f(3) = 12$, $f(7) = 21$, $f(42) = 210$, $f(89) = 1\\,121\\,222$.
+したがって、$f(2) = 2$, $f(3) = 12$, $f(7) = 21$, $f(42) = 210$, $f(89) = 1\\,121\\,222$ です。
-Also, $\displaystyle\sum_{n = 1}^{100} \frac{f(n)}{n} = 11\\,363\\,107$.
+また、$\displaystyle\sum_{n = 1}^{100} \frac{f(n)}{n} = 11\\,363\\,107$ です。
-Find $\displaystyle\sum_{n = 1}^{10\\,000} \frac{f(n)}{n}$.
+$\displaystyle\sum_{n = 1}^{10\\000} \frac{f(n)}{n} $ を求めなさい。
# --hints--
-`multiplesWithSmallDigits()` should return `1111981904675169`.
+`multiplesWithSmallDigits()` は `1111981904675169` を返す必要があります。
```js
assert.strictEqual(multiplesWithSmallDigits(), 1111981904675169);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md
index add0b83c8b..08d604c715 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-304-primonacci.md
@@ -1,6 +1,6 @@
---
id: 5900f49d1000cf542c50ffaf
-title: 'Problem 304: Primonacci'
+title: '問題 304: 素数フィボナッチ数列 (Primonacci)'
challengeType: 5
forumTopicId: 301958
dashedName: problem-304-primonacci
@@ -8,19 +8,19 @@ dashedName: problem-304-primonacci
# --description--
-For any positive integer $n$ the function $\text{next_prime}(n)$ returns the smallest prime $p$ such that $p > n$.
+任意の正の整数 $n$ について、関数 $\text{next_prime}(n)$ は、$p > n$ を満たす最小の素数 $p$ を返します。
-The sequence $a(n)$ is defined by: $a(1) = \text{next_prime}({10}^{14})$ and $a(n) = \text{next_prime}(a(n - 1))$ for $n > 1$.
+数列 $a(n)$ は次のように定義されます: $n > 1$ のとき、$a(1) = \text{next_prime}({10}^{14})$, $a(n) = \text{next_prime}(a(n - 1))$
-The fibonacci sequence $f(n)$ is defined by: $f(0) = 0$, $f(1) = 1$ and $f(n) = f(n - 1) + f(n - 2)$ for $n > 1$.
+フィボナッチ数列 $f(n)$ は次のように定義されます: $n > 1$ のとき、$f(0) = 0$, $f(1) = 1$, $f(n) = f(n - 1) + f(n - 2)$
-The sequence $b(n)$ is defined as $f(a(n))$.
+数列 $b(n)$ は $f(a(n))$ と定義されます。
-Find $\sum b(n)$ for $1≤n≤100\\,000$. Give your answer $\bmod 1\\,234\\,567\\,891\\,011$.
+$1 ≤ n ≤ 100\\,000$ のとき、$\sum b(n)$ を求めなさい。 $\bmod 1\\,234\\,567\\,891\\,011$ で答えること。
# --hints--
-`primonacci()` should return `283988410192`.
+`primonacci()` は `283988410192` を返す必要があります。
```js
assert.strictEqual(primonacci(), 283988410192);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md
index eff1a148a8..6a7128bd4b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-305-reflexive-position.md
@@ -1,6 +1,6 @@
---
id: 5900f49d1000cf542c50ffb0
-title: 'Problem 305: Reflexive Position'
+title: '問題 305: 再帰位置'
challengeType: 5
forumTopicId: 301959
dashedName: problem-305-reflexive-position
@@ -8,19 +8,19 @@ dashedName: problem-305-reflexive-position
# --description--
-Let's call $S$ the (infinite) string that is made by concatenating the consecutive positive integers (starting from 1) written down in base 10.
+10 進数表記の (1から始まる) 連続する正の整数を連結した (無限の) 文字列を、$S$ とします。
-Thus, $S = 1234567891011121314151617181920212223242\ldots$
+したがって、$S = 1234567891011121314151617181920212223242\ldots$ です。
-It's easy to see that any number will show up an infinite number of times in $S$.
+一見して分かるとおり、$S$ にはどの数字も無限に現れます。
-Let's call $f(n)$ the starting position of the $n^{\text{th}}$ occurrence of $n$ in $S$. For example, $f(1) = 1$, $f(5) = 81$, $f(12) = 271$ and $f(7780) = 111\\,111\\,365$.
+$S$ 内で $n$ が $n$ 回目に現れた開始位置を、$f(n)$ と定義します。 例えば、$f(1) = 1$, $f(5) = 81$, $f(12) = 271$, $f(7780) = 111\\,111\\,365$ です。
-Find $\sum f(3^k) for 1 ≤ k ≤ 13$.
+$1 ≤ k ≤ 13$ のとき、$\sum f(3^k) を求めなさい。
# --hints--
-`reflexivePosition()` should return `18174995535140`.
+`reflexivePosition()` は `18174995535140` を返す必要があります。
```js
assert.strictEqual(reflexivePosition(), 18174995535140);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md
index ac028b63fb..16494b4fee 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-306-paper-strip-game.md
@@ -1,6 +1,6 @@
---
id: 5900f49f1000cf542c50ffb1
-title: 'Problem 306: Paper-strip Game'
+title: '問題 306: 短冊ゲーム'
challengeType: 5
forumTopicId: 301960
dashedName: problem-306-paper-strip-game
@@ -8,27 +8,27 @@ dashedName: problem-306-paper-strip-game
# --description--
-The following game is a classic example of Combinatorial Game Theory:
+次のゲームは、組み合わせゲーム理論の古典的な例です。
-Two players start with a strip of $n$ white squares and they take alternate turns. On each turn, a player picks two contiguous white squares and paints them black. The first player who cannot make a move loses.
+一列に並べた $n$ 個の白いマスが最初にあり、2 人のプレイヤーが交互にプレイしていきます。 それぞれのターンで、プレイヤーは連続する白いマスを 2 つ選び、それらを黒く塗ります。 先にどこも塗れなくなったプレイヤーの負けです。
-- $n = 1$: No valid moves, so the first player loses automatically.
-- $n = 2$: Only one valid move, after which the second player loses.
-- $n = 3$: Two valid moves, but both leave a situation where the second player loses.
-- $n = 4$: There are three valid moves for the first player; who is able to win the game by painting the two middle squares.
-- $n = 5$: Four valid moves for the first player (shown below in red); but no matter what the player does, the second player (blue) wins.
+- $n = 1$: 有効な塗り方がないため、先手が自動的に負けます。
+- $n = 2$: 有効な塗り方は 1 通りのみです。その後、後手が負けます。
+- $n = 3$: 有効な塗り方が 2 通りありますが、いずれでも後手が負けます。
+- $n = 4$: 先手には 3 通りの有効な塗り方があります。中央の 2 マスを塗れば勝てます。
+- $n = 5$: 先手には有効な塗り方が 4 通りありますが (下図の赤色)、いずれでも後手 (青) が勝ちます。
-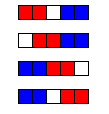 +
+ -So, for $1 ≤ n ≤ 5$, there are 3 values of $n$ for which the first player can force a win.
+したがって、$1 ≤ n ≤ 5$ のとき、先手が必ず勝てるような $n$ の値は 3 つあります。
-Similarly, for $1 ≤ n ≤ 50$, there are 40 values of $n$ for which the first player can force a win.
+同様に、$1 ≤ n ≤ 50$ のとき、先手が必ず勝てるような $n$ の値は 40 個あります。
-For $1 ≤ n ≤ 1\\,000\\,000$, how many values of $n$ are there for which the first player can force a win?
+$1 ≤ n ≤ 1\\,000\\,000$ のとき、先手が必ず勝てるような $n$ の値はいつくありますか。
# --hints--
-`paperStripGame()` should return `852938`.
+`paperStripGame()` は `852938` を返す必要があります。
```js
assert.strictEqual(paperStripGame(), 852938);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md
index b23c87918d..b2b5cbb8dc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md
@@ -1,6 +1,6 @@
---
id: 5900f4a01000cf542c50ffb2
-title: 'Problem 307: Chip Defects'
+title: '問題 307: IC チップの不良'
challengeType: 5
forumTopicId: 301961
dashedName: problem-307-chip-defects
@@ -8,15 +8,15 @@ dashedName: problem-307-chip-defects
# --description--
-$k$ defects are randomly distributed amongst $n$ integrated-circuit chips produced by a factory (any number of defects may be found on a chip and each defect is independent of the other defects).
+工場で製造される IC チップ $n$ 個において $k$ 件の不良が不規則に生じます (1 個のチップに何件でも不良が生じる可能性があり、それぞれの不良は他の不良から独立しています)。
-Let $p(k,n)$ represent the probability that there is a chip with at least 3 defects. For instance $p(3,7) ≈ 0.0204081633$.
+少なくとも 3 件の不良を持つチップが存在する確率を、$p(k,n)$ とします。 例えば、$p(3,7) ≈ 0.0204081633$ です。
-Find $p(20\\,000, 1\\,000\\,000)$ and give your answer rounded to 10 decimal places in the form 0.abcdefghij
+$p(20\\,000, 1\\,000\\,000)$ を求め、小数第 10 位に四捨五入して 0.abcdefghij の形式弟答えなさい。
# --hints--
-`chipDefects()` should return `0.7311720251`.
+`chipDefects()` は `0.7311720251` を返す必要があります。
```js
assert.strictEqual(chipDefects(), 0.7311720251);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md
index 066f71c105..360f652d3b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md
@@ -1,6 +1,6 @@
---
id: 5900f4a11000cf542c50ffb3
-title: 'Problem 308: An amazing Prime-generating Automaton'
+title: '問題 308: 驚くべき素数生成オートマトン'
challengeType: 5
forumTopicId: 301962
dashedName: problem-308-an-amazing-prime-generating-automaton
@@ -8,27 +8,27 @@ dashedName: problem-308-an-amazing-prime-generating-automaton
# --description--
-A program written in the programming language Fractran consists of a list of fractions.
+プログラミング言語 Fractran で書かれたプログラムは、分数のリストで構成されています。
-The internal state of the Fractran Virtual Machine is a positive integer, which is initially set to a seed value. Each iteration of a Fractran program multiplies the state integer by the first fraction in the list which will leave it an integer.
+Fractran 仮想マシンの内部状態は正の整数で、最初はシード値に設定されます。 Fractran プログラムは 1 回の反復ごとに、状態整数にリストの最初の分数を乗じて整数を得ます。
-For example, one of the Fractran programs that John Horton Conway wrote for prime-generation consists of the following 14 fractions:
+例えば、ジョン・ホートン・コンウェイが素数生成用に作成した Fractran プログラムの一つは、次の 14 個の分数で構成されています。
$$\frac{17}{91}, \frac{78}{85}, \frac{19}{51}, \frac{23}{38}, \frac{29}{33}, \frac{77}{29}, \frac{95}{23}, \frac{77}{19}, \frac{1}{17}, \frac{11}{13}, \frac{13}{11}, \frac{15}{2}, \frac{1}{7}, \frac{55}{1}$$
-Starting with the seed integer 2, successive iterations of the program produce the sequence:
+整数 2 のシード値から始めてプログラムの反復を続けると、次の数列が生成されます。
$$15, 825, 725, 1925, 2275, 425, \ldots, 68, \mathbf{4}, 30, \ldots, 136, \mathbf{8}, 60, \ldots, 544, \mathbf{32}, 240, \ldots$$
-The powers of 2 that appear in this sequence are $2^2, 2^3, 2^5, \ldots$.
+この数列に現れる 2 の累乗は $2^2, 2^3, 2^5, \ldots$ です。
-It can be shown that all the powers of 2 in this sequence have prime exponents and that all the primes appear as exponents of powers of 2, in proper order!
+この数列にある 2 の累乗はいずれも指数が素数であること、および、すべての素数が 2 の累乗の指数として順序通りに現れるということを示せます。
-If someone uses the above Fractran program to solve Project Euler Problem 7 (find the ${10001}^{\text{st}}$ prime), how many iterations would be needed until the program produces $2^{10001^{\text{st}}\text{ prime}}$?
+上の Fractran のプログラムを使用してプロジェクト・オイラーの問題 7 (${10001}$ 番目の素数を求める) を解くとしたら、$2^{10001 {\text{ 番目の}}\text{素数}}$ を生成するまでにプログラムを何回反復する必要がありますか。
# --hints--
-`primeGeneratingAutomation()` should return `1539669807660924`.
+`primeGeneratingAutomation()` は `1539669807660924` を返す必要があります 。
```js
assert.strictEqual(primeGeneratingAutomation(), 1539669807660924);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md
index 96e3664b5f..365a1c7d63 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md
@@ -1,6 +1,6 @@
---
id: 5900f4a11000cf542c50ffb4
-title: 'Problem 309: Integer Ladders'
+title: '問題 309: 整数のはしご'
challengeType: 5
forumTopicId: 301963
dashedName: problem-309-integer-ladders
@@ -8,19 +8,19 @@ dashedName: problem-309-integer-ladders
# --description--
-In the classic "Crossing Ladders" problem, we are given the lengths $x$ and $y$ of two ladders resting on the opposite walls of a narrow, level street. We are also given the height $h$ above the street where the two ladders cross and we are asked to find the width of the street ($w$).
+古典的な「交差するはしご」問題では、それぞれの長さが $x$ と $y$ のはしご 2 本が、狭く平らな道の両壁に 1 本ずつ立て掛けられています。 また、2 本のはしごが交差する個所の、路面からの高さ $h$ が与えられ、道幅 ($w$) を導くよう求められます。
-
-So, for $1 ≤ n ≤ 5$, there are 3 values of $n$ for which the first player can force a win.
+したがって、$1 ≤ n ≤ 5$ のとき、先手が必ず勝てるような $n$ の値は 3 つあります。
-Similarly, for $1 ≤ n ≤ 50$, there are 40 values of $n$ for which the first player can force a win.
+同様に、$1 ≤ n ≤ 50$ のとき、先手が必ず勝てるような $n$ の値は 40 個あります。
-For $1 ≤ n ≤ 1\\,000\\,000$, how many values of $n$ are there for which the first player can force a win?
+$1 ≤ n ≤ 1\\,000\\,000$ のとき、先手が必ず勝てるような $n$ の値はいつくありますか。
# --hints--
-`paperStripGame()` should return `852938`.
+`paperStripGame()` は `852938` を返す必要があります。
```js
assert.strictEqual(paperStripGame(), 852938);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md
index b23c87918d..b2b5cbb8dc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-307-chip-defects.md
@@ -1,6 +1,6 @@
---
id: 5900f4a01000cf542c50ffb2
-title: 'Problem 307: Chip Defects'
+title: '問題 307: IC チップの不良'
challengeType: 5
forumTopicId: 301961
dashedName: problem-307-chip-defects
@@ -8,15 +8,15 @@ dashedName: problem-307-chip-defects
# --description--
-$k$ defects are randomly distributed amongst $n$ integrated-circuit chips produced by a factory (any number of defects may be found on a chip and each defect is independent of the other defects).
+工場で製造される IC チップ $n$ 個において $k$ 件の不良が不規則に生じます (1 個のチップに何件でも不良が生じる可能性があり、それぞれの不良は他の不良から独立しています)。
-Let $p(k,n)$ represent the probability that there is a chip with at least 3 defects. For instance $p(3,7) ≈ 0.0204081633$.
+少なくとも 3 件の不良を持つチップが存在する確率を、$p(k,n)$ とします。 例えば、$p(3,7) ≈ 0.0204081633$ です。
-Find $p(20\\,000, 1\\,000\\,000)$ and give your answer rounded to 10 decimal places in the form 0.abcdefghij
+$p(20\\,000, 1\\,000\\,000)$ を求め、小数第 10 位に四捨五入して 0.abcdefghij の形式弟答えなさい。
# --hints--
-`chipDefects()` should return `0.7311720251`.
+`chipDefects()` は `0.7311720251` を返す必要があります。
```js
assert.strictEqual(chipDefects(), 0.7311720251);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md
index 066f71c105..360f652d3b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-308-an-amazing-prime-generating-automaton.md
@@ -1,6 +1,6 @@
---
id: 5900f4a11000cf542c50ffb3
-title: 'Problem 308: An amazing Prime-generating Automaton'
+title: '問題 308: 驚くべき素数生成オートマトン'
challengeType: 5
forumTopicId: 301962
dashedName: problem-308-an-amazing-prime-generating-automaton
@@ -8,27 +8,27 @@ dashedName: problem-308-an-amazing-prime-generating-automaton
# --description--
-A program written in the programming language Fractran consists of a list of fractions.
+プログラミング言語 Fractran で書かれたプログラムは、分数のリストで構成されています。
-The internal state of the Fractran Virtual Machine is a positive integer, which is initially set to a seed value. Each iteration of a Fractran program multiplies the state integer by the first fraction in the list which will leave it an integer.
+Fractran 仮想マシンの内部状態は正の整数で、最初はシード値に設定されます。 Fractran プログラムは 1 回の反復ごとに、状態整数にリストの最初の分数を乗じて整数を得ます。
-For example, one of the Fractran programs that John Horton Conway wrote for prime-generation consists of the following 14 fractions:
+例えば、ジョン・ホートン・コンウェイが素数生成用に作成した Fractran プログラムの一つは、次の 14 個の分数で構成されています。
$$\frac{17}{91}, \frac{78}{85}, \frac{19}{51}, \frac{23}{38}, \frac{29}{33}, \frac{77}{29}, \frac{95}{23}, \frac{77}{19}, \frac{1}{17}, \frac{11}{13}, \frac{13}{11}, \frac{15}{2}, \frac{1}{7}, \frac{55}{1}$$
-Starting with the seed integer 2, successive iterations of the program produce the sequence:
+整数 2 のシード値から始めてプログラムの反復を続けると、次の数列が生成されます。
$$15, 825, 725, 1925, 2275, 425, \ldots, 68, \mathbf{4}, 30, \ldots, 136, \mathbf{8}, 60, \ldots, 544, \mathbf{32}, 240, \ldots$$
-The powers of 2 that appear in this sequence are $2^2, 2^3, 2^5, \ldots$.
+この数列に現れる 2 の累乗は $2^2, 2^3, 2^5, \ldots$ です。
-It can be shown that all the powers of 2 in this sequence have prime exponents and that all the primes appear as exponents of powers of 2, in proper order!
+この数列にある 2 の累乗はいずれも指数が素数であること、および、すべての素数が 2 の累乗の指数として順序通りに現れるということを示せます。
-If someone uses the above Fractran program to solve Project Euler Problem 7 (find the ${10001}^{\text{st}}$ prime), how many iterations would be needed until the program produces $2^{10001^{\text{st}}\text{ prime}}$?
+上の Fractran のプログラムを使用してプロジェクト・オイラーの問題 7 (${10001}$ 番目の素数を求める) を解くとしたら、$2^{10001 {\text{ 番目の}}\text{素数}}$ を生成するまでにプログラムを何回反復する必要がありますか。
# --hints--
-`primeGeneratingAutomation()` should return `1539669807660924`.
+`primeGeneratingAutomation()` は `1539669807660924` を返す必要があります 。
```js
assert.strictEqual(primeGeneratingAutomation(), 1539669807660924);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md
index 96e3664b5f..365a1c7d63 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-309-integer-ladders.md
@@ -1,6 +1,6 @@
---
id: 5900f4a11000cf542c50ffb4
-title: 'Problem 309: Integer Ladders'
+title: '問題 309: 整数のはしご'
challengeType: 5
forumTopicId: 301963
dashedName: problem-309-integer-ladders
@@ -8,19 +8,19 @@ dashedName: problem-309-integer-ladders
# --description--
-In the classic "Crossing Ladders" problem, we are given the lengths $x$ and $y$ of two ladders resting on the opposite walls of a narrow, level street. We are also given the height $h$ above the street where the two ladders cross and we are asked to find the width of the street ($w$).
+古典的な「交差するはしご」問題では、それぞれの長さが $x$ と $y$ のはしご 2 本が、狭く平らな道の両壁に 1 本ずつ立て掛けられています。 また、2 本のはしごが交差する個所の、路面からの高さ $h$ が与えられ、道幅 ($w$) を導くよう求められます。
-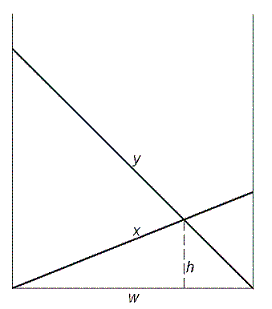 +
+ -Here, we are only concerned with instances where all four variables are positive integers. For example, if $x = 70$, $y = 119$ and $h = 30$, we can calculate that $w = 56$.
+ここでは、4 つの変数がすべて正の整数であるケースのみを扱います。 例えば、$x = 70$, $y = 119$, $h = 30$ の場合、$w = 56$ と計算できます。
-In fact, for integer values $x$, $y$, $h$ and $0 < x < y < 200$, there are only five triplets ($x$, $y$, $h$) producing integer solutions for $w$: (70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35) and (119, 175, 40).
+実は、整数値 $x$, $y$, $h$ および $0 < x < y < 200$ に対し、$w$ の整数解となる三つ組数 ($x$, $y$, $h$) は、(70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35), (119, 175, 40) の 5 つだけです。
-For integer values $x$, $y$, $h$ and $0 < x < y < 1\\,000\\,000$, how many triplets ($x$, $y$, $h$) produce integer solutions for $w$?
+整数値 $x$, $y$, $h$ および $0 < x < y < 1\\,000\\,000$ に対し、$w$ が整数解となる三つ組数 ($x$, $y$, $h$) はいくつありますか。
# --hints--
-`integerLadders()` should return `210139`.
+`integerLadders()` は `210139` を返す必要があります。
```js
assert.strictEqual(integerLadders(), 210139);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md
index db915fad79..314c1c7112 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md
@@ -1,6 +1,6 @@
---
id: 5900f4a21000cf542c50ffb5
-title: 'Problem 310: Nim Square'
+title: '問題 310: ニム平方数'
challengeType: 5
forumTopicId: 301966
dashedName: problem-310-nim-square
@@ -8,19 +8,19 @@ dashedName: problem-310-nim-square
# --description--
-Alice and Bob play the game Nim Square.
+アリスとボブが「ニム平方数」というゲームをします。
-Nim Square is just like ordinary three-heap normal play Nim, but the players may only remove a square number of stones from a heap.
+ニム平方数は、3 つの石の山を使う通常のニムと似ていますが、プレイヤーは 1 つの山から平方数個の石を取らなければなりません。
-The number of stones in the three heaps is represented by the ordered triple ($a$, $b$, $c$).
+3 つの山に積まれた石の数を、3 つの数の順序組 ($a$ $b$, $c$) として表します。
-If $0 ≤ a ≤ b ≤ c ≤ 29$ then the number of losing positions for the next player is 1160.
+$0 ≤ a ≤ b ≤ c ≤ 29$ の場合、次のプレイヤーが負けるポジションは 1160 個あります。
-Find the number of losing positions for the next player if $0 ≤ a ≤ b ≤ c ≤ 100\\,000$.
+$0 ≤ a ≤ b ≤ c ≤ 100\\,000$ の場合に次のプレイヤーが負けるポジションの数を求めなさい。
# --hints--
-`nimSquare()` should return `2586528661783`.
+`nimSquare()` は `2586528661783` を返す必要があります。
```js
assert.strictEqual(nimSquare(), 2586528661783);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md
index a68e5f3c8a..a498d6bffe 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md
@@ -1,6 +1,6 @@
---
id: 5900f4a31000cf542c50ffb6
-title: 'Problem 311: Biclinic Integral Quadrilaterals'
+title: '問題 311: 二斜整数四辺形'
challengeType: 5
forumTopicId: 301967
dashedName: problem-311-biclinic-integral-quadrilaterals
@@ -8,23 +8,23 @@ dashedName: problem-311-biclinic-integral-quadrilaterals
# --description--
-$ABCD$ is a convex, integer sided quadrilateral with $1 ≤ AB < BC < CD < AD$.
+四角形 $ABCD$ は、$1 ≤ AB < BC < CD < AD$ かつ辺長が整数である凸四角形です。
-$BD$ has integer length. $O$ is the midpoint of $BD$. $AO$ has integer length.
+$BD$ の長さは整数です。 $O$ は $BD$ の中点です。 $AO$ の長さは整数です。
-We'll call $ABCD$ a biclinic integral quadrilateral if $AO = CO ≤ BO = DO$.
+$AO = CO ≤ BO = DO$ の場合、$ABCD$ を「二斜整数四辺形」(biclinic integral quadrilateral) と呼ぶことにします。
-For example, the following quadrilateral is a biclinic integral quadrilateral: $AB = 19$, $BC = 29$, $CD = 37$, $AD = 43$, $BD = 48$ and $AO = CO = 23$.
+例えば、下の四辺形は $AB = 19$, $BC = 29$, $CD = 37$, $AD = 43$, $BD = 48$, $AO = CO = 23$ であり、二斜整数四角形です。
-
-Here, we are only concerned with instances where all four variables are positive integers. For example, if $x = 70$, $y = 119$ and $h = 30$, we can calculate that $w = 56$.
+ここでは、4 つの変数がすべて正の整数であるケースのみを扱います。 例えば、$x = 70$, $y = 119$, $h = 30$ の場合、$w = 56$ と計算できます。
-In fact, for integer values $x$, $y$, $h$ and $0 < x < y < 200$, there are only five triplets ($x$, $y$, $h$) producing integer solutions for $w$: (70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35) and (119, 175, 40).
+実は、整数値 $x$, $y$, $h$ および $0 < x < y < 200$ に対し、$w$ の整数解となる三つ組数 ($x$, $y$, $h$) は、(70, 119, 30), (74, 182, 21), (87, 105, 35), (100, 116, 35), (119, 175, 40) の 5 つだけです。
-For integer values $x$, $y$, $h$ and $0 < x < y < 1\\,000\\,000$, how many triplets ($x$, $y$, $h$) produce integer solutions for $w$?
+整数値 $x$, $y$, $h$ および $0 < x < y < 1\\,000\\,000$ に対し、$w$ が整数解となる三つ組数 ($x$, $y$, $h$) はいくつありますか。
# --hints--
-`integerLadders()` should return `210139`.
+`integerLadders()` は `210139` を返す必要があります。
```js
assert.strictEqual(integerLadders(), 210139);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md
index db915fad79..314c1c7112 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-310-nim-square.md
@@ -1,6 +1,6 @@
---
id: 5900f4a21000cf542c50ffb5
-title: 'Problem 310: Nim Square'
+title: '問題 310: ニム平方数'
challengeType: 5
forumTopicId: 301966
dashedName: problem-310-nim-square
@@ -8,19 +8,19 @@ dashedName: problem-310-nim-square
# --description--
-Alice and Bob play the game Nim Square.
+アリスとボブが「ニム平方数」というゲームをします。
-Nim Square is just like ordinary three-heap normal play Nim, but the players may only remove a square number of stones from a heap.
+ニム平方数は、3 つの石の山を使う通常のニムと似ていますが、プレイヤーは 1 つの山から平方数個の石を取らなければなりません。
-The number of stones in the three heaps is represented by the ordered triple ($a$, $b$, $c$).
+3 つの山に積まれた石の数を、3 つの数の順序組 ($a$ $b$, $c$) として表します。
-If $0 ≤ a ≤ b ≤ c ≤ 29$ then the number of losing positions for the next player is 1160.
+$0 ≤ a ≤ b ≤ c ≤ 29$ の場合、次のプレイヤーが負けるポジションは 1160 個あります。
-Find the number of losing positions for the next player if $0 ≤ a ≤ b ≤ c ≤ 100\\,000$.
+$0 ≤ a ≤ b ≤ c ≤ 100\\,000$ の場合に次のプレイヤーが負けるポジションの数を求めなさい。
# --hints--
-`nimSquare()` should return `2586528661783`.
+`nimSquare()` は `2586528661783` を返す必要があります。
```js
assert.strictEqual(nimSquare(), 2586528661783);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md
index a68e5f3c8a..a498d6bffe 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-311-biclinic-integral-quadrilaterals.md
@@ -1,6 +1,6 @@
---
id: 5900f4a31000cf542c50ffb6
-title: 'Problem 311: Biclinic Integral Quadrilaterals'
+title: '問題 311: 二斜整数四辺形'
challengeType: 5
forumTopicId: 301967
dashedName: problem-311-biclinic-integral-quadrilaterals
@@ -8,23 +8,23 @@ dashedName: problem-311-biclinic-integral-quadrilaterals
# --description--
-$ABCD$ is a convex, integer sided quadrilateral with $1 ≤ AB < BC < CD < AD$.
+四角形 $ABCD$ は、$1 ≤ AB < BC < CD < AD$ かつ辺長が整数である凸四角形です。
-$BD$ has integer length. $O$ is the midpoint of $BD$. $AO$ has integer length.
+$BD$ の長さは整数です。 $O$ は $BD$ の中点です。 $AO$ の長さは整数です。
-We'll call $ABCD$ a biclinic integral quadrilateral if $AO = CO ≤ BO = DO$.
+$AO = CO ≤ BO = DO$ の場合、$ABCD$ を「二斜整数四辺形」(biclinic integral quadrilateral) と呼ぶことにします。
-For example, the following quadrilateral is a biclinic integral quadrilateral: $AB = 19$, $BC = 29$, $CD = 37$, $AD = 43$, $BD = 48$ and $AO = CO = 23$.
+例えば、下の四辺形は $AB = 19$, $BC = 29$, $CD = 37$, $AD = 43$, $BD = 48$, $AO = CO = 23$ であり、二斜整数四角形です。
-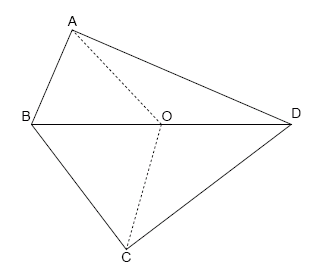 +
+ -Let $B(N)$ be the number of distinct biclinic integral quadrilaterals $ABCD$ that satisfy ${AB}^2 + {BC}^2 + {CD}^2 + {AD}^2 ≤ N$. We can verify that $B(10\\,000) = 49$ and $B(1\\,000\\,000) = 38239$.
+${AB}^2 + {BC}^2 + {CD}^2 + {AD}^2 ≤ N$ を満たす相異なる二斜整数四角形 $ABCD$ の数を、$B(N)$ とします。 $B(10\\000) = 49$, $B(1\\,000\\000) = 38239$ であることを確認できます。
-Find $B(10\\,000\\,000\\,000)$.
+$B(10\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`biclinicIntegralQuadrilaterals()` should return `2466018557`.
+`biclinicIntegralQuadrilaterals()` は `2466018557` を返す必要があります。
```js
assert.strictEqual(biclinicIntegralQuadrilaterals(), 2466018557);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md
index 9621ac1127..6b420cc562 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md
@@ -1,6 +1,6 @@
---
id: 5900f4a51000cf542c50ffb7
-title: 'Problem 312: Cyclic paths on Sierpiński graphs'
+title: '問題 312: シェルピンスキーグラフ上の循環路'
challengeType: 5
forumTopicId: 301968
dashedName: problem-312-cyclic-paths-on-sierpiski-graphs
@@ -8,24 +8,24 @@ dashedName: problem-312-cyclic-paths-on-sierpiski-graphs
# --description--
-- A Sierpiński graph of order-1 ($S_1$) is an equilateral triangle.
-- $S_{n + 1}$ is obtained from $S_n$ by positioning three copies of $S_n$ so that every pair of copies has one common corner.
+- 位数 1 のシェルピンスキーグラフ ($S_1$) は正三角形です。
+- $S_{n + 1}$ は $S_n$ から作られます。3 つの $S_n$ を、それぞれの対が角の 1 つの頂点を共有するように配置したものです。
-
-Let $B(N)$ be the number of distinct biclinic integral quadrilaterals $ABCD$ that satisfy ${AB}^2 + {BC}^2 + {CD}^2 + {AD}^2 ≤ N$. We can verify that $B(10\\,000) = 49$ and $B(1\\,000\\,000) = 38239$.
+${AB}^2 + {BC}^2 + {CD}^2 + {AD}^2 ≤ N$ を満たす相異なる二斜整数四角形 $ABCD$ の数を、$B(N)$ とします。 $B(10\\000) = 49$, $B(1\\,000\\000) = 38239$ であることを確認できます。
-Find $B(10\\,000\\,000\\,000)$.
+$B(10\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`biclinicIntegralQuadrilaterals()` should return `2466018557`.
+`biclinicIntegralQuadrilaterals()` は `2466018557` を返す必要があります。
```js
assert.strictEqual(biclinicIntegralQuadrilaterals(), 2466018557);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md
index 9621ac1127..6b420cc562 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-312-cyclic-paths-on-sierpiski-graphs.md
@@ -1,6 +1,6 @@
---
id: 5900f4a51000cf542c50ffb7
-title: 'Problem 312: Cyclic paths on Sierpiński graphs'
+title: '問題 312: シェルピンスキーグラフ上の循環路'
challengeType: 5
forumTopicId: 301968
dashedName: problem-312-cyclic-paths-on-sierpiski-graphs
@@ -8,24 +8,24 @@ dashedName: problem-312-cyclic-paths-on-sierpiski-graphs
# --description--
-- A Sierpiński graph of order-1 ($S_1$) is an equilateral triangle.
-- $S_{n + 1}$ is obtained from $S_n$ by positioning three copies of $S_n$ so that every pair of copies has one common corner.
+- 位数 1 のシェルピンスキーグラフ ($S_1$) は正三角形です。
+- $S_{n + 1}$ は $S_n$ から作られます。3 つの $S_n$ を、それぞれの対が角の 1 つの頂点を共有するように配置したものです。
- +
+ -Let $C(n)$ be the number of cycles that pass exactly once through all the vertices of $S_n$. For example, $C(3) = 8$ because eight such cycles can be drawn on $S_3$, as shown below:
+$S_n$ のすべての頂点をちょうど 1 回ずつ通る循環路の数を、$C(n)$ とします。 例えば、下図のとおり、$S_3$ にそのような循環路を 8 つ描くことができるので、$C(3) = 8$ です。
-
-Let $C(n)$ be the number of cycles that pass exactly once through all the vertices of $S_n$. For example, $C(3) = 8$ because eight such cycles can be drawn on $S_3$, as shown below:
+$S_n$ のすべての頂点をちょうど 1 回ずつ通る循環路の数を、$C(n)$ とします。 例えば、下図のとおり、$S_3$ にそのような循環路を 8 つ描くことができるので、$C(3) = 8$ です。
- +
+ -It can also be verified that:
+次のことも確認できます。
$$\begin{align} & C(1) = C(2) = 1 \\\\ & C(5) = 71\\,328\\,803\\,586\\,048 \\\\ & C(10 000)\bmod {10}^8 = 37\\,652\\,224 \\\\ & C(10 000)\bmod {13}^8 = 617\\,720\\,485 \\\\ \end{align}$$
-Find $C(C(C(10\\,000)))\bmod {13}^8$.
+$C(C(C(10\\,000)))\bmod {13}^8$ を求めなさい。
# --hints--
-`pathsOnSierpinskiGraphs()` should return `324681947`.
+`pathsOnSierpinskiGraphs()` は `324681947` を返す必要があります。
```js
assert.strictEqual(pathsOnSierpinskiGraphs(), 324681947);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md
index e4f4addb3a..8a8f8a4076 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4a61000cf542c50ffb8
-title: 'Problem 313: Sliding game'
+title: 'Problem 313: スライドゲーム'
challengeType: 5
forumTopicId: 301969
dashedName: problem-313-sliding-game
@@ -8,21 +8,21 @@ dashedName: problem-313-sliding-game
# --description--
-In a sliding game a counter may slide horizontally or vertically into an empty space. The objective of the game is to move the red counter from the top left corner of a grid to the bottom right corner; the space always starts in the bottom right corner. For example, the following sequence of pictures show how the game can be completed in five moves on a 2 by 2 grid.
+スライドゲームでは、カウンターを縦か横にスライドさせて空のスペースに移動します。 ゲームの目的は、赤のカウンターを格子の左上隅から右下隅へ移動することです。開始時は必ず右下隅が空いています。 例えば、次の一連の画像は、2 × 2 の格子上で 5 手でゲームを終える方法を示しています。
-
-It can also be verified that:
+次のことも確認できます。
$$\begin{align} & C(1) = C(2) = 1 \\\\ & C(5) = 71\\,328\\,803\\,586\\,048 \\\\ & C(10 000)\bmod {10}^8 = 37\\,652\\,224 \\\\ & C(10 000)\bmod {13}^8 = 617\\,720\\,485 \\\\ \end{align}$$
-Find $C(C(C(10\\,000)))\bmod {13}^8$.
+$C(C(C(10\\,000)))\bmod {13}^8$ を求めなさい。
# --hints--
-`pathsOnSierpinskiGraphs()` should return `324681947`.
+`pathsOnSierpinskiGraphs()` は `324681947` を返す必要があります。
```js
assert.strictEqual(pathsOnSierpinskiGraphs(), 324681947);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md
index e4f4addb3a..8a8f8a4076 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-313-sliding-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4a61000cf542c50ffb8
-title: 'Problem 313: Sliding game'
+title: 'Problem 313: スライドゲーム'
challengeType: 5
forumTopicId: 301969
dashedName: problem-313-sliding-game
@@ -8,21 +8,21 @@ dashedName: problem-313-sliding-game
# --description--
-In a sliding game a counter may slide horizontally or vertically into an empty space. The objective of the game is to move the red counter from the top left corner of a grid to the bottom right corner; the space always starts in the bottom right corner. For example, the following sequence of pictures show how the game can be completed in five moves on a 2 by 2 grid.
+スライドゲームでは、カウンターを縦か横にスライドさせて空のスペースに移動します。 ゲームの目的は、赤のカウンターを格子の左上隅から右下隅へ移動することです。開始時は必ず右下隅が空いています。 例えば、次の一連の画像は、2 × 2 の格子上で 5 手でゲームを終える方法を示しています。
-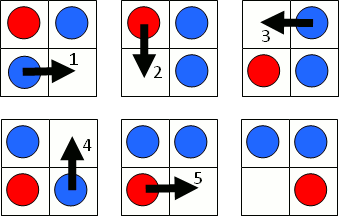 +
+ -Let $S(m, n)$ represent the minimum number of moves to complete the game on an $m$ by $n$ grid. For example, it can be verified that $S(5, 4) = 25$.
+$m$ x $n$ の格子でゲームを終えるための最小移動回数を、$S(m, n)$ とします。 例えば、$S(5, 4) = 25$ であることを確認できます。
-
-Let $S(m, n)$ represent the minimum number of moves to complete the game on an $m$ by $n$ grid. For example, it can be verified that $S(5, 4) = 25$.
+$m$ x $n$ の格子でゲームを終えるための最小移動回数を、$S(m, n)$ とします。 例えば、$S(5, 4) = 25$ であることを確認できます。
-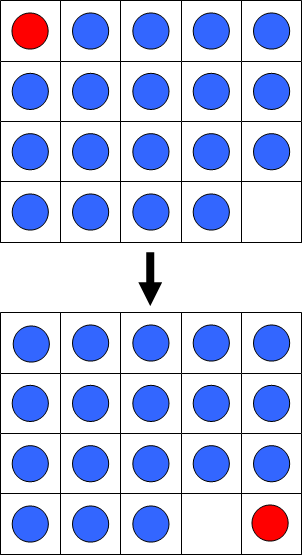 +
+ -There are exactly 5482 grids for which $S(m, n) = p^2$, where $p < 100$ is prime.
+素数 $p < 100$ について、$S(m, n) = p^2$ となる格子はちょうど 5482 個あります。
-How many grids does $S(m, n) = p^2$, where $p < {10}^6$ is prime?
+素数 $p < {10}^6$ について、$S(m, n) = p^2$ となる格子はいくつありますか。
# --hints--
-`slidingGame()` should return `2057774861813004`.
+`slidingGame()` は `2057774861813004` を返す必要があります。
```js
assert.strictEqual(slidingGame(), 2057774861813004);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md
index d367b6956e..b835fd0854 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4a71000cf542c50ffb9
-title: 'Problem 314: The Mouse on the Moon'
+title: '問題 314: 『小鼠 月世界を征服』'
challengeType: 5
forumTopicId: 301970
dashedName: problem-314-the-mouse-on-the-moon
@@ -8,23 +8,23 @@ dashedName: problem-314-the-mouse-on-the-moon
# --description--
-The moon has been opened up, and land can be obtained for free, but there is a catch. You have to build a wall around the land that you stake out, and building a wall on the moon is expensive. Every country has been allotted a 500 m by 500 m square area, but they will possess only that area which they wall in. 251001 posts have been placed in a rectangular grid with 1 meter spacing. The wall must be a closed series of straight lines, each line running from post to post.
+月が開拓され、土地を無料で取得できるようになりました。しかし、1 つ問題があります。 確保した土地を壁で囲まなければなりませんが、月では壁を作るのにとてもお金がかかるのです。 各国には 500 m × 500 m の正方形の土地が割り当てられていますが、所有できるのは壁で囲んだ部分だけです。251001 本の杭が 1 m 間隔で長方形の格子状に配置されています。 壁は、閉じられた連続的直線でなければならず、それぞれの直線は杭と杭を結ぶものでなければなりません。
-The bigger countries of course have built a 2000 m wall enclosing the entire 250 000 $\text{m}^2$ area. The Duchy of Grand Fenwick, has a tighter budget, and has asked you (their Royal Programmer) to compute what shape would get best maximum $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio.
+もちろん大国は 2000 m の壁を建設し、面積 250 000 $\text{m}^2$ の土地の全体を囲んでいます。 グランド・フェンウィック大公国は予算が厳しいため、皇帝プログラマーであるあなたに、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率が最も高くなるのはどのような形状かを計算するよう指示しました。
-You have done some preliminary calculations on a sheet of paper. For a 2000 meter wall enclosing the 250 000 $\text{m}^2$ area the $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio is 125.
+あなたは紙の上で予備的な計算を行いました。 2000 メートルの壁で 250 000 $\text{m}^2$ の土地を囲んだ場合、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率は 125 です。
-Although not allowed, but to get an idea if this is anything better: if you place a circle inside the square area touching the four sides the area will be equal to $π \times {250}^2 \text{m}^2$ and the perimeter will be $π \times 500 \text{m}$, so the $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio will also be 125.
+規則には沿っていませんが、次の方法で比率が高くなるかどうかを考えてみます。正方形の土地の四辺に接するように円を入れると、面積は $π \times {250}^2 \text{m}^2$、周長は $π \times 500 \text{m}$ となり、この場合も、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率は 125 です。
-However, if you cut off from the square four triangles with sides 75 m, 75 m and $75\sqrt{2}$ m the total area becomes 238750 $\text{m}^2$ and the perimeter becomes $1400 + 300\sqrt{2}$ m. So this gives an $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio of 130.87, which is significantly better.
+しかし、辺が 75 m, 75 m, $75\sqrt{2}$ m の 三角形を土地の 4 隅 から切り離すと、面積は238750 $\text{m}^2$、周長は $1400 + 300\sqrt{2}$ m になります。 すると、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率は 130.87 で、先程より大幅に高くなります。
-
-There are exactly 5482 grids for which $S(m, n) = p^2$, where $p < 100$ is prime.
+素数 $p < 100$ について、$S(m, n) = p^2$ となる格子はちょうど 5482 個あります。
-How many grids does $S(m, n) = p^2$, where $p < {10}^6$ is prime?
+素数 $p < {10}^6$ について、$S(m, n) = p^2$ となる格子はいくつありますか。
# --hints--
-`slidingGame()` should return `2057774861813004`.
+`slidingGame()` は `2057774861813004` を返す必要があります。
```js
assert.strictEqual(slidingGame(), 2057774861813004);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md
index d367b6956e..b835fd0854 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-314-the-mouse-on-the-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4a71000cf542c50ffb9
-title: 'Problem 314: The Mouse on the Moon'
+title: '問題 314: 『小鼠 月世界を征服』'
challengeType: 5
forumTopicId: 301970
dashedName: problem-314-the-mouse-on-the-moon
@@ -8,23 +8,23 @@ dashedName: problem-314-the-mouse-on-the-moon
# --description--
-The moon has been opened up, and land can be obtained for free, but there is a catch. You have to build a wall around the land that you stake out, and building a wall on the moon is expensive. Every country has been allotted a 500 m by 500 m square area, but they will possess only that area which they wall in. 251001 posts have been placed in a rectangular grid with 1 meter spacing. The wall must be a closed series of straight lines, each line running from post to post.
+月が開拓され、土地を無料で取得できるようになりました。しかし、1 つ問題があります。 確保した土地を壁で囲まなければなりませんが、月では壁を作るのにとてもお金がかかるのです。 各国には 500 m × 500 m の正方形の土地が割り当てられていますが、所有できるのは壁で囲んだ部分だけです。251001 本の杭が 1 m 間隔で長方形の格子状に配置されています。 壁は、閉じられた連続的直線でなければならず、それぞれの直線は杭と杭を結ぶものでなければなりません。
-The bigger countries of course have built a 2000 m wall enclosing the entire 250 000 $\text{m}^2$ area. The Duchy of Grand Fenwick, has a tighter budget, and has asked you (their Royal Programmer) to compute what shape would get best maximum $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio.
+もちろん大国は 2000 m の壁を建設し、面積 250 000 $\text{m}^2$ の土地の全体を囲んでいます。 グランド・フェンウィック大公国は予算が厳しいため、皇帝プログラマーであるあなたに、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率が最も高くなるのはどのような形状かを計算するよう指示しました。
-You have done some preliminary calculations on a sheet of paper. For a 2000 meter wall enclosing the 250 000 $\text{m}^2$ area the $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio is 125.
+あなたは紙の上で予備的な計算を行いました。 2000 メートルの壁で 250 000 $\text{m}^2$ の土地を囲んだ場合、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率は 125 です。
-Although not allowed, but to get an idea if this is anything better: if you place a circle inside the square area touching the four sides the area will be equal to $π \times {250}^2 \text{m}^2$ and the perimeter will be $π \times 500 \text{m}$, so the $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio will also be 125.
+規則には沿っていませんが、次の方法で比率が高くなるかどうかを考えてみます。正方形の土地の四辺に接するように円を入れると、面積は $π \times {250}^2 \text{m}^2$、周長は $π \times 500 \text{m}$ となり、この場合も、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率は 125 です。
-However, if you cut off from the square four triangles with sides 75 m, 75 m and $75\sqrt{2}$ m the total area becomes 238750 $\text{m}^2$ and the perimeter becomes $1400 + 300\sqrt{2}$ m. So this gives an $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio of 130.87, which is significantly better.
+しかし、辺が 75 m, 75 m, $75\sqrt{2}$ m の 三角形を土地の 4 隅 から切り離すと、面積は238750 $\text{m}^2$、周長は $1400 + 300\sqrt{2}$ m になります。 すると、$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率は 130.87 で、先程より大幅に高くなります。
-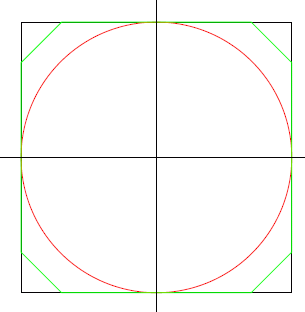 +
+ -Find the maximum $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio. Give your answer rounded to 8 places behind the decimal point in the form abc.defghijk.
+$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率の最大値を求めなさい。 回答は、四捨五入して小数第 8 位まで求め、abc.defghijk の形式にすること。
# --hints--
-`theMouseOnTheMoon()` should return `132.52756426`.
+`theMouseOnTheMoon()` は `132.52756426` を返す必要があります。
```js
assert.strictEqual(theMouseOnTheMoon(), 132.52756426);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md
index 8045152b08..db6ac78131 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md
@@ -1,6 +1,6 @@
---
id: 5900f4a71000cf542c50ffba
-title: 'Problem 315: Digital root clocks'
+title: '問題 315: 数字根時計'
challengeType: 5
forumTopicId: 301971
dashedName: problem-315-digital-root-clocks
@@ -8,45 +8,45 @@ dashedName: problem-315-digital-root-clocks
# --description--
-
-Find the maximum $\frac{\text{enclosed-area}}{\text{wall-length}}$ ratio. Give your answer rounded to 8 places behind the decimal point in the form abc.defghijk.
+$\frac{\text{囲まれた土地の面積}}{\text{壁の長さ}}$の比率の最大値を求めなさい。 回答は、四捨五入して小数第 8 位まで求め、abc.defghijk の形式にすること。
# --hints--
-`theMouseOnTheMoon()` should return `132.52756426`.
+`theMouseOnTheMoon()` は `132.52756426` を返す必要があります。
```js
assert.strictEqual(theMouseOnTheMoon(), 132.52756426);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md
index 8045152b08..db6ac78131 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-315-digital-root-clocks.md
@@ -1,6 +1,6 @@
---
id: 5900f4a71000cf542c50ffba
-title: 'Problem 315: Digital root clocks'
+title: '問題 315: 数字根時計'
challengeType: 5
forumTopicId: 301971
dashedName: problem-315-digital-root-clocks
@@ -8,45 +8,45 @@ dashedName: problem-315-digital-root-clocks
# --description--
- +
+ -Sam and Max are asked to transform two digital clocks into two "digital root" clocks.
+サムとマックスは、2 台のデジタル時計を数字根時計に作り変えるよう頼まれました。
-A digital root clock is a digital clock that calculates digital roots step by step.
+数字根時計とは、数字根を 1 ステップずつ計算するデジタル時計です。
-When a clock is fed a number, it will show it and then it will start the calculation, showing all the intermediate values until it gets to the result. For example, if the clock is fed the number 137, it will show: `137` → `11` → `2` and then it will go black, waiting for the next number.
+数字が入力されると、時計はその数字を表示してから計算を開始し、結果が出るまでの中間値をすべて表示します。 例えば数字 137 が入力されると、`137` → `11` → `2` と表示した後、表示を消して次の数字を待ちます。
-Every digital number consists of some light segments: three horizontal (top, middle, bottom) and four vertical (top-left, top-right, bottom-left, bottom-right). Number `1` is made of vertical top-right and bottom-right, number `4` is made by middle horizontal and vertical top-left, top-right and bottom-right. Number `8` lights them all.
+各デジタル数字を構成する発光セグメントは、横方向に 3 本 (上、中、下) と縦方向に 4 本 (左上、右上、左下、右下) あります。 数字 `1` は右上と右下の縦セグメント、数字 `4` は中央の横セグメントと、左上、右上、右下の縦セグメントで作られます。 数字 `8` では全セグメントが点灯します。
-The clocks consume energy only when segments are turned on/off. To turn on a `2` will cost 5 transitions, while a `7` will cost only 4 transitions.
+この時計は、セグメントを点灯 / 消灯させたときのみエネルギーを消費します。 `2` を点灯させるには 5 回の遷移が必要ですが、`7` では 4 回しか遷移しません。
-Sam and Max built two different clocks.
+サムとマックスはそれぞれ異なる時計を作りました。
-Sam's clock is fed e.g. number 137: the clock shows `137`, then the panel is turned off, then the next number (`11`) is turned on, then the panel is turned off again and finally the last number (`2`) is turned on and, after some time, off.
+サムの時計に例えば 137 が入力されると、時計は `137` を表示した後、表示を消し、次の数字 (`11`) を表示し、再び表示を消し、最終的に最後の数字 (`2`) を表示し、しばらくすると消えます。
-For the example, with number 137, Sam's clock requires:
+この例 (数字 137) では、サムの時計は次のように遷移します。
-- `137`: $(2 + 5 + 4) × 2 = 22$ transitions (`137` on/off).
-- `11`: $(2 + 2) × 2 = 8$ transitions (`11` on/off).
-- `2`: $(5) × 2 = 10$ transitions (`2` on/off).
+- `137`: $(2 + 5 + 4) × 2 = 22$ 回の遷移 (`137` の点灯と消灯)
+- `11`: $(2 + 2) × 2 = 8$ 回の遷移 (`11` の点灯と消灯)
+- `2`: $(5) × 2 = 10$ 回の遷移 (`2` の点灯と消灯)
-For a grand total of 40 transitions.
+計 40 回の遷移があります。
-Max's clock works differently. Instead of turning off the whole panel, it is smart enough to turn off only those segments that won't be needed for the next number.
+マックスの時計は、これとは違う動きをします。 パネル全体を消灯するのではなく、次の数に必要のないセグメントのみを消灯するという賢い方法です。
-For number 137, Max's clock requires:
+137 の場合、マックスの時計は次のように遷移します。
-- `137` : $2 + 5 + 4 = 11$ transitions (`137` on), $7$ transitions (to turn off the segments that are not needed for number `11`).
-- `11` : $0$ transitions (number `11` is already turned on correctly), $3$ transitions (to turn off the first `1` and the bottom part of the second `1`; the top part is common with number `2`).
-- `2` : $4$ transitions (to turn on the remaining segments in order to get a `2`), $5$ transitions (to turn off number `2`).
+- `137`: $(2 + 5 + 4) × 2 = 11$ 回の遷移 (`137` の点灯)、$7$ 回の遷移 (`11` に不要なセグメントを消灯)
+- `11` : $0$ 回の遷移 (数字 `11` は正しく点灯済み)、$3$ 回の遷移 (1 つ目の `1` と、2 つ目の `1` の下部を消灯、上部は数字 `2` と共通)
+- `2` : $4$ 回の遷移 (`2` を作るために残りのセグメントを点灯)、$5$ 回の遷移 (数字 `2` を消灯)
-For a grand total of 30 transitions.
+計 30 回の遷移があります。
-Of course, Max's clock consumes less power than Sam's one. The two clocks are fed all the prime numbers between $A = {10}^7$ and $B = 2 × {10}^7$. Find the difference between the total number of transitions needed by Sam's clock and that needed by Max's one.
+当然ながら、マックスの時計はサムの時計よりも消費電力が少なくなります。 2 台の時計に、$A = {10}^7$ から $B = 2 × {10}^7$ までの全素数を入力します。 サムの時計で必要な遷移の総数と、マックスの時計で必要な遷移の総数との差を求めなさい。
# --hints--
-`digitalRootClocks()` should return `13625242`.
+`digitalRootClocks()` は `13625242` を返す必要があります。
```js
assert.strictEqual(digitalRootClocks(), 13625242);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
index 391ed260ee..6277fdbcaf 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
@@ -1,6 +1,6 @@
---
id: 5900f4a81000cf542c50ffbb
-title: 'Problem 316: Numbers in decimal expansions'
+title: '問題 316: 10 進展開の数字'
challengeType: 5
forumTopicId: 301972
dashedName: problem-316-numbers-in-decimal-expansions
@@ -8,31 +8,31 @@ dashedName: problem-316-numbers-in-decimal-expansions
# --description--
-Let $p = p_1 p_2 p_3 \ldots$ be an infinite sequence of random digits, selected from {0,1,2,3,4,5,6,7,8,9} with equal probability.
+{0,1,2,3,4,5,6,7,8,9} から等しい確率で選択された不規則な数字からなる無限数列を、$p = p_1 p_2 p_3 \ldots$ とします。
-It can be seen that $p$ corresponds to the real number $0.p_1 p_2 p_3 \ldots$.
+$p$ は実数 $0.p_1 p_2 p_3 \ldots$ に対応するということが分かります。
-It can also be seen that choosing a random real number from the interval [0,1) is equivalent to choosing an infinite sequence of random digits selected from {0,1,2,3,4,5,6,7,8,9} with equal probability.
+また、区間 [0,1) から無作為に実数を選ぶことは、{0,1,2,3,4,5,6,7,8,9} から等しい確率で選択した不規則な数字からなる無限数列を選ぶことと同等であることも分かります。
-For any positive integer $n$ with $d$ decimal digits, let $k$ be the smallest index such that $p_k, p_{k + 1}, \ldots p_{k + d - 1}$ are the decimal digits of $n$, in the same order.
+$d$ 個の小数桁を持つ任意の正の整数 $n$ に対して、$p_k, p_{k + 1}, \dots p_{k + d - 1}$ が数字の順序も含めて $n$ の小数桁と同じになるような、最小の添え字を $k$ とします。
-Also, let $g(n)$ be the expected value of $k$; it can be proven that $g(n)$ is always finite and, interestingly, always an integer number.
+また、$k$ の期待値を $g(n)$ とします。$g(n)$ が常に有限であること、そして興味深いことに常に整数であることを証明できます。
-For example, if $n = 535$, then
+例えば、$n = 535$ の場合、
-for $p = 31415926\mathbf{535}897\ldots$, we get $k = 9$
+$p = 31415926\mathbf{535}897\ldots$ のとき、$k = 9$ です。
-for $p = 35528714365004956000049084876408468\mathbf{535}4\ldots$, we get $k = 36$
+$p = 35528714365004956000049084876408468\mathbf{535}4\ldots$ のとき、$k = 36$ です。
-etc and we find that $g(535) = 1008$.
+同様に、$g(535) = 1008$ であることが分かります。
-Given that $\displaystyle\sum_{n = 2}^{999} g\left(\left\lfloor\frac{{10}^6}{n}\right\rfloor\right) = 27280188$, find $\displaystyle\sum_{n = 2}^{999\\,999} g\left(\left\lfloor\frac{{10}^{16}}{n}\right\rfloor\right)$.
+$\displaystyle\sum_{n = 2}^{999} g\left(\left\lfloor\frac{{10}^6}{n}\right\rfloor\right) = 27280188$ が与えられるとき、$\displaystyle\sum_{n = 2}^{999\\,999} g\left(\left\lfloor\frac{{10}^{16}}{n}\right\rfloor\right)$ を求めなさい。
-**Note:** $\lfloor x\rfloor$ represents the floor function.
+**注:** $\lfloor x\rfloor$ は床関数を表します。
# --hints--
-`numbersInDecimalExpansion()` should return `542934735751917760`.
+`numbersInDecimalExpansion()` は `542934735751917760` を返す必要があります。
```js
assert.strictEqual(numbersInDecimalExpansion(), 542934735751917760);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md
index 0a2bd30c68..1a8cf8d658 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md
@@ -1,6 +1,6 @@
---
id: 5900f4aa1000cf542c50ffbc
-title: 'Problem 317: Firecracker'
+title: '問題 317: 爆竹'
challengeType: 5
forumTopicId: 301973
dashedName: problem-317-firecracker
@@ -8,15 +8,15 @@ dashedName: problem-317-firecracker
# --description--
-A firecracker explodes at a height of 100 m above level ground. It breaks into a large number of very small fragments, which move in every direction; all of them have the same initial velocity of 20 $\frac{\text{m}}{\text{s}}$.
+ある爆竹は地上 100 m の高さで爆発します。 爆発すると、無数の微小な破片に分かれてあらゆる方向に飛び散ります。いずれの破片も初速は 20 $\frac{\text{m}}{\text{s}}$ です。
-We assume that the fragments move without air resistance, in a uniform gravitational field with $g=9.81 \frac{\text{m}}{\text{s}^2}$.
+$g=9.81 \frac{\text{m}}{\text{s}^2}$ の一様な重力場で、破片が空気抵抗を受けずに動くと仮定します。
-Find the volume (in $\text{m}^3$) of the region through which the fragments move before reaching the ground. Give your answer rounded to four decimal places.
+破片が地面に到達する前に移動する領域の体積 ($\text{m}^3$) を求めなさい。 回答は、四捨五入して小数第 4 位まで示すこと。
# --hints--
-`firecracker()` should return `1856532.8455`.
+`firecracker()` は `1856532.8455` を返す必要があります。
```js
assert.strictEqual(firecracker(), 1856532.8455);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md
index fea24842c3..c78521e4cc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md
@@ -1,6 +1,6 @@
---
id: 5900f4ab1000cf542c50ffbd
-title: 'Problem 318: 2011 nines'
+title: '問題 318: 2011 個の 9'
challengeType: 5
forumTopicId: 301974
dashedName: problem-318-2011-nines
@@ -8,25 +8,25 @@ dashedName: problem-318-2011-nines
# --description--
-Consider the real number $\sqrt{2} + \sqrt{3}$.
+実数 $\sqrt{2} + \sqrt{3}$ について考えます。
-When we calculate the even powers of $\sqrt{2} + \sqrt{3}$ we get:
+$\sqrt{2} + \sqrt{3}$ の偶数乗を計算すると、次のようになります。
$$\begin{align} & {(\sqrt{2} + \sqrt{3})}^2 = 9.898979485566356\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^4 = 97.98979485566356\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^6 = 969.998969071069263\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^8 = 9601.99989585502907\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{10} = 95049.999989479221\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{12} = 940897.9999989371855\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{14} = 9313929.99999989263\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{16} = 92198401.99999998915\ldots \\\\ \end{align}$$
-It looks like that the number of consecutive nines at the beginning of the fractional part of these powers is non-decreasing. In fact it can be proven that the fractional part of ${(\sqrt{2} + \sqrt{3})}^{2n}$ approaches 1 for large $n$.
+これらの累乗の分数部を見ると、先頭で連続している 9 の個数が非減少であるように見えます。 実際に、$n$ が大きいと ${(\sqrt{2} + \sqrt{3})}^{2n}$ の小数部が 1 に近付くということを証明できます。
-Consider all real numbers of the form $\sqrt{p} + \sqrt{q}$ with $p$ and $q$ positive integers and $p < q$, such that the fractional part of ${(\sqrt{p} + \sqrt{q})}^{2n}$ approaches 1 for large $n$.
+正の整数 $p$ と $q$ ($p < q$) があるとき、$n$ が大きいと ${(\sqrt{p} + \sqrt{q})}^{2n}$ の小数部 が 1 に近付くようなすべての実数 $\sqrt{p} + \sqrt{q}$ について考えます。
-Let $C(p,q,n)$ be the number of consecutive nines at the beginning of the fractional part of ${(\sqrt{p} + \sqrt{q})}^{2n}$.
+${(\sqrt{p} + \sqrt{q})}^{2n}$ の小数部の先頭で連続している 9 の個数を $C(p,q,n)$ とします。
-Let $N(p,q)$ be the minimal value of $n$ such that $C(p,q,n) ≥ 2011$.
+$C(p,q,n) ≥ 2011$ を満たす $n$ の最小値を $N(p,q)$ とします。
-Find $\sum N(p,q)$ for $p + q ≤ 2011$.
+$p + q ≤ 2011$ のとき、$\sum N(p,q)$ を求めなさい。
# --hints--
-`twoThousandElevenNines()` should return `709313889`.
+`twoThousandElevenNines()` は `709313889` を返す必要があります。
```js
assert.strictEqual(twoThousandElevenNines(), 709313889);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md
index c8c65d5531..11c520bd1c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4ab1000cf542c50ffbe
-title: 'Problem 319: Bounded Sequences'
+title: '問題 319: 有界数列'
challengeType: 5
forumTopicId: 301975
dashedName: problem-319-bounded-sequences
@@ -8,21 +8,21 @@ dashedName: problem-319-bounded-sequences
# --description--
-Let $x_1, x_2, \ldots, x_n$ be a sequence of length $n$ such that:
+次の条件を満たす長さ $n$ の数列を $x_1, x_2, \ldots, x_n$ とします。
- $x_1 = 2$
-- for all $1 < i ≤ n : x_{i - 1} < x_i$
-- for all $i$ and $j$ with $1 ≤ i, j ≤ n : {(x_i)}^j < {(x_j + 1)}^i$
+- すべての $1 < i ≤ n について、x_{i - 1} < x_i$
+- $1 ≤ i, j ≤ n を満たすすべての $i$, $j$ について、{(x_i)}^j < {(x_j + 1)}^i$
-There are only five such sequences of length 2, namely: {2,4}, {2,5}, {2,6}, {2,7} and {2,8}. There are 293 such sequences of length 5; three examples are given below: {2,5,11,25,55}, {2,6,14,36,88}, {2,8,22,64,181}.
+これらを満たす長さ 2 の数列は、{2,4}, {2,5}, {2,6}, {2,7}, {2,8} の 5 つしか存在しません。 これらを満たす長さ 5 の数列は 293 個あり、そのうち 3 例は {2,5,11,25,55}, {2,6,14,36,88}, {2,8,22,64,181} です。
-Let $t(n)$ denote the number of such sequences of length $n$. You are given that $t(10) = 86195$ and $t(20) = 5227991891$.
+長さ $n$ のそのような数列を $t(n)$ とします。 $t(10) = 86195$ と $t(20) = 5227991891$ が与えられます。
-Find $t({10}^{10})$ and give your answer modulo $10^9$.
+$t({10}^{10})$ を求め、mod $10^9$ で答えなさい。
# --hints--
-`boundedSequences()` should return `268457129`.
+`boundedSequences()` は `268457129` を返す必要があります。
```js
assert.strictEqual(boundedSequences(), 268457129);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md
index 7695a3cfaa..559bb8dba2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md
@@ -1,6 +1,6 @@
---
id: 5900f4ae1000cf542c50ffbf
-title: 'Problem 320: Factorials divisible by a huge integer'
+title: '問題 320: 巨大な整数で割り切れる階乗'
challengeType: 5
forumTopicId: 301977
dashedName: problem-320-factorials-divisible-by-a-huge-integer
@@ -8,17 +8,17 @@ dashedName: problem-320-factorials-divisible-by-a-huge-integer
# --description--
-Let $N(i)$ be the smallest integer $n$ such that $n!$ is divisible by $(i!)^{1234567890}$
+$n!$ が $(i!)^{1234567890}$ で割り切れるような最小の整数 $n$ を $N(i)$ とします。
-Let $S(u) = \sum N(i)$ for $10 ≤ i ≤ u$.
+$10 ≤ i ≤ u$ に対し、$S(u) = \sum N(i)$ と定義します。
-$S(1000)=614\\,538\\,266\\,565\\,663$.
+$S(1000)=614\\,538\\,266\\,565\\,663$ です。
-Find $S(1\\,000\\,000)\bmod {10}^{18}$.
+$S(1\\,000\\,000)\bmod {10}^{18}$ を求めなさい。
# --hints--
-`divisibleByHugeInteger()` should return `278157919195482660`.
+`divisibleByHugeInteger()` `278157919195482660` を返す必要があります。
```js
assert.strictEqual(divisibleByHugeInteger(), 278157919195482660);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
index e14c6f85cf..717807e1f8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
@@ -1,6 +1,6 @@
---
id: 5900f4ae1000cf542c50ffc0
-title: 'Problem 321: Swapping Counters'
+title: '問題 321: カウンターを入れ替える'
challengeType: 5
forumTopicId: 301978
dashedName: problem-321-swapping-counters
@@ -8,25 +8,25 @@ dashedName: problem-321-swapping-counters
# --description--
-A horizontal row comprising of $2n + 1$ squares has $n$ red counters placed at one end and $n$ blue counters at the other end, being separated by a single empty square in the center. For example, when $n = 3$.
+$2n + 1$ 個のマスが横方向に一列に並べられ、一方の端に $n$ 個の赤のカウンターが置かれ、もう一方の端に $n$ 個の青のカウンターが置かれ、その間の 1 マスは空いています。 例えば、$n = 3$ のときは下図のようになります。
-
-Sam and Max are asked to transform two digital clocks into two "digital root" clocks.
+サムとマックスは、2 台のデジタル時計を数字根時計に作り変えるよう頼まれました。
-A digital root clock is a digital clock that calculates digital roots step by step.
+数字根時計とは、数字根を 1 ステップずつ計算するデジタル時計です。
-When a clock is fed a number, it will show it and then it will start the calculation, showing all the intermediate values until it gets to the result. For example, if the clock is fed the number 137, it will show: `137` → `11` → `2` and then it will go black, waiting for the next number.
+数字が入力されると、時計はその数字を表示してから計算を開始し、結果が出るまでの中間値をすべて表示します。 例えば数字 137 が入力されると、`137` → `11` → `2` と表示した後、表示を消して次の数字を待ちます。
-Every digital number consists of some light segments: three horizontal (top, middle, bottom) and four vertical (top-left, top-right, bottom-left, bottom-right). Number `1` is made of vertical top-right and bottom-right, number `4` is made by middle horizontal and vertical top-left, top-right and bottom-right. Number `8` lights them all.
+各デジタル数字を構成する発光セグメントは、横方向に 3 本 (上、中、下) と縦方向に 4 本 (左上、右上、左下、右下) あります。 数字 `1` は右上と右下の縦セグメント、数字 `4` は中央の横セグメントと、左上、右上、右下の縦セグメントで作られます。 数字 `8` では全セグメントが点灯します。
-The clocks consume energy only when segments are turned on/off. To turn on a `2` will cost 5 transitions, while a `7` will cost only 4 transitions.
+この時計は、セグメントを点灯 / 消灯させたときのみエネルギーを消費します。 `2` を点灯させるには 5 回の遷移が必要ですが、`7` では 4 回しか遷移しません。
-Sam and Max built two different clocks.
+サムとマックスはそれぞれ異なる時計を作りました。
-Sam's clock is fed e.g. number 137: the clock shows `137`, then the panel is turned off, then the next number (`11`) is turned on, then the panel is turned off again and finally the last number (`2`) is turned on and, after some time, off.
+サムの時計に例えば 137 が入力されると、時計は `137` を表示した後、表示を消し、次の数字 (`11`) を表示し、再び表示を消し、最終的に最後の数字 (`2`) を表示し、しばらくすると消えます。
-For the example, with number 137, Sam's clock requires:
+この例 (数字 137) では、サムの時計は次のように遷移します。
-- `137`: $(2 + 5 + 4) × 2 = 22$ transitions (`137` on/off).
-- `11`: $(2 + 2) × 2 = 8$ transitions (`11` on/off).
-- `2`: $(5) × 2 = 10$ transitions (`2` on/off).
+- `137`: $(2 + 5 + 4) × 2 = 22$ 回の遷移 (`137` の点灯と消灯)
+- `11`: $(2 + 2) × 2 = 8$ 回の遷移 (`11` の点灯と消灯)
+- `2`: $(5) × 2 = 10$ 回の遷移 (`2` の点灯と消灯)
-For a grand total of 40 transitions.
+計 40 回の遷移があります。
-Max's clock works differently. Instead of turning off the whole panel, it is smart enough to turn off only those segments that won't be needed for the next number.
+マックスの時計は、これとは違う動きをします。 パネル全体を消灯するのではなく、次の数に必要のないセグメントのみを消灯するという賢い方法です。
-For number 137, Max's clock requires:
+137 の場合、マックスの時計は次のように遷移します。
-- `137` : $2 + 5 + 4 = 11$ transitions (`137` on), $7$ transitions (to turn off the segments that are not needed for number `11`).
-- `11` : $0$ transitions (number `11` is already turned on correctly), $3$ transitions (to turn off the first `1` and the bottom part of the second `1`; the top part is common with number `2`).
-- `2` : $4$ transitions (to turn on the remaining segments in order to get a `2`), $5$ transitions (to turn off number `2`).
+- `137`: $(2 + 5 + 4) × 2 = 11$ 回の遷移 (`137` の点灯)、$7$ 回の遷移 (`11` に不要なセグメントを消灯)
+- `11` : $0$ 回の遷移 (数字 `11` は正しく点灯済み)、$3$ 回の遷移 (1 つ目の `1` と、2 つ目の `1` の下部を消灯、上部は数字 `2` と共通)
+- `2` : $4$ 回の遷移 (`2` を作るために残りのセグメントを点灯)、$5$ 回の遷移 (数字 `2` を消灯)
-For a grand total of 30 transitions.
+計 30 回の遷移があります。
-Of course, Max's clock consumes less power than Sam's one. The two clocks are fed all the prime numbers between $A = {10}^7$ and $B = 2 × {10}^7$. Find the difference between the total number of transitions needed by Sam's clock and that needed by Max's one.
+当然ながら、マックスの時計はサムの時計よりも消費電力が少なくなります。 2 台の時計に、$A = {10}^7$ から $B = 2 × {10}^7$ までの全素数を入力します。 サムの時計で必要な遷移の総数と、マックスの時計で必要な遷移の総数との差を求めなさい。
# --hints--
-`digitalRootClocks()` should return `13625242`.
+`digitalRootClocks()` は `13625242` を返す必要があります。
```js
assert.strictEqual(digitalRootClocks(), 13625242);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
index 391ed260ee..6277fdbcaf 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
@@ -1,6 +1,6 @@
---
id: 5900f4a81000cf542c50ffbb
-title: 'Problem 316: Numbers in decimal expansions'
+title: '問題 316: 10 進展開の数字'
challengeType: 5
forumTopicId: 301972
dashedName: problem-316-numbers-in-decimal-expansions
@@ -8,31 +8,31 @@ dashedName: problem-316-numbers-in-decimal-expansions
# --description--
-Let $p = p_1 p_2 p_3 \ldots$ be an infinite sequence of random digits, selected from {0,1,2,3,4,5,6,7,8,9} with equal probability.
+{0,1,2,3,4,5,6,7,8,9} から等しい確率で選択された不規則な数字からなる無限数列を、$p = p_1 p_2 p_3 \ldots$ とします。
-It can be seen that $p$ corresponds to the real number $0.p_1 p_2 p_3 \ldots$.
+$p$ は実数 $0.p_1 p_2 p_3 \ldots$ に対応するということが分かります。
-It can also be seen that choosing a random real number from the interval [0,1) is equivalent to choosing an infinite sequence of random digits selected from {0,1,2,3,4,5,6,7,8,9} with equal probability.
+また、区間 [0,1) から無作為に実数を選ぶことは、{0,1,2,3,4,5,6,7,8,9} から等しい確率で選択した不規則な数字からなる無限数列を選ぶことと同等であることも分かります。
-For any positive integer $n$ with $d$ decimal digits, let $k$ be the smallest index such that $p_k, p_{k + 1}, \ldots p_{k + d - 1}$ are the decimal digits of $n$, in the same order.
+$d$ 個の小数桁を持つ任意の正の整数 $n$ に対して、$p_k, p_{k + 1}, \dots p_{k + d - 1}$ が数字の順序も含めて $n$ の小数桁と同じになるような、最小の添え字を $k$ とします。
-Also, let $g(n)$ be the expected value of $k$; it can be proven that $g(n)$ is always finite and, interestingly, always an integer number.
+また、$k$ の期待値を $g(n)$ とします。$g(n)$ が常に有限であること、そして興味深いことに常に整数であることを証明できます。
-For example, if $n = 535$, then
+例えば、$n = 535$ の場合、
-for $p = 31415926\mathbf{535}897\ldots$, we get $k = 9$
+$p = 31415926\mathbf{535}897\ldots$ のとき、$k = 9$ です。
-for $p = 35528714365004956000049084876408468\mathbf{535}4\ldots$, we get $k = 36$
+$p = 35528714365004956000049084876408468\mathbf{535}4\ldots$ のとき、$k = 36$ です。
-etc and we find that $g(535) = 1008$.
+同様に、$g(535) = 1008$ であることが分かります。
-Given that $\displaystyle\sum_{n = 2}^{999} g\left(\left\lfloor\frac{{10}^6}{n}\right\rfloor\right) = 27280188$, find $\displaystyle\sum_{n = 2}^{999\\,999} g\left(\left\lfloor\frac{{10}^{16}}{n}\right\rfloor\right)$.
+$\displaystyle\sum_{n = 2}^{999} g\left(\left\lfloor\frac{{10}^6}{n}\right\rfloor\right) = 27280188$ が与えられるとき、$\displaystyle\sum_{n = 2}^{999\\,999} g\left(\left\lfloor\frac{{10}^{16}}{n}\right\rfloor\right)$ を求めなさい。
-**Note:** $\lfloor x\rfloor$ represents the floor function.
+**注:** $\lfloor x\rfloor$ は床関数を表します。
# --hints--
-`numbersInDecimalExpansion()` should return `542934735751917760`.
+`numbersInDecimalExpansion()` は `542934735751917760` を返す必要があります。
```js
assert.strictEqual(numbersInDecimalExpansion(), 542934735751917760);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md
index 0a2bd30c68..1a8cf8d658 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-317-firecracker.md
@@ -1,6 +1,6 @@
---
id: 5900f4aa1000cf542c50ffbc
-title: 'Problem 317: Firecracker'
+title: '問題 317: 爆竹'
challengeType: 5
forumTopicId: 301973
dashedName: problem-317-firecracker
@@ -8,15 +8,15 @@ dashedName: problem-317-firecracker
# --description--
-A firecracker explodes at a height of 100 m above level ground. It breaks into a large number of very small fragments, which move in every direction; all of them have the same initial velocity of 20 $\frac{\text{m}}{\text{s}}$.
+ある爆竹は地上 100 m の高さで爆発します。 爆発すると、無数の微小な破片に分かれてあらゆる方向に飛び散ります。いずれの破片も初速は 20 $\frac{\text{m}}{\text{s}}$ です。
-We assume that the fragments move without air resistance, in a uniform gravitational field with $g=9.81 \frac{\text{m}}{\text{s}^2}$.
+$g=9.81 \frac{\text{m}}{\text{s}^2}$ の一様な重力場で、破片が空気抵抗を受けずに動くと仮定します。
-Find the volume (in $\text{m}^3$) of the region through which the fragments move before reaching the ground. Give your answer rounded to four decimal places.
+破片が地面に到達する前に移動する領域の体積 ($\text{m}^3$) を求めなさい。 回答は、四捨五入して小数第 4 位まで示すこと。
# --hints--
-`firecracker()` should return `1856532.8455`.
+`firecracker()` は `1856532.8455` を返す必要があります。
```js
assert.strictEqual(firecracker(), 1856532.8455);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md
index fea24842c3..c78521e4cc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-318-2011-nines.md
@@ -1,6 +1,6 @@
---
id: 5900f4ab1000cf542c50ffbd
-title: 'Problem 318: 2011 nines'
+title: '問題 318: 2011 個の 9'
challengeType: 5
forumTopicId: 301974
dashedName: problem-318-2011-nines
@@ -8,25 +8,25 @@ dashedName: problem-318-2011-nines
# --description--
-Consider the real number $\sqrt{2} + \sqrt{3}$.
+実数 $\sqrt{2} + \sqrt{3}$ について考えます。
-When we calculate the even powers of $\sqrt{2} + \sqrt{3}$ we get:
+$\sqrt{2} + \sqrt{3}$ の偶数乗を計算すると、次のようになります。
$$\begin{align} & {(\sqrt{2} + \sqrt{3})}^2 = 9.898979485566356\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^4 = 97.98979485566356\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^6 = 969.998969071069263\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^8 = 9601.99989585502907\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{10} = 95049.999989479221\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{12} = 940897.9999989371855\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{14} = 9313929.99999989263\ldots \\\\ & {(\sqrt{2} + \sqrt{3})}^{16} = 92198401.99999998915\ldots \\\\ \end{align}$$
-It looks like that the number of consecutive nines at the beginning of the fractional part of these powers is non-decreasing. In fact it can be proven that the fractional part of ${(\sqrt{2} + \sqrt{3})}^{2n}$ approaches 1 for large $n$.
+これらの累乗の分数部を見ると、先頭で連続している 9 の個数が非減少であるように見えます。 実際に、$n$ が大きいと ${(\sqrt{2} + \sqrt{3})}^{2n}$ の小数部が 1 に近付くということを証明できます。
-Consider all real numbers of the form $\sqrt{p} + \sqrt{q}$ with $p$ and $q$ positive integers and $p < q$, such that the fractional part of ${(\sqrt{p} + \sqrt{q})}^{2n}$ approaches 1 for large $n$.
+正の整数 $p$ と $q$ ($p < q$) があるとき、$n$ が大きいと ${(\sqrt{p} + \sqrt{q})}^{2n}$ の小数部 が 1 に近付くようなすべての実数 $\sqrt{p} + \sqrt{q}$ について考えます。
-Let $C(p,q,n)$ be the number of consecutive nines at the beginning of the fractional part of ${(\sqrt{p} + \sqrt{q})}^{2n}$.
+${(\sqrt{p} + \sqrt{q})}^{2n}$ の小数部の先頭で連続している 9 の個数を $C(p,q,n)$ とします。
-Let $N(p,q)$ be the minimal value of $n$ such that $C(p,q,n) ≥ 2011$.
+$C(p,q,n) ≥ 2011$ を満たす $n$ の最小値を $N(p,q)$ とします。
-Find $\sum N(p,q)$ for $p + q ≤ 2011$.
+$p + q ≤ 2011$ のとき、$\sum N(p,q)$ を求めなさい。
# --hints--
-`twoThousandElevenNines()` should return `709313889`.
+`twoThousandElevenNines()` は `709313889` を返す必要があります。
```js
assert.strictEqual(twoThousandElevenNines(), 709313889);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md
index c8c65d5531..11c520bd1c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-319-bounded-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4ab1000cf542c50ffbe
-title: 'Problem 319: Bounded Sequences'
+title: '問題 319: 有界数列'
challengeType: 5
forumTopicId: 301975
dashedName: problem-319-bounded-sequences
@@ -8,21 +8,21 @@ dashedName: problem-319-bounded-sequences
# --description--
-Let $x_1, x_2, \ldots, x_n$ be a sequence of length $n$ such that:
+次の条件を満たす長さ $n$ の数列を $x_1, x_2, \ldots, x_n$ とします。
- $x_1 = 2$
-- for all $1 < i ≤ n : x_{i - 1} < x_i$
-- for all $i$ and $j$ with $1 ≤ i, j ≤ n : {(x_i)}^j < {(x_j + 1)}^i$
+- すべての $1 < i ≤ n について、x_{i - 1} < x_i$
+- $1 ≤ i, j ≤ n を満たすすべての $i$, $j$ について、{(x_i)}^j < {(x_j + 1)}^i$
-There are only five such sequences of length 2, namely: {2,4}, {2,5}, {2,6}, {2,7} and {2,8}. There are 293 such sequences of length 5; three examples are given below: {2,5,11,25,55}, {2,6,14,36,88}, {2,8,22,64,181}.
+これらを満たす長さ 2 の数列は、{2,4}, {2,5}, {2,6}, {2,7}, {2,8} の 5 つしか存在しません。 これらを満たす長さ 5 の数列は 293 個あり、そのうち 3 例は {2,5,11,25,55}, {2,6,14,36,88}, {2,8,22,64,181} です。
-Let $t(n)$ denote the number of such sequences of length $n$. You are given that $t(10) = 86195$ and $t(20) = 5227991891$.
+長さ $n$ のそのような数列を $t(n)$ とします。 $t(10) = 86195$ と $t(20) = 5227991891$ が与えられます。
-Find $t({10}^{10})$ and give your answer modulo $10^9$.
+$t({10}^{10})$ を求め、mod $10^9$ で答えなさい。
# --hints--
-`boundedSequences()` should return `268457129`.
+`boundedSequences()` は `268457129` を返す必要があります。
```js
assert.strictEqual(boundedSequences(), 268457129);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md
index 7695a3cfaa..559bb8dba2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-320-factorials-divisible-by-a-huge-integer.md
@@ -1,6 +1,6 @@
---
id: 5900f4ae1000cf542c50ffbf
-title: 'Problem 320: Factorials divisible by a huge integer'
+title: '問題 320: 巨大な整数で割り切れる階乗'
challengeType: 5
forumTopicId: 301977
dashedName: problem-320-factorials-divisible-by-a-huge-integer
@@ -8,17 +8,17 @@ dashedName: problem-320-factorials-divisible-by-a-huge-integer
# --description--
-Let $N(i)$ be the smallest integer $n$ such that $n!$ is divisible by $(i!)^{1234567890}$
+$n!$ が $(i!)^{1234567890}$ で割り切れるような最小の整数 $n$ を $N(i)$ とします。
-Let $S(u) = \sum N(i)$ for $10 ≤ i ≤ u$.
+$10 ≤ i ≤ u$ に対し、$S(u) = \sum N(i)$ と定義します。
-$S(1000)=614\\,538\\,266\\,565\\,663$.
+$S(1000)=614\\,538\\,266\\,565\\,663$ です。
-Find $S(1\\,000\\,000)\bmod {10}^{18}$.
+$S(1\\,000\\,000)\bmod {10}^{18}$ を求めなさい。
# --hints--
-`divisibleByHugeInteger()` should return `278157919195482660`.
+`divisibleByHugeInteger()` `278157919195482660` を返す必要があります。
```js
assert.strictEqual(divisibleByHugeInteger(), 278157919195482660);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
index e14c6f85cf..717807e1f8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-321-swapping-counters.md
@@ -1,6 +1,6 @@
---
id: 5900f4ae1000cf542c50ffc0
-title: 'Problem 321: Swapping Counters'
+title: '問題 321: カウンターを入れ替える'
challengeType: 5
forumTopicId: 301978
dashedName: problem-321-swapping-counters
@@ -8,25 +8,25 @@ dashedName: problem-321-swapping-counters
# --description--
-A horizontal row comprising of $2n + 1$ squares has $n$ red counters placed at one end and $n$ blue counters at the other end, being separated by a single empty square in the center. For example, when $n = 3$.
+$2n + 1$ 個のマスが横方向に一列に並べられ、一方の端に $n$ 個の赤のカウンターが置かれ、もう一方の端に $n$ 個の青のカウンターが置かれ、その間の 1 マスは空いています。 例えば、$n = 3$ のときは下図のようになります。
- +
+ -A counter can move from one square to the next (slide) or can jump over another counter (hop) as long as the square next to that counter is unoccupied.
+カウンターは、あるマスから次のマスに移動したり (スライド)、別のカウンターの隣のマスが空いていればそのカウンターを飛び越えたり (ホップ) できます。
-
-A counter can move from one square to the next (slide) or can jump over another counter (hop) as long as the square next to that counter is unoccupied.
+カウンターは、あるマスから次のマスに移動したり (スライド)、別のカウンターの隣のマスが空いていればそのカウンターを飛び越えたり (ホップ) できます。
- +
+ -Let $M(n)$ represent the minimum number of moves/actions to completely reverse the positions of the colored counters; that is, move all the red counters to the right and all the blue counters to the left.
+色付きカウンターの位置を完全に入れ替える (すなわち赤のカウンターをすべて右へ、青のカウンターをすべて左へ移動する) ための移動やアクションの最小回数を、$M(n)$ とします。
-It can be verified $M(3) = 15$, which also happens to be a triangle number.
+$M(3) = 15$ であることを確認できます。これは三角数でもあります。
-If we create a sequence based on the values of n for which $M(n)$ is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
+$M(n)$ が三角数となるような n の値に基づいて数列を作ると、最初の 5 項は 1, 3, 10, 22, 63 で、それらの和は 99 です。
-Find the sum of the first forty terms of this sequence.
+この数列の最初の 40 項の和を求めなさい。
# --hints--
-`swappingCounters()` should return `2470433131948040`.
+`swappingCounters()` は `2470433131948040` を返す必要があります。
```js
assert.strictEqual(swappingCounters(), 2470433131948040);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
index d532a4a95d..1777315329 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
@@ -1,6 +1,6 @@
---
id: 5900f4af1000cf542c50ffc1
-title: 'Problem 322: Binomial coefficients divisible by 10'
+title: '問題 322: 10 で割り切れる二項係数'
challengeType: 5
forumTopicId: 301979
dashedName: problem-322-binomial-coefficients-divisible-by-10
@@ -8,15 +8,15 @@ dashedName: problem-322-binomial-coefficients-divisible-by-10
# --description--
-Let $T(m, n)$ be the number of the binomial coefficients ${}^iC_n$ that are divisible by 10 for $n ≤ i < m$ ($i$, $m$ and $n$ are positive integers).
+$n ≤ i < m$ ($i$, $m$, $n$ は正の整数) のとき、10 で割り切れる二項係数 ${}^iC_n$ の数を $T(m, n)$ とします。
-You are given that $T({10}^9, {10}^7 - 10) = 989\\,697\\,000$.
+$T({10}^9, {10}^7 - 10) = 989\\,697\\,000$ が与えられます。
-Find $T({10}^{18}, {10}^{12} - 10)$.
+$T({10}^{18}, {10}^{12} - 10)$ を求めなさい。
# --hints--
-`binomialCoefficientsDivisibleBy10()` should return `999998760323314000`.
+`binomialCoefficientsDivisibleBy10()` は `999998760323314000` を返す必要があります。
```js
assert.strictEqual(binomialCoefficientsDivisibleBy10(), 999998760323314000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
index 31e36339ea..cc62d803f4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4b01000cf542c50ffc2
-title: 'Problem 323: Bitwise-OR operations on random integers'
+title: '問題 323: 乱数整数のビット論理和演算'
challengeType: 5
forumTopicId: 301980
dashedName: problem-323-bitwise-or-operations-on-random-integers
@@ -8,22 +8,22 @@ dashedName: problem-323-bitwise-or-operations-on-random-integers
# --description--
-Let $y_0, y_1, y_2, \ldots$ be a sequence of random unsigned 32 bit integers
+$y_0, y_1, y_2, \ldots$ を、符号なしの 32 ビット整数の数列とします
-(i.e. $0 ≤ y_i < 2^{32}$, every value equally likely).
+(つまり、$0 ≤ y_i < 2^{32}$ であり、すべての値が等しく現れ得ます)。
-For the sequence $x_i$ the following recursion is given:
+数列 $x_i$ について、次の反復が与えられます。
-- $x_0 = 0$ and
-- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$, for $i > 0$. ($\mathbf{|}$ is the bitwise-OR operator)
+- $x_0 = 0$ かつ
+- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$ ($i > 0$) ($\mathbf{|}$ はビット論理和演算子)
-It can be seen that eventually there will be an index $N$ such that $x_i = 2^{32} - 1$ (a bit-pattern of all ones) for all $i ≥ N$.
+すべての $i ≥ N$ について、$x_i = 2^{32} - 1$ (すべてが 1 であるビットパターン) となるような添え字 $N$ が最終的に存在することが分かります。
-Find the expected value of $N$. Give your answer rounded to 10 digits after the decimal point.
+$N$ の期待値を求めなさい。 回答は、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`bitwiseOrOnRandomIntegers()` should return `6.3551758451`.
+`bitwiseOrOnRandomIntegers()` は `6.3551758451` を返す必要があります。
```js
assert.strictEqual(bitwiseOrOnRandomIntegers(), 6.3551758451);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
index 61700457fc..5e1d822891 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
@@ -1,6 +1,6 @@
---
id: 5900f4b11000cf542c50ffc3
-title: 'Problem 324: Building a tower'
+title: '問題 324: 塔を建設する'
challengeType: 5
forumTopicId: 301981
dashedName: problem-324-building-a-tower
@@ -8,17 +8,17 @@ dashedName: problem-324-building-a-tower
# --description--
-Let $f(n)$ represent the number of ways one can fill a $3×3×n$ tower with blocks of $2×1×1$. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
+$3×3×n$ の塔を $2×1×1×1$ のブロックで埋める方法が何通りあるかを $f(n)$ で表します。 ブロックは自由に回転させることができますが、塔自体に回転、反転などを加えたものは区別してカウントされます。
-For example (with $q = 100\\,000\\,007$):
+次に例を示します ($q = 100\\,000\\,007$ の場合)。
$$\begin{align} & f(2) = 229, \\\\ & f(4) = 117\\,805, \\\\ & f(10)\bmod q = 96\\,149\\,360, \\\\ & f({10}^3)\bmod q = 24\\,806\\,056, \\\\ & f({10}^6)\bmod q = 30\\,808\\,124. \end{align}$$
-Find $f({10}^{10000})\bmod 100\\,000\\,007$.
+$f({10}^{10000})\bmod 100\\,000\\,007$ を求めなさい。
# --hints--
-`buildingTower()` should return `96972774`.
+`buildingTower()` は `96972774` を返す必要があります。
```js
assert.strictEqual(buildingTower(), 96972774);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
index bc828c87e2..6ae458b3b4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f4b11000cf542c50ffc4
-title: 'Problem 325: Stone Game II'
+title: '問題 325: 石取りゲーム (2)'
challengeType: 5
forumTopicId: 301982
dashedName: problem-325-stone-game-ii
@@ -8,23 +8,23 @@ dashedName: problem-325-stone-game-ii
# --description--
-A game is played with two piles of stones and two players. On each player's turn, the player may remove a number of stones from the larger pile. The number of stones removes must be a positive multiple of the number of stones in the smaller pile.
+石を積み上げた 2 つの山と 2 人のプレイヤーでゲームをします。 各プレイヤーは自分のターンで、大きい山から石をいくつか取ります。 取る石の数は、小さい山にある石の数の正の倍数でなければなりません。
-E.g., let the ordered pair (6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
+例えば、小さい山に 6 個、大きい山に 14 個の石がある構成を順序対 (6,14) で表すと、先手は大きい山から 6 個または 12 個の石を取ることができます。
-The player taking all the stones from a pile wins the game.
+1 つの山からすべての石を取ったプレイヤーの勝ちです。
-A winning configuration is one where the first player can force a win. For example, (1,5), (2,6) and (3,12) are winning configurations because the first player can immediately remove all stones in the second pile.
+勝利構成とは、先手が必ず勝てる構成です。 例えば、(1,5), (2,6), (3,12) は、先手が即座に 2 つ目の山からすべての石を取れるので、勝利構成です。
-A losing configuration is one where the second player can force a win, no matter what the first player does. For example, (2,3) and (3,4) are losing configurations: any legal move leaves a winning configuration for the second player.
+敗北構成とは、先手が何をしようと後手が必ず勝てる構成です。 例えば、(2,3) と (3,4) は敗北構成です。ルールに従う限り、何をしても後手の勝利構成になります。
-Define $S(N)$ as the sum of ($x_i + y_i$) for all losing configurations ($x_i$, $y_i$), $0 < x_i < y_i ≤ N$. We can verify that $S(10) = 211$ and $S({10}^4) = 230\\,312\\,207\\,313$.
+$0 < x_i < y_i N$ のとき、すべての敗北構成 ($x_i$, $y_i$) に対する ($x_i + y_i$) の和を、$S(N)$ とします。 $S(10) = 211$, $S({10}^4) = 230\\,312\\,207\\,313$ であることを確認できます。
-Find $S({10}^{16})\bmod 7^{10}$.
+$S({10}^{16})\bmod 7^{10}$ を求めなさい。
# --hints--
-`stoneGameTwo()` should return `54672965`.
+`stoneGameTwo()` は `54672965` を返す必要があります。
```js
assert.strictEqual(stoneGameTwo(), 54672965);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
index ededd29e91..a67f1280bc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
@@ -1,6 +1,6 @@
---
id: 5900f4b21000cf542c50ffc5
-title: 'Problem 326: Modulo Summations'
+title: '問題 326: 剰余の総和 (Modulo Summation)'
challengeType: 5
forumTopicId: 301983
dashedName: problem-326-modulo-summations
@@ -8,23 +8,23 @@ dashedName: problem-326-modulo-summations
# --description--
-Let an be a sequence recursively defined by: $a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$.
+$a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$ によって再帰的に定義される数列を $a_n$ とします。
-So the first 10 elements of $a_n$ are: 1, 1, 0, 3, 0, 3, 5, 4, 1, 9.
+したがって、$a_n$ の最初の 10 項は 1, 1, 0, 3, 0, 3, 5, 4, 1, 9 です。
-Let $f(N, M)$ represent the number of pairs $(p, q)$ such that:
+次の条件を満たす対 $(p, q)$ の個数を $f(N, M)$ とします。
-$$ 1 \le p \le q \le N \\; \text{and} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
+$$ 1 \le p \le q \le N \\; \text{かつ} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
-It can be seen that $f(10, 10) = 4$ with the pairs (3,3), (5,5), (7,9) and (9,10).
+$f(10, 10) = 4 であることが分かります。(3,3), (5,5), (7,9), (9,10) の 4 対です。
-You are also given that $f({10}^4, {10}^3) = 97\\,158$.
+さらに、$f({10}^4, {10}^3) = 97\\,158$ が与えられます。
-Find $f({10}^{12}, {10}^6)$.
+$f({10}^{12}, {10}^6)$ を求めなさい。
# --hints--
-`moduloSummations()` should return `1966666166408794400`.
+`moduloSummations()` は `1966666166408794400` を返す必要があります。
```js
assert.strictEqual(moduloSummations(), 1966666166408794400);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
index a64226ed1b..3838ce7b10 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
@@ -1,6 +1,6 @@
---
id: 5900f4b31000cf542c50ffc6
-title: 'Problem 327: Rooms of Doom'
+title: '問題 327: 運命の部屋'
challengeType: 5
forumTopicId: 301984
dashedName: problem-327-rooms-of-doom
@@ -8,35 +8,35 @@ dashedName: problem-327-rooms-of-doom
# --description--
-A series of three rooms are connected to each other by automatic doors.
+連続する 3 つの部屋が自動ドアでつながっています。
-
-Let $M(n)$ represent the minimum number of moves/actions to completely reverse the positions of the colored counters; that is, move all the red counters to the right and all the blue counters to the left.
+色付きカウンターの位置を完全に入れ替える (すなわち赤のカウンターをすべて右へ、青のカウンターをすべて左へ移動する) ための移動やアクションの最小回数を、$M(n)$ とします。
-It can be verified $M(3) = 15$, which also happens to be a triangle number.
+$M(3) = 15$ であることを確認できます。これは三角数でもあります。
-If we create a sequence based on the values of n for which $M(n)$ is a triangle number then the first five terms would be: 1, 3, 10, 22, and 63, and their sum would be 99.
+$M(n)$ が三角数となるような n の値に基づいて数列を作ると、最初の 5 項は 1, 3, 10, 22, 63 で、それらの和は 99 です。
-Find the sum of the first forty terms of this sequence.
+この数列の最初の 40 項の和を求めなさい。
# --hints--
-`swappingCounters()` should return `2470433131948040`.
+`swappingCounters()` は `2470433131948040` を返す必要があります。
```js
assert.strictEqual(swappingCounters(), 2470433131948040);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
index d532a4a95d..1777315329 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-322-binomial-coefficients-divisible-by-10.md
@@ -1,6 +1,6 @@
---
id: 5900f4af1000cf542c50ffc1
-title: 'Problem 322: Binomial coefficients divisible by 10'
+title: '問題 322: 10 で割り切れる二項係数'
challengeType: 5
forumTopicId: 301979
dashedName: problem-322-binomial-coefficients-divisible-by-10
@@ -8,15 +8,15 @@ dashedName: problem-322-binomial-coefficients-divisible-by-10
# --description--
-Let $T(m, n)$ be the number of the binomial coefficients ${}^iC_n$ that are divisible by 10 for $n ≤ i < m$ ($i$, $m$ and $n$ are positive integers).
+$n ≤ i < m$ ($i$, $m$, $n$ は正の整数) のとき、10 で割り切れる二項係数 ${}^iC_n$ の数を $T(m, n)$ とします。
-You are given that $T({10}^9, {10}^7 - 10) = 989\\,697\\,000$.
+$T({10}^9, {10}^7 - 10) = 989\\,697\\,000$ が与えられます。
-Find $T({10}^{18}, {10}^{12} - 10)$.
+$T({10}^{18}, {10}^{12} - 10)$ を求めなさい。
# --hints--
-`binomialCoefficientsDivisibleBy10()` should return `999998760323314000`.
+`binomialCoefficientsDivisibleBy10()` は `999998760323314000` を返す必要があります。
```js
assert.strictEqual(binomialCoefficientsDivisibleBy10(), 999998760323314000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
index 31e36339ea..cc62d803f4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-323-bitwise-or-operations-on-random-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4b01000cf542c50ffc2
-title: 'Problem 323: Bitwise-OR operations on random integers'
+title: '問題 323: 乱数整数のビット論理和演算'
challengeType: 5
forumTopicId: 301980
dashedName: problem-323-bitwise-or-operations-on-random-integers
@@ -8,22 +8,22 @@ dashedName: problem-323-bitwise-or-operations-on-random-integers
# --description--
-Let $y_0, y_1, y_2, \ldots$ be a sequence of random unsigned 32 bit integers
+$y_0, y_1, y_2, \ldots$ を、符号なしの 32 ビット整数の数列とします
-(i.e. $0 ≤ y_i < 2^{32}$, every value equally likely).
+(つまり、$0 ≤ y_i < 2^{32}$ であり、すべての値が等しく現れ得ます)。
-For the sequence $x_i$ the following recursion is given:
+数列 $x_i$ について、次の反復が与えられます。
-- $x_0 = 0$ and
-- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$, for $i > 0$. ($\mathbf{|}$ is the bitwise-OR operator)
+- $x_0 = 0$ かつ
+- $x_i = x_{i - 1} \mathbf{|} y_{i - 1}$ ($i > 0$) ($\mathbf{|}$ はビット論理和演算子)
-It can be seen that eventually there will be an index $N$ such that $x_i = 2^{32} - 1$ (a bit-pattern of all ones) for all $i ≥ N$.
+すべての $i ≥ N$ について、$x_i = 2^{32} - 1$ (すべてが 1 であるビットパターン) となるような添え字 $N$ が最終的に存在することが分かります。
-Find the expected value of $N$. Give your answer rounded to 10 digits after the decimal point.
+$N$ の期待値を求めなさい。 回答は、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`bitwiseOrOnRandomIntegers()` should return `6.3551758451`.
+`bitwiseOrOnRandomIntegers()` は `6.3551758451` を返す必要があります。
```js
assert.strictEqual(bitwiseOrOnRandomIntegers(), 6.3551758451);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
index 61700457fc..5e1d822891 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-324-building-a-tower.md
@@ -1,6 +1,6 @@
---
id: 5900f4b11000cf542c50ffc3
-title: 'Problem 324: Building a tower'
+title: '問題 324: 塔を建設する'
challengeType: 5
forumTopicId: 301981
dashedName: problem-324-building-a-tower
@@ -8,17 +8,17 @@ dashedName: problem-324-building-a-tower
# --description--
-Let $f(n)$ represent the number of ways one can fill a $3×3×n$ tower with blocks of $2×1×1$. You're allowed to rotate the blocks in any way you like; however, rotations, reflections etc of the tower itself are counted as distinct.
+$3×3×n$ の塔を $2×1×1×1$ のブロックで埋める方法が何通りあるかを $f(n)$ で表します。 ブロックは自由に回転させることができますが、塔自体に回転、反転などを加えたものは区別してカウントされます。
-For example (with $q = 100\\,000\\,007$):
+次に例を示します ($q = 100\\,000\\,007$ の場合)。
$$\begin{align} & f(2) = 229, \\\\ & f(4) = 117\\,805, \\\\ & f(10)\bmod q = 96\\,149\\,360, \\\\ & f({10}^3)\bmod q = 24\\,806\\,056, \\\\ & f({10}^6)\bmod q = 30\\,808\\,124. \end{align}$$
-Find $f({10}^{10000})\bmod 100\\,000\\,007$.
+$f({10}^{10000})\bmod 100\\,000\\,007$ を求めなさい。
# --hints--
-`buildingTower()` should return `96972774`.
+`buildingTower()` は `96972774` を返す必要があります。
```js
assert.strictEqual(buildingTower(), 96972774);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
index bc828c87e2..6ae458b3b4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-325-stone-game-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f4b11000cf542c50ffc4
-title: 'Problem 325: Stone Game II'
+title: '問題 325: 石取りゲーム (2)'
challengeType: 5
forumTopicId: 301982
dashedName: problem-325-stone-game-ii
@@ -8,23 +8,23 @@ dashedName: problem-325-stone-game-ii
# --description--
-A game is played with two piles of stones and two players. On each player's turn, the player may remove a number of stones from the larger pile. The number of stones removes must be a positive multiple of the number of stones in the smaller pile.
+石を積み上げた 2 つの山と 2 人のプレイヤーでゲームをします。 各プレイヤーは自分のターンで、大きい山から石をいくつか取ります。 取る石の数は、小さい山にある石の数の正の倍数でなければなりません。
-E.g., let the ordered pair (6,14) describe a configuration with 6 stones in the smaller pile and 14 stones in the larger pile, then the first player can remove 6 or 12 stones from the larger pile.
+例えば、小さい山に 6 個、大きい山に 14 個の石がある構成を順序対 (6,14) で表すと、先手は大きい山から 6 個または 12 個の石を取ることができます。
-The player taking all the stones from a pile wins the game.
+1 つの山からすべての石を取ったプレイヤーの勝ちです。
-A winning configuration is one where the first player can force a win. For example, (1,5), (2,6) and (3,12) are winning configurations because the first player can immediately remove all stones in the second pile.
+勝利構成とは、先手が必ず勝てる構成です。 例えば、(1,5), (2,6), (3,12) は、先手が即座に 2 つ目の山からすべての石を取れるので、勝利構成です。
-A losing configuration is one where the second player can force a win, no matter what the first player does. For example, (2,3) and (3,4) are losing configurations: any legal move leaves a winning configuration for the second player.
+敗北構成とは、先手が何をしようと後手が必ず勝てる構成です。 例えば、(2,3) と (3,4) は敗北構成です。ルールに従う限り、何をしても後手の勝利構成になります。
-Define $S(N)$ as the sum of ($x_i + y_i$) for all losing configurations ($x_i$, $y_i$), $0 < x_i < y_i ≤ N$. We can verify that $S(10) = 211$ and $S({10}^4) = 230\\,312\\,207\\,313$.
+$0 < x_i < y_i N$ のとき、すべての敗北構成 ($x_i$, $y_i$) に対する ($x_i + y_i$) の和を、$S(N)$ とします。 $S(10) = 211$, $S({10}^4) = 230\\,312\\,207\\,313$ であることを確認できます。
-Find $S({10}^{16})\bmod 7^{10}$.
+$S({10}^{16})\bmod 7^{10}$ を求めなさい。
# --hints--
-`stoneGameTwo()` should return `54672965`.
+`stoneGameTwo()` は `54672965` を返す必要があります。
```js
assert.strictEqual(stoneGameTwo(), 54672965);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
index ededd29e91..a67f1280bc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-326-modulo-summations.md
@@ -1,6 +1,6 @@
---
id: 5900f4b21000cf542c50ffc5
-title: 'Problem 326: Modulo Summations'
+title: '問題 326: 剰余の総和 (Modulo Summation)'
challengeType: 5
forumTopicId: 301983
dashedName: problem-326-modulo-summations
@@ -8,23 +8,23 @@ dashedName: problem-326-modulo-summations
# --description--
-Let an be a sequence recursively defined by: $a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$.
+$a_1 = 1$, $\displaystyle a_n = \left(\sum_{k = 1}^{n - 1} k \times a_k\right)\bmod n$ によって再帰的に定義される数列を $a_n$ とします。
-So the first 10 elements of $a_n$ are: 1, 1, 0, 3, 0, 3, 5, 4, 1, 9.
+したがって、$a_n$ の最初の 10 項は 1, 1, 0, 3, 0, 3, 5, 4, 1, 9 です。
-Let $f(N, M)$ represent the number of pairs $(p, q)$ such that:
+次の条件を満たす対 $(p, q)$ の個数を $f(N, M)$ とします。
-$$ 1 \le p \le q \le N \\; \text{and} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
+$$ 1 \le p \le q \le N \\; \text{かつ} \\; \left(\sum_{i = p}^q a_i\right)\bmod M = 0$$
-It can be seen that $f(10, 10) = 4$ with the pairs (3,3), (5,5), (7,9) and (9,10).
+$f(10, 10) = 4 であることが分かります。(3,3), (5,5), (7,9), (9,10) の 4 対です。
-You are also given that $f({10}^4, {10}^3) = 97\\,158$.
+さらに、$f({10}^4, {10}^3) = 97\\,158$ が与えられます。
-Find $f({10}^{12}, {10}^6)$.
+$f({10}^{12}, {10}^6)$ を求めなさい。
# --hints--
-`moduloSummations()` should return `1966666166408794400`.
+`moduloSummations()` は `1966666166408794400` を返す必要があります。
```js
assert.strictEqual(moduloSummations(), 1966666166408794400);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
index a64226ed1b..3838ce7b10 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-327-rooms-of-doom.md
@@ -1,6 +1,6 @@
---
id: 5900f4b31000cf542c50ffc6
-title: 'Problem 327: Rooms of Doom'
+title: '問題 327: 運命の部屋'
challengeType: 5
forumTopicId: 301984
dashedName: problem-327-rooms-of-doom
@@ -8,35 +8,35 @@ dashedName: problem-327-rooms-of-doom
# --description--
-A series of three rooms are connected to each other by automatic doors.
+連続する 3 つの部屋が自動ドアでつながっています。
-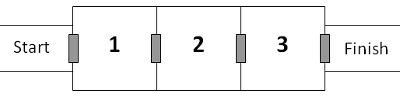 +
+ -Each door is operated by a security card. Once you enter a room, the door automatically closes, and that security card cannot be used again. A machine will dispense an unlimited number of cards at the start, but each room (including the starting room) contains scanners. If they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
+各ドアを開けるにはセキュリティカードを使います。 部屋に入るとドアが自動的に閉まり、そのセキュリティカードは二度と使えません。 開始時、カード発行機から何枚でもカードを入手できますが、各部屋 (開始点となる部屋を含む) には検出器が設置されています。 あなたが 3 枚以上のセキュリティカードを持っていることや、セキュリティカードが床に放置されていることが検出されると、すべてのドアが永久にロックされます。 ただし、各部屋には箱があり、後で使うための任意の枚数のセキュリティカードをその箱に安全に保管できます。
-If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
+単に部屋を一度に通り抜けようとすると、3 つ目の部屋に入った時には 3 枚のカードを使い切っているので、永久にその部屋に閉じ込められます!
-However, if you make use of the storage boxes, then escape is possible. For example, you could enter room 1 using your first card, place one card in the storage box, and use your third card to exit the room back to the start. Then after collecting three more cards from the dispensing machine you could use one to enter room 1 and collect the card you placed in the box a moment ago. You now have three cards again and will be able to travel through the remaining three doors. This method allows you to travel through all three rooms using six security cards in total.
+しかし、保管箱を使えば 脱出できる可能性があります。 例えば、1 枚目のカードを使って 1 つ目の部屋に入り、保管箱にカードを 1 枚入れ、3 枚目のカードを使って開始地点に戻ります。 その後、さらに 3 枚のカードを発行機から入手し、1 枚を使って 1 つ目の部屋に入り、先ほど箱に入れたカードを取り出します。 再び 3 枚のカードを持っているので、残りの 3 つのドアを通過することができます。 この方法なら、計 6 枚のセキュリティカードを使って 3 つの部屋を通り抜けられます。
-It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
+一度に最大 3 枚のカードを持ち、計 123 枚のセキュリティカードを使って 6 つの部屋を通り抜けることができます。
-Let $C$ be the maximum number of cards which can be carried at any time.
+どの時点であれ一度に持つことができるカードの最大枚数を、$C$ とします。
-Let $R$ be the number of rooms to travel through.
+通り抜ける部屋の数を $R$ とします。
-Let $M(C, R)$ be the minimum number of cards required from the dispensing machine to travel through $R$ rooms carrying up to a maximum of $C$ cards at any time.
+どの時点であれ一度に最大 $C$ 枚のカードを持ち、$R$ 個の部屋を通り抜けるために発行機から入手する必要のあるカードの最小枚数を $M(C, R)$ とします。
-For example, $M(3, 6) = 123$ and $M(4, 6) = 23$.
+例えば、$M(3, 6) = 123$, $M(4, 6) = 23$ です。
-And, $\sum M(C, 6) = 146$ for $3 ≤ C ≤ 4$.
+また、$3 ≤ C ≤ 4$ のとき、$\sum M(C, 6) = 146$ です。
-You are given that $\sum M(C, 10) = 10382$ for $3 ≤ C ≤ 10$.
+$3 ≤ C ≤ 10$ のとき、$\sum M(C, 10) = 10382$ が与えられます。
-Find $\sum M(C, 30)$ for $3 ≤ C ≤ 40$.
+$3 ≤ C ≤ 40$ のとき、$\sum M(C, 30)$ を求めなさい。
# --hints--
-`roomsOfDoom()` should return `34315549139516`.
+`roomsOfDoom()` は `34315549139516` を返す必要があります。
```js
assert.strictEqual(roomsOfDoom(), 34315549139516);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
index 7cb9e0d86e..19d27ff859 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
@@ -1,6 +1,6 @@
---
id: 5900f4b41000cf542c50ffc7
-title: 'Problem 328: Lowest-cost Search'
+title: '問題 328: 最低コストを探す'
challengeType: 5
forumTopicId: 301985
dashedName: problem-328-lowest-cost-search
@@ -8,29 +8,29 @@ dashedName: problem-328-lowest-cost-search
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers:
+整数 {1, 2, ..., $n$} から選ばれた秘密の数を、質問をすることで当てます。 それぞれの数 (質問) を尋ねるとき、尋ねた数と同じだけのコストがかかり、得られる答えは次の 3 つのいずれかです。
-- "Your guess is lower than the hidden number", or
-- "Yes, that's it!", or
-- "Your guess is higher than the hidden number".
+- 「あなたの推測は秘密の数よりも小さい」
+- 「当たり!」
+- 「あなたの推測は秘密の数よりも大きい」
-Given the value of $n$, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
+値 $n$ が与えられているとき、最適な戦略に従えば、起こり得る最悪のケースの総コスト (すなわち、尋ねた質問の総和) が最小化します。 次に例を示します。
-If $n = 3$, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
+$n = 3$ の場合、一番良いのはもちろん、秘密の数が "2" であるかどうかを尋ねることです。 答えを聞けば、すぐに秘密の数が分かります (総コスト = 2)。
-If $n = 8$, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be $4 + 6 + 7 = \mathbf{\color{red}{17}}$.
+$n = 8$ の場合は「二分探索」型の戦略が良いかもしれません。まず "4" を尋ね、秘密の数が 4 より大きければ、さらに 1 回か 2 回尋ねる必要があります。 2 回目は "6" を尋ねます。 秘密の数が 6 よりさらに大きければ、7 か 8 かを知るために 3 回目の質問が必要です。 したがって、3 回目の質問は "7" であり、この最悪ケースの総コストは $4 + 6 + 7 = \mathbf{\color{red}{17}}$です。
-We can improve considerably the worst-case cost for $n = 8$, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of $5 + 7 = \mathbf{\color{blue}{12}}$). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of $5 + 3 + 1 = \mathbf{\color{blue}{9}}$. Since $\mathbf{\color{blue}{12 > 9}}$, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for $n = 8$.
+1 回目の質問で "5" を尋ねれば、$n=8$ に対する最悪ケースのコストを大幅に下げることができます。 秘密の数が 5 よりも大きいと言われた場合、2 回目の質問は「7」となり、秘密の数がどれなのかを確実に知ることができます (総コスト $5 + 7 = \mathbf{\color{blue}{12}}$)。 秘密の数が 5 よりも小きいと言われた場合、2 回目の質問は「3」となり、秘密の数が 3 より小さければ、3 回目の質問は "1" であり、総コストは $5 + 3 + 1 = \mathbf{\color{blue}{9}}$ です。 $\mathbf{\color{blue}{12 > 9}}$ なので、この戦略における最悪ケースのコストは 12 です。 これは、先ほどの「二分探索」戦略の結果よりも優れています。また、他のどの戦略よりも優れているか、少なくとも同等です。 さて、ここまで $n = 8$ の最適な戦略を説明してきました。
-Let $C(n)$ be the worst-case cost achieved by an optimal strategy for $n$, as described above. Thus $C(1) = 0$, $C(2) = 1$, $C(3) = 2$ and $C(8) = 12$.
+上のとおり、$n$ に対する最適な戦略によって達成される、最悪ケースのコストを $C(n)$ とします。 したがって、$C(1) = 0$, $C(2) = 1$, $C(3) = 2$, $C(8) = 12$ です。
-Similarly, $C(100) = 400$ and $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$.
+同様に、$C(100) = 400$, $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$ です。
-Find $\displaystyle\sum_{n = 1}^{200\\,000} C(n)$.
+$\displaystyle\sum_{n = 1}^{200\\,000} C(n)$ を求めなさい。
# --hints--
-`lowestCostSearch()` should return `260511850222`.
+`lowestCostSearch()` は `260511850222` を返す必要があります。
```js
assert.strictEqual(lowestCostSearch(), 260511850222);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
index 54f72db23f..24f3c9e9f9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
@@ -1,6 +1,6 @@
---
id: 5900f4b51000cf542c50ffc8
-title: 'Problem 329: Prime Frog'
+title: '問題 329: 素数ガエル'
challengeType: 5
forumTopicId: 301986
dashedName: problem-329-prime-frog
@@ -8,27 +8,27 @@ dashedName: problem-329-prime-frog
# --description--
-Susan has a prime frog.
+スーザンは素数ガエルを飼っています。
-Her frog is jumping around over 500 squares numbered 1 to 500.
+そのカエルは、1 から 500 までの番号が振られた 500 個のマスの上を跳び回ります。
-He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range [1;500]. (if it lands at either end, it automatically jumps to the only available square on the next move.)
+左または右のマスのみへ等しい確率で跳ぶことができ、範囲 [1;500] の外側に跳ぶことはできません。 (いずれかの端に着くと、次に移動できる唯一のマスへ自動的に跳びます。)
-When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability $\frac{2}{3}$ or 'N' (NOT PRIME) with probability $\frac{1}{3}$ just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability $\frac{1}{3}$ or 'N' with probability $\frac{2}{3}$ just before jumping to the next square.
+素数が書かれたマスにいるとき、次のマスへ跳ぶ直前に、確率 $\frac{2}{3}$で 'P' (素数)、または確率 $\frac{1}{3}$ で 'N' (非素数) と鳴きます。 非素数が書かれたマスにいるとき、次のマスへ跳ぶ直前に、確率 $\frac{1}{3}$で 'P' と鳴くか、確率 $\frac{2}{3}$ で 'N' と鳴きます。
-Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
+カエルがどのマスから跳び始めるかは、不規則かつすべてのマスで等確率であるとします。カエルの最初の 15 回の鳴き声が PPPPNNPPPNPPNPN の順になる確率を求めなさい。
-Give your answer as a string as a fraction `p/q` in reduced form.
+回答は、既約分数 `p/q` の形式の文字列にすること。
# --hints--
-`primeFrog()` should return a string.
+`primeFrog()` は文字列を返す必要があります。
```js
assert(typeof primeFrog() === 'string');
```
-`primeFrog()` should return the string `199740353/29386561536000`.
+`primeFrog()` は文字列 `199740353/29386561536000` を返す必要があります。
```js
assert.strictEqual(primeFrog(), '199740353/29386561536000');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
index 91813ffcbf..4f4e623a83 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
@@ -1,6 +1,6 @@
---
id: 5900f4b71000cf542c50ffc9
-title: 'Problem 330: Euler''s Number'
+title: '問題 330: オイラー数'
challengeType: 5
forumTopicId: 301988
dashedName: problem-330-eulers-number
@@ -8,25 +8,25 @@ dashedName: problem-330-eulers-number
# --description--
-An infinite sequence of real numbers $a(n)$ is defined for all integers $n$ as follows:
+すべての整数 $n$ について、実数の無限数列 $a(n)$ は次のように定義されます。
$$ a(n) = \begin{cases} 1 & n < 0 \\\\ \displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0 \end{cases} $$
-For example,
+例えば次のようになります。
$$\begin{align} & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6 \end{align}$$
-with $e = 2.7182818\ldots$ being Euler's constant.
+ここで、$e = 2.7182818\ldots$ はオイラーの定数です。
-It can be shown that $a(n)$ is of the form $\displaystyle\frac{A(n)e + B(n)}{n!}$ for integers $A(n)$ and $B(n)$.
+$a(n)$ は、整数 $A(n)$ と整数 $B(n)$ に対して $\displaystyle\frac{A(n)e + B(n)}{n!}$ の形式であることが分かります。
-For example $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
+例えば、$\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$ です。
-Find $A({10}^9)$ + $B({10}^9)$ and give your answer $\bmod 77\\,777\\,777$.
+$A({10}^9)$ + $B({10}^9)$ を求め、$\bmod 77\\,777\\,777$ で答えなさい。
# --hints--
-`eulersNumber()` should return `15955822`.
+`eulersNumber()` は `15955822` を返す必要があります。
```js
assert.strictEqual(eulersNumber(), 15955822);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
index ab777a2d5d..8f62ddf8d9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
@@ -1,6 +1,6 @@
---
id: 5900f4b71000cf542c50ffca
-title: 'Problem 331: Cross flips'
+title: '問題 331: 十字めくり'
challengeType: 5
forumTopicId: 301989
dashedName: problem-331-cross-flips
@@ -8,25 +8,25 @@ dashedName: problem-331-cross-flips
# --description--
-N×N disks are placed on a square game board. Each disk has a black side and white side.
+N×N 個の円盤が正方形のゲーム盤上に置かれています。 円盤にはそれぞれ黒い面と白い面があります。
-At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus $2 × N - 1$ disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+ターンごとに円盤を 1 枚選び、それと同じ横列および同じ縦列にある円盤をすべて裏返します。したがって、$2 × N - 1$ 枚の円盤が裏返されます。 すべての円盤が白い面になるとゲームは終了です。 次の例は、5×5 の盤を使用したゲームです。
-
-Each door is operated by a security card. Once you enter a room, the door automatically closes, and that security card cannot be used again. A machine will dispense an unlimited number of cards at the start, but each room (including the starting room) contains scanners. If they detect that you are holding more than three security cards or if they detect an unattended security card on the floor, then all the doors will become permanently locked. However, each room contains a box where you may safely store any number of security cards for use at a later stage.
+各ドアを開けるにはセキュリティカードを使います。 部屋に入るとドアが自動的に閉まり、そのセキュリティカードは二度と使えません。 開始時、カード発行機から何枚でもカードを入手できますが、各部屋 (開始点となる部屋を含む) には検出器が設置されています。 あなたが 3 枚以上のセキュリティカードを持っていることや、セキュリティカードが床に放置されていることが検出されると、すべてのドアが永久にロックされます。 ただし、各部屋には箱があり、後で使うための任意の枚数のセキュリティカードをその箱に安全に保管できます。
-If you simply tried to travel through the rooms one at a time then as you entered room 3 you would have used all three cards and would be trapped in that room forever!
+単に部屋を一度に通り抜けようとすると、3 つ目の部屋に入った時には 3 枚のカードを使い切っているので、永久にその部屋に閉じ込められます!
-However, if you make use of the storage boxes, then escape is possible. For example, you could enter room 1 using your first card, place one card in the storage box, and use your third card to exit the room back to the start. Then after collecting three more cards from the dispensing machine you could use one to enter room 1 and collect the card you placed in the box a moment ago. You now have three cards again and will be able to travel through the remaining three doors. This method allows you to travel through all three rooms using six security cards in total.
+しかし、保管箱を使えば 脱出できる可能性があります。 例えば、1 枚目のカードを使って 1 つ目の部屋に入り、保管箱にカードを 1 枚入れ、3 枚目のカードを使って開始地点に戻ります。 その後、さらに 3 枚のカードを発行機から入手し、1 枚を使って 1 つ目の部屋に入り、先ほど箱に入れたカードを取り出します。 再び 3 枚のカードを持っているので、残りの 3 つのドアを通過することができます。 この方法なら、計 6 枚のセキュリティカードを使って 3 つの部屋を通り抜けられます。
-It is possible to travel through six rooms using a total of 123 security cards while carrying a maximum of 3 cards.
+一度に最大 3 枚のカードを持ち、計 123 枚のセキュリティカードを使って 6 つの部屋を通り抜けることができます。
-Let $C$ be the maximum number of cards which can be carried at any time.
+どの時点であれ一度に持つことができるカードの最大枚数を、$C$ とします。
-Let $R$ be the number of rooms to travel through.
+通り抜ける部屋の数を $R$ とします。
-Let $M(C, R)$ be the minimum number of cards required from the dispensing machine to travel through $R$ rooms carrying up to a maximum of $C$ cards at any time.
+どの時点であれ一度に最大 $C$ 枚のカードを持ち、$R$ 個の部屋を通り抜けるために発行機から入手する必要のあるカードの最小枚数を $M(C, R)$ とします。
-For example, $M(3, 6) = 123$ and $M(4, 6) = 23$.
+例えば、$M(3, 6) = 123$, $M(4, 6) = 23$ です。
-And, $\sum M(C, 6) = 146$ for $3 ≤ C ≤ 4$.
+また、$3 ≤ C ≤ 4$ のとき、$\sum M(C, 6) = 146$ です。
-You are given that $\sum M(C, 10) = 10382$ for $3 ≤ C ≤ 10$.
+$3 ≤ C ≤ 10$ のとき、$\sum M(C, 10) = 10382$ が与えられます。
-Find $\sum M(C, 30)$ for $3 ≤ C ≤ 40$.
+$3 ≤ C ≤ 40$ のとき、$\sum M(C, 30)$ を求めなさい。
# --hints--
-`roomsOfDoom()` should return `34315549139516`.
+`roomsOfDoom()` は `34315549139516` を返す必要があります。
```js
assert.strictEqual(roomsOfDoom(), 34315549139516);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
index 7cb9e0d86e..19d27ff859 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-328-lowest-cost-search.md
@@ -1,6 +1,6 @@
---
id: 5900f4b41000cf542c50ffc7
-title: 'Problem 328: Lowest-cost Search'
+title: '問題 328: 最低コストを探す'
challengeType: 5
forumTopicId: 301985
dashedName: problem-328-lowest-cost-search
@@ -8,29 +8,29 @@ dashedName: problem-328-lowest-cost-search
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, has a cost equal to the number asked and we get one of three possible answers:
+整数 {1, 2, ..., $n$} から選ばれた秘密の数を、質問をすることで当てます。 それぞれの数 (質問) を尋ねるとき、尋ねた数と同じだけのコストがかかり、得られる答えは次の 3 つのいずれかです。
-- "Your guess is lower than the hidden number", or
-- "Yes, that's it!", or
-- "Your guess is higher than the hidden number".
+- 「あなたの推測は秘密の数よりも小さい」
+- 「当たり!」
+- 「あなたの推測は秘密の数よりも大きい」
-Given the value of $n$, an optimal strategy minimizes the total cost (i.e. the sum of all the questions asked) for the worst possible case. E.g.
+値 $n$ が与えられているとき、最適な戦略に従えば、起こり得る最悪のケースの総コスト (すなわち、尋ねた質問の総和) が最小化します。 次に例を示します。
-If $n = 3$, the best we can do is obviously to ask the number "2". The answer will immediately lead us to find the hidden number (at a total cost = 2).
+$n = 3$ の場合、一番良いのはもちろん、秘密の数が "2" であるかどうかを尋ねることです。 答えを聞けば、すぐに秘密の数が分かります (総コスト = 2)。
-If $n = 8$, we might decide to use a "binary search" type of strategy: Our first question would be "4" and if the hidden number is higher than 4 we will need one or two additional questions. Let our second question be "6". If the hidden number is still higher than 6, we will need a third question in order to discriminate between 7 and 8. Thus, our third question will be "7" and the total cost for this worst-case scenario will be $4 + 6 + 7 = \mathbf{\color{red}{17}}$.
+$n = 8$ の場合は「二分探索」型の戦略が良いかもしれません。まず "4" を尋ね、秘密の数が 4 より大きければ、さらに 1 回か 2 回尋ねる必要があります。 2 回目は "6" を尋ねます。 秘密の数が 6 よりさらに大きければ、7 か 8 かを知るために 3 回目の質問が必要です。 したがって、3 回目の質問は "7" であり、この最悪ケースの総コストは $4 + 6 + 7 = \mathbf{\color{red}{17}}$です。
-We can improve considerably the worst-case cost for $n = 8$, by asking "5" as our first question. If we are told that the hidden number is higher than 5, our second question will be "7", then we'll know for certain what the hidden number is (for a total cost of $5 + 7 = \mathbf{\color{blue}{12}}$). If we are told that the hidden number is lower than 5, our second question will be "3" and if the hidden number is lower than 3 our third question will be "1", giving a total cost of $5 + 3 + 1 = \mathbf{\color{blue}{9}}$. Since $\mathbf{\color{blue}{12 > 9}}$, the worst-case cost for this strategy is 12. That's better than what we achieved previously with the "binary search" strategy; it is also better than or equal to any other strategy. So, in fact, we have just described an optimal strategy for $n = 8$.
+1 回目の質問で "5" を尋ねれば、$n=8$ に対する最悪ケースのコストを大幅に下げることができます。 秘密の数が 5 よりも大きいと言われた場合、2 回目の質問は「7」となり、秘密の数がどれなのかを確実に知ることができます (総コスト $5 + 7 = \mathbf{\color{blue}{12}}$)。 秘密の数が 5 よりも小きいと言われた場合、2 回目の質問は「3」となり、秘密の数が 3 より小さければ、3 回目の質問は "1" であり、総コストは $5 + 3 + 1 = \mathbf{\color{blue}{9}}$ です。 $\mathbf{\color{blue}{12 > 9}}$ なので、この戦略における最悪ケースのコストは 12 です。 これは、先ほどの「二分探索」戦略の結果よりも優れています。また、他のどの戦略よりも優れているか、少なくとも同等です。 さて、ここまで $n = 8$ の最適な戦略を説明してきました。
-Let $C(n)$ be the worst-case cost achieved by an optimal strategy for $n$, as described above. Thus $C(1) = 0$, $C(2) = 1$, $C(3) = 2$ and $C(8) = 12$.
+上のとおり、$n$ に対する最適な戦略によって達成される、最悪ケースのコストを $C(n)$ とします。 したがって、$C(1) = 0$, $C(2) = 1$, $C(3) = 2$, $C(8) = 12$ です。
-Similarly, $C(100) = 400$ and $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$.
+同様に、$C(100) = 400$, $\displaystyle\sum_{n = 1}^{100} C(n) = 17575$ です。
-Find $\displaystyle\sum_{n = 1}^{200\\,000} C(n)$.
+$\displaystyle\sum_{n = 1}^{200\\,000} C(n)$ を求めなさい。
# --hints--
-`lowestCostSearch()` should return `260511850222`.
+`lowestCostSearch()` は `260511850222` を返す必要があります。
```js
assert.strictEqual(lowestCostSearch(), 260511850222);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
index 54f72db23f..24f3c9e9f9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-329-prime-frog.md
@@ -1,6 +1,6 @@
---
id: 5900f4b51000cf542c50ffc8
-title: 'Problem 329: Prime Frog'
+title: '問題 329: 素数ガエル'
challengeType: 5
forumTopicId: 301986
dashedName: problem-329-prime-frog
@@ -8,27 +8,27 @@ dashedName: problem-329-prime-frog
# --description--
-Susan has a prime frog.
+スーザンは素数ガエルを飼っています。
-Her frog is jumping around over 500 squares numbered 1 to 500.
+そのカエルは、1 から 500 までの番号が振られた 500 個のマスの上を跳び回ります。
-He can only jump one square to the left or to the right, with equal probability, and he cannot jump outside the range [1;500]. (if it lands at either end, it automatically jumps to the only available square on the next move.)
+左または右のマスのみへ等しい確率で跳ぶことができ、範囲 [1;500] の外側に跳ぶことはできません。 (いずれかの端に着くと、次に移動できる唯一のマスへ自動的に跳びます。)
-When he is on a square with a prime number on it, he croaks 'P' (PRIME) with probability $\frac{2}{3}$ or 'N' (NOT PRIME) with probability $\frac{1}{3}$ just before jumping to the next square. When he is on a square with a number on it that is not a prime he croaks 'P' with probability $\frac{1}{3}$ or 'N' with probability $\frac{2}{3}$ just before jumping to the next square.
+素数が書かれたマスにいるとき、次のマスへ跳ぶ直前に、確率 $\frac{2}{3}$で 'P' (素数)、または確率 $\frac{1}{3}$ で 'N' (非素数) と鳴きます。 非素数が書かれたマスにいるとき、次のマスへ跳ぶ直前に、確率 $\frac{1}{3}$で 'P' と鳴くか、確率 $\frac{2}{3}$ で 'N' と鳴きます。
-Given that the frog's starting position is random with the same probability for every square, and given that she listens to his first 15 croaks, what is the probability that she hears the sequence PPPPNNPPPNPPNPN?
+カエルがどのマスから跳び始めるかは、不規則かつすべてのマスで等確率であるとします。カエルの最初の 15 回の鳴き声が PPPPNNPPPNPPNPN の順になる確率を求めなさい。
-Give your answer as a string as a fraction `p/q` in reduced form.
+回答は、既約分数 `p/q` の形式の文字列にすること。
# --hints--
-`primeFrog()` should return a string.
+`primeFrog()` は文字列を返す必要があります。
```js
assert(typeof primeFrog() === 'string');
```
-`primeFrog()` should return the string `199740353/29386561536000`.
+`primeFrog()` は文字列 `199740353/29386561536000` を返す必要があります。
```js
assert.strictEqual(primeFrog(), '199740353/29386561536000');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
index 91813ffcbf..4f4e623a83 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-330-eulers-number.md
@@ -1,6 +1,6 @@
---
id: 5900f4b71000cf542c50ffc9
-title: 'Problem 330: Euler''s Number'
+title: '問題 330: オイラー数'
challengeType: 5
forumTopicId: 301988
dashedName: problem-330-eulers-number
@@ -8,25 +8,25 @@ dashedName: problem-330-eulers-number
# --description--
-An infinite sequence of real numbers $a(n)$ is defined for all integers $n$ as follows:
+すべての整数 $n$ について、実数の無限数列 $a(n)$ は次のように定義されます。
$$ a(n) = \begin{cases} 1 & n < 0 \\\\ \displaystyle \sum_{i = 1}^{\infty} \frac{a(n - 1)}{i!} & n \ge 0 \end{cases} $$
-For example,
+例えば次のようになります。
$$\begin{align} & a(0) = \frac{1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = e − 1 \\\\ & a(1) = \frac{e − 1}{1!} + \frac{1}{2!} + \frac{1}{3!} + \ldots = 2e − 3 \\\\ & a(2) = \frac{2e − 3}{1!} + \frac{e − 1}{2!} + \frac{1}{3!} + \ldots = \frac{7}{2} e − 6 \end{align}$$
-with $e = 2.7182818\ldots$ being Euler's constant.
+ここで、$e = 2.7182818\ldots$ はオイラーの定数です。
-It can be shown that $a(n)$ is of the form $\displaystyle\frac{A(n)e + B(n)}{n!}$ for integers $A(n)$ and $B(n)$.
+$a(n)$ は、整数 $A(n)$ と整数 $B(n)$ に対して $\displaystyle\frac{A(n)e + B(n)}{n!}$ の形式であることが分かります。
-For example $\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$.
+例えば、$\displaystyle a(10) = \frac{328161643e − 652694486}{10!}$ です。
-Find $A({10}^9)$ + $B({10}^9)$ and give your answer $\bmod 77\\,777\\,777$.
+$A({10}^9)$ + $B({10}^9)$ を求め、$\bmod 77\\,777\\,777$ で答えなさい。
# --hints--
-`eulersNumber()` should return `15955822`.
+`eulersNumber()` は `15955822` を返す必要があります。
```js
assert.strictEqual(eulersNumber(), 15955822);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
index ab777a2d5d..8f62ddf8d9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-331-cross-flips.md
@@ -1,6 +1,6 @@
---
id: 5900f4b71000cf542c50ffca
-title: 'Problem 331: Cross flips'
+title: '問題 331: 十字めくり'
challengeType: 5
forumTopicId: 301989
dashedName: problem-331-cross-flips
@@ -8,25 +8,25 @@ dashedName: problem-331-cross-flips
# --description--
-N×N disks are placed on a square game board. Each disk has a black side and white side.
+N×N 個の円盤が正方形のゲーム盤上に置かれています。 円盤にはそれぞれ黒い面と白い面があります。
-At each turn, you may choose a disk and flip all the disks in the same row and the same column as this disk: thus $2 × N - 1$ disks are flipped. The game ends when all disks show their white side. The following example shows a game on a 5×5 board.
+ターンごとに円盤を 1 枚選び、それと同じ横列および同じ縦列にある円盤をすべて裏返します。したがって、$2 × N - 1$ 枚の円盤が裏返されます。 すべての円盤が白い面になるとゲームは終了です。 次の例は、5×5 の盤を使用したゲームです。
-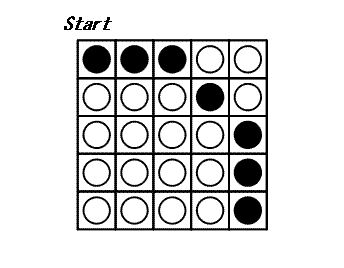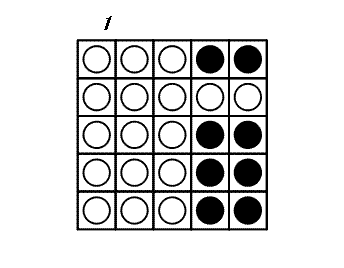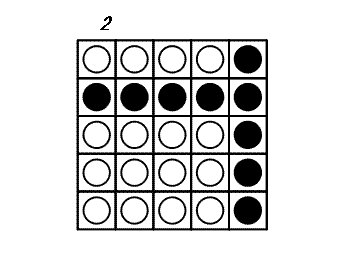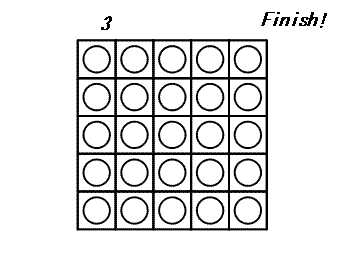 +
+ -It can be proven that 3 is the minimal number of turns to finish this game.
+このゲームを終了するための最小ターン数が 3 であることが分かります。
-The bottom left disk on the $N×N$ board has coordinates (0, 0); the bottom right disk has coordinates ($N - 1$,$0$) and the top left disk has coordinates ($0$,$N - 1$).
+$N×N$ の盤の左下の円盤は座標 (0,0)、右下の円盤は座標 ($N - 1$,$0$)、そして左上の円盤は座標 ($0$,$N - 1$) です。
-Let $C_N$ be the following configuration of a board with $N × N$ disks: A disk at ($x$, $y$) satisfying $N - 1 \le \sqrt{x^2 + y^2} \lt N$, shows its black side; otherwise, it shows its white side. $C_5$ is shown above.
+$N × N$ 枚の円盤を並べた盤について、$N - 1 \le \sqrt{x^2 + y^2} \lt N$ を満たす ($x$, $y$) の円盤は黒い面が見え、それ以外は白い面が見えているような配置を、$C_N$ とします。 上図は $C_5$ です。
-Let $T(N)$ be the minimal number of turns to finish a game starting from configuration $C_N$ or 0 if configuration $C_N$ is unsolvable. We have shown that $T(5) = 3$. You are also given that $T(10) = 29$ and $T(1\\,000) = 395\\,253$.
+配置 $C_N$ からゲームを始めて終了するまでの最小ターン数を $T(N)$ とし、配置 $C_N$ に解が存在しない場合は最小ターン数を 0 とします。 $T(5) = 3$ であることは既に示しました。 さらに、$T(10) = 29$ と $T(1\\000) = 395\\,253$ が与えられます。
-Find $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
+$\displaystyle \sum_{i = 3}^{31} T(2^i - i)$ を求めなさい。
# --hints--
-`crossFlips()` should return `467178235146843500`.
+`crossFlips()` は `467178235146843500` を返す必要があります。
```js
assert.strictEqual(crossFlips(), 467178235146843500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index 726d6184fb..560270f76a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcb
-title: 'Problem 332: Spherical triangles'
+title: '問題 332: 球面三角形'
challengeType: 5
forumTopicId: 301990
dashedName: problem-332-spherical-triangles
@@ -8,25 +8,25 @@ dashedName: problem-332-spherical-triangles
# --description--
-A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
+球面三角形は、3 つの頂点で 2 本ずつ交差する 3 本の大円弧によって球面上に作られる図形です。
-
-It can be proven that 3 is the minimal number of turns to finish this game.
+このゲームを終了するための最小ターン数が 3 であることが分かります。
-The bottom left disk on the $N×N$ board has coordinates (0, 0); the bottom right disk has coordinates ($N - 1$,$0$) and the top left disk has coordinates ($0$,$N - 1$).
+$N×N$ の盤の左下の円盤は座標 (0,0)、右下の円盤は座標 ($N - 1$,$0$)、そして左上の円盤は座標 ($0$,$N - 1$) です。
-Let $C_N$ be the following configuration of a board with $N × N$ disks: A disk at ($x$, $y$) satisfying $N - 1 \le \sqrt{x^2 + y^2} \lt N$, shows its black side; otherwise, it shows its white side. $C_5$ is shown above.
+$N × N$ 枚の円盤を並べた盤について、$N - 1 \le \sqrt{x^2 + y^2} \lt N$ を満たす ($x$, $y$) の円盤は黒い面が見え、それ以外は白い面が見えているような配置を、$C_N$ とします。 上図は $C_5$ です。
-Let $T(N)$ be the minimal number of turns to finish a game starting from configuration $C_N$ or 0 if configuration $C_N$ is unsolvable. We have shown that $T(5) = 3$. You are also given that $T(10) = 29$ and $T(1\\,000) = 395\\,253$.
+配置 $C_N$ からゲームを始めて終了するまでの最小ターン数を $T(N)$ とし、配置 $C_N$ に解が存在しない場合は最小ターン数を 0 とします。 $T(5) = 3$ であることは既に示しました。 さらに、$T(10) = 29$ と $T(1\\000) = 395\\,253$ が与えられます。
-Find $\displaystyle \sum_{i = 3}^{31} T(2^i - i)$.
+$\displaystyle \sum_{i = 3}^{31} T(2^i - i)$ を求めなさい。
# --hints--
-`crossFlips()` should return `467178235146843500`.
+`crossFlips()` は `467178235146843500` を返す必要があります。
```js
assert.strictEqual(crossFlips(), 467178235146843500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
index 726d6184fb..560270f76a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-332-spherical-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcb
-title: 'Problem 332: Spherical triangles'
+title: '問題 332: 球面三角形'
challengeType: 5
forumTopicId: 301990
dashedName: problem-332-spherical-triangles
@@ -8,25 +8,25 @@ dashedName: problem-332-spherical-triangles
# --description--
-A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.
+球面三角形は、3 つの頂点で 2 本ずつ交差する 3 本の大円弧によって球面上に作られる図形です。
-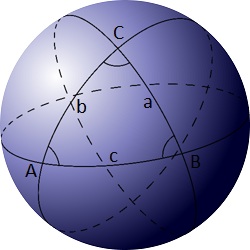 +
+ -Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.
+中心 (0,0,0) と半径 $r$ を持つ球を $C(r)$ とします。
-Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.
+整数座標を持つ $C(r)$ の球面上にある点の集合を $Z(r)$ とします。
-Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are not included in $T(r)$.
+頂点 $Z(r)$ を持つ球面三角形の集合を $T(r)$ とします。 縮退した球面三角形 (同一の大円弧上の 3 点で形成されるもの) は $T(r)$ に含まれません。
-Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.
+$T(r)$ の中で最も小さい球面三角形について、その面積を $A(r)$ とします。
-For example $A(14)$ is 3.294040 rounded to six decimal places.
+例えば、$A(14)$ を四捨五入して小数第 6 位まで求めると 3.294040 です。
-Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.
+$\displaystyle \sum_{r = 1}^{50} A(r)$ を求めなさい。 回答は、四捨五入して小数第 6 位まで示すこと。
# --hints--
-`sphericalTriangles()` should return `2717.751525`.
+`sphericalTriangles()` は `2717.751525` を返す必要があります。
```js
assert.strictEqual(sphericalTriangles(), 2717.751525);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 4f433e9141..41e96d9130 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcc
-title: 'Problem 333: Special partitions'
+title: '問題 333: 特殊な分割'
challengeType: 5
forumTopicId: 301991
dashedName: problem-333-special-partitions
@@ -8,25 +8,25 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as $2^i \times 3^j$, where $i, j ≥ 0$.
+すべての正の整数は、すべての項を $2^i \times 3^j$ (ここで $i, j ≥ 0$) で表せるような形で分割することができます。
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ would not be valid since 2 can divide 6. Neither would the partition $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ since 1 can divide 16. The only valid partition of 17 would be $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
+他の項の約数である項が一つもないような分割のみを考えます。 例えば、$17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ は、2 が 6 を割り切るので有効ではありません。 分割 $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ も、1 が 16 を割り切るので有効ではありません。 17 の場合、唯一の有効な分割は $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$ です。
-Many integers have more than one valid partition, the first being 11 having the following two partitions.
+多くの整数には有効な分割が複数個あります。そのような最初の数は 11 であり、次の 2 つの分割があります。
$$\begin{align} & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1) \end{align}$$
-Let's define $P(n)$ as the number of valid partitions of $n$. For example, $P(11) = 2$.
+$n$ の有効な分割の数を $P(n)$ とします。 例えば、$P(11) = 2$ です。
-Let's consider only the prime integers $q$ which would have a single valid partition such as $P(17)$.
+$P(17)$ のような、有効な分割を 1 つ持つ素数の整数 $q$ のみについて考えます。
-The sum of the primes $q <100$ such that $P(q) = 1$ equals 233.
+$P(q) = 1$ となる $q <100$ の和は 233 です。
-Find the sum of the primes $q < 1\\,000\\,000$ such that $P(q) = 1$.
+$P(q) = 1$ となる素数 $q < 1\\,000\\,000$ の和を求めなさい。
# --hints--
-`specialPartitions()` should return `3053105`.
+`specialPartitions()` は `3053105` を返す必要があります。
```js
assert.strictEqual(specialPartitions(), 3053105);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index 6e1f4eb9f5..f11d2b2891 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4ba1000cf542c50ffcd
-title: 'Problem 334: Spilling the beans'
+title: '問題 334: 豆をこぼす'
challengeType: 5
forumTopicId: 301992
dashedName: problem-334-spilling-the-beans
@@ -8,23 +8,23 @@ dashedName: problem-334-spilling-the-beans
# --description--
-In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.
+プラトンの天国に、無数のボウルが一直線に並べられています。 各ボウルには、有限個の豆が 0 個またはいくつか入っています。 1 人の子供がゲームをします。そのゲームでは、任意のボウルから豆を 2 つ取って両隣のボウルに 1 つずつ入れるという、1 種類の移動だけが許されます。 いずれのボウルにも 1 個または 0 個の豆が入っているとき、ゲームは終了です。
-For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
+例えば、隣り合う 2 つのボウルにそれぞれ 2 つと 3 つの豆が入っており、他のボウルがすべて空であるとします。 次の 8 回の移動でゲームが終了します。
-
-Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.
+中心 (0,0,0) と半径 $r$ を持つ球を $C(r)$ とします。
-Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.
+整数座標を持つ $C(r)$ の球面上にある点の集合を $Z(r)$ とします。
-Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are not included in $T(r)$.
+頂点 $Z(r)$ を持つ球面三角形の集合を $T(r)$ とします。 縮退した球面三角形 (同一の大円弧上の 3 点で形成されるもの) は $T(r)$ に含まれません。
-Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.
+$T(r)$ の中で最も小さい球面三角形について、その面積を $A(r)$ とします。
-For example $A(14)$ is 3.294040 rounded to six decimal places.
+例えば、$A(14)$ を四捨五入して小数第 6 位まで求めると 3.294040 です。
-Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.
+$\displaystyle \sum_{r = 1}^{50} A(r)$ を求めなさい。 回答は、四捨五入して小数第 6 位まで示すこと。
# --hints--
-`sphericalTriangles()` should return `2717.751525`.
+`sphericalTriangles()` は `2717.751525` を返す必要があります。
```js
assert.strictEqual(sphericalTriangles(), 2717.751525);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
index 4f433e9141..41e96d9130 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-333-special-partitions.md
@@ -1,6 +1,6 @@
---
id: 5900f4b91000cf542c50ffcc
-title: 'Problem 333: Special partitions'
+title: '問題 333: 特殊な分割'
challengeType: 5
forumTopicId: 301991
dashedName: problem-333-special-partitions
@@ -8,25 +8,25 @@ dashedName: problem-333-special-partitions
# --description--
-All positive integers can be partitioned in such a way that each and every term of the partition can be expressed as $2^i \times 3^j$, where $i, j ≥ 0$.
+すべての正の整数は、すべての項を $2^i \times 3^j$ (ここで $i, j ≥ 0$) で表せるような形で分割することができます。
-Let's consider only those such partitions where none of the terms can divide any of the other terms. For example, the partition of $17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ would not be valid since 2 can divide 6. Neither would the partition $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ since 1 can divide 16. The only valid partition of 17 would be $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$.
+他の項の約数である項が一つもないような分割のみを考えます。 例えば、$17 = 2 + 6 + 9 = (2^1 \times 3^0 + 2^1 \times 3^1 + 2^0 \times 3^2)$ は、2 が 6 を割り切るので有効ではありません。 分割 $17 = 16 + 1 = (2^4 \times 3^0 + 2^0 \times 3^0)$ も、1 が 16 を割り切るので有効ではありません。 17 の場合、唯一の有効な分割は $8 + 9 = (2^3 \times 3^0 + 2^0 \times 3^2)$ です。
-Many integers have more than one valid partition, the first being 11 having the following two partitions.
+多くの整数には有効な分割が複数個あります。そのような最初の数は 11 であり、次の 2 つの分割があります。
$$\begin{align} & 11 = 2 + 9 = (2^1 \times 3^0 + 2^0 \times 3^2) \\\\ & 11 = 8 + 3 = (2^3 \times 3^0 + 2^0 \times 3^1) \end{align}$$
-Let's define $P(n)$ as the number of valid partitions of $n$. For example, $P(11) = 2$.
+$n$ の有効な分割の数を $P(n)$ とします。 例えば、$P(11) = 2$ です。
-Let's consider only the prime integers $q$ which would have a single valid partition such as $P(17)$.
+$P(17)$ のような、有効な分割を 1 つ持つ素数の整数 $q$ のみについて考えます。
-The sum of the primes $q <100$ such that $P(q) = 1$ equals 233.
+$P(q) = 1$ となる $q <100$ の和は 233 です。
-Find the sum of the primes $q < 1\\,000\\,000$ such that $P(q) = 1$.
+$P(q) = 1$ となる素数 $q < 1\\,000\\,000$ の和を求めなさい。
# --hints--
-`specialPartitions()` should return `3053105`.
+`specialPartitions()` は `3053105` を返す必要があります。
```js
assert.strictEqual(specialPartitions(), 3053105);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index 6e1f4eb9f5..f11d2b2891 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4ba1000cf542c50ffcd
-title: 'Problem 334: Spilling the beans'
+title: '問題 334: 豆をこぼす'
challengeType: 5
forumTopicId: 301992
dashedName: problem-334-spilling-the-beans
@@ -8,23 +8,23 @@ dashedName: problem-334-spilling-the-beans
# --description--
-In Plato's heaven, there exist an infinite number of bowls in a straight line. Each bowl either contains some or none of a finite number of beans. A child plays a game, which allows only one kind of move: removing two beans from any bowl, and putting one in each of the two adjacent bowls. The game ends when each bowl contains either one or no beans.
+プラトンの天国に、無数のボウルが一直線に並べられています。 各ボウルには、有限個の豆が 0 個またはいくつか入っています。 1 人の子供がゲームをします。そのゲームでは、任意のボウルから豆を 2 つ取って両隣のボウルに 1 つずつ入れるという、1 種類の移動だけが許されます。 いずれのボウルにも 1 個または 0 個の豆が入っているとき、ゲームは終了です。
-For example, consider two adjacent bowls containing 2 and 3 beans respectively, all other bowls being empty. The following eight moves will finish the game:
+例えば、隣り合う 2 つのボウルにそれぞれ 2 つと 3 つの豆が入っており、他のボウルがすべて空であるとします。 次の 8 回の移動でゲームが終了します。
-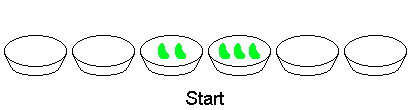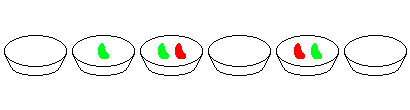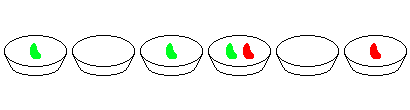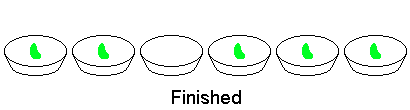 +
+ -You are given the following sequences:
+次の数列が与えられます。
-$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd} \end{cases} \\\\ & \qquad \text{where $⌊x⌋$ is the floor function and $\oplus$ is the bitwise XOR operator.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
+$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{$t_{i - 1}$ が偶数の場合} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{$t_{i - 1}$ が奇数の場合} \end{cases} \\\\ & \qquad \text{ここで、$⌊x⌋$ は床関数、$\oplus$ はビット排他論理和演算子} \\\\ & b_i = (t_i\bmod 2^{11}) + 1 \end{align}$$
-The first two terms of the last sequence are $b_1 = 289$ and $b_2 = 145$. If we start with $b_1$ and $b_2$ beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+最後の数列に含まれる最初の 2 項は $b_1 = 289$ と $b_2 = 145$ です。 隣り合う 2 つのボウルでそれぞれ $b_1$ 個と $b_2$ 個の豆から始めると、ゲームを終えるまでに 3419100 回動かす必要があります。
-Consider now 1500 adjacent bowls containing $b_1, b_2, \ldots, b_{1500}$ beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+隣り合う 1500 個のボウルにそれぞれ $b_1, b_2, \ldots, b_{1500}$ 個の豆が入っており、他のボウルはすべて空であるとします。 ゲームを終了させるのに必要な移動回数を求めなさい。
# --hints--
-`spillingTheBeans()` should return `150320021261690850`.
+`spillingTheBeans()` は `150320021261690850` を返す必要があります。
```js
assert.strictEqual(spillingTheBeans(), 150320021261690850);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index d7fb3ffad9..3d33b9d93e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffce
-title: 'Problem 335: Gathering the beans'
+title: '問題 335: 豆を集める'
challengeType: 5
forumTopicId: 301993
dashedName: problem-335-gathering-the-beans
@@ -8,19 +8,19 @@ dashedName: problem-335-gathering-the-beans
# --description--
-Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+ピーターは退屈に感じるたびに、ボウルをいくつか置き、それぞれに 1 つ豆を入れて円形に並べます。 この後、ある 1 つのボウルからすべての豆を取り出し、右回りに 1つずつボウルに落としていきます。 最後の豆を落としたボウルから再び同じことをします。これを、最初の状態に戻るまで繰り返します。 例えば 5 つのボウルでは次のようにします。
-
-You are given the following sequences:
+次の数列が与えられます。
-$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ is even} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ is odd} \end{cases} \\\\ & \qquad \text{where $⌊x⌋$ is the floor function and $\oplus$ is the bitwise XOR operator.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
+$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{$t_{i - 1}$ が偶数の場合} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{$t_{i - 1}$ が奇数の場合} \end{cases} \\\\ & \qquad \text{ここで、$⌊x⌋$ は床関数、$\oplus$ はビット排他論理和演算子} \\\\ & b_i = (t_i\bmod 2^{11}) + 1 \end{align}$$
-The first two terms of the last sequence are $b_1 = 289$ and $b_2 = 145$. If we start with $b_1$ and $b_2$ beans in two adjacent bowls, 3419100 moves would be required to finish the game.
+最後の数列に含まれる最初の 2 項は $b_1 = 289$ と $b_2 = 145$ です。 隣り合う 2 つのボウルでそれぞれ $b_1$ 個と $b_2$ 個の豆から始めると、ゲームを終えるまでに 3419100 回動かす必要があります。
-Consider now 1500 adjacent bowls containing $b_1, b_2, \ldots, b_{1500}$ beans respectively, all other bowls being empty. Find how many moves it takes before the game ends.
+隣り合う 1500 個のボウルにそれぞれ $b_1, b_2, \ldots, b_{1500}$ 個の豆が入っており、他のボウルはすべて空であるとします。 ゲームを終了させるのに必要な移動回数を求めなさい。
# --hints--
-`spillingTheBeans()` should return `150320021261690850`.
+`spillingTheBeans()` は `150320021261690850` を返す必要があります。
```js
assert.strictEqual(spillingTheBeans(), 150320021261690850);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
index d7fb3ffad9..3d33b9d93e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-335-gathering-the-beans.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffce
-title: 'Problem 335: Gathering the beans'
+title: '問題 335: 豆を集める'
challengeType: 5
forumTopicId: 301993
dashedName: problem-335-gathering-the-beans
@@ -8,19 +8,19 @@ dashedName: problem-335-gathering-the-beans
# --description--
-Whenever Peter feels bored, he places some bowls, containing one bean each, in a circle. After this, he takes all the beans out of a certain bowl and drops them one by one in the bowls going clockwise. He repeats this, starting from the bowl he dropped the last bean in, until the initial situation appears again. For example with 5 bowls he acts as follows:
+ピーターは退屈に感じるたびに、ボウルをいくつか置き、それぞれに 1 つ豆を入れて円形に並べます。 この後、ある 1 つのボウルからすべての豆を取り出し、右回りに 1つずつボウルに落としていきます。 最後の豆を落としたボウルから再び同じことをします。これを、最初の状態に戻るまで繰り返します。 例えば 5 つのボウルでは次のようにします。
- +
+ -So with 5 bowls it takes Peter 15 moves to return to the initial situation.
+したがって、ボウルが 5 つの場合、最初の状況に戻るまでに豆を 15 回動かします。
-Let $M(x)$ represent the number of moves required to return to the initial situation, starting with $x$ bowls. Thus, $M(5) = 15$. It can also be verified that $M(100) = 10920$.
+$x$ 個のボウルで始めて最初の状況に戻るまでに必要な移動回数を、$M(x)$ とします。 したがって、$M(5) = 15$ です。 $M(100) = 10920$ であることも確認できます。
-Find $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Give your answer modulo $7^9$.
+$\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$ を求めなさい。 mod $7^9$ で答えること。
# --hints--
-`gatheringTheBeans()` should return `5032316`.
+`gatheringTheBeans()` は `5032316` を返す必要があります。
```js
assert.strictEqual(gatheringTheBeans(), 5032316);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index f390d18348..df8f8228fc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffcf
-title: 'Problem 336: Maximix Arrangements'
+title: '問題 336: 最も不ぞろいな配置'
challengeType: 5
forumTopicId: 301994
dashedName: problem-336-maximix-arrangements
@@ -8,31 +8,31 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: $ABCD$. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+4 つの貨物 $ABCD$ をこの順序に並べ、機関車で運びます。 しかし、機関車が貨物を受け取るために到着したとき、貨物が正しい順序に並んでいないことがあります。
-To rearrange the carriages, they are all shunted onto a large rotating turntable. After the carriages are uncoupled at a specific point, the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180°. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+順序を入れ替えるために、すべての貨物が大きな回転台に載せられます。 特定の個所で貨物が切り離された後、機関車はそれ自体に連結されている貨物をけん引しながら回転台から離れます。 残りの貨物は 180° 回転されます。 その後、すべての貨物が再び連結され、回転台の使用回数が最も少なくなるような方法で、正しい順序になるまでこの作業が繰り返されます。
-Some arrangements, such as $ADCB$, can be solved easily: the carriages are separated between $A$ and $D$, and after $DCB$ are rotated the correct order has been achieved.
+$ADCB$ などの配置は簡単に直せます。貨物を $A$ と $D$ の間で切り離し、$DCB$ を回転すると正しい順序になります。
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage $A$ in the correct place, then carriage $B$, and so on.
+しかし、機関車を運転するシンプル・サイモンは効率が悪い人なので、いつも最初に貨物 $A$ を正しい位置に置き換え、次に貨物 $B$ を正しい位置に置き換え、以降も同様にすることで正しく並べ替えます。
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are $DACB$ and $DBAC$; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for $DACB$ is shown below.
+貨物が 4 つある場合、サイモンにとって起こり得る最悪の配置 (「最も不ぞろいな配置」と呼ぶことにします) は $DACB$ と $DBAC$ で、それぞれ 5 回の回転が必要です (最も効率的な方法なら 3 回の回転で済むのですが)。 サイモンが $DACB$ に使用した手順を下に示します。
-
-So with 5 bowls it takes Peter 15 moves to return to the initial situation.
+したがって、ボウルが 5 つの場合、最初の状況に戻るまでに豆を 15 回動かします。
-Let $M(x)$ represent the number of moves required to return to the initial situation, starting with $x$ bowls. Thus, $M(5) = 15$. It can also be verified that $M(100) = 10920$.
+$x$ 個のボウルで始めて最初の状況に戻るまでに必要な移動回数を、$M(x)$ とします。 したがって、$M(5) = 15$ です。 $M(100) = 10920$ であることも確認できます。
-Find $\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$. Give your answer modulo $7^9$.
+$\displaystyle\sum_{k = 0}^{{10}^{18}} M(2^k + 1)$ を求めなさい。 mod $7^9$ で答えること。
# --hints--
-`gatheringTheBeans()` should return `5032316`.
+`gatheringTheBeans()` は `5032316` を返す必要があります。
```js
assert.strictEqual(gatheringTheBeans(), 5032316);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
index f390d18348..df8f8228fc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-336-maximix-arrangements.md
@@ -1,6 +1,6 @@
---
id: 5900f4bd1000cf542c50ffcf
-title: 'Problem 336: Maximix Arrangements'
+title: '問題 336: 最も不ぞろいな配置'
challengeType: 5
forumTopicId: 301994
dashedName: problem-336-maximix-arrangements
@@ -8,31 +8,31 @@ dashedName: problem-336-maximix-arrangements
# --description--
-A train is used to transport four carriages in the order: $ABCD$. However, sometimes when the train arrives to collect the carriages they are not in the correct order.
+4 つの貨物 $ABCD$ をこの順序に並べ、機関車で運びます。 しかし、機関車が貨物を受け取るために到着したとき、貨物が正しい順序に並んでいないことがあります。
-To rearrange the carriages, they are all shunted onto a large rotating turntable. After the carriages are uncoupled at a specific point, the train moves off the turntable pulling the carriages still attached with it. The remaining carriages are rotated 180°. All of the carriages are then rejoined and this process is repeated as often as necessary in order to obtain the least number of uses of the turntable.
+順序を入れ替えるために、すべての貨物が大きな回転台に載せられます。 特定の個所で貨物が切り離された後、機関車はそれ自体に連結されている貨物をけん引しながら回転台から離れます。 残りの貨物は 180° 回転されます。 その後、すべての貨物が再び連結され、回転台の使用回数が最も少なくなるような方法で、正しい順序になるまでこの作業が繰り返されます。
-Some arrangements, such as $ADCB$, can be solved easily: the carriages are separated between $A$ and $D$, and after $DCB$ are rotated the correct order has been achieved.
+$ADCB$ などの配置は簡単に直せます。貨物を $A$ と $D$ の間で切り離し、$DCB$ を回転すると正しい順序になります。
-However, Simple Simon, the train driver, is not known for his efficiency, so he always solves the problem by initially getting carriage $A$ in the correct place, then carriage $B$, and so on.
+しかし、機関車を運転するシンプル・サイモンは効率が悪い人なので、いつも最初に貨物 $A$ を正しい位置に置き換え、次に貨物 $B$ を正しい位置に置き換え、以降も同様にすることで正しく並べ替えます。
-Using four carriages, the worst possible arrangements for Simon, which we shall call maximix arrangements, are $DACB$ and $DBAC$; each requiring him five rotations (although, using the most efficient approach, they could be solved using just three rotations). The process he uses for $DACB$ is shown below.
+貨物が 4 つある場合、サイモンにとって起こり得る最悪の配置 (「最も不ぞろいな配置」と呼ぶことにします) は $DACB$ と $DBAC$ で、それぞれ 5 回の回転が必要です (最も効率的な方法なら 3 回の回転で済むのですが)。 サイモンが $DACB$ に使用した手順を下に示します。
-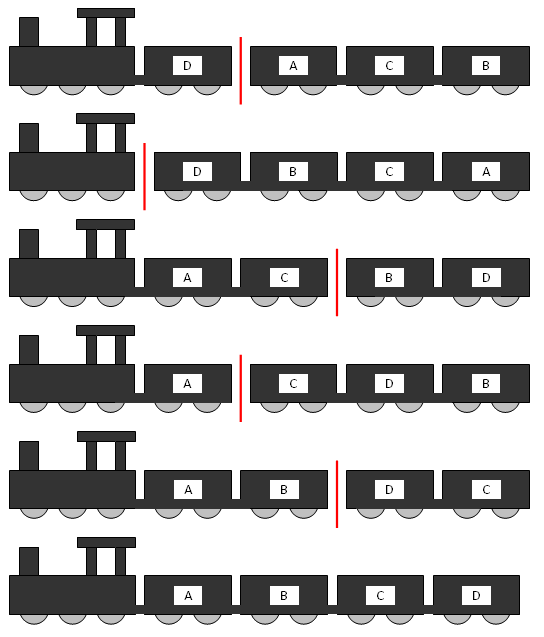 +
+ -It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is $DFAECB$.
+貨物が 6 つある場合、最も不ぞろいな配置は最大 24 個あり、そのうち辞書順で 10 番目の最も不ぞろいな配置が $DFAECB$ であることを確認できます。
-Find the ${2011}^{\text{th}}$ lexicographic maximix arrangement for eleven carriages.
+貨物が 11 個があるとき、辞書順で ${2011}$ 番目の最も不ぞろいな配置を求めなさい。
# --hints--
-`maximixArrangements()` should return a string.
+`maximixArrangements()` は文字列を返す必要があります。
```js
assert(typeof maximixArrangements() === 'string');
```
-`maximixArrangements()` should return the string `CAGBIHEFJDK`.
+`maximixArrangements()` は文字列 `CAGBIHEFJDK` を返す必要があります。
```js
assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index a0298d4170..1b8ba0f661 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd0
-title: 'Problem 337: Totient Stairstep Sequences'
+title: '問題 337: トーティエント階段型数列 (Stairstep Sequence)'
challengeType: 5
forumTopicId: 301995
dashedName: problem-337-totient-stairstep-sequences
@@ -8,25 +8,25 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let $\\{a_1, a_2, \ldots, a_n\\}$ be an integer sequence of length $n$ such that:
+次の条件を満たす長さ $n$ の整数数列を $\\{a_1, a_2, \ldots, a_n\\}$ とします。
- $a_1 = 6$
-- for all $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
+- すべての $1 ≤ i < n$ について、$φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-$φ$ denotes Euler's totient function.
+$φ$ はオイラーのトーティエント関数を表します。
-Let $S(N)$ be the number of such sequences with $a_n ≤ N$.
+そのような数列のうち $a_n ≤ N$ を満たすものの数を $S(N)$ とします。
-For example, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+例: $S(10) = 4$: {6}, {6, 8}, {6, 8, 9}, {6, 10}
-We can verify that $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
+$S(100) = 482\\,073\\,668$, $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$ であることを確認できます。
-Find $S(20\\,000\\,000)\bmod {10}^8$.
+$S(20\\,000\\,000)\bmod {10}^8$ を求めなさい。
# --hints--
-`totientStairstepSequences()` should return `85068035`.
+`totientStairstepSequences()` は `85068035` を返す必要があります。
```js
assert.strictEqual(totientStairstepSequences(), 85068035);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index f152123fd9..ba871db88a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd1
-title: 'Problem 338: Cutting Rectangular Grid Paper'
+title: '問題 338: 長方形の方眼紙を切る'
challengeType: 5
forumTopicId: 301996
dashedName: problem-338-cutting-rectangular-grid-paper
@@ -8,25 +8,25 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions $w$ × $h$ is given. Its grid spacing is 1.
+整数寸法 $w$ × $h$ の長方形の方眼紙が 1 枚与えられます。 格子の間隔は 1 です。
-When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
+この紙を格子線に沿って 2 枚に切り離し、それらの紙を重ねずに並べ替えると、寸法が異なる新しい長方形ができます。
-For example, from a sheet with dimensions 9 × 4, we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+例えば下図のように、寸法 9 × 4 の紙を切り並べ替えると 18 × 2, 12 × 3, 6 × 6 の寸法の長方形を作ることができます。
-
-It can be verified that there are 24 maximix arrangements for six carriages, of which the tenth lexicographic maximix arrangement is $DFAECB$.
+貨物が 6 つある場合、最も不ぞろいな配置は最大 24 個あり、そのうち辞書順で 10 番目の最も不ぞろいな配置が $DFAECB$ であることを確認できます。
-Find the ${2011}^{\text{th}}$ lexicographic maximix arrangement for eleven carriages.
+貨物が 11 個があるとき、辞書順で ${2011}$ 番目の最も不ぞろいな配置を求めなさい。
# --hints--
-`maximixArrangements()` should return a string.
+`maximixArrangements()` は文字列を返す必要があります。
```js
assert(typeof maximixArrangements() === 'string');
```
-`maximixArrangements()` should return the string `CAGBIHEFJDK`.
+`maximixArrangements()` は文字列 `CAGBIHEFJDK` を返す必要があります。
```js
assert.strictEqual(maximixArrangements(), 'CAGBIHEFJDK');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
index a0298d4170..1b8ba0f661 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-337-totient-stairstep-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd0
-title: 'Problem 337: Totient Stairstep Sequences'
+title: '問題 337: トーティエント階段型数列 (Stairstep Sequence)'
challengeType: 5
forumTopicId: 301995
dashedName: problem-337-totient-stairstep-sequences
@@ -8,25 +8,25 @@ dashedName: problem-337-totient-stairstep-sequences
# --description--
-Let $\\{a_1, a_2, \ldots, a_n\\}$ be an integer sequence of length $n$ such that:
+次の条件を満たす長さ $n$ の整数数列を $\\{a_1, a_2, \ldots, a_n\\}$ とします。
- $a_1 = 6$
-- for all $1 ≤ i < n$ : $φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
+- すべての $1 ≤ i < n$ について、$φ(a_i) < φ(a_{i + 1}) < a_i < a_{i + 1}$
-$φ$ denotes Euler's totient function.
+$φ$ はオイラーのトーティエント関数を表します。
-Let $S(N)$ be the number of such sequences with $a_n ≤ N$.
+そのような数列のうち $a_n ≤ N$ を満たすものの数を $S(N)$ とします。
-For example, $S(10) = 4$: {6}, {6, 8}, {6, 8, 9} and {6, 10}.
+例: $S(10) = 4$: {6}, {6, 8}, {6, 8, 9}, {6, 10}
-We can verify that $S(100) = 482\\,073\\,668$ and $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$.
+$S(100) = 482\\,073\\,668$, $S(10\\,000)\bmod {10}^8 = 73\\,808\\,307$ であることを確認できます。
-Find $S(20\\,000\\,000)\bmod {10}^8$.
+$S(20\\,000\\,000)\bmod {10}^8$ を求めなさい。
# --hints--
-`totientStairstepSequences()` should return `85068035`.
+`totientStairstepSequences()` は `85068035` を返す必要があります。
```js
assert.strictEqual(totientStairstepSequences(), 85068035);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
index f152123fd9..ba871db88a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-338-cutting-rectangular-grid-paper.md
@@ -1,6 +1,6 @@
---
id: 5900f4be1000cf542c50ffd1
-title: 'Problem 338: Cutting Rectangular Grid Paper'
+title: '問題 338: 長方形の方眼紙を切る'
challengeType: 5
forumTopicId: 301996
dashedName: problem-338-cutting-rectangular-grid-paper
@@ -8,25 +8,25 @@ dashedName: problem-338-cutting-rectangular-grid-paper
# --description--
-A rectangular sheet of grid paper with integer dimensions $w$ × $h$ is given. Its grid spacing is 1.
+整数寸法 $w$ × $h$ の長方形の方眼紙が 1 枚与えられます。 格子の間隔は 1 です。
-When we cut the sheet along the grid lines into two pieces and rearrange those pieces without overlap, we can make new rectangles with different dimensions.
+この紙を格子線に沿って 2 枚に切り離し、それらの紙を重ねずに並べ替えると、寸法が異なる新しい長方形ができます。
-For example, from a sheet with dimensions 9 × 4, we can make rectangles with dimensions 18 × 2, 12 × 3 and 6 × 6 by cutting and rearranging as below:
+例えば下図のように、寸法 9 × 4 の紙を切り並べ替えると 18 × 2, 12 × 3, 6 × 6 の寸法の長方形を作ることができます。
-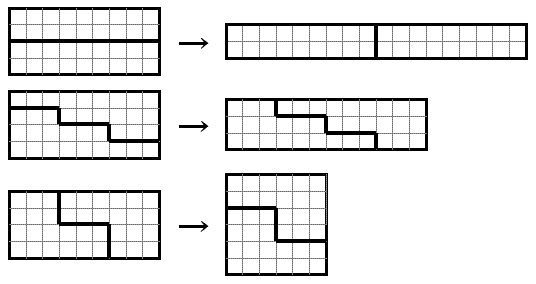 +
+ -Similarly, from a sheet with dimensions 9 × 8, we can make rectangles with dimensions 18 × 4 and 12 × 6.
+同様に、寸法 9 × 8 の紙から、寸法 18 × 4 と 12 × 6 の長方形を作ることができます。
-For a pair $w$ and $h$, let $F(w, h)$ be the number of distinct rectangles that can be made from a sheet with dimensions $w$ × $h$. For example, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ and $F(9, 8) = 2$. Note that rectangles congruent to the initial one are not counted in $F(w, h)$. Note also that rectangles with dimensions $w$ × $h$ and dimensions $h$ × $w$ are not considered distinct.
+$w$ と $h$ の対について、寸法 $w$ × $h$ の紙で作れる相異なる長方形の数を $F(w, h)$ とします。 例えば、$F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$, $F(9, 8) = 2$ です。 注意点として、最初の長方形と一致する長方形は $F(w, h)$ に数えられません。 また、寸法 $w$ × $h$ と寸法 $h$ × $w$ の長方形は区別されません。
-For an integer $N$, let $G(N)$ be the sum of $F(w, h)$ for all pairs $w$ and $h$ which satisfy $0 < h ≤ w ≤ N$. We can verify that $G(10) = 55$, $G({10}^3) = 971\\,745$ and $G({10}^5) = 9\\,992\\,617\\,687$.
+整数 $N$ について、0 < h ≤ w ≤ N$ を満たすような $w$ と $h$ の対のすべてに対する $F(w, h)$ の和を $G(N)$ とします。 $G(10) = 55$, $G({10}^3) = 971\\,745$, $G({10}^5) = 9\\,992\\,617\\,687$ であることを確認できます。
-Find $G({10}^{12})$. Give your answer modulo ${10}^8$.
+$G({10}^{12})$ を求めなさい。 mod ${10}^8$ で答えること。
# --hints--
-`cuttingRectangularGridPaper()` should return `15614292`.
+`cuttingRectangularGridPaper()` は `15614292` を返す必要があります。
```js
assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index c080309b34..a12f28b759 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -1,6 +1,6 @@
---
id: 5900f4c01000cf542c50ffd2
-title: 'Problem 339: Peredur fab Efrawg'
+title: '問題 339: 『エヴラウクの息子ペレドゥルの物語』'
challengeType: 5
forumTopicId: 301997
dashedName: problem-339-peredur-fab-efrawg
@@ -8,17 +8,17 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black." - Peredur the Son of Evrawc
+「そして彼は川が流れる谷へ向かいました。谷の縁は木々に覆われ、川の両側には平らな草地がありました。 片方の川岸には白い羊の群れが、反対側の川岸には黒い羊の群れが見えました。 白い羊が鳴くたびに 1 頭の黒い羊が川を渡って白くなり、黒い羊が鳴くと 1 頭の白い羊が川を渡って黒くなりました。」 - 『エヴラウクの息子ペレドゥルの物語』
-Initially, each flock consists of $n$ sheep. Each sheep (regardless of color) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let $E(n)$ be the expected final number of black sheep if Peredur uses an optimal strategy.
+最初はそれぞれの群れに $n$ 頭います。 (色に関係なく) それぞれの羊は等しい確率で次に鳴きます。 1 頭の羊が鳴き、他方の群れの 1 頭の羊が 渡った後、ペレドゥルは黒い羊の最終的な期待頭数を最大化するために、任意の頭数の白い羊を取り除くことができます。 ペレドゥルが最適な戦略を使った場合の、黒い羊の最終的な期待頭数を $E(n)$ とします。
-You are given that $E(5) = 6.871346$ rounded to 6 places behind the decimal point.
+$E(5) = 6.871346$ (小数第 6 位に四捨五入) が与えられます。
-Find $E(10\\,000)$ and give your answer rounded to 6 places behind the decimal point.
+$E(10\\,000)$ を求め、四捨五入して小数第 6 位まで示しなさい。
# --hints--
-`peredurFabEfrawg()` should return `19823.542204`.
+`peredurFabEfrawg()` は `19823.542204` を返す必要があります。
```js
assert.strictEqual(peredurFabEfrawg(), 19823.542204);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 3f61e86376..9876f78b34 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4c21000cf542c50ffd4
-title: 'Problem 340: Crazy Function'
+title: '問題 340: クレイジー関数'
challengeType: 5
forumTopicId: 301999
dashedName: problem-340-crazy-function
@@ -8,19 +8,19 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers $a$, $b$, $c$, define the crazy function $F(n)$ as follows:
+固定小数点整数 $a$, $b$, $c$ について、クレイジー関数 (crazy function) $F(n)$ を次のように定義します。
-$$\begin{align} & F(n) = n - c \\;\text{ for all } n > b \\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ for all } n ≤ b. \end{align}$$
+$$\begin{align} & F(n) = n - c \\;\text{ (すべての } n > b \text{ に対して)}\\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ (すべての } n ≤ b \text{ に対して)} \end{align}$$
-Also, define $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
+また、$S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$ と定義します。
-For example, if $a = 50$, $b = 2000$ and $c = 40$, then $F(0) = 3240$ and $F(2000) = 2040$. Also, $S(50, 2000, 40) = 5\\,204\\,240$.
+例えば、$a = 50$, $b = 2000$, $c = 40$ の場合、$F(0) = 3240$, $F(2000) = 2040$ です。 また、$S(50, 2000, 40) = 5\\,204\\,240$ です。
-Find the last 9 digits of $S({21}^7, 7^{21}, {12}^7)$.
+$S({21}^7, 7^{21}, {12}^7)$ の下位 9 桁を求めなさい。
# --hints--
-`crazyFunction()` should return `291504964`.
+`crazyFunction()` は `291504964` を返す必要があります。
```js
assert.strictEqual(crazyFunction(), 291504964);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
index de57ab7d25..6396890445 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4c11000cf542c50ffd3
-title: 'Problem 341: Golomb''s self-describing sequence'
+title: '問題 341: ゴロムの自己記述的数列'
challengeType: 5
forumTopicId: 302000
dashedName: problem-341-golombs-self-describing-sequence
@@ -8,19 +8,19 @@ dashedName: problem-341-golombs-self-describing-sequence
# --description--
-The Golomb's self-describing sequence ($G(n)$) is the only nondecreasing sequence of natural numbers such that $n$ appears exactly $G(n)$ times in the sequence. The values of $G(n)$ for the first few $n$ are
+ゴロムの自己記述的数列 ($G(n)$) は、数列内に $n$ がちょうど $G(n)$ 回現れるような、自然数の非減少数列です。 最初の数個の $n$ に対する $G(n)$ の値を次に示します。
$$\begin{array}{c} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & \ldots \\\\ G(n) & 1 & 2 & 2 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & \ldots \end{array}$$
-You are given that $G({10}^3) = 86$, $G({10}^6) = 6137$.
+$G({10}^3) = 86$, $G({10}^6) = 6137$ が与えられます。
-You are also given that $\sum G(n^3) = 153\\,506\\,976$ for $1 ≤ n < {10}^3$.
+また、$1 ≤ n < {10}^3$ のとき、$\sum G(n^3) = 153\\,506\\,976$ です。
-Find $\sum G(n^3)$ for $1 ≤ n < {10}^6$.
+$1 ≤ n < {10}^6$ のとき、$\sum G(n^3)$ を求めなさい。
# --hints--
-`golombsSequence()` should return `56098610614277016`.
+`golombsSequence()` は `56098610614277016` を返す必要があります。
```js
assert.strictEqual(golombsSequence(), 56098610614277016);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
index 950e7d6535..12fa3fb3f6 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c31000cf542c50ffd5
-title: 'Problem 342: The totient of a square is a cube'
+title: '問題 342: 平方数のトーティエントが立方数であるような数'
challengeType: 5
forumTopicId: 302001
dashedName: problem-342-the-totient-of-a-square-is-a-cube
@@ -8,18 +8,18 @@ dashedName: problem-342-the-totient-of-a-square-is-a-cube
# --description--
-Consider the number 50.
+50 という数について考えます。
-${50}^2 = 2500 = 2^2 × 5^4$, so $φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$. $φ$ denotes Euler's totient function.
+${50}^2 = 2500 = 2^2 × 5^4$ なので、$φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$ です。 $φ$ はオイラーのトーティエント関数を表します。
-So 2500 is a square and $φ(2500)$ is a cube.
+したがって、2500 は平方数であり、$φ(2500)$ は立方数です。
-Find the sum of all numbers $n$, $1 < n < {10}^{10}$ such that $φ(n^2)$ is a cube.
+$1 < n < ^ {10}^{10}$ のとき、$φ(n^2)$ が立方数であるような数 $n$ の総和を求めなさい。
# --hints--
-`totientOfSquare()` should return `5943040885644`.
+`totientOfSquare()` は `5943040885644` を返す必要があります。
```js
assert.strictEqual(totientOfSquare(), 5943040885644);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
index 65410d7642..6f3ba8aad5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4c41000cf542c50ffd6
-title: 'Problem 343: Fractional Sequences'
+title: '問題 343: 分数数列'
challengeType: 5
forumTopicId: 302002
dashedName: problem-343-fractional-sequences
@@ -8,28 +8,28 @@ dashedName: problem-343-fractional-sequences
# --description--
-For any positive integer $k$, a finite sequence $a_i$ of fractions $\frac{x_i}{y_i}$ is defined by:
+任意の正の整数 $k$ について、分数 $\frac{x_i}{y_i}$ の有限数列 $a_i$ は次のように定義されます。
-- $a_1 = \displaystyle\frac{1}{k}$ and
-- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ reduced to lowest terms for $i > 1$.
+- $a_1 = \displaystyle\frac{1}{k}$
+- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ ($i > 1$ のときは約分)
-When $a_i$ reaches some integer $n$, the sequence stops. (That is, when $y_i = 1$.)
+$a_i$ が整数 $n$に達すると数列は止まります。 (すなわち、$y_i = 1$ になったとき)
-Define $f(k) = n$.
+$f(k) = n$ と定義します。
-For example, for $k = 20$:
+例えば、$k = 20$ のときは次のようになります。
$$\frac{1}{20} → \frac{2}{19} → \frac{3}{18} = \frac{1}{6} → \frac{2}{5} → \frac{3}{4} → \frac{4}{3} → \frac{5}{2} → \frac{6}{1} = 6$$
-So $f(20) = 6$.
+したがって、$f(20) = 6$ です。
-Also $f(1) = 1$, $f(2) = 2$, $f(3) = 1$ and $\sum f(k^3) = 118\\,937$ for $1 ≤ k ≤ 100$.
+また、$1 ≤ k ≤ 100$ のとき、$f(1) = 1$, $f(2) = 2$, $f(3) = 1$, $\sum f(k^3) = 118\\,937$ です。
-Find $\sum f(k^3)$ for $1 ≤ k ≤ 2 × {10}^6$.
+$1 ≤ k ≤ 2 × {10}^6$ のとき、$\sum f(k^3)$ を求めなさい。
# --hints--
-`fractionalSequences()` should return `269533451410884200`.
+`fractionalSequences()` は `269533451410884200` を返す必要があります。
```js
assert.strictEqual(fractionalSequences(), 269533451410884200);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
index 067c6ee72a..3bbff2c99e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4c51000cf542c50ffd7
-title: 'Problem 344: Silver dollar game'
+title: '問題 344: 銀貨ゲーム'
challengeType: 5
forumTopicId: 302003
dashedName: problem-344-silver-dollar-game
@@ -8,29 +8,29 @@ dashedName: problem-344-silver-dollar-game
# --description--
-One variant of N.G. de Bruijn's silver dollar game can be described as follows:
+ニコラース・ホーヴァート・ ド・ブラウンの銀貨ゲームにはいくつかバリエーションがあり、その一つは次のように説明されます。
-On a strip of squares a number of coins are placed, at most one coin per square. Only one coin, called the silver dollar, has any value. Two players take turns making moves. At each turn a player must make either a regular or a special move.
+マスが並ぶ細長い盤上に硬貨が何枚か置かれています (1 マスにたかだか 1 枚)。 銀貨 (1 ドル硬貨) と呼ばれる 1 枚しかない硬貨に、任意の価値があります。 2 人のプレイヤーが交互にプレイします。 各ターンで、プレイヤーは通常の移動または特別な移動を行う必要があります。
-A regular move consists of selecting one coin and moving it one or more squares to the left. The coin cannot move out of the strip or jump on or over another coin.
+通常の移動とは、硬貨を 1 枚 選び、それを 1 マス以上左へ動かすことです。 硬貨を盤の外に出したり、他のコインの上に置いたり、その上を飛び越えさせたりすることはできません。
-Alternatively, the player can choose to make the special move of pocketing the leftmost coin rather than making a regular move. If no regular moves are possible, the player is forced to pocket the leftmost coin.
+あるいは、通常の移動ではなく、左端の硬貨を取り自分がもらうという特殊な移動を選ぶこともできます。 通常の移動が不可能であれば、必然的に左端の硬貨をもらうことになります。
-The winner is the player who pockets the silver dollar.
+銀貨を手に入れたプレイヤーが勝者です。
-
-Similarly, from a sheet with dimensions 9 × 8, we can make rectangles with dimensions 18 × 4 and 12 × 6.
+同様に、寸法 9 × 8 の紙から、寸法 18 × 4 と 12 × 6 の長方形を作ることができます。
-For a pair $w$ and $h$, let $F(w, h)$ be the number of distinct rectangles that can be made from a sheet with dimensions $w$ × $h$. For example, $F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$ and $F(9, 8) = 2$. Note that rectangles congruent to the initial one are not counted in $F(w, h)$. Note also that rectangles with dimensions $w$ × $h$ and dimensions $h$ × $w$ are not considered distinct.
+$w$ と $h$ の対について、寸法 $w$ × $h$ の紙で作れる相異なる長方形の数を $F(w, h)$ とします。 例えば、$F(2, 1) = 0$, $F(2, 2) = 1$, $F(9, 4) = 3$, $F(9, 8) = 2$ です。 注意点として、最初の長方形と一致する長方形は $F(w, h)$ に数えられません。 また、寸法 $w$ × $h$ と寸法 $h$ × $w$ の長方形は区別されません。
-For an integer $N$, let $G(N)$ be the sum of $F(w, h)$ for all pairs $w$ and $h$ which satisfy $0 < h ≤ w ≤ N$. We can verify that $G(10) = 55$, $G({10}^3) = 971\\,745$ and $G({10}^5) = 9\\,992\\,617\\,687$.
+整数 $N$ について、0 < h ≤ w ≤ N$ を満たすような $w$ と $h$ の対のすべてに対する $F(w, h)$ の和を $G(N)$ とします。 $G(10) = 55$, $G({10}^3) = 971\\,745$, $G({10}^5) = 9\\,992\\,617\\,687$ であることを確認できます。
-Find $G({10}^{12})$. Give your answer modulo ${10}^8$.
+$G({10}^{12})$ を求めなさい。 mod ${10}^8$ で答えること。
# --hints--
-`cuttingRectangularGridPaper()` should return `15614292`.
+`cuttingRectangularGridPaper()` は `15614292` を返す必要があります。
```js
assert.strictEqual(cuttingRectangularGridPaper(), 15614292);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
index c080309b34..a12f28b759 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-339-peredur-fab-efrawg.md
@@ -1,6 +1,6 @@
---
id: 5900f4c01000cf542c50ffd2
-title: 'Problem 339: Peredur fab Efrawg'
+title: '問題 339: 『エヴラウクの息子ペレドゥルの物語』'
challengeType: 5
forumTopicId: 301997
dashedName: problem-339-peredur-fab-efrawg
@@ -8,17 +8,17 @@ dashedName: problem-339-peredur-fab-efrawg
# --description--
-"And he came towards a valley, through which ran a river; and the borders of the valley were wooded, and on each side of the river were level meadows. And on one side of the river he saw a flock of white sheep, and on the other a flock of black sheep. And whenever one of the white sheep bleated, one of the black sheep would cross over and become white; and when one of the black sheep bleated, one of the white sheep would cross over and become black." - Peredur the Son of Evrawc
+「そして彼は川が流れる谷へ向かいました。谷の縁は木々に覆われ、川の両側には平らな草地がありました。 片方の川岸には白い羊の群れが、反対側の川岸には黒い羊の群れが見えました。 白い羊が鳴くたびに 1 頭の黒い羊が川を渡って白くなり、黒い羊が鳴くと 1 頭の白い羊が川を渡って黒くなりました。」 - 『エヴラウクの息子ペレドゥルの物語』
-Initially, each flock consists of $n$ sheep. Each sheep (regardless of color) is equally likely to be the next sheep to bleat. After a sheep has bleated and a sheep from the other flock has crossed over, Peredur may remove a number of white sheep in order to maximize the expected final number of black sheep. Let $E(n)$ be the expected final number of black sheep if Peredur uses an optimal strategy.
+最初はそれぞれの群れに $n$ 頭います。 (色に関係なく) それぞれの羊は等しい確率で次に鳴きます。 1 頭の羊が鳴き、他方の群れの 1 頭の羊が 渡った後、ペレドゥルは黒い羊の最終的な期待頭数を最大化するために、任意の頭数の白い羊を取り除くことができます。 ペレドゥルが最適な戦略を使った場合の、黒い羊の最終的な期待頭数を $E(n)$ とします。
-You are given that $E(5) = 6.871346$ rounded to 6 places behind the decimal point.
+$E(5) = 6.871346$ (小数第 6 位に四捨五入) が与えられます。
-Find $E(10\\,000)$ and give your answer rounded to 6 places behind the decimal point.
+$E(10\\,000)$ を求め、四捨五入して小数第 6 位まで示しなさい。
# --hints--
-`peredurFabEfrawg()` should return `19823.542204`.
+`peredurFabEfrawg()` は `19823.542204` を返す必要があります。
```js
assert.strictEqual(peredurFabEfrawg(), 19823.542204);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
index 3f61e86376..9876f78b34 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-340-crazy-function.md
@@ -1,6 +1,6 @@
---
id: 5900f4c21000cf542c50ffd4
-title: 'Problem 340: Crazy Function'
+title: '問題 340: クレイジー関数'
challengeType: 5
forumTopicId: 301999
dashedName: problem-340-crazy-function
@@ -8,19 +8,19 @@ dashedName: problem-340-crazy-function
# --description--
-For fixed integers $a$, $b$, $c$, define the crazy function $F(n)$ as follows:
+固定小数点整数 $a$, $b$, $c$ について、クレイジー関数 (crazy function) $F(n)$ を次のように定義します。
-$$\begin{align} & F(n) = n - c \\;\text{ for all } n > b \\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ for all } n ≤ b. \end{align}$$
+$$\begin{align} & F(n) = n - c \\;\text{ (すべての } n > b \text{ に対して)}\\\\ & F(n) = F(a + F(a + F(a + F(a + n)))) \\;\text{ (すべての } n ≤ b \text{ に対して)} \end{align}$$
-Also, define $S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$.
+また、$S(a, b, c) = \displaystyle\sum_{n = 0}^b F(n)$ と定義します。
-For example, if $a = 50$, $b = 2000$ and $c = 40$, then $F(0) = 3240$ and $F(2000) = 2040$. Also, $S(50, 2000, 40) = 5\\,204\\,240$.
+例えば、$a = 50$, $b = 2000$, $c = 40$ の場合、$F(0) = 3240$, $F(2000) = 2040$ です。 また、$S(50, 2000, 40) = 5\\,204\\,240$ です。
-Find the last 9 digits of $S({21}^7, 7^{21}, {12}^7)$.
+$S({21}^7, 7^{21}, {12}^7)$ の下位 9 桁を求めなさい。
# --hints--
-`crazyFunction()` should return `291504964`.
+`crazyFunction()` は `291504964` を返す必要があります。
```js
assert.strictEqual(crazyFunction(), 291504964);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
index de57ab7d25..6396890445 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-341-golombs-self-describing-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4c11000cf542c50ffd3
-title: 'Problem 341: Golomb''s self-describing sequence'
+title: '問題 341: ゴロムの自己記述的数列'
challengeType: 5
forumTopicId: 302000
dashedName: problem-341-golombs-self-describing-sequence
@@ -8,19 +8,19 @@ dashedName: problem-341-golombs-self-describing-sequence
# --description--
-The Golomb's self-describing sequence ($G(n)$) is the only nondecreasing sequence of natural numbers such that $n$ appears exactly $G(n)$ times in the sequence. The values of $G(n)$ for the first few $n$ are
+ゴロムの自己記述的数列 ($G(n)$) は、数列内に $n$ がちょうど $G(n)$ 回現れるような、自然数の非減少数列です。 最初の数個の $n$ に対する $G(n)$ の値を次に示します。
$$\begin{array}{c} n & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & \ldots \\\\ G(n) & 1 & 2 & 2 & 3 & 3 & 4 & 4 & 4 & 5 & 5 & 5 & 6 & 6 & 6 & 6 & \ldots \end{array}$$
-You are given that $G({10}^3) = 86$, $G({10}^6) = 6137$.
+$G({10}^3) = 86$, $G({10}^6) = 6137$ が与えられます。
-You are also given that $\sum G(n^3) = 153\\,506\\,976$ for $1 ≤ n < {10}^3$.
+また、$1 ≤ n < {10}^3$ のとき、$\sum G(n^3) = 153\\,506\\,976$ です。
-Find $\sum G(n^3)$ for $1 ≤ n < {10}^6$.
+$1 ≤ n < {10}^6$ のとき、$\sum G(n^3)$ を求めなさい。
# --hints--
-`golombsSequence()` should return `56098610614277016`.
+`golombsSequence()` は `56098610614277016` を返す必要があります。
```js
assert.strictEqual(golombsSequence(), 56098610614277016);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
index 950e7d6535..12fa3fb3f6 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-342-the-totient-of-a-square-is-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c31000cf542c50ffd5
-title: 'Problem 342: The totient of a square is a cube'
+title: '問題 342: 平方数のトーティエントが立方数であるような数'
challengeType: 5
forumTopicId: 302001
dashedName: problem-342-the-totient-of-a-square-is-a-cube
@@ -8,18 +8,18 @@ dashedName: problem-342-the-totient-of-a-square-is-a-cube
# --description--
-Consider the number 50.
+50 という数について考えます。
-${50}^2 = 2500 = 2^2 × 5^4$, so $φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$. $φ$ denotes Euler's totient function.
+${50}^2 = 2500 = 2^2 × 5^4$ なので、$φ(2500) = 2 × 4 × 5^3 = 8 × 5^3 = 2^3 × 5^3$ です。 $φ$ はオイラーのトーティエント関数を表します。
-So 2500 is a square and $φ(2500)$ is a cube.
+したがって、2500 は平方数であり、$φ(2500)$ は立方数です。
-Find the sum of all numbers $n$, $1 < n < {10}^{10}$ such that $φ(n^2)$ is a cube.
+$1 < n < ^ {10}^{10}$ のとき、$φ(n^2)$ が立方数であるような数 $n$ の総和を求めなさい。
# --hints--
-`totientOfSquare()` should return `5943040885644`.
+`totientOfSquare()` は `5943040885644` を返す必要があります。
```js
assert.strictEqual(totientOfSquare(), 5943040885644);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
index 65410d7642..6f3ba8aad5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-343-fractional-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4c41000cf542c50ffd6
-title: 'Problem 343: Fractional Sequences'
+title: '問題 343: 分数数列'
challengeType: 5
forumTopicId: 302002
dashedName: problem-343-fractional-sequences
@@ -8,28 +8,28 @@ dashedName: problem-343-fractional-sequences
# --description--
-For any positive integer $k$, a finite sequence $a_i$ of fractions $\frac{x_i}{y_i}$ is defined by:
+任意の正の整数 $k$ について、分数 $\frac{x_i}{y_i}$ の有限数列 $a_i$ は次のように定義されます。
-- $a_1 = \displaystyle\frac{1}{k}$ and
-- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ reduced to lowest terms for $i > 1$.
+- $a_1 = \displaystyle\frac{1}{k}$
+- $a_i = \displaystyle\frac{(x_{i - 1} + 1)}{(y_{i - 1} - 1)}$ ($i > 1$ のときは約分)
-When $a_i$ reaches some integer $n$, the sequence stops. (That is, when $y_i = 1$.)
+$a_i$ が整数 $n$に達すると数列は止まります。 (すなわち、$y_i = 1$ になったとき)
-Define $f(k) = n$.
+$f(k) = n$ と定義します。
-For example, for $k = 20$:
+例えば、$k = 20$ のときは次のようになります。
$$\frac{1}{20} → \frac{2}{19} → \frac{3}{18} = \frac{1}{6} → \frac{2}{5} → \frac{3}{4} → \frac{4}{3} → \frac{5}{2} → \frac{6}{1} = 6$$
-So $f(20) = 6$.
+したがって、$f(20) = 6$ です。
-Also $f(1) = 1$, $f(2) = 2$, $f(3) = 1$ and $\sum f(k^3) = 118\\,937$ for $1 ≤ k ≤ 100$.
+また、$1 ≤ k ≤ 100$ のとき、$f(1) = 1$, $f(2) = 2$, $f(3) = 1$, $\sum f(k^3) = 118\\,937$ です。
-Find $\sum f(k^3)$ for $1 ≤ k ≤ 2 × {10}^6$.
+$1 ≤ k ≤ 2 × {10}^6$ のとき、$\sum f(k^3)$ を求めなさい。
# --hints--
-`fractionalSequences()` should return `269533451410884200`.
+`fractionalSequences()` は `269533451410884200` を返す必要があります。
```js
assert.strictEqual(fractionalSequences(), 269533451410884200);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
index 067c6ee72a..3bbff2c99e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-344-silver-dollar-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4c51000cf542c50ffd7
-title: 'Problem 344: Silver dollar game'
+title: '問題 344: 銀貨ゲーム'
challengeType: 5
forumTopicId: 302003
dashedName: problem-344-silver-dollar-game
@@ -8,29 +8,29 @@ dashedName: problem-344-silver-dollar-game
# --description--
-One variant of N.G. de Bruijn's silver dollar game can be described as follows:
+ニコラース・ホーヴァート・ ド・ブラウンの銀貨ゲームにはいくつかバリエーションがあり、その一つは次のように説明されます。
-On a strip of squares a number of coins are placed, at most one coin per square. Only one coin, called the silver dollar, has any value. Two players take turns making moves. At each turn a player must make either a regular or a special move.
+マスが並ぶ細長い盤上に硬貨が何枚か置かれています (1 マスにたかだか 1 枚)。 銀貨 (1 ドル硬貨) と呼ばれる 1 枚しかない硬貨に、任意の価値があります。 2 人のプレイヤーが交互にプレイします。 各ターンで、プレイヤーは通常の移動または特別な移動を行う必要があります。
-A regular move consists of selecting one coin and moving it one or more squares to the left. The coin cannot move out of the strip or jump on or over another coin.
+通常の移動とは、硬貨を 1 枚 選び、それを 1 マス以上左へ動かすことです。 硬貨を盤の外に出したり、他のコインの上に置いたり、その上を飛び越えさせたりすることはできません。
-Alternatively, the player can choose to make the special move of pocketing the leftmost coin rather than making a regular move. If no regular moves are possible, the player is forced to pocket the leftmost coin.
+あるいは、通常の移動ではなく、左端の硬貨を取り自分がもらうという特殊な移動を選ぶこともできます。 通常の移動が不可能であれば、必然的に左端の硬貨をもらうことになります。
-The winner is the player who pockets the silver dollar.
+銀貨を手に入れたプレイヤーが勝者です。
-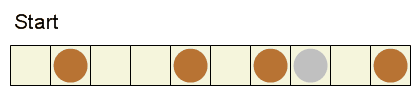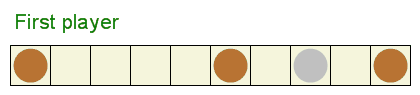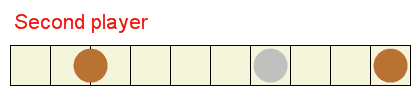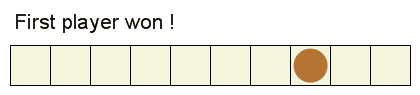 +
+ -A winning configuration is an arrangement of coins on the strip where the first player can force a win no matter what the second player does.
+後手が何をしようが先手が必ず勝てるような硬貨の配列を、「勝利構成」と呼びます。
-Let $W(n, c)$ be the number of winning configurations for a strip of $n$ squares, $c$ worthless coins and one silver dollar.
+$n$ 個のマス、$c$ 枚の無価値硬貨、および 1 枚の銀貨を使用する場合の勝利構成の数を、$W(n, c)$ とします。
-You are given that $W(10, 2) = 324$ and $W(100, 10) = 1\\,514\\,704\\,946\\,113\\,500$.
+$W(10, 2) = 324$, $W(100, 10) = 1\\,514\\,704\\,946\\,113\\,500$ が与えられます。
-Find $W(1\\,000\\,000, 100)$ modulo the semiprime $1000\\,036\\,000\\,099 (= 1\\,000\\,003 \times 1\\,000\\,033)$.
+$W(1\\,000\\,000, 100)$ を求め、半素数 $1000\\,036\\,000\\,099 (= 1\\,000\\,003 \times 1\\,000\\,033)$ で割った余りを答えなさい。
# --hints--
-`silverDollarGame()` should return `65579304332`.
+`silverDollarGame()` は `65579304332` を返す必要があります。
```js
assert.strictEqual(silverDollarGame(), 65579304332);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
index 12e850c9bf..95ddf7a7e9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffda
-title: 'Problem 345: Matrix Sum'
+title: '問題 345: 行列和'
challengeType: 5
forumTopicId: 302004
dashedName: problem-345-matrix-sum
@@ -8,19 +8,19 @@ dashedName: problem-345-matrix-sum
# --description--
-We define the Matrix Sum of a matrix as the maximum sum of matrix elements with each element being the only one in his row and column.
+各行と各列から 1 つずつ選択された行列要素の最大和を、その行列の「行列和」(Matrix Sum) と定義します。
-For example, the Matrix Sum of the matrix below equals $3315 ( = 863 + 383 + 343 + 959 + 767)$:
+例えば次の行列では、行列の和は $3315 (= 863 + 383 + 343 + 959 + 767)$ です。
$$\begin{array}{rrrrr} 7 & 53 & 183 & 439 & \color{lime}{863} \\\\ 497 & \color{lime}{383} & 563 & 79 & 973 \\\\ 287 & 63 & \color{lime}{343} & 169 & 583 \\\\ 627 & 343 & 773 & \color{lime}{959} & 943 \\\\ \color{lime}{767} & 473 & 103 & 699 & 303 \end{array}$$
-Find the Matrix Sum of:
+次の行列の行列和を求めなさい。
$$\\begin{array}{r} 7 & 53 & 183 & 439 & 863 & 497 & 383 & 563 & 79 & 973 & 287 & 63 & 343 & 169 & 583 \\\\ 627 & 343 & 773 & 959 & 943 & 767 & 473 & 103 & 699 & 303 & 957 & 703 & 583 & 639 & 913 \\\\ 447 & 283 & 463 & 29 & 23 & 487 & 463 & 993 & 119 & 883 & 327 & 493 & 423 & 159 & 743 \\\\ 217 & 623 & 3 & 399 & 853 & 407 & 103 & 983 & 89 & 463 & 290 & 516 & 212 & 462 & 350 \\\\ 960 & 376 & 682 & 962 & 300 & 780 & 486 & 502 & 912 & 800 & 250 & 346 & 172 & 812 & 350 \\\\ 870 & 456 & 192 & 162 & 593 & 473 & 915 & 45 & 989 & 873 & 823 & 965 & 425 & 329 & 803 \\\\ 973 & 965 & 905 & 919 & 133 & 673 & 665 & 235 & 509 & 613 & 673 & 815 & 165 & 992 & 326 \\\\ 322 & 148 & 972 & 962 & 286 & 255 & 941 & 541 & 265 & 323 & 925 & 281 & 601 & 95 & 973 \\\\ 445 & 721 & 11 & 525 & 473 & 65 & 511 & 164 & 138 & 672 & 18 & 428 & 154 & 448 & 848 \\\\ 414 & 456 & 310 & 312 & 798 & 104 & 566 & 520 & 302 & 248 & 694 & 976 & 430 & 392 & 198 \\\\ 184 & 829 & 373 & 181 & 631 & 101 & 969 & 613 & 840 & 740 & 778 & 458 & 284 & 760 & 390 \\\\ 821 & 461 & 843 & 513 & 17 & 901 & 711 & 993 & 293 & 157 & 274 & 94 & 192 & 156 & 574 \\\\ 34 & 124 & 4 & 878 & 450 & 476 & 712 & 914 & 838 & 669 & 875 & 299 & 823 & 329 & 699 \\\\ 815 & 559 & 813 & 459 & 522 & 788 & 168 & 586 & 966 & 232 & 308 & 833 & 251 & 631 & 107 \\\\ 813 & 883 & 451 & 509 & 615 & 77 & 281 & 613 & 459 & 205 & 380 & 274 & 302 & 35 & 805 \end{array}$$
# --hints--
-`matrixSum()` should return `13938`.
+`matrixSum()` は `13938` を返す必要があります。
```js
assert.strictEqual(matrixSum(), 13938);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
index 88c4634715..54ed2c701a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
@@ -1,6 +1,6 @@
---
id: 5900f4c71000cf542c50ffd8
-title: 'Problem 346: Strong Repunits'
+title: '問題 346: 強力なレピュニット数'
challengeType: 5
forumTopicId: 302005
dashedName: problem-346-strong-repunits
@@ -8,15 +8,15 @@ dashedName: problem-346-strong-repunits
# --description--
-The number 7 is special, because 7 is 111 written in base 2, and 11 written in base 6 (i.e. $7_{10} = {11}_6 = {111}_2$). In other words, 7 is a repunit in at least two bases $b > 1$.
+7 という数は特殊です。2 進数では 111、6 進数では 11 と表されるからです ($7_{10} = {11}_6 = {111}_2$)。 つまり、7 は少なくとも 2 つの基数 ($b > 1$) のレピュニット数です。
-We shall call a positive integer with this property a strong repunit. It can be verified that there are 8 strong repunits below 50: {1, 7, 13, 15, 21, 31, 40, 43}. Furthermore, the sum of all strong repunits below 1000 equals 15864.
+このような性質を持つ正の整数を「強力なレピュニット数」と呼ぶことにします。 50 未満の強力なレピュニット数は {1, 7, 13, 15, 21, 31, 40, 43} の 8 つであることを確認できます。 さらに、1000 未満の強力なレピュニット数の総和は 15864 です。
-Find the sum of all strong repunits below ${10}^{12}$.
+${10}^{12}$ 未満の強力なレピュニット数の総和を求めなさい。
# --hints--
-`strongRepunits()` should return `336108797689259260`.
+`strongRepunits()` は `336108797689259260` を返す必要があります
```js
assert.strictEqual(strongRepunits(), 336108797689259260);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
index 9924ba3fab..421eee9763 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffd9
-title: 'Problem 347: Largest integer divisible by two primes'
+title: '問題 347: 2 つの素数で割り切れる最大の整数'
challengeType: 5
forumTopicId: 302006
dashedName: problem-347-largest-integer-divisible-by-two-primes
@@ -8,21 +8,21 @@ dashedName: problem-347-largest-integer-divisible-by-two-primes
# --description--
-The largest integer $≤ 100$ that is only divisible by both the primes 2 and 3 is 96, as $96 = 32 \times 3 = 2^5 \times 3$.
+素数のうち 2 と 3 の両方のみで割り切れる最大の整数 ($≤ 100$) は 96 であり、$96 = 32 \times 3 = 2^5 \times 3$ となります。
-For two distinct primes $p$ and $q$ let $M(p, q, N)$ be the largest positive integer $≤ N$ only divisible by both $p$ and $q$ and $M(p, q, N)=0$ if such a positive integer does not exist.
+2 つの相異なる素数 $p$ と $q$ について、$p$ と $q$ の両方のみで割り切れる、$N$ 以下の最大の正の整数を $M(p, q, N)$ とします。そのような正の整数が存在しない場合は $M(p. q, N)=0$ とします。
-E.g. $M(2, 3, 100) = 96$.
+例: $M(2, 3, 100) = 96$
-$M(3, 5, 100) = 75$ and not 90 because 90 is divisible by 2, 3 and 5. Also $M(2, 73, 100) = 0$ because there does not exist a positive integer $≤ 100$ that is divisible by both 2 and 73.
+$M(3, 5, 100) = 75$ であり 90 ではありません。90 は 2, 3, 5 で割り切れるからです。 また、$M(2, 73, 100) = 0$ です。2 と 73 の両方で割り切れる 100 以下の正の整数が存在しないためです。
-Let $S(N)$ be the sum of all distinct $M(p, q, N)$. $S(100)=2262$.
+相異なる $M(p, q, N)$ の総和を $S(N)$ とします。 $S(100)=2262$ となります。
-Find $S(10\\,000\\,000)$.
+$S(10\\,000\\,000)$ を求めなさい。
# --hints--
-`integerDivisibleByTwoPrimes()` should return `11109800204052`.
+`integerDivisibleByTwoPrimes()` は `11109800204052` を返す必要があります。
```js
assert.strictEqual(integerDivisibleByTwoPrimes(), 11109800204052);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
index bd0f9f663b..a436bc71c1 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffdb
-title: 'Problem 348: Sum of a square and a cube'
+title: '問題 348: 平方数と立方数の和'
challengeType: 5
forumTopicId: 302007
dashedName: problem-348-sum-of-a-square-and-a-cube
@@ -8,19 +8,19 @@ dashedName: problem-348-sum-of-a-square-and-a-cube
# --description--
-Many numbers can be expressed as the sum of a square and a cube. Some of them in more than one way.
+多くの数は平方数と立方数の和として表すことができます。 複数の表し方ができる数もあります。
-Consider the palindromic numbers that can be expressed as the sum of a square and a cube, both greater than 1, in exactly 4 different ways.
+1 より大きい平方数と 1 より大きい立方数の和として、ちょうど 4 通りの表し方がある回文数について考えます。
-For example, 5229225 is a palindromic number and it can be expressed in exactly 4 different ways:
+例えば、5229225 は回文数であり、ちょうど 4 通りの表し方があります。
$$\begin{align} & {2285}^2 + {20}^3 \\\\ & {2223}^2 + {66}^3 \\\\ & {1810}^2 + {125}^3 \\\\ & {1197}^2 + {156}^3 \end{align}$$
-Find the sum of the five smallest such palindromic numbers.
+このような回文数のうち最小の数 5 つの和を求めなさい。
# --hints--
-`sumOfSquareAndCube()` should return `1004195061`.
+`sumOfSquareAndCube()` は `1004195061` を返す必要があります。
```js
assert.strictEqual(sumOfSquareAndCube(), 1004195061);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
index 156d06cb3a..980fa9956e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
@@ -1,6 +1,6 @@
---
id: 5900f4ca1000cf542c50ffdc
-title: 'Problem 349: Langton''s ant'
+title: '問題 349: ラングトンのアリ'
challengeType: 5
forumTopicId: 302008
dashedName: problem-349-langtons-ant
@@ -8,18 +8,18 @@ dashedName: problem-349-langtons-ant
# --description--
-An ant moves on a regular grid of squares that are coloured either black or white.
+黒または白に塗られた規則的な格子の上を、アリが歩きます。
-The ant is always oriented in one of the cardinal directions (left, right, up or down) and moves from square to adjacent square according to the following rules:
+アリは常に基本方向 (上下左右) のいずれかを向き、次のルールに従って隣のマスへ移動します。
-- if it is on a black square, it flips the color of the square to white, rotates 90° counterclockwise and moves forward one square.
-- if it is on a white square, it flips the color of the square to black, rotates 90° clockwise and moves forward one square.
+- 黒いマスにアリがいる場合、そのマスの色を白に変え、反時計回りに 90° 方向転換して 1 マス進みます。
+- 白いマスにアリがいる場合、そのマスの色を黒に変え、時計回りに 90° 方向転換して 1 マス進みます。
-Starting with a grid that is entirely white, how many squares are black after ${10}^{18}$ moves of the ant?
+格子全体が白い状態から始め、アリが ${10}^{18}$ 回移動した後、黒いマスはいくつありますか。
# --hints--
-`langtonsAnt()` should return `115384615384614940`.
+`langtonsAnt()` は `115384615384614940` を返す必要があります。
```js
assert.strictEqual(langtonsAnt(), 115384615384614940);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
index 5835ac4cda..9a0c12737a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffdd
-title: 'Problem 350: Constraining the least greatest and the greatest least'
+title: '問題 350: 最小の最大公約数と最大の最小公倍数を制約する'
challengeType: 5
forumTopicId: 302010
dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
@@ -8,21 +8,21 @@ dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
# --description--
-A list of size $n$ is a sequence of $n$ natural numbers. Examples are (2, 4, 6), (2, 6, 4), (10, 6, 15, 6), and (11).
+長さ $n$ のリストとは $n$ 個の自然数の数列です。 例えば、(2, 4, 6), (2, 6, 4), (10, 6, 15, 6), (11) です。
-The greatest common divisor, or $gcd$, of a list is the largest natural number that divides all entries of the list. Examples: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$ and $gcd(11) = 11$.
+リストの最大公約数 ($gcd$) とは、リスト内のすべての項を割り切る最大の自然数です。 例: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$, $gcd(11) = 11$
-The least common multiple, or $lcm$, of a list is the smallest natural number divisible by each entry of the list. Examples: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$ and $lcm(11) = 11$.
+リストの最小公倍数 ($lcm$) とは、リスト内の各項によって割り切れる最小の自然数です。 例: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$, $lcm(11) = 11$
-Let $f(G, L, N)$ be the number of lists of size $N$ with $gcd ≥ G$ and $lcm ≤ L$. For example:
+$gcd ≥ G$ かつ $lcm ≤ L$ を満たすサイズ $N$ のリストの個数を $f(G, L, N)$ とします。 例えば、次のようになります。
$$\begin{align} & f(10, 100, 1) = 91 \\\\ & f(10, 100, 2) = 327 \\\\ & f(10, 100, 3) = 1135 \\\\ & f(10, 100, 1000)\bmod {101}^4 = 3\\,286\\,053 \end{align}$$
-Find $f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$.
+$f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$ を求めなさい。
# --hints--
-`leastGreatestAndGreatestLeast()` should return `84664213`.
+`leastGreatestAndGreatestLeast()` は `84664213` を返す必要があります。
```js
assert.strictEqual(leastGreatestAndGreatestLeast(), 84664213);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
index e7d37e452d..f76f92596d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffde
-title: 'Problem 351: Hexagonal orchards'
+title: '問題 351: 六角形果樹園'
challengeType: 5
forumTopicId: 302011
dashedName: problem-351-hexagonal-orchards
@@ -8,21 +8,21 @@ dashedName: problem-351-hexagonal-orchards
# --description--
-A hexagonal orchard of order $n$ is a triangular lattice made up of points within a regular hexagon with side $n$. The following is an example of a hexagonal orchard of order 5:
+位数 $n$ の六角形果樹園は、辺長 $n$ の正六角形の中の点で構成された三角格子です。 下図は、位数 5 の六角形果樹園の例です。
-
-A winning configuration is an arrangement of coins on the strip where the first player can force a win no matter what the second player does.
+後手が何をしようが先手が必ず勝てるような硬貨の配列を、「勝利構成」と呼びます。
-Let $W(n, c)$ be the number of winning configurations for a strip of $n$ squares, $c$ worthless coins and one silver dollar.
+$n$ 個のマス、$c$ 枚の無価値硬貨、および 1 枚の銀貨を使用する場合の勝利構成の数を、$W(n, c)$ とします。
-You are given that $W(10, 2) = 324$ and $W(100, 10) = 1\\,514\\,704\\,946\\,113\\,500$.
+$W(10, 2) = 324$, $W(100, 10) = 1\\,514\\,704\\,946\\,113\\,500$ が与えられます。
-Find $W(1\\,000\\,000, 100)$ modulo the semiprime $1000\\,036\\,000\\,099 (= 1\\,000\\,003 \times 1\\,000\\,033)$.
+$W(1\\,000\\,000, 100)$ を求め、半素数 $1000\\,036\\,000\\,099 (= 1\\,000\\,003 \times 1\\,000\\,033)$ で割った余りを答えなさい。
# --hints--
-`silverDollarGame()` should return `65579304332`.
+`silverDollarGame()` は `65579304332` を返す必要があります。
```js
assert.strictEqual(silverDollarGame(), 65579304332);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
index 12e850c9bf..95ddf7a7e9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-345-matrix-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffda
-title: 'Problem 345: Matrix Sum'
+title: '問題 345: 行列和'
challengeType: 5
forumTopicId: 302004
dashedName: problem-345-matrix-sum
@@ -8,19 +8,19 @@ dashedName: problem-345-matrix-sum
# --description--
-We define the Matrix Sum of a matrix as the maximum sum of matrix elements with each element being the only one in his row and column.
+各行と各列から 1 つずつ選択された行列要素の最大和を、その行列の「行列和」(Matrix Sum) と定義します。
-For example, the Matrix Sum of the matrix below equals $3315 ( = 863 + 383 + 343 + 959 + 767)$:
+例えば次の行列では、行列の和は $3315 (= 863 + 383 + 343 + 959 + 767)$ です。
$$\begin{array}{rrrrr} 7 & 53 & 183 & 439 & \color{lime}{863} \\\\ 497 & \color{lime}{383} & 563 & 79 & 973 \\\\ 287 & 63 & \color{lime}{343} & 169 & 583 \\\\ 627 & 343 & 773 & \color{lime}{959} & 943 \\\\ \color{lime}{767} & 473 & 103 & 699 & 303 \end{array}$$
-Find the Matrix Sum of:
+次の行列の行列和を求めなさい。
$$\\begin{array}{r} 7 & 53 & 183 & 439 & 863 & 497 & 383 & 563 & 79 & 973 & 287 & 63 & 343 & 169 & 583 \\\\ 627 & 343 & 773 & 959 & 943 & 767 & 473 & 103 & 699 & 303 & 957 & 703 & 583 & 639 & 913 \\\\ 447 & 283 & 463 & 29 & 23 & 487 & 463 & 993 & 119 & 883 & 327 & 493 & 423 & 159 & 743 \\\\ 217 & 623 & 3 & 399 & 853 & 407 & 103 & 983 & 89 & 463 & 290 & 516 & 212 & 462 & 350 \\\\ 960 & 376 & 682 & 962 & 300 & 780 & 486 & 502 & 912 & 800 & 250 & 346 & 172 & 812 & 350 \\\\ 870 & 456 & 192 & 162 & 593 & 473 & 915 & 45 & 989 & 873 & 823 & 965 & 425 & 329 & 803 \\\\ 973 & 965 & 905 & 919 & 133 & 673 & 665 & 235 & 509 & 613 & 673 & 815 & 165 & 992 & 326 \\\\ 322 & 148 & 972 & 962 & 286 & 255 & 941 & 541 & 265 & 323 & 925 & 281 & 601 & 95 & 973 \\\\ 445 & 721 & 11 & 525 & 473 & 65 & 511 & 164 & 138 & 672 & 18 & 428 & 154 & 448 & 848 \\\\ 414 & 456 & 310 & 312 & 798 & 104 & 566 & 520 & 302 & 248 & 694 & 976 & 430 & 392 & 198 \\\\ 184 & 829 & 373 & 181 & 631 & 101 & 969 & 613 & 840 & 740 & 778 & 458 & 284 & 760 & 390 \\\\ 821 & 461 & 843 & 513 & 17 & 901 & 711 & 993 & 293 & 157 & 274 & 94 & 192 & 156 & 574 \\\\ 34 & 124 & 4 & 878 & 450 & 476 & 712 & 914 & 838 & 669 & 875 & 299 & 823 & 329 & 699 \\\\ 815 & 559 & 813 & 459 & 522 & 788 & 168 & 586 & 966 & 232 & 308 & 833 & 251 & 631 & 107 \\\\ 813 & 883 & 451 & 509 & 615 & 77 & 281 & 613 & 459 & 205 & 380 & 274 & 302 & 35 & 805 \end{array}$$
# --hints--
-`matrixSum()` should return `13938`.
+`matrixSum()` は `13938` を返す必要があります。
```js
assert.strictEqual(matrixSum(), 13938);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
index 88c4634715..54ed2c701a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-346-strong-repunits.md
@@ -1,6 +1,6 @@
---
id: 5900f4c71000cf542c50ffd8
-title: 'Problem 346: Strong Repunits'
+title: '問題 346: 強力なレピュニット数'
challengeType: 5
forumTopicId: 302005
dashedName: problem-346-strong-repunits
@@ -8,15 +8,15 @@ dashedName: problem-346-strong-repunits
# --description--
-The number 7 is special, because 7 is 111 written in base 2, and 11 written in base 6 (i.e. $7_{10} = {11}_6 = {111}_2$). In other words, 7 is a repunit in at least two bases $b > 1$.
+7 という数は特殊です。2 進数では 111、6 進数では 11 と表されるからです ($7_{10} = {11}_6 = {111}_2$)。 つまり、7 は少なくとも 2 つの基数 ($b > 1$) のレピュニット数です。
-We shall call a positive integer with this property a strong repunit. It can be verified that there are 8 strong repunits below 50: {1, 7, 13, 15, 21, 31, 40, 43}. Furthermore, the sum of all strong repunits below 1000 equals 15864.
+このような性質を持つ正の整数を「強力なレピュニット数」と呼ぶことにします。 50 未満の強力なレピュニット数は {1, 7, 13, 15, 21, 31, 40, 43} の 8 つであることを確認できます。 さらに、1000 未満の強力なレピュニット数の総和は 15864 です。
-Find the sum of all strong repunits below ${10}^{12}$.
+${10}^{12}$ 未満の強力なレピュニット数の総和を求めなさい。
# --hints--
-`strongRepunits()` should return `336108797689259260`.
+`strongRepunits()` は `336108797689259260` を返す必要があります
```js
assert.strictEqual(strongRepunits(), 336108797689259260);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
index 9924ba3fab..421eee9763 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-347-largest-integer-divisible-by-two-primes.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffd9
-title: 'Problem 347: Largest integer divisible by two primes'
+title: '問題 347: 2 つの素数で割り切れる最大の整数'
challengeType: 5
forumTopicId: 302006
dashedName: problem-347-largest-integer-divisible-by-two-primes
@@ -8,21 +8,21 @@ dashedName: problem-347-largest-integer-divisible-by-two-primes
# --description--
-The largest integer $≤ 100$ that is only divisible by both the primes 2 and 3 is 96, as $96 = 32 \times 3 = 2^5 \times 3$.
+素数のうち 2 と 3 の両方のみで割り切れる最大の整数 ($≤ 100$) は 96 であり、$96 = 32 \times 3 = 2^5 \times 3$ となります。
-For two distinct primes $p$ and $q$ let $M(p, q, N)$ be the largest positive integer $≤ N$ only divisible by both $p$ and $q$ and $M(p, q, N)=0$ if such a positive integer does not exist.
+2 つの相異なる素数 $p$ と $q$ について、$p$ と $q$ の両方のみで割り切れる、$N$ 以下の最大の正の整数を $M(p, q, N)$ とします。そのような正の整数が存在しない場合は $M(p. q, N)=0$ とします。
-E.g. $M(2, 3, 100) = 96$.
+例: $M(2, 3, 100) = 96$
-$M(3, 5, 100) = 75$ and not 90 because 90 is divisible by 2, 3 and 5. Also $M(2, 73, 100) = 0$ because there does not exist a positive integer $≤ 100$ that is divisible by both 2 and 73.
+$M(3, 5, 100) = 75$ であり 90 ではありません。90 は 2, 3, 5 で割り切れるからです。 また、$M(2, 73, 100) = 0$ です。2 と 73 の両方で割り切れる 100 以下の正の整数が存在しないためです。
-Let $S(N)$ be the sum of all distinct $M(p, q, N)$. $S(100)=2262$.
+相異なる $M(p, q, N)$ の総和を $S(N)$ とします。 $S(100)=2262$ となります。
-Find $S(10\\,000\\,000)$.
+$S(10\\,000\\,000)$ を求めなさい。
# --hints--
-`integerDivisibleByTwoPrimes()` should return `11109800204052`.
+`integerDivisibleByTwoPrimes()` は `11109800204052` を返す必要があります。
```js
assert.strictEqual(integerDivisibleByTwoPrimes(), 11109800204052);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
index bd0f9f663b..a436bc71c1 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-348-sum-of-a-square-and-a-cube.md
@@ -1,6 +1,6 @@
---
id: 5900f4c81000cf542c50ffdb
-title: 'Problem 348: Sum of a square and a cube'
+title: '問題 348: 平方数と立方数の和'
challengeType: 5
forumTopicId: 302007
dashedName: problem-348-sum-of-a-square-and-a-cube
@@ -8,19 +8,19 @@ dashedName: problem-348-sum-of-a-square-and-a-cube
# --description--
-Many numbers can be expressed as the sum of a square and a cube. Some of them in more than one way.
+多くの数は平方数と立方数の和として表すことができます。 複数の表し方ができる数もあります。
-Consider the palindromic numbers that can be expressed as the sum of a square and a cube, both greater than 1, in exactly 4 different ways.
+1 より大きい平方数と 1 より大きい立方数の和として、ちょうど 4 通りの表し方がある回文数について考えます。
-For example, 5229225 is a palindromic number and it can be expressed in exactly 4 different ways:
+例えば、5229225 は回文数であり、ちょうど 4 通りの表し方があります。
$$\begin{align} & {2285}^2 + {20}^3 \\\\ & {2223}^2 + {66}^3 \\\\ & {1810}^2 + {125}^3 \\\\ & {1197}^2 + {156}^3 \end{align}$$
-Find the sum of the five smallest such palindromic numbers.
+このような回文数のうち最小の数 5 つの和を求めなさい。
# --hints--
-`sumOfSquareAndCube()` should return `1004195061`.
+`sumOfSquareAndCube()` は `1004195061` を返す必要があります。
```js
assert.strictEqual(sumOfSquareAndCube(), 1004195061);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
index 156d06cb3a..980fa9956e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-349-langtons-ant.md
@@ -1,6 +1,6 @@
---
id: 5900f4ca1000cf542c50ffdc
-title: 'Problem 349: Langton''s ant'
+title: '問題 349: ラングトンのアリ'
challengeType: 5
forumTopicId: 302008
dashedName: problem-349-langtons-ant
@@ -8,18 +8,18 @@ dashedName: problem-349-langtons-ant
# --description--
-An ant moves on a regular grid of squares that are coloured either black or white.
+黒または白に塗られた規則的な格子の上を、アリが歩きます。
-The ant is always oriented in one of the cardinal directions (left, right, up or down) and moves from square to adjacent square according to the following rules:
+アリは常に基本方向 (上下左右) のいずれかを向き、次のルールに従って隣のマスへ移動します。
-- if it is on a black square, it flips the color of the square to white, rotates 90° counterclockwise and moves forward one square.
-- if it is on a white square, it flips the color of the square to black, rotates 90° clockwise and moves forward one square.
+- 黒いマスにアリがいる場合、そのマスの色を白に変え、反時計回りに 90° 方向転換して 1 マス進みます。
+- 白いマスにアリがいる場合、そのマスの色を黒に変え、時計回りに 90° 方向転換して 1 マス進みます。
-Starting with a grid that is entirely white, how many squares are black after ${10}^{18}$ moves of the ant?
+格子全体が白い状態から始め、アリが ${10}^{18}$ 回移動した後、黒いマスはいくつありますか。
# --hints--
-`langtonsAnt()` should return `115384615384614940`.
+`langtonsAnt()` は `115384615384614940` を返す必要があります。
```js
assert.strictEqual(langtonsAnt(), 115384615384614940);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
index 5835ac4cda..9a0c12737a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-350-constraining-the-least-greatest-and-the-greatest-least.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffdd
-title: 'Problem 350: Constraining the least greatest and the greatest least'
+title: '問題 350: 最小の最大公約数と最大の最小公倍数を制約する'
challengeType: 5
forumTopicId: 302010
dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
@@ -8,21 +8,21 @@ dashedName: problem-350-constraining-the-least-greatest-and-the-greatest-least
# --description--
-A list of size $n$ is a sequence of $n$ natural numbers. Examples are (2, 4, 6), (2, 6, 4), (10, 6, 15, 6), and (11).
+長さ $n$ のリストとは $n$ 個の自然数の数列です。 例えば、(2, 4, 6), (2, 6, 4), (10, 6, 15, 6), (11) です。
-The greatest common divisor, or $gcd$, of a list is the largest natural number that divides all entries of the list. Examples: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$ and $gcd(11) = 11$.
+リストの最大公約数 ($gcd$) とは、リスト内のすべての項を割り切る最大の自然数です。 例: $gcd(2, 6, 4) = 2$, $gcd(10, 6, 15, 6) = 1$, $gcd(11) = 11$
-The least common multiple, or $lcm$, of a list is the smallest natural number divisible by each entry of the list. Examples: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$ and $lcm(11) = 11$.
+リストの最小公倍数 ($lcm$) とは、リスト内の各項によって割り切れる最小の自然数です。 例: $lcm(2, 6, 4) = 12$, $lcm(10, 6, 15, 6) = 30$, $lcm(11) = 11$
-Let $f(G, L, N)$ be the number of lists of size $N$ with $gcd ≥ G$ and $lcm ≤ L$. For example:
+$gcd ≥ G$ かつ $lcm ≤ L$ を満たすサイズ $N$ のリストの個数を $f(G, L, N)$ とします。 例えば、次のようになります。
$$\begin{align} & f(10, 100, 1) = 91 \\\\ & f(10, 100, 2) = 327 \\\\ & f(10, 100, 3) = 1135 \\\\ & f(10, 100, 1000)\bmod {101}^4 = 3\\,286\\,053 \end{align}$$
-Find $f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$.
+$f({10}^6, {10}^{12}, {10}^{18})\bmod {101}^4$ を求めなさい。
# --hints--
-`leastGreatestAndGreatestLeast()` should return `84664213`.
+`leastGreatestAndGreatestLeast()` は `84664213` を返す必要があります。
```js
assert.strictEqual(leastGreatestAndGreatestLeast(), 84664213);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
index e7d37e452d..f76f92596d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-351-hexagonal-orchards.md
@@ -1,6 +1,6 @@
---
id: 5900f4cb1000cf542c50ffde
-title: 'Problem 351: Hexagonal orchards'
+title: '問題 351: 六角形果樹園'
challengeType: 5
forumTopicId: 302011
dashedName: problem-351-hexagonal-orchards
@@ -8,21 +8,21 @@ dashedName: problem-351-hexagonal-orchards
# --description--
-A hexagonal orchard of order $n$ is a triangular lattice made up of points within a regular hexagon with side $n$. The following is an example of a hexagonal orchard of order 5:
+位数 $n$ の六角形果樹園は、辺長 $n$ の正六角形の中の点で構成された三角格子です。 下図は、位数 5 の六角形果樹園の例です。
- +
+ -Highlighted in green are the points which are hidden from the center by a point closer to it. It can be seen that for a hexagonal orchard of order 5, 30 points are hidden from the center.
+緑色で強調表示されているのは、中心から見た場合に、より手前の点に隠れるために見えない点です。 位数 5 の六角形果樹園では、30 個の点が中心から見えないことが分かります。
-Let $H(n)$ be the number of points hidden from the center in a hexagonal orchard of order $n$.
+$H(n)$ を、位数 $n$ の六角形果樹園の中心から見えない点の数とします。
-$H(5) = 30$. $H(10) = 138$. $H(1\\,000)$ = $1\\,177\\,848$.
+$H(5) = 30$, $H(10) = 138$, $H(1\\,000)$ = $1\\,177\\,848$ です。
-Find $H(100\\,000\\,000)$.
+$H(100\\,000\\,000)$ を求めなさい。
# --hints--
-`hexagonalOrchards()` should return `11762187201804552`.
+`hexagonalOrchards()` は `11762187201804552` を返す必要があります。
```js
assert.strictEqual(hexagonalOrchards(), 11762187201804552);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
index d9e1197cb3..f583d40f94 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffdf
-title: 'Problem 352: Blood tests'
+title: '問題 352: 血液検査'
challengeType: 5
forumTopicId: 302012
dashedName: problem-352-blood-tests
@@ -8,43 +8,43 @@ dashedName: problem-352-blood-tests
# --description--
-Each one of the 25 sheep in a flock must be tested for a rare virus, known to affect 2% of the sheep population.
+25 頭の羊の群れがいます。これらの一頭ずつに、珍しいウイルスの検査をする必要があります。このウイルスは、羊全体の 2% に感染することが知られています。
-An accurate and extremely sensitive PCR test exists for blood samples, producing a clear positive / negative result, but it is very time-consuming and expensive.
+血液サンプルを検査するための正確な超高感度 PCR 検査があり、これを使えば陽性 / 陰性の結果が明確に得られますが、多大な時間と費用がかかります。
-Because of the high cost, the vet-in-charge suggests that instead of performing 25 separate tests, the following procedure can be used instead:
+コストが高いので、担当の獣医は 25 頭を別々に検査するのではなく次の手順を使用することを提案しています。
-The sheep are split into 5 groups of 5 sheep in each group. For each group, the 5 samples are mixed together and a single test is performed. Then,
+羊を 5 頭ずつ 5 つのグループに分けます。 グループごとに 5 つのサンプルを混合し、1 回のみ検査します。 次に、以下を行います。
-- If the result is negative, all the sheep in that group are deemed to be virus-free.
-- If the result is positive, 5 additional tests will be performed (a separate test for each animal) to determine the affected individual(s).
+- 結果が陰性の場合、そのグループのすべての羊がウイルスに感染していないとみなされます。
+- 結果が陽性の場合、検査をさらに 5 回 (それぞれの羊に 1 回ずつ) を実施して、感染した個体を特定します。
-Since the probability of infection for any specific animal is only 0.02, the first test (on the pooled samples) for each group will be:
+特定の個体への感染率はわずか 0.02 なので、各グループでの (プールしておいたサンプルを使った) 最初の検査は次のようになります。
-- Negative (and no more tests needed) with probability ${0.98}^5 = 0.9039207968$.
-- Positive (5 additional tests needed) with probability $1 - 0.9039207968 = 0.0960792032$.
+- 陰性 (これ以上の検査は不要) の確率: ${0.98}^5 = 0.9039207968$
+- 陽性 (5 回の追加検査が必要) の確率: $1 - 0.9039207968 = 0.0960792032$
-Thus, the expected number of tests for each group is $1 + 0.0960792032 × 5 = 1.480396016$.
+したがって、グループごとの検査の期待回数は $1 + 0.0960792032 × 5 = 1.480396016$ です。
-Consequently, all 5 groups can be screened using an average of only $1.480396016 × 5 = \mathbf{7.40198008}$ tests, which represents a huge saving of more than 70%!
+その結果、 5 つの全グループに対する検査回数は平均 $1.480396016 × 5 = \mathbf{7.40198008}$ 回となり、70% 以上の大幅な節約となります!
-Although the scheme we have just described seems to be very efficient, it can still be improved considerably (always assuming that the test is sufficiently sensitive and no adverse effects are caused by mixing different samples). E.g.:
+上の計画は非常に効率的に見えますが、さらに大幅に改善することができます (検査の感度が十分に高く、異なるサンプルを混合することによる悪影響が生じないと常に仮定すれば)。 次に例を示します。
-- We may start by running a test on a mixture of all the 25 samples. It can be verified that in about 60.35% of the cases this test will be negative, thus no more tests will be needed. Further testing will only be required for the remaining 39.65% of the cases.
-- If we know that at least one animal in a group of 5 is infected and the first 4 individual tests come out negative, there is no need to run a test on the fifth animal (we know that it must be infected).
-- We can try a different number of groups / different number of animals in each group, adjusting those numbers at each level so that the total expected number of tests will be minimised.
+- まず、25 個のサンプルすべてを混合したものを検査します。 この検査の約 60.35% のケースでは、結果が陰性となり追加検査は必要ありません。 追加検査が必要となるのは、残りの 39.65% のケースのみです。
+- 5 頭のグループのうちの少なとも 1 頭の感染が判明しており、最初の 4 頭の個別検査の結果が陰性であれば、5 頭目の検査は必要はありません (間違いなく感染しているからです)。
+- グループの数や各グループ内の頭数を変えて試すことができます。段階ごとにそれらの数を調整して、期待検査総数を最小限に抑えます。
-To simplify the very wide range of possibilities, there is one restriction we place when devising the most cost-efficient testing scheme: whenever we start with a mixed sample, all the sheep contributing to that sample must be fully screened (i.e. a verdict of infected / virus-free must be reached for all of them) before we start examining any other animals.
+非常に幅広い可能性を単純化するため、最も費用対効果の高い検査計画を立てる際の制約を設けます。それは、最初に混合サンプルを使う際は必ず、そのサンプルの元となった羊を完全にスクリーニング (すなわち、サンプルの元となったすべての羊についてウイルス感染の有無を判定) してから、他の羊を検査することです。
-For the current example, it turns out that the most cost-efficient testing scheme (we'll call it the optimal strategy) requires an average of just 4.155452 tests!
+今回の例では、最も費用対効果の高い検査計画 (これを最適戦略と呼ぶことにします) での平均検査回数はわずか 4.155452 回です!
-Using the optimal strategy, let $T(s, p)$ represent the average number of tests needed to screen a flock of $s$ sheep for a virus having probability $p$ to be present in any individual. Thus, rounded to six decimal places, $T(25, 0.02) = 4.155452$ and $T(25, 0.10) = 12.702124$.
+任意の個体に $p$ の確率で感染するウイルスに関して、最適戦略を使用して $s$ 頭の羊の群れをスクリーニングするのに必要な平均検査回数を $T(s, p)$ とします。 したがって、四捨五入して小数第 6 位まで求めると $T(25, 0.02) = 4.155452$, $T(25, 0.10) = 12.702124$ となります。
-Find $\sum T(10\\,000, p)$ for $p = 0.01, 0.02, 0.03, \ldots 0.50$. Give your answer rounded to six decimal places.
+$p = 0.01, 0.02, 0.03, \ldots 0.50$ のとき、$\sum T(10\\,000, p)$ を求めなさい。 回答は、四捨五入して小数第 6 位まで示すこと。
# --hints--
-`bloodTests()` should return `378563.260589`.
+`bloodTests()` は `378563.260589` を返す必要があります。
```js
assert.strictEqual(bloodTests(), 378563.260589);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
index 3973a53ee3..1e3550fce8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffe0
-title: 'Problem 353: Risky moon'
+title: '問題 353: 危険な月'
challengeType: 5
forumTopicId: 302013
dashedName: problem-353-risky-moon
@@ -8,27 +8,27 @@ dashedName: problem-353-risky-moon
# --description--
-A moon could be described by the sphere $C(r)$ with centre (0, 0, 0) and radius $r$.
+月は、中心 (0, 0, 0)、半径 $r$ の球 $C(r)$ で表すことができます。
-There are stations on the moon at the points on the surface of $C(r)$ with integer coordinates. The station at (0, 0, $r$) is called North Pole station, the station at (0, 0, $-r$) is called South Pole station.
+$C(r)$ の月面の整数座標地点に駅があります。 (0, 0, $r$) にある駅は北極駅、(0, 0, $-r$) にある駅は南極駅と呼ばれます。
-All stations are connected with each other via the shortest road on the great arc through the stations. A journey between two stations is risky. If $d$ is the length of the road between two stations, $\{\left(\frac{d}{πr}\right)}^2$ is a measure for the risk of the journey (let us call it the risk of the road). If the journey includes more than two stations, the risk of the journey is the sum of risks of the used roads.
+すべての駅は、それらの駅を通る大円弧上の最短道路で互いに連絡しています。 2 駅間の旅は危険です。 2 駅間の道路の長さが $d$ の場合、旅のリスクの大きさは $\{\left(\frac{d}{πr}\right)}^2$ で示されます (これを道路のリスクと呼びます)。 旅に 2 つ以上の駅が含まれている場合、使用された道路のリスクの和がその旅のリスクとなります。
-A direct journey from the North Pole station to the South Pole station has the length $πr$ and risk 1. The journey from the North Pole station to the South Pole station via (0, $r$, 0) has the same length, but a smaller risk:
+北極駅から南極駅へ直行する際の移動距離は $πr$、リスクは 1 です。 (0, $r$, 0) を経由して北極駅から南極駅へ移動すると、移動距離は同じですが、次のようにリスクは小さくなります。
$${\left(\frac{\frac{1}{2}πr}{πr}\right)}^2+{\left(\frac{\frac{1}{2}πr}{πr}\right)}^2 = 0.5$$
-The minimal risk of a journey from the North Pole station to the South Pole station on $C(r)$ is $M(r)$.
+$C(r)$ 上の北極駅から南極駅まで移動する際の最小リスクは $M(r)$ です。
-You are given that $M(7) = 0.178\\,494\\,399\\,8$ rounded to 10 digits behind the decimal point.
+$M(7) = 0.178\\,494\\,399\\,8$ (小数第 10 位に四捨五入) が与えられます。
-Find $\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$.
+$\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$ を求めなさい。
-Give your answer rounded to 10 digits behind the decimal point in the form a.bcdefghijk.
+回答は、四捨五入して小数第 10 位まで求め、a.bcdefghijk の形式にすること。
# --hints--
-`riskyMoon()` should return `1.2759860331`.
+`riskyMoon()` は `1.2759860331` を返す必要があります。
```js
assert.strictEqual(riskyMoon(), 1.2759860331);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
index 3c9e4c1f60..819d36807f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
@@ -1,6 +1,6 @@
---
id: 5900f4cf1000cf542c50ffe1
-title: 'Problem 354: Distances in a bee''s honeycomb'
+title: '問題 354: 蜂の巣の中における距離'
challengeType: 5
forumTopicId: 302014
dashedName: problem-354-distances-in-a-bees-honeycomb
@@ -8,19 +8,19 @@ dashedName: problem-354-distances-in-a-bees-honeycomb
# --description--
-Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
+それぞれの部屋が辺長1の完全な正六角形であるような蜂の巣について考えます。
-
-Highlighted in green are the points which are hidden from the center by a point closer to it. It can be seen that for a hexagonal orchard of order 5, 30 points are hidden from the center.
+緑色で強調表示されているのは、中心から見た場合に、より手前の点に隠れるために見えない点です。 位数 5 の六角形果樹園では、30 個の点が中心から見えないことが分かります。
-Let $H(n)$ be the number of points hidden from the center in a hexagonal orchard of order $n$.
+$H(n)$ を、位数 $n$ の六角形果樹園の中心から見えない点の数とします。
-$H(5) = 30$. $H(10) = 138$. $H(1\\,000)$ = $1\\,177\\,848$.
+$H(5) = 30$, $H(10) = 138$, $H(1\\,000)$ = $1\\,177\\,848$ です。
-Find $H(100\\,000\\,000)$.
+$H(100\\,000\\,000)$ を求めなさい。
# --hints--
-`hexagonalOrchards()` should return `11762187201804552`.
+`hexagonalOrchards()` は `11762187201804552` を返す必要があります。
```js
assert.strictEqual(hexagonalOrchards(), 11762187201804552);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
index d9e1197cb3..f583d40f94 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-352-blood-tests.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffdf
-title: 'Problem 352: Blood tests'
+title: '問題 352: 血液検査'
challengeType: 5
forumTopicId: 302012
dashedName: problem-352-blood-tests
@@ -8,43 +8,43 @@ dashedName: problem-352-blood-tests
# --description--
-Each one of the 25 sheep in a flock must be tested for a rare virus, known to affect 2% of the sheep population.
+25 頭の羊の群れがいます。これらの一頭ずつに、珍しいウイルスの検査をする必要があります。このウイルスは、羊全体の 2% に感染することが知られています。
-An accurate and extremely sensitive PCR test exists for blood samples, producing a clear positive / negative result, but it is very time-consuming and expensive.
+血液サンプルを検査するための正確な超高感度 PCR 検査があり、これを使えば陽性 / 陰性の結果が明確に得られますが、多大な時間と費用がかかります。
-Because of the high cost, the vet-in-charge suggests that instead of performing 25 separate tests, the following procedure can be used instead:
+コストが高いので、担当の獣医は 25 頭を別々に検査するのではなく次の手順を使用することを提案しています。
-The sheep are split into 5 groups of 5 sheep in each group. For each group, the 5 samples are mixed together and a single test is performed. Then,
+羊を 5 頭ずつ 5 つのグループに分けます。 グループごとに 5 つのサンプルを混合し、1 回のみ検査します。 次に、以下を行います。
-- If the result is negative, all the sheep in that group are deemed to be virus-free.
-- If the result is positive, 5 additional tests will be performed (a separate test for each animal) to determine the affected individual(s).
+- 結果が陰性の場合、そのグループのすべての羊がウイルスに感染していないとみなされます。
+- 結果が陽性の場合、検査をさらに 5 回 (それぞれの羊に 1 回ずつ) を実施して、感染した個体を特定します。
-Since the probability of infection for any specific animal is only 0.02, the first test (on the pooled samples) for each group will be:
+特定の個体への感染率はわずか 0.02 なので、各グループでの (プールしておいたサンプルを使った) 最初の検査は次のようになります。
-- Negative (and no more tests needed) with probability ${0.98}^5 = 0.9039207968$.
-- Positive (5 additional tests needed) with probability $1 - 0.9039207968 = 0.0960792032$.
+- 陰性 (これ以上の検査は不要) の確率: ${0.98}^5 = 0.9039207968$
+- 陽性 (5 回の追加検査が必要) の確率: $1 - 0.9039207968 = 0.0960792032$
-Thus, the expected number of tests for each group is $1 + 0.0960792032 × 5 = 1.480396016$.
+したがって、グループごとの検査の期待回数は $1 + 0.0960792032 × 5 = 1.480396016$ です。
-Consequently, all 5 groups can be screened using an average of only $1.480396016 × 5 = \mathbf{7.40198008}$ tests, which represents a huge saving of more than 70%!
+その結果、 5 つの全グループに対する検査回数は平均 $1.480396016 × 5 = \mathbf{7.40198008}$ 回となり、70% 以上の大幅な節約となります!
-Although the scheme we have just described seems to be very efficient, it can still be improved considerably (always assuming that the test is sufficiently sensitive and no adverse effects are caused by mixing different samples). E.g.:
+上の計画は非常に効率的に見えますが、さらに大幅に改善することができます (検査の感度が十分に高く、異なるサンプルを混合することによる悪影響が生じないと常に仮定すれば)。 次に例を示します。
-- We may start by running a test on a mixture of all the 25 samples. It can be verified that in about 60.35% of the cases this test will be negative, thus no more tests will be needed. Further testing will only be required for the remaining 39.65% of the cases.
-- If we know that at least one animal in a group of 5 is infected and the first 4 individual tests come out negative, there is no need to run a test on the fifth animal (we know that it must be infected).
-- We can try a different number of groups / different number of animals in each group, adjusting those numbers at each level so that the total expected number of tests will be minimised.
+- まず、25 個のサンプルすべてを混合したものを検査します。 この検査の約 60.35% のケースでは、結果が陰性となり追加検査は必要ありません。 追加検査が必要となるのは、残りの 39.65% のケースのみです。
+- 5 頭のグループのうちの少なとも 1 頭の感染が判明しており、最初の 4 頭の個別検査の結果が陰性であれば、5 頭目の検査は必要はありません (間違いなく感染しているからです)。
+- グループの数や各グループ内の頭数を変えて試すことができます。段階ごとにそれらの数を調整して、期待検査総数を最小限に抑えます。
-To simplify the very wide range of possibilities, there is one restriction we place when devising the most cost-efficient testing scheme: whenever we start with a mixed sample, all the sheep contributing to that sample must be fully screened (i.e. a verdict of infected / virus-free must be reached for all of them) before we start examining any other animals.
+非常に幅広い可能性を単純化するため、最も費用対効果の高い検査計画を立てる際の制約を設けます。それは、最初に混合サンプルを使う際は必ず、そのサンプルの元となった羊を完全にスクリーニング (すなわち、サンプルの元となったすべての羊についてウイルス感染の有無を判定) してから、他の羊を検査することです。
-For the current example, it turns out that the most cost-efficient testing scheme (we'll call it the optimal strategy) requires an average of just 4.155452 tests!
+今回の例では、最も費用対効果の高い検査計画 (これを最適戦略と呼ぶことにします) での平均検査回数はわずか 4.155452 回です!
-Using the optimal strategy, let $T(s, p)$ represent the average number of tests needed to screen a flock of $s$ sheep for a virus having probability $p$ to be present in any individual. Thus, rounded to six decimal places, $T(25, 0.02) = 4.155452$ and $T(25, 0.10) = 12.702124$.
+任意の個体に $p$ の確率で感染するウイルスに関して、最適戦略を使用して $s$ 頭の羊の群れをスクリーニングするのに必要な平均検査回数を $T(s, p)$ とします。 したがって、四捨五入して小数第 6 位まで求めると $T(25, 0.02) = 4.155452$, $T(25, 0.10) = 12.702124$ となります。
-Find $\sum T(10\\,000, p)$ for $p = 0.01, 0.02, 0.03, \ldots 0.50$. Give your answer rounded to six decimal places.
+$p = 0.01, 0.02, 0.03, \ldots 0.50$ のとき、$\sum T(10\\,000, p)$ を求めなさい。 回答は、四捨五入して小数第 6 位まで示すこと。
# --hints--
-`bloodTests()` should return `378563.260589`.
+`bloodTests()` は `378563.260589` を返す必要があります。
```js
assert.strictEqual(bloodTests(), 378563.260589);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
index 3973a53ee3..1e3550fce8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-353-risky-moon.md
@@ -1,6 +1,6 @@
---
id: 5900f4cd1000cf542c50ffe0
-title: 'Problem 353: Risky moon'
+title: '問題 353: 危険な月'
challengeType: 5
forumTopicId: 302013
dashedName: problem-353-risky-moon
@@ -8,27 +8,27 @@ dashedName: problem-353-risky-moon
# --description--
-A moon could be described by the sphere $C(r)$ with centre (0, 0, 0) and radius $r$.
+月は、中心 (0, 0, 0)、半径 $r$ の球 $C(r)$ で表すことができます。
-There are stations on the moon at the points on the surface of $C(r)$ with integer coordinates. The station at (0, 0, $r$) is called North Pole station, the station at (0, 0, $-r$) is called South Pole station.
+$C(r)$ の月面の整数座標地点に駅があります。 (0, 0, $r$) にある駅は北極駅、(0, 0, $-r$) にある駅は南極駅と呼ばれます。
-All stations are connected with each other via the shortest road on the great arc through the stations. A journey between two stations is risky. If $d$ is the length of the road between two stations, $\{\left(\frac{d}{πr}\right)}^2$ is a measure for the risk of the journey (let us call it the risk of the road). If the journey includes more than two stations, the risk of the journey is the sum of risks of the used roads.
+すべての駅は、それらの駅を通る大円弧上の最短道路で互いに連絡しています。 2 駅間の旅は危険です。 2 駅間の道路の長さが $d$ の場合、旅のリスクの大きさは $\{\left(\frac{d}{πr}\right)}^2$ で示されます (これを道路のリスクと呼びます)。 旅に 2 つ以上の駅が含まれている場合、使用された道路のリスクの和がその旅のリスクとなります。
-A direct journey from the North Pole station to the South Pole station has the length $πr$ and risk 1. The journey from the North Pole station to the South Pole station via (0, $r$, 0) has the same length, but a smaller risk:
+北極駅から南極駅へ直行する際の移動距離は $πr$、リスクは 1 です。 (0, $r$, 0) を経由して北極駅から南極駅へ移動すると、移動距離は同じですが、次のようにリスクは小さくなります。
$${\left(\frac{\frac{1}{2}πr}{πr}\right)}^2+{\left(\frac{\frac{1}{2}πr}{πr}\right)}^2 = 0.5$$
-The minimal risk of a journey from the North Pole station to the South Pole station on $C(r)$ is $M(r)$.
+$C(r)$ 上の北極駅から南極駅まで移動する際の最小リスクは $M(r)$ です。
-You are given that $M(7) = 0.178\\,494\\,399\\,8$ rounded to 10 digits behind the decimal point.
+$M(7) = 0.178\\,494\\,399\\,8$ (小数第 10 位に四捨五入) が与えられます。
-Find $\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$.
+$\displaystyle\sum_{n = 1}^{15} M(2^n - 1)$ を求めなさい。
-Give your answer rounded to 10 digits behind the decimal point in the form a.bcdefghijk.
+回答は、四捨五入して小数第 10 位まで求め、a.bcdefghijk の形式にすること。
# --hints--
-`riskyMoon()` should return `1.2759860331`.
+`riskyMoon()` は `1.2759860331` を返す必要があります。
```js
assert.strictEqual(riskyMoon(), 1.2759860331);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
index 3c9e4c1f60..819d36807f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-354-distances-in-a-bees-honeycomb.md
@@ -1,6 +1,6 @@
---
id: 5900f4cf1000cf542c50ffe1
-title: 'Problem 354: Distances in a bee''s honeycomb'
+title: '問題 354: 蜂の巣の中における距離'
challengeType: 5
forumTopicId: 302014
dashedName: problem-354-distances-in-a-bees-honeycomb
@@ -8,19 +8,19 @@ dashedName: problem-354-distances-in-a-bees-honeycomb
# --description--
-Consider a honey bee's honeycomb where each cell is a perfect regular hexagon with side length 1.
+それぞれの部屋が辺長1の完全な正六角形であるような蜂の巣について考えます。
-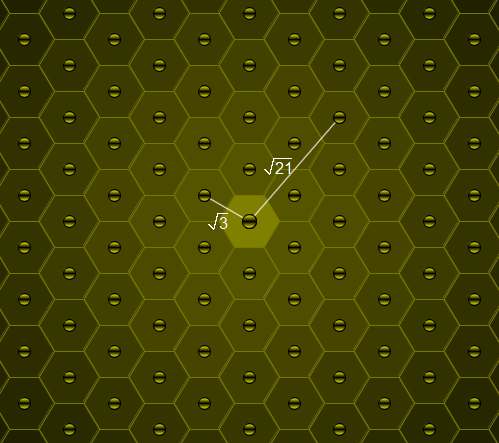 +
+ -One particular cell is occupied by the queen bee. For a positive real number $L$, let $B(L)$ count the cells with distance $L$ from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider.
+ある特定の部屋は女王蜂が占有しています。 正の実数 $L$ を用いて、女王蜂の部屋から $L$ の距離にある部屋 $B(L)$ を数えます (常に、ある部屋の中心から別の部屋の中心までを測ります)。蜂の巣の大きさは、ここで考えるあらゆる距離に対して十分な大きさであると仮定します。
-For example, $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$ and $B(111\\,111\\,111) = 54$.
+例: $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$, $B(111\\,111\\,111) = 54$
-Find the number of $L ≤ 5 \times {10}^{11}$ such that $B(L) = 450$.
+$B(L) = 450$ となるような $L ≤ 5 \times {10}^{11}$ の数を求めなさい。
# --hints--
-`distancesInHoneycomb()` should return `58065134`.
+`distancesInHoneycomb()` は `58065134` を返す必要があります。
```js
assert.strictEqual(distancesInHoneycomb(), 58065134);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
index 8c693f1d43..b8bfc270b7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe2
-title: 'Problem 355: Maximal coprime subset'
+title: '問題 355: 最大の互いに素な部分集合'
challengeType: 5
forumTopicId: 302015
dashedName: problem-355-maximal-coprime-subset
@@ -8,15 +8,15 @@ dashedName: problem-355-maximal-coprime-subset
# --description--
-Define $Co(n)$ to be the maximal possible sum of a set of mutually co-prime elements from $\\{1, 2, \ldots, n\\}$. For example $Co(10)$ is 30 and hits that maximum on the subset $\\{1, 5, 7, 8, 9\\}$.
+$\\{1, 2, \ldots, n\\}$ の要素のうち互いに素な要素の集合の最大和を、$Co(n)$ と定義します。 例えば、 $Co(10)$ は 30 であり、最大の部分集合は $\\{1, 5, 7, 8, 9\\}$ になります。
-You are given that $Co(30) = 193$ and $Co(100) = 1356$.
+$Co(30) = 193$ と $Co(100) = 1356$ が与えられます。
-Find $Co(200\\,000)$.
+$Co(200\\,000)$ を求めなさい。
# --hints--
-`maximalCoprimeSubset()` should return `1726545007`.
+`maximalCoprimeSubset()` は `1726545007` を返す必要があります。
```js
assert.strictEqual(maximalCoprimeSubset(), 1726545007);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
index 07aeae1c6f..042910ccef 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe3
-title: 'Problem 356: Largest roots of cubic polynomials'
+title: '問題 356: 三次多項式の最大根'
challengeType: 5
forumTopicId: 302016
dashedName: problem-356-largest-roots-of-cubic-polynomials
@@ -8,17 +8,17 @@ dashedName: problem-356-largest-roots-of-cubic-polynomials
# --description--
-Let an be the largest real root of a polynomial $g(x) = x^3 - 2^n \times x^2 + n$.
+$a_n$ を、多項式 $g(x) = x^3 - 2^n \times x^2 + n$ の最大の実根とします。
-For example, $a_2 = 3.86619826\ldots$
+例: $a_2 = 3.86619826\ldots$
-Find the last eight digits of $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
+$\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$ の下位 8 桁を求めなさい。
-**Note:** $\lfloor a\rfloor$ represents the floor function.
+**注:** $\lfloor a\rfloor$ は床関数を表します。
# --hints--
-`rootsOfCubicPolynomials()` should return `28010159`.
+`rootsOfCubicPolynomials()` は `28010159` を返す必要があります。
```js
assert.strictEqual(rootsOfCubicPolynomials(), 28010159);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
index 6483905ad4..7516c59549 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d11000cf542c50ffe4
-title: 'Problem 357: Prime generating integers'
+title: '問題 357: 素数を生成する整数'
challengeType: 5
forumTopicId: 302017
dashedName: problem-357-prime-generating-integers
@@ -8,15 +8,15 @@ dashedName: problem-357-prime-generating-integers
# --description--
-Consider the divisors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
+30 の約数である 1, 2, 3, 5, 6, 10, 15, 30 について考えます。
-It can be seen that for every divisor $d$ of 30, $d + \frac{30}{d}$ is prime.
+30 のすべての約数 $d$ について、$d + \frac{30}{d}$ が素数であることが分かります。
-Find the sum of all positive integers $n$ not exceeding $100\\,000\\,000$ such that for every divisor $d$ of $n$, $d + \frac{n}{d}$ is prime.
+$n$ のすべての約数 $d$ について $d + \frac{n}{d}$ が素数となるような、$100\\,000\\,000$ を超えない正の整数 $n$ の総和を求めなさい。
# --hints--
-`primeGeneratingIntegers()` should return `1739023853137`.
+`primeGeneratingIntegers()` は `1739023853137` を返す必要があります。
```js
assert.strictEqual(primeGeneratingIntegers(), 1739023853137);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
index 9370165ecc..184fa5c249 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d21000cf542c50ffe5
-title: 'Problem 358: Cyclic numbers'
+title: '問題 358: 巡回数'
challengeType: 5
forumTopicId: 302018
dashedName: problem-358-cyclic-numbers
@@ -8,25 +8,25 @@ dashedName: problem-358-cyclic-numbers
# --description--
-A cyclic number with $n$ digits has a very interesting property:
+$n$ 桁の巡回数は非常に興味深い性質を持っています:
-When it is multiplied by 1, 2, 3, 4, ... $n$, all the products have exactly the same digits, in the same order, but rotated in a circular fashion!
+1, 2, 3, 4, ... $n$ を乗じると、すべての積に全く同じ数字が使われ、数字を循環させると順序も同じになります!
-The smallest cyclic number is the 6-digit number 142857:
+最小の巡回数は、6 桁の数 142857 です。
$$\begin{align} & 142857 × 1 = 142857 \\\\ & 142857 × 2 = 285714 \\\\ & 142857 × 3 = 428571 \\\\ & 142857 × 4 = 571428 \\\\ & 142857 × 5 = 714285 \\\\ & 142857 × 6 = 857142 \end{align}$$
-The next cyclic number is 0588235294117647 with 16 digits:
+次の巡回数は、16 桁の 0588235294117647 です。
$$\begin{align} & 0588235294117647 × 1 = 0588235294117647 \\\\ & 0588235294117647 × 2 = 1176470588235294 \\\\ & 0588235294117647 × 3 = 1764705882352941 \\\\ & \ldots \\\\ & 0588235294117647 × 16 = 9411764705882352 \end{align}$$
-Note that for cyclic numbers, leading zeros are important.
+なお、巡回数では先行ゼロが重要です。
-There is only one cyclic number for which, the eleven leftmost digits are 00000000137 and the five rightmost digits are 56789 (i.e., it has the form $00000000137\ldots56789$ with an unknown number of digits in the middle). Find the sum of all its digits.
+左端の 11 桁が 00000000137 で、右端の 5 桁が 56789 (すなわち $00000000137\ldots56789$ の形を取り、中間の数字は不明) の巡回数は 1 つしかありません。 この数のすべての桁の和を求めなさい。
# --hints--
-`cyclicNumbers()` should return `3284144505`.
+`cyclicNumbers()` は `3284144505` を返す必要があります。
```js
assert.strictEqual(cyclicNumbers(), 3284144505);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
index d1b78c9dd7..161a623da5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
@@ -1,6 +1,6 @@
---
id: 5900f4d31000cf542c50ffe6
-title: 'Problem 359: Hilbert''s New Hotel'
+title: '問題 359: ヒルベルトの新しいホテル'
challengeType: 5
forumTopicId: 302019
dashedName: problem-359-hilberts-new-hotel
@@ -8,32 +8,32 @@ dashedName: problem-359-hilberts-new-hotel
# --description--
-An infinite number of people (numbered 1, 2, 3, etc.) are lined up to get a room at Hilbert's newest infinite hotel. The hotel contains an infinite number of floors (numbered 1, 2, 3, etc.), and each floor contains an infinite number of rooms (numbered 1, 2, 3, etc.).
+ヒルベルトの最新の無限ホテルで部屋を取ろうと、人々 (1, 2, 3,... の番号付き) が無限に並んでいます。 ホテルには階 (1, 2, 3,... の番号付き) が無限にあり、各階には部屋 (1, 2, 3,... の番号付き) が無限にあります。
-Initially the hotel is empty. Hilbert declares a rule on how the $n^{\text{th}}$ person is assigned a room: person $n$ gets the first vacant room in the lowest numbered floor satisfying either of the following:
+当初、ホテルに客はいませんでした。 ヒルベルトは、$n$ 番目の人にどのように部屋を割り当てるかを宣言しました。それによれば、$n$ 番目の人は、以下のいずれかを満たす最下階の最初の空き部屋を取ります。
-- the floor is empty
-- the floor is not empty, and if the latest person taking a room in that floor is person $m$, then $m + n$ is a perfect square
+- その階が空いている
+- その階が空いておらず、その階で最後に部屋を取った人が $m$ 番目である場合は $m + n$ が完全平方数になる
-Person 1 gets room 1 in floor 1 since floor 1 is empty.
+1 階が空いているので、1 番目の人は 1 階の 1 号室を取ります。
-Person 2 does not get room 2 in floor 1 since 1 + 2 = 3 is not a perfect square.
+1 + 2 = 3 は完全平方数ではないので、2 番目の人は 1 階の 2 号室を取れません。
-Person 2 instead gets room 1 in floor 2 since floor 2 is empty.
+しかし 2 階が空いているので、2 番目の人は代わりに 2 階の 1 号室を取ります。
-Person 3 gets room 2 in floor 1 since 1 + 3 = 4 is a perfect square.
+1 + 3 = 4 は完全平方数なので、3 番目の人は 1 階の 2 号室を取ります。
-Eventually, every person in the line gets a room in the hotel.
+最終的には、並んでいたすべての人がホテルの部屋を取れます。
-Define $P(f, r)$ to be $n$ if person $n$ occupies room $r$ in floor $f$, and 0 if no person occupies the room. Here are a few examples:
+$P(f, r)$ の結果を次のように定義します: $n$ 番目の人が $f$ 階の $r$ 号室を取る場合は $n$、誰もその部屋を取らない場合は 0 になります。 いくつかの例を次に示します。
$$\begin{align} & P(1, 1) = 1 \\\\ & P(1, 2) = 3 \\\\ & P(2, 1) = 2 \\\\ & P(10, 20) = 440 \\\\ & P(25, 75) = 4863 \\\\ & P(99, 100) = 19454 \end{align}$$
-Find the sum of all $P(f, r)$ for all positive $f$ and $r$ such that $f × r = 71\\,328\\,803\\,586\\,048$ and give the last 8 digits as your answer.
+$f × r = 71\\,328\\,803\\,586\\,048$ となるすべての正の数 $f$, $r$ について $P(f, r)$ の総和を求め、下位 8 桁を答えなさい。
# --hints--
-`hilbertsNewHotel()` should return `40632119`.
+`hilbertsNewHotel()` は `40632119` を返す必要があります。
```js
assert.strictEqual(hilbertsNewHotel(), 40632119);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
index f04364484f..07fc4e1462 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
@@ -1,6 +1,6 @@
---
id: 5900f4d41000cf542c50ffe7
-title: 'Problem 360: Scary Sphere'
+title: '問題 360: 恐ろしい球体'
challengeType: 5
forumTopicId: 302021
dashedName: problem-360-scary-sphere
@@ -8,21 +8,21 @@ dashedName: problem-360-scary-sphere
# --description--
-Given two points ($x_1$, $y_1$, $z_1$) and ($x_2$, $y_2$, $z_2$) in three dimensional space, the Manhattan distance between those points is defined as $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$.
+三次元空間に ($x_1$, $y_1$, $z_1$) と ($x_2$, $y_2$, $z_2$) の 2 つの点が与えられるとき、この 2 点間のマンハッタン距離は $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$ と定義されます。
-Let $C(r)$ be a sphere with radius $r$ and center in the origin $O(0, 0, 0)$.
+$C(r)$ を、半径が $r$、中心が原点 $O(0, 0, 0)$ の球とします。
-Let $I(r)$ be the set of all points with integer coordinates on the surface of $C(r)$.
+$I(r)$ を、$C(r)$ の表面に整数座標を持つすべての点の集合とします。
-Let $S(r)$ be the sum of the Manhattan distances of all elements of $I(r)$ to the origin $O$.
+$S(r)$ を、$I(r)$ のすべての要素から原点 $O$ までのマンハッタン距離の和とします。
-E.g. $S(45)=34518$.
+例: $S(45)=34518$
-Find $S({10}^{10})$.
+$S({10}^{10})$ を求めなさい。
# --hints--
-`scarySphere()` should return `878825614395267100`.
+`scarySphere()` は `878825614395267100` を返す必要があります。
```js
assert.strictEqual(scarySphere(), 878825614395267100);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
index 8810eef45f..34f0c93c2f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4d51000cf542c50ffe8
-title: 'Problem 361: Subsequence of Thue-Morse sequence'
+title: '問題 361: トゥエ-モース数列の部分列'
challengeType: 5
forumTopicId: 302022
dashedName: problem-361-subsequence-of-thue-morse-sequence
@@ -8,27 +8,27 @@ dashedName: problem-361-subsequence-of-thue-morse-sequence
# --description--
-The Thue-Morse sequence $\\{T_n\\}$ is a binary sequence satisfying:
+トゥエ-モース数列 $\\{T_n\\}$ は、以下を満たす 2 進数列です。
- $T_0 = 0$
- $T_{2n} = T_n$
- $T_{2n + 1} = 1 - T_n$
-The first several terms of $\\{T_n\\}$ are given as follows: $01101001\color{red}{10010}1101001011001101001\ldots$.
+$\\{T_n\\}$ の最初のいくつかの項が次のように与えられます: $01101001\color{red}{10010}1101001011001101001\ldots$
-We define $\\{A_n\\}$ as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in $\\{T_n\\}$. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in $\\{T_n\\}$ ($T_8$ to $T_{12}$), so 18 is an element of $\\{A_n\\}$. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in $\\{T_n\\}$, so 14 is not an element of $\\{A_n\\}$.
+各要素の 2 進表記が $\\{T_n\\}$ の部分列になるようなソートされた整数数列を、$\\{A_n\\}$ とします。 例えば 10 進数の 18 は、2 進数では 10010 と表現されます。 10010 は $\\{T_n\\}$ ($T_8$ から $T_{12}$) の中に現れるので、18 は $\\{A_n\\}$ の要素です。 10 進数の 14 は、2 進数では 1110 と表現されます。 1110 は $\\{T_n\\}$ の中に現れないので,14 は $\\{A_n\\}$ の要素ではありません。
-The first several terms of $A_n$ are given as follows:
+$A_n$ の最初のいくつかの項が次のように与えられます。
$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
-We can also verify that $A_{100} = 3251$ and $A_{1000} = 80\\,852\\,364\\,498$.
+また、$A_{100} = 3251$ および $A_{1000} = 80\\,852\\,364\\,498$ であることも確認できます。
-Find the last 9 digits of $\displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
+$\displaystyle\sum_{k = 1}^{18} A_{{10}^k}$ の下位 9 桁を求めなさい。
# --hints--
-`subsequenceOfThueMorseSequence()` should return `178476944`.
+`subsequenceOfThueMorseSequence()` は `178476944` を返す必要があります。
```js
assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
index 50d4cc1539..dd609c96a3 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
@@ -1,6 +1,6 @@
---
id: 5900f4d61000cf542c50ffe9
-title: 'Problem 362: Squarefree factors'
+title: '問題 362: 無平方因数'
challengeType: 5
forumTopicId: 302023
dashedName: problem-362-squarefree-factors
@@ -8,25 +8,25 @@ dashedName: problem-362-squarefree-factors
# --description--
-Consider the number 54.
+54 という数について考えます。
-54 can be factored in 7 distinct ways into one or more factors larger than 1:
+1 より大きい因数を 1 つ以上使って 54 を因数分解する方法は、次のように 7 通りあります。
-$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9 \text{ and } 2 × 3 × 3 × 3$$
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9, \text{ および } 2 × 3 × 3 × 3$$
-If we require that the factors are all squarefree only two ways remain: $3 × 3 × 6$ and $2 × 3 × 3 × 3$.
+すべての因数は無平方因数でなければならないとした場合、$3 × 3 × 3$ と $2 × 3 × 3$ の 2 通りに限定されます。
-Let's call $Fsf(n)$ the number of ways $n$ can be factored into one or more squarefree factors larger than 1, so $Fsf(54) = 2$.
+1 より大きい、かつ無平方因数を 1 つ以上使って $n$ を因数分解できる方法の数を $Fsf(n)$ とします。したがって、$Fsf(54) = 2$ です。
-Let $S(n)$ be $\sum Fsf(k)$ for $k = 2$ to $n$.
+2 から $n$ までの $k$ について、$S(n)$ を $\sum Fsf(k)$ とします。
-$S(100) = 193$.
+$S(100) = 193$ です。
-Find $S(10\\,000\\,000\\,000)$.
+$S(10\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`squarefreeFactors()` should return `457895958010`.
+`squarefreeFactors()` は `457895958010` を返す必要があります。
```js
assert.strictEqual(squarefreeFactors(), 457895958010);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
index 821be88ff6..1a8848a425 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffeb
-title: 'Problem 363: Bézier Curves'
+title: '問題 363: ベジェ曲線'
challengeType: 5
forumTopicId: 302024
dashedName: problem-363-bzier-curves
@@ -8,29 +8,29 @@ dashedName: problem-363-bzier-curves
# --description--
-A cubic Bézier curve is defined by four points: $P_0$, $P_1$, $P_2$ and $P_3$.
+三次ベジェ曲線は $P_0$, $P_1$, $P_2$, $P_3$ の 4 点で定義されます。
-The curve is constructed as follows:
+この曲線は次のように形成されます。
-
-One particular cell is occupied by the queen bee. For a positive real number $L$, let $B(L)$ count the cells with distance $L$ from the queen bee cell (all distances are measured from centre to centre); you may assume that the honeycomb is large enough to accommodate for any distance we wish to consider.
+ある特定の部屋は女王蜂が占有しています。 正の実数 $L$ を用いて、女王蜂の部屋から $L$ の距離にある部屋 $B(L)$ を数えます (常に、ある部屋の中心から別の部屋の中心までを測ります)。蜂の巣の大きさは、ここで考えるあらゆる距離に対して十分な大きさであると仮定します。
-For example, $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$ and $B(111\\,111\\,111) = 54$.
+例: $B(\sqrt{3}) = 6$, $B(\sqrt{21}) = 12$, $B(111\\,111\\,111) = 54$
-Find the number of $L ≤ 5 \times {10}^{11}$ such that $B(L) = 450$.
+$B(L) = 450$ となるような $L ≤ 5 \times {10}^{11}$ の数を求めなさい。
# --hints--
-`distancesInHoneycomb()` should return `58065134`.
+`distancesInHoneycomb()` は `58065134` を返す必要があります。
```js
assert.strictEqual(distancesInHoneycomb(), 58065134);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
index 8c693f1d43..b8bfc270b7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-355-maximal-coprime-subset.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe2
-title: 'Problem 355: Maximal coprime subset'
+title: '問題 355: 最大の互いに素な部分集合'
challengeType: 5
forumTopicId: 302015
dashedName: problem-355-maximal-coprime-subset
@@ -8,15 +8,15 @@ dashedName: problem-355-maximal-coprime-subset
# --description--
-Define $Co(n)$ to be the maximal possible sum of a set of mutually co-prime elements from $\\{1, 2, \ldots, n\\}$. For example $Co(10)$ is 30 and hits that maximum on the subset $\\{1, 5, 7, 8, 9\\}$.
+$\\{1, 2, \ldots, n\\}$ の要素のうち互いに素な要素の集合の最大和を、$Co(n)$ と定義します。 例えば、 $Co(10)$ は 30 であり、最大の部分集合は $\\{1, 5, 7, 8, 9\\}$ になります。
-You are given that $Co(30) = 193$ and $Co(100) = 1356$.
+$Co(30) = 193$ と $Co(100) = 1356$ が与えられます。
-Find $Co(200\\,000)$.
+$Co(200\\,000)$ を求めなさい。
# --hints--
-`maximalCoprimeSubset()` should return `1726545007`.
+`maximalCoprimeSubset()` は `1726545007` を返す必要があります。
```js
assert.strictEqual(maximalCoprimeSubset(), 1726545007);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
index 07aeae1c6f..042910ccef 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4d01000cf542c50ffe3
-title: 'Problem 356: Largest roots of cubic polynomials'
+title: '問題 356: 三次多項式の最大根'
challengeType: 5
forumTopicId: 302016
dashedName: problem-356-largest-roots-of-cubic-polynomials
@@ -8,17 +8,17 @@ dashedName: problem-356-largest-roots-of-cubic-polynomials
# --description--
-Let an be the largest real root of a polynomial $g(x) = x^3 - 2^n \times x^2 + n$.
+$a_n$ を、多項式 $g(x) = x^3 - 2^n \times x^2 + n$ の最大の実根とします。
-For example, $a_2 = 3.86619826\ldots$
+例: $a_2 = 3.86619826\ldots$
-Find the last eight digits of $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
+$\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$ の下位 8 桁を求めなさい。
-**Note:** $\lfloor a\rfloor$ represents the floor function.
+**注:** $\lfloor a\rfloor$ は床関数を表します。
# --hints--
-`rootsOfCubicPolynomials()` should return `28010159`.
+`rootsOfCubicPolynomials()` は `28010159` を返す必要があります。
```js
assert.strictEqual(rootsOfCubicPolynomials(), 28010159);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
index 6483905ad4..7516c59549 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-357-prime-generating-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d11000cf542c50ffe4
-title: 'Problem 357: Prime generating integers'
+title: '問題 357: 素数を生成する整数'
challengeType: 5
forumTopicId: 302017
dashedName: problem-357-prime-generating-integers
@@ -8,15 +8,15 @@ dashedName: problem-357-prime-generating-integers
# --description--
-Consider the divisors of 30: 1, 2, 3, 5, 6, 10, 15, 30.
+30 の約数である 1, 2, 3, 5, 6, 10, 15, 30 について考えます。
-It can be seen that for every divisor $d$ of 30, $d + \frac{30}{d}$ is prime.
+30 のすべての約数 $d$ について、$d + \frac{30}{d}$ が素数であることが分かります。
-Find the sum of all positive integers $n$ not exceeding $100\\,000\\,000$ such that for every divisor $d$ of $n$, $d + \frac{n}{d}$ is prime.
+$n$ のすべての約数 $d$ について $d + \frac{n}{d}$ が素数となるような、$100\\,000\\,000$ を超えない正の整数 $n$ の総和を求めなさい。
# --hints--
-`primeGeneratingIntegers()` should return `1739023853137`.
+`primeGeneratingIntegers()` は `1739023853137` を返す必要があります。
```js
assert.strictEqual(primeGeneratingIntegers(), 1739023853137);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
index 9370165ecc..184fa5c249 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-358-cyclic-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4d21000cf542c50ffe5
-title: 'Problem 358: Cyclic numbers'
+title: '問題 358: 巡回数'
challengeType: 5
forumTopicId: 302018
dashedName: problem-358-cyclic-numbers
@@ -8,25 +8,25 @@ dashedName: problem-358-cyclic-numbers
# --description--
-A cyclic number with $n$ digits has a very interesting property:
+$n$ 桁の巡回数は非常に興味深い性質を持っています:
-When it is multiplied by 1, 2, 3, 4, ... $n$, all the products have exactly the same digits, in the same order, but rotated in a circular fashion!
+1, 2, 3, 4, ... $n$ を乗じると、すべての積に全く同じ数字が使われ、数字を循環させると順序も同じになります!
-The smallest cyclic number is the 6-digit number 142857:
+最小の巡回数は、6 桁の数 142857 です。
$$\begin{align} & 142857 × 1 = 142857 \\\\ & 142857 × 2 = 285714 \\\\ & 142857 × 3 = 428571 \\\\ & 142857 × 4 = 571428 \\\\ & 142857 × 5 = 714285 \\\\ & 142857 × 6 = 857142 \end{align}$$
-The next cyclic number is 0588235294117647 with 16 digits:
+次の巡回数は、16 桁の 0588235294117647 です。
$$\begin{align} & 0588235294117647 × 1 = 0588235294117647 \\\\ & 0588235294117647 × 2 = 1176470588235294 \\\\ & 0588235294117647 × 3 = 1764705882352941 \\\\ & \ldots \\\\ & 0588235294117647 × 16 = 9411764705882352 \end{align}$$
-Note that for cyclic numbers, leading zeros are important.
+なお、巡回数では先行ゼロが重要です。
-There is only one cyclic number for which, the eleven leftmost digits are 00000000137 and the five rightmost digits are 56789 (i.e., it has the form $00000000137\ldots56789$ with an unknown number of digits in the middle). Find the sum of all its digits.
+左端の 11 桁が 00000000137 で、右端の 5 桁が 56789 (すなわち $00000000137\ldots56789$ の形を取り、中間の数字は不明) の巡回数は 1 つしかありません。 この数のすべての桁の和を求めなさい。
# --hints--
-`cyclicNumbers()` should return `3284144505`.
+`cyclicNumbers()` は `3284144505` を返す必要があります。
```js
assert.strictEqual(cyclicNumbers(), 3284144505);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
index d1b78c9dd7..161a623da5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-359-hilberts-new-hotel.md
@@ -1,6 +1,6 @@
---
id: 5900f4d31000cf542c50ffe6
-title: 'Problem 359: Hilbert''s New Hotel'
+title: '問題 359: ヒルベルトの新しいホテル'
challengeType: 5
forumTopicId: 302019
dashedName: problem-359-hilberts-new-hotel
@@ -8,32 +8,32 @@ dashedName: problem-359-hilberts-new-hotel
# --description--
-An infinite number of people (numbered 1, 2, 3, etc.) are lined up to get a room at Hilbert's newest infinite hotel. The hotel contains an infinite number of floors (numbered 1, 2, 3, etc.), and each floor contains an infinite number of rooms (numbered 1, 2, 3, etc.).
+ヒルベルトの最新の無限ホテルで部屋を取ろうと、人々 (1, 2, 3,... の番号付き) が無限に並んでいます。 ホテルには階 (1, 2, 3,... の番号付き) が無限にあり、各階には部屋 (1, 2, 3,... の番号付き) が無限にあります。
-Initially the hotel is empty. Hilbert declares a rule on how the $n^{\text{th}}$ person is assigned a room: person $n$ gets the first vacant room in the lowest numbered floor satisfying either of the following:
+当初、ホテルに客はいませんでした。 ヒルベルトは、$n$ 番目の人にどのように部屋を割り当てるかを宣言しました。それによれば、$n$ 番目の人は、以下のいずれかを満たす最下階の最初の空き部屋を取ります。
-- the floor is empty
-- the floor is not empty, and if the latest person taking a room in that floor is person $m$, then $m + n$ is a perfect square
+- その階が空いている
+- その階が空いておらず、その階で最後に部屋を取った人が $m$ 番目である場合は $m + n$ が完全平方数になる
-Person 1 gets room 1 in floor 1 since floor 1 is empty.
+1 階が空いているので、1 番目の人は 1 階の 1 号室を取ります。
-Person 2 does not get room 2 in floor 1 since 1 + 2 = 3 is not a perfect square.
+1 + 2 = 3 は完全平方数ではないので、2 番目の人は 1 階の 2 号室を取れません。
-Person 2 instead gets room 1 in floor 2 since floor 2 is empty.
+しかし 2 階が空いているので、2 番目の人は代わりに 2 階の 1 号室を取ります。
-Person 3 gets room 2 in floor 1 since 1 + 3 = 4 is a perfect square.
+1 + 3 = 4 は完全平方数なので、3 番目の人は 1 階の 2 号室を取ります。
-Eventually, every person in the line gets a room in the hotel.
+最終的には、並んでいたすべての人がホテルの部屋を取れます。
-Define $P(f, r)$ to be $n$ if person $n$ occupies room $r$ in floor $f$, and 0 if no person occupies the room. Here are a few examples:
+$P(f, r)$ の結果を次のように定義します: $n$ 番目の人が $f$ 階の $r$ 号室を取る場合は $n$、誰もその部屋を取らない場合は 0 になります。 いくつかの例を次に示します。
$$\begin{align} & P(1, 1) = 1 \\\\ & P(1, 2) = 3 \\\\ & P(2, 1) = 2 \\\\ & P(10, 20) = 440 \\\\ & P(25, 75) = 4863 \\\\ & P(99, 100) = 19454 \end{align}$$
-Find the sum of all $P(f, r)$ for all positive $f$ and $r$ such that $f × r = 71\\,328\\,803\\,586\\,048$ and give the last 8 digits as your answer.
+$f × r = 71\\,328\\,803\\,586\\,048$ となるすべての正の数 $f$, $r$ について $P(f, r)$ の総和を求め、下位 8 桁を答えなさい。
# --hints--
-`hilbertsNewHotel()` should return `40632119`.
+`hilbertsNewHotel()` は `40632119` を返す必要があります。
```js
assert.strictEqual(hilbertsNewHotel(), 40632119);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
index f04364484f..07fc4e1462 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-360-scary-sphere.md
@@ -1,6 +1,6 @@
---
id: 5900f4d41000cf542c50ffe7
-title: 'Problem 360: Scary Sphere'
+title: '問題 360: 恐ろしい球体'
challengeType: 5
forumTopicId: 302021
dashedName: problem-360-scary-sphere
@@ -8,21 +8,21 @@ dashedName: problem-360-scary-sphere
# --description--
-Given two points ($x_1$, $y_1$, $z_1$) and ($x_2$, $y_2$, $z_2$) in three dimensional space, the Manhattan distance between those points is defined as $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$.
+三次元空間に ($x_1$, $y_1$, $z_1$) と ($x_2$, $y_2$, $z_2$) の 2 つの点が与えられるとき、この 2 点間のマンハッタン距離は $|x_1 - x_2| + |y_1 - y_2| + |z_1 - z_2|$ と定義されます。
-Let $C(r)$ be a sphere with radius $r$ and center in the origin $O(0, 0, 0)$.
+$C(r)$ を、半径が $r$、中心が原点 $O(0, 0, 0)$ の球とします。
-Let $I(r)$ be the set of all points with integer coordinates on the surface of $C(r)$.
+$I(r)$ を、$C(r)$ の表面に整数座標を持つすべての点の集合とします。
-Let $S(r)$ be the sum of the Manhattan distances of all elements of $I(r)$ to the origin $O$.
+$S(r)$ を、$I(r)$ のすべての要素から原点 $O$ までのマンハッタン距離の和とします。
-E.g. $S(45)=34518$.
+例: $S(45)=34518$
-Find $S({10}^{10})$.
+$S({10}^{10})$ を求めなさい。
# --hints--
-`scarySphere()` should return `878825614395267100`.
+`scarySphere()` は `878825614395267100` を返す必要があります。
```js
assert.strictEqual(scarySphere(), 878825614395267100);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
index 8810eef45f..34f0c93c2f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4d51000cf542c50ffe8
-title: 'Problem 361: Subsequence of Thue-Morse sequence'
+title: '問題 361: トゥエ-モース数列の部分列'
challengeType: 5
forumTopicId: 302022
dashedName: problem-361-subsequence-of-thue-morse-sequence
@@ -8,27 +8,27 @@ dashedName: problem-361-subsequence-of-thue-morse-sequence
# --description--
-The Thue-Morse sequence $\\{T_n\\}$ is a binary sequence satisfying:
+トゥエ-モース数列 $\\{T_n\\}$ は、以下を満たす 2 進数列です。
- $T_0 = 0$
- $T_{2n} = T_n$
- $T_{2n + 1} = 1 - T_n$
-The first several terms of $\\{T_n\\}$ are given as follows: $01101001\color{red}{10010}1101001011001101001\ldots$.
+$\\{T_n\\}$ の最初のいくつかの項が次のように与えられます: $01101001\color{red}{10010}1101001011001101001\ldots$
-We define $\\{A_n\\}$ as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in $\\{T_n\\}$. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in $\\{T_n\\}$ ($T_8$ to $T_{12}$), so 18 is an element of $\\{A_n\\}$. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in $\\{T_n\\}$, so 14 is not an element of $\\{A_n\\}$.
+各要素の 2 進表記が $\\{T_n\\}$ の部分列になるようなソートされた整数数列を、$\\{A_n\\}$ とします。 例えば 10 進数の 18 は、2 進数では 10010 と表現されます。 10010 は $\\{T_n\\}$ ($T_8$ から $T_{12}$) の中に現れるので、18 は $\\{A_n\\}$ の要素です。 10 進数の 14 は、2 進数では 1110 と表現されます。 1110 は $\\{T_n\\}$ の中に現れないので,14 は $\\{A_n\\}$ の要素ではありません。
-The first several terms of $A_n$ are given as follows:
+$A_n$ の最初のいくつかの項が次のように与えられます。
$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
-We can also verify that $A_{100} = 3251$ and $A_{1000} = 80\\,852\\,364\\,498$.
+また、$A_{100} = 3251$ および $A_{1000} = 80\\,852\\,364\\,498$ であることも確認できます。
-Find the last 9 digits of $\displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
+$\displaystyle\sum_{k = 1}^{18} A_{{10}^k}$ の下位 9 桁を求めなさい。
# --hints--
-`subsequenceOfThueMorseSequence()` should return `178476944`.
+`subsequenceOfThueMorseSequence()` は `178476944` を返す必要があります。
```js
assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
index 50d4cc1539..dd609c96a3 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
@@ -1,6 +1,6 @@
---
id: 5900f4d61000cf542c50ffe9
-title: 'Problem 362: Squarefree factors'
+title: '問題 362: 無平方因数'
challengeType: 5
forumTopicId: 302023
dashedName: problem-362-squarefree-factors
@@ -8,25 +8,25 @@ dashedName: problem-362-squarefree-factors
# --description--
-Consider the number 54.
+54 という数について考えます。
-54 can be factored in 7 distinct ways into one or more factors larger than 1:
+1 より大きい因数を 1 つ以上使って 54 を因数分解する方法は、次のように 7 通りあります。
-$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9 \text{ and } 2 × 3 × 3 × 3$$
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6, 2 × 3 × 9, \text{ および } 2 × 3 × 3 × 3$$
-If we require that the factors are all squarefree only two ways remain: $3 × 3 × 6$ and $2 × 3 × 3 × 3$.
+すべての因数は無平方因数でなければならないとした場合、$3 × 3 × 3$ と $2 × 3 × 3$ の 2 通りに限定されます。
-Let's call $Fsf(n)$ the number of ways $n$ can be factored into one or more squarefree factors larger than 1, so $Fsf(54) = 2$.
+1 より大きい、かつ無平方因数を 1 つ以上使って $n$ を因数分解できる方法の数を $Fsf(n)$ とします。したがって、$Fsf(54) = 2$ です。
-Let $S(n)$ be $\sum Fsf(k)$ for $k = 2$ to $n$.
+2 から $n$ までの $k$ について、$S(n)$ を $\sum Fsf(k)$ とします。
-$S(100) = 193$.
+$S(100) = 193$ です。
-Find $S(10\\,000\\,000\\,000)$.
+$S(10\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`squarefreeFactors()` should return `457895958010`.
+`squarefreeFactors()` は `457895958010` を返す必要があります。
```js
assert.strictEqual(squarefreeFactors(), 457895958010);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
index 821be88ff6..1a8848a425 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffeb
-title: 'Problem 363: Bézier Curves'
+title: '問題 363: ベジェ曲線'
challengeType: 5
forumTopicId: 302024
dashedName: problem-363-bzier-curves
@@ -8,29 +8,29 @@ dashedName: problem-363-bzier-curves
# --description--
-A cubic Bézier curve is defined by four points: $P_0$, $P_1$, $P_2$ and $P_3$.
+三次ベジェ曲線は $P_0$, $P_1$, $P_2$, $P_3$ の 4 点で定義されます。
-The curve is constructed as follows:
+この曲線は次のように形成されます。
-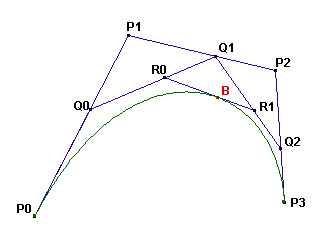 +
+ -On the segments $P_0P_1$, $P_1P_2$ and $P_2P_3$ the points $Q_0$,$Q_1$ and $Q_2$ are drawn such that $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, with $t$ in [0,1].
+線分 $P_0P_1$, $P_1P_2$, $P_2P_3$ 上に点 $Q_0$,$Q_1$, $Q_2$ が、区間 [0,1] 内の $t$ について $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$ となるように描かれます。
-On the segments $Q_0Q_1$ and $Q_1Q_2$ the points $R_0$ and $R_1$ are drawn such that $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ for the same value of $t$.
+線分 $Q_0Q_1$ と $Q_1Q_2$ 上に点 $R_0$ と $R_1$ が、上と同じ $t$ の値について $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ となるように描かれます。
-On the segment $R_0R_1$ the point $B$ is drawn such that $\frac{R_0B}{R_0R_1} = t$ for the same value of $t$.
+線分 $R_0R_1$ 上に点 $B$ が、上と同じ $t$ の値について $\frac{R_0B}{R_0R_1} = t$ となるように描かれます。
-The Bézier curve defined by the points $P_0$, $P_1$, $P_2$, $P_3$ is the locus of $B$ as $Q_0$ takes all possible positions on the segment $P_0P_1$. (Please note that for all points the value of $t$ is the same.)
+点 $P_0$, $P_1$, $P_2$, $P_3$ によって定義されるベジェ曲線は、$Q_0$ が線分 $P_0P_1$ 上の考えられるすべての位置を取る際の $B$ の軌跡です。 (すべての点において $t$ の値が同じであることに注意してください。)
-From the construction it is clear that the Bézier curve will be tangent to the segments $P_0P_1$ in $P_0$ and $P_2P_3$ in $P_3$.
+作成された図を見れば分かるとおり、ベジェ曲線は $P_0$ において線分 $P_0P_1$ と接し、そして $P_3$ において線分 $P_2P_3$ と接しています。
-A cubic Bézier curve with $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ and $P_3 = (0, 1)$ is used to approximate a quarter circle. The value $v > 0$ is chosen such that the area enclosed by the lines $OP_0$, $OP_3$ and the curve is equal to $\frac{π}{4}$ (the area of the quarter circle).
+$P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v. 1)$, $P_3 = (0, 1)$ で定義される三次ベジェ曲線は、4 分の 1 円弧に近付けるために使用されます。 値 $v > 0$ は、直線 $OP_0$, $OP_3$ と曲線で囲まれた部分の面積が $\frac{π}{4}$ (4 分の 1 円弧) と等しくなるように選択されます 。
-By how many percent does the length of the curve differ from the length of the quarter circle? That is, if $L$ is the length of the curve, calculate $100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$. Give your answer rounded to 10 digits behind the decimal point.
+曲線の長さは 4 分の 1 円弧の長さと何パーセント異なりますか。 つまり、$L$ を曲線の長さとすると、$100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$ を計算します。 回答は、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`bezierCurves()` should return `0.0000372091`.
+`bezierCurves()` は `0.0000372091` を返す必要があります。
```js
assert.strictEqual(bezierCurves(), 0.0000372091);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
index c65133ca65..f2b1b83baa 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffea
-title: 'Problem 364: Comfortable distance'
+title: '問題 364: 快適な距離'
challengeType: 5
forumTopicId: 302025
dashedName: problem-364-comfortable-distance
@@ -8,23 +8,23 @@ dashedName: problem-364-comfortable-distance
# --description--
-There are $N$ seats in a row. $N$ people come after each other to fill the seats according to the following rules:
+$N$ 個の席が連続して並んでいます。 ここに $N$ 人が次々とやって来て、次のルールに従って席を埋めていきます。
-1. If there is any seat whose adjacent seat(s) are not occupied take such a seat.
-2. If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
-3. Otherwise take one of the remaining available seats.
+1. 隣席がいずれも空いている席があれば、その席を取ります。
+2. 1 のような席がなく、隣席が 1 つのみ埋まっている席があれば、その席を取ります。
+3. 1, 2 以外の場合は、残っている空席のいずれかを取ります。
-Let $T(N)$ be the number of possibilities that $N$ seats are occupied by $N$ people with the given rules. The following figure shows $T(4) = 8$.
+与えられたルールに従い $N$ 人が $N$ 個の席を取る方法の数を、$T(N)$ とします。 次の図は $T(4) = 8$ を示しています。
-
-On the segments $P_0P_1$, $P_1P_2$ and $P_2P_3$ the points $Q_0$,$Q_1$ and $Q_2$ are drawn such that $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, with $t$ in [0,1].
+線分 $P_0P_1$, $P_1P_2$, $P_2P_3$ 上に点 $Q_0$,$Q_1$, $Q_2$ が、区間 [0,1] 内の $t$ について $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$ となるように描かれます。
-On the segments $Q_0Q_1$ and $Q_1Q_2$ the points $R_0$ and $R_1$ are drawn such that $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ for the same value of $t$.
+線分 $Q_0Q_1$ と $Q_1Q_2$ 上に点 $R_0$ と $R_1$ が、上と同じ $t$ の値について $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ となるように描かれます。
-On the segment $R_0R_1$ the point $B$ is drawn such that $\frac{R_0B}{R_0R_1} = t$ for the same value of $t$.
+線分 $R_0R_1$ 上に点 $B$ が、上と同じ $t$ の値について $\frac{R_0B}{R_0R_1} = t$ となるように描かれます。
-The Bézier curve defined by the points $P_0$, $P_1$, $P_2$, $P_3$ is the locus of $B$ as $Q_0$ takes all possible positions on the segment $P_0P_1$. (Please note that for all points the value of $t$ is the same.)
+点 $P_0$, $P_1$, $P_2$, $P_3$ によって定義されるベジェ曲線は、$Q_0$ が線分 $P_0P_1$ 上の考えられるすべての位置を取る際の $B$ の軌跡です。 (すべての点において $t$ の値が同じであることに注意してください。)
-From the construction it is clear that the Bézier curve will be tangent to the segments $P_0P_1$ in $P_0$ and $P_2P_3$ in $P_3$.
+作成された図を見れば分かるとおり、ベジェ曲線は $P_0$ において線分 $P_0P_1$ と接し、そして $P_3$ において線分 $P_2P_3$ と接しています。
-A cubic Bézier curve with $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ and $P_3 = (0, 1)$ is used to approximate a quarter circle. The value $v > 0$ is chosen such that the area enclosed by the lines $OP_0$, $OP_3$ and the curve is equal to $\frac{π}{4}$ (the area of the quarter circle).
+$P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v. 1)$, $P_3 = (0, 1)$ で定義される三次ベジェ曲線は、4 分の 1 円弧に近付けるために使用されます。 値 $v > 0$ は、直線 $OP_0$, $OP_3$ と曲線で囲まれた部分の面積が $\frac{π}{4}$ (4 分の 1 円弧) と等しくなるように選択されます 。
-By how many percent does the length of the curve differ from the length of the quarter circle? That is, if $L$ is the length of the curve, calculate $100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$. Give your answer rounded to 10 digits behind the decimal point.
+曲線の長さは 4 分の 1 円弧の長さと何パーセント異なりますか。 つまり、$L$ を曲線の長さとすると、$100 × \displaystyle\frac{L − \frac{π}{2}}{\frac{π}{2}}$ を計算します。 回答は、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`bezierCurves()` should return `0.0000372091`.
+`bezierCurves()` は `0.0000372091` を返す必要があります。
```js
assert.strictEqual(bezierCurves(), 0.0000372091);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
index c65133ca65..f2b1b83baa 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffea
-title: 'Problem 364: Comfortable distance'
+title: '問題 364: 快適な距離'
challengeType: 5
forumTopicId: 302025
dashedName: problem-364-comfortable-distance
@@ -8,23 +8,23 @@ dashedName: problem-364-comfortable-distance
# --description--
-There are $N$ seats in a row. $N$ people come after each other to fill the seats according to the following rules:
+$N$ 個の席が連続して並んでいます。 ここに $N$ 人が次々とやって来て、次のルールに従って席を埋めていきます。
-1. If there is any seat whose adjacent seat(s) are not occupied take such a seat.
-2. If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
-3. Otherwise take one of the remaining available seats.
+1. 隣席がいずれも空いている席があれば、その席を取ります。
+2. 1 のような席がなく、隣席が 1 つのみ埋まっている席があれば、その席を取ります。
+3. 1, 2 以外の場合は、残っている空席のいずれかを取ります。
-Let $T(N)$ be the number of possibilities that $N$ seats are occupied by $N$ people with the given rules. The following figure shows $T(4) = 8$.
+与えられたルールに従い $N$ 人が $N$ 個の席を取る方法の数を、$T(N)$ とします。 次の図は $T(4) = 8$ を示しています。
-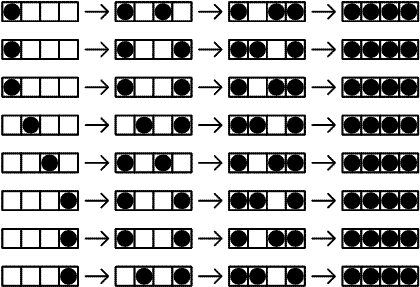 +
+ -We can verify that $T(10) = 61\\,632$ and $T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094$.
+$T(10) = 61\\,632$, $T(1\\,000)\bmod 100\\,007 = 47\\,255\\,094$ であることを確認できます。
-Find $T(1\\,000\\,000)\bmod 100\\,000\\,007$.
+$T(1\\,000\\,000)\bmod 100\\,000\\,007$ を求めなさい。
# --hints--
-`comfortableDistance()` should return `44855254`.
+`comfortableDistance()` は `44855254` を返す必要があります。
```js
assert.strictEqual(comfortableDistance(), 44855254);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
index 3c778cb1f7..041b939d51 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffec
-title: 'Problem 365: A huge binomial coefficient'
+title: '問題 365: 巨大な二項係数'
challengeType: 5
forumTopicId: 302026
dashedName: problem-365-a-huge-binomial-coefficient
@@ -8,15 +8,15 @@ dashedName: problem-365-a-huge-binomial-coefficient
# --description--
-The binomial coefficient $\displaystyle\binom{{10}^{18}}{{10}^9}$ is a number with more than 9 billion ($9 × {10}^9$) digits.
+二項係数 $\displaystyle\binom{{10}^{18}}{{10}^9}$ は 90 億 ($9 × {10}^9$) 桁を超える数です。
-Let $M(n, k, m)$ denote the binomial coefficient $\displaystyle\binom{n}{k}$ modulo $m$.
+$M(n, k, m)$ を、二項係数 $\displaystyle\binom{n}{k}$ mod $m$ とします。
-Calculate $\sum M({10}^{18}, {10}^9, p \times q \times r)$ for $1000 < p < q < r < 5000$ and $p$, $q$, $r$ prime.
+素数 $p$, $q$, $r$ が $1000 < p < q < r < 5000$ を満たすとき、$\sum M({10}^{18}, {10}^9, p \times q \times r)$ を求めなさい。
# --hints--
-`hugeBinomialCoefficient()` should return `162619462356610300`.
+`hugeBinomialCoefficient()` は `162619462356610300` を返す必要があります。
```js
assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
index 85cf7925c3..ec98d5dba4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffed
-title: 'Problem 366: Stone Game III'
+title: '問題 366: 石取りゲーム (3)'
challengeType: 5
forumTopicId: 302027
dashedName: problem-366-stone-game-iii
@@ -8,41 +8,41 @@ dashedName: problem-366-stone-game-iii
# --description--
-Two players, Anton and Bernhard, are playing the following game.
+アントンとベルンハルトという名前の 2 人のプレイヤーが、次のようなゲームをしています。
-There is one pile of $n$ stones.
+$n$ 個の石を積み上げた山が 1 つあります。
-The first player may remove any positive number of stones, but not the whole pile.
+先手は、任意の正の整数分の石を取れますが、山全体を取ることはできません。
-Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+その後、各プレイヤーは、対戦相手が直前に取った数の 2 倍までの数の石を取ります。
-The player who removes the last stone wins.
+最後の石を取ったプレイヤーが勝者です。
-E.g. $n = 5$
+例: $n = 5$ とします。
-If the first player takes anything more than one stone the next player will be able to take all remaining stones.
+先手が 2 個以上の石を取った場合、後手は残りのすべての石を取ることができます。
-If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones.
+先手が石を 1 個取り 4 個残した場合、後手も石を 1 個取ると 3 個残ります。
-The first player cannot take all three because he may take at most $2 \times 1 = 2$ stones. So let's say he also takes one stone, leaving 2.
+先手は多くとも $2 \times 1 = 2$ 個の石しか取れないので、3 個すべてを取ることはできません。 したがって、また石を 1 個取ると仮定します。残りは 2 個になります。
-The second player can take the two remaining stones and wins.
+後手は、残っている 2 個の石を取れば勝つことができます。
-So 5 is a losing position for the first player.
+したがって、石が 5 個ある山は先手にとって敗北ポジション (必ず負ける状況) です。
-For some winning positions there is more than one possible move for the first player.
+いくつかの勝利ポジションでは、先手が取り得る手は複数あります。
-E.g. when $n = 17$ the first player can remove one or four stones.
+例: $n = 17$ の場合、先手は 1 個または 4 個の石を取ることができます。
-Let $M(n)$ be the maximum number of stones the first player can take from a winning position at his first turn and $M(n) = 0$ for any other position.
+先手が最初のターンで勝利ポジションから取れる石の最大数を $M(n)$ とし、他のすべてのポジションでは $M(n) = 0$ とします。
-$\sum M(n)$ for $n ≤ 100$ is 728.
+$n ≤ 100$ のとき、$\sum M(n)$ = 728 です。
-Find $\sum M(n)$ for $n ≤ {10}^{18}$. Give your answer modulo ${10}^8$.
+$n ≤ {10}^{18}$ のとき、$\sum M(n)$ を求めなさい。 mod ${10}^8$ で答えること。
# --hints--
-`stoneGameThree()` should return `88351299`.
+`stoneGameThree()` は `88351299` を返す必要があります。
```js
assert.strictEqual(stoneGameThree(), 88351299);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
index 2497cd85ed..5fa3d3b759 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
@@ -1,6 +1,6 @@
---
id: 5900f4db1000cf542c50ffee
-title: 'Problem 367: Bozo sort'
+title: '問題 367: ボゾソート'
challengeType: 5
forumTopicId: 302028
dashedName: problem-367-bozo-sort
@@ -8,29 +8,29 @@ dashedName: problem-367-bozo-sort
# --description--
-Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+ボゾソートと聞いて、やや効率の低いボゴソートと混同しないでください。ボゾソートは、入力数列がソートされているかをチェックし、ソートされていない場合は無作為に 2 つの要素を交換します。 最終的に数列がソートされるまで、これが繰り返されます。
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all $4!$ input sequences is $24.75$.
+最初の 4 つの自然数が含まれるすべての順列を入力として考えた場合、交換回数の期待値は、$4!$ 個すべての入力数列で平均 $24.75$ になります。
-The already sorted sequence takes 0 steps.
+ソート済みの数列の場合、交換回数は 0 回です。
-In this problem we consider the following variant on bozo sort.
+この問題では、次のような変種のボゾソートについて考えます。
-If the sequence is not in order we pick three elements at random and shuffle these three elements randomly.
+数列がソートされていない場合は、無作為に 3 つの要素を選択し、これら 3 つの要素を無作為に入れ替えます。
-All $3! = 6$ permutations of those three elements are equally likely.
+これら 3 つの要素の $3! = 6$ 個の順列はすべて等確率で現れます。
-The already sorted sequence will take 0 steps.
+ソート済みの数列の場合、交換回数は 0 回です。
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all $4!$ input sequences is $27.5$.
+最初の 4 つの自然数が含まれるすべての順列を入力として考えた場合、交換回数の期待値は、$4!$ 個すべての入力数列で平均 $27.5$ になります。
-Consider as input sequences the permutations of the first 11 natural numbers.
+入力数列として、最初の 11 個の自然数の順列を考えます。
-Averaged over all $11!$ input sequences, what is the expected number of shuffles this sorting algorithm will perform? Give your answer rounded to the nearest integer.
+$11!$ 個すべての入力数列で平均すると、このソートアルゴリズムによる交換回数の期待値はいくつですか? 最も近い整数に四捨五入して答えなさい。
# --hints--
-`bozoSort()` should return `48271207`.
+`bozoSort()` は `48271207` を返す必要があります。
```js
assert.strictEqual(bozoSort(), 48271207);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
index fd8b6c8daf..906bced434 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
@@ -1,6 +1,6 @@
---
id: 5900f4dd1000cf542c50ffef
-title: 'Problem 368: A Kempner-like series'
+title: '問題 368: ケンプナーのような級数'
challengeType: 5
forumTopicId: 302029
dashedName: problem-368-a-kempner-like-series
@@ -8,23 +8,23 @@ dashedName: problem-368-a-kempner-like-series
# --description--
-The harmonic series $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ is well known to be divergent.
+調和級数 $1+\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ が発散することはよく知られています。
-If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+しかし、分母に 9 が含まれる項をすべてこの級数から取り除くと、級数は約 22.9206766193 と驚くほど収束します。 この改良版調和級数はケンプナー級数と呼ばれます。
-Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted.
+次に、同じ数字が 3 桁以上連続して分母に含まれる項をすべて調和級数から省略することで得られる、別の改良版調和級数について考えます。 調和級数の最初の 1200 項のうち、取り除かれるのはわずか 20 項であることを確認できます。
-These 20 omitted terms are:
+削除される 20 項は次のとおりです。
$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\ \dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
-This series converges as well.
+この級数も同様に収束します。
-Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+級数の収束値を求めなさい。 回答は、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`kempnerLikeSeries()` should return `253.6135092068`.
+`kempnerLikeSeries()` は `253.6135092068` を返す必要があります。
```js
assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md
index ce8f9a6e5a..de2e11b65a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff0
-title: 'Problem 369: Badugi'
+title: '問題 369: バドゥーギ'
challengeType: 5
forumTopicId: 302030
dashedName: problem-369-badugi
@@ -8,15 +8,15 @@ dashedName: problem-369-badugi
# --description--
-In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+標準的な 52 枚組のトランプで、ペアがなく、同じスート (マーク) の 2 枚のカードもない 4 枚のカードの組は、バドゥーギと呼ばれます。
-Let $f(n)$ be the number of ways to choose $n$ cards with a 4 card subset that is a Badugi. For example, there are $2\\,598\\,960$ ways to choose five cards from a standard 52 card deck, of which $514\\,800$ contain a 4 card subset that is a Badugi, so $f(5) = 514800$.
+バドゥーギである 4 枚のカードからなる部分集合を持つ $n$ 枚のカードを選ぶ方法の数を、$f(n)$ とします。 例えば、標準的な 52 枚組のトランプから 5 枚のカードを選ぶ法は $2\\,598\\,960$ 通りあり、そのうち $514\\,800$ 通りが、バドゥーギとなる 4 枚のカードからなる部分集合を含んでいるので、$f(5) = 514800$ となります。
-Find $\sum f(n)$ for $4 ≤ n ≤ 13$.
+$4 ≤ n ≤ 13$ のとき、$\sum f(n)$ を求めなさい。
# --hints--
-`badugi()` should return `862400558448`.
+`badugi()` は `862400558448` を返す必要があります。
```js
assert.strictEqual(badugi(), 862400558448);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
index c26ef2220c..86bac84380 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff1
-title: 'Problem 370: Geometric triangles'
+title: '問題 370: 幾何三角形'
challengeType: 5
forumTopicId: 302032
dashedName: problem-370-geometric-triangles
@@ -8,17 +8,17 @@ dashedName: problem-370-geometric-triangles
# --description--
-Let us define a geometric triangle as an integer sided triangle with sides $a ≤ b ≤ c$ so that its sides form a geometric progression, i.e. $b^2 = a \times c$.
+辺 $a ≤ b ≤ c$ を持つ整数辺三角形で、その辺が幾何数列を形成するもの、すなわち $b^2 = a \times c$ であるものを、幾何三角形と定義します。
-An example of such a geometric triangle is the triangle with sides $a = 144$, $b = 156$ and $c = 169$.
+このような幾何三角形の例は、長さ $a = 144$, $b = 156$, $c = 169$ の 3 辺を持つ三角形です。
-There are $861\\,805$ geometric triangles with $\text{perimeter} ≤ {10}^6$.
+$\text{周長} ≤ {10}^6$ を満たす幾何三角形は $861\\,805$ 個あります。
-How many geometric triangles exist with $\text{perimeter} ≤ 2.5 \times {10}^{13}$?
+$\text{周長} ≤ 2.5 \times {10}^{13}$ を満たす幾何三角形はいくつありますか。
# --hints--
-`geometricTriangles()` should return `41791929448408`.
+`geometricTriangles()` は `41791929448408` を返す必要があります。
```js
assert.strictEqual(geometricTriangles(), 41791929448408);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
index 63d7295fe2..3979cf0117 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
@@ -1,6 +1,6 @@
---
id: 5900f4e01000cf542c50fff2
-title: 'Problem 371: Licence plates'
+title: '問題 371: ナンバープレート'
challengeType: 5
forumTopicId: 302033
dashedName: problem-371-licence-plates
@@ -8,21 +8,21 @@ dashedName: problem-371-licence-plates
# --description--
-Oregon licence plates consist of three letters followed by a three digit number (each digit can be from [0...9]).
+オレゴン州のナンバープレートは、3 つの文字の後に 3 桁の数字が続きます (各桁の数字は [0...9] のいずれか)。
-While driving to work Seth plays the following game:
+車での通勤中に、セスは次のようなゲームをします。
-Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+移動中に見た 2 枚のナンバープレートの数字の合計が 1000 になったら勝ちです。
-E.g. `MIC-012` and `HAN-988` is a win and `RYU-500` and `SET-500` too. (as long as he sees them in the same trip).
+例: `MIC-012` と `HAN-988` の組み合わせは勝ちで、`RYU-500` と `SET-500` でも勝ちになります (1 回の移動中に見たものであれば)。
-Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+勝つために見る必要のあるナンバープレートの枚数の期待値を求めなさい。 回答は、四捨五入して小数第 8 位まで示すこと。
-**Note:** We assume that each licence plate seen is equally likely to have any three digit number on it.
+**注:** 見たナンバープレートのいずれでも、3 桁の数字が記されている確率は同じと仮定します。
# --hints--
-`licensePlates()` should return `40.66368097`.
+`licensePlates()` は `40.66368097` を返す必要があります。
```js
assert.strictEqual(licensePlates(), 40.66368097);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
index 9f39453ab4..2a7345e687 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff3
-title: 'Problem 372: Pencils of rays'
+title: '問題 372: 光線束'
challengeType: 5
forumTopicId: 302034
dashedName: problem-372-pencils-of-rays
@@ -8,17 +8,17 @@ dashedName: problem-372-pencils-of-rays
# --description--
-Let $R(M, N)$ be the number of lattice points ($x$, $y$) which satisfy $M \lt x \le N$, $M \lt y \le N$ and $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ is odd.
+$M \lt x \le N$, $M \lt y \le N$ を満たし $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ が奇数になるような格子点 ($x$, $y$) の数を、$R(M, N)$ とします。
-We can verify that $R(0, 100) = 3\\,019$ and $R(100, 10\\,000) = 29\\,750\\,422$.
+$R(0, 100) = 3\\,019$, $R(100, 10\\,000) = 29\\,750\\,422$ であることを確認できます。
-Find $R(2 \times {10}^6, {10}^9)$.
+$R(2 \times {10}^6, {10}^9)$ を求めなさい。
-**Note:** $\lfloor x\rfloor$ represents the floor function.
+**注:** $\lfloor x\rfloor$ は床関数を表します。
# --hints--
-`pencilsOfRays()` should return `301450082318807040`.
+`pencilsOfRays()` は `301450082318807040` を返す必要があります。
```js
assert.strictEqual(pencilsOfRays(), 301450082318807040);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
index c50df93cd8..d778b11e6f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff4
-title: 'Problem 373: Circumscribed Circles'
+title: '問題 373: 外接円'
challengeType: 5
forumTopicId: 302035
dashedName: problem-373-circumscribed-circles
@@ -8,17 +8,17 @@ dashedName: problem-373-circumscribed-circles
# --description--
-Every triangle has a circumscribed circle that goes through the three vertices. Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+あらゆる三角形において、3 つの頂点を通る外接円を描くことができます。 辺の長さが整数で、外接円の半径も整数であるすべての三角形について考えます。
-Let $S(n)$ be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed $n$.
+そのような三角形のうち、半径が $n$ を超えないすべての三角形の外接円の半径の和を $S(n)$ とします。
-$S(100) = 4\\,950$ and $S(1\\,200) = 1\\,653\\,605$.
+$S(100) = 4\\,950$, $S(1\\,200) = 1\\,653\\,605$ です。
-Find $S({10}^7)$.
+$S({10}^7)$ を求めなさい。
# --hints--
-`circumscribedCircles()` should return `727227472448913`.
+`circumscribedCircles()` は `727227472448913` を返す必要があります。
```js
assert.strictEqual(circumscribedCircles(), 727227472448913);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
index febbdf883b..773c99acaa 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff6
-title: 'Problem 374: Maximum Integer Partition Product'
+title: '問題 374: 整数分割の最大の積'
challengeType: 5
forumTopicId: 302036
dashedName: problem-374-maximum-integer-partition-product
@@ -8,27 +8,27 @@ dashedName: problem-374-maximum-integer-partition-product
# --description--
-An integer partition of a number $n$ is a way of writing $n$ as a sum of positive integers.
+数 $n$ の整数分割とは、$n$ を正の整数の和として表す方法です。
-Partitions that differ only in the order of their summands are considered the same. A partition of $n$ into distinct parts is a partition of $n$ in which every part occurs at most once.
+加数や被加数の順序のみが異なる分割は同じものとみなされます。 $n$ を相異なる部分に分割することは、いずれの部分も一度のみ現れるような形で $n$ を分割することです。
-The partitions of 5 into distinct parts are:
+5 を相異なる部分に分割すると、次のようになります。
-5, 4 + 1 and 3 + 2.
+5, 4 + 1, 3 + 2
-Let $f(n)$ be the maximum product of the parts of any such partition of $n$ into distinct parts and let $m(n)$ be the number of elements of any such partition of $n$ with that product.
+$n$ を相異なる部分に分割したとき、各部分の積が最大になるような分割における積を $f(n)$ とします。また、その積をもたらすような $n$ の分割の要素数を $m(n)$ とします。
-So $f(5) = 6$ and $m(5) = 2$.
+したがって、$f(5) = 6$, $m(5) = 2$ となります。
-For $n = 10$ the partition with the largest product is $10 = 2 + 3 + 5$, which gives $f(10) = 30$ and $m(10) = 3$. And their product, $f(10) \times m(10) = 30 \times 3 = 90$
+$n = 10$ の場合、積が最大となる分割は $10 = 2 + 3 + 5$ で、 $f(10) = 30$ と $m(10) = 3$ が導かれます。 そしてそれらの積は $f(10) \times m(10) = 30 \times 3 = 90$ となります。
-It can be verified that $\sum f(n) \times m(n)$ for $1 ≤ n ≤ 100 = 1\\,683\\,550\\,844\\,462$.
+$1 ≤ n ≤ 100 のとき、$\sum f(n) \times m(n)$ = 1\\,683\\,550\\,844\\,462$ となることを確認できます。
-Find $\sum f(n) \times m(n)$ for $1 ≤ n ≤ {10}^{14}$. Give your answer modulo $982\\,451\\,653$, the 50 millionth prime.
+$1 ≤ n ≤ {10}^{14}$ のとき、$\sum f(n) \times m(n)$ を求めなさい。 5000 万番目の素数 $982\\,451\\,653$ で割った余りで答えること。
# --hints--
-`maximumIntegerPartitionProduct()` should return `334420941`.
+`maximumIntegerPartitionProduct()` は `334420941` を返す必要があります。
```js
assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
index 067be0768a..ed619a531f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4e41000cf542c50fff5
-title: 'Problem 375: Minimum of subsequences'
+title: '問題 375: 最小の部分列'
challengeType: 5
forumTopicId: 302037
dashedName: problem-375-minimum-of-subsequences
@@ -8,19 +8,19 @@ dashedName: problem-375-minimum-of-subsequences
# --description--
-Let $S_n$ be an integer sequence produced with the following pseudo-random number generator:
+以下に述べる疑似乱数生成器で作成した整数の数列を $S_n$ とします。
$$\begin{align} S_0 & = 290\\,797 \\\\ S_{n + 1} & = {S_n}^2\bmod 50\\,515\\,093 \end{align}$$
-Let $A(i, j)$ be the minimum of the numbers $S_i, S_{i + 1}, \ldots, S_j$ for $i ≤ j$. Let $M(N) = \sum A(i, j)$ for $1 ≤ i ≤ j ≤ N$.
+$i ≤ j$ に対する数 $S_i, S_{i + 1}, \ldots, S_j$ のうちの最小数を $A(i, j)$ とします。 $1 ≤ i ≤ j ≤ N$ のとき、$M(N) = \sum A(i, j)$ とします。
-We can verify that $M(10) = 432\\,256\\,955$ and $M(10\\,000) = 3\\,264\\,567\\,774\\,119$.
+$M(10) = 432\\,256\\,955$, $M(10\\,000) = 3\\,264\\,567\\,774\\,774\\,119$ となることを確認できます。
-Find $M(2\\,000\\,000\\,000)$.
+$M(2\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`minimumOfSubsequences()` should return `7435327983715286000`.
+`minimumOfSubsequences()` は `7435327983715286000` を返す必要があります。
```js
assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
index c942812e53..58e4ee75bd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff7
-title: 'Problem 376: Nontransitive sets of dice'
+title: '問題 376: サイコロの非推移的集合'
challengeType: 5
forumTopicId: 302038
dashedName: problem-376-nontransitive-sets-of-dice
@@ -8,40 +8,40 @@ dashedName: problem-376-nontransitive-sets-of-dice
# --description--
-Consider the following set of dice with nonstandard pips:
+通常とは異なる目を持つ、以下のようなサイコロの集合について考えます。
-$$\begin{array}{} \text{Die A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{Die B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Die C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
+$$\begin{array}{} \text{サイコロ A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{サイコロ B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{サイコロ C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
-A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+ゲームでは、2 人のプレイヤーが交互にサイコロを選び、振ります。 最大の目を出したプレイヤーが勝者です。
-If the first player picks die $A$ and the second player picks die $B$ we get
+先手がサイコロ $A$ を選び、後手がサイコロ $B$ を選んだ場合
-$P(\text{second player wins}) = \frac{7}{12} > \frac{1}{2}$
+$P(\text{後手が勝つ確率}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die $B$ and the second player picks die $C$ we get
+先手がサイコロの $B$ を選び、後手がサイコロ $C$ を選んだ場合
-$P(\text{second player wins}) = \frac{7}{12} > \frac{1}{2}$
+$P(\text{後手が勝つ確率}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die $C$ and the second player picks die $A$ we get
+先手がサイコロの $C$ を選び、後手がサイコロ $A$ を選んだ場合
-$P(\text{second player wins}) = \frac{25}{36} > \frac{1}{2}$
+$P(\text{後手が勝つ確率}) = \frac{25}{36} > \frac{1}{2}$
-So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+このように、先手がどのサイコロを選んでも、後手が別のサイコロを選んで勝つことができる確率は 50% を超えます。 このような性質を持つサイコロの集合を、サイコロの非推移的集合と呼ぶことにします。
-We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:
+非推移的サイコロの集合がいくつ存在するのかを調べてみます。 以下の条件を仮定します。
-- There are three six-sided dice with each side having between 1 and $N$ pips, inclusive.
-- Dice with the same set of pips are equal, regardless of which side on the die the pips are located.
-- The same pip value may appear on multiple dice; if both players roll the same value neither player wins.
-- The sets of dice $\\{A, B, C\\}$, $\\{B, C, A\\}$ and $\\{C, A, B\\}$ are the same set.
+- 6 面体で、各面に 1 から $N$ までの目が書かれたサイコロが 3 つあります。
+- サイコロのどの面に目が書かれているかに関係なく、同じ目の集合を持つサイコロは同じものとみなされます。
+- 複数のサイコロで同じ目が出る場合があります。両方のプレイヤーが同じ目を出した場合、どちらも勝ちません。
+- サイコロの集合 $\\{A, B, C\\}$, $\\{B, C, A\\}$, $\\{C, A\\}$ は同じ集合です。
-For $N = 7$ we find there are 9780 such sets.
+$N = 7$ のとき、そのような集合は 9780 個存在します。
-How many are there for $N = 30$?
+$N = 30$ のとき、そのような集合はいくつ存在しますか。
# --hints--
-`nontransitiveSetsOfDice()` should return `973059630185670`.
+`nontransitiveSetsOfDice()` は `973059630185670` を返す必要があります。
```js
assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
index 66868c039a..5fa0c426e7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff8
-title: 'Problem 377: Sum of digits, experience 13'
+title: '問題 377: 各位の和 - 13 に注目'
challengeType: 5
forumTopicId: 302039
dashedName: problem-377-sum-of-digits-experience-13
@@ -8,19 +8,19 @@ dashedName: problem-377-sum-of-digits-experience-13
# --description--
-There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+いずれの桁も 0 ではなく各位の和が 5 に等しい正の整数は、次の 16 個です。
-5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111, 11111
-Their sum is 17891.
+これらの和は 17891 になります。
-Let $f(n)$ be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to $n$.
+いずれの桁も 0 ではなく各位の和が $n$ に等しい正の整数の和を、$f(n)$ とします。
-Find $\displaystyle\sum_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+$\displaystyle\sum_{i=1}^{17} f(13^i)$ を求めなさい。 下位 9 桁を答えること。
# --hints--
-`experience13()` should return `732385277`.
+`experience13()` は `732385277` を返す必要があります。
```js
assert.strictEqual(experience13(), 732385277);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
index 5fda48fc4d..f26715c5b9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f4e61000cf542c50fff9
-title: 'Problem 378: Triangle Triples'
+title: '問題 378: 三角数の三つ組数'
challengeType: 5
forumTopicId: 302040
dashedName: problem-378-triangle-triples
@@ -8,17 +8,17 @@ dashedName: problem-378-triangle-triples
# --description--
-Let $T(n)$ be the $n^{\text{th}}$ triangle number, so $T(n) = \frac{n(n + 1)}{2}$.
+$T(n)$ を $n$ 番目の三角数とします。すなわち、$T(n) = \frac{n(n + 1)}{2}$ です。
-Let $dT(n)$ be the number of divisors of $T(n)$. E.g.: $T(7) = 28$ and $dT(7) = 6$.
+$dT(n)$ を $T(n)$ の約数の個数とします。 例えば、$T(7) = 28$, $dT(7) = 6$ です。
-Let $Tr(n)$ be the number of triples ($i$, $j$, $k$) such that $1 ≤ i < j < k ≤ n$ and $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5\\,772$ and $Tr(1000) = 11\\,174\\,776$.
+$1 ≤ i < j < k ≤ n$, $dT(i) > dT(j) > dT(k)$ を満たす三つ組み数 ($i$, $j$, $k$) を $Tr(n)$ とします。 $Tr(20) = 14$, $Tr(100) = 5\\,772$, $Tr(1000) = 11\\,174\\,776$ となります。
-Find $Tr(60\\,000\\,000)$. Give the last 18 digits of your answer.
+$Tr(60\\,000\\,000)$ を求めなさい。 下位 18 桁を答えること。
# --hints--
-`triangleTriples()` should return `147534623725724700`.
+`triangleTriples()` は `147534623725724700` を返す必要があります。
```js
assert.strictEqual(triangleTriples(), 147534623725724700);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
index 9ae9c6d3c1..dceeba60f5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffa
-title: 'Problem 379: Least common multiple count'
+title: '問題 379: 最小公倍数に関する数え上げ'
challengeType: 5
forumTopicId: 302041
dashedName: problem-379-least-common-multiple-count
@@ -8,17 +8,17 @@ dashedName: problem-379-least-common-multiple-count
# --description--
-Let $f(n)$ be the number of couples ($x$, $y$) with $x$ and $y$ positive integers, $x ≤ y$ and the least common multiple of $x$ and $y$ equal to $n$.
+$x ≤ y$ を満たし、$x$ と $y$ の最小公倍数が $n$ に等しくなるような正の整数 $x$, $y$ の組 ($x$, $y$) の個数を $f(n)$ とします。
-Let $g$ be the summatory function of $f$, i.e.: $g(n) = \sum f(i)$ for $1 ≤ i ≤ n$.
+$1 ≤ i ≤ n$ について、$f$ の総和関数を $g$ とします。すなわち、$g(n) = \sum f(i)$ です。
-You are given that $g({10}^6) = 37\\,429\\,395$.
+ここで $g({10}^6) = 37\\,429\\,395$ が与えられます。
-Find $g({10}^{12})$.
+$g({10}^{12})$ を求めなさい。
# --hints--
-`leastCommonMultipleCount()` should return `132314136838185`.
+`leastCommonMultipleCount()` は `132314136838185` を返す必要があります。
```js
assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
index e5998fba22..a252e8e985 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffb
-title: 'Problem 380: Amazing Mazes!'
+title: '問題 380: 驚くべき迷路!'
challengeType: 5
forumTopicId: 302044
dashedName: problem-380-amazing-mazes
@@ -8,27 +8,27 @@ dashedName: problem-380-amazing-mazes
# --description--
-An $m×n$ maze is an $m×n$ rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+$m×n$ の長方形格子で作られた $m×n$ 迷路があります。格子の各マスの間に壁があり、左上のマスからスタートし、他のいずれのマスへ行くにも経路は 1 つしかありません。 下図は、9×12 迷路と15×20 迷路の例です。
-
-We can verify that $T(10) = 61\\,632$ and $T(1\\,000)\bmod 100\\,000\\,007 = 47\\,255\\,094$.
+$T(10) = 61\\,632$, $T(1\\,000)\bmod 100\\,007 = 47\\,255\\,094$ であることを確認できます。
-Find $T(1\\,000\\,000)\bmod 100\\,000\\,007$.
+$T(1\\,000\\,000)\bmod 100\\,000\\,007$ を求めなさい。
# --hints--
-`comfortableDistance()` should return `44855254`.
+`comfortableDistance()` は `44855254` を返す必要があります。
```js
assert.strictEqual(comfortableDistance(), 44855254);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
index 3c778cb1f7..041b939d51 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffec
-title: 'Problem 365: A huge binomial coefficient'
+title: '問題 365: 巨大な二項係数'
challengeType: 5
forumTopicId: 302026
dashedName: problem-365-a-huge-binomial-coefficient
@@ -8,15 +8,15 @@ dashedName: problem-365-a-huge-binomial-coefficient
# --description--
-The binomial coefficient $\displaystyle\binom{{10}^{18}}{{10}^9}$ is a number with more than 9 billion ($9 × {10}^9$) digits.
+二項係数 $\displaystyle\binom{{10}^{18}}{{10}^9}$ は 90 億 ($9 × {10}^9$) 桁を超える数です。
-Let $M(n, k, m)$ denote the binomial coefficient $\displaystyle\binom{n}{k}$ modulo $m$.
+$M(n, k, m)$ を、二項係数 $\displaystyle\binom{n}{k}$ mod $m$ とします。
-Calculate $\sum M({10}^{18}, {10}^9, p \times q \times r)$ for $1000 < p < q < r < 5000$ and $p$, $q$, $r$ prime.
+素数 $p$, $q$, $r$ が $1000 < p < q < r < 5000$ を満たすとき、$\sum M({10}^{18}, {10}^9, p \times q \times r)$ を求めなさい。
# --hints--
-`hugeBinomialCoefficient()` should return `162619462356610300`.
+`hugeBinomialCoefficient()` は `162619462356610300` を返す必要があります。
```js
assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
index 85cf7925c3..ec98d5dba4 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffed
-title: 'Problem 366: Stone Game III'
+title: '問題 366: 石取りゲーム (3)'
challengeType: 5
forumTopicId: 302027
dashedName: problem-366-stone-game-iii
@@ -8,41 +8,41 @@ dashedName: problem-366-stone-game-iii
# --description--
-Two players, Anton and Bernhard, are playing the following game.
+アントンとベルンハルトという名前の 2 人のプレイヤーが、次のようなゲームをしています。
-There is one pile of $n$ stones.
+$n$ 個の石を積み上げた山が 1 つあります。
-The first player may remove any positive number of stones, but not the whole pile.
+先手は、任意の正の整数分の石を取れますが、山全体を取ることはできません。
-Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+その後、各プレイヤーは、対戦相手が直前に取った数の 2 倍までの数の石を取ります。
-The player who removes the last stone wins.
+最後の石を取ったプレイヤーが勝者です。
-E.g. $n = 5$
+例: $n = 5$ とします。
-If the first player takes anything more than one stone the next player will be able to take all remaining stones.
+先手が 2 個以上の石を取った場合、後手は残りのすべての石を取ることができます。
-If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones.
+先手が石を 1 個取り 4 個残した場合、後手も石を 1 個取ると 3 個残ります。
-The first player cannot take all three because he may take at most $2 \times 1 = 2$ stones. So let's say he also takes one stone, leaving 2.
+先手は多くとも $2 \times 1 = 2$ 個の石しか取れないので、3 個すべてを取ることはできません。 したがって、また石を 1 個取ると仮定します。残りは 2 個になります。
-The second player can take the two remaining stones and wins.
+後手は、残っている 2 個の石を取れば勝つことができます。
-So 5 is a losing position for the first player.
+したがって、石が 5 個ある山は先手にとって敗北ポジション (必ず負ける状況) です。
-For some winning positions there is more than one possible move for the first player.
+いくつかの勝利ポジションでは、先手が取り得る手は複数あります。
-E.g. when $n = 17$ the first player can remove one or four stones.
+例: $n = 17$ の場合、先手は 1 個または 4 個の石を取ることができます。
-Let $M(n)$ be the maximum number of stones the first player can take from a winning position at his first turn and $M(n) = 0$ for any other position.
+先手が最初のターンで勝利ポジションから取れる石の最大数を $M(n)$ とし、他のすべてのポジションでは $M(n) = 0$ とします。
-$\sum M(n)$ for $n ≤ 100$ is 728.
+$n ≤ 100$ のとき、$\sum M(n)$ = 728 です。
-Find $\sum M(n)$ for $n ≤ {10}^{18}$. Give your answer modulo ${10}^8$.
+$n ≤ {10}^{18}$ のとき、$\sum M(n)$ を求めなさい。 mod ${10}^8$ で答えること。
# --hints--
-`stoneGameThree()` should return `88351299`.
+`stoneGameThree()` は `88351299` を返す必要があります。
```js
assert.strictEqual(stoneGameThree(), 88351299);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
index 2497cd85ed..5fa3d3b759 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
@@ -1,6 +1,6 @@
---
id: 5900f4db1000cf542c50ffee
-title: 'Problem 367: Bozo sort'
+title: '問題 367: ボゾソート'
challengeType: 5
forumTopicId: 302028
dashedName: problem-367-bozo-sort
@@ -8,29 +8,29 @@ dashedName: problem-367-bozo-sort
# --description--
-Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+ボゾソートと聞いて、やや効率の低いボゴソートと混同しないでください。ボゾソートは、入力数列がソートされているかをチェックし、ソートされていない場合は無作為に 2 つの要素を交換します。 最終的に数列がソートされるまで、これが繰り返されます。
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all $4!$ input sequences is $24.75$.
+最初の 4 つの自然数が含まれるすべての順列を入力として考えた場合、交換回数の期待値は、$4!$ 個すべての入力数列で平均 $24.75$ になります。
-The already sorted sequence takes 0 steps.
+ソート済みの数列の場合、交換回数は 0 回です。
-In this problem we consider the following variant on bozo sort.
+この問題では、次のような変種のボゾソートについて考えます。
-If the sequence is not in order we pick three elements at random and shuffle these three elements randomly.
+数列がソートされていない場合は、無作為に 3 つの要素を選択し、これら 3 つの要素を無作為に入れ替えます。
-All $3! = 6$ permutations of those three elements are equally likely.
+これら 3 つの要素の $3! = 6$ 個の順列はすべて等確率で現れます。
-The already sorted sequence will take 0 steps.
+ソート済みの数列の場合、交換回数は 0 回です。
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all $4!$ input sequences is $27.5$.
+最初の 4 つの自然数が含まれるすべての順列を入力として考えた場合、交換回数の期待値は、$4!$ 個すべての入力数列で平均 $27.5$ になります。
-Consider as input sequences the permutations of the first 11 natural numbers.
+入力数列として、最初の 11 個の自然数の順列を考えます。
-Averaged over all $11!$ input sequences, what is the expected number of shuffles this sorting algorithm will perform? Give your answer rounded to the nearest integer.
+$11!$ 個すべての入力数列で平均すると、このソートアルゴリズムによる交換回数の期待値はいくつですか? 最も近い整数に四捨五入して答えなさい。
# --hints--
-`bozoSort()` should return `48271207`.
+`bozoSort()` は `48271207` を返す必要があります。
```js
assert.strictEqual(bozoSort(), 48271207);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
index fd8b6c8daf..906bced434 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
@@ -1,6 +1,6 @@
---
id: 5900f4dd1000cf542c50ffef
-title: 'Problem 368: A Kempner-like series'
+title: '問題 368: ケンプナーのような級数'
challengeType: 5
forumTopicId: 302029
dashedName: problem-368-a-kempner-like-series
@@ -8,23 +8,23 @@ dashedName: problem-368-a-kempner-like-series
# --description--
-The harmonic series $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ is well known to be divergent.
+調和級数 $1+\dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ が発散することはよく知られています。
-If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+しかし、分母に 9 が含まれる項をすべてこの級数から取り除くと、級数は約 22.9206766193 と驚くほど収束します。 この改良版調和級数はケンプナー級数と呼ばれます。
-Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted.
+次に、同じ数字が 3 桁以上連続して分母に含まれる項をすべて調和級数から省略することで得られる、別の改良版調和級数について考えます。 調和級数の最初の 1200 項のうち、取り除かれるのはわずか 20 項であることを確認できます。
-These 20 omitted terms are:
+削除される 20 項は次のとおりです。
$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\ \dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
-This series converges as well.
+この級数も同様に収束します。
-Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+級数の収束値を求めなさい。 回答は、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`kempnerLikeSeries()` should return `253.6135092068`.
+`kempnerLikeSeries()` は `253.6135092068` を返す必要があります。
```js
assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md
index ce8f9a6e5a..de2e11b65a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-369-badugi.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff0
-title: 'Problem 369: Badugi'
+title: '問題 369: バドゥーギ'
challengeType: 5
forumTopicId: 302030
dashedName: problem-369-badugi
@@ -8,15 +8,15 @@ dashedName: problem-369-badugi
# --description--
-In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+標準的な 52 枚組のトランプで、ペアがなく、同じスート (マーク) の 2 枚のカードもない 4 枚のカードの組は、バドゥーギと呼ばれます。
-Let $f(n)$ be the number of ways to choose $n$ cards with a 4 card subset that is a Badugi. For example, there are $2\\,598\\,960$ ways to choose five cards from a standard 52 card deck, of which $514\\,800$ contain a 4 card subset that is a Badugi, so $f(5) = 514800$.
+バドゥーギである 4 枚のカードからなる部分集合を持つ $n$ 枚のカードを選ぶ方法の数を、$f(n)$ とします。 例えば、標準的な 52 枚組のトランプから 5 枚のカードを選ぶ法は $2\\,598\\,960$ 通りあり、そのうち $514\\,800$ 通りが、バドゥーギとなる 4 枚のカードからなる部分集合を含んでいるので、$f(5) = 514800$ となります。
-Find $\sum f(n)$ for $4 ≤ n ≤ 13$.
+$4 ≤ n ≤ 13$ のとき、$\sum f(n)$ を求めなさい。
# --hints--
-`badugi()` should return `862400558448`.
+`badugi()` は `862400558448` を返す必要があります。
```js
assert.strictEqual(badugi(), 862400558448);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
index c26ef2220c..86bac84380 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff1
-title: 'Problem 370: Geometric triangles'
+title: '問題 370: 幾何三角形'
challengeType: 5
forumTopicId: 302032
dashedName: problem-370-geometric-triangles
@@ -8,17 +8,17 @@ dashedName: problem-370-geometric-triangles
# --description--
-Let us define a geometric triangle as an integer sided triangle with sides $a ≤ b ≤ c$ so that its sides form a geometric progression, i.e. $b^2 = a \times c$.
+辺 $a ≤ b ≤ c$ を持つ整数辺三角形で、その辺が幾何数列を形成するもの、すなわち $b^2 = a \times c$ であるものを、幾何三角形と定義します。
-An example of such a geometric triangle is the triangle with sides $a = 144$, $b = 156$ and $c = 169$.
+このような幾何三角形の例は、長さ $a = 144$, $b = 156$, $c = 169$ の 3 辺を持つ三角形です。
-There are $861\\,805$ geometric triangles with $\text{perimeter} ≤ {10}^6$.
+$\text{周長} ≤ {10}^6$ を満たす幾何三角形は $861\\,805$ 個あります。
-How many geometric triangles exist with $\text{perimeter} ≤ 2.5 \times {10}^{13}$?
+$\text{周長} ≤ 2.5 \times {10}^{13}$ を満たす幾何三角形はいくつありますか。
# --hints--
-`geometricTriangles()` should return `41791929448408`.
+`geometricTriangles()` は `41791929448408` を返す必要があります。
```js
assert.strictEqual(geometricTriangles(), 41791929448408);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
index 63d7295fe2..3979cf0117 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
@@ -1,6 +1,6 @@
---
id: 5900f4e01000cf542c50fff2
-title: 'Problem 371: Licence plates'
+title: '問題 371: ナンバープレート'
challengeType: 5
forumTopicId: 302033
dashedName: problem-371-licence-plates
@@ -8,21 +8,21 @@ dashedName: problem-371-licence-plates
# --description--
-Oregon licence plates consist of three letters followed by a three digit number (each digit can be from [0...9]).
+オレゴン州のナンバープレートは、3 つの文字の後に 3 桁の数字が続きます (各桁の数字は [0...9] のいずれか)。
-While driving to work Seth plays the following game:
+車での通勤中に、セスは次のようなゲームをします。
-Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+移動中に見た 2 枚のナンバープレートの数字の合計が 1000 になったら勝ちです。
-E.g. `MIC-012` and `HAN-988` is a win and `RYU-500` and `SET-500` too. (as long as he sees them in the same trip).
+例: `MIC-012` と `HAN-988` の組み合わせは勝ちで、`RYU-500` と `SET-500` でも勝ちになります (1 回の移動中に見たものであれば)。
-Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+勝つために見る必要のあるナンバープレートの枚数の期待値を求めなさい。 回答は、四捨五入して小数第 8 位まで示すこと。
-**Note:** We assume that each licence plate seen is equally likely to have any three digit number on it.
+**注:** 見たナンバープレートのいずれでも、3 桁の数字が記されている確率は同じと仮定します。
# --hints--
-`licensePlates()` should return `40.66368097`.
+`licensePlates()` は `40.66368097` を返す必要があります。
```js
assert.strictEqual(licensePlates(), 40.66368097);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
index 9f39453ab4..2a7345e687 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff3
-title: 'Problem 372: Pencils of rays'
+title: '問題 372: 光線束'
challengeType: 5
forumTopicId: 302034
dashedName: problem-372-pencils-of-rays
@@ -8,17 +8,17 @@ dashedName: problem-372-pencils-of-rays
# --description--
-Let $R(M, N)$ be the number of lattice points ($x$, $y$) which satisfy $M \lt x \le N$, $M \lt y \le N$ and $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ is odd.
+$M \lt x \le N$, $M \lt y \le N$ を満たし $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ が奇数になるような格子点 ($x$, $y$) の数を、$R(M, N)$ とします。
-We can verify that $R(0, 100) = 3\\,019$ and $R(100, 10\\,000) = 29\\,750\\,422$.
+$R(0, 100) = 3\\,019$, $R(100, 10\\,000) = 29\\,750\\,422$ であることを確認できます。
-Find $R(2 \times {10}^6, {10}^9)$.
+$R(2 \times {10}^6, {10}^9)$ を求めなさい。
-**Note:** $\lfloor x\rfloor$ represents the floor function.
+**注:** $\lfloor x\rfloor$ は床関数を表します。
# --hints--
-`pencilsOfRays()` should return `301450082318807040`.
+`pencilsOfRays()` は `301450082318807040` を返す必要があります。
```js
assert.strictEqual(pencilsOfRays(), 301450082318807040);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
index c50df93cd8..d778b11e6f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff4
-title: 'Problem 373: Circumscribed Circles'
+title: '問題 373: 外接円'
challengeType: 5
forumTopicId: 302035
dashedName: problem-373-circumscribed-circles
@@ -8,17 +8,17 @@ dashedName: problem-373-circumscribed-circles
# --description--
-Every triangle has a circumscribed circle that goes through the three vertices. Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+あらゆる三角形において、3 つの頂点を通る外接円を描くことができます。 辺の長さが整数で、外接円の半径も整数であるすべての三角形について考えます。
-Let $S(n)$ be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed $n$.
+そのような三角形のうち、半径が $n$ を超えないすべての三角形の外接円の半径の和を $S(n)$ とします。
-$S(100) = 4\\,950$ and $S(1\\,200) = 1\\,653\\,605$.
+$S(100) = 4\\,950$, $S(1\\,200) = 1\\,653\\,605$ です。
-Find $S({10}^7)$.
+$S({10}^7)$ を求めなさい。
# --hints--
-`circumscribedCircles()` should return `727227472448913`.
+`circumscribedCircles()` は `727227472448913` を返す必要があります。
```js
assert.strictEqual(circumscribedCircles(), 727227472448913);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
index febbdf883b..773c99acaa 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff6
-title: 'Problem 374: Maximum Integer Partition Product'
+title: '問題 374: 整数分割の最大の積'
challengeType: 5
forumTopicId: 302036
dashedName: problem-374-maximum-integer-partition-product
@@ -8,27 +8,27 @@ dashedName: problem-374-maximum-integer-partition-product
# --description--
-An integer partition of a number $n$ is a way of writing $n$ as a sum of positive integers.
+数 $n$ の整数分割とは、$n$ を正の整数の和として表す方法です。
-Partitions that differ only in the order of their summands are considered the same. A partition of $n$ into distinct parts is a partition of $n$ in which every part occurs at most once.
+加数や被加数の順序のみが異なる分割は同じものとみなされます。 $n$ を相異なる部分に分割することは、いずれの部分も一度のみ現れるような形で $n$ を分割することです。
-The partitions of 5 into distinct parts are:
+5 を相異なる部分に分割すると、次のようになります。
-5, 4 + 1 and 3 + 2.
+5, 4 + 1, 3 + 2
-Let $f(n)$ be the maximum product of the parts of any such partition of $n$ into distinct parts and let $m(n)$ be the number of elements of any such partition of $n$ with that product.
+$n$ を相異なる部分に分割したとき、各部分の積が最大になるような分割における積を $f(n)$ とします。また、その積をもたらすような $n$ の分割の要素数を $m(n)$ とします。
-So $f(5) = 6$ and $m(5) = 2$.
+したがって、$f(5) = 6$, $m(5) = 2$ となります。
-For $n = 10$ the partition with the largest product is $10 = 2 + 3 + 5$, which gives $f(10) = 30$ and $m(10) = 3$. And their product, $f(10) \times m(10) = 30 \times 3 = 90$
+$n = 10$ の場合、積が最大となる分割は $10 = 2 + 3 + 5$ で、 $f(10) = 30$ と $m(10) = 3$ が導かれます。 そしてそれらの積は $f(10) \times m(10) = 30 \times 3 = 90$ となります。
-It can be verified that $\sum f(n) \times m(n)$ for $1 ≤ n ≤ 100 = 1\\,683\\,550\\,844\\,462$.
+$1 ≤ n ≤ 100 のとき、$\sum f(n) \times m(n)$ = 1\\,683\\,550\\,844\\,462$ となることを確認できます。
-Find $\sum f(n) \times m(n)$ for $1 ≤ n ≤ {10}^{14}$. Give your answer modulo $982\\,451\\,653$, the 50 millionth prime.
+$1 ≤ n ≤ {10}^{14}$ のとき、$\sum f(n) \times m(n)$ を求めなさい。 5000 万番目の素数 $982\\,451\\,653$ で割った余りで答えること。
# --hints--
-`maximumIntegerPartitionProduct()` should return `334420941`.
+`maximumIntegerPartitionProduct()` は `334420941` を返す必要があります。
```js
assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
index 067be0768a..ed619a531f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4e41000cf542c50fff5
-title: 'Problem 375: Minimum of subsequences'
+title: '問題 375: 最小の部分列'
challengeType: 5
forumTopicId: 302037
dashedName: problem-375-minimum-of-subsequences
@@ -8,19 +8,19 @@ dashedName: problem-375-minimum-of-subsequences
# --description--
-Let $S_n$ be an integer sequence produced with the following pseudo-random number generator:
+以下に述べる疑似乱数生成器で作成した整数の数列を $S_n$ とします。
$$\begin{align} S_0 & = 290\\,797 \\\\ S_{n + 1} & = {S_n}^2\bmod 50\\,515\\,093 \end{align}$$
-Let $A(i, j)$ be the minimum of the numbers $S_i, S_{i + 1}, \ldots, S_j$ for $i ≤ j$. Let $M(N) = \sum A(i, j)$ for $1 ≤ i ≤ j ≤ N$.
+$i ≤ j$ に対する数 $S_i, S_{i + 1}, \ldots, S_j$ のうちの最小数を $A(i, j)$ とします。 $1 ≤ i ≤ j ≤ N$ のとき、$M(N) = \sum A(i, j)$ とします。
-We can verify that $M(10) = 432\\,256\\,955$ and $M(10\\,000) = 3\\,264\\,567\\,774\\,119$.
+$M(10) = 432\\,256\\,955$, $M(10\\,000) = 3\\,264\\,567\\,774\\,774\\,119$ となることを確認できます。
-Find $M(2\\,000\\,000\\,000)$.
+$M(2\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`minimumOfSubsequences()` should return `7435327983715286000`.
+`minimumOfSubsequences()` は `7435327983715286000` を返す必要があります。
```js
assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
index c942812e53..58e4ee75bd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff7
-title: 'Problem 376: Nontransitive sets of dice'
+title: '問題 376: サイコロの非推移的集合'
challengeType: 5
forumTopicId: 302038
dashedName: problem-376-nontransitive-sets-of-dice
@@ -8,40 +8,40 @@ dashedName: problem-376-nontransitive-sets-of-dice
# --description--
-Consider the following set of dice with nonstandard pips:
+通常とは異なる目を持つ、以下のようなサイコロの集合について考えます。
-$$\begin{array}{} \text{Die A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{Die B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Die C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
+$$\begin{array}{} \text{サイコロ A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{サイコロ B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{サイコロ C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
-A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+ゲームでは、2 人のプレイヤーが交互にサイコロを選び、振ります。 最大の目を出したプレイヤーが勝者です。
-If the first player picks die $A$ and the second player picks die $B$ we get
+先手がサイコロ $A$ を選び、後手がサイコロ $B$ を選んだ場合
-$P(\text{second player wins}) = \frac{7}{12} > \frac{1}{2}$
+$P(\text{後手が勝つ確率}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die $B$ and the second player picks die $C$ we get
+先手がサイコロの $B$ を選び、後手がサイコロ $C$ を選んだ場合
-$P(\text{second player wins}) = \frac{7}{12} > \frac{1}{2}$
+$P(\text{後手が勝つ確率}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die $C$ and the second player picks die $A$ we get
+先手がサイコロの $C$ を選び、後手がサイコロ $A$ を選んだ場合
-$P(\text{second player wins}) = \frac{25}{36} > \frac{1}{2}$
+$P(\text{後手が勝つ確率}) = \frac{25}{36} > \frac{1}{2}$
-So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+このように、先手がどのサイコロを選んでも、後手が別のサイコロを選んで勝つことができる確率は 50% を超えます。 このような性質を持つサイコロの集合を、サイコロの非推移的集合と呼ぶことにします。
-We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:
+非推移的サイコロの集合がいくつ存在するのかを調べてみます。 以下の条件を仮定します。
-- There are three six-sided dice with each side having between 1 and $N$ pips, inclusive.
-- Dice with the same set of pips are equal, regardless of which side on the die the pips are located.
-- The same pip value may appear on multiple dice; if both players roll the same value neither player wins.
-- The sets of dice $\\{A, B, C\\}$, $\\{B, C, A\\}$ and $\\{C, A, B\\}$ are the same set.
+- 6 面体で、各面に 1 から $N$ までの目が書かれたサイコロが 3 つあります。
+- サイコロのどの面に目が書かれているかに関係なく、同じ目の集合を持つサイコロは同じものとみなされます。
+- 複数のサイコロで同じ目が出る場合があります。両方のプレイヤーが同じ目を出した場合、どちらも勝ちません。
+- サイコロの集合 $\\{A, B, C\\}$, $\\{B, C, A\\}$, $\\{C, A\\}$ は同じ集合です。
-For $N = 7$ we find there are 9780 such sets.
+$N = 7$ のとき、そのような集合は 9780 個存在します。
-How many are there for $N = 30$?
+$N = 30$ のとき、そのような集合はいくつ存在しますか。
# --hints--
-`nontransitiveSetsOfDice()` should return `973059630185670`.
+`nontransitiveSetsOfDice()` は `973059630185670` を返す必要があります。
```js
assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
index 66868c039a..5fa0c426e7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff8
-title: 'Problem 377: Sum of digits, experience 13'
+title: '問題 377: 各位の和 - 13 に注目'
challengeType: 5
forumTopicId: 302039
dashedName: problem-377-sum-of-digits-experience-13
@@ -8,19 +8,19 @@ dashedName: problem-377-sum-of-digits-experience-13
# --description--
-There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+いずれの桁も 0 ではなく各位の和が 5 に等しい正の整数は、次の 16 個です。
-5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111, 11111
-Their sum is 17891.
+これらの和は 17891 になります。
-Let $f(n)$ be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to $n$.
+いずれの桁も 0 ではなく各位の和が $n$ に等しい正の整数の和を、$f(n)$ とします。
-Find $\displaystyle\sum_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+$\displaystyle\sum_{i=1}^{17} f(13^i)$ を求めなさい。 下位 9 桁を答えること。
# --hints--
-`experience13()` should return `732385277`.
+`experience13()` は `732385277` を返す必要があります。
```js
assert.strictEqual(experience13(), 732385277);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
index 5fda48fc4d..f26715c5b9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f4e61000cf542c50fff9
-title: 'Problem 378: Triangle Triples'
+title: '問題 378: 三角数の三つ組数'
challengeType: 5
forumTopicId: 302040
dashedName: problem-378-triangle-triples
@@ -8,17 +8,17 @@ dashedName: problem-378-triangle-triples
# --description--
-Let $T(n)$ be the $n^{\text{th}}$ triangle number, so $T(n) = \frac{n(n + 1)}{2}$.
+$T(n)$ を $n$ 番目の三角数とします。すなわち、$T(n) = \frac{n(n + 1)}{2}$ です。
-Let $dT(n)$ be the number of divisors of $T(n)$. E.g.: $T(7) = 28$ and $dT(7) = 6$.
+$dT(n)$ を $T(n)$ の約数の個数とします。 例えば、$T(7) = 28$, $dT(7) = 6$ です。
-Let $Tr(n)$ be the number of triples ($i$, $j$, $k$) such that $1 ≤ i < j < k ≤ n$ and $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5\\,772$ and $Tr(1000) = 11\\,174\\,776$.
+$1 ≤ i < j < k ≤ n$, $dT(i) > dT(j) > dT(k)$ を満たす三つ組み数 ($i$, $j$, $k$) を $Tr(n)$ とします。 $Tr(20) = 14$, $Tr(100) = 5\\,772$, $Tr(1000) = 11\\,174\\,776$ となります。
-Find $Tr(60\\,000\\,000)$. Give the last 18 digits of your answer.
+$Tr(60\\,000\\,000)$ を求めなさい。 下位 18 桁を答えること。
# --hints--
-`triangleTriples()` should return `147534623725724700`.
+`triangleTriples()` は `147534623725724700` を返す必要があります。
```js
assert.strictEqual(triangleTriples(), 147534623725724700);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
index 9ae9c6d3c1..dceeba60f5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffa
-title: 'Problem 379: Least common multiple count'
+title: '問題 379: 最小公倍数に関する数え上げ'
challengeType: 5
forumTopicId: 302041
dashedName: problem-379-least-common-multiple-count
@@ -8,17 +8,17 @@ dashedName: problem-379-least-common-multiple-count
# --description--
-Let $f(n)$ be the number of couples ($x$, $y$) with $x$ and $y$ positive integers, $x ≤ y$ and the least common multiple of $x$ and $y$ equal to $n$.
+$x ≤ y$ を満たし、$x$ と $y$ の最小公倍数が $n$ に等しくなるような正の整数 $x$, $y$ の組 ($x$, $y$) の個数を $f(n)$ とします。
-Let $g$ be the summatory function of $f$, i.e.: $g(n) = \sum f(i)$ for $1 ≤ i ≤ n$.
+$1 ≤ i ≤ n$ について、$f$ の総和関数を $g$ とします。すなわち、$g(n) = \sum f(i)$ です。
-You are given that $g({10}^6) = 37\\,429\\,395$.
+ここで $g({10}^6) = 37\\,429\\,395$ が与えられます。
-Find $g({10}^{12})$.
+$g({10}^{12})$ を求めなさい。
# --hints--
-`leastCommonMultipleCount()` should return `132314136838185`.
+`leastCommonMultipleCount()` は `132314136838185` を返す必要があります。
```js
assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
index e5998fba22..a252e8e985 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffb
-title: 'Problem 380: Amazing Mazes!'
+title: '問題 380: 驚くべき迷路!'
challengeType: 5
forumTopicId: 302044
dashedName: problem-380-amazing-mazes
@@ -8,27 +8,27 @@ dashedName: problem-380-amazing-mazes
# --description--
-An $m×n$ maze is an $m×n$ rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+$m×n$ の長方形格子で作られた $m×n$ 迷路があります。格子の各マスの間に壁があり、左上のマスからスタートし、他のいずれのマスへ行くにも経路は 1 つしかありません。 下図は、9×12 迷路と15×20 迷路の例です。
-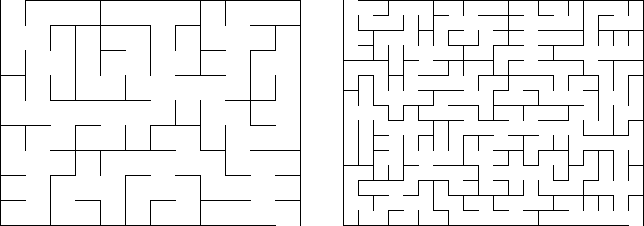 +
+ -Let $C(m, n)$ be the number of distinct $m×n$ mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+相異なる $m×n$ 迷路の数を $C(m, n)$ とします。 別の迷路の回転や反転によって形成される迷路は、相異なる迷路とみなされます。
-It can be verified that $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, and $C(9, 12) = 2.5720\mathrm{e}\\,46$ (in scientific notation rounded to 5 significant digits).
+$C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, $C(9, 12) = 2.5720\mathrm{e}\\,46$ (有効数字 5 桁に四捨五入された科学的記数法) であることを確認できます。
-Find $C(100, 500)$ and write your answer as a string in scientific notation rounded to 5 significant digits.
+$C(100, 500)$ を求め、有効数字 5 桁に四捨五入された科学的記数法の文字列で答えなさい。
-When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be the string `1.2346e12`.
+回答の仮数部と指数部を小文字 e で区切ること。 例: 求めた値が1234567891011 の場合、回答は文字列 `1.2346e12` になります。
# --hints--
-`amazingMazes()` should return a string.
+`amazingMazes()` は文字列を返す必要があります。
```js
assert(typeof amazingMazes() === 'string');
```
-`amazingMazes()` should return the string `6.3202e25093`.
+`amazingMazes()` は文字列 `6.3202e25093` を返す必要があります。
```js
assert.strictEqual(amazingMazes(), '6.3202e25093');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
index 1c5cb8b322..89f38a7735 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
@@ -1,6 +1,6 @@
---
id: 5900f4ea1000cf542c50fffc
-title: 'Problem 381: (prime-k) factorial'
+title: '問題 381: (素数-k) 階乗'
challengeType: 5
forumTopicId: 302045
dashedName: problem-381-prime-k-factorial
@@ -8,21 +8,21 @@ dashedName: problem-381-prime-k-factorial
# --description--
-For a prime $p$ let $S(p) = (\sum (p - k)!)\bmod (p)$ for $1 ≤ k ≤ 5$.
+素数 $p$ について、$1 ≤ k ≤ 5$ のとき $S(p) = (\sum (p - k)!)\bmod (p)$ が成り立つとします。
-For example, if $p = 7$,
+例えば、$p = 7$ のとき、次の式が成り立ちます。
$$(7 - 1)! + (7 - 2)! + (7 - 3)! + (7 - 4)! + (7 - 5)! = 6! + 5! + 4! + 3! + 2! = 720 + 120 + 24 + 6 + 2 = 872$$
-As $872\bmod (7) = 4$, $S(7) = 4$.
+$872\bmod (7) = 4$ なので $S(7) = 4$ となります。
-It can be verified that $\sum S(p) = 480$ for $5 ≤ p < 100$.
+$5 ≤ p < 100$ のとき、$\sum S(p) = 480$ となることを確認できます。
-Find $\sum S(p)$ for $5 ≤ p < {10}^8$.
+$5 ≤ p < {10}^8$ のとき、$\sum S(p)$ を求めなさい。
# --hints--
-`primeKFactorial()` should return `139602943319822`.
+`primeKFactorial()` は`139602943319822` を返す必要があります。
```js
assert.strictEqual(primeKFactorial(), 139602943319822);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
index 9b829c6f05..be752e2ebc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
@@ -1,6 +1,6 @@
---
id: 5900f4eb1000cf542c50fffd
-title: 'Problem 382: Generating polygons'
+title: '問題 382: 多角形を生成する'
challengeType: 5
forumTopicId: 302046
dashedName: problem-382-generating-polygons
@@ -8,38 +8,38 @@ dashedName: problem-382-generating-polygons
# --description--
-A polygon is a flat shape consisting of straight line segments that are joined to form a closed chain or circuit. A polygon consists of at least three sides and does not self-intersect.
+多角形とは、閉路を形成するように結合された直線分からなる平面図形です。 多角形は少なくとも 3 本の辺で構成され、それ自体と交差することはありません。
-A set $S$ of positive numbers is said to generate a polygon $P$ if:
+以下の条件をすべて満たす正の数 $S$ の集合が多角形 $P$ を生成するものとします。
-- no two sides of $P$ are the same length,
-- the length of every side of $P$ is in $S$, and
-- $S$ contains no other value.
+- $P$ のいずれの 2 辺も長さが異なる
+- $P$ の各辺の長さが $S$ に含まれる
+- $S$ にはそれ以外の値が含まれない
-For example:
+以下に例を示します。
-The set {3, 4, 5} generates a polygon with sides 3, 4, and 5 (a triangle).
+集合 {3, 4, 5} は 辺長が 3, 4, 5 の多角形 (三角形) を生成します。
-The set {6, 9, 11, 24} generates a polygon with sides 6, 9, 11, and 24 (a quadrilateral).
+集合 {6, 9, 11, 24} は辺長が 6, 9, 11, 24 の多角形 (四角形) を生成します。
-The sets {1, 2, 3} and {2, 3, 4, 9} do not generate any polygon at all.
+集合 {1, 2, 3} と集合 {2, 3, 4, 9} はいかなる多角形も生成しません。
-Consider the sequence $s$, defined as follows:
+次のように定義される数列 $s$ を考えます。
- $s_1 = 1$, $s_2 = 2$, $s_3 = 3$
-- $s_n = s_{n - 1} + s_{n - 3}$ for $n > 3$.
+- $n > 3$ のとき、$s_n = s_{n - 1} + s_{n - 3}$
-Let $U_n$ be the set $\\{s_1, s_2, \ldots, s_n\\}$. For example, $U_{10} = \\{1, 2, 3, 4, 6, 9, 13, 19, 28, 41\\}$.
+$U_n$ を集合 $\\{s_1, s_2, \ldots, s_n\\}$ と定義します。 例えば、$U_{10} = \\{1, 2, 3, 4, 6, 9, 13, 19, 28, 41\\}$ です。
-Let $f(n)$ be the number of subsets of $U_n$ which generate at least one polygon.
+$U_n$ の部分集合のうち、少なくとも 1 つの多角形を生成する部分集合の数を $f(n)$ とします。
-For example, $f(5) = 7$, $f(10) = 501$ and $f(25) = 18\\,635\\,853$.
+例えば、$f(5) = 7$, $f(10) = 501$, $f(25) = 18\\,635\\,853$ です。
-Find the last 9 digits of $f({10}^{18})$.
+$f({10}^{18})$ の下位 9 桁を求めなさい。
# --hints--
-`generatingPolygons()` should return `697003956`.
+`generatingPolygons()` は `697003956` を返す必要があります。
```js
assert.strictEqual(generatingPolygons(), 697003956);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
index e626c7eb7a..db8b411fdd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
@@ -1,6 +1,6 @@
---
id: 5900f4ed1000cf542c50ffff
-title: 'Problem 383: Divisibility comparison between factorials'
+title: '問題 383: 階乗間の被整除性比較'
challengeType: 5
forumTopicId: 302047
dashedName: problem-383-divisibility-comparison-between-factorials
@@ -8,19 +8,19 @@ dashedName: problem-383-divisibility-comparison-between-factorials
# --description--
-Let $f_5(n)$ be the largest integer $x$ for which $5^x$ divides $n$.
+$5^x$ が $n$ を割り切るような最大の整数 $x$ を $f_5(n)$ とします。
-For example, $f_5(625\\,000) = 7$.
+例えば、$f_5(625\\,000) = 7$ となります。
-Let $T_5(n)$ be the number of integers $i$ which satisfy $f_5((2 \times i - 1)!) < 2 \times f_5(i!)$ and $1 ≤ i ≤ n$.
+次の条件を満たす整数 $i$ の個数を $T_5(n)$ とします: $f_5((2 \times i - 1)!) < 2 \times f_5(i!)$ かつ $1 ≤ i ≤ n$
-It can be verified that $T_5({10}^3) = 68$ and $T_5({10}^9) = 2\\,408\\,210$.
+$T_5({10}^3) = 68$, $T_5({10}^9) = 2\\,408\\,210$ であることを確認できます。
-Find $T_5({10}^{18})$.
+$T_5({10}^{18})$ を求めなさい。
# --hints--
-`factorialDivisibilityComparison()` should return `22173624649806`.
+`factorialDivisibilityComparison()` は `22173624649806` を返す必要があります。
```js
assert.strictEqual(factorialDivisibilityComparison(), 22173624649806);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
index ebe171e2ef..d7f8a24433 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4ed1000cf542c50fffe
-title: 'Problem 384: Rudin-Shapiro sequence'
+title: '問題 384: ルーディン-シャピロ数列'
challengeType: 5
forumTopicId: 302048
dashedName: problem-384-rudin-shapiro-sequence
@@ -8,35 +8,35 @@ dashedName: problem-384-rudin-shapiro-sequence
# --description--
-Define the sequence $a(n)$ as the number of adjacent pairs of ones in the binary expansion of $n$ (possibly overlapping).
+$n$ の 2 進展開における隣接する 1 の対の個数を数列 $a(n)$ とします (1 の対は重複している場合があります)。
-E.g.: $a(5) = a({101}_2) = 0$, $a(6) = a({110}_2) = 1$, $a(7) = a({111}_2) = 2$
+例: $a(5) = a({101}_2) = 0$, $a(6) = a({110}_2) = 1$, $a(7) = a({111}_2) = 2$
-Define the sequence $b(n) = {(-1)}^{a(n)}$. This sequence is called the Rudin-Shapiro sequence.
+続いて、数列 $b(n) = {(-1)}^{a(n)}$ を定義します。 この数列はルーディン-シャピロ数列と呼ばれます。
-Also consider the summatory sequence of $b(n)$: $s(n) = \displaystyle\sum_{i = 0}^{n} b(i)$.
+$b(n)$ の総和数列 $s(n) = \displaystyle\sum_{i = 0}^{n} b(i)$ も考えます。
-The first couple of values of these sequences are:
+これらの数列の最初のいくつかの組み合わせは次のようになります。
$$\begin{array}{lr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\\\ a(n) & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 2 \\\\ b(n) & 1 & 1 & 1 & -1 & 1 & 1 & -1 & 1 \\\\ s(n) & 1 & 2 & 3 & 2 & 3 & 4 & 3 & 4 \end{array}$$
-The sequence $s(n)$ has the remarkable property that all elements are positive and every positive integer $k$ occurs exactly $k$ times.
+数列 $s(n)$ は驚くべき性質を持っています。すべての要素が正の数であり、正の整数 $k$ がいずれもちょうど $k$ 回現れるという性質です。
-Define $g(t, c)$, with $1 ≤ c ≤ t$, as the index in $s(n)$ for which $t$ occurs for the $c$'th time in $s(n)$.
+$s(n)$ の中で $t$ が $c$ 回目に現れたときの $s(n)$ 内でのインデックス (位置) を、$g(t, c)$ と定義します。ここで、$1 ≤ c ≤ t$ です。
-E.g.: $g(3, 3) = 6$, $g(4, 2) = 7$ and $g(54321, 12345) = 1\\,220\\,847\\,710$.
+例: $g(3, 3) = 6$, $g(4, 2) = 7$, $g(54321, 12345) = 1\\,220\\,847\\,710$
-Let $F(n)$ be the fibonacci sequence defined by:
+$F(n)$ を、以下の式で定義されるフィボナッチ数列とします。
-$$\begin{align} & F(0) = F(1) = 1 \text{ and} \\\\ & F(n) = F(n - 1) + F(n - 2) \text{ for } n > 1. \end{align}$$
+$$\begin{align} & F(0) = F(1) = 1 \text{かつ} \\\\ & n > 1 \text{のとき} F(n) = F(n - 1) + F(n - 2) \end{align}$$
-Define $GF(t) = g(F(t), F(t - 1))$.
+$GF(t) = g(F(t), F(t - 1))$ と定義します。
-Find $\sum GF(t)$ for$ 2 ≤ t ≤ 45$.
+$ 2 ≤ t ≤ 45$ のとき、$\sum GF(t)$ を求めなさい。
# --hints--
-`rudinShapiroSequence()` should return `3354706415856333000`.
+`rudinShapiroSequence()` は `3354706415856333000` を返す必要があります。
```js
assert.strictEqual(rudinShapiroSequence(), 3354706415856333000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
index 79d504116d..02f63afae8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4ee1000cf542c510000
-title: 'Problem 385: Ellipses inside triangles'
+title: '問題 385: 三角形の中の楕円'
challengeType: 5
forumTopicId: 302049
dashedName: problem-385-ellipses-inside-triangles
@@ -8,28 +8,28 @@ dashedName: problem-385-ellipses-inside-triangles
# --description--
-For any triangle $T$ in the plane, it can be shown that there is a unique ellipse with largest area that is completely inside $T$.
+平面上の任意の三角形 $T$ について、$T$ に完全に内包され、かつ面積が最大である一意の楕円が存在することが分かっています。
-
-Let $C(m, n)$ be the number of distinct $m×n$ mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+相異なる $m×n$ 迷路の数を $C(m, n)$ とします。 別の迷路の回転や反転によって形成される迷路は、相異なる迷路とみなされます。
-It can be verified that $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, and $C(9, 12) = 2.5720\mathrm{e}\\,46$ (in scientific notation rounded to 5 significant digits).
+$C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$, $C(9, 12) = 2.5720\mathrm{e}\\,46$ (有効数字 5 桁に四捨五入された科学的記数法) であることを確認できます。
-Find $C(100, 500)$ and write your answer as a string in scientific notation rounded to 5 significant digits.
+$C(100, 500)$ を求め、有効数字 5 桁に四捨五入された科学的記数法の文字列で答えなさい。
-When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be the string `1.2346e12`.
+回答の仮数部と指数部を小文字 e で区切ること。 例: 求めた値が1234567891011 の場合、回答は文字列 `1.2346e12` になります。
# --hints--
-`amazingMazes()` should return a string.
+`amazingMazes()` は文字列を返す必要があります。
```js
assert(typeof amazingMazes() === 'string');
```
-`amazingMazes()` should return the string `6.3202e25093`.
+`amazingMazes()` は文字列 `6.3202e25093` を返す必要があります。
```js
assert.strictEqual(amazingMazes(), '6.3202e25093');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
index 1c5cb8b322..89f38a7735 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
@@ -1,6 +1,6 @@
---
id: 5900f4ea1000cf542c50fffc
-title: 'Problem 381: (prime-k) factorial'
+title: '問題 381: (素数-k) 階乗'
challengeType: 5
forumTopicId: 302045
dashedName: problem-381-prime-k-factorial
@@ -8,21 +8,21 @@ dashedName: problem-381-prime-k-factorial
# --description--
-For a prime $p$ let $S(p) = (\sum (p - k)!)\bmod (p)$ for $1 ≤ k ≤ 5$.
+素数 $p$ について、$1 ≤ k ≤ 5$ のとき $S(p) = (\sum (p - k)!)\bmod (p)$ が成り立つとします。
-For example, if $p = 7$,
+例えば、$p = 7$ のとき、次の式が成り立ちます。
$$(7 - 1)! + (7 - 2)! + (7 - 3)! + (7 - 4)! + (7 - 5)! = 6! + 5! + 4! + 3! + 2! = 720 + 120 + 24 + 6 + 2 = 872$$
-As $872\bmod (7) = 4$, $S(7) = 4$.
+$872\bmod (7) = 4$ なので $S(7) = 4$ となります。
-It can be verified that $\sum S(p) = 480$ for $5 ≤ p < 100$.
+$5 ≤ p < 100$ のとき、$\sum S(p) = 480$ となることを確認できます。
-Find $\sum S(p)$ for $5 ≤ p < {10}^8$.
+$5 ≤ p < {10}^8$ のとき、$\sum S(p)$ を求めなさい。
# --hints--
-`primeKFactorial()` should return `139602943319822`.
+`primeKFactorial()` は`139602943319822` を返す必要があります。
```js
assert.strictEqual(primeKFactorial(), 139602943319822);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
index 9b829c6f05..be752e2ebc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
@@ -1,6 +1,6 @@
---
id: 5900f4eb1000cf542c50fffd
-title: 'Problem 382: Generating polygons'
+title: '問題 382: 多角形を生成する'
challengeType: 5
forumTopicId: 302046
dashedName: problem-382-generating-polygons
@@ -8,38 +8,38 @@ dashedName: problem-382-generating-polygons
# --description--
-A polygon is a flat shape consisting of straight line segments that are joined to form a closed chain or circuit. A polygon consists of at least three sides and does not self-intersect.
+多角形とは、閉路を形成するように結合された直線分からなる平面図形です。 多角形は少なくとも 3 本の辺で構成され、それ自体と交差することはありません。
-A set $S$ of positive numbers is said to generate a polygon $P$ if:
+以下の条件をすべて満たす正の数 $S$ の集合が多角形 $P$ を生成するものとします。
-- no two sides of $P$ are the same length,
-- the length of every side of $P$ is in $S$, and
-- $S$ contains no other value.
+- $P$ のいずれの 2 辺も長さが異なる
+- $P$ の各辺の長さが $S$ に含まれる
+- $S$ にはそれ以外の値が含まれない
-For example:
+以下に例を示します。
-The set {3, 4, 5} generates a polygon with sides 3, 4, and 5 (a triangle).
+集合 {3, 4, 5} は 辺長が 3, 4, 5 の多角形 (三角形) を生成します。
-The set {6, 9, 11, 24} generates a polygon with sides 6, 9, 11, and 24 (a quadrilateral).
+集合 {6, 9, 11, 24} は辺長が 6, 9, 11, 24 の多角形 (四角形) を生成します。
-The sets {1, 2, 3} and {2, 3, 4, 9} do not generate any polygon at all.
+集合 {1, 2, 3} と集合 {2, 3, 4, 9} はいかなる多角形も生成しません。
-Consider the sequence $s$, defined as follows:
+次のように定義される数列 $s$ を考えます。
- $s_1 = 1$, $s_2 = 2$, $s_3 = 3$
-- $s_n = s_{n - 1} + s_{n - 3}$ for $n > 3$.
+- $n > 3$ のとき、$s_n = s_{n - 1} + s_{n - 3}$
-Let $U_n$ be the set $\\{s_1, s_2, \ldots, s_n\\}$. For example, $U_{10} = \\{1, 2, 3, 4, 6, 9, 13, 19, 28, 41\\}$.
+$U_n$ を集合 $\\{s_1, s_2, \ldots, s_n\\}$ と定義します。 例えば、$U_{10} = \\{1, 2, 3, 4, 6, 9, 13, 19, 28, 41\\}$ です。
-Let $f(n)$ be the number of subsets of $U_n$ which generate at least one polygon.
+$U_n$ の部分集合のうち、少なくとも 1 つの多角形を生成する部分集合の数を $f(n)$ とします。
-For example, $f(5) = 7$, $f(10) = 501$ and $f(25) = 18\\,635\\,853$.
+例えば、$f(5) = 7$, $f(10) = 501$, $f(25) = 18\\,635\\,853$ です。
-Find the last 9 digits of $f({10}^{18})$.
+$f({10}^{18})$ の下位 9 桁を求めなさい。
# --hints--
-`generatingPolygons()` should return `697003956`.
+`generatingPolygons()` は `697003956` を返す必要があります。
```js
assert.strictEqual(generatingPolygons(), 697003956);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
index e626c7eb7a..db8b411fdd 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
@@ -1,6 +1,6 @@
---
id: 5900f4ed1000cf542c50ffff
-title: 'Problem 383: Divisibility comparison between factorials'
+title: '問題 383: 階乗間の被整除性比較'
challengeType: 5
forumTopicId: 302047
dashedName: problem-383-divisibility-comparison-between-factorials
@@ -8,19 +8,19 @@ dashedName: problem-383-divisibility-comparison-between-factorials
# --description--
-Let $f_5(n)$ be the largest integer $x$ for which $5^x$ divides $n$.
+$5^x$ が $n$ を割り切るような最大の整数 $x$ を $f_5(n)$ とします。
-For example, $f_5(625\\,000) = 7$.
+例えば、$f_5(625\\,000) = 7$ となります。
-Let $T_5(n)$ be the number of integers $i$ which satisfy $f_5((2 \times i - 1)!) < 2 \times f_5(i!)$ and $1 ≤ i ≤ n$.
+次の条件を満たす整数 $i$ の個数を $T_5(n)$ とします: $f_5((2 \times i - 1)!) < 2 \times f_5(i!)$ かつ $1 ≤ i ≤ n$
-It can be verified that $T_5({10}^3) = 68$ and $T_5({10}^9) = 2\\,408\\,210$.
+$T_5({10}^3) = 68$, $T_5({10}^9) = 2\\,408\\,210$ であることを確認できます。
-Find $T_5({10}^{18})$.
+$T_5({10}^{18})$ を求めなさい。
# --hints--
-`factorialDivisibilityComparison()` should return `22173624649806`.
+`factorialDivisibilityComparison()` は `22173624649806` を返す必要があります。
```js
assert.strictEqual(factorialDivisibilityComparison(), 22173624649806);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
index ebe171e2ef..d7f8a24433 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4ed1000cf542c50fffe
-title: 'Problem 384: Rudin-Shapiro sequence'
+title: '問題 384: ルーディン-シャピロ数列'
challengeType: 5
forumTopicId: 302048
dashedName: problem-384-rudin-shapiro-sequence
@@ -8,35 +8,35 @@ dashedName: problem-384-rudin-shapiro-sequence
# --description--
-Define the sequence $a(n)$ as the number of adjacent pairs of ones in the binary expansion of $n$ (possibly overlapping).
+$n$ の 2 進展開における隣接する 1 の対の個数を数列 $a(n)$ とします (1 の対は重複している場合があります)。
-E.g.: $a(5) = a({101}_2) = 0$, $a(6) = a({110}_2) = 1$, $a(7) = a({111}_2) = 2$
+例: $a(5) = a({101}_2) = 0$, $a(6) = a({110}_2) = 1$, $a(7) = a({111}_2) = 2$
-Define the sequence $b(n) = {(-1)}^{a(n)}$. This sequence is called the Rudin-Shapiro sequence.
+続いて、数列 $b(n) = {(-1)}^{a(n)}$ を定義します。 この数列はルーディン-シャピロ数列と呼ばれます。
-Also consider the summatory sequence of $b(n)$: $s(n) = \displaystyle\sum_{i = 0}^{n} b(i)$.
+$b(n)$ の総和数列 $s(n) = \displaystyle\sum_{i = 0}^{n} b(i)$ も考えます。
-The first couple of values of these sequences are:
+これらの数列の最初のいくつかの組み合わせは次のようになります。
$$\begin{array}{lr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\\\ a(n) & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 2 \\\\ b(n) & 1 & 1 & 1 & -1 & 1 & 1 & -1 & 1 \\\\ s(n) & 1 & 2 & 3 & 2 & 3 & 4 & 3 & 4 \end{array}$$
-The sequence $s(n)$ has the remarkable property that all elements are positive and every positive integer $k$ occurs exactly $k$ times.
+数列 $s(n)$ は驚くべき性質を持っています。すべての要素が正の数であり、正の整数 $k$ がいずれもちょうど $k$ 回現れるという性質です。
-Define $g(t, c)$, with $1 ≤ c ≤ t$, as the index in $s(n)$ for which $t$ occurs for the $c$'th time in $s(n)$.
+$s(n)$ の中で $t$ が $c$ 回目に現れたときの $s(n)$ 内でのインデックス (位置) を、$g(t, c)$ と定義します。ここで、$1 ≤ c ≤ t$ です。
-E.g.: $g(3, 3) = 6$, $g(4, 2) = 7$ and $g(54321, 12345) = 1\\,220\\,847\\,710$.
+例: $g(3, 3) = 6$, $g(4, 2) = 7$, $g(54321, 12345) = 1\\,220\\,847\\,710$
-Let $F(n)$ be the fibonacci sequence defined by:
+$F(n)$ を、以下の式で定義されるフィボナッチ数列とします。
-$$\begin{align} & F(0) = F(1) = 1 \text{ and} \\\\ & F(n) = F(n - 1) + F(n - 2) \text{ for } n > 1. \end{align}$$
+$$\begin{align} & F(0) = F(1) = 1 \text{かつ} \\\\ & n > 1 \text{のとき} F(n) = F(n - 1) + F(n - 2) \end{align}$$
-Define $GF(t) = g(F(t), F(t - 1))$.
+$GF(t) = g(F(t), F(t - 1))$ と定義します。
-Find $\sum GF(t)$ for$ 2 ≤ t ≤ 45$.
+$ 2 ≤ t ≤ 45$ のとき、$\sum GF(t)$ を求めなさい。
# --hints--
-`rudinShapiroSequence()` should return `3354706415856333000`.
+`rudinShapiroSequence()` は `3354706415856333000` を返す必要があります。
```js
assert.strictEqual(rudinShapiroSequence(), 3354706415856333000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
index 79d504116d..02f63afae8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4ee1000cf542c510000
-title: 'Problem 385: Ellipses inside triangles'
+title: '問題 385: 三角形の中の楕円'
challengeType: 5
forumTopicId: 302049
dashedName: problem-385-ellipses-inside-triangles
@@ -8,28 +8,28 @@ dashedName: problem-385-ellipses-inside-triangles
# --description--
-For any triangle $T$ in the plane, it can be shown that there is a unique ellipse with largest area that is completely inside $T$.
+平面上の任意の三角形 $T$ について、$T$ に完全に内包され、かつ面積が最大である一意の楕円が存在することが分かっています。
-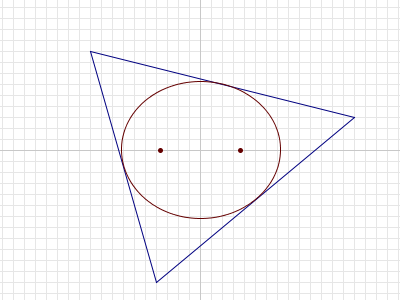 +
+ -For a given $n$, consider triangles $T$ such that:
+与えられた $n$ について、次の両方を満たす三角形 $T$ を考えます。
-- the vertices of $T$ have integer coordinates with absolute value $≤ n$, and
-- the foci1 of the largest-area ellipse inside $T$ are $(\sqrt{13}, 0)$ and $(-\sqrt{13}, 0)$.
+- $T$ の頂点は、絶対値が $n$ 以下である整数座標を持つ。
+- $T$ 内で最大の面積を持つ楕円の焦点 1 は $(\sqrt{13}, 0)$ および $(-\sqrt{13}, 0)$ である。
-Let $A(n)$ be the sum of the areas of all such triangles.
+$A(n)$ を、このような三角形の面積の総和とします。
-For example, if $n = 8$, there are two such triangles. Their vertices are (-4,-3), (-4,3), (8,0) and (4,3), (4,-3), (-8,0), and the area of each triangle is 36. Thus $A(8) = 36 + 36 = 72$.
+例えば $n = 8$ の場合、このような三角形は 2 つあります。 それらの頂点は (-4,-3), (-4,3), (8,0) と (4,3), (4,-3), (-8,0) であり、いずれも三角形の面積は 36 です。 したがって、$A(8) = 36 + 36 = 72$ となります。
-It can be verified that $A(10) = 252$, $A(100) = 34\\,632$ and $A(1000) = 3\\,529\\,008$.
+$A(10) = 252$, $A(100) = 34\\,632$, $A(1000) = 3\\,529\\,008$ であることを確認できます。
-Find $A(1\\,000\\,000\\,000)$.
+$A(1\\,000\\,000\\,000)$ を求めなさい。
-1The foci (plural of focus) of an ellipse are two points $A$ and $B$ such that for every point $P$ on the boundary of the ellipse, $AP + PB$ is constant.
+1 楕円の焦点とは、楕円の境界上にあるすべての点 $P$ について $AP + PB$ が一定になるような 2 点 ($A$ と $B$) を指します。
# --hints--
-`ellipsesInsideTriangles()` should return `3776957309612154000`.
+`ellipsesInsideTriangles()` は `3776957309612154000` を返す必要があります。
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
index 4b9e2557f1..54c96d7bcc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
@@ -1,6 +1,6 @@
---
id: 5900f4ef1000cf542c510001
-title: 'Problem 386: Maximum length of an antichain'
+title: '問題 386: 反鎖の最大長'
challengeType: 5
forumTopicId: 302050
dashedName: problem-386-maximum-length-of-an-antichain
@@ -8,23 +8,23 @@ dashedName: problem-386-maximum-length-of-an-antichain
# --description--
-Let $n$ be an integer and $S(n)$ be the set of factors of $n$.
+$n$ を整数、 $S(n)$ を $n$ の約数の集合とします。
-A subset $A$ of $S(n)$ is called an antichain of $S(n)$ if $A$ contains only one element or if none of the elements of $A$ divides any of the other elements of $A$.
+$A$ に要素が 1 つのみ含まれるか、または、$A$ のいずれの要素も $A$ の他の要素によって割り切れない場合、$S(n)$ の部分集合 $A$ は $S(n)$ の反鎖と呼ばれます。
-For example: $S(30) = \\{1, 2, 3, 5, 6, 10, 15, 30\\}$
+例: $S(30) = \\{1, 2, 3, 5, 6, 10, 15, 30\\}$
-$\\{2, 5, 6\\}$ is not an antichain of $S(30)$.
+$\\{2, 5, 6\\}$ は $S(30)$ の反鎖ではありません。
-$\\{2, 3, 5\\}$ is an antichain of $S(30)$.
+しかし $\\{2, 3, 5\\}$ は $S(30)$ の反鎖です。
-Let $N(n)$ be the maximum length of an antichain of $S(n)$.
+$N(n)$ を $S(n)$ の反鎖の最大長とします。
-Find $\sum N(n)$ for $1 ≤ n ≤ {10}^8$
+$1 ≤ n ≤ {10}^8$ のとき、$\sum N(n)$ を求めなさい。
# --hints--
-`maximumLengthOfAntichain()` should return `528755790`.
+`maximumLengthOfAntichain()` は `528755790` を返す必要があります。
```js
assert.strictEqual(maximumLengthOfAntichain(), 528755790);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
index be8569bcbd..2df28624fb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4f11000cf542c510003
-title: 'Problem 387: Harshad Numbers'
+title: '問題 387: ハーシャッド数'
challengeType: 5
forumTopicId: 302051
dashedName: problem-387-harshad-numbers
@@ -8,31 +8,31 @@ dashedName: problem-387-harshad-numbers
# --description--
-A Harshad or Niven number is a number that is divisible by the sum of its digits.
+ハーシャッド数またはニーベン数とは、その各位の和によって整除できる数のことです。
-201 is a Harshad number because it is divisible by 3 (the sum of its digits.)
+201 は 3 (各位の和) で整除できるのでハーシャッド数です。
-When we truncate the last digit from 201, we get 20, which is a Harshad number.
+201 の最下位の桁を切り詰めると 20 になり、これはハーシャッド数です。
-When we truncate the last digit from 20, we get 2, which is also a Harshad number.
+20 の最下位の桁を切り詰めると 2 になり、これもハーシャッド数です。
-Let's call a Harshad number that, while recursively truncating the last digit, always results in a Harshad number a right truncatable Harshad number.
+最下位の桁を再帰的に切り詰めても結果が常にハーシャッド数になるようなハーシャッド数を、右桁切り詰め可能なハーシャッド数と呼ぶことにします。
-Also:
+また、
-$\frac{201}{3} = 67$ which is prime.
+$\frac{201}{3} = 67$ は素数です。
-Let's call a Harshad number that, when divided by the sum of its digits, results in a prime a strong Harshad number.
+各位の和で割ると素数になるハーシャッド数を、強ハーシャッド数と呼ぶことにします。
-Now take the number 2011 which is prime. When we truncate the last digit from it we get 201, a strong Harshad number that is also right truncatable. Let's call such primes strong, right truncatable Harshad primes.
+ここでは素数 2011 を取り上げます。 最下位の桁を切り詰めると 201 になります。これは強ハルシャッド数であり、右桁が切り詰め可能でもあります。 このような素数を、右桁切り詰め可能な強ハーシャッド素数と呼ぶことにします。
-You are given that the sum of the strong, right truncatable Harshad primes less than 10000 is 90619.
+10000 未満の右桁切り詰め可能な強ハーシャッド素数の和は 90619 です。
-Find the sum of the strong, right truncatable Harshad primes less than ${10}^{14}$.
+${10}^{14}$ 未満の右桁切り詰め可能な強ハーシャッド素数の和を求めなさい。
# --hints--
-`harshadNumbers()` should return `696067597313468`.
+`harshadNumbers()` は `696067597313468` を返す必要があります。
```js
assert.strictEqual(harshadNumbers(), 696067597313468);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
index 0221499351..57fd3199b8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
@@ -1,6 +1,6 @@
---
id: 5900f4f11000cf542c510002
-title: 'Problem 388: Distinct Lines'
+title: '問題 388: 相異なる線'
challengeType: 5
forumTopicId: 302052
dashedName: problem-388-distinct-lines
@@ -8,17 +8,17 @@ dashedName: problem-388-distinct-lines
# --description--
-Consider all lattice points ($a$, $b$, $c$) with $0 ≤ a, b, c ≤ N$.
+$0 ≤ a, b, c ≤ N$ を満たすすべての格子点 ($a$, $b$, $c$) について考えます。
-From the origin $O(0, 0, 0)$ all lines are drawn to the other lattice points. Let $D(N)$ be the number of distinct such lines.
+すべての線は、原点 $O(0, 0, 0)$ から他の格子点まで引かれます。 相異なるこのような線の数を $D(N)$ とします。
-You are given that $D(1\\,000\\,000) = 831\\,909\\,254\\,469\\,114\\,121$.
+$D(1\\,000\\,000) = 831\\,909\\,254\\,469\\,114\\,121$ です。
-Find $D({10}^{10})$. Give as your answer the first nine digits followed by the last nine digits.
+$D({10}^{10})$ を求めなさい。 回答は、上位 9 桁に続けて下位 9 桁を示すこと。
# --hints--
-`distinctLines()` should return `831907372805130000`.
+`distinctLines()` は `831907372805130000` を返す必要があります。
```js
assert.strictEqual(distinctLines(), 831907372805130000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
index 3c82720abc..2fc69899b0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4f21000cf542c510004
-title: 'Problem 389: Platonic Dice'
+title: '問題 389: プラトンのサイコロ'
challengeType: 5
forumTopicId: 302053
dashedName: problem-389-platonic-dice
@@ -8,21 +8,21 @@ dashedName: problem-389-platonic-dice
# --description--
-An unbiased single 4-sided die is thrown and its value, $T$, is noted.
+偏りのない 4 面サイコロを 1 個振り、出た目 $T$ を書き留めます。
-$T$ unbiased 6-sided dice are thrown and their scores are added together. The sum, $C$, is noted.
+次に、偏りのない 6 面サイコロを $T$ 個振り、出た目を合計します。 その合計 $C$ を書き留めます。
-$C$ unbiased 8-sided dice are thrown and their scores are added together. The sum, $O$, is noted.
+続いて、偏りのない 8 面サイコロを $C$ 個振り、出た目を合計します。 その合計 $O$ を書き留めます。
-$O$ unbiased 12-sided dice are thrown and their scores are added together. The sum, $D$, is noted.
+さらに、偏りのない 12 面サイコロを $O$ 個振り、出た目を合計します。 その合計 $D$ を書き留めます。
-$D$ unbiased 20-sided dice are thrown and their scores are added together. The sum, $I$, is noted.
+最後に、偏りのない 20 面サイコロを $D$ 個振り、出た目を合計します。 その合計 $I$ を書き留めます。
-Find the variance of $I$, and give your answer rounded to 4 decimal places.
+$I$ の分散を求め、四捨五入して小数第 4 位まで示しなさい。
# --hints--
-`platonicDice()` should return `2406376.3623`.
+`platonicDice()` は `2406376.3623` を返す必要があります。
```js
assert.strictEqual(platonicDice(), 2406376.3623);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
index 6a8c5ab008..41daae742a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
@@ -1,6 +1,6 @@
---
id: 5900f4f21000cf542c510005
-title: 'Problem 390: Triangles with non rational sides and integral area'
+title: '問題 390: 非有理的な辺と整数の面積を持つ三角形'
challengeType: 5
forumTopicId: 302055
dashedName: problem-390-triangles-with-non-rational-sides-and-integral-area
@@ -8,19 +8,19 @@ dashedName: problem-390-triangles-with-non-rational-sides-and-integral-area
# --description--
-Consider the triangle with sides $\sqrt{5}$, $\sqrt{65}$ and $\sqrt{68}$. It can be shown that this triangle has area 9.
+辺長が $\sqrt{5}$, $\sqrt{65}$, $\sqrt{68} $ である三角形について考えます。 この三角形の面積が 9 であることが分かります。
-$S(n)$ is the sum of the areas of all triangles with sides $\sqrt{1 + b^2}$, $\sqrt{1 + c^2}$ and $\sqrt{b^2 + c^2}$ (for positive integers $b$ and $c$) that have an integral area not exceeding $n$.
+$n$ を超えない整数の面積を持ち、3 辺が $\sqrt{1 + b^2}$, $\sqrt{1 + c^2}$, $\sqrt{b^2 + c^2}$ (ここで $b$ と $c$ は正の整数) である三角形について、それらすべての面積の和を $S(n)$ とします。
-The example triangle has $b = 2$ and $c = 8$.
+例に挙げた三角形では $b = 2$, $c = 8$ です。
-$S({10}^6) = 18\\,018\\,206$.
+$S({10}^6) = 18\\,018\\,206$ です。
-Find $S({10}^{10})$.
+$S({10}^{10})$ を求めなさい。
# --hints--
-`nonRationalSidesAndIntegralArea()` should return `2919133642971`.
+`nonRationalSidesAndIntegralArea()` は `2919133642971` を返す必要があります。
```js
assert.strictEqual(nonRationalSidesAndIntegralArea(), 2919133642971);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
index 9c3d849f7f..9207eab825 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4f31000cf542c510006
-title: 'Problem 391: Hopping Game'
+title: '問題 391: ホッピングゲーム'
challengeType: 5
forumTopicId: 302056
dashedName: problem-391-hopping-game
@@ -8,32 +8,32 @@ dashedName: problem-391-hopping-game
# --description--
-Let $s_k$ be the number of 1’s when writing the numbers from 0 to $k$ in binary.
+0 から $s_k$ までの数を 2 進数で表した場合の 1 の個数を、$k$ とします。
-For example, writing 0 to 5 in binary, we have 0, 1, 10, 11, 100, 101. There are seven 1’s, so $s_5 = 7$.
+例えば、0 から 5 を 2 進数で表すと、0, 1, 10, 11, 100, 101 となります。 1 が 7 個あるので、$s_5 = 7$ です。
-The sequence $S = \\{s_k : k ≥ 0\\}$ starts $\\{0, 1, 2, 4, 5, 7, 9, 12, \ldots\\}$.
+数列 $S = \\{s_k : k ≥ 0\\}$ の最初の部分は $\\{0, 1, 2, 4, 5, 7, 9, 12, \ldots\\}$ です。
-A game is played by two players. Before the game starts, a number $n$ is chosen. A counter $c$ starts at 0. At each turn, the player chooses a number from 1 to $n$ (inclusive) and increases $c$ by that number. The resulting value of $c$ must be a member of $S$. If there are no more valid moves, the player loses.
+あるゲームを 2 人のプレイヤーで行います。 ゲームを始める前に、数 $n$ が選択されます。 カウンター $c$ は 0 から開始します。 各ターンで、プレイヤーは 1 から $n$ (1 と $n$を含む) までの数を 1 つ選び、その数の分だけ $c$ を増加させます。 $c$ の結果の値は $S$ の要素である必要があります。 これ以上は有効な手がない場合、そのプレイヤーは負けます。
-For example, with $n = 5$ and starting with $c = 0$:
+例えば、$n = 5$ であり、$c = 0$ から始めるとします。
-- Player 1 chooses 4, so $c$ becomes $0 + 4 = 4$.
-- Player 2 chooses 5, so $c$ becomes $4 + 5 = 9$.
-- Player 1 chooses 3, so $c$ becomes $9 + 3 = 12$.
-- etc.
+- プレイヤー 1 が 4 を選ぶと、$c$ は $0 + 4 = 4$ になります。
+- プレイヤー 2 が 5を選ぶと、$c$ は $4 + 5 = 9$ になります。
+- プレイヤー 1 が 3 を選ぶと、$c$ は $9 + 3 = 12$ になります。
+- 以降も同様に続けます。
-Note that $c$ must always belong to $S$, and each player can increase $c$ by at most $n$.
+注意点として、$c$ は常に $S$ に属している必要があり、各プレイヤーはたかだか $n$ の分だけ $c$ を増加させることができます。
-Let $M(n)$ be the highest number the first player can choose at her first turn to force a win, and $M(n) = 0$ if there is no such move. For example, $M(2) = 2$, $M(7) = 1$ and $M(20) = 4$.
+ここで、プレイヤー 1 が確実に勝つために最初のターンで選ぶことのできる最大の数を $M(n)$ とし、そのような手がない場合は $M(n)=0$ とします。 例えば、$M(2) = 2$, $M(7) = 1$, $M(20) = 4$ です。
-It can be verified $\sum M{(n)}^3 = 8150$ for $1 ≤ n ≤ 20$.
+$1 ≤ n ≤ 20$ のとき、$\sum M{(n)}^3 = 8150$ であることを確認できます。
-Find $\sum M{(n)}^3$ for $1 ≤ n ≤ 1000$.
+$1 ≤ n ≤ 1000$ のとき、$\sum M{(n)}^3$ を求めなさい。
# --hints--
-`hoppingGame()` should return `61029882288`.
+`hoppingGame()` は `61029882288` を返す必要があります。
```js
assert.strictEqual(hoppingGame(), 61029882288);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
index af4b87d0cf..b0755751ba 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
@@ -1,6 +1,6 @@
---
id: 5900f4f41000cf542c510007
-title: 'Problem 392: Enmeshed unit circle'
+title: '問題 392: 網にかかった単位円'
challengeType: 5
forumTopicId: 302057
dashedName: problem-392-enmeshed-unit-circle
@@ -8,31 +8,31 @@ dashedName: problem-392-enmeshed-unit-circle
# --description--
-A rectilinear grid is an orthogonal grid where the spacing between the gridlines does not have to be equidistant.
+直線格子とは、格子線が必ずしも等間隔でない直交格子です。
-An example of such grid is logarithmic graph paper.
+そのような格子の例として、対数方眼紙が挙げられます。
-Consider rectilinear grids in the Cartesian coordinate system with the following properties:
+ここでは、以下のプロパティを備えたデカルト座標系の直線格子について考えます。
-- The gridlines are parallel to the axes of the Cartesian coordinate system.
-- There are $N + 2$ vertical and $N + 2$ horizontal gridlines. Hence there are $(N + 1) \times (N + 1)$ rectangular cells.
-- The equations of the two outer vertical gridlines are $x = -1$ and $x = 1$.
-- The equations of the two outer horizontal gridlines are $y = -1$ and $y = 1$.
-- The grid cells are colored red if they overlap with the unit circle, black otherwise.
+- 格子線がデカルト座標系の軸と平行である。
+- $N + 2$ 本の垂直格子線と $N + 2$ 本の水平格子線が引かれている。 したがって、長方形のマスが $(N + 1) \times (N + 1)$ 個存在する。
+- 外側の 2 本の垂直格子線の式が $x = -1$ と $x = 1$ である。
+- 外側の 2 本の水平格子線の式が $y = -1$ と $y = 1$ である。
+- 格子のマスは、単位円と重なると赤色になり、それ以外の場合は黒色になる。
-For this problem we would like you to find the positions of the remaining $N$ inner horizontal and $N$ inner vertical gridlines so that the area occupied by the red cells is minimized.
+この問題では、赤色のマスの面積を最小にするには、残りの $N$ 本の内側の水平格子線と $N$ 本の内側の垂直格子線をどこに引けばよいかを求めます。
-E.g. here is a picture of the solution for $N = 10$:
+例: 下図は $N = 10$ のときの解を示しています。
-
-For a given $n$, consider triangles $T$ such that:
+与えられた $n$ について、次の両方を満たす三角形 $T$ を考えます。
-- the vertices of $T$ have integer coordinates with absolute value $≤ n$, and
-- the foci1 of the largest-area ellipse inside $T$ are $(\sqrt{13}, 0)$ and $(-\sqrt{13}, 0)$.
+- $T$ の頂点は、絶対値が $n$ 以下である整数座標を持つ。
+- $T$ 内で最大の面積を持つ楕円の焦点 1 は $(\sqrt{13}, 0)$ および $(-\sqrt{13}, 0)$ である。
-Let $A(n)$ be the sum of the areas of all such triangles.
+$A(n)$ を、このような三角形の面積の総和とします。
-For example, if $n = 8$, there are two such triangles. Their vertices are (-4,-3), (-4,3), (8,0) and (4,3), (4,-3), (-8,0), and the area of each triangle is 36. Thus $A(8) = 36 + 36 = 72$.
+例えば $n = 8$ の場合、このような三角形は 2 つあります。 それらの頂点は (-4,-3), (-4,3), (8,0) と (4,3), (4,-3), (-8,0) であり、いずれも三角形の面積は 36 です。 したがって、$A(8) = 36 + 36 = 72$ となります。
-It can be verified that $A(10) = 252$, $A(100) = 34\\,632$ and $A(1000) = 3\\,529\\,008$.
+$A(10) = 252$, $A(100) = 34\\,632$, $A(1000) = 3\\,529\\,008$ であることを確認できます。
-Find $A(1\\,000\\,000\\,000)$.
+$A(1\\,000\\,000\\,000)$ を求めなさい。
-1The foci (plural of focus) of an ellipse are two points $A$ and $B$ such that for every point $P$ on the boundary of the ellipse, $AP + PB$ is constant.
+1 楕円の焦点とは、楕円の境界上にあるすべての点 $P$ について $AP + PB$ が一定になるような 2 点 ($A$ と $B$) を指します。
# --hints--
-`ellipsesInsideTriangles()` should return `3776957309612154000`.
+`ellipsesInsideTriangles()` は `3776957309612154000` を返す必要があります。
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
index 4b9e2557f1..54c96d7bcc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
@@ -1,6 +1,6 @@
---
id: 5900f4ef1000cf542c510001
-title: 'Problem 386: Maximum length of an antichain'
+title: '問題 386: 反鎖の最大長'
challengeType: 5
forumTopicId: 302050
dashedName: problem-386-maximum-length-of-an-antichain
@@ -8,23 +8,23 @@ dashedName: problem-386-maximum-length-of-an-antichain
# --description--
-Let $n$ be an integer and $S(n)$ be the set of factors of $n$.
+$n$ を整数、 $S(n)$ を $n$ の約数の集合とします。
-A subset $A$ of $S(n)$ is called an antichain of $S(n)$ if $A$ contains only one element or if none of the elements of $A$ divides any of the other elements of $A$.
+$A$ に要素が 1 つのみ含まれるか、または、$A$ のいずれの要素も $A$ の他の要素によって割り切れない場合、$S(n)$ の部分集合 $A$ は $S(n)$ の反鎖と呼ばれます。
-For example: $S(30) = \\{1, 2, 3, 5, 6, 10, 15, 30\\}$
+例: $S(30) = \\{1, 2, 3, 5, 6, 10, 15, 30\\}$
-$\\{2, 5, 6\\}$ is not an antichain of $S(30)$.
+$\\{2, 5, 6\\}$ は $S(30)$ の反鎖ではありません。
-$\\{2, 3, 5\\}$ is an antichain of $S(30)$.
+しかし $\\{2, 3, 5\\}$ は $S(30)$ の反鎖です。
-Let $N(n)$ be the maximum length of an antichain of $S(n)$.
+$N(n)$ を $S(n)$ の反鎖の最大長とします。
-Find $\sum N(n)$ for $1 ≤ n ≤ {10}^8$
+$1 ≤ n ≤ {10}^8$ のとき、$\sum N(n)$ を求めなさい。
# --hints--
-`maximumLengthOfAntichain()` should return `528755790`.
+`maximumLengthOfAntichain()` は `528755790` を返す必要があります。
```js
assert.strictEqual(maximumLengthOfAntichain(), 528755790);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
index be8569bcbd..2df28624fb 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4f11000cf542c510003
-title: 'Problem 387: Harshad Numbers'
+title: '問題 387: ハーシャッド数'
challengeType: 5
forumTopicId: 302051
dashedName: problem-387-harshad-numbers
@@ -8,31 +8,31 @@ dashedName: problem-387-harshad-numbers
# --description--
-A Harshad or Niven number is a number that is divisible by the sum of its digits.
+ハーシャッド数またはニーベン数とは、その各位の和によって整除できる数のことです。
-201 is a Harshad number because it is divisible by 3 (the sum of its digits.)
+201 は 3 (各位の和) で整除できるのでハーシャッド数です。
-When we truncate the last digit from 201, we get 20, which is a Harshad number.
+201 の最下位の桁を切り詰めると 20 になり、これはハーシャッド数です。
-When we truncate the last digit from 20, we get 2, which is also a Harshad number.
+20 の最下位の桁を切り詰めると 2 になり、これもハーシャッド数です。
-Let's call a Harshad number that, while recursively truncating the last digit, always results in a Harshad number a right truncatable Harshad number.
+最下位の桁を再帰的に切り詰めても結果が常にハーシャッド数になるようなハーシャッド数を、右桁切り詰め可能なハーシャッド数と呼ぶことにします。
-Also:
+また、
-$\frac{201}{3} = 67$ which is prime.
+$\frac{201}{3} = 67$ は素数です。
-Let's call a Harshad number that, when divided by the sum of its digits, results in a prime a strong Harshad number.
+各位の和で割ると素数になるハーシャッド数を、強ハーシャッド数と呼ぶことにします。
-Now take the number 2011 which is prime. When we truncate the last digit from it we get 201, a strong Harshad number that is also right truncatable. Let's call such primes strong, right truncatable Harshad primes.
+ここでは素数 2011 を取り上げます。 最下位の桁を切り詰めると 201 になります。これは強ハルシャッド数であり、右桁が切り詰め可能でもあります。 このような素数を、右桁切り詰め可能な強ハーシャッド素数と呼ぶことにします。
-You are given that the sum of the strong, right truncatable Harshad primes less than 10000 is 90619.
+10000 未満の右桁切り詰め可能な強ハーシャッド素数の和は 90619 です。
-Find the sum of the strong, right truncatable Harshad primes less than ${10}^{14}$.
+${10}^{14}$ 未満の右桁切り詰め可能な強ハーシャッド素数の和を求めなさい。
# --hints--
-`harshadNumbers()` should return `696067597313468`.
+`harshadNumbers()` は `696067597313468` を返す必要があります。
```js
assert.strictEqual(harshadNumbers(), 696067597313468);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
index 0221499351..57fd3199b8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
@@ -1,6 +1,6 @@
---
id: 5900f4f11000cf542c510002
-title: 'Problem 388: Distinct Lines'
+title: '問題 388: 相異なる線'
challengeType: 5
forumTopicId: 302052
dashedName: problem-388-distinct-lines
@@ -8,17 +8,17 @@ dashedName: problem-388-distinct-lines
# --description--
-Consider all lattice points ($a$, $b$, $c$) with $0 ≤ a, b, c ≤ N$.
+$0 ≤ a, b, c ≤ N$ を満たすすべての格子点 ($a$, $b$, $c$) について考えます。
-From the origin $O(0, 0, 0)$ all lines are drawn to the other lattice points. Let $D(N)$ be the number of distinct such lines.
+すべての線は、原点 $O(0, 0, 0)$ から他の格子点まで引かれます。 相異なるこのような線の数を $D(N)$ とします。
-You are given that $D(1\\,000\\,000) = 831\\,909\\,254\\,469\\,114\\,121$.
+$D(1\\,000\\,000) = 831\\,909\\,254\\,469\\,114\\,121$ です。
-Find $D({10}^{10})$. Give as your answer the first nine digits followed by the last nine digits.
+$D({10}^{10})$ を求めなさい。 回答は、上位 9 桁に続けて下位 9 桁を示すこと。
# --hints--
-`distinctLines()` should return `831907372805130000`.
+`distinctLines()` は `831907372805130000` を返す必要があります。
```js
assert.strictEqual(distinctLines(), 831907372805130000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
index 3c82720abc..2fc69899b0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4f21000cf542c510004
-title: 'Problem 389: Platonic Dice'
+title: '問題 389: プラトンのサイコロ'
challengeType: 5
forumTopicId: 302053
dashedName: problem-389-platonic-dice
@@ -8,21 +8,21 @@ dashedName: problem-389-platonic-dice
# --description--
-An unbiased single 4-sided die is thrown and its value, $T$, is noted.
+偏りのない 4 面サイコロを 1 個振り、出た目 $T$ を書き留めます。
-$T$ unbiased 6-sided dice are thrown and their scores are added together. The sum, $C$, is noted.
+次に、偏りのない 6 面サイコロを $T$ 個振り、出た目を合計します。 その合計 $C$ を書き留めます。
-$C$ unbiased 8-sided dice are thrown and their scores are added together. The sum, $O$, is noted.
+続いて、偏りのない 8 面サイコロを $C$ 個振り、出た目を合計します。 その合計 $O$ を書き留めます。
-$O$ unbiased 12-sided dice are thrown and their scores are added together. The sum, $D$, is noted.
+さらに、偏りのない 12 面サイコロを $O$ 個振り、出た目を合計します。 その合計 $D$ を書き留めます。
-$D$ unbiased 20-sided dice are thrown and their scores are added together. The sum, $I$, is noted.
+最後に、偏りのない 20 面サイコロを $D$ 個振り、出た目を合計します。 その合計 $I$ を書き留めます。
-Find the variance of $I$, and give your answer rounded to 4 decimal places.
+$I$ の分散を求め、四捨五入して小数第 4 位まで示しなさい。
# --hints--
-`platonicDice()` should return `2406376.3623`.
+`platonicDice()` は `2406376.3623` を返す必要があります。
```js
assert.strictEqual(platonicDice(), 2406376.3623);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
index 6a8c5ab008..41daae742a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
@@ -1,6 +1,6 @@
---
id: 5900f4f21000cf542c510005
-title: 'Problem 390: Triangles with non rational sides and integral area'
+title: '問題 390: 非有理的な辺と整数の面積を持つ三角形'
challengeType: 5
forumTopicId: 302055
dashedName: problem-390-triangles-with-non-rational-sides-and-integral-area
@@ -8,19 +8,19 @@ dashedName: problem-390-triangles-with-non-rational-sides-and-integral-area
# --description--
-Consider the triangle with sides $\sqrt{5}$, $\sqrt{65}$ and $\sqrt{68}$. It can be shown that this triangle has area 9.
+辺長が $\sqrt{5}$, $\sqrt{65}$, $\sqrt{68} $ である三角形について考えます。 この三角形の面積が 9 であることが分かります。
-$S(n)$ is the sum of the areas of all triangles with sides $\sqrt{1 + b^2}$, $\sqrt{1 + c^2}$ and $\sqrt{b^2 + c^2}$ (for positive integers $b$ and $c$) that have an integral area not exceeding $n$.
+$n$ を超えない整数の面積を持ち、3 辺が $\sqrt{1 + b^2}$, $\sqrt{1 + c^2}$, $\sqrt{b^2 + c^2}$ (ここで $b$ と $c$ は正の整数) である三角形について、それらすべての面積の和を $S(n)$ とします。
-The example triangle has $b = 2$ and $c = 8$.
+例に挙げた三角形では $b = 2$, $c = 8$ です。
-$S({10}^6) = 18\\,018\\,206$.
+$S({10}^6) = 18\\,018\\,206$ です。
-Find $S({10}^{10})$.
+$S({10}^{10})$ を求めなさい。
# --hints--
-`nonRationalSidesAndIntegralArea()` should return `2919133642971`.
+`nonRationalSidesAndIntegralArea()` は `2919133642971` を返す必要があります。
```js
assert.strictEqual(nonRationalSidesAndIntegralArea(), 2919133642971);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
index 9c3d849f7f..9207eab825 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4f31000cf542c510006
-title: 'Problem 391: Hopping Game'
+title: '問題 391: ホッピングゲーム'
challengeType: 5
forumTopicId: 302056
dashedName: problem-391-hopping-game
@@ -8,32 +8,32 @@ dashedName: problem-391-hopping-game
# --description--
-Let $s_k$ be the number of 1’s when writing the numbers from 0 to $k$ in binary.
+0 から $s_k$ までの数を 2 進数で表した場合の 1 の個数を、$k$ とします。
-For example, writing 0 to 5 in binary, we have 0, 1, 10, 11, 100, 101. There are seven 1’s, so $s_5 = 7$.
+例えば、0 から 5 を 2 進数で表すと、0, 1, 10, 11, 100, 101 となります。 1 が 7 個あるので、$s_5 = 7$ です。
-The sequence $S = \\{s_k : k ≥ 0\\}$ starts $\\{0, 1, 2, 4, 5, 7, 9, 12, \ldots\\}$.
+数列 $S = \\{s_k : k ≥ 0\\}$ の最初の部分は $\\{0, 1, 2, 4, 5, 7, 9, 12, \ldots\\}$ です。
-A game is played by two players. Before the game starts, a number $n$ is chosen. A counter $c$ starts at 0. At each turn, the player chooses a number from 1 to $n$ (inclusive) and increases $c$ by that number. The resulting value of $c$ must be a member of $S$. If there are no more valid moves, the player loses.
+あるゲームを 2 人のプレイヤーで行います。 ゲームを始める前に、数 $n$ が選択されます。 カウンター $c$ は 0 から開始します。 各ターンで、プレイヤーは 1 から $n$ (1 と $n$を含む) までの数を 1 つ選び、その数の分だけ $c$ を増加させます。 $c$ の結果の値は $S$ の要素である必要があります。 これ以上は有効な手がない場合、そのプレイヤーは負けます。
-For example, with $n = 5$ and starting with $c = 0$:
+例えば、$n = 5$ であり、$c = 0$ から始めるとします。
-- Player 1 chooses 4, so $c$ becomes $0 + 4 = 4$.
-- Player 2 chooses 5, so $c$ becomes $4 + 5 = 9$.
-- Player 1 chooses 3, so $c$ becomes $9 + 3 = 12$.
-- etc.
+- プレイヤー 1 が 4 を選ぶと、$c$ は $0 + 4 = 4$ になります。
+- プレイヤー 2 が 5を選ぶと、$c$ は $4 + 5 = 9$ になります。
+- プレイヤー 1 が 3 を選ぶと、$c$ は $9 + 3 = 12$ になります。
+- 以降も同様に続けます。
-Note that $c$ must always belong to $S$, and each player can increase $c$ by at most $n$.
+注意点として、$c$ は常に $S$ に属している必要があり、各プレイヤーはたかだか $n$ の分だけ $c$ を増加させることができます。
-Let $M(n)$ be the highest number the first player can choose at her first turn to force a win, and $M(n) = 0$ if there is no such move. For example, $M(2) = 2$, $M(7) = 1$ and $M(20) = 4$.
+ここで、プレイヤー 1 が確実に勝つために最初のターンで選ぶことのできる最大の数を $M(n)$ とし、そのような手がない場合は $M(n)=0$ とします。 例えば、$M(2) = 2$, $M(7) = 1$, $M(20) = 4$ です。
-It can be verified $\sum M{(n)}^3 = 8150$ for $1 ≤ n ≤ 20$.
+$1 ≤ n ≤ 20$ のとき、$\sum M{(n)}^3 = 8150$ であることを確認できます。
-Find $\sum M{(n)}^3$ for $1 ≤ n ≤ 1000$.
+$1 ≤ n ≤ 1000$ のとき、$\sum M{(n)}^3$ を求めなさい。
# --hints--
-`hoppingGame()` should return `61029882288`.
+`hoppingGame()` は `61029882288` を返す必要があります。
```js
assert.strictEqual(hoppingGame(), 61029882288);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
index af4b87d0cf..b0755751ba 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
@@ -1,6 +1,6 @@
---
id: 5900f4f41000cf542c510007
-title: 'Problem 392: Enmeshed unit circle'
+title: '問題 392: 網にかかった単位円'
challengeType: 5
forumTopicId: 302057
dashedName: problem-392-enmeshed-unit-circle
@@ -8,31 +8,31 @@ dashedName: problem-392-enmeshed-unit-circle
# --description--
-A rectilinear grid is an orthogonal grid where the spacing between the gridlines does not have to be equidistant.
+直線格子とは、格子線が必ずしも等間隔でない直交格子です。
-An example of such grid is logarithmic graph paper.
+そのような格子の例として、対数方眼紙が挙げられます。
-Consider rectilinear grids in the Cartesian coordinate system with the following properties:
+ここでは、以下のプロパティを備えたデカルト座標系の直線格子について考えます。
-- The gridlines are parallel to the axes of the Cartesian coordinate system.
-- There are $N + 2$ vertical and $N + 2$ horizontal gridlines. Hence there are $(N + 1) \times (N + 1)$ rectangular cells.
-- The equations of the two outer vertical gridlines are $x = -1$ and $x = 1$.
-- The equations of the two outer horizontal gridlines are $y = -1$ and $y = 1$.
-- The grid cells are colored red if they overlap with the unit circle, black otherwise.
+- 格子線がデカルト座標系の軸と平行である。
+- $N + 2$ 本の垂直格子線と $N + 2$ 本の水平格子線が引かれている。 したがって、長方形のマスが $(N + 1) \times (N + 1)$ 個存在する。
+- 外側の 2 本の垂直格子線の式が $x = -1$ と $x = 1$ である。
+- 外側の 2 本の水平格子線の式が $y = -1$ と $y = 1$ である。
+- 格子のマスは、単位円と重なると赤色になり、それ以外の場合は黒色になる。
-For this problem we would like you to find the positions of the remaining $N$ inner horizontal and $N$ inner vertical gridlines so that the area occupied by the red cells is minimized.
+この問題では、赤色のマスの面積を最小にするには、残りの $N$ 本の内側の水平格子線と $N$ 本の内側の垂直格子線をどこに引けばよいかを求めます。
-E.g. here is a picture of the solution for $N = 10$:
+例: 下図は $N = 10$ のときの解を示しています。
- +
+ -The area occupied by the red cells for $N = 10$ rounded to 10 digits behind the decimal point is 3.3469640797.
+$N = 10$ のときに赤色のマスが占める面積を、四捨五入して小数第 10 位まで示すと 3.3469640797 になります。
-Find the positions for $N = 400$. Give as your answer the area occupied by the red cells rounded to 10 digits behind the decimal point.
+$N = 400$ のときの位置を求めなさい。 赤色のマスが占める面積を、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`enmeshedUnitCircle()` should return `3.1486734435`.
+`enmeshedUnitCircle()` は `3.1486734435` を返す必要があります。
```js
assert.strictEqual(enmeshedUnitCircle(), 3.1486734435);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
index db37ca4683..e8fd376a17 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
@@ -1,6 +1,6 @@
---
id: 5900f4f61000cf542c510008
-title: 'Problem 393: Migrating ants'
+title: '問題 393: アリの移動'
challengeType: 5
forumTopicId: 302058
dashedName: problem-393-migrating-ants
@@ -8,19 +8,19 @@ dashedName: problem-393-migrating-ants
# --description--
-An $n × n$ grid of squares contains $n^2$ ants, one ant per square.
+正方形のマスが並ぶ $n × n$ の格子上に、$n^2$ 匹のアリが 1 マスに 1 匹ずついます。
-All ants decide to move simultaneously to an adjacent square (usually 4 possibilities, except for ants on the edge of the grid or at the corners).
+すべてのアリが、隣接するマスに同時に移動するとします (格子の端や角にいるアリを除き、通常は移動方向の選択肢が 4 つあります)。
-We define $f(n)$ to be the number of ways this can happen without any ants ending on the same square and without any two ants crossing the same edge between two squares.
+複数のアリが同じマスに移動することがなく、かつ、2 つのマスの間の境界線を 2 匹のアリが通ることもないような移動方法の数を、$f(n)$ と定義します。
-You are given that $f(4) = 88$.
+$f(4) = 88$ が与えられます。
-Find $f(10)$.
+$f(10)$ を求めなさい。
# --hints--
-`migratingAnts()` should return `112398351350823100`.
+`migratingAnts()` は `112398351350823100` を返す必要があります。
```js
assert.strictEqual(migratingAnts(), 112398351350823100);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
index 9aaf167764..f1ae93fd4f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
@@ -1,6 +1,6 @@
---
id: 5900f4f71000cf542c510009
-title: 'Problem 394: Eating pie'
+title: '問題 394: パイの食べ方'
challengeType: 5
forumTopicId: 302059
dashedName: problem-394-eating-pie
@@ -8,26 +8,26 @@ dashedName: problem-394-eating-pie
# --description--
-Jeff eats a pie in an unusual way.
+ジェフのパイの食べ方は一風変わっています。
-The pie is circular. He starts with slicing an initial cut in the pie along a radius.
+パイは円形です。 まず、彼はパイの半径に沿って最初の切れ目を入れます。
-While there is at least a given fraction $F$ of pie left, he performs the following procedure:
+少なくとも与えられた割合 $F$ のパイが残っている間、彼は以下の手順に従います。
-- He makes two slices from the pie centre to any point of what is remaining of the pie border, any point on the remaining pie border equally likely. This will divide the remaining pie into three pieces.
-- Going counterclockwise from the initial cut, he takes the first two pie pieces and eats them.
+- パイの中心から、残っているパイの縁の任意の点 (点の位置は縁全体から等確率で選ばれます) まで切れ目を入れ切ることにより、2 枚のスライスを作ります。 これによって、残っているパイは 3 つの部分に分割されます。
+- 最初の切れ目から反時計回りに、最初の 2 枚のスライスを取って食べます。
-When less than a fraction $F$ of pie remains, he does not repeat this procedure. Instead, he eats all of the remaining pie.
+パイの残りの割合が $F$ 未満になったら、もうこの手順を繰り返しません。 代わりに、残ったパイを全部食べます。
-
-The area occupied by the red cells for $N = 10$ rounded to 10 digits behind the decimal point is 3.3469640797.
+$N = 10$ のときに赤色のマスが占める面積を、四捨五入して小数第 10 位まで示すと 3.3469640797 になります。
-Find the positions for $N = 400$. Give as your answer the area occupied by the red cells rounded to 10 digits behind the decimal point.
+$N = 400$ のときの位置を求めなさい。 赤色のマスが占める面積を、四捨五入して小数第 10 位まで示すこと。
# --hints--
-`enmeshedUnitCircle()` should return `3.1486734435`.
+`enmeshedUnitCircle()` は `3.1486734435` を返す必要があります。
```js
assert.strictEqual(enmeshedUnitCircle(), 3.1486734435);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
index db37ca4683..e8fd376a17 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
@@ -1,6 +1,6 @@
---
id: 5900f4f61000cf542c510008
-title: 'Problem 393: Migrating ants'
+title: '問題 393: アリの移動'
challengeType: 5
forumTopicId: 302058
dashedName: problem-393-migrating-ants
@@ -8,19 +8,19 @@ dashedName: problem-393-migrating-ants
# --description--
-An $n × n$ grid of squares contains $n^2$ ants, one ant per square.
+正方形のマスが並ぶ $n × n$ の格子上に、$n^2$ 匹のアリが 1 マスに 1 匹ずついます。
-All ants decide to move simultaneously to an adjacent square (usually 4 possibilities, except for ants on the edge of the grid or at the corners).
+すべてのアリが、隣接するマスに同時に移動するとします (格子の端や角にいるアリを除き、通常は移動方向の選択肢が 4 つあります)。
-We define $f(n)$ to be the number of ways this can happen without any ants ending on the same square and without any two ants crossing the same edge between two squares.
+複数のアリが同じマスに移動することがなく、かつ、2 つのマスの間の境界線を 2 匹のアリが通ることもないような移動方法の数を、$f(n)$ と定義します。
-You are given that $f(4) = 88$.
+$f(4) = 88$ が与えられます。
-Find $f(10)$.
+$f(10)$ を求めなさい。
# --hints--
-`migratingAnts()` should return `112398351350823100`.
+`migratingAnts()` は `112398351350823100` を返す必要があります。
```js
assert.strictEqual(migratingAnts(), 112398351350823100);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
index 9aaf167764..f1ae93fd4f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
@@ -1,6 +1,6 @@
---
id: 5900f4f71000cf542c510009
-title: 'Problem 394: Eating pie'
+title: '問題 394: パイの食べ方'
challengeType: 5
forumTopicId: 302059
dashedName: problem-394-eating-pie
@@ -8,26 +8,26 @@ dashedName: problem-394-eating-pie
# --description--
-Jeff eats a pie in an unusual way.
+ジェフのパイの食べ方は一風変わっています。
-The pie is circular. He starts with slicing an initial cut in the pie along a radius.
+パイは円形です。 まず、彼はパイの半径に沿って最初の切れ目を入れます。
-While there is at least a given fraction $F$ of pie left, he performs the following procedure:
+少なくとも与えられた割合 $F$ のパイが残っている間、彼は以下の手順に従います。
-- He makes two slices from the pie centre to any point of what is remaining of the pie border, any point on the remaining pie border equally likely. This will divide the remaining pie into three pieces.
-- Going counterclockwise from the initial cut, he takes the first two pie pieces and eats them.
+- パイの中心から、残っているパイの縁の任意の点 (点の位置は縁全体から等確率で選ばれます) まで切れ目を入れ切ることにより、2 枚のスライスを作ります。 これによって、残っているパイは 3 つの部分に分割されます。
+- 最初の切れ目から反時計回りに、最初の 2 枚のスライスを取って食べます。
-When less than a fraction $F$ of pie remains, he does not repeat this procedure. Instead, he eats all of the remaining pie.
+パイの残りの割合が $F$ 未満になったら、もうこの手順を繰り返しません。 代わりに、残ったパイを全部食べます。
- +
+ -For $x ≥ 1$, let $E(x)$ be the expected number of times Jeff repeats the procedure above with $F = \frac{1}{x}$. It can be verified that $E(1) = 1$, $E(2) ≈ 1.2676536759$, and $E(7.5) ≈ 2.1215732071$.
+$x ≥ 1$, $F = frac{1}{x}$ のとき、ジェフが上の手順を繰り返す回数の期待値を $E(x)$ とします。 $E(1) = 1$, $E(2) ≈ 1.2676536759$, $E(7.5) ≈ 2.1215732071$ であることを確認できます。
-Find $E(40)$ rounded to 10 decimal places behind the decimal point.
+$E(40)$ を求め、四捨五入して小数第 10 位まで示しなさい。
# --hints--
-`eatingPie()` should return `3.2370342194`.
+`eatingPie()` は `3.2370342194` を返す必要があります。
```js
assert.strictEqual(eatingPie(), 3.2370342194);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
index 26c2deffc0..8f2142effc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
@@ -1,6 +1,6 @@
---
id: 5900f4f71000cf542c51000a
-title: 'Problem 395: Pythagorean tree'
+title: '問題 395: ピタゴラスの木'
challengeType: 5
forumTopicId: 302060
dashedName: problem-395-pythagorean-tree
@@ -8,25 +8,25 @@ dashedName: problem-395-pythagorean-tree
# --description--
-The Pythagorean tree is a fractal generated by the following procedure:
+ピタゴラスの木とは、以下の手順で作成されるフラクタル図形です。
-Start with a unit square. Then, calling one of the sides its base (in the animation, the bottom side is the base):
+最初に単位正方形を作ります。 次に、そのいずれかの辺を基点として選びます (アニメーションでは底辺が基点)。
-1. Attach a right triangle to the side opposite the base, with the hypotenuse coinciding with that side and with the sides in a 3-4-5 ratio. Note that the smaller side of the triangle must be on the 'right' side with respect to the base (see animation).
-2. Attach a square to each leg of the right triangle, with one of its sides coinciding with that leg.
-3. Repeat this procedure for both squares, considering as their bases the sides touching the triangle.
+1. 基点の反対側の辺に、直角三角形の斜辺を合わせるようにしてその三角形を付けます。三角形の辺長の比は 3-4-5 にします。 注意点として、三角形の短い方の辺が、基点に対して「右」側に来るようにする必要があります (アニメーション参照)。
+2. 直角三角形の斜辺以外の各辺に、正方形の 1 辺を合わせるようにして正方形を付けます。
+3. 三角形に接する辺を基点とみなして、上の手順を両方の正方形に対して繰り返します。
-The resulting figure, after an infinite number of iterations, is the Pythagorean tree.
+この作業を無限に繰り返して得られる図形がピタゴラスの木です。
-
-For $x ≥ 1$, let $E(x)$ be the expected number of times Jeff repeats the procedure above with $F = \frac{1}{x}$. It can be verified that $E(1) = 1$, $E(2) ≈ 1.2676536759$, and $E(7.5) ≈ 2.1215732071$.
+$x ≥ 1$, $F = frac{1}{x}$ のとき、ジェフが上の手順を繰り返す回数の期待値を $E(x)$ とします。 $E(1) = 1$, $E(2) ≈ 1.2676536759$, $E(7.5) ≈ 2.1215732071$ であることを確認できます。
-Find $E(40)$ rounded to 10 decimal places behind the decimal point.
+$E(40)$ を求め、四捨五入して小数第 10 位まで示しなさい。
# --hints--
-`eatingPie()` should return `3.2370342194`.
+`eatingPie()` は `3.2370342194` を返す必要があります。
```js
assert.strictEqual(eatingPie(), 3.2370342194);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
index 26c2deffc0..8f2142effc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
@@ -1,6 +1,6 @@
---
id: 5900f4f71000cf542c51000a
-title: 'Problem 395: Pythagorean tree'
+title: '問題 395: ピタゴラスの木'
challengeType: 5
forumTopicId: 302060
dashedName: problem-395-pythagorean-tree
@@ -8,25 +8,25 @@ dashedName: problem-395-pythagorean-tree
# --description--
-The Pythagorean tree is a fractal generated by the following procedure:
+ピタゴラスの木とは、以下の手順で作成されるフラクタル図形です。
-Start with a unit square. Then, calling one of the sides its base (in the animation, the bottom side is the base):
+最初に単位正方形を作ります。 次に、そのいずれかの辺を基点として選びます (アニメーションでは底辺が基点)。
-1. Attach a right triangle to the side opposite the base, with the hypotenuse coinciding with that side and with the sides in a 3-4-5 ratio. Note that the smaller side of the triangle must be on the 'right' side with respect to the base (see animation).
-2. Attach a square to each leg of the right triangle, with one of its sides coinciding with that leg.
-3. Repeat this procedure for both squares, considering as their bases the sides touching the triangle.
+1. 基点の反対側の辺に、直角三角形の斜辺を合わせるようにしてその三角形を付けます。三角形の辺長の比は 3-4-5 にします。 注意点として、三角形の短い方の辺が、基点に対して「右」側に来るようにする必要があります (アニメーション参照)。
+2. 直角三角形の斜辺以外の各辺に、正方形の 1 辺を合わせるようにして正方形を付けます。
+3. 三角形に接する辺を基点とみなして、上の手順を両方の正方形に対して繰り返します。
-The resulting figure, after an infinite number of iterations, is the Pythagorean tree.
+この作業を無限に繰り返して得られる図形がピタゴラスの木です。
- +
+ -It can be shown that there exists at least one rectangle, whose sides are parallel to the largest square of the Pythagorean tree, which encloses the Pythagorean tree completely.
+ピタゴラスの木の最大の正方形に対して平行な辺を持ち、ピタゴラスの木を完全に囲むような長方形が、少なくとも 1 つの存在することを証明できます。
-Find the smallest area possible for such a bounding rectangle, and give your answer rounded to 10 decimal places.
+そのような外接矩形が持ち得る最小の面積を求め、四捨五入して小数第 10 位まで示しなさい。
# --hints--
-`pythagoreanTree()` should return `28.2453753155`.
+`pythagoreanTree()` は `28.2453753155` を返す必要があります。
```js
assert.strictEqual(pythagoreanTree(), 28.2453753155);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
index 77684c24d4..b6f210ee54 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4f81000cf542c51000b
-title: 'Problem 396: Weak Goodstein sequence'
+title: '問題 396: 弱いグッドスタイン数列'
challengeType: 5
forumTopicId: 302061
dashedName: problem-396-weak-goodstein-sequence
@@ -8,35 +8,35 @@ dashedName: problem-396-weak-goodstein-sequence
# --description--
-For any positive integer $n$, the $n$th weak Goodstein sequence $\\{g1, g2, g3, \ldots\\}$ is defined as:
+正の整数 $n$ について、$n$ 番目の弱いグッドスタイン数列 $\\{g1, g2, g3, \ldots\\}$ は次のように定義されます。
- $g_1 = n$
-- for $k > 1$, $g_k$ is obtained by writing $g_{k - 1}$ in base $k$, interpreting it as a base $k + 1$ number, and subtracting 1.
+- $k > 1$ のとき、$g_k$ を得るには、$g_{k - 1}$ を基数 $k$ で表し、それを基数 $k + 1$ の数と解釈して、その結果から 1 を引きます。
-The sequence terminates when $g_k$ becomes 0.
+この数列は $g_k$ が 0 になると終了します。
-For example, the $6$th weak Goodstein sequence is $\\{6, 11, 17, 25, \ldots\\}$:
+例えば、$6$ 番目の弱いグッドスタイン数列は $\\{6, 11, 17, 25, \ldots\\}$ です。
-- $g_1 = 6$.
-- $g_2 = 11$ since $6 = 110_2$, $110_3 = 12$, and $12 - 1 = 11$.
-- $g_3 = 17$ since $11 = 102_3$, $102_4 = 18$, and $18 - 1 = 17$.
-- $g_4 = 25$ since $17 = 101_4$, $101_5 = 26$, and $26 - 1 = 25$.
+- $g_1 = 6$
+- $6 = 110_2$, $110_3 = 12$, $12 - 1 = 11$ なので、$g_2 = 11$
+- $11 = 102_3$, $102_4 = 18$, $18 - 1 = 17$ なので、$g_3 = 17$
+- $17 = 101_4$, $101_5 = 26$, $26 - 1 = 25$ なので、$g_4 = 25$
-and so on.
+以降もこのように続きます。
-It can be shown that every weak Goodstein sequence terminates.
+すべての弱いグッドスタイン数列が有限であることが分かっています。
-Let $G(n)$ be the number of nonzero elements in the $n$th weak Goodstein sequence.
+$n$ 番目の弱いグッドスタイン数列に含まれる、0 以外の要素の個数を $G(n)$ とします。
-It can be verified that $G(2) = 3$, $G(4) = 21$ and $G(6) = 381$.
+$G(2) = 3$, $G(4) = 21$, $G(6) = 381$ であることを確認できます。
-It can also be verified that $\sum G(n) = 2517$ for $1 ≤ n < 8$.
+$1 ≤ n < 8$ のとき、$\sum G(n) = 2517$ であることも確認できます。
-Find the last 9 digits of $\sum G(n)$ for $1 ≤ n < 16$.
+$1 ≤ n < 16$ のとき、$\sum G(n)$ の下位 9 桁を求めなさい。
# --hints--
-`weakGoodsteinSequence()` should return `173214653`.
+`weakGoodsteinSequence()` は `173214653` を返す必要があります。
```js
assert.strictEqual(weakGoodsteinSequence(), 173214653);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
index 3b9e67c1cb..855a880c40 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
@@ -1,6 +1,6 @@
---
id: 5900f4f91000cf542c51000c
-title: 'Problem 397: Triangle on parabola'
+title: '問題 397: 放物線上の三角形'
challengeType: 5
forumTopicId: 302062
dashedName: problem-397-triangle-on-parabola
@@ -8,17 +8,17 @@ dashedName: problem-397-triangle-on-parabola
# --description--
-On the parabola $y = \frac{x^2}{k}$, three points $A(a, \frac{a^2}{k})$, $B(b, \frac{b^2}{k})$ and $C(c, \frac{c^2}{k})$ are chosen.
+放物線 $y = \frac{x^2}{k}$ 上の 3 点 $A(a, \frac{a^2}{k})$, $B(b, \frac{b^2}{k})$, $C(c, \frac{c^2}{k})$ を選択します。
-Let $F(K, X)$ be the number of the integer quadruplets $(k, a, b, c)$ such that at least one angle of the triangle $ABC$ is 45°, with $1 ≤ k ≤ K$ and $-X ≤ a < b < c ≤ X$.
+$1 ≤ k ≤ K$, $-X ≤ a < b < c ≤ X$ のとき、三角形 $ABC$ の少なくとも 1 つの角度が 45 度であるような整数の四つ組 $(k, a, b, c)$ の個数を $F(K, X)$ とします。
-For example, $F(1, 10) = 41$ and $F(10, 100) = 12\\,492$.
+例えば、$F(1, 10) = 41$, $F(10, 100) = 12\\,492$ です。
-Find $F({10}^6, {10}^9)$.
+$F({10}^6, {10}^9)$ を求めなさい。
# --hints--
-`triangleOnParabola()` should return `141630459461893730`.
+`triangleOnParabola()` は `141630459461893730` を返す必要があります。
```js
assert.strictEqual(triangleOnParabola(), 141630459461893730);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md
index c51e6f4c20..f24bbaa6ed 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md
@@ -1,6 +1,6 @@
---
id: 5900f4fa1000cf542c51000d
-title: 'Problem 398: Cutting rope'
+title: '問題 398: ロープの切断'
challengeType: 5
forumTopicId: 302063
dashedName: problem-398-cutting-rope
@@ -8,15 +8,15 @@ dashedName: problem-398-cutting-rope
# --description--
-Inside a rope of length $n$, $n - 1$ points are placed with distance 1 from each other and from the endpoints. Among these points, we choose $m - 1$ points at random and cut the rope at these points to create $m$ segments.
+長さ $n$ のロープの内側に$n - 1$ 個の点が付けられています。点の間隔、および点からロープの端までの長さはそれぞれ 1 です。 これら点のうち、$m - 1$ 個の点を無作為に選択し、それらの点でロープを切断して $m$ 本のロープ片を作成します。
-Let $E(n, m)$ be the expected length of the second-shortest segment. For example, $E(3, 2) = 2$ and $E(8, 3) = \frac{16}{7}$. Note that if multiple segments have the same shortest length the length of the second-shortest segment is defined as the same as the shortest length.
+2 番目に短いロープ片の長さの期待値を $E(n, m)$ とします。 例えば、$E(3, 2) = 2$, $E(8, 3) = \frac{16}{7} $ です。 なお、最短の長さのロープ片が複数ある場合、2 番目に短いロープ片の長さは最短の長さと同一であると定義します。
-Find $E({10}^7, 100)$. Give your answer rounded to 5 decimal places behind the decimal point.
+$E({10}^7, 100)$ を求めなさい。 回答は、四捨五入して小数第 5 位まで示すこと。
# --hints--
-`cuttingRope()` should return `2010.59096`.
+`cuttingRope()` は `2010.59096` を返す必要があります。
```js
assert.strictEqual(cuttingRope(), 2010.59096);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md
index 5d21ab4568..0dc8e77c37 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4fc1000cf542c51000e
-title: 'Problem 399: Squarefree Fibonacci Numbers'
+title: '問題 399: 無平方フィボナッチ数'
challengeType: 5
forumTopicId: 302064
dashedName: problem-399-squarefree-fibonacci-numbers
@@ -8,33 +8,33 @@ dashedName: problem-399-squarefree-fibonacci-numbers
# --description--
-The first 15 fibonacci numbers are:
+以下は最初の 15 個のフィボナッチ数です。
-$$1,1,2,3,5,8,13,21,34,55,89,144,233,377,610.$$
+$$1,1,2,3,5,8,13,21,34,55,89,144,233,377,610$$
-It can be seen that 8 and 144 are not squarefree: 8 is divisible by 4 and 144 is divisible by 4 and by 9.
+8 は 4 で割り切れ、144 は 4 と 9 で割り切れるので、8 と 144 は無平方ではないことがわかります。
-So the first 13 squarefree fibonacci numbers are:
+したがって、最初の 13 個の無平方フィボナッチ数は次のようになります。
-$$1,1,2,3,5,13,21,34,55,89,233,377 \text{ and } 610.$$
+$$1,1,2,3,5,13,21,34,55,89,233,377, 610$$
-The $200$th squarefree fibonacci number is: 971183874599339129547649988289594072811608739584170445. The last sixteen digits of this number are: 1608739584170445 and in scientific notation this number can be written as `9.7e53`.
+下に示す数は $200$ 番目の無平方フィボナッチ数です。971183874599339129547649988289594072811608739584170445 この数の下位 16 桁は 1608739584170445 であり、科学的記数法ではこれを `9.7e53` と表すことができます。
-Find the $100\\,000\\,000$th squarefree fibonacci number. Give as your answer as a string with its last sixteen digits followed by a comma followed by the number in scientific notation (rounded to one digit after the decimal point). For the $200$th squarefree number the answer would have been: `1608739584170445,9.7e53`
+$100\\,000\\,000$ 番目の無平方フィボナッチ数を求めなさい。 回答は、下位 16 桁の後にカンマが続き、その後にその数を科学的記数法で表したもの (小数第 1 位に四捨五入) が続く文字列にすること。 $200$ 番目の無平方フィボナッチの場合、回答は `1608739584170445,9.7e53` という形になります。
-**Note:** For this problem, assume that for every prime $p$, the first fibonacci number divisible by $p$ is not divisible by $p^2$ (this is part of Wall's conjecture). This has been verified for primes $≤ 3 \times {10}^{15}$, but has not been proven in general.
+** 注: ** この問題では、すべての素数 $p$ について、$p$ で割り切れる最初のフィボナッチ数は $p^2$ では割り切れないものと仮定します (これは、ウォール予想の一部です)。 この仮定は、素数 $≤ 3 \times {10}^{15}$ に対して確認されていますが、一般的には証明されていません。
-If it happens that the conjecture is false, then the accepted answer to this problem isn't guaranteed to be the $100\\,000\\,000$th squarefree fibonacci number, rather it represents only a lower bound for that number.
+上述の予想が誤りである場合、この問題の想定回答は $100\\,000\\,000$ 番目の無平方フィボナッチ数であると保証されず、正しくは、そのような数の下界のみを表すものとなります。
# --hints--
-`squarefreeFibonacciNumbers()` should return a string.
+`squarefreeFibonacciNumbers()` は文字列を返す必要があります。
```js
assert(typeof squarefreeFibonacciNumbers() === 'string');
```
-`squarefreeFibonacciNumbers()` should return the string `1508395636674243,6.5e27330467`.
+`squarefreeFibonacciNumbers()` は文字列 `1508395636674243,6.5e27330467` を返す必要があります。
```js
assert.strictEqual(squarefreeFibonacciNumbers(), '1508395636674243,6.5e27330467');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md
index d77e1eb45d..f03ab07173 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4fe1000cf542c510010
-title: 'Problem 400: Fibonacci tree game'
+title: '問題 400: フィボナッチ木ゲーム'
challengeType: 5
forumTopicId: 302067
dashedName: problem-400-fibonacci-tree-game
@@ -8,27 +8,27 @@ dashedName: problem-400-fibonacci-tree-game
# --description--
-A Fibonacci tree is a binary tree recursively defined as:
+フィボナッチ木とは、次のように再帰的に定義される二分木です。
-- $T(0)$ is the empty tree.
-- $T(1)$ is the binary tree with only one node.
-- $T(k)$ consists of a root node that has $T(k - 1)$ and $T(k - 2)$ as children.
+- $T(0)$ は空木である。
+- $T(1)$ は 1 つのノードのみを持つ二分木である。
+- $T(k)$ は、$T(k - 1)$, $T(k - 2)$ を子ノードとして持つ根ノードからなる。
-On such a tree two players play a take-away game. On each turn a player selects a node and removes that node along with the subtree rooted at that node. The player who is forced to take the root node of the entire tree loses.
+このような木構造上で 2 人のプレイヤーが削除ゲームをします。 各ターンでプレイヤーがノードを選び、そのノードと、それを根とする部分木を削除します。 木全体の根ノードを取らざるを得なくなったプレイヤーが負けです。
-Here are the winning moves of the first player on the first turn for $T(k)$ from $k = 1$ to $k = 6$.
+$k = 1$ から $k = 6$ までの $T(k)$ において、最初のターンで先手必勝となる手は次のとおりです。
-
-It can be shown that there exists at least one rectangle, whose sides are parallel to the largest square of the Pythagorean tree, which encloses the Pythagorean tree completely.
+ピタゴラスの木の最大の正方形に対して平行な辺を持ち、ピタゴラスの木を完全に囲むような長方形が、少なくとも 1 つの存在することを証明できます。
-Find the smallest area possible for such a bounding rectangle, and give your answer rounded to 10 decimal places.
+そのような外接矩形が持ち得る最小の面積を求め、四捨五入して小数第 10 位まで示しなさい。
# --hints--
-`pythagoreanTree()` should return `28.2453753155`.
+`pythagoreanTree()` は `28.2453753155` を返す必要があります。
```js
assert.strictEqual(pythagoreanTree(), 28.2453753155);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
index 77684c24d4..b6f210ee54 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4f81000cf542c51000b
-title: 'Problem 396: Weak Goodstein sequence'
+title: '問題 396: 弱いグッドスタイン数列'
challengeType: 5
forumTopicId: 302061
dashedName: problem-396-weak-goodstein-sequence
@@ -8,35 +8,35 @@ dashedName: problem-396-weak-goodstein-sequence
# --description--
-For any positive integer $n$, the $n$th weak Goodstein sequence $\\{g1, g2, g3, \ldots\\}$ is defined as:
+正の整数 $n$ について、$n$ 番目の弱いグッドスタイン数列 $\\{g1, g2, g3, \ldots\\}$ は次のように定義されます。
- $g_1 = n$
-- for $k > 1$, $g_k$ is obtained by writing $g_{k - 1}$ in base $k$, interpreting it as a base $k + 1$ number, and subtracting 1.
+- $k > 1$ のとき、$g_k$ を得るには、$g_{k - 1}$ を基数 $k$ で表し、それを基数 $k + 1$ の数と解釈して、その結果から 1 を引きます。
-The sequence terminates when $g_k$ becomes 0.
+この数列は $g_k$ が 0 になると終了します。
-For example, the $6$th weak Goodstein sequence is $\\{6, 11, 17, 25, \ldots\\}$:
+例えば、$6$ 番目の弱いグッドスタイン数列は $\\{6, 11, 17, 25, \ldots\\}$ です。
-- $g_1 = 6$.
-- $g_2 = 11$ since $6 = 110_2$, $110_3 = 12$, and $12 - 1 = 11$.
-- $g_3 = 17$ since $11 = 102_3$, $102_4 = 18$, and $18 - 1 = 17$.
-- $g_4 = 25$ since $17 = 101_4$, $101_5 = 26$, and $26 - 1 = 25$.
+- $g_1 = 6$
+- $6 = 110_2$, $110_3 = 12$, $12 - 1 = 11$ なので、$g_2 = 11$
+- $11 = 102_3$, $102_4 = 18$, $18 - 1 = 17$ なので、$g_3 = 17$
+- $17 = 101_4$, $101_5 = 26$, $26 - 1 = 25$ なので、$g_4 = 25$
-and so on.
+以降もこのように続きます。
-It can be shown that every weak Goodstein sequence terminates.
+すべての弱いグッドスタイン数列が有限であることが分かっています。
-Let $G(n)$ be the number of nonzero elements in the $n$th weak Goodstein sequence.
+$n$ 番目の弱いグッドスタイン数列に含まれる、0 以外の要素の個数を $G(n)$ とします。
-It can be verified that $G(2) = 3$, $G(4) = 21$ and $G(6) = 381$.
+$G(2) = 3$, $G(4) = 21$, $G(6) = 381$ であることを確認できます。
-It can also be verified that $\sum G(n) = 2517$ for $1 ≤ n < 8$.
+$1 ≤ n < 8$ のとき、$\sum G(n) = 2517$ であることも確認できます。
-Find the last 9 digits of $\sum G(n)$ for $1 ≤ n < 16$.
+$1 ≤ n < 16$ のとき、$\sum G(n)$ の下位 9 桁を求めなさい。
# --hints--
-`weakGoodsteinSequence()` should return `173214653`.
+`weakGoodsteinSequence()` は `173214653` を返す必要があります。
```js
assert.strictEqual(weakGoodsteinSequence(), 173214653);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
index 3b9e67c1cb..855a880c40 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
@@ -1,6 +1,6 @@
---
id: 5900f4f91000cf542c51000c
-title: 'Problem 397: Triangle on parabola'
+title: '問題 397: 放物線上の三角形'
challengeType: 5
forumTopicId: 302062
dashedName: problem-397-triangle-on-parabola
@@ -8,17 +8,17 @@ dashedName: problem-397-triangle-on-parabola
# --description--
-On the parabola $y = \frac{x^2}{k}$, three points $A(a, \frac{a^2}{k})$, $B(b, \frac{b^2}{k})$ and $C(c, \frac{c^2}{k})$ are chosen.
+放物線 $y = \frac{x^2}{k}$ 上の 3 点 $A(a, \frac{a^2}{k})$, $B(b, \frac{b^2}{k})$, $C(c, \frac{c^2}{k})$ を選択します。
-Let $F(K, X)$ be the number of the integer quadruplets $(k, a, b, c)$ such that at least one angle of the triangle $ABC$ is 45°, with $1 ≤ k ≤ K$ and $-X ≤ a < b < c ≤ X$.
+$1 ≤ k ≤ K$, $-X ≤ a < b < c ≤ X$ のとき、三角形 $ABC$ の少なくとも 1 つの角度が 45 度であるような整数の四つ組 $(k, a, b, c)$ の個数を $F(K, X)$ とします。
-For example, $F(1, 10) = 41$ and $F(10, 100) = 12\\,492$.
+例えば、$F(1, 10) = 41$, $F(10, 100) = 12\\,492$ です。
-Find $F({10}^6, {10}^9)$.
+$F({10}^6, {10}^9)$ を求めなさい。
# --hints--
-`triangleOnParabola()` should return `141630459461893730`.
+`triangleOnParabola()` は `141630459461893730` を返す必要があります。
```js
assert.strictEqual(triangleOnParabola(), 141630459461893730);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md
index c51e6f4c20..f24bbaa6ed 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-398-cutting-rope.md
@@ -1,6 +1,6 @@
---
id: 5900f4fa1000cf542c51000d
-title: 'Problem 398: Cutting rope'
+title: '問題 398: ロープの切断'
challengeType: 5
forumTopicId: 302063
dashedName: problem-398-cutting-rope
@@ -8,15 +8,15 @@ dashedName: problem-398-cutting-rope
# --description--
-Inside a rope of length $n$, $n - 1$ points are placed with distance 1 from each other and from the endpoints. Among these points, we choose $m - 1$ points at random and cut the rope at these points to create $m$ segments.
+長さ $n$ のロープの内側に$n - 1$ 個の点が付けられています。点の間隔、および点からロープの端までの長さはそれぞれ 1 です。 これら点のうち、$m - 1$ 個の点を無作為に選択し、それらの点でロープを切断して $m$ 本のロープ片を作成します。
-Let $E(n, m)$ be the expected length of the second-shortest segment. For example, $E(3, 2) = 2$ and $E(8, 3) = \frac{16}{7}$. Note that if multiple segments have the same shortest length the length of the second-shortest segment is defined as the same as the shortest length.
+2 番目に短いロープ片の長さの期待値を $E(n, m)$ とします。 例えば、$E(3, 2) = 2$, $E(8, 3) = \frac{16}{7} $ です。 なお、最短の長さのロープ片が複数ある場合、2 番目に短いロープ片の長さは最短の長さと同一であると定義します。
-Find $E({10}^7, 100)$. Give your answer rounded to 5 decimal places behind the decimal point.
+$E({10}^7, 100)$ を求めなさい。 回答は、四捨五入して小数第 5 位まで示すこと。
# --hints--
-`cuttingRope()` should return `2010.59096`.
+`cuttingRope()` は `2010.59096` を返す必要があります。
```js
assert.strictEqual(cuttingRope(), 2010.59096);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md
index 5d21ab4568..0dc8e77c37 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-399-squarefree-fibonacci-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4fc1000cf542c51000e
-title: 'Problem 399: Squarefree Fibonacci Numbers'
+title: '問題 399: 無平方フィボナッチ数'
challengeType: 5
forumTopicId: 302064
dashedName: problem-399-squarefree-fibonacci-numbers
@@ -8,33 +8,33 @@ dashedName: problem-399-squarefree-fibonacci-numbers
# --description--
-The first 15 fibonacci numbers are:
+以下は最初の 15 個のフィボナッチ数です。
-$$1,1,2,3,5,8,13,21,34,55,89,144,233,377,610.$$
+$$1,1,2,3,5,8,13,21,34,55,89,144,233,377,610$$
-It can be seen that 8 and 144 are not squarefree: 8 is divisible by 4 and 144 is divisible by 4 and by 9.
+8 は 4 で割り切れ、144 は 4 と 9 で割り切れるので、8 と 144 は無平方ではないことがわかります。
-So the first 13 squarefree fibonacci numbers are:
+したがって、最初の 13 個の無平方フィボナッチ数は次のようになります。
-$$1,1,2,3,5,13,21,34,55,89,233,377 \text{ and } 610.$$
+$$1,1,2,3,5,13,21,34,55,89,233,377, 610$$
-The $200$th squarefree fibonacci number is: 971183874599339129547649988289594072811608739584170445. The last sixteen digits of this number are: 1608739584170445 and in scientific notation this number can be written as `9.7e53`.
+下に示す数は $200$ 番目の無平方フィボナッチ数です。971183874599339129547649988289594072811608739584170445 この数の下位 16 桁は 1608739584170445 であり、科学的記数法ではこれを `9.7e53` と表すことができます。
-Find the $100\\,000\\,000$th squarefree fibonacci number. Give as your answer as a string with its last sixteen digits followed by a comma followed by the number in scientific notation (rounded to one digit after the decimal point). For the $200$th squarefree number the answer would have been: `1608739584170445,9.7e53`
+$100\\,000\\,000$ 番目の無平方フィボナッチ数を求めなさい。 回答は、下位 16 桁の後にカンマが続き、その後にその数を科学的記数法で表したもの (小数第 1 位に四捨五入) が続く文字列にすること。 $200$ 番目の無平方フィボナッチの場合、回答は `1608739584170445,9.7e53` という形になります。
-**Note:** For this problem, assume that for every prime $p$, the first fibonacci number divisible by $p$ is not divisible by $p^2$ (this is part of Wall's conjecture). This has been verified for primes $≤ 3 \times {10}^{15}$, but has not been proven in general.
+** 注: ** この問題では、すべての素数 $p$ について、$p$ で割り切れる最初のフィボナッチ数は $p^2$ では割り切れないものと仮定します (これは、ウォール予想の一部です)。 この仮定は、素数 $≤ 3 \times {10}^{15}$ に対して確認されていますが、一般的には証明されていません。
-If it happens that the conjecture is false, then the accepted answer to this problem isn't guaranteed to be the $100\\,000\\,000$th squarefree fibonacci number, rather it represents only a lower bound for that number.
+上述の予想が誤りである場合、この問題の想定回答は $100\\,000\\,000$ 番目の無平方フィボナッチ数であると保証されず、正しくは、そのような数の下界のみを表すものとなります。
# --hints--
-`squarefreeFibonacciNumbers()` should return a string.
+`squarefreeFibonacciNumbers()` は文字列を返す必要があります。
```js
assert(typeof squarefreeFibonacciNumbers() === 'string');
```
-`squarefreeFibonacciNumbers()` should return the string `1508395636674243,6.5e27330467`.
+`squarefreeFibonacciNumbers()` は文字列 `1508395636674243,6.5e27330467` を返す必要があります。
```js
assert.strictEqual(squarefreeFibonacciNumbers(), '1508395636674243,6.5e27330467');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md
index d77e1eb45d..f03ab07173 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-400-fibonacci-tree-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4fe1000cf542c510010
-title: 'Problem 400: Fibonacci tree game'
+title: '問題 400: フィボナッチ木ゲーム'
challengeType: 5
forumTopicId: 302067
dashedName: problem-400-fibonacci-tree-game
@@ -8,27 +8,27 @@ dashedName: problem-400-fibonacci-tree-game
# --description--
-A Fibonacci tree is a binary tree recursively defined as:
+フィボナッチ木とは、次のように再帰的に定義される二分木です。
-- $T(0)$ is the empty tree.
-- $T(1)$ is the binary tree with only one node.
-- $T(k)$ consists of a root node that has $T(k - 1)$ and $T(k - 2)$ as children.
+- $T(0)$ は空木である。
+- $T(1)$ は 1 つのノードのみを持つ二分木である。
+- $T(k)$ は、$T(k - 1)$, $T(k - 2)$ を子ノードとして持つ根ノードからなる。
-On such a tree two players play a take-away game. On each turn a player selects a node and removes that node along with the subtree rooted at that node. The player who is forced to take the root node of the entire tree loses.
+このような木構造上で 2 人のプレイヤーが削除ゲームをします。 各ターンでプレイヤーがノードを選び、そのノードと、それを根とする部分木を削除します。 木全体の根ノードを取らざるを得なくなったプレイヤーが負けです。
-Here are the winning moves of the first player on the first turn for $T(k)$ from $k = 1$ to $k = 6$.
+$k = 1$ から $k = 6$ までの $T(k)$ において、最初のターンで先手必勝となる手は次のとおりです。
-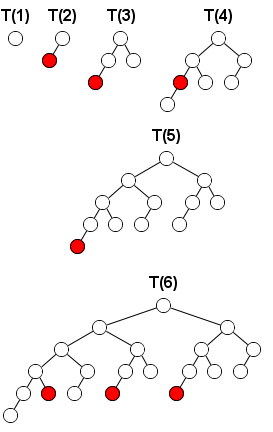 +
+ -Let $f(k)$ be the number of winning moves of the first player (i.e. the moves for which the second player has no winning strategy) on the first turn of the game when this game is played on $T(k)$.
+$T(k)$ の木構造でゲームをするとき、最初のターンにおける先手必勝の手 (すなわち、後手がどのような戦略でも勝てなくなるような手) の数を $f(k)$ とします。
-For example, $f(5) = 1$ and $f(10) = 17$.
+例えば、$f(5) = 1$, $f(10) = 17$ です。
-Find $f(10000)$. Give the last 18 digits of your answer.
+$f(10000)$ を求めなさい。 回答は、下位 18 桁とすること。
# --hints--
-`fibonacciTreeGame()` should return `438505383468410600`.
+`fibonacciTreeGame()` は `438505383468410600` を返す必要があります。
```js
assert.strictEqual(fibonacciTreeGame(), 438505383468410600);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md
index 69bf18c848..9bd3ae3539 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f4fd1000cf542c51000f
-title: 'Problem 401: Sum of squares of divisors'
+title: '問題 401: 約数の平方和'
challengeType: 5
forumTopicId: 302069
dashedName: problem-401-sum-of-squares-of-divisors
@@ -8,19 +8,19 @@ dashedName: problem-401-sum-of-squares-of-divisors
# --description--
-The divisors of 6 are 1, 2, 3 and 6.
+6 の約数は 1, 2, 3, 6 です。
-The sum of the squares of these numbers is $1 + 4 + 9 + 36 = 50$.
+これらの数の平方和は $1 + 4 + 9 + 36 = 50$ です。
-Let $\sigma_2(n)$ represent the sum of the squares of the divisors of $n$. Thus $\sigma_2(6) = 50$.
+$n$ の約数の平方和を $\sigma_2(n)$ で表すことにします。 そうすると、$\sigma_2(6) = 50$ になります。
-Let $\Sigma_2$ represent the summatory function of $\sigma_2$, that is $\Sigma_2(n) = \sum \sigma_2(i)$ for $i=1$ to $n$. The first 6 values of $\Sigma_2$ are: 1, 6, 16, 37, 63 and 113.
+$\sigma_2$ の総和関数を $\Sigma_2$ で表します。つまり、$\Sigma_2(n) = \sum \sigma_2(i)$ ($i=1$ から $n$ まで) です。 $\Sigma_2$ の最初の 6 つの値は 1, 6, 16, 37, 63, 113 です。
-Find $\Sigma_2({10}^{15})$ modulo ${10}^9$.
+$\Sigma_2({10}^{15})$ mod ${10}^9$ を求めなさい。
# --hints--
-`sumOfSquaresDivisors()` should return `281632621`.
+`sumOfSquaresDivisors()` は `281632621` を返す必要があります。
```js
assert.strictEqual(sumOfSquaresDivisors(), 281632621);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md
index 7fd0858e03..658fa15c6b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4ff1000cf542c510011
-title: 'Problem 402: Integer-valued polynomials'
+title: '問題 402: 整数値多項式'
challengeType: 5
forumTopicId: 302070
dashedName: problem-402-integer-valued-polynomials
@@ -8,24 +8,24 @@ dashedName: problem-402-integer-valued-polynomials
# --description--
-It can be shown that the polynomial $n^4 + 4n^3 + 2n^2 + 5n$ is a multiple of 6 for every integer $n$. It can also be shown that 6 is the largest integer satisfying this property.
+すべての整数 $n$ について、多項式 $n^4 + 4n^3 + 2n^2 + 5n$ が 6 の倍数であることが分かっています。 また、このような性質を持つ最大の整数が 6 であることも分かっています。
-Define $M(a, b, c)$ as the maximum $m$ such that $n^4 + an^3 + bn^2 + cn$ is a multiple of $m$ for all integers $n$. For example, $M(4, 2, 5) = 6$.
+$n^4 + an^3 + bn^2 + cn$ がすべての整数 $n$ について $m$ の倍数となるような最大の $m$ を、$M(a, b, c)$ とします。 例えば、$M(4, 2, 5) = 6$ です。
-Also, define $S(N)$ as the sum of $M(a, b, c)$ for all $0 < a, b, c ≤ N$.
+また、$0 < a, b, c ≤ N$ のとき、$M(a, b, c)$ の和を $S(N)$ とします。
-We can verify that $S(10) = 1\\,972$ and $S(10\\,000) = 2\\,024\\,258\\,331\\,114$.
+$S(10) = 1\\,972$, $S(10\\,000) = 2\\,024\\,258\\,331\\,114$ であることを確認できます。
-Let $F_k$ be the Fibonacci sequence:
+次の条件をすべて満たすフィボナッチ数列を $F_k$ とします。
-- $F_0 = 0$, $F_1 = 1$ and
-- $F_k = F_{k - 1} + F_{k - 2}$ for $k ≥ 2$.
+- $F_0 = 0$, $F_1 = 1$
+- $k ≥ 2$ のとき、$F_k = F_{k - 1} + F_{k - 2}$
-Find the last 9 digits of $\sum S(F_k)$ for $2 ≤ k ≤ 1\\,234\\,567\\,890\\,123$.
+$2 ≤ k ≤ 1\\,234\\,567\\,890\\,123$ のとき、$\sum S(F_k)$ の下位 9 桁を求めなさい。
# --hints--
-`integerValuedPolynomials()` should return `356019862`.
+`integerValuedPolynomials()` は `356019862` を返す必要があります。
```js
assert.strictEqual(integerValuedPolynomials(), 356019862);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md
index 1bf202f5db..ab1739775f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md
@@ -1,6 +1,6 @@
---
id: 5900f5001000cf542c510013
-title: 'Problem 403: Lattice points enclosed by parabola and line'
+title: '問題 403: 放物線と線で囲まれた格子点'
challengeType: 5
forumTopicId: 302071
dashedName: problem-403-lattice-points-enclosed-by-parabola-and-line
@@ -8,19 +8,19 @@ dashedName: problem-403-lattice-points-enclosed-by-parabola-and-line
# --description--
-For integers $a$ and $b$, we define $D(a, b)$ as the domain enclosed by the parabola $y = x^2$ and the line $y = ax + b: D(a, b) = \\{ (x, y) | x^2 ≤ y ≤ ax + b \\}$.
+整数 $a$ と $b$ に対し、放物線 $y = x^2$ と線 $y = ax + b で囲まれた領域として $D(a, b)$ を定義します。すなわち、D(a, b) = \\{ (x, y) | x^2 ≤ y ≤ ax + b \\}$ です。
-$L(a, b)$ is defined as the number of lattice points contained in $D(a, b)$. For example, $L(1, 2) = 8$ and $L(2, -1) = 1$.
+$D(a, b)$ に含まれる格子点の数を $L(a, b)$ と定義します。 例えば、$L(1, 2) = 8$, $L(2, -1) = 1$ です。
-We also define $S(N)$ as the sum of $L(a, b)$ for all the pairs ($a$, $b$) such that the area of $D(a, b)$ is a rational number and $|a|,|b| ≤ N$.
+また、$D(a, b)$ の面積が有理数であり、かつ $|a|,|b| ≤ N$ であるようなすべての対 ($a$, $b$) に対して、$L(a, b)$ の和を $S(N)$ と定義します。
-We can verify that $S(5) = 344$ and $S(100) = 26\\,709\\,528$.
+$S(5) = 344$, $S(100) = 26\\,709\\,528$ であることを確認できます。
-Find $S({10}^{12})$. Give your answer $\bmod {10}^8$.
+$S({10}^{12})$ を求めなさい。 $\bmod {10}^8$ で答えること。
# --hints--
-`latticePoints()` should return `18224771`.
+`latticePoints()` は `18224771` を返す必要があります。
```js
assert.strictEqual(latticePoints(), 18224771);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md
index 171955509c..9c7d07aee8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md
@@ -1,6 +1,6 @@
---
id: 5900f5001000cf542c510012
-title: 'Problem 404: Crisscross Ellipses'
+title: '問題 404: 交差楕円'
challengeType: 5
forumTopicId: 302072
dashedName: problem-404-crisscross-ellipses
@@ -8,27 +8,27 @@ dashedName: problem-404-crisscross-ellipses
# --description--
-$E_a$ is an ellipse with an equation of the form $x^2 + 4y^2 = 4a^2$.
+$E_a$ は 式 $x^2 + 4y^2 = 4a^2$ で表される楕円です。
-$E_a'$ is the rotated image of $E_a$ by $θ$ degrees counterclockwise around the origin $O(0, 0)$ for $0° < θ < 90°$.
+$E_a'$ は、原点 $O(0, 0)$ を中心に、$0° < θ < 90°$ の範囲内で、$E_a$ を反時計回りに $θ$ 度回転させた像です。
-
-Let $f(k)$ be the number of winning moves of the first player (i.e. the moves for which the second player has no winning strategy) on the first turn of the game when this game is played on $T(k)$.
+$T(k)$ の木構造でゲームをするとき、最初のターンにおける先手必勝の手 (すなわち、後手がどのような戦略でも勝てなくなるような手) の数を $f(k)$ とします。
-For example, $f(5) = 1$ and $f(10) = 17$.
+例えば、$f(5) = 1$, $f(10) = 17$ です。
-Find $f(10000)$. Give the last 18 digits of your answer.
+$f(10000)$ を求めなさい。 回答は、下位 18 桁とすること。
# --hints--
-`fibonacciTreeGame()` should return `438505383468410600`.
+`fibonacciTreeGame()` は `438505383468410600` を返す必要があります。
```js
assert.strictEqual(fibonacciTreeGame(), 438505383468410600);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md
index 69bf18c848..9bd3ae3539 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-401-sum-of-squares-of-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f4fd1000cf542c51000f
-title: 'Problem 401: Sum of squares of divisors'
+title: '問題 401: 約数の平方和'
challengeType: 5
forumTopicId: 302069
dashedName: problem-401-sum-of-squares-of-divisors
@@ -8,19 +8,19 @@ dashedName: problem-401-sum-of-squares-of-divisors
# --description--
-The divisors of 6 are 1, 2, 3 and 6.
+6 の約数は 1, 2, 3, 6 です。
-The sum of the squares of these numbers is $1 + 4 + 9 + 36 = 50$.
+これらの数の平方和は $1 + 4 + 9 + 36 = 50$ です。
-Let $\sigma_2(n)$ represent the sum of the squares of the divisors of $n$. Thus $\sigma_2(6) = 50$.
+$n$ の約数の平方和を $\sigma_2(n)$ で表すことにします。 そうすると、$\sigma_2(6) = 50$ になります。
-Let $\Sigma_2$ represent the summatory function of $\sigma_2$, that is $\Sigma_2(n) = \sum \sigma_2(i)$ for $i=1$ to $n$. The first 6 values of $\Sigma_2$ are: 1, 6, 16, 37, 63 and 113.
+$\sigma_2$ の総和関数を $\Sigma_2$ で表します。つまり、$\Sigma_2(n) = \sum \sigma_2(i)$ ($i=1$ から $n$ まで) です。 $\Sigma_2$ の最初の 6 つの値は 1, 6, 16, 37, 63, 113 です。
-Find $\Sigma_2({10}^{15})$ modulo ${10}^9$.
+$\Sigma_2({10}^{15})$ mod ${10}^9$ を求めなさい。
# --hints--
-`sumOfSquaresDivisors()` should return `281632621`.
+`sumOfSquaresDivisors()` は `281632621` を返す必要があります。
```js
assert.strictEqual(sumOfSquaresDivisors(), 281632621);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md
index 7fd0858e03..658fa15c6b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-402-integer-valued-polynomials.md
@@ -1,6 +1,6 @@
---
id: 5900f4ff1000cf542c510011
-title: 'Problem 402: Integer-valued polynomials'
+title: '問題 402: 整数値多項式'
challengeType: 5
forumTopicId: 302070
dashedName: problem-402-integer-valued-polynomials
@@ -8,24 +8,24 @@ dashedName: problem-402-integer-valued-polynomials
# --description--
-It can be shown that the polynomial $n^4 + 4n^3 + 2n^2 + 5n$ is a multiple of 6 for every integer $n$. It can also be shown that 6 is the largest integer satisfying this property.
+すべての整数 $n$ について、多項式 $n^4 + 4n^3 + 2n^2 + 5n$ が 6 の倍数であることが分かっています。 また、このような性質を持つ最大の整数が 6 であることも分かっています。
-Define $M(a, b, c)$ as the maximum $m$ such that $n^4 + an^3 + bn^2 + cn$ is a multiple of $m$ for all integers $n$. For example, $M(4, 2, 5) = 6$.
+$n^4 + an^3 + bn^2 + cn$ がすべての整数 $n$ について $m$ の倍数となるような最大の $m$ を、$M(a, b, c)$ とします。 例えば、$M(4, 2, 5) = 6$ です。
-Also, define $S(N)$ as the sum of $M(a, b, c)$ for all $0 < a, b, c ≤ N$.
+また、$0 < a, b, c ≤ N$ のとき、$M(a, b, c)$ の和を $S(N)$ とします。
-We can verify that $S(10) = 1\\,972$ and $S(10\\,000) = 2\\,024\\,258\\,331\\,114$.
+$S(10) = 1\\,972$, $S(10\\,000) = 2\\,024\\,258\\,331\\,114$ であることを確認できます。
-Let $F_k$ be the Fibonacci sequence:
+次の条件をすべて満たすフィボナッチ数列を $F_k$ とします。
-- $F_0 = 0$, $F_1 = 1$ and
-- $F_k = F_{k - 1} + F_{k - 2}$ for $k ≥ 2$.
+- $F_0 = 0$, $F_1 = 1$
+- $k ≥ 2$ のとき、$F_k = F_{k - 1} + F_{k - 2}$
-Find the last 9 digits of $\sum S(F_k)$ for $2 ≤ k ≤ 1\\,234\\,567\\,890\\,123$.
+$2 ≤ k ≤ 1\\,234\\,567\\,890\\,123$ のとき、$\sum S(F_k)$ の下位 9 桁を求めなさい。
# --hints--
-`integerValuedPolynomials()` should return `356019862`.
+`integerValuedPolynomials()` は `356019862` を返す必要があります。
```js
assert.strictEqual(integerValuedPolynomials(), 356019862);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md
index 1bf202f5db..ab1739775f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-403-lattice-points-enclosed-by-parabola-and-line.md
@@ -1,6 +1,6 @@
---
id: 5900f5001000cf542c510013
-title: 'Problem 403: Lattice points enclosed by parabola and line'
+title: '問題 403: 放物線と線で囲まれた格子点'
challengeType: 5
forumTopicId: 302071
dashedName: problem-403-lattice-points-enclosed-by-parabola-and-line
@@ -8,19 +8,19 @@ dashedName: problem-403-lattice-points-enclosed-by-parabola-and-line
# --description--
-For integers $a$ and $b$, we define $D(a, b)$ as the domain enclosed by the parabola $y = x^2$ and the line $y = ax + b: D(a, b) = \\{ (x, y) | x^2 ≤ y ≤ ax + b \\}$.
+整数 $a$ と $b$ に対し、放物線 $y = x^2$ と線 $y = ax + b で囲まれた領域として $D(a, b)$ を定義します。すなわち、D(a, b) = \\{ (x, y) | x^2 ≤ y ≤ ax + b \\}$ です。
-$L(a, b)$ is defined as the number of lattice points contained in $D(a, b)$. For example, $L(1, 2) = 8$ and $L(2, -1) = 1$.
+$D(a, b)$ に含まれる格子点の数を $L(a, b)$ と定義します。 例えば、$L(1, 2) = 8$, $L(2, -1) = 1$ です。
-We also define $S(N)$ as the sum of $L(a, b)$ for all the pairs ($a$, $b$) such that the area of $D(a, b)$ is a rational number and $|a|,|b| ≤ N$.
+また、$D(a, b)$ の面積が有理数であり、かつ $|a|,|b| ≤ N$ であるようなすべての対 ($a$, $b$) に対して、$L(a, b)$ の和を $S(N)$ と定義します。
-We can verify that $S(5) = 344$ and $S(100) = 26\\,709\\,528$.
+$S(5) = 344$, $S(100) = 26\\,709\\,528$ であることを確認できます。
-Find $S({10}^{12})$. Give your answer $\bmod {10}^8$.
+$S({10}^{12})$ を求めなさい。 $\bmod {10}^8$ で答えること。
# --hints--
-`latticePoints()` should return `18224771`.
+`latticePoints()` は `18224771` を返す必要があります。
```js
assert.strictEqual(latticePoints(), 18224771);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md
index 171955509c..9c7d07aee8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-404-crisscross-ellipses.md
@@ -1,6 +1,6 @@
---
id: 5900f5001000cf542c510012
-title: 'Problem 404: Crisscross Ellipses'
+title: '問題 404: 交差楕円'
challengeType: 5
forumTopicId: 302072
dashedName: problem-404-crisscross-ellipses
@@ -8,27 +8,27 @@ dashedName: problem-404-crisscross-ellipses
# --description--
-$E_a$ is an ellipse with an equation of the form $x^2 + 4y^2 = 4a^2$.
+$E_a$ は 式 $x^2 + 4y^2 = 4a^2$ で表される楕円です。
-$E_a'$ is the rotated image of $E_a$ by $θ$ degrees counterclockwise around the origin $O(0, 0)$ for $0° < θ < 90°$.
+$E_a'$ は、原点 $O(0, 0)$ を中心に、$0° < θ < 90°$ の範囲内で、$E_a$ を反時計回りに $θ$ 度回転させた像です。
-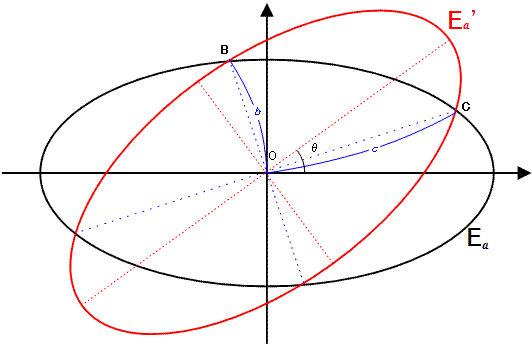 +
+ -$b$ is the distance to the origin of the two intersection points closest to the origin and $c$ is the distance of the two other intersection points.
+原点に最も近い 2 つの交点から原点までの距離を $b$、それ以外の 2 つの交点から原点までの距離を $c$ とします。
-We call an ordered triplet ($a$, $b$, $c$) a canonical ellipsoidal triplet if $a$, $b$ and $c$ are positive integers.
+$a$, $b$, $c$ が正の整数の場合、順序付き三つ組数 ($a$, $b$, $c$) を正準楕円三つ組数と呼びます。
-For example, (209, 247, 286) is a canonical ellipsoidal triplet.
+例えば、(209、247、286) は正準楕円三つ組数です。
-Let $C(N)$ be the number of distinct canonical ellipsoidal triplets ($a$, $b$, $c$) for $a ≤ N$.
+$a ≤ N$ に対し、相異なる正準楕円三つ組数 ($a$, $b$, $c$) の個数を $C(N)$ とします。
-It can be verified that $C({10}^3) = 7$, $C({10}^4) = 106$ and $C({10}^6) = 11\\,845$.
+$C({10}^3) = 7$, $C({10}^4) = 106$, $C({10}^6) = 11\\,845$ であることを確認できます。
-Find $C({10}^{17})$.
+$C({10}^{17})$ を求めなさい。
# --hints--
-`crisscrossEllipses()` should return `1199215615081353`.
+`crisscrossEllipses()` は `1199215615081353` を返す必要があります。
```js
assert.strictEqual(crisscrossEllipses(), 1199215615081353);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md
index 641dcdcb64..b36356d623 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md
@@ -1,6 +1,6 @@
---
id: 5900f5021000cf542c510014
-title: 'Problem 405: A rectangular tiling'
+title: '問題 405: 長方形の敷き詰め'
challengeType: 5
forumTopicId: 302073
dashedName: problem-405-a-rectangular-tiling
@@ -8,25 +8,25 @@ dashedName: problem-405-a-rectangular-tiling
# --description--
-We wish to tile a rectangle whose length is twice its width.
+縦の長さが横の長さの 2 倍である長方形タイルを敷き詰めます。
-Let $T(0)$ be the tiling consisting of a single rectangle.
+1 枚の長方形タイルで敷き詰めたものを $T(0)$ とします。
-For $n > 0$, let $T(n)$ be obtained from $T( n- 1)$ by replacing all tiles in the following manner:
+$n > 0$ のとき、$T(n-1)$ のすべてのタイルを下図のように置き換えることで $T(n)$ を得ます。
-
-$b$ is the distance to the origin of the two intersection points closest to the origin and $c$ is the distance of the two other intersection points.
+原点に最も近い 2 つの交点から原点までの距離を $b$、それ以外の 2 つの交点から原点までの距離を $c$ とします。
-We call an ordered triplet ($a$, $b$, $c$) a canonical ellipsoidal triplet if $a$, $b$ and $c$ are positive integers.
+$a$, $b$, $c$ が正の整数の場合、順序付き三つ組数 ($a$, $b$, $c$) を正準楕円三つ組数と呼びます。
-For example, (209, 247, 286) is a canonical ellipsoidal triplet.
+例えば、(209、247、286) は正準楕円三つ組数です。
-Let $C(N)$ be the number of distinct canonical ellipsoidal triplets ($a$, $b$, $c$) for $a ≤ N$.
+$a ≤ N$ に対し、相異なる正準楕円三つ組数 ($a$, $b$, $c$) の個数を $C(N)$ とします。
-It can be verified that $C({10}^3) = 7$, $C({10}^4) = 106$ and $C({10}^6) = 11\\,845$.
+$C({10}^3) = 7$, $C({10}^4) = 106$, $C({10}^6) = 11\\,845$ であることを確認できます。
-Find $C({10}^{17})$.
+$C({10}^{17})$ を求めなさい。
# --hints--
-`crisscrossEllipses()` should return `1199215615081353`.
+`crisscrossEllipses()` は `1199215615081353` を返す必要があります。
```js
assert.strictEqual(crisscrossEllipses(), 1199215615081353);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md
index 641dcdcb64..b36356d623 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-405-a-rectangular-tiling.md
@@ -1,6 +1,6 @@
---
id: 5900f5021000cf542c510014
-title: 'Problem 405: A rectangular tiling'
+title: '問題 405: 長方形の敷き詰め'
challengeType: 5
forumTopicId: 302073
dashedName: problem-405-a-rectangular-tiling
@@ -8,25 +8,25 @@ dashedName: problem-405-a-rectangular-tiling
# --description--
-We wish to tile a rectangle whose length is twice its width.
+縦の長さが横の長さの 2 倍である長方形タイルを敷き詰めます。
-Let $T(0)$ be the tiling consisting of a single rectangle.
+1 枚の長方形タイルで敷き詰めたものを $T(0)$ とします。
-For $n > 0$, let $T(n)$ be obtained from $T( n- 1)$ by replacing all tiles in the following manner:
+$n > 0$ のとき、$T(n-1)$ のすべてのタイルを下図のように置き換えることで $T(n)$ を得ます。
-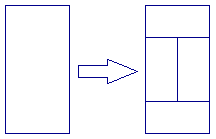 +
+ -The following animation demonstrates the tilings $T(n)$ for $n$ from 0 to 5:
+次のアニメーションは、$n$ が 0 から 5 のときのタイルの敷き詰め方 $T(n)$ を示しています。
-
-The following animation demonstrates the tilings $T(n)$ for $n$ from 0 to 5:
+次のアニメーションは、$n$ が 0 から 5 のときのタイルの敷き詰め方 $T(n)$ を示しています。
- +
+ -Let $f(n)$ be the number of points where four tiles meet in $T(n)$. For example, $f(1) = 0$, $f(4) = 82$ and $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$.
+$T(n)$ で 4 枚のタイルが集まる点の個数を $f(n)$ とします。 例えば、$f(1) = 0$, $f(4) = 82$, $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$ です。
-Find $f({10}^k)$ for $k = {10}^{18}$, give your answer modulo ${17}^7$.
+$k = {10}^{18}$ のとき、$f({10}^k)$ mod ${17}^7$ を求めなさい。
# --hints--
-`rectangularTiling()` should return `237696125`.
+`rectangularTiling()` は `237696125` を返す必要があります。
```js
assert.strictEqual(rectangularTiling(), 237696125);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md
index 770438981f..da4eeed10f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md
@@ -1,6 +1,6 @@
---
id: 5900f5021000cf542c510015
-title: 'Problem 406: Guessing Game'
+title: '問題 406: 推測ゲーム'
challengeType: 5
forumTopicId: 302074
dashedName: problem-406-guessing-game
@@ -8,39 +8,39 @@ dashedName: problem-406-guessing-game
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, we get one of three possible answers:
+整数の集合 {1, 2, ..., $n$} から選ばれた秘密の数を、質問をすることで当てます。 それぞれの数 (質問) で得られる回答は、次の 3 つのいずれかです。
-- "Your guess is lower than the hidden number" (and you incur a cost of a), or
-- "Your guess is higher than the hidden number" (and you incur a cost of b), or
-- "Yes, that's it!" (and the game ends).
+- 「あなたの推測は秘密の数よりも小さい」(a のコストが発生する)
+- 「あなたの推測は秘密の数よりも大きい」(b のコストが発生する)
+- 「当たり!」 (ゲーム終了)
-Given the value of $n$, $a$, and $b$, an optimal strategy minimizes the total cost for the worst possible case.
+値 $n$, $a$, $b$ が与えられているとき、最適な戦略に従えば、起こり得る最悪のケースの総コストが最小化します。
-For example, if $n = 5$, $a = 2$, and $b = 3$, then we may begin by asking "2" as our first question.
+例えば、$n = 5$, $a = 2$, $b = 3$ の場合、最初に秘密の数が "2" であるかどうかを尋ねます。
-If we are told that 2 is higher than the hidden number (for a cost of $b = 3$), then we are sure that "1" is the hidden number (for a total cost of 3).
+2 が秘密の数よりも大きいと告げられた場合 (コストは $b = 3$)、秘密の数が "1" であることが分かります (総コストは 3)。
-If we are told that 2 is lower than the hidden number (for a cost of $a = 2$), then our next question will be "4".
+2 が秘密の数よりも小さいと告げられた場合 (コストは $a = 2$)、次の質問は "4" です。
-If we are told that 4 is higher than the hidden number (for a cost of $b = 3$), then we are sure that "3" is the hidden number (for a total cost of $2 + 3 = \color{blue}{\mathbf{5}}$).
+4 が秘密の数よりも大きいと告げられた場合 (コストは $b = 3$)、秘密の数が "3" であることが分かります (総コストは $2 + 3 = \color{blue}{\mathbf{5}}$)。
-If we are told that 4 is lower than the hidden number (for a cost of $a = 2$), then we are sure that "5" is the hidden number (for a total cost of $2 + 2 = \color{blue}{\mathbf{4}}$).
+4 が秘密の数よりも小さいと告げられた場合 (コスト $a = 2$)、秘密の数が "5" であることが分かります (総コストは $2 + 2 = \color{blue}{\mathbf{4}}$)。
-Thus, the worst-case cost achieved by this strategy is 5. It can also be shown that this is the lowest worst-case cost that can be achieved. So, in fact, we have just described an optimal strategy for the given values of $n$, $a$, and $b$.
+したがって、この戦略によって達成される、最悪ケースのコストは 5 です。 また、達成可能な最悪ケースのコストの中でこれが最も低いコストであることも分かっています。 つまり、与えられた値 $n$, $a$, $b$ に対してこれが最適な戦略です。
-Let $C(n, a, b)$ be the worst-case cost achieved by an optimal strategy for the given values of $n$, $a$, and $b$.
+与えられた値 $n$, $a$, $b$ に対する最適な戦略によって達成される、最悪ケースのコストを $C(n, a, b)$ とします。
-Here are a few examples:
+いくつかの例を次に示します。
$$\begin{align} & C(5, 2, 3) = 5 \\\\ & C(500, \sqrt{2}, \sqrt{3}) = 13.220\\,731\\,97\ldots \\\\ & C(20\\,000, 5, 7) = 82 \\\\ & C(2\\,000\\,000, √5, √7) = 49.637\\,559\\,55\ldots \\\\ \end{align}$$
-Let $F_k$ be the Fibonacci numbers: $F_k = F_{k - 1} + F_{k - 2}$ with base cases $F_1 = F_2 = 1$.
+$F_1 = F_2 = 1$ を初期条件とするフィボナッチ数 $F_k = F_{k - 1} + F_{k - 2}$ を $F_k$ と定義します。
-Find $\displaystyle\sum_{k = 1}^{30} C({10}^{12}, \sqrt{k}, \sqrt{F_k})$, and give your answer rounded to 8 decimal places behind the decimal point.
+$\displaystyle\sum_{k = 1}^{30} C({10}^{12}, \sqrt{k}, \sqrt{F_k})$ を求め、四捨五入して小数第 8 位まで示しなさい。
# --hints--
-`guessingGame()` should return `36813.12757207`.
+`guessingGame()` は `36813.12757207` を返す必要があります。
```js
assert.strictEqual(guessingGame(), 36813.12757207);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md
index bae66db99c..e262a008f2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md
@@ -1,6 +1,6 @@
---
id: 5900f5041000cf542c510016
-title: 'Problem 407: Idempotents'
+title: '冪等元'
challengeType: 5
forumTopicId: 302075
dashedName: problem-407-idempotents
@@ -8,17 +8,17 @@ dashedName: problem-407-idempotents
# --description--
-If we calculate $a^2\bmod 6$ for $0 ≤ a ≤ 5$ we get: 0, 1, 4, 3, 4, 1.
+$0 ≤ a ≤ 5$ のとき $a^2\bmod 6$ を求めると、0, 1, 4, 3, 4, 1 になります。
-The largest value of a such that $a^2 ≡ a\bmod 6$ is $4$.
+$a^2 ≡ a\bmod 6$ となる a の最大値は $4$ です。
-Let's call $M(n)$ the largest value of $a < n$ such that $a^2 ≡ a (\text{mod } n)$. So $M(6) = 4$.
+$a^2 ≡ a (\text{mod } n)$ となる $a < n$ の最大値を $M(n)$ とします。 したがって、$M(6) = 4$ です。
-Find $\sum M(n)$ for $1 ≤ n ≤ {10}^7$.
+$1 ≤ n ≤ {10}^7$ のとき、$\sum M(n)$ を求めなさい。
# --hints--
-`idempotents()` should return `39782849136421`.
+`idempotents()` は `39782849136421` を返す必要があります。
```js
assert.strictEqual(idempotents(), 39782849136421);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md
index 94e93e63c8..0f11bd9ee2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md
@@ -1,6 +1,6 @@
---
id: 5900f5091000cf542c51001b
-title: 'Problem 408: Admissible paths through a grid'
+title: '問題 408: 格子内の許容的経路'
challengeType: 5
forumTopicId: 302076
dashedName: problem-408-admissible-paths-through-a-grid
@@ -8,19 +8,19 @@ dashedName: problem-408-admissible-paths-through-a-grid
# --description--
-Let's call a lattice point ($x$, $y$) inadmissible if $x$, $y$ and $x + y$ are all positive perfect squares.
+$x$, $y$, $x + y$ がすべて正の完全平方数の場合、格子点 ($x$, $y$) を「非許容的」と表現することにします。
-For example, (9, 16) is inadmissible, while (0, 4), (3, 1) and (9, 4) are not.
+例えば、(9, 16) は非許容的な点ですが、(0, 4), (3, 1), (9, 4) はそうではありません。
-Consider a path from point ($x_1$, $y_1$) to point ($x_2$, $y_2$) using only unit steps north or east. Let's call such a path admissible if none of its intermediate points are inadmissible.
+点 ($x_1$, $y_1$) から点 ($x_2$, $y_2$) へ、北方向または東方向への単位ステップのみで移動する場合の経路を考えます。 経路上の中間点がいずれも非許容的ではない場合、そのような経路を「許容的」と表現することにします。
-Let $P(n)$ be the number of admissible paths from (0, 0) to ($n$, $n$). It can be verified that $P(5) = 252$, $P(16) = 596\\,994\\,440$ and $P(1\\,000)\bmod 1\\,000\\,000\\,007 = 341\\,920\\,854$.
+(0, 0) から ($n$, $n$) までの許容的な経路の数を $P(n)$ とします。 $P(5) = 252$, $P(16) = 596\\,994\\,440$, $P(1\\,000)\bmod 1\\,000\\,000\\,007 = 341\\,920\\,854$ であることを確認できます。
-Find $P(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+$P(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`admissiblePaths()` should return `299742733`.
+`admissiblePaths()`は `299742733` を返す必要があります。
```js
assert.strictEqual(admissiblePaths(), 299742733);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md
index b751cb412b..30729a0915 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md
@@ -1,6 +1,6 @@
---
id: 5900f5061000cf542c510017
-title: 'Problem 409: Nim Extreme'
+title: '問題 409: 極端なニム (石取りゲーム)'
challengeType: 5
forumTopicId: 302077
dashedName: problem-409-nim-extreme
@@ -8,21 +8,21 @@ dashedName: problem-409-nim-extreme
# --description--
-Let $n$ be a positive integer. Consider nim positions where:
+$n$ を正の整数とします。 次のような二ム (石取りゲーム) の配置について考えます。
-- There are $n$ non-empty piles.
-- Each pile has size less than $2^n$.
-- No two piles have the same size.
+- 空でない山が $n$ 個ある。
+- それぞれの山のサイズは $2^n$ 未満である。
+- 同じサイズの山はない。
-Let $W(n)$ be the number of winning nim positions satisfying the above conditions (a position is winning if the first player has a winning strategy).
+上の条件を満たすような、二ムの勝利ポジション (先手が必勝戦略を持つようなポジション) の数を $W(n)$ とします 。
-For example, $W(1) = 1$, $W(2) = 6$, $W(3) = 168$, $W(5) = 19\\,764\\,360$ and $W(100)\bmod 1\\,000\\,000\\,007 = 384\\,777\\,056$.
+例えば、$W(1) = 1$, $W(2) = 6$, $W(3) = 168$, $W(5) = 19\\,764\\,360$, $W(100)\bmod 1\\,000\\,000\\,007 = 384\\,777\\,056$ です。
-Find $W(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+$W(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`nimExtreme()` should return `253223948`.
+`nimExtreme()` は `253223948` を返す必要があります。
```js
assert.strictEqual(nimExtreme(), 253223948);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md
index 81ab40a2c9..4d1932896a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md
@@ -1,6 +1,6 @@
---
id: 5900f5071000cf542c510018
-title: 'Problem 410: Circle and tangent line'
+title: '問題 410: 円と接線'
challengeType: 5
forumTopicId: 302079
dashedName: problem-410-circle-and-tangent-line
@@ -8,19 +8,19 @@ dashedName: problem-410-circle-and-tangent-line
# --description--
-Let $C$ be the circle with radius $r$, $x^2 + y^2 = r^2$. We choose two points $P(a, b)$ and $Q(-a, c)$ so that the line passing through $P$ and $Q$ is tangent to $C$.
+半径 $r$, $x^2 + y^2 = r^2$ の円を $C$ とします。 2 つの点 $P(a, b)$, $Q(-a, c)$ を通過する線が $C$ の接線となるように、$P$, $Q$ を選びます。
-For example, the quadruplet $(r, a, b, c) = (2, 6, 2, -7)$ satisfies this property.
+例えば、四つ組数 $(r, a, b, c) = (2, 6, 2, -7)$ はこの性質を満たしています。
-Let $F(R, X)$ be the number of the integer quadruplets $(r, a, b, c)$ with this property, and with $0 < r ≤ R$ and $0 < a ≤ X$.
+$0 < r ≤ R$, $0 < a ≤ X$ のとき、この性質を持つ四つ組整数 $(r, a, b, c)$ の個数を $F(R, X)$ とします。
-We can verify that $F(1, 5) = 10$, $F(2, 10) = 52$ and $F(10, 100) = 3384$.
+$F(1, 5) = 10$, $F(2, 10) = 52$, $F(10, 100) = 3384$ であることを確認できます。
-Find $F({10}^8, {10}^9) + F({10}^9, {10}^8)$.
+$F({10}^8, {10}^9) + F({10}^9, {10}^8)$ を求めなさい。
# --hints--
-`circleAndTangentLine()` should return `799999783589946600`.
+`circleAndTangentLine()` は `799999783589946600` を返す必要があります 。
```js
assert.strictEqual(circleAndTangentLine(), 799999783589946600);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md
index 732059154b..a8f3f70493 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md
@@ -1,6 +1,6 @@
---
id: 5900f5081000cf542c510019
-title: 'Problem 411: Uphill paths'
+title: '問題 411: 登り坂を描く経路'
challengeType: 5
forumTopicId: 302080
dashedName: problem-411-uphill-paths
@@ -8,23 +8,23 @@ dashedName: problem-411-uphill-paths
# --description--
-Let $n$ be a positive integer. Suppose there are stations at the coordinates $(x, y) = (2^i\bmod n, 3^i\bmod n)$ for $0 ≤ i ≤ 2n$. We will consider stations with the same coordinates as the same station.
+$n$ を正の整数とします。 $0 ≤ i ≤ 2n$ のとき、座標 $(x, y) = (2^i\bmod n, 3^i\bmod n)$ に駅があるとします。 同じ座標を持つ駅が複数ある場合、それらは同じ駅であると考えます。
-We wish to form a path from (0, 0) to ($n$, $n$) such that the $x$ and $y$ coordinates never decrease.
+$x$, $y$ 座標の値が減少することのない経路を、(0, 0) から ($n$, $n$) まで作成するとします。
-Let $S(n)$ be the maximum number of stations such a path can pass through.
+その経路が通過できる駅の最大数を $S(n)$ とします。
-For example, if $n = 22$, there are 11 distinct stations, and a valid path can pass through at most 5 stations. Therefore, $S(22) = 5$. The case is illustrated below, with an example of an optimal path:
+例えば、$n = 22$ のとき、11 の相異なる駅があり、1 本の有効な経路がたかだか 5 駅を通ることができます。 したがって、$S(22) = 5$ となります。 下図に、このケースを最適な経路の例と共に示します。
-
-Let $f(n)$ be the number of points where four tiles meet in $T(n)$. For example, $f(1) = 0$, $f(4) = 82$ and $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$.
+$T(n)$ で 4 枚のタイルが集まる点の個数を $f(n)$ とします。 例えば、$f(1) = 0$, $f(4) = 82$, $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$ です。
-Find $f({10}^k)$ for $k = {10}^{18}$, give your answer modulo ${17}^7$.
+$k = {10}^{18}$ のとき、$f({10}^k)$ mod ${17}^7$ を求めなさい。
# --hints--
-`rectangularTiling()` should return `237696125`.
+`rectangularTiling()` は `237696125` を返す必要があります。
```js
assert.strictEqual(rectangularTiling(), 237696125);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md
index 770438981f..da4eeed10f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-406-guessing-game.md
@@ -1,6 +1,6 @@
---
id: 5900f5021000cf542c510015
-title: 'Problem 406: Guessing Game'
+title: '問題 406: 推測ゲーム'
challengeType: 5
forumTopicId: 302074
dashedName: problem-406-guessing-game
@@ -8,39 +8,39 @@ dashedName: problem-406-guessing-game
# --description--
-We are trying to find a hidden number selected from the set of integers {1, 2, ..., $n$} by asking questions. Each number (question) we ask, we get one of three possible answers:
+整数の集合 {1, 2, ..., $n$} から選ばれた秘密の数を、質問をすることで当てます。 それぞれの数 (質問) で得られる回答は、次の 3 つのいずれかです。
-- "Your guess is lower than the hidden number" (and you incur a cost of a), or
-- "Your guess is higher than the hidden number" (and you incur a cost of b), or
-- "Yes, that's it!" (and the game ends).
+- 「あなたの推測は秘密の数よりも小さい」(a のコストが発生する)
+- 「あなたの推測は秘密の数よりも大きい」(b のコストが発生する)
+- 「当たり!」 (ゲーム終了)
-Given the value of $n$, $a$, and $b$, an optimal strategy minimizes the total cost for the worst possible case.
+値 $n$, $a$, $b$ が与えられているとき、最適な戦略に従えば、起こり得る最悪のケースの総コストが最小化します。
-For example, if $n = 5$, $a = 2$, and $b = 3$, then we may begin by asking "2" as our first question.
+例えば、$n = 5$, $a = 2$, $b = 3$ の場合、最初に秘密の数が "2" であるかどうかを尋ねます。
-If we are told that 2 is higher than the hidden number (for a cost of $b = 3$), then we are sure that "1" is the hidden number (for a total cost of 3).
+2 が秘密の数よりも大きいと告げられた場合 (コストは $b = 3$)、秘密の数が "1" であることが分かります (総コストは 3)。
-If we are told that 2 is lower than the hidden number (for a cost of $a = 2$), then our next question will be "4".
+2 が秘密の数よりも小さいと告げられた場合 (コストは $a = 2$)、次の質問は "4" です。
-If we are told that 4 is higher than the hidden number (for a cost of $b = 3$), then we are sure that "3" is the hidden number (for a total cost of $2 + 3 = \color{blue}{\mathbf{5}}$).
+4 が秘密の数よりも大きいと告げられた場合 (コストは $b = 3$)、秘密の数が "3" であることが分かります (総コストは $2 + 3 = \color{blue}{\mathbf{5}}$)。
-If we are told that 4 is lower than the hidden number (for a cost of $a = 2$), then we are sure that "5" is the hidden number (for a total cost of $2 + 2 = \color{blue}{\mathbf{4}}$).
+4 が秘密の数よりも小さいと告げられた場合 (コスト $a = 2$)、秘密の数が "5" であることが分かります (総コストは $2 + 2 = \color{blue}{\mathbf{4}}$)。
-Thus, the worst-case cost achieved by this strategy is 5. It can also be shown that this is the lowest worst-case cost that can be achieved. So, in fact, we have just described an optimal strategy for the given values of $n$, $a$, and $b$.
+したがって、この戦略によって達成される、最悪ケースのコストは 5 です。 また、達成可能な最悪ケースのコストの中でこれが最も低いコストであることも分かっています。 つまり、与えられた値 $n$, $a$, $b$ に対してこれが最適な戦略です。
-Let $C(n, a, b)$ be the worst-case cost achieved by an optimal strategy for the given values of $n$, $a$, and $b$.
+与えられた値 $n$, $a$, $b$ に対する最適な戦略によって達成される、最悪ケースのコストを $C(n, a, b)$ とします。
-Here are a few examples:
+いくつかの例を次に示します。
$$\begin{align} & C(5, 2, 3) = 5 \\\\ & C(500, \sqrt{2}, \sqrt{3}) = 13.220\\,731\\,97\ldots \\\\ & C(20\\,000, 5, 7) = 82 \\\\ & C(2\\,000\\,000, √5, √7) = 49.637\\,559\\,55\ldots \\\\ \end{align}$$
-Let $F_k$ be the Fibonacci numbers: $F_k = F_{k - 1} + F_{k - 2}$ with base cases $F_1 = F_2 = 1$.
+$F_1 = F_2 = 1$ を初期条件とするフィボナッチ数 $F_k = F_{k - 1} + F_{k - 2}$ を $F_k$ と定義します。
-Find $\displaystyle\sum_{k = 1}^{30} C({10}^{12}, \sqrt{k}, \sqrt{F_k})$, and give your answer rounded to 8 decimal places behind the decimal point.
+$\displaystyle\sum_{k = 1}^{30} C({10}^{12}, \sqrt{k}, \sqrt{F_k})$ を求め、四捨五入して小数第 8 位まで示しなさい。
# --hints--
-`guessingGame()` should return `36813.12757207`.
+`guessingGame()` は `36813.12757207` を返す必要があります。
```js
assert.strictEqual(guessingGame(), 36813.12757207);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md
index bae66db99c..e262a008f2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-407-idempotents.md
@@ -1,6 +1,6 @@
---
id: 5900f5041000cf542c510016
-title: 'Problem 407: Idempotents'
+title: '冪等元'
challengeType: 5
forumTopicId: 302075
dashedName: problem-407-idempotents
@@ -8,17 +8,17 @@ dashedName: problem-407-idempotents
# --description--
-If we calculate $a^2\bmod 6$ for $0 ≤ a ≤ 5$ we get: 0, 1, 4, 3, 4, 1.
+$0 ≤ a ≤ 5$ のとき $a^2\bmod 6$ を求めると、0, 1, 4, 3, 4, 1 になります。
-The largest value of a such that $a^2 ≡ a\bmod 6$ is $4$.
+$a^2 ≡ a\bmod 6$ となる a の最大値は $4$ です。
-Let's call $M(n)$ the largest value of $a < n$ such that $a^2 ≡ a (\text{mod } n)$. So $M(6) = 4$.
+$a^2 ≡ a (\text{mod } n)$ となる $a < n$ の最大値を $M(n)$ とします。 したがって、$M(6) = 4$ です。
-Find $\sum M(n)$ for $1 ≤ n ≤ {10}^7$.
+$1 ≤ n ≤ {10}^7$ のとき、$\sum M(n)$ を求めなさい。
# --hints--
-`idempotents()` should return `39782849136421`.
+`idempotents()` は `39782849136421` を返す必要があります。
```js
assert.strictEqual(idempotents(), 39782849136421);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md
index 94e93e63c8..0f11bd9ee2 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-408-admissible-paths-through-a-grid.md
@@ -1,6 +1,6 @@
---
id: 5900f5091000cf542c51001b
-title: 'Problem 408: Admissible paths through a grid'
+title: '問題 408: 格子内の許容的経路'
challengeType: 5
forumTopicId: 302076
dashedName: problem-408-admissible-paths-through-a-grid
@@ -8,19 +8,19 @@ dashedName: problem-408-admissible-paths-through-a-grid
# --description--
-Let's call a lattice point ($x$, $y$) inadmissible if $x$, $y$ and $x + y$ are all positive perfect squares.
+$x$, $y$, $x + y$ がすべて正の完全平方数の場合、格子点 ($x$, $y$) を「非許容的」と表現することにします。
-For example, (9, 16) is inadmissible, while (0, 4), (3, 1) and (9, 4) are not.
+例えば、(9, 16) は非許容的な点ですが、(0, 4), (3, 1), (9, 4) はそうではありません。
-Consider a path from point ($x_1$, $y_1$) to point ($x_2$, $y_2$) using only unit steps north or east. Let's call such a path admissible if none of its intermediate points are inadmissible.
+点 ($x_1$, $y_1$) から点 ($x_2$, $y_2$) へ、北方向または東方向への単位ステップのみで移動する場合の経路を考えます。 経路上の中間点がいずれも非許容的ではない場合、そのような経路を「許容的」と表現することにします。
-Let $P(n)$ be the number of admissible paths from (0, 0) to ($n$, $n$). It can be verified that $P(5) = 252$, $P(16) = 596\\,994\\,440$ and $P(1\\,000)\bmod 1\\,000\\,000\\,007 = 341\\,920\\,854$.
+(0, 0) から ($n$, $n$) までの許容的な経路の数を $P(n)$ とします。 $P(5) = 252$, $P(16) = 596\\,994\\,440$, $P(1\\,000)\bmod 1\\,000\\,000\\,007 = 341\\,920\\,854$ であることを確認できます。
-Find $P(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+$P(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`admissiblePaths()` should return `299742733`.
+`admissiblePaths()`は `299742733` を返す必要があります。
```js
assert.strictEqual(admissiblePaths(), 299742733);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md
index b751cb412b..30729a0915 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-409-nim-extreme.md
@@ -1,6 +1,6 @@
---
id: 5900f5061000cf542c510017
-title: 'Problem 409: Nim Extreme'
+title: '問題 409: 極端なニム (石取りゲーム)'
challengeType: 5
forumTopicId: 302077
dashedName: problem-409-nim-extreme
@@ -8,21 +8,21 @@ dashedName: problem-409-nim-extreme
# --description--
-Let $n$ be a positive integer. Consider nim positions where:
+$n$ を正の整数とします。 次のような二ム (石取りゲーム) の配置について考えます。
-- There are $n$ non-empty piles.
-- Each pile has size less than $2^n$.
-- No two piles have the same size.
+- 空でない山が $n$ 個ある。
+- それぞれの山のサイズは $2^n$ 未満である。
+- 同じサイズの山はない。
-Let $W(n)$ be the number of winning nim positions satisfying the above conditions (a position is winning if the first player has a winning strategy).
+上の条件を満たすような、二ムの勝利ポジション (先手が必勝戦略を持つようなポジション) の数を $W(n)$ とします 。
-For example, $W(1) = 1$, $W(2) = 6$, $W(3) = 168$, $W(5) = 19\\,764\\,360$ and $W(100)\bmod 1\\,000\\,000\\,007 = 384\\,777\\,056$.
+例えば、$W(1) = 1$, $W(2) = 6$, $W(3) = 168$, $W(5) = 19\\,764\\,360$, $W(100)\bmod 1\\,000\\,000\\,007 = 384\\,777\\,056$ です。
-Find $W(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+$W(10\\,000\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`nimExtreme()` should return `253223948`.
+`nimExtreme()` は `253223948` を返す必要があります。
```js
assert.strictEqual(nimExtreme(), 253223948);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md
index 81ab40a2c9..4d1932896a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-410-circle-and-tangent-line.md
@@ -1,6 +1,6 @@
---
id: 5900f5071000cf542c510018
-title: 'Problem 410: Circle and tangent line'
+title: '問題 410: 円と接線'
challengeType: 5
forumTopicId: 302079
dashedName: problem-410-circle-and-tangent-line
@@ -8,19 +8,19 @@ dashedName: problem-410-circle-and-tangent-line
# --description--
-Let $C$ be the circle with radius $r$, $x^2 + y^2 = r^2$. We choose two points $P(a, b)$ and $Q(-a, c)$ so that the line passing through $P$ and $Q$ is tangent to $C$.
+半径 $r$, $x^2 + y^2 = r^2$ の円を $C$ とします。 2 つの点 $P(a, b)$, $Q(-a, c)$ を通過する線が $C$ の接線となるように、$P$, $Q$ を選びます。
-For example, the quadruplet $(r, a, b, c) = (2, 6, 2, -7)$ satisfies this property.
+例えば、四つ組数 $(r, a, b, c) = (2, 6, 2, -7)$ はこの性質を満たしています。
-Let $F(R, X)$ be the number of the integer quadruplets $(r, a, b, c)$ with this property, and with $0 < r ≤ R$ and $0 < a ≤ X$.
+$0 < r ≤ R$, $0 < a ≤ X$ のとき、この性質を持つ四つ組整数 $(r, a, b, c)$ の個数を $F(R, X)$ とします。
-We can verify that $F(1, 5) = 10$, $F(2, 10) = 52$ and $F(10, 100) = 3384$.
+$F(1, 5) = 10$, $F(2, 10) = 52$, $F(10, 100) = 3384$ であることを確認できます。
-Find $F({10}^8, {10}^9) + F({10}^9, {10}^8)$.
+$F({10}^8, {10}^9) + F({10}^9, {10}^8)$ を求めなさい。
# --hints--
-`circleAndTangentLine()` should return `799999783589946600`.
+`circleAndTangentLine()` は `799999783589946600` を返す必要があります 。
```js
assert.strictEqual(circleAndTangentLine(), 799999783589946600);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md
index 732059154b..a8f3f70493 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-411-uphill-paths.md
@@ -1,6 +1,6 @@
---
id: 5900f5081000cf542c510019
-title: 'Problem 411: Uphill paths'
+title: '問題 411: 登り坂を描く経路'
challengeType: 5
forumTopicId: 302080
dashedName: problem-411-uphill-paths
@@ -8,23 +8,23 @@ dashedName: problem-411-uphill-paths
# --description--
-Let $n$ be a positive integer. Suppose there are stations at the coordinates $(x, y) = (2^i\bmod n, 3^i\bmod n)$ for $0 ≤ i ≤ 2n$. We will consider stations with the same coordinates as the same station.
+$n$ を正の整数とします。 $0 ≤ i ≤ 2n$ のとき、座標 $(x, y) = (2^i\bmod n, 3^i\bmod n)$ に駅があるとします。 同じ座標を持つ駅が複数ある場合、それらは同じ駅であると考えます。
-We wish to form a path from (0, 0) to ($n$, $n$) such that the $x$ and $y$ coordinates never decrease.
+$x$, $y$ 座標の値が減少することのない経路を、(0, 0) から ($n$, $n$) まで作成するとします。
-Let $S(n)$ be the maximum number of stations such a path can pass through.
+その経路が通過できる駅の最大数を $S(n)$ とします。
-For example, if $n = 22$, there are 11 distinct stations, and a valid path can pass through at most 5 stations. Therefore, $S(22) = 5$. The case is illustrated below, with an example of an optimal path:
+例えば、$n = 22$ のとき、11 の相異なる駅があり、1 本の有効な経路がたかだか 5 駅を通ることができます。 したがって、$S(22) = 5$ となります。 下図に、このケースを最適な経路の例と共に示します。
-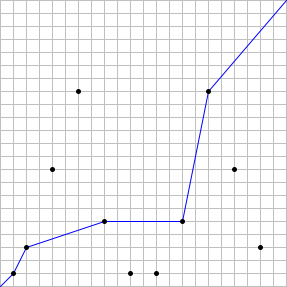 +
+ -It can also be verified that $S(123) = 14$ and $S(10\\,000) = 48$.
+$S(123) = 14$, $S(10\\,000) = 48$ であることも確認できます。
-Find $\sum S(k^5)$ for $1 ≤ k ≤ 30$.
+$1 ≤ k ≤ 30$ のとき、$\sum S(k^5)$ を求めなさい。
# --hints--
-`uphillPaths()` should return `9936352`.
+`uphillPaths()` は `9936352` を返す必要があります。
```js
assert.strictEqual(uphillPaths(), 9936352);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md
index f69590e22b..953bcdaf91 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md
@@ -1,6 +1,6 @@
---
id: 5900f5081000cf542c51001a
-title: 'Problem 412: Gnomon numbering'
+title: '問題 412: グノモンの番号付け'
challengeType: 5
forumTopicId: 302081
dashedName: problem-412-gnomon-numbering
@@ -8,25 +8,25 @@ dashedName: problem-412-gnomon-numbering
# --description--
-For integers $m$, $n$ ($0 ≤ n < m$), let $L(m, n)$ be an $m×m$ grid with the top-right $n×n$ grid removed.
+整数 $m$, $n$ ($0 ≤ n < m$) について、$m×m$ の格子の右上から $n×n$ の格子を取り除いたものを $L(m, n)$ とします。
-For example, $L(5, 3)$ looks like this:
+例えば、$L(5, 3)$ は下図のようになります。
-
-It can also be verified that $S(123) = 14$ and $S(10\\,000) = 48$.
+$S(123) = 14$, $S(10\\,000) = 48$ であることも確認できます。
-Find $\sum S(k^5)$ for $1 ≤ k ≤ 30$.
+$1 ≤ k ≤ 30$ のとき、$\sum S(k^5)$ を求めなさい。
# --hints--
-`uphillPaths()` should return `9936352`.
+`uphillPaths()` は `9936352` を返す必要があります。
```js
assert.strictEqual(uphillPaths(), 9936352);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md
index f69590e22b..953bcdaf91 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-412-gnomon-numbering.md
@@ -1,6 +1,6 @@
---
id: 5900f5081000cf542c51001a
-title: 'Problem 412: Gnomon numbering'
+title: '問題 412: グノモンの番号付け'
challengeType: 5
forumTopicId: 302081
dashedName: problem-412-gnomon-numbering
@@ -8,25 +8,25 @@ dashedName: problem-412-gnomon-numbering
# --description--
-For integers $m$, $n$ ($0 ≤ n < m$), let $L(m, n)$ be an $m×m$ grid with the top-right $n×n$ grid removed.
+整数 $m$, $n$ ($0 ≤ n < m$) について、$m×m$ の格子の右上から $n×n$ の格子を取り除いたものを $L(m, n)$ とします。
-For example, $L(5, 3)$ looks like this:
+例えば、$L(5, 3)$ は下図のようになります。
- +
+ -We want to number each cell of $L(m, n)$ with consecutive integers 1, 2, 3, ... such that the number in every cell is smaller than the number below it and to the left of it.
+すべてのマスの数字が下のマスと左のマスにある数字よりも小さくなるように、$L(m, n)$ の各マスに連続整数 1, 2, 3, ... を付けるとします。
-For example, here are two valid numberings of $L(5, 3)$:
+下図は、$L(5, 3)$ に対する有効な番号付けの 2 例です。
-
-We want to number each cell of $L(m, n)$ with consecutive integers 1, 2, 3, ... such that the number in every cell is smaller than the number below it and to the left of it.
+すべてのマスの数字が下のマスと左のマスにある数字よりも小さくなるように、$L(m, n)$ の各マスに連続整数 1, 2, 3, ... を付けるとします。
-For example, here are two valid numberings of $L(5, 3)$:
+下図は、$L(5, 3)$ に対する有効な番号付けの 2 例です。
-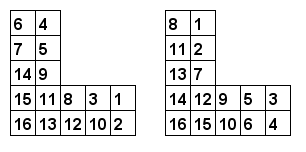 +
+ -Let $LC(m, n)$ be the number of valid numberings of $L(m, n)$. It can be verified that $LC(3, 0) = 42$, $LC(5, 3) = 250\\,250$, $LC(6, 3) = 406\\,029\\,023\\,400$ and $LC(10, 5)\bmod 76\\,543\\,217 = 61\\,251\\,715$.
+$L(m, n)$ の有効な番号付けの個数を $LC(m, n)$ とします。 $LC(3, 0) = 42$, $LC(5, 3) = 250\\,250$, $LC(6, 3) = 406\\,029\\,023\\,400$, $LC(10, 5)\bmod 76\\,543\\,217 = 61\\,251\\,715$ であることを確認できます。
-Find $LC(10\\,000, 5\\,000)\bmod 76\\,543\\,217$.
+$LC(10\\,000, 5\\,000)\bmod 76\\,543\\,217$ を求めなさい。
# --hints--
-`gnomonNumbering()` should return `38788800`.
+`gnomonNumbering()` は `38788800` を返す必要があります。
```js
assert.strictEqual(gnomonNumbering(), 38788800);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md
index 2db9542a81..6d8f695d38 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f50a1000cf542c51001c
-title: 'Problem 413: One-child Numbers'
+title: '問題 413: 一人っ子数'
challengeType: 5
forumTopicId: 302082
dashedName: problem-413-one-child-numbers
@@ -8,19 +8,19 @@ dashedName: problem-413-one-child-numbers
# --description--
-We say that a $d$-digit positive number (no leading zeros) is a one-child number if exactly one of its sub-strings is divisible by $d$.
+$d$ 桁の正の数 (先行ゼロなし) の部分文字列のうちちょうど 1 つが $d$ で割り切れる場合、その正の数を「一人っ子数」と呼ぶことにします。
-For example, 5671 is a 4-digit one-child number. Among all its sub-strings 5, 6, 7, 1, 56, 67, 71, 567, 671 and 5671, only 56 is divisible by 4.
+例えば、5671 は 4 桁の一人っ子数です。 すべての部分文字列 5, 6, 7, 1, 56, 67, 71, 567, 671, 5671 の中で、4 で割り切れるのは 56 のみです。
-Similarly, 104 is a 3-digit one-child number because only 0 is divisible by 3. 1132451 is a 7-digit one-child number because only 245 is divisible by 7.
+同様に、104 は 3 桁の 一人っ子数であり、3 で割り切れるのは 0 のみです。 また、1132451 は 7 桁の一人っ子数であり、7 で割り切れるのは 245 のみです。
-Let $F(N)$ be the number of the one-child numbers less than $N$. We can verify that $F(10) = 9$, $F({10}^3) = 389$ and $F({10}^7) = 277\\,674$.
+$N$ 未満の一人っ子数の個数を $F(N)$ とします。 $F(10) = 9$, $F({10}^3) = 389$, $F({10}^7) = 277\\,674$ であることを確認できます。
-Find $F({10}^{19})$.
+$F({10}^{19})$ を求めなさい
# --hints--
-`oneChildNumbers()` should return `3079418648040719`.
+`oneChildNumbers()` は `3079418648040719` を返す必要があります。
```js
assert.strictEqual(oneChildNumbers(), 3079418648040719);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md
index 1c36bede5e..c67af69889 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md
@@ -1,6 +1,6 @@
---
id: 5900f50b1000cf542c51001d
-title: 'Problem 414: Kaprekar constant'
+title: '問題 414: カプレカ定数'
challengeType: 5
forumTopicId: 302083
dashedName: problem-414-kaprekar-constant
@@ -8,36 +8,36 @@ dashedName: problem-414-kaprekar-constant
# --description--
-6174 is a remarkable number; if we sort its digits in increasing order and subtract that number from the number you get when you sort the digits in decreasing order, we get $7641 - 1467 = 6174$.
+6174 は驚くべき数です。その各位を降順に並べ替えた数から昇順に並べ替えた数を引くと、$7641 - 1467 = 6174$ となるのです。
-Even more remarkable is that if we start from any 4 digit number and repeat this process of sorting and subtracting, we'll eventually end up with 6174 or immediately with 0 if all digits are equal.
+さらに驚くべきことに、いずれの 4 桁の数から始めても、並べ替えと減算を繰り返すと最終的に 6174 になるか、または、すべての桁の数字が同じである場合は即座に 0 になります。
-This also works with numbers that have less than 4 digits if we pad the number with leading zeroes until we have 4 digits.
+4 桁より少ない桁の数についても、4 桁になるまで先行ゼロを付けることで上と同様のことが起こります。
-E.g. let's start with the number 0837:
+例えば、 数 0837 から始めると次のようになります。
$$\begin{align} & 8730 - 0378 = 8352 \\\\ & 8532 - 2358 = 6174 \end{align}$$
-6174 is called the Kaprekar constant. The process of sorting and subtracting and repeating this until either 0 or the Kaprekar constant is reached is called the Kaprekar routine.
+6174 はカプレカ定数と呼ばれます。 0 かカプレカ定数になるまでこのように並べ替えと減算を繰り返すプロセスは、カプレカ操作と呼ばれます。
-We can consider the Kaprekar routine for other bases and number of digits. Unfortunately, it is not guaranteed a Kaprekar constant exists in all cases; either the routine can end up in a cycle for some input numbers or the constant the routine arrives at can be different for different input numbers. However, it can be shown that for 5 digits and a base $b = 6t + 3 ≠ 9$, a Kaprekar constant exists.
+基数や桁数が異なる数に対するカプレカ操作を考えることができます。 残念ながら、すべてのケースに必ずカプレカ定数があるわけではありません。一部の入力値が最終的に循環に入るか、または入力値ごとに定数が異なるかのいずれかが起こります。 しかし、5 桁かつ基数が $b = 6t + 3 ≠ 9$ の場合にカプレカ定数が存在することが分かっています。
-E.g. base 15: ${(10, 4, 14, 9, 5)}\_{15}$ base 21: $(14, 6, 20, 13, 7)_{21}$
+例えば、 基数が 15 のとき: ${(10, 4, 14, 9, 5)}\_{15}$、基数が 21 のとき: $(14, 6, 20, 13, 7)_{21}$ です。
-Define $C_b$ to be the Kaprekar constant in base $b$ for 5 digits. Define the function $sb(i)$ to be:
+5 桁かつ基数が $b$ の場合のカプレカ定数を $C_b$ と定義します。 また、関数 $sb(i)$ を次のように定義します。
-- 0 if $i = C_b$ or if $i$ written in base $b$ consists of 5 identical digits
-- the number of iterations it takes the Kaprekar routine in base $b$ to arrive at $C_b$, otherwise
+- $i = C_b$ のとき、または、$i$ が $b$ を基数とし 5 つの同じ数字からなるときは、値は 0 である。
+- それ以外のときの値は、$C_b$ に到達するまでに基数 $b$ でカプレカ操作を繰り返す必要のある回数である。
-Note that we can define $sb(i)$ for all integers $i < b^5$. If $i$ written in base $b$ takes less than 5 digits, the number is padded with leading zero digits until we have 5 digits before applying the Kaprekar routine.
+なお、すべての整数 $i < b^5$ に対して $sb(i)$ を定義することができます。 $b$ を基数として表される $i$ が 5 桁未満の数である場合、カプレカ操作を行う前にその数が 5 桁になるまで先行ゼロを付けます。
-Define $S(b)$ as the sum of $sb(i)$ for $0 < i < b^5$. E.g. $S(15) = 5\\,274\\,369$ $S(111) = 400\\,668\\,930\\,299$
+$0 < i < b^5$ のとき、$sb(i)$ の和を $S(b)$ と定義します。 例: $S(15) = 5\\,274\\,369$ $S(111) = 400\\,668\\,930\\,299$
-Find the sum of $S(6k + 3)$ for $2 ≤ k ≤ 300$. Give the last 18 digits as your answer.
+$2 ≤ k ≤ 300$ のとき、$S(6k + 3)$ の和を求めなさい。 回答は、下位 18 桁とすること。
# --hints--
-`kaprekarConstant()` should return `552506775824935500`.
+`kaprekarConstant()` は `552506775824935500` を返す必要があります。
```js
assert.strictEqual(kaprekarConstant(), 552506775824935500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
index 1a7139764e..f45a2f4a6a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
@@ -1,6 +1,6 @@
---
id: 5900f50c1000cf542c51001e
-title: 'Problem 415: Titanic sets'
+title: '問題 415: タイタニック集合'
challengeType: 5
forumTopicId: 302084
dashedName: problem-415-titanic-sets
@@ -8,19 +8,19 @@ dashedName: problem-415-titanic-sets
# --description--
-A set of lattice points $S$ is called a titanic set if there exists a line passing through exactly two points in $S$.
+格子点の集合 $S$ に含まれる格子点のうちちょうど 2 点を通る直線がある場合、その格子点の集合 $S$ をタイタニック集合と呼びます。
-An example of a titanic set is $S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (2, 0), (1, 0)\\}$, where the line passing through (0, 1) and (2, 0) does not pass through any other point in $S$.
+タイタニック集合の例を挙げます。$S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (2, 0), (1, 0)\\}$ ここで、(0, 1) と (2, 0) を通る線は $S$ の他のいずれの点も通りません。
-On the other hand, the set {(0, 0), (1, 1), (2, 2), (4, 4)} is not a titanic set since the line passing through any two points in the set also passes through the other two.
+一方、集合 {(0, 0), (1, 1), (2, 2), (4, 4)} はタイタニック集合ではありません。なぜなら、集合内のいずれの 2 点を通る線も、さらに他の 2 点を通るからです。
-For any positive integer $N$, let $T(N)$ be the number of titanic sets $S$ whose every point ($x$, $y$) satisfies $0 ≤ x$, $y ≤ N$. It can be verified that $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$ and $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$.
+任意の正の整数 $N$ について、すべての点 ($x$, $y$) が $0 ≤ x$, $y ≤ N$ を満たすようなタイタニック集合 $S$ の数を $T(N)$ とします。 $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$, $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$ であることを確認できます。
-Find $T({10}^{11})\bmod {10}^8$.
+$T({10}^{11})\bmod {10}^8$ を求めなさい。
# --hints--
-`titanicSets()` should return `55859742`.
+`titanicSets()` は `55859742` を返す必要があります。
```js
assert.strictEqual(titanicSets(), 55859742);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
index 8465a868b1..903f92f92a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
@@ -1,6 +1,6 @@
---
id: 5900f50e1000cf542c510020
-title: 'Problem 416: A frog''s trip'
+title: '問題 416: カエルの旅'
challengeType: 5
forumTopicId: 302085
dashedName: problem-416-a-frogs-trip
@@ -8,17 +8,17 @@ dashedName: problem-416-a-frogs-trip
# --description--
-A row of $n$ squares contains a frog in the leftmost square. By successive jumps the frog goes to the rightmost square and then back to the leftmost square. On the outward trip he jumps one, two or three squares to the right, and on the homeward trip he jumps to the left in a similar manner. He cannot jump outside the squares. He repeats the round-trip travel $m$ times.
+$n$ 個のマスが一列に並べられ、左端のマスにカエルがいます。 カエルは連続して跳ぶことにより、右端のマスへ移動してから左端のマスに戻ります。 左端から右へ向かうとき、カエルは右へ 1 マス、2 マス、または 3 マス跳びます。右端から左へ戻るときも同様に跳びます。 マスの外へ跳ぶことはできません。 カエルは、この往復を $m$ 回繰り返します。
-Let $F(m, n)$ be the number of the ways the frog can travel so that at most one square remains unvisited.
+カエルが途中で一度も着地しないマスがたかだか 1 つになるような旅のしかたの数を、$F(m, n)$ とします。
-For example, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ and $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$.
+例えば、$F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$, $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$ です。
-Find the last 9 digits of $F(10, {10}^{12})$.
+$F(10, {10}^{12})$ の下位 9 桁 を求めなさい。
# --hints--
-`frogsTrip()` should return `898082747`.
+`frogsTrip()` は `898082747` を返す必要があります。
```js
assert.strictEqual(frogsTrip(), 898082747);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
index 32da63b51b..1d8f868712 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f50d1000cf542c51001f
-title: 'Problem 417: Reciprocal cycles II'
+title: '問題 417: 逆数の循環節 (2)'
challengeType: 5
forumTopicId: 302086
dashedName: problem-417-reciprocal-cycles-ii
@@ -8,21 +8,21 @@ dashedName: problem-417-reciprocal-cycles-ii
# --description--
-A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with denominators 2 to 10 are given:
+単位分数とは分子が 1 である分数です。 分母が 2 から 10 までの単位分数を小数で表すと、次のようになります。
$$\begin{align} & \frac{1}{2} = 0.5 \\\\ & \frac{1}{3} = 0.(3) \\\\ & \frac{1}{4} = 0.25 \\\\ & \frac{1}{5} = 0.2 \\\\ & \frac{1}{6} = 0.1(6) \\\\ & \frac{1}{7} = 0.(142857) \\\\ & \frac{1}{8} = 0.125 \\\\ & \frac{1}{9} = 0.(1) \\\\ & \frac{1}{10} = 0.1 \\\\ \end{align}$$
-Where $0.1(6)$ means $0.166666\ldots$, and has a 1-digit recurring cycle. It can be seen that $\frac{1}{7}$ has a 6-digit recurring cycle.
+この中の $0.1(6)$ は $0.16666\ldots$ を意味し、1 桁の循環節を持ちます。 $\frac{1}{7}$ には 6 桁の循環節があることが分かります。
-Unit fractions whose denominator has no other prime factors than 2 and/or 5 are not considered to have a recurring cycle. We define the length of the recurring cycle of those unit fractions as 0.
+分母の素因数が 2 または 5、あるいはその両方のみであるとき、その単位分数は循環節を持たないとみなされます。 これらの単位分数の循環節の長さを 0 と定義します。
-Let $L(n)$ denote the length of the recurring cycle of $\frac{1}{n}$. You are given that $\sum L(n)$ for $3 ≤ n ≤ 1\\,000\\,000$ equals $55\\,535\\,191\\,115$.
+$L(n)$ を $\frac{1}{n}$ の循環節の長さと定義します。 $3 ≤ n ≤ 1\\,000\\,000$ のとき、$\sum L(n)$ = $55\\,535\\,191\\,115$ です。
-Find $\sum L(n)$ for $3 ≤ n ≤ 100\\,000\\,000$.
+$3 ≤ n ≤ 100\\,000\\,000$ のとき、$\sum L(n)$ を求めなさい。
# --hints--
-`reciprocalCyclesTwo()` should return `446572970925740`.
+`reciprocalCyclesTwo()` は `446572970925740` を返す必要があります。
```js
assert.strictEqual(reciprocalCyclesTwo(), 446572970925740);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
index 43a5d24736..c7484654ce 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f50f1000cf542c510021
-title: 'Problem 418: Factorisation triples'
+title: '問題 418: 因数分解の三つ組数'
challengeType: 5
forumTopicId: 302087
dashedName: problem-418-factorisation-triples
@@ -8,20 +8,20 @@ dashedName: problem-418-factorisation-triples
# --description--
-Let $n$ be a positive integer. An integer triple ($a$, $b$, $c$) is called a factorisation triple of $n$ if:
+$n$ を正の整数とします。 三つ組整数 ($a$, $b$, $c$) が次の条件を満たすとき、それを $n$ の因数分解の三つ組数と呼びます。
- $1 ≤ a ≤ b ≤ c$
-- $a \times b \times c = n$.
+- $a \times b \times c = n$
-Define $f(n)$ to be $a + b + c$ for the factorisation triple ($a$, $b$, $c$) of $n$ which minimises $\frac{c}{a}$. One can show that this triple is unique.
+$\frac{c}{a}$ が最小となるような $n$ の因数分解三つ組数 ($a$, $b$, $c$) について、$a + b + c$ を $f(n)$ と定義します。 この三つ組数が一意であることが分かっています。
-For example, $f(165) = 19$, $f(100\\,100) = 142$ and $f(20!) = 4\\,034\\,872$.
+例えば、$f(165) = 19$, $f(100\\,100) = 142$, $f(20!) = 4\\,034\\,872$ です。
-Find $f(43!)$.
+$f(43!)$ を求めなさい。
# --hints--
-`factorisationTriples()` should return `1177163565297340400`.
+`factorisationTriples()` は `1177163565297340400` を返す必要があります。
```js
assert.strictEqual(factorisationTriples(), 1177163565297340400);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
index 12e5c58bad..8e1dd23df1 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f5101000cf542c510022
-title: 'Problem 419: Look and say sequence'
+title: '問題 419: 読み上げ数列'
challengeType: 5
forumTopicId: 302088
dashedName: problem-419-look-and-say-sequence
@@ -8,38 +8,38 @@ dashedName: problem-419-look-and-say-sequence
# --description--
-The look and say sequence goes 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ...
+読み上げ数列は、1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ... と続きます。
-The sequence starts with 1 and all other members are obtained by describing the previous member in terms of consecutive digits.
+この数列は 1 から始まり、他のすべての項は、連続する桁によって前項の数を説明しています。
-It helps to do this out loud:
+声に出して読むとすぐ分かります。
-1 is 'one one' $→ 11$
+1 は 「1 個の 1」$→ 11$
-11 is 'two ones' $→ 21$
+11 は 「2 個の 1」$→ 21 $
-21 is 'one two and one one' $→ 1211$
+21 は「1 個の 2 と 1 個の 1」$→ 1211$
-1211 is 'one one, one two and two ones' $→ 111221$
+1211 は 「1 個の 1、1 個の 2、2 個の 1」$→ 111221$
-111221 is 'three ones, two twos and one one' $→ 312211$
+111221 は 「3 個の 1、2 個の 2、1 個の 1」$→ 312211$
-...
+このように続いていきます。
-Define $A(n)$, $B(n)$ and $C(n)$ as the number of ones, twos and threes in the $n$'th element of the sequence respectively. One can verify that $A(40) = 31\\,254$, $B(40) = 20\\,259$ and $C(40) = 11\\,625$.
+この数列の第 $n$ 項に含まれる 1, 2, 3 の個数をそれぞれ $A(n)$, $B(n)$, $C(n)$ とします。 $A(40) = 31\\,254$, $B(40) = 20\\,259$, $C(40) = 11\\,625$ であることを確認できます。
-Find $A(n)$, $B(n)$ and $C(n)$ for $n = {10}^{12}$. Give your answer modulo $2^{30}$ as a string and separate your values for $A$, $B$ and $C$ by a comma. E.g. for $n = 40$ the answer would be `31254,20259,11625`.
+$n = {10}^{12}$ のとき、$A(n)$, $B(n)$, $C(n)$ を求めなさい。 回答は mod $2^{30}$ の文字列とし、値 $A$, $B$, $C$ をカンマで区切ること。 例: $n = 40$ のとき、回答は `31254,20259,11625` になります。
# --hints--
-`lookAndSaySequence()` should return a string.
+`lookAndSaySequence()` は文字列を返す必要があります。
```js
assert(typeof lookAndSaySequence() === 'string');
```
-`lookAndSaySequence()` should return the string `998567458,1046245404,43363922`.
+`lookAndSaySequence()` は文字列 `998567458,1046245404,43363922` を返す必要があります。
```js
assert.strictEqual(lookAndSaySequence(), '998567458,1046245404,43363922');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md
index 38356bd296..a5fa40b5e0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md
@@ -1,6 +1,6 @@
---
id: 5900f5111000cf542c510023
-title: 'Problem 420: 2x2 positive integer matrix'
+title: '問題 420: 2x2 の正整数行列'
challengeType: 5
forumTopicId: 302090
dashedName: problem-420-2x2-positive-integer-matrix
@@ -8,25 +8,25 @@ dashedName: problem-420-2x2-positive-integer-matrix
# --description--
-A positive integer matrix is a matrix whose elements are all positive integers.
+正整数行列とは、要素がすべて正の整数である行列です。
-Some positive integer matrices can be expressed as a square of a positive integer matrix in two different ways. Here is an example:
+一部の正整数行列中は、正整数行列の 2 乗として 2 通りに表すことができます。 次に例を示します。
-$$\begin{pmatrix} 40 & 12 \\\\ 48 & 40 \end{pmatrix} =
+$$\begin{pmatrix} 40 & 12 \\\\ 48 & 40 \end{pmatrix}=
{\begin{pmatrix}
2 & 3 \\\\ 12 & 2 \end{pmatrix}}^2 =
{\begin{pmatrix}
6 & 1 \\\\ 4 & 6 \end{pmatrix}}^2$$
-We define $F(N)$ as the number of the 2x2 positive integer matrices which have a trace less than N and which can be expressed as a square of a positive integer matrix in two different ways.
+対角和が N 未満であり、かつ、正整数行列の 2 乗として 2 通りに表せる 2x2 の正整数行列の個数を $F(N)$ とします。
-We can verify that $F(50) = 7$ and $F(1000) = 1019$.
+$F(50) = 7$, $F(1000) = 1019$ であることを確認できます。
-Find $F({10}^7)$.
+$F({10}^7)$ を求めなさい。
# --hints--
-`positiveIntegerMatrix()` should return `145159332`.
+`positiveIntegerMatrix()` は `145159332` を返す必要があります。
```js
assert.strictEqual(positiveIntegerMatrix(), 145159332);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
index 9e9bb64894..3161af301c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
@@ -1,6 +1,6 @@
---
id: 5900f5131000cf542c510024
-title: 'Problem 421: Prime factors of n15+1'
+title: '問題 421: $n^{15}$ + 1 の素因数'
challengeType: 5
forumTopicId: 302091
dashedName: problem-421-prime-factors-of-n151
@@ -8,23 +8,23 @@ dashedName: problem-421-prime-factors-of-n151
# --description--
-Numbers of the form $n^{15} + 1$ are composite for every integer $n > 1$.
+$n > 1$ を満たすすべての整数について、$n^{15} + 1$ で表される数は合成数です。
-For positive integers $n$ and $m$ let $s(n, m)$ be defined as the sum of the distinct prime factors of $n^{15} + 1$ not exceeding $m$.
+正の整数 $n$, $m$ について、$m$ を超えない $n^{15} + 1$ の相異なる素因数の和を $s(n, m)$ と定義します。
-E.g. $2^{15} + 1 = 3 × 3 × 11 × 331$.
+例: $2^{15} + 1 = 3 × 3 × 11 × 331$
-So $s(2, 10) = 3$ and $s(2, 1000) = 3 + 11 + 331 = 345$.
+したがって、$s(2, 10) = 3$, $s(2, 1000) = 3 + 11 + 331 = 345$ となります。
-Also ${10}^{15} + 1 = 7 × 11 × 13 × 211 × 241 × 2161 × 9091$.
+同様に、${10}^{15} + 1 = 7 × 11 × 13 × 211 × 241 × 2161 × 9091$ です。
-So $s(10, 100) = 31$ and $s(10, 1000) = 483$.
+したがって、$s(10, 100) = 31$, $s(10, 1000) = 483$ となります。
-Find $\sum s(n, {10}^8)$ for $1 ≤ n ≤ {10}^{11}$.
+$1 ≤ n ≤ {10}^{11}$ のとき、$\sum s(n, {10}^8)$ を求めなさい。
# --hints--
-`primeFactorsOfN15Plus1()` should return `2304215802083466200`.
+`primeFactorsOfN15Plus1()` は `2304215802083466200` を返す必要があります。
```js
assert.strictEqual(primeFactorsOfN15Plus1(), 2304215802083466200);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
index 26f0034471..ad35ce952e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
@@ -1,6 +1,6 @@
---
id: 5900f5131000cf542c510025
-title: 'Problem 422: Sequence of points on a hyperbola'
+title: '問題 422: 双曲線上の点列'
challengeType: 5
forumTopicId: 302092
dashedName: problem-422-sequence-of-points-on-a-hyperbola
@@ -8,27 +8,27 @@ dashedName: problem-422-sequence-of-points-on-a-hyperbola
# --description--
-Let $H$ be the hyperbola defined by the equation $12x^2 + 7xy - 12y^2 = 625$.
+式 $12x^2 + 7xy - 12y^2 = 625$ で定義される双曲線を $H$ とします。
-Next, define $X$ as the point (7, 1). It can be seen that $X$ is in $H$.
+次に、点 (7, 1) を $X$ と定義します。 $X$ が $H$ 上にあることが分かります。
-Now we define a sequence of points in $H, \\{P_i : i ≥ 1\\}$, as:
+ここで、$H, \\{P_i : i ≥ 1\\}$ の点列を次のように定義します。
-- $P_1 = (13, \frac{61}{4})$.
-- $P_2 = (\frac{-43}{6}, -4)$.
-- For $i > 2$, $P_i$ is the unique point in $H$ that is different from $P_{i - 1}$ and such that line $P_iP_{i - 1}$ is parallel to line $P_{i - 2}X$. It can be shown that $P_i$ is well-defined, and that its coordinates are always rational.
+- $P_1 = (13, \frac{61}{4})$
+- $P_2 = (\frac{-43}{6}, -4)$
+- $i > 2$ のとき、$P_i$ は、線 $P_iP_{i - 1}$ が線 $P_{i - 2}X$ と平行になるような点のうち $P_{i - 1}$ ではない方の、$H$ 上の一意の点である。 $P_i$ を明確に定義できること、および、それらの座標が常に有理数であることを示せる。
-
-Let $LC(m, n)$ be the number of valid numberings of $L(m, n)$. It can be verified that $LC(3, 0) = 42$, $LC(5, 3) = 250\\,250$, $LC(6, 3) = 406\\,029\\,023\\,400$ and $LC(10, 5)\bmod 76\\,543\\,217 = 61\\,251\\,715$.
+$L(m, n)$ の有効な番号付けの個数を $LC(m, n)$ とします。 $LC(3, 0) = 42$, $LC(5, 3) = 250\\,250$, $LC(6, 3) = 406\\,029\\,023\\,400$, $LC(10, 5)\bmod 76\\,543\\,217 = 61\\,251\\,715$ であることを確認できます。
-Find $LC(10\\,000, 5\\,000)\bmod 76\\,543\\,217$.
+$LC(10\\,000, 5\\,000)\bmod 76\\,543\\,217$ を求めなさい。
# --hints--
-`gnomonNumbering()` should return `38788800`.
+`gnomonNumbering()` は `38788800` を返す必要があります。
```js
assert.strictEqual(gnomonNumbering(), 38788800);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md
index 2db9542a81..6d8f695d38 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-413-one-child-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f50a1000cf542c51001c
-title: 'Problem 413: One-child Numbers'
+title: '問題 413: 一人っ子数'
challengeType: 5
forumTopicId: 302082
dashedName: problem-413-one-child-numbers
@@ -8,19 +8,19 @@ dashedName: problem-413-one-child-numbers
# --description--
-We say that a $d$-digit positive number (no leading zeros) is a one-child number if exactly one of its sub-strings is divisible by $d$.
+$d$ 桁の正の数 (先行ゼロなし) の部分文字列のうちちょうど 1 つが $d$ で割り切れる場合、その正の数を「一人っ子数」と呼ぶことにします。
-For example, 5671 is a 4-digit one-child number. Among all its sub-strings 5, 6, 7, 1, 56, 67, 71, 567, 671 and 5671, only 56 is divisible by 4.
+例えば、5671 は 4 桁の一人っ子数です。 すべての部分文字列 5, 6, 7, 1, 56, 67, 71, 567, 671, 5671 の中で、4 で割り切れるのは 56 のみです。
-Similarly, 104 is a 3-digit one-child number because only 0 is divisible by 3. 1132451 is a 7-digit one-child number because only 245 is divisible by 7.
+同様に、104 は 3 桁の 一人っ子数であり、3 で割り切れるのは 0 のみです。 また、1132451 は 7 桁の一人っ子数であり、7 で割り切れるのは 245 のみです。
-Let $F(N)$ be the number of the one-child numbers less than $N$. We can verify that $F(10) = 9$, $F({10}^3) = 389$ and $F({10}^7) = 277\\,674$.
+$N$ 未満の一人っ子数の個数を $F(N)$ とします。 $F(10) = 9$, $F({10}^3) = 389$, $F({10}^7) = 277\\,674$ であることを確認できます。
-Find $F({10}^{19})$.
+$F({10}^{19})$ を求めなさい
# --hints--
-`oneChildNumbers()` should return `3079418648040719`.
+`oneChildNumbers()` は `3079418648040719` を返す必要があります。
```js
assert.strictEqual(oneChildNumbers(), 3079418648040719);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md
index 1c36bede5e..c67af69889 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-414-kaprekar-constant.md
@@ -1,6 +1,6 @@
---
id: 5900f50b1000cf542c51001d
-title: 'Problem 414: Kaprekar constant'
+title: '問題 414: カプレカ定数'
challengeType: 5
forumTopicId: 302083
dashedName: problem-414-kaprekar-constant
@@ -8,36 +8,36 @@ dashedName: problem-414-kaprekar-constant
# --description--
-6174 is a remarkable number; if we sort its digits in increasing order and subtract that number from the number you get when you sort the digits in decreasing order, we get $7641 - 1467 = 6174$.
+6174 は驚くべき数です。その各位を降順に並べ替えた数から昇順に並べ替えた数を引くと、$7641 - 1467 = 6174$ となるのです。
-Even more remarkable is that if we start from any 4 digit number and repeat this process of sorting and subtracting, we'll eventually end up with 6174 or immediately with 0 if all digits are equal.
+さらに驚くべきことに、いずれの 4 桁の数から始めても、並べ替えと減算を繰り返すと最終的に 6174 になるか、または、すべての桁の数字が同じである場合は即座に 0 になります。
-This also works with numbers that have less than 4 digits if we pad the number with leading zeroes until we have 4 digits.
+4 桁より少ない桁の数についても、4 桁になるまで先行ゼロを付けることで上と同様のことが起こります。
-E.g. let's start with the number 0837:
+例えば、 数 0837 から始めると次のようになります。
$$\begin{align} & 8730 - 0378 = 8352 \\\\ & 8532 - 2358 = 6174 \end{align}$$
-6174 is called the Kaprekar constant. The process of sorting and subtracting and repeating this until either 0 or the Kaprekar constant is reached is called the Kaprekar routine.
+6174 はカプレカ定数と呼ばれます。 0 かカプレカ定数になるまでこのように並べ替えと減算を繰り返すプロセスは、カプレカ操作と呼ばれます。
-We can consider the Kaprekar routine for other bases and number of digits. Unfortunately, it is not guaranteed a Kaprekar constant exists in all cases; either the routine can end up in a cycle for some input numbers or the constant the routine arrives at can be different for different input numbers. However, it can be shown that for 5 digits and a base $b = 6t + 3 ≠ 9$, a Kaprekar constant exists.
+基数や桁数が異なる数に対するカプレカ操作を考えることができます。 残念ながら、すべてのケースに必ずカプレカ定数があるわけではありません。一部の入力値が最終的に循環に入るか、または入力値ごとに定数が異なるかのいずれかが起こります。 しかし、5 桁かつ基数が $b = 6t + 3 ≠ 9$ の場合にカプレカ定数が存在することが分かっています。
-E.g. base 15: ${(10, 4, 14, 9, 5)}\_{15}$ base 21: $(14, 6, 20, 13, 7)_{21}$
+例えば、 基数が 15 のとき: ${(10, 4, 14, 9, 5)}\_{15}$、基数が 21 のとき: $(14, 6, 20, 13, 7)_{21}$ です。
-Define $C_b$ to be the Kaprekar constant in base $b$ for 5 digits. Define the function $sb(i)$ to be:
+5 桁かつ基数が $b$ の場合のカプレカ定数を $C_b$ と定義します。 また、関数 $sb(i)$ を次のように定義します。
-- 0 if $i = C_b$ or if $i$ written in base $b$ consists of 5 identical digits
-- the number of iterations it takes the Kaprekar routine in base $b$ to arrive at $C_b$, otherwise
+- $i = C_b$ のとき、または、$i$ が $b$ を基数とし 5 つの同じ数字からなるときは、値は 0 である。
+- それ以外のときの値は、$C_b$ に到達するまでに基数 $b$ でカプレカ操作を繰り返す必要のある回数である。
-Note that we can define $sb(i)$ for all integers $i < b^5$. If $i$ written in base $b$ takes less than 5 digits, the number is padded with leading zero digits until we have 5 digits before applying the Kaprekar routine.
+なお、すべての整数 $i < b^5$ に対して $sb(i)$ を定義することができます。 $b$ を基数として表される $i$ が 5 桁未満の数である場合、カプレカ操作を行う前にその数が 5 桁になるまで先行ゼロを付けます。
-Define $S(b)$ as the sum of $sb(i)$ for $0 < i < b^5$. E.g. $S(15) = 5\\,274\\,369$ $S(111) = 400\\,668\\,930\\,299$
+$0 < i < b^5$ のとき、$sb(i)$ の和を $S(b)$ と定義します。 例: $S(15) = 5\\,274\\,369$ $S(111) = 400\\,668\\,930\\,299$
-Find the sum of $S(6k + 3)$ for $2 ≤ k ≤ 300$. Give the last 18 digits as your answer.
+$2 ≤ k ≤ 300$ のとき、$S(6k + 3)$ の和を求めなさい。 回答は、下位 18 桁とすること。
# --hints--
-`kaprekarConstant()` should return `552506775824935500`.
+`kaprekarConstant()` は `552506775824935500` を返す必要があります。
```js
assert.strictEqual(kaprekarConstant(), 552506775824935500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
index 1a7139764e..f45a2f4a6a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
@@ -1,6 +1,6 @@
---
id: 5900f50c1000cf542c51001e
-title: 'Problem 415: Titanic sets'
+title: '問題 415: タイタニック集合'
challengeType: 5
forumTopicId: 302084
dashedName: problem-415-titanic-sets
@@ -8,19 +8,19 @@ dashedName: problem-415-titanic-sets
# --description--
-A set of lattice points $S$ is called a titanic set if there exists a line passing through exactly two points in $S$.
+格子点の集合 $S$ に含まれる格子点のうちちょうど 2 点を通る直線がある場合、その格子点の集合 $S$ をタイタニック集合と呼びます。
-An example of a titanic set is $S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (2, 0), (1, 0)\\}$, where the line passing through (0, 1) and (2, 0) does not pass through any other point in $S$.
+タイタニック集合の例を挙げます。$S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (2, 0), (1, 0)\\}$ ここで、(0, 1) と (2, 0) を通る線は $S$ の他のいずれの点も通りません。
-On the other hand, the set {(0, 0), (1, 1), (2, 2), (4, 4)} is not a titanic set since the line passing through any two points in the set also passes through the other two.
+一方、集合 {(0, 0), (1, 1), (2, 2), (4, 4)} はタイタニック集合ではありません。なぜなら、集合内のいずれの 2 点を通る線も、さらに他の 2 点を通るからです。
-For any positive integer $N$, let $T(N)$ be the number of titanic sets $S$ whose every point ($x$, $y$) satisfies $0 ≤ x$, $y ≤ N$. It can be verified that $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$ and $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$.
+任意の正の整数 $N$ について、すべての点 ($x$, $y$) が $0 ≤ x$, $y ≤ N$ を満たすようなタイタニック集合 $S$ の数を $T(N)$ とします。 $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$, $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$ であることを確認できます。
-Find $T({10}^{11})\bmod {10}^8$.
+$T({10}^{11})\bmod {10}^8$ を求めなさい。
# --hints--
-`titanicSets()` should return `55859742`.
+`titanicSets()` は `55859742` を返す必要があります。
```js
assert.strictEqual(titanicSets(), 55859742);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
index 8465a868b1..903f92f92a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
@@ -1,6 +1,6 @@
---
id: 5900f50e1000cf542c510020
-title: 'Problem 416: A frog''s trip'
+title: '問題 416: カエルの旅'
challengeType: 5
forumTopicId: 302085
dashedName: problem-416-a-frogs-trip
@@ -8,17 +8,17 @@ dashedName: problem-416-a-frogs-trip
# --description--
-A row of $n$ squares contains a frog in the leftmost square. By successive jumps the frog goes to the rightmost square and then back to the leftmost square. On the outward trip he jumps one, two or three squares to the right, and on the homeward trip he jumps to the left in a similar manner. He cannot jump outside the squares. He repeats the round-trip travel $m$ times.
+$n$ 個のマスが一列に並べられ、左端のマスにカエルがいます。 カエルは連続して跳ぶことにより、右端のマスへ移動してから左端のマスに戻ります。 左端から右へ向かうとき、カエルは右へ 1 マス、2 マス、または 3 マス跳びます。右端から左へ戻るときも同様に跳びます。 マスの外へ跳ぶことはできません。 カエルは、この往復を $m$ 回繰り返します。
-Let $F(m, n)$ be the number of the ways the frog can travel so that at most one square remains unvisited.
+カエルが途中で一度も着地しないマスがたかだか 1 つになるような旅のしかたの数を、$F(m, n)$ とします。
-For example, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ and $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$.
+例えば、$F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$, $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$ です。
-Find the last 9 digits of $F(10, {10}^{12})$.
+$F(10, {10}^{12})$ の下位 9 桁 を求めなさい。
# --hints--
-`frogsTrip()` should return `898082747`.
+`frogsTrip()` は `898082747` を返す必要があります。
```js
assert.strictEqual(frogsTrip(), 898082747);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
index 32da63b51b..1d8f868712 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f50d1000cf542c51001f
-title: 'Problem 417: Reciprocal cycles II'
+title: '問題 417: 逆数の循環節 (2)'
challengeType: 5
forumTopicId: 302086
dashedName: problem-417-reciprocal-cycles-ii
@@ -8,21 +8,21 @@ dashedName: problem-417-reciprocal-cycles-ii
# --description--
-A unit fraction contains 1 in the numerator. The decimal representation of the unit fractions with denominators 2 to 10 are given:
+単位分数とは分子が 1 である分数です。 分母が 2 から 10 までの単位分数を小数で表すと、次のようになります。
$$\begin{align} & \frac{1}{2} = 0.5 \\\\ & \frac{1}{3} = 0.(3) \\\\ & \frac{1}{4} = 0.25 \\\\ & \frac{1}{5} = 0.2 \\\\ & \frac{1}{6} = 0.1(6) \\\\ & \frac{1}{7} = 0.(142857) \\\\ & \frac{1}{8} = 0.125 \\\\ & \frac{1}{9} = 0.(1) \\\\ & \frac{1}{10} = 0.1 \\\\ \end{align}$$
-Where $0.1(6)$ means $0.166666\ldots$, and has a 1-digit recurring cycle. It can be seen that $\frac{1}{7}$ has a 6-digit recurring cycle.
+この中の $0.1(6)$ は $0.16666\ldots$ を意味し、1 桁の循環節を持ちます。 $\frac{1}{7}$ には 6 桁の循環節があることが分かります。
-Unit fractions whose denominator has no other prime factors than 2 and/or 5 are not considered to have a recurring cycle. We define the length of the recurring cycle of those unit fractions as 0.
+分母の素因数が 2 または 5、あるいはその両方のみであるとき、その単位分数は循環節を持たないとみなされます。 これらの単位分数の循環節の長さを 0 と定義します。
-Let $L(n)$ denote the length of the recurring cycle of $\frac{1}{n}$. You are given that $\sum L(n)$ for $3 ≤ n ≤ 1\\,000\\,000$ equals $55\\,535\\,191\\,115$.
+$L(n)$ を $\frac{1}{n}$ の循環節の長さと定義します。 $3 ≤ n ≤ 1\\,000\\,000$ のとき、$\sum L(n)$ = $55\\,535\\,191\\,115$ です。
-Find $\sum L(n)$ for $3 ≤ n ≤ 100\\,000\\,000$.
+$3 ≤ n ≤ 100\\,000\\,000$ のとき、$\sum L(n)$ を求めなさい。
# --hints--
-`reciprocalCyclesTwo()` should return `446572970925740`.
+`reciprocalCyclesTwo()` は `446572970925740` を返す必要があります。
```js
assert.strictEqual(reciprocalCyclesTwo(), 446572970925740);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
index 43a5d24736..c7484654ce 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f50f1000cf542c510021
-title: 'Problem 418: Factorisation triples'
+title: '問題 418: 因数分解の三つ組数'
challengeType: 5
forumTopicId: 302087
dashedName: problem-418-factorisation-triples
@@ -8,20 +8,20 @@ dashedName: problem-418-factorisation-triples
# --description--
-Let $n$ be a positive integer. An integer triple ($a$, $b$, $c$) is called a factorisation triple of $n$ if:
+$n$ を正の整数とします。 三つ組整数 ($a$, $b$, $c$) が次の条件を満たすとき、それを $n$ の因数分解の三つ組数と呼びます。
- $1 ≤ a ≤ b ≤ c$
-- $a \times b \times c = n$.
+- $a \times b \times c = n$
-Define $f(n)$ to be $a + b + c$ for the factorisation triple ($a$, $b$, $c$) of $n$ which minimises $\frac{c}{a}$. One can show that this triple is unique.
+$\frac{c}{a}$ が最小となるような $n$ の因数分解三つ組数 ($a$, $b$, $c$) について、$a + b + c$ を $f(n)$ と定義します。 この三つ組数が一意であることが分かっています。
-For example, $f(165) = 19$, $f(100\\,100) = 142$ and $f(20!) = 4\\,034\\,872$.
+例えば、$f(165) = 19$, $f(100\\,100) = 142$, $f(20!) = 4\\,034\\,872$ です。
-Find $f(43!)$.
+$f(43!)$ を求めなさい。
# --hints--
-`factorisationTriples()` should return `1177163565297340400`.
+`factorisationTriples()` は `1177163565297340400` を返す必要があります。
```js
assert.strictEqual(factorisationTriples(), 1177163565297340400);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
index 12e5c58bad..8e1dd23df1 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f5101000cf542c510022
-title: 'Problem 419: Look and say sequence'
+title: '問題 419: 読み上げ数列'
challengeType: 5
forumTopicId: 302088
dashedName: problem-419-look-and-say-sequence
@@ -8,38 +8,38 @@ dashedName: problem-419-look-and-say-sequence
# --description--
-The look and say sequence goes 1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ...
+読み上げ数列は、1, 11, 21, 1211, 111221, 312211, 13112221, 1113213211, ... と続きます。
-The sequence starts with 1 and all other members are obtained by describing the previous member in terms of consecutive digits.
+この数列は 1 から始まり、他のすべての項は、連続する桁によって前項の数を説明しています。
-It helps to do this out loud:
+声に出して読むとすぐ分かります。
-1 is 'one one' $→ 11$
+1 は 「1 個の 1」$→ 11$
-11 is 'two ones' $→ 21$
+11 は 「2 個の 1」$→ 21 $
-21 is 'one two and one one' $→ 1211$
+21 は「1 個の 2 と 1 個の 1」$→ 1211$
-1211 is 'one one, one two and two ones' $→ 111221$
+1211 は 「1 個の 1、1 個の 2、2 個の 1」$→ 111221$
-111221 is 'three ones, two twos and one one' $→ 312211$
+111221 は 「3 個の 1、2 個の 2、1 個の 1」$→ 312211$
-...
+このように続いていきます。
-Define $A(n)$, $B(n)$ and $C(n)$ as the number of ones, twos and threes in the $n$'th element of the sequence respectively. One can verify that $A(40) = 31\\,254$, $B(40) = 20\\,259$ and $C(40) = 11\\,625$.
+この数列の第 $n$ 項に含まれる 1, 2, 3 の個数をそれぞれ $A(n)$, $B(n)$, $C(n)$ とします。 $A(40) = 31\\,254$, $B(40) = 20\\,259$, $C(40) = 11\\,625$ であることを確認できます。
-Find $A(n)$, $B(n)$ and $C(n)$ for $n = {10}^{12}$. Give your answer modulo $2^{30}$ as a string and separate your values for $A$, $B$ and $C$ by a comma. E.g. for $n = 40$ the answer would be `31254,20259,11625`.
+$n = {10}^{12}$ のとき、$A(n)$, $B(n)$, $C(n)$ を求めなさい。 回答は mod $2^{30}$ の文字列とし、値 $A$, $B$, $C$ をカンマで区切ること。 例: $n = 40$ のとき、回答は `31254,20259,11625` になります。
# --hints--
-`lookAndSaySequence()` should return a string.
+`lookAndSaySequence()` は文字列を返す必要があります。
```js
assert(typeof lookAndSaySequence() === 'string');
```
-`lookAndSaySequence()` should return the string `998567458,1046245404,43363922`.
+`lookAndSaySequence()` は文字列 `998567458,1046245404,43363922` を返す必要があります。
```js
assert.strictEqual(lookAndSaySequence(), '998567458,1046245404,43363922');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md
index 38356bd296..a5fa40b5e0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-420-2x2-positive-integer-matrix.md
@@ -1,6 +1,6 @@
---
id: 5900f5111000cf542c510023
-title: 'Problem 420: 2x2 positive integer matrix'
+title: '問題 420: 2x2 の正整数行列'
challengeType: 5
forumTopicId: 302090
dashedName: problem-420-2x2-positive-integer-matrix
@@ -8,25 +8,25 @@ dashedName: problem-420-2x2-positive-integer-matrix
# --description--
-A positive integer matrix is a matrix whose elements are all positive integers.
+正整数行列とは、要素がすべて正の整数である行列です。
-Some positive integer matrices can be expressed as a square of a positive integer matrix in two different ways. Here is an example:
+一部の正整数行列中は、正整数行列の 2 乗として 2 通りに表すことができます。 次に例を示します。
-$$\begin{pmatrix} 40 & 12 \\\\ 48 & 40 \end{pmatrix} =
+$$\begin{pmatrix} 40 & 12 \\\\ 48 & 40 \end{pmatrix}=
{\begin{pmatrix}
2 & 3 \\\\ 12 & 2 \end{pmatrix}}^2 =
{\begin{pmatrix}
6 & 1 \\\\ 4 & 6 \end{pmatrix}}^2$$
-We define $F(N)$ as the number of the 2x2 positive integer matrices which have a trace less than N and which can be expressed as a square of a positive integer matrix in two different ways.
+対角和が N 未満であり、かつ、正整数行列の 2 乗として 2 通りに表せる 2x2 の正整数行列の個数を $F(N)$ とします。
-We can verify that $F(50) = 7$ and $F(1000) = 1019$.
+$F(50) = 7$, $F(1000) = 1019$ であることを確認できます。
-Find $F({10}^7)$.
+$F({10}^7)$ を求めなさい。
# --hints--
-`positiveIntegerMatrix()` should return `145159332`.
+`positiveIntegerMatrix()` は `145159332` を返す必要があります。
```js
assert.strictEqual(positiveIntegerMatrix(), 145159332);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
index 9e9bb64894..3161af301c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
@@ -1,6 +1,6 @@
---
id: 5900f5131000cf542c510024
-title: 'Problem 421: Prime factors of n15+1'
+title: '問題 421: $n^{15}$ + 1 の素因数'
challengeType: 5
forumTopicId: 302091
dashedName: problem-421-prime-factors-of-n151
@@ -8,23 +8,23 @@ dashedName: problem-421-prime-factors-of-n151
# --description--
-Numbers of the form $n^{15} + 1$ are composite for every integer $n > 1$.
+$n > 1$ を満たすすべての整数について、$n^{15} + 1$ で表される数は合成数です。
-For positive integers $n$ and $m$ let $s(n, m)$ be defined as the sum of the distinct prime factors of $n^{15} + 1$ not exceeding $m$.
+正の整数 $n$, $m$ について、$m$ を超えない $n^{15} + 1$ の相異なる素因数の和を $s(n, m)$ と定義します。
-E.g. $2^{15} + 1 = 3 × 3 × 11 × 331$.
+例: $2^{15} + 1 = 3 × 3 × 11 × 331$
-So $s(2, 10) = 3$ and $s(2, 1000) = 3 + 11 + 331 = 345$.
+したがって、$s(2, 10) = 3$, $s(2, 1000) = 3 + 11 + 331 = 345$ となります。
-Also ${10}^{15} + 1 = 7 × 11 × 13 × 211 × 241 × 2161 × 9091$.
+同様に、${10}^{15} + 1 = 7 × 11 × 13 × 211 × 241 × 2161 × 9091$ です。
-So $s(10, 100) = 31$ and $s(10, 1000) = 483$.
+したがって、$s(10, 100) = 31$, $s(10, 1000) = 483$ となります。
-Find $\sum s(n, {10}^8)$ for $1 ≤ n ≤ {10}^{11}$.
+$1 ≤ n ≤ {10}^{11}$ のとき、$\sum s(n, {10}^8)$ を求めなさい。
# --hints--
-`primeFactorsOfN15Plus1()` should return `2304215802083466200`.
+`primeFactorsOfN15Plus1()` は `2304215802083466200` を返す必要があります。
```js
assert.strictEqual(primeFactorsOfN15Plus1(), 2304215802083466200);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
index 26f0034471..ad35ce952e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
@@ -1,6 +1,6 @@
---
id: 5900f5131000cf542c510025
-title: 'Problem 422: Sequence of points on a hyperbola'
+title: '問題 422: 双曲線上の点列'
challengeType: 5
forumTopicId: 302092
dashedName: problem-422-sequence-of-points-on-a-hyperbola
@@ -8,27 +8,27 @@ dashedName: problem-422-sequence-of-points-on-a-hyperbola
# --description--
-Let $H$ be the hyperbola defined by the equation $12x^2 + 7xy - 12y^2 = 625$.
+式 $12x^2 + 7xy - 12y^2 = 625$ で定義される双曲線を $H$ とします。
-Next, define $X$ as the point (7, 1). It can be seen that $X$ is in $H$.
+次に、点 (7, 1) を $X$ と定義します。 $X$ が $H$ 上にあることが分かります。
-Now we define a sequence of points in $H, \\{P_i : i ≥ 1\\}$, as:
+ここで、$H, \\{P_i : i ≥ 1\\}$ の点列を次のように定義します。
-- $P_1 = (13, \frac{61}{4})$.
-- $P_2 = (\frac{-43}{6}, -4)$.
-- For $i > 2$, $P_i$ is the unique point in $H$ that is different from $P_{i - 1}$ and such that line $P_iP_{i - 1}$ is parallel to line $P_{i - 2}X$. It can be shown that $P_i$ is well-defined, and that its coordinates are always rational.
+- $P_1 = (13, \frac{61}{4})$
+- $P_2 = (\frac{-43}{6}, -4)$
+- $i > 2$ のとき、$P_i$ は、線 $P_iP_{i - 1}$ が線 $P_{i - 2}X$ と平行になるような点のうち $P_{i - 1}$ ではない方の、$H$ 上の一意の点である。 $P_i$ を明確に定義できること、および、それらの座標が常に有理数であることを示せる。
-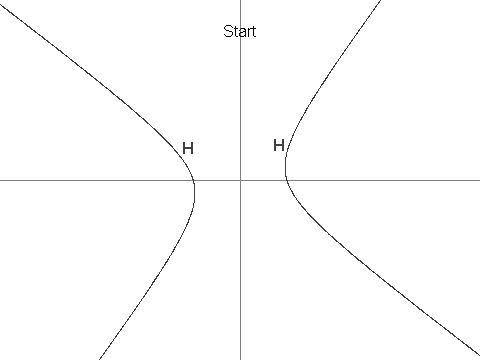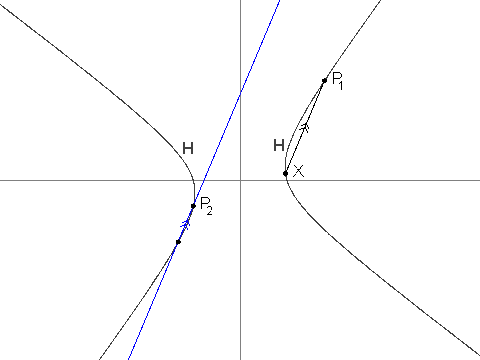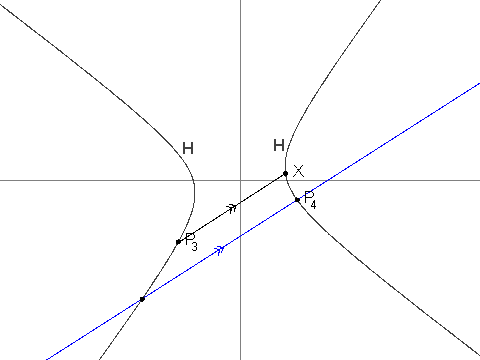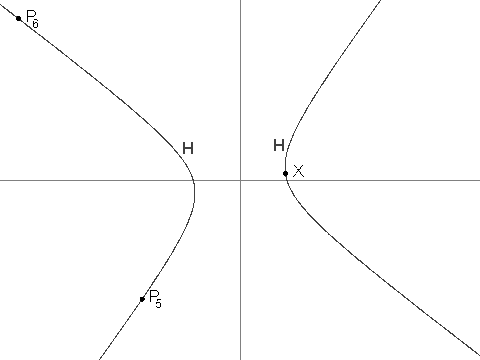 +
+ -You are given that $P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$ and $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$.
+$P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$, $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$ が与えられます。
-Find $P_n$ for $n = {11}^{14}$ in the following format: If $P_n = (\frac{a}{b}, \frac{c}{d})$ where the fractions are in lowest terms and the denominators are positive, then the answer is $(a + b + c + d)\bmod 1\\,000\\,000\\,007$.
+$n = {11}^{14}$ のとき、$P_n$ を次の形式で求めなさい: $P_n = (\frac{a}{b}, \frac{c}{d})$ が既約分数かつ分母が正の数である場合、回答は $(a + b + c + d)\bmod 1\\,000\\,000\\,007$ となります。
-For $n = 7$, the answer would have been: $806\\,236\\,837$.
+$n = 7$ のとき、回答は $806\\,236\\,837$ です。
# --hints--
-`sequenceOfPointsOnHyperbola()` should return `92060460`.
+`sequenceOfPointsOnHyperbola()` は `92060460` を返す必要があります。
```js
assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
index db865909c7..4a0ca26368 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
@@ -1,6 +1,6 @@
---
id: 5900f5141000cf542c510027
-title: 'Problem 423: Consecutive die throws'
+title: '問題 423: 連続サイコロ投げ'
challengeType: 5
forumTopicId: 302093
dashedName: problem-423-consecutive-die-throws
@@ -8,31 +8,31 @@ dashedName: problem-423-consecutive-die-throws
# --description--
-Let $n$ be a positive integer.
+$n$ を正の整数とします。
-A 6-sided die is thrown $n$ times. Let $c$ be the number of pairs of consecutive throws that give the same value.
+6 面サイコロを $n$ 回投げます。 連続する同じ出目の対がいくつあるかを $c$ で表します。
-For example, if $n = 7$ and the values of the die throws are (1, 1, 5, 6, 6, 6, 3), then the following pairs of consecutive throws give the same value:
+例えば、$n = 7$、サイコロの出目が (1, 1, 5, 6, 6, 6, 3) の場合、連続する同じ出目の対は次のとおりです。
$$\begin{align} & (\underline{1}, \underline{1}, 5, 6, 6, 6, 3) \\\\ & (1, 1, 5, \underline{6}, \underline{6}, 6, 3) \\\\ & (1, 1, 5, 6, \underline{6}, \underline{6}, 3) \end{align}$$
-Therefore, $c = 3$ for (1, 1, 5, 6, 6, 6, 3).
+したがって、(1, 1, 5, 6, 6, 6, 3) のとき、$c = 3$ になります。
-Define $C(n)$ as the number of outcomes of throwing a 6-sided die $n$ times such that $c$ does not exceed $π(n)$.1
+6 面サイコロを $n$ 回投げた結果のうち、$c$ が $π(n)$ を超えない結果の数を $C(n)$ とします1。
-For example, $C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$ and $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$.
+例えば、$C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$, $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$ です。
-Define $S(L)$ as $\sum C(n)$ for $1 ≤ n ≤ L$.
+$1 ≤ n ≤ L$ のとき、$\sum C(n)$ を $S(L)$ と定義します。
-For example, $S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$.
+例えば、$S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$ です。
-Find $S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+$S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
-1 $π$ denotes the prime-counting function, i.e. $π(n)$ is the number of primes $≤ n$.
+1 $π$ は素数計数関数を意味します。すなわち、$π(n)$ は $n$ 以下の素数の数です。
# --hints--
-`consecutiveDieThrows()` should return `653972374`.
+`consecutiveDieThrows()` は `653972374` を返す必要があります。
```js
assert.strictEqual(consecutiveDieThrows(), 653972374);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md
index 74fbac4d30..add049d78f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md
@@ -1,6 +1,6 @@
---
id: 5900f5141000cf542c510026
-title: 'Problem 424: Kakuro'
+title: '問題 424: カックロ'
challengeType: 5
forumTopicId: 302094
dashedName: problem-424-kakuro
@@ -8,37 +8,37 @@ dashedName: problem-424-kakuro
# --description--
-
-You are given that $P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$ and $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$.
+$P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$, $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$ が与えられます。
-Find $P_n$ for $n = {11}^{14}$ in the following format: If $P_n = (\frac{a}{b}, \frac{c}{d})$ where the fractions are in lowest terms and the denominators are positive, then the answer is $(a + b + c + d)\bmod 1\\,000\\,000\\,007$.
+$n = {11}^{14}$ のとき、$P_n$ を次の形式で求めなさい: $P_n = (\frac{a}{b}, \frac{c}{d})$ が既約分数かつ分母が正の数である場合、回答は $(a + b + c + d)\bmod 1\\,000\\,000\\,007$ となります。
-For $n = 7$, the answer would have been: $806\\,236\\,837$.
+$n = 7$ のとき、回答は $806\\,236\\,837$ です。
# --hints--
-`sequenceOfPointsOnHyperbola()` should return `92060460`.
+`sequenceOfPointsOnHyperbola()` は `92060460` を返す必要があります。
```js
assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
index db865909c7..4a0ca26368 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
@@ -1,6 +1,6 @@
---
id: 5900f5141000cf542c510027
-title: 'Problem 423: Consecutive die throws'
+title: '問題 423: 連続サイコロ投げ'
challengeType: 5
forumTopicId: 302093
dashedName: problem-423-consecutive-die-throws
@@ -8,31 +8,31 @@ dashedName: problem-423-consecutive-die-throws
# --description--
-Let $n$ be a positive integer.
+$n$ を正の整数とします。
-A 6-sided die is thrown $n$ times. Let $c$ be the number of pairs of consecutive throws that give the same value.
+6 面サイコロを $n$ 回投げます。 連続する同じ出目の対がいくつあるかを $c$ で表します。
-For example, if $n = 7$ and the values of the die throws are (1, 1, 5, 6, 6, 6, 3), then the following pairs of consecutive throws give the same value:
+例えば、$n = 7$、サイコロの出目が (1, 1, 5, 6, 6, 6, 3) の場合、連続する同じ出目の対は次のとおりです。
$$\begin{align} & (\underline{1}, \underline{1}, 5, 6, 6, 6, 3) \\\\ & (1, 1, 5, \underline{6}, \underline{6}, 6, 3) \\\\ & (1, 1, 5, 6, \underline{6}, \underline{6}, 3) \end{align}$$
-Therefore, $c = 3$ for (1, 1, 5, 6, 6, 6, 3).
+したがって、(1, 1, 5, 6, 6, 6, 3) のとき、$c = 3$ になります。
-Define $C(n)$ as the number of outcomes of throwing a 6-sided die $n$ times such that $c$ does not exceed $π(n)$.1
+6 面サイコロを $n$ 回投げた結果のうち、$c$ が $π(n)$ を超えない結果の数を $C(n)$ とします1。
-For example, $C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$ and $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$.
+例えば、$C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$, $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$ です。
-Define $S(L)$ as $\sum C(n)$ for $1 ≤ n ≤ L$.
+$1 ≤ n ≤ L$ のとき、$\sum C(n)$ を $S(L)$ と定義します。
-For example, $S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$.
+例えば、$S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$ です。
-Find $S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+$S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
-1 $π$ denotes the prime-counting function, i.e. $π(n)$ is the number of primes $≤ n$.
+1 $π$ は素数計数関数を意味します。すなわち、$π(n)$ は $n$ 以下の素数の数です。
# --hints--
-`consecutiveDieThrows()` should return `653972374`.
+`consecutiveDieThrows()` は `653972374` を返す必要があります。
```js
assert.strictEqual(consecutiveDieThrows(), 653972374);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md
index 74fbac4d30..add049d78f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-424-kakuro.md
@@ -1,6 +1,6 @@
---
id: 5900f5141000cf542c510026
-title: 'Problem 424: Kakuro'
+title: '問題 424: カックロ'
challengeType: 5
forumTopicId: 302094
dashedName: problem-424-kakuro
@@ -8,37 +8,37 @@ dashedName: problem-424-kakuro
# --description--
-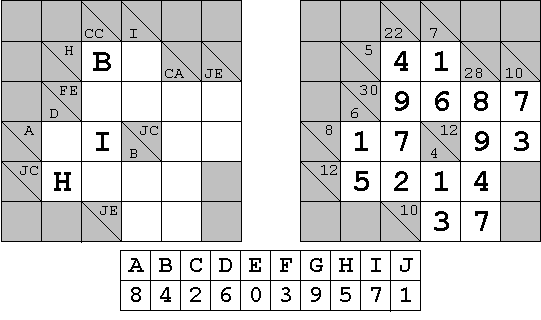 +
+ -The above is an example of a cryptic kakuro (also known as cross sums, or even sums cross) puzzle, with its final solution on the right. (The common rules of kakuro puzzles can be found easily on numerous internet sites. Other related information can also be currently found at krazydad.com whose author has provided the puzzle data for this challenge.)
+上図は暗号カックロ (別名: クロスサム、サムクロス) というパズルの例であり、右側はその最終解です。 (カックロパズルの一般ルールは、数多くのインターネットサイトで簡単に見つかります。 その他の関連情報は現在、このチャレンジにパズルデータを提供した方が運営する krazydad.com でも見つかります。)
-The `testPuzzles` array contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as string as follows:
+`testPuzzles` 配列には、このようなパズルの 5x5 タイプと 6x6 のタイプが計 200 問含まれています。 このファイルにある最初のパズルが上の例であり、次の文字列で書かれています。
`6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X`
-The first character is a numerical digit indicating the size of the information grid. It would be either a 6 (for a 5x5 kakuro puzzle) or a 7 (for a 6x6 puzzle) followed by a comma (,). The extra top line and left column are needed to insert information.
+最初の文字は、情報格子のサイズを表す数字です。 6 (5x5 のカックロパズルの場合) または 7 (6x6 のカックロパズルの場合) の後にカンマ (,) が続きます。 追加情報を入れるために、最上行と最左列が付加されています。
-The content of each cell is then described and followed by a comma, going left to right and starting with the top line.
+各マスの内容は、最上行から始まり、左から右へカンマ区切りで記述されます。
-`X` = Gray cell, not required to be filled by a digit.
+`X`: 灰色のマスであり、数字を埋める必要はありません。
-`O` (upper case letter)= White empty cell to be filled by a digit.
+`O` (大文字): 数字を埋める必要のある空白のマスです。
-`A` = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle.
+`A` (大文字の A から J までのすべて): パズルを解くときにそれに相当する数字に置き換えられます。
-`( )` = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
+`( )`: 暗号化された和の位置です。 横方向の和のは小文字の "h" で始まり、縦方向の和は小文字の "v" で始まります。 その後に、和が 1 桁か 2 桁かに応じて 1 つまたは 2 つの大文字のアルファベットが続きます。 和が 2 桁のとき、1 つ目のアルファベットは 10 の位、2 つ目のアルファベットは 1 の位を表します。 マスが縦方向と横方向の両方の和を持つ必要があるとき、1 つ目は常に横方向の和であり、両方の和が同じ括弧内でカンマで区切られます。例えば、(hFE,vD) となります。 左括弧から右括弧までの各まとまりの直後にも、カンマが続きます。
-The description of the last cell is followed by a Carriage Return/Line Feed (CRLF) instead of a comma.
+最後のマスの記述の後は、カンマではなく改行 (CRLF) が続きます。
-The required answer to each puzzle is based on the value of each letter necessary to arrive at the solution and according to the alphabetical order. As indicated under the example puzzle, its answer would be 8426039571. At least 9 out of the 10 encrypting letters are always part of the problem description. When only 9 are given, the missing one must be assigned the remaining digit.
+それぞれのパズルの解は、パズルを解くのに必要となる各文字の値をアルファベット順に並べたものに基づきます。 例題の解は、パズルの下に示すとおり 8426039571 です。 暗号化文字 10 個のうち少なくとも 9 個が必ずパズル記述に含まれています。 9 個のみ含まれている場合、含まれていない 1 個には残りの数字が割り当てられる必要があります。
-You are given that the sum of the answers for the first 10 puzzles in `testPuzzles` is 64414157580.
+最初の 10 問のパズルの解の和は `testPuzzles` であることが与えられます。
-Find the sum of the answers for `puzzles` array.
+`puzzles` 配列の解の和を求めなさい。
# --hints--
-`kakuro(testPuzzles)` should return `1059760019628`.
+`kakuro(testPuzzles)` は `1059760019628` を返す必要があります。
```js
assert.strictEqual(kakuro(_testPuzzles), 1059760019628);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
index 72f5393017..94afbcfe2a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
@@ -1,6 +1,6 @@
---
id: 5900f5151000cf542c510028
-title: 'Problem 425: Prime connection'
+title: '問題 425: 素数の親類関係'
challengeType: 5
forumTopicId: 302095
dashedName: problem-425-prime-connection
@@ -8,26 +8,26 @@ dashedName: problem-425-prime-connection
# --description--
-Two positive numbers $A$ and $B$ are said to be connected (denoted by "$A ↔ B$") if one of these conditions holds:
+2 つの正の整数 $A$ と $B$ が次の条件のいずれか 1 つを満たすとき、それらは親類関係にある ("$A ↔ B$" で表記) ものとします。
-1. $A$ and $B$ have the same length and differ in exactly one digit; for example, $123 ↔ 173$.
-2. Adding one digit to the left of $A$ (or $B$) makes $B$ (or $A$); for example, $23 ↔ 223$ and $123 ↔ 23$.
+1. $A$ と $B$ の桁数が同じで、ちょうど 1 桁が異なる。例: 123 ↔ 173
+2. $A$ (または $B$) の左側に 1 桁追加すると $B$ (または $A$) になる。例: 23 ↔ 223 および 123 ↔ 23
-We call a prime $P$ a 2's relative if there exists a chain of connected primes between 2 and $P$ and no prime in the chain exceeds $P$.
+親類関係にある素数の連鎖が 2 と 素数 $P$ の間にあり、その連鎖の中に $P$ を超える素数がないとき、$P$ を 2 の親類と呼ぶことにします。
-For example, 127 is a 2's relative. One of the possible chains is shown below:
+例えば、127 は 2 の親類です。 考えられる連鎖の一つを次に示します。
$$2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127$$
-However, 11 and 103 are not 2's relatives.
+しかし、11 と 103 は 2 の親類ではありません。
-Let $F(N)$ be the sum of the primes $≤ N$ which are not 2's relatives. We can verify that $F({10}^3) = 431$ and $F({10}^4) = 78\\,728$.
+2 の親類ではない N 以下の素数の和を $F(N)$ とします。 $F({10}^3) = 431$, $F({10}^4) = 78\\,728$ であることを確認できます。
-Find $F({10}^7)$.
+$F({10}^7)$ を求めなさい。
# --hints--
-`primeConnection()` should return `46479497324`.
+`primeConnection()` は `46479497324` を返す必要があります。
```js
assert.strictEqual(primeConnection(), 46479497324);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
index d42c63f115..d465aeb08b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
@@ -1,6 +1,6 @@
---
id: 5900f5171000cf542c510029
-title: 'Problem 426: Box-ball system'
+title: '問題 426: 箱玉系'
challengeType: 5
forumTopicId: 302096
dashedName: problem-426-box-ball-system
@@ -8,33 +8,33 @@ dashedName: problem-426-box-ball-system
# --description--
-Consider an infinite row of boxes. Some of the boxes contain a ball. For example, an initial configuration of 2 consecutive occupied boxes followed by 2 empty boxes, 2 occupied boxes, 1 empty box, and 2 occupied boxes can be denoted by the sequence (2, 2, 2, 1, 2), in which the number of consecutive occupied and empty boxes appear alternately.
+無限に並べられた箱について考えます。 いくつかの箱には玉が入っています。 例えば、玉入りの箱が 2 個連続し、その後に空箱が 2 個、玉入りの箱が 2 個、空箱が 1 個、玉入りの箱が 2 個並んでいる初期配置は、数列 (2, 2, 2, 1, 2) と表すことができます。これは、玉入りの箱の連続数と空箱の連続数とを交互に表したものです。
-A turn consists of moving each ball exactly once according to the following rule: Transfer the leftmost ball which has not been moved to the nearest empty box to its right.
+1 回の操作は、「まだ移動していない最も左にある玉を、その玉より右側の最も近い空箱に入れる」というルールに従って、それぞれの玉をちょうど 1 回移動させることです。
-After one turn the sequence (2, 2, 2, 1, 2) becomes (2, 2, 1, 2, 3) as can be seen below; note that we begin the new sequence starting at the first occupied box.
+1 回の操作の後、下図のように数列 (2, 2, 2, 1, 2) が (2, 2, 1, 2, 3) になります。新たにできた数列が最初の玉入りの箱から始まっていることに注意してください。
-
-The above is an example of a cryptic kakuro (also known as cross sums, or even sums cross) puzzle, with its final solution on the right. (The common rules of kakuro puzzles can be found easily on numerous internet sites. Other related information can also be currently found at krazydad.com whose author has provided the puzzle data for this challenge.)
+上図は暗号カックロ (別名: クロスサム、サムクロス) というパズルの例であり、右側はその最終解です。 (カックロパズルの一般ルールは、数多くのインターネットサイトで簡単に見つかります。 その他の関連情報は現在、このチャレンジにパズルデータを提供した方が運営する krazydad.com でも見つかります。)
-The `testPuzzles` array contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as string as follows:
+`testPuzzles` 配列には、このようなパズルの 5x5 タイプと 6x6 のタイプが計 200 問含まれています。 このファイルにある最初のパズルが上の例であり、次の文字列で書かれています。
`6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X`
-The first character is a numerical digit indicating the size of the information grid. It would be either a 6 (for a 5x5 kakuro puzzle) or a 7 (for a 6x6 puzzle) followed by a comma (,). The extra top line and left column are needed to insert information.
+最初の文字は、情報格子のサイズを表す数字です。 6 (5x5 のカックロパズルの場合) または 7 (6x6 のカックロパズルの場合) の後にカンマ (,) が続きます。 追加情報を入れるために、最上行と最左列が付加されています。
-The content of each cell is then described and followed by a comma, going left to right and starting with the top line.
+各マスの内容は、最上行から始まり、左から右へカンマ区切りで記述されます。
-`X` = Gray cell, not required to be filled by a digit.
+`X`: 灰色のマスであり、数字を埋める必要はありません。
-`O` (upper case letter)= White empty cell to be filled by a digit.
+`O` (大文字): 数字を埋める必要のある空白のマスです。
-`A` = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle.
+`A` (大文字の A から J までのすべて): パズルを解くときにそれに相当する数字に置き換えられます。
-`( )` = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
+`( )`: 暗号化された和の位置です。 横方向の和のは小文字の "h" で始まり、縦方向の和は小文字の "v" で始まります。 その後に、和が 1 桁か 2 桁かに応じて 1 つまたは 2 つの大文字のアルファベットが続きます。 和が 2 桁のとき、1 つ目のアルファベットは 10 の位、2 つ目のアルファベットは 1 の位を表します。 マスが縦方向と横方向の両方の和を持つ必要があるとき、1 つ目は常に横方向の和であり、両方の和が同じ括弧内でカンマで区切られます。例えば、(hFE,vD) となります。 左括弧から右括弧までの各まとまりの直後にも、カンマが続きます。
-The description of the last cell is followed by a Carriage Return/Line Feed (CRLF) instead of a comma.
+最後のマスの記述の後は、カンマではなく改行 (CRLF) が続きます。
-The required answer to each puzzle is based on the value of each letter necessary to arrive at the solution and according to the alphabetical order. As indicated under the example puzzle, its answer would be 8426039571. At least 9 out of the 10 encrypting letters are always part of the problem description. When only 9 are given, the missing one must be assigned the remaining digit.
+それぞれのパズルの解は、パズルを解くのに必要となる各文字の値をアルファベット順に並べたものに基づきます。 例題の解は、パズルの下に示すとおり 8426039571 です。 暗号化文字 10 個のうち少なくとも 9 個が必ずパズル記述に含まれています。 9 個のみ含まれている場合、含まれていない 1 個には残りの数字が割り当てられる必要があります。
-You are given that the sum of the answers for the first 10 puzzles in `testPuzzles` is 64414157580.
+最初の 10 問のパズルの解の和は `testPuzzles` であることが与えられます。
-Find the sum of the answers for `puzzles` array.
+`puzzles` 配列の解の和を求めなさい。
# --hints--
-`kakuro(testPuzzles)` should return `1059760019628`.
+`kakuro(testPuzzles)` は `1059760019628` を返す必要があります。
```js
assert.strictEqual(kakuro(_testPuzzles), 1059760019628);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
index 72f5393017..94afbcfe2a 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
@@ -1,6 +1,6 @@
---
id: 5900f5151000cf542c510028
-title: 'Problem 425: Prime connection'
+title: '問題 425: 素数の親類関係'
challengeType: 5
forumTopicId: 302095
dashedName: problem-425-prime-connection
@@ -8,26 +8,26 @@ dashedName: problem-425-prime-connection
# --description--
-Two positive numbers $A$ and $B$ are said to be connected (denoted by "$A ↔ B$") if one of these conditions holds:
+2 つの正の整数 $A$ と $B$ が次の条件のいずれか 1 つを満たすとき、それらは親類関係にある ("$A ↔ B$" で表記) ものとします。
-1. $A$ and $B$ have the same length and differ in exactly one digit; for example, $123 ↔ 173$.
-2. Adding one digit to the left of $A$ (or $B$) makes $B$ (or $A$); for example, $23 ↔ 223$ and $123 ↔ 23$.
+1. $A$ と $B$ の桁数が同じで、ちょうど 1 桁が異なる。例: 123 ↔ 173
+2. $A$ (または $B$) の左側に 1 桁追加すると $B$ (または $A$) になる。例: 23 ↔ 223 および 123 ↔ 23
-We call a prime $P$ a 2's relative if there exists a chain of connected primes between 2 and $P$ and no prime in the chain exceeds $P$.
+親類関係にある素数の連鎖が 2 と 素数 $P$ の間にあり、その連鎖の中に $P$ を超える素数がないとき、$P$ を 2 の親類と呼ぶことにします。
-For example, 127 is a 2's relative. One of the possible chains is shown below:
+例えば、127 は 2 の親類です。 考えられる連鎖の一つを次に示します。
$$2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127$$
-However, 11 and 103 are not 2's relatives.
+しかし、11 と 103 は 2 の親類ではありません。
-Let $F(N)$ be the sum of the primes $≤ N$ which are not 2's relatives. We can verify that $F({10}^3) = 431$ and $F({10}^4) = 78\\,728$.
+2 の親類ではない N 以下の素数の和を $F(N)$ とします。 $F({10}^3) = 431$, $F({10}^4) = 78\\,728$ であることを確認できます。
-Find $F({10}^7)$.
+$F({10}^7)$ を求めなさい。
# --hints--
-`primeConnection()` should return `46479497324`.
+`primeConnection()` は `46479497324` を返す必要があります。
```js
assert.strictEqual(primeConnection(), 46479497324);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
index d42c63f115..d465aeb08b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
@@ -1,6 +1,6 @@
---
id: 5900f5171000cf542c510029
-title: 'Problem 426: Box-ball system'
+title: '問題 426: 箱玉系'
challengeType: 5
forumTopicId: 302096
dashedName: problem-426-box-ball-system
@@ -8,33 +8,33 @@ dashedName: problem-426-box-ball-system
# --description--
-Consider an infinite row of boxes. Some of the boxes contain a ball. For example, an initial configuration of 2 consecutive occupied boxes followed by 2 empty boxes, 2 occupied boxes, 1 empty box, and 2 occupied boxes can be denoted by the sequence (2, 2, 2, 1, 2), in which the number of consecutive occupied and empty boxes appear alternately.
+無限に並べられた箱について考えます。 いくつかの箱には玉が入っています。 例えば、玉入りの箱が 2 個連続し、その後に空箱が 2 個、玉入りの箱が 2 個、空箱が 1 個、玉入りの箱が 2 個並んでいる初期配置は、数列 (2, 2, 2, 1, 2) と表すことができます。これは、玉入りの箱の連続数と空箱の連続数とを交互に表したものです。
-A turn consists of moving each ball exactly once according to the following rule: Transfer the leftmost ball which has not been moved to the nearest empty box to its right.
+1 回の操作は、「まだ移動していない最も左にある玉を、その玉より右側の最も近い空箱に入れる」というルールに従って、それぞれの玉をちょうど 1 回移動させることです。
-After one turn the sequence (2, 2, 2, 1, 2) becomes (2, 2, 1, 2, 3) as can be seen below; note that we begin the new sequence starting at the first occupied box.
+1 回の操作の後、下図のように数列 (2, 2, 2, 1, 2) が (2, 2, 1, 2, 3) になります。新たにできた数列が最初の玉入りの箱から始まっていることに注意してください。
- +
+ -A system like this is called a Box-Ball System or BBS for short.
+このような系は箱玉系、または略して BBS (Box-Ball System) と呼ばれます。
-It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to [1, 2, 3]; we shall call this the final state.
+この操作を十分に繰り返すと、玉入りの箱の連続数が一定となる状態へと箱玉系が発展することが分かっています。 下の例では、玉入りの箱の連続数が [1, 2, 3] に発展します。これを最終状態と呼ぶことにします。
-
-A system like this is called a Box-Ball System or BBS for short.
+このような系は箱玉系、または略して BBS (Box-Ball System) と呼ばれます。
-It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to [1, 2, 3]; we shall call this the final state.
+この操作を十分に繰り返すと、玉入りの箱の連続数が一定となる状態へと箱玉系が発展することが分かっています。 下の例では、玉入りの箱の連続数が [1, 2, 3] に発展します。これを最終状態と呼ぶことにします。
-![four turns from occupied boxes [2, 2, 2] to final state [1, 2, 3]](https://cdn.freecodecamp.org/curriculum/project-euler/box-ball-system-2.gif) +
+![玉入りの箱 [2, 2, 2] から最終状態 [1, 2, 3] までの 4 操作](https://cdn.freecodecamp.org/curriculum/project-euler/box-ball-system-2.gif) -We define the sequence $\\{t_i\\}$:
+数列 $\\{t_i\\}$ を次のように定義します。
$$\begin{align} & s_0 = 290\\,797 \\\\ & s_{k + 1} = {s_k}^2\bmod 50\\,515\\,093 \\\\ & t_k = (s_k\bmod 64) + 1 \end{align}$$
-Starting from the initial configuration $(t_0, t_1, \ldots, t_{10})$, the final state becomes [1, 3, 10, 24, 51, 75].
+初期配置 $(t_0, t_1, \ldots, t_{10})$ から開始すると、最終状態は [1, 3, 10, 24, 51, 75] となります。
-Starting from the initial configuration $(t_0, t_1, \ldots, t_{10\\,000\\,000})$, find the final state.
+初期配置 $(t_0, t_1, \ldots, t_{10\\,000\\,000})$ から開始したときの最終状態を求めなさい。
-Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is [1, 2, 3] then $14 (= 1^2 + 2^2 + 3^2)$ is your answer.
+回答は、最終状態の各要素の 2 乗の和とすること。 例えば、最終状態が [1, 2, 3] のとき、回答は $14 (= 1^2 + 2^2 + 3^2)$ となります。
# --hints--
-`boxBallSystem()` should return `31591886008`.
+`boxBallSystem()` は `31591886008` を返す必要があります。
```js
assert.strictEqual(boxBallSystem(), 31591886008);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
index bc840f45c8..a9af23c02e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f5181000cf542c51002a
-title: 'Problem 427: n-sequences'
+title: '問題 427: n の数列'
challengeType: 5
forumTopicId: 302097
dashedName: problem-427-n-sequences
@@ -8,21 +8,21 @@ dashedName: problem-427-n-sequences
# --description--
-A sequence of integers $S = \\{s_i\\}$ is called an $n$-sequence if it has $n$ elements and each element $s_i$ satisfies $1 ≤ s_i ≤ n$. Thus there are $n^n$ distinct $n$-sequences in total.
+整数の数列 $S = \\{s_i\\}$ が $n$ 個の要素を持ち、各要素 $s_i$ が $1 ≤ s_i ≤ n$ を満たすとき、これを $n$ の数列と呼びます。 したがって、全体で $n^n$ 個の相異なる $n$ の数列があります。
-For example, the sequence $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ is a 10-sequence.
+例えば、数列 $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ は 10 の数列の一例です。
-For any sequence $S$, let $L(S)$ be the length of the longest contiguous subsequence of $S$ with the same value. For example, for the given sequence $S$ above, $L(S) = 3$, because of the three consecutive 7's.
+任意の数列 $S$ について、同じ値が最も長く連続している、$S$ の部分列の長さを $L(S)$ とします。 例えば、上で与えられた数列 $S$ の場合、7 が 3 回連続で現れるので、$L(S) = 3$ です。
-Let $f(n) = \sum L(S)$ for all $n$-sequences $S$.
+すべての $n$ の数列 $S$ について、$f(n) = \sum L(S)$ とします。
-For example, $f(3) = 45$, $f(7) = 1\\,403\\,689$ and $f(11) = 481\\,496\\,895\\,121$.
+例: $f(3) = 45$, $f(7) = 1\\,403\\,689$, $f(11) = 481\\,496\\,895\\,121$
-Find $f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$.
+$f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$ を求めなさい。
# --hints--
-`nSequences()` should return `97138867`.
+`nSequences()` は `97138867` を返す必要があります。
```js
assert.strictEqual(nSequences(), 97138867);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
index 6a9135f923..e43e21568c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f5191000cf542c51002b
-title: 'Problem 428: Necklace of Circles'
+title: '問題 428: 円のネックレス'
challengeType: 5
forumTopicId: 302098
dashedName: problem-428-necklace-of-circles
@@ -8,32 +8,32 @@ dashedName: problem-428-necklace-of-circles
# --description--
-Let $a$, $b$ and $c$ be positive numbers.
+$a$, $b$, $c$ を正の数とします。
-Let $W$, $X$, $Y$, $Z$ be four collinear points where $|WX| = a$, $|XY| = b$, $|YZ| = c$ and $|WZ| = a + b + c$.
+$|WX| = a$, $|XY| = b$, $|YZ| = c$, $|WZ| = a + b + c$ となる同一直線上の 4 点 を $W$, $X$, $Y$, $Z$ とします。
-Let $C_{\text{in}}$ be the circle having the diameter $XY$.
+直径が $XY$ である円を $C_{\text{in}}$ とします。
-Let $C_{\text{out}}$ be the circle having the diameter $WZ$.
+直径が $WZ$ である円を $C_{\text{out}}$ とします。
-The triplet ($a$, $b$, $c$) is called a *necklace triplet* if you can place $k ≥ 3$ distinct circles $C_1, C_2, \ldots, C_k$ such that:
+$k (≥ 3)$ 個の相異なる円 $C_1, C_2, \ldots, C_k$ を、以下の条件をすべて満たすように配置できる場合、三つ組数 ($a$, $b$, $c$) は*ネックレス三つ組数*と呼ばれます。
-- $C_i$ has no common interior points with any $C_j$ for $1 ≤ i$, $j ≤ k$ and $i ≠ j$,
-- $C_i$ is tangent to both $C_{\text{in}}$ and $C_{\text{out}}$ for $1 ≤ i ≤ k$,
-- $C_i$ is tangent to $C_{i + 1}$ for $1 ≤ i < k$, and
-- $C_k$ is tangent to $C_1$.
+- $C_i$ は、$1 ≤ i$, $j ≤ k$ かつ $i ≠ j$ のとき、いずれの $C_j$ とも内点を共有しない。
+- $C_i$ は、$1 ≤ i ≤ k$ のとき、$C_{\text{in}}$ および $C_{\text{out}}$ の両方に接している。
+- $C_i$ は、$1 ≤ i < k$ のとき、$C_{i + 1}$ に接している。
+- $C_k$ は $C_1$ に接している。
-For example, (5, 5, 5) and (4, 3, 21) are necklace triplets, while it can be shown that (2, 2, 5) is not.
+例えば、(5, 5, 5) と (4, 3, 21) はネックレス三つ組数です。しかし、(2, 2, 5) はそうではないことが分かっています。
-
-We define the sequence $\\{t_i\\}$:
+数列 $\\{t_i\\}$ を次のように定義します。
$$\begin{align} & s_0 = 290\\,797 \\\\ & s_{k + 1} = {s_k}^2\bmod 50\\,515\\,093 \\\\ & t_k = (s_k\bmod 64) + 1 \end{align}$$
-Starting from the initial configuration $(t_0, t_1, \ldots, t_{10})$, the final state becomes [1, 3, 10, 24, 51, 75].
+初期配置 $(t_0, t_1, \ldots, t_{10})$ から開始すると、最終状態は [1, 3, 10, 24, 51, 75] となります。
-Starting from the initial configuration $(t_0, t_1, \ldots, t_{10\\,000\\,000})$, find the final state.
+初期配置 $(t_0, t_1, \ldots, t_{10\\,000\\,000})$ から開始したときの最終状態を求めなさい。
-Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is [1, 2, 3] then $14 (= 1^2 + 2^2 + 3^2)$ is your answer.
+回答は、最終状態の各要素の 2 乗の和とすること。 例えば、最終状態が [1, 2, 3] のとき、回答は $14 (= 1^2 + 2^2 + 3^2)$ となります。
# --hints--
-`boxBallSystem()` should return `31591886008`.
+`boxBallSystem()` は `31591886008` を返す必要があります。
```js
assert.strictEqual(boxBallSystem(), 31591886008);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
index bc840f45c8..a9af23c02e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
@@ -1,6 +1,6 @@
---
id: 5900f5181000cf542c51002a
-title: 'Problem 427: n-sequences'
+title: '問題 427: n の数列'
challengeType: 5
forumTopicId: 302097
dashedName: problem-427-n-sequences
@@ -8,21 +8,21 @@ dashedName: problem-427-n-sequences
# --description--
-A sequence of integers $S = \\{s_i\\}$ is called an $n$-sequence if it has $n$ elements and each element $s_i$ satisfies $1 ≤ s_i ≤ n$. Thus there are $n^n$ distinct $n$-sequences in total.
+整数の数列 $S = \\{s_i\\}$ が $n$ 個の要素を持ち、各要素 $s_i$ が $1 ≤ s_i ≤ n$ を満たすとき、これを $n$ の数列と呼びます。 したがって、全体で $n^n$ 個の相異なる $n$ の数列があります。
-For example, the sequence $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ is a 10-sequence.
+例えば、数列 $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ は 10 の数列の一例です。
-For any sequence $S$, let $L(S)$ be the length of the longest contiguous subsequence of $S$ with the same value. For example, for the given sequence $S$ above, $L(S) = 3$, because of the three consecutive 7's.
+任意の数列 $S$ について、同じ値が最も長く連続している、$S$ の部分列の長さを $L(S)$ とします。 例えば、上で与えられた数列 $S$ の場合、7 が 3 回連続で現れるので、$L(S) = 3$ です。
-Let $f(n) = \sum L(S)$ for all $n$-sequences $S$.
+すべての $n$ の数列 $S$ について、$f(n) = \sum L(S)$ とします。
-For example, $f(3) = 45$, $f(7) = 1\\,403\\,689$ and $f(11) = 481\\,496\\,895\\,121$.
+例: $f(3) = 45$, $f(7) = 1\\,403\\,689$, $f(11) = 481\\,496\\,895\\,121$
-Find $f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$.
+$f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$ を求めなさい。
# --hints--
-`nSequences()` should return `97138867`.
+`nSequences()` は `97138867` を返す必要があります。
```js
assert.strictEqual(nSequences(), 97138867);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
index 6a9135f923..e43e21568c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f5191000cf542c51002b
-title: 'Problem 428: Necklace of Circles'
+title: '問題 428: 円のネックレス'
challengeType: 5
forumTopicId: 302098
dashedName: problem-428-necklace-of-circles
@@ -8,32 +8,32 @@ dashedName: problem-428-necklace-of-circles
# --description--
-Let $a$, $b$ and $c$ be positive numbers.
+$a$, $b$, $c$ を正の数とします。
-Let $W$, $X$, $Y$, $Z$ be four collinear points where $|WX| = a$, $|XY| = b$, $|YZ| = c$ and $|WZ| = a + b + c$.
+$|WX| = a$, $|XY| = b$, $|YZ| = c$, $|WZ| = a + b + c$ となる同一直線上の 4 点 を $W$, $X$, $Y$, $Z$ とします。
-Let $C_{\text{in}}$ be the circle having the diameter $XY$.
+直径が $XY$ である円を $C_{\text{in}}$ とします。
-Let $C_{\text{out}}$ be the circle having the diameter $WZ$.
+直径が $WZ$ である円を $C_{\text{out}}$ とします。
-The triplet ($a$, $b$, $c$) is called a *necklace triplet* if you can place $k ≥ 3$ distinct circles $C_1, C_2, \ldots, C_k$ such that:
+$k (≥ 3)$ 個の相異なる円 $C_1, C_2, \ldots, C_k$ を、以下の条件をすべて満たすように配置できる場合、三つ組数 ($a$, $b$, $c$) は*ネックレス三つ組数*と呼ばれます。
-- $C_i$ has no common interior points with any $C_j$ for $1 ≤ i$, $j ≤ k$ and $i ≠ j$,
-- $C_i$ is tangent to both $C_{\text{in}}$ and $C_{\text{out}}$ for $1 ≤ i ≤ k$,
-- $C_i$ is tangent to $C_{i + 1}$ for $1 ≤ i < k$, and
-- $C_k$ is tangent to $C_1$.
+- $C_i$ は、$1 ≤ i$, $j ≤ k$ かつ $i ≠ j$ のとき、いずれの $C_j$ とも内点を共有しない。
+- $C_i$ は、$1 ≤ i ≤ k$ のとき、$C_{\text{in}}$ および $C_{\text{out}}$ の両方に接している。
+- $C_i$ は、$1 ≤ i < k$ のとき、$C_{i + 1}$ に接している。
+- $C_k$ は $C_1$ に接している。
-For example, (5, 5, 5) and (4, 3, 21) are necklace triplets, while it can be shown that (2, 2, 5) is not.
+例えば、(5, 5, 5) と (4, 3, 21) はネックレス三つ組数です。しかし、(2, 2, 5) はそうではないことが分かっています。
-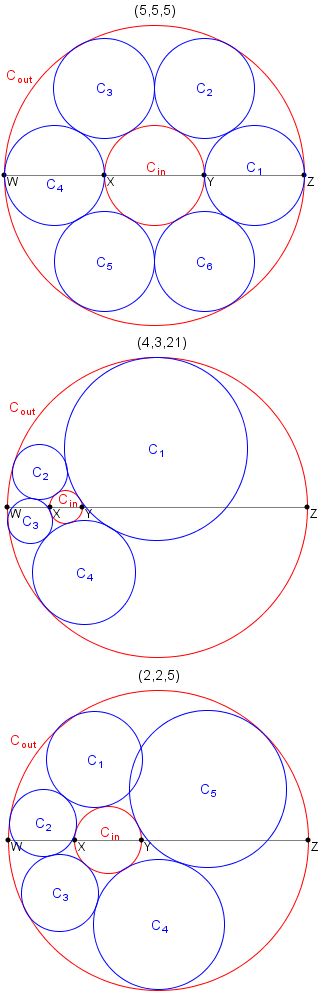 +
+ -Let $T(n)$ be the number of necklace triplets $(a, b, c)$ such that $a$, $b$ and $c$ are positive integers, and $b ≤ n$. For example, $T(1) = 9$, $T(20) = 732$ and $T(3\\,000) = 438\\,106$.
+$a$, $b$, $c$ が正の整数で、かつ $b ≤ n$ のときのネックレス三つ組数の個数を $T(n)$ とします。 例えば、$T(1) = 9$, $T(20) = 732$, $T(3\\,000) = 438\\,106$ です。
-Find $T(1\\,000\\,000\\,000)$.
+$T(1\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`necklace(1000000000)` should return `747215561862`.
+`necklace(1000000000)` は `747215561862` を返す必要があります。
```js
assert.strictEqual(necklace(1000000000), 747215561862);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
index 8735e80e53..91995ee9a9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f5191000cf542c51002c
-title: 'Problem 429: Sum of squares of unitary divisors'
+title: '問題 429: 単約数の平方和'
challengeType: 5
forumTopicId: 302099
dashedName: problem-429-sum-of-squares-of-unitary-divisors
@@ -8,19 +8,19 @@ dashedName: problem-429-sum-of-squares-of-unitary-divisors
# --description--
-A unitary divisor $d$ of a number $n$ is a divisor of $n$ that has the property $gcd(d, \frac{n}{d}) = 1$.
+ある数 $n$ の単約数 $d$ とは、$gcd(d, \frac{n}{d}) = 1$ という性質を持つような $n$ の約数です。
The unitary divisors of $4! = 24$ are 1, 3, 8 and 24.
-The sum of their squares is $12 + 32 + 82 + 242 = 650$.
+これらの平方数の和は $12 + 32 + 82 + 242 = 650$ です。
-Let $S(n)$ represent the sum of the squares of the unitary divisors of $n$. Thus $S(4!) = 650$.
+$n$ の単約数の平方和を $S(n)$ で表します。 Thus $S(4!) = 650$.
-Find $S(100\\,000\\,000!)$ modulo $1\\,000\\,000\\,009$.
+$S(100\\,000\\,000!)$ mod $1\\,000\\,000\\,009$ を求めなさい。
# --hints--
-`sumSquaresOfUnitaryDivisors()` should return `98792821`.
+`sumSquaresOfUnitaryDivisors()` は `98792821` を返す必要があります。
```js
assert.strictEqual(sumSquaresOfUnitaryDivisors(), 98792821);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md
index aeb7359d02..be0c8bdb77 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md
@@ -1,6 +1,6 @@
---
id: 5900f51a1000cf542c51002d
-title: 'Problem 430: Range flips'
+title: '問題 430: 範囲めくり'
challengeType: 5
forumTopicId: 302101
dashedName: problem-430-range-flips
@@ -8,23 +8,23 @@ dashedName: problem-430-range-flips
# --description--
-$N$ disks are placed in a row, indexed 1 to $N$ from left to right.
+$N$ 枚の円盤が一列に並べられ、左から右に 1 から $N$ までの番号が振られています。
-Each disk has a black side and white side. Initially all disks show their white side.
+円盤にはそれぞれ黒い面と白い面があります。 最初は、すべての円盤の白い面が見えています。
-At each turn, two, not necessarily distinct, integers $A$ and $B$ between 1 and $N$ (inclusive) are chosen uniformly at random. All disks with an index from $A$ to $B$ (inclusive) are flipped.
+各ターンで、相異なるとは限らない 2 つの整数 $A$, $B$ が、1 から $N$ までの間 (1 と $N$ を含む) から一様かつ無作為に選ばれます。 $A$ から $B$ まで ($A$ と $B$ を含む) の番号が振られたすべての円盤が裏返されます。
-The following example shows the case $N = 8$. At the first turn $A = 5$ and $B = 2$, and at the second turn $A = 4$ and $B = 6$.
+下図は $N = 8$ の場合の例です。 最初のターンでは $A = 5$ と $B = 2$、2 回目のターンでは $A = 4$ と $B = 6$ が選ばれます。
-
-Let $T(n)$ be the number of necklace triplets $(a, b, c)$ such that $a$, $b$ and $c$ are positive integers, and $b ≤ n$. For example, $T(1) = 9$, $T(20) = 732$ and $T(3\\,000) = 438\\,106$.
+$a$, $b$, $c$ が正の整数で、かつ $b ≤ n$ のときのネックレス三つ組数の個数を $T(n)$ とします。 例えば、$T(1) = 9$, $T(20) = 732$, $T(3\\,000) = 438\\,106$ です。
-Find $T(1\\,000\\,000\\,000)$.
+$T(1\\,000\\,000\\,000)$ を求めなさい。
# --hints--
-`necklace(1000000000)` should return `747215561862`.
+`necklace(1000000000)` は `747215561862` を返す必要があります。
```js
assert.strictEqual(necklace(1000000000), 747215561862);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
index 8735e80e53..91995ee9a9 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f5191000cf542c51002c
-title: 'Problem 429: Sum of squares of unitary divisors'
+title: '問題 429: 単約数の平方和'
challengeType: 5
forumTopicId: 302099
dashedName: problem-429-sum-of-squares-of-unitary-divisors
@@ -8,19 +8,19 @@ dashedName: problem-429-sum-of-squares-of-unitary-divisors
# --description--
-A unitary divisor $d$ of a number $n$ is a divisor of $n$ that has the property $gcd(d, \frac{n}{d}) = 1$.
+ある数 $n$ の単約数 $d$ とは、$gcd(d, \frac{n}{d}) = 1$ という性質を持つような $n$ の約数です。
The unitary divisors of $4! = 24$ are 1, 3, 8 and 24.
-The sum of their squares is $12 + 32 + 82 + 242 = 650$.
+これらの平方数の和は $12 + 32 + 82 + 242 = 650$ です。
-Let $S(n)$ represent the sum of the squares of the unitary divisors of $n$. Thus $S(4!) = 650$.
+$n$ の単約数の平方和を $S(n)$ で表します。 Thus $S(4!) = 650$.
-Find $S(100\\,000\\,000!)$ modulo $1\\,000\\,000\\,009$.
+$S(100\\,000\\,000!)$ mod $1\\,000\\,000\\,009$ を求めなさい。
# --hints--
-`sumSquaresOfUnitaryDivisors()` should return `98792821`.
+`sumSquaresOfUnitaryDivisors()` は `98792821` を返す必要があります。
```js
assert.strictEqual(sumSquaresOfUnitaryDivisors(), 98792821);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md
index aeb7359d02..be0c8bdb77 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-430-range-flips.md
@@ -1,6 +1,6 @@
---
id: 5900f51a1000cf542c51002d
-title: 'Problem 430: Range flips'
+title: '問題 430: 範囲めくり'
challengeType: 5
forumTopicId: 302101
dashedName: problem-430-range-flips
@@ -8,23 +8,23 @@ dashedName: problem-430-range-flips
# --description--
-$N$ disks are placed in a row, indexed 1 to $N$ from left to right.
+$N$ 枚の円盤が一列に並べられ、左から右に 1 から $N$ までの番号が振られています。
-Each disk has a black side and white side. Initially all disks show their white side.
+円盤にはそれぞれ黒い面と白い面があります。 最初は、すべての円盤の白い面が見えています。
-At each turn, two, not necessarily distinct, integers $A$ and $B$ between 1 and $N$ (inclusive) are chosen uniformly at random. All disks with an index from $A$ to $B$ (inclusive) are flipped.
+各ターンで、相異なるとは限らない 2 つの整数 $A$, $B$ が、1 から $N$ までの間 (1 と $N$ を含む) から一様かつ無作為に選ばれます。 $A$ から $B$ まで ($A$ と $B$ を含む) の番号が振られたすべての円盤が裏返されます。
-The following example shows the case $N = 8$. At the first turn $A = 5$ and $B = 2$, and at the second turn $A = 4$ and $B = 6$.
+下図は $N = 8$ の場合の例です。 最初のターンでは $A = 5$ と $B = 2$、2 回目のターンでは $A = 4$ と $B = 6$ が選ばれます。
- +
+ -Let $E(N, M)$ be the expected number of disks that show their white side after $M$ turns. We can verify that $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$ and $E(100, 10) ≈ 51.893$.
+$M$ 回のターンの後に白い面が見えている円盤の枚数の期待値を $E(N, M)$ とします。 $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$, $E(100, 10) ≈ 51.893$ であることを確認できます。
-Find $E({10}^{10}, 4000)$. Give your answer rounded to 2 decimal places behind the decimal point.
+$E({10}^{10}, 4000)$ を求めなさい。 回答は、四捨五入して小数第 2 位まで示すこと。
# --hints--
-`rangeFlips()` should return `5000624921.38`.
+`rangeFlips()` は `5000624921.38` を返す必要があります。
```js
assert.strictEqual(rangeFlips(), 5000624921.38);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
index 92f1965578..10076001d6 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
@@ -1,6 +1,6 @@
---
id: 5900f51b1000cf542c51002e
-title: 'Problem 431: Square Space Silo'
+title: '問題 431: 空間が平方数であるサイロ'
challengeType: 5
forumTopicId: 302102
dashedName: problem-431-square-space-silo
@@ -8,21 +8,21 @@ dashedName: problem-431-square-space-silo
# --description--
-Fred the farmer arranges to have a new storage silo installed on his farm and having an obsession for all things square he is absolutely devastated when he discovers that it is circular. Quentin, the representative from the company that installed the silo, explains that they only manufacture cylindrical silos, but he points out that it is resting on a square base. Fred is not amused and insists that it is removed from his property.
+農場主のフレッドは、農場にサイロを新設するための手配をしました。彼は四角い物への執着が強く、丸い物を見つけるとひどく落ち込みます。 サイロを新設した会社の代表者クエンティンは、円柱状のサイロしか製造していないと説明しましたが、ただしサイロは四角い土台の上に載っていると指摘しました。 それでもフレッドは不快感を抱き、サイロを農場から撤去するよう求めました。
-Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\alpha = 30°$, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
+クエンティンは機転を利かせて次のことを説明しました。サイロの上から粒状のものが投入されるとき、円錐状の斜面ができ、その際に斜面と水平な線によって自然にできる角度は安息角と呼ばれます。 例えば、安息角が $\alpha = 30°$ で、サイロの中央に穀物を投入する場合、円柱の最上部に向けて完全な円錐が形作られます。 直径 6 m のこのサイロの場合、無駄になる空間の体積は約 32.648388556 m3 です。 一方で、最上面の中心から水平に $x$ メートル離れた点から穀物を投入すると、円錐の底面は奇妙に曲がり傾斜します。 クエンティンはフレッドに図を見せました。
-
-Let $E(N, M)$ be the expected number of disks that show their white side after $M$ turns. We can verify that $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$ and $E(100, 10) ≈ 51.893$.
+$M$ 回のターンの後に白い面が見えている円盤の枚数の期待値を $E(N, M)$ とします。 $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$, $E(100, 10) ≈ 51.893$ であることを確認できます。
-Find $E({10}^{10}, 4000)$. Give your answer rounded to 2 decimal places behind the decimal point.
+$E({10}^{10}, 4000)$ を求めなさい。 回答は、四捨五入して小数第 2 位まで示すこと。
# --hints--
-`rangeFlips()` should return `5000624921.38`.
+`rangeFlips()` は `5000624921.38` を返す必要があります。
```js
assert.strictEqual(rangeFlips(), 5000624921.38);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
index 92f1965578..10076001d6 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
@@ -1,6 +1,6 @@
---
id: 5900f51b1000cf542c51002e
-title: 'Problem 431: Square Space Silo'
+title: '問題 431: 空間が平方数であるサイロ'
challengeType: 5
forumTopicId: 302102
dashedName: problem-431-square-space-silo
@@ -8,21 +8,21 @@ dashedName: problem-431-square-space-silo
# --description--
-Fred the farmer arranges to have a new storage silo installed on his farm and having an obsession for all things square he is absolutely devastated when he discovers that it is circular. Quentin, the representative from the company that installed the silo, explains that they only manufacture cylindrical silos, but he points out that it is resting on a square base. Fred is not amused and insists that it is removed from his property.
+農場主のフレッドは、農場にサイロを新設するための手配をしました。彼は四角い物への執着が強く、丸い物を見つけるとひどく落ち込みます。 サイロを新設した会社の代表者クエンティンは、円柱状のサイロしか製造していないと説明しましたが、ただしサイロは四角い土台の上に載っていると指摘しました。 それでもフレッドは不快感を抱き、サイロを農場から撤去するよう求めました。
-Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\alpha = 30°$, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
+クエンティンは機転を利かせて次のことを説明しました。サイロの上から粒状のものが投入されるとき、円錐状の斜面ができ、その際に斜面と水平な線によって自然にできる角度は安息角と呼ばれます。 例えば、安息角が $\alpha = 30°$ で、サイロの中央に穀物を投入する場合、円柱の最上部に向けて完全な円錐が形作られます。 直径 6 m のこのサイロの場合、無駄になる空間の体積は約 32.648388556 m3 です。 一方で、最上面の中心から水平に $x$ メートル離れた点から穀物を投入すると、円錐の底面は奇妙に曲がり傾斜します。 クエンティンはフレッドに図を見せました。
- +
+ -We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114\\,785\\,284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114\\,785\\,284) \approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511\\,167\\,869) \approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
+無駄になる空間の体積 (単位: 立方メートル) を $V(x)$ で表します。 $x = 1.114\\,785\\,284$ の場合 (偶然にも、小数点以下の桁数が 3 の 平方数すなわち 9)、無駄になる空間の体積は $V(1.114\\,785\\,284) \approx 36$ となります。 この問題に対して考えられる解の範囲内に、他の選択肢がちょうど 1 つあります。それは、$V(2.511\\,167\\,869) \approx 49$ です。 これで、(平方数と四角形の両方を意味する) "square" がサイロの主になり、輝く栄誉の中で穀物の山の頂に座しているかのようになります。
-Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40°. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+この的確な解決法にフレッドの表情が喜びで輝きました。しかしクエンティンの図と計算を詳しく調べてみると、喜びが再び落胆に変わりました。 フレッドは、 6 m はサイロの直径ではなく半径であり、さらに穀物の安息角は 40 度であるとクエンティンに指摘しました。 しかし、クエンティンが今回のサイロに対する解決策一式を見つけられれば、フレッドは喜んでサイロをこのまま保有するはずです。
-If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\sum x$ correct to 9 decimal places.
+機転の利くクエンティンが、苛立たしいほど気難しい農場主フレッドの四角い物への欲求を満たそうとする場合について、無駄な空間が平方数となるすべての可能な選択肢に対する $x$ の値を決定し、$\sum x$ を小数第 9 位まで求めなさい。
# --hints--
-`squareSpaceSilo()` should return `23.386029052`.
+`squareSpaceSilo()` は `23.386029052` を返す必要があります。
```js
assert.strictEqual(squareSpaceSilo(), 23.386029052);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
index 845ee38a53..97b5e3c0a6 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f51e1000cf542c510030
-title: 'Problem 432: Totient sum'
+title: '問題 432: トーティエント和'
challengeType: 5
forumTopicId: 302103
dashedName: problem-432-totient-sum
@@ -8,15 +8,15 @@ dashedName: problem-432-totient-sum
# --description--
-Let $S(n, m) = \sum φ(n × i)$ for $1 ≤ i ≤ m$. ($φ$ is Euler's totient function)
+$1 ≤ i ≤ m$ のとき、$S(n, m) = \sum φ(n × i)$ とします。 ($φ$ はオイラーのトーティエント関数を表します。)
-You are given that $S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$.
+$S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$ が与えられます。
-Find $S(510\\,510, {10}^{11})$. Give the last 9 digits of your answer.
+$S(510\\,510, {10}^{11})$ を求めなさい。 回答は、下位 9 桁とすること。
# --hints--
-`totientSum()` should return `754862080`.
+`totientSum()` は `754862080` を返す必要があります。
```js
assert.strictEqual(totientSum(), 754862080);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
index 5120b44733..b828530ee0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
@@ -1,6 +1,6 @@
---
id: 5900f51d1000cf542c51002f
-title: 'Problem 433: Steps in Euclid''s algorithm'
+title: '問題 433: ユークリッドの互除法のステップ数'
challengeType: 5
forumTopicId: 302104
dashedName: problem-433-steps-in-euclids-algorithm
@@ -8,23 +8,23 @@ dashedName: problem-433-steps-in-euclids-algorithm
# --description--
-Let $E(x_0, y_0)$ be the number of steps it takes to determine the greatest common divisor of $x_0$ and $y_0$ with Euclid's algorithm. More formally:
+$x_0$ と $y_0$ の最大公約数をユークリッドの互除法によって決定するために必要なステップ数を、$E(x_0, y_0)$ とします。 より形式的に表すと、次のようになります。
$$\begin{align} & x_1 = y_0, y_1 = x_0\bmod y_0 \\\\ & x_n = y_{n - 1}, y_n = x_{n - 1}\bmod y_{n - 1} \end{align}$$
-$E(x_0, y_0)$ is the smallest $n$ such that $y_n = 0$.
+$E(x_0, y_0)$ は $y_n = 0$ となるような最小の $n$ です。
-We have $E(1, 1) = 1$, $E(10, 6) = 3$ and $E(6, 10) = 4$.
+$E(1, 1) = 1$, $E(10, 6) = 3$, $E(6, 10) = 4$ が与えられます。
-Define $S(N)$ as the sum of $E(x, y)$ for $1 ≤ x$, $y ≤ N$.
+$1 ≤ x$, $y ≤ N$ のとき、$E(x, y)$ の和を $S(N)$ と定義します。
-We have $S(1) = 1$, $S(10) = 221$ and $S(100) = 39\\,826$.
+$S(1) = 1$, $S(10) = 221$, $S(100) = 39\\,826$ が与えられます。
-Find $S(5 \times {10}^6)$.
+$S(5 \times {10}^6)$ を求めなさい。
# --hints--
-`stepsInEuclidsAlgorithm()` should return `326624372659664`.
+`stepsInEuclidsAlgorithm()` は `326624372659664` を返す必要があります。
```js
assert.strictEqual(stepsInEuclidsAlgorithm(), 326624372659664);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
index ae1a4b0aae..8b7063775d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
@@ -1,6 +1,6 @@
---
id: 5900f51f1000cf542c510031
-title: 'Problem 434: Rigid graphs'
+title: '問題 434: 剛なグラフ'
challengeType: 5
forumTopicId: 302105
dashedName: problem-434-rigid-graphs
@@ -8,39 +8,39 @@ dashedName: problem-434-rigid-graphs
# --description--
-Recall that a graph is a collection of vertices and edges connecting the vertices, and that two vertices connected by an edge are called adjacent.
+まず、次のことを思い出してください。グラフとは、頂点と、頂点間を結ぶ辺との集まりであり、辺によって結ばれた 2 つの頂点は「隣接している」と表現されます。
-Graphs can be embedded in Euclidean space by associating each vertex with a point in the Euclidean space.
+グラフは、各頂点をユークリッド空間上の点と関連付けることでユークリッド空間に埋め込むことができます。
-A flexible graph is an embedding of a graph where it is possible to move one or more vertices continuously so that the distance between at least two nonadjacent vertices is altered while the distances between each pair of adjacent vertices is kept constant.
+柔軟なグラフとは、隣接する 2 頂点の対のそれぞれで 2 頂点間の距離が一定に保たれたまま、 少なくとも 2 つの隣接していない頂点間の距離が変化するような方法で、1 つ以上の頂点を連続的に動すことができるグラフの埋め込みのことです。
-A rigid graph is an embedding of a graph which is not flexible.
+剛なグラフとは、柔軟でないグラフの埋め込みのことでです。
-Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
+平たく言えば、頂点を 360 度回転する蝶番とに置き換え、辺を弾力のない固い棒に置き換えたときに、グラフの残りの部分から独立して動かすことのできる部分がないグラフは剛なグラフです。
-The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
+ユークリッド平面に埋め込まれた格子グラフは、下のアニメーションが示すように剛なグラフではありません。
-
-We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114\\,785\\,284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114\\,785\\,284) \approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511\\,167\\,869) \approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
+無駄になる空間の体積 (単位: 立方メートル) を $V(x)$ で表します。 $x = 1.114\\,785\\,284$ の場合 (偶然にも、小数点以下の桁数が 3 の 平方数すなわち 9)、無駄になる空間の体積は $V(1.114\\,785\\,284) \approx 36$ となります。 この問題に対して考えられる解の範囲内に、他の選択肢がちょうど 1 つあります。それは、$V(2.511\\,167\\,869) \approx 49$ です。 これで、(平方数と四角形の両方を意味する) "square" がサイロの主になり、輝く栄誉の中で穀物の山の頂に座しているかのようになります。
-Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40°. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+この的確な解決法にフレッドの表情が喜びで輝きました。しかしクエンティンの図と計算を詳しく調べてみると、喜びが再び落胆に変わりました。 フレッドは、 6 m はサイロの直径ではなく半径であり、さらに穀物の安息角は 40 度であるとクエンティンに指摘しました。 しかし、クエンティンが今回のサイロに対する解決策一式を見つけられれば、フレッドは喜んでサイロをこのまま保有するはずです。
-If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\sum x$ correct to 9 decimal places.
+機転の利くクエンティンが、苛立たしいほど気難しい農場主フレッドの四角い物への欲求を満たそうとする場合について、無駄な空間が平方数となるすべての可能な選択肢に対する $x$ の値を決定し、$\sum x$ を小数第 9 位まで求めなさい。
# --hints--
-`squareSpaceSilo()` should return `23.386029052`.
+`squareSpaceSilo()` は `23.386029052` を返す必要があります。
```js
assert.strictEqual(squareSpaceSilo(), 23.386029052);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
index 845ee38a53..97b5e3c0a6 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f51e1000cf542c510030
-title: 'Problem 432: Totient sum'
+title: '問題 432: トーティエント和'
challengeType: 5
forumTopicId: 302103
dashedName: problem-432-totient-sum
@@ -8,15 +8,15 @@ dashedName: problem-432-totient-sum
# --description--
-Let $S(n, m) = \sum φ(n × i)$ for $1 ≤ i ≤ m$. ($φ$ is Euler's totient function)
+$1 ≤ i ≤ m$ のとき、$S(n, m) = \sum φ(n × i)$ とします。 ($φ$ はオイラーのトーティエント関数を表します。)
-You are given that $S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$.
+$S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$ が与えられます。
-Find $S(510\\,510, {10}^{11})$. Give the last 9 digits of your answer.
+$S(510\\,510, {10}^{11})$ を求めなさい。 回答は、下位 9 桁とすること。
# --hints--
-`totientSum()` should return `754862080`.
+`totientSum()` は `754862080` を返す必要があります。
```js
assert.strictEqual(totientSum(), 754862080);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
index 5120b44733..b828530ee0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
@@ -1,6 +1,6 @@
---
id: 5900f51d1000cf542c51002f
-title: 'Problem 433: Steps in Euclid''s algorithm'
+title: '問題 433: ユークリッドの互除法のステップ数'
challengeType: 5
forumTopicId: 302104
dashedName: problem-433-steps-in-euclids-algorithm
@@ -8,23 +8,23 @@ dashedName: problem-433-steps-in-euclids-algorithm
# --description--
-Let $E(x_0, y_0)$ be the number of steps it takes to determine the greatest common divisor of $x_0$ and $y_0$ with Euclid's algorithm. More formally:
+$x_0$ と $y_0$ の最大公約数をユークリッドの互除法によって決定するために必要なステップ数を、$E(x_0, y_0)$ とします。 より形式的に表すと、次のようになります。
$$\begin{align} & x_1 = y_0, y_1 = x_0\bmod y_0 \\\\ & x_n = y_{n - 1}, y_n = x_{n - 1}\bmod y_{n - 1} \end{align}$$
-$E(x_0, y_0)$ is the smallest $n$ such that $y_n = 0$.
+$E(x_0, y_0)$ は $y_n = 0$ となるような最小の $n$ です。
-We have $E(1, 1) = 1$, $E(10, 6) = 3$ and $E(6, 10) = 4$.
+$E(1, 1) = 1$, $E(10, 6) = 3$, $E(6, 10) = 4$ が与えられます。
-Define $S(N)$ as the sum of $E(x, y)$ for $1 ≤ x$, $y ≤ N$.
+$1 ≤ x$, $y ≤ N$ のとき、$E(x, y)$ の和を $S(N)$ と定義します。
-We have $S(1) = 1$, $S(10) = 221$ and $S(100) = 39\\,826$.
+$S(1) = 1$, $S(10) = 221$, $S(100) = 39\\,826$ が与えられます。
-Find $S(5 \times {10}^6)$.
+$S(5 \times {10}^6)$ を求めなさい。
# --hints--
-`stepsInEuclidsAlgorithm()` should return `326624372659664`.
+`stepsInEuclidsAlgorithm()` は `326624372659664` を返す必要があります。
```js
assert.strictEqual(stepsInEuclidsAlgorithm(), 326624372659664);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
index ae1a4b0aae..8b7063775d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
@@ -1,6 +1,6 @@
---
id: 5900f51f1000cf542c510031
-title: 'Problem 434: Rigid graphs'
+title: '問題 434: 剛なグラフ'
challengeType: 5
forumTopicId: 302105
dashedName: problem-434-rigid-graphs
@@ -8,39 +8,39 @@ dashedName: problem-434-rigid-graphs
# --description--
-Recall that a graph is a collection of vertices and edges connecting the vertices, and that two vertices connected by an edge are called adjacent.
+まず、次のことを思い出してください。グラフとは、頂点と、頂点間を結ぶ辺との集まりであり、辺によって結ばれた 2 つの頂点は「隣接している」と表現されます。
-Graphs can be embedded in Euclidean space by associating each vertex with a point in the Euclidean space.
+グラフは、各頂点をユークリッド空間上の点と関連付けることでユークリッド空間に埋め込むことができます。
-A flexible graph is an embedding of a graph where it is possible to move one or more vertices continuously so that the distance between at least two nonadjacent vertices is altered while the distances between each pair of adjacent vertices is kept constant.
+柔軟なグラフとは、隣接する 2 頂点の対のそれぞれで 2 頂点間の距離が一定に保たれたまま、 少なくとも 2 つの隣接していない頂点間の距離が変化するような方法で、1 つ以上の頂点を連続的に動すことができるグラフの埋め込みのことです。
-A rigid graph is an embedding of a graph which is not flexible.
+剛なグラフとは、柔軟でないグラフの埋め込みのことでです。
-Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
+平たく言えば、頂点を 360 度回転する蝶番とに置き換え、辺を弾力のない固い棒に置き換えたときに、グラフの残りの部分から独立して動かすことのできる部分がないグラフは剛なグラフです。
-The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
+ユークリッド平面に埋め込まれた格子グラフは、下のアニメーションが示すように剛なグラフではありません。
-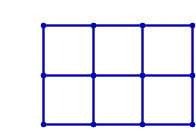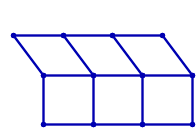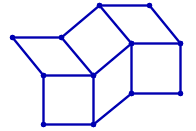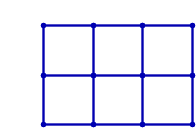 +
+ -However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid:
+ただし、マスに対角線の辺を追加すれば剛なグラフになります。 例えば、2x3 の格子グラフの場合、剛なグラフにする方法は次のように 19 通りあります。
-
-However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid:
+ただし、マスに対角線の辺を追加すれば剛なグラフになります。 例えば、2x3 の格子グラフの場合、剛なグラフにする方法は次のように 19 通りあります。
- +
+ -Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+なお、この問題の目的上、格子グラフに剛性を持たせる別の方法として、対角線の向きを変えたり 1 つのセルに対角線を 2 本追加したりすることは考えないものとします。
-Let $R(m, n)$ be the number of ways to make the $m × n$ grid graph rigid.
+$m × n$ の格子グラフを剛なグラフにする方法の数を $R(m, n)$ とします。
-E.g. $R(2, 3) = 19$ and $R(5, 5) = 23\\,679\\,901$.
+例: $R(2, 3) = 19$, $R(5, 5) = 23\\,679\\,901$
-Define $S(N)$ as $\sum R(i, j)$ for $1 ≤ i$, $j ≤ N$.
+$1 ≤ i$, $j ≤ N のとき、$\sum R(i, j) を $S(N)$ とします。
-E.g. $S(5) = 25\\,021\\,721$.
+例: $S(5) = 25\\,021\\,721$
-Find $S(100)$, give your answer modulo $1\\,000\\,000\\,033$.
+$S(100)$ を求め、mod $1\\,000\\,000\\,033$ で答えなさい。
# --hints--
-`rigidGraphs()` should return `863253606`.
+`rigidGraphs()` は `863253606` を返す必要があります。
```js
assert.strictEqual(rigidGraphs(), 863253606);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
index 9be0b43a51..a0910cebe7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f5201000cf542c510032
-title: 'Problem 435: Polynomials of Fibonacci numbers'
+title: '問題 435: フィボナッチ数の多項式'
challengeType: 5
forumTopicId: 302106
dashedName: problem-435-polynomials-of-fibonacci-numbers
@@ -8,17 +8,17 @@ dashedName: problem-435-polynomials-of-fibonacci-numbers
# --description--
-The Fibonacci numbers $\\{f_n, n ≥ 0\\}$ are defined recursively as $f_n = f_{n - 1} + f_{n - 2}$ with base cases $f_0 = 0$ and $f_1 = 1$.
+フィボナッチ数 $\\{f_n, n ≥ 0\\}$ は、$f_0 = 0$, $f_1 = 1$ を初期条件として $f_n = f_{n - 1} + f_{n - 2}$ と再帰的に定義されます。
-Define the polynomials $\\{F_n, n ≥ 0\\}$ as $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$.
+多項式 $\\{F_n, n ≥ 0\\}$ を $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$ と定義します。
-For example, $F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, and $F_7(11) = 268\\,357\\,683$.
+例えば、$F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, $F_7(11) = 268\\,357\\,683$ です。
-Let $n = {10}^{15}$. Find the sum $\displaystyle\sum_{x = 0}^{100} F_n(x)$ and give your answer modulo $1\\,307\\,674\\,368\\,000 \\, (= 15!)$.
+$n = {10}^{15}$ とします。 和 $\displaystyle\sum_{x = 0}^{100} F_n(x)$ を求め、mod $1\\,307\\,674\\,368\\,000 \\, (= 15!)$ で答えなさい。
# --hints--
-`polynomialsOfFibonacciNumbers()` should return `252541322550`.
+`polynomialsOfFibonacciNumbers()` は`252541322550` を返す必要があります。
```js
assert.strictEqual(polynomialsOfFibonacciNumbers(), 252541322550);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
index d5dfcc5920..21532b293b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
@@ -1,6 +1,6 @@
---
id: 5900f5221000cf542c510033
-title: 'Problem 436: Unfair wager'
+title: '問題 436: 不公平な賭け'
challengeType: 5
forumTopicId: 302107
dashedName: problem-436-unfair-wager
@@ -8,29 +8,29 @@ dashedName: problem-436-unfair-wager
# --description--
-Julie proposes the following wager to her sister Louise.
+ジュリーは、姉のルイーズに次のような賭けを提案しました。
-She suggests they play a game of chance to determine who will wash the dishes.
+誰が皿を洗うかを決めるために、運で決まるゲームをするというものです。
-For this game, they shall use a generator of independent random numbers uniformly distributed between 0 and 1.
+このゲームでは、0 から 1 の間に一様に分布する独立的な乱数を作る生成器を使います。
-The game starts with $S = 0$.
+ゲームは $S = 0$ から開始します。
-The first player, Louise, adds to $S$ different random numbers from the generator until $S > 1$ and records her last random number '$x$'.
+先手であるルイーズは、生成器から得られるさまざまな乱数を $S$ に加えていき、$S > 1$ になったら止め、最後の乱数 '$x$' を記録します。
-The second player, Julie, continues adding to $S$ different random numbers from the generator until $S > 2$ and records her last random number '$y$'.
+後手のジュリーは、生成器から得られる色々な乱数を引き続き $S$ に加えていき、$S > 2$ になったら止め、最後の乱数 '$y$' を記録します。
-The player with the highest number wins and the loser washes the dishes, i.e. if $y > x$ the second player wins.
+最大の数を記録した方が勝ち、負けた方は皿洗いをします。すなわち、$y > x$ であれば後手の勝ちです。
-For example, if the first player draws 0.62 and 0.44, the first player turn ends since $0.62 + 0.44 > 1$ and $x = 0.44$. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since $0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ and $y = 0.91$. Since $y > x$, the second player wins.
+例えば、先手が生成器から 0.62 と 0.44 を得た場合、$0.62 + 0.44 > 1$ なので先手のターンが終わり、$x = 0.44$ となります。 後手が 0.1, 0.27, 0.91 を得た場合、$0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ なので後手のターンが終わり、$y = 0.91$ となります。 $y > x$ なので後手の勝ちです。
-Louise thinks about it for a second, and objects: "That's not fair".
+ルイーズは少し考えてから、「不公平だわ」と抗議しました。
-What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
+後手が勝つ確率を求めなさい。 回答は、四捨五入して小数第 10 位まで求め、0.abcdefghij の形式にすること。
# --hints--
-`unfairWager()` should return `0.5276662759`.
+`unfairWager()` は `0.5276662759` を返す必要があります。
```js
assert.strictEqual(unfairWager(), 0.5276662759);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
index b36feea460..315a4b7796 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
@@ -1,6 +1,6 @@
---
id: 5900f5241000cf542c510036
-title: 'Problem 437: Fibonacci primitive roots'
+title: '問題 437: フィボナッチ原始根'
challengeType: 5
forumTopicId: 302108
dashedName: problem-437-fibonacci-primitive-roots
@@ -8,25 +8,25 @@ dashedName: problem-437-fibonacci-primitive-roots
# --description--
-When we calculate $8^n$ modulo 11 for $n = 0$ to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
+$n$ が 0 から 9 のとき、$8^n$ mod 11 を求めると 1, 8, 9, 6, 4, 10, 3, 2, 5, 7 が得られます。
-As we see all possible values from 1 to 10 occur. So 8 is a primitive root of 11.
+このように、1 から 10 までのすべての値が現れます。 したがって、 8 は 11 の原始根です。
-But there is more:
+しかし、話はここで終わりません。
-If we take a closer look we see:
+よく見ると次のことが分かります。
$$\begin{align} & 1 + 8 = 9 \\\\ & 8 + 9 = 17 ≡ 6\bmod 11 \\\\ & 9 + 6 = 15 ≡ 4\bmod 11 \\\\ & 6 + 4 = 10 \\\\ & 4 + 10 = 14 ≡ 3\bmod 11 \\\\ & 10 + 3 = 13 ≡ 2\bmod 11 \\\\ & 3 + 2 = 5 \\\\ & 2 + 5 = 7 \\\\ & 5 + 7 = 12 ≡ 1\bmod 11. \end{align}$$
-So the powers of 8 mod 11 are cyclic with period 10, and $8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$. 8 is called a Fibonacci primitive root of 11.
+したがって、8 の累乗を 11 で除した余りは周期 10 で循環し、$8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$ です。 8 は 11 のフィボナッチ原始根と呼ばれます。
-Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491.
+すべての素数がフィボナッチ原始根を持つわけではありません。 1 つ以上のフィボナッチ原始根を持つ 10000 未満の素数は 323 個あり、それらの和は 1480491 です。
-Find the sum of the primes less than $100\\,000\\,000$ with at least one Fibonacci primitive root.
+少なくとも 1 つのフィボナッチ原始根を持つ $100\\,000\\,000$ 未満の素数の和を求めなさい。
# --hints--
-`fibonacciPrimitiveRoots()` should return `74204709657207`.
+`fibonacciPrimitiveRoots()` は `74204709657207` を返す必要があります。
```js
assert.strictEqual(fibonacciPrimitiveRoots(), 74204709657207);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
index e247069b3d..40ea595de5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
@@ -1,6 +1,6 @@
---
id: 5900f5231000cf542c510034
-title: 'Problem 438: Integer part of polynomial equation''s solutions'
+title: '問題 438: 多項式の解の整数部'
challengeType: 5
forumTopicId: 302109
dashedName: problem-438-integer-part-of-polynomial-equations-solutions
@@ -8,24 +8,24 @@ dashedName: problem-438-integer-part-of-polynomial-equations-solutions
# --description--
-For an $n$-tuple of integers $t = (a_1, \ldots, a_n)$, let $(x_1, \ldots, x_n)$ be the solutions of the polynomial equation $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$.
+$n$ 個の整数の組 $t = (a_1, \ldots, a_n)$ について、多項式 $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$ の解を $(x_1, \ldots, x_n)$ とします。
-Consider the following two conditions:
+以下の 2 つの条件について考えます。
-- $x_1, \ldots, x_n$ are all real.
-- If $x_1, ..., x_n$ are sorted, $⌊x_i⌋ = i$ for $1 ≤ i ≤ n$. ($⌊·⌋:$ floor function.)
+- $x_1, \ldots, x_n$ はすべて実数である。
+- $x_1, ..., x_n$ を並べ替えると、$1 ≤ i ≤ n$ に対し $⌊x_i⌋ = i$ となる。 ($⌊·⌋:$ は床関数。)
-In the case of $n = 4$, there are 12 $n$-tuples of integers which satisfy both conditions.
+$n = 4$ のとき、両方の条件を満たす $n$ 個の整数の組は 12 個あります。
-We define $S(t)$ as the sum of the absolute values of the integers in $t$.
+$t$ 内の整数の絶対値の和を $S(t)$ とします。
-For $n = 4$ we can verify that $\sum S(t) = 2087$ for all $n$-tuples t which satisfy both conditions.
+$n = 4$ のとき、両方の条件を満たす $n$ 個の整数の組 $t$ のすべてについて $\sum S(t) = 2087$ となることを確認できます。
-Find $\sum S(t)$ for $n = 7$.
+$n = 7$ のとき、$\sum S(t)$ を求めなさい。
# --hints--
-`polynomialIntegerPart()` should return `2046409616809`.
+`polynomialIntegerPart()` は `2046409616809` を返す必要があります。
```js
assert.strictEqual(polynomialIntegerPart(), 2046409616809);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
index 264dfaf572..3e93ae3566 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f5231000cf542c510035
-title: 'Problem 439: Sum of sum of divisors'
+title: '問題 439: 約数の和の和'
challengeType: 5
forumTopicId: 302110
dashedName: problem-439-sum-of-sum-of-divisors
@@ -8,19 +8,19 @@ dashedName: problem-439-sum-of-sum-of-divisors
# --description--
-Let $d(k)$ be the sum of all divisors of $k$.
+$k$ の約数の総和を $d(k)$ とします。
-We define the function $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$.
+関数 $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$ を定義します。
-For example, $S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$.
+例えば、$S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$ です。
-You are given that $S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$.
+$S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$ が与えられます。
-Find $S({10}^{11})\bmod {10}^9$.
+$S({10}^{11})\bmod {10}^9$ を求めなさい。
# --hints--
-`sumOfSumOfDivisors()` should return `968697378`.
+`sumOfSumOfDivisors()` は `968697378` を返す必要があります。
```js
assert.strictEqual(sumOfSumOfDivisors(), 968697378);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
index 5078487086..8603afc3d8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
@@ -1,6 +1,6 @@
---
id: 5900f5241000cf542c510037
-title: 'Problem 440: GCD and Tiling'
+title: '問題 440: 最大公約数とタイル貼り'
challengeType: 5
forumTopicId: 302112
dashedName: problem-440-gcd-and-tiling
@@ -8,29 +8,29 @@ dashedName: problem-440-gcd-and-tiling
# --description--
-We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
+1 × 2 のタイル、または下図のように 1 桁の 10 進数が書かれた 1 × 1 のタイルを、長さ$n$、高さ 1 の板全体に貼ります。
-
-Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+なお、この問題の目的上、格子グラフに剛性を持たせる別の方法として、対角線の向きを変えたり 1 つのセルに対角線を 2 本追加したりすることは考えないものとします。
-Let $R(m, n)$ be the number of ways to make the $m × n$ grid graph rigid.
+$m × n$ の格子グラフを剛なグラフにする方法の数を $R(m, n)$ とします。
-E.g. $R(2, 3) = 19$ and $R(5, 5) = 23\\,679\\,901$.
+例: $R(2, 3) = 19$, $R(5, 5) = 23\\,679\\,901$
-Define $S(N)$ as $\sum R(i, j)$ for $1 ≤ i$, $j ≤ N$.
+$1 ≤ i$, $j ≤ N のとき、$\sum R(i, j) を $S(N)$ とします。
-E.g. $S(5) = 25\\,021\\,721$.
+例: $S(5) = 25\\,021\\,721$
-Find $S(100)$, give your answer modulo $1\\,000\\,000\\,033$.
+$S(100)$ を求め、mod $1\\,000\\,000\\,033$ で答えなさい。
# --hints--
-`rigidGraphs()` should return `863253606`.
+`rigidGraphs()` は `863253606` を返す必要があります。
```js
assert.strictEqual(rigidGraphs(), 863253606);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
index 9be0b43a51..a0910cebe7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f5201000cf542c510032
-title: 'Problem 435: Polynomials of Fibonacci numbers'
+title: '問題 435: フィボナッチ数の多項式'
challengeType: 5
forumTopicId: 302106
dashedName: problem-435-polynomials-of-fibonacci-numbers
@@ -8,17 +8,17 @@ dashedName: problem-435-polynomials-of-fibonacci-numbers
# --description--
-The Fibonacci numbers $\\{f_n, n ≥ 0\\}$ are defined recursively as $f_n = f_{n - 1} + f_{n - 2}$ with base cases $f_0 = 0$ and $f_1 = 1$.
+フィボナッチ数 $\\{f_n, n ≥ 0\\}$ は、$f_0 = 0$, $f_1 = 1$ を初期条件として $f_n = f_{n - 1} + f_{n - 2}$ と再帰的に定義されます。
-Define the polynomials $\\{F_n, n ≥ 0\\}$ as $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$.
+多項式 $\\{F_n, n ≥ 0\\}$ を $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$ と定義します。
-For example, $F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, and $F_7(11) = 268\\,357\\,683$.
+例えば、$F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, $F_7(11) = 268\\,357\\,683$ です。
-Let $n = {10}^{15}$. Find the sum $\displaystyle\sum_{x = 0}^{100} F_n(x)$ and give your answer modulo $1\\,307\\,674\\,368\\,000 \\, (= 15!)$.
+$n = {10}^{15}$ とします。 和 $\displaystyle\sum_{x = 0}^{100} F_n(x)$ を求め、mod $1\\,307\\,674\\,368\\,000 \\, (= 15!)$ で答えなさい。
# --hints--
-`polynomialsOfFibonacciNumbers()` should return `252541322550`.
+`polynomialsOfFibonacciNumbers()` は`252541322550` を返す必要があります。
```js
assert.strictEqual(polynomialsOfFibonacciNumbers(), 252541322550);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
index d5dfcc5920..21532b293b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
@@ -1,6 +1,6 @@
---
id: 5900f5221000cf542c510033
-title: 'Problem 436: Unfair wager'
+title: '問題 436: 不公平な賭け'
challengeType: 5
forumTopicId: 302107
dashedName: problem-436-unfair-wager
@@ -8,29 +8,29 @@ dashedName: problem-436-unfair-wager
# --description--
-Julie proposes the following wager to her sister Louise.
+ジュリーは、姉のルイーズに次のような賭けを提案しました。
-She suggests they play a game of chance to determine who will wash the dishes.
+誰が皿を洗うかを決めるために、運で決まるゲームをするというものです。
-For this game, they shall use a generator of independent random numbers uniformly distributed between 0 and 1.
+このゲームでは、0 から 1 の間に一様に分布する独立的な乱数を作る生成器を使います。
-The game starts with $S = 0$.
+ゲームは $S = 0$ から開始します。
-The first player, Louise, adds to $S$ different random numbers from the generator until $S > 1$ and records her last random number '$x$'.
+先手であるルイーズは、生成器から得られるさまざまな乱数を $S$ に加えていき、$S > 1$ になったら止め、最後の乱数 '$x$' を記録します。
-The second player, Julie, continues adding to $S$ different random numbers from the generator until $S > 2$ and records her last random number '$y$'.
+後手のジュリーは、生成器から得られる色々な乱数を引き続き $S$ に加えていき、$S > 2$ になったら止め、最後の乱数 '$y$' を記録します。
-The player with the highest number wins and the loser washes the dishes, i.e. if $y > x$ the second player wins.
+最大の数を記録した方が勝ち、負けた方は皿洗いをします。すなわち、$y > x$ であれば後手の勝ちです。
-For example, if the first player draws 0.62 and 0.44, the first player turn ends since $0.62 + 0.44 > 1$ and $x = 0.44$. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since $0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ and $y = 0.91$. Since $y > x$, the second player wins.
+例えば、先手が生成器から 0.62 と 0.44 を得た場合、$0.62 + 0.44 > 1$ なので先手のターンが終わり、$x = 0.44$ となります。 後手が 0.1, 0.27, 0.91 を得た場合、$0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ なので後手のターンが終わり、$y = 0.91$ となります。 $y > x$ なので後手の勝ちです。
-Louise thinks about it for a second, and objects: "That's not fair".
+ルイーズは少し考えてから、「不公平だわ」と抗議しました。
-What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
+後手が勝つ確率を求めなさい。 回答は、四捨五入して小数第 10 位まで求め、0.abcdefghij の形式にすること。
# --hints--
-`unfairWager()` should return `0.5276662759`.
+`unfairWager()` は `0.5276662759` を返す必要があります。
```js
assert.strictEqual(unfairWager(), 0.5276662759);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
index b36feea460..315a4b7796 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
@@ -1,6 +1,6 @@
---
id: 5900f5241000cf542c510036
-title: 'Problem 437: Fibonacci primitive roots'
+title: '問題 437: フィボナッチ原始根'
challengeType: 5
forumTopicId: 302108
dashedName: problem-437-fibonacci-primitive-roots
@@ -8,25 +8,25 @@ dashedName: problem-437-fibonacci-primitive-roots
# --description--
-When we calculate $8^n$ modulo 11 for $n = 0$ to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
+$n$ が 0 から 9 のとき、$8^n$ mod 11 を求めると 1, 8, 9, 6, 4, 10, 3, 2, 5, 7 が得られます。
-As we see all possible values from 1 to 10 occur. So 8 is a primitive root of 11.
+このように、1 から 10 までのすべての値が現れます。 したがって、 8 は 11 の原始根です。
-But there is more:
+しかし、話はここで終わりません。
-If we take a closer look we see:
+よく見ると次のことが分かります。
$$\begin{align} & 1 + 8 = 9 \\\\ & 8 + 9 = 17 ≡ 6\bmod 11 \\\\ & 9 + 6 = 15 ≡ 4\bmod 11 \\\\ & 6 + 4 = 10 \\\\ & 4 + 10 = 14 ≡ 3\bmod 11 \\\\ & 10 + 3 = 13 ≡ 2\bmod 11 \\\\ & 3 + 2 = 5 \\\\ & 2 + 5 = 7 \\\\ & 5 + 7 = 12 ≡ 1\bmod 11. \end{align}$$
-So the powers of 8 mod 11 are cyclic with period 10, and $8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$. 8 is called a Fibonacci primitive root of 11.
+したがって、8 の累乗を 11 で除した余りは周期 10 で循環し、$8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$ です。 8 は 11 のフィボナッチ原始根と呼ばれます。
-Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491.
+すべての素数がフィボナッチ原始根を持つわけではありません。 1 つ以上のフィボナッチ原始根を持つ 10000 未満の素数は 323 個あり、それらの和は 1480491 です。
-Find the sum of the primes less than $100\\,000\\,000$ with at least one Fibonacci primitive root.
+少なくとも 1 つのフィボナッチ原始根を持つ $100\\,000\\,000$ 未満の素数の和を求めなさい。
# --hints--
-`fibonacciPrimitiveRoots()` should return `74204709657207`.
+`fibonacciPrimitiveRoots()` は `74204709657207` を返す必要があります。
```js
assert.strictEqual(fibonacciPrimitiveRoots(), 74204709657207);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
index e247069b3d..40ea595de5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
@@ -1,6 +1,6 @@
---
id: 5900f5231000cf542c510034
-title: 'Problem 438: Integer part of polynomial equation''s solutions'
+title: '問題 438: 多項式の解の整数部'
challengeType: 5
forumTopicId: 302109
dashedName: problem-438-integer-part-of-polynomial-equations-solutions
@@ -8,24 +8,24 @@ dashedName: problem-438-integer-part-of-polynomial-equations-solutions
# --description--
-For an $n$-tuple of integers $t = (a_1, \ldots, a_n)$, let $(x_1, \ldots, x_n)$ be the solutions of the polynomial equation $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$.
+$n$ 個の整数の組 $t = (a_1, \ldots, a_n)$ について、多項式 $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$ の解を $(x_1, \ldots, x_n)$ とします。
-Consider the following two conditions:
+以下の 2 つの条件について考えます。
-- $x_1, \ldots, x_n$ are all real.
-- If $x_1, ..., x_n$ are sorted, $⌊x_i⌋ = i$ for $1 ≤ i ≤ n$. ($⌊·⌋:$ floor function.)
+- $x_1, \ldots, x_n$ はすべて実数である。
+- $x_1, ..., x_n$ を並べ替えると、$1 ≤ i ≤ n$ に対し $⌊x_i⌋ = i$ となる。 ($⌊·⌋:$ は床関数。)
-In the case of $n = 4$, there are 12 $n$-tuples of integers which satisfy both conditions.
+$n = 4$ のとき、両方の条件を満たす $n$ 個の整数の組は 12 個あります。
-We define $S(t)$ as the sum of the absolute values of the integers in $t$.
+$t$ 内の整数の絶対値の和を $S(t)$ とします。
-For $n = 4$ we can verify that $\sum S(t) = 2087$ for all $n$-tuples t which satisfy both conditions.
+$n = 4$ のとき、両方の条件を満たす $n$ 個の整数の組 $t$ のすべてについて $\sum S(t) = 2087$ となることを確認できます。
-Find $\sum S(t)$ for $n = 7$.
+$n = 7$ のとき、$\sum S(t)$ を求めなさい。
# --hints--
-`polynomialIntegerPart()` should return `2046409616809`.
+`polynomialIntegerPart()` は `2046409616809` を返す必要があります。
```js
assert.strictEqual(polynomialIntegerPart(), 2046409616809);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
index 264dfaf572..3e93ae3566 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f5231000cf542c510035
-title: 'Problem 439: Sum of sum of divisors'
+title: '問題 439: 約数の和の和'
challengeType: 5
forumTopicId: 302110
dashedName: problem-439-sum-of-sum-of-divisors
@@ -8,19 +8,19 @@ dashedName: problem-439-sum-of-sum-of-divisors
# --description--
-Let $d(k)$ be the sum of all divisors of $k$.
+$k$ の約数の総和を $d(k)$ とします。
-We define the function $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$.
+関数 $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$ を定義します。
-For example, $S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$.
+例えば、$S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$ です。
-You are given that $S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$.
+$S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$ が与えられます。
-Find $S({10}^{11})\bmod {10}^9$.
+$S({10}^{11})\bmod {10}^9$ を求めなさい。
# --hints--
-`sumOfSumOfDivisors()` should return `968697378`.
+`sumOfSumOfDivisors()` は `968697378` を返す必要があります。
```js
assert.strictEqual(sumOfSumOfDivisors(), 968697378);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
index 5078487086..8603afc3d8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
@@ -1,6 +1,6 @@
---
id: 5900f5241000cf542c510037
-title: 'Problem 440: GCD and Tiling'
+title: '問題 440: 最大公約数とタイル貼り'
challengeType: 5
forumTopicId: 302112
dashedName: problem-440-gcd-and-tiling
@@ -8,29 +8,29 @@ dashedName: problem-440-gcd-and-tiling
# --description--
-We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
+1 × 2 のタイル、または下図のように 1 桁の 10 進数が書かれた 1 × 1 のタイルを、長さ$n$、高さ 1 の板全体に貼ります。
-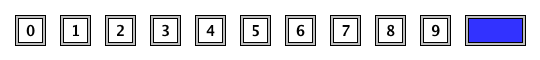 +
+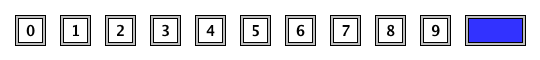 -For example, here are some of the ways to tile a board of length $n = 8$:
+例えば、$n = 8$ のときに板にタイルを貼る方法をいくつか示します。
-
-For example, here are some of the ways to tile a board of length $n = 8$:
+例えば、$n = 8$ のときに板にタイルを貼る方法をいくつか示します。
-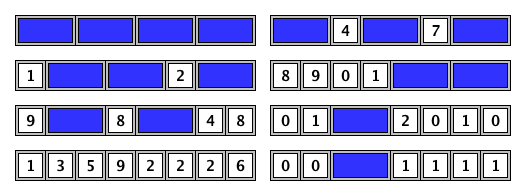 +
+ -Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
+上述の長さ $n$ の板にタイルを貼る方法の数を $T(n)$ とします。
-For example, $T(1) = 10$ and $T(2) = 101$.
+例えば、$T(1) = 10$, $T(2) = 101$ です。
-Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
+$1 ≤ a, b, c ≤ L$ のとき、三重和 $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ を $S(L)$ とします。
-For example:
+例えば、次のようになります。
$$\begin{align} & S(2) = 10\\,444 \\\\ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}$$
-Find $S(2000)\bmod 987\\,898\\,789$.
+$S(2000)\bmod 987\\,898\\,789$ を求めなさい。
# --hints--
-`gcdAndTiling()` should return `970746056`.
+`gcdAndTiling()` は `970746056` を返す必要があります。
```js
assert.strictEqual(gcdAndTiling(), 970746056);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md
index 4113a4c75b..8e611327ae 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md
@@ -1,6 +1,6 @@
---
id: 5900f5261000cf542c510038
-title: 'Problem 441: The inverse summation of coprime couples'
+title: '問題 441: 互いに素な組の逆数の総和'
challengeType: 5
forumTopicId: 302113
dashedName: problem-441-the-inverse-summation-of-coprime-couples
@@ -8,21 +8,21 @@ dashedName: problem-441-the-inverse-summation-of-coprime-couples
# --description--
-For an integer $M$, we define $R(M)$ as the sum of $\frac{1}{p·q}$ for all the integer pairs $p$ and $q$ which satisfy all of these conditions:
+整数 $M$ について、以下の条件をすべて満たすすべての整数対 $p$, $q$ に対する $\frac{1}{p·q}$ の和を$R(M)$ と定義します。
- $1 ≤ p < q ≤ M$
- $p + q ≥ M$
-- $p$ and $q$ are coprime.
+- $p$ と $q$ は互いに素である。
-We also define $S(N)$ as the sum of $R(i)$ for $2 ≤ i ≤ N$.
+$2 ≤ i ≤ N$ のとき、$R(i)$ の和を $S(N)$ と定義します。
-We can verify that $S(2) = R(2) = \frac{1}{2}$, $S(10) ≈ 6.9147$ and $S(100) ≈ 58.2962$.
+$S(2) = R(2) = \frac{1}{2}$, $S(10) ≈ 6.9147$ and $S(100) ≈ 58.2962$ であることを確認できます。
-Find $S({10}^7)$. Give your answer rounded to four decimal places.
+$S({10}^7)$ を求めなさい。 回答は、四捨五入して小数第 4 位まで示すこと。
# --hints--
-`inverseSummationCoprimeCouples()` should return `5000088.8395`.
+`inverseSummationCoprimeCouples()` は `5000088.8395` を返す必要があります。
```js
assert.strictEqual(inverseSummationCoprimeCouples(), 5000088.8395);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md
index 3b010b021e..56d20e408d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f5271000cf542c510039
-title: 'Problem 442: Eleven-free integers'
+title: '問題 442: イレブン・フリー整数'
challengeType: 5
forumTopicId: 302114
dashedName: problem-442-eleven-free-integers
@@ -8,17 +8,17 @@ dashedName: problem-442-eleven-free-integers
# --description--
-An integer is called eleven-free if its decimal expansion does not contain any substring representing a power of 11 except 1.
+10 進展開したときに 1 を除く 11 の累乗を表す部分文字列を一切含まないような整数を、「イレブン・フリー整数」と呼ぶことにします。
-For example, 2404 and 13431 are eleven-free, while 911 and 4121331 are not.
+例えば、2404 と 13431 はイレブン・フリーですが、 911 と 4121331 はそうではありません。
-Let $E(n)$ be the $n$th positive eleven-free integer. For example, $E(3) = 3$, $E(200) = 213$ and $E(500\\,000) = 531\\,563$.
+イレブン・フリーである $n$ 番目の正の整数を $E(n)$ とします。 例えば、$E(3) = 3$, $E(200) = 213$, $E(500\\,000) = 531\\,563$ です。
-Find $E({10}^{18})$.
+$E({10}^{18})$ を求めなさい。
# --hints--
-`elevenFreeIntegers()` should return `1295552661530920200`.
+`elevenFreeIntegers()` は `1295552661530920200` を返す必要があります。
```js
assert.strictEqual(elevenFreeIntegers(), 1295552661530920200);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md
index 102d3a37d0..0e684863d7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f5271000cf542c51003a
-title: 'Problem 443: GCD sequence'
+title: '問題 443: 最大公約数の数列'
challengeType: 5
forumTopicId: 302115
dashedName: problem-443-gcd-sequence
@@ -8,21 +8,21 @@ dashedName: problem-443-gcd-sequence
# --description--
-Let $g(n)$ be a sequence defined as follows:
+次のように定義される数列を $g(n)$ とします。
-$$\begin{align} & g(4) = 13, \\\\ & g(n) = g(n-1) + gcd(n, g(n - 1)) \text{ for } n > 4. \end{align}$$
+$$\begin{align} & g(4) = 13, \\\\ & n > 4 \text{ のとき、} g(n) = g(n-1) + gcd(n, g(n - 1)) \end{align}$$
-The first few values are:
+最初のいくつかの値は次のようになります。
$$\begin{array}{l} n & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & \ldots \\\\ g(n) & 13 & 14 & 16 & 17 & 18 & 27 & 28 & 29 & 30 & 31 & 32 & 33 & 34 & 51 & 54 & 55 & 60 & \ldots \end{array}$$
-You are given that $g(1\\,000) = 2\\,524$ and $g(1\\,000\\,000) = 2\\,624\\,152$.
+$g(1\\,000) = 2\\,524$, $g(1\\,000\\,000) = 2\\,624\\,152$ が与えられます。
-Find $g({10}^{15})$.
+$g({10}^{15})$ を求めなさい。
# --hints--
-`gcdSequence()` should return `2744233049300770`.
+`gcdSequence()` は `2744233049300770` を返す必要があります。
```js
assert.strictEqual(gcdSequence(), 2744233049300770);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md
index 7ea868fbe2..3590a27223 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md
@@ -1,6 +1,6 @@
---
id: 5900f52a1000cf542c51003b
-title: 'Problem 444: The Roundtable Lottery'
+title: '問題 444: 円卓宝くじ'
challengeType: 5
forumTopicId: 302116
dashedName: problem-444-the-roundtable-lottery
@@ -8,34 +8,34 @@ dashedName: problem-444-the-roundtable-lottery
# --description--
-A group of $p$ people decide to sit down at a round table and play a lottery-ticket trading game. Each person starts off with a randomly-assigned, unscratched lottery ticket. Each ticket, when scratched, reveals a whole-pound prize ranging anywhere from £1 to £$p$, with no two tickets alike. The goal of the game is for each person to maximize his ticket winnings upon leaving the game.
+$p$ 人のグループで円卓に座り、宝くじのトレーディングゲームを行うことにしました。 最初に、まだスクラッチが削られていない宝くじが、1 人に 1 枚ずつ無作為に割り当てられます。 それぞれのくじのスクラッチを削ると 1 ポンドから $p$ ポンドまでの賞金 (1 ポンド単位) が書いてあり、金額はすべて異なります。 ゲームの目的は、各自が自分のくじの賞金を最大にしてゲームから退場することです。
-An arbitrary person is chosen to be the first player. Going around the table, each player has only one of two options:
+任意の人が最初のプレイヤーに選ばれます。 円卓の席の順に、各プレイヤーは 2 つの選択肢のうち 1 つを選択します。
-1. The player can scratch his ticket and reveal its worth to everyone at the table.
-2. The player can trade his unscratched ticket for a previous player's scratched ticket, and then leave the game with that ticket. The previous player then scratches his newly-acquired ticket and reveals its worth to everyone at the table.
+1. くじを削り、プレイヤー全員にくじの賞金額を伝える。
+2. まだ削られていない自分のくじを前のプレイヤーの削られたくじと交換し、そのくじを受け取ってゲームから退場する。 前のプレイヤーは新たに割り当てられたくじを削り、プレイヤー全員にくじの賞金額を伝える。
-The game ends once all tickets have been scratched. All players still remaining at the table must leave with their currently-held tickets.
+すべてのくじが削られたときにゲームが終了します。 円卓に残ったすべてのプレイヤーは、その時点で持っているくじを持って退場しなければなりません。
-Assume that each player uses the optimal strategy for maximizing the expected value of his ticket winnings.
+各プレイヤーが、自分のくじの賞金額の期待値を最大化するための最適な戦略を使用すると仮定します。
-Let $E(p)$ represent the expected number of players left at the table when the game ends in a game consisting of $p$ players (e.g. $E(111) = 5.2912$ when rounded to 5 significant digits).
+$p$ 人のプレイヤーで行うゲームが終了するときに円卓に残っているプレイヤーの期待人数を、$E(p)$ で表します (例: 有効数字 5 桁に四捨五入すると $E(111) = 5.2912$)。
-Let $S_1(N) = \displaystyle\sum_{p = 1}^N E(p)$.
+$S_1(N) = \displaystyle\sum_{p = 1}^N E(p)$ とします。
-Let $S_k(N) = \displaystyle\sum_{p = 1}^N S_{k - 1}(p)$ for $k > 1$.
+$k > 1$ のとき、$S_k(N) = \displaystyle\sum_{p = 1}^N S_{k - 1}(p)$ とします。
-Find $S_{20}({10}^{14})$ and write the answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent. For example, the answer for $S_3(100)$ would be `5.983679014e5`.
+$S_{20}({10}^{14})$ を求め、有効数字 10 桁に四捨五入された科学的記数法の文字列で答えなさい。 小文字 `e` で仮数部と指数部を区切ること。 例えば、$S_3(100)$ の回答は `5.983679014e5` になります。
# --hints--
-`roundtableLottery()` should return a string.
+`roundtableLottery()` は文字列を返す必要があります。
```js
assert(typeof roundtableLottery() === 'string');
```
-`roundtableLottery()` should return the string `1.200856722e263`.
+`roundtableLottery()` は文字列 `1.200856722e263` を返す必要があります。
```js
assert.strictEqual(roundtableLottery(), '1.200856722e263');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md
index 678660f8fe..4e996860ca 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md
@@ -1,6 +1,6 @@
---
id: 5900f52a1000cf542c51003c
-title: 'Problem 445: Retractions A'
+title: '問題 445: レトラクション A'
challengeType: 5
forumTopicId: 302117
dashedName: problem-445-retractions-a
@@ -8,23 +8,23 @@ dashedName: problem-445-retractions-a
# --description--
-For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+$n > 1$ のすべての整数について、関数族 $f_{n, a, b}$ は次のように定義されます。
-$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+整数 $a, b, x$ および $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$ について、$f_{n, a, b}(x) ≡ ax + b\bmod n$
-We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+$0 \le x \lt n$ のすべてにおいて、$f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ のとき、$f_{n, a, b}$ をレトラクションと呼ぶことにします。
-Let $R(n)$ be the number of retractions for $n$.
+$n$ のレトラクションの個数を $R(n)$ とします。
-You are given that
+次が与えられます。
$$\sum_{k = 1}^{99\\,999} R(\displaystyle\binom{100\\,000}{k}) \equiv 628\\,701\\,600\bmod 1\\,000\\,000\\,007$$
-Find $$\sum_{k = 1}^{9\\,999\\,999} R(\displaystyle\binom{10\\,000\\,000}{k})$$ Give your answer modulo $1\\,000\\,000\\,007$.
+$$\sum_{k = 1}^{9\\,999\\,999} R(\displaystyle\binom{10\\,000\\,000}{k})$$ を求め、mod $1\\,000\\,000\\,007$ で答えなさい。
# --hints--
-`retractionsA()` should return `659104042`.
+`retractionsA()` は `659104042` を返す必要があります。
```js
assert.strictEqual(retractionsA(), 659104042);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md
index 04954f5265..e620e72022 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md
@@ -1,6 +1,6 @@
---
id: 5900f52c1000cf542c51003d
-title: 'Problem 446: Retractions B'
+title: '問題 446: レトラクション B'
challengeType: 5
forumTopicId: 302118
dashedName: problem-446-retractions-b
@@ -8,23 +8,23 @@ dashedName: problem-446-retractions-b
# --description--
-For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+$n > 1$ のすべての整数について、関数族 $f_{n, a, b}$ を次のように定義します。
-$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+整数 $a, b, x$ および $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$ について、$f_{n, a, b}(x) ≡ ax + b\bmod n$
-We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+$0 \le x \lt n$ のすべてにおいて、$f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ のとき、$f_{n, a, b}$ をレトラクションと呼ぶことにします。
-Let $R(n)$ be the number of retractions for $n$.
+$n$ のレトラクションの個数を $R(n)$ とします。
-$F(N) = \displaystyle\sum_{n = 1}^N R(n^4 + 4)$.
+$F(N) = \displaystyle\sum_{n = 1}^N R(n^4 + 4)$
-$F(1024) = 77\\,532\\,377\\,300\\,600$.
+$F(1024) = 77\\,532\\,377\\,300\\,600$
-Find $F({10}^7)$. Give your answer modulo $1\\,000\\,000\\,007$.
+$F({10}^7)$ を求めなさい。 mod $1\\,000\\,000\\,007$ で答えること。
# --hints--
-`retractionsB()` should return `907803852`.
+`retractionsB()` は `907803852` を返す必要があります。
```js
assert.strictEqual(retractionsB(), 907803852);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md
index 19a690c2a0..710a3e8a0c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md
@@ -1,6 +1,6 @@
---
id: 5900f52c1000cf542c51003e
-title: 'Problem 447: Retractions C'
+title: '問題 447: レトラクション C'
challengeType: 5
forumTopicId: 302119
dashedName: problem-447-retractions-c
@@ -8,23 +8,23 @@ dashedName: problem-447-retractions-c
# --description--
-For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+$n > 1$ のすべての整数について、関数族 $f_{n, a, b}$ を次のように定義します。
-$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+整数 $a, b, x$ および $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$ について、$f_{n, a, b}(x) ≡ ax + b\bmod n$
-We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+$0 \le x \lt n$ のすべてにおいて、$f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ のとき、$f_{n, a, b}$ をレトラクションと呼ぶことにします。
-Let $R(n)$ be the number of retractions for $n$.
+$n$ のレトラクションの個数を $R(n)$ とします。
-$F(N) = \displaystyle\sum_{n = 2}^N R(n)$.
+$F(N) = \displaystyle\sum_{n = 2}^N R(n)$
-$F({10}^7) ≡ 638\\,042\\,271\bmod 1\\,000\\,000\\,007$.
+$F({10}^7) ≡ 638\\,042\\,271\bmod 1\\,000\\,000\\,007$
-Find $F({10}^{14})$. Give your answer modulo $1\\,000\\,000\\,007$.
+$F({10}^{14})$ を求めなさい。 mod $1\\,000\\,000\\,007$ で答えること。
# --hints--
-`retractionsC()` should return `530553372`.
+`retractionsC()` は `530553372` を返す必要があります。
```js
assert.strictEqual(retractionsC(), 530553372);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md
index 6d551bfdb8..25433f86f0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md
@@ -1,6 +1,6 @@
---
id: 5900f52c1000cf542c51003f
-title: 'Problem 448: Average least common multiple'
+title: '問題 448: 平均最小公倍数'
challengeType: 5
forumTopicId: 302120
dashedName: problem-448-average-least-common-multiple
@@ -8,21 +8,21 @@ dashedName: problem-448-average-least-common-multiple
# --description--
-The function $lcm(a, b)$ denotes the least common multiple of $a$ and $b$.
+関数 $lcm(a, b)$ は $a$ と $b$ の最小公倍数を表します。
-Let $A(n)$ be the average of the values of $lcm(n, i)$ for $1 ≤ i ≤ n$.
+$1 ≤ i ≤ n$ のとき、$lcm(n, i)$ の値の平均を $A(n)$ とします。
-E.g: $A(2) = \frac{2 + 2}{2} = 2$ and $A(10) = \frac{10 + 10 + 30 + 20 + 10 + 30 + 70 + 40 + 90 + 10}{10} = 32$.
+例: $A(2) = \frac{2 + 2}{2} = 2$ および $A(10) = \frac{10 + 30 + 20 + 30 + 70 + 40 + 90 + 10}{10} = 32$
-Let $S(n) = \sum A(k)$ for $1 ≤ k ≤ n$.
+$1 ≤ k ≤ n$ のとき、$S(n) = \sum A(k)$ とします。
-$S(100) = 122\\,726$.
+$S(100) = 122\\,726$
-Find $S(99\\,999\\,999\\,019)\bmod 999\\,999\\,017$.
+$S(99\\,999\\,999\\,019)\bmod 999\\,999\\,017$ を求めなさい。
# --hints--
-`averageLCM()` should return `106467648`.
+`averageLCM()` は `106467648` を返す必要があります。
```js
assert.strictEqual(averageLCM(), 106467648);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md
index 5983812636..246dde7df8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md
@@ -1,6 +1,6 @@
---
id: 5900f52d1000cf542c510040
-title: 'Problem 449: Chocolate covered candy'
+title: '問題 449: チョコレートでコーティングされたキャンディー'
challengeType: 5
forumTopicId: 302121
dashedName: problem-449-chocolate-covered-candy
@@ -8,19 +8,19 @@ dashedName: problem-449-chocolate-covered-candy
# --description--
-Phil the confectioner is making a new batch of chocolate covered candy. Each candy centre is shaped like an ellipsoid of revolution defined by the equation: $b^2x^2 + b^2y^2 + a^2z^2 = a^2b^2$.
+菓子職人のフィルは、チョコレートでコーティングされたキャンディーを新たに 1 回分作っています。 各キャンディーの中心部は、方程式 $b^2x^2 + b^2y^2 + a^2z^2 = a^2b^2$ により定義される回転楕円体のような形をしています。
-Phil wants to know how much chocolate is needed to cover one candy centre with a uniform coat of chocolate one millimeter thick.
+フィルは、1 つのキャンディーを厚さ 1 ミリの均一なチョコレートコーティングで覆うのにどれだけのチョコレートが必要かを知りたいと思っています。
-If $a = 1$ mm and $b = 1$ mm, the amount of chocolate required is $\frac{28}{3} \pi$ mm3
+$a = 1$ mm, $b = 1$ mm の場合、必要なチョコレートの量は $\frac{28}{3} \pi$ mm3 です。
-If $a = 2$ mm and $b = 1$ mm, the amount of chocolate required is approximately 60.35475635 mm3.
+$a = 2$ mm, $b = 1$ mm の場合、必要なチョコレートの量は約 60.35475635 mm3 です。
-Find the amount of chocolate in mm3 required if $a = 3$ mm and $b = 1$ mm. Give your answer as the number rounded to 8 decimal places behind the decimal point.
+$a = 3$ mm, $b = 1$ mm のときに必要なチョコレートの量を mm3 単位で求めなさい。 回答は、四捨五入して小数第 8 位まで示すこと。
# --hints--
-`chocolateCoveredCandy()` should return `103.37870096`.
+`chocolateCoveredCandy()` は `103.37870096` を返す必要があります。
```js
assert.strictEqual(chocolateCoveredCandy(), 103.37870096);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md
index 7995e5b066..1d1e64d0ed 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md
@@ -1,6 +1,6 @@
---
id: 5900f52e1000cf542c510041
-title: 'Problem 450: Hypocycloid and Lattice points'
+title: '問題 450: 内サイクロイドと格子点'
challengeType: 5
forumTopicId: 302123
dashedName: problem-450-hypocycloid-and-lattice-points
@@ -8,35 +8,35 @@ dashedName: problem-450-hypocycloid-and-lattice-points
# --description--
-A hypocycloid is the curve drawn by a point on a small circle rolling inside a larger circle. The parametric equations of a hypocycloid centered at the origin, and starting at the right most point is given by:
+内サイクロイドとは、大きな円の内部で回転する小さな円上の点によって描かれる曲線のことです。 原点を中心とし、右端の点から始まる内サイクロイドのパラメトリック方程式を次に示します。
$$x(t) = (R - r) \cos(t) + r \cos(\frac{R - r}{r}t)$$
$$y(t) = (R - r) \sin(t) - r \sin(\frac{R - r}{r} t)$$
-Where $R$ is the radius of the large circle and $r$ the radius of the small circle.
+ここで、$R$ は大きな円の半径、$r$ は小さな円の半径です。
-Let $C(R, r)$ be the set of distinct points with integer coordinates on the hypocycloid with radius $R$ and $r$ and for which there is a corresponding value of $t$ such that $\sin(t)$ and $\cos(t)$ are rational numbers.
+半径 $R$ と $r$ を持つ内サイクロイド上の整数座標の点であり、$\sin(t)$ と $\cos(t)$ が有理数となる $t$ の相当値が存在するような、相異なる点の集合を $C(R, r)$ とします。
-Let $S(R, r) = \sum\_{(x,y) \in C(R, r)} |x| + |y|$ be the sum of the absolute values of the $x$ and $y$ coordinates of the points in $C(R, r)$.
+$C(R, r)$ に含まれる点の $x$ 座標と $y$ 座標の絶対値の総和を $S(R, r) = \sum\_{(x,y) \in C(R, r)} |x| + |y|$ とします。
-Let $T(N) = \sum_{R = 3}^N \sum_{r=1}^{\left\lfloor \frac{R - 1}{2} \right\rfloor} S(R, r)$ be the sum of $S(R, r)$ for $R$ and $r$ positive integers, $R\leq N$ and $2r < R$.
+正の整数 $R$ と $r$ について、$R\leq N$ かつ $2r < R$のとき、$S(R, r)$ の和を $T(N) = \sum_{R = 3}^N \sum_{r=1}^{\left\lfloor \frac{R - 1}{2} \right\rfloor} S(R, r)$ とします。
-You are given:
+次が与えられます。
$$\begin{align} C(3, 1) = & \\{(3, 0), (-1, 2), (-1,0), (-1,-2)\\} \\\\ C(2500, 1000) = & \\{(2500, 0), (772, 2376), (772, -2376), (516, 1792), (516, -1792), (500, 0), (68, 504), \\\\ &(68, -504),(-1356, 1088), (-1356, -1088), (-1500, 1000), (-1500, -1000)\\} \end{align}$$
-**Note:** (-625, 0) is not an element of $C(2500, 1000)$ because $\sin(t)$ is not a rational number for the corresponding values of t.
+** 注:** (-625, 0) は $C(2500, 1000)$ の要素ではありません。なぜなら、$t$ の相当値で $\sin(t)$ が有理数とならないからです。
$S(3, 1) = (|3| + |0|) + (|-1| + |2|) + (|-1| + |0|) + (|-1| + |-2|) = 10$
-$T(3) = 10$; $T(10) = 524$; $T(100) = 580\\,442$; $T({10}^3) = 583\\,108\\,600$.
+$T(3) = 10$; $T(10) = 524$; $T(100) = 580\\,442$; $T({10}^3) = 583\\,108\\,600$
-Find $T({10}^6)$.
+$T({10}^6)$ を求めなさい。
# --hints--
-`hypocycloidAndLatticePoints()` should return `583333163984220900`.
+`hypocycloidAndLatticePoints()` は `583333163984220900` を返す必要があります。
```js
assert.strictEqual(hypocycloidAndLatticePoints(), 583333163984220900);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md
index 071cdcc083..4923c39549 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md
@@ -1,6 +1,6 @@
---
id: 5900f5311000cf542c510042
-title: 'Problem 451: Modular inverses'
+title: '問題 451: モジュラ逆数'
challengeType: 5
forumTopicId: 302124
dashedName: problem-451-modular-inverses
@@ -8,25 +8,25 @@ dashedName: problem-451-modular-inverses
# --description--
-Consider the number 15.
+数 15 について考えます。
-There are eight positive numbers less than 15 which are coprime to 15: 1, 2, 4, 7, 8, 11, 13, 14.
+15 と互いに素である 15 未満の正の数は 1, 2, 4, 7, 8, 11, 13, 14 の 8 つです。
-The modular inverses of these numbers modulo 15 are: 1, 8, 4, 13, 2, 11, 7, 14 because
+それらの数の 15 を法とするモジュラ逆数は、1, 8, 4, 13, 2, 11, 7, 14 です。理由は次のとおりです。
$$\begin{align} & 1 \times 1\bmod 15 = 1 \\\\ & 2 \times 8 = 16\bmod 15 = 1 \\\\ & 4 \times 4 = 16\bmod 15 = 1 \\\\ & 7 \times 13 = 91\bmod 15 = 1 \\\\ & 11 \times 11 = 121\bmod 15 = 1 \\\\ & 14 \times 14 = 196\bmod 15 = 1 \end{align}$$
-Let $I(n)$ be the largest positive number $m$ smaller than $n - 1$ such that the modular inverse of $m$ modulo $n$ equals $m$ itself.
+$m$ の $n$ を法とするモジュラ逆数が $m$ 自体に等しくなるような、$n - 1$ 未満の最大の正の数 $m$ を $I(n)$ とします。
-So $I(15) = 11$.
+したがって、$I(15) = 11$ です。
-Also $I(100) = 51$ and $I(7) = 1$.
+また、$I(100) = 51$ および $I(7) = 1$ です。
-Find $\sum I(n)$ for $3 ≤ n ≤ 2 \times {10}^7$
+$3 ≤ n ≤ 2 \times {10}^7$のとき、$\sum I(n)$ を求めなさい。
# --hints--
-`modularInverses()` should return `153651073760956`.
+`modularInverses()` は `153651073760956` を返す必要があります。
```js
assert.strictEqual(modularInverses(), 153651073760956);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md
index 32246622d7..1fb56d743f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md
@@ -1,6 +1,6 @@
---
id: 5900f5311000cf542c510043
-title: 'Problem 452: Long Products'
+title: '問題 452: 長い積'
challengeType: 5
forumTopicId: 302125
dashedName: problem-452-long-products
@@ -8,17 +8,17 @@ dashedName: problem-452-long-products
# --description--
-Define $F(m, n)$ as the number of $n$-tuples of positive integers for which the product of the elements doesn't exceed $m$.
+要素の積が $m$ を超えないような、$n$ 個の正の整数からなる組の数を $F(m, n)$ とします。
-$F(10, 10) = 571$.
+$F(10, 10) = 571$
-$F({10}^6, {10}^6)\bmod 1\\,234\\,567\\,891 = 252\\,903\\,833$.
+$F({10}^6, {10}^6)\bmod 1\\,234\\,567\\,891 = 252\\,903\\,833$
-Find $F({10}^9, {10}^9)\bmod 1\\,234\\,567\\,891$.
+$F({10}^9, {10}^9)\bmod 1\\,234\\,567\\,891$ を求めなさい。
# --hints--
-`longProducts()` should return `345558983`.
+`longProducts()` は `345558983` を返す必要があります。
```js
assert.strictEqual(longProducts(), 345558983);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md
index 91dce06f6d..91b4a79f24 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md
@@ -1,6 +1,6 @@
---
id: 5900f5311000cf542c510044
-title: 'Problem 453: Lattice Quadrilaterals'
+title: '問題 453: 格子四角形'
challengeType: 5
forumTopicId: 302126
dashedName: problem-453-lattice-quadrilaterals
@@ -8,21 +8,21 @@ dashedName: problem-453-lattice-quadrilaterals
# --description--
-A simple quadrilateral is a polygon that has four distinct vertices, has no straight angles and does not self-intersect.
+単純四角形とは、4 つの相異なる頂点を持ち、平角を持たず、かつ自己交差していない多角形のことです。
-Let $Q(m, n)$ be the number of simple quadrilaterals whose vertices are lattice points with coordinates ($x$, $y$) satisfying $0 ≤ x ≤ m$ and $0 ≤ y ≤ n$.
+$0 ≤ x ≤ m$, $0 ≤ y ≤ m$ を満たす座標 ($x$, $y$) の格子点を頂点とする単純四角形の個数を、$Q(m, n)$ とします。
-For example, $Q(2, 2) = 94$ as can be seen below:
+例えば、下図のとおり $Q(2, 2) = 94$ です。
-
-Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
+上述の長さ $n$ の板にタイルを貼る方法の数を $T(n)$ とします。
-For example, $T(1) = 10$ and $T(2) = 101$.
+例えば、$T(1) = 10$, $T(2) = 101$ です。
-Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
+$1 ≤ a, b, c ≤ L$ のとき、三重和 $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ を $S(L)$ とします。
-For example:
+例えば、次のようになります。
$$\begin{align} & S(2) = 10\\,444 \\\\ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}$$
-Find $S(2000)\bmod 987\\,898\\,789$.
+$S(2000)\bmod 987\\,898\\,789$ を求めなさい。
# --hints--
-`gcdAndTiling()` should return `970746056`.
+`gcdAndTiling()` は `970746056` を返す必要があります。
```js
assert.strictEqual(gcdAndTiling(), 970746056);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md
index 4113a4c75b..8e611327ae 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-441-the-inverse-summation-of-coprime-couples.md
@@ -1,6 +1,6 @@
---
id: 5900f5261000cf542c510038
-title: 'Problem 441: The inverse summation of coprime couples'
+title: '問題 441: 互いに素な組の逆数の総和'
challengeType: 5
forumTopicId: 302113
dashedName: problem-441-the-inverse-summation-of-coprime-couples
@@ -8,21 +8,21 @@ dashedName: problem-441-the-inverse-summation-of-coprime-couples
# --description--
-For an integer $M$, we define $R(M)$ as the sum of $\frac{1}{p·q}$ for all the integer pairs $p$ and $q$ which satisfy all of these conditions:
+整数 $M$ について、以下の条件をすべて満たすすべての整数対 $p$, $q$ に対する $\frac{1}{p·q}$ の和を$R(M)$ と定義します。
- $1 ≤ p < q ≤ M$
- $p + q ≥ M$
-- $p$ and $q$ are coprime.
+- $p$ と $q$ は互いに素である。
-We also define $S(N)$ as the sum of $R(i)$ for $2 ≤ i ≤ N$.
+$2 ≤ i ≤ N$ のとき、$R(i)$ の和を $S(N)$ と定義します。
-We can verify that $S(2) = R(2) = \frac{1}{2}$, $S(10) ≈ 6.9147$ and $S(100) ≈ 58.2962$.
+$S(2) = R(2) = \frac{1}{2}$, $S(10) ≈ 6.9147$ and $S(100) ≈ 58.2962$ であることを確認できます。
-Find $S({10}^7)$. Give your answer rounded to four decimal places.
+$S({10}^7)$ を求めなさい。 回答は、四捨五入して小数第 4 位まで示すこと。
# --hints--
-`inverseSummationCoprimeCouples()` should return `5000088.8395`.
+`inverseSummationCoprimeCouples()` は `5000088.8395` を返す必要があります。
```js
assert.strictEqual(inverseSummationCoprimeCouples(), 5000088.8395);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md
index 3b010b021e..56d20e408d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-442-eleven-free-integers.md
@@ -1,6 +1,6 @@
---
id: 5900f5271000cf542c510039
-title: 'Problem 442: Eleven-free integers'
+title: '問題 442: イレブン・フリー整数'
challengeType: 5
forumTopicId: 302114
dashedName: problem-442-eleven-free-integers
@@ -8,17 +8,17 @@ dashedName: problem-442-eleven-free-integers
# --description--
-An integer is called eleven-free if its decimal expansion does not contain any substring representing a power of 11 except 1.
+10 進展開したときに 1 を除く 11 の累乗を表す部分文字列を一切含まないような整数を、「イレブン・フリー整数」と呼ぶことにします。
-For example, 2404 and 13431 are eleven-free, while 911 and 4121331 are not.
+例えば、2404 と 13431 はイレブン・フリーですが、 911 と 4121331 はそうではありません。
-Let $E(n)$ be the $n$th positive eleven-free integer. For example, $E(3) = 3$, $E(200) = 213$ and $E(500\\,000) = 531\\,563$.
+イレブン・フリーである $n$ 番目の正の整数を $E(n)$ とします。 例えば、$E(3) = 3$, $E(200) = 213$, $E(500\\,000) = 531\\,563$ です。
-Find $E({10}^{18})$.
+$E({10}^{18})$ を求めなさい。
# --hints--
-`elevenFreeIntegers()` should return `1295552661530920200`.
+`elevenFreeIntegers()` は `1295552661530920200` を返す必要があります。
```js
assert.strictEqual(elevenFreeIntegers(), 1295552661530920200);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md
index 102d3a37d0..0e684863d7 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-443-gcd-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f5271000cf542c51003a
-title: 'Problem 443: GCD sequence'
+title: '問題 443: 最大公約数の数列'
challengeType: 5
forumTopicId: 302115
dashedName: problem-443-gcd-sequence
@@ -8,21 +8,21 @@ dashedName: problem-443-gcd-sequence
# --description--
-Let $g(n)$ be a sequence defined as follows:
+次のように定義される数列を $g(n)$ とします。
-$$\begin{align} & g(4) = 13, \\\\ & g(n) = g(n-1) + gcd(n, g(n - 1)) \text{ for } n > 4. \end{align}$$
+$$\begin{align} & g(4) = 13, \\\\ & n > 4 \text{ のとき、} g(n) = g(n-1) + gcd(n, g(n - 1)) \end{align}$$
-The first few values are:
+最初のいくつかの値は次のようになります。
$$\begin{array}{l} n & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & 13 & 14 & 15 & 16 & 17 & 18 & 19 & 20 & \ldots \\\\ g(n) & 13 & 14 & 16 & 17 & 18 & 27 & 28 & 29 & 30 & 31 & 32 & 33 & 34 & 51 & 54 & 55 & 60 & \ldots \end{array}$$
-You are given that $g(1\\,000) = 2\\,524$ and $g(1\\,000\\,000) = 2\\,624\\,152$.
+$g(1\\,000) = 2\\,524$, $g(1\\,000\\,000) = 2\\,624\\,152$ が与えられます。
-Find $g({10}^{15})$.
+$g({10}^{15})$ を求めなさい。
# --hints--
-`gcdSequence()` should return `2744233049300770`.
+`gcdSequence()` は `2744233049300770` を返す必要があります。
```js
assert.strictEqual(gcdSequence(), 2744233049300770);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md
index 7ea868fbe2..3590a27223 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-444-the-roundtable-lottery.md
@@ -1,6 +1,6 @@
---
id: 5900f52a1000cf542c51003b
-title: 'Problem 444: The Roundtable Lottery'
+title: '問題 444: 円卓宝くじ'
challengeType: 5
forumTopicId: 302116
dashedName: problem-444-the-roundtable-lottery
@@ -8,34 +8,34 @@ dashedName: problem-444-the-roundtable-lottery
# --description--
-A group of $p$ people decide to sit down at a round table and play a lottery-ticket trading game. Each person starts off with a randomly-assigned, unscratched lottery ticket. Each ticket, when scratched, reveals a whole-pound prize ranging anywhere from £1 to £$p$, with no two tickets alike. The goal of the game is for each person to maximize his ticket winnings upon leaving the game.
+$p$ 人のグループで円卓に座り、宝くじのトレーディングゲームを行うことにしました。 最初に、まだスクラッチが削られていない宝くじが、1 人に 1 枚ずつ無作為に割り当てられます。 それぞれのくじのスクラッチを削ると 1 ポンドから $p$ ポンドまでの賞金 (1 ポンド単位) が書いてあり、金額はすべて異なります。 ゲームの目的は、各自が自分のくじの賞金を最大にしてゲームから退場することです。
-An arbitrary person is chosen to be the first player. Going around the table, each player has only one of two options:
+任意の人が最初のプレイヤーに選ばれます。 円卓の席の順に、各プレイヤーは 2 つの選択肢のうち 1 つを選択します。
-1. The player can scratch his ticket and reveal its worth to everyone at the table.
-2. The player can trade his unscratched ticket for a previous player's scratched ticket, and then leave the game with that ticket. The previous player then scratches his newly-acquired ticket and reveals its worth to everyone at the table.
+1. くじを削り、プレイヤー全員にくじの賞金額を伝える。
+2. まだ削られていない自分のくじを前のプレイヤーの削られたくじと交換し、そのくじを受け取ってゲームから退場する。 前のプレイヤーは新たに割り当てられたくじを削り、プレイヤー全員にくじの賞金額を伝える。
-The game ends once all tickets have been scratched. All players still remaining at the table must leave with their currently-held tickets.
+すべてのくじが削られたときにゲームが終了します。 円卓に残ったすべてのプレイヤーは、その時点で持っているくじを持って退場しなければなりません。
-Assume that each player uses the optimal strategy for maximizing the expected value of his ticket winnings.
+各プレイヤーが、自分のくじの賞金額の期待値を最大化するための最適な戦略を使用すると仮定します。
-Let $E(p)$ represent the expected number of players left at the table when the game ends in a game consisting of $p$ players (e.g. $E(111) = 5.2912$ when rounded to 5 significant digits).
+$p$ 人のプレイヤーで行うゲームが終了するときに円卓に残っているプレイヤーの期待人数を、$E(p)$ で表します (例: 有効数字 5 桁に四捨五入すると $E(111) = 5.2912$)。
-Let $S_1(N) = \displaystyle\sum_{p = 1}^N E(p)$.
+$S_1(N) = \displaystyle\sum_{p = 1}^N E(p)$ とします。
-Let $S_k(N) = \displaystyle\sum_{p = 1}^N S_{k - 1}(p)$ for $k > 1$.
+$k > 1$ のとき、$S_k(N) = \displaystyle\sum_{p = 1}^N S_{k - 1}(p)$ とします。
-Find $S_{20}({10}^{14})$ and write the answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent. For example, the answer for $S_3(100)$ would be `5.983679014e5`.
+$S_{20}({10}^{14})$ を求め、有効数字 10 桁に四捨五入された科学的記数法の文字列で答えなさい。 小文字 `e` で仮数部と指数部を区切ること。 例えば、$S_3(100)$ の回答は `5.983679014e5` になります。
# --hints--
-`roundtableLottery()` should return a string.
+`roundtableLottery()` は文字列を返す必要があります。
```js
assert(typeof roundtableLottery() === 'string');
```
-`roundtableLottery()` should return the string `1.200856722e263`.
+`roundtableLottery()` は文字列 `1.200856722e263` を返す必要があります。
```js
assert.strictEqual(roundtableLottery(), '1.200856722e263');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md
index 678660f8fe..4e996860ca 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-445-retractions-a.md
@@ -1,6 +1,6 @@
---
id: 5900f52a1000cf542c51003c
-title: 'Problem 445: Retractions A'
+title: '問題 445: レトラクション A'
challengeType: 5
forumTopicId: 302117
dashedName: problem-445-retractions-a
@@ -8,23 +8,23 @@ dashedName: problem-445-retractions-a
# --description--
-For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+$n > 1$ のすべての整数について、関数族 $f_{n, a, b}$ は次のように定義されます。
-$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+整数 $a, b, x$ および $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$ について、$f_{n, a, b}(x) ≡ ax + b\bmod n$
-We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+$0 \le x \lt n$ のすべてにおいて、$f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ のとき、$f_{n, a, b}$ をレトラクションと呼ぶことにします。
-Let $R(n)$ be the number of retractions for $n$.
+$n$ のレトラクションの個数を $R(n)$ とします。
-You are given that
+次が与えられます。
$$\sum_{k = 1}^{99\\,999} R(\displaystyle\binom{100\\,000}{k}) \equiv 628\\,701\\,600\bmod 1\\,000\\,000\\,007$$
-Find $$\sum_{k = 1}^{9\\,999\\,999} R(\displaystyle\binom{10\\,000\\,000}{k})$$ Give your answer modulo $1\\,000\\,000\\,007$.
+$$\sum_{k = 1}^{9\\,999\\,999} R(\displaystyle\binom{10\\,000\\,000}{k})$$ を求め、mod $1\\,000\\,000\\,007$ で答えなさい。
# --hints--
-`retractionsA()` should return `659104042`.
+`retractionsA()` は `659104042` を返す必要があります。
```js
assert.strictEqual(retractionsA(), 659104042);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md
index 04954f5265..e620e72022 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-446-retractions-b.md
@@ -1,6 +1,6 @@
---
id: 5900f52c1000cf542c51003d
-title: 'Problem 446: Retractions B'
+title: '問題 446: レトラクション B'
challengeType: 5
forumTopicId: 302118
dashedName: problem-446-retractions-b
@@ -8,23 +8,23 @@ dashedName: problem-446-retractions-b
# --description--
-For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+$n > 1$ のすべての整数について、関数族 $f_{n, a, b}$ を次のように定義します。
-$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+整数 $a, b, x$ および $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$ について、$f_{n, a, b}(x) ≡ ax + b\bmod n$
-We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+$0 \le x \lt n$ のすべてにおいて、$f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ のとき、$f_{n, a, b}$ をレトラクションと呼ぶことにします。
-Let $R(n)$ be the number of retractions for $n$.
+$n$ のレトラクションの個数を $R(n)$ とします。
-$F(N) = \displaystyle\sum_{n = 1}^N R(n^4 + 4)$.
+$F(N) = \displaystyle\sum_{n = 1}^N R(n^4 + 4)$
-$F(1024) = 77\\,532\\,377\\,300\\,600$.
+$F(1024) = 77\\,532\\,377\\,300\\,600$
-Find $F({10}^7)$. Give your answer modulo $1\\,000\\,000\\,007$.
+$F({10}^7)$ を求めなさい。 mod $1\\,000\\,000\\,007$ で答えること。
# --hints--
-`retractionsB()` should return `907803852`.
+`retractionsB()` は `907803852` を返す必要があります。
```js
assert.strictEqual(retractionsB(), 907803852);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md
index 19a690c2a0..710a3e8a0c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-447-retractions-c.md
@@ -1,6 +1,6 @@
---
id: 5900f52c1000cf542c51003e
-title: 'Problem 447: Retractions C'
+title: '問題 447: レトラクション C'
challengeType: 5
forumTopicId: 302119
dashedName: problem-447-retractions-c
@@ -8,23 +8,23 @@ dashedName: problem-447-retractions-c
# --description--
-For every integer $n > 1$, the family of functions $f_{n, a, b}$ is defined by:
+$n > 1$ のすべての整数について、関数族 $f_{n, a, b}$ を次のように定義します。
-$f_{n, a, b}(x) ≡ ax + b\bmod n$ for $a, b, x$ integer and $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$.
+整数 $a, b, x$ および $0 \lt a \lt n$, $0 \le b \lt n$, $0 \le x \lt n$ について、$f_{n, a, b}(x) ≡ ax + b\bmod n$
-We will call $f_{n, a, b}$ a retraction if $f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ for every $0 \le x \lt n$.
+$0 \le x \lt n$ のすべてにおいて、$f_{n, a, b}(f_{n, a, b}(x)) \equiv f_{n, a, b}(x)\bmod n$ のとき、$f_{n, a, b}$ をレトラクションと呼ぶことにします。
-Let $R(n)$ be the number of retractions for $n$.
+$n$ のレトラクションの個数を $R(n)$ とします。
-$F(N) = \displaystyle\sum_{n = 2}^N R(n)$.
+$F(N) = \displaystyle\sum_{n = 2}^N R(n)$
-$F({10}^7) ≡ 638\\,042\\,271\bmod 1\\,000\\,000\\,007$.
+$F({10}^7) ≡ 638\\,042\\,271\bmod 1\\,000\\,000\\,007$
-Find $F({10}^{14})$. Give your answer modulo $1\\,000\\,000\\,007$.
+$F({10}^{14})$ を求めなさい。 mod $1\\,000\\,000\\,007$ で答えること。
# --hints--
-`retractionsC()` should return `530553372`.
+`retractionsC()` は `530553372` を返す必要があります。
```js
assert.strictEqual(retractionsC(), 530553372);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md
index 6d551bfdb8..25433f86f0 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-448-average-least-common-multiple.md
@@ -1,6 +1,6 @@
---
id: 5900f52c1000cf542c51003f
-title: 'Problem 448: Average least common multiple'
+title: '問題 448: 平均最小公倍数'
challengeType: 5
forumTopicId: 302120
dashedName: problem-448-average-least-common-multiple
@@ -8,21 +8,21 @@ dashedName: problem-448-average-least-common-multiple
# --description--
-The function $lcm(a, b)$ denotes the least common multiple of $a$ and $b$.
+関数 $lcm(a, b)$ は $a$ と $b$ の最小公倍数を表します。
-Let $A(n)$ be the average of the values of $lcm(n, i)$ for $1 ≤ i ≤ n$.
+$1 ≤ i ≤ n$ のとき、$lcm(n, i)$ の値の平均を $A(n)$ とします。
-E.g: $A(2) = \frac{2 + 2}{2} = 2$ and $A(10) = \frac{10 + 10 + 30 + 20 + 10 + 30 + 70 + 40 + 90 + 10}{10} = 32$.
+例: $A(2) = \frac{2 + 2}{2} = 2$ および $A(10) = \frac{10 + 30 + 20 + 30 + 70 + 40 + 90 + 10}{10} = 32$
-Let $S(n) = \sum A(k)$ for $1 ≤ k ≤ n$.
+$1 ≤ k ≤ n$ のとき、$S(n) = \sum A(k)$ とします。
-$S(100) = 122\\,726$.
+$S(100) = 122\\,726$
-Find $S(99\\,999\\,999\\,019)\bmod 999\\,999\\,017$.
+$S(99\\,999\\,999\\,019)\bmod 999\\,999\\,017$ を求めなさい。
# --hints--
-`averageLCM()` should return `106467648`.
+`averageLCM()` は `106467648` を返す必要があります。
```js
assert.strictEqual(averageLCM(), 106467648);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md
index 5983812636..246dde7df8 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-449-chocolate-covered-candy.md
@@ -1,6 +1,6 @@
---
id: 5900f52d1000cf542c510040
-title: 'Problem 449: Chocolate covered candy'
+title: '問題 449: チョコレートでコーティングされたキャンディー'
challengeType: 5
forumTopicId: 302121
dashedName: problem-449-chocolate-covered-candy
@@ -8,19 +8,19 @@ dashedName: problem-449-chocolate-covered-candy
# --description--
-Phil the confectioner is making a new batch of chocolate covered candy. Each candy centre is shaped like an ellipsoid of revolution defined by the equation: $b^2x^2 + b^2y^2 + a^2z^2 = a^2b^2$.
+菓子職人のフィルは、チョコレートでコーティングされたキャンディーを新たに 1 回分作っています。 各キャンディーの中心部は、方程式 $b^2x^2 + b^2y^2 + a^2z^2 = a^2b^2$ により定義される回転楕円体のような形をしています。
-Phil wants to know how much chocolate is needed to cover one candy centre with a uniform coat of chocolate one millimeter thick.
+フィルは、1 つのキャンディーを厚さ 1 ミリの均一なチョコレートコーティングで覆うのにどれだけのチョコレートが必要かを知りたいと思っています。
-If $a = 1$ mm and $b = 1$ mm, the amount of chocolate required is $\frac{28}{3} \pi$ mm3
+$a = 1$ mm, $b = 1$ mm の場合、必要なチョコレートの量は $\frac{28}{3} \pi$ mm3 です。
-If $a = 2$ mm and $b = 1$ mm, the amount of chocolate required is approximately 60.35475635 mm3.
+$a = 2$ mm, $b = 1$ mm の場合、必要なチョコレートの量は約 60.35475635 mm3 です。
-Find the amount of chocolate in mm3 required if $a = 3$ mm and $b = 1$ mm. Give your answer as the number rounded to 8 decimal places behind the decimal point.
+$a = 3$ mm, $b = 1$ mm のときに必要なチョコレートの量を mm3 単位で求めなさい。 回答は、四捨五入して小数第 8 位まで示すこと。
# --hints--
-`chocolateCoveredCandy()` should return `103.37870096`.
+`chocolateCoveredCandy()` は `103.37870096` を返す必要があります。
```js
assert.strictEqual(chocolateCoveredCandy(), 103.37870096);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md
index 7995e5b066..1d1e64d0ed 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-450-hypocycloid-and-lattice-points.md
@@ -1,6 +1,6 @@
---
id: 5900f52e1000cf542c510041
-title: 'Problem 450: Hypocycloid and Lattice points'
+title: '問題 450: 内サイクロイドと格子点'
challengeType: 5
forumTopicId: 302123
dashedName: problem-450-hypocycloid-and-lattice-points
@@ -8,35 +8,35 @@ dashedName: problem-450-hypocycloid-and-lattice-points
# --description--
-A hypocycloid is the curve drawn by a point on a small circle rolling inside a larger circle. The parametric equations of a hypocycloid centered at the origin, and starting at the right most point is given by:
+内サイクロイドとは、大きな円の内部で回転する小さな円上の点によって描かれる曲線のことです。 原点を中心とし、右端の点から始まる内サイクロイドのパラメトリック方程式を次に示します。
$$x(t) = (R - r) \cos(t) + r \cos(\frac{R - r}{r}t)$$
$$y(t) = (R - r) \sin(t) - r \sin(\frac{R - r}{r} t)$$
-Where $R$ is the radius of the large circle and $r$ the radius of the small circle.
+ここで、$R$ は大きな円の半径、$r$ は小さな円の半径です。
-Let $C(R, r)$ be the set of distinct points with integer coordinates on the hypocycloid with radius $R$ and $r$ and for which there is a corresponding value of $t$ such that $\sin(t)$ and $\cos(t)$ are rational numbers.
+半径 $R$ と $r$ を持つ内サイクロイド上の整数座標の点であり、$\sin(t)$ と $\cos(t)$ が有理数となる $t$ の相当値が存在するような、相異なる点の集合を $C(R, r)$ とします。
-Let $S(R, r) = \sum\_{(x,y) \in C(R, r)} |x| + |y|$ be the sum of the absolute values of the $x$ and $y$ coordinates of the points in $C(R, r)$.
+$C(R, r)$ に含まれる点の $x$ 座標と $y$ 座標の絶対値の総和を $S(R, r) = \sum\_{(x,y) \in C(R, r)} |x| + |y|$ とします。
-Let $T(N) = \sum_{R = 3}^N \sum_{r=1}^{\left\lfloor \frac{R - 1}{2} \right\rfloor} S(R, r)$ be the sum of $S(R, r)$ for $R$ and $r$ positive integers, $R\leq N$ and $2r < R$.
+正の整数 $R$ と $r$ について、$R\leq N$ かつ $2r < R$のとき、$S(R, r)$ の和を $T(N) = \sum_{R = 3}^N \sum_{r=1}^{\left\lfloor \frac{R - 1}{2} \right\rfloor} S(R, r)$ とします。
-You are given:
+次が与えられます。
$$\begin{align} C(3, 1) = & \\{(3, 0), (-1, 2), (-1,0), (-1,-2)\\} \\\\ C(2500, 1000) = & \\{(2500, 0), (772, 2376), (772, -2376), (516, 1792), (516, -1792), (500, 0), (68, 504), \\\\ &(68, -504),(-1356, 1088), (-1356, -1088), (-1500, 1000), (-1500, -1000)\\} \end{align}$$
-**Note:** (-625, 0) is not an element of $C(2500, 1000)$ because $\sin(t)$ is not a rational number for the corresponding values of t.
+** 注:** (-625, 0) は $C(2500, 1000)$ の要素ではありません。なぜなら、$t$ の相当値で $\sin(t)$ が有理数とならないからです。
$S(3, 1) = (|3| + |0|) + (|-1| + |2|) + (|-1| + |0|) + (|-1| + |-2|) = 10$
-$T(3) = 10$; $T(10) = 524$; $T(100) = 580\\,442$; $T({10}^3) = 583\\,108\\,600$.
+$T(3) = 10$; $T(10) = 524$; $T(100) = 580\\,442$; $T({10}^3) = 583\\,108\\,600$
-Find $T({10}^6)$.
+$T({10}^6)$ を求めなさい。
# --hints--
-`hypocycloidAndLatticePoints()` should return `583333163984220900`.
+`hypocycloidAndLatticePoints()` は `583333163984220900` を返す必要があります。
```js
assert.strictEqual(hypocycloidAndLatticePoints(), 583333163984220900);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md
index 071cdcc083..4923c39549 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-451-modular-inverses.md
@@ -1,6 +1,6 @@
---
id: 5900f5311000cf542c510042
-title: 'Problem 451: Modular inverses'
+title: '問題 451: モジュラ逆数'
challengeType: 5
forumTopicId: 302124
dashedName: problem-451-modular-inverses
@@ -8,25 +8,25 @@ dashedName: problem-451-modular-inverses
# --description--
-Consider the number 15.
+数 15 について考えます。
-There are eight positive numbers less than 15 which are coprime to 15: 1, 2, 4, 7, 8, 11, 13, 14.
+15 と互いに素である 15 未満の正の数は 1, 2, 4, 7, 8, 11, 13, 14 の 8 つです。
-The modular inverses of these numbers modulo 15 are: 1, 8, 4, 13, 2, 11, 7, 14 because
+それらの数の 15 を法とするモジュラ逆数は、1, 8, 4, 13, 2, 11, 7, 14 です。理由は次のとおりです。
$$\begin{align} & 1 \times 1\bmod 15 = 1 \\\\ & 2 \times 8 = 16\bmod 15 = 1 \\\\ & 4 \times 4 = 16\bmod 15 = 1 \\\\ & 7 \times 13 = 91\bmod 15 = 1 \\\\ & 11 \times 11 = 121\bmod 15 = 1 \\\\ & 14 \times 14 = 196\bmod 15 = 1 \end{align}$$
-Let $I(n)$ be the largest positive number $m$ smaller than $n - 1$ such that the modular inverse of $m$ modulo $n$ equals $m$ itself.
+$m$ の $n$ を法とするモジュラ逆数が $m$ 自体に等しくなるような、$n - 1$ 未満の最大の正の数 $m$ を $I(n)$ とします。
-So $I(15) = 11$.
+したがって、$I(15) = 11$ です。
-Also $I(100) = 51$ and $I(7) = 1$.
+また、$I(100) = 51$ および $I(7) = 1$ です。
-Find $\sum I(n)$ for $3 ≤ n ≤ 2 \times {10}^7$
+$3 ≤ n ≤ 2 \times {10}^7$のとき、$\sum I(n)$ を求めなさい。
# --hints--
-`modularInverses()` should return `153651073760956`.
+`modularInverses()` は `153651073760956` を返す必要があります。
```js
assert.strictEqual(modularInverses(), 153651073760956);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md
index 32246622d7..1fb56d743f 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-452-long-products.md
@@ -1,6 +1,6 @@
---
id: 5900f5311000cf542c510043
-title: 'Problem 452: Long Products'
+title: '問題 452: 長い積'
challengeType: 5
forumTopicId: 302125
dashedName: problem-452-long-products
@@ -8,17 +8,17 @@ dashedName: problem-452-long-products
# --description--
-Define $F(m, n)$ as the number of $n$-tuples of positive integers for which the product of the elements doesn't exceed $m$.
+要素の積が $m$ を超えないような、$n$ 個の正の整数からなる組の数を $F(m, n)$ とします。
-$F(10, 10) = 571$.
+$F(10, 10) = 571$
-$F({10}^6, {10}^6)\bmod 1\\,234\\,567\\,891 = 252\\,903\\,833$.
+$F({10}^6, {10}^6)\bmod 1\\,234\\,567\\,891 = 252\\,903\\,833$
-Find $F({10}^9, {10}^9)\bmod 1\\,234\\,567\\,891$.
+$F({10}^9, {10}^9)\bmod 1\\,234\\,567\\,891$ を求めなさい。
# --hints--
-`longProducts()` should return `345558983`.
+`longProducts()` は `345558983` を返す必要があります。
```js
assert.strictEqual(longProducts(), 345558983);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md
index 91dce06f6d..91b4a79f24 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-453-lattice-quadrilaterals.md
@@ -1,6 +1,6 @@
---
id: 5900f5311000cf542c510044
-title: 'Problem 453: Lattice Quadrilaterals'
+title: '問題 453: 格子四角形'
challengeType: 5
forumTopicId: 302126
dashedName: problem-453-lattice-quadrilaterals
@@ -8,21 +8,21 @@ dashedName: problem-453-lattice-quadrilaterals
# --description--
-A simple quadrilateral is a polygon that has four distinct vertices, has no straight angles and does not self-intersect.
+単純四角形とは、4 つの相異なる頂点を持ち、平角を持たず、かつ自己交差していない多角形のことです。
-Let $Q(m, n)$ be the number of simple quadrilaterals whose vertices are lattice points with coordinates ($x$, $y$) satisfying $0 ≤ x ≤ m$ and $0 ≤ y ≤ n$.
+$0 ≤ x ≤ m$, $0 ≤ y ≤ m$ を満たす座標 ($x$, $y$) の格子点を頂点とする単純四角形の個数を、$Q(m, n)$ とします。
-For example, $Q(2, 2) = 94$ as can be seen below:
+例えば、下図のとおり $Q(2, 2) = 94$ です。
- +
+ -It can also be verified that $Q(3, 7) = 39\\,590$, $Q(12, 3) = 309\\,000$ and $Q(123, 45) = 70\\,542\\,215\\,894\\,646$.
+$Q(3, 7) = 39\\,590$, $Q(12, 3) = 309\\,000$, $Q(123, 45) = 70\\,542\\,215\\,894\\,646$ であることも確認できます。
-Find $Q(12\\,345, 6\\,789)\bmod 135\\,707\\,531$.
+$Q(12\\,345, 6\\,789)\bmod 135\\,707\\,531$ を求めなさい。
# --hints--
-`latticeQuadrilaterals()` should return `104354107`.
+`latticeQuadrilaterals()` は `104354107` を返す必要があります。
```js
assert.strictEqual(latticeQuadrilaterals(), 104354107);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md
index 28b97f569e..5ca61d10ba 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f5331000cf542c510045
-title: 'Problem 454: Diophantine reciprocals III'
+title: '問題 454: ディオファントス逆数 (3)'
challengeType: 5
forumTopicId: 302127
dashedName: problem-454-diophantine-reciprocals-iii
@@ -8,19 +8,19 @@ dashedName: problem-454-diophantine-reciprocals-iii
# --description--
-In the following equation $x$, $y$, and $n$ are positive integers.
+次の式の $x$, $y$, $n$ は正の整数です。
$$\frac{1}{x} + \frac{1}{y} = \frac{1}{n}$$
-For a limit $L$ we define $F(L)$ as the number of solutions which satisfy $x < y ≤ L$.
+上限が $L$ のとき、$x < y ≤ L$ を満たす解の個数を $F(L)$ とします。
-We can verify that $F(15) = 4$ and $F(1000) = 1069$.
+$F(15) = 4$, $F(1000) = 1069$ であることを確認できます。
-Find $F({10}^{12})$.
+$F({10}^{12})$ を求めなさい。
# --hints--
-`diophantineReciprocalsThree()` should return `5435004633092`.
+`diophantineReciprocalsThree()` は `5435004633092` を返す必要があります。
```js
assert.strictEqual(diophantineReciprocalsThree(), 5435004633092);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md
index 76b107407d..301e79e215 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md
@@ -1,6 +1,6 @@
---
id: 5900f5331000cf542c510046
-title: 'Problem 455: Powers With Trailing Digits'
+title: '問題 455: 累乗の下位桁'
challengeType: 5
forumTopicId: 302129
dashedName: problem-455-powers-with-trailing-digits
@@ -8,17 +8,17 @@ dashedName: problem-455-powers-with-trailing-digits
# --description--
-Let $f(n)$ be the largest positive integer $x$ less than ${10}^9$ such that the last 9 digits of $n^x$ form the number $x$ (including leading zeros), or zero if no such integer exists.
+$n^x$ の下位 9 桁が $x$ (先行ゼロを含む) になるような ${10}^9$ 未満の最大の正の整数 $x$ を $f(n)$ とし、そのような整数が存在しないときはその関数の結果を 0 とします。
-For example:
+次に例を示します。
$$\begin{align} & f(4) = 411\\,728\\,896 (4^{411\\,728\\,896} = ...490\underline{411728896}) \\\\ & f(10) = 0 \\\\ & f(157) = 743\\,757 (157^{743\\,757} = ...567\underline{000743757}) \\\\ & Σf(n), 2 ≤ n ≤ 103 = 442\\,530\\,011\\,399 \end{align}$$
-Find $\sum f(n)$, $2 ≤ n ≤ {10}^6$.
+$2 ≤ n ≤ {10}^6$ のとき、$\sum f(n)$ を求めなさい。
# --hints--
-`powersWithTrailingDigits()` should return `450186511399999`.
+`powersWithTrailingDigits()` は `450186511399999` を返す必要があります。
```js
assert.strictEqual(powersWithTrailingDigits(), 450186511399999);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
index c81a11ca17..5ad2a16c11 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f5351000cf542c510047
-title: 'Problem 456: Triangles containing the origin II'
+title: '問題 456: 原点を内包する三角形 (2)'
challengeType: 5
forumTopicId: 302130
dashedName: problem-456-triangles-containing-the-origin-ii
@@ -8,23 +8,23 @@ dashedName: problem-456-triangles-containing-the-origin-ii
# --description--
-Define:
+以下のように定義します。
$$\begin{align} & x_n = ({1248}^n\bmod 32323) - 16161 \\\\ & y_n = ({8421}^n\bmod 30103) - 15051 \\\\ & P_n = \\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\\} \end{align}$$
-For example, $$P_8 = \\{(-14913, -6630), (-10161, 5625), (5226, 11896), (8340, -10778), (15852, -5203), (-15165, 11295), (-1427, -14495), (12407, 1060)\\}$$
+例: $$P_8 = \\{(-14913, -6630), (-10161, 5625), (5226, 11896), (8340, -10778), (15852, -5203), (-15165, 11295), (-1427, -14495), (12407, 1060)\\}$$
-Let $C(n)$ be the number of triangles whose vertices are in $P_n$ which contain the origin in the interior.
+$P_n$ に含まれる点を頂点とし、かつ原点を内包するような三角形の個数を $C(n)$ とします。
-Examples:
+例:
$$\begin{align} & C(8) = 20 \\\\ & C(600) = 8\\,950\\,634 \\\\ & C(40\\,000) = 2\\,666\\,610\\,948\\,988 \end{align}$$
-Find $C(2\\,000\\,000)$.
+$C(2\\,000\\,000)$ を求めなさい。
# --hints--
-`trianglesContainingOriginTwo()` should return `333333208685971500`.
+`trianglesContainingOriginTwo()` は `333333208685971500` を返す必要があります。
```js
assert.strictEqual(trianglesContainingOriginTwo(), 333333208685971500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
index d57d106ed0..cb45f2656d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
@@ -1,6 +1,6 @@
---
id: 5900f5361000cf542c510048
-title: 'Problem 457: A polynomial modulo the square of a prime'
+title: '問題 457: 素数の平方数を法とする多項式'
challengeType: 5
forumTopicId: 302131
dashedName: problem-457-a-polynomial-modulo-the-square-of-a-prime
@@ -8,19 +8,19 @@ dashedName: problem-457-a-polynomial-modulo-the-square-of-a-prime
# --description--
-Let $f(n) = n^2 - 3n - 1$.
+$f(n) = n^2 - 3n - 1$ と定義します。
-Let $p$ be a prime.
+$p$ を素数とします。
-Let $R(p)$ be the smallest positive integer $n$ such that $f(n)\bmod p^2 = 0$ if such an integer $n$ exists, otherwise $R(p) = 0$.
+$f(n)\bmod p^2 = 0$ が成り立つ最小の正の整数 $n$ が存在するときは $R(p)$ = $n$ とし、存在しないときは $R(p) = 0$ と定義します。
-Let $SR(L)$ be $\sum R(p)$ for all primes not exceeding $L$.
+$L$ を超えないすべての素数について、$\sum R(p)$ を $SR(L)$ とします。
-Find $SR({10}^7)$.
+$SR({10}^7)$ を求めなさい。
# --hints--
-`polynomialModuloSquareOfPrime()` should return `2647787126797397000`.
+`polynomialModuloSquareOfPrime()` は `2647787126797397000` を返す必要があります。
```js
assert.strictEqual(polynomialModuloSquareOfPrime(), 2647787126797397000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md
index e6abd5b68d..7f62717f2d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md
@@ -1,6 +1,6 @@
---
id: 5900f5361000cf542c510049
-title: 'Problem 458: Permutations of Project'
+title: '問題 458: "Project" の順列'
challengeType: 5
forumTopicId: 302132
dashedName: problem-458-permutations-of-project
@@ -8,17 +8,17 @@ dashedName: problem-458-permutations-of-project
# --description--
-Consider the alphabet $A$ made out of the letters of the word `project`: $A = \\{c, e, j, o, p, r, t\\}$.
+"`project`"という単語に含まれる文字からなるアルファベットの集合 $A$、すなわち $A = \\{c, e, j, o, p, r, t\\}$ について考えます。
-Let $T(n)$ be the number of strings of length $n$ consisting of letters from $A$ that do not have a substring that is one of the 5040 permutations of `project`.
+$A$ の文字で構成される長さ $n$ の文字列のうち、"`project`" の 5040 通りの順列の一つである部分文字列を持たない文字列の数を、$T(n)$ とします。
-$T(7) = 7^7 - 7! = 818\\,503$.
+$T(7) = 7^7 - 7! = 818\\,503$ です。
-Find $T({10}^{12})$. Give the last 9 digits of your answer.
+$T({10}^{12})$ を求めなさい。 回答は、下位 9 桁とすること。
# --hints--
-`permutationsOfProject()` should return `423341841`.
+`permutationsOfProject()` は `423341841` を返す必要があります。
```js
assert.strictEqual(permutationsOfProject(), 423341841);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md
index 87122d0e2a..9aa8b01658 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md
@@ -1,6 +1,6 @@
---
id: 5900f5371000cf542c51004a
-title: 'Problem 459: Flipping game'
+title: '問題 459: 裏返しゲーム'
challengeType: 5
forumTopicId: 302133
dashedName: problem-459-flipping-game
@@ -8,35 +8,35 @@ dashedName: problem-459-flipping-game
# --description--
-The flipping game is a two player game played on a $N$ by $N$ square board.
+裏返しゲームは、$N$ × $N$ 個のマスがある盤を使って 2 人で行うゲームです。
-Each square contains a disk with one side white and one side black.
+各マスには、白と黒の面を持つ円盤が置いてあります。
-The game starts with all disks showing their white side.
+ゲーム開始時は、すべての円盤の白い面が上になっています。
-A turn consists of flipping all disks in a rectangle with the following properties:
+各ターンで、以下の性質を持つ長方形の範囲内にあるすべての円盤を裏返します。
-- the upper right corner of the rectangle contains a white disk
-- the rectangle width is a perfect square (1, 4, 9, 16, ...)
-- the rectangle height is a triangular number (1, 3, 6, 10, ...)
+- 長方形の右上隅に白い円盤がある
+- 長方形の幅が完全正方数 (1, 4, 9, 16, ...) である
+- 長方形の高さが三角数 (1, 3, 6, 10, ...) である
-
-It can also be verified that $Q(3, 7) = 39\\,590$, $Q(12, 3) = 309\\,000$ and $Q(123, 45) = 70\\,542\\,215\\,894\\,646$.
+$Q(3, 7) = 39\\,590$, $Q(12, 3) = 309\\,000$, $Q(123, 45) = 70\\,542\\,215\\,894\\,646$ であることも確認できます。
-Find $Q(12\\,345, 6\\,789)\bmod 135\\,707\\,531$.
+$Q(12\\,345, 6\\,789)\bmod 135\\,707\\,531$ を求めなさい。
# --hints--
-`latticeQuadrilaterals()` should return `104354107`.
+`latticeQuadrilaterals()` は `104354107` を返す必要があります。
```js
assert.strictEqual(latticeQuadrilaterals(), 104354107);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md
index 28b97f569e..5ca61d10ba 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-454-diophantine-reciprocals-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f5331000cf542c510045
-title: 'Problem 454: Diophantine reciprocals III'
+title: '問題 454: ディオファントス逆数 (3)'
challengeType: 5
forumTopicId: 302127
dashedName: problem-454-diophantine-reciprocals-iii
@@ -8,19 +8,19 @@ dashedName: problem-454-diophantine-reciprocals-iii
# --description--
-In the following equation $x$, $y$, and $n$ are positive integers.
+次の式の $x$, $y$, $n$ は正の整数です。
$$\frac{1}{x} + \frac{1}{y} = \frac{1}{n}$$
-For a limit $L$ we define $F(L)$ as the number of solutions which satisfy $x < y ≤ L$.
+上限が $L$ のとき、$x < y ≤ L$ を満たす解の個数を $F(L)$ とします。
-We can verify that $F(15) = 4$ and $F(1000) = 1069$.
+$F(15) = 4$, $F(1000) = 1069$ であることを確認できます。
-Find $F({10}^{12})$.
+$F({10}^{12})$ を求めなさい。
# --hints--
-`diophantineReciprocalsThree()` should return `5435004633092`.
+`diophantineReciprocalsThree()` は `5435004633092` を返す必要があります。
```js
assert.strictEqual(diophantineReciprocalsThree(), 5435004633092);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md
index 76b107407d..301e79e215 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-455-powers-with-trailing-digits.md
@@ -1,6 +1,6 @@
---
id: 5900f5331000cf542c510046
-title: 'Problem 455: Powers With Trailing Digits'
+title: '問題 455: 累乗の下位桁'
challengeType: 5
forumTopicId: 302129
dashedName: problem-455-powers-with-trailing-digits
@@ -8,17 +8,17 @@ dashedName: problem-455-powers-with-trailing-digits
# --description--
-Let $f(n)$ be the largest positive integer $x$ less than ${10}^9$ such that the last 9 digits of $n^x$ form the number $x$ (including leading zeros), or zero if no such integer exists.
+$n^x$ の下位 9 桁が $x$ (先行ゼロを含む) になるような ${10}^9$ 未満の最大の正の整数 $x$ を $f(n)$ とし、そのような整数が存在しないときはその関数の結果を 0 とします。
-For example:
+次に例を示します。
$$\begin{align} & f(4) = 411\\,728\\,896 (4^{411\\,728\\,896} = ...490\underline{411728896}) \\\\ & f(10) = 0 \\\\ & f(157) = 743\\,757 (157^{743\\,757} = ...567\underline{000743757}) \\\\ & Σf(n), 2 ≤ n ≤ 103 = 442\\,530\\,011\\,399 \end{align}$$
-Find $\sum f(n)$, $2 ≤ n ≤ {10}^6$.
+$2 ≤ n ≤ {10}^6$ のとき、$\sum f(n)$ を求めなさい。
# --hints--
-`powersWithTrailingDigits()` should return `450186511399999`.
+`powersWithTrailingDigits()` は `450186511399999` を返す必要があります。
```js
assert.strictEqual(powersWithTrailingDigits(), 450186511399999);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
index c81a11ca17..5ad2a16c11 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f5351000cf542c510047
-title: 'Problem 456: Triangles containing the origin II'
+title: '問題 456: 原点を内包する三角形 (2)'
challengeType: 5
forumTopicId: 302130
dashedName: problem-456-triangles-containing-the-origin-ii
@@ -8,23 +8,23 @@ dashedName: problem-456-triangles-containing-the-origin-ii
# --description--
-Define:
+以下のように定義します。
$$\begin{align} & x_n = ({1248}^n\bmod 32323) - 16161 \\\\ & y_n = ({8421}^n\bmod 30103) - 15051 \\\\ & P_n = \\{(x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n)\\} \end{align}$$
-For example, $$P_8 = \\{(-14913, -6630), (-10161, 5625), (5226, 11896), (8340, -10778), (15852, -5203), (-15165, 11295), (-1427, -14495), (12407, 1060)\\}$$
+例: $$P_8 = \\{(-14913, -6630), (-10161, 5625), (5226, 11896), (8340, -10778), (15852, -5203), (-15165, 11295), (-1427, -14495), (12407, 1060)\\}$$
-Let $C(n)$ be the number of triangles whose vertices are in $P_n$ which contain the origin in the interior.
+$P_n$ に含まれる点を頂点とし、かつ原点を内包するような三角形の個数を $C(n)$ とします。
-Examples:
+例:
$$\begin{align} & C(8) = 20 \\\\ & C(600) = 8\\,950\\,634 \\\\ & C(40\\,000) = 2\\,666\\,610\\,948\\,988 \end{align}$$
-Find $C(2\\,000\\,000)$.
+$C(2\\,000\\,000)$ を求めなさい。
# --hints--
-`trianglesContainingOriginTwo()` should return `333333208685971500`.
+`trianglesContainingOriginTwo()` は `333333208685971500` を返す必要があります。
```js
assert.strictEqual(trianglesContainingOriginTwo(), 333333208685971500);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
index d57d106ed0..cb45f2656d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-457-a-polynomial-modulo-the-square-of-a-prime.md
@@ -1,6 +1,6 @@
---
id: 5900f5361000cf542c510048
-title: 'Problem 457: A polynomial modulo the square of a prime'
+title: '問題 457: 素数の平方数を法とする多項式'
challengeType: 5
forumTopicId: 302131
dashedName: problem-457-a-polynomial-modulo-the-square-of-a-prime
@@ -8,19 +8,19 @@ dashedName: problem-457-a-polynomial-modulo-the-square-of-a-prime
# --description--
-Let $f(n) = n^2 - 3n - 1$.
+$f(n) = n^2 - 3n - 1$ と定義します。
-Let $p$ be a prime.
+$p$ を素数とします。
-Let $R(p)$ be the smallest positive integer $n$ such that $f(n)\bmod p^2 = 0$ if such an integer $n$ exists, otherwise $R(p) = 0$.
+$f(n)\bmod p^2 = 0$ が成り立つ最小の正の整数 $n$ が存在するときは $R(p)$ = $n$ とし、存在しないときは $R(p) = 0$ と定義します。
-Let $SR(L)$ be $\sum R(p)$ for all primes not exceeding $L$.
+$L$ を超えないすべての素数について、$\sum R(p)$ を $SR(L)$ とします。
-Find $SR({10}^7)$.
+$SR({10}^7)$ を求めなさい。
# --hints--
-`polynomialModuloSquareOfPrime()` should return `2647787126797397000`.
+`polynomialModuloSquareOfPrime()` は `2647787126797397000` を返す必要があります。
```js
assert.strictEqual(polynomialModuloSquareOfPrime(), 2647787126797397000);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md
index e6abd5b68d..7f62717f2d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-458-permutations-of-project.md
@@ -1,6 +1,6 @@
---
id: 5900f5361000cf542c510049
-title: 'Problem 458: Permutations of Project'
+title: '問題 458: "Project" の順列'
challengeType: 5
forumTopicId: 302132
dashedName: problem-458-permutations-of-project
@@ -8,17 +8,17 @@ dashedName: problem-458-permutations-of-project
# --description--
-Consider the alphabet $A$ made out of the letters of the word `project`: $A = \\{c, e, j, o, p, r, t\\}$.
+"`project`"という単語に含まれる文字からなるアルファベットの集合 $A$、すなわち $A = \\{c, e, j, o, p, r, t\\}$ について考えます。
-Let $T(n)$ be the number of strings of length $n$ consisting of letters from $A$ that do not have a substring that is one of the 5040 permutations of `project`.
+$A$ の文字で構成される長さ $n$ の文字列のうち、"`project`" の 5040 通りの順列の一つである部分文字列を持たない文字列の数を、$T(n)$ とします。
-$T(7) = 7^7 - 7! = 818\\,503$.
+$T(7) = 7^7 - 7! = 818\\,503$ です。
-Find $T({10}^{12})$. Give the last 9 digits of your answer.
+$T({10}^{12})$ を求めなさい。 回答は、下位 9 桁とすること。
# --hints--
-`permutationsOfProject()` should return `423341841`.
+`permutationsOfProject()` は `423341841` を返す必要があります。
```js
assert.strictEqual(permutationsOfProject(), 423341841);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md
index 87122d0e2a..9aa8b01658 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-459-flipping-game.md
@@ -1,6 +1,6 @@
---
id: 5900f5371000cf542c51004a
-title: 'Problem 459: Flipping game'
+title: '問題 459: 裏返しゲーム'
challengeType: 5
forumTopicId: 302133
dashedName: problem-459-flipping-game
@@ -8,35 +8,35 @@ dashedName: problem-459-flipping-game
# --description--
-The flipping game is a two player game played on a $N$ by $N$ square board.
+裏返しゲームは、$N$ × $N$ 個のマスがある盤を使って 2 人で行うゲームです。
-Each square contains a disk with one side white and one side black.
+各マスには、白と黒の面を持つ円盤が置いてあります。
-The game starts with all disks showing their white side.
+ゲーム開始時は、すべての円盤の白い面が上になっています。
-A turn consists of flipping all disks in a rectangle with the following properties:
+各ターンで、以下の性質を持つ長方形の範囲内にあるすべての円盤を裏返します。
-- the upper right corner of the rectangle contains a white disk
-- the rectangle width is a perfect square (1, 4, 9, 16, ...)
-- the rectangle height is a triangular number (1, 3, 6, 10, ...)
+- 長方形の右上隅に白い円盤がある
+- 長方形の幅が完全正方数 (1, 4, 9, 16, ...) である
+- 長方形の高さが三角数 (1, 3, 6, 10, ...) である
- +
+ -Players alternate turns. A player wins by turning the grid all black.
+プレイヤーは交互に手を打ちます。 すべてのマスを黒にしたプレイヤーの勝ちです。
-Let $W(N)$ be the number of winning moves for the first player on a $N$ by $N$ board with all disks white, assuming perfect play.
+すべての円盤が白である $N$ x $N$ 個のマスから始めて完璧なプレイをすると仮定して、先手必勝の手の数を $W(N)$ とします。
-$W(1) = 1$, $W(2) = 0$, $W(5) = 8$ and $W({10}^2) = 31\\,395$.
+$W(1) = 1$, $W(2) = 0$, $W(5) = 8$, $W({10}^2) = 31\\,395$ となります。
-For $N = 5$, the first player's eight winning first moves are:
+$N = 5$ のとき、先手必勝の第 1 手は次の 8 つです。
-
-Players alternate turns. A player wins by turning the grid all black.
+プレイヤーは交互に手を打ちます。 すべてのマスを黒にしたプレイヤーの勝ちです。
-Let $W(N)$ be the number of winning moves for the first player on a $N$ by $N$ board with all disks white, assuming perfect play.
+すべての円盤が白である $N$ x $N$ 個のマスから始めて完璧なプレイをすると仮定して、先手必勝の手の数を $W(N)$ とします。
-$W(1) = 1$, $W(2) = 0$, $W(5) = 8$ and $W({10}^2) = 31\\,395$.
+$W(1) = 1$, $W(2) = 0$, $W(5) = 8$, $W({10}^2) = 31\\,395$ となります。
-For $N = 5$, the first player's eight winning first moves are:
+$N = 5$ のとき、先手必勝の第 1 手は次の 8 つです。
- +
+ -Find $W({10}^6)$.
+$W({10}^6)$ を求めなさい。
# --hints--
-`flippingGame()` should return `3996390106631`.
+`flippingGame()` は `3996390106631` を返す必要があります。
```js
assert.strictEqual(flippingGame(), 3996390106631);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md
index 01da7401b3..a726366f0b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md
@@ -1,6 +1,6 @@
---
id: 5900f5381000cf542c51004b
-title: 'Problem 460: An ant on the move'
+title: '問題 460: 歩き回るアリ'
challengeType: 5
forumTopicId: 302135
dashedName: problem-460-an-ant-on-the-move
@@ -8,30 +8,30 @@ dashedName: problem-460-an-ant-on-the-move
# --description--
-On the Euclidean plane, an ant travels from point $A(0, 1)$ to point $B(d, 1)$ for an integer $d$.
+ユークリッド平面上で、アリが点 $A(0, 1)$ から点 $B(d, 1)$ へ移動します。ここで、$d$ は整数です。
-In each step, the ant at point ($x_0$, $y_0$) chooses one of the lattice points ($x_1$, $y_1$) which satisfy $x_1 ≥ 0$ and $y_1 ≥ 1$ and goes straight to ($x_1$, $y_1$) at a constant velocity $v$. The value of $v$ depends on $y_0$ and $y_1$ as follows:
+各ステップにおいて、点 ($x_0$, $y_0$) にいるアリは、$x_1 ≥ 0$, $y_1 ≥ 1$ を満たす格子点 ($x_1$, $y_1$) のうち 1 つを選び、一定の速度 $v$ で ($x_1$, $y_1$) に向かって直進します。 $v$ の値は、$y_0$ と $y_1$ によって次のように決まります。
-- If $y_0 = y_1$, the value of $v$ equals $y_0$.
-- If $y_0 ≠ y_1$, the value of $v$ equals $\frac{y_1 - y_0}{\ln y_1 - \ln y_0}$.
+- $y_0 = y_1$ の場合、$v$ の値は $y_0$ に等しい。
+- $y_0 ≠ y_1$ の場合、$v$ の値は $\frac{y_1 - y_0}{\ln y_1 - \ln y_0}$ に等しい。
-The left image is one of the possible paths for $d = 4$. First the ant goes from $A(0, 1)$ to $P_1(1, 3)$ at velocity $\frac{3 - 1}{\ln 3 - \ln 1} ≈ 1.8205$. Then the required time is $\frac{\sqrt{5}}{1.820} ≈ 1.2283$.
+左側の図は、$d = 4$ の場合に考えられる経路の一つです。 まず、アリは $A(0, 1)$ から $P_1(1, 3)$ まで、速度 $\frac{3 - 1}{\ln 3 - \ln 1} ≈ 1.8205$ で進みます。 したがって、所要時間は $\frac{\sqrt{5}}{1.820} ≈ 1.2283$ です。
-From $P_1(1, 3)$ to $P_2(3, 3)$ the ant travels at velocity 3 so the required time is $\frac{2}{3} ≈ 0.6667$. From $P_2(3, 3)$ to $B(4, 1)$ the ant travels at velocity $\frac{1 - 3}{\ln 1 - \ln 3} ≈ 1.8205$ so the required time is $\frac{\sqrt{5}}{1.8205} ≈ 1.2283$.
+$P_1(1, 3)$ から $P_2(3, 3)$ までは速度 3 で移動するので、所要時間は $\frac{2}{3} ≈ 0.6667$ です。 $P_2(3, 3)$ から $B(4, 1)$ までのアリの移動速度は $\frac{1 - 3}{\ln 1 -\ln 3} ≈ 1.8205$なので、所要時間は $\frac{\sqrt{5}}{1.8205} ≈ 1.2283$ となります。
-Thus the total required time is $1.2283 + 0.6667 + 1.2283 = 3.1233$.
+したがって、合計所要時間は $1.2283 + 0.6667 + 1.2283 = 3.1233$ です。
-The right image is another path. The total required time is calculated as $0.98026 + 1 + 0.98026 = 2.96052$. It can be shown that this is the quickest path for $d = 4$.
+右側の図は別の経路です。 合計所要時間は $0.98026 + 1 + 0.98026 = 2.96052$ となります。 これが $d = 4$ に対する最速経路であることが分かっています。
-
-Find $W({10}^6)$.
+$W({10}^6)$ を求めなさい。
# --hints--
-`flippingGame()` should return `3996390106631`.
+`flippingGame()` は `3996390106631` を返す必要があります。
```js
assert.strictEqual(flippingGame(), 3996390106631);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md
index 01da7401b3..a726366f0b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-460-an-ant-on-the-move.md
@@ -1,6 +1,6 @@
---
id: 5900f5381000cf542c51004b
-title: 'Problem 460: An ant on the move'
+title: '問題 460: 歩き回るアリ'
challengeType: 5
forumTopicId: 302135
dashedName: problem-460-an-ant-on-the-move
@@ -8,30 +8,30 @@ dashedName: problem-460-an-ant-on-the-move
# --description--
-On the Euclidean plane, an ant travels from point $A(0, 1)$ to point $B(d, 1)$ for an integer $d$.
+ユークリッド平面上で、アリが点 $A(0, 1)$ から点 $B(d, 1)$ へ移動します。ここで、$d$ は整数です。
-In each step, the ant at point ($x_0$, $y_0$) chooses one of the lattice points ($x_1$, $y_1$) which satisfy $x_1 ≥ 0$ and $y_1 ≥ 1$ and goes straight to ($x_1$, $y_1$) at a constant velocity $v$. The value of $v$ depends on $y_0$ and $y_1$ as follows:
+各ステップにおいて、点 ($x_0$, $y_0$) にいるアリは、$x_1 ≥ 0$, $y_1 ≥ 1$ を満たす格子点 ($x_1$, $y_1$) のうち 1 つを選び、一定の速度 $v$ で ($x_1$, $y_1$) に向かって直進します。 $v$ の値は、$y_0$ と $y_1$ によって次のように決まります。
-- If $y_0 = y_1$, the value of $v$ equals $y_0$.
-- If $y_0 ≠ y_1$, the value of $v$ equals $\frac{y_1 - y_0}{\ln y_1 - \ln y_0}$.
+- $y_0 = y_1$ の場合、$v$ の値は $y_0$ に等しい。
+- $y_0 ≠ y_1$ の場合、$v$ の値は $\frac{y_1 - y_0}{\ln y_1 - \ln y_0}$ に等しい。
-The left image is one of the possible paths for $d = 4$. First the ant goes from $A(0, 1)$ to $P_1(1, 3)$ at velocity $\frac{3 - 1}{\ln 3 - \ln 1} ≈ 1.8205$. Then the required time is $\frac{\sqrt{5}}{1.820} ≈ 1.2283$.
+左側の図は、$d = 4$ の場合に考えられる経路の一つです。 まず、アリは $A(0, 1)$ から $P_1(1, 3)$ まで、速度 $\frac{3 - 1}{\ln 3 - \ln 1} ≈ 1.8205$ で進みます。 したがって、所要時間は $\frac{\sqrt{5}}{1.820} ≈ 1.2283$ です。
-From $P_1(1, 3)$ to $P_2(3, 3)$ the ant travels at velocity 3 so the required time is $\frac{2}{3} ≈ 0.6667$. From $P_2(3, 3)$ to $B(4, 1)$ the ant travels at velocity $\frac{1 - 3}{\ln 1 - \ln 3} ≈ 1.8205$ so the required time is $\frac{\sqrt{5}}{1.8205} ≈ 1.2283$.
+$P_1(1, 3)$ から $P_2(3, 3)$ までは速度 3 で移動するので、所要時間は $\frac{2}{3} ≈ 0.6667$ です。 $P_2(3, 3)$ から $B(4, 1)$ までのアリの移動速度は $\frac{1 - 3}{\ln 1 -\ln 3} ≈ 1.8205$なので、所要時間は $\frac{\sqrt{5}}{1.8205} ≈ 1.2283$ となります。
-Thus the total required time is $1.2283 + 0.6667 + 1.2283 = 3.1233$.
+したがって、合計所要時間は $1.2283 + 0.6667 + 1.2283 = 3.1233$ です。
-The right image is another path. The total required time is calculated as $0.98026 + 1 + 0.98026 = 2.96052$. It can be shown that this is the quickest path for $d = 4$.
+右側の図は別の経路です。 合計所要時間は $0.98026 + 1 + 0.98026 = 2.96052$ となります。 これが $d = 4$ に対する最速経路であることが分かっています。
-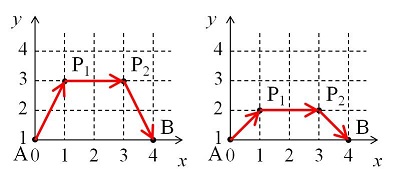 +
+ -Let $F(d)$ be the total required time if the ant chooses the quickest path. For example, $F(4) ≈ 2.960\\,516\\,287$. We can verify that $F(10) ≈ 4.668\\,187\\,834$ and $F(100) ≈ 9.217\\,221\\,972$.
+アリが最速経路を選んだ場合の合計所要時間を $F(d)$ とします。 例えば、$F(4) ≈ 2.960\\,516\\,287$ です。 $F(10) ≈ 4.668\\,187\\,834$, $F(100) ≈ 9.217\\,221\\,972$ であることを確認できます。
-Find $F(10\\,000)$. Give your answer rounded to nine decimal places.
+$F(10\\,000)$ を求めなさい。 回答は、四捨五入して小数第 9 位まで示すこと。
# --hints--
-`antOnTheMove()` should return `18.420738199`.
+`antOnTheMove()` は `18.420738199` を返す必要があります。
```js
assert.strictEqual(antOnTheMove(), 18.420738199);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md
index 9903fbe010..1ec9c45f62 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md
@@ -1,6 +1,6 @@
---
id: 5900f53a1000cf542c51004c
-title: 'Problem 461: Almost Pi'
+title: '問題 461: ほぼ Pi'
challengeType: 5
forumTopicId: 302136
dashedName: problem-461-almost-pi
@@ -8,43 +8,43 @@ dashedName: problem-461-almost-pi
# --description--
-Let `f(k, n)` = $e^\frac{k}{n} - 1$, for all non-negative integers `k`.
+すべての非負整数 `k` に対して `f(k, n)` = $e^\frac{k}{n} - 1$ と定義します。
-Remarkably, `f(6, 200) + f(75, 200) + f(89, 200) + f(226, 200)` = 3.1415926… ≈ π.
+驚くべきことに、`f(6, 200) + f(75, 200) + f(89, 200) + f(226, 200)` = 3.1415926… ≈ π となります。
-In fact, it is the best approximation of π of the form `f(a, 200) + f(b, 200) + f(c, 200) + f(d, 200)`.
+実際、これは式 `f(a, 200) + f(b, 200) + f(c, 200) + f(d, 200)` の π の最良近似です。
-Let `almostPi(n)` = a2 + b2 + c2 + d2 for a, b, c, d that minimize the error: $\lvert f(a,n) + f(b,n) + f(c,n) + f(d,n) - \Pi\rvert$
+誤差 $\lvert f(a,n) + f(b,n) + f(c,n) + f(d,n) - \Pi\rvert$ が最小となる a, b, c, d に対して、`almostPi(n)` = a2 + b2 + c2 + d2 と定義します。
-You are given `almostPi(200)` = 62 + 752 + 892 + 2262 = 64658.
+`almostPi(200)` = 62 + 752 + 892 + 2262 = 64658 が与えられます。
# --hints--
-`almostPi` should be a function.
+`almostPi` は関数でなければなりません。
```js
assert(typeof almostPi === 'function')
```
-`almostPi` should return a number.
+`almostPi` は数値を返す必要があります。
```js
assert.strictEqual(typeof almostPi(10), 'number');
```
-`almostPi(29)` should return `1208`.
+`almostPi(29)` は `1208` を返す必要があります。
```js
assert.strictEqual(almostPi(29), 1208);
```
-`almostPi(50)` should return `4152`.
+`almostPi(50)` は `4152` を返す必要があります。
```js
assert.strictEqual(almostPi(50), 4152);
```
-`almostPi(200)` should return `64658`.
+`almostPi(200)` は `64658` を返す必要があります。
```js
assert.strictEqual(almostPi(200), 64658);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
index 550715f701..8c04e8e694 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f53b1000cf542c51004d
-title: 'Problem 462: Permutation of 3-smooth numbers'
+title: '問題 462: 3-smooth 数の順列'
challengeType: 5
forumTopicId: 302137
dashedName: problem-462-permutation-of-3-smooth-numbers
@@ -8,31 +8,31 @@ dashedName: problem-462-permutation-of-3-smooth-numbers
# --description--
-A 3-smooth number is an integer which has no prime factor larger than 3. For an integer $N$, we define $S(N)$ as the set of 3-smooth numbers less than or equal to $N$. For example, $S(20) = \\{1, 2, 3, 4, 6, 8, 9, 12, 16, 18\\}$.
+3-smooth 数とは、3 より大きい素因数を持たない整数のことです。 整数 $N$ に対して、$N$ 以下の 3-smooth 数の集合を $S(N)$ とします。 例えば、$S(20) = \\{1, 2, 3, 4, 6, 8, 9, 12, 16, 18\\}$ です。
-We define $F(N)$ as the number of permutations of $S(N)$ in which each element comes after all of its proper divisors.
+各要素のすべての真の約数の後にその要素が現れるような $S(N)$ の順列の個数を、$F(N)$ とします。
-This is one of the possible permutations for $N = 20$.
+$N = 20$ に対して考えられる順列の一例を下に示します。
-- 1, 2, 4, 3, 9, 8, 16, 6, 18, 12.
+- 1, 2, 4, 3, 9, 8, 16, 6, 18, 12
-This is not a valid permutation because 12 comes before its divisor 6.
+下の例は、12 が約数 6 の前に現れるので有効な順列ではありません。
-- 1, 2, 4, 3, 9, 8, 12, 16, 6, 18.
+- 1, 2, 4, 3, 9, 8, 12, 16, 6, 18
-We can verify that $F(6) = 5$, $F(8) = 9$, $F(20) = 450$ and $F(1000) ≈ 8.8521816557e\\,21$.
+$F(6) = 5$, $F(8) = 9$, $F(20) = 450$, $F(1000) ≈ 8.8521816557e\\21$ であることを確認できます。
-Find $F({10}^{18})$. Give as your answer as a string in its scientific notation rounded to ten digits after the decimal point. When giving your answer, use a lowercase `e` to separate mantissa and exponent. E.g. if the answer is $112\\,233\\,445\\,566\\,778\\,899$ then the answer format would be `1.1223344557e17`.
+$F({10}^{18})$ を求めなさい。 回答は、科学的記数法による文字列を四捨五入して小数第 10 位まで示すこと。 回答は、小文字 `e` で仮数部と指数部を区切って書くこと。 例えば、 答えが $112\\,233\\,445\\,566\\,778\\,899$ の場合、`1.1223344557e17` の形式にします。
# --hints--
-`permutationOf3SmoothNumbers()` should return a string.
+`permutationOf3SmoothNumbers()` は文字列を返す必要があります。
```js
assert.strictEqual(typeof permutationOf3SmoothNumbers() === 'string');
```
-`permutationOf3SmoothNumbers()` should return the string `5.5350769703e1512`.
+`permutationOf3SmoothNumbers()` は文字列 `5.5350769703e1512` を返す必要があります。
```js
assert.strictEqual(permutationOf3SmoothNumbers(), '5.5350769703e1512');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
index 159aacceb3..d699d8d745 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
@@ -1,6 +1,6 @@
---
id: 5900f53c1000cf542c51004e
-title: 'Problem 463: A weird recurrence relation'
+title: '問題 463: 風変わりな漸化式'
challengeType: 5
forumTopicId: 302138
dashedName: problem-463-a-weird-recurrence-relation
@@ -8,19 +8,19 @@ dashedName: problem-463-a-weird-recurrence-relation
# --description--
-The function $f$ is defined for all positive integers as follows:
+すべての正の整数に対して関数 $f$ が次のように定義されます。
$$\begin{align} & f(1) = 1 \\\\ & f(3) = 3 \\\\ & f(2n) = f(n) \\\\ & f(4n + 1) = 2f(2n + 1) - f(n) \\\\ & f(4n + 3) = 3f(2n + 1) - 2f(n) \end{align}$$
-The function $S(n)$ is defined as $\sum_{i=1}^{n} f(i)$.
+関数 $S(n)$ は $\sum_{i=1}^{n} f(i)$ と定義されます。
-$S(8) = 22$ and $S(100) = 3604$.
+$S(8) = 22$, $S(100) = 3604$ です。
-Find $S(3^{37})$. Give the last 9 digits of your answer.
+$S(3^{37})$ を求めなさい。 回答は、下位 9 桁とすること。
# --hints--
-`weirdRecurrenceRelation()` should return `808981553`.
+`weirdRecurrenceRelation()` は `808981553` を返す必要があります。
```js
assert.strictEqual(weirdRecurrenceRelation(), 808981553);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
index 2e12caa276..3946777551 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
@@ -1,6 +1,6 @@
---
id: 5900f53d1000cf542c51004f
-title: 'Problem 464: Möbius function and intervals'
+title: '問題 464: メビウス関数と区間'
challengeType: 5
forumTopicId: 302139
dashedName: problem-464-mbius-function-and-intervals
@@ -8,30 +8,30 @@ dashedName: problem-464-mbius-function-and-intervals
# --description--
-The Möbius function, denoted $μ(n)$, is defined as:
+$μ(n)$ で表されるメビウス関数は次のように定義されます。
-- $μ(n) = (-1)^{ω(n)}$ if $n$ is squarefree (where $ω(n)$ is the number of distinct prime factors of $n$)
-- $μ(n) = 0$ if $n$ is not squarefree.
+- $n$ が無平方数のとき、$μ(n) = (-1)^{ω(n)}$ (ここで、$ω(n)$ は $n$ の相異なる素因数)
+- $n$ が無平方数でないとき、$μ(n) = 0$
-Let $P(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = 1$.
+区間 $[a, b]$ において $μ(n) = 1$ となる整数 $n$ の数を、$P(a, b)$ とします。
-Let $N(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = -1$.
+区間 $[a, b]$ において $μ(n) = -1$ となる整数 $n$ の数を、$N(a, b)$ とします。
-For example, $P(2, 10) = 2$ and $N(2, 10) = 4$.
+例えば、$P(2, 10) = 2$, $N(2, 10) = 4$ です。
-Let $C(n)$ be the number of integer pairs $(a, b)$ such that:
+次の条件をすべて満たす整数の対 $(a, b)$ を $C(n)$ とします。
-- $1 ≤ a ≤ b ≤ n$,
-- $99 \times N(a, b) ≤ 100 \times P(a, b)$, and
-- $99 \times P(a, b) ≤ 100 \times N(a, b)$.
+- $1 ≤ a ≤ b ≤ n$
+- $99 \times N(a, b) ≤ 100 \times P(a, b)$
+- $99 \times P(a, b) ≤ 100 \times N(a, b)$
-For example, $C(10) = 13$, $C(500) = 16\\,676$ and $C(10\\,000) = 20\\,155\\,319$.
+例えば、$C(10) = 13$, $C(500) = 16\\,676$, $C(10\\,000) = 20\\,155\\,319$ です。
-Find $C(20\\,000\\,000)$.
+$C(20\\,000\\,000)$ を求めなさい。
# --hints--
-`mobiusFunctionAndIntervals()` should return `198775297232878`.
+`mobiusFunctionAndIntervals()` は `198775297232878` を返す必要があります。
```js
assert.strictEqual(mobiusFunctionAndIntervals(), 198775297232878);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
index 8de90ab899..28001c5ebc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
@@ -1,6 +1,6 @@
---
id: 5900f53d1000cf542c510050
-title: 'Problem 465: Polar polygons'
+title: '問題 465: 極の多角形'
challengeType: 5
forumTopicId: 302140
dashedName: problem-465-polar-polygons
@@ -8,27 +8,27 @@ dashedName: problem-465-polar-polygons
# --description--
-The kernel of a polygon is defined by the set of points from which the entire polygon's boundary is visible. We define a polar polygon as a polygon for which the origin is strictly contained inside its kernel.
+多角形の核は、その多角形の全範囲をそこから見渡せるような点の集合として定義されます。 原点が核の中に厳密に含まれている多角形を「極の多角形」と定義します。
-For this problem, a polygon can have collinear consecutive vertices. However, a polygon still cannot have self-intersection and cannot have zero area.
+この問題では、多角形は同一線上に連続する頂点を持つことができます。 しかし、多角形は自己交差してはならず、面積が 0 であってはいけません。
-For example, only the first of the following is a polar polygon (the kernels of the second, third, and fourth do not strictly contain the origin, and the fifth does not have a kernel at all):
+例えば、次のうち 1 つ目だけが極の多角形です (2 つ目、3 つ目、4 つ目の多角形の核は厳密には原点を含んでおらず、5 つ目には核が全くありません)。
-
-Let $F(d)$ be the total required time if the ant chooses the quickest path. For example, $F(4) ≈ 2.960\\,516\\,287$. We can verify that $F(10) ≈ 4.668\\,187\\,834$ and $F(100) ≈ 9.217\\,221\\,972$.
+アリが最速経路を選んだ場合の合計所要時間を $F(d)$ とします。 例えば、$F(4) ≈ 2.960\\,516\\,287$ です。 $F(10) ≈ 4.668\\,187\\,834$, $F(100) ≈ 9.217\\,221\\,972$ であることを確認できます。
-Find $F(10\\,000)$. Give your answer rounded to nine decimal places.
+$F(10\\,000)$ を求めなさい。 回答は、四捨五入して小数第 9 位まで示すこと。
# --hints--
-`antOnTheMove()` should return `18.420738199`.
+`antOnTheMove()` は `18.420738199` を返す必要があります。
```js
assert.strictEqual(antOnTheMove(), 18.420738199);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md
index 9903fbe010..1ec9c45f62 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-461-almost-pi.md
@@ -1,6 +1,6 @@
---
id: 5900f53a1000cf542c51004c
-title: 'Problem 461: Almost Pi'
+title: '問題 461: ほぼ Pi'
challengeType: 5
forumTopicId: 302136
dashedName: problem-461-almost-pi
@@ -8,43 +8,43 @@ dashedName: problem-461-almost-pi
# --description--
-Let `f(k, n)` = $e^\frac{k}{n} - 1$, for all non-negative integers `k`.
+すべての非負整数 `k` に対して `f(k, n)` = $e^\frac{k}{n} - 1$ と定義します。
-Remarkably, `f(6, 200) + f(75, 200) + f(89, 200) + f(226, 200)` = 3.1415926… ≈ π.
+驚くべきことに、`f(6, 200) + f(75, 200) + f(89, 200) + f(226, 200)` = 3.1415926… ≈ π となります。
-In fact, it is the best approximation of π of the form `f(a, 200) + f(b, 200) + f(c, 200) + f(d, 200)`.
+実際、これは式 `f(a, 200) + f(b, 200) + f(c, 200) + f(d, 200)` の π の最良近似です。
-Let `almostPi(n)` = a2 + b2 + c2 + d2 for a, b, c, d that minimize the error: $\lvert f(a,n) + f(b,n) + f(c,n) + f(d,n) - \Pi\rvert$
+誤差 $\lvert f(a,n) + f(b,n) + f(c,n) + f(d,n) - \Pi\rvert$ が最小となる a, b, c, d に対して、`almostPi(n)` = a2 + b2 + c2 + d2 と定義します。
-You are given `almostPi(200)` = 62 + 752 + 892 + 2262 = 64658.
+`almostPi(200)` = 62 + 752 + 892 + 2262 = 64658 が与えられます。
# --hints--
-`almostPi` should be a function.
+`almostPi` は関数でなければなりません。
```js
assert(typeof almostPi === 'function')
```
-`almostPi` should return a number.
+`almostPi` は数値を返す必要があります。
```js
assert.strictEqual(typeof almostPi(10), 'number');
```
-`almostPi(29)` should return `1208`.
+`almostPi(29)` は `1208` を返す必要があります。
```js
assert.strictEqual(almostPi(29), 1208);
```
-`almostPi(50)` should return `4152`.
+`almostPi(50)` は `4152` を返す必要があります。
```js
assert.strictEqual(almostPi(50), 4152);
```
-`almostPi(200)` should return `64658`.
+`almostPi(200)` は `64658` を返す必要があります。
```js
assert.strictEqual(almostPi(200), 64658);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
index 550715f701..8c04e8e694 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-462-permutation-of-3-smooth-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f53b1000cf542c51004d
-title: 'Problem 462: Permutation of 3-smooth numbers'
+title: '問題 462: 3-smooth 数の順列'
challengeType: 5
forumTopicId: 302137
dashedName: problem-462-permutation-of-3-smooth-numbers
@@ -8,31 +8,31 @@ dashedName: problem-462-permutation-of-3-smooth-numbers
# --description--
-A 3-smooth number is an integer which has no prime factor larger than 3. For an integer $N$, we define $S(N)$ as the set of 3-smooth numbers less than or equal to $N$. For example, $S(20) = \\{1, 2, 3, 4, 6, 8, 9, 12, 16, 18\\}$.
+3-smooth 数とは、3 より大きい素因数を持たない整数のことです。 整数 $N$ に対して、$N$ 以下の 3-smooth 数の集合を $S(N)$ とします。 例えば、$S(20) = \\{1, 2, 3, 4, 6, 8, 9, 12, 16, 18\\}$ です。
-We define $F(N)$ as the number of permutations of $S(N)$ in which each element comes after all of its proper divisors.
+各要素のすべての真の約数の後にその要素が現れるような $S(N)$ の順列の個数を、$F(N)$ とします。
-This is one of the possible permutations for $N = 20$.
+$N = 20$ に対して考えられる順列の一例を下に示します。
-- 1, 2, 4, 3, 9, 8, 16, 6, 18, 12.
+- 1, 2, 4, 3, 9, 8, 16, 6, 18, 12
-This is not a valid permutation because 12 comes before its divisor 6.
+下の例は、12 が約数 6 の前に現れるので有効な順列ではありません。
-- 1, 2, 4, 3, 9, 8, 12, 16, 6, 18.
+- 1, 2, 4, 3, 9, 8, 12, 16, 6, 18
-We can verify that $F(6) = 5$, $F(8) = 9$, $F(20) = 450$ and $F(1000) ≈ 8.8521816557e\\,21$.
+$F(6) = 5$, $F(8) = 9$, $F(20) = 450$, $F(1000) ≈ 8.8521816557e\\21$ であることを確認できます。
-Find $F({10}^{18})$. Give as your answer as a string in its scientific notation rounded to ten digits after the decimal point. When giving your answer, use a lowercase `e` to separate mantissa and exponent. E.g. if the answer is $112\\,233\\,445\\,566\\,778\\,899$ then the answer format would be `1.1223344557e17`.
+$F({10}^{18})$ を求めなさい。 回答は、科学的記数法による文字列を四捨五入して小数第 10 位まで示すこと。 回答は、小文字 `e` で仮数部と指数部を区切って書くこと。 例えば、 答えが $112\\,233\\,445\\,566\\,778\\,899$ の場合、`1.1223344557e17` の形式にします。
# --hints--
-`permutationOf3SmoothNumbers()` should return a string.
+`permutationOf3SmoothNumbers()` は文字列を返す必要があります。
```js
assert.strictEqual(typeof permutationOf3SmoothNumbers() === 'string');
```
-`permutationOf3SmoothNumbers()` should return the string `5.5350769703e1512`.
+`permutationOf3SmoothNumbers()` は文字列 `5.5350769703e1512` を返す必要があります。
```js
assert.strictEqual(permutationOf3SmoothNumbers(), '5.5350769703e1512');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
index 159aacceb3..d699d8d745 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-463-a-weird-recurrence-relation.md
@@ -1,6 +1,6 @@
---
id: 5900f53c1000cf542c51004e
-title: 'Problem 463: A weird recurrence relation'
+title: '問題 463: 風変わりな漸化式'
challengeType: 5
forumTopicId: 302138
dashedName: problem-463-a-weird-recurrence-relation
@@ -8,19 +8,19 @@ dashedName: problem-463-a-weird-recurrence-relation
# --description--
-The function $f$ is defined for all positive integers as follows:
+すべての正の整数に対して関数 $f$ が次のように定義されます。
$$\begin{align} & f(1) = 1 \\\\ & f(3) = 3 \\\\ & f(2n) = f(n) \\\\ & f(4n + 1) = 2f(2n + 1) - f(n) \\\\ & f(4n + 3) = 3f(2n + 1) - 2f(n) \end{align}$$
-The function $S(n)$ is defined as $\sum_{i=1}^{n} f(i)$.
+関数 $S(n)$ は $\sum_{i=1}^{n} f(i)$ と定義されます。
-$S(8) = 22$ and $S(100) = 3604$.
+$S(8) = 22$, $S(100) = 3604$ です。
-Find $S(3^{37})$. Give the last 9 digits of your answer.
+$S(3^{37})$ を求めなさい。 回答は、下位 9 桁とすること。
# --hints--
-`weirdRecurrenceRelation()` should return `808981553`.
+`weirdRecurrenceRelation()` は `808981553` を返す必要があります。
```js
assert.strictEqual(weirdRecurrenceRelation(), 808981553);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
index 2e12caa276..3946777551 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-464-mbius-function-and-intervals.md
@@ -1,6 +1,6 @@
---
id: 5900f53d1000cf542c51004f
-title: 'Problem 464: Möbius function and intervals'
+title: '問題 464: メビウス関数と区間'
challengeType: 5
forumTopicId: 302139
dashedName: problem-464-mbius-function-and-intervals
@@ -8,30 +8,30 @@ dashedName: problem-464-mbius-function-and-intervals
# --description--
-The Möbius function, denoted $μ(n)$, is defined as:
+$μ(n)$ で表されるメビウス関数は次のように定義されます。
-- $μ(n) = (-1)^{ω(n)}$ if $n$ is squarefree (where $ω(n)$ is the number of distinct prime factors of $n$)
-- $μ(n) = 0$ if $n$ is not squarefree.
+- $n$ が無平方数のとき、$μ(n) = (-1)^{ω(n)}$ (ここで、$ω(n)$ は $n$ の相異なる素因数)
+- $n$ が無平方数でないとき、$μ(n) = 0$
-Let $P(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = 1$.
+区間 $[a, b]$ において $μ(n) = 1$ となる整数 $n$ の数を、$P(a, b)$ とします。
-Let $N(a, b)$ be the number of integers $n$ in the interval $[a, b]$ such that $μ(n) = -1$.
+区間 $[a, b]$ において $μ(n) = -1$ となる整数 $n$ の数を、$N(a, b)$ とします。
-For example, $P(2, 10) = 2$ and $N(2, 10) = 4$.
+例えば、$P(2, 10) = 2$, $N(2, 10) = 4$ です。
-Let $C(n)$ be the number of integer pairs $(a, b)$ such that:
+次の条件をすべて満たす整数の対 $(a, b)$ を $C(n)$ とします。
-- $1 ≤ a ≤ b ≤ n$,
-- $99 \times N(a, b) ≤ 100 \times P(a, b)$, and
-- $99 \times P(a, b) ≤ 100 \times N(a, b)$.
+- $1 ≤ a ≤ b ≤ n$
+- $99 \times N(a, b) ≤ 100 \times P(a, b)$
+- $99 \times P(a, b) ≤ 100 \times N(a, b)$
-For example, $C(10) = 13$, $C(500) = 16\\,676$ and $C(10\\,000) = 20\\,155\\,319$.
+例えば、$C(10) = 13$, $C(500) = 16\\,676$, $C(10\\,000) = 20\\,155\\,319$ です。
-Find $C(20\\,000\\,000)$.
+$C(20\\,000\\,000)$ を求めなさい。
# --hints--
-`mobiusFunctionAndIntervals()` should return `198775297232878`.
+`mobiusFunctionAndIntervals()` は `198775297232878` を返す必要があります。
```js
assert.strictEqual(mobiusFunctionAndIntervals(), 198775297232878);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
index 8de90ab899..28001c5ebc 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-465-polar-polygons.md
@@ -1,6 +1,6 @@
---
id: 5900f53d1000cf542c510050
-title: 'Problem 465: Polar polygons'
+title: '問題 465: 極の多角形'
challengeType: 5
forumTopicId: 302140
dashedName: problem-465-polar-polygons
@@ -8,27 +8,27 @@ dashedName: problem-465-polar-polygons
# --description--
-The kernel of a polygon is defined by the set of points from which the entire polygon's boundary is visible. We define a polar polygon as a polygon for which the origin is strictly contained inside its kernel.
+多角形の核は、その多角形の全範囲をそこから見渡せるような点の集合として定義されます。 原点が核の中に厳密に含まれている多角形を「極の多角形」と定義します。
-For this problem, a polygon can have collinear consecutive vertices. However, a polygon still cannot have self-intersection and cannot have zero area.
+この問題では、多角形は同一線上に連続する頂点を持つことができます。 しかし、多角形は自己交差してはならず、面積が 0 であってはいけません。
-For example, only the first of the following is a polar polygon (the kernels of the second, third, and fourth do not strictly contain the origin, and the fifth does not have a kernel at all):
+例えば、次のうち 1 つ目だけが極の多角形です (2 つ目、3 つ目、4 つ目の多角形の核は厳密には原点を含んでおらず、5 つ目には核が全くありません)。
-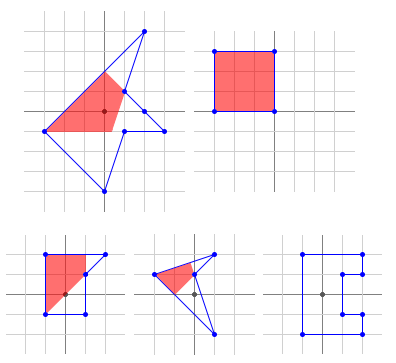 +
+ -Notice that the first polygon has three consecutive collinear vertices.
+1 つ目の多角形で、3 つの頂点が同一線上で連続していることに注目してください。
-Let $P(n)$ be the number of polar polygons such that the vertices $(x, y)$ have integer coordinates whose absolute values are not greater than $n$.
+絶対値が $n$ を超えない整数座標 $(x, y)$ に頂点があるような極の多角形の個数を、$P(n)$ とします。
-Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices [(0,0), (0,3), (1,1), (3,0)] is distinct from the polygon with vertices [(0,0), (0,3), (1,1), (3,0), (1,0)].
+注意点として、たとえ同じ領域を囲んでいても、辺の集合が異なる多角形は区別して数えられます。 例えば、[(0,0), (0,3), (1,1), (3,0)] を頂点とする多角形は、[(0,0), (0,3), (1,1), (3,0), (1,0)] を頂点とする多角形と区別されます。
-For example, $P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$ and $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$.
+例えば、$P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$, $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$ です。
-Find $P(7^{13})\bmod 1\\,000\\,000\\,007$.
+$P(7^{13})\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`polarPolygons()` should return `585965659`.
+`polarPolygons()` は `585965659` を返す必要があります。
```js
assert.strictEqual(polarPolygons(), 585965659);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
index 8e39b55b74..c6b84f0d53 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
@@ -1,6 +1,6 @@
---
id: 5900f53e1000cf542c510051
-title: 'Problem 466: Distinct terms in a multiplication table'
+title: '問題 466: 掛け算表の相異なる項'
challengeType: 5
forumTopicId: 302141
dashedName: problem-466-distinct-terms-in-a-multiplication-table
@@ -8,23 +8,23 @@ dashedName: problem-466-distinct-terms-in-a-multiplication-table
# --description--
-Let $P(m,n)$ be the number of distinct terms in an $m×n$ multiplication table.
+$m×n$ の掛け算表の相異なる項の個数を $P(m,n)$ とします。
-For example, a 3×4 multiplication table looks like this:
+例えば、3×4 の掛け算表は次のようになります。
$$\begin{array}{c} × & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} \\\\ \mathbf{1} & 1 & 2 & 3 & 4 \\\\ \mathbf{2} & 2 & 4 & 6 & 8 \\\\ \mathbf{3} & 3 & 6 & 9 & 12 \end{array}$$
-There are 8 distinct terms {1, 2, 3, 4, 6, 8, 9, 12}, therefore $P(3, 4) = 8$.
+8 つの相異なる項 {1, 2, 3, 4, 6, 8, 9, 12} があるので、$P(3, 4) = 8$ です。
-You are given that:
+次が与えられます。
-$$\begin{align} & P(64, 64) = 1\\,263, \\\\ & P(12, 345) = 1\\,998, \text{ and} \\\\ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302. \\\\ \end{align}$$
+$$\begin{align} & P(64, 64) = 1\\,263\\\\ & P(12, 345) = 1\\,998 \text{ および} \\\\ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302 \\\\ \end{align}$$
-Find $P(64, {10}^{16})$.
+$P(64, {10}^{16})$ を求めなさい。
# --hints--
-`multiplicationTable()` should return `258381958195474750`.
+`multiplicationTable()` は `258381958195474750` を返す必要があります。
```js
assert.strictEqual(multiplicationTable(), 258381958195474750);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md
index 6c0d5894ec..4bec04a004 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md
@@ -1,6 +1,6 @@
---
id: 5900f5411000cf542c510052
-title: 'Problem 467: Superinteger'
+title: '問題 467: 超越整数'
challengeType: 5
forumTopicId: 302142
dashedName: problem-467-superinteger
@@ -8,29 +8,29 @@ dashedName: problem-467-superinteger
# --description--
-An integer $s$ is called a superinteger of another integer $n$ if the digits of $n$ form a subsequence of the digits of $s$.
+整数 $n$ の数字が別の整数 $s$ の数字の部分列になる場合、整数 $s$ を整数 $n$ の「超越整数」と呼ぶことにします。
-For example, 2718281828 is a superinteger of 18828, while 314159 is not a superinteger of 151.
+例えば、2718281828 は 18828 の超越整数ですが、314159 は 151 の超越整数ではありません。
-Let $p(n)$ be the $n$th prime number, and let $c(n)$ be the $n$th composite number. For example, $p(1) = 2$, $p(10) = 29$, $c(1) = 4$ and $c(10) = 18$.
+$p(n)$ を $n$ 番目の素数とし、$c(n)$ を $n$ 番目の合成数とします。 例えば、$p(1) = 2$, $p(10) = 29$, $c(1) = 4$, $c(10) = 18$ です。
$$\begin{align} & \\{p(i) : i ≥ 1\\} = \\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots \\} \\\\ & \\{c(i) : i ≥ 1\\} = \\{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, \ldots \\} \end{align}$$
-Let $P^D$ the sequence of the digital roots of $\\{p(i)\\}$ ($C^D$ is defined similarly for $\\{c(i)\\}$):
+$\\{p(i)\\}$ の数字根からなる数列を $P^D$ とすると、次のようになります ($C^D$ は $\\{c(i)\\}$ に対して同様に定義されます)。
$$\begin{align} & P^D = \\{2, 3, 5, 7, 2, 4, 8, 1, 5, 2, \ldots \\} \\\\ & C^D = \\{4, 6, 8, 9, 1, 3, 5, 6, 7, 9, \ldots \\} \end{align}$$
-Let $P_n$ be the integer formed by concatenating the first $n$ elements of $P^D$ ($C_n$ is defined similarly for $C^D$).
+$P^D$ の最初の $n$ 個の要素をつなげた整数を $P_n$ とします ($C_n$ は $C^D$ に対して同様に定義されます)。
$$\begin{align} & P_{10} = 2\\,357\\,248\\,152 \\\\ & C_{10} = 4\\,689\\,135\\,679 \end{align}$$
-Let $f(n)$ be the smallest positive integer that is a common superinteger of $P_n$ and $C_n$. For example, $f(10) = 2\\,357\\,246\\,891\\,352\\,679$, and $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$.
+$P_n$ と $C_n$ の共通の超越整数である最小の正の整数を、$f(n)$ とします。 例えば、$f(10) = 2\\,357\\,246\\,891\\,352\\,679$, $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$ です。
-Find $f(10\\,000)\bmod 1\\,000\\,000\\,007$.
+$f(10\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`superinteger()` should return `775181359`.
+`superinteger()` は `775181359` を返す必要があります。
```js
assert.strictEqual(superinteger(), 775181359);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
index 54837616df..8ce0c4ae11 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
@@ -1,6 +1,6 @@
---
id: 5900f5411000cf542c510054
-title: 'Problem 468: Smooth divisors of binomial coefficients'
+title: '問題 468: 二項係数の Smooth 約数'
challengeType: 5
forumTopicId: 302143
dashedName: problem-468-smooth-divisors-of-binomial-coefficients
@@ -8,25 +8,25 @@ dashedName: problem-468-smooth-divisors-of-binomial-coefficients
# --description--
-An integer is called B-smooth if none of its prime factors is greater than $B$.
+$B$ より大きい素因数を持たない整数は B-smooth と呼ばれます。
-Let $SB(n)$ be the largest B-smooth divisor of $n$.
+$n$ の最大の B-smooth 約数を $SB(n)$ とします。
-Examples:
+例:
$$\begin{align} & S_1(10) = 1 \\\\ & S_4(2\\,100) = 12 \\\\ & S_{17}(2\\,496\\,144) = 5\\,712 \end{align}$$
-Define $F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$. Here, $\displaystyle\binom{n}{r}$ denotes the binomial coefficient.
+$F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$ と定義します。 ここで、$\displaystyle\binom{n}{r}$ は二項係数を表します。
-Examples:
+例:
$$\begin{align} & F(11) = 3132 \\\\ & F(1\\,111)\bmod 1\\,000\\,000\\,993 = 706\\,036\\,312 \\\\ & F(111\\,111)\bmod 1\\,000\\,000\\,993 = 22\\,156\\,169 \end{align}$$
-Find $F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$.
+$F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$ を求めなさい。
# --hints--
-`smoothDivisorsOfBinomialCoefficients()` should return `852950321`.
+`smoothDivisorsOfBinomialCoefficients()` は `852950321` を返す必要があります。
```js
assert.strictEqual(smoothDivisorsOfBinomialCoefficients(), 852950321);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
index d1db21f4f4..569938bd53 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
@@ -1,6 +1,6 @@
---
id: 5900f5411000cf542c510053
-title: 'Problem 469: Empty chairs'
+title: '問題 469: 空席'
challengeType: 5
forumTopicId: 302144
dashedName: problem-469-empty-chairs
@@ -8,21 +8,21 @@ dashedName: problem-469-empty-chairs
# --description--
-In a room $N$ chairs are placed around a round table.
+部屋の中の円卓の周りに $N$ 脚の椅子が置かれています。
-Knights enter the room one by one and choose at random an available empty chair.
+騎士が部屋に 1 人ずつ入り、座って良い空席を無作為に選びます。
-To have enough elbow room the knights always leave at least one empty chair between each other.
+肘を置く余裕を十分持たせるために、騎士達は常に互いの間で少なくとも 1 脚の椅子を空席のままにします。
-When there aren't any suitable chairs left, the fraction $C$ of empty chairs is determined. We also define $E(N)$ as the expected value of $C$.
+座って良い椅子がなくなったとき、空席の割合 $C$ が決まります。 また、$C$ の期待値を $E(N)$ とします。
-We can verify that $E(4) = \frac{1}{2}$ and $E(6) = \frac{5}{9}$.
+$E(4) = \frac{1}{2}$, $E(6) = \frac{5}{9} $ であることを確認できます。
-Find $E({10}^{18})$. Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
+$E({10}^{18})$ を求めなさい。 回答は、四捨五入して小数第 14 位まで求め、0.abcdefghijklmn の形式にすること。
# --hints--
-`emptyChairs()` should return `0.56766764161831`.
+`emptyChairs()` は `0.56766764161831` を返す必要があります。
```js
assert.strictEqual(emptyChairs(), 0.56766764161831);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
index a8f59ece37..2a30df1638 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
@@ -1,6 +1,6 @@
---
id: 5900f5431000cf542c510055
-title: 'Problem 470: Super Ramvok'
+title: '問題 470: スーパー Ramvok'
challengeType: 5
forumTopicId: 302146
dashedName: problem-470-super-ramvok
@@ -8,23 +8,23 @@ dashedName: problem-470-super-ramvok
# --description--
-Consider a single game of Ramvok:
+Ramvok というゲームを 1 回プレイすることについて考えます。
-Let $t$ represent the maximum number of turns the game lasts. If $t = 0$, then the game ends immediately. Otherwise, on each turn $i$, the player rolls a die. After rolling, if $i < t$ the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If $i = t$, then the roll cannot be discarded and the prize must be accepted. Before the game begins, $t$ is chosen by the player, who must then pay an up-front cost $ct$ for some constant $c$. For $c = 0$, $t$ can be chosen to be infinite (with an up-front cost of 0). Let $R(d, c)$ be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair $d$-sided die and cost constant $c$. For example, $R(4, 0.2) = 2.65$. Assume that the player has sufficient funds for paying any/all up-front costs.
+ゲームが続いている間のターンの最大数を $t$ とします。 $t = 0$ の場合、ゲームはすぐに終了します。 それ以外の場合、各ターン $i$ でプレイヤーがサイコロを振ります。 サイコロを振った後、$i < t$ の場合は、そのプレイヤーはゲームをやめてサイコロの目と同額の賞金を受け取るか、または、出目を捨てて次のターンで再挑戦することができます。 $i = t$の場合、出目を捨てることはできず、賞金を受け入れなければなりません。 ゲーム開始前、プレイヤーは $t$ を選び、そのプレイヤーはある定数 $c$ に対して前金 $ct$ を支払う必要があります。 $c = 0$ の場合、(前金なしで) $t$ を無制限にすることを選択できます 。 偏りのない $d$ 面のサイコロとコスト定数 $c$ が与えられるとき、Ramvok のゲームを最適に 1 回プレイすることでプレイヤーが受け取る期待利益 (純利益) を $R(d, c)$ とします。 例えば、$R(4, 0.2) = 2.65$ です。 プレイヤーが前金をいくらでも支払えるほどの資金を持っていると仮定します。
-Now consider a game of Super Ramvok:
+次に、スーパー Ramvok を 1 回プレイすることについて考えます。
-In Super Ramvok, the game of Ramvok is played repeatedly, but with a slight modification. After each game, the die is altered. The alteration process is as follows: The die is rolled once, and if the resulting face has its pips visible, then that face is altered to be blank instead. If the face is already blank, then it is changed back to its original value. After the alteration is made, another game of Ramvok can begin (and during such a game, at each turn, the die is rolled until a face with a value on it appears). The player knows which faces are blank and which are not at all times. The game of Super Ramvok ends once all faces of the die are blank.
+スーパー Ramvokでも Ramvok のゲームが繰り返し行われますが、ルールが少し異なります。 各ゲームの後、サイコロが変更されるのです。 変更のプロセスは次のとおりです。サイコロが 1 回振られ、上になった面に目があれば、その面は目のない面に変えられます。 上になった面がすでに空白の場合は、元の目の値に戻されます。 変更が行われた後、Ramvok ゲームの次の 1 回をスタートできます (そのような 1 回のゲーム中に、各ターンで、目のある面が出るまでサイコロを振ります)。 プレイヤーは、どの面が空白で、どの面が空白でないかを常に知っています。 スーパー Ramvok のゲームは、サイコロのすべての面が空白になると終了です。
-Let $S(d, c)$ be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair $d$-sided die to start (with all sides visible), and cost constant $c$. For example, $S(6, 1) = 208.3$.
+偏りのない $d$ 面のサイコロ (開始時はすべての面に目がある) とコスト定数 $c$ が与えられるとき、スーパー Ramvok を最適に 1 回プレイすることでプレイヤーが受け取る期待利益を $S(d, c)$ とします。 例えば、$S(6, 1) = 208.3$ です。
-Let $F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$.
+$F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$ と定義します。
-Calculate $F(20)$, rounded to the nearest integer.
+$F(20)$ を計算し、最も近い整数に四捨五入して答えなさい。
# --hints--
-`superRamvok()` should return `147668794`.
+`superRamvok()` は `147668794` を返す必要があります。
```js
assert.strictEqual(superRamvok(), 147668794);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
index 250ddfce2d..b27f8c698d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
@@ -1,6 +1,6 @@
---
id: 5900f5431000cf542c510056
-title: 'Problem 471: Triangle inscribed in ellipse'
+title: '問題 471: 楕円に内接する三角形'
challengeType: 5
forumTopicId: 302148
dashedName: problem-471-triangle-inscribed-in-ellipse
@@ -8,33 +8,33 @@ dashedName: problem-471-triangle-inscribed-in-ellipse
# --description--
-The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
+$0 < 2b < a$ を満たす整数 $a$, $b$ について、三角形 $ΔABC$ は式 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ で表される楕円に内接しています。
-Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
+三角形 $ΔABC$ の内接円の中心が $(2b, 0)$ で、$A$ の座標が $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$ のとき、その内接円の半径を $r(a, b)$ とします。
-For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
+たとえば、$r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$ です。
-
-Notice that the first polygon has three consecutive collinear vertices.
+1 つ目の多角形で、3 つの頂点が同一線上で連続していることに注目してください。
-Let $P(n)$ be the number of polar polygons such that the vertices $(x, y)$ have integer coordinates whose absolute values are not greater than $n$.
+絶対値が $n$ を超えない整数座標 $(x, y)$ に頂点があるような極の多角形の個数を、$P(n)$ とします。
-Note that polygons should be counted as different if they have different set of edges, even if they enclose the same area. For example, the polygon with vertices [(0,0), (0,3), (1,1), (3,0)] is distinct from the polygon with vertices [(0,0), (0,3), (1,1), (3,0), (1,0)].
+注意点として、たとえ同じ領域を囲んでいても、辺の集合が異なる多角形は区別して数えられます。 例えば、[(0,0), (0,3), (1,1), (3,0)] を頂点とする多角形は、[(0,0), (0,3), (1,1), (3,0), (1,0)] を頂点とする多角形と区別されます。
-For example, $P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$ and $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$.
+例えば、$P(1) = 131$, $P(2) = 1\\,648\\,531$, $P(3) = 1\\,099\\,461\\,296\\,175$, $P(343)\bmod 1\\,000\\,000\\,007 = 937\\,293\\,740$ です。
-Find $P(7^{13})\bmod 1\\,000\\,000\\,007$.
+$P(7^{13})\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`polarPolygons()` should return `585965659`.
+`polarPolygons()` は `585965659` を返す必要があります。
```js
assert.strictEqual(polarPolygons(), 585965659);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
index 8e39b55b74..c6b84f0d53 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-466-distinct-terms-in-a-multiplication-table.md
@@ -1,6 +1,6 @@
---
id: 5900f53e1000cf542c510051
-title: 'Problem 466: Distinct terms in a multiplication table'
+title: '問題 466: 掛け算表の相異なる項'
challengeType: 5
forumTopicId: 302141
dashedName: problem-466-distinct-terms-in-a-multiplication-table
@@ -8,23 +8,23 @@ dashedName: problem-466-distinct-terms-in-a-multiplication-table
# --description--
-Let $P(m,n)$ be the number of distinct terms in an $m×n$ multiplication table.
+$m×n$ の掛け算表の相異なる項の個数を $P(m,n)$ とします。
-For example, a 3×4 multiplication table looks like this:
+例えば、3×4 の掛け算表は次のようになります。
$$\begin{array}{c} × & \mathbf{1} & \mathbf{2} & \mathbf{3} & \mathbf{4} \\\\ \mathbf{1} & 1 & 2 & 3 & 4 \\\\ \mathbf{2} & 2 & 4 & 6 & 8 \\\\ \mathbf{3} & 3 & 6 & 9 & 12 \end{array}$$
-There are 8 distinct terms {1, 2, 3, 4, 6, 8, 9, 12}, therefore $P(3, 4) = 8$.
+8 つの相異なる項 {1, 2, 3, 4, 6, 8, 9, 12} があるので、$P(3, 4) = 8$ です。
-You are given that:
+次が与えられます。
-$$\begin{align} & P(64, 64) = 1\\,263, \\\\ & P(12, 345) = 1\\,998, \text{ and} \\\\ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302. \\\\ \end{align}$$
+$$\begin{align} & P(64, 64) = 1\\,263\\\\ & P(12, 345) = 1\\,998 \text{ および} \\\\ & P(32, {10}^{15}) = 13\\,826\\,382\\,602\\,124\\,302 \\\\ \end{align}$$
-Find $P(64, {10}^{16})$.
+$P(64, {10}^{16})$ を求めなさい。
# --hints--
-`multiplicationTable()` should return `258381958195474750`.
+`multiplicationTable()` は `258381958195474750` を返す必要があります。
```js
assert.strictEqual(multiplicationTable(), 258381958195474750);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md
index 6c0d5894ec..4bec04a004 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-467-superinteger.md
@@ -1,6 +1,6 @@
---
id: 5900f5411000cf542c510052
-title: 'Problem 467: Superinteger'
+title: '問題 467: 超越整数'
challengeType: 5
forumTopicId: 302142
dashedName: problem-467-superinteger
@@ -8,29 +8,29 @@ dashedName: problem-467-superinteger
# --description--
-An integer $s$ is called a superinteger of another integer $n$ if the digits of $n$ form a subsequence of the digits of $s$.
+整数 $n$ の数字が別の整数 $s$ の数字の部分列になる場合、整数 $s$ を整数 $n$ の「超越整数」と呼ぶことにします。
-For example, 2718281828 is a superinteger of 18828, while 314159 is not a superinteger of 151.
+例えば、2718281828 は 18828 の超越整数ですが、314159 は 151 の超越整数ではありません。
-Let $p(n)$ be the $n$th prime number, and let $c(n)$ be the $n$th composite number. For example, $p(1) = 2$, $p(10) = 29$, $c(1) = 4$ and $c(10) = 18$.
+$p(n)$ を $n$ 番目の素数とし、$c(n)$ を $n$ 番目の合成数とします。 例えば、$p(1) = 2$, $p(10) = 29$, $c(1) = 4$, $c(10) = 18$ です。
$$\begin{align} & \\{p(i) : i ≥ 1\\} = \\{2, 3, 5, 7, 11, 13, 17, 19, 23, 29, \ldots \\} \\\\ & \\{c(i) : i ≥ 1\\} = \\{4, 6, 8, 9, 10, 12, 14, 15, 16, 18, \ldots \\} \end{align}$$
-Let $P^D$ the sequence of the digital roots of $\\{p(i)\\}$ ($C^D$ is defined similarly for $\\{c(i)\\}$):
+$\\{p(i)\\}$ の数字根からなる数列を $P^D$ とすると、次のようになります ($C^D$ は $\\{c(i)\\}$ に対して同様に定義されます)。
$$\begin{align} & P^D = \\{2, 3, 5, 7, 2, 4, 8, 1, 5, 2, \ldots \\} \\\\ & C^D = \\{4, 6, 8, 9, 1, 3, 5, 6, 7, 9, \ldots \\} \end{align}$$
-Let $P_n$ be the integer formed by concatenating the first $n$ elements of $P^D$ ($C_n$ is defined similarly for $C^D$).
+$P^D$ の最初の $n$ 個の要素をつなげた整数を $P_n$ とします ($C_n$ は $C^D$ に対して同様に定義されます)。
$$\begin{align} & P_{10} = 2\\,357\\,248\\,152 \\\\ & C_{10} = 4\\,689\\,135\\,679 \end{align}$$
-Let $f(n)$ be the smallest positive integer that is a common superinteger of $P_n$ and $C_n$. For example, $f(10) = 2\\,357\\,246\\,891\\,352\\,679$, and $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$.
+$P_n$ と $C_n$ の共通の超越整数である最小の正の整数を、$f(n)$ とします。 例えば、$f(10) = 2\\,357\\,246\\,891\\,352\\,679$, $f(100)\bmod 1\\,000\\,000\\,007 = 771\\,661\\,825$ です。
-Find $f(10\\,000)\bmod 1\\,000\\,000\\,007$.
+$f(10\\,000)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`superinteger()` should return `775181359`.
+`superinteger()` は `775181359` を返す必要があります。
```js
assert.strictEqual(superinteger(), 775181359);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
index 54837616df..8ce0c4ae11 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-468-smooth-divisors-of-binomial-coefficients.md
@@ -1,6 +1,6 @@
---
id: 5900f5411000cf542c510054
-title: 'Problem 468: Smooth divisors of binomial coefficients'
+title: '問題 468: 二項係数の Smooth 約数'
challengeType: 5
forumTopicId: 302143
dashedName: problem-468-smooth-divisors-of-binomial-coefficients
@@ -8,25 +8,25 @@ dashedName: problem-468-smooth-divisors-of-binomial-coefficients
# --description--
-An integer is called B-smooth if none of its prime factors is greater than $B$.
+$B$ より大きい素因数を持たない整数は B-smooth と呼ばれます。
-Let $SB(n)$ be the largest B-smooth divisor of $n$.
+$n$ の最大の B-smooth 約数を $SB(n)$ とします。
-Examples:
+例:
$$\begin{align} & S_1(10) = 1 \\\\ & S_4(2\\,100) = 12 \\\\ & S_{17}(2\\,496\\,144) = 5\\,712 \end{align}$$
-Define $F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$. Here, $\displaystyle\binom{n}{r}$ denotes the binomial coefficient.
+$F(n) = \displaystyle\sum_{B = 1}^n \sum_{r = 0}^n S_B(\displaystyle\binom{n}{r})$ と定義します。 ここで、$\displaystyle\binom{n}{r}$ は二項係数を表します。
-Examples:
+例:
$$\begin{align} & F(11) = 3132 \\\\ & F(1\\,111)\bmod 1\\,000\\,000\\,993 = 706\\,036\\,312 \\\\ & F(111\\,111)\bmod 1\\,000\\,000\\,993 = 22\\,156\\,169 \end{align}$$
-Find $F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$.
+$F(11\\,111\\,111)\bmod 1\\,000\\,000\\,993$ を求めなさい。
# --hints--
-`smoothDivisorsOfBinomialCoefficients()` should return `852950321`.
+`smoothDivisorsOfBinomialCoefficients()` は `852950321` を返す必要があります。
```js
assert.strictEqual(smoothDivisorsOfBinomialCoefficients(), 852950321);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
index d1db21f4f4..569938bd53 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-469-empty-chairs.md
@@ -1,6 +1,6 @@
---
id: 5900f5411000cf542c510053
-title: 'Problem 469: Empty chairs'
+title: '問題 469: 空席'
challengeType: 5
forumTopicId: 302144
dashedName: problem-469-empty-chairs
@@ -8,21 +8,21 @@ dashedName: problem-469-empty-chairs
# --description--
-In a room $N$ chairs are placed around a round table.
+部屋の中の円卓の周りに $N$ 脚の椅子が置かれています。
-Knights enter the room one by one and choose at random an available empty chair.
+騎士が部屋に 1 人ずつ入り、座って良い空席を無作為に選びます。
-To have enough elbow room the knights always leave at least one empty chair between each other.
+肘を置く余裕を十分持たせるために、騎士達は常に互いの間で少なくとも 1 脚の椅子を空席のままにします。
-When there aren't any suitable chairs left, the fraction $C$ of empty chairs is determined. We also define $E(N)$ as the expected value of $C$.
+座って良い椅子がなくなったとき、空席の割合 $C$ が決まります。 また、$C$ の期待値を $E(N)$ とします。
-We can verify that $E(4) = \frac{1}{2}$ and $E(6) = \frac{5}{9}$.
+$E(4) = \frac{1}{2}$, $E(6) = \frac{5}{9} $ であることを確認できます。
-Find $E({10}^{18})$. Give your answer rounded to fourteen decimal places in the form 0.abcdefghijklmn.
+$E({10}^{18})$ を求めなさい。 回答は、四捨五入して小数第 14 位まで求め、0.abcdefghijklmn の形式にすること。
# --hints--
-`emptyChairs()` should return `0.56766764161831`.
+`emptyChairs()` は `0.56766764161831` を返す必要があります。
```js
assert.strictEqual(emptyChairs(), 0.56766764161831);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
index a8f59ece37..2a30df1638 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-470-super-ramvok.md
@@ -1,6 +1,6 @@
---
id: 5900f5431000cf542c510055
-title: 'Problem 470: Super Ramvok'
+title: '問題 470: スーパー Ramvok'
challengeType: 5
forumTopicId: 302146
dashedName: problem-470-super-ramvok
@@ -8,23 +8,23 @@ dashedName: problem-470-super-ramvok
# --description--
-Consider a single game of Ramvok:
+Ramvok というゲームを 1 回プレイすることについて考えます。
-Let $t$ represent the maximum number of turns the game lasts. If $t = 0$, then the game ends immediately. Otherwise, on each turn $i$, the player rolls a die. After rolling, if $i < t$ the player can either stop the game and receive a prize equal to the value of the current roll, or discard the roll and try again next turn. If $i = t$, then the roll cannot be discarded and the prize must be accepted. Before the game begins, $t$ is chosen by the player, who must then pay an up-front cost $ct$ for some constant $c$. For $c = 0$, $t$ can be chosen to be infinite (with an up-front cost of 0). Let $R(d, c)$ be the expected profit (i.e. net gain) that the player receives from a single game of optimally-played Ramvok, given a fair $d$-sided die and cost constant $c$. For example, $R(4, 0.2) = 2.65$. Assume that the player has sufficient funds for paying any/all up-front costs.
+ゲームが続いている間のターンの最大数を $t$ とします。 $t = 0$ の場合、ゲームはすぐに終了します。 それ以外の場合、各ターン $i$ でプレイヤーがサイコロを振ります。 サイコロを振った後、$i < t$ の場合は、そのプレイヤーはゲームをやめてサイコロの目と同額の賞金を受け取るか、または、出目を捨てて次のターンで再挑戦することができます。 $i = t$の場合、出目を捨てることはできず、賞金を受け入れなければなりません。 ゲーム開始前、プレイヤーは $t$ を選び、そのプレイヤーはある定数 $c$ に対して前金 $ct$ を支払う必要があります。 $c = 0$ の場合、(前金なしで) $t$ を無制限にすることを選択できます 。 偏りのない $d$ 面のサイコロとコスト定数 $c$ が与えられるとき、Ramvok のゲームを最適に 1 回プレイすることでプレイヤーが受け取る期待利益 (純利益) を $R(d, c)$ とします。 例えば、$R(4, 0.2) = 2.65$ です。 プレイヤーが前金をいくらでも支払えるほどの資金を持っていると仮定します。
-Now consider a game of Super Ramvok:
+次に、スーパー Ramvok を 1 回プレイすることについて考えます。
-In Super Ramvok, the game of Ramvok is played repeatedly, but with a slight modification. After each game, the die is altered. The alteration process is as follows: The die is rolled once, and if the resulting face has its pips visible, then that face is altered to be blank instead. If the face is already blank, then it is changed back to its original value. After the alteration is made, another game of Ramvok can begin (and during such a game, at each turn, the die is rolled until a face with a value on it appears). The player knows which faces are blank and which are not at all times. The game of Super Ramvok ends once all faces of the die are blank.
+スーパー Ramvokでも Ramvok のゲームが繰り返し行われますが、ルールが少し異なります。 各ゲームの後、サイコロが変更されるのです。 変更のプロセスは次のとおりです。サイコロが 1 回振られ、上になった面に目があれば、その面は目のない面に変えられます。 上になった面がすでに空白の場合は、元の目の値に戻されます。 変更が行われた後、Ramvok ゲームの次の 1 回をスタートできます (そのような 1 回のゲーム中に、各ターンで、目のある面が出るまでサイコロを振ります)。 プレイヤーは、どの面が空白で、どの面が空白でないかを常に知っています。 スーパー Ramvok のゲームは、サイコロのすべての面が空白になると終了です。
-Let $S(d, c)$ be the expected profit that the player receives from an optimally-played game of Super Ramvok, given a fair $d$-sided die to start (with all sides visible), and cost constant $c$. For example, $S(6, 1) = 208.3$.
+偏りのない $d$ 面のサイコロ (開始時はすべての面に目がある) とコスト定数 $c$ が与えられるとき、スーパー Ramvok を最適に 1 回プレイすることでプレイヤーが受け取る期待利益を $S(d, c)$ とします。 例えば、$S(6, 1) = 208.3$ です。
-Let $F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$.
+$F(n) = \sum_{4 ≤ d ≤ n} \sum_{0 ≤ c ≤ n} S(d, c)$ と定義します。
-Calculate $F(20)$, rounded to the nearest integer.
+$F(20)$ を計算し、最も近い整数に四捨五入して答えなさい。
# --hints--
-`superRamvok()` should return `147668794`.
+`superRamvok()` は `147668794` を返す必要があります。
```js
assert.strictEqual(superRamvok(), 147668794);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
index 250ddfce2d..b27f8c698d 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-471-triangle-inscribed-in-ellipse.md
@@ -1,6 +1,6 @@
---
id: 5900f5431000cf542c510056
-title: 'Problem 471: Triangle inscribed in ellipse'
+title: '問題 471: 楕円に内接する三角形'
challengeType: 5
forumTopicId: 302148
dashedName: problem-471-triangle-inscribed-in-ellipse
@@ -8,33 +8,33 @@ dashedName: problem-471-triangle-inscribed-in-ellipse
# --description--
-The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
+$0 < 2b < a$ を満たす整数 $a$, $b$ について、三角形 $ΔABC$ は式 $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$ で表される楕円に内接しています。
-Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
+三角形 $ΔABC$ の内接円の中心が $(2b, 0)$ で、$A$ の座標が $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$ のとき、その内接円の半径を $r(a, b)$ とします。
-For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
+たとえば、$r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$ です。
-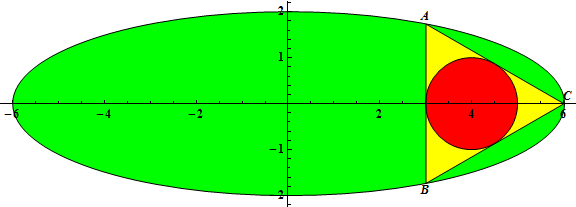 +
+ -
-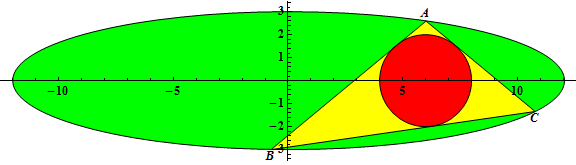 +
+ -Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
+$G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$ と定義します。
-You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
+$G(10) = 20.59722222$, $G(100) = 19223.60980$ (有効数字 10 桁に四捨五入) が与えられます。
-Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
+$G({10}^{11})$ を求めなさい。 回答は、有効数字 10 桁に四捨五入された科学的記数法の文字列にすること。 また、小文字 `e` で仮数部と指数部を区切ること。
-For $G(10)$ the answer would have been `2.059722222e1`
+$G(10)$ の場合、回答は `2.059722222e1` となります。
# --hints--
-`triangleInscribedInEllipse()` should return a string.
+`triangleInscribedInEllipse()` は文字列を返す必要があります。
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
-`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
+`triangleInscribedInEllipse()` は文字列 `1.895093981e31` を返す必要があります。
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
index 638c796c8d..0bd4c83926 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f5451000cf542c510057
-title: 'Problem 472: Comfortable Distance II'
+title: '問題 472: 快適な距離 (2)'
challengeType: 5
forumTopicId: 302149
dashedName: problem-472-comfortable-distance-ii
@@ -8,29 +8,29 @@ dashedName: problem-472-comfortable-distance-ii
# --description--
-There are $N$ seats in a row. $N$ people come one after another to fill the seats according to the following rules:
+$N$ 個の席が一列に並んでいます。 $N$ 人の人が次々とやって来て、次のルールに従って席を埋めていきます。
-1. No person sits beside another.
-1. The first person chooses any seat.
-1. Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
+1. 他の人の隣りに座らない。
+1. 最初の人が任意の席を選択する。
+1. 2 人目以降はそれぞれ、ルール 1 に反しない席のうち、既に人が座っている席から最も遠い席を選ぶ。 この条件を満たす席が複数ある場合は、一番左の席を選ぶ。
-Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than $N$ (for $N > 1$).
+注意点として、ルール 1 に基づき席の一部は空席のままであり、座れる人数は最大で $N$ 未満です ($N > 1$)。
-Here are the possible seating arrangements for $N = 15$:
+$N = 15$ のとき、考えられる座席配置は次のとおりです。
-
-Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
+$G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$ と定義します。
-You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
+$G(10) = 20.59722222$, $G(100) = 19223.60980$ (有効数字 10 桁に四捨五入) が与えられます。
-Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
+$G({10}^{11})$ を求めなさい。 回答は、有効数字 10 桁に四捨五入された科学的記数法の文字列にすること。 また、小文字 `e` で仮数部と指数部を区切ること。
-For $G(10)$ the answer would have been `2.059722222e1`
+$G(10)$ の場合、回答は `2.059722222e1` となります。
# --hints--
-`triangleInscribedInEllipse()` should return a string.
+`triangleInscribedInEllipse()` は文字列を返す必要があります。
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
-`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
+`triangleInscribedInEllipse()` は文字列 `1.895093981e31` を返す必要があります。
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
index 638c796c8d..0bd4c83926 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-472-comfortable-distance-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f5451000cf542c510057
-title: 'Problem 472: Comfortable Distance II'
+title: '問題 472: 快適な距離 (2)'
challengeType: 5
forumTopicId: 302149
dashedName: problem-472-comfortable-distance-ii
@@ -8,29 +8,29 @@ dashedName: problem-472-comfortable-distance-ii
# --description--
-There are $N$ seats in a row. $N$ people come one after another to fill the seats according to the following rules:
+$N$ 個の席が一列に並んでいます。 $N$ 人の人が次々とやって来て、次のルールに従って席を埋めていきます。
-1. No person sits beside another.
-1. The first person chooses any seat.
-1. Each subsequent person chooses the seat furthest from anyone else already seated, as long as it does not violate rule 1. If there is more than one choice satisfying this condition, then the person chooses the leftmost choice.
+1. 他の人の隣りに座らない。
+1. 最初の人が任意の席を選択する。
+1. 2 人目以降はそれぞれ、ルール 1 に反しない席のうち、既に人が座っている席から最も遠い席を選ぶ。 この条件を満たす席が複数ある場合は、一番左の席を選ぶ。
-Note that due to rule 1, some seats will surely be left unoccupied, and the maximum number of people that can be seated is less than $N$ (for $N > 1$).
+注意点として、ルール 1 に基づき席の一部は空席のままであり、座れる人数は最大で $N$ 未満です ($N > 1$)。
-Here are the possible seating arrangements for $N = 15$:
+$N = 15$ のとき、考えられる座席配置は次のとおりです。
-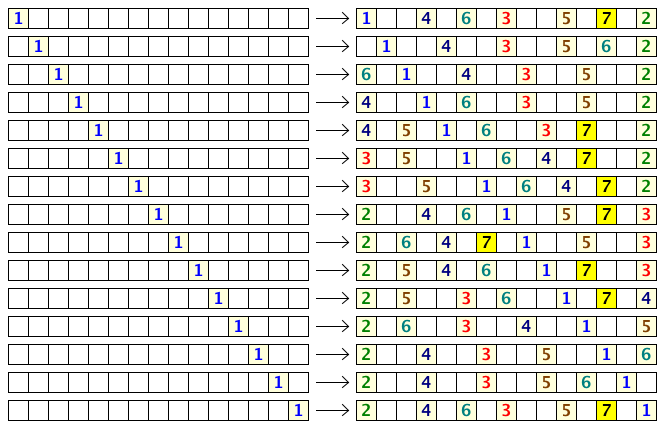 +
+ -We see that if the first person chooses correctly, the 15 seats can seat up to 7 people. We can also see that the first person has 9 choices to maximize the number of people that may be seated.
+最初の人が席を正しく選択すると、15 席に最大 7 人が座れることが分かります。 また、最初の人が持つ選択肢のうち、座れる人数が最大になる選択肢が 9 つであることも分かります。
-Let $f(N)$ be the number of choices the first person has to maximize the number of occupants for $N$ seats in a row. Thus, $f(1) = 1$, $f(15) = 9$, $f(20) = 6$, and $f(500) = 16$.
+$N$ 個の席が一列に並んでいるとき、最初の人が持つ選択肢のうち、座れる人数が最大になる選択肢の数を $f(N)$ とします。 したがって、$f(1) = 1$, $f(15) = 9$, $f(20) = 6$, $f(500) = 16$ です。
-Also, $\sum f(N) = 83$ for $1 ≤ N ≤ 20$ and $\sum f(N) = 13\\,343$ for $1 ≤ N ≤ 500$.
+また、$1 ≤ N ≤ 20$ のときは $\sum f(N) = 83$ であり、$1 ≤ N ≤ 500$ のときは $\sum f(N) = 13\\,343$ です。
-Find $\sum f(N)$ for $1 ≤ N ≤ {10}^{12}$. Give the last 8 digits of your answer.
+$1 ≤ N ≤ {10}^{12}$ のとき、$\sum f(N)$ を求めなさい。 回答は、下位 8 桁とすること。
# --hints--
-`comfortableDistanceTwo()` should return `73811586`.
+`comfortableDistanceTwo()` は `73811586` を返す必要があります。
```js
assert.strictEqual(comfortableDistanceTwo(), 73811586);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
index 0936140110..ff847fa8a5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
@@ -1,6 +1,6 @@
---
id: 5900f5461000cf542c510058
-title: 'Problem 473: Phigital number base'
+title: '問題 473: フィジタル進数'
challengeType: 5
forumTopicId: 302150
dashedName: problem-473-phigital-number-base
@@ -8,29 +8,29 @@ dashedName: problem-473-phigital-number-base
# --description--
-Let $\varphi$ be the golden ratio: $\varphi = \frac{1+\sqrt{5}}{2}.$
+黄金比 $\varphi = \frac{1+\sqrt{5}}{2}$ を $\varphi$ とします。
-Remarkably it is possible to write every positive integer as a sum of powers of $\varphi$ even if we require that every power of $\varphi$ is used at most once in this sum.
+驚くべきことに、すべての正の整数は $\varphi$ の累乗の和として表すことができます。たとえこの和の中で $\varphi$ のすべての累乗をたかだか 1 度しか使えないとしても、それが可能なのです。
-Even then this representation is not unique.
+しかも、この表し方は唯一のものではありません。
-We can make it unique by requiring that no powers with consecutive exponents are used and that the representation is finite.
+指数が連続するような累乗を使わないこと、および、その表し方が有限であることを条件にすれば、表し方を一意にできます。
-E.g:
+例:
-$2 = \varphi + \varphi^{-2}$ and $3 = \varphi^{2} + \varphi^{-2}$
+$2 = \varphi + \varphi^{-2}$, $3 = \varphi^{2} + \varphi^{-2}$
-To represent this sum of powers of $\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase.
+$\varphi$ の累乗の和を表すために、0 と 1 からなり、負の指数の開始点が小数点で示されている文字列を使用します。 この表記法を「フィジタル進数」と呼ぶことにします。
-So $1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$ and $14 = 100100.001001_{\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
+したがって、$1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$, $14 = 100100.001001_{\varphi}$ となります。 フィジタル進数の 1, 2, 14 を表す文字列は回文数で、3 を表す文字列は回文数ではありません (フィジタル進数の小数点が中央の文字ではありません)。
-The sum of the positive integers not exceeding 1000 whose phigital representation is palindromic is 4345.
+フィジタル進数で表すと回文数になる 1000 以下の正の整数の和は 4345 です。
-Find the sum of the positive integers not exceeding $10^{10}$ whose phigital representation is palindromic.
+フィジタル進数で表すと回文数になる $10^{10}$ 以下の正の整数の和を求めなさい。
# --hints--
-`phigitalNumberBase()` should return `35856681704365`.
+`phigitalNumberBase()` は `35856681704365` を返す必要があります。
```js
assert.strictEqual(phigitalNumberBase(), 35856681704365);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
index 04123a2b35..8ad8d4efa5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f5471000cf542c510059
-title: 'Problem 474: Last digits of divisors'
+title: '問題 474: 約数の下位桁'
challengeType: 5
forumTopicId: 302151
dashedName: problem-474-last-digits-of-divisors
@@ -8,17 +8,17 @@ dashedName: problem-474-last-digits-of-divisors
# --description--
-For a positive integer $n$ and digits $d$, we define $F(n, d)$ as the number of the divisors of $n$ whose last digits equal $d$.
+正の整数 $n$ と桁の数字 $d$ について、$n$ の約数のうち下位桁が $d$ と等しいものの個数を $F(n, d)$ と定義します。
-For example, $F(84, 4) = 3$. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
+例えば、$F(84, 4) = 3$ です。 84 の約数 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84) のうち、最下位の桁が 4 であるのは 3 つ (4, 14, 84) だからです。
-We can also verify that $F(12!, 12) = 11$ and $F(50!, 123) = 17\\,888$.
+$F(12!, 12) = 11$, $F(50!, 123) = 17\\,888$ であることも確認できます。
-Find $F({10}^6!, 65\\,432) \text{ modulo } ({10}^{16} + 61)$.
+$F({10}^6!, 65\\,432) \text{ mod } ({10}^{16} + 61)$ を求めなさい。
# --hints--
-`lastDigitsOfDivisors()` should return `9690646731515010`.
+`lastDigitsOfDivisors()` は `9690646731515010` を返す必要があります。
```js
assert.strictEqual(lastDigitsOfDivisors(), 9690646731515010);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md
index 4ab0b69b3a..53975cbb46 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md
@@ -1,6 +1,6 @@
---
id: 5900f5481000cf542c51005a
-title: 'Problem 475: Music festival'
+title: '問題 475: 音楽祭'
challengeType: 5
forumTopicId: 302152
dashedName: problem-475-music-festival
@@ -8,21 +8,21 @@ dashedName: problem-475-music-festival
# --description--
-$12n$ musicians participate at a music festival. On the first day, they form $3n$ quartets and practice all day.
+$12n$ 人の演奏家が音楽祭に参加します。 初日に $3n$ 組のカルテットを編成し、終日練習します。
-It is a disaster. At the end of the day, all musicians decide they will never again agree to play with any member of their quartet.
+そして大変な事態が起こります。 練習の後、すべての演奏家が自分のカルテットのいずれのメンバーとも共演しないと決めたのです。
-On the second day, they form $4n$ trios, each musician avoiding his previous quartet partners.
+2 日目に、演奏家たちは以前のカルテットのパートナーを避けて $4n$ 組のトリオを編成します。
-Let $f(12n)$ be the number of ways to organize the trios amongst the $12n$ musicians.
+$12n$ 人の演奏家の間でトリオを編成する方法が何通りあるかを、$f(12n)$ で表します。
-You are given $f(12) = 576$ and $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$.
+$f(12) = 576$ および $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$ が与えられます。
-Find $f(600)\bmod 1\\,000\\,000\\,007$.
+$f(600)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`musicFestival()` should return `75780067`.
+`musicFestival()` は `75780067` を返す必要があります。
```js
assert.strictEqual(musicFestival(), 75780067);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
index b87eca74b7..e20ba89154 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f5481000cf542c51005b
-title: 'Problem 476: Circle Packing II'
+title: '問題 476: 円を詰める (2)'
challengeType: 5
forumTopicId: 302153
dashedName: problem-476-circle-packing-ii
@@ -8,17 +8,17 @@ dashedName: problem-476-circle-packing-ii
# --description--
-Let $R(a, b, c)$ be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths $a$, $b$ and $c$.
+辺の長さが $a$, $b$, $c$ の三角形の内側で、重ならない 3 つの円で覆うことができる最大面積を $R(a, b, c)$ とします。
-Let $S(n)$ be the average value of $R(a, b, c)$ over all integer triplets $(a, b, c)$ such that $1 ≤ a ≤ b ≤ c < a + b ≤ n$.
+$1 ≤ a ≤ b ≤ c < a + b ≤ n$ が成り立つすべての三つ組整数 $(a, b, c)$ における $R(a, b, c)$ の平均値を $S(n)$ とします。
-You are given $S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$.
+$S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$ が与えられます。
-Find $S(1803)$ rounded to 5 decimal places behind the decimal point.
+$S(1803)$ を求め、四捨五入して小数第 5 位まで示しなさい。
# --hints--
-`circlePackingTwo()` should return `110242.87794`.
+`circlePackingTwo()` は `110242.87794` を返す必要があります。
```js
assert.strictEqual(circlePackingTwo(), 110242.87794);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
index 24fa79f131..2fdf8e440e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
@@ -1,6 +1,6 @@
---
id: 5900f54a1000cf542c51005c
-title: 'Problem 477: Number Sequence Game'
+title: '問題 477: 数列ゲーム'
challengeType: 5
forumTopicId: 302154
dashedName: problem-477-number-sequence-game
@@ -8,35 +8,35 @@ dashedName: problem-477-number-sequence-game
# --description--
-The number sequence game starts with a sequence $S$ of $N$ numbers written on a line.
+数列ゲームは、一列に書かれた $N$ 個の数からなる数列 $S$ で始まります。
-Two players alternate turns. At his turn, a player must select and remove either the first or the last number remaining in the sequence.
+2 人のプレイヤーが交互にプレイします。 プレイヤーは自分のターンで、数列に残っている最初の数または最後の数を選択し、取り除きます。
-The player score is the sum of all the numbers he has taken. Each player attempts to maximize his own sum.
+取った数の和がそのプレイヤーのスコアになります。 各プレイヤーは自分の数の和を最大にしようとします。
-If $N = 4$ and $S = \\{1, 2, 10, 3\\}$, then each player maximizes his score as follows:
+$N = 4$ かつ $S = \\{1, 2, 10, 3\\}$ の場合、各プレイヤーは次のようにスコアを最大化します。
-- Player 1: removes the first number (1)
-- Player 2: removes the last number from the remaining sequence (3)
-- Player 1: removes the last number from the remaining sequence (10)
-- Player 2: removes the remaining number (2)
+- プレイヤー 1: 最初の数 (1) を取り除く
+- プレイヤー 2: 残りの数列から最後の数 (3) を取り除く
+- プレイヤー 1: 残りの数列から最後の数 (10) を取り除く
+- プレイヤー 2: 残りの数 (2) を取り除く
-Player 1 score is $1 + 10 = 11$.
+プレイヤー 1 のスコアは $1 + 10 = 11$ です。
-Let $F(N)$ be the score of player 1 if both players follow the optimal strategy for the sequence $S = \\{s_1, s_2, \ldots, s_N\\}$ defined as:
+次のように定義される数列 $S = \\{s_1, s_2, \ldots, s_N\\}$ の最適な戦略に両プレイヤーが従った場合の、プレイヤー 1 のスコアを $F(N)$ とします。
- $s_1 = 0$
-- $s_{i + 1} = ({s_i}^2 + 45)$ modulo $1\\,000\\,000\\,007$
+- $s_{i + 1} = ({s_i}^2 + 45)$ mod $1\\,000\\,000\\,007$
-The sequence begins with $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,107\\,844, 894\\,218\\,625, \ldots\\}$.
+数列は $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,844, 894\\,218\\,625, \ldots\\}$ で始まります。
-You are given $F(2) = 45$, $F(4) = 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$.
+$F(2) = 45$, $F= 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$ が与えられます。
-Find $F({10}^8)$.
+$F({10}^8)$ を求めなさい。
# --hints--
-`numberSequenceGame()` should return `25044905874565164`.
+`numberSequenceGame()` は `25044905874565164` を返す必要があります。
```js
assert.strictEqual(numberSequenceGame(), 25044905874565164);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md
index 745aefc824..e3eedcf632 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md
@@ -1,6 +1,6 @@
---
id: 5900f54c1000cf542c51005e
-title: 'Problem 478: Mixtures'
+title: '問題 478: 混合物'
challengeType: 5
forumTopicId: 302155
dashedName: problem-478-mixtures
@@ -8,29 +8,29 @@ dashedName: problem-478-mixtures
# --description--
-Let us consider mixtures of three substances: $A$, $B$ and $C$. A mixture can be described by a ratio of the amounts of $A$, $B$, and $C$ in it, i.e., $(a : b : c)$. For example, a mixture described by the ratio (2 : 3 : 5) contains 20% $A$, 30% $B$ and 50% $C$.
+3 つの物質 $A$, $B$, $C$ の混合物について考えます。 混合物は、それに含まれる $A$, $B$, $C$ の比率によって $(a : b : c)$ と表すことができます。 例えば、比率 (2 : 3 : 5) で表された混合物には、$A$ が20%、$B$ が30%、そして $C$ が 50% 含まれています。
-For the purposes of this problem, we cannot separate the individual components from a mixture. However, we can combine different amounts of different mixtures to form mixtures with new ratios.
+この問題の目的上、混合物から各物質を分離することはできないものとします。 しかし、異なる混合物をさまざまな量で組み合わせ、新しい比率の混合物を作ることはできます。
-For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: ($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9)
+例えば、3 つの比率 (3 : 0 : 2), (3 : 6 : 11), (3 : 3 : 4) の混合物があるとします。 1 つ目の混合物を 10 単位、2 つ目の混合物を 20 単位、3 つ目の混合物を 30 単位使って混合すると、比率が (6 : 5 : 9) の混合物ができます。なぜなら、($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9) だからです。
-However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of $B$ is always less than the amount of $C$.
+しかし、上と同じ 3 つの混合物を使って比率を (3 : 2 : 1) にすることは不可能です。どのように組み合わせても $B$ の量が $C$ の量より少なくなるからです。
-Let $n$ be a positive integer. Suppose that for every triple of integers $(a, b, c)$ with $0 ≤ a, b, c ≤ n$ and $gcd(a, b, c) = 1$, we have a mixture with ratio $(a : b : c)$. Let $M(n)$ be the set of all such mixtures.
+$n$ を正の整数とします。 $0 ≤ a, b, c ≤ n$ かつ $gcd(a, b, c) = 1$ を満たす整数の三つ組 $(a, b, c)$ に対して、比率 $(a : b : c)$ の混合物が常にあるとします。 そのようなすべての混合物の集合を $M(n)$ とします。
-For example, $M(2)$ contains the 19 mixtures with the following ratios:
+例えば、$M(2)$ には次の比率で 19 の混合物が含まれています。
-{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}
-Let $E(n)$ be the number of subsets of $M(n)$ which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts $A$, $B$ and $C$.
+比率 (1 : 1 : 1)、すなわち $A$, $B$, $C$ が等しく配合された混合物を作れる $M(n)$ の部分集合の個数を $E(n)$ とします。
-We can verify that $E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$ and $E(500)\bmod {11}^8 = 13\\,801\\,403$.
+$E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$, $E(500)\bmod {11}^8 = 13\\,801\\,403$ であることを確認できます。
-Find $E(10\\,000\\,000)\bmod {11}^8$.
+$E(10\\,000\\,000)\bmod {11}^8$ を求めなさい。
# --hints--
-`mixtures()` should return `59510340`.
+`mixtures()` は `59510340` を返す必要があります。
```js
assert.strictEqual(mixtures(), 59510340);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
index f2114e53c2..a02d502558 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
@@ -1,6 +1,6 @@
---
id: 5900f54b1000cf542c51005d
-title: 'Problem 479: Roots on the Rise'
+title: '問題 479: 根の増大'
challengeType: 5
forumTopicId: 302156
dashedName: problem-479-roots-on-the-rise
@@ -8,19 +8,19 @@ dashedName: problem-479-roots-on-the-rise
# --description--
-Let $a_k$, $b_k$, and $c_k$ represent the three solutions (real or complex numbers) to the expression $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$.
+式 $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$ の 3 つの解 (実数または複素数) を、$a_k$, $b_k$, $c_k$ で表します。
-For instance, for $k = 5$, we see that $\\{a_5, b_5, c_5\\}$ is approximately $\\{5.727244, -0.363622 + 2.057397i, -0.363622 - 2.057397i\\}$.
+例えば $k = 5$ の場合、$\\{a_5, b_5, c_5\\}$ は約 $\\{5.727244, -0.3622 + 2.057397i, -0.363622 - 2.057397i\\}$ であることが分かります。
-Let $S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ for all integers $p$, $k$ such that $1 ≤ p, k ≤ n$.
+$1 ≤ p, k ≤ n$ を満たすすべての整数 $p$, $k$ に対して、$S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ と定義します。
-Interestingly, $S(n)$ is always an integer. For example, $S(4) = 51\\,160$.
+興味深いことに、$S(n)$ は常に整数です。 例えば、$S(4) ≈ 51\\,160$ です。
-Find $S({10}^6) \text{ modulo } 1\\,000\\,000\\,007$.
+$S({10}^6) \text{ mod } 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`rootsOnTheRise()` should return `191541795`.
+`rootsOnTheRise()` は `191541795` を返す必要があります。
```js
assert.strictEqual(rootsOnTheRise(), 191541795);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
index 8ffff17076..a4b94b7028 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
@@ -1,6 +1,6 @@
---
id: 5900f54c1000cf542c51005f
-title: 'Problem 480: The Last Question'
+title: '問題 480: 最後の質問'
challengeType: 5
forumTopicId: 302158
dashedName: problem-480-the-last-question
@@ -8,39 +8,39 @@ dashedName: problem-480-the-last-question
# --description--
-Consider all the words which can be formed by selecting letters, in any order, from the phrase:
+次のフレーズから任意の順序で文字を選んで作ることができる、すべての単語を考えます。
$$\mathbf{\text{thereisasyetinsufficientdataforameaningfulanswer}}$$
-Suppose those with 15 letters or less are listed in alphabetical order and numbered sequentially starting at 1.
+15 個以下の文字がアルファベット順に列挙され、1 から順に番号が振られているとします。
-The list would include:
+そのリストには以下が含まれるでしょう。
$$\begin{align} & 1: \text{a} \\\\ & 2: \text{aa} \\\\ & 3: \text{aaa} \\\\ & 4: \text{aaaa} \\\\ & 5: \text{aaaaa} \\\\ & 6: \text{aaaaaa} \\\\ & 7: \text{aaaaaac} \\\\ & 8: \text{aaaaaacd} \\\\ & 9: \text{aaaaaacde} \\\\ & 10: \text{aaaaaacdee} \\\\ & 11: \text{aaaaaacdeee} \\\\ & 12: \text{aaaaaacdeeee} \\\\ & 13: \text{aaaaaacdeeeee} \\\\ & 14: \text{aaaaaacdeeeeee} \\\\ & 15: \text{aaaaaacdeeeeeef} \\\\ & 16: \text{aaaaaacdeeeeeeg} \\\\ & 17: \text{aaaaaacdeeeeeeh} \\\\ & \ldots \\\\ & 28: \text{aaaaaacdeeeeeey} \\\\ & 29: \text{aaaaaacdeeeeef} \\\\ & 30: \text{aaaaaacdeeeeefe} \\\\ & \ldots \\\\ & 115246685191495242: \text{euleoywuttttsss} \\\\ & 115246685191495243: \text{euler} \\\\ & 115246685191495244: \text{eulera} \\\\ & ... \\\\ & 525069350231428029: \text{ywuuttttssssrrr} \\\\ \end{align}$$
-Define $P(w)$ as the position of the word $w$.
+$P(w)$ を、単語 $w$ の位置とします。
-Define $W(p)$ as the word in position $p$.
+$W(p)$ を、位置 $p$ にある単語とします。
-We can see that $P(w)$ and $W(p)$ are inverses: $P(W(p)) = p$ and $W(P(w)) = w$.
+$P(w)$ と $W(p)$ は逆元であることがわかります。つまり、$P(W(p)) = p$ および $W(P(w)) = w$ です。
-Examples:
+例:
$$\begin{align} & W(10) = \text{ aaaaaacdee} \\\\ & P(\text{aaaaaacdee}) = 10 \\\\ & W(115246685191495243) = \text{ euler} \\\\ & P(\text{euler}) = 115246685191495243 \\\\ \end{align}$$
-Find $$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering})).$$
+$$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering}))$$ を求めなさい。
-Give your answer using lowercase characters (no punctuation or space).
+回答は、 (句読点やスペースを含めずに) 小文字で書くこと 。
# --hints--
-`euler480()` should return a string.
+`euler480()` は文字列を返す必要があります。
```js
assert(typeof euler480() === 'string');
```
-`euler480()` should return the string `turnthestarson`.
+`euler480()` は文字列 `turnthestarson` を返す必要があります。
```js
assert.strictEqual(euler480(), 'turnthestarson');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md
index e791c06558..c8c3e0b001 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md
@@ -1,6 +1,6 @@
---
id: 594810f028c0303b75339acb
-title: 100 doors
+title: 100個のドア
challengeType: 5
forumTopicId: 302217
dashedName: 100-doors
@@ -8,27 +8,27 @@ dashedName: 100-doors
# --description--
-There are 100 doors in a row that are all initially closed. You make 100 passes by the doors. The first time through, visit every door and 'toggle' the door (if the door is closed, open it; if it is open, close it). The second time, only visit every 2nd door (i.e., door #2, #4, #6, ...) and toggle it. The third time, visit every 3rd door (i.e., door #3, #6, #9, ...), etc., until you only visit the 100th door.
+100個のドアが連続してあり、最初はすべてのドアは閉じています。 100個のドア全てを対象とします。 1回目はすべてのドアを訪問し、ドアを「切り替え」(ドアが閉じられている場合は、開き、開いている場合は、閉じる)ます。 2回目は、2の倍数のドア(#2のドア、#4のドア、#6のドア...)に訪問し、それぞれの開閉を「切り替え」ます。 3回目は、3の倍数のドア(#3のドア、#6のドア、#9のドア...)を訪問して「切替」を行い、100番目のドアまで続けます。
# --instructions--
-Implement a function to determine the state of the doors after the last pass. Return the final result in an array, with only the door number included in the array if it is open.
+3回の訪問が終了した時点でのドアの状態を示す関数を作成します。 配列形式で最終的な結果を返します。開いている状態のドアの番号を配列形式で返します。
# --hints--
-`getFinalOpenedDoors` should be a function.
+`getFinalOpenedDoors` という関数です。
```js
assert(typeof getFinalOpenedDoors === 'function');
```
-`getFinalOpenedDoors` should return an array.
+`getFinalOpenedDoors` は配列を返します。
```js
assert(Array.isArray(getFinalOpenedDoors(100)));
```
-`getFinalOpenedDoors` should produce the correct result.
+`getFinalOpenedDoors` は正確な結果を返します。
```js
assert.deepEqual(getFinalOpenedDoors(100), solution);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md
index 7bf28fe4df..58760ce94b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md
@@ -8,23 +8,23 @@ dashedName: 24-game
# --description--
-The [24 Game](https://en.wikipedia.org/wiki/24_Game) tests a person's mental arithmetic.
+[24 Game](https://en.wikipedia.org/wiki/24_Game) では、人の暗算能力をテストします。
-The aim of the game is to arrange four numbers in a way that when evaluated, the result is 24
+ゲームの目的は、算出結果が24になるように4つの数字を配置することです。
# --instructions--
-Implement a function that takes a string of four digits as its argument, with each digit from 1 to 9 (inclusive) with repetitions allowed, and returns an arithmetic expression that evaluates to the number 24. If no such solution exists, return "no solution exists".
+4桁の文字列を引数とする関数を作成します。 各桁は、1 から 9 までの数字で、繰り返しも可能です。この関数は、算出結果が数値 24 になる算術式を返します。 そのような解が存在しない場合は、「解が存在しません」を返します。
-**Rules:**
+**ルール:**
-We see that if the first person chooses correctly, the 15 seats can seat up to 7 people. We can also see that the first person has 9 choices to maximize the number of people that may be seated.
+最初の人が席を正しく選択すると、15 席に最大 7 人が座れることが分かります。 また、最初の人が持つ選択肢のうち、座れる人数が最大になる選択肢が 9 つであることも分かります。
-Let $f(N)$ be the number of choices the first person has to maximize the number of occupants for $N$ seats in a row. Thus, $f(1) = 1$, $f(15) = 9$, $f(20) = 6$, and $f(500) = 16$.
+$N$ 個の席が一列に並んでいるとき、最初の人が持つ選択肢のうち、座れる人数が最大になる選択肢の数を $f(N)$ とします。 したがって、$f(1) = 1$, $f(15) = 9$, $f(20) = 6$, $f(500) = 16$ です。
-Also, $\sum f(N) = 83$ for $1 ≤ N ≤ 20$ and $\sum f(N) = 13\\,343$ for $1 ≤ N ≤ 500$.
+また、$1 ≤ N ≤ 20$ のときは $\sum f(N) = 83$ であり、$1 ≤ N ≤ 500$ のときは $\sum f(N) = 13\\,343$ です。
-Find $\sum f(N)$ for $1 ≤ N ≤ {10}^{12}$. Give the last 8 digits of your answer.
+$1 ≤ N ≤ {10}^{12}$ のとき、$\sum f(N)$ を求めなさい。 回答は、下位 8 桁とすること。
# --hints--
-`comfortableDistanceTwo()` should return `73811586`.
+`comfortableDistanceTwo()` は `73811586` を返す必要があります。
```js
assert.strictEqual(comfortableDistanceTwo(), 73811586);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
index 0936140110..ff847fa8a5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-473-phigital-number-base.md
@@ -1,6 +1,6 @@
---
id: 5900f5461000cf542c510058
-title: 'Problem 473: Phigital number base'
+title: '問題 473: フィジタル進数'
challengeType: 5
forumTopicId: 302150
dashedName: problem-473-phigital-number-base
@@ -8,29 +8,29 @@ dashedName: problem-473-phigital-number-base
# --description--
-Let $\varphi$ be the golden ratio: $\varphi = \frac{1+\sqrt{5}}{2}.$
+黄金比 $\varphi = \frac{1+\sqrt{5}}{2}$ を $\varphi$ とします。
-Remarkably it is possible to write every positive integer as a sum of powers of $\varphi$ even if we require that every power of $\varphi$ is used at most once in this sum.
+驚くべきことに、すべての正の整数は $\varphi$ の累乗の和として表すことができます。たとえこの和の中で $\varphi$ のすべての累乗をたかだか 1 度しか使えないとしても、それが可能なのです。
-Even then this representation is not unique.
+しかも、この表し方は唯一のものではありません。
-We can make it unique by requiring that no powers with consecutive exponents are used and that the representation is finite.
+指数が連続するような累乗を使わないこと、および、その表し方が有限であることを条件にすれば、表し方を一意にできます。
-E.g:
+例:
-$2 = \varphi + \varphi^{-2}$ and $3 = \varphi^{2} + \varphi^{-2}$
+$2 = \varphi + \varphi^{-2}$, $3 = \varphi^{2} + \varphi^{-2}$
-To represent this sum of powers of $\varphi$ we use a string of 0's and 1's with a point to indicate where the negative exponents start. We call this the representation in the phigital numberbase.
+$\varphi$ の累乗の和を表すために、0 と 1 からなり、負の指数の開始点が小数点で示されている文字列を使用します。 この表記法を「フィジタル進数」と呼ぶことにします。
-So $1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$ and $14 = 100100.001001_{\varphi}$. The strings representing 1, 2 and 14 in the phigital number base are palindromic, while the string representing 3 is not. (the phigital point is not the middle character).
+したがって、$1 = 1_{\varphi}$, $2 = 10.01_{\varphi}$, $3 = 100.01_{\varphi}$, $14 = 100100.001001_{\varphi}$ となります。 フィジタル進数の 1, 2, 14 を表す文字列は回文数で、3 を表す文字列は回文数ではありません (フィジタル進数の小数点が中央の文字ではありません)。
-The sum of the positive integers not exceeding 1000 whose phigital representation is palindromic is 4345.
+フィジタル進数で表すと回文数になる 1000 以下の正の整数の和は 4345 です。
-Find the sum of the positive integers not exceeding $10^{10}$ whose phigital representation is palindromic.
+フィジタル進数で表すと回文数になる $10^{10}$ 以下の正の整数の和を求めなさい。
# --hints--
-`phigitalNumberBase()` should return `35856681704365`.
+`phigitalNumberBase()` は `35856681704365` を返す必要があります。
```js
assert.strictEqual(phigitalNumberBase(), 35856681704365);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
index 04123a2b35..8ad8d4efa5 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-474-last-digits-of-divisors.md
@@ -1,6 +1,6 @@
---
id: 5900f5471000cf542c510059
-title: 'Problem 474: Last digits of divisors'
+title: '問題 474: 約数の下位桁'
challengeType: 5
forumTopicId: 302151
dashedName: problem-474-last-digits-of-divisors
@@ -8,17 +8,17 @@ dashedName: problem-474-last-digits-of-divisors
# --description--
-For a positive integer $n$ and digits $d$, we define $F(n, d)$ as the number of the divisors of $n$ whose last digits equal $d$.
+正の整数 $n$ と桁の数字 $d$ について、$n$ の約数のうち下位桁が $d$ と等しいものの個数を $F(n, d)$ と定義します。
-For example, $F(84, 4) = 3$. Among the divisors of 84 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84), three of them (4, 14, 84) have the last digit 4.
+例えば、$F(84, 4) = 3$ です。 84 の約数 (1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84) のうち、最下位の桁が 4 であるのは 3 つ (4, 14, 84) だからです。
-We can also verify that $F(12!, 12) = 11$ and $F(50!, 123) = 17\\,888$.
+$F(12!, 12) = 11$, $F(50!, 123) = 17\\,888$ であることも確認できます。
-Find $F({10}^6!, 65\\,432) \text{ modulo } ({10}^{16} + 61)$.
+$F({10}^6!, 65\\,432) \text{ mod } ({10}^{16} + 61)$ を求めなさい。
# --hints--
-`lastDigitsOfDivisors()` should return `9690646731515010`.
+`lastDigitsOfDivisors()` は `9690646731515010` を返す必要があります。
```js
assert.strictEqual(lastDigitsOfDivisors(), 9690646731515010);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md
index 4ab0b69b3a..53975cbb46 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-475-music-festival.md
@@ -1,6 +1,6 @@
---
id: 5900f5481000cf542c51005a
-title: 'Problem 475: Music festival'
+title: '問題 475: 音楽祭'
challengeType: 5
forumTopicId: 302152
dashedName: problem-475-music-festival
@@ -8,21 +8,21 @@ dashedName: problem-475-music-festival
# --description--
-$12n$ musicians participate at a music festival. On the first day, they form $3n$ quartets and practice all day.
+$12n$ 人の演奏家が音楽祭に参加します。 初日に $3n$ 組のカルテットを編成し、終日練習します。
-It is a disaster. At the end of the day, all musicians decide they will never again agree to play with any member of their quartet.
+そして大変な事態が起こります。 練習の後、すべての演奏家が自分のカルテットのいずれのメンバーとも共演しないと決めたのです。
-On the second day, they form $4n$ trios, each musician avoiding his previous quartet partners.
+2 日目に、演奏家たちは以前のカルテットのパートナーを避けて $4n$ 組のトリオを編成します。
-Let $f(12n)$ be the number of ways to organize the trios amongst the $12n$ musicians.
+$12n$ 人の演奏家の間でトリオを編成する方法が何通りあるかを、$f(12n)$ で表します。
-You are given $f(12) = 576$ and $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$.
+$f(12) = 576$ および $f(24)\bmod 1\\,000\\,000\\,007 = 509\\,089\\,824$ が与えられます。
-Find $f(600)\bmod 1\\,000\\,000\\,007$.
+$f(600)\bmod 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`musicFestival()` should return `75780067`.
+`musicFestival()` は `75780067` を返す必要があります。
```js
assert.strictEqual(musicFestival(), 75780067);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
index b87eca74b7..e20ba89154 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-476-circle-packing-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f5481000cf542c51005b
-title: 'Problem 476: Circle Packing II'
+title: '問題 476: 円を詰める (2)'
challengeType: 5
forumTopicId: 302153
dashedName: problem-476-circle-packing-ii
@@ -8,17 +8,17 @@ dashedName: problem-476-circle-packing-ii
# --description--
-Let $R(a, b, c)$ be the maximum area covered by three non-overlapping circles inside a triangle with edge lengths $a$, $b$ and $c$.
+辺の長さが $a$, $b$, $c$ の三角形の内側で、重ならない 3 つの円で覆うことができる最大面積を $R(a, b, c)$ とします。
-Let $S(n)$ be the average value of $R(a, b, c)$ over all integer triplets $(a, b, c)$ such that $1 ≤ a ≤ b ≤ c < a + b ≤ n$.
+$1 ≤ a ≤ b ≤ c < a + b ≤ n$ が成り立つすべての三つ組整数 $(a, b, c)$ における $R(a, b, c)$ の平均値を $S(n)$ とします。
-You are given $S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$.
+$S(2) = R(1, 1, 1) ≈ 0.31998$, $S(5) ≈ 1.25899$ が与えられます。
-Find $S(1803)$ rounded to 5 decimal places behind the decimal point.
+$S(1803)$ を求め、四捨五入して小数第 5 位まで示しなさい。
# --hints--
-`circlePackingTwo()` should return `110242.87794`.
+`circlePackingTwo()` は `110242.87794` を返す必要があります。
```js
assert.strictEqual(circlePackingTwo(), 110242.87794);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
index 24fa79f131..2fdf8e440e 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-477-number-sequence-game.md
@@ -1,6 +1,6 @@
---
id: 5900f54a1000cf542c51005c
-title: 'Problem 477: Number Sequence Game'
+title: '問題 477: 数列ゲーム'
challengeType: 5
forumTopicId: 302154
dashedName: problem-477-number-sequence-game
@@ -8,35 +8,35 @@ dashedName: problem-477-number-sequence-game
# --description--
-The number sequence game starts with a sequence $S$ of $N$ numbers written on a line.
+数列ゲームは、一列に書かれた $N$ 個の数からなる数列 $S$ で始まります。
-Two players alternate turns. At his turn, a player must select and remove either the first or the last number remaining in the sequence.
+2 人のプレイヤーが交互にプレイします。 プレイヤーは自分のターンで、数列に残っている最初の数または最後の数を選択し、取り除きます。
-The player score is the sum of all the numbers he has taken. Each player attempts to maximize his own sum.
+取った数の和がそのプレイヤーのスコアになります。 各プレイヤーは自分の数の和を最大にしようとします。
-If $N = 4$ and $S = \\{1, 2, 10, 3\\}$, then each player maximizes his score as follows:
+$N = 4$ かつ $S = \\{1, 2, 10, 3\\}$ の場合、各プレイヤーは次のようにスコアを最大化します。
-- Player 1: removes the first number (1)
-- Player 2: removes the last number from the remaining sequence (3)
-- Player 1: removes the last number from the remaining sequence (10)
-- Player 2: removes the remaining number (2)
+- プレイヤー 1: 最初の数 (1) を取り除く
+- プレイヤー 2: 残りの数列から最後の数 (3) を取り除く
+- プレイヤー 1: 残りの数列から最後の数 (10) を取り除く
+- プレイヤー 2: 残りの数 (2) を取り除く
-Player 1 score is $1 + 10 = 11$.
+プレイヤー 1 のスコアは $1 + 10 = 11$ です。
-Let $F(N)$ be the score of player 1 if both players follow the optimal strategy for the sequence $S = \\{s_1, s_2, \ldots, s_N\\}$ defined as:
+次のように定義される数列 $S = \\{s_1, s_2, \ldots, s_N\\}$ の最適な戦略に両プレイヤーが従った場合の、プレイヤー 1 のスコアを $F(N)$ とします。
- $s_1 = 0$
-- $s_{i + 1} = ({s_i}^2 + 45)$ modulo $1\\,000\\,000\\,007$
+- $s_{i + 1} = ({s_i}^2 + 45)$ mod $1\\,000\\,000\\,007$
-The sequence begins with $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,107\\,844, 894\\,218\\,625, \ldots\\}$.
+数列は $S = \\{0, 45, 2\\,070, 4\\,284\\,945, 753\\,524\\,550, 478\\,844, 894\\,218\\,625, \ldots\\}$ で始まります。
-You are given $F(2) = 45$, $F(4) = 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$.
+$F(2) = 45$, $F= 4\\,284\\,990$, $F(100) = 26\\,365\\,463\\,243$, $F(104) = 2\\,495\\,838\\,522\\,951$ が与えられます。
-Find $F({10}^8)$.
+$F({10}^8)$ を求めなさい。
# --hints--
-`numberSequenceGame()` should return `25044905874565164`.
+`numberSequenceGame()` は `25044905874565164` を返す必要があります。
```js
assert.strictEqual(numberSequenceGame(), 25044905874565164);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md
index 745aefc824..e3eedcf632 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-478-mixtures.md
@@ -1,6 +1,6 @@
---
id: 5900f54c1000cf542c51005e
-title: 'Problem 478: Mixtures'
+title: '問題 478: 混合物'
challengeType: 5
forumTopicId: 302155
dashedName: problem-478-mixtures
@@ -8,29 +8,29 @@ dashedName: problem-478-mixtures
# --description--
-Let us consider mixtures of three substances: $A$, $B$ and $C$. A mixture can be described by a ratio of the amounts of $A$, $B$, and $C$ in it, i.e., $(a : b : c)$. For example, a mixture described by the ratio (2 : 3 : 5) contains 20% $A$, 30% $B$ and 50% $C$.
+3 つの物質 $A$, $B$, $C$ の混合物について考えます。 混合物は、それに含まれる $A$, $B$, $C$ の比率によって $(a : b : c)$ と表すことができます。 例えば、比率 (2 : 3 : 5) で表された混合物には、$A$ が20%、$B$ が30%、そして $C$ が 50% 含まれています。
-For the purposes of this problem, we cannot separate the individual components from a mixture. However, we can combine different amounts of different mixtures to form mixtures with new ratios.
+この問題の目的上、混合物から各物質を分離することはできないものとします。 しかし、異なる混合物をさまざまな量で組み合わせ、新しい比率の混合物を作ることはできます。
-For example, say we have three mixtures with ratios (3 : 0 : 2), (3 : 6 : 11) and (3 : 3 : 4). By mixing 10 units of the first, 20 units of the second and 30 units of the third, we get a new mixture with ratio (6 : 5 : 9), since: ($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9)
+例えば、3 つの比率 (3 : 0 : 2), (3 : 6 : 11), (3 : 3 : 4) の混合物があるとします。 1 つ目の混合物を 10 単位、2 つ目の混合物を 20 単位、3 つ目の混合物を 30 単位使って混合すると、比率が (6 : 5 : 9) の混合物ができます。なぜなら、($10 \times \frac{3}{5} + 20 \times \frac{3}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{0}{5} + 20 \times \frac{6}{20} + 30 \times \frac{3}{10}$ : $10 \times \frac{2}{5} + 20 \times \frac{11}{20} + 30 \times \frac{4}{10}$) = (18 : 15 : 27) = (6 : 5 : 9) だからです。
-However, with the same three mixtures, it is impossible to form the ratio (3 : 2 : 1), since the amount of $B$ is always less than the amount of $C$.
+しかし、上と同じ 3 つの混合物を使って比率を (3 : 2 : 1) にすることは不可能です。どのように組み合わせても $B$ の量が $C$ の量より少なくなるからです。
-Let $n$ be a positive integer. Suppose that for every triple of integers $(a, b, c)$ with $0 ≤ a, b, c ≤ n$ and $gcd(a, b, c) = 1$, we have a mixture with ratio $(a : b : c)$. Let $M(n)$ be the set of all such mixtures.
+$n$ を正の整数とします。 $0 ≤ a, b, c ≤ n$ かつ $gcd(a, b, c) = 1$ を満たす整数の三つ組 $(a, b, c)$ に対して、比率 $(a : b : c)$ の混合物が常にあるとします。 そのようなすべての混合物の集合を $M(n)$ とします。
-For example, $M(2)$ contains the 19 mixtures with the following ratios:
+例えば、$M(2)$ には次の比率で 19 の混合物が含まれています。
-{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}.
+{(0 : 0 : 1), (0 : 1 : 0), (0 : 1 : 1), (0 : 1 : 2), (0 : 2 : 1), (1 : 0 : 0), (1 : 0 : 1), (1 : 0 : 2), (1 : 1 : 0), (1 : 1 : 1), (1 : 1 : 2), (1 : 2 : 0), (1 : 2 : 1), (1 : 2 : 2), (2 : 0 : 1), (2 : 1 : 0), (2 : 1 : 1), (2 : 1 : 2), (2 : 2 : 1)}
-Let $E(n)$ be the number of subsets of $M(n)$ which can produce the mixture with ratio (1 : 1 : 1), i.e., the mixture with equal parts $A$, $B$ and $C$.
+比率 (1 : 1 : 1)、すなわち $A$, $B$, $C$ が等しく配合された混合物を作れる $M(n)$ の部分集合の個数を $E(n)$ とします。
-We can verify that $E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$ and $E(500)\bmod {11}^8 = 13\\,801\\,403$.
+$E(1) = 103$, $E(2) = 520\\,447$, $E(10)\bmod {11}^8 = 82\\,608\\,406$, $E(500)\bmod {11}^8 = 13\\,801\\,403$ であることを確認できます。
-Find $E(10\\,000\\,000)\bmod {11}^8$.
+$E(10\\,000\\,000)\bmod {11}^8$ を求めなさい。
# --hints--
-`mixtures()` should return `59510340`.
+`mixtures()` は `59510340` を返す必要があります。
```js
assert.strictEqual(mixtures(), 59510340);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
index f2114e53c2..a02d502558 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-479-roots-on-the-rise.md
@@ -1,6 +1,6 @@
---
id: 5900f54b1000cf542c51005d
-title: 'Problem 479: Roots on the Rise'
+title: '問題 479: 根の増大'
challengeType: 5
forumTopicId: 302156
dashedName: problem-479-roots-on-the-rise
@@ -8,19 +8,19 @@ dashedName: problem-479-roots-on-the-rise
# --description--
-Let $a_k$, $b_k$, and $c_k$ represent the three solutions (real or complex numbers) to the expression $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$.
+式 $\frac{1}{x} = {\left(\frac{k}{x} \right)}^2 (k + x^2) - kx$ の 3 つの解 (実数または複素数) を、$a_k$, $b_k$, $c_k$ で表します。
-For instance, for $k = 5$, we see that $\\{a_5, b_5, c_5\\}$ is approximately $\\{5.727244, -0.363622 + 2.057397i, -0.363622 - 2.057397i\\}$.
+例えば $k = 5$ の場合、$\\{a_5, b_5, c_5\\}$ は約 $\\{5.727244, -0.3622 + 2.057397i, -0.363622 - 2.057397i\\}$ であることが分かります。
-Let $S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ for all integers $p$, $k$ such that $1 ≤ p, k ≤ n$.
+$1 ≤ p, k ≤ n$ を満たすすべての整数 $p$, $k$ に対して、$S(n) = \displaystyle\sum_{p = 1}^n \sum_{k = 1}^n {(a_k + b_k)}^p {(b_k + c_k)}^p {(c_k + a_k)}^p$ と定義します。
-Interestingly, $S(n)$ is always an integer. For example, $S(4) = 51\\,160$.
+興味深いことに、$S(n)$ は常に整数です。 例えば、$S(4) ≈ 51\\,160$ です。
-Find $S({10}^6) \text{ modulo } 1\\,000\\,000\\,007$.
+$S({10}^6) \text{ mod } 1\\,000\\,000\\,007$ を求めなさい。
# --hints--
-`rootsOnTheRise()` should return `191541795`.
+`rootsOnTheRise()` は `191541795` を返す必要があります。
```js
assert.strictEqual(rootsOnTheRise(), 191541795);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
index 8ffff17076..a4b94b7028 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/project-euler/problem-480-the-last-question.md
@@ -1,6 +1,6 @@
---
id: 5900f54c1000cf542c51005f
-title: 'Problem 480: The Last Question'
+title: '問題 480: 最後の質問'
challengeType: 5
forumTopicId: 302158
dashedName: problem-480-the-last-question
@@ -8,39 +8,39 @@ dashedName: problem-480-the-last-question
# --description--
-Consider all the words which can be formed by selecting letters, in any order, from the phrase:
+次のフレーズから任意の順序で文字を選んで作ることができる、すべての単語を考えます。
$$\mathbf{\text{thereisasyetinsufficientdataforameaningfulanswer}}$$
-Suppose those with 15 letters or less are listed in alphabetical order and numbered sequentially starting at 1.
+15 個以下の文字がアルファベット順に列挙され、1 から順に番号が振られているとします。
-The list would include:
+そのリストには以下が含まれるでしょう。
$$\begin{align} & 1: \text{a} \\\\ & 2: \text{aa} \\\\ & 3: \text{aaa} \\\\ & 4: \text{aaaa} \\\\ & 5: \text{aaaaa} \\\\ & 6: \text{aaaaaa} \\\\ & 7: \text{aaaaaac} \\\\ & 8: \text{aaaaaacd} \\\\ & 9: \text{aaaaaacde} \\\\ & 10: \text{aaaaaacdee} \\\\ & 11: \text{aaaaaacdeee} \\\\ & 12: \text{aaaaaacdeeee} \\\\ & 13: \text{aaaaaacdeeeee} \\\\ & 14: \text{aaaaaacdeeeeee} \\\\ & 15: \text{aaaaaacdeeeeeef} \\\\ & 16: \text{aaaaaacdeeeeeeg} \\\\ & 17: \text{aaaaaacdeeeeeeh} \\\\ & \ldots \\\\ & 28: \text{aaaaaacdeeeeeey} \\\\ & 29: \text{aaaaaacdeeeeef} \\\\ & 30: \text{aaaaaacdeeeeefe} \\\\ & \ldots \\\\ & 115246685191495242: \text{euleoywuttttsss} \\\\ & 115246685191495243: \text{euler} \\\\ & 115246685191495244: \text{eulera} \\\\ & ... \\\\ & 525069350231428029: \text{ywuuttttssssrrr} \\\\ \end{align}$$
-Define $P(w)$ as the position of the word $w$.
+$P(w)$ を、単語 $w$ の位置とします。
-Define $W(p)$ as the word in position $p$.
+$W(p)$ を、位置 $p$ にある単語とします。
-We can see that $P(w)$ and $W(p)$ are inverses: $P(W(p)) = p$ and $W(P(w)) = w$.
+$P(w)$ と $W(p)$ は逆元であることがわかります。つまり、$P(W(p)) = p$ および $W(P(w)) = w$ です。
-Examples:
+例:
$$\begin{align} & W(10) = \text{ aaaaaacdee} \\\\ & P(\text{aaaaaacdee}) = 10 \\\\ & W(115246685191495243) = \text{ euler} \\\\ & P(\text{euler}) = 115246685191495243 \\\\ \end{align}$$
-Find $$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering})).$$
+$$W(P(\text{legionary}) + P(\text{calorimeters}) - P(\text{annihilate}) + P(\text{orchestrated}) - P(\text{fluttering}))$$ を求めなさい。
-Give your answer using lowercase characters (no punctuation or space).
+回答は、 (句読点やスペースを含めずに) 小文字で書くこと 。
# --hints--
-`euler480()` should return a string.
+`euler480()` は文字列を返す必要があります。
```js
assert(typeof euler480() === 'string');
```
-`euler480()` should return the string `turnthestarson`.
+`euler480()` は文字列 `turnthestarson` を返す必要があります。
```js
assert.strictEqual(euler480(), 'turnthestarson');
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md
index e791c06558..c8c3e0b001 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/100-doors.md
@@ -1,6 +1,6 @@
---
id: 594810f028c0303b75339acb
-title: 100 doors
+title: 100個のドア
challengeType: 5
forumTopicId: 302217
dashedName: 100-doors
@@ -8,27 +8,27 @@ dashedName: 100-doors
# --description--
-There are 100 doors in a row that are all initially closed. You make 100 passes by the doors. The first time through, visit every door and 'toggle' the door (if the door is closed, open it; if it is open, close it). The second time, only visit every 2nd door (i.e., door #2, #4, #6, ...) and toggle it. The third time, visit every 3rd door (i.e., door #3, #6, #9, ...), etc., until you only visit the 100th door.
+100個のドアが連続してあり、最初はすべてのドアは閉じています。 100個のドア全てを対象とします。 1回目はすべてのドアを訪問し、ドアを「切り替え」(ドアが閉じられている場合は、開き、開いている場合は、閉じる)ます。 2回目は、2の倍数のドア(#2のドア、#4のドア、#6のドア...)に訪問し、それぞれの開閉を「切り替え」ます。 3回目は、3の倍数のドア(#3のドア、#6のドア、#9のドア...)を訪問して「切替」を行い、100番目のドアまで続けます。
# --instructions--
-Implement a function to determine the state of the doors after the last pass. Return the final result in an array, with only the door number included in the array if it is open.
+3回の訪問が終了した時点でのドアの状態を示す関数を作成します。 配列形式で最終的な結果を返します。開いている状態のドアの番号を配列形式で返します。
# --hints--
-`getFinalOpenedDoors` should be a function.
+`getFinalOpenedDoors` という関数です。
```js
assert(typeof getFinalOpenedDoors === 'function');
```
-`getFinalOpenedDoors` should return an array.
+`getFinalOpenedDoors` は配列を返します。
```js
assert(Array.isArray(getFinalOpenedDoors(100)));
```
-`getFinalOpenedDoors` should produce the correct result.
+`getFinalOpenedDoors` は正確な結果を返します。
```js
assert.deepEqual(getFinalOpenedDoors(100), solution);
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md
index 7bf28fe4df..58760ce94b 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/24-game.md
@@ -8,23 +8,23 @@ dashedName: 24-game
# --description--
-The [24 Game](https://en.wikipedia.org/wiki/24_Game) tests a person's mental arithmetic.
+[24 Game](https://en.wikipedia.org/wiki/24_Game) では、人の暗算能力をテストします。
-The aim of the game is to arrange four numbers in a way that when evaluated, the result is 24
+ゲームの目的は、算出結果が24になるように4つの数字を配置することです。
# --instructions--
-Implement a function that takes a string of four digits as its argument, with each digit from 1 to 9 (inclusive) with repetitions allowed, and returns an arithmetic expression that evaluates to the number 24. If no such solution exists, return "no solution exists".
+4桁の文字列を引数とする関数を作成します。 各桁は、1 から 9 までの数字で、繰り返しも可能です。この関数は、算出結果が数値 24 になる算術式を返します。 そのような解が存在しない場合は、「解が存在しません」を返します。
-**Rules:**
+**ルール:**
solve24("4878"); | (7-8/8)\*4 |
| solve24("1234"); | 3\*1\*4\*2 |
@@ -33,31 +33,31 @@ Implement a function that takes a string of four digits as its argument, with ea
# --hints--
-`solve24` should be a function.
+`solve24` という関数です。
```js
assert(typeof solve24 === 'function');
```
-`solve24("4878")` should return `(7-8/8)*4` or `4*(7-8/8)`
+`solve24("4878")` は `(7-8/8)*4` または `4*(7-8/8)` を返します。
```js
assert(include(answers[0], removeParentheses(solve24(testCases[0]))));
```
-`solve24("1234")` should return any arrangement of `1*2*3*4`
+`solve24("1234")` は任意の配列で `1*2*3*4` を返します。
```js
assert(include(answers[1], removeParentheses(solve24(testCases[1]))));
```
-`solve24("6789")` should return `(6*8)/(9-7)` or `(8*6)/(9-7)`
+`solve24("6789")` は `(6*8)/(9-7)` または `(8*6)/(9-7)` を返します。
```js
assert(include(answers[2], removeParentheses(solve24(testCases[2]))));
```
-`solve24("1127")` should return a permutation of `(1+7)*(1+2)`
+`solve24("1127")` は `(1+7)*(1+2)` の順列を返します。
```js
assert(include(answers[3], removeParentheses(solve24(testCases[3]))));
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/9-billion-names-of-god-the-integer.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/9-billion-names-of-god-the-integer.md
index 125236ca75..a7b9c9d210 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/9-billion-names-of-god-the-integer.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/9-billion-names-of-god-the-integer.md
@@ -1,6 +1,6 @@
---
id: 5949b579404977fbaefcd736
-title: 9 billion names of God the integer
+title: 90億の神の御名 整数
challengeType: 5
forumTopicId: 302219
dashedName: 9-billion-names-of-god-the-integer
@@ -8,77 +8,77 @@ dashedName: 9-billion-names-of-god-the-integer
# --description--
-This task is a variation of the [short story by Arthur C. Clarke](https://en.wikipedia.org/wiki/The Nine Billion Names of God#Plot_summary "wp: The Nine Billion Names of God#Plot_summary").
+このタスクは、[アーサー・C・クラークの短編](https://en.wikipedia.org/wiki/The Nine Billion Names of God#Plot_summary "wp: The Nine Billion Names of God#Plot_summary")のバリエーションです。
-(Solvers should be aware of the consequences of completing this task.)
+(ソルバーは、このタスクの完了結果を認識している必要があります。)
-In detail, to specify what is meant by a "name":
+「名前」が意味するものを詳細に示します。
1 - 1 1 - 1 1 1 - 1 2 1 1 - 1 2 2 1 1 -1 3 3 2 1 1 + 1 1 + 1 1 1 + 1 2 1 1 + 1 2 1 1 1 +1 3 3 2 1 1-Where row $n$ corresponds to integer $n$, and each column $C$ in row $m$ from left to right corresponds to the number of names beginning with $C$. +$n$ 行は、整数 $n$に相当し、左から右への $m$行内の$C$の各列は、$C$で始まる名前の数に相当します。 -Optionally note that the sum of the $n$-th row $P(n)$ is the integer partition function. +また、$n$番目の $P(n)$ 行の合計は、整数パーティション関数であることに注意してください。 # --instructions-- -Implement a function that returns the sum of the $n$-th row. +$n$番目の行の合計を返す関数を作成します。 # --hints-- -`numberOfNames` should be function. +`numberOfNames` という関数です。 ```js assert(typeof numberOfNames === 'function'); ``` -`numberOfNames(5)` should equal 7. +`numberOfNames(5)` は7に等しいです。 ```js assert.equal(numberOfNames(5), 7); ``` -`numberOfNames(12)` should equal 77. +`numberOfNames(12)` は77に等しいです。 ```js assert.equal(numberOfNames(12), 77); ``` -`numberOfNames(18)` should equal 385. +`numberOfNames(18)` は385に等しいです。 ```js assert.equal(numberOfNames(18), 385); ``` -`numberOfNames(23)` should equal 1255. +`numberOfNames(23)` は1255に等しいです。 ```js assert.equal(numberOfNames(23), 1255); ``` -`numberOfNames(42)` should equal 53174. +`numberOfNames(42)` は53174に等しいです。 ```js assert.equal(numberOfNames(42), 53174); ``` -`numberOfNames(123)` should equal 2552338241. +`numberOfNames(123)` は2552338241に等しいです。 ```js assert.equal(numberOfNames(123), 2552338241); diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/abc-problem.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/abc-problem.md index b42b619749..d6e1b9edb8 100644 --- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/abc-problem.md +++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/abc-problem.md @@ -1,6 +1,6 @@ --- id: 594810f028c0303b75339acc -title: ABC Problem +title: ABC問題 challengeType: 5 forumTopicId: 302220 dashedName: abc-problem @@ -8,7 +8,7 @@ dashedName: abc-problem # --description-- -You are given a collection of ABC blocks (e.g., childhood alphabet blocks). There are 20 blocks with two letters on each block. A complete alphabet is guaranteed amongst all sides of the blocks. The sample collection of blocks: +ABCブロック一式が与えられます (例えば、子供用のアルファベットブロック)。 20個のブロックがあり、各ブロックに2文字入っています。 ブロックの全側面を見れば、すべてのアルファベットが必ずあります。 ブロックのサンプル一式:
(B O) (X K) @@ -34,60 +34,60 @@ You are given a collection of ABC blocks (e.g., childhood alphabet blocks). Ther # --instructions-- -Implement a function that takes a string (word) and determines whether the word can be spelled with the given collection of blocks. +文字列(単語)を取って、与えられたブロック一式で単語が作れるかを判定する関数を作成します。 -Some rules to keep in mind: +留意すべきルール:
- What is the smallest positive integer whose square ends in the digits 269,696? + 2乗の末尾が269,696になる最小の正の整数は何ですか?-He thought the answer might be 99,736, whose square is 9,947,269,696; but he couldn't be certain. +答えは99,736で、その2乗は9,947,269,696であると考えましたが、確信はありませんでした。 -The task is to find out if Babbage had the right answer. +バベッジの答えが正しかったかどうかを調べましょう。 # --instructions-- -Implement a function to return the lowest integer that satisfies the Babbage problem. If Babbage was right, return Babbage's number. +バベッジの問題の答えとなる最小の整数を返す関数を作成します。 バベッジが正しかった場合は、バベッジが答えた数値を返します。 # --hints-- -`babbage` should be a function. +`babbage` という関数です。 ```js assert(typeof babbage === 'function'); ``` -`babbage(99736, 269696)` should not return 99736 (there is a smaller answer). +`babbage(99736, 269696)` は 99736 を返さないはずです(もっと小さな答えがあります)。 ```js assert.equal(babbage(babbageAns, endDigits), answer); diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/balanced-brackets.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/balanced-brackets.md index 5045fbd2ca..1614664350 100644 --- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/balanced-brackets.md +++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/balanced-brackets.md @@ -1,6 +1,6 @@ --- id: 594dc6c729e5700999302b45 -title: Balanced brackets +title: 対の括弧 challengeType: 5 forumTopicId: 302230 dashedName: balanced-brackets @@ -8,129 +8,129 @@ dashedName: balanced-brackets # --description-- -Determine whether a generated string of brackets is balanced; that is, whether it consists entirely of pairs of opening/closing brackets (in that order), none of which mis-nest. +生成された括弧が対になっているかどうかを確認します。括弧が開き括弧と閉じ括弧の順番で対になっているかどうか、誤った入れ子になっていないかどうかを確認します。 -**Examples:** -| Input | Output | -| ------------------------- | ------ | -|
\[] | true |
-| ]\[ | false |
-| [][] | true |
-| ]\[] | false |
-| \[]]\[\[] | false |
-| \[\[\[\[]]]] | true |
+**例:**
+| 入力 | 出力 |
+| ------------------------- | -- |
+| \[] | 真 |
+| ]\[ | 偽 |
+| [][] | 真 |
+| ]\[] | 偽 |
+| \[]]\[\[] | 偽 |
+| \[\[\[\[]]]] | 真 |
# --hints--
-`isBalanced` should be a function.
+`isBalanced` という関数です。
```js
assert(typeof isBalanced === 'function');
```
-`isBalanced("[]")` should return true.
+`isBalanced("[]")` は真を返します。
```js
assert(isBalanced(testCases[0]));
```
-`isBalanced("]][[[][][][]][")` should return false.
+`isBalanced("]][[[][][][]][")` は偽を返します。
```js
assert(!isBalanced(testCases[1]));
```
-`isBalanced("[][[[[][][[[]]]]]]")` should return true.
+`isBalanced("[][[[[][][[[]]]]]]")` は真を返します。
```js
assert(isBalanced(testCases[2]));
```
-`isBalanced("][")` should return false.
+`isBalanced("][")` は偽を返します。
```js
assert(!isBalanced(testCases[3]));
```
-`isBalanced("[[[]]]][[]")` should return false.
+`isBalanced("[[[]]]][[]")` は偽を返します。
```js
assert(!isBalanced(testCases[4]));
```
-`isBalanced("][[]")` should return false.
+`isBalanced("][[]")` は偽を返します。
```js
assert(!isBalanced(testCases[5]));
```
-`isBalanced("][[][]][[[]]")` should return false.
+`isBalanced("][[][]][[[]]")` は偽を返します。
```js
assert(!isBalanced(testCases[6]));
```
-`isBalanced("[[][]]][")` should return false.
+`isBalanced("[[][]]][")` は偽を返します。
```js
assert(!isBalanced(testCases[7]));
```
-`isBalanced("[[[]]][[]]]][][[")` should return false.
+`isBalanced("[[[]]][[]]]][][[")` は偽を返します。
```js
assert(!isBalanced(testCases[8]));
```
-`isBalanced("[]][[]]][[[[][]]")` should return false.
+`isBalanced("[]][[]]][[[[][]]")` は偽を返します。
```js
assert(!isBalanced(testCases[9]));
```
-`isBalanced("][]][[][")` should return false.
+`isBalanced("][]][[][")` は偽を返します。
```js
assert(!isBalanced(testCases[10]));
```
-`isBalanced("[[]][[][]]")` should return true.
+`isBalanced("[[]][[][]]")` は真を返します。
```js
assert(isBalanced(testCases[11]));
```
-`isBalanced("[[]]")` should return true.
+`isBalanced("[[]]")` は真を返します。
```js
assert(isBalanced(testCases[12]));
```
-`isBalanced("]][]][[]][[[")` should return false.
+`isBalanced("]][]][[]][[[")` は偽を返します。
```js
assert(!isBalanced(testCases[13]));
```
-`isBalanced("][]][][[")` should return false.
+`isBalanced("][]][][[")` は偽を返します。
```js
assert(!isBalanced(testCases[14]));
```
-`isBalanced("][][")` should return false.
+`isBalanced("][][")` は偽を返します。
```js
assert(!isBalanced(testCases[15]));
```
-`isBalanced("[]]]")` should return false.
+`isBalanced("[]]]")` は偽を返します。
```js
assert(!isBalanced(testCases[16]));
```
-`isBalanced("")` should return true.
+`isBalanced("")` は真を返します。
```js
assert(isBalanced(testCases[17]));
diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/circles-of-given-radius-through-two-points.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/circles-of-given-radius-through-two-points.md
index bbd910fb6c..396f67965c 100644
--- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/circles-of-given-radius-through-two-points.md
+++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/circles-of-given-radius-through-two-points.md
@@ -1,6 +1,6 @@
---
id: 5951815dd895584b06884620
-title: Circles of given radius through two points
+title: 2点を通る指定半径の円
challengeType: 5
forumTopicId: 302231
dashedName: circles-of-given-radius-through-two-points
@@ -8,30 +8,30 @@ dashedName: circles-of-given-radius-through-two-points
# --description--
-Given two points on a plane and a radius, usually two circles of given radius can be drawn through the points.
+平面上の2点と半径が指定されると、指定半径の円が2点を通って2つ描かれます。
-**Exceptions:**
+**例外:**
"Radius Zero"."Coincident point. Infinite solutions"."No intersection. Points further apart than circle diameter"."Radius Zero" を返します。"Coincident point. Infinite solutions" を返します。"No intersection. Points further apart than circle diameter" を返します。p1 p2 r 0.1234, 0.9876 0.8765, 0.2345 2.0 @@ -43,37 +43,37 @@ Implement a function that takes two points and a radius and returns the two circ # --hints-- -`getCircles` should be a function. +`getCircles` という関数です。 ```js assert(typeof getCircles === 'function'); ``` -`getCircles([0.1234, 0.9876], [0.8765, 0.2345], 2.0)` should return `[[1.8631, 1.9742], [-0.8632, -0.7521]]`. +`getCircles([0.1234, 0.9876], [0.8765, 0.2345], 2.0)` は `[[1.8631, 1.9742], [-0.8632, -0.7521]]` を返します。 ```js assert.deepEqual(getCircles(...testCases[0]), answers[0]); ``` -`getCircles([0.0000, 2.0000], [0.0000, 0.0000], 1.0)` should return `[0, 1]` +`getCircles([0.0000, 2.0000], [0.0000, 0.0000], 1.0)` は `[0, 1]` を返します。 ```js assert.deepEqual(getCircles(...testCases[1]), answers[1]); ``` -`getCircles([0.1234, 0.9876], [0.1234, 0.9876], 2.0)` should return `Coincident point. Infinite solutions` +`getCircles([0.1234, 0.9876], [0.1234, 0.9876], 2.0)` は `Coincident point. Infinite solutions `を返します。 ```js assert.deepEqual(getCircles(...testCases[2]), answers[2]); ``` -`getCircles([0.1234, 0.9876], [0.8765, 0.2345], 0.5)` should return `No intersection. Points further apart than circle diameter` +`getCircles([0.1234, 0.9876], [0.8765, 0.2345], 0.5)` は、`No intersection. Points further apart than circle diameter ` を返します。 ```js assert.deepEqual(getCircles(...testCases[3]), answers[3]); ``` -`getCircles([0.1234, 0.9876], [0.1234, 0.9876], 0.0)` should return `Radius Zero` +`getCircles([0.1234, 0.9876], [0.1234, 0.9876], 0.0)` は`Radius Zero` を返します。 ```js assert.deepEqual(getCircles(...testCases[4]), answers[4]); diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/closest-pair-problem.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/closest-pair-problem.md index 9221d424b3..015271b19c 100644 --- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/closest-pair-problem.md +++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/closest-pair-problem.md @@ -1,6 +1,6 @@ --- id: 5951a53863c8a34f02bf1bdc -title: Closest-pair problem +title: 最近点対の問題 challengeType: 5 forumTopicId: 302232 dashedName: closest-pair-problem @@ -8,9 +8,9 @@ dashedName: closest-pair-problem # --description-- -Provide a function to find the closest two points among a set of given points in two dimensions. +2次元の任意の点の集合の中から最も近い2点を見つける関数を提供します。 -The straightforward solution is a $O(n^2)$ algorithm (which we can call *brute-force algorithm*); the pseudo-code (using indexes) could be simply: +簡単な解決策は、(*brute-force algorithm*と呼ばれる)$O(n^2)$ アルゴリズムを使用することです。疑似コード(インデックス使用)は単純に以下のようになります。bruteForceClosestPair of P(1), P(2), ... P(N) if N < 2 then @@ -30,7 +30,7 @@ The straightforward solution is a $O(n^2)$ algorithm (which we can call *brute-f endif-A better algorithm is based on the recursive divide and conquer approach, which is $O(n\log n)$ a pseudo-code could be: +より好ましいアルゴリズムは、$O(n\log n)$の再帰的な分割統治法に基づいており、疑似コードは以下のようになります。closestPair of (xP, yP) where xP is P(1) .. P(N) sorted by x coordinate, and @@ -65,9 +65,9 @@ A better algorithm is based on the recursive divide and conquer approach, which endif-For the input, expect the argument to be an array of `Point` objects with `x` and `y` members set to numbers. Return an object containing the key:value pairs for `distance` and `pair` (the pair of two closest points). +入力には、引数を `x` と `y` メンバーが数字に設定されている `Point` オブジェクトの配列であると想定します。 `distance` と `pair` の key:value ペア (最も近い2点のペア) を含むオブジェクトを返します。 -For example `getClosestPair` with input array `points`: +例えば、入力配列 `points` を持つ `getClosestPair` の場合 ```js const points = [ @@ -77,7 +77,7 @@ const points = [ ]; ``` -Would return: +次のものを返します。 ```js { @@ -95,24 +95,24 @@ Would return: } ``` -**Note:** Sort the `pair` array by their `x` values in incrementing order. +**注記: ** `pair` 配列を `x` の値で昇順に並べ替えます。 # --hints-- -`getClosestPair` should be a function. +`getClosestPair` という関数です。 ```js assert(typeof getClosestPair === 'function'); ``` -`getClosestPair(points1).distance` should be `0.0894096443343775`. +`getClosestPair(points1).distance` は `0.0894096443343775` になります。 ```js assert.equal(getClosestPair(points1).distance, answer1.distance); ``` -`getClosestPair(points1).pair` should be `[ { x: 7.46489, y: 4.6268 }, { x: 7.46911, y: 4.71611 } ]`. +`getClosestPair(points1).pair` は `[ { x: 7.46489, y: 4.6268 }, { x: 7.46911, y: 4.71611 } ]` になります。 ```js assert.deepEqual( @@ -121,13 +121,13 @@ assert.deepEqual( ); ``` -`getClosestPair(points2).distance` should be `65.06919393998976`. +`getClosestPair(points2).distance` は `65.06919393998976` になります。 ```js assert.equal(getClosestPair(points2).distance, answer2.distance); ``` -`getClosestPair(points2).pair` should be `[ { x: 37134, y: 1963 }, { x: 37181, y: 2008 } ]`. +`getClosestPair(points2).pair` は `[ { x: 37134, y: 1963 }, { x: 37181, y: 2008 } ]` になります。 ```js assert.deepEqual( @@ -136,13 +136,13 @@ assert.deepEqual( ); ``` -`getClosestPair(points3).distance` should be `6754.625082119658`. +`getClosestPair(points3).distance` は `6754.625082119658` になります。 ```js assert.equal(getClosestPair(points3).distance, answer3.distance); ``` -`getClosestPair(points3).pair` should be `[ { x: 46817, y: 64975 }, { x: 48953, y: 58567 } ]`. +`getClosestPair(points3).pair` は `[ { x: 46817, y: 64975 }, { x: 48953, y: 58567 } ]` になります。 ```js assert.deepEqual( diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/combinations.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/combinations.md index 27e9a3fa6d..6c76c0d53b 100644 --- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/combinations.md +++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/combinations.md @@ -1,6 +1,6 @@ --- id: 5958469238c0d8d2632f46db -title: Combinations +title: 組み合わせ challengeType: 5 forumTopicId: 302233 dashedName: combinations @@ -8,11 +8,11 @@ dashedName: combinations # --description-- -Given non-negative integers `m` and `n`, generate all size `m` combinations of the integers from `0` (zero) to `n-1` in sorted order (each combination is sorted and the entire table is sorted). +負でない整数 `m` と `n` が与えられると、`0` (ゼロ) から `n-1` までの整数におけるすべての `m` の組み合わせをソート順に生成します (各組合せとテーブル全体を並べ替えます)。 -**Example:** +**例:** -`3` comb `5` is: +`3` と `5` の組み合わせは以下の通りです。0 1 2 0 1 3 @@ -28,19 +28,19 @@ Given non-negative integers `m` and `n`, generate all size `m` combinations of t # --hints-- -`combinations` should be a function. +`combinations` という関数です。 ```js assert(typeof combinations === 'function'); ``` -`combinations(3, 5)` should return `[[0, 1, 2], [0, 1, 3], [0, 1, 4], [0, 2, 3], [0, 2, 4], [0, 3, 4], [1, 2, 3], [1, 2, 4], [1, 3, 4], [2, 3, 4]]`. +`combinations(3, 5)` は `[[0, 1, 2], [0, 1, 3], [0, 1, 4], [0, 2, 3], [0, 2, 4], [0, 3, 4], [1, 2, 3], [1, 2, 4], [1, 3, 4], [2, 3, 4]]` を返します。 ```js assert.deepEqual(combinations(testInput1[0], testInput1[1]), testOutput1); ``` -`combinations(4, 6)` should return `[[0,1,2,3], [0,1,2,4], [0,1,2,5], [0,1,3,4], [0,1,3,5], [0,1,4,5], [0,2,3,4], [0,2,3,5], [0,2,4,5], [0,3,4,5], [1,2,3,4], [1,2,3,5], [1,2,4,5], [1,3,4,5], [2,3,4,5]]` +`combinations(4, 6)` は `[[0,1,2,3], [0,1,2,4], [0,1,2,5], [0,1,3,4], [0,1,3,5], [0,1,4,5], [0,2,3,4], [0,2,3,5], [0,2,4,5], [0,3,4,5], [1,2,3,4], [1,2,3,5], [1,2,4,5], [1,3,4,5], [2,3,4,5]]` を返します。 ```js assert.deepEqual(combinations(testInput2[0], testInput2[1]), testOutput2); diff --git a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/comma-quibbling.md b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/comma-quibbling.md index 6223a523ce..713372d49a 100644 --- a/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/comma-quibbling.md +++ b/curriculum/challenges/japanese/10-coding-interview-prep/rosetta-code/comma-quibbling.md @@ -1,6 +1,6 @@ --- id: 596e414344c3b2872167f0fe -title: Comma quibbling +title: コンマキブリング challengeType: 5 forumTopicId: 302234 dashedName: comma-quibbling @@ -8,63 +8,63 @@ dashedName: comma-quibbling # --description-- -Comma quibbling is a task originally set by Eric Lippert in his [blog](https://blogs.msdn.com/b/ericlippert/archive/2009/04/15/comma-quibbling.aspx). +カンマキブリング はもともとエリック・リッパートが彼の [ブログ](https://blogs.msdn.com/b/ericlippert/archive/2009/04/15/comma-quibbling.aspx) で提示したタスクです。 # --instructions-- -Write a function to generate a string output which is the concatenation of input words from a list/sequence where: +リスト/シーケンスからの入力単語の連結である文字列を出力する関数を作成します。-
-Test your function with the following series of inputs showing your output here on this page: +次の一連の入力によりこのページに出力表示して、関数をテストします。- An input of no words produces the output string of just the two brace characters (
-"{}")- An input of just one word, e.g.
-["ABC"], produces the output string of the word inside the two braces, e.g."{ABC}"- An input of two words, e.g.
-["ABC", "DEF"], produces the output string of the two words inside the two braces with the words separated by the string" and ", e.g."{ABC and DEF}"- An input of three or more words, e.g.
+["ABC", "DEF", "G", "H"], produces the output string of all but the last word separated by", "with the last word separated by" and "and all within braces; e.g."{ABC, DEF, G and H}"- 単語を入力しなかった場合、2つの中括弧文字 (
+"{}") だけの出力文字列が生成されます。- 1単語、例えば
+["ABC"]、だけを入力した場合、"{ABC}"のように、2つの中括弧の中にその単語が出力文字列として生成されます。- 2つの単語、例えば
+["ABC", "DEF"]、を入力した場合、"{ABC and DEF}"のように、文字列" and "に区切られた2つの単語が、2つの中括弧の中に出力文字列として生成されます。- 3つ以上の単語、 例えば
["ABC", "DEF", "G", "H"]を入力した場合、"{ABC, DEF, G and H}"のように、最後の単語以外のすべての単語は、", "で区切られ、最後の単語は" and "で区切られ、すべての単語が中括弧の中に出力文字列として生成されます。
100), and1 min, 40 sec).100)。1 min, 40 sec)。2 hr, 59 sec |
-| 86400 | 1 d |
-| 6000000 | 9 wk, 6 d, 10 hr, 40 min |
+| 入力した数字 | 出力された数字 |
+| ------- | ------------------------- |
+| 7259 | 2 hr, 59 sec |
+| 86400 | 1 d |
+| 6000000 | 9 wk, 6 d, 10 hr, 40 min |
-1 d and not 0 wk, 1 d, 0 hr, 0 min, 0 sec).
+ ただし、ゼロではない値 のみ が出力されます(例えば 0 wk, 1 d, 0 hr, 0 min, 0 secではなく、1 dを返します)。
2 min, 10 sec and not 1 min, 70 sec or 130 sec).
+ 可能な限り小さな単位よりも大きな単位を優先します (例えば 1 min, 70 sec または 130 sec ではなく、2 min, 10 sec を返します)。
There are six ways to make change for 15 cents:
+15セントを両替するには6つの組み合わせがあります。