From 47fc3c6761c69369f58f7016ac53156a1b41ca08 Mon Sep 17 00:00:00 2001
From: gikf <60067306+gikf@users.noreply.github.com>
Date: Thu, 22 Jul 2021 05:38:46 +0200
Subject: [PATCH] fix(curriculum): clean-up Project Euler 281-300 (#42922)
* fix: clean-up Project Euler 281-300
* fix: missing image extension
* fix: missing power
Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
* fix: missing subscript
Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
Co-authored-by: Tom <20648924+moT01@users.noreply.github.com>
---
.../problem-281-pizza-toppings.md | 18 +++++-----
.../problem-282-the-ackermann-function.md | 21 ++++++++----
...h-the-area--perimeter-ratio-is-integral.md | 12 +++----
.../problem-284-steady-squares.md | 22 ++++++++-----
.../problem-285-pythagorean-odds.md | 18 +++++-----
.../problem-286-scoring-probabilities.md | 14 ++++----
...encoding-a-simple-compression-algorithm.md | 33 +++++++++++--------
.../problem-288-an-enormous-factorial.md | 24 ++++++++------
.../problem-289-eulerian-cycles.md | 22 +++++++------
.../problem-290-digital-signature.md | 10 +++---
.../problem-291-panaitopol-primes.md | 12 +++----
.../problem-292-pythagorean-polygons.md | 23 +++++++------
.../problem-293-pseudo-fortunate-numbers.md | 18 +++++-----
...oblem-294-sum-of-digits---experience-23.md | 19 ++++++-----
.../problem-295-lenticular-holes.md | 32 ++++++++++--------
...roblem-296-angular-bisector-and-tangent.md | 16 +++++----
.../problem-297-zeckendorf-representation.md | 20 +++++++----
.../problem-298-selective-amnesia.md | 25 ++++++++++----
.../problem-299-three-similar-triangles.md | 28 +++++++++-------
.../problem-300-protein-folding.md | 20 +++++++----
20 files changed, 238 insertions(+), 169 deletions(-)
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
index 9ac6cf33a6..46837ff79b 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-281-pizza-toppings.md
@@ -8,20 +8,22 @@ dashedName: problem-281-pizza-toppings
# --description--
-You are given a pizza (perfect circle) that has been cut into m·n equal pieces and you want to have exactly one topping on each slice.
+You are given a pizza (perfect circle) that has been cut into $m·n$ equal pieces and you want to have exactly one topping on each slice.
-Let f(m,n) denote the number of ways you can have toppings on the pizza with m different toppings (m ≥ 2), using each topping on exactly n slices (n ≥ 1). Reflections are considered distinct, rotations are not.
+Let $f(m,n)$ denote the number of ways you can have toppings on the pizza with $m$ different toppings ($m ≥ 2$), using each topping on exactly $n$ slices ($n ≥ 1$). Reflections are considered distinct, rotations are not.
-Thus, for instance, f(2,1) = 1, f(2,2) = f(3,1) = 2 and f(3,2) = 16. f(3,2) is shown below:
+Thus, for instance, $f(2,1) = 1$, $f(2,2) = f(3,1) = 2$ and $f(3,2) = 16$. $f(3,2)$ is shown below:
-Find the sum of all f(m,n) such that f(m,n) ≤ 1015.
+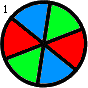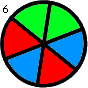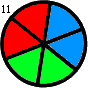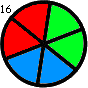 +
+Find the sum of all $f(m,n)$ such that $f(m,n) ≤ {10}^{15}$.
# --hints--
-`euler281()` should return 1485776387445623.
+`pizzaToppings()` should return `1485776387445623`.
```js
-assert.strictEqual(euler281(), 1485776387445623);
+assert.strictEqual(pizzaToppings(), 1485776387445623);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler281(), 1485776387445623);
## --seed-contents--
```js
-function euler281() {
+function pizzaToppings() {
return true;
}
-euler281();
+pizzaToppings();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
index 5abd58ec44..aaaf1c46b6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
@@ -8,18 +8,25 @@ dashedName: problem-282-the-ackermann-function
# --description--
-For non-negative integers m, n, the Ackermann function A(m, n) is defined as follows:
+For non-negative integers $m$, $n$, the Ackermann function $A(m, n)$ is defined as follows:
-For example A(1, 0) = 2, A(2, 2) = 7 and A(3, 4) = 125.
+$$A(m, n) =
+\begin{cases}
+n + 1 & \text{if $m = 0$} \\\\
+A(m - 1, 1) & \text{if $m > 0$ and $n = 0$} \\\\
+A(m - 1, A(m, n - 1)) & \text{if $m > 0$ and $n > 0$}
+\end{cases}$$
-Find A(n, n) and give your answer mod 148.
+For example $A(1, 0) = 2$, $A(2, 2) = 7$ and $A(3, 4) = 125$.
+
+Find $\displaystyle\sum_{n = 0}^6 A(n, n)$ and give your answer mod ${14}^8$.
# --hints--
-`euler282()` should return 1098988351.
+`ackermanFunction()` should return `1098988351`.
```js
-assert.strictEqual(euler282(), 1098988351);
+assert.strictEqual(ackermanFunction(), 1098988351);
```
# --seed--
@@ -27,12 +34,12 @@ assert.strictEqual(euler282(), 1098988351);
## --seed-contents--
```js
-function euler282() {
+function ackermanFunction() {
return true;
}
-euler282();
+ackermanFunction();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
index 7073e7c431..84e8ca4f4f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
@@ -13,20 +13,20 @@ dashedName: >-
Consider the triangle with sides 6, 8 and 10. It can be seen that the perimeter and the area are both equal to 24.
-So the area/perimeter ratio is equal to 1.
+So the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 1.
Consider also the triangle with sides 13, 14 and 15. The perimeter equals 42 while the area is equal to 84.
-So for this triangle the area/perimeter ratio is equal to 2.
+So for this triangle the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 2.
Find the sum of the perimeters of all integer sided triangles for which the area/perimeter ratios are equal to positive integers not exceeding 1000.
# --hints--
-`euler283()` should return 28038042525570324.
+`integralAreaPerimeterRatio()` should return `28038042525570324`.
```js
-assert.strictEqual(euler283(), 28038042525570324);
+assert.strictEqual(integralAreaPerimeterRatio(), 28038042525570324);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler283(), 28038042525570324);
## --seed-contents--
```js
-function euler283() {
+function integralAreaPerimeterRatio() {
return true;
}
-euler283();
+integralAreaPerimeterRatio();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
index 818483669e..417ddd2948 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
@@ -8,20 +8,26 @@ dashedName: problem-284-steady-squares
# --description--
-The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: 3762 = 141376. Let's call a number with this property a steady square.
+The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: ${376}^2 = 141376$. Let's call a number with this property a steady square.
-Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number c37 is also a steady square: c372 = aa0c37, and the sum of its digits is c+3+7=18 in the same numbering system. The letters a, b, c and d are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
+Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number $c37$ is also a steady square: $c37^2 = aa0c37$, and the sum of its digits is $c+3+7=18$ in the same numbering system. The letters $a$, $b$, $c$ and $d$ are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
-For 1 ≤ n ≤ 9, the sum of the digits of all the n-digit steady squares in the base 14 numbering system is 2d8 (582 decimal). Steady squares with leading 0's are not allowed.
+For $1 ≤ n ≤ 9$, the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system is $2d8$ (582 decimal). Steady squares with leading 0's are not allowed.
-Find the sum of the digits of all the n-digit steady squares in the base 14 numbering system for 1 ≤ n ≤ 10000 (decimal) and give your answer in the base 14 system using lower case letters where necessary.
+Find the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system for $1 ≤ n ≤ 10000$ (decimal) and give your answer as a string in the base 14 system using lower case letters where necessary.
# --hints--
-`euler284()` should return 5a411d7b.
+`steadySquares()` should return a string.
```js
-assert.strictEqual(euler284(), '5a411d7b');
+assert(typeof steadySquares() === 'string');
+```
+
+`steadySquares()` should return the string `5a411d7b`.
+
+```js
+assert.strictEqual(steadySquares(), '5a411d7b');
```
# --seed--
@@ -29,12 +35,12 @@ assert.strictEqual(euler284(), '5a411d7b');
## --seed-contents--
```js
-function euler284() {
+function steadySquares() {
return true;
}
-euler284();
+steadySquares();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
index 12ddabd722..ad75e381a1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
@@ -8,22 +8,22 @@ dashedName: problem-285-pythagorean-odds
# --description--
-Albert chooses a positive integer k, then two real numbers a, b are randomly chosen in the interval \[0,1] with uniform distribution.
+Albert chooses a positive integer $k$, then two real numbers $a$, $b$ are randomly chosen in the interval [0,1] with uniform distribution.
-The square root of the sum (k·a+1)2 + (k·b+1)2 is then computed and rounded to the nearest integer. If the result is equal to k, he scores k points; otherwise he scores nothing.
+The square root of the sum ${(ka + 1)}^2 + {(kb + 1)}^2$ is then computed and rounded to the nearest integer. If the result is equal to $k$, he scores $k$ points; otherwise he scores nothing.
-For example, if k = 6, a = 0.2 and b = 0.85, then (k·a+1)2 + (k·b+1)2 = 42.05. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to k, so he scores 6 points.
+For example, if $k = 6$, $a = 0.2$ and $b = 0.85$, then ${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to $k$, so he scores 6 points.
-It can be shown that if he plays 10 turns with k = 1, k = 2, ..., k = 10, the expected value of his total score, rounded to five decimal places, is 10.20914.
+It can be shown that if he plays 10 turns with $k = 1, k = 2, \ldots, k = 10$, the expected value of his total score, rounded to five decimal places, is 10.20914.
-If he plays 105 turns with k = 1, k = 2, k = 3, ..., k = 105, what is the expected value of his total score, rounded to five decimal places?
+If he plays ${10}^5$ turns with $k = 1, k = 2, k = 3, \ldots, k = {10}^5$, what is the expected value of his total score, rounded to five decimal places?
# --hints--
-`euler285()` should return 157055.80999.
+`pythagoreanOdds()` should return `157055.80999`.
```js
-assert.strictEqual(euler285(), 157055.80999);
+assert.strictEqual(pythagoreanOdds(), 157055.80999);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler285(), 157055.80999);
## --seed-contents--
```js
-function euler285() {
+function pythagoreanOdds() {
return true;
}
-euler285();
+pythagoreanOdds();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
index abb357c47a..1e5a4445df 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
@@ -8,18 +8,18 @@ dashedName: problem-286-scoring-probabilities
# --description--
-Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance x is exactly (1 - x/q), where q is a real constant greater than 50.
+Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance $x$ is exactly ($1 - \frac{x}{q}$), where $q$ is a real constant greater than 50.
-During each practice run, she takes shots from distances x = 1, x = 2, ..., x = 50 and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
+During each practice run, she takes shots from distances $x = 1, x = 2, \ldots, x = 50$ and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
-Find q and give your answer rounded to 10 decimal places.
+Find $q$ and give your answer rounded to 10 decimal places.
# --hints--
-`euler286()` should return 52.6494571953.
+`scoringProbabilities()` should return `52.6494571953`.
```js
-assert.strictEqual(euler286(), 52.6494571953);
+assert.strictEqual(scoringProbabilities(), 52.6494571953);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler286(), 52.6494571953);
## --seed-contents--
```js
-function euler286() {
+function scoringProbabilities() {
return true;
}
-euler286();
+scoringProbabilities();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
index 8d11a248e2..c6b5bee51e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
@@ -8,30 +8,35 @@ dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
# --description--
-The quadtree encoding allows us to describe a 2N×2N black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
+The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
-the first bit deals with the complete 2N×2N region;
+- the first bit deals with the complete $2^N×2^N$ region;
+- "0" denotes a split:
+ - the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
+ - the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+- "10" indicates that the current region contains only black pixels;
+- "11" indicates that the current region contains only white pixels.
-"0" denotes a split:
+Consider the following 4×4 image (colored marks denote places where a split can occur):
-the current 2n×2n region is divided into 4 sub-regions of dimension 2n-1×2n-1,
+
+
+Find the sum of all $f(m,n)$ such that $f(m,n) ≤ {10}^{15}$.
# --hints--
-`euler281()` should return 1485776387445623.
+`pizzaToppings()` should return `1485776387445623`.
```js
-assert.strictEqual(euler281(), 1485776387445623);
+assert.strictEqual(pizzaToppings(), 1485776387445623);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler281(), 1485776387445623);
## --seed-contents--
```js
-function euler281() {
+function pizzaToppings() {
return true;
}
-euler281();
+pizzaToppings();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
index 5abd58ec44..aaaf1c46b6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
@@ -8,18 +8,25 @@ dashedName: problem-282-the-ackermann-function
# --description--
-For non-negative integers m, n, the Ackermann function A(m, n) is defined as follows:
+For non-negative integers $m$, $n$, the Ackermann function $A(m, n)$ is defined as follows:
-For example A(1, 0) = 2, A(2, 2) = 7 and A(3, 4) = 125.
+$$A(m, n) =
+\begin{cases}
+n + 1 & \text{if $m = 0$} \\\\
+A(m - 1, 1) & \text{if $m > 0$ and $n = 0$} \\\\
+A(m - 1, A(m, n - 1)) & \text{if $m > 0$ and $n > 0$}
+\end{cases}$$
-Find A(n, n) and give your answer mod 148.
+For example $A(1, 0) = 2$, $A(2, 2) = 7$ and $A(3, 4) = 125$.
+
+Find $\displaystyle\sum_{n = 0}^6 A(n, n)$ and give your answer mod ${14}^8$.
# --hints--
-`euler282()` should return 1098988351.
+`ackermanFunction()` should return `1098988351`.
```js
-assert.strictEqual(euler282(), 1098988351);
+assert.strictEqual(ackermanFunction(), 1098988351);
```
# --seed--
@@ -27,12 +34,12 @@ assert.strictEqual(euler282(), 1098988351);
## --seed-contents--
```js
-function euler282() {
+function ackermanFunction() {
return true;
}
-euler282();
+ackermanFunction();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
index 7073e7c431..84e8ca4f4f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
@@ -13,20 +13,20 @@ dashedName: >-
Consider the triangle with sides 6, 8 and 10. It can be seen that the perimeter and the area are both equal to 24.
-So the area/perimeter ratio is equal to 1.
+So the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 1.
Consider also the triangle with sides 13, 14 and 15. The perimeter equals 42 while the area is equal to 84.
-So for this triangle the area/perimeter ratio is equal to 2.
+So for this triangle the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 2.
Find the sum of the perimeters of all integer sided triangles for which the area/perimeter ratios are equal to positive integers not exceeding 1000.
# --hints--
-`euler283()` should return 28038042525570324.
+`integralAreaPerimeterRatio()` should return `28038042525570324`.
```js
-assert.strictEqual(euler283(), 28038042525570324);
+assert.strictEqual(integralAreaPerimeterRatio(), 28038042525570324);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler283(), 28038042525570324);
## --seed-contents--
```js
-function euler283() {
+function integralAreaPerimeterRatio() {
return true;
}
-euler283();
+integralAreaPerimeterRatio();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
index 818483669e..417ddd2948 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
@@ -8,20 +8,26 @@ dashedName: problem-284-steady-squares
# --description--
-The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: 3762 = 141376. Let's call a number with this property a steady square.
+The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: ${376}^2 = 141376$. Let's call a number with this property a steady square.
-Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number c37 is also a steady square: c372 = aa0c37, and the sum of its digits is c+3+7=18 in the same numbering system. The letters a, b, c and d are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
+Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number $c37$ is also a steady square: $c37^2 = aa0c37$, and the sum of its digits is $c+3+7=18$ in the same numbering system. The letters $a$, $b$, $c$ and $d$ are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
-For 1 ≤ n ≤ 9, the sum of the digits of all the n-digit steady squares in the base 14 numbering system is 2d8 (582 decimal). Steady squares with leading 0's are not allowed.
+For $1 ≤ n ≤ 9$, the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system is $2d8$ (582 decimal). Steady squares with leading 0's are not allowed.
-Find the sum of the digits of all the n-digit steady squares in the base 14 numbering system for 1 ≤ n ≤ 10000 (decimal) and give your answer in the base 14 system using lower case letters where necessary.
+Find the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system for $1 ≤ n ≤ 10000$ (decimal) and give your answer as a string in the base 14 system using lower case letters where necessary.
# --hints--
-`euler284()` should return 5a411d7b.
+`steadySquares()` should return a string.
```js
-assert.strictEqual(euler284(), '5a411d7b');
+assert(typeof steadySquares() === 'string');
+```
+
+`steadySquares()` should return the string `5a411d7b`.
+
+```js
+assert.strictEqual(steadySquares(), '5a411d7b');
```
# --seed--
@@ -29,12 +35,12 @@ assert.strictEqual(euler284(), '5a411d7b');
## --seed-contents--
```js
-function euler284() {
+function steadySquares() {
return true;
}
-euler284();
+steadySquares();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
index 12ddabd722..ad75e381a1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
@@ -8,22 +8,22 @@ dashedName: problem-285-pythagorean-odds
# --description--
-Albert chooses a positive integer k, then two real numbers a, b are randomly chosen in the interval \[0,1] with uniform distribution.
+Albert chooses a positive integer $k$, then two real numbers $a$, $b$ are randomly chosen in the interval [0,1] with uniform distribution.
-The square root of the sum (k·a+1)2 + (k·b+1)2 is then computed and rounded to the nearest integer. If the result is equal to k, he scores k points; otherwise he scores nothing.
+The square root of the sum ${(ka + 1)}^2 + {(kb + 1)}^2$ is then computed and rounded to the nearest integer. If the result is equal to $k$, he scores $k$ points; otherwise he scores nothing.
-For example, if k = 6, a = 0.2 and b = 0.85, then (k·a+1)2 + (k·b+1)2 = 42.05. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to k, so he scores 6 points.
+For example, if $k = 6$, $a = 0.2$ and $b = 0.85$, then ${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to $k$, so he scores 6 points.
-It can be shown that if he plays 10 turns with k = 1, k = 2, ..., k = 10, the expected value of his total score, rounded to five decimal places, is 10.20914.
+It can be shown that if he plays 10 turns with $k = 1, k = 2, \ldots, k = 10$, the expected value of his total score, rounded to five decimal places, is 10.20914.
-If he plays 105 turns with k = 1, k = 2, k = 3, ..., k = 105, what is the expected value of his total score, rounded to five decimal places?
+If he plays ${10}^5$ turns with $k = 1, k = 2, k = 3, \ldots, k = {10}^5$, what is the expected value of his total score, rounded to five decimal places?
# --hints--
-`euler285()` should return 157055.80999.
+`pythagoreanOdds()` should return `157055.80999`.
```js
-assert.strictEqual(euler285(), 157055.80999);
+assert.strictEqual(pythagoreanOdds(), 157055.80999);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler285(), 157055.80999);
## --seed-contents--
```js
-function euler285() {
+function pythagoreanOdds() {
return true;
}
-euler285();
+pythagoreanOdds();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
index abb357c47a..1e5a4445df 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
@@ -8,18 +8,18 @@ dashedName: problem-286-scoring-probabilities
# --description--
-Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance x is exactly (1 - x/q), where q is a real constant greater than 50.
+Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance $x$ is exactly ($1 - \frac{x}{q}$), where $q$ is a real constant greater than 50.
-During each practice run, she takes shots from distances x = 1, x = 2, ..., x = 50 and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
+During each practice run, she takes shots from distances $x = 1, x = 2, \ldots, x = 50$ and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
-Find q and give your answer rounded to 10 decimal places.
+Find $q$ and give your answer rounded to 10 decimal places.
# --hints--
-`euler286()` should return 52.6494571953.
+`scoringProbabilities()` should return `52.6494571953`.
```js
-assert.strictEqual(euler286(), 52.6494571953);
+assert.strictEqual(scoringProbabilities(), 52.6494571953);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler286(), 52.6494571953);
## --seed-contents--
```js
-function euler286() {
+function scoringProbabilities() {
return true;
}
-euler286();
+scoringProbabilities();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
index 8d11a248e2..c6b5bee51e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
@@ -8,30 +8,35 @@ dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
# --description--
-The quadtree encoding allows us to describe a 2N×2N black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
+The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
-the first bit deals with the complete 2N×2N region;
+- the first bit deals with the complete $2^N×2^N$ region;
+- "0" denotes a split:
+ - the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
+ - the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+- "10" indicates that the current region contains only black pixels;
+- "11" indicates that the current region contains only white pixels.
-"0" denotes a split:
+Consider the following 4×4 image (colored marks denote places where a split can occur):
-the current 2n×2n region is divided into 4 sub-regions of dimension 2n-1×2n-1,
+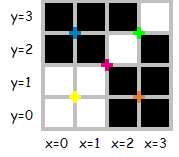 -the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-"10" indicates that the current region contains only black pixels;
+For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
-"11" indicates that the current region contains only white pixels.Consider the following 4×4 image (colored marks denote places where a split can occur):
+- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
+- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
+- otherwise the pixel is white.
-This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-
-For a positive integer N, define DN as the 2N×2N image with the following coloring scheme: the pixel with coordinates x = 0, y = 0 corresponds to the bottom left pixel, if (x - 2N-1)2 + (y - 2N-1)2 ≤ 22N-2 then the pixel is black, otherwise the pixel is white.What is the length of the minimal sequence describing D24 ?
+What is the length of the minimal sequence describing $D_{24}$?
# --hints--
-`euler287()` should return 313135496.
+`quadtreeEncoding()` should return `313135496`.
```js
-assert.strictEqual(euler287(), 313135496);
+assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
@@ -39,12 +44,12 @@ assert.strictEqual(euler287(), 313135496);
## --seed-contents--
```js
-function euler287() {
+function quadtreeEncoding() {
return true;
}
-euler287();
+quadtreeEncoding();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
index 28a2e301ce..6a4b1ea589 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
@@ -8,24 +8,28 @@ dashedName: problem-288-an-enormous-factorial
# --description--
-For any prime p the number N(p,q) is defined by
+For any prime $p$ the number $N(p,q)$ is defined by $N(p,q) = \sum_{n=0}^q T_n \times p^n$ with $T_n$ generated by the following random number generator:
-N(p,q) = ∑n=0 to q Tn\*pn with Tn generated by the following random number generator:
+$$\begin{align}
+ & S_0 = 290797 \\\\
+ & S_{n + 1} = {S_n}^2\bmod 50\\,515\\,093 \\\\
+ & T_n = S_n\bmod p
+\end{align}$$
-S0 = 290797 Sn+1 = Sn2 mod 50515093 Tn = Sn mod p
+Let $Nfac(p,q)$ be the factorial of $N(p,q)$.
-Let Nfac(p,q) be the factorial of N(p,q). Let NF(p,q) be the number of factors p in Nfac(p,q).
+Let $NF(p,q)$ be the number of factors $p$ in $Nfac(p,q)$.
-You are given that NF(3,10000) mod 320=624955285.
+You are given that $NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$.
-Find NF(61,107) mod 6110
+Find $NF(61,{10}^7)\bmod {61}^{10}$.
# --hints--
-`euler288()` should return 605857431263982000.
+`enormousFactorial()` should return `605857431263982000`.
```js
-assert.strictEqual(euler288(), 605857431263982000);
+assert.strictEqual(enormousFactorial(), 605857431263982000);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler288(), 605857431263982000);
## --seed-contents--
```js
-function euler288() {
+function enormousFactorial() {
return true;
}
-euler288();
+enormousFactorial();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
index fcac68664d..d313645a22 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
@@ -8,24 +8,26 @@ dashedName: problem-289-eulerian-cycles
# --description--
-Let C(x,y) be a circle passing through the points (x, y), (x, y+1), (x+1, y) and (x+1, y+1).
+Let $C(x,y)$ be a circle passing through the points ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$) and ($x + 1$, $y + 1$).
-For positive integers m and n, let E(m,n) be a configuration which consists of the m·n circles: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x and y are integers }
+For positive integers $m$ and $n$, let $E(m,n)$ be a configuration which consists of the $m·n$ circles: { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ and $y$ are integers }
-An Eulerian cycle on E(m,n) is a closed path that passes through each arc exactly once. Many such paths are possible on E(m,n), but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
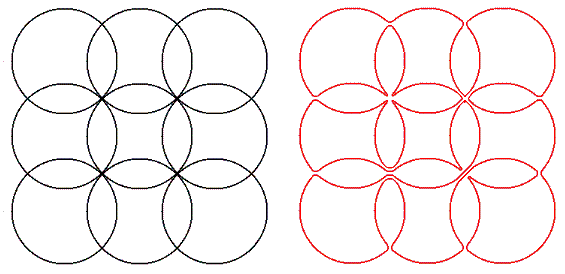
+An Eulerian cycle on $E(m,n)$ is a closed path that passes through each arc exactly once. Many such paths are possible on $E(m,n)$, but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
-The image below shows E(3,3) and an example of an Eulerian non-crossing path.
+The image below shows $E(3,3)$ and an example of an Eulerian non-crossing path.
-Let L(m,n) be the number of Eulerian non-crossing paths on E(m,n). For example, L(1,2) = 2, L(2,2) = 37 and L(3,3) = 104290.
+
-the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-"10" indicates that the current region contains only black pixels;
+For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
-"11" indicates that the current region contains only white pixels.Consider the following 4×4 image (colored marks denote places where a split can occur):
+- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
+- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
+- otherwise the pixel is white.
-This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-
-For a positive integer N, define DN as the 2N×2N image with the following coloring scheme: the pixel with coordinates x = 0, y = 0 corresponds to the bottom left pixel, if (x - 2N-1)2 + (y - 2N-1)2 ≤ 22N-2 then the pixel is black, otherwise the pixel is white.What is the length of the minimal sequence describing D24 ?
+What is the length of the minimal sequence describing $D_{24}$?
# --hints--
-`euler287()` should return 313135496.
+`quadtreeEncoding()` should return `313135496`.
```js
-assert.strictEqual(euler287(), 313135496);
+assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
@@ -39,12 +44,12 @@ assert.strictEqual(euler287(), 313135496);
## --seed-contents--
```js
-function euler287() {
+function quadtreeEncoding() {
return true;
}
-euler287();
+quadtreeEncoding();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
index 28a2e301ce..6a4b1ea589 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
@@ -8,24 +8,28 @@ dashedName: problem-288-an-enormous-factorial
# --description--
-For any prime p the number N(p,q) is defined by
+For any prime $p$ the number $N(p,q)$ is defined by $N(p,q) = \sum_{n=0}^q T_n \times p^n$ with $T_n$ generated by the following random number generator:
-N(p,q) = ∑n=0 to q Tn\*pn with Tn generated by the following random number generator:
+$$\begin{align}
+ & S_0 = 290797 \\\\
+ & S_{n + 1} = {S_n}^2\bmod 50\\,515\\,093 \\\\
+ & T_n = S_n\bmod p
+\end{align}$$
-S0 = 290797 Sn+1 = Sn2 mod 50515093 Tn = Sn mod p
+Let $Nfac(p,q)$ be the factorial of $N(p,q)$.
-Let Nfac(p,q) be the factorial of N(p,q). Let NF(p,q) be the number of factors p in Nfac(p,q).
+Let $NF(p,q)$ be the number of factors $p$ in $Nfac(p,q)$.
-You are given that NF(3,10000) mod 320=624955285.
+You are given that $NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$.
-Find NF(61,107) mod 6110
+Find $NF(61,{10}^7)\bmod {61}^{10}$.
# --hints--
-`euler288()` should return 605857431263982000.
+`enormousFactorial()` should return `605857431263982000`.
```js
-assert.strictEqual(euler288(), 605857431263982000);
+assert.strictEqual(enormousFactorial(), 605857431263982000);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler288(), 605857431263982000);
## --seed-contents--
```js
-function euler288() {
+function enormousFactorial() {
return true;
}
-euler288();
+enormousFactorial();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
index fcac68664d..d313645a22 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
@@ -8,24 +8,26 @@ dashedName: problem-289-eulerian-cycles
# --description--
-Let C(x,y) be a circle passing through the points (x, y), (x, y+1), (x+1, y) and (x+1, y+1).
+Let $C(x,y)$ be a circle passing through the points ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$) and ($x + 1$, $y + 1$).
-For positive integers m and n, let E(m,n) be a configuration which consists of the m·n circles: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x and y are integers }
+For positive integers $m$ and $n$, let $E(m,n)$ be a configuration which consists of the $m·n$ circles: { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ and $y$ are integers }
-An Eulerian cycle on E(m,n) is a closed path that passes through each arc exactly once. Many such paths are possible on E(m,n), but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
+An Eulerian cycle on $E(m,n)$ is a closed path that passes through each arc exactly once. Many such paths are possible on $E(m,n)$, but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
-The image below shows E(3,3) and an example of an Eulerian non-crossing path.
+The image below shows $E(3,3)$ and an example of an Eulerian non-crossing path.
-Let L(m,n) be the number of Eulerian non-crossing paths on E(m,n). For example, L(1,2) = 2, L(2,2) = 37 and L(3,3) = 104290.
+ -Find L(6,10) mod 1010.
+Let $L(m,n)$ be the number of Eulerian non-crossing paths on $E(m,n)$. For example, $L(1,2) = 2$, $L(2,2) = 37$ and $L(3,3) = 104290$.
+
+Find $L(6,10)\bmod {10}^{10}$.
# --hints--
-`euler289()` should return 6567944538.
+`eulerianCycles()` should return `6567944538`.
```js
-assert.strictEqual(euler289(), 6567944538);
+assert.strictEqual(eulerianCycles(), 6567944538);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler289(), 6567944538);
## --seed-contents--
```js
-function euler289() {
+function eulerianCycles() {
return true;
}
-euler289();
+eulerianCycles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
index e46dfedd83..9439010175 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
@@ -8,14 +8,14 @@ dashedName: problem-290-digital-signature
# --description--
-How many integers 0 ≤ n < 1018 have the property that the sum of the digits of n equals the sum of digits of 137n?
+How many integers $0 ≤ n < {10}^{18}$ have the property that the sum of the digits of $n$ equals the sum of digits of $137n$?
# --hints--
-`euler290()` should return 20444710234716470.
+`digitalSignature()` should return `20444710234716470`.
```js
-assert.strictEqual(euler290(), 20444710234716470);
+assert.strictEqual(digitalSignature(), 20444710234716470);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler290(), 20444710234716470);
## --seed-contents--
```js
-function euler290() {
+function digitalSignature() {
return true;
}
-euler290();
+digitalSignature();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
index 0c7d704d9f..2922bdcbe5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
@@ -8,16 +8,16 @@ dashedName: problem-291-panaitopol-primes
# --description--
-A prime number p is called a Panaitopol prime if for some positive integersx and y.
+A prime number $p$ is called a Panaitopol prime if $p = \frac{x^4 - y^4}{x^3 + y^3}$ for some positive integers $x$ and $y$.
-Find how many Panaitopol primes are less than 5×1015.
+Find how many Panaitopol primes are less than $5 × {10}^{15}$.
# --hints--
-`euler291()` should return 4037526.
+`panaitopolPrimes()` should return `4037526`.
```js
-assert.strictEqual(euler291(), 4037526);
+assert.strictEqual(panaitopolPrimes(), 4037526);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler291(), 4037526);
## --seed-contents--
```js
-function euler291() {
+function panaitopolPrimes() {
return true;
}
-euler291();
+panaitopolPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
index 446e875531..7f4ae44273 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
@@ -8,24 +8,27 @@ dashedName: problem-292-pythagorean-polygons
# --description--
-We shall define a pythagorean polygon to be a convex polygon with the following properties:there are at least three vertices,
+We shall define a pythagorean polygon to be a convex polygon with the following properties:
-no three vertices are aligned,
+- there are at least three vertices,
+- no three vertices are aligned,
+- each vertex has integer coordinates,
+- each edge has integer length.
-each vertex has integer coordinates,
-
-each edge has integer length.For a given integer n, define P(n) as the number of distinct pythagorean polygons for which the perimeter is ≤ n.
+For a given integer $n$, define $P(n)$ as the number of distinct pythagorean polygons for which the perimeter is $≤ n$.
Pythagorean polygons should be considered distinct as long as none is a translation of another.
-You are given that P(4) = 1, P(30) = 3655 and P(60) = 891045. Find P(120).
+You are given that $P(4) = 1$, $P(30) = 3655$ and $P(60) = 891045$.
+
+Find $P(120)$.
# --hints--
-`euler292()` should return 3600060866.
+`pythagoreanPolygons()` should return `3600060866`.
```js
-assert.strictEqual(euler292(), 3600060866);
+assert.strictEqual(pythagoreanPolygons(), 3600060866);
```
# --seed--
@@ -33,12 +36,12 @@ assert.strictEqual(euler292(), 3600060866);
## --seed-contents--
```js
-function euler292() {
+function pythagoreanPolygons() {
return true;
}
-euler292();
+pythagoreanPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
index 18307e7b04..2da024c967 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
@@ -8,22 +8,22 @@ dashedName: problem-293-pseudo-fortunate-numbers
# --description--
-An even positive integer N will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
+An even positive integer $N$ will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
-The first twelve admissible numbers are 2,4,6,8,12,16,18,24,30,32,36,48.
+The first twelve admissible numbers are 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48.
-If N is admissible, the smallest integer M > 1 such that N+M is prime, will be called the pseudo-Fortunate number for N.
+If $N$ is admissible, the smallest integer $M > 1$ such that $N + M$ is prime, will be called the pseudo-Fortunate number for $N$.
-For example, N=630 is admissible since it is even and its distinct prime factors are the consecutive primes 2,3,5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is M=11. It can also be seen that the pseudo-Fortunate number for 16 is 3.
+For example, $N = 630$ is admissible since it is even and its distinct prime factors are the consecutive primes 2, 3, 5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is $M = 11$. It can also be seen that the pseudo-Fortunate number for 16 is 3.
-Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers N less than 109.
+Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers $N$ less than ${10}^9$.
# --hints--
-`euler293()` should return 2209.
+`pseudoFortunateNumbers()` should return `2209`.
```js
-assert.strictEqual(euler293(), 2209);
+assert.strictEqual(pseudoFortunateNumbers(), 2209);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler293(), 2209);
## --seed-contents--
```js
-function euler293() {
+function pseudoFortunateNumbers() {
return true;
}
-euler293();
+pseudoFortunateNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
index b7bc62a5f1..20216ace66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
@@ -8,22 +8,23 @@ dashedName: problem-294-sum-of-digits---experience-23
# --description--
-For a positive integer k, define d(k) as the sum of the digits of k in its usual decimal representation.
+For a positive integer $k$, define $d(k)$ as the sum of the digits of $k$ in its usual decimal representation. Thus $d(42) = 4 + 2 = 6$.
-Thus d(42) = 4+2 = 6.
+For a positive integer $n$, define $S(n)$ as the number of positive integers $k < {10}^n$ with the following properties:
-For a positive integer n, define S(n) as the number of positive integers k < 10n with the following properties : k is divisible by 23 and d(k) = 23.
+- $k$ is divisible by 23 and,
+- $d(k) = 23$.
-You are given that S(9) = 263626 and S(42) = 6377168878570056.
+You are given that $S(9) = 263\\,626$ and $S(42) = 6\\,377\\,168\\,878\\,570\\,056$.
-Find S(1112) and give your answer mod 109.
+Find $S({11}^{12})$ and give your answer $\bmod {10}^9$.
# --hints--
-`euler294()` should return 789184709.
+`experience23()` should return `789184709`.
```js
-assert.strictEqual(euler294(), 789184709);
+assert.strictEqual(experience23(), 789184709);
```
# --seed--
@@ -31,12 +32,12 @@ assert.strictEqual(euler294(), 789184709);
## --seed-contents--
```js
-function euler294() {
+function experience23() {
return true;
}
-euler294();
+experience23();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
index 70d1de6d60..c6cb54cc6a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
@@ -10,30 +10,36 @@ dashedName: problem-295-lenticular-holes
We call the convex area enclosed by two circles a lenticular hole if:
-The centres of both circles are on lattice points.
+- The centres of both circles are on lattice points.
+- The two circles intersect at two distinct lattice points.
+- The interior of the convex area enclosed by both circles does not contain any lattice points.
-The two circles intersect at two distinct lattice points.
+Consider the circles:
-The interior of the convex area enclosed by both circles does not contain any lattice points.
+$$\begin{align}
+ & C_0: x^2 + y^2 = 25 \\\\
+ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\
+ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65
+\end{align}$$
-Consider the circles: C0: x2+y2=25 C1: (x+4)2+(y-4)2=1 C2: (x-12)2+(y-4)2=65
+The circles $C_0$, $C_1$ and $C_2$ are drawn in the picture below.
-The circles C0, C1 and C2 are drawn in the picture below.
+
-Find L(6,10) mod 1010.
+Let $L(m,n)$ be the number of Eulerian non-crossing paths on $E(m,n)$. For example, $L(1,2) = 2$, $L(2,2) = 37$ and $L(3,3) = 104290$.
+
+Find $L(6,10)\bmod {10}^{10}$.
# --hints--
-`euler289()` should return 6567944538.
+`eulerianCycles()` should return `6567944538`.
```js
-assert.strictEqual(euler289(), 6567944538);
+assert.strictEqual(eulerianCycles(), 6567944538);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler289(), 6567944538);
## --seed-contents--
```js
-function euler289() {
+function eulerianCycles() {
return true;
}
-euler289();
+eulerianCycles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
index e46dfedd83..9439010175 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
@@ -8,14 +8,14 @@ dashedName: problem-290-digital-signature
# --description--
-How many integers 0 ≤ n < 1018 have the property that the sum of the digits of n equals the sum of digits of 137n?
+How many integers $0 ≤ n < {10}^{18}$ have the property that the sum of the digits of $n$ equals the sum of digits of $137n$?
# --hints--
-`euler290()` should return 20444710234716470.
+`digitalSignature()` should return `20444710234716470`.
```js
-assert.strictEqual(euler290(), 20444710234716470);
+assert.strictEqual(digitalSignature(), 20444710234716470);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler290(), 20444710234716470);
## --seed-contents--
```js
-function euler290() {
+function digitalSignature() {
return true;
}
-euler290();
+digitalSignature();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
index 0c7d704d9f..2922bdcbe5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
@@ -8,16 +8,16 @@ dashedName: problem-291-panaitopol-primes
# --description--
-A prime number p is called a Panaitopol prime if for some positive integersx and y.
+A prime number $p$ is called a Panaitopol prime if $p = \frac{x^4 - y^4}{x^3 + y^3}$ for some positive integers $x$ and $y$.
-Find how many Panaitopol primes are less than 5×1015.
+Find how many Panaitopol primes are less than $5 × {10}^{15}$.
# --hints--
-`euler291()` should return 4037526.
+`panaitopolPrimes()` should return `4037526`.
```js
-assert.strictEqual(euler291(), 4037526);
+assert.strictEqual(panaitopolPrimes(), 4037526);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler291(), 4037526);
## --seed-contents--
```js
-function euler291() {
+function panaitopolPrimes() {
return true;
}
-euler291();
+panaitopolPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
index 446e875531..7f4ae44273 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
@@ -8,24 +8,27 @@ dashedName: problem-292-pythagorean-polygons
# --description--
-We shall define a pythagorean polygon to be a convex polygon with the following properties:there are at least three vertices,
+We shall define a pythagorean polygon to be a convex polygon with the following properties:
-no three vertices are aligned,
+- there are at least three vertices,
+- no three vertices are aligned,
+- each vertex has integer coordinates,
+- each edge has integer length.
-each vertex has integer coordinates,
-
-each edge has integer length.For a given integer n, define P(n) as the number of distinct pythagorean polygons for which the perimeter is ≤ n.
+For a given integer $n$, define $P(n)$ as the number of distinct pythagorean polygons for which the perimeter is $≤ n$.
Pythagorean polygons should be considered distinct as long as none is a translation of another.
-You are given that P(4) = 1, P(30) = 3655 and P(60) = 891045. Find P(120).
+You are given that $P(4) = 1$, $P(30) = 3655$ and $P(60) = 891045$.
+
+Find $P(120)$.
# --hints--
-`euler292()` should return 3600060866.
+`pythagoreanPolygons()` should return `3600060866`.
```js
-assert.strictEqual(euler292(), 3600060866);
+assert.strictEqual(pythagoreanPolygons(), 3600060866);
```
# --seed--
@@ -33,12 +36,12 @@ assert.strictEqual(euler292(), 3600060866);
## --seed-contents--
```js
-function euler292() {
+function pythagoreanPolygons() {
return true;
}
-euler292();
+pythagoreanPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
index 18307e7b04..2da024c967 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
@@ -8,22 +8,22 @@ dashedName: problem-293-pseudo-fortunate-numbers
# --description--
-An even positive integer N will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
+An even positive integer $N$ will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
-The first twelve admissible numbers are 2,4,6,8,12,16,18,24,30,32,36,48.
+The first twelve admissible numbers are 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48.
-If N is admissible, the smallest integer M > 1 such that N+M is prime, will be called the pseudo-Fortunate number for N.
+If $N$ is admissible, the smallest integer $M > 1$ such that $N + M$ is prime, will be called the pseudo-Fortunate number for $N$.
-For example, N=630 is admissible since it is even and its distinct prime factors are the consecutive primes 2,3,5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is M=11. It can also be seen that the pseudo-Fortunate number for 16 is 3.
+For example, $N = 630$ is admissible since it is even and its distinct prime factors are the consecutive primes 2, 3, 5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is $M = 11$. It can also be seen that the pseudo-Fortunate number for 16 is 3.
-Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers N less than 109.
+Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers $N$ less than ${10}^9$.
# --hints--
-`euler293()` should return 2209.
+`pseudoFortunateNumbers()` should return `2209`.
```js
-assert.strictEqual(euler293(), 2209);
+assert.strictEqual(pseudoFortunateNumbers(), 2209);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler293(), 2209);
## --seed-contents--
```js
-function euler293() {
+function pseudoFortunateNumbers() {
return true;
}
-euler293();
+pseudoFortunateNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
index b7bc62a5f1..20216ace66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
@@ -8,22 +8,23 @@ dashedName: problem-294-sum-of-digits---experience-23
# --description--
-For a positive integer k, define d(k) as the sum of the digits of k in its usual decimal representation.
+For a positive integer $k$, define $d(k)$ as the sum of the digits of $k$ in its usual decimal representation. Thus $d(42) = 4 + 2 = 6$.
-Thus d(42) = 4+2 = 6.
+For a positive integer $n$, define $S(n)$ as the number of positive integers $k < {10}^n$ with the following properties:
-For a positive integer n, define S(n) as the number of positive integers k < 10n with the following properties : k is divisible by 23 and d(k) = 23.
+- $k$ is divisible by 23 and,
+- $d(k) = 23$.
-You are given that S(9) = 263626 and S(42) = 6377168878570056.
+You are given that $S(9) = 263\\,626$ and $S(42) = 6\\,377\\,168\\,878\\,570\\,056$.
-Find S(1112) and give your answer mod 109.
+Find $S({11}^{12})$ and give your answer $\bmod {10}^9$.
# --hints--
-`euler294()` should return 789184709.
+`experience23()` should return `789184709`.
```js
-assert.strictEqual(euler294(), 789184709);
+assert.strictEqual(experience23(), 789184709);
```
# --seed--
@@ -31,12 +32,12 @@ assert.strictEqual(euler294(), 789184709);
## --seed-contents--
```js
-function euler294() {
+function experience23() {
return true;
}
-euler294();
+experience23();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
index 70d1de6d60..c6cb54cc6a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
@@ -10,30 +10,36 @@ dashedName: problem-295-lenticular-holes
We call the convex area enclosed by two circles a lenticular hole if:
-The centres of both circles are on lattice points.
+- The centres of both circles are on lattice points.
+- The two circles intersect at two distinct lattice points.
+- The interior of the convex area enclosed by both circles does not contain any lattice points.
-The two circles intersect at two distinct lattice points.
+Consider the circles:
-The interior of the convex area enclosed by both circles does not contain any lattice points.
+$$\begin{align}
+ & C_0: x^2 + y^2 = 25 \\\\
+ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\
+ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65
+\end{align}$$
-Consider the circles: C0: x2+y2=25 C1: (x+4)2+(y-4)2=1 C2: (x-12)2+(y-4)2=65
+The circles $C_0$, $C_1$ and $C_2$ are drawn in the picture below.
-The circles C0, C1 and C2 are drawn in the picture below.
+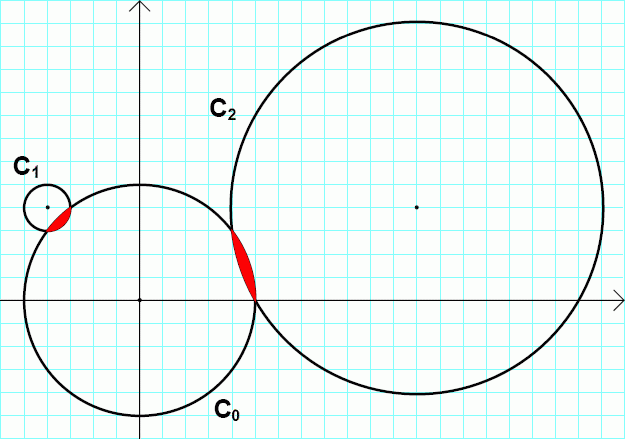 -C0 and C1 form a lenticular hole, as well as C0 and C2.
+$C_0$ and $C_1$ form a lenticular hole, as well as $C_0$ and $C_2$.
-We call an ordered pair of positive real numbers (r1, r2) a lenticular pair if there exist two circles with radii r1 and r2 that form a lenticular hole. We can verify that (1, 5) and (5, √65) are the lenticular pairs of the example above.
+We call an ordered pair of positive real numbers ($r_1$, $r_2$) a lenticular pair if there exist two circles with radii $r_1$ and $r_2$ that form a lenticular hole. We can verify that ($1$, $5$) and ($5$, $\sqrt{65}$) are the lenticular pairs of the example above.
-Let L(N) be the number of distinct lenticular pairs (r1, r2) for which 0 < r1 ≤ r2 ≤ N. We can verify that L(10) = 30 and L(100) = 3442.
+Let $L(N)$ be the number of distinct lenticular pairs ($r_1$, $r_2$) for which $0 < r_1 ≤ r_2 ≤ N$. We can verify that $L(10) = 30$ and $L(100) = 3442$.
-Find L(100 000).
+Find $L(100\\,000)$.
# --hints--
-`euler295()` should return 4884650818.
+`lenticularHoles()` should return `4884650818`.
```js
-assert.strictEqual(euler295(), 4884650818);
+assert.strictEqual(lenticularHoles(), 4884650818);
```
# --seed--
@@ -41,12 +47,12 @@ assert.strictEqual(euler295(), 4884650818);
## --seed-contents--
```js
-function euler295() {
+function lenticularHoles() {
return true;
}
-euler295();
+lenticularHoles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
index 0d269dca3c..9001b02c5f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
@@ -8,18 +8,20 @@ dashedName: problem-296-angular-bisector-and-tangent
# --description--
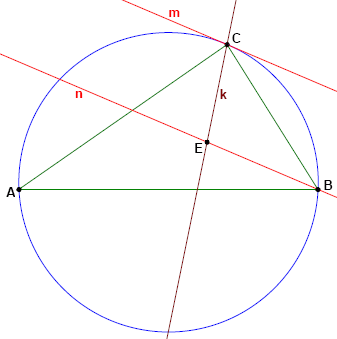
-Given is an integer sided triangle ABC with BC ≤ AC ≤ AB.k is the angular bisector of angle ACB.m is the tangent at C to the circumscribed circle of ABC.n is a line parallel to m through B.
+Given is an integer sided triangle $ABC$ with $BC ≤ AC ≤ AB$. $k$ is the angular bisector of angle $ACB$. $m$ is the tangent at $C$ to the circumscribed circle of $ABC$. $n$ is a line parallel to $m$ through $B$.
-The intersection of n and k is called E.
+The intersection of $n$ and $k$ is called $E$.
-How many triangles ABC with a perimeter not exceeding 100 000 exist such that BE has integral length?
+
-C0 and C1 form a lenticular hole, as well as C0 and C2.
+$C_0$ and $C_1$ form a lenticular hole, as well as $C_0$ and $C_2$.
-We call an ordered pair of positive real numbers (r1, r2) a lenticular pair if there exist two circles with radii r1 and r2 that form a lenticular hole. We can verify that (1, 5) and (5, √65) are the lenticular pairs of the example above.
+We call an ordered pair of positive real numbers ($r_1$, $r_2$) a lenticular pair if there exist two circles with radii $r_1$ and $r_2$ that form a lenticular hole. We can verify that ($1$, $5$) and ($5$, $\sqrt{65}$) are the lenticular pairs of the example above.
-Let L(N) be the number of distinct lenticular pairs (r1, r2) for which 0 < r1 ≤ r2 ≤ N. We can verify that L(10) = 30 and L(100) = 3442.
+Let $L(N)$ be the number of distinct lenticular pairs ($r_1$, $r_2$) for which $0 < r_1 ≤ r_2 ≤ N$. We can verify that $L(10) = 30$ and $L(100) = 3442$.
-Find L(100 000).
+Find $L(100\\,000)$.
# --hints--
-`euler295()` should return 4884650818.
+`lenticularHoles()` should return `4884650818`.
```js
-assert.strictEqual(euler295(), 4884650818);
+assert.strictEqual(lenticularHoles(), 4884650818);
```
# --seed--
@@ -41,12 +47,12 @@ assert.strictEqual(euler295(), 4884650818);
## --seed-contents--
```js
-function euler295() {
+function lenticularHoles() {
return true;
}
-euler295();
+lenticularHoles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
index 0d269dca3c..9001b02c5f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
@@ -8,18 +8,20 @@ dashedName: problem-296-angular-bisector-and-tangent
# --description--
-Given is an integer sided triangle ABC with BC ≤ AC ≤ AB.k is the angular bisector of angle ACB.m is the tangent at C to the circumscribed circle of ABC.n is a line parallel to m through B.
+Given is an integer sided triangle $ABC$ with $BC ≤ AC ≤ AB$. $k$ is the angular bisector of angle $ACB$. $m$ is the tangent at $C$ to the circumscribed circle of $ABC$. $n$ is a line parallel to $m$ through $B$.
-The intersection of n and k is called E.
+The intersection of $n$ and $k$ is called $E$.
-How many triangles ABC with a perimeter not exceeding 100 000 exist such that BE has integral length?
+ +
+How many triangles $ABC$ with a perimeter not exceeding $100\\,000$ exist such that $BE$ has integral length?
# --hints--
-`euler296()` should return 1137208419.
+`angularBisectorAndTangent()` should return `1137208419`.
```js
-assert.strictEqual(euler296(), 1137208419);
+assert.strictEqual(angularBisectorAndTangent(), 1137208419);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler296(), 1137208419);
## --seed-contents--
```js
-function euler296() {
+function angularBisectorAndTangent() {
return true;
}
-euler296();
+angularBisectorAndTangent();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
index 55d96b520c..8178fce31e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
@@ -12,18 +12,24 @@ Each new term in the Fibonacci sequence is generated by adding the previous two
Starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
-Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89. Such a sum is called the Zeckendorf representation of the number.
+Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89.
-For any integer n>0, let z(n) be the number of terms in the Zeckendorf representation of n. Thus, z(5) = 1, z(14) = 2, z(100) = 3 etc. Also, for 0<n<106, ∑ z(n) = 7894453.
+Such a sum is called the Zeckendorf representation of the number.
-Find ∑ z(n) for 0<n<1017.
+For any integer $n>0$, let $z(n)$ be the number of terms in the Zeckendorf representation of $n$.
+
+Thus, $z(5) = 1$, $z(14) = 2$, $z(100) = 3$ etc.
+
+Also, for $0 < n < {10}^6$, $\sum z(n) = 7\\,894\\,453$.
+
+Find $\sum z(n)$ for $0 < n < {10}^{17}$.
# --hints--
-`euler297()` should return 2252639041804718000.
+`zeckendorfRepresentation()` should return `2252639041804718000`.
```js
-assert.strictEqual(euler297(), 2252639041804718000);
+assert.strictEqual(zeckendorfRepresentation(), 2252639041804718000);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler297(), 2252639041804718000);
## --seed-contents--
```js
-function euler297() {
+function zeckendorfRepresentation() {
return true;
}
-euler297();
+zeckendorfRepresentation();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
index a9c0c8ad7e..66e95010d5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
@@ -12,16 +12,29 @@ Larry and Robin play a memory game involving of a sequence of random numbers bet
Both players start with empty memories. Both players always add new missed numbers to their memory but use a different strategy in deciding which number to remove: Larry's strategy is to remove the number that hasn't been called in the longest time. Robin's strategy is to remove the number that's been in the memory the longest time.
-Example game:Turn Callednumber Larry'smemory Larry'sscore Robin'smemory Robin'sscore 1 1 1 0 1 0 2 2 1,2 0 1,2 0 3 4 1,2,4 0 1,2,4 0 4 6 1,2,4,6 0 1,2,4,6 0 5 1 1,2,4,6 1 1,2,4,6 1 6 8 1,2,4,6,8 1 1,2,4,6,8 1 7 10 1,4,6,8,10 1 2,4,6,8,10 1 8 2 1,2,6,8,10 1 2,4,6,8,10 2 9 4 1,2,4,8,10 1 2,4,6,8,10 3 10 1 1,2,4,8,10 2 1,4,6,8,10 3
+Example game:
-Denoting Larry's score by L and Robin's score by R, what is the expected value of |L-R| after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+| Turn | Called number | Larry's memory | Larry's score | Robin's memory | Robin's score |
+|------|---------------|---------------:|---------------|----------------|---------------|
+| 1 | 1 | 1 | 0 | 1 | 0 |
+| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
+| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
+| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
+| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
+| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
+| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
+| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
+| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
+| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
+
+Denoting Larry's score by $L$ and Robin's score by $R$, what is the expected value of $|L - R|$ after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
# --hints--
-`euler298()` should return 1.76882294.
+`selectiveAmnesia()` should return `1.76882294`.
```js
-assert.strictEqual(euler298(), 1.76882294);
+assert.strictEqual(selectiveAmnesia(), 1.76882294);
```
# --seed--
@@ -29,12 +42,12 @@ assert.strictEqual(euler298(), 1.76882294);
## --seed-contents--
```js
-function euler298() {
+function selectiveAmnesia() {
return true;
}
-euler298();
+selectiveAmnesia();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
index 586b589068..20a21fc782 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
@@ -8,26 +8,32 @@ dashedName: problem-299-three-similar-triangles
# --description--
-Four points with integer coordinates are selected:A(a, 0), B(b, 0), C(0, c) and D(0, d),
+Four points with integer coordinates are selected:
-with 0 < a < b and 0 < c < d.
+$A(a, 0)$, $B(b, 0)$, $C(0, c)$ and $D(0, d)$, with $0 < a < b$ and $0 < c < d$.
-Point P, also with integer coordinates, is chosen on the line AC so that the three triangles ABP, CDP and BDP are all similar.
+Point $P$, also with integer coordinates, is chosen on the line $AC$ so that the three triangles $ABP$, $CDP$ and $BDP$ are all similar.
-It is easy to prove that the three triangles can be similar, only if a=c.
+
+
+How many triangles $ABC$ with a perimeter not exceeding $100\\,000$ exist such that $BE$ has integral length?
# --hints--
-`euler296()` should return 1137208419.
+`angularBisectorAndTangent()` should return `1137208419`.
```js
-assert.strictEqual(euler296(), 1137208419);
+assert.strictEqual(angularBisectorAndTangent(), 1137208419);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler296(), 1137208419);
## --seed-contents--
```js
-function euler296() {
+function angularBisectorAndTangent() {
return true;
}
-euler296();
+angularBisectorAndTangent();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
index 55d96b520c..8178fce31e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
@@ -12,18 +12,24 @@ Each new term in the Fibonacci sequence is generated by adding the previous two
Starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
-Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89. Such a sum is called the Zeckendorf representation of the number.
+Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89.
-For any integer n>0, let z(n) be the number of terms in the Zeckendorf representation of n. Thus, z(5) = 1, z(14) = 2, z(100) = 3 etc. Also, for 0<n<106, ∑ z(n) = 7894453.
+Such a sum is called the Zeckendorf representation of the number.
-Find ∑ z(n) for 0<n<1017.
+For any integer $n>0$, let $z(n)$ be the number of terms in the Zeckendorf representation of $n$.
+
+Thus, $z(5) = 1$, $z(14) = 2$, $z(100) = 3$ etc.
+
+Also, for $0 < n < {10}^6$, $\sum z(n) = 7\\,894\\,453$.
+
+Find $\sum z(n)$ for $0 < n < {10}^{17}$.
# --hints--
-`euler297()` should return 2252639041804718000.
+`zeckendorfRepresentation()` should return `2252639041804718000`.
```js
-assert.strictEqual(euler297(), 2252639041804718000);
+assert.strictEqual(zeckendorfRepresentation(), 2252639041804718000);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler297(), 2252639041804718000);
## --seed-contents--
```js
-function euler297() {
+function zeckendorfRepresentation() {
return true;
}
-euler297();
+zeckendorfRepresentation();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
index a9c0c8ad7e..66e95010d5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
@@ -12,16 +12,29 @@ Larry and Robin play a memory game involving of a sequence of random numbers bet
Both players start with empty memories. Both players always add new missed numbers to their memory but use a different strategy in deciding which number to remove: Larry's strategy is to remove the number that hasn't been called in the longest time. Robin's strategy is to remove the number that's been in the memory the longest time.
-Example game:Turn Callednumber Larry'smemory Larry'sscore Robin'smemory Robin'sscore 1 1 1 0 1 0 2 2 1,2 0 1,2 0 3 4 1,2,4 0 1,2,4 0 4 6 1,2,4,6 0 1,2,4,6 0 5 1 1,2,4,6 1 1,2,4,6 1 6 8 1,2,4,6,8 1 1,2,4,6,8 1 7 10 1,4,6,8,10 1 2,4,6,8,10 1 8 2 1,2,6,8,10 1 2,4,6,8,10 2 9 4 1,2,4,8,10 1 2,4,6,8,10 3 10 1 1,2,4,8,10 2 1,4,6,8,10 3
+Example game:
-Denoting Larry's score by L and Robin's score by R, what is the expected value of |L-R| after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+| Turn | Called number | Larry's memory | Larry's score | Robin's memory | Robin's score |
+|------|---------------|---------------:|---------------|----------------|---------------|
+| 1 | 1 | 1 | 0 | 1 | 0 |
+| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
+| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
+| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
+| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
+| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
+| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
+| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
+| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
+| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
+
+Denoting Larry's score by $L$ and Robin's score by $R$, what is the expected value of $|L - R|$ after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
# --hints--
-`euler298()` should return 1.76882294.
+`selectiveAmnesia()` should return `1.76882294`.
```js
-assert.strictEqual(euler298(), 1.76882294);
+assert.strictEqual(selectiveAmnesia(), 1.76882294);
```
# --seed--
@@ -29,12 +42,12 @@ assert.strictEqual(euler298(), 1.76882294);
## --seed-contents--
```js
-function euler298() {
+function selectiveAmnesia() {
return true;
}
-euler298();
+selectiveAmnesia();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
index 586b589068..20a21fc782 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
@@ -8,26 +8,32 @@ dashedName: problem-299-three-similar-triangles
# --description--
-Four points with integer coordinates are selected:A(a, 0), B(b, 0), C(0, c) and D(0, d),
+Four points with integer coordinates are selected:
-with 0 < a < b and 0 < c < d.
+$A(a, 0)$, $B(b, 0)$, $C(0, c)$ and $D(0, d)$, with $0 < a < b$ and $0 < c < d$.
-Point P, also with integer coordinates, is chosen on the line AC so that the three triangles ABP, CDP and BDP are all similar.
+Point $P$, also with integer coordinates, is chosen on the line $AC$ so that the three triangles $ABP$, $CDP$ and $BDP$ are all similar.
-It is easy to prove that the three triangles can be similar, only if a=c.
+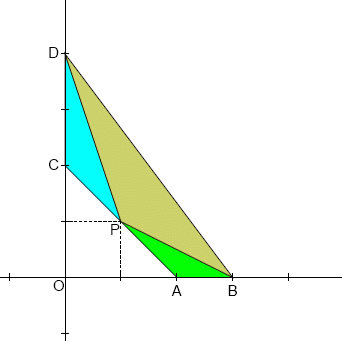 -So, given that a=c, we are looking for triplets (a,b,d) such that at least one point P (with integer coordinates) exists on AC, making the three triangles ABP, CDP and BDP all similar.
+It is easy to prove that the three triangles can be similar, only if $a = c$.
-For example, if (a,b,d)=(2,3,4), it can be easily verified that point P(1,1) satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point P(1,1) is common for both.
+So, given that $a = c$, we are looking for triplets ($a$, $b$, $d$) such that at least one point $P$ (with integer coordinates) exists on $AC$, making the three triangles $ABP$, $CDP$ and $BDP$ all similar.
-If b+d < 100, there are 92 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000, there are 320471 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000 000, how many distinct triplets (a,b,d) are there such that point P exists?
+For example, if $(a, b, d) = (2, 3, 4)$, it can be easily verified that point $P(1, 1)$ satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point $P(1, 1)$ is common for both.
+
+If $b + d < 100$, there are 92 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000$, there are 320471 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000\\,000$, how many distinct triplets ($a$, $b$, $d$) are there such that point $P$ exists?
# --hints--
-`euler299()` should return 549936643.
+`threeSimilarTriangles()` should return `549936643`.
```js
-assert.strictEqual(euler299(), 549936643);
+assert.strictEqual(threeSimilarTriangles(), 549936643);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler299(), 549936643);
## --seed-contents--
```js
-function euler299() {
+function threeSimilarTriangles() {
return true;
}
-euler299();
+threeSimilarTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
index 52c5f272c6..0d58795ae2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
@@ -10,24 +10,30 @@ dashedName: problem-300-protein-folding
In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
-For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are 2n distinct proteins consisting of n elements.
+For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are $2^n$ distinct proteins consisting of $n$ elements.
-When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous. As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside. Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
+When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
+
+As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
+
+Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
+
-So, given that a=c, we are looking for triplets (a,b,d) such that at least one point P (with integer coordinates) exists on AC, making the three triangles ABP, CDP and BDP all similar.
+It is easy to prove that the three triangles can be similar, only if $a = c$.
-For example, if (a,b,d)=(2,3,4), it can be easily verified that point P(1,1) satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point P(1,1) is common for both.
+So, given that $a = c$, we are looking for triplets ($a$, $b$, $d$) such that at least one point $P$ (with integer coordinates) exists on $AC$, making the three triangles $ABP$, $CDP$ and $BDP$ all similar.
-If b+d < 100, there are 92 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000, there are 320471 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000 000, how many distinct triplets (a,b,d) are there such that point P exists?
+For example, if $(a, b, d) = (2, 3, 4)$, it can be easily verified that point $P(1, 1)$ satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point $P(1, 1)$ is common for both.
+
+If $b + d < 100$, there are 92 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000$, there are 320471 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000\\,000$, how many distinct triplets ($a$, $b$, $d$) are there such that point $P$ exists?
# --hints--
-`euler299()` should return 549936643.
+`threeSimilarTriangles()` should return `549936643`.
```js
-assert.strictEqual(euler299(), 549936643);
+assert.strictEqual(threeSimilarTriangles(), 549936643);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler299(), 549936643);
## --seed-contents--
```js
-function euler299() {
+function threeSimilarTriangles() {
return true;
}
-euler299();
+threeSimilarTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
index 52c5f272c6..0d58795ae2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
@@ -10,24 +10,30 @@ dashedName: problem-300-protein-folding
In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
-For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are 2n distinct proteins consisting of n elements.
+For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are $2^n$ distinct proteins consisting of $n$ elements.
-When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous. As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside. Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
+When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
+
+As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
+
+Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
+ +
The folding on the left has only six H-H contact points, thus it would never occur naturally. On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
-Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be 850 / 28=3.3203125.
+Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be $\frac{850}{2^8} = 3.3203125$.
What is the average number of H-H contact points in an optimal folding of a random protein string of length 15? Give your answer using as many decimal places as necessary for an exact result.
# --hints--
-`euler300()` should return 8.0540771484375.
+`proteinFolding()` should return `8.0540771484375`.
```js
-assert.strictEqual(euler300(), 8.0540771484375);
+assert.strictEqual(proteinFolding(), 8.0540771484375);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler300(), 8.0540771484375);
## --seed-contents--
```js
-function euler300() {
+function proteinFolding() {
return true;
}
-euler300();
+proteinFolding();
```
# --solutions--
+
The folding on the left has only six H-H contact points, thus it would never occur naturally. On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
-Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be 850 / 28=3.3203125.
+Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be $\frac{850}{2^8} = 3.3203125$.
What is the average number of H-H contact points in an optimal folding of a random protein string of length 15? Give your answer using as many decimal places as necessary for an exact result.
# --hints--
-`euler300()` should return 8.0540771484375.
+`proteinFolding()` should return `8.0540771484375`.
```js
-assert.strictEqual(euler300(), 8.0540771484375);
+assert.strictEqual(proteinFolding(), 8.0540771484375);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler300(), 8.0540771484375);
## --seed-contents--
```js
-function euler300() {
+function proteinFolding() {
return true;
}
-euler300();
+proteinFolding();
```
# --solutions--
 +
+Find the sum of all $f(m,n)$ such that $f(m,n) ≤ {10}^{15}$.
# --hints--
-`euler281()` should return 1485776387445623.
+`pizzaToppings()` should return `1485776387445623`.
```js
-assert.strictEqual(euler281(), 1485776387445623);
+assert.strictEqual(pizzaToppings(), 1485776387445623);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler281(), 1485776387445623);
## --seed-contents--
```js
-function euler281() {
+function pizzaToppings() {
return true;
}
-euler281();
+pizzaToppings();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
index 5abd58ec44..aaaf1c46b6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
@@ -8,18 +8,25 @@ dashedName: problem-282-the-ackermann-function
# --description--
-For non-negative integers m, n, the Ackermann function A(m, n) is defined as follows:
+For non-negative integers $m$, $n$, the Ackermann function $A(m, n)$ is defined as follows:
-For example A(1, 0) = 2, A(2, 2) = 7 and A(3, 4) = 125.
+$$A(m, n) =
+\begin{cases}
+n + 1 & \text{if $m = 0$} \\\\
+A(m - 1, 1) & \text{if $m > 0$ and $n = 0$} \\\\
+A(m - 1, A(m, n - 1)) & \text{if $m > 0$ and $n > 0$}
+\end{cases}$$
-Find A(n, n) and give your answer mod 148.
+For example $A(1, 0) = 2$, $A(2, 2) = 7$ and $A(3, 4) = 125$.
+
+Find $\displaystyle\sum_{n = 0}^6 A(n, n)$ and give your answer mod ${14}^8$.
# --hints--
-`euler282()` should return 1098988351.
+`ackermanFunction()` should return `1098988351`.
```js
-assert.strictEqual(euler282(), 1098988351);
+assert.strictEqual(ackermanFunction(), 1098988351);
```
# --seed--
@@ -27,12 +34,12 @@ assert.strictEqual(euler282(), 1098988351);
## --seed-contents--
```js
-function euler282() {
+function ackermanFunction() {
return true;
}
-euler282();
+ackermanFunction();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
index 7073e7c431..84e8ca4f4f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
@@ -13,20 +13,20 @@ dashedName: >-
Consider the triangle with sides 6, 8 and 10. It can be seen that the perimeter and the area are both equal to 24.
-So the area/perimeter ratio is equal to 1.
+So the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 1.
Consider also the triangle with sides 13, 14 and 15. The perimeter equals 42 while the area is equal to 84.
-So for this triangle the area/perimeter ratio is equal to 2.
+So for this triangle the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 2.
Find the sum of the perimeters of all integer sided triangles for which the area/perimeter ratios are equal to positive integers not exceeding 1000.
# --hints--
-`euler283()` should return 28038042525570324.
+`integralAreaPerimeterRatio()` should return `28038042525570324`.
```js
-assert.strictEqual(euler283(), 28038042525570324);
+assert.strictEqual(integralAreaPerimeterRatio(), 28038042525570324);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler283(), 28038042525570324);
## --seed-contents--
```js
-function euler283() {
+function integralAreaPerimeterRatio() {
return true;
}
-euler283();
+integralAreaPerimeterRatio();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
index 818483669e..417ddd2948 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
@@ -8,20 +8,26 @@ dashedName: problem-284-steady-squares
# --description--
-The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: 3762 = 141376. Let's call a number with this property a steady square.
+The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: ${376}^2 = 141376$. Let's call a number with this property a steady square.
-Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number c37 is also a steady square: c372 = aa0c37, and the sum of its digits is c+3+7=18 in the same numbering system. The letters a, b, c and d are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
+Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number $c37$ is also a steady square: $c37^2 = aa0c37$, and the sum of its digits is $c+3+7=18$ in the same numbering system. The letters $a$, $b$, $c$ and $d$ are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
-For 1 ≤ n ≤ 9, the sum of the digits of all the n-digit steady squares in the base 14 numbering system is 2d8 (582 decimal). Steady squares with leading 0's are not allowed.
+For $1 ≤ n ≤ 9$, the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system is $2d8$ (582 decimal). Steady squares with leading 0's are not allowed.
-Find the sum of the digits of all the n-digit steady squares in the base 14 numbering system for 1 ≤ n ≤ 10000 (decimal) and give your answer in the base 14 system using lower case letters where necessary.
+Find the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system for $1 ≤ n ≤ 10000$ (decimal) and give your answer as a string in the base 14 system using lower case letters where necessary.
# --hints--
-`euler284()` should return 5a411d7b.
+`steadySquares()` should return a string.
```js
-assert.strictEqual(euler284(), '5a411d7b');
+assert(typeof steadySquares() === 'string');
+```
+
+`steadySquares()` should return the string `5a411d7b`.
+
+```js
+assert.strictEqual(steadySquares(), '5a411d7b');
```
# --seed--
@@ -29,12 +35,12 @@ assert.strictEqual(euler284(), '5a411d7b');
## --seed-contents--
```js
-function euler284() {
+function steadySquares() {
return true;
}
-euler284();
+steadySquares();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
index 12ddabd722..ad75e381a1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
@@ -8,22 +8,22 @@ dashedName: problem-285-pythagorean-odds
# --description--
-Albert chooses a positive integer k, then two real numbers a, b are randomly chosen in the interval \[0,1] with uniform distribution.
+Albert chooses a positive integer $k$, then two real numbers $a$, $b$ are randomly chosen in the interval [0,1] with uniform distribution.
-The square root of the sum (k·a+1)2 + (k·b+1)2 is then computed and rounded to the nearest integer. If the result is equal to k, he scores k points; otherwise he scores nothing.
+The square root of the sum ${(ka + 1)}^2 + {(kb + 1)}^2$ is then computed and rounded to the nearest integer. If the result is equal to $k$, he scores $k$ points; otherwise he scores nothing.
-For example, if k = 6, a = 0.2 and b = 0.85, then (k·a+1)2 + (k·b+1)2 = 42.05. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to k, so he scores 6 points.
+For example, if $k = 6$, $a = 0.2$ and $b = 0.85$, then ${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to $k$, so he scores 6 points.
-It can be shown that if he plays 10 turns with k = 1, k = 2, ..., k = 10, the expected value of his total score, rounded to five decimal places, is 10.20914.
+It can be shown that if he plays 10 turns with $k = 1, k = 2, \ldots, k = 10$, the expected value of his total score, rounded to five decimal places, is 10.20914.
-If he plays 105 turns with k = 1, k = 2, k = 3, ..., k = 105, what is the expected value of his total score, rounded to five decimal places?
+If he plays ${10}^5$ turns with $k = 1, k = 2, k = 3, \ldots, k = {10}^5$, what is the expected value of his total score, rounded to five decimal places?
# --hints--
-`euler285()` should return 157055.80999.
+`pythagoreanOdds()` should return `157055.80999`.
```js
-assert.strictEqual(euler285(), 157055.80999);
+assert.strictEqual(pythagoreanOdds(), 157055.80999);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler285(), 157055.80999);
## --seed-contents--
```js
-function euler285() {
+function pythagoreanOdds() {
return true;
}
-euler285();
+pythagoreanOdds();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
index abb357c47a..1e5a4445df 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
@@ -8,18 +8,18 @@ dashedName: problem-286-scoring-probabilities
# --description--
-Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance x is exactly (1 - x/q), where q is a real constant greater than 50.
+Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance $x$ is exactly ($1 - \frac{x}{q}$), where $q$ is a real constant greater than 50.
-During each practice run, she takes shots from distances x = 1, x = 2, ..., x = 50 and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
+During each practice run, she takes shots from distances $x = 1, x = 2, \ldots, x = 50$ and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
-Find q and give your answer rounded to 10 decimal places.
+Find $q$ and give your answer rounded to 10 decimal places.
# --hints--
-`euler286()` should return 52.6494571953.
+`scoringProbabilities()` should return `52.6494571953`.
```js
-assert.strictEqual(euler286(), 52.6494571953);
+assert.strictEqual(scoringProbabilities(), 52.6494571953);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler286(), 52.6494571953);
## --seed-contents--
```js
-function euler286() {
+function scoringProbabilities() {
return true;
}
-euler286();
+scoringProbabilities();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
index 8d11a248e2..c6b5bee51e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
@@ -8,30 +8,35 @@ dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
# --description--
-The quadtree encoding allows us to describe a 2N×2N black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
+The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
-the first bit deals with the complete 2N×2N region;
+- the first bit deals with the complete $2^N×2^N$ region;
+- "0" denotes a split:
+ - the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
+ - the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+- "10" indicates that the current region contains only black pixels;
+- "11" indicates that the current region contains only white pixels.
-"0" denotes a split:
+Consider the following 4×4 image (colored marks denote places where a split can occur):
-the current 2n×2n region is divided into 4 sub-regions of dimension 2n-1×2n-1,
+
+
+Find the sum of all $f(m,n)$ such that $f(m,n) ≤ {10}^{15}$.
# --hints--
-`euler281()` should return 1485776387445623.
+`pizzaToppings()` should return `1485776387445623`.
```js
-assert.strictEqual(euler281(), 1485776387445623);
+assert.strictEqual(pizzaToppings(), 1485776387445623);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler281(), 1485776387445623);
## --seed-contents--
```js
-function euler281() {
+function pizzaToppings() {
return true;
}
-euler281();
+pizzaToppings();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
index 5abd58ec44..aaaf1c46b6 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-282-the-ackermann-function.md
@@ -8,18 +8,25 @@ dashedName: problem-282-the-ackermann-function
# --description--
-For non-negative integers m, n, the Ackermann function A(m, n) is defined as follows:
+For non-negative integers $m$, $n$, the Ackermann function $A(m, n)$ is defined as follows:
-For example A(1, 0) = 2, A(2, 2) = 7 and A(3, 4) = 125.
+$$A(m, n) =
+\begin{cases}
+n + 1 & \text{if $m = 0$} \\\\
+A(m - 1, 1) & \text{if $m > 0$ and $n = 0$} \\\\
+A(m - 1, A(m, n - 1)) & \text{if $m > 0$ and $n > 0$}
+\end{cases}$$
-Find A(n, n) and give your answer mod 148.
+For example $A(1, 0) = 2$, $A(2, 2) = 7$ and $A(3, 4) = 125$.
+
+Find $\displaystyle\sum_{n = 0}^6 A(n, n)$ and give your answer mod ${14}^8$.
# --hints--
-`euler282()` should return 1098988351.
+`ackermanFunction()` should return `1098988351`.
```js
-assert.strictEqual(euler282(), 1098988351);
+assert.strictEqual(ackermanFunction(), 1098988351);
```
# --seed--
@@ -27,12 +34,12 @@ assert.strictEqual(euler282(), 1098988351);
## --seed-contents--
```js
-function euler282() {
+function ackermanFunction() {
return true;
}
-euler282();
+ackermanFunction();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
index 7073e7c431..84e8ca4f4f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-283-integer-sided-triangles-for-which-the-area--perimeter-ratio-is-integral.md
@@ -13,20 +13,20 @@ dashedName: >-
Consider the triangle with sides 6, 8 and 10. It can be seen that the perimeter and the area are both equal to 24.
-So the area/perimeter ratio is equal to 1.
+So the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 1.
Consider also the triangle with sides 13, 14 and 15. The perimeter equals 42 while the area is equal to 84.
-So for this triangle the area/perimeter ratio is equal to 2.
+So for this triangle the $\frac{\text{area}}{\text{perimeter}}$ ratio is equal to 2.
Find the sum of the perimeters of all integer sided triangles for which the area/perimeter ratios are equal to positive integers not exceeding 1000.
# --hints--
-`euler283()` should return 28038042525570324.
+`integralAreaPerimeterRatio()` should return `28038042525570324`.
```js
-assert.strictEqual(euler283(), 28038042525570324);
+assert.strictEqual(integralAreaPerimeterRatio(), 28038042525570324);
```
# --seed--
@@ -34,12 +34,12 @@ assert.strictEqual(euler283(), 28038042525570324);
## --seed-contents--
```js
-function euler283() {
+function integralAreaPerimeterRatio() {
return true;
}
-euler283();
+integralAreaPerimeterRatio();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
index 818483669e..417ddd2948 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-284-steady-squares.md
@@ -8,20 +8,26 @@ dashedName: problem-284-steady-squares
# --description--
-The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: 3762 = 141376. Let's call a number with this property a steady square.
+The 3-digit number 376 in the decimal numbering system is an example of numbers with the special property that its square ends with the same digits: ${376}^2 = 141376$. Let's call a number with this property a steady square.
-Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number c37 is also a steady square: c372 = aa0c37, and the sum of its digits is c+3+7=18 in the same numbering system. The letters a, b, c and d are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
+Steady squares can also be observed in other numbering systems. In the base 14 numbering system, the 3-digit number $c37$ is also a steady square: $c37^2 = aa0c37$, and the sum of its digits is $c+3+7=18$ in the same numbering system. The letters $a$, $b$, $c$ and $d$ are used for the 10, 11, 12 and 13 digits respectively, in a manner similar to the hexadecimal numbering system.
-For 1 ≤ n ≤ 9, the sum of the digits of all the n-digit steady squares in the base 14 numbering system is 2d8 (582 decimal). Steady squares with leading 0's are not allowed.
+For $1 ≤ n ≤ 9$, the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system is $2d8$ (582 decimal). Steady squares with leading 0's are not allowed.
-Find the sum of the digits of all the n-digit steady squares in the base 14 numbering system for 1 ≤ n ≤ 10000 (decimal) and give your answer in the base 14 system using lower case letters where necessary.
+Find the sum of the digits of all the $n$-digit steady squares in the base 14 numbering system for $1 ≤ n ≤ 10000$ (decimal) and give your answer as a string in the base 14 system using lower case letters where necessary.
# --hints--
-`euler284()` should return 5a411d7b.
+`steadySquares()` should return a string.
```js
-assert.strictEqual(euler284(), '5a411d7b');
+assert(typeof steadySquares() === 'string');
+```
+
+`steadySquares()` should return the string `5a411d7b`.
+
+```js
+assert.strictEqual(steadySquares(), '5a411d7b');
```
# --seed--
@@ -29,12 +35,12 @@ assert.strictEqual(euler284(), '5a411d7b');
## --seed-contents--
```js
-function euler284() {
+function steadySquares() {
return true;
}
-euler284();
+steadySquares();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
index 12ddabd722..ad75e381a1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-285-pythagorean-odds.md
@@ -8,22 +8,22 @@ dashedName: problem-285-pythagorean-odds
# --description--
-Albert chooses a positive integer k, then two real numbers a, b are randomly chosen in the interval \[0,1] with uniform distribution.
+Albert chooses a positive integer $k$, then two real numbers $a$, $b$ are randomly chosen in the interval [0,1] with uniform distribution.
-The square root of the sum (k·a+1)2 + (k·b+1)2 is then computed and rounded to the nearest integer. If the result is equal to k, he scores k points; otherwise he scores nothing.
+The square root of the sum ${(ka + 1)}^2 + {(kb + 1)}^2$ is then computed and rounded to the nearest integer. If the result is equal to $k$, he scores $k$ points; otherwise he scores nothing.
-For example, if k = 6, a = 0.2 and b = 0.85, then (k·a+1)2 + (k·b+1)2 = 42.05. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to k, so he scores 6 points.
+For example, if $k = 6$, $a = 0.2$ and $b = 0.85$, then ${(ka + 1)}^2 + {(kb + 1)}^2 = 42.05$. The square root of 42.05 is 6.484... and when rounded to the nearest integer, it becomes 6. This is equal to $k$, so he scores 6 points.
-It can be shown that if he plays 10 turns with k = 1, k = 2, ..., k = 10, the expected value of his total score, rounded to five decimal places, is 10.20914.
+It can be shown that if he plays 10 turns with $k = 1, k = 2, \ldots, k = 10$, the expected value of his total score, rounded to five decimal places, is 10.20914.
-If he plays 105 turns with k = 1, k = 2, k = 3, ..., k = 105, what is the expected value of his total score, rounded to five decimal places?
+If he plays ${10}^5$ turns with $k = 1, k = 2, k = 3, \ldots, k = {10}^5$, what is the expected value of his total score, rounded to five decimal places?
# --hints--
-`euler285()` should return 157055.80999.
+`pythagoreanOdds()` should return `157055.80999`.
```js
-assert.strictEqual(euler285(), 157055.80999);
+assert.strictEqual(pythagoreanOdds(), 157055.80999);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler285(), 157055.80999);
## --seed-contents--
```js
-function euler285() {
+function pythagoreanOdds() {
return true;
}
-euler285();
+pythagoreanOdds();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
index abb357c47a..1e5a4445df 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-286-scoring-probabilities.md
@@ -8,18 +8,18 @@ dashedName: problem-286-scoring-probabilities
# --description--
-Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance x is exactly (1 - x/q), where q is a real constant greater than 50.
+Barbara is a mathematician and a basketball player. She has found that the probability of scoring a point when shooting from a distance $x$ is exactly ($1 - \frac{x}{q}$), where $q$ is a real constant greater than 50.
-During each practice run, she takes shots from distances x = 1, x = 2, ..., x = 50 and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
+During each practice run, she takes shots from distances $x = 1, x = 2, \ldots, x = 50$ and, according to her records, she has precisely a 2 % chance to score a total of exactly 20 points.
-Find q and give your answer rounded to 10 decimal places.
+Find $q$ and give your answer rounded to 10 decimal places.
# --hints--
-`euler286()` should return 52.6494571953.
+`scoringProbabilities()` should return `52.6494571953`.
```js
-assert.strictEqual(euler286(), 52.6494571953);
+assert.strictEqual(scoringProbabilities(), 52.6494571953);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler286(), 52.6494571953);
## --seed-contents--
```js
-function euler286() {
+function scoringProbabilities() {
return true;
}
-euler286();
+scoringProbabilities();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
index 8d11a248e2..c6b5bee51e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-287-quadtree-encoding-a-simple-compression-algorithm.md
@@ -8,30 +8,35 @@ dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
# --description--
-The quadtree encoding allows us to describe a 2N×2N black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
+The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
-the first bit deals with the complete 2N×2N region;
+- the first bit deals with the complete $2^N×2^N$ region;
+- "0" denotes a split:
+ - the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
+ - the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+- "10" indicates that the current region contains only black pixels;
+- "11" indicates that the current region contains only white pixels.
-"0" denotes a split:
+Consider the following 4×4 image (colored marks denote places where a split can occur):
-the current 2n×2n region is divided into 4 sub-regions of dimension 2n-1×2n-1,
+ -the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-"10" indicates that the current region contains only black pixels;
+For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
-"11" indicates that the current region contains only white pixels.Consider the following 4×4 image (colored marks denote places where a split can occur):
+- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
+- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
+- otherwise the pixel is white.
-This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-
-For a positive integer N, define DN as the 2N×2N image with the following coloring scheme: the pixel with coordinates x = 0, y = 0 corresponds to the bottom left pixel, if (x - 2N-1)2 + (y - 2N-1)2 ≤ 22N-2 then the pixel is black, otherwise the pixel is white.What is the length of the minimal sequence describing D24 ?
+What is the length of the minimal sequence describing $D_{24}$?
# --hints--
-`euler287()` should return 313135496.
+`quadtreeEncoding()` should return `313135496`.
```js
-assert.strictEqual(euler287(), 313135496);
+assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
@@ -39,12 +44,12 @@ assert.strictEqual(euler287(), 313135496);
## --seed-contents--
```js
-function euler287() {
+function quadtreeEncoding() {
return true;
}
-euler287();
+quadtreeEncoding();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
index 28a2e301ce..6a4b1ea589 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
@@ -8,24 +8,28 @@ dashedName: problem-288-an-enormous-factorial
# --description--
-For any prime p the number N(p,q) is defined by
+For any prime $p$ the number $N(p,q)$ is defined by $N(p,q) = \sum_{n=0}^q T_n \times p^n$ with $T_n$ generated by the following random number generator:
-N(p,q) = ∑n=0 to q Tn\*pn with Tn generated by the following random number generator:
+$$\begin{align}
+ & S_0 = 290797 \\\\
+ & S_{n + 1} = {S_n}^2\bmod 50\\,515\\,093 \\\\
+ & T_n = S_n\bmod p
+\end{align}$$
-S0 = 290797 Sn+1 = Sn2 mod 50515093 Tn = Sn mod p
+Let $Nfac(p,q)$ be the factorial of $N(p,q)$.
-Let Nfac(p,q) be the factorial of N(p,q). Let NF(p,q) be the number of factors p in Nfac(p,q).
+Let $NF(p,q)$ be the number of factors $p$ in $Nfac(p,q)$.
-You are given that NF(3,10000) mod 320=624955285.
+You are given that $NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$.
-Find NF(61,107) mod 6110
+Find $NF(61,{10}^7)\bmod {61}^{10}$.
# --hints--
-`euler288()` should return 605857431263982000.
+`enormousFactorial()` should return `605857431263982000`.
```js
-assert.strictEqual(euler288(), 605857431263982000);
+assert.strictEqual(enormousFactorial(), 605857431263982000);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler288(), 605857431263982000);
## --seed-contents--
```js
-function euler288() {
+function enormousFactorial() {
return true;
}
-euler288();
+enormousFactorial();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
index fcac68664d..d313645a22 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
@@ -8,24 +8,26 @@ dashedName: problem-289-eulerian-cycles
# --description--
-Let C(x,y) be a circle passing through the points (x, y), (x, y+1), (x+1, y) and (x+1, y+1).
+Let $C(x,y)$ be a circle passing through the points ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$) and ($x + 1$, $y + 1$).
-For positive integers m and n, let E(m,n) be a configuration which consists of the m·n circles: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x and y are integers }
+For positive integers $m$ and $n$, let $E(m,n)$ be a configuration which consists of the $m·n$ circles: { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ and $y$ are integers }
-An Eulerian cycle on E(m,n) is a closed path that passes through each arc exactly once. Many such paths are possible on E(m,n), but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
+An Eulerian cycle on $E(m,n)$ is a closed path that passes through each arc exactly once. Many such paths are possible on $E(m,n)$, but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
-The image below shows E(3,3) and an example of an Eulerian non-crossing path.
+The image below shows $E(3,3)$ and an example of an Eulerian non-crossing path.
-Let L(m,n) be the number of Eulerian non-crossing paths on E(m,n). For example, L(1,2) = 2, L(2,2) = 37 and L(3,3) = 104290.
+
-the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
+This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-"10" indicates that the current region contains only black pixels;
+For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
-"11" indicates that the current region contains only white pixels.Consider the following 4×4 image (colored marks denote places where a split can occur):
+- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
+- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
+- otherwise the pixel is white.
-This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
-
-For a positive integer N, define DN as the 2N×2N image with the following coloring scheme: the pixel with coordinates x = 0, y = 0 corresponds to the bottom left pixel, if (x - 2N-1)2 + (y - 2N-1)2 ≤ 22N-2 then the pixel is black, otherwise the pixel is white.What is the length of the minimal sequence describing D24 ?
+What is the length of the minimal sequence describing $D_{24}$?
# --hints--
-`euler287()` should return 313135496.
+`quadtreeEncoding()` should return `313135496`.
```js
-assert.strictEqual(euler287(), 313135496);
+assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
@@ -39,12 +44,12 @@ assert.strictEqual(euler287(), 313135496);
## --seed-contents--
```js
-function euler287() {
+function quadtreeEncoding() {
return true;
}
-euler287();
+quadtreeEncoding();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
index 28a2e301ce..6a4b1ea589 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-288-an-enormous-factorial.md
@@ -8,24 +8,28 @@ dashedName: problem-288-an-enormous-factorial
# --description--
-For any prime p the number N(p,q) is defined by
+For any prime $p$ the number $N(p,q)$ is defined by $N(p,q) = \sum_{n=0}^q T_n \times p^n$ with $T_n$ generated by the following random number generator:
-N(p,q) = ∑n=0 to q Tn\*pn with Tn generated by the following random number generator:
+$$\begin{align}
+ & S_0 = 290797 \\\\
+ & S_{n + 1} = {S_n}^2\bmod 50\\,515\\,093 \\\\
+ & T_n = S_n\bmod p
+\end{align}$$
-S0 = 290797 Sn+1 = Sn2 mod 50515093 Tn = Sn mod p
+Let $Nfac(p,q)$ be the factorial of $N(p,q)$.
-Let Nfac(p,q) be the factorial of N(p,q). Let NF(p,q) be the number of factors p in Nfac(p,q).
+Let $NF(p,q)$ be the number of factors $p$ in $Nfac(p,q)$.
-You are given that NF(3,10000) mod 320=624955285.
+You are given that $NF(3,10000) \bmod 3^{20} = 624\\,955\\,285$.
-Find NF(61,107) mod 6110
+Find $NF(61,{10}^7)\bmod {61}^{10}$.
# --hints--
-`euler288()` should return 605857431263982000.
+`enormousFactorial()` should return `605857431263982000`.
```js
-assert.strictEqual(euler288(), 605857431263982000);
+assert.strictEqual(enormousFactorial(), 605857431263982000);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler288(), 605857431263982000);
## --seed-contents--
```js
-function euler288() {
+function enormousFactorial() {
return true;
}
-euler288();
+enormousFactorial();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
index fcac68664d..d313645a22 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-289-eulerian-cycles.md
@@ -8,24 +8,26 @@ dashedName: problem-289-eulerian-cycles
# --description--
-Let C(x,y) be a circle passing through the points (x, y), (x, y+1), (x+1, y) and (x+1, y+1).
+Let $C(x,y)$ be a circle passing through the points ($x$, $y$), ($x$, $y + 1$), ($x + 1$, $y$) and ($x + 1$, $y + 1$).
-For positive integers m and n, let E(m,n) be a configuration which consists of the m·n circles: { C(x,y): 0 ≤ x < m, 0 ≤ y < n, x and y are integers }
+For positive integers $m$ and $n$, let $E(m,n)$ be a configuration which consists of the $m·n$ circles: { $C(x,y)$: $0 ≤ x < m$, $0 ≤ y < n$, $x$ and $y$ are integers }
-An Eulerian cycle on E(m,n) is a closed path that passes through each arc exactly once. Many such paths are possible on E(m,n), but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
+An Eulerian cycle on $E(m,n)$ is a closed path that passes through each arc exactly once. Many such paths are possible on $E(m,n)$, but we are only interested in those which are not self-crossing: A non-crossing path just touches itself at lattice points, but it never crosses itself.
-The image below shows E(3,3) and an example of an Eulerian non-crossing path.
+The image below shows $E(3,3)$ and an example of an Eulerian non-crossing path.
-Let L(m,n) be the number of Eulerian non-crossing paths on E(m,n). For example, L(1,2) = 2, L(2,2) = 37 and L(3,3) = 104290.
+ -Find L(6,10) mod 1010.
+Let $L(m,n)$ be the number of Eulerian non-crossing paths on $E(m,n)$. For example, $L(1,2) = 2$, $L(2,2) = 37$ and $L(3,3) = 104290$.
+
+Find $L(6,10)\bmod {10}^{10}$.
# --hints--
-`euler289()` should return 6567944538.
+`eulerianCycles()` should return `6567944538`.
```js
-assert.strictEqual(euler289(), 6567944538);
+assert.strictEqual(eulerianCycles(), 6567944538);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler289(), 6567944538);
## --seed-contents--
```js
-function euler289() {
+function eulerianCycles() {
return true;
}
-euler289();
+eulerianCycles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
index e46dfedd83..9439010175 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
@@ -8,14 +8,14 @@ dashedName: problem-290-digital-signature
# --description--
-How many integers 0 ≤ n < 1018 have the property that the sum of the digits of n equals the sum of digits of 137n?
+How many integers $0 ≤ n < {10}^{18}$ have the property that the sum of the digits of $n$ equals the sum of digits of $137n$?
# --hints--
-`euler290()` should return 20444710234716470.
+`digitalSignature()` should return `20444710234716470`.
```js
-assert.strictEqual(euler290(), 20444710234716470);
+assert.strictEqual(digitalSignature(), 20444710234716470);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler290(), 20444710234716470);
## --seed-contents--
```js
-function euler290() {
+function digitalSignature() {
return true;
}
-euler290();
+digitalSignature();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
index 0c7d704d9f..2922bdcbe5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
@@ -8,16 +8,16 @@ dashedName: problem-291-panaitopol-primes
# --description--
-A prime number p is called a Panaitopol prime if for some positive integersx and y.
+A prime number $p$ is called a Panaitopol prime if $p = \frac{x^4 - y^4}{x^3 + y^3}$ for some positive integers $x$ and $y$.
-Find how many Panaitopol primes are less than 5×1015.
+Find how many Panaitopol primes are less than $5 × {10}^{15}$.
# --hints--
-`euler291()` should return 4037526.
+`panaitopolPrimes()` should return `4037526`.
```js
-assert.strictEqual(euler291(), 4037526);
+assert.strictEqual(panaitopolPrimes(), 4037526);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler291(), 4037526);
## --seed-contents--
```js
-function euler291() {
+function panaitopolPrimes() {
return true;
}
-euler291();
+panaitopolPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
index 446e875531..7f4ae44273 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
@@ -8,24 +8,27 @@ dashedName: problem-292-pythagorean-polygons
# --description--
-We shall define a pythagorean polygon to be a convex polygon with the following properties:there are at least three vertices,
+We shall define a pythagorean polygon to be a convex polygon with the following properties:
-no three vertices are aligned,
+- there are at least three vertices,
+- no three vertices are aligned,
+- each vertex has integer coordinates,
+- each edge has integer length.
-each vertex has integer coordinates,
-
-each edge has integer length.For a given integer n, define P(n) as the number of distinct pythagorean polygons for which the perimeter is ≤ n.
+For a given integer $n$, define $P(n)$ as the number of distinct pythagorean polygons for which the perimeter is $≤ n$.
Pythagorean polygons should be considered distinct as long as none is a translation of another.
-You are given that P(4) = 1, P(30) = 3655 and P(60) = 891045. Find P(120).
+You are given that $P(4) = 1$, $P(30) = 3655$ and $P(60) = 891045$.
+
+Find $P(120)$.
# --hints--
-`euler292()` should return 3600060866.
+`pythagoreanPolygons()` should return `3600060866`.
```js
-assert.strictEqual(euler292(), 3600060866);
+assert.strictEqual(pythagoreanPolygons(), 3600060866);
```
# --seed--
@@ -33,12 +36,12 @@ assert.strictEqual(euler292(), 3600060866);
## --seed-contents--
```js
-function euler292() {
+function pythagoreanPolygons() {
return true;
}
-euler292();
+pythagoreanPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
index 18307e7b04..2da024c967 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
@@ -8,22 +8,22 @@ dashedName: problem-293-pseudo-fortunate-numbers
# --description--
-An even positive integer N will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
+An even positive integer $N$ will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
-The first twelve admissible numbers are 2,4,6,8,12,16,18,24,30,32,36,48.
+The first twelve admissible numbers are 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48.
-If N is admissible, the smallest integer M > 1 such that N+M is prime, will be called the pseudo-Fortunate number for N.
+If $N$ is admissible, the smallest integer $M > 1$ such that $N + M$ is prime, will be called the pseudo-Fortunate number for $N$.
-For example, N=630 is admissible since it is even and its distinct prime factors are the consecutive primes 2,3,5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is M=11. It can also be seen that the pseudo-Fortunate number for 16 is 3.
+For example, $N = 630$ is admissible since it is even and its distinct prime factors are the consecutive primes 2, 3, 5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is $M = 11$. It can also be seen that the pseudo-Fortunate number for 16 is 3.
-Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers N less than 109.
+Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers $N$ less than ${10}^9$.
# --hints--
-`euler293()` should return 2209.
+`pseudoFortunateNumbers()` should return `2209`.
```js
-assert.strictEqual(euler293(), 2209);
+assert.strictEqual(pseudoFortunateNumbers(), 2209);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler293(), 2209);
## --seed-contents--
```js
-function euler293() {
+function pseudoFortunateNumbers() {
return true;
}
-euler293();
+pseudoFortunateNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
index b7bc62a5f1..20216ace66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
@@ -8,22 +8,23 @@ dashedName: problem-294-sum-of-digits---experience-23
# --description--
-For a positive integer k, define d(k) as the sum of the digits of k in its usual decimal representation.
+For a positive integer $k$, define $d(k)$ as the sum of the digits of $k$ in its usual decimal representation. Thus $d(42) = 4 + 2 = 6$.
-Thus d(42) = 4+2 = 6.
+For a positive integer $n$, define $S(n)$ as the number of positive integers $k < {10}^n$ with the following properties:
-For a positive integer n, define S(n) as the number of positive integers k < 10n with the following properties : k is divisible by 23 and d(k) = 23.
+- $k$ is divisible by 23 and,
+- $d(k) = 23$.
-You are given that S(9) = 263626 and S(42) = 6377168878570056.
+You are given that $S(9) = 263\\,626$ and $S(42) = 6\\,377\\,168\\,878\\,570\\,056$.
-Find S(1112) and give your answer mod 109.
+Find $S({11}^{12})$ and give your answer $\bmod {10}^9$.
# --hints--
-`euler294()` should return 789184709.
+`experience23()` should return `789184709`.
```js
-assert.strictEqual(euler294(), 789184709);
+assert.strictEqual(experience23(), 789184709);
```
# --seed--
@@ -31,12 +32,12 @@ assert.strictEqual(euler294(), 789184709);
## --seed-contents--
```js
-function euler294() {
+function experience23() {
return true;
}
-euler294();
+experience23();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
index 70d1de6d60..c6cb54cc6a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
@@ -10,30 +10,36 @@ dashedName: problem-295-lenticular-holes
We call the convex area enclosed by two circles a lenticular hole if:
-The centres of both circles are on lattice points.
+- The centres of both circles are on lattice points.
+- The two circles intersect at two distinct lattice points.
+- The interior of the convex area enclosed by both circles does not contain any lattice points.
-The two circles intersect at two distinct lattice points.
+Consider the circles:
-The interior of the convex area enclosed by both circles does not contain any lattice points.
+$$\begin{align}
+ & C_0: x^2 + y^2 = 25 \\\\
+ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\
+ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65
+\end{align}$$
-Consider the circles: C0: x2+y2=25 C1: (x+4)2+(y-4)2=1 C2: (x-12)2+(y-4)2=65
+The circles $C_0$, $C_1$ and $C_2$ are drawn in the picture below.
-The circles C0, C1 and C2 are drawn in the picture below.
+
-Find L(6,10) mod 1010.
+Let $L(m,n)$ be the number of Eulerian non-crossing paths on $E(m,n)$. For example, $L(1,2) = 2$, $L(2,2) = 37$ and $L(3,3) = 104290$.
+
+Find $L(6,10)\bmod {10}^{10}$.
# --hints--
-`euler289()` should return 6567944538.
+`eulerianCycles()` should return `6567944538`.
```js
-assert.strictEqual(euler289(), 6567944538);
+assert.strictEqual(eulerianCycles(), 6567944538);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler289(), 6567944538);
## --seed-contents--
```js
-function euler289() {
+function eulerianCycles() {
return true;
}
-euler289();
+eulerianCycles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
index e46dfedd83..9439010175 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-290-digital-signature.md
@@ -8,14 +8,14 @@ dashedName: problem-290-digital-signature
# --description--
-How many integers 0 ≤ n < 1018 have the property that the sum of the digits of n equals the sum of digits of 137n?
+How many integers $0 ≤ n < {10}^{18}$ have the property that the sum of the digits of $n$ equals the sum of digits of $137n$?
# --hints--
-`euler290()` should return 20444710234716470.
+`digitalSignature()` should return `20444710234716470`.
```js
-assert.strictEqual(euler290(), 20444710234716470);
+assert.strictEqual(digitalSignature(), 20444710234716470);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler290(), 20444710234716470);
## --seed-contents--
```js
-function euler290() {
+function digitalSignature() {
return true;
}
-euler290();
+digitalSignature();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
index 0c7d704d9f..2922bdcbe5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-291-panaitopol-primes.md
@@ -8,16 +8,16 @@ dashedName: problem-291-panaitopol-primes
# --description--
-A prime number p is called a Panaitopol prime if for some positive integersx and y.
+A prime number $p$ is called a Panaitopol prime if $p = \frac{x^4 - y^4}{x^3 + y^3}$ for some positive integers $x$ and $y$.
-Find how many Panaitopol primes are less than 5×1015.
+Find how many Panaitopol primes are less than $5 × {10}^{15}$.
# --hints--
-`euler291()` should return 4037526.
+`panaitopolPrimes()` should return `4037526`.
```js
-assert.strictEqual(euler291(), 4037526);
+assert.strictEqual(panaitopolPrimes(), 4037526);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler291(), 4037526);
## --seed-contents--
```js
-function euler291() {
+function panaitopolPrimes() {
return true;
}
-euler291();
+panaitopolPrimes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
index 446e875531..7f4ae44273 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-292-pythagorean-polygons.md
@@ -8,24 +8,27 @@ dashedName: problem-292-pythagorean-polygons
# --description--
-We shall define a pythagorean polygon to be a convex polygon with the following properties:there are at least three vertices,
+We shall define a pythagorean polygon to be a convex polygon with the following properties:
-no three vertices are aligned,
+- there are at least three vertices,
+- no three vertices are aligned,
+- each vertex has integer coordinates,
+- each edge has integer length.
-each vertex has integer coordinates,
-
-each edge has integer length.For a given integer n, define P(n) as the number of distinct pythagorean polygons for which the perimeter is ≤ n.
+For a given integer $n$, define $P(n)$ as the number of distinct pythagorean polygons for which the perimeter is $≤ n$.
Pythagorean polygons should be considered distinct as long as none is a translation of another.
-You are given that P(4) = 1, P(30) = 3655 and P(60) = 891045. Find P(120).
+You are given that $P(4) = 1$, $P(30) = 3655$ and $P(60) = 891045$.
+
+Find $P(120)$.
# --hints--
-`euler292()` should return 3600060866.
+`pythagoreanPolygons()` should return `3600060866`.
```js
-assert.strictEqual(euler292(), 3600060866);
+assert.strictEqual(pythagoreanPolygons(), 3600060866);
```
# --seed--
@@ -33,12 +36,12 @@ assert.strictEqual(euler292(), 3600060866);
## --seed-contents--
```js
-function euler292() {
+function pythagoreanPolygons() {
return true;
}
-euler292();
+pythagoreanPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
index 18307e7b04..2da024c967 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-293-pseudo-fortunate-numbers.md
@@ -8,22 +8,22 @@ dashedName: problem-293-pseudo-fortunate-numbers
# --description--
-An even positive integer N will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
+An even positive integer $N$ will be called admissible, if it is a power of 2 or its distinct prime factors are consecutive primes.
-The first twelve admissible numbers are 2,4,6,8,12,16,18,24,30,32,36,48.
+The first twelve admissible numbers are 2, 4, 6, 8, 12, 16, 18, 24, 30, 32, 36, 48.
-If N is admissible, the smallest integer M > 1 such that N+M is prime, will be called the pseudo-Fortunate number for N.
+If $N$ is admissible, the smallest integer $M > 1$ such that $N + M$ is prime, will be called the pseudo-Fortunate number for $N$.
-For example, N=630 is admissible since it is even and its distinct prime factors are the consecutive primes 2,3,5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is M=11. It can also be seen that the pseudo-Fortunate number for 16 is 3.
+For example, $N = 630$ is admissible since it is even and its distinct prime factors are the consecutive primes 2, 3, 5 and 7. The next prime number after 631 is 641; hence, the pseudo-Fortunate number for 630 is $M = 11$. It can also be seen that the pseudo-Fortunate number for 16 is 3.
-Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers N less than 109.
+Find the sum of all distinct pseudo-Fortunate numbers for admissible numbers $N$ less than ${10}^9$.
# --hints--
-`euler293()` should return 2209.
+`pseudoFortunateNumbers()` should return `2209`.
```js
-assert.strictEqual(euler293(), 2209);
+assert.strictEqual(pseudoFortunateNumbers(), 2209);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler293(), 2209);
## --seed-contents--
```js
-function euler293() {
+function pseudoFortunateNumbers() {
return true;
}
-euler293();
+pseudoFortunateNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
index b7bc62a5f1..20216ace66 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-294-sum-of-digits---experience-23.md
@@ -8,22 +8,23 @@ dashedName: problem-294-sum-of-digits---experience-23
# --description--
-For a positive integer k, define d(k) as the sum of the digits of k in its usual decimal representation.
+For a positive integer $k$, define $d(k)$ as the sum of the digits of $k$ in its usual decimal representation. Thus $d(42) = 4 + 2 = 6$.
-Thus d(42) = 4+2 = 6.
+For a positive integer $n$, define $S(n)$ as the number of positive integers $k < {10}^n$ with the following properties:
-For a positive integer n, define S(n) as the number of positive integers k < 10n with the following properties : k is divisible by 23 and d(k) = 23.
+- $k$ is divisible by 23 and,
+- $d(k) = 23$.
-You are given that S(9) = 263626 and S(42) = 6377168878570056.
+You are given that $S(9) = 263\\,626$ and $S(42) = 6\\,377\\,168\\,878\\,570\\,056$.
-Find S(1112) and give your answer mod 109.
+Find $S({11}^{12})$ and give your answer $\bmod {10}^9$.
# --hints--
-`euler294()` should return 789184709.
+`experience23()` should return `789184709`.
```js
-assert.strictEqual(euler294(), 789184709);
+assert.strictEqual(experience23(), 789184709);
```
# --seed--
@@ -31,12 +32,12 @@ assert.strictEqual(euler294(), 789184709);
## --seed-contents--
```js
-function euler294() {
+function experience23() {
return true;
}
-euler294();
+experience23();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
index 70d1de6d60..c6cb54cc6a 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-295-lenticular-holes.md
@@ -10,30 +10,36 @@ dashedName: problem-295-lenticular-holes
We call the convex area enclosed by two circles a lenticular hole if:
-The centres of both circles are on lattice points.
+- The centres of both circles are on lattice points.
+- The two circles intersect at two distinct lattice points.
+- The interior of the convex area enclosed by both circles does not contain any lattice points.
-The two circles intersect at two distinct lattice points.
+Consider the circles:
-The interior of the convex area enclosed by both circles does not contain any lattice points.
+$$\begin{align}
+ & C_0: x^2 + y^2 = 25 \\\\
+ & C_1: {(x + 4)}^2 + {(y - 4)}^2 = 1 \\\\
+ & C_2: {(x - 12)}^2 + {(y - 4)}^2 = 65
+\end{align}$$
-Consider the circles: C0: x2+y2=25 C1: (x+4)2+(y-4)2=1 C2: (x-12)2+(y-4)2=65
+The circles $C_0$, $C_1$ and $C_2$ are drawn in the picture below.
-The circles C0, C1 and C2 are drawn in the picture below.
+ -C0 and C1 form a lenticular hole, as well as C0 and C2.
+$C_0$ and $C_1$ form a lenticular hole, as well as $C_0$ and $C_2$.
-We call an ordered pair of positive real numbers (r1, r2) a lenticular pair if there exist two circles with radii r1 and r2 that form a lenticular hole. We can verify that (1, 5) and (5, √65) are the lenticular pairs of the example above.
+We call an ordered pair of positive real numbers ($r_1$, $r_2$) a lenticular pair if there exist two circles with radii $r_1$ and $r_2$ that form a lenticular hole. We can verify that ($1$, $5$) and ($5$, $\sqrt{65}$) are the lenticular pairs of the example above.
-Let L(N) be the number of distinct lenticular pairs (r1, r2) for which 0 < r1 ≤ r2 ≤ N. We can verify that L(10) = 30 and L(100) = 3442.
+Let $L(N)$ be the number of distinct lenticular pairs ($r_1$, $r_2$) for which $0 < r_1 ≤ r_2 ≤ N$. We can verify that $L(10) = 30$ and $L(100) = 3442$.
-Find L(100 000).
+Find $L(100\\,000)$.
# --hints--
-`euler295()` should return 4884650818.
+`lenticularHoles()` should return `4884650818`.
```js
-assert.strictEqual(euler295(), 4884650818);
+assert.strictEqual(lenticularHoles(), 4884650818);
```
# --seed--
@@ -41,12 +47,12 @@ assert.strictEqual(euler295(), 4884650818);
## --seed-contents--
```js
-function euler295() {
+function lenticularHoles() {
return true;
}
-euler295();
+lenticularHoles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
index 0d269dca3c..9001b02c5f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
@@ -8,18 +8,20 @@ dashedName: problem-296-angular-bisector-and-tangent
# --description--
-Given is an integer sided triangle ABC with BC ≤ AC ≤ AB.k is the angular bisector of angle ACB.m is the tangent at C to the circumscribed circle of ABC.n is a line parallel to m through B.
+Given is an integer sided triangle $ABC$ with $BC ≤ AC ≤ AB$. $k$ is the angular bisector of angle $ACB$. $m$ is the tangent at $C$ to the circumscribed circle of $ABC$. $n$ is a line parallel to $m$ through $B$.
-The intersection of n and k is called E.
+The intersection of $n$ and $k$ is called $E$.
-How many triangles ABC with a perimeter not exceeding 100 000 exist such that BE has integral length?
+
-C0 and C1 form a lenticular hole, as well as C0 and C2.
+$C_0$ and $C_1$ form a lenticular hole, as well as $C_0$ and $C_2$.
-We call an ordered pair of positive real numbers (r1, r2) a lenticular pair if there exist two circles with radii r1 and r2 that form a lenticular hole. We can verify that (1, 5) and (5, √65) are the lenticular pairs of the example above.
+We call an ordered pair of positive real numbers ($r_1$, $r_2$) a lenticular pair if there exist two circles with radii $r_1$ and $r_2$ that form a lenticular hole. We can verify that ($1$, $5$) and ($5$, $\sqrt{65}$) are the lenticular pairs of the example above.
-Let L(N) be the number of distinct lenticular pairs (r1, r2) for which 0 < r1 ≤ r2 ≤ N. We can verify that L(10) = 30 and L(100) = 3442.
+Let $L(N)$ be the number of distinct lenticular pairs ($r_1$, $r_2$) for which $0 < r_1 ≤ r_2 ≤ N$. We can verify that $L(10) = 30$ and $L(100) = 3442$.
-Find L(100 000).
+Find $L(100\\,000)$.
# --hints--
-`euler295()` should return 4884650818.
+`lenticularHoles()` should return `4884650818`.
```js
-assert.strictEqual(euler295(), 4884650818);
+assert.strictEqual(lenticularHoles(), 4884650818);
```
# --seed--
@@ -41,12 +47,12 @@ assert.strictEqual(euler295(), 4884650818);
## --seed-contents--
```js
-function euler295() {
+function lenticularHoles() {
return true;
}
-euler295();
+lenticularHoles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
index 0d269dca3c..9001b02c5f 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-296-angular-bisector-and-tangent.md
@@ -8,18 +8,20 @@ dashedName: problem-296-angular-bisector-and-tangent
# --description--
-Given is an integer sided triangle ABC with BC ≤ AC ≤ AB.k is the angular bisector of angle ACB.m is the tangent at C to the circumscribed circle of ABC.n is a line parallel to m through B.
+Given is an integer sided triangle $ABC$ with $BC ≤ AC ≤ AB$. $k$ is the angular bisector of angle $ACB$. $m$ is the tangent at $C$ to the circumscribed circle of $ABC$. $n$ is a line parallel to $m$ through $B$.
-The intersection of n and k is called E.
+The intersection of $n$ and $k$ is called $E$.
-How many triangles ABC with a perimeter not exceeding 100 000 exist such that BE has integral length?
+ +
+How many triangles $ABC$ with a perimeter not exceeding $100\\,000$ exist such that $BE$ has integral length?
# --hints--
-`euler296()` should return 1137208419.
+`angularBisectorAndTangent()` should return `1137208419`.
```js
-assert.strictEqual(euler296(), 1137208419);
+assert.strictEqual(angularBisectorAndTangent(), 1137208419);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler296(), 1137208419);
## --seed-contents--
```js
-function euler296() {
+function angularBisectorAndTangent() {
return true;
}
-euler296();
+angularBisectorAndTangent();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
index 55d96b520c..8178fce31e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
@@ -12,18 +12,24 @@ Each new term in the Fibonacci sequence is generated by adding the previous two
Starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
-Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89. Such a sum is called the Zeckendorf representation of the number.
+Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89.
-For any integer n>0, let z(n) be the number of terms in the Zeckendorf representation of n. Thus, z(5) = 1, z(14) = 2, z(100) = 3 etc. Also, for 0<n<106, ∑ z(n) = 7894453.
+Such a sum is called the Zeckendorf representation of the number.
-Find ∑ z(n) for 0<n<1017.
+For any integer $n>0$, let $z(n)$ be the number of terms in the Zeckendorf representation of $n$.
+
+Thus, $z(5) = 1$, $z(14) = 2$, $z(100) = 3$ etc.
+
+Also, for $0 < n < {10}^6$, $\sum z(n) = 7\\,894\\,453$.
+
+Find $\sum z(n)$ for $0 < n < {10}^{17}$.
# --hints--
-`euler297()` should return 2252639041804718000.
+`zeckendorfRepresentation()` should return `2252639041804718000`.
```js
-assert.strictEqual(euler297(), 2252639041804718000);
+assert.strictEqual(zeckendorfRepresentation(), 2252639041804718000);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler297(), 2252639041804718000);
## --seed-contents--
```js
-function euler297() {
+function zeckendorfRepresentation() {
return true;
}
-euler297();
+zeckendorfRepresentation();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
index a9c0c8ad7e..66e95010d5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
@@ -12,16 +12,29 @@ Larry and Robin play a memory game involving of a sequence of random numbers bet
Both players start with empty memories. Both players always add new missed numbers to their memory but use a different strategy in deciding which number to remove: Larry's strategy is to remove the number that hasn't been called in the longest time. Robin's strategy is to remove the number that's been in the memory the longest time.
-Example game:Turn Callednumber Larry'smemory Larry'sscore Robin'smemory Robin'sscore 1 1 1 0 1 0 2 2 1,2 0 1,2 0 3 4 1,2,4 0 1,2,4 0 4 6 1,2,4,6 0 1,2,4,6 0 5 1 1,2,4,6 1 1,2,4,6 1 6 8 1,2,4,6,8 1 1,2,4,6,8 1 7 10 1,4,6,8,10 1 2,4,6,8,10 1 8 2 1,2,6,8,10 1 2,4,6,8,10 2 9 4 1,2,4,8,10 1 2,4,6,8,10 3 10 1 1,2,4,8,10 2 1,4,6,8,10 3
+Example game:
-Denoting Larry's score by L and Robin's score by R, what is the expected value of |L-R| after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+| Turn | Called number | Larry's memory | Larry's score | Robin's memory | Robin's score |
+|------|---------------|---------------:|---------------|----------------|---------------|
+| 1 | 1 | 1 | 0 | 1 | 0 |
+| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
+| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
+| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
+| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
+| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
+| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
+| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
+| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
+| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
+
+Denoting Larry's score by $L$ and Robin's score by $R$, what is the expected value of $|L - R|$ after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
# --hints--
-`euler298()` should return 1.76882294.
+`selectiveAmnesia()` should return `1.76882294`.
```js
-assert.strictEqual(euler298(), 1.76882294);
+assert.strictEqual(selectiveAmnesia(), 1.76882294);
```
# --seed--
@@ -29,12 +42,12 @@ assert.strictEqual(euler298(), 1.76882294);
## --seed-contents--
```js
-function euler298() {
+function selectiveAmnesia() {
return true;
}
-euler298();
+selectiveAmnesia();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
index 586b589068..20a21fc782 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
@@ -8,26 +8,32 @@ dashedName: problem-299-three-similar-triangles
# --description--
-Four points with integer coordinates are selected:A(a, 0), B(b, 0), C(0, c) and D(0, d),
+Four points with integer coordinates are selected:
-with 0 < a < b and 0 < c < d.
+$A(a, 0)$, $B(b, 0)$, $C(0, c)$ and $D(0, d)$, with $0 < a < b$ and $0 < c < d$.
-Point P, also with integer coordinates, is chosen on the line AC so that the three triangles ABP, CDP and BDP are all similar.
+Point $P$, also with integer coordinates, is chosen on the line $AC$ so that the three triangles $ABP$, $CDP$ and $BDP$ are all similar.
-It is easy to prove that the three triangles can be similar, only if a=c.
+
+
+How many triangles $ABC$ with a perimeter not exceeding $100\\,000$ exist such that $BE$ has integral length?
# --hints--
-`euler296()` should return 1137208419.
+`angularBisectorAndTangent()` should return `1137208419`.
```js
-assert.strictEqual(euler296(), 1137208419);
+assert.strictEqual(angularBisectorAndTangent(), 1137208419);
```
# --seed--
@@ -27,12 +29,12 @@ assert.strictEqual(euler296(), 1137208419);
## --seed-contents--
```js
-function euler296() {
+function angularBisectorAndTangent() {
return true;
}
-euler296();
+angularBisectorAndTangent();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
index 55d96b520c..8178fce31e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-297-zeckendorf-representation.md
@@ -12,18 +12,24 @@ Each new term in the Fibonacci sequence is generated by adding the previous two
Starting with 1 and 2, the first 10 terms will be: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89.
-Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89. Such a sum is called the Zeckendorf representation of the number.
+Every positive integer can be uniquely written as a sum of nonconsecutive terms of the Fibonacci sequence. For example, 100 = 3 + 8 + 89.
-For any integer n>0, let z(n) be the number of terms in the Zeckendorf representation of n. Thus, z(5) = 1, z(14) = 2, z(100) = 3 etc. Also, for 0<n<106, ∑ z(n) = 7894453.
+Such a sum is called the Zeckendorf representation of the number.
-Find ∑ z(n) for 0<n<1017.
+For any integer $n>0$, let $z(n)$ be the number of terms in the Zeckendorf representation of $n$.
+
+Thus, $z(5) = 1$, $z(14) = 2$, $z(100) = 3$ etc.
+
+Also, for $0 < n < {10}^6$, $\sum z(n) = 7\\,894\\,453$.
+
+Find $\sum z(n)$ for $0 < n < {10}^{17}$.
# --hints--
-`euler297()` should return 2252639041804718000.
+`zeckendorfRepresentation()` should return `2252639041804718000`.
```js
-assert.strictEqual(euler297(), 2252639041804718000);
+assert.strictEqual(zeckendorfRepresentation(), 2252639041804718000);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler297(), 2252639041804718000);
## --seed-contents--
```js
-function euler297() {
+function zeckendorfRepresentation() {
return true;
}
-euler297();
+zeckendorfRepresentation();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
index a9c0c8ad7e..66e95010d5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-298-selective-amnesia.md
@@ -12,16 +12,29 @@ Larry and Robin play a memory game involving of a sequence of random numbers bet
Both players start with empty memories. Both players always add new missed numbers to their memory but use a different strategy in deciding which number to remove: Larry's strategy is to remove the number that hasn't been called in the longest time. Robin's strategy is to remove the number that's been in the memory the longest time.
-Example game:Turn Callednumber Larry'smemory Larry'sscore Robin'smemory Robin'sscore 1 1 1 0 1 0 2 2 1,2 0 1,2 0 3 4 1,2,4 0 1,2,4 0 4 6 1,2,4,6 0 1,2,4,6 0 5 1 1,2,4,6 1 1,2,4,6 1 6 8 1,2,4,6,8 1 1,2,4,6,8 1 7 10 1,4,6,8,10 1 2,4,6,8,10 1 8 2 1,2,6,8,10 1 2,4,6,8,10 2 9 4 1,2,4,8,10 1 2,4,6,8,10 3 10 1 1,2,4,8,10 2 1,4,6,8,10 3
+Example game:
-Denoting Larry's score by L and Robin's score by R, what is the expected value of |L-R| after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
+| Turn | Called number | Larry's memory | Larry's score | Robin's memory | Robin's score |
+|------|---------------|---------------:|---------------|----------------|---------------|
+| 1 | 1 | 1 | 0 | 1 | 0 |
+| 2 | 2 | 1,2 | 0 | 1,2 | 0 |
+| 3 | 4 | 1,2,4 | 0 | 1,2,4 | 0 |
+| 4 | 6 | 1,2,4,6 | 0 | 1,2,4,6 | 0 |
+| 5 | 1 | 1,2,4,6 | 1 | 1,2,4,6 | 1 |
+| 6 | 8 | 1,2,4,6,8 | 1 | 1,2,4,6,8 | 1 |
+| 7 | 10 | 1,4,6,8,10 | 1 | 2,4,6,8,10 | 1 |
+| 8 | 2 | 1,2,6,8,10 | 1 | 2,4,6,8,10 | 2 |
+| 9 | 4 | 1,2,4,8,10 | 1 | 2,4,6,8,10 | 3 |
+| 10 | 1 | 1,2,4,8,10 | 2 | 1,4,6,8,10 | 3 |
+
+Denoting Larry's score by $L$ and Robin's score by $R$, what is the expected value of $|L - R|$ after 50 turns? Give your answer rounded to eight decimal places using the format x.xxxxxxxx .
# --hints--
-`euler298()` should return 1.76882294.
+`selectiveAmnesia()` should return `1.76882294`.
```js
-assert.strictEqual(euler298(), 1.76882294);
+assert.strictEqual(selectiveAmnesia(), 1.76882294);
```
# --seed--
@@ -29,12 +42,12 @@ assert.strictEqual(euler298(), 1.76882294);
## --seed-contents--
```js
-function euler298() {
+function selectiveAmnesia() {
return true;
}
-euler298();
+selectiveAmnesia();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
index 586b589068..20a21fc782 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-299-three-similar-triangles.md
@@ -8,26 +8,32 @@ dashedName: problem-299-three-similar-triangles
# --description--
-Four points with integer coordinates are selected:A(a, 0), B(b, 0), C(0, c) and D(0, d),
+Four points with integer coordinates are selected:
-with 0 < a < b and 0 < c < d.
+$A(a, 0)$, $B(b, 0)$, $C(0, c)$ and $D(0, d)$, with $0 < a < b$ and $0 < c < d$.
-Point P, also with integer coordinates, is chosen on the line AC so that the three triangles ABP, CDP and BDP are all similar.
+Point $P$, also with integer coordinates, is chosen on the line $AC$ so that the three triangles $ABP$, $CDP$ and $BDP$ are all similar.
-It is easy to prove that the three triangles can be similar, only if a=c.
+ -So, given that a=c, we are looking for triplets (a,b,d) such that at least one point P (with integer coordinates) exists on AC, making the three triangles ABP, CDP and BDP all similar.
+It is easy to prove that the three triangles can be similar, only if $a = c$.
-For example, if (a,b,d)=(2,3,4), it can be easily verified that point P(1,1) satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point P(1,1) is common for both.
+So, given that $a = c$, we are looking for triplets ($a$, $b$, $d$) such that at least one point $P$ (with integer coordinates) exists on $AC$, making the three triangles $ABP$, $CDP$ and $BDP$ all similar.
-If b+d < 100, there are 92 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000, there are 320471 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000 000, how many distinct triplets (a,b,d) are there such that point P exists?
+For example, if $(a, b, d) = (2, 3, 4)$, it can be easily verified that point $P(1, 1)$ satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point $P(1, 1)$ is common for both.
+
+If $b + d < 100$, there are 92 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000$, there are 320471 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000\\,000$, how many distinct triplets ($a$, $b$, $d$) are there such that point $P$ exists?
# --hints--
-`euler299()` should return 549936643.
+`threeSimilarTriangles()` should return `549936643`.
```js
-assert.strictEqual(euler299(), 549936643);
+assert.strictEqual(threeSimilarTriangles(), 549936643);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler299(), 549936643);
## --seed-contents--
```js
-function euler299() {
+function threeSimilarTriangles() {
return true;
}
-euler299();
+threeSimilarTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
index 52c5f272c6..0d58795ae2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
@@ -10,24 +10,30 @@ dashedName: problem-300-protein-folding
In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
-For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are 2n distinct proteins consisting of n elements.
+For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are $2^n$ distinct proteins consisting of $n$ elements.
-When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous. As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside. Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
+When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
+
+As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
+
+Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
+
-So, given that a=c, we are looking for triplets (a,b,d) such that at least one point P (with integer coordinates) exists on AC, making the three triangles ABP, CDP and BDP all similar.
+It is easy to prove that the three triangles can be similar, only if $a = c$.
-For example, if (a,b,d)=(2,3,4), it can be easily verified that point P(1,1) satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point P(1,1) is common for both.
+So, given that $a = c$, we are looking for triplets ($a$, $b$, $d$) such that at least one point $P$ (with integer coordinates) exists on $AC$, making the three triangles $ABP$, $CDP$ and $BDP$ all similar.
-If b+d < 100, there are 92 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000, there are 320471 distinct triplets (a,b,d) such that point P exists. If b+d < 100 000 000, how many distinct triplets (a,b,d) are there such that point P exists?
+For example, if $(a, b, d) = (2, 3, 4)$, it can be easily verified that point $P(1, 1)$ satisfies the above condition. Note that the triplets (2,3,4) and (2,4,3) are considered as distinct, although point $P(1, 1)$ is common for both.
+
+If $b + d < 100$, there are 92 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000$, there are 320471 distinct triplets ($a$, $b$, $d$) such that point $P$ exists.
+
+If $b + d < 100\\,000\\,000$, how many distinct triplets ($a$, $b$, $d$) are there such that point $P$ exists?
# --hints--
-`euler299()` should return 549936643.
+`threeSimilarTriangles()` should return `549936643`.
```js
-assert.strictEqual(euler299(), 549936643);
+assert.strictEqual(threeSimilarTriangles(), 549936643);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler299(), 549936643);
## --seed-contents--
```js
-function euler299() {
+function threeSimilarTriangles() {
return true;
}
-euler299();
+threeSimilarTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
index 52c5f272c6..0d58795ae2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-300-protein-folding.md
@@ -10,24 +10,30 @@ dashedName: problem-300-protein-folding
In a very simplified form, we can consider proteins as strings consisting of hydrophobic (H) and polar (P) elements, e.g. HHPPHHHPHHPH.
-For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are 2n distinct proteins consisting of n elements.
+For this problem, the orientation of a protein is important; e.g. HPP is considered distinct from PPH. Thus, there are $2^n$ distinct proteins consisting of $n$ elements.
-When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous. As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside. Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
+When one encounters these strings in nature, they are always folded in such a way that the number of H-H contact points is as large as possible, since this is energetically advantageous.
+
+As a result, the H-elements tend to accumulate in the inner part, with the P-elements on the outside.
+
+Natural proteins are folded in three dimensions of course, but we will only consider protein folding in two dimensions.
The figure below shows two possible ways that our example protein could be folded (H-H contact points are shown with red dots).
+ +
The folding on the left has only six H-H contact points, thus it would never occur naturally. On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
-Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be 850 / 28=3.3203125.
+Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be $\frac{850}{2^8} = 3.3203125$.
What is the average number of H-H contact points in an optimal folding of a random protein string of length 15? Give your answer using as many decimal places as necessary for an exact result.
# --hints--
-`euler300()` should return 8.0540771484375.
+`proteinFolding()` should return `8.0540771484375`.
```js
-assert.strictEqual(euler300(), 8.0540771484375);
+assert.strictEqual(proteinFolding(), 8.0540771484375);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler300(), 8.0540771484375);
## --seed-contents--
```js
-function euler300() {
+function proteinFolding() {
return true;
}
-euler300();
+proteinFolding();
```
# --solutions--
+
The folding on the left has only six H-H contact points, thus it would never occur naturally. On the other hand, the folding on the right has nine H-H contact points, which is optimal for this string.
-Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be 850 / 28=3.3203125.
+Assuming that H and P elements are equally likely to occur in any position along the string, the average number of H-H contact points in an optimal folding of a random protein string of length 8 turns out to be $\frac{850}{2^8} = 3.3203125$.
What is the average number of H-H contact points in an optimal folding of a random protein string of length 15? Give your answer using as many decimal places as necessary for an exact result.
# --hints--
-`euler300()` should return 8.0540771484375.
+`proteinFolding()` should return `8.0540771484375`.
```js
-assert.strictEqual(euler300(), 8.0540771484375);
+assert.strictEqual(proteinFolding(), 8.0540771484375);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler300(), 8.0540771484375);
## --seed-contents--
```js
-function euler300() {
+function proteinFolding() {
return true;
}
-euler300();
+proteinFolding();
```
# --solutions--