diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
index 34fda8a4ee..070bfdee09 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
@@ -1,6 +1,6 @@
---
id: 5900f3f51000cf542c50ff07
-title: 'Problem 136: Singleton difference'
+title: 'Problema 136: Diferenças de solitários'
challengeType: 5
forumTopicId: 301764
dashedName: problem-136-singleton-difference
@@ -8,20 +8,20 @@ dashedName: problem-136-singleton-difference
# --description--
-The positive integers, x, y, and z, are consecutive terms of an arithmetic progression. Given that n is a positive integer, the equation, x2 − y2 − z2 = n, has exactly one solution when n = 20:
+Os números inteiros positivos, $x$, $y$e $z$, são termos consecutivos de uma progressão aritmética. Dado que $n$ é um número inteiro positivo, a equação, $x^2 - y^2 - z^2 = n$, tem exatamente uma solução quando $n = 20$:
-132 − 102 − 72 = 20
+$$13^2 − 10^2 − 7^2 = 20$$
-In fact there are twenty-five values of n below one hundred for which the equation has a unique solution.
+De fato, há vinte e cinco valores de $n$ abaixo de cem para os quais a equação tem uma solução única.
-How many values of n less than fifty million have exactly one solution?
+Quantos valores de $n$ abaixo de cinquenta milhões têm exatamente uma solução?
# --hints--
-`euler136()` should return 2544559.
+`singletonDifference()` deve retornar `2544559`.
```js
-assert.strictEqual(euler136(), 2544559);
+assert.strictEqual(singletonDifference(), 2544559);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler136(), 2544559);
## --seed-contents--
```js
-function euler136() {
+function singletonDifference() {
return true;
}
-euler136();
+singletonDifference();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
index 2863f66aa1..cf0f9558d5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
@@ -1,6 +1,6 @@
---
id: 5900f3f51000cf542c50ff08
-title: 'Problem 137: Fibonacci golden nuggets'
+title: 'Problema 137: Pepitas de ouro de Fibonacci'
challengeType: 5
forumTopicId: 301765
dashedName: problem-137-fibonacci-golden-nuggets
@@ -8,30 +8,34 @@ dashedName: problem-137-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AF(x) = xF1 + x2F2 + x3F3 + ..., where Fk is the kth term in the Fibonacci sequence: 1, 1, 2, 3, 5, 8, ... ; that is, Fk = Fk−1 + Fk−2, F1 = 1 and F2 = 1.
+Considere a série polinomial infinita $A_{F}(x) = xF_1 + x^2F_2 + x^3F_3 + \ldots$, onde $F_k$ é o $k$º termo na sequência de Fibonacci: $1, 1, 2, 3, 5, 8, \ldots$; ou seja, $F_k = F_{k − 1} + F_{k − 2}, F_1 = 1$ e $F_2 = 1$.
-For this problem we shall be interested in values of x for which AF(x) is a positive integer.
+Para este problema, estaremos interessados em valores de $x$ para os quais $A_{F}(x)$ é um número inteiro positivo.
-Surprisingly AF(1/2)
+Surpreendentemente,
-=
+$$\begin{align} A_F(\frac{1}{2}) & = (\frac{1}{2}) × 1 + {(\frac{1}{2})}^2 × 1 + {(\frac{1}{2})}^3 × 2 + {(\frac{1}{2})}^4 × 3 + {(\frac{1}{2})}^5 × 5 + \cdots \\\\ & = \frac{1}{2} + \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{5}{32} + \cdots \\\\ & = 2 \end{align}$$
-(1/2).1 + (1/2)2.1 + (1/2)3.2 + (1/2)4.3 + (1/2)5.5 + ...
+Os valores correspondentes de $x$ para os primeiros cinco números naturais são mostrados abaixo.
-= 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ...
+| $x$ | $A_F(x)$ |
+| --------------------------- | -------- |
+| $\sqrt{2} − 1$ | $1$ |
+| $\frac{1}{2}$ | $2$ |
+| $\frac{\sqrt{13} − 2}{3}$ | $3$ |
+| $\frac{\sqrt{89} − 5}{8}$ | $4$ |
+| $\frac{\sqrt{34} − 3}{5}$ | $5$ |
-= 2 The corresponding values of x for the first five natural numbers are shown below.
+Vamos chamar $A_F(x)$ de pepita de ouro se $x$ for racional, porque eles se tornam cada vez mais raros (por exemplo, a 10ª pepita de ouro é 74049690).
-xAF(x) √2−11 1/22 (√13−2)/33 (√89−5)/84 (√34−3)/55
-
-We shall call AF(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690. Find the 15th golden nugget.
+Encontre a 15ª pepita dourada.
# --hints--
-`euler137()` should return 1120149658760.
+`goldenNugget()` deve retornar `1120149658760`.
```js
-assert.strictEqual(euler137(), 1120149658760);
+assert.strictEqual(goldenNugget(), 1120149658760);
```
# --seed--
@@ -39,12 +43,12 @@ assert.strictEqual(euler137(), 1120149658760);
## --seed-contents--
```js
-function euler137() {
+function goldenNugget() {
return true;
}
-euler137();
+goldenNugget();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
index 5675e1f938..6af82710da 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f3f61000cf542c50ff09
-title: 'Problem 138: Special isosceles triangles'
+title: 'Problema 138: Triângulos isósceles especiais'
challengeType: 5
forumTopicId: 301766
dashedName: problem-138-special-isosceles-triangles
@@ -8,16 +8,22 @@ dashedName: problem-138-special-isosceles-triangles
# --description--
-Consider the isosceles triangle with base length, b = 16, and legs, L = 17.
+Considere o triângulo isósceles com o comprimento de base, $b = 16$, e os lados iguais, $L = 17$.
-By using the Pythagorean theorem it can be seen that the height of the triangle, h = √(172 − 82) = 15, which is one less than the base length. With b = 272 and L = 305, we get h = 273, which is one more than the base length, and this is the second smallest isosceles triangle with the property that h = b ± 1. Find ∑ L for the twelve smallest isosceles triangles for which h = b ± 1 and b, L are positive integers.
+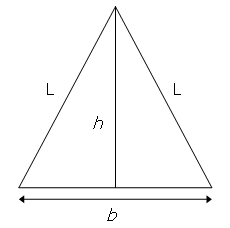 +
+Usando o teorema de Pitágoras, pode ser visto que a altura do triângulo, $h = \sqrt{{17}^2 - 8^2} = 15$, que é uma unidade menor que o comprimento da base.
+
+Com $b = 272$ e $L = 305$, obtemos $h = 273$, que é um a mais do que o comprimento da base, e este é o segundo menor triângulo isósceles com a propriedade $h = b ± 1$.
+
+Encontre $\sum{L}$ para os doze menores triângulos isósceles para os quais $h = b ± 1$ e $b$, $L$ são números inteiros positivos.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` deve retornar `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..c97bce63ec 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -1,6 +1,6 @@
---
id: 5900f3f71000cf542c50ff0a
-title: 'Problem 139: Pythagorean tiles'
+title: 'Problema 139: Blocos de Pitágoras'
challengeType: 5
forumTopicId: 301767
dashedName: problem-139-pythagorean-tiles
@@ -8,18 +8,22 @@ dashedName: problem-139-pythagorean-tiles
# --description--
-Let (a, b, c) represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length c.
+Considere que (a, b, c) representam os três lados de um triângulo retângulo com lados cujo comprimento são números inteiros. É possível posicionar quatro desses triângulos juntos para formar um quadrado com comprimento c.
-For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
+Por exemplo, triângulos de lados (3, 4, 5) podem ser colocados juntos para formar um quadrado de 5 por 5 com um orifício de 1 por 1 no meio. Também pode-se ver que o quadrado de 5 por 5 pode ser preenchido com vinte e cinco blocos quadrados de 1 por 1.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+
+
+Usando o teorema de Pitágoras, pode ser visto que a altura do triângulo, $h = \sqrt{{17}^2 - 8^2} = 15$, que é uma unidade menor que o comprimento da base.
+
+Com $b = 272$ e $L = 305$, obtemos $h = 273$, que é um a mais do que o comprimento da base, e este é o segundo menor triângulo isósceles com a propriedade $h = b ± 1$.
+
+Encontre $\sum{L}$ para os doze menores triângulos isósceles para os quais $h = b ± 1$ e $b$, $L$ são números inteiros positivos.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` deve retornar `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..c97bce63ec 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -1,6 +1,6 @@
---
id: 5900f3f71000cf542c50ff0a
-title: 'Problem 139: Pythagorean tiles'
+title: 'Problema 139: Blocos de Pitágoras'
challengeType: 5
forumTopicId: 301767
dashedName: problem-139-pythagorean-tiles
@@ -8,18 +8,22 @@ dashedName: problem-139-pythagorean-tiles
# --description--
-Let (a, b, c) represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length c.
+Considere que (a, b, c) representam os três lados de um triângulo retângulo com lados cujo comprimento são números inteiros. É possível posicionar quatro desses triângulos juntos para formar um quadrado com comprimento c.
-For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
+Por exemplo, triângulos de lados (3, 4, 5) podem ser colocados juntos para formar um quadrado de 5 por 5 com um orifício de 1 por 1 no meio. Também pode-se ver que o quadrado de 5 por 5 pode ser preenchido com vinte e cinco blocos quadrados de 1 por 1.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+ +
+No entanto, se os triângulos de (5, 12, 13) fossem usados, o orifício mediria 7 por 7. Esses quadrados de 7 por 7 não poderiam ser usados para preencher o quadrado de 13 por 13.
+
+Dado que o perímetro do triângulo retângulo é inferior a cem milhões, quantos triângulos trigonométricos pitagóricos permitiriam que tal preenchimento acontecesse?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` deve retornar `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..c027721b5a 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -1,6 +1,6 @@
---
id: 5900f3fa1000cf542c50ff0c
-title: 'Problem 140: Modified Fibonacci golden nuggets'
+title: 'Problema 140: Pepitas de ouro de Fibonacci modificado'
challengeType: 5
forumTopicId: 301769
dashedName: problem-140-modified-fibonacci-golden-nuggets
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Considere a série polinomial infinita $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, onde $G_k$ é o $k$º termo da relação de recorrência de segunda ordem $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ e $G_2 = 4$; ou seja, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+Para este problema, estaremos interessados nos valores de $x$ para os quais $A_G(x)$ é um número inteiro positivo.
-The corresponding values of x for the first five natural numbers are shown below.
+Os valores correspondentes de $x$ para os primeiros cinco números naturais são mostrados abaixo.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+| ----------------------------- | -------- |
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+Vamos chamar $A_G(x)$ de pepita de ouro se $x$ for racional, porque eles se tornam cada vez mais raros (por exemplo, a 20ª pepita de ouro é 211345365). Encontre a soma das primeiras trinta pepitas douradas.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` deve retornar `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
index 13babe893b..b0bf0827f0 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff14
-title: 'Problem 148: Exploring Pascal''s triangle'
+title: 'Problema 148: Explorando o triângulo de Pascal'
challengeType: 5
forumTopicId: 301777
dashedName: problem-148-exploring-pascals-triangle
@@ -8,9 +8,9 @@ dashedName: problem-148-exploring-pascals-triangle
# --description--
-We can easily verify that none of the entries in the first seven rows of Pascal's triangle are divisible by 7:
+Podemos facilmente verificar que nenhuma das entradas das primeiras sete linhas do triângulo Pascal é divisível por 7:
-
+
+No entanto, se os triângulos de (5, 12, 13) fossem usados, o orifício mediria 7 por 7. Esses quadrados de 7 por 7 não poderiam ser usados para preencher o quadrado de 13 por 13.
+
+Dado que o perímetro do triângulo retângulo é inferior a cem milhões, quantos triângulos trigonométricos pitagóricos permitiriam que tal preenchimento acontecesse?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` deve retornar `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..c027721b5a 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -1,6 +1,6 @@
---
id: 5900f3fa1000cf542c50ff0c
-title: 'Problem 140: Modified Fibonacci golden nuggets'
+title: 'Problema 140: Pepitas de ouro de Fibonacci modificado'
challengeType: 5
forumTopicId: 301769
dashedName: problem-140-modified-fibonacci-golden-nuggets
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Considere a série polinomial infinita $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, onde $G_k$ é o $k$º termo da relação de recorrência de segunda ordem $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ e $G_2 = 4$; ou seja, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+Para este problema, estaremos interessados nos valores de $x$ para os quais $A_G(x)$ é um número inteiro positivo.
-The corresponding values of x for the first five natural numbers are shown below.
+Os valores correspondentes de $x$ para os primeiros cinco números naturais são mostrados abaixo.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+| ----------------------------- | -------- |
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+Vamos chamar $A_G(x)$ de pepita de ouro se $x$ for racional, porque eles se tornam cada vez mais raros (por exemplo, a 20ª pepita de ouro é 211345365). Encontre a soma das primeiras trinta pepitas douradas.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` deve retornar `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
index 13babe893b..b0bf0827f0 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff14
-title: 'Problem 148: Exploring Pascal''s triangle'
+title: 'Problema 148: Explorando o triângulo de Pascal'
challengeType: 5
forumTopicId: 301777
dashedName: problem-148-exploring-pascals-triangle
@@ -8,9 +8,9 @@ dashedName: problem-148-exploring-pascals-triangle
# --description--
-We can easily verify that none of the entries in the first seven rows of Pascal's triangle are divisible by 7:
+Podemos facilmente verificar que nenhuma das entradas das primeiras sete linhas do triângulo Pascal é divisível por 7:
-
+```
1
1 1
1 2 1
@@ -18,20 +18,20 @@ We can easily verify that none of the entries in the first seven rows of Pascal'
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
-
+```
-However, if we check the first one hundred rows, we will find that only 2361 of the 5050 entries are not divisible by 7.
+No entanto, se verificarmos as primeiras cem linhas, descobriremos que apenas 2361 das 5050 entradas não são divisíveis por 7.
# --instructions--
-Find the number of entries which are not divisible by 7 in the first one billion (109) rows of Pascal's triangle.
+Encontre o número de entradas que não são divisíveis por 7 no primeiro bilhão (${10}^9$) de linhas do triângulo de Pascal.
# --hints--
-`euler148()` should return 2129970655314432.
+`entriesOfPascalsTriangle()` deve retornar `2129970655314432`.
```js
-assert.strictEqual(euler148(), 2129970655314432);
+assert.strictEqual(entriesOfPascalsTriangle(), 2129970655314432);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler148(), 2129970655314432);
## --seed-contents--
```js
-function euler148() {
+function entriesOfPascalsTriangle() {
return true;
}
-euler148();
+entriesOfPascalsTriangle();
```
# --solutions--
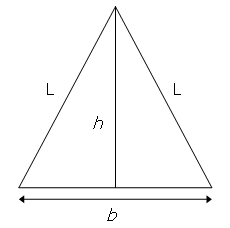 +
+Usando o teorema de Pitágoras, pode ser visto que a altura do triângulo, $h = \sqrt{{17}^2 - 8^2} = 15$, que é uma unidade menor que o comprimento da base.
+
+Com $b = 272$ e $L = 305$, obtemos $h = 273$, que é um a mais do que o comprimento da base, e este é o segundo menor triângulo isósceles com a propriedade $h = b ± 1$.
+
+Encontre $\sum{L}$ para os doze menores triângulos isósceles para os quais $h = b ± 1$ e $b$, $L$ são números inteiros positivos.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` deve retornar `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..c97bce63ec 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -1,6 +1,6 @@
---
id: 5900f3f71000cf542c50ff0a
-title: 'Problem 139: Pythagorean tiles'
+title: 'Problema 139: Blocos de Pitágoras'
challengeType: 5
forumTopicId: 301767
dashedName: problem-139-pythagorean-tiles
@@ -8,18 +8,22 @@ dashedName: problem-139-pythagorean-tiles
# --description--
-Let (a, b, c) represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length c.
+Considere que (a, b, c) representam os três lados de um triângulo retângulo com lados cujo comprimento são números inteiros. É possível posicionar quatro desses triângulos juntos para formar um quadrado com comprimento c.
-For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
+Por exemplo, triângulos de lados (3, 4, 5) podem ser colocados juntos para formar um quadrado de 5 por 5 com um orifício de 1 por 1 no meio. Também pode-se ver que o quadrado de 5 por 5 pode ser preenchido com vinte e cinco blocos quadrados de 1 por 1.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+
+
+Usando o teorema de Pitágoras, pode ser visto que a altura do triângulo, $h = \sqrt{{17}^2 - 8^2} = 15$, que é uma unidade menor que o comprimento da base.
+
+Com $b = 272$ e $L = 305$, obtemos $h = 273$, que é um a mais do que o comprimento da base, e este é o segundo menor triângulo isósceles com a propriedade $h = b ± 1$.
+
+Encontre $\sum{L}$ para os doze menores triângulos isósceles para os quais $h = b ± 1$ e $b$, $L$ são números inteiros positivos.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` deve retornar `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..c97bce63ec 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -1,6 +1,6 @@
---
id: 5900f3f71000cf542c50ff0a
-title: 'Problem 139: Pythagorean tiles'
+title: 'Problema 139: Blocos de Pitágoras'
challengeType: 5
forumTopicId: 301767
dashedName: problem-139-pythagorean-tiles
@@ -8,18 +8,22 @@ dashedName: problem-139-pythagorean-tiles
# --description--
-Let (a, b, c) represent the three sides of a right angle triangle with integral length sides. It is possible to place four such triangles together to form a square with length c.
+Considere que (a, b, c) representam os três lados de um triângulo retângulo com lados cujo comprimento são números inteiros. É possível posicionar quatro desses triângulos juntos para formar um quadrado com comprimento c.
-For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
+Por exemplo, triângulos de lados (3, 4, 5) podem ser colocados juntos para formar um quadrado de 5 por 5 com um orifício de 1 por 1 no meio. Também pode-se ver que o quadrado de 5 por 5 pode ser preenchido com vinte e cinco blocos quadrados de 1 por 1.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+ +
+No entanto, se os triângulos de (5, 12, 13) fossem usados, o orifício mediria 7 por 7. Esses quadrados de 7 por 7 não poderiam ser usados para preencher o quadrado de 13 por 13.
+
+Dado que o perímetro do triângulo retângulo é inferior a cem milhões, quantos triângulos trigonométricos pitagóricos permitiriam que tal preenchimento acontecesse?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` deve retornar `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..c027721b5a 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -1,6 +1,6 @@
---
id: 5900f3fa1000cf542c50ff0c
-title: 'Problem 140: Modified Fibonacci golden nuggets'
+title: 'Problema 140: Pepitas de ouro de Fibonacci modificado'
challengeType: 5
forumTopicId: 301769
dashedName: problem-140-modified-fibonacci-golden-nuggets
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Considere a série polinomial infinita $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, onde $G_k$ é o $k$º termo da relação de recorrência de segunda ordem $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ e $G_2 = 4$; ou seja, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+Para este problema, estaremos interessados nos valores de $x$ para os quais $A_G(x)$ é um número inteiro positivo.
-The corresponding values of x for the first five natural numbers are shown below.
+Os valores correspondentes de $x$ para os primeiros cinco números naturais são mostrados abaixo.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+| ----------------------------- | -------- |
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+Vamos chamar $A_G(x)$ de pepita de ouro se $x$ for racional, porque eles se tornam cada vez mais raros (por exemplo, a 20ª pepita de ouro é 211345365). Encontre a soma das primeiras trinta pepitas douradas.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` deve retornar `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
index 13babe893b..b0bf0827f0 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff14
-title: 'Problem 148: Exploring Pascal''s triangle'
+title: 'Problema 148: Explorando o triângulo de Pascal'
challengeType: 5
forumTopicId: 301777
dashedName: problem-148-exploring-pascals-triangle
@@ -8,9 +8,9 @@ dashedName: problem-148-exploring-pascals-triangle
# --description--
-We can easily verify that none of the entries in the first seven rows of Pascal's triangle are divisible by 7:
+Podemos facilmente verificar que nenhuma das entradas das primeiras sete linhas do triângulo Pascal é divisível por 7:
-
+
+No entanto, se os triângulos de (5, 12, 13) fossem usados, o orifício mediria 7 por 7. Esses quadrados de 7 por 7 não poderiam ser usados para preencher o quadrado de 13 por 13.
+
+Dado que o perímetro do triângulo retângulo é inferior a cem milhões, quantos triângulos trigonométricos pitagóricos permitiriam que tal preenchimento acontecesse?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` deve retornar `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..c027721b5a 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -1,6 +1,6 @@
---
id: 5900f3fa1000cf542c50ff0c
-title: 'Problem 140: Modified Fibonacci golden nuggets'
+title: 'Problema 140: Pepitas de ouro de Fibonacci modificado'
challengeType: 5
forumTopicId: 301769
dashedName: problem-140-modified-fibonacci-golden-nuggets
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Considere a série polinomial infinita $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, onde $G_k$ é o $k$º termo da relação de recorrência de segunda ordem $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ e $G_2 = 4$; ou seja, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+Para este problema, estaremos interessados nos valores de $x$ para os quais $A_G(x)$ é um número inteiro positivo.
-The corresponding values of x for the first five natural numbers are shown below.
+Os valores correspondentes de $x$ para os primeiros cinco números naturais são mostrados abaixo.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+| ----------------------------- | -------- |
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+Vamos chamar $A_G(x)$ de pepita de ouro se $x$ for racional, porque eles se tornam cada vez mais raros (por exemplo, a 20ª pepita de ouro é 211345365). Encontre a soma das primeiras trinta pepitas douradas.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` deve retornar `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
index 13babe893b..b0bf0827f0 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff14
-title: 'Problem 148: Exploring Pascal''s triangle'
+title: 'Problema 148: Explorando o triângulo de Pascal'
challengeType: 5
forumTopicId: 301777
dashedName: problem-148-exploring-pascals-triangle
@@ -8,9 +8,9 @@ dashedName: problem-148-exploring-pascals-triangle
# --description--
-We can easily verify that none of the entries in the first seven rows of Pascal's triangle are divisible by 7:
+Podemos facilmente verificar que nenhuma das entradas das primeiras sete linhas do triângulo Pascal é divisível por 7:
-