Update index.md by fixing typos (#20410)

* Update index.md by fixing typos 

Also, added section for learning about Depth-first searching and Breadth-first searching.

* Update index.md - reverting back to original verbiage.

guide/english/algorithms/binary-search-trees/index.md

@@ -5,9 +5,9 @@ title: Binary Search Trees
 ![Binary Search Tree](https://cdn-images-1.medium.com/max/1320/0*x5o1G1UpM1RfLpyx.png)
 
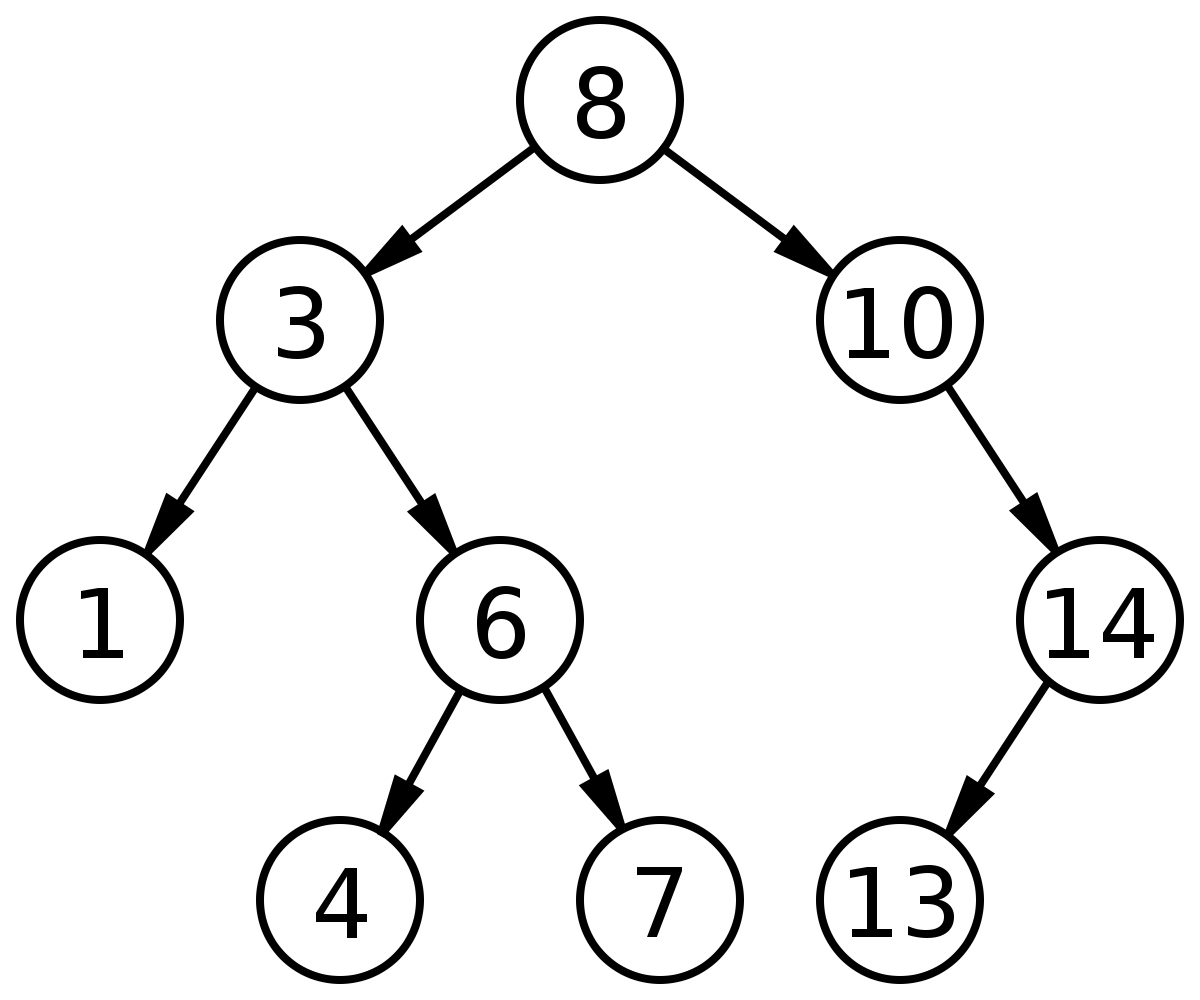
 A tree is a data structure composed of nodes that has the following characteristics:
-1. Each tree has a root node (at the top) having some value.
+1. Each tree has a root node (at the top) - containing some value (can be any datatype).
 2. The root node has zero or more child nodes.
-3. Each child node has zero or more child nodes, and so on. This create a subtree in the tree. Every node has it's own subtree made up of his children and their children, etc. This means that every node on its own can be a tree.
+3. Each child node has zero or more child nodes, and so on. This creates a subtree in the tree. Every node has its own subtree made up of its children and their children, etc. This means that every node on its own can be a tree.
 
 A binary search tree (BST) adds these two characteristics:
 1. Each node has a maximum of up to two children.
@@ -31,6 +31,12 @@ Initially an empty tree without any nodes is created. The variable/identifier wh
 #### Search
 You always start searching the tree at the root node and go down from there. You compare the data in each node with the one you are looking for. If the compared node doesn't match then you either proceed to the right child or the left child, which depends on the outcome of the following comparison: If the node that you are searching for is lower than the one you were comparing it with, you proceed to to the left child, otherwise (if it's larger) you go to the right child. Why? Because the BST is structured (as per its definition), that the right child is always larger than the parent and the left child is always lesser.
 
+###### Breadth-first search (BFS)
+Breadth first search is an algorithm used to traverse a BST. It begins at the root node and travels in a lateral manner (side to side), searching for the desired node. This type of search can be described as O(n) given that each node is visited once and the size of the tree directly correlates to the length of the search.
+
+###### Depth-first search (DFS)
+With a Depth-first search approach, we start with the root node and travel down a single branch. If the desired node is found along that branch, great, but if not, continue upwards and search unvisited nodes. This type of search also has a big O notation of O(n). 
+
 #### Insert
 It is very similar to the search function. You again start at the root of the tree and go down recursively, searching for the right place to insert our new node, in the same way as explained in the search function. If a node with the same value is already in the tree, you can choose to either insert the duplicate or not. Some trees allow duplicates, some don't. It depends on the certain implementation.
 
@@ -46,7 +52,7 @@ The time complexity for creating a tree is `O(1)`. The time complexity for searc
 Predecessors can be described as the node that would come right before the node you are currently at. To find the predecessor of the current node, look at the right-most/largest leaf node in the left subtree.
 
 #### Successor of a node
-Successors can be described as the node that would come right after the node you are currently at. To find the successor of the current node, look at the left-most/smallest leaf node in the right subtree.
+Successors can be described as the node that would come right after the the current node. To find the successor of the current node, look at the left-most/smallest leaf node in the right subtree.
 
 ### Special types of BT
 - Heap