From 637d1966921b7fc8af239ce4364c8e7ba727547f Mon Sep 17 00:00:00 2001
From: Alexander Molnar <37451552+BTmathic@users.noreply.github.com>
Date: Thu, 21 Mar 2019 09:06:58 -0400
Subject: [PATCH] Added content to stub (#30728)
Provided definition, examples, as well as applications for their use and importance.
---
.../mathematics/geometric-series/index.md | 160 +++++++++++++++---
1 file changed, 132 insertions(+), 28 deletions(-)
diff --git a/guide/english/mathematics/geometric-series/index.md b/guide/english/mathematics/geometric-series/index.md
index f2209395ef..f49694ac52 100644
--- a/guide/english/mathematics/geometric-series/index.md
+++ b/guide/english/mathematics/geometric-series/index.md
@@ -3,42 +3,146 @@ title: Geometric Series
---
## Geometric Series
+A geometric series is a sum of numbers, such as
+```
+1 + 1/2 + 1/4 + 1/8 + 1/16 + ...
+```
+where the first term is not zero and each consecutive pair of terms in the sum has the same ratio, called the *common ratio*. In the example above we have `1/(1/2) = 2`, `(1/2)/(1/4) = 2`, etc... While seemingly fairly simple this type of sum is found extensively in many areas including [geometry of real numbers](https://en.wikipedia.org/wiki/Cantor_set), [fractals](https://en.wikipedia.org/wiki/Geometric_series#Fractal_geometry), [probability](https://math.stackexchange.com/questions/1164163/introduction-to-probability-dice), [economics](https://en.wikipedia.org/wiki/Annuity#Proof_of_annuity-immediate_formula), converting rational numbers from decimal form to fraction form (see below) and more.
-A geometric progression is a sequence of numbers, whose first term is non zero and each term is obtained by multiplying its proceding term by a constant quantity. This constant quantity is called common ratio of the GP.
+We will show how to sum a geometric series when possible, give the formulas and then give some examples of this below.
-The sum of this progression is called geometric series.
+It is common to see the common ratio between terms denoted by `r`, so if a geometric series starts with first term `a`, the series is
+```
+a + a*r + a*r^2 + a*r^3 + a*r^4 + ...
+```
+When summing an infinite number of terms (such as 1 + 1 + 1 + 1 + ...) it is not clear the sum should be a number, but a remarkable property about geometric series is that the sum is always a number when `-1 < r < 1` and otherwise the sum is not a number (e.g., our `1 + 1 + 1 + ...` series tends to infinite, so is not a number). To see why, suppose we are only interested in the first `n + 1` terms of the series,
+```
+a + a*r + a*r^2 + ... + a*r^n
+```
+This is a sum of a `n + 1` numbers, so is certainly a real number itself. If we call this number `S_n`, so
+```
+S_0 = a,
+S_1 = a + a*r,
+S_2 = a + a*r + a*r^2,
+etc...
+```
+we have
+```
+S_n = a + a*r + a*r^2 + ... + a*r^n
+```
+and multiplying both sides by `r` gives
+```
+S_n*r = a*r + a*r^2 + a*r^3 + ... + a*r^n + a*r^(n+1)
+```
+which looks almost like our original sum `S_n` on the right. We have an extra `a*r^(n+1)` and we are missing the first term `a`, so writing
+```
+S_n*r = 0 + a*r + a*r^2 + a*r^n + a*r^(n+1)
+ = (a - a) + a*r + a*r^2 + ... + a*r^n + a*r^(n+1)
+ = a + a*r + a*r^2 + ... + a*r^n + a*r^(n+1) - a
+```
+we can now see `S_n` on the right hand side again. Indeed, we see that
+```
+S_n*r = S_n + a*r^(n+1) - a
+```
+and
+```
+a - a*r(n+1) = S_n - S_n*r = S_n*(1 - r)
+```
+so that
+```
+S_n = [a - a*r^(n+1)]/(1 - r) = a*[1 - r^(n+1)]/(1 - r).
+```
+when `r` is not equal to 1 (we cannot divide by 0!). Now if `-1 < r < 1` then we know that `r^(n+1)` tends to 0 as `n` tends to infinity, so our sum `S_n` tends to
+```
+S = a*[1 - 0]/(1 - r) = a/(1 - r).
+```
+On the other hand, when `r > 1` or `r < 1` we know that `r^(n_1)` does not tend to a finite number, so the `S_n` do not tend to a finite number either. The only case we have not mentioned yet is when `r = 1`, but then the series is
+```
+S_n = a + a*1 + a*1^2 + ... + a*1^n = a + a + ... + a = (n + 1)*a
+```
+which certainly does not equal a number when `n` tends to infinity.
-We can say if a1,a2,a3,....,an are in GP then
+### Formula for geometric series
- +If we have some real number `a` and some `r` such that `-1 < r < 1`, then the *finite* geometric series
+```
+a + a*r + a*r^2 + ... + a*r^(n+1)
+```
+has the sum
+```
+a*[1 - r^(n+1)]/(1 - r)
+```
+while the *infinite* geometric series
+```
+a + a*r + a*r^2 + ...
+```
+has the sum
+```
+a/(1 - r).
+```
-
+If we have some real number `a` and some `r` such that `-1 < r < 1`, then the *finite* geometric series
+```
+a + a*r + a*r^2 + ... + a*r^(n+1)
+```
+has the sum
+```
+a*[1 - r^(n+1)]/(1 - r)
+```
+while the *infinite* geometric series
+```
+a + a*r + a*r^2 + ...
+```
+has the sum
+```
+a/(1 - r).
+```
- is known as common ratio of GP.
-
- if a is the first term then GP can be written as
is known as common ratio of GP.
-
- if a is the first term then GP can be written as  +### Examples
-example of a GP : 2,4,8,16,....
+For example, the series with `a = 1` and `r = 1/2` above has sum
+```
+1/(1 - 1/2) = 1/(1/2) = 2.
+```
+(This particular sum is well known for [one](https://www.reddit.com/r/Jokes/comments/1423a4/an_infinite_number_of_mathematicians_walk_into_a/) or [two](https://www.reddit.com/r/Jokes/comments/929r9g/an_infinite_number_of_mathematicians_walk_into_a/) jokes.)
-## The nth term of GP (Also known as General term)
+The geometric series with first term `a = 2.5` and common ratio `r = -1/3` has a sum of
+```
+2.5/[1 - (-1/3)] = 2.5/[1 + 1/3] = (5/2)/(4/3) = (5/2)*(3/4) = 15/8
+```
+whereas if we started with `a = -2.5` instead, the series has a sum of
+```
+-2.5/[1 - (-1/3)] = -15/8.
+```
-Let a be the first term, r be the common ratio and l be the last term of a GP, then nth term is given by
+### Application for converting decimals to fractions
-
+### Examples
-example of a GP : 2,4,8,16,....
+For example, the series with `a = 1` and `r = 1/2` above has sum
+```
+1/(1 - 1/2) = 1/(1/2) = 2.
+```
+(This particular sum is well known for [one](https://www.reddit.com/r/Jokes/comments/1423a4/an_infinite_number_of_mathematicians_walk_into_a/) or [two](https://www.reddit.com/r/Jokes/comments/929r9g/an_infinite_number_of_mathematicians_walk_into_a/) jokes.)
-## The nth term of GP (Also known as General term)
+The geometric series with first term `a = 2.5` and common ratio `r = -1/3` has a sum of
+```
+2.5/[1 - (-1/3)] = 2.5/[1 + 1/3] = (5/2)/(4/3) = (5/2)*(3/4) = 15/8
+```
+whereas if we started with `a = -2.5` instead, the series has a sum of
+```
+-2.5/[1 - (-1/3)] = -15/8.
+```
-Let a be the first term, r be the common ratio and l be the last term of a GP, then nth term is given by
+### Application for converting decimals to fractions
-  -
- where
-
- where  -
- # The sum of n terms of a GP
-
- Let a be the first term, r be the common ratio and l be the last term of a GP, then sum of n terms is given by:
-
-
- # The sum of n terms of a GP
-
- Let a be the first term, r be the common ratio and l be the last term of a GP, then sum of n terms is given by:
- }{r-1},&space;r>1&space;&&space;\\&space;\frac{a\left&space;(&space;1-r^{n}&space;\right&space;)}{1-r},&space;r<1&space;&&space;\end{matrix}\right.) -
- and
-
- and 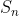 is not defined for r=1
+To see how this can be useful converting decimal numbers to fractions, consider the number `0.1111111...` with 1s repeating. As
+```
+0.1 = 1/10,
+0.01 = 1/100,
+0.001 = 1/1000,
+etc...
+```
+we can rewrite this as
+```
+0.11111... = 1/10 + 1/100 + 1/1000 + ...
+```
+which is a geometric sum with first term `a = 1/10` and common ratio `r = 1/10`, so using our formula for the sum above,
+```
+0.111... = (1/10)/(1 - 1/10) = (1/10)/(9/10) = (1/10)*(10/9) = 1/9.
+```
-# Geometric Mean
-
-if we insert geometric mean between two numbers
is not defined for r=1
+To see how this can be useful converting decimal numbers to fractions, consider the number `0.1111111...` with 1s repeating. As
+```
+0.1 = 1/10,
+0.01 = 1/100,
+0.001 = 1/1000,
+etc...
+```
+we can rewrite this as
+```
+0.11111... = 1/10 + 1/100 + 1/1000 + ...
+```
+which is a geometric sum with first term `a = 1/10` and common ratio `r = 1/10`, so using our formula for the sum above,
+```
+0.111... = (1/10)/(1 - 1/10) = (1/10)/(9/10) = (1/10)*(10/9) = 1/9.
+```
-# Geometric Mean
-
-if we insert geometric mean between two numbers 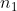 and
and 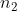 , then
+For a more complicated decimal, consider `0.124312431243...` where the repeating part is 1243. The decimal is equivalent to
+```
+1243/10000 + 1243/10000^2 + 1243/10000^3 + ...
+```
+and so our simple sum formula gives
+```
+0.124312431243... = (1243/10000)/(1 - 1/10000)
+ = (1243/10000)*(10000/9999)
+ = 1243/9999 = 113/909
+```
-Geometric mean =
, then
+For a more complicated decimal, consider `0.124312431243...` where the repeating part is 1243. The decimal is equivalent to
+```
+1243/10000 + 1243/10000^2 + 1243/10000^3 + ...
+```
+and so our simple sum formula gives
+```
+0.124312431243... = (1243/10000)/(1 - 1/10000)
+ = (1243/10000)*(10000/9999)
+ = 1243/9999 = 113/909
+```
-Geometric mean =  -
-
-
-
+For the most complicated type of repeating decimal, consider one that starts with something different from the repeating pattern, e.g., `0.42567676767...` where after the initial 425 we repeat with 67 forever. This is simply
+```
+0.425 + 0.000676767...
+```
+and so we have
+```
+0.425676767... = 425/1000 + 67/100000 + 67/(100000*100) + 67/(100000*100^2) + ...
+ = 425/1000 + (67/100000)/(1 - 1/100)
+ = 425/1000 + 67/99000)
+ = (425*99 + 67)/99000 = 21071/49500.
+```
+This may be less pleasant without a calculator, but just as simple as the examples above with our wonderful formula!
+
+This also gives a nice validation that `0.999... = 1`. Indeed, we have
+```
+0.999 = 9/10 + 9/100 + 9/1000 + ...
+ = (9/10)/(1 - 1/10)
+ = (9/10)/(9/10) = 1.
+```
\ No newline at end of file
-
-
-
-
+For the most complicated type of repeating decimal, consider one that starts with something different from the repeating pattern, e.g., `0.42567676767...` where after the initial 425 we repeat with 67 forever. This is simply
+```
+0.425 + 0.000676767...
+```
+and so we have
+```
+0.425676767... = 425/1000 + 67/100000 + 67/(100000*100) + 67/(100000*100^2) + ...
+ = 425/1000 + (67/100000)/(1 - 1/100)
+ = 425/1000 + 67/99000)
+ = (425*99 + 67)/99000 = 21071/49500.
+```
+This may be less pleasant without a calculator, but just as simple as the examples above with our wonderful formula!
+
+This also gives a nice validation that `0.999... = 1`. Indeed, we have
+```
+0.999 = 9/10 + 9/100 + 9/1000 + ...
+ = (9/10)/(1 - 1/10)
+ = (9/10)/(9/10) = 1.
+```
\ No newline at end of file