```js
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-queue-class.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-queue-class.english.md
index 2f9665c081..32e18427ef 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-queue-class.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-queue-class.english.md
@@ -9,13 +9,11 @@ challengeType: 1
Like stacks, queues are a collection of elements. But unlike stacks, queues follow the FIFO (First-In First-Out) principle. Elements added to a queue are pushed to the tail, or the end, of the queue, and only the element at the front of the queue is allowed to be removed.
We could use an array to represent a queue, but just like stacks, we want to limit the amount of control we have over our queues.
The two main methods of a queue class is the enqueue and the dequeue method. The enqueue method pushes an element to the tail of the queue, and the dequeue method removes and returns the element at the front of the queue. Other useful methods are the front, size, and isEmpty methods.
-Instructions
-Write an enqueue method that pushes an element to the tail of the queue, a dequeue method that removes and returns the front element, a front method that lets us see the front element, a size method that shows the length, and an isEmpty method to check if the queue is empty.
## Instructions
-
+Write an
## Tests
@@ -41,32 +39,29 @@ tests:
testString: assert((function(){var test = new Queue(); test.enqueue('Smith'); return (test.size() === 1)}()), 'The
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-set-class.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-set-class.english.md
index c0a6b015f3..0b60b4d628 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-set-class.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-set-class.english.md
@@ -63,7 +63,6 @@ tests:
## Challenge Seed
-
## Solution
@@ -133,5 +130,4 @@ class Set {
}
}
```
-
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-stack-class.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-stack-class.english.md
index d6eedeea1b..2bb0393150 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-stack-class.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-stack-class.english.md
@@ -9,14 +9,12 @@ challengeType: 1
In the last section, we talked about what a stack is and how we can use an array to represent a stack. In this section, we will be creating our own stack class.
Although you can use arrays to create stacks, sometimes it is best to limit the amount of control we have with our stacks.
Apart from the
-
+Write a
## Tests
@@ -42,32 +40,25 @@ tests:
testString: assert((function(){var test = new Stack(); return test.isEmpty()}()), 'The
-
## Solution
@@ -75,27 +66,27 @@ function Stack() {
```js
class Stack {
- constructor() {
- this.collection = [];
- }
- print(){
- console.log(this.collection);
- }
- push(val){
- this.collection.push(val);
- }
- pop(){
- return this.collection.pop();
- }
- peek(){
- return this.collection[this.collection.length-1];
- }
- isEmpty(){
- return this.collection.length === 0;
- }
- clear(){
- return this.collection.length = 0;
- }
+ constructor() {
+ this.collection = [];
+ }
+ print() {
+ console.log(this.collection);
+ }
+ push(val) {
+ this.collection.push(val);
+ }
+ pop() {
+ return this.collection.pop();
+ }
+ peek() {
+ return this.collection[this.collection.length - 1];
+ }
+ isEmpty() {
+ return this.collection.length === 0;
+ }
+ clear() {
+ return (this.collection.length = 0);
+ }
}
```
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-trie-search-tree.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-trie-search-tree.english.md
index ff00f87952..50e2e435c3 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-trie-search-tree.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-a-trie-search-tree.english.md
@@ -9,13 +9,12 @@ challengeType: 1
Here we will move on from binary search trees and take a look at another type of tree structure called a trie. A trie is an ordered search tree commonly used to hold strings, or more generically associative arrays or dynamic datasets in which the keys are strings. They are very good at storing sets of data when many keys will have overlapping prefixes, for example, all the words in a dictionary.
Unlike a binary tree, nodes are not associated with actual values. Instead, the path to a node represents a specific key. For instance, if we wanted to store the string code in a trie, we would have four nodes, one for each letter: c — o — d — e. Following that path through all these nodes will then create code as a string — that path is the key we stored. Then, if we wanted to add the string coding, it would share the first three nodes of code before branching away after the d. In this way, large datasets can be stored very compactly. In addition, search can be very quick because it is effectively limited to the length of the string you are storing. Furthermore, unlike binary trees a node can store any number of child nodes.
As you might have guessed from the above example, some metadata is commonly stored at nodes that hold the end of a key so that on later traversals that key can still be retrieved. For instance, if we added codes in our example above we would need some way to know that the e in code represents the end of a key that was previously entered. Otherwise, this information would effectively be lost when we add codes.
-Instructions: Let's create a trie to store words. It will accept words through an add method and store these in a trie data structure. It will also allow us to query if a given string is a word with an isWord method, and retrieve all the words entered into the trie with a print method. isWord should return a boolean value and print should return an array of all these words as string values.
-In order for us to verify that this data structure is implemented correctly, we've provided a Node structure for each node in the tree. Each node will be an object with a keys property which is a JavaScript Map object. This will hold the individual letters that are valid keys of each node. We've also created an end property on the nodes that can be set to true if the node represents the termination of a word.
## Instructions
-
+Let's create a trie to store words. It will accept words through an
## Tests
@@ -33,18 +32,16 @@ tests:
testString: assert((function testTrie() { var test = false; if (typeof Trie !== 'undefined') { test = new Trie() } else { return false; }; test.add('jump'); test.add('jumps'); test.add('jumped'); test.add('house'); test.add('mouse'); var added = test.print(); return (added.indexOf('jump') != -1 && added.indexOf('jumps') != -1 && added.indexOf('jumped') != -1 && added.indexOf('house') != -1 && added.indexOf('mouse') != -1 && added.length == 5); }()), 'The print method returns all items added to the trie as strings in an array.');
- text: The isWord method returns true only for words added to the trie and false for all other words.
testString: assert((function testTrie() { var test = false; if (typeof Trie !== 'undefined') { test = new Trie() } else { return false; }; test.add('hop'); test.add('hops'); test.add('hopped'); test.add('hoppy'); test.add('hope'); return (test.isWord('hop') && !test.isWord('ho') && test.isWord('hopped') && !test.isWord('hopp') && test.isWord('hoppy') && !test.isWord('hoping')); }()), 'The isWord method returns true only for words added to the trie and false for all other words.');
-
```
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-an-es6-javascript-map.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-an-es6-javascript-map.english.md
index 5b61a0b70c..10aa284aad 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-an-es6-javascript-map.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-an-es6-javascript-map.english.md
@@ -14,12 +14,11 @@ The new version of JavaScript provides us with a built-in Map object which provi
-
+Define a JavaScript Map object and assign to it a variable called myMap. Add the key, value pair
## Tests
@@ -31,24 +30,17 @@ tests:
testString: assert(typeof myMap === 'object', 'The myMap object exists.');
- text: myMap contains the key value pair
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-and-add-to-sets-in-es6.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-and-add-to-sets-in-es6.english.md
index ed726ad1b7..dc7bbe6dd6 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-and-add-to-sets-in-es6.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/create-and-add-to-sets-in-es6.english.md
@@ -48,7 +48,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/incidence-matrix.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/incidence-matrix.english.md
index 56d235207d..ede94d9dae 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/incidence-matrix.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/incidence-matrix.english.md
@@ -66,7 +66,6 @@ tests:
## Challenge Seed
-
## Solution
-
```js
function Set() {
// the var collection will hold the set
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-subset-check-on-two-sets-of-data.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-subset-check-on-two-sets-of-data.english.md
index 2c9e74e3e4..ea459fc547 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-subset-check-on-two-sets-of-data.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-subset-check-on-two-sets-of-data.english.md
@@ -39,7 +39,6 @@ tests:
## Challenge Seed
-
## Solution
-
```js
function Set() {var collection = []; this.has = function(e){return(collection.indexOf(e) !== -1);};this.values = function() {return collection;};this.add = function(element) {if (!this.has(element)) {collection.push(element);return true;} else {return false;}};this.remove = function(element) {if(this.has(element)) {var i = collection.indexOf(element);collection.splice(i, 1);return true;}return false;};this.size = function() {return collection.length;};this.union = function(set) {var u = new Set();var c = this.values();var s = set.values();c.forEach(function(element){u.add(element);});s.forEach(function(element){u.add(element);});return u;};this.intersection = function(set) {var i = new Set();var c = this.values();c.forEach(function(element){if(s.has(element)) i.add(element);});};this.difference = function(set) {var d = new Set();var c = this.values();c.forEach(function(e){if(!set.has(e)) d.add(e);});};this.subset = function(set) {var isSubset = true;var c = this.values();c.forEach(function(e){if(!set.has(e)) isSubset = false;});return isSubset;};}
```
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-union-on-two-sets.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-union-on-two-sets.english.md
index 34659b7bc9..91ad249c5a 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-union-on-two-sets.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-union-on-two-sets.english.md
@@ -30,7 +30,6 @@ tests:
## Challenge Seed
-
## Solution
-
```js
function Set() {
var collection = [];
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-an-intersection-on-two-sets-of-data.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-an-intersection-on-two-sets-of-data.english.md
index 48c992b571..0a0e3fa447 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-an-intersection-on-two-sets-of-data.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-an-intersection-on-two-sets-of-data.english.md
@@ -31,7 +31,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-an-element-from-a-max-heap.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-an-element-from-a-max-heap.english.md
index a9b58cad35..1ed0ce80a5 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-an-element-from-a-max-heap.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-an-element-from-a-max-heap.english.md
@@ -40,7 +40,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list-by-index.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list-by-index.english.md
index 1f7c9a17ec..483c7ed822 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list-by-index.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list-by-index.english.md
@@ -41,7 +41,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list.english.md
index 8454833c31..6b68deecd0 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-elements-from-a-linked-list.english.md
@@ -40,7 +40,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/typed-arrays.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/typed-arrays.english.md
index d1682d1518..ea45bfff84 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/typed-arrays.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/typed-arrays.english.md
@@ -76,14 +76,11 @@ var i32View;
-
-
enqueue method that pushes an element to the tail of the queue, a dequeue method that removes and returns the front element, a front method that lets us see the front element, a size method that shows the length, and an isEmpty method to check if the queue is empty.
size method should return the length of the queue');
- text: The isEmpty method should return false if there are elements in the queue
testString: assert((function(){var test = new Queue(); test.enqueue('Smith'); return !(test.isEmpty())}()), 'The isEmpty method should return false if there are elements in the queue');
-
```
## Challenge Seed
+
```js
-function Queue () {
- var collection = [];
- this.print = function() {
- console.log(collection);
- };
- // Only change code below this line
+function Queue() {
+ var collection = [];
+ this.print = function() {
+ console.log(collection);
+ };
+ // Only change code below this line
- // Only change code above this line
+ // Only change code above this line
}
```
-
-
-
```js
@@ -93,8 +92,6 @@ class Set {
```
-
-
push and pop method, stacks have other useful methods. Let's add a peek, isEmpty, and clear method to our stack class.
-Instructions
-Write a push method that pushes an element to the top of the stack, a pop method that removes the element on the top of the stack, a peek method that looks at the first element in the stack, an isEmpty method that checks if the stack is empty, and a clear method that removes all elements from the stack.
-Normally stacks don't have this, but we've added a print helper method that console logs the collection.
## Instructions
push method that pushes an element to the top of the stack, a pop method that removes the element on the top of the stack, a peek method that looks at the first element in the stack, an isEmpty method that checks if the stack is empty, and a clear method that removes all elements from the stack.
+Normally stacks don't have this, but we've added a print helper method that console logs the collection.
isEmpty method should return true if a stack does not contain any elements');
- text: The clear method should remove all element from the stack
testString: assert((function(){var test = new Stack(); test.push('CS50'); test.clear(); return (test.isEmpty())}()), 'The clear method should remove all element from the stack');
-
```
-
## Challenge Seed
```js
function Stack() {
- var collection = [];
- this.print = function() {
- console.log(collection);
- };
- // Only change code below this line
+ var collection = [];
+ this.print = function() {
+ console.log(collection);
+ };
+ // Only change code below this line
- // Only change code above this line
+ // Only change code above this line
}
```
-
-
-
-
add method and store these in a trie data structure. It will also allow us to query if a given string is a word with an isWord method, and retrieve all the words entered into the trie with a print method. isWord should return a boolean value and print should return an array of all these words as string values.
+In order for us to verify that this data structure is implemented correctly, we've provided a Node structure for each node in the tree. Each node will be an object with a keys property which is a JavaScript Map object. This will hold the individual letters that are valid keys of each node. We've also created an end property on the nodes that can be set to true if the node represents the termination of a word.
```js
-var displayTree = (tree) => console.log(JSON.stringify(tree, null, 2));
+var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
var Node = function() {
this.keys = new Map();
this.end = false;
@@ -60,11 +57,7 @@ var Trie = function() {
// change code above this line
};
```
-
-
-
-
.clear() removes all key, value pairs
.entries() returns an array of all the keys in insertion order
.values() returns an array of all the values in insertion order
-Instructions: Define a JavaScript Map object and assign to it a variable called myMap. Add the key, value pair freeCodeCamp, Awesome! to it.
## Instructions
freeCodeCamp, Awesome! to it.
freeCodeCamp, Awesome!.
testString: assert(myMap.get('freeCodeCamp') === 'Awesome!', 'myMap contains the key value pair freeCodeCamp, Awesome!.');
-
```
-
## Challenge Seed
```js
// change code below this line
```
-
-
-
-
```js
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-leaf-node-in-a-binary-search-tree.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-leaf-node-in-a-binary-search-tree.english.md
index f92bd9bc4b..f7c000be0f 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-leaf-node-in-a-binary-search-tree.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-leaf-node-in-a-binary-search-tree.english.md
@@ -5,19 +5,20 @@ challengeType: 1
---
## Description
+
This is the first of three challenges where we will implement a more difficult operation in binary search trees: deletion. Deletion is difficult because removing nodes breaks links in the tree. These links must be carefully reestablished to ensure the binary tree structure is maintained. For some deletions, this means the tree must be rearranged. In general, you will encounter one of three cases when trying to delete a node:
Leaf Node: The target to delete has zero children.
One Child: The target to delete only has one child.
Two Children: The target to delete has two child nodes.
Removing a leaf node is easy, we simply remove it. Deleting a node with one child is also relatively easy, we simply remove it and link its parent to child of the node we deleted. Removing a node with two children is more difficult, however, because this creates two child nodes that need to be reconnected to the parent tree. We'll see how to deal with this case in the third challenge. Additionally, you need to be mindful of some edge cases when handling deletion. What if the tree is empty? What if the node to delete is the root node? What if there are only two elements in the tree? For now, let's handle the first case where we delete a leaf node.
-Instructions: Create a method on our binary tree called
## Instructions
-
+
+Create a method on our binary tree called
## Tests
@@ -35,116 +36,111 @@ tests:
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.remove !== 'function') { return false; }; test.add(500); test.remove(500); return (test.inorder() == null); })(), 'If the root node has no children, deleting it sets the root to
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-one-child-in-a-binary-search-tree.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-one-child-in-a-binary-search-tree.english.md
index 94df686519..892b298414 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-one-child-in-a-binary-search-tree.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-one-child-in-a-binary-search-tree.english.md
@@ -7,12 +7,11 @@ challengeType: 1
## Description
Now that we can delete leaf nodes let's move on to the second case: deleting a node with one child. For this case, say we have a tree with the following nodes 1 — 2 — 3 where 1 is the root. To delete 2, we simply need to make the right reference in 1 point to 3. More generally to delete a node with only one child, we make that node's parent reference the next node in the tree.
-Instructions: We've provided some code in our
## Instructions
-
+We've provided some code in our
## Tests
@@ -34,18 +33,15 @@ tests:
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.remove !== 'function') { return false; }; test.add(-1); test.add(3); test.add(7); test.add(16); test.remove(16); test.remove(7); test.remove(3); return (test.inorder().join('') == '-1'); })(), 'The
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-two-children-in-a-binary-search-tree.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-two-children-in-a-binary-search-tree.english.md
index 33bb315702..98a566ac86 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-two-children-in-a-binary-search-tree.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/delete-a-node-with-two-children-in-a-binary-search-tree.english.md
@@ -8,12 +8,11 @@ challengeType: 1
Removing nodes that have two children is the hardest case to implement. Removing a node like this produces two subtrees that are no longer connected to the original tree structure. How can we reconnect them? One method is to find the smallest value in the right subtree of the target node and replace the target node with this value. Selecting the replacement in this way ensures that it is greater than every node in the left subtree it becomes the new parent of but also less than every node in the right subtree it becomes the new parent of.
Once this replacement is made the replacement node must be removed from the right subtree. Even this operation is tricky because the replacement may be a leaf or it may itself be the parent of a right subtree. If it is a leaf we must remove its parent's reference to it. Otherwise, it must be the right child of the target. In this case, we must replace the target value with the replacement value and make the target reference the replacement's right child.
-Instructions: Let's finish our
## Instructions
-
+Let's finish our
## Tests
@@ -26,11 +25,11 @@ tests:
- text: The binary search tree has a method called
-
## Solution
@@ -212,4 +206,5 @@ BinarySearchTree.prototype = {
```js
// solution required
```
+
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-height-of-a-binary-search-tree.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-height-of-a-binary-search-tree.english.md
index 8c6c81efa5..07dcf2caaa 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-height-of-a-binary-search-tree.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-height-of-a-binary-search-tree.english.md
@@ -8,13 +8,12 @@ challengeType: 1
In the last challenge we described a scenario in which a tree could become unbalanced. To understand the concept of balance, let's take a look at another tree property: height. Height in a tree represents the distance from the root node to any given leaf node. Different paths in a highly branched tree structure may have different heights, but for a given tree there will be a minimum and maximum height. If the tree is balanced, these values will differ at most by one. This means that in a balanced tree, all the leaf nodes exist within the same level, or if they are not within the same level they are at most one level apart.
The property of balance is important for trees because it is what determines the efficiency of tree operations. As we explained in the last challenge, we face worst case time complexity for heavily unbalanced trees. Self-balancing trees are commonly used to account for this issue in trees with dynamic data sets. Common examples of these include AVL trees, red-black trees, and B-trees. These trees all contain additional internal logic which re-balance the tree when insertions or deletions create a state of imbalance.
-Note: A similar property to height is depth, which refers to how far a given node is from the root node.
-Instructions: Write two methods for our binary tree:
## Instructions
-
+Write two methods for our binary tree:
## Tests
@@ -38,150 +37,146 @@ tests:
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.findMaxHeight !== 'function') { return false; }; return (test.findMaxHeight() == -1); })(), 'An empty tree returns a height of
-
## Solution
```js
-var displayTree = (tree) => console.log(JSON.stringify(tree, null, 2));
+var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
- this.value = value;
- this.left = null;
- this.right = null;
+ this.value = value;
+ this.left = null;
+ this.right = null;
}
function BinarySearchTree() {
- this.root = null;
- // change code below this line
- // change code above this line
- this.findMinHeight = function(root = this.root) {
- // empty tree.
- if(root === null) {
- return -1;
- }
- // leaf node.
- if(root.left === null && root.right === null) {
- return 0;
- }
- if(root.left === null){
- return this.findMinHeight(root.right) + 1;
- }
- if(root.right === null){
- return this.findMinHeight(root.left) + 1;
- }
- const lHeight = this.findMinHeight(root.left);
- const rHeight = this.findMinHeight(root.right);
- return Math.min(lHeight, rHeight) + 1;
- };
- this.findMaxHeight = function(root = this.root) {
- // empty tree.
- if(root === null) {
- return -1;
- }
- // leaf node.
- if(root.left === null && root.right === null) {
- return 0;
- }
- if(root.left === null){
- return this.findMaxHeight(root.right) + 1;
- }
- if(root.right === null){
- return this.findMaxHeight(root.left) + 1;
- }
- const lHeight = this.findMaxHeight(root.left);
- const rHeight = this.findMaxHeight(root.right);
- return Math.max(lHeight, rHeight) + 1;
- };
- this.isBalanced = function(root = this.root) {
+ this.root = null;
+ // change code below this line
+ // change code above this line
+ this.findMinHeight = function(root = this.root) {
+ // empty tree.
+ if (root === null) {
+ return -1;
+ }
+ // leaf node.
+ if (root.left === null && root.right === null) {
+ return 0;
+ }
+ if (root.left === null) {
+ return this.findMinHeight(root.right) + 1;
+ }
+ if (root.right === null) {
+ return this.findMinHeight(root.left) + 1;
+ }
+ const lHeight = this.findMinHeight(root.left);
+ const rHeight = this.findMinHeight(root.right);
+ return Math.min(lHeight, rHeight) + 1;
+ };
+ this.findMaxHeight = function(root = this.root) {
+ // empty tree.
+ if (root === null) {
+ return -1;
+ }
+ // leaf node.
+ if (root.left === null && root.right === null) {
+ return 0;
+ }
+ if (root.left === null) {
+ return this.findMaxHeight(root.right) + 1;
+ }
+ if (root.right === null) {
+ return this.findMaxHeight(root.left) + 1;
+ }
+ const lHeight = this.findMaxHeight(root.left);
+ const rHeight = this.findMaxHeight(root.right);
+ return Math.max(lHeight, rHeight) + 1;
+ };
+ this.isBalanced = function(root = this.root) {
+ if (root === null) {
+ return true;
+ }
- if(root === null) {
- return true;
- }
+ if (root.left === null && root.right === null) {
+ return true;
+ }
- if(root.left === null && root.right === null){
- return true;
- }
+ if (root.left === null) {
+ return this.findMaxHeight(root.right) <= 0;
+ }
- if(root.left === null) {
- return this.findMaxHeight(root.right) <= 0;
- }
+ if (root.right === null) {
+ return this.findMaxHeight(root.left) <= 0;
+ }
- if(root.right === null) {
- return this.findMaxHeight(root.left) <= 0;
- }
-
- const lHeight = this.findMaxHeight(root.left);
- const rHeight = this.findMaxHeight(root.right);
- if(Math.abs(lHeight - rHeight) > 1){
- return false;
- }
- return this.isBalanced(root.left) && this.isBalanced(root.right);
- };
+ const lHeight = this.findMaxHeight(root.left);
+ const rHeight = this.findMaxHeight(root.right);
+ if (Math.abs(lHeight - rHeight) > 1) {
+ return false;
+ }
+ return this.isBalanced(root.left) && this.isBalanced(root.right);
+ };
}
```
+
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-value-in-a-binary-search-tree.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-value-in-a-binary-search-tree.english.md
index 1f5900c1c4..f9442f1fe7 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-value-in-a-binary-search-tree.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/find-the-minimum-and-maximum-value-in-a-binary-search-tree.english.md
@@ -12,12 +12,11 @@ To begin, we will discuss a particular type of a tree, the binary tree. In fact,
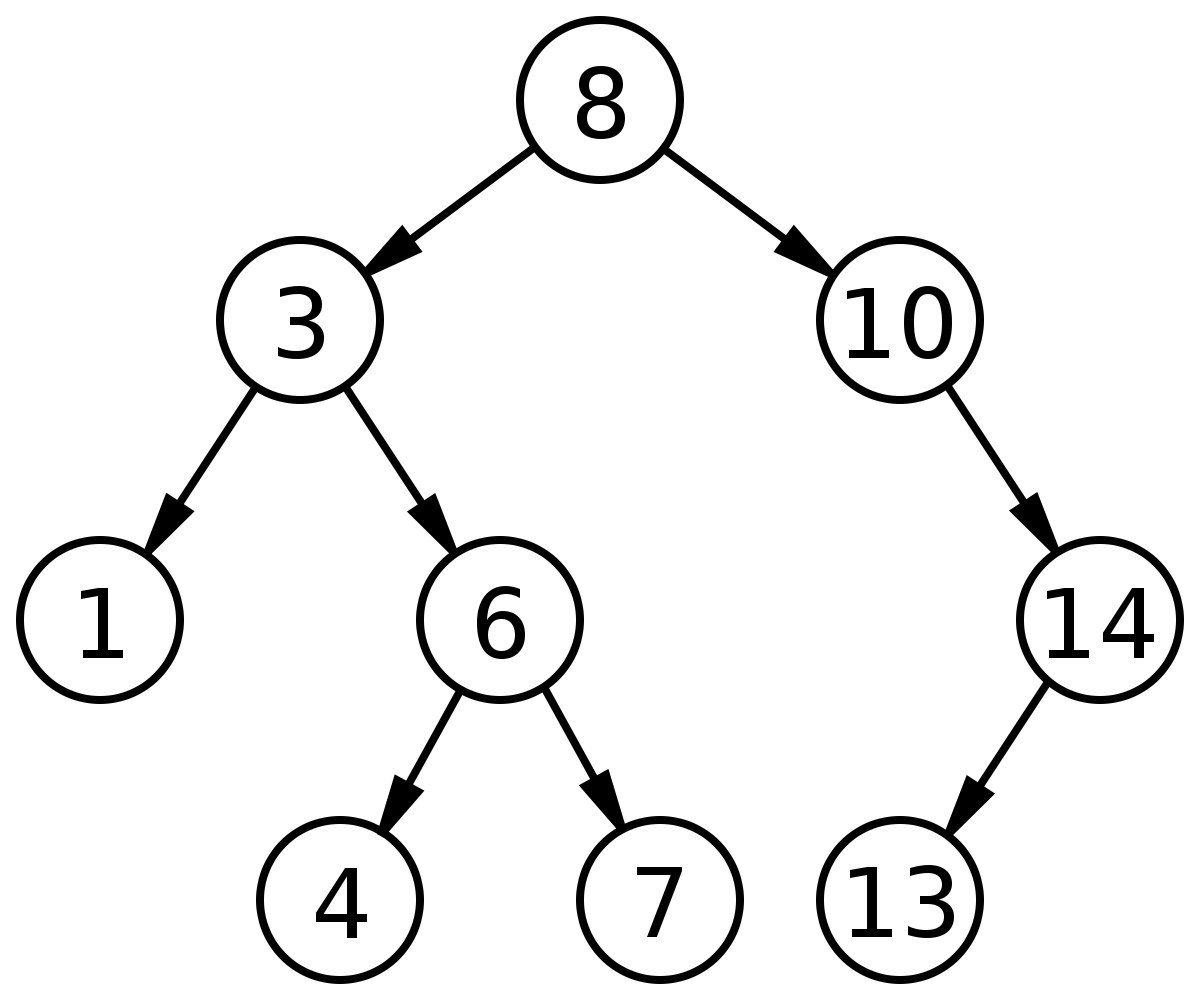 Now this ordered relationship is very easy to see. Note that every value to the left of 8, the root node, is less than 8, and every value to the right is greater than 8. Also notice that this relationship applies to each of the subtrees as well. For example, the first left child is a subtree. 3 is the parent node, and it has exactly two child nodes — by the rules governing binary search trees, we know without even looking that the left child of this node (and any of its children) will be less than 3, and the right child (and any of its children) will be greater than 3 (but also less than the structure's root value), and so on.
Binary search trees are very common and useful data structures because they provide logarithmic time in the average case for several common operations such as lookup, insertion, and deletion.
-Instructions: We'll start simple. We've defined the skeleton of a binary search tree structure here in addition to a function to create nodes for our tree. Observe that each node may have a left and right value. These will be assigned child subtrees if they exist. In our binary search tree, define two methods,
Now this ordered relationship is very easy to see. Note that every value to the left of 8, the root node, is less than 8, and every value to the right is greater than 8. Also notice that this relationship applies to each of the subtrees as well. For example, the first left child is a subtree. 3 is the parent node, and it has exactly two child nodes — by the rules governing binary search trees, we know without even looking that the left child of this node (and any of its children) will be less than 3, and the right child (and any of its children) will be greater than 3 (but also less than the structure's root value), and so on.
Binary search trees are very common and useful data structures because they provide logarithmic time in the average case for several common operations such as lookup, insertion, and deletion.
-Instructions: We'll start simple. We've defined the skeleton of a binary search tree structure here in addition to a function to create nodes for our tree. Observe that each node may have a left and right value. These will be assigned child subtrees if they exist. In our binary search tree, define two methods,
-
+We'll start simple. We've defined the skeleton of a binary search tree structure here in addition to a function to create nodes for our tree. Observe that each node may have a left and right value. These will be assigned child subtrees if they exist. In our binary search tree, define two methods,
## Tests
@@ -37,7 +36,6 @@ tests:
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.findMax !== 'function') { return false; }; test.add(4); test.add(1); test.add(7); test.add(87); test.add(34); test.add(45); test.add(73); test.add(8); return test.findMax() == 87; })(), 'The
Now that we can add and remove elements let's see some of the applications heaps can be used for. Heaps are commonly used to implement priority queues because they always store an item of greatest or least value in first position. In addition, they are used to implement a sorting algorithm called heap sort. We'll see how to do this here. Heap sort uses a min heap, the reverse of a max heap. A min heap always stores the element of least value in the root position.
Heap sort works by taking an unsorted array, adding each item in the array into a min heap, and then extracting every item out of the min heap into a new array. The min heap structure ensures that the new array will contain the original items in least to greatest order. This is one of the most efficient sorting algorithms with average and worst case performance of O(nlog(n)).
-Instructions: Let's implement heap sort with a min heap. Feel free to adapt your max heap code here. Create an object MinHeap with insert, remove, and sort methods. The sort method should return an array of all the elements in the min heap sorted from smallest to largest.
## Instructions
-
+Let's implement heap sort with a min heap. Feel free to adapt your max heap code here. Create an object
## Tests
@@ -31,7 +30,6 @@ tests:
testString: assert((function() { var test = false; if (typeof MinHeap !== 'undefined') { test = new MinHeap() } else { return false; }; return (typeof test.sort == 'function')})(), 'MinHeap has a method called sort.');
- text: The sort method returns an array containing all items added to the min heap in sorted order.
testString: assert((function() { var test = false; if (typeof MinHeap !== 'undefined') { test = new MinHeap() } else { return false; }; test.insert(3); test.insert(12); test.insert(5); test.insert(10); test.insert(1); test.insert(27); test.insert(42); test.insert(57); test.insert(5); var result = test.sort(); return (isSorted(result)); })(), 'The sort method returns an array containing all items added to the min heap in sorted order.');
-
```
@@ -44,14 +42,15 @@ tests:
```js
// check if array is sorted
function isSorted(arr) {
- var check = (i) => (i == arr.length - 1) ? true : (arr[i] > arr[i + 1]) ? false : check(i + 1);
+ var check = i =>
+ i == arr.length - 1 ? true : arr[i] > arr[i + 1] ? false : check(i + 1);
return check(0);
}
// generate a randomly filled array
var array = new Array();
(function createArray(size = 5) {
array.push(+(Math.random() * 100).toFixed(0));
- return (size > 1) ? createArray(size - 1) : undefined;
+ return size > 1 ? createArray(size - 1) : undefined;
})(25);
var MinHeap = function() {
// change code below this line
@@ -60,9 +59,6 @@ var MinHeap = function() {
```
-
-
-
remove. We'll build the logic for our deletion operation in here. First, you'll want to create a function within remove that finds the node we are trying to delete in the current tree. If the node is not present in the tree, remove should return null. Now, if the target node is a leaf node with no children, then the parent reference to it should be set to null. This effectively deletes the node from the tree. To do this, you will have to keep track of the parent of the node we are trying to delete as well. It will also be useful to create a way to track the number of children the target node has, as this will determine which case our deletion falls under.
-We will handle the second and third cases in the next challenges. Good luck!
remove. We'll build the logic for our deletion operation in here. First, you'll want to create a function within remove that finds the node we are trying to delete in the current tree. If the node is not present in the tree, remove should return null. Now, if the target node is a leaf node with no children, then the parent reference to it should be set to null. This effectively deletes the node from the tree. To do this, you will have to keep track of the parent of the node we are trying to delete as well. It will also be useful to create a way to track the number of children the target node has, as this will determine which case our deletion falls under.
+We will handle the second and third cases in the next challenges. Good luck!
null.');
- text: The remove method removes leaf nodes from the tree
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.remove !== 'function') { return false; }; test.add(5); test.add(3); test.add(7); test.add(6); test.add(10); test.add(12); test.remove(3); test.remove(12); test.remove(10); return (test.inorder().join('') == '567'); })(), 'The remove method removes leaf nodes from the tree');
-
```
-
```js
-var displayTree = (tree) => console.log(JSON.stringify(tree, null, 2));
+var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
- this.value = value;
- this.left = null;
- this.right = null;
+ this.value = value;
+ this.left = null;
+ this.right = null;
}
function BinarySearchTree() {
- this.root = null;
- // case 1: target has no children, change code below this line
+ this.root = null;
+ // case 1: target has no children, change code below this line
}
```
-
### After Test
```js
BinarySearchTree.prototype = {
- add: function(value) {
- var node = this.root;
- if (node == null) {
- this.root = new Node(value);
- return;
- } else {
- function searchTree(node) {
- if (value < node.value) {
- if (node.left == null) {
- node.left = new Node(value);
- return;
- } else if (node.left != null) {
- return searchTree(node.left)
- };
- } else if (value > node.value) {
- if (node.right == null) {
- node.right = new Node(value);
- return;
- } else if (node.right != null) {
- return searchTree(node.right);
- };
- } else {
- return null;
- };
- };
- return searchTree(node);
- };
- },
- inorder: function() {
- if (this.root == null) {
- return null;
- } else {
- var result = new Array();
- function traverseInOrder(node) {
- if (node.left != null) {
- traverseInOrder(node.left);
- };
- result.push(node.value);
- if (node.right != null) {
- traverseInOrder(node.right);
- };
+ add: function(value) {
+ var node = this.root;
+ if (node == null) {
+ this.root = new Node(value);
+ return;
+ } else {
+ function searchTree(node) {
+ if (value < node.value) {
+ if (node.left == null) {
+ node.left = new Node(value);
+ return;
+ } else if (node.left != null) {
+ return searchTree(node.left);
+ }
+ } else if (value > node.value) {
+ if (node.right == null) {
+ node.right = new Node(value);
+ return;
+ } else if (node.right != null) {
+ return searchTree(node.right);
}
- traverseInOrder(this.root);
- return result;
- };
- },
- isBinarySearchTree() {
- if (this.root == null) {
- return null;
} else {
- var check = true;
- function checkTree(node) {
- if (node.left != null) {
- var left = node.left;
- if (left.value > node.value) {
- check = false;
- } else {
- checkTree(left);
- }
- }
- if (node.right != null) {
- var right = node.right;
- if (right.value < node.value) {
- check = false;
- } else {
- checkTree(right);
- };
- };
- };
- checkTree(this.root);
- return check;
+ return null;
}
+ }
+ return searchTree(node);
}
+ },
+ inorder: function() {
+ if (this.root == null) {
+ return null;
+ } else {
+ var result = new Array();
+ function traverseInOrder(node) {
+ if (node.left != null) {
+ traverseInOrder(node.left);
+ }
+ result.push(node.value);
+ if (node.right != null) {
+ traverseInOrder(node.right);
+ }
+ }
+ traverseInOrder(this.root);
+ return result;
+ }
+ },
+ isBinarySearchTree() {
+ if (this.root == null) {
+ return null;
+ } else {
+ var check = true;
+ function checkTree(node) {
+ if (node.left != null) {
+ var left = node.left;
+ if (left.value > node.value) {
+ check = false;
+ } else {
+ checkTree(left);
+ }
+ }
+ if (node.right != null) {
+ var right = node.right;
+ if (right.value < node.value) {
+ check = false;
+ } else {
+ checkTree(right);
+ }
+ }
+ }
+ checkTree(this.root);
+ return check;
+ }
+ }
};
```
-
remove method that accomplishes the tasks from the last challenge. We find the target to delete and its parent and define the number of children the target node has. Let's add the next case here for target nodes with only one child. Here, we'll have to determine if the single child is a left or right branch in the tree and then set the correct reference in the parent to point to this node. In addition, let's account for the case where the target is the root node (this means the parent node will be null). Feel free to replace all the starter code with your own as long as it passes the tests.
remove method that accomplishes the tasks from the last challenge. We find the target to delete and its parent and define the number of children the target node has. Let's add the next case here for target nodes with only one child. Here, we'll have to determine if the single child is a left or right branch in the tree and then set the correct reference in the parent to point to this node. In addition, let's account for the case where the target is the root node (this means the parent node will be null). Feel free to replace all the starter code with your own as long as it passes the tests.
remove method removes nodes with one child.');
- text: Removing the root in a tree with two nodes sets the second to be the root.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.remove !== 'function') { return false; }; test.add(15); test.add(27); test.remove(15); return (test.inorder().join('') == '27'); })(), 'Removing the root in a tree with two nodes sets the second to be the root.');
-
```
-
## Challenge Seed
```js
-var displayTree = (tree) => console.log(JSON.stringify(tree, null, 2));
+var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
this.value = value;
this.left = null;
@@ -75,18 +71,18 @@ function BinarySearchTree() {
} else {
return null;
}
- }).bind(this)();
+ }.bind(this)());
if (target === null) {
return null;
}
// count the children of the target to delete
- var children = (target.left !== null ? 1 : 0) + (target.right !== null ? 1 : 0);
+ var children =
+ (target.left !== null ? 1 : 0) + (target.right !== null ? 1 : 0);
// case 1: target has no children
if (children === 0) {
if (target == this.root) {
this.root = null;
- }
- else {
+ } else {
if (parent.left == target) {
parent.left = null;
} else {
@@ -101,90 +97,88 @@ function BinarySearchTree() {
-
### After Test
```js
BinarySearchTree.prototype = {
- add: function(value) {
- var node = this.root;
- if (node == null) {
- this.root = new Node(value);
- return;
- } else {
- function searchTree(node) {
- if (value < node.value) {
- if (node.left == null) {
- node.left = new Node(value);
- return;
- } else if (node.left != null) {
- return searchTree(node.left)
- };
- } else if (value > node.value) {
- if (node.right == null) {
- node.right = new Node(value);
- return;
- } else if (node.right != null) {
- return searchTree(node.right);
- };
- } else {
- return null;
- };
- };
- return searchTree(node);
- };
- },
- inorder: function() {
- if (this.root == null) {
- return null;
- } else {
- var result = new Array();
- function traverseInOrder(node) {
- if (node.left != null) {
- traverseInOrder(node.left);
- };
- result.push(node.value);
- if (node.right != null) {
- traverseInOrder(node.right);
- };
+ add: function(value) {
+ var node = this.root;
+ if (node == null) {
+ this.root = new Node(value);
+ return;
+ } else {
+ function searchTree(node) {
+ if (value < node.value) {
+ if (node.left == null) {
+ node.left = new Node(value);
+ return;
+ } else if (node.left != null) {
+ return searchTree(node.left);
+ }
+ } else if (value > node.value) {
+ if (node.right == null) {
+ node.right = new Node(value);
+ return;
+ } else if (node.right != null) {
+ return searchTree(node.right);
}
- traverseInOrder(this.root);
- return result;
- };
- },
- isBinarySearchTree() {
- if (this.root == null) {
- return null;
} else {
- var check = true;
- function checkTree(node) {
- if (node.left != null) {
- var left = node.left;
- if (left.value > node.value) {
- check = false;
- } else {
- checkTree(left);
- }
- }
- if (node.right != null) {
- var right = node.right;
- if (right.value < node.value) {
- check = false;
- } else {
- checkTree(right);
- };
- };
- };
- checkTree(this.root);
- return check;
+ return null;
}
+ }
+ return searchTree(node);
}
+ },
+ inorder: function() {
+ if (this.root == null) {
+ return null;
+ } else {
+ var result = new Array();
+ function traverseInOrder(node) {
+ if (node.left != null) {
+ traverseInOrder(node.left);
+ }
+ result.push(node.value);
+ if (node.right != null) {
+ traverseInOrder(node.right);
+ }
+ }
+ traverseInOrder(this.root);
+ return result;
+ }
+ },
+ isBinarySearchTree() {
+ if (this.root == null) {
+ return null;
+ } else {
+ var check = true;
+ function checkTree(node) {
+ if (node.left != null) {
+ var left = node.left;
+ if (left.value > node.value) {
+ check = false;
+ } else {
+ checkTree(left);
+ }
+ }
+ if (node.right != null) {
+ var right = node.right;
+ if (right.value < node.value) {
+ check = false;
+ } else {
+ checkTree(right);
+ }
+ }
+ }
+ checkTree(this.root);
+ return check;
+ }
+ }
};
```
-
remove method by handling the third case. We've provided some code again for the first two cases. Add some code now to handle target nodes with two children. Any edge cases to be aware of? What if the tree has only three nodes? Once you are finished this will complete our deletion operation for binary search trees. Nice job, this is a pretty hard problem!
remove method by handling the third case. We've provided some code again for the first two cases. Add some code now to handle target nodes with two children. Any edge cases to be aware of? What if the tree has only three nodes? Once you are finished this will complete our deletion operation for binary search trees. Nice job, this is a pretty hard problem!
remove.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; return (typeof test.remove == 'function')})(), 'The binary search tree has a method called remove.');
- text: Trying to remove an element that does not exist returns null.
- testString: 'assert((function() { var test = false; if (typeof BinarySearchTree !== ''undefined'') { test = new BinarySearchTree() } else { return false; }; return (typeof test.remove == ''function'') ? (test.remove(100) == null) : false})(), ''Trying to remove an element that does not exist returns null.'');'
+ testString: "assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; return (typeof test.remove == 'function') ? (test.remove(100) == null) : false})(), 'Trying to remove an element that does not exist returns null.');"
- text: If the root node has no children, deleting it sets the root to null.
- testString: 'assert((function() { var test = false; if (typeof BinarySearchTree !== ''undefined'') { test = new BinarySearchTree() } else { return false; }; test.add(500); test.remove(500); return (typeof test.remove == ''function'') ? (test.inorder() == null) : false})(), ''If the root node has no children, deleting it sets the root to null.'');'
+ testString: "assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; test.add(500); test.remove(500); return (typeof test.remove == 'function') ? (test.inorder() == null) : false})(), 'If the root node has no children, deleting it sets the root to null.');"
- text: The remove method removes leaf nodes from the tree
- testString: 'assert((function() { var test = false; if (typeof BinarySearchTree !== ''undefined'') { test = new BinarySearchTree() } else { return false; }; test.add(5); test.add(3); test.add(7); test.add(6); test.add(10); test.add(12); test.remove(3); test.remove(12); test.remove(10); return (typeof test.remove == ''function'') ? (test.inorder().join('''') == ''567'') : false})(), ''The remove method removes leaf nodes from the tree'');'
+ testString: "assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; test.add(5); test.add(3); test.add(7); test.add(6); test.add(10); test.add(12); test.remove(3); test.remove(12); test.remove(10); return (typeof test.remove == 'function') ? (test.inorder().join('') == '567') : false})(), 'The remove method removes leaf nodes from the tree');"
- text: The remove method removes nodes with one child.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.remove !== 'function') { return false; }; test.add(-1); test.add(3); test.add(7); test.add(16); test.remove(16); test.remove(7); test.remove(3); return (test.inorder().join('') == '-1'); })(), 'The remove method removes nodes with one child.');
- text: Removing the root in a tree with two nodes sets the second to be the root.
@@ -39,18 +38,15 @@ tests:
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.remove !== 'function') { return false; }; test.add(1); test.add(4); test.add(3); test.add(7); test.add(9); test.add(11); test.add(14); test.add(15); test.add(19); test.add(50); test.remove(9); if (!test.isBinarySearchTree()) { return false; }; test.remove(11); if (!test.isBinarySearchTree()) { return false; }; test.remove(14); if (!test.isBinarySearchTree()) { return false; }; test.remove(19); if (!test.isBinarySearchTree()) { return false; }; test.remove(3); if (!test.isBinarySearchTree()) { return false; }; test.remove(50); if (!test.isBinarySearchTree()) { return false; }; test.remove(15); if (!test.isBinarySearchTree()) { return false; }; return (test.inorder().join('') == '147'); })(), 'The remove method removes nodes with two children while maintaining the binary search tree structure.');
- text: The root can be removed on a tree of three nodes.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.remove !== 'function') { return false; }; test.add(100); test.add(50); test.add(300); test.remove(100); return (test.inorder().join('') == 50300); })(), 'The root can be removed on a tree of three nodes.');
-
```
-
## Challenge Seed
```js
-var displayTree = (tree) => console.log(JSON.stringify(tree, null, 2));
+var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
this.value = value;
this.left = null;
@@ -80,18 +76,18 @@ function BinarySearchTree() {
} else {
return null;
}
- }).bind(this)();
+ }.bind(this)());
if (target === null) {
return null;
}
// count the children of the target to delete
- var children = (target.left !== null ? 1 : 0) + (target.right !== null ? 1 : 0);
+ var children =
+ (target.left !== null ? 1 : 0) + (target.right !== null ? 1 : 0);
// case 1: target has no children
if (children === 0) {
if (target == this.root) {
this.root = null;
- }
- else {
+ } else {
if (parent.left == target) {
parent.left = null;
} else {
@@ -101,7 +97,7 @@ function BinarySearchTree() {
}
// case 2: target has one child
else if (children == 1) {
- var newChild = (target.left !== null) ? target.left : target.right;
+ var newChild = target.left !== null ? target.left : target.right;
if (parent === null) {
target.value = newChild.value;
target.left = null;
@@ -120,90 +116,88 @@ function BinarySearchTree() {
-
### After Test
```js
BinarySearchTree.prototype = {
- add: function(value) {
- var node = this.root;
- if (node == null) {
- this.root = new Node(value);
- return;
- } else {
- function searchTree(node) {
- if (value < node.value) {
- if (node.left == null) {
- node.left = new Node(value);
- return;
- } else if (node.left != null) {
- return searchTree(node.left)
- };
- } else if (value > node.value) {
- if (node.right == null) {
- node.right = new Node(value);
- return;
- } else if (node.right != null) {
- return searchTree(node.right);
- };
- } else {
- return null;
- };
- };
- return searchTree(node);
- };
- },
- inorder: function() {
- if (this.root == null) {
- return null;
- } else {
- var result = new Array();
- function traverseInOrder(node) {
- if (node.left != null) {
- traverseInOrder(node.left);
- };
- result.push(node.value);
- if (node.right != null) {
- traverseInOrder(node.right);
- };
+ add: function(value) {
+ var node = this.root;
+ if (node == null) {
+ this.root = new Node(value);
+ return;
+ } else {
+ function searchTree(node) {
+ if (value < node.value) {
+ if (node.left == null) {
+ node.left = new Node(value);
+ return;
+ } else if (node.left != null) {
+ return searchTree(node.left);
+ }
+ } else if (value > node.value) {
+ if (node.right == null) {
+ node.right = new Node(value);
+ return;
+ } else if (node.right != null) {
+ return searchTree(node.right);
}
- traverseInOrder(this.root);
- return result;
- };
- },
- isBinarySearchTree() {
- if (this.root == null) {
- return null;
} else {
- var check = true;
- function checkTree(node) {
- if (node.left != null) {
- var left = node.left;
- if (left.value > node.value) {
- check = false;
- } else {
- checkTree(left);
- }
- }
- if (node.right != null) {
- var right = node.right;
- if (right.value < node.value) {
- check = false;
- } else {
- checkTree(right);
- };
- };
- };
- checkTree(this.root);
- return check;
+ return null;
}
+ }
+ return searchTree(node);
}
+ },
+ inorder: function() {
+ if (this.root == null) {
+ return null;
+ } else {
+ var result = new Array();
+ function traverseInOrder(node) {
+ if (node.left != null) {
+ traverseInOrder(node.left);
+ }
+ result.push(node.value);
+ if (node.right != null) {
+ traverseInOrder(node.right);
+ }
+ }
+ traverseInOrder(this.root);
+ return result;
+ }
+ },
+ isBinarySearchTree() {
+ if (this.root == null) {
+ return null;
+ } else {
+ var check = true;
+ function checkTree(node) {
+ if (node.left != null) {
+ var left = node.left;
+ if (left.value > node.value) {
+ check = false;
+ } else {
+ checkTree(left);
+ }
+ }
+ if (node.right != null) {
+ var right = node.right;
+ if (right.value < node.value) {
+ check = false;
+ } else {
+ checkTree(right);
+ }
+ }
+ }
+ checkTree(this.root);
+ return check;
+ }
+ }
};
```
-
findMinHeight and findMaxHeight. These methods should return an integer value for the minimum and maximum height within a given binary tree, respectively. If the node is empty let's assign it a height of -1 (that's the base case). Finally, add a third method isBalanced which returns true or false depending on whether the tree is balanced or not. You can use the first two methods you just wrote to determine this.
+Note: A similar property to height is depth, which refers to how far a given node is from the root node.
findMinHeight and findMaxHeight. These methods should return an integer value for the minimum and maximum height within a given binary tree, respectively. If the node is empty let's assign it a height of -1 (that's the base case). Finally, add a third method isBalanced which returns true or false depending on whether the tree is balanced or not. You can use the first two methods you just wrote to determine this.
-1.');
- text: The isBalanced method returns true if the tree is a balanced binary search tree.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.isBalanced !== 'function') { return false; }; test.add(4); test.add(1); test.add(7); test.add(87); test.add(34); test.add(45); test.add(73); test.add(8); return !test.isBalanced(); })(), 'The isBalanced method returns true if the tree is a balanced binary search tree.');
-
```
## Challenge Seed
```js
-var displayTree = (tree) => console.log(JSON.stringify(tree, null, 2));
+var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
- this.value = value;
- this.left = null;
- this.right = null;
+ this.value = value;
+ this.left = null;
+ this.right = null;
}
function BinarySearchTree() {
- this.root = null;
- // change code below this line
- // change code above this line
+ this.root = null;
+ // change code below this line
+ // change code above this line
}
```
-
### After Test
```js
BinarySearchTree.prototype = {
- add: function(value) {
- var node = this.root;
- if (node == null) {
- this.root = new Node(value);
- return;
+ add: function(value) {
+ var node = this.root;
+ if (node == null) {
+ this.root = new Node(value);
+ return;
+ } else {
+ function searchTree(node) {
+ if (value < node.value) {
+ if (node.left == null) {
+ node.left = new Node(value);
+ return;
+ } else if (node.left != null) {
+ return searchTree(node.left);
+ }
+ } else if (value > node.value) {
+ if (node.right == null) {
+ node.right = new Node(value);
+ return;
+ } else if (node.right != null) {
+ return searchTree(node.right);
+ }
} else {
- function searchTree(node) {
- if (value < node.value) {
- if (node.left == null) {
- node.left = new Node(value);
- return;
- } else if (node.left != null) {
- return searchTree(node.left)
- };
- } else if (value > node.value) {
- if (node.right == null) {
- node.right = new Node(value);
- return;
- } else if (node.right != null) {
- return searchTree(node.right);
- };
- } else {
- return null;
- };
- };
- return searchTree(node);
- };
+ return null;
+ }
+ }
+ return searchTree(node);
}
+ }
};
```
-

findMin and findMax. These methods should return the minimum and maximum value held in the binary search tree (don't worry about adding values to the tree for now, we have added some in the background). If you get stuck, reflect on the invariant that must be true for binary search trees: each left subtree is less than or equal to its parent and each right subtree is greater than or equal to its parent. Let's also say that our tree can only store integer values. If the tree is empty, either method should return null.
## Instructions
findMin and findMax. These methods should return the minimum and maximum value held in the binary search tree (don't worry about adding values to the tree for now, we have added some in the background). If you get stuck, reflect on the invariant that must be true for binary search trees: each left subtree is less than or equal to its parent and each right subtree is greater than or equal to its parent. Let's also say that our tree can only store integer values. If the tree is empty, either method should return null.
findMax method returns the maximum value in the binary search tree.');
- text: The findMin and findMax methods return null for an empty tree.
testString: assert((function() { var test = false; if (typeof BinarySearchTree !== 'undefined') { test = new BinarySearchTree() } else { return false; }; if (typeof test.findMin !== 'function') { return false; }; if (typeof test.findMax !== 'function') { return false; }; return (test.findMin() == null && test.findMax() == null) })(), 'The findMin and findMax methods return null for an empty tree.');
-
```
@@ -48,60 +46,58 @@ tests:
```js
-var displayTree = (tree) => console.log(JSON.stringify(tree, null, 2));
+var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
- this.value = value;
- this.left = null;
- this.right = null;
+ this.value = value;
+ this.left = null;
+ this.right = null;
}
function BinarySearchTree() {
- this.root = null;
- // change code below this line
- // change code above this line
+ this.root = null;
+ // change code below this line
+ // change code above this line
}
```
-
### After Test
```js
BinarySearchTree.prototype = {
- add: function(value) {
- var node = this.root;
- if (node == null) {
- this.root = new Node(value);
- return;
+ add: function(value) {
+ var node = this.root;
+ if (node == null) {
+ this.root = new Node(value);
+ return;
+ } else {
+ function searchTree(node) {
+ if (value < node.value) {
+ if (node.left == null) {
+ node.left = new Node(value);
+ return;
+ } else if (node.left != null) {
+ return searchTree(node.left);
+ }
+ } else if (value > node.value) {
+ if (node.right == null) {
+ node.right = new Node(value);
+ return;
+ } else if (node.right != null) {
+ return searchTree(node.right);
+ }
} else {
- function searchTree(node) {
- if (value < node.value) {
- if (node.left == null) {
- node.left = new Node(value);
- return;
- } else if (node.left != null) {
- return searchTree(node.left)
- };
- } else if (value > node.value) {
- if (node.right == null) {
- node.right = new Node(value);
- return;
- } else if (node.right != null) {
- return searchTree(node.right);
- };
- } else {
- return null;
- };
- };
- return searchTree(node);
- };
+ return null;
+ }
+ }
+ return searchTree(node);
}
+ }
};
```
-
## Solution
@@ -111,173 +107,174 @@ BinarySearchTree.prototype = {
var displayTree = tree => console.log(JSON.stringify(tree, null, 2));
function Node(value) {
- this.value = value;
- this.left = null;
- this.right = null;
+ this.value = value;
+ this.left = null;
+ this.right = null;
}
function BinarySearchTree() {
- this.root = null;
- this.findMin = function() {
- // Empty tree.
- if (!this.root) {
- return null;
- }
- let currentNode = this.root;
- while (currentNode.left) {
- currentNode = currentNode.left;
- }
- return currentNode.value;
- };
- this.findMax = function() {
- // Empty tree.
- if (!this.root) {
- return null;
- }
- let currentNode = this.root;
- while (currentNode.right) {
- currentNode = currentNode.right;
- }
- return currentNode.value;
- };
- this.add = function(value) {
- // Empty tree.
- if (!this.root) {
- this.root = new Node(value);
- return undefined;
- }
- return this.addNode(this.root, value);
- };
- this.addNode = function(node, value) {
- // Check if value already exists.
- if (node.value === value) return null;
- if (value < node.value) {
- if (node.left) {
- return this.addNode(node.left, value);
- } else {
- node.left = new Node(value);
- return undefined;
- }
- } else {
- if (node.right) {
- return this.addNode(node.right, value);
- } else {
- node.right = new Node(value);
- return undefined;
- }
- }
- };
- this.isPresent = function(value) {
- if (!this.root) {
- return null;
- }
- return this.isNodePresent(this.root, value);
- };
- this.isNodePresent = function(node, value) {
- if (node.value === value) return true;
- if (value < node.value) {
- return node.left ? this.isNodePresent(node.left, value) : false;
- } else {
- return node.right ? this.isNodePresent(node.right, value) : false;
- }
- return false;
- };
- this.findMinHeight = function() {
- if (!this.root) {
- return -1;
- }
- let heights = {};
- let height = 0;
- this.traverseTree(this.root, height, heights);
- return Math.min(...Object.keys(heights));
- };
- this.findMaxHeight = function() {
- if (!this.root) {
- return -1;
- }
- let heights = {};
- let height = 0;
- this.traverseTree(this.root, height, heights);
- return Math.max(...Object.keys(heights));
- };
- this.traverseTree = function(node, height, heights) {
- if (node.left === null && node.right === null) {
- return (heights[height] = true);
- }
- if (node.left) {
- this.traverseTree(node.left, height + 1, heights);
- }
- if (node.right) {
- this.traverseTree(node.right, height + 1, heights);
- }
- };
- this.isBalanced = function() {
- return this.findMaxHeight() > this.findMinHeight() + 1;
- };
- // DFS tree traversal.
- this.inorder = function() {
- if (!this.root) return null;
- let result = [];
+ this.root = null;
+ this.findMin = function() {
+ // Empty tree.
+ if (!this.root) {
+ return null;
+ }
+ let currentNode = this.root;
+ while (currentNode.left) {
+ currentNode = currentNode.left;
+ }
+ return currentNode.value;
+ };
+ this.findMax = function() {
+ // Empty tree.
+ if (!this.root) {
+ return null;
+ }
+ let currentNode = this.root;
+ while (currentNode.right) {
+ currentNode = currentNode.right;
+ }
+ return currentNode.value;
+ };
+ this.add = function(value) {
+ // Empty tree.
+ if (!this.root) {
+ this.root = new Node(value);
+ return undefined;
+ }
+ return this.addNode(this.root, value);
+ };
+ this.addNode = function(node, value) {
+ // Check if value already exists.
+ if (node.value === value) return null;
+ if (value < node.value) {
+ if (node.left) {
+ return this.addNode(node.left, value);
+ } else {
+ node.left = new Node(value);
+ return undefined;
+ }
+ } else {
+ if (node.right) {
+ return this.addNode(node.right, value);
+ } else {
+ node.right = new Node(value);
+ return undefined;
+ }
+ }
+ };
+ this.isPresent = function(value) {
+ if (!this.root) {
+ return null;
+ }
+ return this.isNodePresent(this.root, value);
+ };
+ this.isNodePresent = function(node, value) {
+ if (node.value === value) return true;
+ if (value < node.value) {
+ return node.left ? this.isNodePresent(node.left, value) : false;
+ } else {
+ return node.right ? this.isNodePresent(node.right, value) : false;
+ }
+ return false;
+ };
+ this.findMinHeight = function() {
+ if (!this.root) {
+ return -1;
+ }
+ let heights = {};
+ let height = 0;
+ this.traverseTree(this.root, height, heights);
+ return Math.min(...Object.keys(heights));
+ };
+ this.findMaxHeight = function() {
+ if (!this.root) {
+ return -1;
+ }
+ let heights = {};
+ let height = 0;
+ this.traverseTree(this.root, height, heights);
+ return Math.max(...Object.keys(heights));
+ };
+ this.traverseTree = function(node, height, heights) {
+ if (node.left === null && node.right === null) {
+ return (heights[height] = true);
+ }
+ if (node.left) {
+ this.traverseTree(node.left, height + 1, heights);
+ }
+ if (node.right) {
+ this.traverseTree(node.right, height + 1, heights);
+ }
+ };
+ this.isBalanced = function() {
+ return this.findMaxHeight() > this.findMinHeight() + 1;
+ };
+ // DFS tree traversal.
+ this.inorder = function() {
+ if (!this.root) return null;
+ let result = [];
- function traverseInOrder(node) {
- if (node.left) traverseInOrder(node.left);
- result.push(node.value);
- if (node.right) traverseInOrder(node.right);
- }
- traverseInOrder(this.root);
- return result;
- };
- this.preorder = function() {
- if (!this.root) return null;
- let result = [];
+ function traverseInOrder(node) {
+ if (node.left) traverseInOrder(node.left);
+ result.push(node.value);
+ if (node.right) traverseInOrder(node.right);
+ }
+ traverseInOrder(this.root);
+ return result;
+ };
+ this.preorder = function() {
+ if (!this.root) return null;
+ let result = [];
- function traverseInOrder(node) {
- result.push(node.value);
- if (node.left) traverseInOrder(node.left);
- if (node.right) traverseInOrder(node.right);
- }
- traverseInOrder(this.root);
- return result;
- };
- this.postorder = function() {
- if (!this.root) return null;
- let result = [];
+ function traverseInOrder(node) {
+ result.push(node.value);
+ if (node.left) traverseInOrder(node.left);
+ if (node.right) traverseInOrder(node.right);
+ }
+ traverseInOrder(this.root);
+ return result;
+ };
+ this.postorder = function() {
+ if (!this.root) return null;
+ let result = [];
- function traverseInOrder(node) {
- if (node.left) traverseInOrder(node.left);
- if (node.right) traverseInOrder(node.right);
- result.push(node.value);
- }
- traverseInOrder(this.root);
- return result;
- };
- // BFS tree traversal.
- this.levelOrder = function() {
- if (!this.root) return null;
- let queue = [this.root];
- let result = [];
- while (queue.length) {
- let node = queue.shift();
- result.push(node.value);
- if (node.left) queue.push(node.left);
- if (node.right) queue.push(node.right);
- }
- return result;
- };
- this.reverseLevelOrder = function() {
- if (!this.root) return null;
- let queue = [this.root];
- let result = [];
- while (queue.length) {
- let node = queue.shift();
- result.push(node.value);
- if (node.right) queue.push(node.right);
- if (node.left) queue.push(node.left);
- }
- return result;
- };
- // Delete a leaf node.
+ function traverseInOrder(node) {
+ if (node.left) traverseInOrder(node.left);
+ if (node.right) traverseInOrder(node.right);
+ result.push(node.value);
+ }
+ traverseInOrder(this.root);
+ return result;
+ };
+ // BFS tree traversal.
+ this.levelOrder = function() {
+ if (!this.root) return null;
+ let queue = [this.root];
+ let result = [];
+ while (queue.length) {
+ let node = queue.shift();
+ result.push(node.value);
+ if (node.left) queue.push(node.left);
+ if (node.right) queue.push(node.right);
+ }
+ return result;
+ };
+ this.reverseLevelOrder = function() {
+ if (!this.root) return null;
+ let queue = [this.root];
+ let result = [];
+ while (queue.length) {
+ let node = queue.shift();
+ result.push(node.value);
+ if (node.right) queue.push(node.right);
+ if (node.left) queue.push(node.left);
+ }
+ return result;
+ };
+ // Delete a leaf node.
}
let bst = new BinarySearchTree();
```
+
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/implement-heap-sort-with-a-min-heap.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/implement-heap-sort-with-a-min-heap.english.md
index 6b88755369..192b5d3f71 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/implement-heap-sort-with-a-min-heap.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/implement-heap-sort-with-a-min-heap.english.md
@@ -8,12 +8,11 @@ challengeType: 1
MinHeap with insert, remove, and sort methods. The sort method should return an array of all the elements in the min heap sorted from smallest to largest.
```js
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/insert-an-element-into-a-max-heap.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/insert-an-element-into-a-max-heap.english.md
index 9214e34aff..5d02437b40 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/insert-an-element-into-a-max-heap.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/insert-an-element-into-a-max-heap.english.md
@@ -48,7 +48,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/invert-a-binary-tree.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/invert-a-binary-tree.english.md
index 812c538d4d..7e299cfa59 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/invert-a-binary-tree.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/invert-a-binary-tree.english.md
@@ -34,7 +34,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/learn-how-a-stack-works.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/learn-how-a-stack-works.english.md
index 9b634f9edc..7ec1d4ca23 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/learn-how-a-stack-works.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/learn-how-a-stack-works.english.md
@@ -39,7 +39,6 @@ tests:
## Challenge Seed
-
## Solution
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-difference-on-two-sets-of-data.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-difference-on-two-sets-of-data.english.md
index c799c997e2..5a9e881dcd 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-difference-on-two-sets-of-data.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/perform-a-difference-on-two-sets-of-data.english.md
@@ -97,15 +97,11 @@ function Set() {
```
-
-
-
```js
@@ -59,9 +58,6 @@ var MaxHeap = function() {
```
-
-
-
```js
@@ -109,7 +108,6 @@ BinarySearchTree.prototype = {
```
-
```js
@@ -50,8 +49,6 @@ var homeworkStack = ["BIO12","HIS80","MAT122","PSY44"];
-
-
```js
@@ -116,15 +115,11 @@ function Set() {
```
-
-
-
```js
@@ -73,15 +72,11 @@ function Set() {
```
-
-
-
```js
@@ -86,9 +85,6 @@ function Set() {
```
-
-
-
```js
@@ -51,9 +50,6 @@ var MaxHeap = function() {
```
-
-
-
```js
@@ -86,9 +85,6 @@ function LinkedList() {
```
-
-
-
```js
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-items-from-a-set-in-es6.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-items-from-a-set-in-es6.english.md
index d0dbe75b09..14a7dab2c3 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-items-from-a-set-in-es6.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/remove-items-from-a-set-in-es6.english.md
@@ -38,7 +38,6 @@ tests:
## Challenge Seed
-
## Solution
-
```js
function checkSet(){
var set = new Set([1,2,3,4,5]);
diff --git a/curriculum/challenges/english/08-coding-interview-prep/data-structures/search-within-a-linked-list.english.md b/curriculum/challenges/english/08-coding-interview-prep/data-structures/search-within-a-linked-list.english.md
index 06a5eaeced..28cfc6f375 100644
--- a/curriculum/challenges/english/08-coding-interview-prep/data-structures/search-within-a-linked-list.english.md
+++ b/curriculum/challenges/english/08-coding-interview-prep/data-structures/search-within-a-linked-list.english.md
@@ -101,8 +101,6 @@ function LinkedList() {
-
-
```js
@@ -52,15 +51,11 @@ function checkSet(){
```
-
-
-