diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-121-disc-game-prize-fund.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-121-disc-game-prize-fund.md
index 1cc716c41c..c8db41a350 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-121-disc-game-prize-fund.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-121-disc-game-prize-fund.md
@@ -18,10 +18,10 @@ Find the maximum prize fund that should be allocated to a single game in which f
# --hints--
-`euler121()` should return 2269.
+`discGamePrize()` should return `2269`.
```js
-assert.strictEqual(euler121(), 2269);
+assert.strictEqual(discGamePrize(), 2269);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler121(), 2269);
## --seed-contents--
```js
-function euler121() {
+function discGamePrize() {
return true;
}
-euler121();
+discGamePrize();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-122-efficient-exponentiation.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-122-efficient-exponentiation.md
index 7da1b4274e..a023244489 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-122-efficient-exponentiation.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-122-efficient-exponentiation.md
@@ -8,28 +8,41 @@ dashedName: problem-122-efficient-exponentiation
# --description--
-The most naive way of computing n15 requires fourteen multiplications:
+The most naive way of computing $n^{15}$ requires fourteen multiplications:
-n × n × ... × n = n15
+$$n × n × \ldots × n = n^{15}$$
But using a "binary" method you can compute it in six multiplications:
-n × n = n2n2 × n2 = n4n4 × n4 = n8n8 × n4 = n12n12 × n2 = n14n14 × n = n15
+$$\begin{align}
+ & n × n = n^2\\\\
+ & n^2 × n^2 = n^4\\\\
+ & n^4 × n^4 = n^8\\\\
+ & n^8 × n^4 = n^{12}\\\\
+ & n^{12} × n^2 = n^{14}\\\\
+ & n^{14} × n = n^{15}
+\end{align}$$
However it is yet possible to compute it in only five multiplications:
-n × n = n2n2 × n = n3n3 × n3 = n6n6 × n6 = n12n12 × n3 = n15
+$$\begin{align}
+ & n × n = n^2\\\\
+ & n^2 × n = n^3\\\\
+ & n^3 × n^3 = n^6\\\\
+ & n^6 × n^6 = n^{12}\\\\
+ & n^{12} × n^3 = n^{15}
+\end{align}$$
-We shall define m(k) to be the minimum number of multiplications to compute nk; for example m(15) = 5.
+We shall define $m(k)$ to be the minimum number of multiplications to compute $n^k$; for example $m(15) = 5$.
-For 1 ≤ k ≤ 200, find ∑ m(k).
+For $1 ≤ k ≤ 200$, find $\sum{m(k)}$.
# --hints--
-`euler122()` should return 1582.
+`efficientExponentation()` should return `1582`.
```js
-assert.strictEqual(euler122(), 1582);
+assert.strictEqual(efficientExponentation(), 1582);
```
# --seed--
@@ -37,12 +50,12 @@ assert.strictEqual(euler122(), 1582);
## --seed-contents--
```js
-function euler122() {
+function efficientExponentation() {
return true;
}
-euler122();
+efficientExponentation();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
index cb7b7afda1..6b5de785eb 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
@@ -8,20 +8,20 @@ dashedName: problem-123-prime-square-remainders
# --description--
-Let pn be the nth prime: 2, 3, 5, 7, 11, ..., and let r be the remainder when (pn−1)n + (pn+1)n is divided by pn2.
+Let $p_n$ be the $n$th prime: 2, 3, 5, 7, 11, ..., and let $r$ be the remainder when ${(p_n−1)}^n + {(p_n+1)}^n$ is divided by ${p_n}^2$.
-For example, when n = 3, p3 = 5, and 43 + 63 = 280 ≡ 5 mod 25.
+For example, when $n = 3, p_3 = 5$, and $4^3 + 6^3 = 280 ≡ 5\\ mod\\ 25$.
-The least value of n for which the remainder first exceeds 109 is 7037.
+The least value of $n$ for which the remainder first exceeds $10^9$ is 7037.
-Find the least value of n for which the remainder first exceeds 1010.
+Find the least value of $n$ for which the remainder first exceeds $10^{10}$.
# --hints--
-`euler123()` should return 21035.
+`primeSquareRemainders()` should return `21035`.
```js
-assert.strictEqual(euler123(), 21035);
+assert.strictEqual(primeSquareRemainders(), 21035);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler123(), 21035);
## --seed-contents--
```js
-function euler123() {
+function primeSquareRemainders() {
return true;
}
-euler123();
+primeSquareRemainders();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-124-ordered-radicals.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-124-ordered-radicals.md
index 1dfc34dc9b..5376e15f59 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-124-ordered-radicals.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-124-ordered-radicals.md
@@ -8,42 +8,118 @@ dashedName: problem-124-ordered-radicals
# --description--
-The radical of n, rad(n), is the product of the distinct prime factors of n. For example, 504 = 23 × 32 × 7, so rad(504) = 2 × 3 × 7 = 42.
+The radical of $n, rad(n)$, is the product of the distinct prime factors of $n$. For example, $504 = 2^3 × 3^2 × 7$, so $rad(504) = 2 × 3 × 7 = 42$.
-If we calculate rad(n) for 1 ≤ n ≤ 10, then sort them on rad(n), and sorting on n if the radical values are equal, we get:
+If we calculate $rad(n)$ for $1 ≤ n ≤ 10$, then sort them on $rad(n)$, and sorting on $n$ if the radical values are equal, we get:
-Unsorted
+
+
+
+
+ | $Unsorted$ |
+ |
+ $Sorted$ |
+
+
+ | $n$ |
+ $rad(n)$ |
+ |
+ $n$ |
+ $rad(n)$ |
+ $k$ |
+
+
+ | 1 |
+ 1 |
+ |
+ 1 |
+ 1 |
+ 1 |
+
+
+ | 2 |
+ 2 |
+ |
+ 2 |
+ 2 |
+ 2 |
+
+
+ | 3 |
+ 3 |
+ |
+ 4 |
+ 2 |
+ 3 |
+
+
+ | 4 |
+ 2 |
+ |
+ 8 |
+ 2 |
+ 4 |
+
+
+ | 5 |
+ 5 |
+ |
+ 3 |
+ 3 |
+ 5 |
+
+
+ | 6 |
+ 6 |
+ |
+ 9 |
+ 3 |
+ 6 |
+
+
+ | 7 |
+ 7 |
+ |
+ 5 |
+ 5 |
+ 7 |
+
+
+ | 8 |
+ 2 |
+ |
+ 6 |
+ 6 |
+ 8 |
+
+
+ | 9 |
+ 3 |
+ |
+ 7 |
+ 7 |
+ 9 |
+
+
+ | 10 |
+ 10 |
+ |
+ 10 |
+ 10 |
+ 10 |
+
+
+
+
-Sorted n rad(n)
-
-n rad(n) k 11
-
-111 22
-
-222 33
-
-423 42
-
-824 55
-
-335 66
-
-936 77
-
-557 82
-
-668 93
-
-779 1010
-
-101010 Let E(k) be the kth element in the sorted n column; for example, E(4) = 8 and E(6) = 9. If rad(n) is sorted for 1 ≤ n ≤ 100000, find E(10000).
+Let $E(k)$ be the $k$th element in the sorted $n$ column; for example, $E(4) = 8$ and $E(6) = 9$. If $rad(n)$ is sorted for $1 ≤ n ≤ 100000$, find $E(10000)$.
# --hints--
-`euler124()` should return 21417.
+`orderedRadicals()` should return `21417`.
```js
-assert.strictEqual(euler124(), 21417);
+assert.strictEqual(orderedRadicals(), 21417);
```
# --seed--
@@ -51,12 +127,12 @@ assert.strictEqual(euler124(), 21417);
## --seed-contents--
```js
-function euler124() {
+function orderedRadicals() {
return true;
}
-euler124();
+orderedRadicals();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-125-palindromic-sums.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-125-palindromic-sums.md
index 460f5e2a23..c54c796409 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-125-palindromic-sums.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-125-palindromic-sums.md
@@ -8,18 +8,18 @@ dashedName: problem-125-palindromic-sums
# --description--
-The palindromic number 595 is interesting because it can be written as the sum of consecutive squares: 62 + 72 + 82 + 92 + 102 + 112 + 122.
+The palindromic number 595 is interesting because it can be written as the sum of consecutive squares: $6^2 + 7^2 + 8^2 + 9^2 + 10^2 + 11^2 + 12^2$.
-There are exactly eleven palindromes below one-thousand that can be written as consecutive square sums, and the sum of these palindromes is 4164. Note that 1 = 02 + 12 has not been included as this problem is concerned with the squares of positive integers.
+There are exactly eleven palindromes below one-thousand that can be written as consecutive square sums, and the sum of these palindromes is 4164. Note that $1 = 0^2 + 1^2$ has not been included as this problem is concerned with the squares of positive integers.
-Find the sum of all the numbers less than 108 that are both palindromic and can be written as the sum of consecutive squares.
+Find the sum of all the numbers less than $10^8$ that are both palindromic and can be written as the sum of consecutive squares.
# --hints--
-`euler125()` should return 2906969179.
+`palindromicSums()` should return `2906969179`.
```js
-assert.strictEqual(euler125(), 2906969179);
+assert.strictEqual(palindromicSums(), 2906969179);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler125(), 2906969179);
## --seed-contents--
```js
-function euler125() {
+function palindromicSums() {
return true;
}
-euler125();
+palindromicSums();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-126-cuboid-layers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-126-cuboid-layers.md
index fe9b4a6aa8..61e8b8c58d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-126-cuboid-layers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-126-cuboid-layers.md
@@ -10,14 +10,24 @@ dashedName: problem-126-cuboid-layers
The minimum number of cubes to cover every visible face on a cuboid measuring 3 x 2 x 1 is twenty-two.
-If we then add a second layer to this solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face. However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, and 11 x 1 x 1 all contain forty-six cubes. We shall define C(n) to represent the number of cuboids that contain n cubes in one of its layers. So C(22) = 2, C(46) = 4, C(78) = 5, and C(118) = 8. It turns out that 154 is the least value of n for which C(n) = 10. Find the least value of n for which C(n) = 1000.
+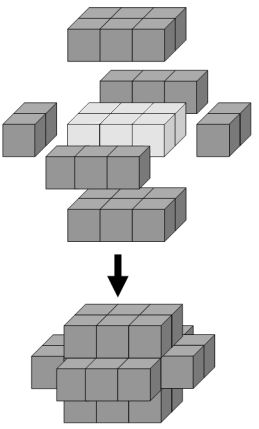 +
+If we add a second layer to this solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
+
+However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly, the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, and 11 x 1 x 1 all contain forty-six cubes.
+
+We shall define $C(n)$ to represent the number of cuboids that contain $n$ cubes in one of its layers. So $C(22) = 2$, $C(46) = 4$, $C(78) = 5$, and $C(118) = 8$.
+
+It turns out that 154 is the least value of $n$ for which $C(n) = 10$.
+
+Find the least value of $n$ for which $C(n) = 1000$.
# --hints--
-`euler126()` should return 18522.
+`cuboidLayers()` should return `18522`.
```js
-assert.strictEqual(euler126(), 18522);
+assert.strictEqual(cuboidLayers(), 18522);
```
# --seed--
@@ -25,12 +35,12 @@ assert.strictEqual(euler126(), 18522);
## --seed-contents--
```js
-function euler126() {
+function cuboidLayers() {
return true;
}
-euler126();
+cuboidLayers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
index 665e17c0a7..075655d7f5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
@@ -8,38 +8,32 @@ dashedName: problem-127-abc-hits
# --description--
-The radical of n, rad(n), is the product of distinct prime factors of n. For example, 504 = 23 × 32 × 7, so rad(504) = 2 × 3 × 7 = 42.
+The radical of $n$, $rad(n)$, is the product of distinct prime factors of $n$. For example, $504 = 2^3 × 3^2 × 7$, so $rad(504) = 2 × 3 × 7 = 42$.
We shall define the triplet of positive integers (a, b, c) to be an abc-hit if:
-GCD(a, b) = GCD(a, c) = GCD(b, c) = 1
-
-a < b
-
-a + b = c
-
-rad(abc) < c
+1. $GCD(a, b) = GCD(a, c) = GCD(b, c) = 1$
+2. $a < b$
+3. $a + b = c$
+4. $rad(abc) < c$
For example, (5, 27, 32) is an abc-hit, because:
-GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1
+1. $GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1$
+2. $5 < 27$
+3. $5 + 27 = 32$
+4. $rad(4320) = 30 < 32$
-5 < 27
+It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for $c < 1000$, with $\sum{c} = 12523$.
-5 + 27 = 32
-
-rad(4320) = 30 < 32
-
-It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for c < 1000, with ∑c = 12523.
-
-Find ∑c for c < 120000.
+Find $\sum{c}$ for $c < 120000$.
# --hints--
-`euler127()` should return 18407904.
+`abcHits()` should return `18407904`.
```js
-assert.strictEqual(euler127(), 18407904);
+assert.strictEqual(abcHits(), 18407904);
```
# --seed--
@@ -47,12 +41,12 @@ assert.strictEqual(euler127(), 18407904);
## --seed-contents--
```js
-function euler127() {
+function abcHits() {
return true;
}
-euler127();
+abcHits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
index 7bdd624234..8e4e1889aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
@@ -12,14 +12,26 @@ A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, s
New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
-By finding the difference between tile n and each of its six neighbours we shall define PD(n) to be the number of those differences which are prime. For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So PD(8) = 3. In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2. It can be shown that the maximum value of PD(n) is 3. If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271. Find the 2000th tile in this sequence.
+
+
+If we add a second layer to this solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
+
+However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly, the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, and 11 x 1 x 1 all contain forty-six cubes.
+
+We shall define $C(n)$ to represent the number of cuboids that contain $n$ cubes in one of its layers. So $C(22) = 2$, $C(46) = 4$, $C(78) = 5$, and $C(118) = 8$.
+
+It turns out that 154 is the least value of $n$ for which $C(n) = 10$.
+
+Find the least value of $n$ for which $C(n) = 1000$.
# --hints--
-`euler126()` should return 18522.
+`cuboidLayers()` should return `18522`.
```js
-assert.strictEqual(euler126(), 18522);
+assert.strictEqual(cuboidLayers(), 18522);
```
# --seed--
@@ -25,12 +35,12 @@ assert.strictEqual(euler126(), 18522);
## --seed-contents--
```js
-function euler126() {
+function cuboidLayers() {
return true;
}
-euler126();
+cuboidLayers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
index 665e17c0a7..075655d7f5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
@@ -8,38 +8,32 @@ dashedName: problem-127-abc-hits
# --description--
-The radical of n, rad(n), is the product of distinct prime factors of n. For example, 504 = 23 × 32 × 7, so rad(504) = 2 × 3 × 7 = 42.
+The radical of $n$, $rad(n)$, is the product of distinct prime factors of $n$. For example, $504 = 2^3 × 3^2 × 7$, so $rad(504) = 2 × 3 × 7 = 42$.
We shall define the triplet of positive integers (a, b, c) to be an abc-hit if:
-GCD(a, b) = GCD(a, c) = GCD(b, c) = 1
-
-a < b
-
-a + b = c
-
-rad(abc) < c
+1. $GCD(a, b) = GCD(a, c) = GCD(b, c) = 1$
+2. $a < b$
+3. $a + b = c$
+4. $rad(abc) < c$
For example, (5, 27, 32) is an abc-hit, because:
-GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1
+1. $GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1$
+2. $5 < 27$
+3. $5 + 27 = 32$
+4. $rad(4320) = 30 < 32$
-5 < 27
+It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for $c < 1000$, with $\sum{c} = 12523$.
-5 + 27 = 32
-
-rad(4320) = 30 < 32
-
-It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for c < 1000, with ∑c = 12523.
-
-Find ∑c for c < 120000.
+Find $\sum{c}$ for $c < 120000$.
# --hints--
-`euler127()` should return 18407904.
+`abcHits()` should return `18407904`.
```js
-assert.strictEqual(euler127(), 18407904);
+assert.strictEqual(abcHits(), 18407904);
```
# --seed--
@@ -47,12 +41,12 @@ assert.strictEqual(euler127(), 18407904);
## --seed-contents--
```js
-function euler127() {
+function abcHits() {
return true;
}
-euler127();
+abcHits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
index 7bdd624234..8e4e1889aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
@@ -12,14 +12,26 @@ A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, s
New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
-By finding the difference between tile n and each of its six neighbours we shall define PD(n) to be the number of those differences which are prime. For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So PD(8) = 3. In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2. It can be shown that the maximum value of PD(n) is 3. If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271. Find the 2000th tile in this sequence.
+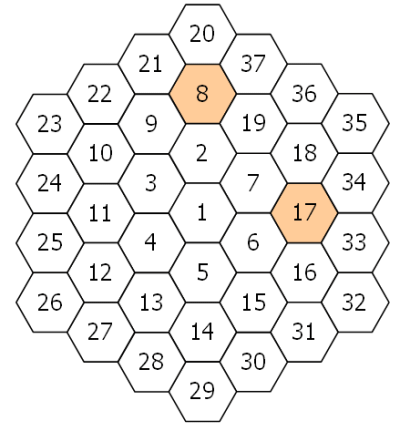 +
+By finding the difference between tile $n$ and each of its six neighbours we shall define $PD(n)$ to be the number of those differences which are prime.
+
+For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So $PD(8) = 3$.
+
+In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence $PD(17) = 2$.
+
+It can be shown that the maximum value of $PD(n)$ is $3$.
+
+If all of the tiles for which $PD(n) = 3$ are listed in ascending order to form a sequence, the 10th tile would be 271.
+
+Find the 2000th tile in this sequence.
# --hints--
-`euler128()` should return 14516824220.
+`hexagonalTile()` should return `14516824220`.
```js
-assert.strictEqual(euler128(), 14516824220);
+assert.strictEqual(hexagonalTile(), 14516824220);
```
# --seed--
@@ -27,12 +39,12 @@ assert.strictEqual(euler128(), 14516824220);
## --seed-contents--
```js
-function euler128() {
+function hexagonalTile() {
return true;
}
-euler128();
+hexagonalTile();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
index 0d8f6c2916..8fef3216aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
@@ -8,20 +8,20 @@ dashedName: problem-129-repunit-divisibility
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-The least value of n for which A(n) first exceeds ten is 17.
+The least value of $n$ for which $A(n)$ first exceeds ten is 17.
-Find the least value of n for which A(n) first exceeds one-million.
+Find the least value of $n$ for which $A(n)$ first exceeds one-million.
# --hints--
-`euler129()` should return 1000023.
+`repunitDivisibility()` should return `1000023`.
```js
-assert.strictEqual(euler129(), 1000023);
+assert.strictEqual(repunitDivisibility(), 1000023);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler129(), 1000023);
## --seed-contents--
```js
-function euler129() {
+function repunitDivisibility() {
return true;
}
-euler129();
+repunitDivisibility();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
index 0f3c2c7a3c..49525947cc 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
@@ -8,22 +8,22 @@ dashedName: problem-130-composites-with-prime-repunit-property
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-You are given that for all primes, p > 5, that p − 1 is divisible by A(p). For example, when p = 41, A(41) = 5, and 40 is divisible by 5.
+You are given that for all primes, $p > 5$, that $p − 1$ is divisible by $A(p)$. For example, when $p = 41, A(41) = 5$, and 40 is divisible by 5.
However, there are rare composite values for which this is also true; the first five examples being 91, 259, 451, 481, and 703.
-Find the sum of the first twenty-five composite values of n for whichGCD(n, 10) = 1 and n − 1 is divisible by A(n).
+Find the sum of the first twenty-five composite values of $n$ for which $GCD(n, 10) = 1$ and $n − 1$ is divisible by $A(n)$.
# --hints--
-`euler130()` should return 149253.
+`compositeRepunit()` should return `149253`.
```js
-assert.strictEqual(euler130(), 149253);
+assert.strictEqual(compositeRepunit(), 149253);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler130(), 149253);
## --seed-contents--
```js
-function euler130() {
+function compositeRepunit() {
return true;
}
-euler130();
+compositeRepunit();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
index 729f8689fb..a88b77db0d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
@@ -8,20 +8,20 @@ dashedName: problem-131-prime-cube-partnership
# --description--
-There are some prime values, p, for which there exists a positive integer, n, such that the expression n3 + n2p is a perfect cube.
+There are some prime values, $p$, for which there exists a positive integer, $n$, such that the expression $n^3 + n^{2}p$ is a perfect cube.
-For example, when p = 19, 83 + 82×19 = 123.
+For example, when $p = 19,\\ 8^3 + 8^2 × 19 = {12}^3$.
-What is perhaps most surprising is that for each prime with this property the value of n is unique, and there are only four such primes below one-hundred.
+What is perhaps most surprising is that the value of $n$ is unique for each prime with this property, and there are only four such primes below one hundred.
How many primes below one million have this remarkable property?
# --hints--
-`euler131()` should return 173.
+`primeCubePartnership()` should return `173`.
```js
-assert.strictEqual(euler131(), 173);
+assert.strictEqual(primeCubePartnership(), 173);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler131(), 173);
## --seed-contents--
```js
-function euler131() {
+function primeCubePartnership() {
return true;
}
-euler131();
+primeCubePartnership();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
index d71927659b..bda0bad006 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
@@ -8,18 +8,18 @@ dashedName: problem-132-large-repunit-factors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$.
-For example, R(10) = 1111111111 = 11×41×271×9091, and the sum of these prime factors is 9414.
+For example, $R(10) = 1111111111 = 11 × 41 × 271 × 9091$, and the sum of these prime factors is 9414.
-Find the sum of the first forty prime factors of R(109).
+Find the sum of the first forty prime factors of $R({10}^9)$.
# --hints--
-`euler132()` should return 843296.
+`largeRepunitFactors()` should return `843296`.
```js
-assert.strictEqual(euler132(), 843296);
+assert.strictEqual(largeRepunitFactors(), 843296);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler132(), 843296);
## --seed-contents--
```js
-function euler132() {
+function largeRepunitFactors() {
return true;
}
-euler132();
+largeRepunitFactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
index 649dd7f1f3..022bba6228 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
@@ -8,20 +8,20 @@ dashedName: problem-133-repunit-nonfactors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Let us consider repunits of the form R(10n).
+Let us consider repunits of the form $R({10}^n)$.
-Although R(10), R(100), or R(1000) are not divisible by 17, R(10000) is divisible by 17. Yet there is no value of n for which R(10n) will divide by 19. In fact, it is remarkable that 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of R(10n).
+Although $R(10)$, $R(100)$, or $R(1000)$ are not divisible by 17, $R(10000)$ is divisible by 17. Yet there is no value of n for which $R({10}^n)$ will divide by 19. Remarkably, 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of $R({10}^n)$.
-Find the sum of all the primes below one-hundred thousand that will never be a factor of R(10n).
+Find the sum of all the primes below one-hundred thousand that will never be a factor of $R({10}^n)$.
# --hints--
-`euler133()` should return 453647705.
+`repunitNonfactors()` should return `453647705`.
```js
-assert.strictEqual(euler133(), 453647705);
+assert.strictEqual(repunitNonfactors(), 453647705);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler133(), 453647705);
## --seed-contents--
```js
-function euler133() {
+function repunitNonfactors() {
return true;
}
-euler133();
+repunitNonfactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
index a21b71ea01..27bfeef13c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
@@ -8,18 +8,18 @@ dashedName: problem-134-prime-pair-connection
# --description--
-Consider the consecutive primes p1 = 19 and p2 = 23. It can be verified that 1219 is the smallest number such that the last digits are formed by p1 whilst also being divisible by p2.
+Consider the consecutive primes $p_1 = 19$ and $p_2 = 23$. It can be verified that 1219 is the smallest number such that the last digits are formed by $p_1$ whilst also being divisible by $p_2$.
-In fact, with the exception of p1 = 3 and p2 = 5, for every pair of consecutive primes, p2 > p1, there exist values of n for which the last digits are formed by p1 and n is divisible by p2. Let S be the smallest of these values of n.
+In fact, with the exception of $p_1 = 3$ and $p_2 = 5$, for every pair of consecutive primes, $p_2 > p_1$, there exist values of $n$ for which the last digits are formed by $p_1$ and $n$ is divisible by $p_2$. Let $S$ be the smallest of these values of $n$.
-Find ∑ S for every pair of consecutive primes with 5 ≤ p1 ≤ 1000000.
+Find $\sum{S}$ for every pair of consecutive primes with $5 ≤ p_1 ≤ 1000000$.
# --hints--
-`euler134()` should return 18613426663617120.
+`primePairConnection()` should return `18613426663617120`.
```js
-assert.strictEqual(euler134(), 18613426663617120);
+assert.strictEqual(primePairConnection(), 18613426663617120);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler134(), 18613426663617120);
## --seed-contents--
```js
-function euler134() {
+function primePairConnection() {
return true;
}
-euler134();
+primePairConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
index f0de3b5c58..2b6509bbb9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
@@ -8,20 +8,20 @@ dashedName: problem-135-same-differences
# --description--
-Given the positive integers, x, y, and z, are consecutive terms of an arithmetic progression, the least value of the positive integer, n, for which the equation, x2 − y2 − z2 = n, has exactly two solutions is n = 27:
+Given the positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression, the least value of the positive integer, $n$, for which the equation, $x^2 − y^2 − z^2 = n$, has exactly two solutions is $n = 27$:
-342 − 272 − 202 = 122 − 92 − 62 = 27
+$$34^2 − 27^2 − 20^2 = 12^2 − 9^2 − 6^2 = 27$$
-It turns out that n = 1155 is the least value which has exactly ten solutions.
+It turns out that $n = 1155$ is the least value which has exactly ten solutions.
-How many values of n less than one million have exactly ten distinct solutions?
+How many values of $n$ less than one million have exactly ten distinct solutions?
# --hints--
-`euler135()` should return 4989.
+`sameDifferences()` should return `4989`.
```js
-assert.strictEqual(euler135(), 4989);
+assert.strictEqual(sameDifferences(), 4989);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler135(), 4989);
## --seed-contents--
```js
-function euler135() {
+function sameDifferences() {
return true;
}
-euler135();
+sameDifferences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
index 34fda8a4ee..971f6ae2ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
@@ -8,20 +8,20 @@ dashedName: problem-136-singleton-difference
# --description--
-The positive integers, x, y, and z, are consecutive terms of an arithmetic progression. Given that n is a positive integer, the equation, x2 − y2 − z2 = n, has exactly one solution when n = 20:
+The positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression. Given that $n$ is a positive integer, the equation, $x^2 − y^2 − z^2 = n$, has exactly one solution when $n = 20$:
-132 − 102 − 72 = 20
+$$13^2 − 10^2 − 7^2 = 20$$
-In fact there are twenty-five values of n below one hundred for which the equation has a unique solution.
+In fact, there are twenty-five values of $n$ below one hundred for which the equation has a unique solution.
-How many values of n less than fifty million have exactly one solution?
+How many values of $n$ less than fifty million have exactly one solution?
# --hints--
-`euler136()` should return 2544559.
+`singletonDifference()` should return `2544559`.
```js
-assert.strictEqual(euler136(), 2544559);
+assert.strictEqual(singletonDifference(), 2544559);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler136(), 2544559);
## --seed-contents--
```js
-function euler136() {
+function singletonDifference() {
return true;
}
-euler136();
+singletonDifference();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
index 2863f66aa1..6f1ea61389 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
@@ -8,30 +8,38 @@ dashedName: problem-137-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AF(x) = xF1 + x2F2 + x3F3 + ..., where Fk is the kth term in the Fibonacci sequence: 1, 1, 2, 3, 5, 8, ... ; that is, Fk = Fk−1 + Fk−2, F1 = 1 and F2 = 1.
+Consider the infinite polynomial series $A_{F}(x) = xF_1 + x^2F_2 + x^3F_3 + \ldots$, where $F_k$ is the $k$th term in the Fibonacci sequence: $1, 1, 2, 3, 5, 8, \ldots$; that is, $F_k = F_{k − 1} + F_{k − 2}, F_1 = 1$ and $F_2 = 1$.
-For this problem we shall be interested in values of x for which AF(x) is a positive integer.
+For this problem we shall be interested in values of $x$ for which $A_{F}(x)$ is a positive integer.
-Surprisingly AF(1/2)
+Surprisingly
-=
+$$\begin{align}
+A_F(\frac{1}{2}) & = (\frac{1}{2}) × 1 + {(\frac{1}{2})}^2 × 1 + {(\frac{1}{2})}^3 × 2 + {(\frac{1}{2})}^4 × 3 + {(\frac{1}{2})}^5 × 5 + \cdots \\\\
+ & = \frac{1}{2} + \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{5}{32} + \cdots \\\\
+ & = 2
+\end{align}$$
-(1/2).1 + (1/2)2.1 + (1/2)3.2 + (1/2)4.3 + (1/2)5.5 + ...
+The corresponding values of $x$ for the first five natural numbers are shown below.
-= 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ...
+| $x$ | $A_F(x)$ |
+|---------------------------|----------|
+| $\sqrt{2} − 1$ | $1$ |
+| $\frac{1}{2}$ | $2$ |
+| $\frac{\sqrt{13} − 2}{3}$ | $3$ |
+| $\frac{\sqrt{89} − 5}{8}$ | $4$ |
+| $\frac{\sqrt{34} − 3}{5}$ | $5$ |
-= 2 The corresponding values of x for the first five natural numbers are shown below.
+We shall call $A_F(x)$ a golden nugget if $x$ is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690.
-xAF(x) √2−11 1/22 (√13−2)/33 (√89−5)/84 (√34−3)/55
-
-We shall call AF(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690. Find the 15th golden nugget.
+Find the 15th golden nugget.
# --hints--
-`euler137()` should return 1120149658760.
+`goldenNugget()` should return `1120149658760`.
```js
-assert.strictEqual(euler137(), 1120149658760);
+assert.strictEqual(goldenNugget(), 1120149658760);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler137(), 1120149658760);
## --seed-contents--
```js
-function euler137() {
+function goldenNugget() {
return true;
}
-euler137();
+goldenNugget();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
index 5675e1f938..6b94842d02 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
@@ -8,16 +8,22 @@ dashedName: problem-138-special-isosceles-triangles
# --description--
-Consider the isosceles triangle with base length, b = 16, and legs, L = 17.
+Consider the isosceles triangle with base length, $b = 16$, and legs, $L = 17$.
-By using the Pythagorean theorem it can be seen that the height of the triangle, h = √(172 − 82) = 15, which is one less than the base length. With b = 272 and L = 305, we get h = 273, which is one more than the base length, and this is the second smallest isosceles triangle with the property that h = b ± 1. Find ∑ L for the twelve smallest isosceles triangles for which h = b ± 1 and b, L are positive integers.
+
+
+By finding the difference between tile $n$ and each of its six neighbours we shall define $PD(n)$ to be the number of those differences which are prime.
+
+For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So $PD(8) = 3$.
+
+In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence $PD(17) = 2$.
+
+It can be shown that the maximum value of $PD(n)$ is $3$.
+
+If all of the tiles for which $PD(n) = 3$ are listed in ascending order to form a sequence, the 10th tile would be 271.
+
+Find the 2000th tile in this sequence.
# --hints--
-`euler128()` should return 14516824220.
+`hexagonalTile()` should return `14516824220`.
```js
-assert.strictEqual(euler128(), 14516824220);
+assert.strictEqual(hexagonalTile(), 14516824220);
```
# --seed--
@@ -27,12 +39,12 @@ assert.strictEqual(euler128(), 14516824220);
## --seed-contents--
```js
-function euler128() {
+function hexagonalTile() {
return true;
}
-euler128();
+hexagonalTile();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
index 0d8f6c2916..8fef3216aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
@@ -8,20 +8,20 @@ dashedName: problem-129-repunit-divisibility
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-The least value of n for which A(n) first exceeds ten is 17.
+The least value of $n$ for which $A(n)$ first exceeds ten is 17.
-Find the least value of n for which A(n) first exceeds one-million.
+Find the least value of $n$ for which $A(n)$ first exceeds one-million.
# --hints--
-`euler129()` should return 1000023.
+`repunitDivisibility()` should return `1000023`.
```js
-assert.strictEqual(euler129(), 1000023);
+assert.strictEqual(repunitDivisibility(), 1000023);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler129(), 1000023);
## --seed-contents--
```js
-function euler129() {
+function repunitDivisibility() {
return true;
}
-euler129();
+repunitDivisibility();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
index 0f3c2c7a3c..49525947cc 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
@@ -8,22 +8,22 @@ dashedName: problem-130-composites-with-prime-repunit-property
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-You are given that for all primes, p > 5, that p − 1 is divisible by A(p). For example, when p = 41, A(41) = 5, and 40 is divisible by 5.
+You are given that for all primes, $p > 5$, that $p − 1$ is divisible by $A(p)$. For example, when $p = 41, A(41) = 5$, and 40 is divisible by 5.
However, there are rare composite values for which this is also true; the first five examples being 91, 259, 451, 481, and 703.
-Find the sum of the first twenty-five composite values of n for whichGCD(n, 10) = 1 and n − 1 is divisible by A(n).
+Find the sum of the first twenty-five composite values of $n$ for which $GCD(n, 10) = 1$ and $n − 1$ is divisible by $A(n)$.
# --hints--
-`euler130()` should return 149253.
+`compositeRepunit()` should return `149253`.
```js
-assert.strictEqual(euler130(), 149253);
+assert.strictEqual(compositeRepunit(), 149253);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler130(), 149253);
## --seed-contents--
```js
-function euler130() {
+function compositeRepunit() {
return true;
}
-euler130();
+compositeRepunit();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
index 729f8689fb..a88b77db0d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
@@ -8,20 +8,20 @@ dashedName: problem-131-prime-cube-partnership
# --description--
-There are some prime values, p, for which there exists a positive integer, n, such that the expression n3 + n2p is a perfect cube.
+There are some prime values, $p$, for which there exists a positive integer, $n$, such that the expression $n^3 + n^{2}p$ is a perfect cube.
-For example, when p = 19, 83 + 82×19 = 123.
+For example, when $p = 19,\\ 8^3 + 8^2 × 19 = {12}^3$.
-What is perhaps most surprising is that for each prime with this property the value of n is unique, and there are only four such primes below one-hundred.
+What is perhaps most surprising is that the value of $n$ is unique for each prime with this property, and there are only four such primes below one hundred.
How many primes below one million have this remarkable property?
# --hints--
-`euler131()` should return 173.
+`primeCubePartnership()` should return `173`.
```js
-assert.strictEqual(euler131(), 173);
+assert.strictEqual(primeCubePartnership(), 173);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler131(), 173);
## --seed-contents--
```js
-function euler131() {
+function primeCubePartnership() {
return true;
}
-euler131();
+primeCubePartnership();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
index d71927659b..bda0bad006 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
@@ -8,18 +8,18 @@ dashedName: problem-132-large-repunit-factors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$.
-For example, R(10) = 1111111111 = 11×41×271×9091, and the sum of these prime factors is 9414.
+For example, $R(10) = 1111111111 = 11 × 41 × 271 × 9091$, and the sum of these prime factors is 9414.
-Find the sum of the first forty prime factors of R(109).
+Find the sum of the first forty prime factors of $R({10}^9)$.
# --hints--
-`euler132()` should return 843296.
+`largeRepunitFactors()` should return `843296`.
```js
-assert.strictEqual(euler132(), 843296);
+assert.strictEqual(largeRepunitFactors(), 843296);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler132(), 843296);
## --seed-contents--
```js
-function euler132() {
+function largeRepunitFactors() {
return true;
}
-euler132();
+largeRepunitFactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
index 649dd7f1f3..022bba6228 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
@@ -8,20 +8,20 @@ dashedName: problem-133-repunit-nonfactors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Let us consider repunits of the form R(10n).
+Let us consider repunits of the form $R({10}^n)$.
-Although R(10), R(100), or R(1000) are not divisible by 17, R(10000) is divisible by 17. Yet there is no value of n for which R(10n) will divide by 19. In fact, it is remarkable that 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of R(10n).
+Although $R(10)$, $R(100)$, or $R(1000)$ are not divisible by 17, $R(10000)$ is divisible by 17. Yet there is no value of n for which $R({10}^n)$ will divide by 19. Remarkably, 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of $R({10}^n)$.
-Find the sum of all the primes below one-hundred thousand that will never be a factor of R(10n).
+Find the sum of all the primes below one-hundred thousand that will never be a factor of $R({10}^n)$.
# --hints--
-`euler133()` should return 453647705.
+`repunitNonfactors()` should return `453647705`.
```js
-assert.strictEqual(euler133(), 453647705);
+assert.strictEqual(repunitNonfactors(), 453647705);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler133(), 453647705);
## --seed-contents--
```js
-function euler133() {
+function repunitNonfactors() {
return true;
}
-euler133();
+repunitNonfactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
index a21b71ea01..27bfeef13c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
@@ -8,18 +8,18 @@ dashedName: problem-134-prime-pair-connection
# --description--
-Consider the consecutive primes p1 = 19 and p2 = 23. It can be verified that 1219 is the smallest number such that the last digits are formed by p1 whilst also being divisible by p2.
+Consider the consecutive primes $p_1 = 19$ and $p_2 = 23$. It can be verified that 1219 is the smallest number such that the last digits are formed by $p_1$ whilst also being divisible by $p_2$.
-In fact, with the exception of p1 = 3 and p2 = 5, for every pair of consecutive primes, p2 > p1, there exist values of n for which the last digits are formed by p1 and n is divisible by p2. Let S be the smallest of these values of n.
+In fact, with the exception of $p_1 = 3$ and $p_2 = 5$, for every pair of consecutive primes, $p_2 > p_1$, there exist values of $n$ for which the last digits are formed by $p_1$ and $n$ is divisible by $p_2$. Let $S$ be the smallest of these values of $n$.
-Find ∑ S for every pair of consecutive primes with 5 ≤ p1 ≤ 1000000.
+Find $\sum{S}$ for every pair of consecutive primes with $5 ≤ p_1 ≤ 1000000$.
# --hints--
-`euler134()` should return 18613426663617120.
+`primePairConnection()` should return `18613426663617120`.
```js
-assert.strictEqual(euler134(), 18613426663617120);
+assert.strictEqual(primePairConnection(), 18613426663617120);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler134(), 18613426663617120);
## --seed-contents--
```js
-function euler134() {
+function primePairConnection() {
return true;
}
-euler134();
+primePairConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
index f0de3b5c58..2b6509bbb9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
@@ -8,20 +8,20 @@ dashedName: problem-135-same-differences
# --description--
-Given the positive integers, x, y, and z, are consecutive terms of an arithmetic progression, the least value of the positive integer, n, for which the equation, x2 − y2 − z2 = n, has exactly two solutions is n = 27:
+Given the positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression, the least value of the positive integer, $n$, for which the equation, $x^2 − y^2 − z^2 = n$, has exactly two solutions is $n = 27$:
-342 − 272 − 202 = 122 − 92 − 62 = 27
+$$34^2 − 27^2 − 20^2 = 12^2 − 9^2 − 6^2 = 27$$
-It turns out that n = 1155 is the least value which has exactly ten solutions.
+It turns out that $n = 1155$ is the least value which has exactly ten solutions.
-How many values of n less than one million have exactly ten distinct solutions?
+How many values of $n$ less than one million have exactly ten distinct solutions?
# --hints--
-`euler135()` should return 4989.
+`sameDifferences()` should return `4989`.
```js
-assert.strictEqual(euler135(), 4989);
+assert.strictEqual(sameDifferences(), 4989);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler135(), 4989);
## --seed-contents--
```js
-function euler135() {
+function sameDifferences() {
return true;
}
-euler135();
+sameDifferences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
index 34fda8a4ee..971f6ae2ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
@@ -8,20 +8,20 @@ dashedName: problem-136-singleton-difference
# --description--
-The positive integers, x, y, and z, are consecutive terms of an arithmetic progression. Given that n is a positive integer, the equation, x2 − y2 − z2 = n, has exactly one solution when n = 20:
+The positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression. Given that $n$ is a positive integer, the equation, $x^2 − y^2 − z^2 = n$, has exactly one solution when $n = 20$:
-132 − 102 − 72 = 20
+$$13^2 − 10^2 − 7^2 = 20$$
-In fact there are twenty-five values of n below one hundred for which the equation has a unique solution.
+In fact, there are twenty-five values of $n$ below one hundred for which the equation has a unique solution.
-How many values of n less than fifty million have exactly one solution?
+How many values of $n$ less than fifty million have exactly one solution?
# --hints--
-`euler136()` should return 2544559.
+`singletonDifference()` should return `2544559`.
```js
-assert.strictEqual(euler136(), 2544559);
+assert.strictEqual(singletonDifference(), 2544559);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler136(), 2544559);
## --seed-contents--
```js
-function euler136() {
+function singletonDifference() {
return true;
}
-euler136();
+singletonDifference();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
index 2863f66aa1..6f1ea61389 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
@@ -8,30 +8,38 @@ dashedName: problem-137-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AF(x) = xF1 + x2F2 + x3F3 + ..., where Fk is the kth term in the Fibonacci sequence: 1, 1, 2, 3, 5, 8, ... ; that is, Fk = Fk−1 + Fk−2, F1 = 1 and F2 = 1.
+Consider the infinite polynomial series $A_{F}(x) = xF_1 + x^2F_2 + x^3F_3 + \ldots$, where $F_k$ is the $k$th term in the Fibonacci sequence: $1, 1, 2, 3, 5, 8, \ldots$; that is, $F_k = F_{k − 1} + F_{k − 2}, F_1 = 1$ and $F_2 = 1$.
-For this problem we shall be interested in values of x for which AF(x) is a positive integer.
+For this problem we shall be interested in values of $x$ for which $A_{F}(x)$ is a positive integer.
-Surprisingly AF(1/2)
+Surprisingly
-=
+$$\begin{align}
+A_F(\frac{1}{2}) & = (\frac{1}{2}) × 1 + {(\frac{1}{2})}^2 × 1 + {(\frac{1}{2})}^3 × 2 + {(\frac{1}{2})}^4 × 3 + {(\frac{1}{2})}^5 × 5 + \cdots \\\\
+ & = \frac{1}{2} + \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{5}{32} + \cdots \\\\
+ & = 2
+\end{align}$$
-(1/2).1 + (1/2)2.1 + (1/2)3.2 + (1/2)4.3 + (1/2)5.5 + ...
+The corresponding values of $x$ for the first five natural numbers are shown below.
-= 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ...
+| $x$ | $A_F(x)$ |
+|---------------------------|----------|
+| $\sqrt{2} − 1$ | $1$ |
+| $\frac{1}{2}$ | $2$ |
+| $\frac{\sqrt{13} − 2}{3}$ | $3$ |
+| $\frac{\sqrt{89} − 5}{8}$ | $4$ |
+| $\frac{\sqrt{34} − 3}{5}$ | $5$ |
-= 2 The corresponding values of x for the first five natural numbers are shown below.
+We shall call $A_F(x)$ a golden nugget if $x$ is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690.
-xAF(x) √2−11 1/22 (√13−2)/33 (√89−5)/84 (√34−3)/55
-
-We shall call AF(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690. Find the 15th golden nugget.
+Find the 15th golden nugget.
# --hints--
-`euler137()` should return 1120149658760.
+`goldenNugget()` should return `1120149658760`.
```js
-assert.strictEqual(euler137(), 1120149658760);
+assert.strictEqual(goldenNugget(), 1120149658760);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler137(), 1120149658760);
## --seed-contents--
```js
-function euler137() {
+function goldenNugget() {
return true;
}
-euler137();
+goldenNugget();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
index 5675e1f938..6b94842d02 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
@@ -8,16 +8,22 @@ dashedName: problem-138-special-isosceles-triangles
# --description--
-Consider the isosceles triangle with base length, b = 16, and legs, L = 17.
+Consider the isosceles triangle with base length, $b = 16$, and legs, $L = 17$.
-By using the Pythagorean theorem it can be seen that the height of the triangle, h = √(172 − 82) = 15, which is one less than the base length. With b = 272 and L = 305, we get h = 273, which is one more than the base length, and this is the second smallest isosceles triangle with the property that h = b ± 1. Find ∑ L for the twelve smallest isosceles triangles for which h = b ± 1 and b, L are positive integers.
+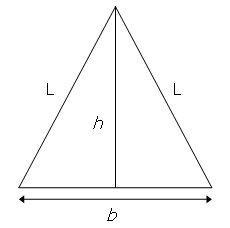 +
+By using the Pythagorean theorem, it can be seen that the height of the triangle, $h = \sqrt{{17}^2 − 8^2} = 15$, which is one less than the base length.
+
+With $b = 272$ and $L = 305$, we get $h = 273$, which is one more than the base length, and this is the second smallest isosceles triangle with the property that $h = b ± 1$.
+
+Find $\sum{L}$ for the twelve smallest isosceles triangles for which $h = b ± 1$ and $b$, $L$ are positive integers.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` should return `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..cd05d680b1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -12,14 +12,18 @@ Let (a, b, c) represent the three sides of a right angle triangle with integral
For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+
+
+By using the Pythagorean theorem, it can be seen that the height of the triangle, $h = \sqrt{{17}^2 − 8^2} = 15$, which is one less than the base length.
+
+With $b = 272$ and $L = 305$, we get $h = 273$, which is one more than the base length, and this is the second smallest isosceles triangle with the property that $h = b ± 1$.
+
+Find $\sum{L}$ for the twelve smallest isosceles triangles for which $h = b ± 1$ and $b$, $L$ are positive integers.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` should return `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..cd05d680b1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -12,14 +12,18 @@ Let (a, b, c) represent the three sides of a right angle triangle with integral
For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+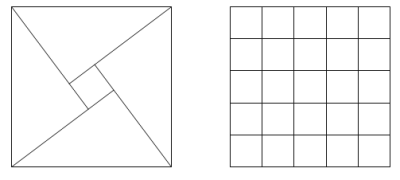 +
+However, if (5, 12, 13) triangles were used, the hole would measure 7 by 7. These 7 by 7 squares could not be used to tile the 13 by 13 square.
+
+Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to occur?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` should return `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..e05d7096ec 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Consider the infinite polynomial series $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, where $G_k$ is the $k$th term of the second order recurrence relation $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ and $G_2 = 4$; that is, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+For this problem we shall be concerned with values of $x$ for which $A_G(x)$ is a positive integer.
-The corresponding values of x for the first five natural numbers are shown below.
+The corresponding values of $x$ for the first five natural numbers are shown below.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+|-----------------------------|----------|
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+We shall call $A_G(x)$ a golden nugget if $x$ is rational because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` should return `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
+
+However, if (5, 12, 13) triangles were used, the hole would measure 7 by 7. These 7 by 7 squares could not be used to tile the 13 by 13 square.
+
+Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to occur?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` should return `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..e05d7096ec 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Consider the infinite polynomial series $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, where $G_k$ is the $k$th term of the second order recurrence relation $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ and $G_2 = 4$; that is, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+For this problem we shall be concerned with values of $x$ for which $A_G(x)$ is a positive integer.
-The corresponding values of x for the first five natural numbers are shown below.
+The corresponding values of $x$ for the first five natural numbers are shown below.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+|-----------------------------|----------|
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+We shall call $A_G(x)$ a golden nugget if $x$ is rational because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` should return `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
 +
+If we add a second layer to this solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
+
+However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly, the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, and 11 x 1 x 1 all contain forty-six cubes.
+
+We shall define $C(n)$ to represent the number of cuboids that contain $n$ cubes in one of its layers. So $C(22) = 2$, $C(46) = 4$, $C(78) = 5$, and $C(118) = 8$.
+
+It turns out that 154 is the least value of $n$ for which $C(n) = 10$.
+
+Find the least value of $n$ for which $C(n) = 1000$.
# --hints--
-`euler126()` should return 18522.
+`cuboidLayers()` should return `18522`.
```js
-assert.strictEqual(euler126(), 18522);
+assert.strictEqual(cuboidLayers(), 18522);
```
# --seed--
@@ -25,12 +35,12 @@ assert.strictEqual(euler126(), 18522);
## --seed-contents--
```js
-function euler126() {
+function cuboidLayers() {
return true;
}
-euler126();
+cuboidLayers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
index 665e17c0a7..075655d7f5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
@@ -8,38 +8,32 @@ dashedName: problem-127-abc-hits
# --description--
-The radical of n, rad(n), is the product of distinct prime factors of n. For example, 504 = 23 × 32 × 7, so rad(504) = 2 × 3 × 7 = 42.
+The radical of $n$, $rad(n)$, is the product of distinct prime factors of $n$. For example, $504 = 2^3 × 3^2 × 7$, so $rad(504) = 2 × 3 × 7 = 42$.
We shall define the triplet of positive integers (a, b, c) to be an abc-hit if:
-GCD(a, b) = GCD(a, c) = GCD(b, c) = 1
-
-a < b
-
-a + b = c
-
-rad(abc) < c
+1. $GCD(a, b) = GCD(a, c) = GCD(b, c) = 1$
+2. $a < b$
+3. $a + b = c$
+4. $rad(abc) < c$
For example, (5, 27, 32) is an abc-hit, because:
-GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1
+1. $GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1$
+2. $5 < 27$
+3. $5 + 27 = 32$
+4. $rad(4320) = 30 < 32$
-5 < 27
+It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for $c < 1000$, with $\sum{c} = 12523$.
-5 + 27 = 32
-
-rad(4320) = 30 < 32
-
-It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for c < 1000, with ∑c = 12523.
-
-Find ∑c for c < 120000.
+Find $\sum{c}$ for $c < 120000$.
# --hints--
-`euler127()` should return 18407904.
+`abcHits()` should return `18407904`.
```js
-assert.strictEqual(euler127(), 18407904);
+assert.strictEqual(abcHits(), 18407904);
```
# --seed--
@@ -47,12 +41,12 @@ assert.strictEqual(euler127(), 18407904);
## --seed-contents--
```js
-function euler127() {
+function abcHits() {
return true;
}
-euler127();
+abcHits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
index 7bdd624234..8e4e1889aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
@@ -12,14 +12,26 @@ A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, s
New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
-By finding the difference between tile n and each of its six neighbours we shall define PD(n) to be the number of those differences which are prime. For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So PD(8) = 3. In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2. It can be shown that the maximum value of PD(n) is 3. If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271. Find the 2000th tile in this sequence.
+
+
+If we add a second layer to this solid it would require forty-six cubes to cover every visible face, the third layer would require seventy-eight cubes, and the fourth layer would require one-hundred and eighteen cubes to cover every visible face.
+
+However, the first layer on a cuboid measuring 5 x 1 x 1 also requires twenty-two cubes; similarly, the first layer on cuboids measuring 5 x 3 x 1, 7 x 2 x 1, and 11 x 1 x 1 all contain forty-six cubes.
+
+We shall define $C(n)$ to represent the number of cuboids that contain $n$ cubes in one of its layers. So $C(22) = 2$, $C(46) = 4$, $C(78) = 5$, and $C(118) = 8$.
+
+It turns out that 154 is the least value of $n$ for which $C(n) = 10$.
+
+Find the least value of $n$ for which $C(n) = 1000$.
# --hints--
-`euler126()` should return 18522.
+`cuboidLayers()` should return `18522`.
```js
-assert.strictEqual(euler126(), 18522);
+assert.strictEqual(cuboidLayers(), 18522);
```
# --seed--
@@ -25,12 +35,12 @@ assert.strictEqual(euler126(), 18522);
## --seed-contents--
```js
-function euler126() {
+function cuboidLayers() {
return true;
}
-euler126();
+cuboidLayers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
index 665e17c0a7..075655d7f5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-127-abc-hits.md
@@ -8,38 +8,32 @@ dashedName: problem-127-abc-hits
# --description--
-The radical of n, rad(n), is the product of distinct prime factors of n. For example, 504 = 23 × 32 × 7, so rad(504) = 2 × 3 × 7 = 42.
+The radical of $n$, $rad(n)$, is the product of distinct prime factors of $n$. For example, $504 = 2^3 × 3^2 × 7$, so $rad(504) = 2 × 3 × 7 = 42$.
We shall define the triplet of positive integers (a, b, c) to be an abc-hit if:
-GCD(a, b) = GCD(a, c) = GCD(b, c) = 1
-
-a < b
-
-a + b = c
-
-rad(abc) < c
+1. $GCD(a, b) = GCD(a, c) = GCD(b, c) = 1$
+2. $a < b$
+3. $a + b = c$
+4. $rad(abc) < c$
For example, (5, 27, 32) is an abc-hit, because:
-GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1
+1. $GCD(5, 27) = GCD(5, 32) = GCD(27, 32) = 1$
+2. $5 < 27$
+3. $5 + 27 = 32$
+4. $rad(4320) = 30 < 32$
-5 < 27
+It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for $c < 1000$, with $\sum{c} = 12523$.
-5 + 27 = 32
-
-rad(4320) = 30 < 32
-
-It turns out that abc-hits are quite rare and there are only thirty-one abc-hits for c < 1000, with ∑c = 12523.
-
-Find ∑c for c < 120000.
+Find $\sum{c}$ for $c < 120000$.
# --hints--
-`euler127()` should return 18407904.
+`abcHits()` should return `18407904`.
```js
-assert.strictEqual(euler127(), 18407904);
+assert.strictEqual(abcHits(), 18407904);
```
# --seed--
@@ -47,12 +41,12 @@ assert.strictEqual(euler127(), 18407904);
## --seed-contents--
```js
-function euler127() {
+function abcHits() {
return true;
}
-euler127();
+abcHits();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
index 7bdd624234..8e4e1889aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-128-hexagonal-tile-differences.md
@@ -12,14 +12,26 @@ A hexagonal tile with number 1 is surrounded by a ring of six hexagonal tiles, s
New rings are added in the same fashion, with the next rings being numbered 8 to 19, 20 to 37, 38 to 61, and so on. The diagram below shows the first three rings.
-By finding the difference between tile n and each of its six neighbours we shall define PD(n) to be the number of those differences which are prime. For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So PD(8) = 3. In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence PD(17) = 2. It can be shown that the maximum value of PD(n) is 3. If all of the tiles for which PD(n) = 3 are listed in ascending order to form a sequence, the 10th tile would be 271. Find the 2000th tile in this sequence.
+ +
+By finding the difference between tile $n$ and each of its six neighbours we shall define $PD(n)$ to be the number of those differences which are prime.
+
+For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So $PD(8) = 3$.
+
+In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence $PD(17) = 2$.
+
+It can be shown that the maximum value of $PD(n)$ is $3$.
+
+If all of the tiles for which $PD(n) = 3$ are listed in ascending order to form a sequence, the 10th tile would be 271.
+
+Find the 2000th tile in this sequence.
# --hints--
-`euler128()` should return 14516824220.
+`hexagonalTile()` should return `14516824220`.
```js
-assert.strictEqual(euler128(), 14516824220);
+assert.strictEqual(hexagonalTile(), 14516824220);
```
# --seed--
@@ -27,12 +39,12 @@ assert.strictEqual(euler128(), 14516824220);
## --seed-contents--
```js
-function euler128() {
+function hexagonalTile() {
return true;
}
-euler128();
+hexagonalTile();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
index 0d8f6c2916..8fef3216aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
@@ -8,20 +8,20 @@ dashedName: problem-129-repunit-divisibility
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-The least value of n for which A(n) first exceeds ten is 17.
+The least value of $n$ for which $A(n)$ first exceeds ten is 17.
-Find the least value of n for which A(n) first exceeds one-million.
+Find the least value of $n$ for which $A(n)$ first exceeds one-million.
# --hints--
-`euler129()` should return 1000023.
+`repunitDivisibility()` should return `1000023`.
```js
-assert.strictEqual(euler129(), 1000023);
+assert.strictEqual(repunitDivisibility(), 1000023);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler129(), 1000023);
## --seed-contents--
```js
-function euler129() {
+function repunitDivisibility() {
return true;
}
-euler129();
+repunitDivisibility();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
index 0f3c2c7a3c..49525947cc 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
@@ -8,22 +8,22 @@ dashedName: problem-130-composites-with-prime-repunit-property
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-You are given that for all primes, p > 5, that p − 1 is divisible by A(p). For example, when p = 41, A(41) = 5, and 40 is divisible by 5.
+You are given that for all primes, $p > 5$, that $p − 1$ is divisible by $A(p)$. For example, when $p = 41, A(41) = 5$, and 40 is divisible by 5.
However, there are rare composite values for which this is also true; the first five examples being 91, 259, 451, 481, and 703.
-Find the sum of the first twenty-five composite values of n for whichGCD(n, 10) = 1 and n − 1 is divisible by A(n).
+Find the sum of the first twenty-five composite values of $n$ for which $GCD(n, 10) = 1$ and $n − 1$ is divisible by $A(n)$.
# --hints--
-`euler130()` should return 149253.
+`compositeRepunit()` should return `149253`.
```js
-assert.strictEqual(euler130(), 149253);
+assert.strictEqual(compositeRepunit(), 149253);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler130(), 149253);
## --seed-contents--
```js
-function euler130() {
+function compositeRepunit() {
return true;
}
-euler130();
+compositeRepunit();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
index 729f8689fb..a88b77db0d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
@@ -8,20 +8,20 @@ dashedName: problem-131-prime-cube-partnership
# --description--
-There are some prime values, p, for which there exists a positive integer, n, such that the expression n3 + n2p is a perfect cube.
+There are some prime values, $p$, for which there exists a positive integer, $n$, such that the expression $n^3 + n^{2}p$ is a perfect cube.
-For example, when p = 19, 83 + 82×19 = 123.
+For example, when $p = 19,\\ 8^3 + 8^2 × 19 = {12}^3$.
-What is perhaps most surprising is that for each prime with this property the value of n is unique, and there are only four such primes below one-hundred.
+What is perhaps most surprising is that the value of $n$ is unique for each prime with this property, and there are only four such primes below one hundred.
How many primes below one million have this remarkable property?
# --hints--
-`euler131()` should return 173.
+`primeCubePartnership()` should return `173`.
```js
-assert.strictEqual(euler131(), 173);
+assert.strictEqual(primeCubePartnership(), 173);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler131(), 173);
## --seed-contents--
```js
-function euler131() {
+function primeCubePartnership() {
return true;
}
-euler131();
+primeCubePartnership();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
index d71927659b..bda0bad006 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
@@ -8,18 +8,18 @@ dashedName: problem-132-large-repunit-factors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$.
-For example, R(10) = 1111111111 = 11×41×271×9091, and the sum of these prime factors is 9414.
+For example, $R(10) = 1111111111 = 11 × 41 × 271 × 9091$, and the sum of these prime factors is 9414.
-Find the sum of the first forty prime factors of R(109).
+Find the sum of the first forty prime factors of $R({10}^9)$.
# --hints--
-`euler132()` should return 843296.
+`largeRepunitFactors()` should return `843296`.
```js
-assert.strictEqual(euler132(), 843296);
+assert.strictEqual(largeRepunitFactors(), 843296);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler132(), 843296);
## --seed-contents--
```js
-function euler132() {
+function largeRepunitFactors() {
return true;
}
-euler132();
+largeRepunitFactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
index 649dd7f1f3..022bba6228 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
@@ -8,20 +8,20 @@ dashedName: problem-133-repunit-nonfactors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Let us consider repunits of the form R(10n).
+Let us consider repunits of the form $R({10}^n)$.
-Although R(10), R(100), or R(1000) are not divisible by 17, R(10000) is divisible by 17. Yet there is no value of n for which R(10n) will divide by 19. In fact, it is remarkable that 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of R(10n).
+Although $R(10)$, $R(100)$, or $R(1000)$ are not divisible by 17, $R(10000)$ is divisible by 17. Yet there is no value of n for which $R({10}^n)$ will divide by 19. Remarkably, 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of $R({10}^n)$.
-Find the sum of all the primes below one-hundred thousand that will never be a factor of R(10n).
+Find the sum of all the primes below one-hundred thousand that will never be a factor of $R({10}^n)$.
# --hints--
-`euler133()` should return 453647705.
+`repunitNonfactors()` should return `453647705`.
```js
-assert.strictEqual(euler133(), 453647705);
+assert.strictEqual(repunitNonfactors(), 453647705);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler133(), 453647705);
## --seed-contents--
```js
-function euler133() {
+function repunitNonfactors() {
return true;
}
-euler133();
+repunitNonfactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
index a21b71ea01..27bfeef13c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
@@ -8,18 +8,18 @@ dashedName: problem-134-prime-pair-connection
# --description--
-Consider the consecutive primes p1 = 19 and p2 = 23. It can be verified that 1219 is the smallest number such that the last digits are formed by p1 whilst also being divisible by p2.
+Consider the consecutive primes $p_1 = 19$ and $p_2 = 23$. It can be verified that 1219 is the smallest number such that the last digits are formed by $p_1$ whilst also being divisible by $p_2$.
-In fact, with the exception of p1 = 3 and p2 = 5, for every pair of consecutive primes, p2 > p1, there exist values of n for which the last digits are formed by p1 and n is divisible by p2. Let S be the smallest of these values of n.
+In fact, with the exception of $p_1 = 3$ and $p_2 = 5$, for every pair of consecutive primes, $p_2 > p_1$, there exist values of $n$ for which the last digits are formed by $p_1$ and $n$ is divisible by $p_2$. Let $S$ be the smallest of these values of $n$.
-Find ∑ S for every pair of consecutive primes with 5 ≤ p1 ≤ 1000000.
+Find $\sum{S}$ for every pair of consecutive primes with $5 ≤ p_1 ≤ 1000000$.
# --hints--
-`euler134()` should return 18613426663617120.
+`primePairConnection()` should return `18613426663617120`.
```js
-assert.strictEqual(euler134(), 18613426663617120);
+assert.strictEqual(primePairConnection(), 18613426663617120);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler134(), 18613426663617120);
## --seed-contents--
```js
-function euler134() {
+function primePairConnection() {
return true;
}
-euler134();
+primePairConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
index f0de3b5c58..2b6509bbb9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
@@ -8,20 +8,20 @@ dashedName: problem-135-same-differences
# --description--
-Given the positive integers, x, y, and z, are consecutive terms of an arithmetic progression, the least value of the positive integer, n, for which the equation, x2 − y2 − z2 = n, has exactly two solutions is n = 27:
+Given the positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression, the least value of the positive integer, $n$, for which the equation, $x^2 − y^2 − z^2 = n$, has exactly two solutions is $n = 27$:
-342 − 272 − 202 = 122 − 92 − 62 = 27
+$$34^2 − 27^2 − 20^2 = 12^2 − 9^2 − 6^2 = 27$$
-It turns out that n = 1155 is the least value which has exactly ten solutions.
+It turns out that $n = 1155$ is the least value which has exactly ten solutions.
-How many values of n less than one million have exactly ten distinct solutions?
+How many values of $n$ less than one million have exactly ten distinct solutions?
# --hints--
-`euler135()` should return 4989.
+`sameDifferences()` should return `4989`.
```js
-assert.strictEqual(euler135(), 4989);
+assert.strictEqual(sameDifferences(), 4989);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler135(), 4989);
## --seed-contents--
```js
-function euler135() {
+function sameDifferences() {
return true;
}
-euler135();
+sameDifferences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
index 34fda8a4ee..971f6ae2ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
@@ -8,20 +8,20 @@ dashedName: problem-136-singleton-difference
# --description--
-The positive integers, x, y, and z, are consecutive terms of an arithmetic progression. Given that n is a positive integer, the equation, x2 − y2 − z2 = n, has exactly one solution when n = 20:
+The positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression. Given that $n$ is a positive integer, the equation, $x^2 − y^2 − z^2 = n$, has exactly one solution when $n = 20$:
-132 − 102 − 72 = 20
+$$13^2 − 10^2 − 7^2 = 20$$
-In fact there are twenty-five values of n below one hundred for which the equation has a unique solution.
+In fact, there are twenty-five values of $n$ below one hundred for which the equation has a unique solution.
-How many values of n less than fifty million have exactly one solution?
+How many values of $n$ less than fifty million have exactly one solution?
# --hints--
-`euler136()` should return 2544559.
+`singletonDifference()` should return `2544559`.
```js
-assert.strictEqual(euler136(), 2544559);
+assert.strictEqual(singletonDifference(), 2544559);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler136(), 2544559);
## --seed-contents--
```js
-function euler136() {
+function singletonDifference() {
return true;
}
-euler136();
+singletonDifference();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
index 2863f66aa1..6f1ea61389 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
@@ -8,30 +8,38 @@ dashedName: problem-137-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AF(x) = xF1 + x2F2 + x3F3 + ..., where Fk is the kth term in the Fibonacci sequence: 1, 1, 2, 3, 5, 8, ... ; that is, Fk = Fk−1 + Fk−2, F1 = 1 and F2 = 1.
+Consider the infinite polynomial series $A_{F}(x) = xF_1 + x^2F_2 + x^3F_3 + \ldots$, where $F_k$ is the $k$th term in the Fibonacci sequence: $1, 1, 2, 3, 5, 8, \ldots$; that is, $F_k = F_{k − 1} + F_{k − 2}, F_1 = 1$ and $F_2 = 1$.
-For this problem we shall be interested in values of x for which AF(x) is a positive integer.
+For this problem we shall be interested in values of $x$ for which $A_{F}(x)$ is a positive integer.
-Surprisingly AF(1/2)
+Surprisingly
-=
+$$\begin{align}
+A_F(\frac{1}{2}) & = (\frac{1}{2}) × 1 + {(\frac{1}{2})}^2 × 1 + {(\frac{1}{2})}^3 × 2 + {(\frac{1}{2})}^4 × 3 + {(\frac{1}{2})}^5 × 5 + \cdots \\\\
+ & = \frac{1}{2} + \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{5}{32} + \cdots \\\\
+ & = 2
+\end{align}$$
-(1/2).1 + (1/2)2.1 + (1/2)3.2 + (1/2)4.3 + (1/2)5.5 + ...
+The corresponding values of $x$ for the first five natural numbers are shown below.
-= 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ...
+| $x$ | $A_F(x)$ |
+|---------------------------|----------|
+| $\sqrt{2} − 1$ | $1$ |
+| $\frac{1}{2}$ | $2$ |
+| $\frac{\sqrt{13} − 2}{3}$ | $3$ |
+| $\frac{\sqrt{89} − 5}{8}$ | $4$ |
+| $\frac{\sqrt{34} − 3}{5}$ | $5$ |
-= 2 The corresponding values of x for the first five natural numbers are shown below.
+We shall call $A_F(x)$ a golden nugget if $x$ is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690.
-xAF(x) √2−11 1/22 (√13−2)/33 (√89−5)/84 (√34−3)/55
-
-We shall call AF(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690. Find the 15th golden nugget.
+Find the 15th golden nugget.
# --hints--
-`euler137()` should return 1120149658760.
+`goldenNugget()` should return `1120149658760`.
```js
-assert.strictEqual(euler137(), 1120149658760);
+assert.strictEqual(goldenNugget(), 1120149658760);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler137(), 1120149658760);
## --seed-contents--
```js
-function euler137() {
+function goldenNugget() {
return true;
}
-euler137();
+goldenNugget();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
index 5675e1f938..6b94842d02 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
@@ -8,16 +8,22 @@ dashedName: problem-138-special-isosceles-triangles
# --description--
-Consider the isosceles triangle with base length, b = 16, and legs, L = 17.
+Consider the isosceles triangle with base length, $b = 16$, and legs, $L = 17$.
-By using the Pythagorean theorem it can be seen that the height of the triangle, h = √(172 − 82) = 15, which is one less than the base length. With b = 272 and L = 305, we get h = 273, which is one more than the base length, and this is the second smallest isosceles triangle with the property that h = b ± 1. Find ∑ L for the twelve smallest isosceles triangles for which h = b ± 1 and b, L are positive integers.
+
+
+By finding the difference between tile $n$ and each of its six neighbours we shall define $PD(n)$ to be the number of those differences which are prime.
+
+For example, working clockwise around tile 8 the differences are 12, 29, 11, 6, 1, and 13. So $PD(8) = 3$.
+
+In the same way, the differences around tile 17 are 1, 17, 16, 1, 11, and 10, hence $PD(17) = 2$.
+
+It can be shown that the maximum value of $PD(n)$ is $3$.
+
+If all of the tiles for which $PD(n) = 3$ are listed in ascending order to form a sequence, the 10th tile would be 271.
+
+Find the 2000th tile in this sequence.
# --hints--
-`euler128()` should return 14516824220.
+`hexagonalTile()` should return `14516824220`.
```js
-assert.strictEqual(euler128(), 14516824220);
+assert.strictEqual(hexagonalTile(), 14516824220);
```
# --seed--
@@ -27,12 +39,12 @@ assert.strictEqual(euler128(), 14516824220);
## --seed-contents--
```js
-function euler128() {
+function hexagonalTile() {
return true;
}
-euler128();
+hexagonalTile();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
index 0d8f6c2916..8fef3216aa 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-129-repunit-divisibility.md
@@ -8,20 +8,20 @@ dashedName: problem-129-repunit-divisibility
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-The least value of n for which A(n) first exceeds ten is 17.
+The least value of $n$ for which $A(n)$ first exceeds ten is 17.
-Find the least value of n for which A(n) first exceeds one-million.
+Find the least value of $n$ for which $A(n)$ first exceeds one-million.
# --hints--
-`euler129()` should return 1000023.
+`repunitDivisibility()` should return `1000023`.
```js
-assert.strictEqual(euler129(), 1000023);
+assert.strictEqual(repunitDivisibility(), 1000023);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler129(), 1000023);
## --seed-contents--
```js
-function euler129() {
+function repunitDivisibility() {
return true;
}
-euler129();
+repunitDivisibility();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
index 0f3c2c7a3c..49525947cc 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-130-composites-with-prime-repunit-property.md
@@ -8,22 +8,22 @@ dashedName: problem-130-composites-with-prime-repunit-property
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Given that n is a positive integer and GCD(n, 10) = 1, it can be shown that there always exists a value, k, for which R(k) is divisible by n, and let A(n) be the least such value of k; for example, A(7) = 6 and A(41) = 5.
+Given that $n$ is a positive integer and $GCD(n, 10) = 1$, it can be shown that there always exists a value, $k$, for which $R(k)$ is divisible by $n$, and let $A(n)$ be the least such value of $k$; for example, $A(7) = 6$ and $A(41) = 5$.
-You are given that for all primes, p > 5, that p − 1 is divisible by A(p). For example, when p = 41, A(41) = 5, and 40 is divisible by 5.
+You are given that for all primes, $p > 5$, that $p − 1$ is divisible by $A(p)$. For example, when $p = 41, A(41) = 5$, and 40 is divisible by 5.
However, there are rare composite values for which this is also true; the first five examples being 91, 259, 451, 481, and 703.
-Find the sum of the first twenty-five composite values of n for whichGCD(n, 10) = 1 and n − 1 is divisible by A(n).
+Find the sum of the first twenty-five composite values of $n$ for which $GCD(n, 10) = 1$ and $n − 1$ is divisible by $A(n)$.
# --hints--
-`euler130()` should return 149253.
+`compositeRepunit()` should return `149253`.
```js
-assert.strictEqual(euler130(), 149253);
+assert.strictEqual(compositeRepunit(), 149253);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler130(), 149253);
## --seed-contents--
```js
-function euler130() {
+function compositeRepunit() {
return true;
}
-euler130();
+compositeRepunit();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
index 729f8689fb..a88b77db0d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-131-prime-cube-partnership.md
@@ -8,20 +8,20 @@ dashedName: problem-131-prime-cube-partnership
# --description--
-There are some prime values, p, for which there exists a positive integer, n, such that the expression n3 + n2p is a perfect cube.
+There are some prime values, $p$, for which there exists a positive integer, $n$, such that the expression $n^3 + n^{2}p$ is a perfect cube.
-For example, when p = 19, 83 + 82×19 = 123.
+For example, when $p = 19,\\ 8^3 + 8^2 × 19 = {12}^3$.
-What is perhaps most surprising is that for each prime with this property the value of n is unique, and there are only four such primes below one-hundred.
+What is perhaps most surprising is that the value of $n$ is unique for each prime with this property, and there are only four such primes below one hundred.
How many primes below one million have this remarkable property?
# --hints--
-`euler131()` should return 173.
+`primeCubePartnership()` should return `173`.
```js
-assert.strictEqual(euler131(), 173);
+assert.strictEqual(primeCubePartnership(), 173);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler131(), 173);
## --seed-contents--
```js
-function euler131() {
+function primeCubePartnership() {
return true;
}
-euler131();
+primeCubePartnership();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
index d71927659b..bda0bad006 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-132-large-repunit-factors.md
@@ -8,18 +8,18 @@ dashedName: problem-132-large-repunit-factors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$.
-For example, R(10) = 1111111111 = 11×41×271×9091, and the sum of these prime factors is 9414.
+For example, $R(10) = 1111111111 = 11 × 41 × 271 × 9091$, and the sum of these prime factors is 9414.
-Find the sum of the first forty prime factors of R(109).
+Find the sum of the first forty prime factors of $R({10}^9)$.
# --hints--
-`euler132()` should return 843296.
+`largeRepunitFactors()` should return `843296`.
```js
-assert.strictEqual(euler132(), 843296);
+assert.strictEqual(largeRepunitFactors(), 843296);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler132(), 843296);
## --seed-contents--
```js
-function euler132() {
+function largeRepunitFactors() {
return true;
}
-euler132();
+largeRepunitFactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
index 649dd7f1f3..022bba6228 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-133-repunit-nonfactors.md
@@ -8,20 +8,20 @@ dashedName: problem-133-repunit-nonfactors
# --description--
-A number consisting entirely of ones is called a repunit. We shall define R(k) to be a repunit of length k; for example, R(6) = 111111.
+A number consisting entirely of ones is called a repunit. We shall define $R(k)$ to be a repunit of length $k$; for example, $R(6) = 111111$.
-Let us consider repunits of the form R(10n).
+Let us consider repunits of the form $R({10}^n)$.
-Although R(10), R(100), or R(1000) are not divisible by 17, R(10000) is divisible by 17. Yet there is no value of n for which R(10n) will divide by 19. In fact, it is remarkable that 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of R(10n).
+Although $R(10)$, $R(100)$, or $R(1000)$ are not divisible by 17, $R(10000)$ is divisible by 17. Yet there is no value of n for which $R({10}^n)$ will divide by 19. Remarkably, 11, 17, 41, and 73 are the only four primes below one-hundred that can be a factor of $R({10}^n)$.
-Find the sum of all the primes below one-hundred thousand that will never be a factor of R(10n).
+Find the sum of all the primes below one-hundred thousand that will never be a factor of $R({10}^n)$.
# --hints--
-`euler133()` should return 453647705.
+`repunitNonfactors()` should return `453647705`.
```js
-assert.strictEqual(euler133(), 453647705);
+assert.strictEqual(repunitNonfactors(), 453647705);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler133(), 453647705);
## --seed-contents--
```js
-function euler133() {
+function repunitNonfactors() {
return true;
}
-euler133();
+repunitNonfactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
index a21b71ea01..27bfeef13c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-134-prime-pair-connection.md
@@ -8,18 +8,18 @@ dashedName: problem-134-prime-pair-connection
# --description--
-Consider the consecutive primes p1 = 19 and p2 = 23. It can be verified that 1219 is the smallest number such that the last digits are formed by p1 whilst also being divisible by p2.
+Consider the consecutive primes $p_1 = 19$ and $p_2 = 23$. It can be verified that 1219 is the smallest number such that the last digits are formed by $p_1$ whilst also being divisible by $p_2$.
-In fact, with the exception of p1 = 3 and p2 = 5, for every pair of consecutive primes, p2 > p1, there exist values of n for which the last digits are formed by p1 and n is divisible by p2. Let S be the smallest of these values of n.
+In fact, with the exception of $p_1 = 3$ and $p_2 = 5$, for every pair of consecutive primes, $p_2 > p_1$, there exist values of $n$ for which the last digits are formed by $p_1$ and $n$ is divisible by $p_2$. Let $S$ be the smallest of these values of $n$.
-Find ∑ S for every pair of consecutive primes with 5 ≤ p1 ≤ 1000000.
+Find $\sum{S}$ for every pair of consecutive primes with $5 ≤ p_1 ≤ 1000000$.
# --hints--
-`euler134()` should return 18613426663617120.
+`primePairConnection()` should return `18613426663617120`.
```js
-assert.strictEqual(euler134(), 18613426663617120);
+assert.strictEqual(primePairConnection(), 18613426663617120);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler134(), 18613426663617120);
## --seed-contents--
```js
-function euler134() {
+function primePairConnection() {
return true;
}
-euler134();
+primePairConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
index f0de3b5c58..2b6509bbb9 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-135-same-differences.md
@@ -8,20 +8,20 @@ dashedName: problem-135-same-differences
# --description--
-Given the positive integers, x, y, and z, are consecutive terms of an arithmetic progression, the least value of the positive integer, n, for which the equation, x2 − y2 − z2 = n, has exactly two solutions is n = 27:
+Given the positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression, the least value of the positive integer, $n$, for which the equation, $x^2 − y^2 − z^2 = n$, has exactly two solutions is $n = 27$:
-342 − 272 − 202 = 122 − 92 − 62 = 27
+$$34^2 − 27^2 − 20^2 = 12^2 − 9^2 − 6^2 = 27$$
-It turns out that n = 1155 is the least value which has exactly ten solutions.
+It turns out that $n = 1155$ is the least value which has exactly ten solutions.
-How many values of n less than one million have exactly ten distinct solutions?
+How many values of $n$ less than one million have exactly ten distinct solutions?
# --hints--
-`euler135()` should return 4989.
+`sameDifferences()` should return `4989`.
```js
-assert.strictEqual(euler135(), 4989);
+assert.strictEqual(sameDifferences(), 4989);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler135(), 4989);
## --seed-contents--
```js
-function euler135() {
+function sameDifferences() {
return true;
}
-euler135();
+sameDifferences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
index 34fda8a4ee..971f6ae2ea 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-136-singleton-difference.md
@@ -8,20 +8,20 @@ dashedName: problem-136-singleton-difference
# --description--
-The positive integers, x, y, and z, are consecutive terms of an arithmetic progression. Given that n is a positive integer, the equation, x2 − y2 − z2 = n, has exactly one solution when n = 20:
+The positive integers, $x$, $y$, and $z$, are consecutive terms of an arithmetic progression. Given that $n$ is a positive integer, the equation, $x^2 − y^2 − z^2 = n$, has exactly one solution when $n = 20$:
-132 − 102 − 72 = 20
+$$13^2 − 10^2 − 7^2 = 20$$
-In fact there are twenty-five values of n below one hundred for which the equation has a unique solution.
+In fact, there are twenty-five values of $n$ below one hundred for which the equation has a unique solution.
-How many values of n less than fifty million have exactly one solution?
+How many values of $n$ less than fifty million have exactly one solution?
# --hints--
-`euler136()` should return 2544559.
+`singletonDifference()` should return `2544559`.
```js
-assert.strictEqual(euler136(), 2544559);
+assert.strictEqual(singletonDifference(), 2544559);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler136(), 2544559);
## --seed-contents--
```js
-function euler136() {
+function singletonDifference() {
return true;
}
-euler136();
+singletonDifference();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
index 2863f66aa1..6f1ea61389 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-137-fibonacci-golden-nuggets.md
@@ -8,30 +8,38 @@ dashedName: problem-137-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AF(x) = xF1 + x2F2 + x3F3 + ..., where Fk is the kth term in the Fibonacci sequence: 1, 1, 2, 3, 5, 8, ... ; that is, Fk = Fk−1 + Fk−2, F1 = 1 and F2 = 1.
+Consider the infinite polynomial series $A_{F}(x) = xF_1 + x^2F_2 + x^3F_3 + \ldots$, where $F_k$ is the $k$th term in the Fibonacci sequence: $1, 1, 2, 3, 5, 8, \ldots$; that is, $F_k = F_{k − 1} + F_{k − 2}, F_1 = 1$ and $F_2 = 1$.
-For this problem we shall be interested in values of x for which AF(x) is a positive integer.
+For this problem we shall be interested in values of $x$ for which $A_{F}(x)$ is a positive integer.
-Surprisingly AF(1/2)
+Surprisingly
-=
+$$\begin{align}
+A_F(\frac{1}{2}) & = (\frac{1}{2}) × 1 + {(\frac{1}{2})}^2 × 1 + {(\frac{1}{2})}^3 × 2 + {(\frac{1}{2})}^4 × 3 + {(\frac{1}{2})}^5 × 5 + \cdots \\\\
+ & = \frac{1}{2} + \frac{1}{4} + \frac{2}{8} + \frac{3}{16} + \frac{5}{32} + \cdots \\\\
+ & = 2
+\end{align}$$
-(1/2).1 + (1/2)2.1 + (1/2)3.2 + (1/2)4.3 + (1/2)5.5 + ...
+The corresponding values of $x$ for the first five natural numbers are shown below.
-= 1/2 + 1/4 + 2/8 + 3/16 + 5/32 + ...
+| $x$ | $A_F(x)$ |
+|---------------------------|----------|
+| $\sqrt{2} − 1$ | $1$ |
+| $\frac{1}{2}$ | $2$ |
+| $\frac{\sqrt{13} − 2}{3}$ | $3$ |
+| $\frac{\sqrt{89} − 5}{8}$ | $4$ |
+| $\frac{\sqrt{34} − 3}{5}$ | $5$ |
-= 2 The corresponding values of x for the first five natural numbers are shown below.
+We shall call $A_F(x)$ a golden nugget if $x$ is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690.
-xAF(x) √2−11 1/22 (√13−2)/33 (√89−5)/84 (√34−3)/55
-
-We shall call AF(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 10th golden nugget is 74049690. Find the 15th golden nugget.
+Find the 15th golden nugget.
# --hints--
-`euler137()` should return 1120149658760.
+`goldenNugget()` should return `1120149658760`.
```js
-assert.strictEqual(euler137(), 1120149658760);
+assert.strictEqual(goldenNugget(), 1120149658760);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler137(), 1120149658760);
## --seed-contents--
```js
-function euler137() {
+function goldenNugget() {
return true;
}
-euler137();
+goldenNugget();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
index 5675e1f938..6b94842d02 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-138-special-isosceles-triangles.md
@@ -8,16 +8,22 @@ dashedName: problem-138-special-isosceles-triangles
# --description--
-Consider the isosceles triangle with base length, b = 16, and legs, L = 17.
+Consider the isosceles triangle with base length, $b = 16$, and legs, $L = 17$.
-By using the Pythagorean theorem it can be seen that the height of the triangle, h = √(172 − 82) = 15, which is one less than the base length. With b = 272 and L = 305, we get h = 273, which is one more than the base length, and this is the second smallest isosceles triangle with the property that h = b ± 1. Find ∑ L for the twelve smallest isosceles triangles for which h = b ± 1 and b, L are positive integers.
+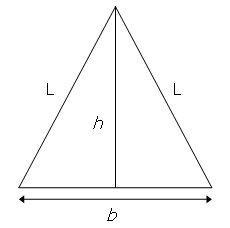 +
+By using the Pythagorean theorem, it can be seen that the height of the triangle, $h = \sqrt{{17}^2 − 8^2} = 15$, which is one less than the base length.
+
+With $b = 272$ and $L = 305$, we get $h = 273$, which is one more than the base length, and this is the second smallest isosceles triangle with the property that $h = b ± 1$.
+
+Find $\sum{L}$ for the twelve smallest isosceles triangles for which $h = b ± 1$ and $b$, $L$ are positive integers.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` should return `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..cd05d680b1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -12,14 +12,18 @@ Let (a, b, c) represent the three sides of a right angle triangle with integral
For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+
+
+By using the Pythagorean theorem, it can be seen that the height of the triangle, $h = \sqrt{{17}^2 − 8^2} = 15$, which is one less than the base length.
+
+With $b = 272$ and $L = 305$, we get $h = 273$, which is one more than the base length, and this is the second smallest isosceles triangle with the property that $h = b ± 1$.
+
+Find $\sum{L}$ for the twelve smallest isosceles triangles for which $h = b ± 1$ and $b$, $L$ are positive integers.
# --hints--
-`euler138()` should return 1118049290473932.
+`isoscelesTriangles()` should return `1118049290473932`.
```js
-assert.strictEqual(euler138(), 1118049290473932);
+assert.strictEqual(isoscelesTriangles(), 1118049290473932);
```
# --seed--
@@ -25,12 +31,12 @@ assert.strictEqual(euler138(), 1118049290473932);
## --seed-contents--
```js
-function euler138() {
+function isoscelesTriangles() {
return true;
}
-euler138();
+isoscelesTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
index 800c0ccbab..cd05d680b1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-139-pythagorean-tiles.md
@@ -12,14 +12,18 @@ Let (a, b, c) represent the three sides of a right angle triangle with integral
For example, (3, 4, 5) triangles can be placed together to form a 5 by 5 square with a 1 by 1 hole in the middle and it can be seen that the 5 by 5 square can be tiled with twenty-five 1 by 1 squares.
-However, if (5, 12, 13) triangles were used then the hole would measure 7 by 7 and these could not be used to tile the 13 by 13 square. Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to take place?
+ +
+However, if (5, 12, 13) triangles were used, the hole would measure 7 by 7. These 7 by 7 squares could not be used to tile the 13 by 13 square.
+
+Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to occur?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` should return `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..e05d7096ec 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Consider the infinite polynomial series $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, where $G_k$ is the $k$th term of the second order recurrence relation $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ and $G_2 = 4$; that is, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+For this problem we shall be concerned with values of $x$ for which $A_G(x)$ is a positive integer.
-The corresponding values of x for the first five natural numbers are shown below.
+The corresponding values of $x$ for the first five natural numbers are shown below.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+|-----------------------------|----------|
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+We shall call $A_G(x)$ a golden nugget if $x$ is rational because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` should return `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
+
+However, if (5, 12, 13) triangles were used, the hole would measure 7 by 7. These 7 by 7 squares could not be used to tile the 13 by 13 square.
+
+Given that the perimeter of the right triangle is less than one-hundred million, how many Pythagorean triangles would allow such a tiling to occur?
# --hints--
-`euler139()` should return 10057761.
+`pythagoreanTiles()` should return `10057761`.
```js
-assert.strictEqual(euler139(), 10057761);
+assert.strictEqual(pythagoreanTiles(), 10057761);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler139(), 10057761);
## --seed-contents--
```js
-function euler139() {
+function pythagoreanTiles() {
return true;
}
-euler139();
+pythagoreanTiles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..e05d7096ec 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+Consider the infinite polynomial series $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$, where $G_k$ is the $k$th term of the second order recurrence relation $G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$ and $G_2 = 4$; that is, $1, 4, 5, 9, 14, 23, \ldots$.
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+For this problem we shall be concerned with values of $x$ for which $A_G(x)$ is a positive integer.
-The corresponding values of x for the first five natural numbers are shown below.
+The corresponding values of $x$ for the first five natural numbers are shown below.
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+|-----------------------------|----------|
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+We shall call $A_G(x)$ a golden nugget if $x$ is rational because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` should return `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--