 -This looks very similar to the Pythagorean Theorem, and if C was 90 degrees (a right triange), the expression acctually simplifies to the Pythagorean Thoerem. So, the Pythagorean Theorem is a special case of the Law of Cosines.
+This looks very similar to the Pythagorean Theorem, and if C was 90 degrees (a right triange), then cos(C) = 0 and the expression simplifies to the Pythagorean Thoerem. So, the Pythagorean Theorem is a special case of the Law of Cosines.
-You can also switch the angle C with either A or B, but make sure to change the respective side (c) to a or b.
+You can also switch the angle C with either A or B, but need to change the respective side (c) to a or b:
-
-This looks very similar to the Pythagorean Theorem, and if C was 90 degrees (a right triange), the expression acctually simplifies to the Pythagorean Thoerem. So, the Pythagorean Theorem is a special case of the Law of Cosines.
+This looks very similar to the Pythagorean Theorem, and if C was 90 degrees (a right triange), then cos(C) = 0 and the expression simplifies to the Pythagorean Thoerem. So, the Pythagorean Theorem is a special case of the Law of Cosines.
-You can also switch the angle C with either A or B, but make sure to change the respective side (c) to a or b.
+You can also switch the angle C with either A or B, but need to change the respective side (c) to a or b:
-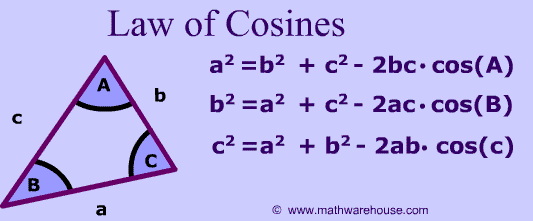 +
+
+ a2 = b2 + c2 - 2bc · cos(A)
+ b2 = a2 + c2 - 2ac · cos(B)
+ c2 = a2 + b2 - 2ab · cos(C)
+
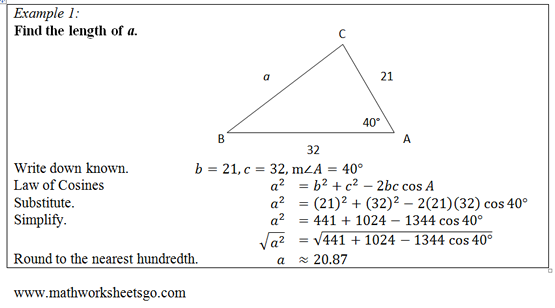 -
+To start, let's find a. Since we know b, c and A, the first of the three formulas above will be best to use. We have
+
+
-
+To start, let's find a. Since we know b, c and A, the first of the three formulas above will be best to use. We have
+
++ a2 = 212 + 322 - 2 · 21 · 32 · cos(40°) +
+ +so simplifying and taking square roots we have a = sqrt(1465 - 1344 · cos(40°)) or approximately, a ≈ 20.87. + +Similarly, if we want to find the angle B, we now have the length of all three sides so the second formula above will be helpful. Rearranging we have + ++ cos(B) = [a2 + c2 - b2]/(2ac) +
+ +and so taking the inverse cosine (or arccosine) of both sides gives the angle B. Plugging in the lengths of our sides (using the exact expression for a found above, and only simplyfing at the end) we find B is approximately 40.31°. + +Now to find C we have two approaches, either use the third formula above, or recall that the angles of our triangle should add up to 180 degrees, so if A is 40° and B was found above, we have + ++ C = (180 - 40 - B)° ≈ 99.69° +
+ +(Checking with the cosine formula we get the same approximate answer, so we can rest easy knowing we haven't likely made a mistake in any of the calculations.) #### More Information: -https://www.varsitytutors.com/hotmath/hotmath_help/topics/law-of-cosines -http://mathworld.wolfram.com/LawofCosines.html - +- https://www.varsitytutors.com/hotmath/hotmath_help/topics/law-of-cosines +- http://mathworld.wolfram.com/LawofCosines.html