diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
index 61e0b86a92..9e9bb64894 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-421-prime-factors-of-n151.md
@@ -8,20 +8,26 @@ dashedName: problem-421-prime-factors-of-n151
# --description--
-Numbers of the form n15+1 are composite for every integer n > 1.
+Numbers of the form $n^{15} + 1$ are composite for every integer $n > 1$.
-For positive integers n and m let s(n,m) be defined as the sum of the distinct prime factors of n15+1 not exceeding m.
+For positive integers $n$ and $m$ let $s(n, m)$ be defined as the sum of the distinct prime factors of $n^{15} + 1$ not exceeding $m$.
-E.g. 215+1 = 3×3×11×331. So s(2,10) = 3 and s(2,1000) = 3+11+331 = 345.
+E.g. $2^{15} + 1 = 3 × 3 × 11 × 331$.
-Also 1015+1 = 7×11×13×211×241×2161×9091. So s(10,100) = 31 and s(10,1000) = 483. Find ∑ s(n,108) for 1 ≤ n ≤ 1011.
+So $s(2, 10) = 3$ and $s(2, 1000) = 3 + 11 + 331 = 345$.
+
+Also ${10}^{15} + 1 = 7 × 11 × 13 × 211 × 241 × 2161 × 9091$.
+
+So $s(10, 100) = 31$ and $s(10, 1000) = 483$.
+
+Find $\sum s(n, {10}^8)$ for $1 ≤ n ≤ {10}^{11}$.
# --hints--
-`euler421()` should return 2304215802083466200.
+`primeFactorsOfN15Plus1()` should return `2304215802083466200`.
```js
-assert.strictEqual(euler421(), 2304215802083466200);
+assert.strictEqual(primeFactorsOfN15Plus1(), 2304215802083466200);
```
# --seed--
@@ -29,12 +35,12 @@ assert.strictEqual(euler421(), 2304215802083466200);
## --seed-contents--
```js
-function euler421() {
+function primeFactorsOfN15Plus1() {
return true;
}
-euler421();
+primeFactorsOfN15Plus1();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
index cf7455ac9d..07ec19e1ed 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-422-sequence-of-points-on-a-hyperbola.md
@@ -8,22 +8,30 @@ dashedName: problem-422-sequence-of-points-on-a-hyperbola
# --description--
-Let H be the hyperbola defined by the equation 12x2 + 7xy - 12y2 = 625.
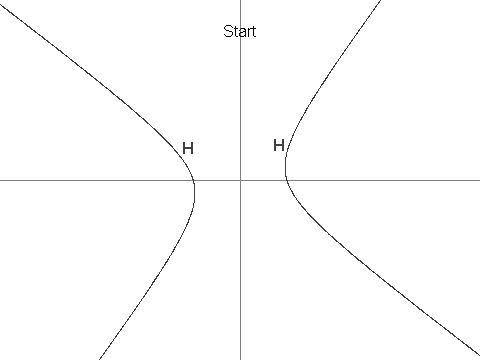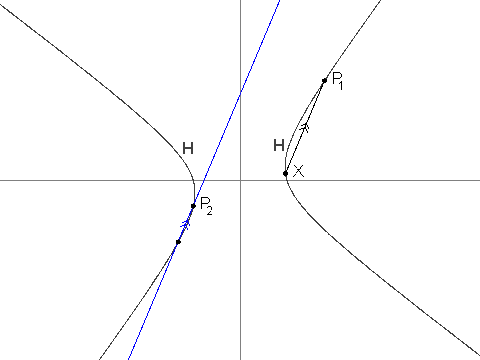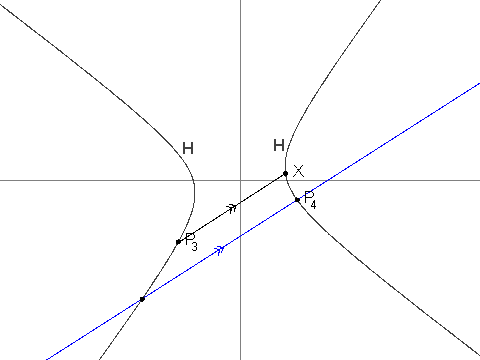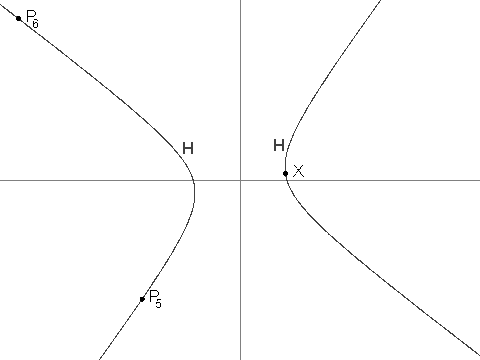
+Let $H$ be the hyperbola defined by the equation $12x^2 + 7xy - 12y^2 = 625$.
-Next, define X as the point (7, 1). It can be seen that X is in H.
+Next, define $X$ as the point (7, 1). It can be seen that $X$ is in $H$.
-Now we define a sequence of points in H, {Pi : i ≥ 1}, as: P1 = (13, 61/4). P2 = (-43/6, -4). For i > 2, Pi is the unique point in H that is different from Pi-1 and such that line PiPi-1 is parallel to line Pi-2X. It can be shown that Pi is well-defined, and that its coordinates are always rational. You are given that P3 = (-19/2, -229/24), P4 = (1267/144, -37/12) and P7 = (17194218091/143327232, 274748766781/1719926784).
+Now we define a sequence of points in $H, \\{P_i : i ≥ 1\\}$, as:
-Find Pn for n = 1114 in the following format:If Pn = (a/b, c/d) where the fractions are in lowest terms and the denominators are positive, then the answer is (a + b + c + d) mod 1 000 000 007.
+- $P_1 = (13, \frac{61}{4})$.
+- $P_2 = (\frac{-43}{6}, -4)$.
+- For $i > 2$, $P_i$ is the unique point in $H$ that is different from $P_{i - 1}$ and such that line $P_iP_{i - 1}$ is parallel to line $P_{i - 2}X$. It can be shown that $P_i$ is well-defined, and that its coordinates are always rational.
-For n = 7, the answer would have been: 806236837.
+ +
+You are given that $P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$ and $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$.
+
+Find $P_n$ for $n = {11}^{14}$ in the following format: If $P_n = (\frac{a}{b}, \frac{c}{d})$ where the fractions are in lowest terms and the denominators are positive, then the answer is $(a + b + c + d)\bmod 1\\,000\\,000\\,007$.
+
+For $n = 7$, the answer would have been: $806\\,236\\,837$.
# --hints--
-`euler422()` should return 92060460.
+`sequenceOfPointsOnHyperbola()` should return `92060460`.
```js
-assert.strictEqual(euler422(), 92060460);
+assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
```
# --seed--
@@ -31,12 +39,12 @@ assert.strictEqual(euler422(), 92060460);
## --seed-contents--
```js
-function euler422() {
+function sequenceOfPointsOnHyperbola() {
return true;
}
-euler422();
+sequenceOfPointsOnHyperbola();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
index a19a5ce19d..d63900393e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
@@ -8,26 +8,38 @@ dashedName: problem-423-consecutive-die-throws
# --description--
-Let n be a positive integer.
+Let $n$ be a positive integer.
-A 6-sided die is thrown n times. Let c be the number of pairs of consecutive throws that give the same value.
+A 6-sided die is thrown $n$ times. Let $c$ be the number of pairs of consecutive throws that give the same value.
-For example, if n = 7 and the values of the die throws are (1,1,5,6,6,6,3), then the following pairs of consecutive throws give the same value: (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) Therefore, c = 3 for (1,1,5,6,6,6,3).
+For example, if $n = 7$ and the values of the die throws are (1, 1, 5, 6, 6, 6, 3), then the following pairs of consecutive throws give the same value:
-Define C(n) as the number of outcomes of throwing a 6-sided die n times such that c does not exceed π(n).1 For example, C(3) = 216, C(4) = 1290, C(11) = 361912500 and C(24) = 4727547363281250000.
+$$\begin{align}
+ & (\underline{1}, \underline{1}, 5, 6, 6, 6, 3) \\\\
+ & (1, 1, 5, \underline{6}, \underline{6}, 6, 3) \\\\
+ & (1, 1, 5, 6, \underline{6}, \underline{6}, 3)
+\end{align}$$
-Define S(L) as ∑ C(n) for 1 ≤ n ≤ L. For example, S(50) mod 1 000 000 007 = 832833871.
+Therefore, $c = 3$ for (1, 1, 5, 6, 6, 6, 3).
-Find S(50 000 000) mod 1 000 000 007.
+Define $C(n)$ as the number of outcomes of throwing a 6-sided die $n$ times such that $c$ does not exceed $π(n)$.1
-1 π denotes the prime-counting function, i.e. π(n) is the number of primes ≤ n.
+For example, $C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$ and $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$.
+
+Define $S(L)$ as $\sum C(n)$ for $1 ≤ n ≤ L$.
+
+For example, $S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$.
+
+Find $S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+
+1 $π$ denotes the prime-counting function, i.e. $π(n)$ is the number of primes $≤ n$.
# --hints--
-`euler423()` should return 653972374.
+`consecutiveDieThrows()` should return `653972374`.
```js
-assert.strictEqual(euler423(), 653972374);
+assert.strictEqual(consecutiveDieThrows(), 653972374);
```
# --seed--
@@ -35,12 +47,12 @@ assert.strictEqual(euler423(), 653972374);
## --seed-contents--
```js
-function euler423() {
+function consecutiveDieThrows() {
return true;
}
-euler423();
+consecutiveDieThrows();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
index 827b969ce6..a8a4030906 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
@@ -8,43 +8,66 @@ dashedName: problem-424-kakuro
# --description--
+
+
+You are given that $P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$ and $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$.
+
+Find $P_n$ for $n = {11}^{14}$ in the following format: If $P_n = (\frac{a}{b}, \frac{c}{d})$ where the fractions are in lowest terms and the denominators are positive, then the answer is $(a + b + c + d)\bmod 1\\,000\\,000\\,007$.
+
+For $n = 7$, the answer would have been: $806\\,236\\,837$.
# --hints--
-`euler422()` should return 92060460.
+`sequenceOfPointsOnHyperbola()` should return `92060460`.
```js
-assert.strictEqual(euler422(), 92060460);
+assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
```
# --seed--
@@ -31,12 +39,12 @@ assert.strictEqual(euler422(), 92060460);
## --seed-contents--
```js
-function euler422() {
+function sequenceOfPointsOnHyperbola() {
return true;
}
-euler422();
+sequenceOfPointsOnHyperbola();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
index a19a5ce19d..d63900393e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
@@ -8,26 +8,38 @@ dashedName: problem-423-consecutive-die-throws
# --description--
-Let n be a positive integer.
+Let $n$ be a positive integer.
-A 6-sided die is thrown n times. Let c be the number of pairs of consecutive throws that give the same value.
+A 6-sided die is thrown $n$ times. Let $c$ be the number of pairs of consecutive throws that give the same value.
-For example, if n = 7 and the values of the die throws are (1,1,5,6,6,6,3), then the following pairs of consecutive throws give the same value: (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) Therefore, c = 3 for (1,1,5,6,6,6,3).
+For example, if $n = 7$ and the values of the die throws are (1, 1, 5, 6, 6, 6, 3), then the following pairs of consecutive throws give the same value:
-Define C(n) as the number of outcomes of throwing a 6-sided die n times such that c does not exceed π(n).1 For example, C(3) = 216, C(4) = 1290, C(11) = 361912500 and C(24) = 4727547363281250000.
+$$\begin{align}
+ & (\underline{1}, \underline{1}, 5, 6, 6, 6, 3) \\\\
+ & (1, 1, 5, \underline{6}, \underline{6}, 6, 3) \\\\
+ & (1, 1, 5, 6, \underline{6}, \underline{6}, 3)
+\end{align}$$
-Define S(L) as ∑ C(n) for 1 ≤ n ≤ L. For example, S(50) mod 1 000 000 007 = 832833871.
+Therefore, $c = 3$ for (1, 1, 5, 6, 6, 6, 3).
-Find S(50 000 000) mod 1 000 000 007.
+Define $C(n)$ as the number of outcomes of throwing a 6-sided die $n$ times such that $c$ does not exceed $π(n)$.1
-1 π denotes the prime-counting function, i.e. π(n) is the number of primes ≤ n.
+For example, $C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$ and $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$.
+
+Define $S(L)$ as $\sum C(n)$ for $1 ≤ n ≤ L$.
+
+For example, $S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$.
+
+Find $S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+
+1 $π$ denotes the prime-counting function, i.e. $π(n)$ is the number of primes $≤ n$.
# --hints--
-`euler423()` should return 653972374.
+`consecutiveDieThrows()` should return `653972374`.
```js
-assert.strictEqual(euler423(), 653972374);
+assert.strictEqual(consecutiveDieThrows(), 653972374);
```
# --seed--
@@ -35,12 +47,12 @@ assert.strictEqual(euler423(), 653972374);
## --seed-contents--
```js
-function euler423() {
+function consecutiveDieThrows() {
return true;
}
-euler423();
+consecutiveDieThrows();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
index 827b969ce6..a8a4030906 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
@@ -8,43 +8,66 @@ dashedName: problem-424-kakuro
# --description--
+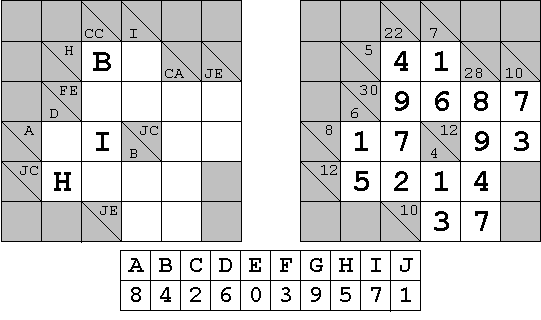 +
The above is an example of a cryptic kakuro (also known as cross sums, or even sums cross) puzzle, with its final solution on the right. (The common rules of kakuro puzzles can be found easily on numerous internet sites. Other related information can also be currently found at krazydad.com whose author has provided the puzzle data for this challenge.)
-The downloadable text file (kakuro200.txt) contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as follows:
+The `testPuzzles` array contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as string as follows:
-6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X
+`6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X`
The first character is a numerical digit indicating the size of the information grid. It would be either a 6 (for a 5x5 kakuro puzzle) or a 7 (for a 6x6 puzzle) followed by a comma (,). The extra top line and left column are needed to insert information.
-The content of each cell is then described and followed by a comma, going left to right and starting with the top line. X = Gray cell, not required to be filled by a digit. O (upper case letter)= White empty cell to be filled by a digit. A = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle. ( ) = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
+The content of each cell is then described and followed by a comma, going left to right and starting with the top line.
+
+`X` = Gray cell, not required to be filled by a digit.
+
+`O` (upper case letter)= White empty cell to be filled by a digit.
+
+`A` = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle.
+
+`( )` = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
The description of the last cell is followed by a Carriage Return/Line Feed (CRLF) instead of a comma.
The required answer to each puzzle is based on the value of each letter necessary to arrive at the solution and according to the alphabetical order. As indicated under the example puzzle, its answer would be 8426039571. At least 9 out of the 10 encrypting letters are always part of the problem description. When only 9 are given, the missing one must be assigned the remaining digit.
-You are given that the sum of the answers for the first 10 puzzles in the file is 64414157580.
+You are given that the sum of the answers for the first 10 puzzles in `testPuzzles` is 64414157580.
-Find the sum of the answers for the 200 puzzles.
+Find the sum of the answers for `puzzles` array.
# --hints--
-`euler424()` should return 1059760019628.
+`kakuro(testPuzzles)` should return `1059760019628`.
```js
-assert.strictEqual(euler424(), 1059760019628);
+assert.strictEqual(kakuro(_testPuzzles), 1059760019628);
```
# --seed--
+
+## --after-user-code--
+
+```js
+const _testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+```
+
## --seed-contents--
```js
-function euler424() {
+function kakuro(puzzles) {
return true;
}
-euler424();
+const testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+
+kakuro(testPuzzles);
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
index d46740b0d5..72f5393017 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
@@ -8,26 +8,29 @@ dashedName: problem-425-prime-connection
# --description--
-Two positive numbers A and B are said to be connected (denoted by "A ↔ B") if one of these conditions holds:
+Two positive numbers $A$ and $B$ are said to be connected (denoted by "$A ↔ B$") if one of these conditions holds:
-(1) A and B have the same length and differ in exactly one digit; for example, 123 ↔ 173.
+1. $A$ and $B$ have the same length and differ in exactly one digit; for example, $123 ↔ 173$.
+2. Adding one digit to the left of $A$ (or $B$) makes $B$ (or $A$); for example, $23 ↔ 223$ and $123 ↔ 23$.
-(2) Adding one digit to the left of A (or B) makes B (or A); for example, 23 ↔ 223 and 123 ↔ 23.
+We call a prime $P$ a 2's relative if there exists a chain of connected primes between 2 and $P$ and no prime in the chain exceeds $P$.
-We call a prime P a 2's relative if there exists a chain of connected primes between 2 and P and no prime in the chain exceeds P.
+For example, 127 is a 2's relative. One of the possible chains is shown below:
-For example, 127 is a 2's relative. One of the possible chains is shown below: 2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127 However, 11 and 103 are not 2's relatives.
+$$2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127$$
-Let F(N) be the sum of the primes ≤ N which are not 2's relatives. We can verify that F(103) = 431 and F(104) = 78728.
+However, 11 and 103 are not 2's relatives.
-Find F(107).
+Let $F(N)$ be the sum of the primes $≤ N$ which are not 2's relatives. We can verify that $F({10}^3) = 431$ and $F({10}^4) = 78\\,728$.
+
+Find $F({10}^7)$.
# --hints--
-`euler425()` should return 46479497324.
+`primeConnection()` should return `46479497324`.
```js
-assert.strictEqual(euler425(), 46479497324);
+assert.strictEqual(primeConnection(), 46479497324);
```
# --seed--
@@ -35,12 +38,12 @@ assert.strictEqual(euler425(), 46479497324);
## --seed-contents--
```js
-function euler425() {
+function primeConnection() {
return true;
}
-euler425();
+primeConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
index 5e2c48c34e..3f1e34d156 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
@@ -14,20 +14,34 @@ A turn consists of moving each ball exactly once according to the following rule
After one turn the sequence (2, 2, 2, 1, 2) becomes (2, 2, 1, 2, 3) as can be seen below; note that we begin the new sequence starting at the first occupied box.
+
+
The above is an example of a cryptic kakuro (also known as cross sums, or even sums cross) puzzle, with its final solution on the right. (The common rules of kakuro puzzles can be found easily on numerous internet sites. Other related information can also be currently found at krazydad.com whose author has provided the puzzle data for this challenge.)
-The downloadable text file (kakuro200.txt) contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as follows:
+The `testPuzzles` array contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as string as follows:
-6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X
+`6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X`
The first character is a numerical digit indicating the size of the information grid. It would be either a 6 (for a 5x5 kakuro puzzle) or a 7 (for a 6x6 puzzle) followed by a comma (,). The extra top line and left column are needed to insert information.
-The content of each cell is then described and followed by a comma, going left to right and starting with the top line. X = Gray cell, not required to be filled by a digit. O (upper case letter)= White empty cell to be filled by a digit. A = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle. ( ) = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
+The content of each cell is then described and followed by a comma, going left to right and starting with the top line.
+
+`X` = Gray cell, not required to be filled by a digit.
+
+`O` (upper case letter)= White empty cell to be filled by a digit.
+
+`A` = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle.
+
+`( )` = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
The description of the last cell is followed by a Carriage Return/Line Feed (CRLF) instead of a comma.
The required answer to each puzzle is based on the value of each letter necessary to arrive at the solution and according to the alphabetical order. As indicated under the example puzzle, its answer would be 8426039571. At least 9 out of the 10 encrypting letters are always part of the problem description. When only 9 are given, the missing one must be assigned the remaining digit.
-You are given that the sum of the answers for the first 10 puzzles in the file is 64414157580.
+You are given that the sum of the answers for the first 10 puzzles in `testPuzzles` is 64414157580.
-Find the sum of the answers for the 200 puzzles.
+Find the sum of the answers for `puzzles` array.
# --hints--
-`euler424()` should return 1059760019628.
+`kakuro(testPuzzles)` should return `1059760019628`.
```js
-assert.strictEqual(euler424(), 1059760019628);
+assert.strictEqual(kakuro(_testPuzzles), 1059760019628);
```
# --seed--
+
+## --after-user-code--
+
+```js
+const _testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+```
+
## --seed-contents--
```js
-function euler424() {
+function kakuro(puzzles) {
return true;
}
-euler424();
+const testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+
+kakuro(testPuzzles);
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
index d46740b0d5..72f5393017 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
@@ -8,26 +8,29 @@ dashedName: problem-425-prime-connection
# --description--
-Two positive numbers A and B are said to be connected (denoted by "A ↔ B") if one of these conditions holds:
+Two positive numbers $A$ and $B$ are said to be connected (denoted by "$A ↔ B$") if one of these conditions holds:
-(1) A and B have the same length and differ in exactly one digit; for example, 123 ↔ 173.
+1. $A$ and $B$ have the same length and differ in exactly one digit; for example, $123 ↔ 173$.
+2. Adding one digit to the left of $A$ (or $B$) makes $B$ (or $A$); for example, $23 ↔ 223$ and $123 ↔ 23$.
-(2) Adding one digit to the left of A (or B) makes B (or A); for example, 23 ↔ 223 and 123 ↔ 23.
+We call a prime $P$ a 2's relative if there exists a chain of connected primes between 2 and $P$ and no prime in the chain exceeds $P$.
-We call a prime P a 2's relative if there exists a chain of connected primes between 2 and P and no prime in the chain exceeds P.
+For example, 127 is a 2's relative. One of the possible chains is shown below:
-For example, 127 is a 2's relative. One of the possible chains is shown below: 2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127 However, 11 and 103 are not 2's relatives.
+$$2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127$$
-Let F(N) be the sum of the primes ≤ N which are not 2's relatives. We can verify that F(103) = 431 and F(104) = 78728.
+However, 11 and 103 are not 2's relatives.
-Find F(107).
+Let $F(N)$ be the sum of the primes $≤ N$ which are not 2's relatives. We can verify that $F({10}^3) = 431$ and $F({10}^4) = 78\\,728$.
+
+Find $F({10}^7)$.
# --hints--
-`euler425()` should return 46479497324.
+`primeConnection()` should return `46479497324`.
```js
-assert.strictEqual(euler425(), 46479497324);
+assert.strictEqual(primeConnection(), 46479497324);
```
# --seed--
@@ -35,12 +38,12 @@ assert.strictEqual(euler425(), 46479497324);
## --seed-contents--
```js
-function euler425() {
+function primeConnection() {
return true;
}
-euler425();
+primeConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
index 5e2c48c34e..3f1e34d156 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
@@ -14,20 +14,34 @@ A turn consists of moving each ball exactly once according to the following rule
After one turn the sequence (2, 2, 2, 1, 2) becomes (2, 2, 1, 2, 3) as can be seen below; note that we begin the new sequence starting at the first occupied box.
+ +
A system like this is called a Box-Ball System or BBS for short.
-It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to \[1, 2, 3]; we shall call this the final state.
+It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to [1, 2, 3]; we shall call this the final state.
-We define the sequence {ti}:s0 = 290797 sk+1 = sk2 mod 50515093 tk = (sk mod 64) + 1
+
+
A system like this is called a Box-Ball System or BBS for short.
-It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to \[1, 2, 3]; we shall call this the final state.
+It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to [1, 2, 3]; we shall call this the final state.
-We define the sequence {ti}:s0 = 290797 sk+1 = sk2 mod 50515093 tk = (sk mod 64) + 1
+![four turns from occupied boxes [2, 2, 2] to final state [1, 2, 3]](https://cdn.freecodecamp.org/curriculum/project-euler/box-ball-system-2.gif) -Starting from the initial configuration (t0, t1, …, t10), the final state becomes \[1, 3, 10, 24, 51, 75]. Starting from the initial configuration (t0, t1, …, t10 000 000), find the final state. Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is \[1, 2, 3] then 14 ( = 12 + 22 + 32) is your answer.
+We define the sequence $\\{t_i\\}$:
+
+$$\begin{align}
+ & s_0 = 290\\,797 \\\\
+ & s_{k + 1} = {s_k}^2\bmod 50\\,515\\,093 \\\\
+ & t_k = (s_k\bmod 64) + 1
+\end{align}$$
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10})$, the final state becomes [1, 3, 10, 24, 51, 75].
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10\\,000\\,000})$, find the final state.
+
+Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is [1, 2, 3] then $14 (= 1^2 + 2^2 + 3^2)$ is your answer.
# --hints--
-`euler426()` should return 31591886008.
+`boxBallSystem()` should return `31591886008`.
```js
-assert.strictEqual(euler426(), 31591886008);
+assert.strictEqual(boxBallSystem(), 31591886008);
```
# --seed--
@@ -35,12 +49,12 @@ assert.strictEqual(euler426(), 31591886008);
## --seed-contents--
```js
-function euler426() {
+function boxBallSystem() {
return true;
}
-euler426();
+boxBallSystem();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
index 8f399eeaf0..bc840f45c8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
@@ -8,24 +8,24 @@ dashedName: problem-427-n-sequences
# --description--
-A sequence of integers S = {si} is called an n-sequence if it has n elements and each element si satisfies 1 ≤ si ≤ n. Thus there are nn distinct n-sequences in total.
+A sequence of integers $S = \\{s_i\\}$ is called an $n$-sequence if it has $n$ elements and each element $s_i$ satisfies $1 ≤ s_i ≤ n$. Thus there are $n^n$ distinct $n$-sequences in total.
-For example, the sequence S = {1, 5, 5, 10, 7, 7, 7, 2, 3, 7} is a 10-sequence.
+For example, the sequence $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ is a 10-sequence.
-For any sequence S, let L(S) be the length of the longest contiguous subsequence of S with the same value. For example, for the given sequence S above, L(S) = 3, because of the three consecutive 7's.
+For any sequence $S$, let $L(S)$ be the length of the longest contiguous subsequence of $S$ with the same value. For example, for the given sequence $S$ above, $L(S) = 3$, because of the three consecutive 7's.
-Let f(n) = ∑ L(S) for all n-sequences S.
+Let $f(n) = \sum L(S)$ for all $n$-sequences $S$.
-For example, f(3) = 45, f(7) = 1403689 and f(11) = 481496895121.
+For example, $f(3) = 45$, $f(7) = 1\\,403\\,689$ and $f(11) = 481\\,496\\,895\\,121$.
-Find f(7 500 000) mod 1 000 000 009.
+Find $f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$.
# --hints--
-`euler427()` should return 97138867.
+`nSequences()` should return `97138867`.
```js
-assert.strictEqual(euler427(), 97138867);
+assert.strictEqual(nSequences(), 97138867);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler427(), 97138867);
## --seed-contents--
```js
-function euler427() {
+function nSequences() {
return true;
}
-euler427();
+nSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
index e3b2460e6d..30d46ed11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
@@ -8,27 +8,32 @@ dashedName: problem-428-necklace-of-circles
# --description--
-Let `a`, `b` and `c` be positive numbers.
+Let $a$, $b$ and $c$ be positive numbers.
-Let W, X, Y, Z be four collinear points where |WX| = `a`, |XY| = `b`, |YZ| = `c` and |WZ| = `a` + `b` + `c`.
+Let $W$, $X$, $Y$, $Z$ be four collinear points where $|WX| = a$, $|XY| = b$, $|YZ| = c$ and $|WZ| = a + b + c$.
-Let Cin be the circle having the diameter XY.
+Let $C_{\text{in}}$ be the circle having the diameter $XY$.
-Let Cout be the circle having the diameter WZ.
+Let $C_{\text{out}}$ be the circle having the diameter $WZ$.
-The triplet (`a`, `b`, `c`) is called a *necklace triplet* if you can place `k` ≥ 3 distinct circles C1, C2, ..., Ck such that:
+The triplet ($a$, $b$, $c$) is called a *necklace triplet* if you can place $k ≥ 3$ distinct circles $C_1, C_2, \ldots, C_k$ such that:
+
+- $C_i$ has no common interior points with any $C_j$ for $1 ≤ i$, $j ≤ k$ and $i ≠ j$,
+- $C_i$ is tangent to both $C_{\text{in}}$ and $C_{\text{out}}$ for $1 ≤ i ≤ k$,
+- $C_i$ is tangent to $C_{i + 1}$ for $1 ≤ i < k$, and
+- $C_k$ is tangent to $C_1$.
-
-Starting from the initial configuration (t0, t1, …, t10), the final state becomes \[1, 3, 10, 24, 51, 75]. Starting from the initial configuration (t0, t1, …, t10 000 000), find the final state. Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is \[1, 2, 3] then 14 ( = 12 + 22 + 32) is your answer.
+We define the sequence $\\{t_i\\}$:
+
+$$\begin{align}
+ & s_0 = 290\\,797 \\\\
+ & s_{k + 1} = {s_k}^2\bmod 50\\,515\\,093 \\\\
+ & t_k = (s_k\bmod 64) + 1
+\end{align}$$
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10})$, the final state becomes [1, 3, 10, 24, 51, 75].
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10\\,000\\,000})$, find the final state.
+
+Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is [1, 2, 3] then $14 (= 1^2 + 2^2 + 3^2)$ is your answer.
# --hints--
-`euler426()` should return 31591886008.
+`boxBallSystem()` should return `31591886008`.
```js
-assert.strictEqual(euler426(), 31591886008);
+assert.strictEqual(boxBallSystem(), 31591886008);
```
# --seed--
@@ -35,12 +49,12 @@ assert.strictEqual(euler426(), 31591886008);
## --seed-contents--
```js
-function euler426() {
+function boxBallSystem() {
return true;
}
-euler426();
+boxBallSystem();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
index 8f399eeaf0..bc840f45c8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
@@ -8,24 +8,24 @@ dashedName: problem-427-n-sequences
# --description--
-A sequence of integers S = {si} is called an n-sequence if it has n elements and each element si satisfies 1 ≤ si ≤ n. Thus there are nn distinct n-sequences in total.
+A sequence of integers $S = \\{s_i\\}$ is called an $n$-sequence if it has $n$ elements and each element $s_i$ satisfies $1 ≤ s_i ≤ n$. Thus there are $n^n$ distinct $n$-sequences in total.
-For example, the sequence S = {1, 5, 5, 10, 7, 7, 7, 2, 3, 7} is a 10-sequence.
+For example, the sequence $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ is a 10-sequence.
-For any sequence S, let L(S) be the length of the longest contiguous subsequence of S with the same value. For example, for the given sequence S above, L(S) = 3, because of the three consecutive 7's.
+For any sequence $S$, let $L(S)$ be the length of the longest contiguous subsequence of $S$ with the same value. For example, for the given sequence $S$ above, $L(S) = 3$, because of the three consecutive 7's.
-Let f(n) = ∑ L(S) for all n-sequences S.
+Let $f(n) = \sum L(S)$ for all $n$-sequences $S$.
-For example, f(3) = 45, f(7) = 1403689 and f(11) = 481496895121.
+For example, $f(3) = 45$, $f(7) = 1\\,403\\,689$ and $f(11) = 481\\,496\\,895\\,121$.
-Find f(7 500 000) mod 1 000 000 009.
+Find $f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$.
# --hints--
-`euler427()` should return 97138867.
+`nSequences()` should return `97138867`.
```js
-assert.strictEqual(euler427(), 97138867);
+assert.strictEqual(nSequences(), 97138867);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler427(), 97138867);
## --seed-contents--
```js
-function euler427() {
+function nSequences() {
return true;
}
-euler427();
+nSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
index e3b2460e6d..30d46ed11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
@@ -8,27 +8,32 @@ dashedName: problem-428-necklace-of-circles
# --description--
-Let `a`, `b` and `c` be positive numbers.
+Let $a$, $b$ and $c$ be positive numbers.
-Let W, X, Y, Z be four collinear points where |WX| = `a`, |XY| = `b`, |YZ| = `c` and |WZ| = `a` + `b` + `c`.
+Let $W$, $X$, $Y$, $Z$ be four collinear points where $|WX| = a$, $|XY| = b$, $|YZ| = c$ and $|WZ| = a + b + c$.
-Let Cin be the circle having the diameter XY.
+Let $C_{\text{in}}$ be the circle having the diameter $XY$.
-Let Cout be the circle having the diameter WZ.
+Let $C_{\text{out}}$ be the circle having the diameter $WZ$.
-The triplet (`a`, `b`, `c`) is called a *necklace triplet* if you can place `k` ≥ 3 distinct circles C1, C2, ..., Ck such that:
+The triplet ($a$, $b$, $c$) is called a *necklace triplet* if you can place $k ≥ 3$ distinct circles $C_1, C_2, \ldots, C_k$ such that:
+
+- $C_i$ has no common interior points with any $C_j$ for $1 ≤ i$, $j ≤ k$ and $i ≠ j$,
+- $C_i$ is tangent to both $C_{\text{in}}$ and $C_{\text{out}}$ for $1 ≤ i ≤ k$,
+- $C_i$ is tangent to $C_{i + 1}$ for $1 ≤ i < k$, and
+- $C_k$ is tangent to $C_1$.
-- Ci has no common interior points with any Cj for 1 ≤ i, j ≤ k and i ≠ j,
- Ci is tangent to both Cin and Cout for 1 ≤ i ≤ k,
- Ci is tangent to Ci+1 for 1 ≤ i < k, and
- Ck is tangent to C1.
For example, (5, 5, 5) and (4, 3, 21) are necklace triplets, while it can be shown that (2, 2, 5) is not.
- -Let T(`n`) be the number of necklace triplets (`a`, `b`, `c`) such that `a`, `b` and `c` are positive integers, and `b` ≤ `n`. For example, T(1) = 9, T(20) = 732 and T(3000) = 438106.
+
-Let T(`n`) be the number of necklace triplets (`a`, `b`, `c`) such that `a`, `b` and `c` are positive integers, and `b` ≤ `n`. For example, T(1) = 9, T(20) = 732 and T(3000) = 438106.
+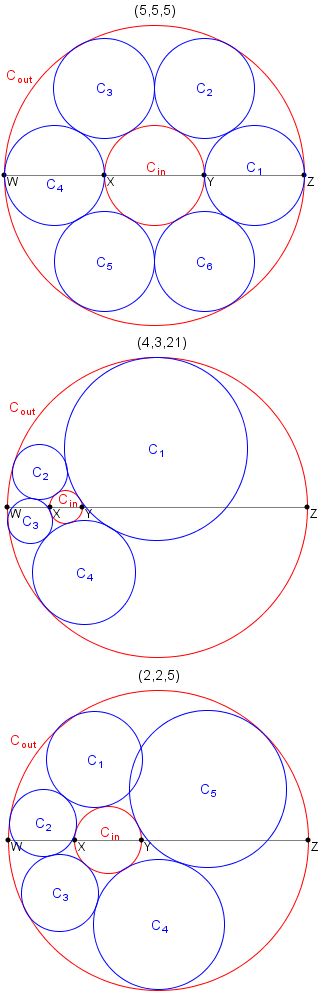 -Find T(1 000 000 000).
+Let $T(n)$ be the number of necklace triplets $(a, b, c)$ such that $a$, $b$ and $c$ are positive integers, and $b ≤ n$. For example, $T(1) = 9$, $T(20) = 732$ and $T(3\\,000) = 438\\,106$.
+
+Find $T(1\\,000\\,000\\,000)$.
# --hints--
-`necklace(1000000000)` should return 747215561862.
+`necklace(1000000000)` should return `747215561862`.
```js
assert.strictEqual(necklace(1000000000), 747215561862);
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
index 8b9c108829..8735e80e53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
@@ -8,22 +8,22 @@ dashedName: problem-429-sum-of-squares-of-unitary-divisors
# --description--
-A unitary divisor d of a number n is a divisor of n that has the property gcd(d, n/d) = 1.
+A unitary divisor $d$ of a number $n$ is a divisor of $n$ that has the property $gcd(d, \frac{n}{d}) = 1$.
-The unitary divisors of 4! = 24 are 1, 3, 8 and 24.
+The unitary divisors of $4! = 24$ are 1, 3, 8 and 24.
-The sum of their squares is 12 + 32 + 82 + 242 = 650.
+The sum of their squares is $12 + 32 + 82 + 242 = 650$.
-Let S(n) represent the sum of the squares of the unitary divisors of n. Thus S(4!)=650.
+Let $S(n)$ represent the sum of the squares of the unitary divisors of $n$. Thus $S(4!) = 650$.
-Find S(100 000 000!) modulo 1 000 000 009.
+Find $S(100\\,000\\,000!)$ modulo $1\\,000\\,000\\,009$.
# --hints--
-`euler429()` should return 98792821.
+`sumSquaresOfUnitaryDivisors()` should return `98792821`.
```js
-assert.strictEqual(euler429(), 98792821);
+assert.strictEqual(sumSquaresOfUnitaryDivisors(), 98792821);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler429(), 98792821);
## --seed-contents--
```js
-function euler429() {
+function sumSquaresOfUnitaryDivisors() {
return true;
}
-euler429();
+sumSquaresOfUnitaryDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
index ba66983c7b..ded4becfce 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
@@ -8,24 +8,26 @@ dashedName: problem-430-range-flips
# --description--
-N disks are placed in a row, indexed 1 to N from left to right.
+$N$ disks are placed in a row, indexed 1 to $N$ from left to right.
Each disk has a black side and white side. Initially all disks show their white side.
-At each turn, two, not necessarily distinct, integers A and B between 1 and N (inclusive) are chosen uniformly at random. All disks with an index from A to B (inclusive) are flipped.
+At each turn, two, not necessarily distinct, integers $A$ and $B$ between 1 and $N$ (inclusive) are chosen uniformly at random. All disks with an index from $A$ to $B$ (inclusive) are flipped.
-The following example shows the case N = 8. At the first turn A = 5 and B = 2, and at the second turn A = 4 and B = 6.
+The following example shows the case $N = 8$. At the first turn $A = 5$ and $B = 2$, and at the second turn $A = 4$ and $B = 6$.
-Let E(N, M) be the expected number of disks that show their white side after M turns. We can verify that E(3, 1) = 10/9, E(3, 2) = 5/3, E(10, 4) ≈ 5.157 and E(100, 10) ≈ 51.893.
+
-Find T(1 000 000 000).
+Let $T(n)$ be the number of necklace triplets $(a, b, c)$ such that $a$, $b$ and $c$ are positive integers, and $b ≤ n$. For example, $T(1) = 9$, $T(20) = 732$ and $T(3\\,000) = 438\\,106$.
+
+Find $T(1\\,000\\,000\\,000)$.
# --hints--
-`necklace(1000000000)` should return 747215561862.
+`necklace(1000000000)` should return `747215561862`.
```js
assert.strictEqual(necklace(1000000000), 747215561862);
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
index 8b9c108829..8735e80e53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
@@ -8,22 +8,22 @@ dashedName: problem-429-sum-of-squares-of-unitary-divisors
# --description--
-A unitary divisor d of a number n is a divisor of n that has the property gcd(d, n/d) = 1.
+A unitary divisor $d$ of a number $n$ is a divisor of $n$ that has the property $gcd(d, \frac{n}{d}) = 1$.
-The unitary divisors of 4! = 24 are 1, 3, 8 and 24.
+The unitary divisors of $4! = 24$ are 1, 3, 8 and 24.
-The sum of their squares is 12 + 32 + 82 + 242 = 650.
+The sum of their squares is $12 + 32 + 82 + 242 = 650$.
-Let S(n) represent the sum of the squares of the unitary divisors of n. Thus S(4!)=650.
+Let $S(n)$ represent the sum of the squares of the unitary divisors of $n$. Thus $S(4!) = 650$.
-Find S(100 000 000!) modulo 1 000 000 009.
+Find $S(100\\,000\\,000!)$ modulo $1\\,000\\,000\\,009$.
# --hints--
-`euler429()` should return 98792821.
+`sumSquaresOfUnitaryDivisors()` should return `98792821`.
```js
-assert.strictEqual(euler429(), 98792821);
+assert.strictEqual(sumSquaresOfUnitaryDivisors(), 98792821);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler429(), 98792821);
## --seed-contents--
```js
-function euler429() {
+function sumSquaresOfUnitaryDivisors() {
return true;
}
-euler429();
+sumSquaresOfUnitaryDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
index ba66983c7b..ded4becfce 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
@@ -8,24 +8,26 @@ dashedName: problem-430-range-flips
# --description--
-N disks are placed in a row, indexed 1 to N from left to right.
+$N$ disks are placed in a row, indexed 1 to $N$ from left to right.
Each disk has a black side and white side. Initially all disks show their white side.
-At each turn, two, not necessarily distinct, integers A and B between 1 and N (inclusive) are chosen uniformly at random. All disks with an index from A to B (inclusive) are flipped.
+At each turn, two, not necessarily distinct, integers $A$ and $B$ between 1 and $N$ (inclusive) are chosen uniformly at random. All disks with an index from $A$ to $B$ (inclusive) are flipped.
-The following example shows the case N = 8. At the first turn A = 5 and B = 2, and at the second turn A = 4 and B = 6.
+The following example shows the case $N = 8$. At the first turn $A = 5$ and $B = 2$, and at the second turn $A = 4$ and $B = 6$.
-Let E(N, M) be the expected number of disks that show their white side after M turns. We can verify that E(3, 1) = 10/9, E(3, 2) = 5/3, E(10, 4) ≈ 5.157 and E(100, 10) ≈ 51.893.
+ -Find E(1010, 4000). Give your answer rounded to 2 decimal places behind the decimal point.
+Let $E(N, M)$ be the expected number of disks that show their white side after $M$ turns. We can verify that $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$ and $E(100, 10) ≈ 51.893$.
+
+Find $E({10}^{10}, 4000)$. Give your answer rounded to 2 decimal places behind the decimal point.
# --hints--
-`euler430()` should return 5000624921.38.
+`rangeFlips()` should return `5000624921.38`.
```js
-assert.strictEqual(euler430(), 5000624921.38);
+assert.strictEqual(rangeFlips(), 5000624921.38);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler430(), 5000624921.38);
## --seed-contents--
```js
-function euler430() {
+function rangeFlips() {
return true;
}
-euler430();
+rangeFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
index 51a104b47a..96f109a2e8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
@@ -10,20 +10,22 @@ dashedName: problem-431-square-space-silo
Fred the farmer arranges to have a new storage silo installed on his farm and having an obsession for all things square he is absolutely devastated when he discovers that it is circular. Quentin, the representative from the company that installed the silo, explains that they only manufacture cylindrical silos, but he points out that it is resting on a square base. Fred is not amused and insists that it is removed from his property.
-Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\\alpha = 30$ degrees, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
+Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\alpha = 30°$, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
-We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114785284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114785284) \\approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511167869) \\approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
+
-Find E(1010, 4000). Give your answer rounded to 2 decimal places behind the decimal point.
+Let $E(N, M)$ be the expected number of disks that show their white side after $M$ turns. We can verify that $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$ and $E(100, 10) ≈ 51.893$.
+
+Find $E({10}^{10}, 4000)$. Give your answer rounded to 2 decimal places behind the decimal point.
# --hints--
-`euler430()` should return 5000624921.38.
+`rangeFlips()` should return `5000624921.38`.
```js
-assert.strictEqual(euler430(), 5000624921.38);
+assert.strictEqual(rangeFlips(), 5000624921.38);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler430(), 5000624921.38);
## --seed-contents--
```js
-function euler430() {
+function rangeFlips() {
return true;
}
-euler430();
+rangeFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
index 51a104b47a..96f109a2e8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
@@ -10,20 +10,22 @@ dashedName: problem-431-square-space-silo
Fred the farmer arranges to have a new storage silo installed on his farm and having an obsession for all things square he is absolutely devastated when he discovers that it is circular. Quentin, the representative from the company that installed the silo, explains that they only manufacture cylindrical silos, but he points out that it is resting on a square base. Fred is not amused and insists that it is removed from his property.
-Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\\alpha = 30$ degrees, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
+Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\alpha = 30°$, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
-We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114785284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114785284) \\approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511167869) \\approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
+ -Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40 degrees. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114\\,785\\,284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114\\,785\\,284) \approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511\\,167\\,869) \approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
-If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\\sum x$ correct to 9 decimal places.
+Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40°. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+
+If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\sum x$ correct to 9 decimal places.
# --hints--
-`euler431()` should return 23.386029052.
+`squareSpaceSilo()` should return `23.386029052`.
```js
-assert.strictEqual(euler431(), 23.386029052);
+assert.strictEqual(squareSpaceSilo(), 23.386029052);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler431(), 23.386029052);
## --seed-contents--
```js
-function euler431() {
+function squareSpaceSilo() {
return true;
}
-euler431();
+squareSpaceSilo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
index 4f0f5928ef..845ee38a53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
@@ -8,18 +8,18 @@ dashedName: problem-432-totient-sum
# --description--
-Let S(n,m) = ∑φ(n × i) for 1 ≤ i ≤ m. (φ is Euler's totient function)
+Let $S(n, m) = \sum φ(n × i)$ for $1 ≤ i ≤ m$. ($φ$ is Euler's totient function)
-You are given that S(510510,106 )= 45480596821125120.
+You are given that $S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$.
-Find S(510510,1011). Give the last 9 digits of your answer.
+Find $S(510\\,510, {10}^{11})$. Give the last 9 digits of your answer.
# --hints--
-`euler432()` should return 754862080.
+`totientSum()` should return `754862080`.
```js
-assert.strictEqual(euler432(), 754862080);
+assert.strictEqual(totientSum(), 754862080);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler432(), 754862080);
## --seed-contents--
```js
-function euler432() {
+function totientSum() {
return true;
}
-euler432();
+totientSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
index 5423c8691c..1999a6f26c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
@@ -8,22 +8,29 @@ dashedName: problem-433-steps-in-euclids-algorithm
# --description--
-Let E(x0, y0) be the number of steps it takes to determine the greatest common divisor of x0 and y0 with Euclid's algorithm. More formally:x1 = y0, y1 = x0 mod y0xn = yn-1, yn = xn-1 mod yn-1
+Let $E(x_0, y_0)$ be the number of steps it takes to determine the greatest common divisor of $x_0$ and $y_0$ with Euclid's algorithm. More formally:
-E(x0, y0) is the smallest n such that yn = 0.
+$$\begin{align}
+ & x_1 = y_0, y_1 = x_0\bmod y_0 \\\\
+ & x_n = y_{n - 1}, y_n = x_{n - 1}\bmod y_{n - 1}
+\end{align}$$
-We have E(1,1) = 1, E(10,6) = 3 and E(6,10) = 4.
+$E(x_0, y_0)$ is the smallest $n$ such that $y_n = 0$.
-Define S(N) as the sum of E(x,y) for 1 ≤ x,y ≤ N. We have S(1) = 1, S(10) = 221 and S(100) = 39826.
+We have $E(1, 1) = 1$, $E(10, 6) = 3$ and $E(6, 10) = 4$.
-Find S(5·106).
+Define $S(N)$ as the sum of $E(x, y)$ for $1 ≤ x$, $y ≤ N$.
+
+We have $S(1) = 1$, $S(10) = 221$ and $S(100) = 39\\,826$.
+
+Find $S(5 \times {10}^6)$.
# --hints--
-`euler433()` should return 326624372659664.
+`stepsInEuclidsAlgorithm()` should return `326624372659664`.
```js
-assert.strictEqual(euler433(), 326624372659664);
+assert.strictEqual(stepsInEuclidsAlgorithm(), 326624372659664);
```
# --seed--
@@ -31,12 +38,12 @@ assert.strictEqual(euler433(), 326624372659664);
## --seed-contents--
```js
-function euler433() {
+function stepsInEuclidsAlgorithm() {
return true;
}
-euler433();
+stepsInEuclidsAlgorithm();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
index 48a01b7a3b..a598aebb10 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
@@ -18,18 +18,32 @@ A rigid graph is an embedding of a graph which is not flexible.
Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
-The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates: However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid: Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
-Let R(m,n) be the number of ways to make the m × n grid graph rigid. E.g. R(2,3) = 19 and R(5,5) = 23679901
+
-Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40 degrees. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114\\,785\\,284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114\\,785\\,284) \approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511\\,167\\,869) \approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
-If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\\sum x$ correct to 9 decimal places.
+Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40°. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+
+If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\sum x$ correct to 9 decimal places.
# --hints--
-`euler431()` should return 23.386029052.
+`squareSpaceSilo()` should return `23.386029052`.
```js
-assert.strictEqual(euler431(), 23.386029052);
+assert.strictEqual(squareSpaceSilo(), 23.386029052);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler431(), 23.386029052);
## --seed-contents--
```js
-function euler431() {
+function squareSpaceSilo() {
return true;
}
-euler431();
+squareSpaceSilo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
index 4f0f5928ef..845ee38a53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
@@ -8,18 +8,18 @@ dashedName: problem-432-totient-sum
# --description--
-Let S(n,m) = ∑φ(n × i) for 1 ≤ i ≤ m. (φ is Euler's totient function)
+Let $S(n, m) = \sum φ(n × i)$ for $1 ≤ i ≤ m$. ($φ$ is Euler's totient function)
-You are given that S(510510,106 )= 45480596821125120.
+You are given that $S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$.
-Find S(510510,1011). Give the last 9 digits of your answer.
+Find $S(510\\,510, {10}^{11})$. Give the last 9 digits of your answer.
# --hints--
-`euler432()` should return 754862080.
+`totientSum()` should return `754862080`.
```js
-assert.strictEqual(euler432(), 754862080);
+assert.strictEqual(totientSum(), 754862080);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler432(), 754862080);
## --seed-contents--
```js
-function euler432() {
+function totientSum() {
return true;
}
-euler432();
+totientSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
index 5423c8691c..1999a6f26c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
@@ -8,22 +8,29 @@ dashedName: problem-433-steps-in-euclids-algorithm
# --description--
-Let E(x0, y0) be the number of steps it takes to determine the greatest common divisor of x0 and y0 with Euclid's algorithm. More formally:x1 = y0, y1 = x0 mod y0xn = yn-1, yn = xn-1 mod yn-1
+Let $E(x_0, y_0)$ be the number of steps it takes to determine the greatest common divisor of $x_0$ and $y_0$ with Euclid's algorithm. More formally:
-E(x0, y0) is the smallest n such that yn = 0.
+$$\begin{align}
+ & x_1 = y_0, y_1 = x_0\bmod y_0 \\\\
+ & x_n = y_{n - 1}, y_n = x_{n - 1}\bmod y_{n - 1}
+\end{align}$$
-We have E(1,1) = 1, E(10,6) = 3 and E(6,10) = 4.
+$E(x_0, y_0)$ is the smallest $n$ such that $y_n = 0$.
-Define S(N) as the sum of E(x,y) for 1 ≤ x,y ≤ N. We have S(1) = 1, S(10) = 221 and S(100) = 39826.
+We have $E(1, 1) = 1$, $E(10, 6) = 3$ and $E(6, 10) = 4$.
-Find S(5·106).
+Define $S(N)$ as the sum of $E(x, y)$ for $1 ≤ x$, $y ≤ N$.
+
+We have $S(1) = 1$, $S(10) = 221$ and $S(100) = 39\\,826$.
+
+Find $S(5 \times {10}^6)$.
# --hints--
-`euler433()` should return 326624372659664.
+`stepsInEuclidsAlgorithm()` should return `326624372659664`.
```js
-assert.strictEqual(euler433(), 326624372659664);
+assert.strictEqual(stepsInEuclidsAlgorithm(), 326624372659664);
```
# --seed--
@@ -31,12 +38,12 @@ assert.strictEqual(euler433(), 326624372659664);
## --seed-contents--
```js
-function euler433() {
+function stepsInEuclidsAlgorithm() {
return true;
}
-euler433();
+stepsInEuclidsAlgorithm();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
index 48a01b7a3b..a598aebb10 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
@@ -18,18 +18,32 @@ A rigid graph is an embedding of a graph which is not flexible.
Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
-The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates: However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid: Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
-Let R(m,n) be the number of ways to make the m × n grid graph rigid. E.g. R(2,3) = 19 and R(5,5) = 23679901
+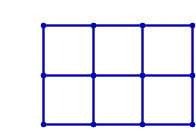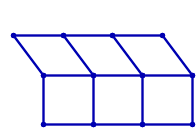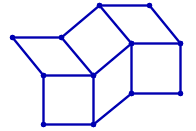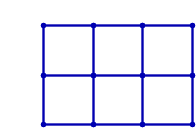 -Define S(N) as ∑R(i,j) for 1 ≤ i, j ≤ N. E.g. S(5) = 25021721. Find S(100), give your answer modulo 1000000033
+However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid:
+
+
-Define S(N) as ∑R(i,j) for 1 ≤ i, j ≤ N. E.g. S(5) = 25021721. Find S(100), give your answer modulo 1000000033
+However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid:
+
+ +
+Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+
+Let $R(m, n)$ be the number of ways to make the $m × n$ grid graph rigid.
+
+E.g. $R(2, 3) = 19$ and $R(5, 5) = 23\\,679\\,901$.
+
+Define $S(N)$ as $\sum R(i, j)$ for $1 ≤ i$, $j ≤ N$.
+
+E.g. $S(5) = 25\\,021\\,721$.
+
+Find $S(100)$, give your answer modulo $1\\,000\\,000\\,033$.
# --hints--
-`euler434()` should return 863253606.
+`rigidGraphs()` should return `863253606`.
```js
-assert.strictEqual(euler434(), 863253606);
+assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
@@ -37,12 +51,12 @@ assert.strictEqual(euler434(), 863253606);
## --seed-contents--
```js
-function euler434() {
+function rigidGraphs() {
return true;
}
-euler434();
+rigidGraphs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
index ee078a7382..9be0b43a51 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
@@ -8,20 +8,20 @@ dashedName: problem-435-polynomials-of-fibonacci-numbers
# --description--
-The Fibonacci numbers {fn, n ≥ 0} are defined recursively as fn = fn-1 + fn-2 with base cases f0 = 0 and f1 = 1.
+The Fibonacci numbers $\\{f_n, n ≥ 0\\}$ are defined recursively as $f_n = f_{n - 1} + f_{n - 2}$ with base cases $f_0 = 0$ and $f_1 = 1$.
-Define the polynomials {Fn, n ≥ 0} as Fn(x) = ∑fixi for 0 ≤ i ≤ n.
+Define the polynomials $\\{F_n, n ≥ 0\\}$ as $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$.
-For example, F7(x) = x + x2 + 2x3 + 3x4 + 5x5 + 8x6 + 13x7, and F7(11) = 268357683.
+For example, $F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, and $F_7(11) = 268\\,357\\,683$.
-Let n = 1015. Find the sum \[∑0≤x≤100 Fn(x)] mod 1307674368000 (= 15!).
+Let $n = {10}^{15}$. Find the sum $\displaystyle\sum_{x = 0}^{100} F_n(x)$ and give your answer modulo $1\\,307\\,674\\,368\\,000 \\, (= 15!)$.
# --hints--
-`euler435()` should return 252541322550.
+`polynomialsOfFibonacciNumbers()` should return `252541322550`.
```js
-assert.strictEqual(euler435(), 252541322550);
+assert.strictEqual(polynomialsOfFibonacciNumbers(), 252541322550);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler435(), 252541322550);
## --seed-contents--
```js
-function euler435() {
+function polynomialsOfFibonacciNumbers() {
return true;
}
-euler435();
+polynomialsOfFibonacciNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
index 43b111b868..d5dfcc5920 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
@@ -14,24 +14,26 @@ She suggests they play a game of chance to determine who will wash the dishes.
For this game, they shall use a generator of independent random numbers uniformly distributed between 0 and 1.
-The game starts with S = 0.
+The game starts with $S = 0$.
-The first player, Louise, adds to S different random numbers from the generator until S > 1 and records her last random number 'x'.
+The first player, Louise, adds to $S$ different random numbers from the generator until $S > 1$ and records her last random number '$x$'.
-The second player, Julie, continues adding to S different random numbers from the generator until S > 2 and records her last random number 'y'.
+The second player, Julie, continues adding to $S$ different random numbers from the generator until $S > 2$ and records her last random number '$y$'.
-The player with the highest number wins and the loser washes the dishes, i.e. if y > x the second player wins.
+The player with the highest number wins and the loser washes the dishes, i.e. if $y > x$ the second player wins.
-For example, if the first player draws 0.62 and 0.44, the first player turn ends since 0.62+0.44 > 1 and x = 0.44. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since 0.62+0.44+0.1+0.27+0.91 > 2 and y = 0.91. Since y > x, the second player wins.
+For example, if the first player draws 0.62 and 0.44, the first player turn ends since $0.62 + 0.44 > 1$ and $x = 0.44$. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since $0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ and $y = 0.91$. Since $y > x$, the second player wins.
-Louise thinks about it for a second, and objects: "That's not fair". What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
+Louise thinks about it for a second, and objects: "That's not fair".
+
+What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
# --hints--
-`euler436()` should return 0.5276662759.
+`unfairWager()` should return `0.5276662759`.
```js
-assert.strictEqual(euler436(), 0.5276662759);
+assert.strictEqual(unfairWager(), 0.5276662759);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler436(), 0.5276662759);
## --seed-contents--
```js
-function euler436() {
+function unfairWager() {
return true;
}
-euler436();
+unfairWager();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
index 0072d0f9a9..8a109549c1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
@@ -8,7 +8,7 @@ dashedName: problem-437-fibonacci-primitive-roots
# --description--
-When we calculate 8n modulo 11 for n=0 to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
+When we calculate $8^n$ modulo 11 for $n = 0$ to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
As we see all possible values from 1 to 10 occur. So 8 is a primitive root of 11.
@@ -16,32 +16,30 @@ But there is more:
If we take a closer look we see:
-1+8=9
+$$\begin{align}
+ & 1 + 8 = 9 \\\\
+ & 8 + 9 = 17 ≡ 6\bmod 11 \\\\
+ & 9 + 6 = 15 ≡ 4\bmod 11 \\\\
+ & 6 + 4 = 10 \\\\
+ & 4 + 10 = 14 ≡ 3\bmod 11 \\\\
+ & 10 + 3 = 13 ≡ 2\bmod 11 \\\\
+ & 3 + 2 = 5 \\\\
+ & 2 + 5 = 7 \\\\
+ & 5 + 7 = 12 ≡ 1\bmod 11.
+\end{align}$$
-8+9=17≡6 mod 11
+So the powers of 8 mod 11 are cyclic with period 10, and $8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$. 8 is called a Fibonacci primitive root of 11.
-9+6=15≡4 mod 11
+Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491.
-6+4=10
-
-4+10=14≡3 mod 11
-
-10+3=13≡2 mod 11
-
-3+2=5
-
-2+5=7
-
-5+7=12≡1 mod 11.
-
-So the powers of 8 mod 11 are cyclic with period 10, and 8n + 8n+1 ≡ 8n+2 (mod 11). 8 is called a Fibonacci primitive root of 11. Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491. Find the sum of the primes less than 100,000,000 with at least one Fibonacci primitive root.
+Find the sum of the primes less than $100\\,000\\,000$ with at least one Fibonacci primitive root.
# --hints--
-`euler437()` should return 74204709657207.
+`fibonacciPrimitiveRoots()` should return `74204709657207`.
```js
-assert.strictEqual(euler437(), 74204709657207);
+assert.strictEqual(fibonacciPrimitiveRoots(), 74204709657207);
```
# --seed--
@@ -49,12 +47,12 @@ assert.strictEqual(euler437(), 74204709657207);
## --seed-contents--
```js
-function euler437() {
+function fibonacciPrimitiveRoots() {
return true;
}
-euler437();
+fibonacciPrimitiveRoots();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
index 112326a2fa..e247069b3d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
@@ -8,20 +8,27 @@ dashedName: problem-438-integer-part-of-polynomial-equations-solutions
# --description--
-For an n-tuple of integers t = (a1, ..., an), let (x1, ..., xn) be the solutions of the polynomial equation xn + a1xn-1 + a2xn-2 + ... + an-1x + an = 0.
+For an $n$-tuple of integers $t = (a_1, \ldots, a_n)$, let $(x_1, \ldots, x_n)$ be the solutions of the polynomial equation $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$.
-Consider the following two conditions: x1, ..., xn are all real. If x1, ..., xn are sorted, ⌊xi⌋ = i for 1 ≤ i ≤ n. (⌊·⌋: floor function.)
+Consider the following two conditions:
-In the case of n = 4, there are 12 n-tuples of integers which satisfy both conditions. We define S(t) as the sum of the absolute values of the integers in t. For n = 4 we can verify that ∑S(t) = 2087 for all n-tuples t which satisfy both conditions.
+- $x_1, \ldots, x_n$ are all real.
+- If $x_1, ..., x_n$ are sorted, $⌊x_i⌋ = i$ for $1 ≤ i ≤ n$. ($⌊·⌋:$ floor function.)
-Find ∑S(t) for n = 7.
+In the case of $n = 4$, there are 12 $n$-tuples of integers which satisfy both conditions.
+
+We define $S(t)$ as the sum of the absolute values of the integers in $t$.
+
+For $n = 4$ we can verify that $\sum S(t) = 2087$ for all $n$-tuples t which satisfy both conditions.
+
+Find $\sum S(t)$ for $n = 7$.
# --hints--
-`euler438()` should return 2046409616809.
+`polynomialIntegerPart()` should return `2046409616809`.
```js
-assert.strictEqual(euler438(), 2046409616809);
+assert.strictEqual(polynomialIntegerPart(), 2046409616809);
```
# --seed--
@@ -29,12 +36,12 @@ assert.strictEqual(euler438(), 2046409616809);
## --seed-contents--
```js
-function euler438() {
+function polynomialIntegerPart() {
return true;
}
-euler438();
+polynomialIntegerPart();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
index 4fb1871a85..264dfaf572 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
@@ -8,20 +8,22 @@ dashedName: problem-439-sum-of-sum-of-divisors
# --description--
-Let d(k) be the sum of all divisors of k.
+Let $d(k)$ be the sum of all divisors of $k$.
-We define the function S(N) = ∑1≤i≤N ∑1≤j≤Nd(i·j).
+We define the function $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$.
-For example, S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59.
+For example, $S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$.
-You are given that S(103) = 563576517282 and S(105) mod 109 = 215766508. Find S(1011) mod 109.
+You are given that $S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$.
+
+Find $S({10}^{11})\bmod {10}^9$.
# --hints--
-`euler439()` should return 968697378.
+`sumOfSumOfDivisors()` should return `968697378`.
```js
-assert.strictEqual(euler439(), 968697378);
+assert.strictEqual(sumOfSumOfDivisors(), 968697378);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler439(), 968697378);
## --seed-contents--
```js
-function euler439() {
+function sumOfSumOfDivisors() {
return true;
}
-euler439();
+sumOfSumOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
index a68f99a00a..21d7100bbd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
@@ -8,24 +8,36 @@ dashedName: problem-440-gcd-and-tiling
# --description--
-We want to tile a board of length n and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
+We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
-For example, here are some of the ways to tile a board of length n = 8:
+
+
+Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+
+Let $R(m, n)$ be the number of ways to make the $m × n$ grid graph rigid.
+
+E.g. $R(2, 3) = 19$ and $R(5, 5) = 23\\,679\\,901$.
+
+Define $S(N)$ as $\sum R(i, j)$ for $1 ≤ i$, $j ≤ N$.
+
+E.g. $S(5) = 25\\,021\\,721$.
+
+Find $S(100)$, give your answer modulo $1\\,000\\,000\\,033$.
# --hints--
-`euler434()` should return 863253606.
+`rigidGraphs()` should return `863253606`.
```js
-assert.strictEqual(euler434(), 863253606);
+assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
@@ -37,12 +51,12 @@ assert.strictEqual(euler434(), 863253606);
## --seed-contents--
```js
-function euler434() {
+function rigidGraphs() {
return true;
}
-euler434();
+rigidGraphs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
index ee078a7382..9be0b43a51 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
@@ -8,20 +8,20 @@ dashedName: problem-435-polynomials-of-fibonacci-numbers
# --description--
-The Fibonacci numbers {fn, n ≥ 0} are defined recursively as fn = fn-1 + fn-2 with base cases f0 = 0 and f1 = 1.
+The Fibonacci numbers $\\{f_n, n ≥ 0\\}$ are defined recursively as $f_n = f_{n - 1} + f_{n - 2}$ with base cases $f_0 = 0$ and $f_1 = 1$.
-Define the polynomials {Fn, n ≥ 0} as Fn(x) = ∑fixi for 0 ≤ i ≤ n.
+Define the polynomials $\\{F_n, n ≥ 0\\}$ as $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$.
-For example, F7(x) = x + x2 + 2x3 + 3x4 + 5x5 + 8x6 + 13x7, and F7(11) = 268357683.
+For example, $F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, and $F_7(11) = 268\\,357\\,683$.
-Let n = 1015. Find the sum \[∑0≤x≤100 Fn(x)] mod 1307674368000 (= 15!).
+Let $n = {10}^{15}$. Find the sum $\displaystyle\sum_{x = 0}^{100} F_n(x)$ and give your answer modulo $1\\,307\\,674\\,368\\,000 \\, (= 15!)$.
# --hints--
-`euler435()` should return 252541322550.
+`polynomialsOfFibonacciNumbers()` should return `252541322550`.
```js
-assert.strictEqual(euler435(), 252541322550);
+assert.strictEqual(polynomialsOfFibonacciNumbers(), 252541322550);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler435(), 252541322550);
## --seed-contents--
```js
-function euler435() {
+function polynomialsOfFibonacciNumbers() {
return true;
}
-euler435();
+polynomialsOfFibonacciNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
index 43b111b868..d5dfcc5920 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
@@ -14,24 +14,26 @@ She suggests they play a game of chance to determine who will wash the dishes.
For this game, they shall use a generator of independent random numbers uniformly distributed between 0 and 1.
-The game starts with S = 0.
+The game starts with $S = 0$.
-The first player, Louise, adds to S different random numbers from the generator until S > 1 and records her last random number 'x'.
+The first player, Louise, adds to $S$ different random numbers from the generator until $S > 1$ and records her last random number '$x$'.
-The second player, Julie, continues adding to S different random numbers from the generator until S > 2 and records her last random number 'y'.
+The second player, Julie, continues adding to $S$ different random numbers from the generator until $S > 2$ and records her last random number '$y$'.
-The player with the highest number wins and the loser washes the dishes, i.e. if y > x the second player wins.
+The player with the highest number wins and the loser washes the dishes, i.e. if $y > x$ the second player wins.
-For example, if the first player draws 0.62 and 0.44, the first player turn ends since 0.62+0.44 > 1 and x = 0.44. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since 0.62+0.44+0.1+0.27+0.91 > 2 and y = 0.91. Since y > x, the second player wins.
+For example, if the first player draws 0.62 and 0.44, the first player turn ends since $0.62 + 0.44 > 1$ and $x = 0.44$. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since $0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ and $y = 0.91$. Since $y > x$, the second player wins.
-Louise thinks about it for a second, and objects: "That's not fair". What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
+Louise thinks about it for a second, and objects: "That's not fair".
+
+What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
# --hints--
-`euler436()` should return 0.5276662759.
+`unfairWager()` should return `0.5276662759`.
```js
-assert.strictEqual(euler436(), 0.5276662759);
+assert.strictEqual(unfairWager(), 0.5276662759);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler436(), 0.5276662759);
## --seed-contents--
```js
-function euler436() {
+function unfairWager() {
return true;
}
-euler436();
+unfairWager();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
index 0072d0f9a9..8a109549c1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
@@ -8,7 +8,7 @@ dashedName: problem-437-fibonacci-primitive-roots
# --description--
-When we calculate 8n modulo 11 for n=0 to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
+When we calculate $8^n$ modulo 11 for $n = 0$ to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
As we see all possible values from 1 to 10 occur. So 8 is a primitive root of 11.
@@ -16,32 +16,30 @@ But there is more:
If we take a closer look we see:
-1+8=9
+$$\begin{align}
+ & 1 + 8 = 9 \\\\
+ & 8 + 9 = 17 ≡ 6\bmod 11 \\\\
+ & 9 + 6 = 15 ≡ 4\bmod 11 \\\\
+ & 6 + 4 = 10 \\\\
+ & 4 + 10 = 14 ≡ 3\bmod 11 \\\\
+ & 10 + 3 = 13 ≡ 2\bmod 11 \\\\
+ & 3 + 2 = 5 \\\\
+ & 2 + 5 = 7 \\\\
+ & 5 + 7 = 12 ≡ 1\bmod 11.
+\end{align}$$
-8+9=17≡6 mod 11
+So the powers of 8 mod 11 are cyclic with period 10, and $8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$. 8 is called a Fibonacci primitive root of 11.
-9+6=15≡4 mod 11
+Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491.
-6+4=10
-
-4+10=14≡3 mod 11
-
-10+3=13≡2 mod 11
-
-3+2=5
-
-2+5=7
-
-5+7=12≡1 mod 11.
-
-So the powers of 8 mod 11 are cyclic with period 10, and 8n + 8n+1 ≡ 8n+2 (mod 11). 8 is called a Fibonacci primitive root of 11. Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491. Find the sum of the primes less than 100,000,000 with at least one Fibonacci primitive root.
+Find the sum of the primes less than $100\\,000\\,000$ with at least one Fibonacci primitive root.
# --hints--
-`euler437()` should return 74204709657207.
+`fibonacciPrimitiveRoots()` should return `74204709657207`.
```js
-assert.strictEqual(euler437(), 74204709657207);
+assert.strictEqual(fibonacciPrimitiveRoots(), 74204709657207);
```
# --seed--
@@ -49,12 +47,12 @@ assert.strictEqual(euler437(), 74204709657207);
## --seed-contents--
```js
-function euler437() {
+function fibonacciPrimitiveRoots() {
return true;
}
-euler437();
+fibonacciPrimitiveRoots();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
index 112326a2fa..e247069b3d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
@@ -8,20 +8,27 @@ dashedName: problem-438-integer-part-of-polynomial-equations-solutions
# --description--
-For an n-tuple of integers t = (a1, ..., an), let (x1, ..., xn) be the solutions of the polynomial equation xn + a1xn-1 + a2xn-2 + ... + an-1x + an = 0.
+For an $n$-tuple of integers $t = (a_1, \ldots, a_n)$, let $(x_1, \ldots, x_n)$ be the solutions of the polynomial equation $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$.
-Consider the following two conditions: x1, ..., xn are all real. If x1, ..., xn are sorted, ⌊xi⌋ = i for 1 ≤ i ≤ n. (⌊·⌋: floor function.)
+Consider the following two conditions:
-In the case of n = 4, there are 12 n-tuples of integers which satisfy both conditions. We define S(t) as the sum of the absolute values of the integers in t. For n = 4 we can verify that ∑S(t) = 2087 for all n-tuples t which satisfy both conditions.
+- $x_1, \ldots, x_n$ are all real.
+- If $x_1, ..., x_n$ are sorted, $⌊x_i⌋ = i$ for $1 ≤ i ≤ n$. ($⌊·⌋:$ floor function.)
-Find ∑S(t) for n = 7.
+In the case of $n = 4$, there are 12 $n$-tuples of integers which satisfy both conditions.
+
+We define $S(t)$ as the sum of the absolute values of the integers in $t$.
+
+For $n = 4$ we can verify that $\sum S(t) = 2087$ for all $n$-tuples t which satisfy both conditions.
+
+Find $\sum S(t)$ for $n = 7$.
# --hints--
-`euler438()` should return 2046409616809.
+`polynomialIntegerPart()` should return `2046409616809`.
```js
-assert.strictEqual(euler438(), 2046409616809);
+assert.strictEqual(polynomialIntegerPart(), 2046409616809);
```
# --seed--
@@ -29,12 +36,12 @@ assert.strictEqual(euler438(), 2046409616809);
## --seed-contents--
```js
-function euler438() {
+function polynomialIntegerPart() {
return true;
}
-euler438();
+polynomialIntegerPart();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
index 4fb1871a85..264dfaf572 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
@@ -8,20 +8,22 @@ dashedName: problem-439-sum-of-sum-of-divisors
# --description--
-Let d(k) be the sum of all divisors of k.
+Let $d(k)$ be the sum of all divisors of $k$.
-We define the function S(N) = ∑1≤i≤N ∑1≤j≤Nd(i·j).
+We define the function $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$.
-For example, S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59.
+For example, $S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$.
-You are given that S(103) = 563576517282 and S(105) mod 109 = 215766508. Find S(1011) mod 109.
+You are given that $S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$.
+
+Find $S({10}^{11})\bmod {10}^9$.
# --hints--
-`euler439()` should return 968697378.
+`sumOfSumOfDivisors()` should return `968697378`.
```js
-assert.strictEqual(euler439(), 968697378);
+assert.strictEqual(sumOfSumOfDivisors(), 968697378);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler439(), 968697378);
## --seed-contents--
```js
-function euler439() {
+function sumOfSumOfDivisors() {
return true;
}
-euler439();
+sumOfSumOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
index a68f99a00a..21d7100bbd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
@@ -8,24 +8,36 @@ dashedName: problem-440-gcd-and-tiling
# --description--
-We want to tile a board of length n and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
+We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
-For example, here are some of the ways to tile a board of length n = 8:
+ -Let T(n) be the number of ways to tile a board of length n as described above.
+For example, here are some of the ways to tile a board of length $n = 8$:
-For example, T(1) = 10 and T(2) = 101.
+
-Let T(n) be the number of ways to tile a board of length n as described above.
+For example, here are some of the ways to tile a board of length $n = 8$:
-For example, T(1) = 10 and T(2) = 101.
+ -Let S(L) be the triple sum ∑a,b,c gcd(T(ca), T(cb)) for 1 ≤ a, b, c ≤ L. For example: S(2) = 10444 S(3) = 1292115238446807016106539989 S(4) mod 987 898 789 = 670616280.
+Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
-Find S(2000) mod 987 898 789.
+For example, $T(1) = 10$ and $T(2) = 101$.
+
+Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
+
+For example:
+
+$$\begin{align}
+ & S(2) = 10\\,444 \\\\
+ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
+ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
+\end{align}$$
+
+Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
-`euler440()` should return 970746056.
+`gcdAndTiling()` should return `970746056`.
```js
-assert.strictEqual(euler440(), 970746056);
+assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
@@ -33,12 +45,12 @@ assert.strictEqual(euler440(), 970746056);
## --seed-contents--
```js
-function euler440() {
+function gcdAndTiling() {
return true;
}
-euler440();
+gcdAndTiling();
```
# --solutions--
-Let S(L) be the triple sum ∑a,b,c gcd(T(ca), T(cb)) for 1 ≤ a, b, c ≤ L. For example: S(2) = 10444 S(3) = 1292115238446807016106539989 S(4) mod 987 898 789 = 670616280.
+Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
-Find S(2000) mod 987 898 789.
+For example, $T(1) = 10$ and $T(2) = 101$.
+
+Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
+
+For example:
+
+$$\begin{align}
+ & S(2) = 10\\,444 \\\\
+ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
+ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
+\end{align}$$
+
+Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
-`euler440()` should return 970746056.
+`gcdAndTiling()` should return `970746056`.
```js
-assert.strictEqual(euler440(), 970746056);
+assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
@@ -33,12 +45,12 @@ assert.strictEqual(euler440(), 970746056);
## --seed-contents--
```js
-function euler440() {
+function gcdAndTiling() {
return true;
}
-euler440();
+gcdAndTiling();
```
# --solutions--
 +
+You are given that $P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$ and $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$.
+
+Find $P_n$ for $n = {11}^{14}$ in the following format: If $P_n = (\frac{a}{b}, \frac{c}{d})$ where the fractions are in lowest terms and the denominators are positive, then the answer is $(a + b + c + d)\bmod 1\\,000\\,000\\,007$.
+
+For $n = 7$, the answer would have been: $806\\,236\\,837$.
# --hints--
-`euler422()` should return 92060460.
+`sequenceOfPointsOnHyperbola()` should return `92060460`.
```js
-assert.strictEqual(euler422(), 92060460);
+assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
```
# --seed--
@@ -31,12 +39,12 @@ assert.strictEqual(euler422(), 92060460);
## --seed-contents--
```js
-function euler422() {
+function sequenceOfPointsOnHyperbola() {
return true;
}
-euler422();
+sequenceOfPointsOnHyperbola();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
index a19a5ce19d..d63900393e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
@@ -8,26 +8,38 @@ dashedName: problem-423-consecutive-die-throws
# --description--
-Let n be a positive integer.
+Let $n$ be a positive integer.
-A 6-sided die is thrown n times. Let c be the number of pairs of consecutive throws that give the same value.
+A 6-sided die is thrown $n$ times. Let $c$ be the number of pairs of consecutive throws that give the same value.
-For example, if n = 7 and the values of the die throws are (1,1,5,6,6,6,3), then the following pairs of consecutive throws give the same value: (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) Therefore, c = 3 for (1,1,5,6,6,6,3).
+For example, if $n = 7$ and the values of the die throws are (1, 1, 5, 6, 6, 6, 3), then the following pairs of consecutive throws give the same value:
-Define C(n) as the number of outcomes of throwing a 6-sided die n times such that c does not exceed π(n).1 For example, C(3) = 216, C(4) = 1290, C(11) = 361912500 and C(24) = 4727547363281250000.
+$$\begin{align}
+ & (\underline{1}, \underline{1}, 5, 6, 6, 6, 3) \\\\
+ & (1, 1, 5, \underline{6}, \underline{6}, 6, 3) \\\\
+ & (1, 1, 5, 6, \underline{6}, \underline{6}, 3)
+\end{align}$$
-Define S(L) as ∑ C(n) for 1 ≤ n ≤ L. For example, S(50) mod 1 000 000 007 = 832833871.
+Therefore, $c = 3$ for (1, 1, 5, 6, 6, 6, 3).
-Find S(50 000 000) mod 1 000 000 007.
+Define $C(n)$ as the number of outcomes of throwing a 6-sided die $n$ times such that $c$ does not exceed $π(n)$.1
-1 π denotes the prime-counting function, i.e. π(n) is the number of primes ≤ n.
+For example, $C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$ and $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$.
+
+Define $S(L)$ as $\sum C(n)$ for $1 ≤ n ≤ L$.
+
+For example, $S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$.
+
+Find $S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+
+1 $π$ denotes the prime-counting function, i.e. $π(n)$ is the number of primes $≤ n$.
# --hints--
-`euler423()` should return 653972374.
+`consecutiveDieThrows()` should return `653972374`.
```js
-assert.strictEqual(euler423(), 653972374);
+assert.strictEqual(consecutiveDieThrows(), 653972374);
```
# --seed--
@@ -35,12 +47,12 @@ assert.strictEqual(euler423(), 653972374);
## --seed-contents--
```js
-function euler423() {
+function consecutiveDieThrows() {
return true;
}
-euler423();
+consecutiveDieThrows();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
index 827b969ce6..a8a4030906 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
@@ -8,43 +8,66 @@ dashedName: problem-424-kakuro
# --description--
+
+
+You are given that $P_3 = (\frac{-19}{2}, \frac{-229}{24})$, $P_4 = (\frac{1267}{144}, \frac{-37}{12})$ and $P_7 = (\frac{17\\,194\\,218\\,091}{143\\,327\\,232}, \frac{274\\,748\\,766\\,781}{1\\,719\\,926\\,784})$.
+
+Find $P_n$ for $n = {11}^{14}$ in the following format: If $P_n = (\frac{a}{b}, \frac{c}{d})$ where the fractions are in lowest terms and the denominators are positive, then the answer is $(a + b + c + d)\bmod 1\\,000\\,000\\,007$.
+
+For $n = 7$, the answer would have been: $806\\,236\\,837$.
# --hints--
-`euler422()` should return 92060460.
+`sequenceOfPointsOnHyperbola()` should return `92060460`.
```js
-assert.strictEqual(euler422(), 92060460);
+assert.strictEqual(sequenceOfPointsOnHyperbola(), 92060460);
```
# --seed--
@@ -31,12 +39,12 @@ assert.strictEqual(euler422(), 92060460);
## --seed-contents--
```js
-function euler422() {
+function sequenceOfPointsOnHyperbola() {
return true;
}
-euler422();
+sequenceOfPointsOnHyperbola();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
index a19a5ce19d..d63900393e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-423-consecutive-die-throws.md
@@ -8,26 +8,38 @@ dashedName: problem-423-consecutive-die-throws
# --description--
-Let n be a positive integer.
+Let $n$ be a positive integer.
-A 6-sided die is thrown n times. Let c be the number of pairs of consecutive throws that give the same value.
+A 6-sided die is thrown $n$ times. Let $c$ be the number of pairs of consecutive throws that give the same value.
-For example, if n = 7 and the values of the die throws are (1,1,5,6,6,6,3), then the following pairs of consecutive throws give the same value: (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) (1,1,5,6,6,6,3) Therefore, c = 3 for (1,1,5,6,6,6,3).
+For example, if $n = 7$ and the values of the die throws are (1, 1, 5, 6, 6, 6, 3), then the following pairs of consecutive throws give the same value:
-Define C(n) as the number of outcomes of throwing a 6-sided die n times such that c does not exceed π(n).1 For example, C(3) = 216, C(4) = 1290, C(11) = 361912500 and C(24) = 4727547363281250000.
+$$\begin{align}
+ & (\underline{1}, \underline{1}, 5, 6, 6, 6, 3) \\\\
+ & (1, 1, 5, \underline{6}, \underline{6}, 6, 3) \\\\
+ & (1, 1, 5, 6, \underline{6}, \underline{6}, 3)
+\end{align}$$
-Define S(L) as ∑ C(n) for 1 ≤ n ≤ L. For example, S(50) mod 1 000 000 007 = 832833871.
+Therefore, $c = 3$ for (1, 1, 5, 6, 6, 6, 3).
-Find S(50 000 000) mod 1 000 000 007.
+Define $C(n)$ as the number of outcomes of throwing a 6-sided die $n$ times such that $c$ does not exceed $π(n)$.1
-1 π denotes the prime-counting function, i.e. π(n) is the number of primes ≤ n.
+For example, $C(3) = 216$, $C(4) = 1290$, $C(11) = 361\\,912\\,500$ and $C(24) = 4\\,727\\,547\\,363\\,281\\,250\\,000$.
+
+Define $S(L)$ as $\sum C(n)$ for $1 ≤ n ≤ L$.
+
+For example, $S(50)\bmod 1\\,000\\,000\\,007 = 832\\,833\\,871$.
+
+Find $S(50\\,000\\,000)\bmod 1\\,000\\,000\\,007$.
+
+1 $π$ denotes the prime-counting function, i.e. $π(n)$ is the number of primes $≤ n$.
# --hints--
-`euler423()` should return 653972374.
+`consecutiveDieThrows()` should return `653972374`.
```js
-assert.strictEqual(euler423(), 653972374);
+assert.strictEqual(consecutiveDieThrows(), 653972374);
```
# --seed--
@@ -35,12 +47,12 @@ assert.strictEqual(euler423(), 653972374);
## --seed-contents--
```js
-function euler423() {
+function consecutiveDieThrows() {
return true;
}
-euler423();
+consecutiveDieThrows();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
index 827b969ce6..a8a4030906 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-424-kakuro.md
@@ -8,43 +8,66 @@ dashedName: problem-424-kakuro
# --description--
+ +
The above is an example of a cryptic kakuro (also known as cross sums, or even sums cross) puzzle, with its final solution on the right. (The common rules of kakuro puzzles can be found easily on numerous internet sites. Other related information can also be currently found at krazydad.com whose author has provided the puzzle data for this challenge.)
-The downloadable text file (kakuro200.txt) contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as follows:
+The `testPuzzles` array contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as string as follows:
-6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X
+`6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X`
The first character is a numerical digit indicating the size of the information grid. It would be either a 6 (for a 5x5 kakuro puzzle) or a 7 (for a 6x6 puzzle) followed by a comma (,). The extra top line and left column are needed to insert information.
-The content of each cell is then described and followed by a comma, going left to right and starting with the top line. X = Gray cell, not required to be filled by a digit. O (upper case letter)= White empty cell to be filled by a digit. A = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle. ( ) = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
+The content of each cell is then described and followed by a comma, going left to right and starting with the top line.
+
+`X` = Gray cell, not required to be filled by a digit.
+
+`O` (upper case letter)= White empty cell to be filled by a digit.
+
+`A` = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle.
+
+`( )` = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
The description of the last cell is followed by a Carriage Return/Line Feed (CRLF) instead of a comma.
The required answer to each puzzle is based on the value of each letter necessary to arrive at the solution and according to the alphabetical order. As indicated under the example puzzle, its answer would be 8426039571. At least 9 out of the 10 encrypting letters are always part of the problem description. When only 9 are given, the missing one must be assigned the remaining digit.
-You are given that the sum of the answers for the first 10 puzzles in the file is 64414157580.
+You are given that the sum of the answers for the first 10 puzzles in `testPuzzles` is 64414157580.
-Find the sum of the answers for the 200 puzzles.
+Find the sum of the answers for `puzzles` array.
# --hints--
-`euler424()` should return 1059760019628.
+`kakuro(testPuzzles)` should return `1059760019628`.
```js
-assert.strictEqual(euler424(), 1059760019628);
+assert.strictEqual(kakuro(_testPuzzles), 1059760019628);
```
# --seed--
+
+## --after-user-code--
+
+```js
+const _testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+```
+
## --seed-contents--
```js
-function euler424() {
+function kakuro(puzzles) {
return true;
}
-euler424();
+const testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+
+kakuro(testPuzzles);
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
index d46740b0d5..72f5393017 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
@@ -8,26 +8,29 @@ dashedName: problem-425-prime-connection
# --description--
-Two positive numbers A and B are said to be connected (denoted by "A ↔ B") if one of these conditions holds:
+Two positive numbers $A$ and $B$ are said to be connected (denoted by "$A ↔ B$") if one of these conditions holds:
-(1) A and B have the same length and differ in exactly one digit; for example, 123 ↔ 173.
+1. $A$ and $B$ have the same length and differ in exactly one digit; for example, $123 ↔ 173$.
+2. Adding one digit to the left of $A$ (or $B$) makes $B$ (or $A$); for example, $23 ↔ 223$ and $123 ↔ 23$.
-(2) Adding one digit to the left of A (or B) makes B (or A); for example, 23 ↔ 223 and 123 ↔ 23.
+We call a prime $P$ a 2's relative if there exists a chain of connected primes between 2 and $P$ and no prime in the chain exceeds $P$.
-We call a prime P a 2's relative if there exists a chain of connected primes between 2 and P and no prime in the chain exceeds P.
+For example, 127 is a 2's relative. One of the possible chains is shown below:
-For example, 127 is a 2's relative. One of the possible chains is shown below: 2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127 However, 11 and 103 are not 2's relatives.
+$$2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127$$
-Let F(N) be the sum of the primes ≤ N which are not 2's relatives. We can verify that F(103) = 431 and F(104) = 78728.
+However, 11 and 103 are not 2's relatives.
-Find F(107).
+Let $F(N)$ be the sum of the primes $≤ N$ which are not 2's relatives. We can verify that $F({10}^3) = 431$ and $F({10}^4) = 78\\,728$.
+
+Find $F({10}^7)$.
# --hints--
-`euler425()` should return 46479497324.
+`primeConnection()` should return `46479497324`.
```js
-assert.strictEqual(euler425(), 46479497324);
+assert.strictEqual(primeConnection(), 46479497324);
```
# --seed--
@@ -35,12 +38,12 @@ assert.strictEqual(euler425(), 46479497324);
## --seed-contents--
```js
-function euler425() {
+function primeConnection() {
return true;
}
-euler425();
+primeConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
index 5e2c48c34e..3f1e34d156 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
@@ -14,20 +14,34 @@ A turn consists of moving each ball exactly once according to the following rule
After one turn the sequence (2, 2, 2, 1, 2) becomes (2, 2, 1, 2, 3) as can be seen below; note that we begin the new sequence starting at the first occupied box.
+
+
The above is an example of a cryptic kakuro (also known as cross sums, or even sums cross) puzzle, with its final solution on the right. (The common rules of kakuro puzzles can be found easily on numerous internet sites. Other related information can also be currently found at krazydad.com whose author has provided the puzzle data for this challenge.)
-The downloadable text file (kakuro200.txt) contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as follows:
+The `testPuzzles` array contains the description of 200 such puzzles, a mix of 5x5 and 6x6 types. The first puzzle in the file is the above example which is coded as string as follows:
-6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X
+`6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X`
The first character is a numerical digit indicating the size of the information grid. It would be either a 6 (for a 5x5 kakuro puzzle) or a 7 (for a 6x6 puzzle) followed by a comma (,). The extra top line and left column are needed to insert information.
-The content of each cell is then described and followed by a comma, going left to right and starting with the top line. X = Gray cell, not required to be filled by a digit. O (upper case letter)= White empty cell to be filled by a digit. A = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle. ( ) = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
+The content of each cell is then described and followed by a comma, going left to right and starting with the top line.
+
+`X` = Gray cell, not required to be filled by a digit.
+
+`O` (upper case letter)= White empty cell to be filled by a digit.
+
+`A` = Or any one of the upper case letters from A to J to be replaced by its equivalent digit in the solved puzzle.
+
+`( )` = Location of the encrypted sums. Horizontal sums are preceded by a lower case "h" and vertical sums are preceded by a lower case "v". Those are followed by one or two upper case letters depending if the sum is a single digit or double digit one. For double digit sums, the first letter would be for the "tens" and the second one for the "units". When the cell must contain information for both a horizontal and a vertical sum, the first one is always for the horizontal sum and the two are separated by a comma within the same set of brackets, ex.: (hFE,vD). Each set of brackets is also immediately followed by a comma.
The description of the last cell is followed by a Carriage Return/Line Feed (CRLF) instead of a comma.
The required answer to each puzzle is based on the value of each letter necessary to arrive at the solution and according to the alphabetical order. As indicated under the example puzzle, its answer would be 8426039571. At least 9 out of the 10 encrypting letters are always part of the problem description. When only 9 are given, the missing one must be assigned the remaining digit.
-You are given that the sum of the answers for the first 10 puzzles in the file is 64414157580.
+You are given that the sum of the answers for the first 10 puzzles in `testPuzzles` is 64414157580.
-Find the sum of the answers for the 200 puzzles.
+Find the sum of the answers for `puzzles` array.
# --hints--
-`euler424()` should return 1059760019628.
+`kakuro(testPuzzles)` should return `1059760019628`.
```js
-assert.strictEqual(euler424(), 1059760019628);
+assert.strictEqual(kakuro(_testPuzzles), 1059760019628);
```
# --seed--
+
+## --after-user-code--
+
+```js
+const _testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+```
+
## --seed-contents--
```js
-function euler424() {
+function kakuro(puzzles) {
return true;
}
-euler424();
+const testPuzzles = [
+ '6,X,X,(vCC),(vI),X,X,X,(hH),B,O,(vCA),(vJE),X,(hFE,vD),O,O,O,O,(hA),O,I,(hJC,vB),O,O,(hJC),H,O,O,O,X,X,X,(hJE),O,O,X','7,X,X,X,X,(vJJ),(vCD),X,X,X,X,(hCG),O,O,(vCE),X,X,X,(hCI,vJB),C,O,O,X,(vB),(hJF,vJF),O,F,O,O,(hJA),F,G,O,O,X,X,(hCA),O,A,O,X,X,X,X,(hCF),O,O,X,X,X','7,X,X,X,(vE),(vCB),X,X,X,X,(hJ),O,O,(vCA),X,X,(vCH),(hCG,vCJ),O,O,O,(vJ),(hCE),O,O,O,(hJ,vGG),O,O,(hD),I,O,(hCD,vCB),H,O,O,X,(hCE),O,O,E,X,X,X,X,(hCE),O,O,X,X','6,X,X,X,(vEA),(vJF),X,X,X,(hI),O,O,(vJA),X,(vA),(hEI,vEB),O,O,O,(hIG),C,O,J,O,D,(hJD),O,O,O,X,X,X,(hJD),O,O,X,X','7,X,(vH),(vG),X,X,(vI),(vDH),(hG),B,O,(vDI),(hDB,vDE),O,O,(hBC),I,O,F,O,O,J,X,X,(hG),O,O,X,X,X,(vDG),(hH,vDD),O,O,(vDJ),(vC),(hBI),O,O,O,O,O,O,(hDJ),O,O,X,(hA),O,O','6,X,(vID),(vIJ),X,X,X,(hH),F,I,(vF),(vIA),X,(hIA),G,B,O,C,X,X,(hID),O,O,O,(vIF),X,(hIA),E,O,I,O,X,X,X,(hII),O,G','6,X,X,(vAF),(vAI),X,X,X,(hJ,vAC),O,B,(vGJ),X,(hGH),J,O,O,O,(vAF),(hAG),O,O,(hH,vF),A,D,X,(hGF),O,E,O,O,X,X,(hD),O,O,X','7,X,X,X,X,(vCE),(vGB),X,X,(vJG),(vCI),(hCD,vCJ),O,O,X,(hCI),O,O,O,O,B,(vJB),(hCF),O,O,O,(hCA,vH),O,O,(hCJ),O,O,(hJB,vCJ),O,O,O,X,(hJD),O,O,O,O,O,X,(hF),I,O,X,X,X','7,X,(vBB),(vBD),X,X,X,X,(hBB),C,E,(vEE),(vEC),X,X,(hBC),O,O,O,O,X,X,X,(hEF),H,O,A,(vJ),X,X,X,(hBD),O,O,O,(vI),X,X,(hBE),F,O,O,O,X,X,X,X,(hG),O,O','7,X,X,(vGG),(vGD),X,(vI),(vGI),X,(hGB),O,O,(hGH,vIC),O,O,X,(hGA),O,O,O,J,O,X,X,(hGI),O,O,X,X,X,(vGD),(hE,vE),O,O,(vGF),X,(hIH),O,O,O,O,O,X,(hE),A,O,(hGF),O,O,X','6,X,(vIJ),(vIE),X,X,X,(hF),O,C,(vIA),X,X,(hCA),O,O,D,(vIH),X,X,(hIB),E,O,O,(vF),X,X,(hD),O,A,O,X,X,X,(hID),O,G','6,X,(vAD),(vGI),(vI),X,X,(hB),O,O,O,(vAF),X,(hGC),O,O,O,O,(vGA),(hGE),O,O,(hJ,vB),O,O,X,(hGD),D,O,E,O,X,X,(hAI),O,C,O','6,X,X,X,(vAB),(vFA),X,X,X,(hHI),O,O,(vHJ),X,(vA),(hFJ,vHE),I,D,O,(hFH),O,O,O,O,O,(hHJ),O,O,O,X,X,X,(hC),O,J,X,X','7,X,X,X,(vJ),(vEF),X,X,X,X,(hI,vGD),C,E,(vEF),(vA),X,(hEH),O,O,O,O,O,X,(hH,vJ),O,O,(hJ,vEJ),O,O,(hD),O,A,(hEF,vEB),O,O,X,(hCC),O,O,A,O,O,X,X,X,(hH),O,O,X,X','7,X,X,X,(vAG),(vAJ),(vFH),X,X,X,(hFD),O,O,O,X,X,(vH),(hAJ,vAB),O,O,O,(vB),(hAH),O,H,O,(hC,vAI),O,O,(hE),O,O,(hAI,vAE),O,O,O,X,(hJ),O,O,O,X,X,X,(hFG),E,O,O,X,X','7,X,(vAI),(vHB),X,X,(vJE),(vAA),(hD),O,O,X,(hG),O,O,(hAJ),O,O,(vE),(hAA,vAI),O,O,X,(hHF),O,O,O,O,X,X,(hJF,vAE),O,O,O,J,(vH),(hAI),D,O,X,(hB),O,O,(hAG),O,O,X,(hAA),O,O','7,X,X,(vHJ),(vC),(vAF),X,X,X,(hHF),O,O,O,(vHI),(vHD),X,(hHB,vAB),O,O,O,O,E,(hAI),O,O,X,(hAB),O,O,(hD),O,O,(vAB),(hAI,vE),J,O,(hHH),O,O,O,B,O,X,X,X,(hG),O,A,O,X','6,X,X,(vDF),(vHE),X,X,X,(hHJ,vE),C,O,X,X,(hHI),O,O,O,(vDF),(vHH),(hFA),A,O,B,O,O,X,X,(hE),O,I,O,X,X,(hHH),O,O,X','6,X,(vA),(vA),X,X,X,(hE),O,O,(vCJ),X,X,(hG),O,O,O,(vHI),X,X,(hHC),O,O,H,(vB),X,X,(hCE),O,O,D,X,X,X,(hE),O,O','6,X,X,X,X,(vEH),(vEC),X,X,X,(hEB,vEJ),O,O,X,X,(hEC,vEF),O,O,B,X,(hDD,vEI),O,B,C,X,(hB),O,D,A,X,X,(hEC),O,O,X,X,X','6,X,X,X,X,(vIF),(vH),X,X,X,(hIJ,vGJ),B,I,X,X,(hIB,vIC),O,O,G,X,(hIA,vC),O,O,O,X,(hE),O,O,O,X,X,(hIA),E,O,X,X,X','7,X,(vC),(vFB),X,X,X,X,(hFH),O,O,(vFA),(vFJ),(vC),X,(hFJ),O,O,O,O,O,X,X,X,(hA,vJ),O,O,O,X,X,(hG),D,O,O,(vC),(vFC),X,(hBH),A,O,O,O,E,X,X,X,X,(hFH),O,I','6,X,X,(vFD),(vC),X,X,X,(hDH),E,F,(vDG),(vDD),X,(hDF,vDI),O,O,A,O,(hDG),O,O,(hDG,vDG),O,O,(hDJ),O,D,J,O,X,X,X,(hJ),E,O,X','6,X,X,X,(vE),(vGH),(vIC),X,X,(hD,vIG),O,O,A,X,(hIF,vJ),O,J,E,O,(hJ),O,D,(hGG,vGH),O,O,(hGG),O,O,O,O,X,(hIC),O,O,O,X,X','7,X,X,X,X,(vAG),(vJA),(vH),X,X,X,(hAJ,vDJ),O,O,O,X,X,(hJF),O,O,O,O,X,X,(hG),D,O,X,X,X,(vJH),(hJE,vJD),C,I,X,X,(hAE),B,O,O,O,X,X,(hAJ),O,O,E,X,X,X','7,X,X,X,X,(vGG),(vIA),(vGF),X,X,X,(hGF),O,O,D,X,X,X,(hGJ,vIB),O,O,O,X,X,(hGH,vGD),O,O,O,X,X,(hII,vC),O,J,O,X,X,(hIH),J,O,O,X,X,X,(hGE),O,I,O,X,X,X','6,X,X,(vFA),(vEC),X,X,X,(hI,vFI),F,O,X,X,(hDE),O,O,O,(vFF),(vFF),(hDI),G,J,O,F,O,X,X,(hFJ),O,D,O,X,X,(hFH),J,A,X','7,X,X,X,X,X,(vID),(vBB),X,X,X,X,(hBC),O,I,X,X,(vIH),(vBH),(hBF,vF),O,O,X,(hIE,vD),O,O,I,O,O,(hAG),O,O,O,O,F,X,(hA),O,O,X,X,X,X,(hD),O,O,X,X,X,X','7,X,(vCD),(vCC),X,X,X,X,(hE),B,C,(vCE),X,X,X,(hCD),O,O,O,(vE),(vCG),X,X,(hCH),O,O,O,O,X,X,(hFC),B,J,G,O,(vCC),X,X,X,(hCI),O,O,O,X,X,X,X,(hG),O,O','7,X,X,X,(vID),(vD),(vFB),X,X,X,(hIB,vID),O,O,O,X,X,(hJE,vIA),J,C,O,D,(vF),(hIB),O,O,X,(hIG),O,O,(hIJ),O,O,(vD),(hA,vID),O,O,X,(hJF),O,O,O,O,X,X,(hIE),O,O,O,X,X','7,X,X,(vAC),(vAH),X,X,X,X,(hD),O,O,(vAD),X,X,X,(hCH,vAD),O,O,O,(vAA),(vF),(hAC),O,H,(hAB,vAJ),O,O,A,(hAE),O,O,O,(hD,vAD),O,O,X,X,(hAC),O,O,O,X,X,X,X,(hG),O,O,X','6,X,X,(vBB),(vBE),X,X,X,(hBH),O,I,(vBG),(vBB),X,(hHE,vBD),H,D,O,O,(hBA),C,O,(hA,vG),O,O,(hBF),I,O,O,O,X,X,X,(hG),O,O,X','6,X,X,(vEC),(vD),X,X,X,(hD,vH),O,O,(vIB),X,(hIA),O,O,O,O,(vE),(hII),O,F,(hII,vIG),O,O,X,(hIH),O,O,O,O,X,X,(hIA),O,D,X','6,X,X,X,X,(vEH),(vEG),X,X,X,(hEB,vEF),O,O,X,X,(hAC,vG),O,B,O,X,(hEE,vEC),O,D,O,X,(hEE),O,O,O,X,X,(hEJ),D,O,X,X,X','6,X,(vD),(vB),X,X,X,(hA),O,O,(vE),X,X,(hE),A,O,O,(vCJ),X,X,(hCH),O,A,O,(vCI),X,X,(hB),O,D,O,X,X,X,(hCB),G,O','7,X,X,X,X,(vHJ),(vIF),(vIB),X,X,X,(hIH,vJI),O,O,J,X,X,(hIA),O,O,O,F,X,X,(hIG),O,C,X,X,X,(vD),(hA,vIB),O,J,X,X,(hHB),O,O,O,O,X,X,(hHB),O,O,O,X,X,X','7,X,X,X,(vBJ),(vIB),X,X,X,(vIF),(hBB,vBB),O,O,(vBA),X,(hIC),O,O,O,O,O,(vBA),(hBD),O,O,(hC,vC),O,O,O,(hBJ),E,O,O,(hBC,vBI),G,H,X,(hBA),O,O,O,O,O,X,X,(hBF),O,O,X,X','7,X,(vHI),(vHE),X,X,X,X,(hA),O,O,X,X,X,X,(hHG),O,O,(vHH),(vHE),(vIJ),X,(hHA),O,O,O,O,O,(vHI),X,(hID),H,O,O,B,I,X,X,X,X,(hHB),F,O,X,X,X,X,(hHE),O,H','6,X,X,(vAJ),(vAJ),X,X,X,(hAF,vAA),G,A,X,X,(hDA),O,O,O,(vDE),(vAH),(hAJ),O,O,O,O,I,X,X,(hAG),D,C,O,X,X,(hAI),O,O,X','6,X,X,X,X,(vDH),(vDA),X,X,X,(hG,vDG),O,E,X,X,(hBJ,vBC),O,O,O,X,(hBI,vE),O,E,O,X,(hE),O,O,O,X,X,(hDH),O,E,X,X,X','6,X,X,X,X,(vHJ),(vHH),X,X,X,(hHE,vCC),O,O,X,X,(hF,vG),A,O,O,X,(hHC,vHJ),O,B,O,X,(hHH),O,O,O,X,X,(hHI),O,O,X,X,X','7,X,(vJ),(vDG),X,X,(vDF),(vEF),(hC),E,B,X,(hEA),O,O,(hEE),C,O,(vH),(hED,vEF),A,O,X,(hEC),O,O,O,O,X,X,(hDD,vEF),O,O,O,O,(vEA),(hEJ),O,F,X,(hJ),O,O,(hEF),O,O,X,(hEF),O,O','7,X,X,X,(vCC),(vD),X,X,X,(vJE),(hI,vCH),O,O,(vBF),X,(hCC),O,O,O,O,A,(vJB),(hCB),G,O,O,(hJA,vJF),O,O,(hJA),O,O,(hG,vH),O,O,O,X,(hCE),O,O,O,O,O,X,X,(hH),O,O,X,X','7,X,X,(vEI),(vEB),(vG),X,X,X,(hEF),E,O,O,(vHE),X,X,(hEF,vH),O,O,O,O,(vEI),(hH),O,O,X,(hEH),O,B,(hG),O,O,(vG),(hEI,vED),O,O,X,(hAG),C,O,O,O,X,X,X,(hEE),O,O,O,X','6,X,X,X,X,(vJE),(vF),X,X,X,(hI,vJJ),O,O,X,X,(hEC,vJJ),H,O,O,X,(hF,vJB),O,O,O,X,(hJI),A,C,E,X,X,(hJD),O,J,X,X,X','6,X,X,X,(vH),(vAE),X,X,X,(hCB,vCJ),O,O,(vCB),X,(hCA,vD),O,O,O,O,(hD),C,O,(hCC,vJ),O,O,(hAB),A,O,F,O,X,X,(hB),G,O,X,X','6,X,X,(vEC),(vEG),X,X,X,(hEF),O,O,(vFC),(vEI),X,(hHJ,vJ),E,O,O,A,(hJ),O,O,(hEA,vEA),O,O,(hHH),O,O,O,B,X,X,X,(hEF),O,O,X','7,X,(vEI),(vEC),X,X,X,X,(hH),O,O,X,X,X,X,(hED),O,O,(vEB),(vEG),(vGB),X,(hEJ),O,O,O,O,O,(vD),X,(hIA),O,O,O,O,C,X,X,X,X,(hA),O,I,X,X,X,X,(hEB),A,O','7,X,X,X,(vF),(vG),(vIB),X,X,(vG),(hBA,vIH),J,I,D,X,(hBG),O,O,O,O,O,(vBG),(hA),O,O,X,(hE),O,O,(hBB),O,C,(vA),(hBI,vBE),O,O,X,(hBA),O,O,O,O,O,X,(hBF),O,O,O,X,X','7,X,X,(vEF),(vDI),X,X,X,X,(hDG),O,O,(vDA),X,X,X,(hEA,vG),O,O,O,(vEJ),(vJ),(hF),O,G,(hDH,vDI),O,O,F,(hED),O,O,O,(hDD,vB),O,O,X,X,(hDB),O,O,A,X,X,X,X,(hH),O,O,X','7,X,X,X,X,(vJH),(vD),(vAJ),X,X,X,(hAC,vDH),O,O,O,X,X,(hAA),O,O,O,O,X,X,(hC),F,O,X,X,X,(vC),(hAJ,vAA),I,H,X,X,(hJA),O,D,O,G,X,X,(hJB),O,C,O,X,X,X','6,X,X,X,(vDC),(vG),X,X,X,(hA),O,O,(vCH),X,(vCI),(hCB,vB),O,O,O,(hDF),O,H,O,O,O,(hH),O,O,O,X,X,X,(hH),J,O,X,X','6,X,X,(vCG),(vGA),X,X,X,(hE),O,O,(vGG),(vGB),X,(hCI,vF),O,O,O,I,(hGI),O,O,(hI,vD),O,A,(hGH),O,B,O,O,X,X,X,(hA),O,O,X','6,X,X,X,(vJ),(vHF),X,X,(vF),(hHG,vHD),O,A,X,(hHI),A,O,O,O,(vHE),(hB),G,O,(hD,vHE),O,F,X,(hGJ),O,O,O,O,X,(hHD),O,O,X,X','6,X,X,X,X,(vBD),(vD),X,X,X,(hD,vBB),O,O,X,X,(hI,vHD),O,O,O,X,(hHD,vBE),O,O,A,X,(hHF),C,O,G,X,X,(hBI),O,O,X,X,X','7,X,(vJ),(vFB),(vDB),X,X,X,(hFC),O,O,O,(vFE),X,X,(hFB),O,O,O,O,X,X,X,X,(hG),I,O,X,X,X,X,(hA),O,O,(vFG),(vE),X,X,(hDD),O,O,O,A,X,X,X,(hFD),D,E,J','6,X,X,X,(vAD),(vAH),X,X,(vB),(hF,vEB),O,O,X,(hED),O,O,O,O,(vD),(hD),O,O,(hJ,vI),O,O,X,(hEH),O,A,O,C,X,(hB),G,O,X,X','6,X,X,X,X,(vFG),(vFB),X,X,X,(hFD,vB),O,O,X,X,(hFG,vFG),O,O,O,X,(hI,vH),O,O,C,X,(hGA),E,H,O,X,X,(hD),O,G,X,X,X','7,X,X,X,(vBH),(vBB),X,X,X,X,(hBJ,vBJ),I,O,(vHE),(vI),X,(hBF,vBA),O,O,O,O,O,(hBE),O,D,X,(hA),O,O,(hBC),O,O,(vA),(hBB,vBH),O,O,(hDA),B,H,O,O,O,X,X,X,(hI),O,O,X,X','7,X,X,X,(vEC),(vD),X,X,X,(vJ),(hEB,vEJ),O,O,X,X,(hFC),O,O,O,F,(vEG),X,(hG),O,O,(hH,vFI),O,E,(vEH),X,(hEB),A,O,(hED,vJ),O,O,X,X,(hFI),O,O,O,O,X,X,(hED),O,O,X,X','6,X,(vGH),(vGG),X,X,X,(hGE),O,O,(vFI),(vGJ),X,(hGF),O,O,D,O,X,X,(hGB),O,C,O,(vGG),X,(hFG),O,O,O,O,X,X,X,(hE),O,I','7,X,X,X,(vF),(vGI),X,X,X,(vJ),(hB,vGA),H,G,X,X,(hHF),O,O,O,A,(vHH),X,(hB),O,O,(hGB,vGA),C,O,(vC),X,(hGC),O,O,(hGI,vGF),O,O,X,X,(hHB),O,E,O,O,X,X,(hA),O,O,X,X','7,X,X,X,X,X,(vED),(vIG),X,X,X,X,(hEC),O,O,X,X,(vAC),(vA),(hH,vEG),O,O,X,(hAE,vB),O,O,H,O,O,(hIJ),O,O,O,B,O,X,(hEC),O,O,X,X,X,X,(hEI),O,O,X,X,X,X','7,X,X,(vAI),(vAA),X,X,X,X,(hAD,vAG),O,O,(vAE),X,X,(hAH),O,O,O,O,(vBH),(vD),(hG),O,O,(hI,vE),O,O,O,(hAI),O,O,O,(hG,vAC),D,F,X,X,(hAH),O,O,O,O,X,X,X,(hAJ),O,O,X','7,X,X,(vGD),(vFB),(vJ),X,X,X,(hGD),O,O,O,(vFA),(vGG),X,(hFA),O,O,O,O,O,X,(hGE,vGF),O,O,(hH,vFB),O,O,(hH),O,G,(hGC,vD),O,G,X,(hEB),O,O,O,O,O,X,X,X,(hGC),O,A,O,X','6,X,X,(vAD),(vEE),X,X,X,(hEC),G,O,(vAJ),(vH),X,(hEC,vEG),O,A,O,O,(hEG),F,O,(hEG,vEG),O,O,(hAB),O,E,F,A,X,X,X,(hEG),O,O,X','6,X,X,X,X,(vIB),(vJ),X,X,X,(hB,vIJ),O,O,X,X,(hE,vIF),O,O,C,X,(hFC,vIF),O,A,O,X,(hG),O,O,H,X,X,(hIJ),O,O,X,X,X','6,X,X,X,(vIB),(vEB),X,X,X,(hD,vAE),O,O,(vE),X,(hIJ,vE),O,O,O,O,(hII),O,O,(hJ,vC),H,O,(hAE),O,O,G,J,X,X,(hC),O,O,X,X','6,X,X,(vFF),(vB),X,X,X,(hC,vI),O,J,(vJE),X,(hJJ),O,O,I,G,(vA),(hJJ),O,O,(hJD,vJE),O,O,X,(hJB),O,O,F,O,X,X,(hJH),C,J,X','7,X,X,X,(vEI),(vJI),X,X,X,X,(hJA),O,O,(vJE),(vJJ),X,X,(hJI,vJB),O,E,O,D,X,(hJI,vC),O,H,(hJB,vJE),O,O,(hB),O,O,(hF,vD),O,O,X,(hJB),O,O,O,O,X,X,X,X,(hJE),O,O,X,X','7,X,(vJB),(vFD),X,X,(vFE),(vH),(hJF),O,O,X,(hH),O,O,(hJC),O,O,(vH),(hJF,vJF),O,O,X,(hJI),H,O,O,O,X,X,(hFJ,vJJ),J,O,O,O,(vJA),(hA),G,O,X,(hJF),O,C,(hJC),O,O,X,(hD),O,O','7,X,(vI),(vDH),X,X,X,X,(hB),O,I,X,X,X,X,(hC),O,O,(vA),(vI),(vDJ),X,(hDH),O,B,O,O,O,(vDH),X,(hGG),O,O,O,J,O,X,X,X,X,(hHH),B,O,X,X,X,X,(hHE),O,O','6,X,X,(vDI),(vE),X,X,X,(hA,vDA),E,O,(vHI),X,(hHI),F,A,O,O,(vDF),(hDD),O,O,(hDJ,vDJ),O,O,X,(hDG),O,O,H,O,X,X,(hB),O,D,X','6,X,(vJ),(vDH),X,X,X,(hDA),G,O,(vDA),(vDB),X,(hDB),O,O,I,F,X,X,(hG),O,F,O,(vDI),X,(hED),G,O,O,F,X,X,X,(hDE),O,H','6,X,X,(vCJ),(vD),X,X,X,(hG),O,O,(vAD),(vAE),X,(hCC,vI),O,O,A,O,(hJ),O,F,(hAD,vAD),I,H,(hCD),O,O,O,F,X,X,X,(hAJ),O,G,X','7,X,X,X,X,(vEF),(vEC),(vF),X,X,X,(hED,vEB),O,O,O,X,X,(hEB),O,O,O,O,X,X,(hC),O,D,X,X,X,(vI),(hB,vEE),O,O,X,X,(hEB),E,H,D,O,X,X,(hHJ),O,G,O,X,X,X','7,X,X,X,X,(vJF),(vIC),X,X,X,(vIA),(hD,vJE),O,O,X,X,(hIJ,vD),J,O,O,D,(vG),(hJC),I,O,O,(hJA,vC),O,O,(hJF),J,C,(hJF,vJE),O,O,O,X,(hIB),O,O,O,O,X,X,(hJF),O,O,X,X,X','6,X,(vH),(vJE),X,X,X,(hC),J,O,(vJJ),(vJC),X,(hJJ),A,I,O,H,X,X,(hD),O,O,A,(vC),X,(hAI),F,B,O,O,X,X,X,(hC),J,O','7,X,(vA),(vEE),X,X,(vD),(vF),(hEC),O,O,(vIH),(hI,vEB),O,O,(hBD),O,O,O,O,F,O,X,X,(hA),O,O,X,X,X,(vJ),(hEJ,vEG),F,O,(vA),(vG),(hBG),O,O,O,O,O,O,(hEH),O,O,X,(hG),O,O','6,X,X,X,(vFG),(vFC),X,X,(vE),(hFE,vFF),A,O,X,(hBF),O,O,O,O,(vH),(hE),O,O,(hD,vFF),I,O,X,(hFF),O,O,E,D,X,(hFI),O,O,X,X','6,X,X,(vHA),(vFH),X,X,X,(hFF),O,O,(vFH),(vE),X,(hDI,vFG),O,O,O,O,(hFG),B,O,(hC,vFB),O,O,(hDC),O,G,O,F,X,X,X,(hFF),O,O,X','7,X,X,(vBE),(vBB),(vA),X,X,X,(hH),O,O,O,(vBA),(vH),X,(hGI,vBB),O,J,O,O,O,(hBG),O,O,X,(hI),O,O,(hC),O,O,(vBG),(hE,vBD),H,C,(hBI),O,O,O,O,O,X,X,X,(hGG),O,O,O,X','7,X,X,X,X,X,(vHC),(vF),X,X,X,X,(hF,vC),O,E,X,X,(vEJ),(hEF,vEG),F,O,H,X,(hHD),C,O,O,O,X,X,(hHC,vI),A,O,O,O,X,(hJ),D,O,O,X,X,X,(hF),O,O,X,X,X,X','6,X,X,(vH),(vDC),X,X,X,(hCI,vCD),O,O,X,X,(hH),O,O,O,(vCA),(vCB),(hCJ),O,I,O,D,E,X,X,(hDI),E,H,O,X,X,(hG),O,O,X','7,X,X,X,X,(vJ),(vHE),X,X,X,X,(hHA,vHF),O,B,(vHE),X,X,(hEC,vHG),O,O,O,O,X,(hHE,vHG),O,O,(hA,vHB),O,O,(hJ),O,O,(hHE,vJ),O,O,X,(hED),O,J,O,O,X,X,X,(hB),O,O,X,X,X','6,X,X,(vJG),(vA),X,X,X,(hI),B,O,(vJC),(vJH),X,(hJH,vJC),O,E,O,O,(hB),O,O,(hJJ,vF),O,O,(hCE),O,O,D,I,X,X,X,(hB),O,H,X','6,X,X,X,X,(vDG),(vHH),X,X,(vDH),(hJ,vHB),O,O,X,(hJF),O,O,O,O,X,(hHF,vE),O,O,O,X,(hDJ),H,O,O,I,X,(hHC),G,O,X,X,X','7,X,(vAI),(vHC),X,X,X,X,(hD),O,G,X,X,(vHI),(vG),(hAJ),O,O,(vB),(hH,vAH),O,O,X,(hHF,vH),O,O,F,O,O,(hCA),O,O,O,O,O,(vF),(hH),O,O,X,(hG),O,O,X,X,X,X,(hAH),O,O','7,X,X,X,X,(vFG),(vFI),X,X,X,X,(hFI,vFB),O,O,(vFJ),X,(vFA),(hFG,vGA),O,B,O,O,(hIB),O,O,O,(hH,vJ),O,O,(hJ),O,O,(hFD,vD),O,C,O,(hII),O,O,O,O,X,X,X,(hE),O,O,X,X,X','7,X,X,X,(vI),(vEG),(vFD),X,X,(vED),(hA,vEB),O,O,O,X,(hJC),O,O,A,O,O,X,(hEG),O,O,(hEG,vEC),O,O,(vB),X,(hH),O,O,(hJ,vEB),O,O,X,(hEI),O,O,O,O,J,X,(hFF),O,H,O,X,X','6,X,X,(vEI),(vEB),X,X,X,(hEC,vB),O,O,(vEB),X,(hHC),J,O,O,F,(vEC),(hH),O,O,(hB,vEC),O,O,X,(hEH),O,O,O,O,X,X,(hEA),D,O,X','6,X,X,(vAF),(vBF),X,X,X,(hBI),O,G,(vAD),(vBD),X,(hBI,vF),O,J,O,E,(hBB),A,G,(hBI,vBI),O,H,(hAJ),B,O,O,O,X,X,X,(hBA),O,O,X','6,X,(vCB),(vJ),X,X,X,(hCE),A,O,(vCI),X,X,(hCG),D,O,O,(vCC),X,X,(hCA),O,O,O,(vB),X,X,(hB),O,E,G,X,X,X,(hG),O,H','7,X,X,X,X,X,(vFI),(vHG),X,X,X,X,(hHJ,vHH),O,O,X,X,(vHC),(hHD,vHG),O,O,O,X,(hHH),O,O,O,O,X,X,(hFE,vHC),O,O,O,D,X,(hHE),H,O,O,X,X,X,(hHE),I,A,X,X,X,X','7,X,X,(vFA),(vC),X,X,X,X,(hE),O,B,(vAC),(vGJ),X,X,(hFF,vG),O,O,O,O,(vAI),(hAA),O,D,(hAB,vAC),O,O,O,(hAH),O,O,O,(hAB,vAB),O,O,X,(hFJ),O,O,O,O,X,X,X,X,(hAH),O,J,X','7,X,X,X,(vIF),(vIB),X,X,X,X,(hID),O,O,(vC),X,X,(vIF),(hIH,vEE),O,O,O,(vII),(hEB),O,O,O,(hIB,vIF),D,J,(hIF),O,O,(hII,vIE),O,O,O,X,(hJ),O,G,O,X,X,X,X,(hIF),O,O,X,X','7,X,(vDJ),(vDB),X,X,X,X,(hDJ),O,O,(vDF),(vCE),(vI),X,(hCH),O,O,O,O,O,X,X,X,(hDC,vDB),O,A,G,X,X,(hFE),O,O,O,(vDJ),(vI),X,(hCF),O,O,O,O,O,X,X,X,X,(hDE),O,O','6,X,X,(vCI),(vJ),X,X,X,(hA),O,E,(vEG),(vCC),X,(hEG,vCF),O,O,D,O,(hJ),C,G,(hB,vCC),C,O,(hED),O,O,A,O,X,X,X,(hCD),O,O,X','6,X,X,X,(vG),(vFE),X,X,X,(hG,vBC),O,O,(vBC),X,(hFJ,vC),O,E,O,I,(hG),O,O,(hBF,vBC),O,O,(hEJ),O,O,O,O,X,X,(hBA),D,O,X,X','6,X,X,(vAJ),(vE),X,X,X,(hFH,vH),O,O,(vFA),X,(hFH),O,O,O,O,(vFI),(hI),O,C,(hFI,vFD),O,O,X,(hAC),O,O,I,G,X,X,(hC),O,O,X','6,X,X,X,(vE),(vCJ),X,X,(vFF),(hA,vHJ),C,O,X,(hFC),O,O,O,F,(vD),(hFI),O,O,(hFE,vFJ),O,O,X,(hFG),O,O,O,O,X,(hFD),O,O,X,X','7,X,X,X,(vBJ),(vBI),X,X,X,X,(hA),O,O,(vCH),(vBJ),X,(vCJ),(hCB,vG),H,O,I,B,(hBA),O,O,O,(hBE,vG),O,O,(hBB),F,O,(hBE,vBI),O,O,O,(hBI),O,O,O,O,X,X,X,X,(hBC),O,O,X,X','6,X,X,(vCJ),(vD),X,X,X,(hH),O,O,(vBD),(vJ),X,(hCI,vCH),O,J,F,O,(hCG),O,E,(hA,vCD),O,F,(hBF),O,O,O,O,X,X,X,(hCG),O,O,X','6,X,X,X,X,(vJB),(vG),X,X,X,(hA,vH),I,O,X,X,(hCD,vCG),O,O,B,X,(hCF,vCD),O,O,O,X,(hJD),O,H,O,X,X,(hB),O,O,X,X,X','7,X,(vI),(vEH),X,X,(vCC),(vF),(hG),O,O,X,(hH),O,C,(hJ),O,O,(vAD),(hAG,vG),O,O,X,(hEI),F,O,O,O,X,X,(hAD,vAB),O,O,I,O,(vI),(hG),O,O,X,(hC),O,O,(hAJ),O,O,X,(hAA),O,O','7,X,X,X,X,X,(vEC),(vEA),X,X,X,X,(hB),O,O,X,X,(vDF),(vEH),(hEC,vH),H,O,X,(hEA,vI),O,B,E,O,O,(hDB),E,J,O,D,O,X,(hEH),O,A,X,X,X,X,(hI),O,O,X,X,X,X','6,X,X,X,(vBC),(vBC),X,X,X,(hBJ,vEC),H,O,(vBB),X,(hBE,vA),D,J,O,O,(hC),O,O,(hBE,vBG),O,O,(hEG),H,O,B,O,X,X,(hBI),O,O,X,X','7,X,(vE),(vCF),X,X,X,X,(hJ),O,O,(vFB),X,X,X,(hCJ),O,O,A,(vFE),(vCA),X,X,(hIH),O,O,O,O,X,X,(hFF),O,O,O,B,(vFA),X,X,X,(hCI),O,O,O,X,X,X,X,(hFG),O,O','7,X,X,X,X,(vBH),(vH),X,X,X,X,(hI),O,O,(vE),X,X,X,(hJG,vBF),O,O,O,X,(vH),(hBA,vJE),O,O,O,O,(hDG),O,O,O,O,X,X,(hBG),O,F,O,X,X,X,X,(hA),J,O,X,X,X','7,X,X,X,X,X,(vIC),(vA),X,X,X,(vII),(hG,vIH),F,I,X,X,(hIG),O,O,O,D,X,X,(hC,vC),O,O,J,X,X,(hIF,vE),O,G,A,X,X,(hIH),O,O,O,O,X,X,(hJ),F,D,X,X,X,X','7,X,X,X,(vH),(vCJ),X,X,X,(vCG),(hCB,vEG),O,O,X,X,(hEF),O,I,O,O,(vCI),X,(hCD),O,J,(hCB,vCJ),E,O,(vCC),X,(hCE),O,O,(hCI,vH),O,O,X,X,(hEB),O,O,O,O,X,X,(hD),O,O,X,X','6,X,(vGA),(vBE),X,X,X,(hGC),H,O,(vGF),X,X,(hGG),O,O,O,(vGD),X,X,(hBG),O,J,O,(vGD),X,X,(hGD),O,O,E,X,X,X,(hGH),O,O','6,X,X,(vEE),(vEJ),X,X,X,(hI,vEF),O,O,(vEH),X,(hEA),O,O,O,E,(vB),(hEE),O,O,(hB,vB),O,O,X,(hEG),A,O,I,O,X,X,(hA),D,B,X','6,X,(vJ),(vHA),X,X,X,(hHH),D,O,(vHG),X,X,(hI),O,O,F,(vDG),X,X,(hDJ),O,O,O,(vHF),X,X,(hHF),O,O,E,X,X,X,(hHE),B,O','6,X,X,X,X,(vFI),(vE),X,X,X,(hH,vA),J,I,X,X,(hGF,vD),O,O,F,X,(hGF,vC),O,O,A,X,(hD),O,O,O,X,X,(hD),O,O,X,X,X','7,X,X,(vHG),(vE),X,X,X,X,(hGD),O,O,(vGA),(vHC),(vAJ),X,(hGD,vAC),O,O,O,O,O,(hGC),O,O,(hAA,vGC),O,O,O,(hAC),O,O,F,(hGD,vD),O,O,(hHB),O,O,O,O,O,X,X,X,X,(hI),O,D,X','7,X,X,(vBG),(vBJ),X,(vBD),(vE),X,(hC),O,O,(hBB,vAG),O,C,X,(hBE),O,O,O,O,D,X,(hBG),O,O,O,(vBE),X,X,(vE),(hBI,vJ),O,O,O,X,(hCG),F,G,O,O,O,X,(hC),O,O,(hBJ),O,O,X','7,X,X,X,X,X,(vEA),(vJJ),X,X,(vED),(vJI),(hF),O,O,X,(hB),O,O,(hJH,vB),O,O,X,(hED),O,B,O,O,X,X,(hJI,vJI),O,O,C,O,X,(hJH),O,O,(hJJ),O,O,X,(hF),J,E,X,X,X,X','6,X,(vF),(vED),X,X,X,(hEI),O,O,(vEA),X,X,(hEJ),O,O,J,(vB),X,X,(hB),O,O,O,(vG),X,X,(hJ),B,O,C,X,X,X,(hF),O,E','6,X,X,X,X,(vCH),(vCD),X,X,X,(hG,vCH),O,O,X,X,(hCH,vCI),O,O,O,X,(hFA,vCE),O,O,J,X,(hFF),O,O,O,X,X,(hI),F,C,X,X,X','6,X,X,(vCH),(vA),X,X,X,(hE,vE),D,O,(vAG),(vHC),(hHB),O,O,C,O,I,(hHA),O,O,(hE,vJ),O,O,(hCH),A,O,O,O,O,X,X,(hHD),O,O,X','7,X,(vF),(vDG),(vGD),X,X,X,(hA),O,D,O,(vI),(vGE),X,(hDG),O,C,O,O,O,X,(hGC),H,O,(hH,vA),O,O,(vGF),X,(hH),O,O,(hGB,vGD),O,O,X,(hDH),O,D,O,O,O,X,X,X,(hA),O,O,G','7,X,X,X,X,(vIG),(vIG),X,X,X,X,(hCJ),O,O,(vCE),X,X,X,(hIE,vEA),O,O,O,X,(vJ),(hEA,vIE),O,O,O,O,(hCH),O,F,O,O,X,X,(hCH),I,B,O,X,X,X,X,(hCH),O,O,X,X,X','7,X,X,X,X,(vJ),(vDB),X,X,X,X,(hDG,vH),O,O,X,X,(vB),(hJ,vEB),E,O,O,(vG),(hDJ),O,F,D,(hI,vDC),O,O,(hA),O,O,(hJ,vA),O,O,I,X,(hDA),O,O,O,X,X,X,(hDH),O,O,X,X,X','6,X,X,X,(vEE),(vJA),(vEI),X,X,(hD,vEE),O,F,O,X,(hED,vEC),O,O,O,O,(hJ),O,O,(hEH,vEI),O,O,(hIB),O,O,O,O,X,(hII),O,O,O,X,X','6,X,(vE),(vGH),X,X,X,(hC),O,J,(vFJ),X,X,(hGH),O,O,O,(vJ),X,X,(hFA),B,O,I,(vFF),X,X,(hFG),O,O,O,X,X,X,(hB),F,G','6,X,X,(vIF),(vIJ),X,X,X,(hD,vIC),O,O,X,X,(hIB),O,O,O,(vIG),(vA),(hBF),O,O,F,I,O,X,X,(hE),D,O,F,X,X,(hIF),O,C,X','7,X,(vCD),(vB),X,X,X,X,(hII),O,D,(vA),X,X,X,(hIJ),O,O,O,(vII),X,X,(hID),O,O,O,O,(vIJ),(vCJ),X,X,(hCA),H,O,F,O,X,X,X,(hA),O,O,G,X,X,X,X,(hII),J,O','7,X,(vC),(vFF),X,X,(vHF),(vD),(hFD),O,O,(vHG),(hA,vFJ),O,O,(hHF),O,O,O,O,O,O,X,X,(hFG,vFH),O,O,O,X,X,(hFB,vI),O,O,O,(vFB),(vB),(hIG),O,O,O,O,D,J,(hG),O,I,X,(hFE),O,O','7,X,(vHJ),(vDE),X,X,(vDI),(vHH),(hHG),O,J,(vHJ),(hJ),O,O,(hHE),O,O,O,(hHJ,vB),O,O,X,(hHH),O,O,O,O,X,X,(hDJ,vHA),D,O,E,O,(vF),(hHJ),O,O,(hA),O,O,E,(hHA),O,O,X,(hI),O,O','7,X,(vEH),(vFA),X,X,X,X,(hEB),O,O,(vFA),X,X,X,(hFD),O,O,O,(vEE),(vID),X,X,(hFB),O,O,O,O,X,X,(hFJ),O,O,O,O,(vEE),X,X,X,(hJ),O,B,O,X,X,X,X,(hEH),C,O','6,X,(vJ),(vE),X,X,X,(hA),B,C,(vCJ),X,X,(hCG),O,O,O,(vCD),X,X,(hHF),O,O,O,(vJ),X,X,(hE),O,O,H,X,X,X,(hCE),O,O','6,X,(vGC),(vGH),X,X,X,(hGG),O,O,(vGB),X,X,(hGI),E,O,I,(vGG),X,X,(hIJ),O,C,O,(vA),X,X,(hD),G,O,O,X,X,X,(hD),O,O','6,X,X,X,X,(vIG),(vII),X,X,X,(hE,vIA),I,G,X,X,(hGJ,vGF),O,C,O,X,(hIE,vII),D,O,O,X,(hGJ),O,B,O,X,X,(hA),O,J,X,X,X','6,X,X,X,X,(vIA),(vE),X,X,(vJB),(hB,vII),I,J,X,(hIF),O,O,O,H,X,(hIB,vG),D,J,O,X,(hJG),C,O,O,F,X,(hB),O,O,X,X,X','7,X,X,X,(vDB),(vGG),X,X,X,X,(hGH),O,O,(vGA),(vGA),X,X,(hGF,vGA),O,O,O,O,X,(hGA,vGE),B,O,(hGD,vI),O,O,(hJ),O,I,(hGE,vGG),O,O,X,(hDA),O,D,O,O,X,X,X,X,(hF),O,O,X,X','6,X,X,X,(vFB),(vI),X,X,X,(hGF),O,O,(vGA),X,(vH),(hGA,vFD),O,O,O,(hFF),O,A,O,O,C,(hGG),O,J,O,X,X,X,(hGH),O,D,X,X','6,X,X,(vGA),(vA),X,X,X,(hB,vGE),O,O,(vHJ),X,(hBD),O,O,O,O,(vGH),(hGC),O,O,(hGJ,vGE),O,O,X,(hGG),O,F,O,O,X,X,(hGC),O,O,X','7,X,X,(vCE),(vG),(vI),X,X,X,(hEE),A,O,E,(vCD),(vCH),X,(hEG,vCD),O,O,O,O,O,(hA),G,C,X,(hEH),O,O,(hEE),O,O,(vI),(hA,vD),O,O,(hCF),O,O,O,O,O,X,X,X,(hED),O,O,B,X','7,X,(vG),(vDC),X,(vBA),(vDG),X,(hJ),O,G,(hDA,vBA),O,O,X,(hBC),O,O,G,O,O,X,X,(hDH),O,O,O,(vG),X,X,X,(hG,vDI),O,O,O,(vJ),X,(hBB),E,O,O,O,O,X,(hH),O,J,(hB),O,O','6,X,X,X,(vJG),(vCG),X,X,(vJG),(hJB,vJH),O,O,X,(hJH),I,B,O,O,(vD),(hJB),O,O,(hA,vJG),O,O,X,(hJB),O,B,O,O,X,(hF),I,C,X,X','7,X,(vA),(vE),X,X,(vD),(vB),(hF),O,O,(vJJ),(hI,vGD),O,O,(hGD),O,O,O,O,I,O,X,X,(hJI),O,O,X,X,X,(vJE),(hA,vF),I,O,(vD),(vJJ),(hGA),O,O,O,J,O,O,(hH),O,O,X,(hI),O,O','7,X,X,(vEH),(vEF),X,X,X,X,(hEI,vIH),O,O,(vEI),X,X,(hEI),O,O,O,O,(vIE),(vEJ),(hD),O,O,(hEH,vH),O,O,O,(hEC),O,O,O,(hD,vC),H,G,X,X,(hIA),O,O,O,O,X,X,X,(hD),E,O,X','7,X,X,X,X,X,(vEA),(vCJ),X,X,X,X,(hCD,vCC),O,O,X,X,(vCI),(hCJ,vEH),O,O,O,X,(hDH),O,J,B,O,X,X,(hCH,vD),O,O,O,O,X,(hCJ),O,O,O,X,X,X,(hJ),O,G,X,X,X,X','7,X,(vB),(vFF),X,(vEI),(vFE),X,(hH),O,O,(hFC,vIB),G,O,X,(hFC),O,O,O,O,O,X,X,X,(hFH),O,D,X,X,X,X,(hFF,vFG),O,O,(vFE),(vFH),X,(hEE),O,O,J,O,O,X,(hFG),O,O,(hFG),O,O','6,X,(vHE),(vII),X,X,X,(hHB),O,O,(vHF),(vHJ),X,(hHD),B,O,O,O,X,X,(hG),H,O,O,(vHE),X,(hCA),O,O,E,B,X,X,X,(hHB),O,G','6,X,(vH),(vAF),X,X,X,(hAC),O,O,(vAD),X,X,(hDI),J,O,O,(vAH),X,X,(hAC),O,O,O,(vAI),X,X,(hH),O,O,B,X,X,X,(hAH),O,E','6,X,(vC),(vHA),X,X,X,(hC),O,J,(vHA),X,X,(hF),J,O,O,(vHC),X,X,(hI),O,J,O,(vF),X,X,(hEJ),O,O,B,X,X,X,(hG),O,O','6,X,X,X,(vFJ),(vJC),X,X,(vFF),(hFF,vJE),O,O,X,(hFH),O,F,O,O,(vD),(hFI),O,C,(hE,vH),D,O,X,(hJC),O,O,O,A,X,(hFG),O,J,X,X','7,X,X,X,X,X,(vDE),(vBB),X,(vC),(vDF),X,(hBF),O,O,(hH),O,O,(vE),(hH,vBI),B,O,(hDF),O,O,O,O,D,(vE),X,(hDI,vBE),O,O,C,O,B,(hBF),O,A,X,(hG),E,D,(hG),O,O,X,X,X,X','7,X,(vJ),(vFH),X,X,X,X,(hHH),F,A,X,X,(vGE),(vA),(hI),O,O,(vC),(hF,vD),O,O,X,(hHC,vF),H,O,O,O,O,(hGJ),O,O,O,O,O,(vE),(hE),O,O,X,(hHI),O,O,X,X,X,X,(hA),O,O','7,X,X,(vCD),(vCB),(vF),X,X,X,(hCA,vCJ),O,O,O,(vFH),X,(hCD),O,O,O,O,O,(vCB),(hH),O,O,X,(hI),O,O,(hCE),O,B,(vCE),(hCH,vCI),O,G,X,(hFA),O,G,O,O,O,X,X,(hBC),H,O,O,X','6,X,X,X,X,(vHD),(vHH),X,X,X,(hA,vHH),H,I,X,X,(hHJ,vIG),O,C,O,X,(hHC,vE),O,O,O,X,(hIG),J,O,O,X,X,(hHF),O,O,X,X,X','6,X,X,(vFD),(vJB),X,X,X,(hH,vH),O,O,(vJD),X,(hFH),O,O,O,O,(vJI),(hJD),O,O,(hJD,vG),J,E,X,(hJD),O,O,O,O,X,X,(hB),A,O,X','6,X,X,X,(vC),(vDC),X,X,(vF),(hHB,vDI),O,O,(vDJ),(hDG),O,O,E,O,O,(hHA),O,O,(hHD,vG),O,O,(hEJ),O,O,F,O,O,X,(hJ),O,O,X,X','7,X,X,X,X,X,(vEJ),(vG),X,X,X,X,(hD,vI),C,O,X,X,(vEG),(hFE,vFE),O,O,O,X,(hFD),O,O,O,O,X,X,(hEC,vFI),O,O,O,O,X,(hEC),B,O,H,X,X,X,(hJ),O,O,X,X,X,X','7,X,(vI),(vAC),X,X,(vAI),(vCG),(hB),O,I,X,(hCB,vCD),O,O,(hH),A,D,(hCD,vAF),O,O,O,X,(hAC),O,O,O,O,X,X,(hCF,vCC),O,O,O,O,(vB),(hCB),O,O,O,(hCF),O,O,(hCB),O,J,X,(hB),O,O','6,X,X,X,(vJB),(vIG),X,X,(vA),(hJI,vJC),O,F,X,(hJB),O,O,O,O,(vJE),(hJD),B,O,(hJB,vD),O,H,X,(hJG),O,I,O,O,X,(hA),O,E,X,X','7,X,X,X,X,(vCD),(vCC),(vB),X,X,X,(hCC,vEC),O,I,O,X,X,(hCH),C,O,O,O,X,X,(hCA),F,O,X,X,X,(vA),(hCH,vCE),O,E,X,X,(hGA),C,O,O,O,X,X,(hCE),O,O,O,X,X,X','6,X,X,X,X,(vJI),(vA),X,X,(vJH),(hJE,vJI),O,G,X,(hJE),F,O,O,D,X,(hC,vB),O,E,O,X,(hJH),O,O,O,O,X,(hJD),O,E,X,X,X','6,X,X,X,X,(vAJ),(vAJ),X,X,X,(hAF,vGB),O,O,X,X,(hAE,vD),O,O,O,X,(hAJ,vF),O,J,O,X,(hAF),O,O,H,X,X,(hB),O,I,X,X,X','7,X,X,X,X,(vH),(vIE),X,X,X,X,(hA,vA),O,O,X,X,(vID),(hF,vCH),O,O,A,(vIE),(hIH),O,O,O,(hIA,vIH),O,O,(hIE),O,O,(hIG,vIA),B,O,O,X,(hIF),O,G,A,X,X,X,(hIE),O,D,X,X,X','7,X,(vEF),(vB),(vFC),X,X,X,(hH),O,O,O,(vEA),X,X,(hED),C,O,O,O,X,X,X,X,(hEG),O,F,X,X,X,X,(hEI),O,O,(vEH),(vI),X,X,(hFH),O,O,O,O,X,X,X,(hEE),O,I,O','6,X,(vHI),(vDG),X,X,X,(hHE),J,O,(vDG),X,X,(hHC),H,O,O,(vHA),X,X,(hDH),F,O,G,(vHE),X,X,(hHC),O,O,O,X,X,X,(hHE),O,O','6,X,X,(vAD),(vAE),X,X,X,(hAA),O,O,(vAD),(vAA),X,(hAI,vI),O,F,D,J,(hC),A,O,(hB,vJ),A,E,(hAB),O,I,C,J,X,X,X,(hI),O,H,X','6,X,X,(vDA),(vE),X,X,X,(hJ,vDE),O,F,(vGG),X,(hDJ),O,O,O,O,(vC),(hDD),O,O,(hJ,vI),O,O,X,(hGG),O,D,O,O,X,X,(hDA),G,B,X','7,X,X,(vJD),(vG),(vI),X,X,X,(hG),O,O,H,(vEB),(vEF),X,(hEB),O,O,B,O,J,X,(hEJ,vA),O,H,(hEE,vEA),O,O,(hA),O,O,(hEJ,vG),O,O,X,(hJF),O,O,O,O,O,X,X,X,(hG),F,O,O,X','6,X,X,X,X,(vEJ),(vG),X,X,X,(hDE,vF),O,O,X,X,(hDJ,vF),O,O,O,X,(hA,vDA),O,O,O,X,(hDI),B,O,O,X,X,(hDE),C,O,X,X,X','6,X,X,(vAC),(vD),X,X,X,(hD,vEI),O,O,(vBC),X,(hBA),O,O,O,O,(vH),(hEF),O,O,(hEI,vF),O,O,X,(hEF),O,O,A,O,X,X,(hEE),G,D,X','6,X,X,(vGB),(vD),X,X,X,(hGG),A,C,(vGJ),(vC),X,(hGG,vGC),O,O,O,J,(hGH),O,O,(hE,vI),G,H,(hHF),O,H,O,O,X,X,X,(hE),O,O,X','6,X,X,(vIJ),(vCD),X,X,X,(hCD),O,O,(vCI),(vCG),X,(hIH,vCC),G,O,O,O,(hCE),O,I,(hCH,vCD),G,O,(hIC),B,D,O,O,X,X,X,(hA),O,O,X','7,X,(vII),(vDH),(vID),X,X,X,(hIG),O,O,O,X,X,X,(hDA),O,C,J,(vII),X,X,X,(hID),F,O,O,(vDH),X,X,X,(hID),O,O,O,(vID),X,X,X,(hIE),A,O,O,X,X,X,(hDD),O,O,O','7,X,(vEB),(vF),X,X,X,X,(hED),O,O,(vAJ),(vED),(vD),X,(hIB),O,O,O,G,O,X,X,X,(hF,vA),O,O,O,X,X,(hED),O,O,F,(vA),(vEB),X,(hIE),O,H,O,O,O,X,X,X,X,(hEE),O,O','7,X,X,X,X,(vCA),(vCE),(vB),X,X,X,(hF),O,O,O,X,X,X,(hJG,vCD),I,O,O,X,X,(hF,vB),O,O,O,X,X,(hJI,vCI),O,F,O,X,X,(hD),O,O,O,X,X,X,(hCI),O,O,O,X,X,X','6,X,(vJI),(vI),X,X,X,(hH),O,O,(vD),X,X,(hJA),F,O,O,(vJH),X,X,(hJI),C,G,O,(vJJ),X,X,(hD),O,O,O,X,X,X,(hJE),O,O','6,X,X,X,(vDC),(vAE),X,X,X,(hI),O,B,(vI),X,(vC),(hJ,vDE),O,O,O,(hAF),A,D,O,O,O,(hI),O,O,G,X,X,X,(hDA),H,O,X,X','7,X,X,X,(vFD),(vAF),X,X,X,(vFD),(hFE,vFA),B,O,X,X,(hHI),O,O,O,O,(vFF),X,(hFI),O,O,(hC,vG),O,H,(vFA),X,(hE),O,O,(hFB,vC),O,O,X,X,(hFJ),O,G,O,O,X,X,(hH),O,O,X,X','7,X,X,X,X,(vD),(vHD),X,X,X,(vDH),(hA,vJJ),O,O,(vE),X,(hHB,vJH),O,O,O,E,J,(hJE),H,O,O,(hD,vF),O,O,(hJG),E,O,(hJE,vJG),C,O,O,(hHH),J,O,O,O,O,X,X,(hJJ),O,O,X,X,X','7,X,X,X,X,(vBA),(vEB),X,X,X,(vBG),(hC,vBB),O,O,X,X,(hBD,vBA),O,O,O,O,(vBJ),(hBC),O,O,O,(hBG,vBD),A,O,(hBB),O,O,(hEE,vBF),O,O,D,X,(hBJ),O,O,O,I,X,X,(hBD),O,O,X,X,X','7,X,X,X,X,X,(vDG),(vC),X,(vB),(vFH),X,(hC),E,O,(hA),O,O,(vDD),(hH,vDB),O,O,(hDA),C,O,O,O,O,(vE),X,(hFH,vDE),O,O,H,O,F,(hDH),O,O,X,(hDI),O,O,(hJ),O,O,X,X,X,X','6,X,(vB),(vE),X,X,X,(hA),D,O,(vA),X,X,(hH),O,C,O,(vIG),X,X,(hDI),O,O,O,(vDF),X,X,(hIF),O,O,O,X,X,X,(hH),O,O','7,X,(vHF),(vC),X,X,(vC),(vHF),(hC),O,O,(vBC),(hA,vBF),O,O,(hBE),O,O,O,O,O,O,X,X,(hHD),A,O,X,X,X,(vD),(hJ,vHA),O,O,(vHI),(vC),(hCH),J,O,O,O,O,B,(hHH),O,O,X,(hE),O,O','6,X,X,X,(vJ),(vDA),X,X,(vFD),(hB,vFE),O,O,(vDA),(hDJ),O,O,O,O,O,(hDE),O,O,(hDA,vC),O,H,(hBA),O,I,O,G,O,X,(hJ),E,O,X,X','6,X,(vGA),(vA),X,X,X,(hGE),O,O,(vGD),X,X,(hGA),O,G,A,(vED),X,X,(hGE),O,O,O,(vGD),X,X,(hEB),C,H,F,X,X,X,(hGE),A,I','6,X,(vIC),(vFD),X,X,X,(hIG),O,C,(vIB),X,X,(hFJ),O,O,O,(vII),X,X,(hIE),O,O,F,(vIA),X,X,(hIJ),F,I,O,X,X,X,(hIC),O,O','6,X,X,X,(vJG),(vHH),X,X,X,(hHA),O,O,(vHD),X,(vE),(hJF,vHJ),O,O,O,(hHB),F,O,D,O,O,(hE),O,J,O,X,X,X,(hHE),I,O,X,X','7,X,X,X,(vGG),(vI),(vEC),X,X,(vBH),(hJ,vBI),O,O,O,X,(hBJ),O,O,O,O,O,(vJ),(hGJ),O,O,X,(hA),O,O,(hGC),O,O,(vC),(hGB,vGJ),O,O,X,(hBF),O,O,O,O,B,X,(hBH),O,O,O,X,X','7,X,X,X,X,X,(vD),(vHB),X,X,(vG),(vFC),(hHA,vAI),O,O,X,(hAB),O,O,O,O,O,X,(hAD),O,O,O,(vHB),X,X,(vF),(hAF,vHI),O,O,O,X,(hAB),O,O,O,O,O,X,(hB),O,E,X,X,X,X','6,X,(vBC),(vDF),X,X,X,(hBE),O,O,(vDB),X,X,(hDG),O,J,O,(vC),X,X,(hBI),O,O,O,(vBB),X,X,(hBA),O,O,D,X,X,X,(hBG),F,O','6,X,X,X,(vH),(vDC),(vGA),X,X,(hA,vIE),O,O,O,X,(hIG,vGG),O,O,O,O,(hF),O,O,(hGF,vJ),J,O,(hGA),O,O,O,O,X,(hIE),O,O,O,X,X','6,X,(vHC),(vHJ),X,X,X,(hHC),A,B,(vA),X,X,(hHI),O,O,O,(vHA),X,X,(hD),F,O,O,(vB),X,X,(hII),G,O,O,X,X,X,(hB),O,O','7,X,(vH),(vJA),X,X,(vIE),(vJI),(hJC),O,O,(vDG),(hJE,vIG),O,O,(hDD),I,O,O,O,O,O,X,X,(hII,vIG),O,O,O,X,X,(hIE,vJA),O,O,O,(vB),(vJI),(hDG),C,O,O,O,O,O,(hJF),O,O,X,(hH),O,O','7,X,(vHH),(vBE),X,X,X,X,(hE),B,O,X,(vHF),(vBJ),X,(hHI),C,O,(hJ,vHI),O,O,X,X,(hBC),D,O,O,O,X,X,(hHH),O,O,D,O,(vHF),X,(hHD),F,O,(hHD),G,O,X,X,X,X,(hHE),O,O','7,X,X,X,X,X,(vIF),(vI),X,X,X,X,(hB,vGF),O,O,X,X,(vEG),(hGG,vB),O,O,O,X,(hGJ),O,O,O,H,X,X,(hGA,vA),O,O,O,O,X,(hGC),I,H,O,X,X,X,(hH),G,J,X,X,X,X','7,X,X,X,X,X,(vJF),(vJF),X,X,X,X,(hJD),A,O,X,X,(vBG),(vJB),(hI,vI),O,O,X,(hBD,vJF),F,O,O,E,O,(hIB),O,O,O,O,C,X,(hJG),O,B,X,X,X,X,(hI),O,J,X,X,X,X','6,X,X,(vEI),(vC),X,X,X,(hH,vGG),O,O,(vGD),X,(hBJ),O,O,O,O,(vD),(hGI),O,O,(hD,vD),E,G,X,(hBG),O,O,A,O,X,X,(hJ),O,O,X','7,X,X,X,X,(vFI),(vJF),X,X,X,X,(hJH),O,O,(vJC),X,X,X,(hEE,vEC),O,O,O,X,(vJE),(hED,vEF),O,O,O,G,(hJB),O,O,O,O,X,X,(hEH),O,O,G,X,X,X,X,(hJG),O,O,X,X,X','7,X,X,X,(vJ),(vEI),X,X,X,X,(hJ,vEC),O,A,(vBD),X,X,(hHC,vEA),O,O,O,I,(vF),(hEE),O,O,(hEE,vHD),B,J,O,(hHE),O,O,O,(hG,vED),O,O,X,(hHD),O,O,O,O,X,X,X,(hEA),O,O,X,X','7,X,X,X,X,X,(vFH),(vED),X,X,X,X,(hEC,vEA),O,O,X,X,(vED),(hFI,vEH),O,O,O,X,(hEE),O,O,A,D,X,X,(hFB,vJ),O,O,O,J,X,(hFI),O,O,O,X,X,X,(hI),O,A,X,X,X,X','6,X,(vB),(vHI),X,X,X,(hHH),O,O,(vHJ),(vGA),X,(hHH),O,O,O,I,X,X,(hGE),O,A,O,(vHE),X,(hHJ),H,B,F,D,X,X,X,(hHJ),O,C'
+]
+
+kakuro(testPuzzles);
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
index d46740b0d5..72f5393017 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-425-prime-connection.md
@@ -8,26 +8,29 @@ dashedName: problem-425-prime-connection
# --description--
-Two positive numbers A and B are said to be connected (denoted by "A ↔ B") if one of these conditions holds:
+Two positive numbers $A$ and $B$ are said to be connected (denoted by "$A ↔ B$") if one of these conditions holds:
-(1) A and B have the same length and differ in exactly one digit; for example, 123 ↔ 173.
+1. $A$ and $B$ have the same length and differ in exactly one digit; for example, $123 ↔ 173$.
+2. Adding one digit to the left of $A$ (or $B$) makes $B$ (or $A$); for example, $23 ↔ 223$ and $123 ↔ 23$.
-(2) Adding one digit to the left of A (or B) makes B (or A); for example, 23 ↔ 223 and 123 ↔ 23.
+We call a prime $P$ a 2's relative if there exists a chain of connected primes between 2 and $P$ and no prime in the chain exceeds $P$.
-We call a prime P a 2's relative if there exists a chain of connected primes between 2 and P and no prime in the chain exceeds P.
+For example, 127 is a 2's relative. One of the possible chains is shown below:
-For example, 127 is a 2's relative. One of the possible chains is shown below: 2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127 However, 11 and 103 are not 2's relatives.
+$$2 ↔ 3 ↔ 13 ↔ 113 ↔ 103 ↔ 107 ↔ 127$$
-Let F(N) be the sum of the primes ≤ N which are not 2's relatives. We can verify that F(103) = 431 and F(104) = 78728.
+However, 11 and 103 are not 2's relatives.
-Find F(107).
+Let $F(N)$ be the sum of the primes $≤ N$ which are not 2's relatives. We can verify that $F({10}^3) = 431$ and $F({10}^4) = 78\\,728$.
+
+Find $F({10}^7)$.
# --hints--
-`euler425()` should return 46479497324.
+`primeConnection()` should return `46479497324`.
```js
-assert.strictEqual(euler425(), 46479497324);
+assert.strictEqual(primeConnection(), 46479497324);
```
# --seed--
@@ -35,12 +38,12 @@ assert.strictEqual(euler425(), 46479497324);
## --seed-contents--
```js
-function euler425() {
+function primeConnection() {
return true;
}
-euler425();
+primeConnection();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
index 5e2c48c34e..3f1e34d156 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-426-box-ball-system.md
@@ -14,20 +14,34 @@ A turn consists of moving each ball exactly once according to the following rule
After one turn the sequence (2, 2, 2, 1, 2) becomes (2, 2, 1, 2, 3) as can be seen below; note that we begin the new sequence starting at the first occupied box.
+ +
A system like this is called a Box-Ball System or BBS for short.
-It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to \[1, 2, 3]; we shall call this the final state.
+It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to [1, 2, 3]; we shall call this the final state.
-We define the sequence {ti}:s0 = 290797 sk+1 = sk2 mod 50515093 tk = (sk mod 64) + 1
+
+
A system like this is called a Box-Ball System or BBS for short.
-It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to \[1, 2, 3]; we shall call this the final state.
+It can be shown that after a sufficient number of turns, the system evolves to a state where the consecutive numbers of occupied boxes is invariant. In the example below, the consecutive numbers of occupied boxes evolves to [1, 2, 3]; we shall call this the final state.
-We define the sequence {ti}:s0 = 290797 sk+1 = sk2 mod 50515093 tk = (sk mod 64) + 1
+![four turns from occupied boxes [2, 2, 2] to final state [1, 2, 3]](https://cdn.freecodecamp.org/curriculum/project-euler/box-ball-system-2.gif) -Starting from the initial configuration (t0, t1, …, t10), the final state becomes \[1, 3, 10, 24, 51, 75]. Starting from the initial configuration (t0, t1, …, t10 000 000), find the final state. Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is \[1, 2, 3] then 14 ( = 12 + 22 + 32) is your answer.
+We define the sequence $\\{t_i\\}$:
+
+$$\begin{align}
+ & s_0 = 290\\,797 \\\\
+ & s_{k + 1} = {s_k}^2\bmod 50\\,515\\,093 \\\\
+ & t_k = (s_k\bmod 64) + 1
+\end{align}$$
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10})$, the final state becomes [1, 3, 10, 24, 51, 75].
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10\\,000\\,000})$, find the final state.
+
+Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is [1, 2, 3] then $14 (= 1^2 + 2^2 + 3^2)$ is your answer.
# --hints--
-`euler426()` should return 31591886008.
+`boxBallSystem()` should return `31591886008`.
```js
-assert.strictEqual(euler426(), 31591886008);
+assert.strictEqual(boxBallSystem(), 31591886008);
```
# --seed--
@@ -35,12 +49,12 @@ assert.strictEqual(euler426(), 31591886008);
## --seed-contents--
```js
-function euler426() {
+function boxBallSystem() {
return true;
}
-euler426();
+boxBallSystem();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
index 8f399eeaf0..bc840f45c8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
@@ -8,24 +8,24 @@ dashedName: problem-427-n-sequences
# --description--
-A sequence of integers S = {si} is called an n-sequence if it has n elements and each element si satisfies 1 ≤ si ≤ n. Thus there are nn distinct n-sequences in total.
+A sequence of integers $S = \\{s_i\\}$ is called an $n$-sequence if it has $n$ elements and each element $s_i$ satisfies $1 ≤ s_i ≤ n$. Thus there are $n^n$ distinct $n$-sequences in total.
-For example, the sequence S = {1, 5, 5, 10, 7, 7, 7, 2, 3, 7} is a 10-sequence.
+For example, the sequence $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ is a 10-sequence.
-For any sequence S, let L(S) be the length of the longest contiguous subsequence of S with the same value. For example, for the given sequence S above, L(S) = 3, because of the three consecutive 7's.
+For any sequence $S$, let $L(S)$ be the length of the longest contiguous subsequence of $S$ with the same value. For example, for the given sequence $S$ above, $L(S) = 3$, because of the three consecutive 7's.
-Let f(n) = ∑ L(S) for all n-sequences S.
+Let $f(n) = \sum L(S)$ for all $n$-sequences $S$.
-For example, f(3) = 45, f(7) = 1403689 and f(11) = 481496895121.
+For example, $f(3) = 45$, $f(7) = 1\\,403\\,689$ and $f(11) = 481\\,496\\,895\\,121$.
-Find f(7 500 000) mod 1 000 000 009.
+Find $f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$.
# --hints--
-`euler427()` should return 97138867.
+`nSequences()` should return `97138867`.
```js
-assert.strictEqual(euler427(), 97138867);
+assert.strictEqual(nSequences(), 97138867);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler427(), 97138867);
## --seed-contents--
```js
-function euler427() {
+function nSequences() {
return true;
}
-euler427();
+nSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
index e3b2460e6d..30d46ed11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
@@ -8,27 +8,32 @@ dashedName: problem-428-necklace-of-circles
# --description--
-Let `a`, `b` and `c` be positive numbers.
+Let $a$, $b$ and $c$ be positive numbers.
-Let W, X, Y, Z be four collinear points where |WX| = `a`, |XY| = `b`, |YZ| = `c` and |WZ| = `a` + `b` + `c`.
+Let $W$, $X$, $Y$, $Z$ be four collinear points where $|WX| = a$, $|XY| = b$, $|YZ| = c$ and $|WZ| = a + b + c$.
-Let Cin be the circle having the diameter XY.
+Let $C_{\text{in}}$ be the circle having the diameter $XY$.
-Let Cout be the circle having the diameter WZ.
+Let $C_{\text{out}}$ be the circle having the diameter $WZ$.
-The triplet (`a`, `b`, `c`) is called a *necklace triplet* if you can place `k` ≥ 3 distinct circles C1, C2, ..., Ck such that:
+The triplet ($a$, $b$, $c$) is called a *necklace triplet* if you can place $k ≥ 3$ distinct circles $C_1, C_2, \ldots, C_k$ such that:
+
+- $C_i$ has no common interior points with any $C_j$ for $1 ≤ i$, $j ≤ k$ and $i ≠ j$,
+- $C_i$ is tangent to both $C_{\text{in}}$ and $C_{\text{out}}$ for $1 ≤ i ≤ k$,
+- $C_i$ is tangent to $C_{i + 1}$ for $1 ≤ i < k$, and
+- $C_k$ is tangent to $C_1$.
-
-Starting from the initial configuration (t0, t1, …, t10), the final state becomes \[1, 3, 10, 24, 51, 75]. Starting from the initial configuration (t0, t1, …, t10 000 000), find the final state. Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is \[1, 2, 3] then 14 ( = 12 + 22 + 32) is your answer.
+We define the sequence $\\{t_i\\}$:
+
+$$\begin{align}
+ & s_0 = 290\\,797 \\\\
+ & s_{k + 1} = {s_k}^2\bmod 50\\,515\\,093 \\\\
+ & t_k = (s_k\bmod 64) + 1
+\end{align}$$
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10})$, the final state becomes [1, 3, 10, 24, 51, 75].
+
+Starting from the initial configuration $(t_0, t_1, \ldots, t_{10\\,000\\,000})$, find the final state.
+
+Give as your answer the sum of the squares of the elements of the final state. For example, if the final state is [1, 2, 3] then $14 (= 1^2 + 2^2 + 3^2)$ is your answer.
# --hints--
-`euler426()` should return 31591886008.
+`boxBallSystem()` should return `31591886008`.
```js
-assert.strictEqual(euler426(), 31591886008);
+assert.strictEqual(boxBallSystem(), 31591886008);
```
# --seed--
@@ -35,12 +49,12 @@ assert.strictEqual(euler426(), 31591886008);
## --seed-contents--
```js
-function euler426() {
+function boxBallSystem() {
return true;
}
-euler426();
+boxBallSystem();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
index 8f399eeaf0..bc840f45c8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-427-n-sequences.md
@@ -8,24 +8,24 @@ dashedName: problem-427-n-sequences
# --description--
-A sequence of integers S = {si} is called an n-sequence if it has n elements and each element si satisfies 1 ≤ si ≤ n. Thus there are nn distinct n-sequences in total.
+A sequence of integers $S = \\{s_i\\}$ is called an $n$-sequence if it has $n$ elements and each element $s_i$ satisfies $1 ≤ s_i ≤ n$. Thus there are $n^n$ distinct $n$-sequences in total.
-For example, the sequence S = {1, 5, 5, 10, 7, 7, 7, 2, 3, 7} is a 10-sequence.
+For example, the sequence $S = \\{1, 5, 5, 10, 7, 7, 7, 2, 3, 7\\}$ is a 10-sequence.
-For any sequence S, let L(S) be the length of the longest contiguous subsequence of S with the same value. For example, for the given sequence S above, L(S) = 3, because of the three consecutive 7's.
+For any sequence $S$, let $L(S)$ be the length of the longest contiguous subsequence of $S$ with the same value. For example, for the given sequence $S$ above, $L(S) = 3$, because of the three consecutive 7's.
-Let f(n) = ∑ L(S) for all n-sequences S.
+Let $f(n) = \sum L(S)$ for all $n$-sequences $S$.
-For example, f(3) = 45, f(7) = 1403689 and f(11) = 481496895121.
+For example, $f(3) = 45$, $f(7) = 1\\,403\\,689$ and $f(11) = 481\\,496\\,895\\,121$.
-Find f(7 500 000) mod 1 000 000 009.
+Find $f(7\\,500\\,000)\bmod 1\\,000\\,000\\,009$.
# --hints--
-`euler427()` should return 97138867.
+`nSequences()` should return `97138867`.
```js
-assert.strictEqual(euler427(), 97138867);
+assert.strictEqual(nSequences(), 97138867);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler427(), 97138867);
## --seed-contents--
```js
-function euler427() {
+function nSequences() {
return true;
}
-euler427();
+nSequences();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
index e3b2460e6d..30d46ed11e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-428-necklace-of-circles.md
@@ -8,27 +8,32 @@ dashedName: problem-428-necklace-of-circles
# --description--
-Let `a`, `b` and `c` be positive numbers.
+Let $a$, $b$ and $c$ be positive numbers.
-Let W, X, Y, Z be four collinear points where |WX| = `a`, |XY| = `b`, |YZ| = `c` and |WZ| = `a` + `b` + `c`.
+Let $W$, $X$, $Y$, $Z$ be four collinear points where $|WX| = a$, $|XY| = b$, $|YZ| = c$ and $|WZ| = a + b + c$.
-Let Cin be the circle having the diameter XY.
+Let $C_{\text{in}}$ be the circle having the diameter $XY$.
-Let Cout be the circle having the diameter WZ.
+Let $C_{\text{out}}$ be the circle having the diameter $WZ$.
-The triplet (`a`, `b`, `c`) is called a *necklace triplet* if you can place `k` ≥ 3 distinct circles C1, C2, ..., Ck such that:
+The triplet ($a$, $b$, $c$) is called a *necklace triplet* if you can place $k ≥ 3$ distinct circles $C_1, C_2, \ldots, C_k$ such that:
+
+- $C_i$ has no common interior points with any $C_j$ for $1 ≤ i$, $j ≤ k$ and $i ≠ j$,
+- $C_i$ is tangent to both $C_{\text{in}}$ and $C_{\text{out}}$ for $1 ≤ i ≤ k$,
+- $C_i$ is tangent to $C_{i + 1}$ for $1 ≤ i < k$, and
+- $C_k$ is tangent to $C_1$.
- -Let T(`n`) be the number of necklace triplets (`a`, `b`, `c`) such that `a`, `b` and `c` are positive integers, and `b` ≤ `n`. For example, T(1) = 9, T(20) = 732 and T(3000) = 438106.
+
-Let T(`n`) be the number of necklace triplets (`a`, `b`, `c`) such that `a`, `b` and `c` are positive integers, and `b` ≤ `n`. For example, T(1) = 9, T(20) = 732 and T(3000) = 438106.
+ -Find T(1 000 000 000).
+Let $T(n)$ be the number of necklace triplets $(a, b, c)$ such that $a$, $b$ and $c$ are positive integers, and $b ≤ n$. For example, $T(1) = 9$, $T(20) = 732$ and $T(3\\,000) = 438\\,106$.
+
+Find $T(1\\,000\\,000\\,000)$.
# --hints--
-`necklace(1000000000)` should return 747215561862.
+`necklace(1000000000)` should return `747215561862`.
```js
assert.strictEqual(necklace(1000000000), 747215561862);
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
index 8b9c108829..8735e80e53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
@@ -8,22 +8,22 @@ dashedName: problem-429-sum-of-squares-of-unitary-divisors
# --description--
-A unitary divisor d of a number n is a divisor of n that has the property gcd(d, n/d) = 1.
+A unitary divisor $d$ of a number $n$ is a divisor of $n$ that has the property $gcd(d, \frac{n}{d}) = 1$.
-The unitary divisors of 4! = 24 are 1, 3, 8 and 24.
+The unitary divisors of $4! = 24$ are 1, 3, 8 and 24.
-The sum of their squares is 12 + 32 + 82 + 242 = 650.
+The sum of their squares is $12 + 32 + 82 + 242 = 650$.
-Let S(n) represent the sum of the squares of the unitary divisors of n. Thus S(4!)=650.
+Let $S(n)$ represent the sum of the squares of the unitary divisors of $n$. Thus $S(4!) = 650$.
-Find S(100 000 000!) modulo 1 000 000 009.
+Find $S(100\\,000\\,000!)$ modulo $1\\,000\\,000\\,009$.
# --hints--
-`euler429()` should return 98792821.
+`sumSquaresOfUnitaryDivisors()` should return `98792821`.
```js
-assert.strictEqual(euler429(), 98792821);
+assert.strictEqual(sumSquaresOfUnitaryDivisors(), 98792821);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler429(), 98792821);
## --seed-contents--
```js
-function euler429() {
+function sumSquaresOfUnitaryDivisors() {
return true;
}
-euler429();
+sumSquaresOfUnitaryDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
index ba66983c7b..ded4becfce 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
@@ -8,24 +8,26 @@ dashedName: problem-430-range-flips
# --description--
-N disks are placed in a row, indexed 1 to N from left to right.
+$N$ disks are placed in a row, indexed 1 to $N$ from left to right.
Each disk has a black side and white side. Initially all disks show their white side.
-At each turn, two, not necessarily distinct, integers A and B between 1 and N (inclusive) are chosen uniformly at random. All disks with an index from A to B (inclusive) are flipped.
+At each turn, two, not necessarily distinct, integers $A$ and $B$ between 1 and $N$ (inclusive) are chosen uniformly at random. All disks with an index from $A$ to $B$ (inclusive) are flipped.
-The following example shows the case N = 8. At the first turn A = 5 and B = 2, and at the second turn A = 4 and B = 6.
+The following example shows the case $N = 8$. At the first turn $A = 5$ and $B = 2$, and at the second turn $A = 4$ and $B = 6$.
-Let E(N, M) be the expected number of disks that show their white side after M turns. We can verify that E(3, 1) = 10/9, E(3, 2) = 5/3, E(10, 4) ≈ 5.157 and E(100, 10) ≈ 51.893.
+
-Find T(1 000 000 000).
+Let $T(n)$ be the number of necklace triplets $(a, b, c)$ such that $a$, $b$ and $c$ are positive integers, and $b ≤ n$. For example, $T(1) = 9$, $T(20) = 732$ and $T(3\\,000) = 438\\,106$.
+
+Find $T(1\\,000\\,000\\,000)$.
# --hints--
-`necklace(1000000000)` should return 747215561862.
+`necklace(1000000000)` should return `747215561862`.
```js
assert.strictEqual(necklace(1000000000), 747215561862);
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
index 8b9c108829..8735e80e53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-429-sum-of-squares-of-unitary-divisors.md
@@ -8,22 +8,22 @@ dashedName: problem-429-sum-of-squares-of-unitary-divisors
# --description--
-A unitary divisor d of a number n is a divisor of n that has the property gcd(d, n/d) = 1.
+A unitary divisor $d$ of a number $n$ is a divisor of $n$ that has the property $gcd(d, \frac{n}{d}) = 1$.
-The unitary divisors of 4! = 24 are 1, 3, 8 and 24.
+The unitary divisors of $4! = 24$ are 1, 3, 8 and 24.
-The sum of their squares is 12 + 32 + 82 + 242 = 650.
+The sum of their squares is $12 + 32 + 82 + 242 = 650$.
-Let S(n) represent the sum of the squares of the unitary divisors of n. Thus S(4!)=650.
+Let $S(n)$ represent the sum of the squares of the unitary divisors of $n$. Thus $S(4!) = 650$.
-Find S(100 000 000!) modulo 1 000 000 009.
+Find $S(100\\,000\\,000!)$ modulo $1\\,000\\,000\\,009$.
# --hints--
-`euler429()` should return 98792821.
+`sumSquaresOfUnitaryDivisors()` should return `98792821`.
```js
-assert.strictEqual(euler429(), 98792821);
+assert.strictEqual(sumSquaresOfUnitaryDivisors(), 98792821);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler429(), 98792821);
## --seed-contents--
```js
-function euler429() {
+function sumSquaresOfUnitaryDivisors() {
return true;
}
-euler429();
+sumSquaresOfUnitaryDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
index ba66983c7b..ded4becfce 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-430-range-flips.md
@@ -8,24 +8,26 @@ dashedName: problem-430-range-flips
# --description--
-N disks are placed in a row, indexed 1 to N from left to right.
+$N$ disks are placed in a row, indexed 1 to $N$ from left to right.
Each disk has a black side and white side. Initially all disks show their white side.
-At each turn, two, not necessarily distinct, integers A and B between 1 and N (inclusive) are chosen uniformly at random. All disks with an index from A to B (inclusive) are flipped.
+At each turn, two, not necessarily distinct, integers $A$ and $B$ between 1 and $N$ (inclusive) are chosen uniformly at random. All disks with an index from $A$ to $B$ (inclusive) are flipped.
-The following example shows the case N = 8. At the first turn A = 5 and B = 2, and at the second turn A = 4 and B = 6.
+The following example shows the case $N = 8$. At the first turn $A = 5$ and $B = 2$, and at the second turn $A = 4$ and $B = 6$.
-Let E(N, M) be the expected number of disks that show their white side after M turns. We can verify that E(3, 1) = 10/9, E(3, 2) = 5/3, E(10, 4) ≈ 5.157 and E(100, 10) ≈ 51.893.
+ -Find E(1010, 4000). Give your answer rounded to 2 decimal places behind the decimal point.
+Let $E(N, M)$ be the expected number of disks that show their white side after $M$ turns. We can verify that $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$ and $E(100, 10) ≈ 51.893$.
+
+Find $E({10}^{10}, 4000)$. Give your answer rounded to 2 decimal places behind the decimal point.
# --hints--
-`euler430()` should return 5000624921.38.
+`rangeFlips()` should return `5000624921.38`.
```js
-assert.strictEqual(euler430(), 5000624921.38);
+assert.strictEqual(rangeFlips(), 5000624921.38);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler430(), 5000624921.38);
## --seed-contents--
```js
-function euler430() {
+function rangeFlips() {
return true;
}
-euler430();
+rangeFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
index 51a104b47a..96f109a2e8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
@@ -10,20 +10,22 @@ dashedName: problem-431-square-space-silo
Fred the farmer arranges to have a new storage silo installed on his farm and having an obsession for all things square he is absolutely devastated when he discovers that it is circular. Quentin, the representative from the company that installed the silo, explains that they only manufacture cylindrical silos, but he points out that it is resting on a square base. Fred is not amused and insists that it is removed from his property.
-Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\\alpha = 30$ degrees, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
+Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\alpha = 30°$, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
-We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114785284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114785284) \\approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511167869) \\approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
+
-Find E(1010, 4000). Give your answer rounded to 2 decimal places behind the decimal point.
+Let $E(N, M)$ be the expected number of disks that show their white side after $M$ turns. We can verify that $E(3, 1) = \frac{10}{9}$, $E(3, 2) = \frac{5}{3}$, $E(10, 4) ≈ 5.157$ and $E(100, 10) ≈ 51.893$.
+
+Find $E({10}^{10}, 4000)$. Give your answer rounded to 2 decimal places behind the decimal point.
# --hints--
-`euler430()` should return 5000624921.38.
+`rangeFlips()` should return `5000624921.38`.
```js
-assert.strictEqual(euler430(), 5000624921.38);
+assert.strictEqual(rangeFlips(), 5000624921.38);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler430(), 5000624921.38);
## --seed-contents--
```js
-function euler430() {
+function rangeFlips() {
return true;
}
-euler430();
+rangeFlips();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
index 51a104b47a..96f109a2e8 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-431-square-space-silo.md
@@ -10,20 +10,22 @@ dashedName: problem-431-square-space-silo
Fred the farmer arranges to have a new storage silo installed on his farm and having an obsession for all things square he is absolutely devastated when he discovers that it is circular. Quentin, the representative from the company that installed the silo, explains that they only manufacture cylindrical silos, but he points out that it is resting on a square base. Fred is not amused and insists that it is removed from his property.
-Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\\alpha = 30$ degrees, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
+Quick thinking Quentin explains that when granular materials are delivered from above a conical slope is formed and the natural angle made with the horizontal is called the angle of repose. For example if the angle of repose, $\alpha = 30°$, and grain is delivered at the centre of the silo then a perfect cone will form towards the top of the cylinder. In the case of this silo, which has a diameter of 6m, the amount of space wasted would be approximately 32.648388556 m3. However, if grain is delivered at a point on the top which has a horizontal distance of $x$ metres from the centre then a cone with a strangely curved and sloping base is formed. He shows Fred a picture.
-We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114785284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114785284) \\approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511167869) \\approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
+ -Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40 degrees. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114\\,785\\,284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114\\,785\\,284) \approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511\\,167\\,869) \approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
-If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\\sum x$ correct to 9 decimal places.
+Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40°. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+
+If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\sum x$ correct to 9 decimal places.
# --hints--
-`euler431()` should return 23.386029052.
+`squareSpaceSilo()` should return `23.386029052`.
```js
-assert.strictEqual(euler431(), 23.386029052);
+assert.strictEqual(squareSpaceSilo(), 23.386029052);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler431(), 23.386029052);
## --seed-contents--
```js
-function euler431() {
+function squareSpaceSilo() {
return true;
}
-euler431();
+squareSpaceSilo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
index 4f0f5928ef..845ee38a53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
@@ -8,18 +8,18 @@ dashedName: problem-432-totient-sum
# --description--
-Let S(n,m) = ∑φ(n × i) for 1 ≤ i ≤ m. (φ is Euler's totient function)
+Let $S(n, m) = \sum φ(n × i)$ for $1 ≤ i ≤ m$. ($φ$ is Euler's totient function)
-You are given that S(510510,106 )= 45480596821125120.
+You are given that $S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$.
-Find S(510510,1011). Give the last 9 digits of your answer.
+Find $S(510\\,510, {10}^{11})$. Give the last 9 digits of your answer.
# --hints--
-`euler432()` should return 754862080.
+`totientSum()` should return `754862080`.
```js
-assert.strictEqual(euler432(), 754862080);
+assert.strictEqual(totientSum(), 754862080);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler432(), 754862080);
## --seed-contents--
```js
-function euler432() {
+function totientSum() {
return true;
}
-euler432();
+totientSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
index 5423c8691c..1999a6f26c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
@@ -8,22 +8,29 @@ dashedName: problem-433-steps-in-euclids-algorithm
# --description--
-Let E(x0, y0) be the number of steps it takes to determine the greatest common divisor of x0 and y0 with Euclid's algorithm. More formally:x1 = y0, y1 = x0 mod y0xn = yn-1, yn = xn-1 mod yn-1
+Let $E(x_0, y_0)$ be the number of steps it takes to determine the greatest common divisor of $x_0$ and $y_0$ with Euclid's algorithm. More formally:
-E(x0, y0) is the smallest n such that yn = 0.
+$$\begin{align}
+ & x_1 = y_0, y_1 = x_0\bmod y_0 \\\\
+ & x_n = y_{n - 1}, y_n = x_{n - 1}\bmod y_{n - 1}
+\end{align}$$
-We have E(1,1) = 1, E(10,6) = 3 and E(6,10) = 4.
+$E(x_0, y_0)$ is the smallest $n$ such that $y_n = 0$.
-Define S(N) as the sum of E(x,y) for 1 ≤ x,y ≤ N. We have S(1) = 1, S(10) = 221 and S(100) = 39826.
+We have $E(1, 1) = 1$, $E(10, 6) = 3$ and $E(6, 10) = 4$.
-Find S(5·106).
+Define $S(N)$ as the sum of $E(x, y)$ for $1 ≤ x$, $y ≤ N$.
+
+We have $S(1) = 1$, $S(10) = 221$ and $S(100) = 39\\,826$.
+
+Find $S(5 \times {10}^6)$.
# --hints--
-`euler433()` should return 326624372659664.
+`stepsInEuclidsAlgorithm()` should return `326624372659664`.
```js
-assert.strictEqual(euler433(), 326624372659664);
+assert.strictEqual(stepsInEuclidsAlgorithm(), 326624372659664);
```
# --seed--
@@ -31,12 +38,12 @@ assert.strictEqual(euler433(), 326624372659664);
## --seed-contents--
```js
-function euler433() {
+function stepsInEuclidsAlgorithm() {
return true;
}
-euler433();
+stepsInEuclidsAlgorithm();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
index 48a01b7a3b..a598aebb10 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
@@ -18,18 +18,32 @@ A rigid graph is an embedding of a graph which is not flexible.
Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
-The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates: However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid: Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
-Let R(m,n) be the number of ways to make the m × n grid graph rigid. E.g. R(2,3) = 19 and R(5,5) = 23679901
+
-Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40 degrees. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+We shall let the amount of space wasted in cubic metres be given by $V(x)$. If $x = 1.114\\,785\\,284$, which happens to have three squared decimal places, then the amount of space wasted, $V(1.114\\,785\\,284) \approx 36$. Given the range of possible solutions to this problem there is exactly one other option: $V(2.511\\,167\\,869) \approx 49$. It would be like knowing that the square is king of the silo, sitting in splendid glory on top of your grain.
-If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\\sum x$ correct to 9 decimal places.
+Fred's eyes light up with delight at this elegant resolution, but on closer inspection of Quentin's drawings and calculations his happiness turns to despondency once more. Fred points out to Quentin that it's the radius of the silo that is 6 metres, not the diameter, and the angle of repose for his grain is 40°. However, if Quentin can find a set of solutions for this particular silo then he will be more than happy to keep it.
+
+If Quick thinking Quentin is to satisfy frustratingly fussy Fred the farmer's appetite for all things square then determine the values of $x$ for all possible square space wastage options and calculate $\sum x$ correct to 9 decimal places.
# --hints--
-`euler431()` should return 23.386029052.
+`squareSpaceSilo()` should return `23.386029052`.
```js
-assert.strictEqual(euler431(), 23.386029052);
+assert.strictEqual(squareSpaceSilo(), 23.386029052);
```
# --seed--
@@ -31,12 +33,12 @@ assert.strictEqual(euler431(), 23.386029052);
## --seed-contents--
```js
-function euler431() {
+function squareSpaceSilo() {
return true;
}
-euler431();
+squareSpaceSilo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
index 4f0f5928ef..845ee38a53 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-432-totient-sum.md
@@ -8,18 +8,18 @@ dashedName: problem-432-totient-sum
# --description--
-Let S(n,m) = ∑φ(n × i) for 1 ≤ i ≤ m. (φ is Euler's totient function)
+Let $S(n, m) = \sum φ(n × i)$ for $1 ≤ i ≤ m$. ($φ$ is Euler's totient function)
-You are given that S(510510,106 )= 45480596821125120.
+You are given that $S(510\\,510, {10}^6) = 45\\,480\\,596\\,821\\,125\\,120$.
-Find S(510510,1011). Give the last 9 digits of your answer.
+Find $S(510\\,510, {10}^{11})$. Give the last 9 digits of your answer.
# --hints--
-`euler432()` should return 754862080.
+`totientSum()` should return `754862080`.
```js
-assert.strictEqual(euler432(), 754862080);
+assert.strictEqual(totientSum(), 754862080);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler432(), 754862080);
## --seed-contents--
```js
-function euler432() {
+function totientSum() {
return true;
}
-euler432();
+totientSum();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
index 5423c8691c..1999a6f26c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-433-steps-in-euclids-algorithm.md
@@ -8,22 +8,29 @@ dashedName: problem-433-steps-in-euclids-algorithm
# --description--
-Let E(x0, y0) be the number of steps it takes to determine the greatest common divisor of x0 and y0 with Euclid's algorithm. More formally:x1 = y0, y1 = x0 mod y0xn = yn-1, yn = xn-1 mod yn-1
+Let $E(x_0, y_0)$ be the number of steps it takes to determine the greatest common divisor of $x_0$ and $y_0$ with Euclid's algorithm. More formally:
-E(x0, y0) is the smallest n such that yn = 0.
+$$\begin{align}
+ & x_1 = y_0, y_1 = x_0\bmod y_0 \\\\
+ & x_n = y_{n - 1}, y_n = x_{n - 1}\bmod y_{n - 1}
+\end{align}$$
-We have E(1,1) = 1, E(10,6) = 3 and E(6,10) = 4.
+$E(x_0, y_0)$ is the smallest $n$ such that $y_n = 0$.
-Define S(N) as the sum of E(x,y) for 1 ≤ x,y ≤ N. We have S(1) = 1, S(10) = 221 and S(100) = 39826.
+We have $E(1, 1) = 1$, $E(10, 6) = 3$ and $E(6, 10) = 4$.
-Find S(5·106).
+Define $S(N)$ as the sum of $E(x, y)$ for $1 ≤ x$, $y ≤ N$.
+
+We have $S(1) = 1$, $S(10) = 221$ and $S(100) = 39\\,826$.
+
+Find $S(5 \times {10}^6)$.
# --hints--
-`euler433()` should return 326624372659664.
+`stepsInEuclidsAlgorithm()` should return `326624372659664`.
```js
-assert.strictEqual(euler433(), 326624372659664);
+assert.strictEqual(stepsInEuclidsAlgorithm(), 326624372659664);
```
# --seed--
@@ -31,12 +38,12 @@ assert.strictEqual(euler433(), 326624372659664);
## --seed-contents--
```js
-function euler433() {
+function stepsInEuclidsAlgorithm() {
return true;
}
-euler433();
+stepsInEuclidsAlgorithm();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
index 48a01b7a3b..a598aebb10 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-434-rigid-graphs.md
@@ -18,18 +18,32 @@ A rigid graph is an embedding of a graph which is not flexible.
Informally, a graph is rigid if by replacing the vertices with fully rotating hinges and the edges with rods that are unbending and inelastic, no parts of the graph can be moved independently from the rest of the graph.
-The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates: However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid: Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+The grid graphs embedded in the Euclidean plane are not rigid, as the following animation demonstrates:
-Let R(m,n) be the number of ways to make the m × n grid graph rigid. E.g. R(2,3) = 19 and R(5,5) = 23679901
+ -Define S(N) as ∑R(i,j) for 1 ≤ i, j ≤ N. E.g. S(5) = 25021721. Find S(100), give your answer modulo 1000000033
+However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid:
+
+
-Define S(N) as ∑R(i,j) for 1 ≤ i, j ≤ N. E.g. S(5) = 25021721. Find S(100), give your answer modulo 1000000033
+However, one can make them rigid by adding diagonal edges to the cells. For example, for the 2x3 grid graph, there are 19 ways to make the graph rigid:
+
+ +
+Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+
+Let $R(m, n)$ be the number of ways to make the $m × n$ grid graph rigid.
+
+E.g. $R(2, 3) = 19$ and $R(5, 5) = 23\\,679\\,901$.
+
+Define $S(N)$ as $\sum R(i, j)$ for $1 ≤ i$, $j ≤ N$.
+
+E.g. $S(5) = 25\\,021\\,721$.
+
+Find $S(100)$, give your answer modulo $1\\,000\\,000\\,033$.
# --hints--
-`euler434()` should return 863253606.
+`rigidGraphs()` should return `863253606`.
```js
-assert.strictEqual(euler434(), 863253606);
+assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
@@ -37,12 +51,12 @@ assert.strictEqual(euler434(), 863253606);
## --seed-contents--
```js
-function euler434() {
+function rigidGraphs() {
return true;
}
-euler434();
+rigidGraphs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
index ee078a7382..9be0b43a51 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
@@ -8,20 +8,20 @@ dashedName: problem-435-polynomials-of-fibonacci-numbers
# --description--
-The Fibonacci numbers {fn, n ≥ 0} are defined recursively as fn = fn-1 + fn-2 with base cases f0 = 0 and f1 = 1.
+The Fibonacci numbers $\\{f_n, n ≥ 0\\}$ are defined recursively as $f_n = f_{n - 1} + f_{n - 2}$ with base cases $f_0 = 0$ and $f_1 = 1$.
-Define the polynomials {Fn, n ≥ 0} as Fn(x) = ∑fixi for 0 ≤ i ≤ n.
+Define the polynomials $\\{F_n, n ≥ 0\\}$ as $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$.
-For example, F7(x) = x + x2 + 2x3 + 3x4 + 5x5 + 8x6 + 13x7, and F7(11) = 268357683.
+For example, $F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, and $F_7(11) = 268\\,357\\,683$.
-Let n = 1015. Find the sum \[∑0≤x≤100 Fn(x)] mod 1307674368000 (= 15!).
+Let $n = {10}^{15}$. Find the sum $\displaystyle\sum_{x = 0}^{100} F_n(x)$ and give your answer modulo $1\\,307\\,674\\,368\\,000 \\, (= 15!)$.
# --hints--
-`euler435()` should return 252541322550.
+`polynomialsOfFibonacciNumbers()` should return `252541322550`.
```js
-assert.strictEqual(euler435(), 252541322550);
+assert.strictEqual(polynomialsOfFibonacciNumbers(), 252541322550);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler435(), 252541322550);
## --seed-contents--
```js
-function euler435() {
+function polynomialsOfFibonacciNumbers() {
return true;
}
-euler435();
+polynomialsOfFibonacciNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
index 43b111b868..d5dfcc5920 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
@@ -14,24 +14,26 @@ She suggests they play a game of chance to determine who will wash the dishes.
For this game, they shall use a generator of independent random numbers uniformly distributed between 0 and 1.
-The game starts with S = 0.
+The game starts with $S = 0$.
-The first player, Louise, adds to S different random numbers from the generator until S > 1 and records her last random number 'x'.
+The first player, Louise, adds to $S$ different random numbers from the generator until $S > 1$ and records her last random number '$x$'.
-The second player, Julie, continues adding to S different random numbers from the generator until S > 2 and records her last random number 'y'.
+The second player, Julie, continues adding to $S$ different random numbers from the generator until $S > 2$ and records her last random number '$y$'.
-The player with the highest number wins and the loser washes the dishes, i.e. if y > x the second player wins.
+The player with the highest number wins and the loser washes the dishes, i.e. if $y > x$ the second player wins.
-For example, if the first player draws 0.62 and 0.44, the first player turn ends since 0.62+0.44 > 1 and x = 0.44. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since 0.62+0.44+0.1+0.27+0.91 > 2 and y = 0.91. Since y > x, the second player wins.
+For example, if the first player draws 0.62 and 0.44, the first player turn ends since $0.62 + 0.44 > 1$ and $x = 0.44$. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since $0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ and $y = 0.91$. Since $y > x$, the second player wins.
-Louise thinks about it for a second, and objects: "That's not fair". What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
+Louise thinks about it for a second, and objects: "That's not fair".
+
+What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
# --hints--
-`euler436()` should return 0.5276662759.
+`unfairWager()` should return `0.5276662759`.
```js
-assert.strictEqual(euler436(), 0.5276662759);
+assert.strictEqual(unfairWager(), 0.5276662759);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler436(), 0.5276662759);
## --seed-contents--
```js
-function euler436() {
+function unfairWager() {
return true;
}
-euler436();
+unfairWager();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
index 0072d0f9a9..8a109549c1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
@@ -8,7 +8,7 @@ dashedName: problem-437-fibonacci-primitive-roots
# --description--
-When we calculate 8n modulo 11 for n=0 to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
+When we calculate $8^n$ modulo 11 for $n = 0$ to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
As we see all possible values from 1 to 10 occur. So 8 is a primitive root of 11.
@@ -16,32 +16,30 @@ But there is more:
If we take a closer look we see:
-1+8=9
+$$\begin{align}
+ & 1 + 8 = 9 \\\\
+ & 8 + 9 = 17 ≡ 6\bmod 11 \\\\
+ & 9 + 6 = 15 ≡ 4\bmod 11 \\\\
+ & 6 + 4 = 10 \\\\
+ & 4 + 10 = 14 ≡ 3\bmod 11 \\\\
+ & 10 + 3 = 13 ≡ 2\bmod 11 \\\\
+ & 3 + 2 = 5 \\\\
+ & 2 + 5 = 7 \\\\
+ & 5 + 7 = 12 ≡ 1\bmod 11.
+\end{align}$$
-8+9=17≡6 mod 11
+So the powers of 8 mod 11 are cyclic with period 10, and $8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$. 8 is called a Fibonacci primitive root of 11.
-9+6=15≡4 mod 11
+Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491.
-6+4=10
-
-4+10=14≡3 mod 11
-
-10+3=13≡2 mod 11
-
-3+2=5
-
-2+5=7
-
-5+7=12≡1 mod 11.
-
-So the powers of 8 mod 11 are cyclic with period 10, and 8n + 8n+1 ≡ 8n+2 (mod 11). 8 is called a Fibonacci primitive root of 11. Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491. Find the sum of the primes less than 100,000,000 with at least one Fibonacci primitive root.
+Find the sum of the primes less than $100\\,000\\,000$ with at least one Fibonacci primitive root.
# --hints--
-`euler437()` should return 74204709657207.
+`fibonacciPrimitiveRoots()` should return `74204709657207`.
```js
-assert.strictEqual(euler437(), 74204709657207);
+assert.strictEqual(fibonacciPrimitiveRoots(), 74204709657207);
```
# --seed--
@@ -49,12 +47,12 @@ assert.strictEqual(euler437(), 74204709657207);
## --seed-contents--
```js
-function euler437() {
+function fibonacciPrimitiveRoots() {
return true;
}
-euler437();
+fibonacciPrimitiveRoots();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
index 112326a2fa..e247069b3d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
@@ -8,20 +8,27 @@ dashedName: problem-438-integer-part-of-polynomial-equations-solutions
# --description--
-For an n-tuple of integers t = (a1, ..., an), let (x1, ..., xn) be the solutions of the polynomial equation xn + a1xn-1 + a2xn-2 + ... + an-1x + an = 0.
+For an $n$-tuple of integers $t = (a_1, \ldots, a_n)$, let $(x_1, \ldots, x_n)$ be the solutions of the polynomial equation $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$.
-Consider the following two conditions: x1, ..., xn are all real. If x1, ..., xn are sorted, ⌊xi⌋ = i for 1 ≤ i ≤ n. (⌊·⌋: floor function.)
+Consider the following two conditions:
-In the case of n = 4, there are 12 n-tuples of integers which satisfy both conditions. We define S(t) as the sum of the absolute values of the integers in t. For n = 4 we can verify that ∑S(t) = 2087 for all n-tuples t which satisfy both conditions.
+- $x_1, \ldots, x_n$ are all real.
+- If $x_1, ..., x_n$ are sorted, $⌊x_i⌋ = i$ for $1 ≤ i ≤ n$. ($⌊·⌋:$ floor function.)
-Find ∑S(t) for n = 7.
+In the case of $n = 4$, there are 12 $n$-tuples of integers which satisfy both conditions.
+
+We define $S(t)$ as the sum of the absolute values of the integers in $t$.
+
+For $n = 4$ we can verify that $\sum S(t) = 2087$ for all $n$-tuples t which satisfy both conditions.
+
+Find $\sum S(t)$ for $n = 7$.
# --hints--
-`euler438()` should return 2046409616809.
+`polynomialIntegerPart()` should return `2046409616809`.
```js
-assert.strictEqual(euler438(), 2046409616809);
+assert.strictEqual(polynomialIntegerPart(), 2046409616809);
```
# --seed--
@@ -29,12 +36,12 @@ assert.strictEqual(euler438(), 2046409616809);
## --seed-contents--
```js
-function euler438() {
+function polynomialIntegerPart() {
return true;
}
-euler438();
+polynomialIntegerPart();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
index 4fb1871a85..264dfaf572 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
@@ -8,20 +8,22 @@ dashedName: problem-439-sum-of-sum-of-divisors
# --description--
-Let d(k) be the sum of all divisors of k.
+Let $d(k)$ be the sum of all divisors of $k$.
-We define the function S(N) = ∑1≤i≤N ∑1≤j≤Nd(i·j).
+We define the function $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$.
-For example, S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59.
+For example, $S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$.
-You are given that S(103) = 563576517282 and S(105) mod 109 = 215766508. Find S(1011) mod 109.
+You are given that $S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$.
+
+Find $S({10}^{11})\bmod {10}^9$.
# --hints--
-`euler439()` should return 968697378.
+`sumOfSumOfDivisors()` should return `968697378`.
```js
-assert.strictEqual(euler439(), 968697378);
+assert.strictEqual(sumOfSumOfDivisors(), 968697378);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler439(), 968697378);
## --seed-contents--
```js
-function euler439() {
+function sumOfSumOfDivisors() {
return true;
}
-euler439();
+sumOfSumOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
index a68f99a00a..21d7100bbd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
@@ -8,24 +8,36 @@ dashedName: problem-440-gcd-and-tiling
# --description--
-We want to tile a board of length n and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
+We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
-For example, here are some of the ways to tile a board of length n = 8:
+
+
+Note that for the purposes of this problem, we do not consider changing the orientation of a diagonal edge or adding both diagonal edges to a cell as a different way of making a grid graph rigid.
+
+Let $R(m, n)$ be the number of ways to make the $m × n$ grid graph rigid.
+
+E.g. $R(2, 3) = 19$ and $R(5, 5) = 23\\,679\\,901$.
+
+Define $S(N)$ as $\sum R(i, j)$ for $1 ≤ i$, $j ≤ N$.
+
+E.g. $S(5) = 25\\,021\\,721$.
+
+Find $S(100)$, give your answer modulo $1\\,000\\,000\\,033$.
# --hints--
-`euler434()` should return 863253606.
+`rigidGraphs()` should return `863253606`.
```js
-assert.strictEqual(euler434(), 863253606);
+assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
@@ -37,12 +51,12 @@ assert.strictEqual(euler434(), 863253606);
## --seed-contents--
```js
-function euler434() {
+function rigidGraphs() {
return true;
}
-euler434();
+rigidGraphs();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
index ee078a7382..9be0b43a51 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-435-polynomials-of-fibonacci-numbers.md
@@ -8,20 +8,20 @@ dashedName: problem-435-polynomials-of-fibonacci-numbers
# --description--
-The Fibonacci numbers {fn, n ≥ 0} are defined recursively as fn = fn-1 + fn-2 with base cases f0 = 0 and f1 = 1.
+The Fibonacci numbers $\\{f_n, n ≥ 0\\}$ are defined recursively as $f_n = f_{n - 1} + f_{n - 2}$ with base cases $f_0 = 0$ and $f_1 = 1$.
-Define the polynomials {Fn, n ≥ 0} as Fn(x) = ∑fixi for 0 ≤ i ≤ n.
+Define the polynomials $\\{F_n, n ≥ 0\\}$ as $F_n(x) = \displaystyle\sum_{i = 0}^n f_ix^i$.
-For example, F7(x) = x + x2 + 2x3 + 3x4 + 5x5 + 8x6 + 13x7, and F7(11) = 268357683.
+For example, $F_7(x) = x + x^2 + 2x^3 + 3x^4 + 5x^5 + 8x^6 + 13x^7$, and $F_7(11) = 268\\,357\\,683$.
-Let n = 1015. Find the sum \[∑0≤x≤100 Fn(x)] mod 1307674368000 (= 15!).
+Let $n = {10}^{15}$. Find the sum $\displaystyle\sum_{x = 0}^{100} F_n(x)$ and give your answer modulo $1\\,307\\,674\\,368\\,000 \\, (= 15!)$.
# --hints--
-`euler435()` should return 252541322550.
+`polynomialsOfFibonacciNumbers()` should return `252541322550`.
```js
-assert.strictEqual(euler435(), 252541322550);
+assert.strictEqual(polynomialsOfFibonacciNumbers(), 252541322550);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler435(), 252541322550);
## --seed-contents--
```js
-function euler435() {
+function polynomialsOfFibonacciNumbers() {
return true;
}
-euler435();
+polynomialsOfFibonacciNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
index 43b111b868..d5dfcc5920 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-436-unfair-wager.md
@@ -14,24 +14,26 @@ She suggests they play a game of chance to determine who will wash the dishes.
For this game, they shall use a generator of independent random numbers uniformly distributed between 0 and 1.
-The game starts with S = 0.
+The game starts with $S = 0$.
-The first player, Louise, adds to S different random numbers from the generator until S > 1 and records her last random number 'x'.
+The first player, Louise, adds to $S$ different random numbers from the generator until $S > 1$ and records her last random number '$x$'.
-The second player, Julie, continues adding to S different random numbers from the generator until S > 2 and records her last random number 'y'.
+The second player, Julie, continues adding to $S$ different random numbers from the generator until $S > 2$ and records her last random number '$y$'.
-The player with the highest number wins and the loser washes the dishes, i.e. if y > x the second player wins.
+The player with the highest number wins and the loser washes the dishes, i.e. if $y > x$ the second player wins.
-For example, if the first player draws 0.62 and 0.44, the first player turn ends since 0.62+0.44 > 1 and x = 0.44. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since 0.62+0.44+0.1+0.27+0.91 > 2 and y = 0.91. Since y > x, the second player wins.
+For example, if the first player draws 0.62 and 0.44, the first player turn ends since $0.62 + 0.44 > 1$ and $x = 0.44$. If the second players draws 0.1, 0.27 and 0.91, the second player turn ends since $0.62 + 0.44 + 0.1 + 0.27 + 0.91 > 2$ and $y = 0.91$. Since $y > x$, the second player wins.
-Louise thinks about it for a second, and objects: "That's not fair". What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
+Louise thinks about it for a second, and objects: "That's not fair".
+
+What is the probability that the second player wins? Give your answer rounded to 10 places behind the decimal point in the form 0.abcdefghij
# --hints--
-`euler436()` should return 0.5276662759.
+`unfairWager()` should return `0.5276662759`.
```js
-assert.strictEqual(euler436(), 0.5276662759);
+assert.strictEqual(unfairWager(), 0.5276662759);
```
# --seed--
@@ -39,12 +41,12 @@ assert.strictEqual(euler436(), 0.5276662759);
## --seed-contents--
```js
-function euler436() {
+function unfairWager() {
return true;
}
-euler436();
+unfairWager();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
index 0072d0f9a9..8a109549c1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-437-fibonacci-primitive-roots.md
@@ -8,7 +8,7 @@ dashedName: problem-437-fibonacci-primitive-roots
# --description--
-When we calculate 8n modulo 11 for n=0 to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
+When we calculate $8^n$ modulo 11 for $n = 0$ to 9 we get: 1, 8, 9, 6, 4, 10, 3, 2, 5, 7.
As we see all possible values from 1 to 10 occur. So 8 is a primitive root of 11.
@@ -16,32 +16,30 @@ But there is more:
If we take a closer look we see:
-1+8=9
+$$\begin{align}
+ & 1 + 8 = 9 \\\\
+ & 8 + 9 = 17 ≡ 6\bmod 11 \\\\
+ & 9 + 6 = 15 ≡ 4\bmod 11 \\\\
+ & 6 + 4 = 10 \\\\
+ & 4 + 10 = 14 ≡ 3\bmod 11 \\\\
+ & 10 + 3 = 13 ≡ 2\bmod 11 \\\\
+ & 3 + 2 = 5 \\\\
+ & 2 + 5 = 7 \\\\
+ & 5 + 7 = 12 ≡ 1\bmod 11.
+\end{align}$$
-8+9=17≡6 mod 11
+So the powers of 8 mod 11 are cyclic with period 10, and $8^n + 8^{n + 1} ≡ 8^{n + 2} (\text{mod } 11)$. 8 is called a Fibonacci primitive root of 11.
-9+6=15≡4 mod 11
+Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491.
-6+4=10
-
-4+10=14≡3 mod 11
-
-10+3=13≡2 mod 11
-
-3+2=5
-
-2+5=7
-
-5+7=12≡1 mod 11.
-
-So the powers of 8 mod 11 are cyclic with period 10, and 8n + 8n+1 ≡ 8n+2 (mod 11). 8 is called a Fibonacci primitive root of 11. Not every prime has a Fibonacci primitive root. There are 323 primes less than 10000 with one or more Fibonacci primitive roots and the sum of these primes is 1480491. Find the sum of the primes less than 100,000,000 with at least one Fibonacci primitive root.
+Find the sum of the primes less than $100\\,000\\,000$ with at least one Fibonacci primitive root.
# --hints--
-`euler437()` should return 74204709657207.
+`fibonacciPrimitiveRoots()` should return `74204709657207`.
```js
-assert.strictEqual(euler437(), 74204709657207);
+assert.strictEqual(fibonacciPrimitiveRoots(), 74204709657207);
```
# --seed--
@@ -49,12 +47,12 @@ assert.strictEqual(euler437(), 74204709657207);
## --seed-contents--
```js
-function euler437() {
+function fibonacciPrimitiveRoots() {
return true;
}
-euler437();
+fibonacciPrimitiveRoots();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
index 112326a2fa..e247069b3d 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-438-integer-part-of-polynomial-equations-solutions.md
@@ -8,20 +8,27 @@ dashedName: problem-438-integer-part-of-polynomial-equations-solutions
# --description--
-For an n-tuple of integers t = (a1, ..., an), let (x1, ..., xn) be the solutions of the polynomial equation xn + a1xn-1 + a2xn-2 + ... + an-1x + an = 0.
+For an $n$-tuple of integers $t = (a_1, \ldots, a_n)$, let $(x_1, \ldots, x_n)$ be the solutions of the polynomial equation $x^n + a_1x^{n - 1} + a_2x^{n - 2} + \ldots + a_{n - 1}x + a_n = 0$.
-Consider the following two conditions: x1, ..., xn are all real. If x1, ..., xn are sorted, ⌊xi⌋ = i for 1 ≤ i ≤ n. (⌊·⌋: floor function.)
+Consider the following two conditions:
-In the case of n = 4, there are 12 n-tuples of integers which satisfy both conditions. We define S(t) as the sum of the absolute values of the integers in t. For n = 4 we can verify that ∑S(t) = 2087 for all n-tuples t which satisfy both conditions.
+- $x_1, \ldots, x_n$ are all real.
+- If $x_1, ..., x_n$ are sorted, $⌊x_i⌋ = i$ for $1 ≤ i ≤ n$. ($⌊·⌋:$ floor function.)
-Find ∑S(t) for n = 7.
+In the case of $n = 4$, there are 12 $n$-tuples of integers which satisfy both conditions.
+
+We define $S(t)$ as the sum of the absolute values of the integers in $t$.
+
+For $n = 4$ we can verify that $\sum S(t) = 2087$ for all $n$-tuples t which satisfy both conditions.
+
+Find $\sum S(t)$ for $n = 7$.
# --hints--
-`euler438()` should return 2046409616809.
+`polynomialIntegerPart()` should return `2046409616809`.
```js
-assert.strictEqual(euler438(), 2046409616809);
+assert.strictEqual(polynomialIntegerPart(), 2046409616809);
```
# --seed--
@@ -29,12 +36,12 @@ assert.strictEqual(euler438(), 2046409616809);
## --seed-contents--
```js
-function euler438() {
+function polynomialIntegerPart() {
return true;
}
-euler438();
+polynomialIntegerPart();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
index 4fb1871a85..264dfaf572 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-439-sum-of-sum-of-divisors.md
@@ -8,20 +8,22 @@ dashedName: problem-439-sum-of-sum-of-divisors
# --description--
-Let d(k) be the sum of all divisors of k.
+Let $d(k)$ be the sum of all divisors of $k$.
-We define the function S(N) = ∑1≤i≤N ∑1≤j≤Nd(i·j).
+We define the function $S(N) = \sum_{i = 1}^N \sum_{j = 1}^N d(i \times j)$.
-For example, S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59.
+For example, $S(3) = d(1) + d(2) + d(3) + d(2) + d(4) + d(6) + d(3) + d(6) + d(9) = 59$.
-You are given that S(103) = 563576517282 and S(105) mod 109 = 215766508. Find S(1011) mod 109.
+You are given that $S({10}^3) = 563\\,576\\,517\\,282$ and $S({10}^5)\bmod {10}^9 = 215\\,766\\,508$.
+
+Find $S({10}^{11})\bmod {10}^9$.
# --hints--
-`euler439()` should return 968697378.
+`sumOfSumOfDivisors()` should return `968697378`.
```js
-assert.strictEqual(euler439(), 968697378);
+assert.strictEqual(sumOfSumOfDivisors(), 968697378);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler439(), 968697378);
## --seed-contents--
```js
-function euler439() {
+function sumOfSumOfDivisors() {
return true;
}
-euler439();
+sumOfSumOfDivisors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
index a68f99a00a..21d7100bbd 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-440-gcd-and-tiling.md
@@ -8,24 +8,36 @@ dashedName: problem-440-gcd-and-tiling
# --description--
-We want to tile a board of length n and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
+We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
-For example, here are some of the ways to tile a board of length n = 8:
+ -Let T(n) be the number of ways to tile a board of length n as described above.
+For example, here are some of the ways to tile a board of length $n = 8$:
-For example, T(1) = 10 and T(2) = 101.
+
-Let T(n) be the number of ways to tile a board of length n as described above.
+For example, here are some of the ways to tile a board of length $n = 8$:
-For example, T(1) = 10 and T(2) = 101.
+ -Let S(L) be the triple sum ∑a,b,c gcd(T(ca), T(cb)) for 1 ≤ a, b, c ≤ L. For example: S(2) = 10444 S(3) = 1292115238446807016106539989 S(4) mod 987 898 789 = 670616280.
+Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
-Find S(2000) mod 987 898 789.
+For example, $T(1) = 10$ and $T(2) = 101$.
+
+Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
+
+For example:
+
+$$\begin{align}
+ & S(2) = 10\\,444 \\\\
+ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
+ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
+\end{align}$$
+
+Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
-`euler440()` should return 970746056.
+`gcdAndTiling()` should return `970746056`.
```js
-assert.strictEqual(euler440(), 970746056);
+assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
@@ -33,12 +45,12 @@ assert.strictEqual(euler440(), 970746056);
## --seed-contents--
```js
-function euler440() {
+function gcdAndTiling() {
return true;
}
-euler440();
+gcdAndTiling();
```
# --solutions--
-Let S(L) be the triple sum ∑a,b,c gcd(T(ca), T(cb)) for 1 ≤ a, b, c ≤ L. For example: S(2) = 10444 S(3) = 1292115238446807016106539989 S(4) mod 987 898 789 = 670616280.
+Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
-Find S(2000) mod 987 898 789.
+For example, $T(1) = 10$ and $T(2) = 101$.
+
+Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
+
+For example:
+
+$$\begin{align}
+ & S(2) = 10\\,444 \\\\
+ & S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
+ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
+\end{align}$$
+
+Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
-`euler440()` should return 970746056.
+`gcdAndTiling()` should return `970746056`.
```js
-assert.strictEqual(euler440(), 970746056);
+assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
@@ -33,12 +45,12 @@ assert.strictEqual(euler440(), 970746056);
## --seed-contents--
```js
-function euler440() {
+function gcdAndTiling() {
return true;
}
-euler440();
+gcdAndTiling();
```
# --solutions--