gaspersic/freeCodeCamp
1
0
Fork 0
Code Issues Pull Requests Projects Releases Wiki Activity

update translation greedy-algorithms (#36388)

Browse Source 
* update translation greedy-algorithms

* updated translation after review
This commit is contained in:
Cleo Aguiar
2019-08-20 13:26:25 -03:00
committed by Randell Dawson
parent b6ffe92a84
commit ad5b99ed09
1 changed files with 19 additions and 11 deletions
Download Patch File Download Diff File Expand all files Collapse all files

28
guide/portuguese/algorithms/greedy-algorithms/index.md
View File

@ -2,7 +2,7 @@
title: Greedy Algorithms title: Greedy Algorithms
localeTitle: Algoritmos Greedy localeTitle: Algoritmos Greedy
--- ---
## O que é um algoritmo ganancioso ## O que é um algoritmo guloso
Você deve ter ouvido falar sobre muitas técnicas de design algorítmico enquanto analisa alguns dos artigos aqui. Alguns deles são: Você deve ter ouvido falar sobre muitas técnicas de design algorítmico enquanto analisa alguns dos artigos aqui. Alguns deles são:
@ -11,15 +11,15 @@ Você deve ter ouvido falar sobre muitas técnicas de design algorítmico enquan
* Programação gananciosa * Programação gananciosa
* Programação dinâmica para nomear alguns. Neste artigo, você aprenderá sobre o que é um algoritmo guloso e como você pode usar essa técnica para resolver muitos problemas de programação que, de outra forma, não parecem triviais. * Programação dinâmica para nomear alguns. Neste artigo, você aprenderá sobre o que é um algoritmo guloso e como você pode usar essa técnica para resolver muitos problemas de programação que, de outra forma, não parecem triviais.
Imagine que você está indo para caminhadas e seu objetivo é atingir o maior pico possível. Você já tem o mapa antes de começar, mas existem milhares de caminhos possíveis mostrados no mapa. Você é muito preguiçoso e simplesmente não tem tempo para avaliar cada um deles. Aparafuse o mapa! Você começou a caminhar com uma estratégia simples - ser ganancioso e míope. Apenas pegue caminhos que se inclinem mais para cima. Esta parece ser uma boa estratégia para caminhadas. Mas é sempre o melhor? Imagine que você está indo para caminhadas e seu objetivo é atingir o maior pico possível. Você já tem o mapa antes de começar, mas existem milhares de caminhos possíveis mostrados no mapa. Você é muito preguiçoso e simplesmente não tem tempo para avaliar cada um deles. Dane-se o mapa! Você começou a caminhar com uma estratégia simples - ser ganancioso e míope. Apenas pegue caminhos que se inclinem mais para cima. Esta parece ser uma boa estratégia para caminhadas. Mas é sempre o melhor?
Depois que a viagem termina e todo o seu corpo está dolorido e cansado, você olha para o mapa de trilhas pela primeira vez. Meu Deus! Há um rio lamacento que eu deveria ter atravessado, em vez de continuar subindo. Isso significa que um algoritmo guloso escolhe a melhor opção imediata e nunca reconsidera suas escolhas. Em termos de otimização de uma solução, isso significa simplesmente que a solução gulosa tentará encontrar soluções ótimas locais - que podem ser muitas - e poderá perder uma solução global ideal. Depois que a viagem termina e todo o seu corpo está dolorido e cansado, você olha para o mapa de trilhas pela primeira vez. Meu Deus! Há um rio lamacento que eu deveria ter atravessado, em vez de continuar subindo. Isso significa que um algoritmo guloso escolhe a melhor opção imediata e nunca reconsidera suas escolhas. Em termos de otimização de uma solução, isso significa simplesmente que a solução gulosa tentará encontrar soluções ótimas locais - que podem ser muitas - e poderá perder uma solução global ideal.
## Definição formal ## Definição formal
Suponha que você tenha uma função objetiva que precisa ser otimizada (maximizada ou minimizada) em um determinado ponto. Um algoritmo Greedy faz escolhas gananciosas em cada etapa para garantir que a função objetivo seja otimizada. O algoritmo Greedy tem apenas uma chance para calcular a solução ótima, para que ela nunca retorne e reverta a decisão. Suponha que você tenha uma função objetiva que precisa ser otimizada (maximizada ou minimizada) em um determinado ponto. Um algoritmo guloso faz escolhas gananciosas em cada etapa para garantir que a função objetivo seja otimizada. O algoritmo guloso tem apenas uma chance para calcular a solução ótima, para que ela nunca retorne e reverta a decisão.
### Algoritmos gananciosos têm algumas vantagens e desvantagens: ### Algoritmos gulosos têm algumas vantagens e desvantagens:
* É muito fácil criar um algoritmo guloso (ou mesmo vários algoritmos gulosos) para um problema. Analisar o tempo de execução para algoritmos gulosos geralmente será muito mais fácil do que para outras técnicas (como Dividir e conquistar). Para a técnica de dividir e conquistar, não está claro se a técnica é rápida ou lenta. Isso ocorre porque, em cada nível de recursão, o tamanho diminui e o número de subproblemas aumenta. * É muito fácil criar um algoritmo guloso (ou mesmo vários algoritmos gulosos) para um problema. Analisar o tempo de execução para algoritmos gulosos geralmente será muito mais fácil do que para outras técnicas (como Dividir e conquistar). Para a técnica de dividir e conquistar, não está claro se a técnica é rápida ou lenta. Isso ocorre porque, em cada nível de recursão, o tamanho diminui e o número de subproblemas aumenta.
@ -49,7 +49,7 @@ Vamos examinar as várias abordagens para resolver esse problema.
1. **Primeira Hora de Início Primeiro,** ou seja, selecione o intervalo que tem a hora de início mais antiga. Dê uma olhada no exemplo a seguir que quebra essa solução. Essa solução falhou porque pode haver um intervalo que começa muito cedo, mas isso é muito longo. Isso significa que a próxima estratégia que poderíamos tentar seria onde nós olhamos em intervalos menores primeiro. 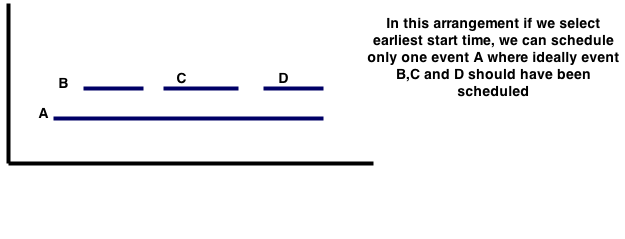![Primeiras Horas Iniciais Primeiro](https://algorithmsandme.files.wordpress.com/2015/03/f268b-jobs.png?w=840) 1. **Primeira Hora de Início Primeiro,** ou seja, selecione o intervalo que tem a hora de início mais antiga. Dê uma olhada no exemplo a seguir que quebra essa solução. Essa solução falhou porque pode haver um intervalo que começa muito cedo, mas isso é muito longo. Isso significa que a próxima estratégia que poderíamos tentar seria onde nós olhamos em intervalos menores primeiro. 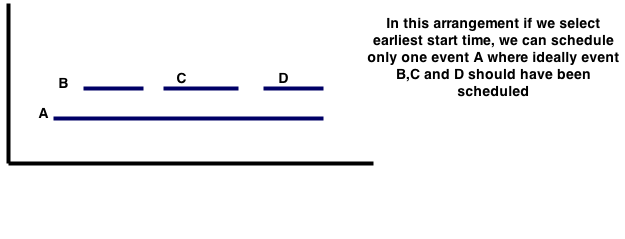![Primeiras Horas Iniciais Primeiro](https://algorithmsandme.files.wordpress.com/2015/03/f268b-jobs.png?w=840)
2. **Intervalo Menor Primeiro,** ou seja, você acaba selecionando as palestras na ordem de seu intervalo geral, que não é nada além do `finish time - start time` . Mais uma vez, esta solução não está correta. Olhe o seguinte caso. 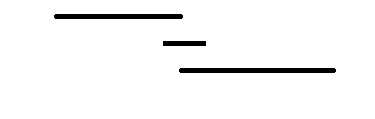![Intervalo mais curto primeiro](https://cdn-media-1.freecodecamp.org/imgr/4bz2N.png) 2. **Intervalo Menor Primeiro,** ou seja, você acaba selecionando as palestras na ordem de seu intervalo geral, que não é nada além do `hora de término - hora de início` . Mais uma vez, esta solução não está correta. Olhe o seguinte caso. 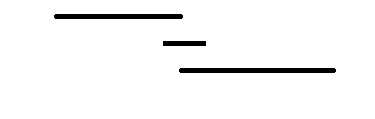![Intervalo mais curto primeiro](https://cdn-media-1.freecodecamp.org/imgr/4bz2N.png)
Você pode ver claramente que a palestra de intervalo mais curta é a do meio, mas essa não é a solução ideal aqui. Vamos ver outra solução para esse problema, derivando insights dessa solução. Você pode ver claramente que a palestra de intervalo mais curta é a do meio, mas essa não é a solução ideal aqui. Vamos ver outra solução para esse problema, derivando insights dessa solução.
@ -71,11 +71,11 @@ function interval_scheduling_problem(requests)
end end
``` ```
## Quando usamos Algoritmos Greedy? ## Quando usamos Algoritmos Guloso?
Algoritmos Greedy podem ajudá-lo a encontrar soluções para muitos problemas aparentemente difíceis. O único problema com eles é que você pode encontrar a solução correta, mas talvez não consiga verificar se é a correta. Todos os problemas gananciosos compartilham uma propriedade comum que um ótimo local pode eventualmente levar a um mínimo global sem reconsiderar o conjunto de escolhas já considerado. Algoritmos guloso podem ajudá-lo a encontrar soluções para muitos problemas aparentemente difíceis. O único problema com eles é que você pode encontrar a solução correta, mas talvez não consiga verificar se é a correta. Todos os problemas gananciosos compartilham uma propriedade comum que um ótimo local pode eventualmente levar a um mínimo global sem reconsiderar o conjunto de escolhas já considerado.
Algoritmos Greedy nos ajudam a resolver muitos tipos diferentes de problemas. Fique atento aos próximos tutoriais sobre cada um deles. Algoritmos gulosos nos ajudam a resolver muitos tipos diferentes de problemas. Fique atento aos próximos tutoriais sobre cada um deles.
1. Problema do caminho mais curto. 1. Problema do caminho mais curto.
2. Problema Mínimo da Árvore de Abrangência em um Gráfico. 2. Problema Mínimo da Árvore de Abrangência em um Gráfico.
@ -84,6 +84,14 @@ Algoritmos Greedy nos ajudam a resolver muitos tipos diferentes de problemas. Fi
#### Mais Informações: #### Mais Informações:
[![Problemas gananciosos](http://img.youtube.com/vi/HzeK7g8cD0Y/0.jpg)](https://www.youtube.com/watch?v=HzeK7g8cD0Y) <a href="https://www.youtube.com/watch?v=HzeK7g8cD0Y" target="_blank">
<img src="http://img.youtube.com/vi/HzeK7g8cD0Y/0.jpg" alt="Greedy Problems" width="240" height="180" border="10" />
</a>
[![Problemas gananciosos](http://img.youtube.com/vi/poWB2UCuozA/0.jpg)](https://www.youtube.com/watch?v=poWB2UCuozA) <a href="https://www.youtube.com/watch?v=poWB2UCuozA" target="_blank">
<img src="http://img.youtube.com/vi/poWB2UCuozA/0.jpg" alt="Greedy Problems" width="240" height="180" border="10" />
</a>
<a href="https://www.youtube.com/watch?v=tKwnms5iRBU" target="_blank">
<img src="http://img.youtube.com/vi/tKwnms5iRBU/0.jpg" alt="Greedy Problems" width="240" height="180" border="10" />
</a>