diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md
index 1e65da5610..18513a26a1 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f3df1000cf542c50fef1
-title: 'Problem 115: Counting block combinations II'
+title: '問題 115：計數塊組合 II'
challengeType: 5
forumTopicId: 301741
dashedName: problem-115-counting-block-combinations-ii
@@ -8,23 +8,23 @@ dashedName: problem-115-counting-block-combinations-ii
# --description--
-A row measuring `n` units in length has red blocks with a minimum length of `m` units placed on it, such that any two red blocks (which are allowed to be different lengths) are separated by at least one black square.
+一排長度爲 `n` 個單位的行上放置了最小長度爲 `m` 個單位的紅色塊，這樣任何兩個紅色塊（允許長度不同）至少被一個黑色方塊隔開。
-Let the fill-count function, $F(m, n)$, represent the number of ways that a row can be filled.
+讓填充計數函數，$F(m, n)$，表示可以填充的行數。
-For example, $F(3, 29) = 673135$ and $F(3, 30) = 1089155$.
+例如， $F(3, 29) = 673135$，$F(3, 30) = 1089155$。
-That is, for m = 3, it can be seen that n = 30 is the smallest value for which the fill-count function first exceeds one million.
+就是說，對於 m = 3，可以看出 n = 30 是函數結果超過 100 萬的最小 n 值。
-In the same way, for m = 10, it can be verified that $F(10, 56) = 880711$ and $F(10, 57) = 1148904$, so n = 57 is the least value for which the fill-count function first exceeds one million.
+同樣，對於 m = 10，可以驗證 $F(10, 56) = 880711$ 和 $F(10, 57) = 1148904$。即函數第一次超過 100 萬的 n 最小值爲 57。
-For m = 50, find the least value of `n` for which the fill-count function first exceeds one million.
+對於 m = 50，找到最小值 `n` 的值，讓函數第一次超過 100 萬。
-**Note:** This is a more difficult version of Problem 114.
+**注意：** 這是問題 114 的一個困難版本。
# --hints--
-`countingBlockTwo()` should return `168`.
+`countingBlockTwo()` 應該返回 `168`。
```js
assert.strictEqual(countingBlockTwo(), 168);
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-120-square-remainders.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-120-square-remainders.md
index 828f12b906..63d75ff5e3 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-120-square-remainders.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-120-square-remainders.md
@@ -1,6 +1,6 @@
---
id: 5900f3e41000cf542c50fef7
-title: 'Problem 120: Square remainders'
+title: '問題 120：平方餘數'
challengeType: 5
forumTopicId: 301747
dashedName: problem-120-square-remainders
@@ -8,15 +8,15 @@ dashedName: problem-120-square-remainders
# --description--
-Let `r` be the remainder when ${(a − 1)}^n + {(a + 1)}^n$ is divided by $a^2$.
+將 `r` 記爲當 ${(a − 1)}^n + {(a + 1)}^n$ 除以 $a^2$ 的餘數。
-For example, if $a = 7$ and $n = 3$, then $r = 42: 6^3 + 8^3 = 728 ≡ 42 \\ \text{mod}\\ 49$. And as `n` varies, so too will `r`, but for $a = 7$ it turns out that $r_{max} = 42$.
+例如，如果 $a = 7$ 且 $n = 3$，則 $r = 42: 6^3 + 8^3 = 728 ≡ 42 \\ \text{mod}\\ 49$。 `r` 會隨着 `n` 的變化而變化，但對於 $a = 7$，會有 $r_{max} = 42$。
-For $3 ≤ a ≤ 1000$, find $\sum{r}_{max}$.
+對於 $3 ≤ a ≤ 1000$，求 $\sum{r}_{max}$。
# --hints--
-`squareRemainders()` should return `333082500`.
+`squareRemainders()` 應該返回 `333082500`。
```js
assert.strictEqual(squareRemainders(), 333082500);
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
index cb7b7afda1..5ed311c7e9 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
@@ -1,6 +1,6 @@
---
id: 5900f3e71000cf542c50fefa
-title: 'Problem 123: Prime square remainders'
+title: '問題 123：素數平方餘數'
challengeType: 5
forumTopicId: 301750
dashedName: problem-123-prime-square-remainders
@@ -8,20 +8,20 @@ dashedName: problem-123-prime-square-remainders
# --description--
-Let pn be the nth prime: 2, 3, 5, 7, 11, ..., and let r be the remainder when (pn−1)n + (pn+1)n is divided by pn2.
+令 $p_n$ 爲第 $n$ 個素數：2, 3, 5, 7, 11, ...，並令 $r$ 爲當 ${(p_n−1)}^n + {(p_n+ 1)}^n$ 除以 ${p_n}^2$ 的餘數。
-For example, when n = 3, p3 = 5, and 43 + 63 = 280 ≡ 5 mod 25.
+例如，當 $n = 3, p_3 = 5$，$4^3 + 6^3 = 280 ≡ 5\\ mod\\ 25$。
-The least value of n for which the remainder first exceeds 109 is 7037.
+餘數超過 $10^9$ 的 $n$ 的最小值是 7037。
-Find the least value of n for which the remainder first exceeds 1010.
+求餘數超過 $10^{10}$ 時的 $n$ 的最小值。
# --hints--
-`euler123()` should return 21035.
+`primeSquareRemainders()` 應該返回 `21035`。
```js
-assert.strictEqual(euler123(), 21035);
+assert.strictEqual(primeSquareRemainders(), 21035);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler123(), 21035);
## --seed-contents--
```js
-function euler123() {
+function primeSquareRemainders() {
return true;
}
-euler123();
+primeSquareRemainders();
```
# --solutions--
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..57662565e5 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -1,6 +1,6 @@
---
id: 5900f3fa1000cf542c50ff0c
-title: 'Problem 140: Modified Fibonacci golden nuggets'
+title: '問題 140：改進的斐波那契金塊'
challengeType: 5
forumTopicId: 301769
dashedName: problem-140-modified-fibonacci-golden-nuggets
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+考慮無窮級數 $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$，其中 $G_k$ 是二階遞歸關係的第 $k$ 項，$G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$，且 $G_2 = 4$；該數列爲 $1, 4, 5, 9, 14, 23, \ldots$。
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+在這個問題中，我們關注的是那些使得 $A_G(x)$ 爲正整數的 $x$ 的值。
-The corresponding values of x for the first five natural numbers are shown below.
+前五個對應的自然數 $x$ 如下。
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+| ----------------------------- | -------- |
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+當 $x$ 是有理數時，我們稱 $A_G(x)$ 是一個金磚，因爲這樣的數字逐漸變得稀少；例如，第 20 個金磚是 211345365。 請計算出前三十個金磚之和。
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` 應該返回 `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md
index fd11d827b7..242f5a648a 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f3fc1000cf542c50ff0e
-title: 'Problem 143: Investigating the Torricelli point of a triangle'
+title: '問題 143：三角形托裏拆利點的研究'
challengeType: 5
forumTopicId: 301772
dashedName: problem-143-investigating-the-torricelli-point-of-a-triangle
@@ -8,20 +8,22 @@ dashedName: problem-143-investigating-the-torricelli-point-of-a-triangle
# --description--
-Let ABC be a triangle with all interior angles being less than 120 degrees. Let X be any point inside the triangle and let XA = p, XC = q, and XB = r.
+設三角形 ABC 的內角均小於120度。 取三角形內任意一點 X，令 $XA = p$，$XC = q$，$XB = r$。
-Fermat challenged Torricelli to find the position of X such that p + q + r was minimised.
+費馬曾經向托裏拆利提出挑戰：找到令 p + q + r 最小的點 X 的位置。
-Torricelli was able to prove that if equilateral triangles AOB, BNC and AMC are constructed on each side of triangle ABC, the circumscribed circles of AOB, BNC, and AMC will intersect at a single point, T, inside the triangle. Moreover he proved that T, called the Torricelli/Fermat point, minimises p + q + r. Even more remarkable, it can be shown that when the sum is minimised, AN = BM = CO = p + q + r and that AN, BM and CO also intersect at T.
+托裏拆利證明，若對三角形 ABC 三邊分別構造等邊三角形 AOB、BNC 和 AMC，則三角形 AOB、BNC 和 AMC 的外接圓相交於三角形 ABC 內的一點 T。 此外，他還證明這個後來被稱爲托裏拆利點或費馬點的點 T，就是使得 $p + q + r$ 最小的點。 更值得注意的是，當和最小時，滿足 $AN = BM = CO = p + q + r$ 且 AN、BM 和 CO 也相交於點 T。
-If the sum is minimised and a, b, c, p, q and r are all positive integers we shall call triangle ABC a Torricelli triangle. For example, a = 399, b = 455, c = 511 is an example of a Torricelli triangle, with p + q + r = 784. Find the sum of all distinct values of p + q + r ≤ 120000 for Torricelli triangles.
+
+
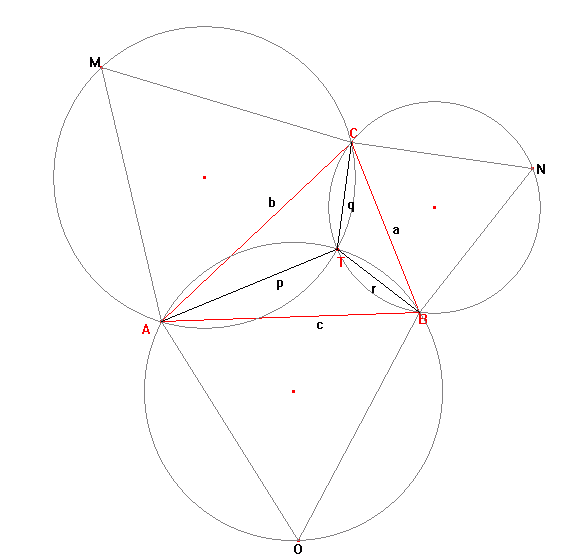+如果當和最小時且有 a、b、c、p、q 和 r 均爲正整數，我們就稱三角形 ABC 爲托裏拆利三角形。 例如，$a = 399$、$b = 455$、$c = 511$ 就是一個托裏拆利三角形，此時 $p + q + r = 784$。 對於所有滿足 $p + q + r ≤ 120000$ 的托裏拆利三角形，求出所有不同值的總和。
# --hints--
-`euler143()` should return 30758397.
+`sumTorricelliTriangles()` 應該返回 `30758397`。
```js
-assert.strictEqual(euler143(), 30758397);
+assert.strictEqual(sumTorricelliTriangles(), 30758397);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler143(), 30758397);
## --seed-contents--
```js
-function euler143() {
+function sumTorricelliTriangles() {
return true;
}
-euler143();
+sumTorricelliTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md
index ddfec6766b..1ac5c816e6 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md
@@ -1,6 +1,6 @@
---
id: 5900f3fe1000cf542c50ff11
-title: 'Problem 146: Investigating a Prime Pattern'
+title: '問題 146：素數模式的研究'
challengeType: 5
forumTopicId: 301775
dashedName: problem-146-investigating-a-prime-pattern
@@ -8,16 +8,16 @@ dashedName: problem-146-investigating-a-prime-pattern
# --description--
-The smallest positive integer n for which the numbers n2+1, n2+3, n2+7, n2+9, n2+13, and n2+27 are consecutive primes is 10. The sum of all such integers n below one-million is 1242490.
+使得數字 $n^2 + 1$、$n^2 + 3$、$n^2 + 7$、$n^2 + 9$、$n^2 + 13$ 及 $n^2 + 27$ 爲連續素數的最小正整數 $n$ 是 10。 在小於一百萬的整數中，所有滿足該條件的整數 $n$ 之和爲 1242490。
-What is the sum of all such integers n below 150 million?
+請求出在小於一億五千萬的整數中，所有滿足該條件的整數 $n$ 之和是多少？
# --hints--
-`euler146()` should return 676333270.
+`primePattern()` 應該返回 `676333270`。
```js
-assert.strictEqual(euler146(), 676333270);
+assert.strictEqual(primePattern(), 676333270);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler146(), 676333270);
## --seed-contents--
```js
-function euler146() {
+function primePattern() {
return true;
}
-euler146();
+primePattern();
```
# --solutions--
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
index 13babe893b..4c1b03a3b7 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff14
-title: 'Problem 148: Exploring Pascal''s triangle'
+title: '問題 148：帕斯卡三角形的研究'
challengeType: 5
forumTopicId: 301777
dashedName: problem-148-exploring-pascals-triangle
@@ -8,9 +8,9 @@ dashedName: problem-148-exploring-pascals-triangle
# --description--
-We can easily verify that none of the entries in the first seven rows of Pascal's triangle are divisible by 7:
+可以輕易證明，帕斯卡三角形前七行中，沒有一個數字可以被 7 整除。
-
+```
1
1 1
1 2 1
@@ -18,20 +18,20 @@ We can easily verify that none of the entries in the first seven rows of Pascal'
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
-
+```
-However, if we check the first one hundred rows, we will find that only 2361 of the 5050 entries are not divisible by 7.
+但是如果我們檢查前一百行，會發現在 5050 個數中只有 2361 個數字不能被 7 整除。
# --instructions--
-Find the number of entries which are not divisible by 7 in the first one billion (109) rows of Pascal's triangle.
+請找出帕斯卡三角形前十億（${10}^9$）行中不能被 7 整除的數的個數。
# --hints--
-`euler148()` should return 2129970655314432.
+`entriesOfPascalsTriangle()` 應該返回 `2129970655314432`。
```js
-assert.strictEqual(euler148(), 2129970655314432);
+assert.strictEqual(entriesOfPascalsTriangle(), 2129970655314432);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler148(), 2129970655314432);
## --seed-contents--
```js
-function euler148() {
+function entriesOfPascalsTriangle() {
return true;
}
-euler148();
+entriesOfPascalsTriangle();
```
# --solutions--
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md
index c76d5370c2..c081b79def 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff13
-title: 'Problem 149: Searching for a maximum-sum subsequence'
+title: '問題 149：搜索最大和子序列'
challengeType: 5
forumTopicId: 301778
dashedName: problem-149-searching-for-a-maximum-sum-subsequence
@@ -8,28 +8,30 @@ dashedName: problem-149-searching-for-a-maximum-sum-subsequence
# --description--
-Looking at the table below, it is easy to verify that the maximum possible sum of adjacent numbers in any direction (horizontal, vertical, diagonal or anti-diagonal) is 16 (= 8 + 7 + 1).
+觀察下表，可以輕易驗證任意方向（水平、垂直、對角線或反對角線）上相鄰數字最大和爲 $16 (= 8 + 7 + 1)$。
-−25329−6513273−18−4 8
+$$\begin{array}{|r|r|r|r|} \hline −2 & 5 & 3 & 2 \\\\ \hline 9 & −6 & 5 & 1 \\\\ \hline 3 & 2 & 7 & 3 \\\\ \hline −1 & 8 & −4 & 8 \\\\ \hline \end{array}$$
-Now, let us repeat the search, but on a much larger scale:
+現在我們重複一遍搜索過程，但是這次是在一個更大規模的表格中：
-First, generate four million pseudo-random numbers using a specific form of what is known as a "Lagged Fibonacci Generator":
+首先，使用被稱爲“滯後斐波那契生成器”的特殊方法，生成四百萬個僞隨機數：
-For 1 ≤ k ≤ 55, sk = \[100003 − 200003k + 300007k3] (modulo 1000000) − 500000. For 56 ≤ k ≤ 4000000, sk = \[sk−24 + sk−55 + 1000000] (modulo 1000000) − 500000.
+對於 $1 ≤ k ≤ 55$，$s_k = (100003 − 200003k + 300007{k}^3) \\ (modulo\\ 1000000) − 500000$。
-Thus, s10 = −393027 and s100 = 86613.
+對於 $56 ≤ k ≤ 4000000$，$s_k = (s_{k − 24} + s_{k − 55} + 1000000) \\ (modulo\\ 1000000) − 500000$。
-The terms of s are then arranged in a 2000×2000 table, using the first 2000 numbers to fill the first row (sequentially), the next 2000 numbers to fill the second row, and so on.
+可得，$s_{10} = −393027$，$s_{100} = 86613$。
-Finally, find the greatest sum of (any number of) adjacent entries in any direction (horizontal, vertical, diagonal or anti-diagonal).
+這些數字 $s$ 隨後排列在一個 2000 x 2000 的表格中，前 2000 個數字填入第一行（順序填入），後 2000 個數字填充第二行，依次類推。
+
+最後，請找到任意方向（水平、垂直、對象線或反對角線）上相鄰數字（任意數量）的最大和。
# --hints--
-`euler149()` should return 52852124.
+`maximumSubSequence()` 應該返回 `52852124`。
```js
-assert.strictEqual(euler149(), 52852124);
+assert.strictEqual(maximumSubSequence(), 52852124);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler149(), 52852124);
## --seed-contents--
```js
-function euler149() {
+function maximumSubSequence() {
return true;
}
-euler149();
+maximumSubSequence();
```
# --solutions--
diff --git a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/rosetta-code/sha-256.md b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/rosetta-code/sha-256.md
index 9ce0ca4260..1b0f529c0b 100644
--- a/curriculum/challenges/chinese-traditional/10-coding-interview-prep/rosetta-code/sha-256.md
+++ b/curriculum/challenges/chinese-traditional/10-coding-interview-prep/rosetta-code/sha-256.md
@@ -8,27 +8,27 @@ dashedName: sha-256
# --description--
-The `SHA-2` family is a stronger alternative to `SHA-1`. The main difference between them is the length of the hash. Meaning `SHA-1` provides a shorter code with fewer possibilities for unique combinations. `SHA-2` or `SHA-256` creates a longer and thus more complex hash with more possibilities.
+`SHA-2` 家族是比 `SHA-1` 更強大的替代。 兩者最主要的不同是散列的長度。 即 `SHA-1` 提供了更短的編碼，也意味着組合的唯一性概率更低。 `SHA-2` 或 `SHA-256` 創建了較長的散列，從而增加了唯一性的概率。
# --instructions--
-Research implemenation details and write a function that takes a string as the parameter and returns a hash using `SHA-256`
+研究實現細節並編寫一個函數，該函數以字符串爲參數並使用 `SHA-256` 返回哈希值
# --hints--
-`SHA256` should be a function.
+`SHA256` 應該是一個函數。
```js
assert(typeof SHA256 === 'function');
```
-`SHA256("Rosetta code")` should return a string.
+`SHA256("Rosetta code")` 應該返回一個字符串。
```js
assert(typeof SHA256('Rosetta code') === 'string');
```
-`SHA256("Rosetta code")` should return `"764faf5c61ac315f1497f9dfa542713965b785e5cc2f707d6468d7d1124cdfcf"`.
+`SHA256("Rosetta code")` 應該返回 `"764faf5c61ac315f1497f9dfa542713965b785e5cc2f707d6468d7d1124cdfcf"`。
```js
assert.equal(
@@ -37,7 +37,7 @@ assert.equal(
);
```
-`SHA256("SHA-256 Hash")` should return `"bee8c0cabdcf8c7835f40217dd35a8b0dba9134520e633f1c57285f35ca7ee3e"`.
+`SHA256("SHA-256 Hash")` 應該返回 `"bee8c0cabdcf8c7835f40217dd35a8b0dba9134520e633f1c57285f35ca7ee3e"`。
```js
assert.equal(
@@ -46,7 +46,7 @@ assert.equal(
);
```
-`SHA256("implementation")` should return `"da31012c40330e7e21538e7dd57503b16e8a0839159e96137090cccc9910b171"`.
+`SHA256("implementation")` 應該返回 `"da31012c40330e7e21538e7dd57503b16e8a0839159e96137090cccc9910b171"`。
```js
assert.equal(
@@ -55,7 +55,7 @@ assert.equal(
);
```
-`SHA256("algorithm")` should return `"b1eb2ec8ac9f31ff7918231e67f96e6deda83a9ff33ed2c67443f1df81e5ed14"`.
+`SHA256("algorithm")` 應該返回 `"b1eb2ec8ac9f31ff7918231e67f96e6deda83a9ff33ed2c67443f1df81e5ed14"`。
```js
assert.equal(
@@ -64,7 +64,7 @@ assert.equal(
);
```
-`SHA256("language")` should return `"a4ef304ba42a200bafd78b046e0869af9183f6eee5524aead5dcb3a5ab5f8f3f"`.
+`SHA256("language")` 應該返回 `"a4ef304ba42a200bafd78b046e0869af9183f6eee5524aead5dcb3a5ab5f8f3f"`
```js
assert.equal(
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md
index 1e65da5610..fd7a1446e4 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-115-counting-block-combinations-ii.md
@@ -1,6 +1,6 @@
---
id: 5900f3df1000cf542c50fef1
-title: 'Problem 115: Counting block combinations II'
+title: '问题 115：计数块组合 II'
challengeType: 5
forumTopicId: 301741
dashedName: problem-115-counting-block-combinations-ii
@@ -8,23 +8,23 @@ dashedName: problem-115-counting-block-combinations-ii
# --description--
-A row measuring `n` units in length has red blocks with a minimum length of `m` units placed on it, such that any two red blocks (which are allowed to be different lengths) are separated by at least one black square.
+一排长度为 `n` 个单位的行上放置了最小长度为 `m` 个单位的红色块，这样任何两个红色块（允许长度不同）至少被一个黑色方块隔开。
-Let the fill-count function, $F(m, n)$, represent the number of ways that a row can be filled.
+让填充计数函数，$F(m, n)$，表示可以填充的行数。
-For example, $F(3, 29) = 673135$ and $F(3, 30) = 1089155$.
+例如， $F(3, 29) = 673135$，$F(3, 30) = 1089155$。
-That is, for m = 3, it can be seen that n = 30 is the smallest value for which the fill-count function first exceeds one million.
+就是说，对于 m = 3，可以看出 n = 30 是函数结果超过 100 万的最小 n 值。
-In the same way, for m = 10, it can be verified that $F(10, 56) = 880711$ and $F(10, 57) = 1148904$, so n = 57 is the least value for which the fill-count function first exceeds one million.
+同样，对于 m = 10，可以验证 $F(10, 56) = 880711$ 和 $F(10, 57) = 1148904$。即函数第一次超过 100 万的 n 最小值为 57。
-For m = 50, find the least value of `n` for which the fill-count function first exceeds one million.
+对于 m = 50，找到最小值 `n` 的值，让函数第一次超过 100 万。
-**Note:** This is a more difficult version of Problem 114.
+**注意：** 这是问题 114 的一个困难版本。
# --hints--
-`countingBlockTwo()` should return `168`.
+`countingBlockTwo()` 应该返回 `168`。
```js
assert.strictEqual(countingBlockTwo(), 168);
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-120-square-remainders.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-120-square-remainders.md
index 828f12b906..d9f802b95a 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-120-square-remainders.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-120-square-remainders.md
@@ -1,6 +1,6 @@
---
id: 5900f3e41000cf542c50fef7
-title: 'Problem 120: Square remainders'
+title: '问题 120：平方余数'
challengeType: 5
forumTopicId: 301747
dashedName: problem-120-square-remainders
@@ -8,15 +8,15 @@ dashedName: problem-120-square-remainders
# --description--
-Let `r` be the remainder when ${(a − 1)}^n + {(a + 1)}^n$ is divided by $a^2$.
+将 `r` 记为当 ${(a − 1)}^n + {(a + 1)}^n$ 除以 $a^2$ 的余数。
-For example, if $a = 7$ and $n = 3$, then $r = 42: 6^3 + 8^3 = 728 ≡ 42 \\ \text{mod}\\ 49$. And as `n` varies, so too will `r`, but for $a = 7$ it turns out that $r_{max} = 42$.
+例如，如果 $a = 7$ 且 $n = 3$，则 $r = 42: 6^3 + 8^3 = 728 ≡ 42 \\ \text{mod}\\ 49$。 `r` 会随着 `n` 的变化而变化，但对于 $a = 7$，会有 $r_{max} = 42$。
-For $3 ≤ a ≤ 1000$, find $\sum{r}_{max}$.
+对于 $3 ≤ a ≤ 1000$，求 $\sum{r}_{max}$。
# --hints--
-`squareRemainders()` should return `333082500`.
+`squareRemainders()` 应该返回 `333082500`。
```js
assert.strictEqual(squareRemainders(), 333082500);
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
index cb7b7afda1..a1f9d05f78 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-123-prime-square-remainders.md
@@ -1,6 +1,6 @@
---
id: 5900f3e71000cf542c50fefa
-title: 'Problem 123: Prime square remainders'
+title: '问题 123：素数平方余数'
challengeType: 5
forumTopicId: 301750
dashedName: problem-123-prime-square-remainders
@@ -8,20 +8,20 @@ dashedName: problem-123-prime-square-remainders
# --description--
-Let pn be the nth prime: 2, 3, 5, 7, 11, ..., and let r be the remainder when (pn−1)n + (pn+1)n is divided by pn2.
+令 $p_n$ 为第 $n$ 个素数：2, 3, 5, 7, 11, ...，并令 $r$ 为当 ${(p_n−1)}^n + {(p_n+ 1)}^n$ 除以 ${p_n}^2$ 的余数。
-For example, when n = 3, p3 = 5, and 43 + 63 = 280 ≡ 5 mod 25.
+例如，当 $n = 3, p_3 = 5$，$4^3 + 6^3 = 280 ≡ 5\\ mod\\ 25$。
-The least value of n for which the remainder first exceeds 109 is 7037.
+余数超过 $10^9$ 的 $n$ 的最小值是 7037。
-Find the least value of n for which the remainder first exceeds 1010.
+求余数超过 $10^{10}$ 时的 $n$ 的最小值。
# --hints--
-`euler123()` should return 21035.
+`primeSquareRemainders()` 应该返回 `21035`。
```js
-assert.strictEqual(euler123(), 21035);
+assert.strictEqual(primeSquareRemainders(), 21035);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler123(), 21035);
## --seed-contents--
```js
-function euler123() {
+function primeSquareRemainders() {
return true;
}
-euler123();
+primeSquareRemainders();
```
# --solutions--
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
index 01664be7ae..3a9b0f02be 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-140-modified-fibonacci-golden-nuggets.md
@@ -1,6 +1,6 @@
---
id: 5900f3fa1000cf542c50ff0c
-title: 'Problem 140: Modified Fibonacci golden nuggets'
+title: '问题 140：改进的斐波那契金块'
challengeType: 5
forumTopicId: 301769
dashedName: problem-140-modified-fibonacci-golden-nuggets
@@ -8,22 +8,28 @@ dashedName: problem-140-modified-fibonacci-golden-nuggets
# --description--
-Consider the infinite polynomial series AG(x) = xG1 + x2G2 + x3G3 + ..., where Gk is the kth term of the second order recurrence relation Gk = Gk−1 + Gk−2, G1 = 1 and G2 = 4; that is, 1, 4, 5, 9, 14, 23, ... .
+考虑无穷级数 $A_G(x) = xG_1 + x^2G_2 + x^3G_3 + \cdots$，其中 $G_k$ 是二阶递归关系的第 $k$ 项，$G_k = G_{k − 1} + G_{k − 2}, G_1 = 1$，且 $G_2 = 4$；该数列为 $1, 4, 5, 9, 14, 23, \ldots$。
-For this problem we shall be concerned with values of x for which AG(x) is a positive integer.
+在这个问题中，我们关注的是那些使得 $A_G(x)$ 为正整数的 $x$ 的值。
-The corresponding values of x for the first five natural numbers are shown below.
+前五个对应的自然数 $x$ 如下。
-xAG(x) (√5−1)/41 2/52 (√22−2)/63 (√137−5)/144 1/25
+| $x$ | $A_G(x)$ |
+| ----------------------------- | -------- |
+| $\frac{\sqrt{5} − 1}{4}$ | $1$ |
+| $\frac{2}{5}$ | $2$ |
+| $\frac{\sqrt{22} − 2}{6}$ | $3$ |
+| $\frac{\sqrt{137} − 5}{14}$ | $4$ |
+| $\frac{1}{2}$ | $5$ |
-We shall call AG(x) a golden nugget if x is rational, because they become increasingly rarer; for example, the 20th golden nugget is 211345365. Find the sum of the first thirty golden nuggets.
+当 $x$ 是有理数时，我们称 $A_G(x)$ 是一个金砖，因为这样的数字逐渐变得稀少；例如，第 20 个金砖是 211345365。 请计算出前三十个金砖之和。
# --hints--
-`euler140()` should return 5673835352990.
+`modifiedGoldenNuggets()` 应该返回 `5673835352990`
```js
-assert.strictEqual(euler140(), 5673835352990);
+assert.strictEqual(modifiedGoldenNuggets(), 5673835352990);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler140(), 5673835352990);
## --seed-contents--
```js
-function euler140() {
+function modifiedGoldenNuggets() {
return true;
}
-euler140();
+modifiedGoldenNuggets();
```
# --solutions--
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md
index fd11d827b7..4cbe3700b5 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-143-investigating-the-torricelli-point-of-a-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f3fc1000cf542c50ff0e
-title: 'Problem 143: Investigating the Torricelli point of a triangle'
+title: '问题 143：三角形托里拆利点的研究'
challengeType: 5
forumTopicId: 301772
dashedName: problem-143-investigating-the-torricelli-point-of-a-triangle
@@ -8,20 +8,22 @@ dashedName: problem-143-investigating-the-torricelli-point-of-a-triangle
# --description--
-Let ABC be a triangle with all interior angles being less than 120 degrees. Let X be any point inside the triangle and let XA = p, XC = q, and XB = r.
+设三角形 ABC 的内角均小于120度。 取三角形内任意一点 X，令 $XA = p$，$XC = q$，$XB = r$。
-Fermat challenged Torricelli to find the position of X such that p + q + r was minimised.
+费马曾经向托里拆利提出挑战：找到令 p + q + r 最小的点 X 的位置。
-Torricelli was able to prove that if equilateral triangles AOB, BNC and AMC are constructed on each side of triangle ABC, the circumscribed circles of AOB, BNC, and AMC will intersect at a single point, T, inside the triangle. Moreover he proved that T, called the Torricelli/Fermat point, minimises p + q + r. Even more remarkable, it can be shown that when the sum is minimised, AN = BM = CO = p + q + r and that AN, BM and CO also intersect at T.
+托里拆利证明，若对三角形 ABC 三边分别构造等边三角形 AOB、BNC 和 AMC，则三角形 AOB、BNC 和 AMC 的外接圆相交于三角形 ABC 内的一点 T。 此外，他还证明这个后来被称为托里拆利点或费马点的点 T，就是使得 $p + q + r$ 最小的点。 更值得注意的是，当和最小时，满足 $AN = BM = CO = p + q + r$ 且 AN、BM 和 CO 也相交于点 T。
-If the sum is minimised and a, b, c, p, q and r are all positive integers we shall call triangle ABC a Torricelli triangle. For example, a = 399, b = 455, c = 511 is an example of a Torricelli triangle, with p + q + r = 784. Find the sum of all distinct values of p + q + r ≤ 120000 for Torricelli triangles.
+
+
+如果当和最小时且有 a、b、c、p、q 和 r 均为正整数，我们就称三角形 ABC 为托里拆利三角形。 例如，$a = 399$、$b = 455$、$c = 511$ 就是一个托里拆利三角形，此时 $p + q + r = 784$。 对于所有满足 $p + q + r ≤ 120000$ 的托里拆利三角形，求出所有不同值的总和。
# --hints--
-`euler143()` should return 30758397.
+`sumTorricelliTriangles()` 应该返回 `30758397`。
```js
-assert.strictEqual(euler143(), 30758397);
+assert.strictEqual(sumTorricelliTriangles(), 30758397);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler143(), 30758397);
## --seed-contents--
```js
-function euler143() {
+function sumTorricelliTriangles() {
return true;
}
-euler143();
+sumTorricelliTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md
index ddfec6766b..762f769008 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-146-investigating-a-prime-pattern.md
@@ -1,6 +1,6 @@
---
id: 5900f3fe1000cf542c50ff11
-title: 'Problem 146: Investigating a Prime Pattern'
+title: '问题 146：素数模式的研究'
challengeType: 5
forumTopicId: 301775
dashedName: problem-146-investigating-a-prime-pattern
@@ -8,16 +8,16 @@ dashedName: problem-146-investigating-a-prime-pattern
# --description--
-The smallest positive integer n for which the numbers n2+1, n2+3, n2+7, n2+9, n2+13, and n2+27 are consecutive primes is 10. The sum of all such integers n below one-million is 1242490.
+使得数字 $n^2 + 1$、$n^2 + 3$、$n^2 + 7$、$n^2 + 9$、$n^2 + 13$ 及 $n^2 + 27$ 为连续素数的最小正整数 $n$ 是 10。 在小于一百万的整数中，所有满足该条件的整数 $n$ 之和为 1242490。
-What is the sum of all such integers n below 150 million?
+请求出在小于一亿五千万的整数中，所有满足该条件的整数 $n$ 之和是多少？
# --hints--
-`euler146()` should return 676333270.
+`primePattern()` 应该返回 `676333270`。
```js
-assert.strictEqual(euler146(), 676333270);
+assert.strictEqual(primePattern(), 676333270);
```
# --seed--
@@ -25,12 +25,12 @@ assert.strictEqual(euler146(), 676333270);
## --seed-contents--
```js
-function euler146() {
+function primePattern() {
return true;
}
-euler146();
+primePattern();
```
# --solutions--
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
index 13babe893b..7d931e84bc 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-148-exploring-pascals-triangle.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff14
-title: 'Problem 148: Exploring Pascal''s triangle'
+title: '问题 148：帕斯卡三角形的研究'
challengeType: 5
forumTopicId: 301777
dashedName: problem-148-exploring-pascals-triangle
@@ -8,9 +8,9 @@ dashedName: problem-148-exploring-pascals-triangle
# --description--
-We can easily verify that none of the entries in the first seven rows of Pascal's triangle are divisible by 7:
+可以轻易证明，帕斯卡三角形前七行中，没有一个数字可以被 7 整除。
-
+```
1
1 1
1 2 1
@@ -18,20 +18,20 @@ We can easily verify that none of the entries in the first seven rows of Pascal'
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
-
+```
-However, if we check the first one hundred rows, we will find that only 2361 of the 5050 entries are not divisible by 7.
+但是如果我们检查前一百行，会发现在 5050 个数中只有 2361 个数字不能被 7 整除。
# --instructions--
-Find the number of entries which are not divisible by 7 in the first one billion (109) rows of Pascal's triangle.
+请找出帕斯卡三角形前十亿（${10}^9$）行中不能被 7 整除的数的个数。
# --hints--
-`euler148()` should return 2129970655314432.
+`entriesOfPascalsTriangle()` 应该返回 `2129970655314432`。
```js
-assert.strictEqual(euler148(), 2129970655314432);
+assert.strictEqual(entriesOfPascalsTriangle(), 2129970655314432);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler148(), 2129970655314432);
## --seed-contents--
```js
-function euler148() {
+function entriesOfPascalsTriangle() {
return true;
}
-euler148();
+entriesOfPascalsTriangle();
```
# --solutions--
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md
index c76d5370c2..33c622c1eb 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/project-euler/problem-149-searching-for-a-maximum-sum-subsequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4021000cf542c50ff13
-title: 'Problem 149: Searching for a maximum-sum subsequence'
+title: '问题 149：搜索最大和子序列'
challengeType: 5
forumTopicId: 301778
dashedName: problem-149-searching-for-a-maximum-sum-subsequence
@@ -8,28 +8,30 @@ dashedName: problem-149-searching-for-a-maximum-sum-subsequence
# --description--
-Looking at the table below, it is easy to verify that the maximum possible sum of adjacent numbers in any direction (horizontal, vertical, diagonal or anti-diagonal) is 16 (= 8 + 7 + 1).
+观察下表，可以轻易验证任意方向（水平、垂直、对角线或反对角线）上相邻数字最大和为 $16 (= 8 + 7 + 1)$。
-−25329−6513273−18−4 8
+$$\begin{array}{|r|r|r|r|} \hline −2 & 5 & 3 & 2 \\\\ \hline 9 & −6 & 5 & 1 \\\\ \hline 3 & 2 & 7 & 3 \\\\ \hline −1 & 8 & −4 & 8 \\\\ \hline \end{array}$$
-Now, let us repeat the search, but on a much larger scale:
+现在我们重复一遍搜索过程，但是这次是在一个更大规模的表格中：
-First, generate four million pseudo-random numbers using a specific form of what is known as a "Lagged Fibonacci Generator":
+首先，使用被称为“滞后斐波那契生成器”的特殊方法，生成四百万个伪随机数：
-For 1 ≤ k ≤ 55, sk = \[100003 − 200003k + 300007k3] (modulo 1000000) − 500000. For 56 ≤ k ≤ 4000000, sk = \[sk−24 + sk−55 + 1000000] (modulo 1000000) − 500000.
+对于 $1 ≤ k ≤ 55$，$s_k = (100003 − 200003k + 300007{k}^3) \\ (modulo\\ 1000000) − 500000$。
-Thus, s10 = −393027 and s100 = 86613.
+对于 $56 ≤ k ≤ 4000000$，$s_k = (s_{k − 24} + s_{k − 55} + 1000000) \\ (modulo\\ 1000000) − 500000$。
-The terms of s are then arranged in a 2000×2000 table, using the first 2000 numbers to fill the first row (sequentially), the next 2000 numbers to fill the second row, and so on.
+可得，$s_{10} = −393027$，$s_{100} = 86613$。
-Finally, find the greatest sum of (any number of) adjacent entries in any direction (horizontal, vertical, diagonal or anti-diagonal).
+这些数字 $s$ 随后排列在一个 2000 x 2000 的表格中，前 2000 个数字填入第一行（顺序填入），后 2000 个数字填充第二行，依次类推。
+
+最后，请找到任意方向（水平、垂直、对象线或反对角线）上相邻数字（任意数量）的最大和。
# --hints--
-`euler149()` should return 52852124.
+`maximumSubSequence()` 应该返回 `52852124`。
```js
-assert.strictEqual(euler149(), 52852124);
+assert.strictEqual(maximumSubSequence(), 52852124);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler149(), 52852124);
## --seed-contents--
```js
-function euler149() {
+function maximumSubSequence() {
return true;
}
-euler149();
+maximumSubSequence();
```
# --solutions--
diff --git a/curriculum/challenges/chinese/10-coding-interview-prep/rosetta-code/sha-256.md b/curriculum/challenges/chinese/10-coding-interview-prep/rosetta-code/sha-256.md
index 9ce0ca4260..83c648b79b 100644
--- a/curriculum/challenges/chinese/10-coding-interview-prep/rosetta-code/sha-256.md
+++ b/curriculum/challenges/chinese/10-coding-interview-prep/rosetta-code/sha-256.md
@@ -8,27 +8,27 @@ dashedName: sha-256
# --description--
-The `SHA-2` family is a stronger alternative to `SHA-1`. The main difference between them is the length of the hash. Meaning `SHA-1` provides a shorter code with fewer possibilities for unique combinations. `SHA-2` or `SHA-256` creates a longer and thus more complex hash with more possibilities.
+`SHA-2` 家族是比 `SHA-1` 更强大的替代。 两者最主要的不同是散列的长度。 即 `SHA-1` 提供了更短的编码，也意味着组合的唯一性概率更低。 `SHA-2` 或 `SHA-256` 创建了较长的散列，从而增加了唯一性的概率。
# --instructions--
-Research implemenation details and write a function that takes a string as the parameter and returns a hash using `SHA-256`
+研究实现细节并编写一个函数，该函数以字符串为参数并使用 `SHA-256` 返回哈希值
# --hints--
-`SHA256` should be a function.
+`SHA256` 应该是一个函数。
```js
assert(typeof SHA256 === 'function');
```
-`SHA256("Rosetta code")` should return a string.
+`SHA256("Rosetta code")` 应该返回一个字符串。
```js
assert(typeof SHA256('Rosetta code') === 'string');
```
-`SHA256("Rosetta code")` should return `"764faf5c61ac315f1497f9dfa542713965b785e5cc2f707d6468d7d1124cdfcf"`.
+`SHA256("Rosetta code")` 应该返回 `"764faf5c61ac315f1497f9dfa542713965b785e5cc2f707d6468d7d1124cdfcf"`。
```js
assert.equal(
@@ -37,7 +37,7 @@ assert.equal(
);
```
-`SHA256("SHA-256 Hash")` should return `"bee8c0cabdcf8c7835f40217dd35a8b0dba9134520e633f1c57285f35ca7ee3e"`.
+`SHA256("SHA-256 Hash")` 应该返回 `"bee8c0cabdcf8c7835f40217dd35a8b0dba9134520e633f1c57285f35ca7ee3e"`。
```js
assert.equal(
@@ -46,7 +46,7 @@ assert.equal(
);
```
-`SHA256("implementation")` should return `"da31012c40330e7e21538e7dd57503b16e8a0839159e96137090cccc9910b171"`.
+`SHA256("implementation")` 应该返回 `"da31012c40330e7e21538e7dd57503b16e8a0839159e96137090cccc9910b171"`。
```js
assert.equal(
@@ -55,7 +55,7 @@ assert.equal(
);
```
-`SHA256("algorithm")` should return `"b1eb2ec8ac9f31ff7918231e67f96e6deda83a9ff33ed2c67443f1df81e5ed14"`.
+`SHA256("algorithm")` 应该返回 `"b1eb2ec8ac9f31ff7918231e67f96e6deda83a9ff33ed2c67443f1df81e5ed14"`。
```js
assert.equal(
@@ -64,7 +64,7 @@ assert.equal(
);
```
-`SHA256("language")` should return `"a4ef304ba42a200bafd78b046e0869af9183f6eee5524aead5dcb3a5ab5f8f3f"`.
+`SHA256("language")` 应该返回 `"a4ef304ba42a200bafd78b046e0869af9183f6eee5524aead5dcb3a5ab5f8f3f"`
```js
assert.equal(
diff --git a/curriculum/challenges/portuguese/01-responsive-web-design/applied-visual-design/create-a-more-complex-shape-using-css-and-html.md b/curriculum/challenges/portuguese/01-responsive-web-design/applied-visual-design/create-a-more-complex-shape-using-css-and-html.md
index 5ba0cf1563..33686a84bc 100644
--- a/curriculum/challenges/portuguese/01-responsive-web-design/applied-visual-design/create-a-more-complex-shape-using-css-and-html.md
+++ b/curriculum/challenges/portuguese/01-responsive-web-design/applied-visual-design/create-a-more-complex-shape-using-css-and-html.md
@@ -9,7 +9,7 @@ dashedName: create-a-more-complex-shape-using-css-and-html
# --description--
-Uma das formas mais populares do mundo é a forma de coração e, neste desafio, você criará um usando CSS puro. Mas primeiro, você precisa entender os pseudo-elementos `::before` e `::after`. Esses pseudo-elementos são usados para adicionar algo antes ou depois de um elemento selecionado. No exemplo a seguir, um pseudo-elemento `::before` é usado para adicionar um retângulo a um elemento com a classe `heart`:
+Uma das formas mais populares do mundo é a forma de coração e, neste desafio, você criará um usando CSS puro. Mas primeiro, você precisa entender os pseudo-elementos `::before` e `::after`. ::before cria um pseudoelemento que é o primeiro filho do elemento selecionado; ::after cria um pseudoelemento que é o último filho do elemento selecionado. No exemplo a seguir, um pseudo-elemento `::before` é usado para adicionar um retângulo a um elemento com a classe `heart`:
```css
.heart::before {
diff --git a/curriculum/challenges/portuguese/02-javascript-algorithms-and-data-structures/regular-expressions/positive-and-negative-lookahead.md b/curriculum/challenges/portuguese/02-javascript-algorithms-and-data-structures/regular-expressions/positive-and-negative-lookahead.md
index 196fb9fbf1..e8a6ae1c2f 100644
--- a/curriculum/challenges/portuguese/02-javascript-algorithms-and-data-structures/regular-expressions/positive-and-negative-lookahead.md
+++ b/curriculum/challenges/portuguese/02-javascript-algorithms-and-data-structures/regular-expressions/positive-and-negative-lookahead.md
@@ -39,7 +39,7 @@ checkPass.test(password);
# --instructions--
-Faça com que `pwRegex` capture senhas que têm 5 ou mais caracteres e dois dígitos consecutivos usando lookaheads.
+Use os lookaheads na `pwRegex` para que correspondam a senhas de mais de 5 caracteres e que tenham dois algarismos consecutivos.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence.md
index 8c4e51a3e8..71cbfcd927 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-197-investigating-the-behaviour-of-a-recursively-defined-sequence.md
@@ -8,7 +8,7 @@ dashedName: problem-197-investigating-the-behaviour-of-a-recursively-defined-seq
# --description--
-Dada a função $f(x) = ⌊{2}^{30.403243784 - x^2}⌋ × {10}^{-9}$ (onde ⌊ ⌋ é a função de base), a sequência $u_n$ é definida por $u_0 = -1$ e $u_{n + 1} = f(u_n)$.
+Dada a função $f(x) = ⌊{2}^{30.403243784 - x^2}⌋ × {10}^{-9}$ (onde ⌊ ⌋ é a função piso), a sequência $u_n$ é definida por $u_0 = -1$ e $u_{n + 1} = f(u_n)$.
Encontre $u_n + u_{n + 1}$ para $n = {10}^{12}$. Dê sua resposta com 9 algarismos após o ponto (9 casas depois da vírgula).
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md
index ca403ef871..c295087021 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md
@@ -14,7 +14,7 @@ Considere $s(n) = \sum_{k=1 \ldots n} u(k)$.
Encontre o valor de $r$ para o qual $s(5000) = -600.000.000.000$.
-Dê sua resposta arredondada para 12 casas antes da vírgula.
+Dê sua resposta arredondada para 12 casas depois da vírgula.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-255-rounded-square-roots.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-255-rounded-square-roots.md
index c310ff0702..2035360b26 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-255-rounded-square-roots.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-255-rounded-square-roots.md
@@ -36,7 +36,7 @@ O número de iterações necessárias ao usar este método é surpreendentemente
Usando o procedimento descrito acima, qual é o número médio de iterações necessárias para encontrar a raiz quadrada arredondada de um número de 14 algarismos (${10}^{13} ≤ n < {10}^{14}$)? Dê sua resposta arredondada para 10 casas decimais.
-**Observação:** os símbolos $⌊x⌋$ e $⌈x⌉$ representam a função floor (piso) e ceiling (teto), respectivamente.
+**Observação:** os símbolos $⌊x⌋$ e $⌈x⌉$ representam as funções piso e teto, respectivamente.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
index 56725ea20d..c81d2cf044 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-316-numbers-in-decimal-expansions.md
@@ -28,7 +28,7 @@ etc. e vemos que $g(535) = 1008$.
Dado que $\displaystyle\sum_{n = 2}^{999} g\left(\left\lfloor\frac{{10}^6}{n}\right\rfloor\right) = 27280188$, find $\displaystyle\sum_{n = 2}^{999.999} g\left(\left\lfloor\frac{{10}^{16}}{n}\right\rfloor\right)$.
-**Observação:** $\lfloor x\rfloor$ representa a função de base.
+**Observação:** $\lfloor x\rfloor$ representa a função piso.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
index e02c93ec28..4492cb51bd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-334-spilling-the-beans.md
@@ -16,7 +16,7 @@ Por exemplo, considere duas tigelas adjacentes contendo 2 e 3 feijões, respecti
Você recebe as seguintes sequências:
-$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ é par} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ é ímpar} \end{cases} \\\\ & \qquad \text{onde $⌊x⌋$ é a função de base e $\oplus$ é o operador bitwise XOR.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
+$$\begin{align} & t_0 = 123456, \\\\ & t_i = \begin{cases} \frac{t_{i - 1}}{2}, & \text{if $t_{i - 1}$ é par} \\\\ \left\lfloor\frac{t_{i - 1}}{2}\right\rfloor \oplus 926252, & \text{if $t_{i - 1}$ é ímpar} \end{cases} \\\\ & \qquad \text{onde $⌊x⌋$ é a função piso e $\oplus$ é o operador bitwise XOR.} \\\\ & b_i = (t_i\bmod 2^{11}) + 1. \end{align}$$
Os dois primeiros termos da última sequência são $b_1 = 289$ e $b_2 = 145$. Se começarmos com $b_1$ e $b_2$ feijões em duas tigelas adjacentes, 3419100 movimentos seriam necessários para terminar o jogo.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
index 377c82d2fd..5711c272a7 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-356-largest-roots-of-cubic-polynomials.md
@@ -14,7 +14,7 @@ Por exemplo, $a_2 = 3.86619826\ldots$
Encontre os oito últimos algarismos de $\displaystyle\sum_{i = 1}^{30} \lfloor {a_i}^{987654321}\rfloor$.
-**Observação:** $\lfloor a\rfloor$ representa a função de base.
+**Observação:** $\lfloor a\rfloor$ representa a função piso.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
index bc13159789..50bf34c0cf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-361-subsequence-of-thue-morse-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4d51000cf542c50ffe8
-title: 'Problem 361: Subsequence of Thue-Morse sequence'
+title: 'Problema 361: Subsequência da sequência de Thue-Morse'
challengeType: 5
forumTopicId: 302022
dashedName: problem-361-subsequence-of-thue-morse-sequence
@@ -8,30 +8,30 @@ dashedName: problem-361-subsequence-of-thue-morse-sequence
# --description--
-The Thue-Morse sequence {Tn} is a binary sequence satisfying:
+A sequência Thue-Morse $\\{T_n\\}$ é uma sequência binária satisfatória:
-T0 = 0
+- $T_0 = 0$
+- $T_{2n} = T_n$
+- $T_{2n + 1} = 1 - T_n$
-T2n = Tn
+Os primeiros termos de $\\{T_n\\}$ são atribuídos da seguinte forma: $01101001\color{red}{10010}1101001011001101001\ldots$.
-T2n+1 = 1 - Tn
+Definimos $\\{A_n\\}$ como uma sequência ordenada de inteiros, de forma que a expressão binária de cada elemento apareça como uma subsequência em $\\{T_n\\}$. Por exemplo, o número decimal 18 é expresso como 10010 em binário. 10010 aparece em $\\{T_n\\}$ ($T_8$ a $T_{12}$), portanto 18 é um elemento de $\\{A_n\\}$. O número decimal 14 é expresso como 1110 no binário. 1110 nunca aparece em $\\{T_n\\}$, portanto 14 não é um elemento de $\\{A_n\\}$.
-The first several terms of {Tn} are given as follows: 01101001100101101001011001101001....
+Os primeiros termos de $A_n$ são atribuídos da seguinte forma:
-We define {An} as the sorted sequence of integers such that the binary expression of each element appears as a subsequence in {Tn}. For example, the decimal number 18 is expressed as 10010 in binary. 10010 appears in {Tn} (T8 to T12), so 18 is an element of {An}. The decimal number 14 is expressed as 1110 in binary. 1110 never appears in {Tn}, so 14 is not an element of {An}.
+$$\begin{array}{cr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 & 8 & 9 & 10 & 11 & 12 & \ldots \\\\ A_n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 9 & 10 & 11 & 12 & 13 & 18 & \ldots \end{array}$$
-The first several terms of An are given as follows: n0123456789101112…An012345691011121318…
+Também podemos verificar que $A_{100} = 3251$ e $A_{1000} = 80.852.364.498$.
-We can also verify that A100 = 3251 and A1000 = 80852364498.
-
-Find the last 9 digits of .
+Encontre os últimos 9 dígitos de $\displaystyle\sum_{k = 1}^{18} A_{{10}^k}$.
# --hints--
-`euler361()` should return 178476944.
+`subsequenceOfThueMorseSequence()` deve retornar `178476944`.
```js
-assert.strictEqual(euler361(), 178476944);
+assert.strictEqual(subsequenceOfThueMorseSequence(), 178476944);
```
# --seed--
@@ -39,12 +39,12 @@ assert.strictEqual(euler361(), 178476944);
## --seed-contents--
```js
-function euler361() {
+function subsequenceOfThueMorseSequence() {
return true;
}
-euler361();
+subsequenceOfThueMorseSequence();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
index 4d6bc3f4a9..901ff5fa41 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-362-squarefree-factors.md
@@ -1,6 +1,6 @@
---
id: 5900f4d61000cf542c50ffe9
-title: 'Problem 362: Squarefree factors'
+title: 'Problema 362: Fatores não quadráticos'
challengeType: 5
forumTopicId: 302023
dashedName: problem-362-squarefree-factors
@@ -8,28 +8,28 @@ dashedName: problem-362-squarefree-factors
# --description--
-Consider the number 54.
+Considere o número 54.
-54 can be factored in 7 distinct ways into one or more factors larger than 1:
+54 pode ser fatorado de 7 formas distintas em um ou mais fatores maiores que 1:
-54, 2×27, 3×18, 6×9, 3×3×6, 2×3×9 and 2×3×3×3.
+$$54, 2 × 27, 3 × 18, 6 × 9, 3 × 3 × 6 2 × 3 × 9 \text{ e } 2 × 3 × 3 × 3$$
-If we require that the factors are all squarefree only two ways remain: 3×3×6 and 2×3×3×3.
+Se precisarmos que todos os fatores não sejam quadráticos, apenas duas formas permanecem: $3 × 3 × 6$ e $2 × 3 × 3 × 3 × 3$.
-Let's call Fsf(n) the number of ways n can be factored into one or more squarefree factors larger than 1, so Fsf(54)=2.
+Vamos chamar $Fsf(n)$ o número de formas $n$ que pode ser fatorado em um ou mais fatores não quadráticos maiores que 1, então $Fsf(54) = 2$.
-Let S(n) be ∑Fsf(k) for k=2 to n.
+Considere $S(n)$ como $\sum Fsf(k)$ para $k = 2$ a $n$.
-S(100)=193.
+$S(100)=193$.
-Find S(10 000 000 000).
+Encontre $S(10.000.000.000)$.
# --hints--
-`euler362()` should return 457895958010.
+`squarefreeFactors()` deve retornar `457895958010`.
```js
-assert.strictEqual(euler362(), 457895958010);
+assert.strictEqual(squarefreeFactors(), 457895958010);
```
# --seed--
@@ -37,12 +37,12 @@ assert.strictEqual(euler362(), 457895958010);
## --seed-contents--
```js
-function euler362() {
+function squarefreeFactors() {
return true;
}
-euler362();
+squarefreeFactors();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
index 2fde41d1eb..64a652680a 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-363-bzier-curves.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffeb
-title: 'Problem 363: Bézier Curves'
+title: 'Problema 363: Curva de Bézier'
challengeType: 5
forumTopicId: 302024
dashedName: problem-363-bzier-curves
@@ -8,24 +8,32 @@ dashedName: problem-363-bzier-curves
# --description--
-A cubic Bézier curve is defined by four points: P0, P1, P2 and P3.
+Uma curva cúbica de Bézier é definida por quatro pontos: $P_0$, $P_1$, $P_2$ e $P_3$.
-The curve is constructed as follows: On the segments P0P1, P1P2 and P2P3 the points Q0,Q1 and Q2 are drawn such that P0Q0 / P0P1 = P1Q1 / P1P2 = P2Q2 / P2P3 = t (t in \[0,1]). On the segments Q0Q1 and Q1Q2 the points R0 and R1 are drawn such that Q0R0 / Q0Q1 = Q1R1 / Q1Q2 = t for the same value of t. On the segment R0R1 the point B is drawn such that R0B / R0R1 = t for the same value of t. The Bézier curve defined by the points P0, P1, P2, P3 is the locus of B as Q0 takes all possible positions on the segment P0P1. (Please note that for all points the value of t is the same.)
+A curva é construída da seguinte forma:
-At this (external) web address you will find an applet that allows you to drag the points P0, P1, P2 and P3 to see what the Bézier curve (green curve) defined by those points looks like. You can also drag the point Q0 along the segment P0P1.
+
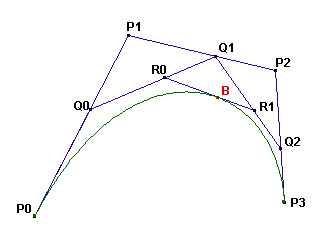-From the construction it is clear that the Bézier curve will be tangent to the segments P0P1 in P0 and P2P3 in P3.
+Nos segmentos $P_0P_1$, $P_1P_2$ e $P_2P_3$ os pontos $Q_0$,$Q_1$ e $Q_2$ estão desenhados tal que $\frac{P_0Q_0}{P_0P_1} = \frac{P_1Q_1}{P_1P_2} = \frac{P_2Q_2}{P_2P_3} = t$, com $t$ em [0,1].
-A cubic Bézier curve with P0=(1,0), P1=(1,v), P2=(v,1) and P3=(0,1) is used to approximate a quarter circle. The value v > 0 is chosen such that the area enclosed by the lines OP0, OP3 and the curve is equal to π/4 (the area of the quarter circle).
+Nos segmentos $Q_0Q_1$ e $Q_1Q_2$ os pontos $R_0$ e $R_1$ estão desenhados, tal que $\frac{Q_0R_0}{Q_0Q_1} = \frac{Q_1R_1}{Q_1Q_2} = t$ pelo mesmo valor de $t$.
-By how many percent does the length of the curve differ from the length of the quarter circle? That is, if L is the length of the curve, calculate 100 × L − π/2π/2Give your answer rounded to 10 digits behind the decimal point.
+No segmento $R_0R_1$ o ponto $B$ é desenhado de forma que $\frac{R_0B}{R_0R_1} = t$ tenha o mesmo valor de $t$.
+
+A curva de Bézier definida pelos pontos $P_0$, $P_1$, $P_2$, $P_3$ é a localidade de $B$ pois $Q_0$ ocupa todas as posições possíveis no segmento $P_0P_1$. Observe que, para todos os pontos, o valor de $t$ é o mesmo.
+
+A partir da construção, fica claro que a curva de Bézier será tangente aos segmentos $P_0P_1$ em $P_0$ e $P_2P_3$ em $P_3$.
+
+Uma curva de Bézier cúbica com $P_0 = (1, 0)$, $P_1 = (1, v)$, $P_2 = (v, 1)$ e $P_3 = (0, 1)$ é usada para aproximar um quarto de círculo. O valor $v > 0$ foi escolhido de modo que a área circundada pelas linhas $OP_0$, $OP_3$ e a curva é igual a $\frac{π}{4}$ (a área do quarto de círculo).
+
+Qual a porcentagem do comprimento da curva que difere do comprimento do quarto de círculo? Ou seja, se $L$ for o comprimento da curva, calcule $100 × \displaystyle\frac{L – \frac{π}{2}}{\frac{π}{2}}$. Dê sua resposta arredondada para 10 casas depois da vírgula.
# --hints--
-`euler363()` should return 0.0000372091.
+`bezierCurves()` deve retornar `0.0000372091`.
```js
-assert.strictEqual(euler363(), 0.0000372091);
+assert.strictEqual(bezierCurves(), 0.0000372091);
```
# --seed--
@@ -33,12 +41,12 @@ assert.strictEqual(euler363(), 0.0000372091);
## --seed-contents--
```js
-function euler363() {
+function bezierCurves() {
return true;
}
-euler363();
+bezierCurves();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
index 84637798b8..d3d083c0c7 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-364-comfortable-distance.md
@@ -1,6 +1,6 @@
---
id: 5900f4d91000cf542c50ffea
-title: 'Problem 364: Comfortable distance'
+title: 'Problema 364: Distância confortável'
challengeType: 5
forumTopicId: 302025
dashedName: problem-364-comfortable-distance
@@ -8,24 +8,26 @@ dashedName: problem-364-comfortable-distance
# --description--
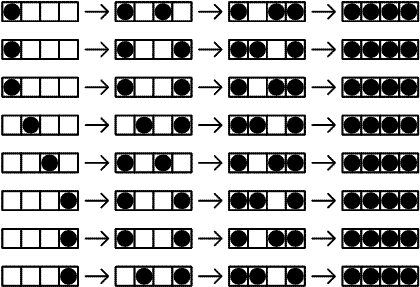
-There are N seats in a row. N people come after each other to fill the seats according to the following rules:
+Existem $N$ assentos em uma fila. $N$ pessoas vêm atrás umas das outras para preencher os lugares de acordo com as seguintes regras:
-If there is any seat whose adjacent seat(s) are not occupied take such a seat.
+1. Se houver algum lugar no qual os assentos adjacentes não estejam ocupados, tome esse lugar.
+2. Se não existir esse lugar e se houver algum lugar para o qual apenas um lugar adjacente esteja ocupado, tome esse lugar.
+3. Caso contrário, pegue um dos lugares restantes disponíveis.
-If there is no such seat and there is any seat for which only one adjacent seat is occupied take such a seat.
+Considere $T(N)$ como o número de possibilidades de que $N$ assentos estejam ocupados por $N$ pessoas com as regras dadas. A figura a seguir mostra $T(4) = 8$.
-Otherwise take one of the remaining available seats.
+
-Let T(N) be the number of possibilities that N seats are occupied by N people with the given rules. The following figure shows T(4)=8.
+Podemos verificar que $T(10) = 61.632$ e $T(1.000)\bmod 100.000.007 = 47.255.094$.
-We can verify that T(10) = 61632 and T(1 000) mod 100 000 007 = 47255094. Find T(1 000 000) mod 100 000 007.
+Encontre $T(1.000.000)\bmod 100.000.007$.
# --hints--
-`euler364()` should return 44855254.
+`comfortableDistance()` deve retornar `44855254`.
```js
-assert.strictEqual(euler364(), 44855254);
+assert.strictEqual(comfortableDistance(), 44855254);
```
# --seed--
@@ -33,12 +35,12 @@ assert.strictEqual(euler364(), 44855254);
## --seed-contents--
```js
-function euler364() {
+function comfortableDistance() {
return true;
}
-euler364();
+comfortableDistance();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
index 1647ff46ea..2a8c7adc20 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-365-a-huge-binomial-coefficient.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffec
-title: 'Problem 365: A huge binomial coefficient'
+title: 'Problema 365: Um coeficiente binomial enorme'
challengeType: 5
forumTopicId: 302026
dashedName: problem-365-a-huge-binomial-coefficient
@@ -8,18 +8,18 @@ dashedName: problem-365-a-huge-binomial-coefficient
# --description--
-The binomial coefficient C(1018,109) is a number with more than 9 billion (9×109) digits.
+O coeficiente binomial $\displaystyle\binom{{10}^{18}}{{10}^9}$ é um número com mais de 9 bilhões de algarismos ($9 × {10}^9$).
-Let M(n,k,m) denote the binomial coefficient C(n,k) modulo m.
+Considere $M(n, k, m)$ como o coeficiente binomial $\displaystyle\binom{n}{k}$ modulo $m$.
-Calculate ∑M(1018,109,p*q*r) for 1000<p<q<r<5000 and p,q,r prime.
+Calcule $\sum M({10}^{18}, {10}^9, p \times q \times r)$ para$1000 < p < q < r < 5000$ e com $p$, $q$, $r$ sendo números primos.
# --hints--
-`euler365()` should return 162619462356610300.
+`hugeBinomialCoefficient()` deve retornar `162619462356610300`.
```js
-assert.strictEqual(euler365(), 162619462356610300);
+assert.strictEqual(hugeBinomialCoefficient(), 162619462356610300);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler365(), 162619462356610300);
## --seed-contents--
```js
-function euler365() {
+function hugeBinomialCoefficient() {
return true;
}
-euler365();
+hugeBinomialCoefficient();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
index b7f832ebf4..d81f73beb7 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-366-stone-game-iii.md
@@ -1,6 +1,6 @@
---
id: 5900f4da1000cf542c50ffed
-title: 'Problem 366: Stone Game III'
+title: 'Problema 366: Jogo da pedra III'
challengeType: 5
forumTopicId: 302027
dashedName: problem-366-stone-game-iii
@@ -8,30 +8,44 @@ dashedName: problem-366-stone-game-iii
# --description--
-Two players, Anton and Bernhard, are playing the following game.
+Dois jogadores, Anton e Bernhard, estão jogando o seguinte jogo.
-There is one pile of n stones.
+Existe uma pilha de $n$ pedras.
-The first player may remove any positive number of stones, but not the whole pile.
+O primeiro jogador pode remover qualquer número positivo de pedras, mas não a pilha toda.
-Thereafter, each player may remove at most twice the number of stones his opponent took on the previous move.
+Depois disso, cada jogador pode remover, no máximo, o dobro das pedras que seu oponente removeu no movimento anterior.
-The player who removes the last stone wins.
+O jogador que remover a última pedra ganha.
-E.g. n=5 If the first player takes anything more than one stone the next player will be able to take all remaining stones. If the first player takes one stone, leaving four, his opponent will take also one stone, leaving three stones. The first player cannot take all three because he may take at most 2x1=2 stones. So let's say he takes also one stone, leaving 2. The second player can take the two remaining stones and wins. So 5 is a losing position for the first player. For some winning positions there is more than one possible move for the first player. E.g. when n=17 the first player can remove one or four stones.
+Ex: $n = 5$
-Let M(n) be the maximum number of stones the first player can take from a winning position at his first turn and M(n)=0 for any other position.
+Se o primeiro jogador pegar mais do que uma pedra, o próximo jogador será capaz de pegar todas as pedras restantes.
-∑M(n) for n≤100 is 728.
+Se o primeiro jogador pegar uma pedra, deixando quatro, o oponente dele pegará também uma pedra, deixando três pedras.
-Find ∑M(n) for n≤1018. Give your answer modulo 108.
+O primeiro jogador não pode pegar todas as três pedras restantes porque ele pode pegar no máximo $2 \times 1 = 2$ pedras. Então digamos que ele também leve uma pedra, deixando 2.
+
+O segundo jogador pode pegar as duas pedras restantes e ganhar.
+
+Portanto, 5 é uma posição em que o primeiro jogador perde.
+
+Para algumas posições vencedoras, há mais de um movimento possível para o primeiro jogador.
+
+Ex: quando $n = 17$, o primeiro jogador pode remover uma ou quatro pedras.
+
+Considere $M(n)$ como o número máximo de pedras que o primeiro jogador pode remover em uma posição vencedora em seu primeiro movimento e $M(n) = 0$ para qualquer outra posição.
+
+A $\sum M(n)$ para $n ≤ 100$ é 728.
+
+Encontre a $\sum M(n)$ para $n ≤ {10}^{18}$. Dê sua resposta modulo ${10}^8$.
# --hints--
-`euler366()` should return 88351299.
+`stoneGameThree()` deve retornar `88351299`.
```js
-assert.strictEqual(euler366(), 88351299);
+assert.strictEqual(stoneGameThree(), 88351299);
```
# --seed--
@@ -39,12 +53,12 @@ assert.strictEqual(euler366(), 88351299);
## --seed-contents--
```js
-function euler366() {
+function stoneGameThree() {
return true;
}
-euler366();
+stoneGameThree();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
index 979702592a..c841db192c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-367-bozo-sort.md
@@ -1,6 +1,6 @@
---
id: 5900f4db1000cf542c50ffee
-title: 'Problem 367: Bozo sort'
+title: 'Problema 367: Ordenação do Bozo'
challengeType: 5
forumTopicId: 302028
dashedName: problem-367-bozo-sort
@@ -8,20 +8,32 @@ dashedName: problem-367-bozo-sort
# --description--
-Bozo sort, not to be confused with the slightly less efficient bogo sort, consists out of checking if the input sequence is sorted and if not swapping randomly two elements. This is repeated until eventually the sequence is sorted.
+A ordenação do Bozo – não confunda com a ordenação Bogo, ligeiramente menos eficiente – consiste em verificar se a sequência de entrada está ordenada e, se não estiver, trocar aleatoriamente dois elementos. Isso é repetido até que a sequência esteja ordenada.
-If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of swaps, averaged over all 4! input sequences is 24.75. The already sorted sequence takes 0 steps.
+Se considerarmos todas as permutações dos primeiros 4 números naturais como entrada, o valor da expectativa do número de trocas, na média sobre todas as sequências de entrada $4!$, é $24,75$.
-In this problem we consider the following variant on bozo sort. If the sequence is not in order we pick three elements at random and shuffle these three elements randomly. All 3!=6 permutations of those three elements are equally likely. The already sorted sequence will take 0 steps. If we consider all permutations of the first 4 natural numbers as input the expectation value of the number of shuffles, averaged over all 4! input sequences is 27.5. Consider as input sequences the permutations of the first 11 natural numbers. Averaged over all 11! input sequences, what is the expected number of shuffles this sorting algorithm will perform?
+A sequência já classificada leva 0 etapas.
-Give your answer rounded to the nearest integer.
+Neste problema, consideramos a seguinte variante na ordenação do Bozo.
+
+Se a sequência não estiver em ordem, selecionamos três elementos aleatoriamente e embaralhamos esses três elementos aleatoriamente.
+
+Todas as permutações $3! = 6$ desses três elementos são igualmente prováveis.
+
+A sequência já classificada levará 0 etapas.
+
+Se considerarmos todas as permutações dos primeiros 4 números naturais como entrada, o valor da expectativa do número de embaralhamentos, na média sobre todas as sequências de entrada $4!$, é $27,5$.
+
+Considere como sequências de entrada as permutações dos primeiros 11 números naturais.
+
+Com a média sobre todas as sequências de entrada $11!$, qual é o número esperado de embaralhamentos que este algoritmo de ordenação executará? Dê a sua resposta arredondada para o número inteiro mais próximo.
# --hints--
-`euler367()` should return 48271207.
+`bozoSort()` deve retornar `48271207`.
```js
-assert.strictEqual(euler367(), 48271207);
+assert.strictEqual(bozoSort(), 48271207);
```
# --seed--
@@ -29,12 +41,12 @@ assert.strictEqual(euler367(), 48271207);
## --seed-contents--
```js
-function euler367() {
+function bozoSort() {
return true;
}
-euler367();
+bozoSort();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
index dc9cf2f919..cebfef535d 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-368-a-kempner-like-series.md
@@ -1,6 +1,6 @@
---
id: 5900f4dd1000cf542c50ffef
-title: 'Problem 368: A Kempner-like series'
+title: 'Problema 368: Uma série semelhante à de Kempner'
challengeType: 5
forumTopicId: 302029
dashedName: problem-368-a-kempner-like-series
@@ -8,22 +8,26 @@ dashedName: problem-368-a-kempner-like-series
# --description--
-The harmonic series $1 + \\dfrac{1}{2} + \\dfrac{1}{3} + \\dfrac{1}{4} + ...$ is well known to be divergent.
+A série harmônica $1 + \dfrac{1}{2} + \dfrac{1}{3} + \dfrac{1}{4} + \ldots$ é conhecido por ser divergente.
-If we however omit from this series every term where the denominator has a 9 in it, the series remarkably enough converges to approximately 22.9206766193. This modified harmonic series is called the Kempner series.
+No entanto, se omitirmos desta série todos os termos em que o denominador tem um 9, a série converge consideravelmente para aproximadamente 22,9206766193. Esta série harmônica modificada é chamada de série de Kempner.
-Let us now consider another modified harmonic series by omitting from the harmonic series every term where the denominator has 3 or more equal consecutive digits. One can verify that out of the first 1200 terms of the harmonic series, only 20 terms will be omitted. These 20 omitted terms are: $$\\dfrac{1}{111}, \\dfrac{1}{222}, \\dfrac{1}{333}, \\dfrac{1}{444}, \\dfrac{1}{555}, \\dfrac{1}{666}, \\dfrac{1}{777}, \\dfrac{1}{888}, \\dfrac{1}{999}, \\dfrac{1}{1000}, \\dfrac{1}{1110}, \\\\ \\dfrac{1}{1111}, \\dfrac{1}{1112}, \\dfrac{1}{1113}, \\dfrac{1}{1114}, \\dfrac{1}{1115}, \\dfrac{1}{1116}, \\dfrac{1}{1117}, \\dfrac{1}{1118}, \\dfrac{1}{1119}$$
+Consideremos agora outra série harmônica modificada, omitindo da série harmônica todos os termos em que o denominador tem 3 ou mais algarismos iguais consecutivos. Pode-se verificar que, dos primeiros 1200 termos da série harmônica, apenas 20 termos serão omitidos.
-This series converges as well.
+Estes 20 termos omitidos são:
-Find the value the series converges to. Give your answer rounded to 10 digits behind the decimal point.
+$$\dfrac{1}{111}, \dfrac{1}{222}, \dfrac{1}{333}, \dfrac{1}{444}, \dfrac{1}{555}, \dfrac{1}{666}, \dfrac{1}{777}, \dfrac{1}{888}, \dfrac{1}{999}, \dfrac{1}{1000}, \dfrac{1}{1110}, \\\\ \dfrac{1}{1111}, \dfrac{1}{1112}, \dfrac{1}{1113}, \dfrac{1}{1114}, \dfrac{1}{1115}, \dfrac{1}{1116}, \dfrac{1}{1117}, \dfrac{1}{1118}, \dfrac{1}{1119}$$
+
+Esta série também converge.
+
+Encontre o valor para o qual a série converge. Dê sua resposta arredondada para 10 casas depois da vírgula.
# --hints--
-`euler368()` should return 253.6135092068.
+`kempnerLikeSeries()` deve retornar `253.6135092068`.
```js
-assert.strictEqual(euler368(), 253.6135092068);
+assert.strictEqual(kempnerLikeSeries(), 253.6135092068);
```
# --seed--
@@ -31,12 +35,12 @@ assert.strictEqual(euler368(), 253.6135092068);
## --seed-contents--
```js
-function euler368() {
+function kempnerLikeSeries() {
return true;
}
-euler368();
+kempnerLikeSeries();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-369-badugi.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-369-badugi.md
index abdcb4c810..bf2eede118 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-369-badugi.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-369-badugi.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff0
-title: 'Problem 369: Badugi'
+title: 'Problema 369: Badugi'
challengeType: 5
forumTopicId: 302030
dashedName: problem-369-badugi
@@ -8,18 +8,18 @@ dashedName: problem-369-badugi
# --description--
-In a standard 52 card deck of playing cards, a set of 4 cards is a Badugi if it contains 4 cards with no pairs and no two cards of the same suit.
+Em um baralho padrão de 52 cartas, um conjunto de 4 cartas é um Badugi caso tenha 4 cartas sem pares e se não houver duas cartas do mesmo naipe.
-Let f(n) be the number of ways to choose n cards with a 4 card subset that is a Badugi. For example, there are 2598960 ways to choose five cards from a standard 52 card deck, of which 514800 contain a 4 card subset that is a Badugi, so f(5) = 514800.
+Considere $f(n)$ como o número de maneiras de escolher $n$ cartas com um subconjunto de 4 cartas que é um Badugi. Por exemplo, há $2.598.960$ maneiras de escolher cinco cartas de um baralho padrão de 52 cartas. Dessas, $514.800$ contêm um subconjunto que é um Badugi. Assim, $f(5) = 514800$.
-Find ∑f(n) for 4 ≤ n ≤ 13.
+Encontre $\sum f(n)$ para $4 ≤ n ≤ 13$.
# --hints--
-`euler369()` should return 862400558448.
+`badugi()` deve retornar `862400558448`.
```js
-assert.strictEqual(euler369(), 862400558448);
+assert.strictEqual(badugi(), 862400558448);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler369(), 862400558448);
## --seed-contents--
```js
-function euler369() {
+function badugi() {
return true;
}
-euler369();
+badugi();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
index 469f9151e0..bb72f1a9b9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-370-geometric-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4de1000cf542c50fff1
-title: 'Problem 370: Geometric triangles'
+title: 'Problema 370: Triângulos geométricos'
challengeType: 5
forumTopicId: 302032
dashedName: problem-370-geometric-triangles
@@ -8,20 +8,20 @@ dashedName: problem-370-geometric-triangles
# --description--
-Let us define a geometric triangle as an integer sided triangle with sides a ≤ b ≤ c so that its sides form a geometric progression, i.e. b2 = a · c .
+Vamos definir um triângulo geométrico como um triângulo de lados compostos de números inteiros, com os lados $a ≤ b ≤ c$, de modo que seus lados formem uma progressão geométrica, ou seja, $b^2 = a \times c$.
-An example of such a geometric triangle is the triangle with sides a = 144, b = 156 and c = 169.
+Um exemplo de um triângulo geométrico como este é o triângulo de lados $a = 144$, $b = 156$ e $c = 169$.
-There are 861805 geometric triangles with perimeter ≤ 106 .
+Existem $861.805$ triângulos geométricos com $\text{perímetro} ≤ {10}^6$.
-How many geometric triangles exist with perimeter ≤ 2.5·1013 ?
+Quantos triângulos geométricos existem com $\text{perímetro} ≤ 2,5 \times {10}^{13}$?
# --hints--
-`euler370()` should return 41791929448408.
+`geometricTriangles()` deve retornar `41791929448408`.
```js
-assert.strictEqual(euler370(), 41791929448408);
+assert.strictEqual(geometricTriangles(), 41791929448408);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler370(), 41791929448408);
## --seed-contents--
```js
-function euler370() {
+function geometricTriangles() {
return true;
}
-euler370();
+geometricTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
index 005b5aaf07..f85e6deb98 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-371-licence-plates.md
@@ -1,6 +1,6 @@
---
id: 5900f4e01000cf542c50fff2
-title: 'Problem 371: Licence plates'
+title: 'Problema 371: Placas de carro'
challengeType: 5
forumTopicId: 302033
dashedName: problem-371-licence-plates
@@ -8,24 +8,24 @@ dashedName: problem-371-licence-plates
# --description--
-Oregon licence plates consist of three letters followed by a three digit number (each digit can be from \[0..9]).
+As placas de carro do Oregon consistem em três letras seguidas por um número de três algarismos (cada algarismo podendo estar entre [0...9]).
-While driving to work Seth plays the following game:
+Enquanto conduz para o trabalho, Seth joga o seguinte jogo:
-Whenever the numbers of two licence plates seen on his trip add to 1000 that's a win.
+Sempre que o número de duas placas de carro que ele vê na viagem somar 1000, é uma vitória.
-E.g. MIC-012 and HAN-988 is a win and RYU-500 and SET-500 too. (as long as he sees them in the same trip).
+Ex: `MIC-012` e `HAN-988` é uma vitória e `RYU-500` e `SET-500` também. (contanto que ele os veja na mesma viagem).
-Find the expected number of plates he needs to see for a win. Give your answer rounded to 8 decimal places behind the decimal point.
+Encontre o número esperado de licenças que ele precisa ver para a vitória. Dê sua resposta arredondada para 8 casas depois da vírgula.
-Note: We assume that each licence plate seen is equally likely to have any three digit number on it.
+**Observação:** consideramos que cada placa de carro vista tem igual probabilidade de ter um número de três algarismos nela.
# --hints--
-`euler371()` should return 40.66368097.
+`licensePlates()` deve retornar `40.66368097`.
```js
-assert.strictEqual(euler371(), 40.66368097);
+assert.strictEqual(licensePlates(), 40.66368097);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler371(), 40.66368097);
## --seed-contents--
```js
-function euler371() {
+function licensePlates() {
return true;
}
-euler371();
+licensePlates();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
index 1a04cacb71..0665ccea04 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-372-pencils-of-rays.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff3
-title: 'Problem 372: Pencils of rays'
+title: 'Problema 372: Feixe de raios'
challengeType: 5
forumTopicId: 302034
dashedName: problem-372-pencils-of-rays
@@ -8,16 +8,20 @@ dashedName: problem-372-pencils-of-rays
# --description--
-Let R(M, N) be the number of lattice points (x, y) which satisfy M
+Considere $R(M, N)$ como o número de pontos da rede($x$, $y$) que satisfaz $M \lt x \le N$, $M \lt y \le N$ e que $\left\lfloor\frac{y^2}{x^2}\right\rfloor$ é ímpar.
-Note: represents the floor function.
+Podemos verificar que $R(0, 100) = 3.019$ e $R(100, 10.000) = 29.750.422$.
+
+Encontre $R(2 \times {10}^6, {10}^9)$.
+
+**Observação:** $\lfloor x\rfloor$ representa a função piso.
# --hints--
-`euler372()` should return 301450082318807040.
+`pencilsOfRays()` deve retornar `301450082318807040`.
```js
-assert.strictEqual(euler372(), 301450082318807040);
+assert.strictEqual(pencilsOfRays(), 301450082318807040);
```
# --seed--
@@ -25,12 +29,12 @@ assert.strictEqual(euler372(), 301450082318807040);
## --seed-contents--
```js
-function euler372() {
+function pencilsOfRays() {
return true;
}
-euler372();
+pencilsOfRays();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
index 534c32ea25..9ac9ba041d 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-373-circumscribed-circles.md
@@ -1,6 +1,6 @@
---
id: 5900f4e11000cf542c50fff4
-title: 'Problem 373: Circumscribed Circles'
+title: 'Problema 373: Círculos circunscritos'
challengeType: 5
forumTopicId: 302035
dashedName: problem-373-circumscribed-circles
@@ -8,22 +8,20 @@ dashedName: problem-373-circumscribed-circles
# --description--
-Every triangle has a circumscribed circle that goes through the three vertices.
+Todo triângulo tem um círculo circunscrito que atravessa os três vértices. Considere todos os triângulos com os lados compostos de números inteiros para os quais o raio do círculo circunscrito também é um número inteiro.
-Consider all integer sided triangles for which the radius of the circumscribed circle is integral as well.
+Considere $S(n)$ como a soma dos raios dos círculos circunscritos de todos os triângulos para os quais o raio não excede $n$.
-Let S(n) be the sum of the radii of the circumscribed circles of all such triangles for which the radius does not exceed n.
+$S(100) = 4.950$ e $S(1.200) = 1.653.605$.
-S(100)=4950 and S(1200)=1653605.
-
-Find S(107).
+Encontre $S({10}^7)$.
# --hints--
-`euler373()` should return 727227472448913.
+`circumscribedCircles()` deve retornar `727227472448913`.
```js
-assert.strictEqual(euler373(), 727227472448913);
+assert.strictEqual(circumscribedCircles(), 727227472448913);
```
# --seed--
@@ -31,12 +29,12 @@ assert.strictEqual(euler373(), 727227472448913);
## --seed-contents--
```js
-function euler373() {
+function circumscribedCircles() {
return true;
}
-euler373();
+circumscribedCircles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
index 10fe621891..f1a501bca6 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-374-maximum-integer-partition-product.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff6
-title: 'Problem 374: Maximum Integer Partition Product'
+title: 'Problema 374: Produto da partição inteira máxima'
challengeType: 5
forumTopicId: 302036
dashedName: problem-374-maximum-integer-partition-product
@@ -8,28 +8,30 @@ dashedName: problem-374-maximum-integer-partition-product
# --description--
-An integer partition of a number n is a way of writing n as a sum of positive integers.
+Uma partição inteira de um número $n$ é uma maneira de escrever $n$ como uma soma dos números inteiros positivos.
-Partitions that differ only in the order of their summands are considered the same. A partition of n into distinct parts is a partition of n in which every part occurs at most once.
+Partições que diferem apenas da ordem de seus somandos são consideradas iguais. Uma partição de $n$ em partes distintas é uma partição de $n$ na qual cada parte ocorre no máximo uma vez.
-The partitions of 5 into distinct parts are: 5, 4+1 and 3+2.
+As partições de 5 em partes distintas são:
-Let f(n) be the maximum product of the parts of any such partition of n into distinct parts and let m(n) be the number of elements of any such partition of n with that product.
+5, 4 + 1 e 3 + 2.
-So f(5)=6 and m(5)=2.
+Considere $f(n)$ como o produto máximo das partes de qualquer partição de $n$ em partes distintas e $m(n)$ o número de elementos de qualquer partição $n$ com esse produto.
-For n=10 the partition with the largest product is 10=2+3+5, which gives f(10)=30 and m(10)=3. And their product, f(10)·m(10) = 30·3 = 90
+Assim, $f(5) = 6$ e $m(5) = 2$.
-It can be verified that ∑f(n)·m(n) for 1 ≤ n ≤ 100 = 1683550844462.
+Para $n = 10$, a partição com o maior produto é $10 = 2 + 3 + 5$, o que dá $f(10) = 30$ e $m(10) = 3$. E seu produto, $f(10) \times m(10) = 30 \times 3 = 90$
-Find ∑f(n)·m(n) for 1 ≤ n ≤ 1014. Give your answer modulo 982451653, the 50 millionth prime.
+Pode-se verificar que $\sum f(n) \times m(n)$ para $1 ≤ n ≤ 100 = 1.683.550.844.462$.
+
+Encontre a $\sum f(n) \times m(n)$ para $1 ≤ n ≤ {10}^{14}$. Dê sua resposta modulo $982.451.653$, o quinquagésimo milionésimo número primo.
# --hints--
-`euler374()` should return 334420941.
+`maximumIntegerPartitionProduct()` deve retornar `334420941`.
```js
-assert.strictEqual(euler374(), 334420941);
+assert.strictEqual(maximumIntegerPartitionProduct(), 334420941);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler374(), 334420941);
## --seed-contents--
```js
-function euler374() {
+function maximumIntegerPartitionProduct() {
return true;
}
-euler374();
+maximumIntegerPartitionProduct();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
index 684613a235..49589b217a 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-375-minimum-of-subsequences.md
@@ -1,6 +1,6 @@
---
id: 5900f4e41000cf542c50fff5
-title: 'Problem 375: Minimum of subsequences'
+title: 'Problema 375: Mínimo das subsequências'
challengeType: 5
forumTopicId: 302037
dashedName: problem-375-minimum-of-subsequences
@@ -8,30 +8,22 @@ dashedName: problem-375-minimum-of-subsequences
# --description--
-Let Sn be an integer sequence produced with the following pseudo-random number generator:
+Considere $S_n$ como uma sequência de números inteiros produzida com o seguinte gerador de números pseudoaleatórios:
-S0
+$$\begin{align} S_0 & = 290.797 \\\\ S_{n + 1} & = {S_n}^2\bmod 50.515.093 \end{align}$$
-=
+Considere $A(i, j)$ como o mínimo dos números $S_i, S_{i + 1}, \ldots, S_j$ para $i ≤ j$. Considere $M(N) = \sum A(i, j)$ para $1 ≤ i ≤ j ≤ N$.
-290797
+Podemos verificar que $M(10) = 432.256.955$ e $M(10.000) = 3.264.567.774.119$.
-Sn+1
-
-=
-
-Sn2 mod 50515093
-
-Let A(i, j) be the minimum of the numbers Si, Si+1, ... , Sj for i ≤ j. Let M(N) = ΣA(i, j) for 1 ≤ i ≤ j ≤ N. We can verify that M(10) = 432256955 and M(10 000) = 3264567774119.
-
-Find M(2 000 000 000).
+Encontre $M(2.000.000.000)$.
# --hints--
-`euler375()` should return 7435327983715286000.
+`minimumOfSubsequences()` deve retornar `7435327983715286000`.
```js
-assert.strictEqual(euler375(), 7435327983715286000);
+assert.strictEqual(minimumOfSubsequences(), 7435327983715286000);
```
# --seed--
@@ -39,12 +31,12 @@ assert.strictEqual(euler375(), 7435327983715286000);
## --seed-contents--
```js
-function euler375() {
+function minimumOfSubsequences() {
return true;
}
-euler375();
+minimumOfSubsequences();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
index b76c4d26e8..89aaca2074 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-376-nontransitive-sets-of-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff7
-title: 'Problem 376: Nontransitive sets of dice'
+title: 'Problema 376: Conjuntos de dados não transitivos'
challengeType: 5
forumTopicId: 302038
dashedName: problem-376-nontransitive-sets-of-dice
@@ -8,30 +8,43 @@ dashedName: problem-376-nontransitive-sets-of-dice
# --description--
-Consider the following set of dice with nonstandard pips:
+Considere o seguinte conjunto de dados com valores fora do padrão de 1 a 6:
-Die A: 1 4 4 4 4 4 Die B: 2 2 2 5 5 5 Die C: 3 3 3 3 3 6
+$$\begin{array}{} \text{Die A: } & 1 & 4 & 4 & 4 & 4 & 4 \\\\ \text{Die B: } & 2 & 2 & 2 & 5 & 5 & 5 \\\\ \text{Die C: } & 3 & 3 & 3 & 3 & 3 & 6 \\\\ \end{array}$$
-A game is played by two players picking a die in turn and rolling it. The player who rolls the highest value wins.
+Um jogo é disputado por dois jogadores que escolhem um dado por vez e o rolam. O jogador que rolar nos dados o maior valor ganha.
-If the first player picks die A and the second player picks die B we get P(second player wins) = 7/12 > 1/2
+Se o primeiro jogador escolher o dado $A$ e o segundo jogador escolher o dado $B$, temos
-If the first player picks die B and the second player picks die C we get P(second player wins) = 7/12 > 1/2
+$P(\text{vitória do segundo jogador}) = \frac{7}{12} > \frac{1}{2}$
-If the first player picks die C and the second player picks die A we get P(second player wins) = 25/36 > 1/2
+Se o primeiro jogador escolher o dado $B$ e o segundo jogador escolher o dado $C$, temos
-So whatever die the first player picks, the second player can pick another die and have a larger than 50% chance of winning. A set of dice having this property is called a nontransitive set of dice.
+$P(\text{vitória do segundo jogador}) = \frac{7}{12} > \frac{1}{2}$
-We wish to investigate how many sets of nontransitive dice exist. We will assume the following conditions:There are three six-sided dice with each side having between 1 and N pips, inclusive. Dice with the same set of pips are equal, regardless of which side on the die the pips are located. The same pip value may appear on multiple dice; if both players roll the same value neither player wins. The sets of dice {A,B,C}, {B,C,A} and {C,A,B} are the same set.
+Se o primeiro jogador escolher o dado $C$ e o segundo jogador escolher o dado $A$, nós temos
-For N = 7 we find there are 9780 such sets. How many are there for N = 30 ?
+$P(\text{vitória do segundo jogador}) = \frac{25}{36} > \frac{1}{2}$
+
+Portanto, seja qual for o dado que o primeiro jogador escolher, o segundo jogador pode escolher outro dado e ter mais de 50% de chance de ganhar. Um conjunto de dados com esta propriedade é denominado conjunto de dados não transitivo.
+
+Queremos investigar quantos conjuntos de dados não transitivos existem. Assumiremos as seguintes condições:
+
+- Existem três dados de seis lados com cada lado tendo entre 1 e $N$ pontos, inclusive.
+- Dados com o mesmo conjunto de pontos são iguais, independentemente de qual lado no dado o ponto está localizado.
+- O mesmo valor de pontos pode aparecer em vários dados. Se ambos os jogadores obtiverem o mesmo valor, nenhum deles ganhará.
+- Os conjuntos de dados $\\{A, B, C\\}$, $\\{B, C, A\\}$ e $\\{C, A, B\\}$ são o mesmo conjunto.
+
+Para $N = 7$ encontramos 9780 desses conjuntos.
+
+Quantos são para $N = 30$?
# --hints--
-`euler376()` should return 973059630185670.
+`nontransitiveSetsOfDice()` deve retornar `973059630185670`.
```js
-assert.strictEqual(euler376(), 973059630185670);
+assert.strictEqual(nontransitiveSetsOfDice(), 973059630185670);
```
# --seed--
@@ -39,12 +52,12 @@ assert.strictEqual(euler376(), 973059630185670);
## --seed-contents--
```js
-function euler376() {
+function nontransitiveSetsOfDice() {
return true;
}
-euler376();
+nontransitiveSetsOfDice();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
index 660508c234..f573944ee7 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-377-sum-of-digits-experience-13.md
@@ -1,6 +1,6 @@
---
id: 5900f4e51000cf542c50fff8
-title: 'Problem 377: Sum of digits, experience 13'
+title: 'Problema 377: Soma dos algarismos, experiência nº 13'
challengeType: 5
forumTopicId: 302039
dashedName: problem-377-sum-of-digits-experience-13
@@ -8,22 +8,22 @@ dashedName: problem-377-sum-of-digits-experience-13
# --description--
-There are 16 positive integers that do not have a zero in their digits and that have a digital sum equal to 5, namely:
+Existem 16 números inteiros positivos que não têm zero nos seus algarismos e que têm uma soma de algarismos igual a 5. São eles:
-5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 and 11111.
+5, 14, 23, 32, 41, 113, 122, 131, 212, 221, 311, 1112, 1121, 1211, 2111 e 11111.
-Their sum is 17891.
+A soma deles é de 17891.
-Let f(n) be the sum of all positive integers that do not have a zero in their digits and have a digital sum equal to n.
+Considere $f(n)$ como a soma de todos os números inteiros positivos que não têm zero nos seus algarismos e que têm uma soma dos algarismos igual a $n$.
-Find $\\displaystyle \\sum\_{i=1}^{17} f(13^i)$. Give the last 9 digits as your answer.
+Encontre $\displaystyle\sum_{i=1}^{17} f(13^i)$. Dê os últimos 9 algarismos da sua resposta.
# --hints--
-`euler377()` should return 732385277.
+`experience13()` deve retornar `732385277`.
```js
-assert.strictEqual(euler377(), 732385277);
+assert.strictEqual(experience13(), 732385277);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler377(), 732385277);
## --seed-contents--
```js
-function euler377() {
+function experience13() {
return true;
}
-euler377();
+experience13();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
index 22589747fe..4ade6a2e45 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-378-triangle-triples.md
@@ -1,6 +1,6 @@
---
id: 5900f4e61000cf542c50fff9
-title: 'Problem 378: Triangle Triples'
+title: 'Problema 378: Trios de triângulos'
challengeType: 5
forumTopicId: 302040
dashedName: problem-378-triangle-triples
@@ -8,24 +8,20 @@ dashedName: problem-378-triangle-triples
# --description--
-Let T(n) be the nth triangle number, so T(n) =
+Considere $T(n)$ como o $n^{\text{º}}$ número triangular. Assim, $T(n) = \frac{n(n + 1)}{2}$.
-n (n+1)2
+Considere $dT(n)$ como o número de divisores de $T(n)$. Ex.: $T(7) = 28$ e $dT(7) = 6$.
-.
+Considere $Tr(n)$ como o número de trios ($i$, $j$, $k$), tal que $1 ≤ i < j < k ≤ n$ e $dT(i) > dT(j) > dT(k)$. $Tr(20) = 14$, $Tr(100) = 5.772$ e $Tr(1000) = 11.174.776$.
-Let dT(n) be the number of divisors of T(n). E.g.: T(7) = 28 and dT(7) = 6.
-
-Let Tr(n) be the number of triples (i, j, k) such that 1 ≤ i < j < k ≤ n and dT(i) > dT(j) > dT(k). Tr(20) = 14, Tr(100) = 5772 and Tr(1000) = 11174776.
-
-Find Tr(60 000 000). Give the last 18 digits of your answer.
+Encontre $Tr(60.000.000)$. Dê os últimos 18 dígitos da sua resposta.
# --hints--
-`euler378()` should return 147534623725724700.
+`triangleTriples()` deve retornar `147534623725724700`.
```js
-assert.strictEqual(euler378(), 147534623725724700);
+assert.strictEqual(triangleTriples(), 147534623725724700);
```
# --seed--
@@ -33,12 +29,12 @@ assert.strictEqual(euler378(), 147534623725724700);
## --seed-contents--
```js
-function euler378() {
+function triangleTriples() {
return true;
}
-euler378();
+triangleTriples();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
index 3933d82ea2..815095067e 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-379-least-common-multiple-count.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffa
-title: 'Problem 379: Least common multiple count'
+title: 'Problema 379: Contagem de mínimos múltiplos comuns'
challengeType: 5
forumTopicId: 302041
dashedName: problem-379-least-common-multiple-count
@@ -8,20 +8,20 @@ dashedName: problem-379-least-common-multiple-count
# --description--
-Let f(n) be the number of couples (x,y) with x and y positive integers, x ≤ y and the least common multiple of x and y equal to n.
+Considere $f(n)$ como o número de pares ($x$, $y$) com $x$ e $y$ sendo números inteiros positivos, $x ≤ y$ e o mínimo múltiplo comum de $x$ e $y$ sendo igual a $n$.
-Let g be the summatory function of f, i.e.: g(n) = ∑ f(i) for 1 ≤ i ≤ n.
+Considere $g$ como a função somatória de $f$, ou seja, $g(n) = \sum f(i)$ para $1 ≤ i ≤ n$.
-You are given that g(106) = 37429395.
+Você é informado de que $g({10}^6) = 37.429.395$.
-Find g(1012).
+Encontre $g({10}^{12})$.
# --hints--
-`euler379()` should return 132314136838185.
+`leastCommonMultipleCount()` deve retornar `132314136838185`.
```js
-assert.strictEqual(euler379(), 132314136838185);
+assert.strictEqual(leastCommonMultipleCount(), 132314136838185);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler379(), 132314136838185);
## --seed-contents--
```js
-function euler379() {
+function leastCommonMultipleCount() {
return true;
}
-euler379();
+leastCommonMultipleCount();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
index 8596f52fa7..de819fa0b7 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-380-amazing-mazes.md
@@ -1,6 +1,6 @@
---
id: 5900f4e81000cf542c50fffb
-title: 'Problem 380: Amazing Mazes!'
+title: 'Problema 380: Labirintos fantásticos!'
challengeType: 5
forumTopicId: 302044
dashedName: problem-380-amazing-mazes
@@ -8,20 +8,30 @@ dashedName: problem-380-amazing-mazes
# --description--
-An m×n maze is an m×n rectangular grid with walls placed between grid cells such that there is exactly one path from the top-left square to any other square. The following are examples of a 9×12 maze and a 15×20 maze:
+Um labirinto $m×n$ é uma grade retangular $m×n$ com paredes colocadas entre as células da malha de forma que haja exatamente um caminho do quadrado superior esquerdo para qualquer outro quadrado. Os exemplos a seguir são de um labirinto 9×12 e de um labirinto 15×20:
-Let C(m,n) be the number of distinct m×n mazes. Mazes which can be formed by rotation and reflection from another maze are considered distinct.
+
-It can be verified that C(1,1) = 1, C(2,2) = 4, C(3,4) = 2415, and C(9,12) = 2.5720e46 (in scientific notation rounded to 5 significant digits). Find C(100,500) and write your answer in scientific notation rounded to 5 significant digits.
+Considere $C(m, n)$ como o número de labirintos distintos $m×n$. Os labirintos que podem ser criados por rotação e reflexão de outro labirinto são considerados distintos.
-When giving your answer, use a lowercase e to separate mantissa and exponent. E.g. if the answer is 1234567891011 then the answer format would be 1.2346e12.
+Pode-se verificar que $C(1, 1) = 1$, $C(2, 2) = 4$, $C(3, 4) = 2415$ e $C(9, 12) = 2.5720\mathrm{e}\\,46$ (na notação científica, arredondado para 5 algarismos significantes).
+
+Encontre $C(100, 500)$ e escreva sua resposta em uma string em notação científica arredondada para 5 algarismos significativos.
+
+Ao dar sua resposta, use letra minúscula para separar a mantissa e o expoente. Ex: se a resposta for 1234567891011, o formato da resposta deve ser a string `1.2346e12`.
# --hints--
-`euler380()` should return Infinity.
+`amazingMazes()` deve retornar uma string.
```js
-assert.strictEqual(euler380(), Infinity);
+assert(typeof amazingMazes() === 'string');
+```
+
+`amazingMazes()` deve retornar a string `6.3202e25093`.
+
+```js
+assert.strictEqual(amazingMazes(), '6.3202e25093');
```
# --seed--
@@ -29,12 +39,12 @@ assert.strictEqual(euler380(), Infinity);
## --seed-contents--
```js
-function euler380() {
+function amazingMazes() {
return true;
}
-euler380();
+amazingMazes();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
index f64768a5c7..dd32001ff3 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-381-prime-k-factorial.md
@@ -1,6 +1,6 @@
---
id: 5900f4ea1000cf542c50fffc
-title: 'Problem 381: (prime-k) factorial'
+title: 'Problema 381: Fatorial (k-primo)'
challengeType: 5
forumTopicId: 302045
dashedName: problem-381-prime-k-factorial
@@ -8,20 +8,24 @@ dashedName: problem-381-prime-k-factorial
# --description--
-For a prime p let S(p) = (∑(p-k)!) mod(p) for 1 ≤ k ≤ 5.
+Para um número primo $p$, considere $S(p) = (\sum (p - k)!)\bmod (p)$ para $1 ≤ k ≤ 5$.
-For example, if p=7, (7-1)! + (7-2)! + (7-3)! + (7-4)! + (7-5)! = 6! + 5! + 4! + 3! + 2! = 720+120+24+6+2 = 872. As 872 mod(7) = 4, S(7) = 4.
+Por exemplo, se $p = 7$,
-It can be verified that ∑S(p) = 480 for 5 ≤ p < 100.
+$$(7 - 1)! + (7 - 2)! + (7 - 3)! + (7 - 4)! + (7 - 5)! = 6! + 5! + 4! + 3! + 2! = 720 + 120 + 24 + 6 + 2 = 872$$
-Find ∑S(p) for 5 ≤ p < 108.
+Como $872\bmod (7) = 4$, $S(7) = 4$.
+
+Pode-se verificar que $\sum S(p) = 480$ para $5 ≤ p < 100$.
+
+Encontre a $\sum S(p)$ para $5 ≤ p < {10}^8$.
# --hints--
-`euler381()` should return 139602943319822.
+`primeKFactorial()` deve retornar `139602943319822`.
```js
-assert.strictEqual(euler381(), 139602943319822);
+assert.strictEqual(primeKFactorial(), 139602943319822);
```
# --seed--
@@ -29,12 +33,12 @@ assert.strictEqual(euler381(), 139602943319822);
## --seed-contents--
```js
-function euler381() {
+function primeKFactorial() {
return true;
}
-euler381();
+primeKFactorial();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
index ae95128f6b..78d4d75c7e 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-382-generating-polygons.md
@@ -1,6 +1,6 @@
---
id: 5900f4eb1000cf542c50fffd
-title: 'Problem 382: Generating polygons'
+title: 'Problema 382: Geração de polígonos'
challengeType: 5
forumTopicId: 302046
dashedName: problem-382-generating-polygons
@@ -8,24 +8,41 @@ dashedName: problem-382-generating-polygons
# --description--
-A polygon is a flat shape consisting of straight line segments that are joined to form a closed chain or circuit. A polygon consists of at least three sides and does not self-intersect.
+Um polígono é uma forma plana composta por segmentos de retas que são reunidos para formar uma cadeia ou circuito fechado. Um polígono consiste em, pelo menos, três lados e não se cruzam.
-A set S of positive numbers is said to generate a polygon P if: no two sides of P are the same length, the length of every side of P is in S, and S contains no other value.
+Dizem que um conjunto $S$ de números positivos gera um polígono $P$ se:
-For example: The set {3, 4, 5} generates a polygon with sides 3, 4, and 5 (a triangle). The set {6, 9, 11, 24} generates a polygon with sides 6, 9, 11, and 24 (a quadrilateral). The sets {1, 2, 3} and {2, 3, 4, 9} do not generate any polygon at all.
+- não há dois lados de $P$ que sejam do mesmo tamanho,
+- o comprimento de cada lado de $P$ está em $S$, e
+- $S$ não contém nenhum outro valor.
-Consider the sequence s, defined as follows:s1 = 1, s2 = 2, s3 = 3 sn = sn-1 + sn-3 for n > 3.
+Por exemplo:
-Let Un be the set {s1, s2, ..., sn}. For example, U10 = {1, 2, 3, 4, 6, 9, 13, 19, 28, 41}. Let f(n) be the number of subsets of Un which generate at least one polygon. For example, f(5) = 7, f(10) = 501 and f(25) = 18635853.
+O conjunto {3, 4, 5} gera um polígono com lados 3, 4 e 5 (um triângulo).
-Find the last 9 digits of f(1018).
+O conjunto {6, 9, 11, 24} gera um polígono com lados 6, 9, 11 e 24 (um quadrilátero).
+
+Os conjuntos {1, 2, 3} e {2, 3, 4, 9} não geram nenhum polígono.
+
+Considere a sequência $s$, definida da seguinte forma:
+
+- $s_1 = 1$, $s_2 = 2$, $s_3 = 3$
+- $s_n = s_{n - 1} + s_{n - 3}$ para $n > 3$.
+
+Considere $U_n$ como o conjunto $\\{s_1, s_2, \ldots, s_n\\}$. Por exemplo, $U_{10} = \\{1, 2, 3, 4, 6, 9, 13, 19, 28, 41\\}$.
+
+Considere $f(n)$ como o número de subconjuntos de $U_n$ que geram pelo menos um polígono.
+
+Por exemplo, $f(5) = 7$, $f(10) = 501$ e $f(25) = 18.635.853$.
+
+Encontre os 9 últimos algarismos de $f({10}^{18})$.
# --hints--
-`euler382()` should return 697003956.
+`generatingPolygons()` deve retornar `697003956`.
```js
-assert.strictEqual(euler382(), 697003956);
+assert.strictEqual(generatingPolygons(), 697003956);
```
# --seed--
@@ -33,12 +50,12 @@ assert.strictEqual(euler382(), 697003956);
## --seed-contents--
```js
-function euler382() {
+function generatingPolygons() {
return true;
}
-euler382();
+generatingPolygons();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
index f199cb4f94..832467b794 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-383-divisibility-comparison-between-factorials.md
@@ -1,6 +1,6 @@
---
id: 5900f4ed1000cf542c50ffff
-title: 'Problem 383: Divisibility comparison between factorials'
+title: 'Problema 383: Comparação de divisibilidade entre fatoriais'
challengeType: 5
forumTopicId: 302047
dashedName: problem-383-divisibility-comparison-between-factorials
@@ -8,20 +8,22 @@ dashedName: problem-383-divisibility-comparison-between-factorials
# --description--
-Let f5(n) be the largest integer x for which 5x divides n.
+Considere $f_5(n)$ como o maior número inteiro $x$ para o qual $5^x$ divide $n$.
-For example, f5(625000) = 7.
+Por exemplo, $f_5(625.000) = 7$.
-Let T5(n) be the number of integers i which satisfy f5((2·i-1)!) < 2·f5(i!) and 1 ≤ i ≤ n. It can be verified that T5(103) = 68 and T5(109) = 2408210.
+Considere $T_5(n)$ como a quantidade de números inteiros $i$ que satisfazem $f_5((2 \times i - 1)!) < 2 \times f_5(i!)$ e $1 ≤ i ≤ n$.
-Find T5(1018).
+Pode-se verificar que $T_5({10}^3) = 68$ e que $T_5({10}^9) = 2.408.210$.
+
+Encontre $T_5({10}^{18})$.
# --hints--
-`euler383()` should return 22173624649806.
+`factorialDivisibilityComparison()` deve retornar `22173624649806`.
```js
-assert.strictEqual(euler383(), 22173624649806);
+assert.strictEqual(factorialDivisibilityComparison(), 22173624649806);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler383(), 22173624649806);
## --seed-contents--
```js
-function euler383() {
+function factorialDivisibilityComparison() {
return true;
}
-euler383();
+factorialDivisibilityComparison();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
index c57f0ee2f9..eeb0866933 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-384-rudin-shapiro-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4ed1000cf542c50fffe
-title: 'Problem 384: Rudin-Shapiro sequence'
+title: 'Problema 384: Sequência de Rudin-Shapiro'
challengeType: 5
forumTopicId: 302048
dashedName: problem-384-rudin-shapiro-sequence
@@ -8,30 +8,38 @@ dashedName: problem-384-rudin-shapiro-sequence
# --description--
-Define the sequence a(n) as the number of adjacent pairs of ones in the binary expansion of n (possibly overlapping).
+Defina a sequência $a(n)$ como o número de pares adjacentes de uns na expansão binária de $n$ (possivelmente sobrepostos).
-E.g.: a(5) = a(1012) = 0, a(6) = a(1102) = 1, a(7) = a(1112) = 2
+Por exemplo: $a(5) = a({101}_2) = 0$, $a(6) = a({110}_2) = 1$, $a(7) = a({111}_2) = 2$
-Define the sequence b(n) = (-1)a(n). This sequence is called the Rudin-Shapiro sequence. Also consider the summatory sequence of b(n): .
+Defina a sequência $b(n) = {(-1)}^{a(n)}$. Essa sequência é chamada de sequência de Rudin-Shapiro.
-The first couple of values of these sequences are: n 0 1 2 3 4 5 6 7 a(n) 0 0 0 1 0 0 1 2 b(n) 1 1 1 -1 1 1 -1 1 s(n) 1 2 3 2 3 4 3 4
+Além disso, considere a sequência somatória de $b(n)$: $s(n) = \displaystyle\sum_{i = 0}^{n} b(i)$.
-The sequence s(n) has the remarkable property that all elements are positive and every positive integer k occurs exactly k times.
+Os primeiros valores destas sequências são:
-Define g(t,c), with 1 ≤ c ≤ t, as the index in s(n) for which t occurs for the c'th time in s(n). E.g.: g(3,3) = 6, g(4,2) = 7 and g(54321,12345) = 1220847710.
+$$\begin{array}{lr} n & 0 & 1 & 2 & 3 & 4 & 5 & 6 & 7 \\\\ a(n) & 0 & 0 & 0 & 1 & 0 & 0 & 1 & 2 \\\\ b(n) & 1 & 1 & 1 & -1 & 1 & 1 & -1 & 1 \\\\ s(n) & 1 & 2 & 3 & 2 & 3 & 4 & 3 & 4 \end{array}$$
-Let F(n) be the fibonacci sequence defined by: F(0)=F(1)=1 and F(n)=F(n-1)+F(n-2) for n>1.
+A sequência $s(n)$ tem a incrível propriedade de que todos os elementos são positivos e de que todo número inteiro positivo $k$ ocorre exatamente $k$ vezes.
-Define GF(t)=g(F(t),F(t-1)).
+Defina $g(t, c)$, com $1 ≤ c ≤ t$, como o índice em $s(n)$ para o qual $t$ ocorre pela $c$ª vez em $s(n)$.
-Find ΣGF(t) for 2≤t≤45.
+Ex.: $g(3, 3) = 6$, $g(4, 2) = 7$ e $g(54321, 12345) = 1.220.847.710$.
+
+Considere $F(n)$ como a sequência de Fibonacci definida por:
+
+$$\begin{align} & F(0) = F(1) = 1 \text{ e} \\\\ & F(n) = F(n - 1) + F(n - 2) \text{ para } n > 1. \end{align}$$
+
+Defina $GF(t) = g(F(t), F(t - 1))$.
+
+Encontre a $\sum GF(t)$ para $2 ≤ t ≤ 45$.
# --hints--
-`euler384()` should return 3354706415856333000.
+`rudinShapiroSequence()` deve retornar `3354706415856333000`.
```js
-assert.strictEqual(euler384(), 3354706415856333000);
+assert.strictEqual(rudinShapiroSequence(), 3354706415856333000);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler384(), 3354706415856333000);
## --seed-contents--
```js
-function euler384() {
+function rudinShapiroSequence() {
return true;
}
-euler384();
+rudinShapiroSequence();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
index 3cb1e30763..f86e3ddd7c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-385-ellipses-inside-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4ee1000cf542c510000
-title: 'Problem 385: Ellipses inside triangles'
+title: 'Problema 385: Elipses dentro de triângulos'
challengeType: 5
forumTopicId: 302049
dashedName: problem-385-ellipses-inside-triangles
@@ -8,29 +8,31 @@ dashedName: problem-385-ellipses-inside-triangles
# --description--
-For any triangle T in the plane, it can be shown that there is a unique ellipse with largest area that is completely inside T.
+Para qualquer triângulo $T$ no plano, pode-se mostrar que há uma elipse única com a maior área completamente dentro de $T$.
-For a given n, consider triangles T such that:
+
-- the vertices of T have integer coordinates with absolute value ≤ n, and
-- the foci1 of the largest-area ellipse inside T are (√13,0) and (-√13,0).
+Para um $n$ dado, considere os triângulos $T$, tal que:
-Let A(n) be the sum of the areas of all such triangles.
+- os vértices de $T$ têm coordenadas em números inteiros, com valor absoluto $≤ n$, e
+- os focos1 da elipse de maior área dentro de $T$ são $(\sqrt{13}, 0)$ e $(-\sqrt{13}, 0)$.
-For example, if n = 8, there are two such triangles. Their vertices are (-4,-3),(-4,3),(8,0) and (4,3),(4,-3),(-8,0), and the area of each triangle is 36. Thus A(8) = 36 + 36 = 72.
+Considere $A(n)$ como a soma das áreas de todos esses triângulos.
-It can be verified that A(10) = 252, A(100) = 34632 and A(1000) = 3529008.
+Por exemplo, se $n = 8$, existem dois triângulos desse tipo. Seus vértices são (-4,-3), (-4,3), (8,0) e (4,3), (4,-3), (-8,0). A área de cada triângulo é 36. Portanto, $A(8) = 36 + 36 = 72$.
-Find A(1 000 000 000).
+Pode-se verificar que $A(10) = 252$, $A(100) = 34.632$ e $A(1000) = 3.529.008$.
-1The foci (plural of focus) of an ellipse are two points A and B such that for every point P on the boundary of the ellipse, AP + PB is constant.
+Encontre $A(1.000.000.000)$.
+
+1Os focos de uma elipse são dois pontos $A$ e $B$, tal que, para qualquer ponto $P$ no limite da elipse, $AP + PB$ é constante.
# --hints--
-`euler385()` should return 3776957309612154000.
+`ellipsesInsideTriangles()` deve retornar `3776957309612154000`.
```js
-assert.strictEqual(euler385(), 3776957309612154000);
+assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
@@ -38,12 +40,12 @@ assert.strictEqual(euler385(), 3776957309612154000);
## --seed-contents--
```js
-function euler385() {
+function ellipsesInsideTriangles() {
return true;
}
-euler385();
+ellipsesInsideTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
index 36a6ce965c..054326d3ec 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-386-maximum-length-of-an-antichain.md
@@ -1,6 +1,6 @@
---
id: 5900f4ef1000cf542c510001
-title: 'Problem 386: Maximum length of an antichain'
+title: 'Problema 386: Comprimento máximo de uma anticadeia'
challengeType: 5
forumTopicId: 302050
dashedName: problem-386-maximum-length-of-an-antichain
@@ -8,22 +8,26 @@ dashedName: problem-386-maximum-length-of-an-antichain
# --description--
-Let n be an integer and S(n) be the set of factors of n.
+Considere $n$ como um número inteiro e $S(n)$ como o conjunto de fatores de $n$.
-A subset A of S(n) is called an antichain of S(n) if A contains only one element or if none of the elements of A divides any of the other elements of A.
+Um subconjunto $A$ de $S(n)$ é chamado de anticadeia de $S(n)$ se $A$ tiver apenas um elemento ou se nenhum dos elementos de $A$ divide qualquer um dos outros elementos de $A$.
-For example: S(30) = {1, 2, 3, 5, 6, 10, 15, 30} {2, 5, 6} is not an antichain of S(30). {2, 3, 5} is an antichain of S(30).
+Por exemplo: $S(30) = \\{1, 2, 3, 5, 6, 10, 15, 30\\}$
-Let N(n) be the maximum length of an antichain of S(n).
+$\\{2, 5, 6\\}$ não é uma anticadeia de $S(30)$.
-Find ΣN(n) for 1 ≤ n ≤ 108
+$\\{2, 3, 5\\}$ é uma anticadeia de $S(30)$.
+
+Considere $N(n)$ como o comprimento máximo de uma anticadeia de $S(n)$.
+
+Encontre a $\sum N(n)$ para $1 ≤ n ≤ {10}^8$
# --hints--
-`euler386()` should return 528755790.
+`maximumLengthOfAntichain()` deve retornar `528755790`.
```js
-assert.strictEqual(euler386(), 528755790);
+assert.strictEqual(maximumLengthOfAntichain(), 528755790);
```
# --seed--
@@ -31,12 +35,12 @@ assert.strictEqual(euler386(), 528755790);
## --seed-contents--
```js
-function euler386() {
+function maximumLengthOfAntichain() {
return true;
}
-euler386();
+maximumLengthOfAntichain();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
index aa3caddfe3..aea39abb84 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-387-harshad-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4f11000cf542c510003
-title: 'Problem 387: Harshad Numbers'
+title: 'Problema 387: Números de Harshad'
challengeType: 5
forumTopicId: 302051
dashedName: problem-387-harshad-numbers
@@ -8,30 +8,34 @@ dashedName: problem-387-harshad-numbers
# --description--
-A Harshad or Niven number is a number that is divisible by the sum of its digits.
+Um número de Harshad ou número de Niven é um número divisível pela soma de seus algarismos.
-201 is a Harshad number because it is divisible by 3 (the sum of its digits.)
+201 é um número de Harshad, pois é divisível por 3 (a soma de seus algarismos).
-When we truncate the last digit from 201, we get 20, which is a Harshad number.
+Quando truncamos o último algarismo de 201, obtemos 20, que é um número de Harshad.
-When we truncate the last digit from 20, we get 2, which is also a Harshad number.
+Quando truncamos o último algarismo de 20, obtemos 2, que também é um número de Harshad.
-Let's call a Harshad number that, while recursively truncating the last digit, always results in a Harshad number a right truncatable Harshad number.
+Vamos chamar um número de Harshad que, embora truncando recursivamente o último algarismo, sempre resulte em um número de Harshad, de um número de Harshad corretamente truncável.
-Also: 201/3=67 which is prime. Let's call a Harshad number that, when divided by the sum of its digits, results in a prime a strong Harshad number.
+Além disso:
-Now take the number 2011 which is prime. When we truncate the last digit from it we get 201, a strong Harshad number that is also right truncatable. Let's call such primes strong, right truncatable Harshad primes.
+$\frac{201}{3} = 67$, que é um número primo.
-You are given that the sum of the strong, right truncatable Harshad primes less than 10000 is 90619.
+Vamos chamar um número de Harshad que, quando dividido pela soma de seus algarismos, resulte em um número primo, de número de Harshad forte.
-Find the sum of the strong, right truncatable Harshad primes less than 1014.
+Vejamos agora o número 2011, que é um número primo. Quando truncamos o último algarismo dele chegamos em 201, um número forte de Harshad, que também é corretamente truncável. Vamos chamar esses números primos e fortes de números primos de Harshad corretamente truncáveis.
+
+Você é informado de que a soma dos números primos de Harshad corretamente truncáveis e fortes inferiores a 10000 é de 90619.
+
+Encontre a soma dos números primos de Harshad corretamente truncáveis e fortes inferiores a ${10}^{14}$.
# --hints--
-`euler387()` should return 696067597313468.
+`harshadNumbers()` deve retornar `696067597313468`.
```js
-assert.strictEqual(euler387(), 696067597313468);
+assert.strictEqual(harshadNumbers(), 696067597313468);
```
# --seed--
@@ -39,12 +43,12 @@ assert.strictEqual(euler387(), 696067597313468);
## --seed-contents--
```js
-function euler387() {
+function harshadNumbers() {
return true;
}
-euler387();
+harshadNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
index ba13e9be3c..b42389b1d5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-388-distinct-lines.md
@@ -1,6 +1,6 @@
---
id: 5900f4f11000cf542c510002
-title: 'Problem 388: Distinct Lines'
+title: 'Problema 388: Linhas distintas'
challengeType: 5
forumTopicId: 302052
dashedName: problem-388-distinct-lines
@@ -8,20 +8,20 @@ dashedName: problem-388-distinct-lines
# --description--
-Consider all lattice points (a,b,c) with 0 ≤ a,b,c ≤ N.
+Considere todos os pontos da rede ($a$, $b$, $c$) com $0 ≤ a, b, c ≤ N$.
-From the origin O(0,0,0) all lines are drawn to the other lattice points. Let D(N) be the number of distinct such lines.
+A partir da origem $O(0, 0, 0)$ todas as linhas são desenhadas até outros pontos da rede. Considere $D(N)$ como o número de linhas distintas feitas dessa forma.
-You are given that D(1 000 000) = 831909254469114121.
+Você é informado de que $D(1.000.000) = 831.909.254.469.114.121$.
-Find D(1010). Give as your answer the first nine digits followed by the last nine digits.
+Encontre $D({10}^{10})$. Dê como resposta os primeiros nove algarismos seguidos pelos últimos nove algarismos.
# --hints--
-`euler388()` should return 831907372805130000.
+`distinctLines()` deve retornar `831907372805130000`.
```js
-assert.strictEqual(euler388(), 831907372805130000);
+assert.strictEqual(distinctLines(), 831907372805130000);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler388(), 831907372805130000);
## --seed-contents--
```js
-function euler388() {
+function distinctLines() {
return true;
}
-euler388();
+distinctLines();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
index 0fb6bb2688..014059d6fe 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-389-platonic-dice.md
@@ -1,6 +1,6 @@
---
id: 5900f4f21000cf542c510004
-title: 'Problem 389: Platonic Dice'
+title: 'Problema 389: Dados platônicos'
challengeType: 5
forumTopicId: 302053
dashedName: problem-389-platonic-dice
@@ -8,16 +8,24 @@ dashedName: problem-389-platonic-dice
# --description--
-An unbiased single 4-sided die is thrown and its value, T, is noted.T unbiased 6-sided dice are thrown and their scores are added together. The sum, C, is noted.C unbiased 8-sided dice are thrown and their scores are added together. The sum, O, is noted.O unbiased 12-sided dice are thrown and their scores are added together. The sum, D, is noted.D unbiased 20-sided dice are thrown and their scores are added together. The sum, I, is noted.
+Um único dado de 4 lados sem viés é lançado e seu valor, $T$, é registrado.
-Find the variance of I, and give your answer rounded to 4 decimal places.
+$T$ dados de 6 lados sem viés são lançados e sua pontuação é somada. A soma, $C$, é registrada.
+
+$C$ dados de 8 lados sem viés são lançados e sua pontuação é somada. A soma, $O$, é registrada.
+
+$O$ dados de 12 lados sem viés são lançados e sua pontuação é somada. A soma, $D$, é registrada.
+
+$D$ dados de 20 lados sem viés são lançados e sua pontuação é somada. A soma, $I$, é registrada.
+
+Encontre a variância de $I$ e dê sua resposta arredondada para 4 casas decimais.
# --hints--
-`euler389()` should return 2406376.3623.
+`platonicDice()` deve retornar `2406376.3623`.
```js
-assert.strictEqual(euler389(), 2406376.3623);
+assert.strictEqual(platonicDice(), 2406376.3623);
```
# --seed--
@@ -25,12 +33,12 @@ assert.strictEqual(euler389(), 2406376.3623);
## --seed-contents--
```js
-function euler389() {
+function platonicDice() {
return true;
}
-euler389();
+platonicDice();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
index e582b23f2d..aa39d56f85 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-390-triangles-with-non-rational-sides-and-integral-area.md
@@ -1,6 +1,6 @@
---
id: 5900f4f21000cf542c510005
-title: 'Problem 390: Triangles with non rational sides and integral area'
+title: 'Problema 390: Triângulos com lados não racionais e ângulo em números inteiros'
challengeType: 5
forumTopicId: 302055
dashedName: problem-390-triangles-with-non-rational-sides-and-integral-area
@@ -8,24 +8,22 @@ dashedName: problem-390-triangles-with-non-rational-sides-and-integral-area
# --description--
-Consider the triangle with sides √5, √65 and √68.
+Considere o triângulo com lados $\sqrt{5}$, $\sqrt{65}$ e $\sqrt{68}$. Pode-se demonstrar que a área desse triângulo é 9.
-It can be shown that this triangle has area 9.
+$S(n)$ é a soma das áreas de todos os triângulos com lados $\sqrt{1 + b^2}$, $\sqrt{1 + c^2}$ e $\sqrt{b^2 + c^2}$ (para números inteiros positivos $b$ e $c$) que tenham uma área em número inteiros não excedendo $n$.
-S(n) is the sum of the areas of all triangles with sides √(1+b2), √(1+c2) and √(b2+c2) (for positive integers b and c ) that have an integral area not exceeding n.
+O triângulo de exemplo tem $b = 2$ e $c = 8$.
-The example triangle has b=2 and c=8.
+$S({10}^6) = 18.018.206$.
-S(106)=18018206.
-
-Find S(1010).
+Encontre $S({10}^{10})$.
# --hints--
-`euler390()` should return 2919133642971.
+`nonRationalSidesAndIntegralArea()` deve retornar `2919133642971`.
```js
-assert.strictEqual(euler390(), 2919133642971);
+assert.strictEqual(nonRationalSidesAndIntegralArea(), 2919133642971);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler390(), 2919133642971);
## --seed-contents--
```js
-function euler390() {
+function nonRationalSidesAndIntegralArea() {
return true;
}
-euler390();
+nonRationalSidesAndIntegralArea();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
index 4eda36c0a4..2cfa393023 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-391-hopping-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4f31000cf542c510006
-title: 'Problem 391: Hopping Game'
+title: 'Problema 391: Jogo de saltos'
challengeType: 5
forumTopicId: 302056
dashedName: problem-391-hopping-game
@@ -8,28 +8,35 @@ dashedName: problem-391-hopping-game
# --description--
-Let sk be the number of 1’s when writing the numbers from 0 to k in binary.
+Considere $s_k$ como o número de 1s ao escrever os números de 0 a $k$ em binário.
-For example, writing 0 to 5 in binary, we have 0, 1, 10, 11, 100, 101. There are seven 1’s, so s5 = 7.
+Por exemplo, escrevendo de 0 a 5 em binário, temos 0, 1, 10, 11, 100 e 101. São sete números 1, portanto $s_5 = 7$.
-The sequence S = {sk : k ≥ 0} starts {0, 1, 2, 4, 5, 7, 9, 12, ...}.
+A sequência $S = \\{s_k : k ≥ 0\\}$ começa com $\\{0, 1, 2, 4, 5, 7, 9, 12, \ldots\\}$.
-A game is played by two players. Before the game starts, a number n is chosen. A counter c starts at 0. At each turn, the player chooses a number from 1 to n (inclusive) and increases c by that number. The resulting value of c must be a member of S. If there are no more valid moves, the player loses.
+Dois jogadores jogam. Antes de o jogo começar, um número $n$ é selecionado. Um contador $c$ começa em 0. A cada turno, o jogador escolhe um número de 1 a $n$ (inclusive) e aumenta $c$ por aquele número. O valor resultante de $c$ deve pertencer a $S$. Se não houver mais movimentos válidos, o jogador perde.
-For example: Let n = 5. c starts at 0. Player 1 chooses 4, so c becomes 0 + 4 = 4. Player 2 chooses 5, so c becomes 4 + 5 = 9. Player 1 chooses 3, so c becomes 9 + 3 = 12. etc. Note that c must always belong to S, and each player can increase c by at most n.
+Por exemplo, com $n = 5$ e começando com $c = 0$:
-Let M(n) be the highest number the first player can choose at her first turn to force a win, and M(n) = 0 if there is no such move. For example, M(2) = 2, M(7) = 1 and M(20) = 4.
+- O jogador 1 escolhe 4, então $c$ passa a ser $0 + 4 = 4$.
+- O jogador 2 escolhe 5, então $c$ passa a ser $4 + 5 = 9$.
+- O jogador 1 escolhe 3, então $c$ passa a ser $9 + 3 = 12$.
+- etc.
-Given Σ(M(n))3 = 8150 for 1 ≤ n ≤ 20.
+Observe que $c$ deve sempre pertencer a $S$ e que cada jogador pode aumentar $c$ em, no máximo, $n$.
-Find Σ(M(n))3 for 1 ≤ n ≤ 1000.
+Considere $M(n)$ como o maior número que o primeiro jogador pode escolher em sua primeira jogada para forçar uma vitórias, e que $M(n) = 0$ se esse movimento não existir. Por exemplo, $M(2) = 2$, $M(7) = 1$ e $M(20) = 4$.
+
+Pode-se verificar que $\sum M{(n)}^3 = 8150$ para $1 ≤ n ≤ 20$.
+
+Encontre a $\sum M{(n)}^3$ para $1 ≤ n ≤ 1000$.
# --hints--
-`euler391()` should return 61029882288.
+`hoppingGame()` deve retornar `61029882288`.
```js
-assert.strictEqual(euler391(), 61029882288);
+assert.strictEqual(hoppingGame(), 61029882288);
```
# --seed--
@@ -37,12 +44,12 @@ assert.strictEqual(euler391(), 61029882288);
## --seed-contents--
```js
-function euler391() {
+function hoppingGame() {
return true;
}
-euler391();
+hoppingGame();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
index cd4d53f17d..a174d2034c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-392-enmeshed-unit-circle.md
@@ -1,6 +1,6 @@
---
id: 5900f4f41000cf542c510007
-title: 'Problem 392: Enmeshed unit circle'
+title: 'Problema 392: Círculo unitário em malha'
challengeType: 5
forumTopicId: 302057
dashedName: problem-392-enmeshed-unit-circle
@@ -8,24 +8,34 @@ dashedName: problem-392-enmeshed-unit-circle
# --description--
-A rectilinear grid is an orthogonal grid where the spacing between the gridlines does not have to be equidistant.
+Uma grade retilinear é uma grade ortogonal onde o espaçamento entre as linhas da grade não precisa ser equidistante.
-An example of such grid is logarithmic graph paper.
+Um exemplo desse tipo de grade é o papel gráfico logarítmico.
-Consider rectilinear grids in the Cartesian coordinate system with the following properties:The gridlines are parallel to the axes of the Cartesian coordinate system.There are N+2 vertical and N+2 horizontal gridlines. Hence there are (N+1) x (N+1) rectangular cells.The equations of the two outer vertical gridlines are x = -1 and x = 1.The equations of the two outer horizontal gridlines are y = -1 and y = 1.The grid cells are colored red if they overlap with the unit circle, black otherwise.For this problem we would like you to find the positions of the remaining N inner horizontal and N inner vertical gridlines so that the area occupied by the red cells is minimized.
+Considere as grades retilineares no sistema de coordenadas cartesiano com as seguintes propriedades:
-E.g. here is a picture of the solution for N = 10:
+- As linhas da grade são paralelas aos eixos do sistema de coordenadas cartesiano.
+- Existem $N + 2$ linhas de grade verticais e $N + 2$ linhas de grade horizontais. Portanto, existem $(N + 1) \times (N + 1)$ células retangulares.
+- As equações das duas linhas da grade verticais externas são $x = -1$ e $x = 1$.
+- As equações das duas linhas da grade horizontais externas são $y = -1$ e $y = 1$.
+- As células da grade são coloridas de vermelho se elas estiveres sobre o círculo unitário. Do contrário, elas serão pretas.
-The area occupied by the red cells for N = 10 rounded to 10 digits behind the decimal point is 3.3469640797.
+Para esse problema, gostaríamos que você encontrasse as posições das $N$ linhas de grade internas horizontais e das $N$ linhas de grade internas verticais restantes, de modo que a área ocupada pelas células vermelhas seja minimizada.
-Find the positions for N = 400. Give as your answer the area occupied by the red cells rounded to 10 digits behind the decimal point.
+Ex: aqui vemos uma imagem da solução para $N = 10$:
+
+
+
+A área ocupada pelas células vermelhas para $N = 10$, arredondada para 10 casas depois da vírgula, é de 3,3469640797.
+
+Encontre as posições para $N = 400$. Dê sua resposta como a área ocupada pelas células vermelhas arredondada para 10 casas depois da vírgula.
# --hints--
-`euler392()` should return 3.1486734435.
+`enmeshedUnitCircle()` deve retornar `3.1486734435`.
```js
-assert.strictEqual(euler392(), 3.1486734435);
+assert.strictEqual(enmeshedUnitCircle(), 3.1486734435);
```
# --seed--
@@ -33,12 +43,12 @@ assert.strictEqual(euler392(), 3.1486734435);
## --seed-contents--
```js
-function euler392() {
+function enmeshedUnitCircle() {
return true;
}
-euler392();
+enmeshedUnitCircle();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
index 21f98ec10c..b9d2e775c8 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-393-migrating-ants.md
@@ -1,6 +1,6 @@
---
id: 5900f4f61000cf542c510008
-title: 'Problem 393: Migrating ants'
+title: 'Problema 393: Formigas migratórias'
challengeType: 5
forumTopicId: 302058
dashedName: problem-393-migrating-ants
@@ -8,20 +8,22 @@ dashedName: problem-393-migrating-ants
# --description--
-An n×n grid of squares contains n2 ants, one ant per square.
+Uma grade de $n × n$ quadrados contém $n^2$ formigas, uma por quadrado.
-All ants decide to move simultaneously to an adjacent square (usually 4 possibilities, except for ants on the edge of the grid or at the corners).
+Todas as formigas decidem se mover simultaneamente para um quadrado adjacente (em geral, 4 possibilidades, exceto para as formigas nas arestas ou nos vértices da grade).
-We define f(n) to be the number of ways this can happen without any ants ending on the same square and without any two ants crossing the same edge between two squares.
+Definimos $f(n)$ como o número de formas pelas quais isso pode acontecer sem que qualquer formiga acabe no mesmo quadrado em que estava e sem que duas formigas cruzem a mesma aresta entre dois quadrados.
-You are given that f(4) = 88. Find f(10).
+Você é informado de que $f(4) = 88$.
+
+Encontre $f(10)$.
# --hints--
-`euler393()` should return 112398351350823100.
+`migratingAnts()` deve retornar `112398351350823100`.
```js
-assert.strictEqual(euler393(), 112398351350823100);
+assert.strictEqual(migratingAnts(), 112398351350823100);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler393(), 112398351350823100);
## --seed-contents--
```js
-function euler393() {
+function migratingAnts() {
return true;
}
-euler393();
+migratingAnts();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
index 26c7bce3a9..3aaf2070e2 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-394-eating-pie.md
@@ -1,6 +1,6 @@
---
id: 5900f4f71000cf542c510009
-title: 'Problem 394: Eating pie'
+title: 'Problema 394: Comendo tortas'
challengeType: 5
forumTopicId: 302059
dashedName: problem-394-eating-pie
@@ -8,28 +8,29 @@ dashedName: problem-394-eating-pie
# --description--
-Jeff eats a pie in an unusual way.
+Jeff come uma torta de maneira incomum.
-The pie is circular. He starts with slicing an initial cut in the pie along a radius.
+A torta é circular. Ele começa cortando uma fatia inicial da torta ao longo de seu raio.
-While there is at least a given fraction F of pie left, he performs the following procedure:
+Enquanto houver ao menos uma fração $F$ determinada da torta restando, ele realiza o seguinte procedimento:
-\- He makes two slices from the pie centre to any point of what is remaining of the pie border, any point on the remaining pie border equally likely. This will divide the remaining pie into three pieces.
+- Ele faz duas fatias a partir do centro da torta até qualquer ponto do que resta da borda, qualquer ponto na borda restante da torta sendo igualmente provável. Isso dividirá o restante da torta em três pedaços.
+- Indo no sentido anti-horário a partir do corte inicial, ele pega os dois primeiros pedaços da torta e os come.
-\- Going counterclockwise from the initial cut, he takes the first two pie pieces and eats them.
+Quando menos que uma fração $F$ da torta restar, ele para de repetir esse procedimento. Em vez disso, ele come toda a torta que resta.
-When less than a fraction F of pie remains, he does not repeat this procedure. Instead, he eats all of the remaining pie.
+
-For x ≥ 1, let E(x) be the expected number of times Jeff repeats the procedure above with F = 1/x. It can be verified that E(1) = 1, E(2) ≈ 1.2676536759, and E(7.5) ≈ 2.1215732071.
+Para $x ≥ 1$, considere $E(x)$ como o número esperado de vezes que Jeff repetirá o procedimento acima com $F = \frac{1}{x}$. Pode-se verificar que $E(1) = 1$, $E(2) ≈ 1,2676536759$, e $E(7,5) ≈ 2,1215732071$.
-Find E(40) rounded to 10 decimal places behind the decimal point.
+Encontre $E(40)$ arredondado para 10 casas decimais depois da vírgula.
# --hints--
-`euler394()` should return 3.2370342194.
+`eatingPie()` deve retornar `3.2370342194`.
```js
-assert.strictEqual(euler394(), 3.2370342194);
+assert.strictEqual(eatingPie(), 3.2370342194);
```
# --seed--
@@ -37,12 +38,12 @@ assert.strictEqual(euler394(), 3.2370342194);
## --seed-contents--
```js
-function euler394() {
+function eatingPie() {
return true;
}
-euler394();
+eatingPie();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
index 80903ac0ef..b96e3f6933 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-395-pythagorean-tree.md
@@ -1,6 +1,6 @@
---
id: 5900f4f71000cf542c51000a
-title: 'Problem 395: Pythagorean tree'
+title: 'Problema 395: Árvore de Pitágoras'
challengeType: 5
forumTopicId: 302060
dashedName: problem-395-pythagorean-tree
@@ -8,22 +8,28 @@ dashedName: problem-395-pythagorean-tree
# --description--
-The Pythagorean tree is a fractal generated by the following procedure:
+A árvore de Pitágoras é um fractal gerado pelo seguinte procedimento:
-Start with a unit square. Then, calling one of the sides its base (in the animation, the bottom side is the base): Attach a right triangle to the side opposite the base, with the hypotenuse coinciding with that side and with the sides in a 3-4-5 ratio. Note that the smaller side of the triangle must be on the 'right' side with respect to the base (see animation). Attach a square to each leg of the right triangle, with one of its sides coinciding with that leg. Repeat this procedure for both squares, considering as their bases the sides touching the triangle.
+Comece com um quadrado unitário. Em seguida, chamando um dos lados de sua base (na animação, o lado inferior é a base):
-The resulting figure, after an infinite number of iterations, is the Pythagorean tree.
+1. Conecte um triângulo retângulo ao lado oposto da base, com a hipotenusa coincidindo com aquele lado e com os lados em uma relação de 3-4-5. Observe que o lado menor do triângulo deve estar no lado direito em relação à base (ver animação).
+2. Anexe um quadrado a cada cateto do triângulo reto, com um de seus lados coincidindo com aquele cateto.
+3. Repita este procedimento para ambos os quadrados, considerando que as suas bases tocam o triângulo.
-It can be shown that there exists at least one rectangle, whose sides are parallel to the largest square of the Pythagorean tree, which encloses the Pythagorean tree completely.
+A figura resultante, após um número infinito de iterações, é a árvore de Pitágoras.
-Find the smallest area possible for such a bounding rectangle, and give your answer rounded to 10 decimal places.
+
+
+É possível mostrar que existe pelo menos um retângulo, cujos lados são paralelos ao quadrado maior da árvore de Pitágoras, e que envolve a árvore completamente.
+
+Encontre a menor área possível para esse triângulo limitador, dando sua resposta arredondada para 10 casas decimais.
# --hints--
-`euler395()` should return 28.2453753155.
+`pythagoreanTree()` deve retornar `28.2453753155`.
```js
-assert.strictEqual(euler395(), 28.2453753155);
+assert.strictEqual(pythagoreanTree(), 28.2453753155);
```
# --seed--
@@ -31,12 +37,12 @@ assert.strictEqual(euler395(), 28.2453753155);
## --seed-contents--
```js
-function euler395() {
+function pythagoreanTree() {
return true;
}
-euler395();
+pythagoreanTree();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
index bb98b389ba..78502f30f2 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-396-weak-goodstein-sequence.md
@@ -1,6 +1,6 @@
---
id: 5900f4f81000cf542c51000b
-title: 'Problem 396: Weak Goodstein sequence'
+title: 'Problema 396: Sequência fraca de Goodstein'
challengeType: 5
forumTopicId: 302061
dashedName: problem-396-weak-goodstein-sequence
@@ -8,30 +8,38 @@ dashedName: problem-396-weak-goodstein-sequence
# --description--
-For any positive integer n, the nth weak Goodstein sequence {g1, g2, g3, ...} is defined as:
+Para qualquer número inteiro positivo $n$, a $n$ª sequência fraca de Goodstein $\\{g1, g2, g3, \ldots\\}$ é definida como:
-g1 = n
+- $g_1 = n$
+- para $k > 1$, $g_k$ é obtido escrevendo $g_{k - 1}$ na base $k$, interpretando-a como uma base de número $k + 1$, e subtraindo 1.
-for k > 1, gk is obtained by writing gk-1 in base k, interpreting it as a base k + 1 number, and subtracting 1.
+A sequência termina quando $g_k$ passa a ser 0.
-The sequence terminates when gk becomes 0.
+Por exemplo, a $6$ª sequência fraca de Goodstein é $\\{6, 11, 17, 25, \ldots\\}$:
-For example, the 6th weak Goodstein sequence is {6, 11, 17, 25, ...}: g1 = 6. g2 = 11 since 6 = 1102, 1103 = 12, and 12 - 1 = 11. g3 = 17 since 11 = 1023, 1024 = 18, and 18 - 1 = 17. g4 = 25 since 17 = 1014, 1015 = 26, and 26 - 1 = 25.
+- $g_1 = 6$.
+- $g_2 = 11$, já que $6 = 110_2$, $110_3 = 12$ e $12 - 1 = 11$.
+- $g_3 = 17$, já que $11 = 102_3$, $102_4 = 18$ e $18 - 1 = 17$.
+- $g_4 = 25$, já que $17 = 101_4$, $101_5 = 26$ e $26 - 1 = 25$.
-and so on.
+e assim por diante.
-It can be shown that every weak Goodstein sequence terminates.
+Pode-se mostrar que toda a sequência fraca de Goodstein termina.
-Let G(n) be the number of nonzero elements in the nth weak Goodstein sequence. It can be verified that G(2) = 3, G(4) = 21 and G(6) = 381. It can also be verified that ΣG(n) = 2517 for 1 ≤ n < 8.
+Considere $G(n)$ como o número de elementos diferentes de zero na $n$ª sequência fraca de Goodstein.
-Find the last 9 digits of ΣG(n) for 1 ≤ n < 16.
+Pode-se verificar que $G(2) = 3$, $G(4) = 21$ e $G(6) = 381$.
+
+Também é possível verificar que $\sum G(n) = 2517$ para $1 ≤ n < 8$.
+
+Encontre os últimos 9 algarismos de $\sum G(n)$ para $1 ≤ n < 16$.
# --hints--
-`euler396()` should return 173214653.
+`weakGoodsteinSequence()` deve retornar `173214653`.
```js
-assert.strictEqual(euler396(), 173214653);
+assert.strictEqual(weakGoodsteinSequence(), 173214653);
```
# --seed--
@@ -39,12 +47,12 @@ assert.strictEqual(euler396(), 173214653);
## --seed-contents--
```js
-function euler396() {
+function weakGoodsteinSequence() {
return true;
}
-euler396();
+weakGoodsteinSequence();
```
# --solutions--