diff --git a/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/announce-new-users.md b/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/announce-new-users.md
index fca0105f3d..f4a2a2b988 100644
--- a/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/announce-new-users.md
+++ b/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/announce-new-users.md
@@ -1,6 +1,6 @@
---
id: 589fc832f9fc0f352b528e78
-title: Announce New Users
+title: Anuncia nuevos usuarios
challengeType: 2
forumTopicId: 301546
dashedName: announce-new-users
@@ -8,9 +8,9 @@ dashedName: announce-new-users
# --description--
-Many chat rooms are able to announce when a user connects or disconnects and then display that to all of the connected users in the chat. Seeing as though you already are emitting an event on connect and disconnect, you will just have to modify this event to support such a feature. The most logical way of doing so is sending 3 pieces of data with the event: the name of the user who connected/disconnected, the current user count, and if that name connected or disconnected.
+Muchas salas de chat son capaces de anunciar cuando un usuario se conecta o se desconecta y luego lo muestra a todos los usuarios conectados en el chat. Viendo como si ya estuvieras emitiendo un evento al conectar y desconectar, sólo tendrás que modificar este evento para soportar una característica de este tipo. La forma más lógica de hacerlo es enviando 3 datos con el evento: el nombre del usuario que se conectó/desconectó, el recuento actual de usuarios y si ese nombre se conectó o desconectó.
-Change the event name to `'user'`, and pass an object along containing the fields 'name', 'currentUsers', and 'connected' (to be `true` in case of connection, or `false` for disconnection of the user sent). Be sure to change both 'user count' events and set the disconnect one to send `false` for the field 'connected' instead of `true` like the event emitted on connect.
+Cambia el nombre del evento a `'user'`, y pasa un objeto a lo largo de los campos que contengan 'name', 'currentUsers', and 'connected' (esto será `true` en caso de conexión, o `false` para desconexión del usuario enviado). Asegúrate de cambiar los dos eventos 'user count' y configura el de desconexión para que envíe `false` para el campo 'connected' en lugar de `true` como el evento emitido al conectar.
```js
io.emit('user', {
@@ -20,9 +20,9 @@ io.emit('user', {
});
```
-Now your client will have all the necessary information to correctly display the current user count and announce when a user connects or disconnects! To handle this event on the client side we should listen for `'user'`, then update the current user count by using jQuery to change the text of `#num-users` to `'{NUMBER} users online'`, as well as append a `` to the unordered list with id `messages` with `'{NAME} has {joined/left} the chat.'`.
+¡Ahora tu cliente tendrá toda la información necesaria para mostrar correctamente el recuento de usuarios actual y anunciar cuando un usuario se conecta o se desconecta! Para manejar este evento en el lado del cliente debemos escuchar `'user'`, luego actualiza el recuento de usuarios usando jQuery para cambiar el texto de `#num-users` a `'{NUMBER} users online'`, así como añadir un `` a la lista desordenada con id `messages` con `'{NAME} has {joined/left} the chat.'`.
-An implementation of this could look like the following:
+Una implementación de esto podría parecerse a lo siguiente:
```js
socket.on('user', data => {
@@ -34,11 +34,11 @@ socket.on('user', data => {
});
```
-Submit your page when you think you've got it right. If you're running into errors, you can check out the project completed up to this point [here](https://gist.github.com/camperbot/bf95a0f74b756cf0771cd62c087b8286).
+Envía tu página cuando creas que lo has hecho bien. Si te encuentras con errores, puedes revisar el proyecto completado hasta este punto [aquí](https://gist.github.com/camperbot/bf95a0f74b756cf0771cd62c087b8286).
# --hints--
-Event `'user'` should be emitted with name, currentUsers, and connected.
+El evento `'user'` debe emitirse con name, currentUsers, y connected.
```js
(getUserInput) =>
@@ -56,7 +56,7 @@ Event `'user'` should be emitted with name, currentUsers, and connected.
);
```
-Client should properly handle and display the new data from event `'user'`.
+El cliente debe manejar y mostrar correctamente los nuevos datos del evento `'user'`.
```js
(getUserInput) =>
diff --git a/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md b/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
index bdafd11935..c1cb929b27 100644
--- a/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
+++ b/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/polygon-area-calculator.md
@@ -8,22 +8,96 @@ dashedName: polygon-area-calculator
# --description--
+Você [trabalhará neste projeto com nosso código inicial do Replit](https://replit.com/github/freeCodeCamp/boilerplate-polygon-area-calculator).
+
+Ainda estamos desenvolvendo a parte instrucional interativa do currículo Python. Por enquanto, aqui estão alguns vídeos no canal do freeCodeCamp.org do YouTube que ensinarão tudo o que você precisa saber para completar este projeto:
+
+- [Curso de Python em vídeo para todos](https://www.freecodecamp.org/news/python-for-everybody/) (14 horas)
+
+- [Curso Aprenda Python em vídeo](https://www.freecodecamp.org/news/learn-python-video-course/) (10 horas)
+
+# --instructions--
+
Neste projeto, você usará programação orientada a objetos para criar a classe Rectangle, para um retângulo, e a classe Square, para um quadrado. A classe Square deve ser uma subclasse da classe Rectangle e herdar métodos e atributos.
-Você pode acessar [a descrição completa do projeto e o código inicial no Replit](https://replit.com/github/freeCodeCamp/boilerplate-polygon-area-calculator).
+## Classe do retângulo
-Depois de ir para esse link, faça fork no projeto. Depois que você completar o projeto com baseado nas instruções do 'README.md', envie o link do seu projeto abaixo.
+Quando um objeto de retângulo é criado, ele deve ser inicializado com atributos `width` (largura) e `height` (altura). A classe também deve conter os seguintes métodos:
-Ainda estamos desenvolvendo a parte instrucional interativa do currículo Python. Por enquanto, aqui estão alguns vídeos no canal freeCodeCamp.org do YouTube que ensinarão tudo o que você precisa saber para completar este projeto:
+- `set_width`
+- `set_height`
+- `get_area`: retorna a área (`width * height`)
+- `get_perimeter`: retorna o perímetro (`2 * width + 2 * height`)
+- `get_diagonal`: retorna a diagonal (`(width ** 2 + height ** 2) ** .5`)
+- `get_picture`: retorna uma string que representa a forma usando as linhas de "\*". O número de linhas deve ser igual à altura e o número de "\*" em cada linha deve ser igual à largura. Deve haver uma nova linha (`\n`) no final de cada linha. Se a largura ou altura for maior do que 50, é preciso retornar a string: "Too big for picture." (Muito grande para a imagem).
+- `get_amount_inside`: Pega outra forma (quadrado ou retângulo) como um argumento. Retorna o número de vezes que a forma passada como argumento poderia caber dentro da forma (sem rotações). Por exemplo, um retângulo com uma largura de 4 e uma altura de 8 poderia caber em dois quadrados com lados de 4.
-
+Além disso, se uma instância de um retângulo for representada como uma string, ela deve ter a seguinte aparência: `Rectangle(width=5, height=10)`
+
+## Classe do quadrado
+
+A classe Square (Quadrado) deve ser uma subclasse de Rectangle (Retângulo). Quando um objeto Square é criado, um único comprimento lateral é passado. O método `__init__` deve armazenar o comprimento do lado nos atributos `width` e `height` da classe Rectangle.
+
+A classe Square deve ser capaz de acessar os métodos da classe Rectangle, mas também deve conter um método `set_side`. Se uma instância de Square for representada como uma string, ela deve ter a seguinte aparência: `Square(side=9)`
+
+Além disso, os métodos `set_width` e `set_height` na classe Square devem definir a largura e a altura.
+
+## Exemplo de uso
+
+```py
+rect = shape_calculator.Rectangle(10, 5)
+print(rect.get_area())
+rect.set_height(3)
+print(rect.get_perimeter())
+print(rect)
+print(rect.get_picture())
+
+sq = shape_calculator.Square(9)
+print(sq.get_area())
+sq.set_side(4)
+print(sq.get_diagonal())
+print(sq)
+print(sq.get_picture())
+
+rect.set_height(8)
+rect.set_width(16)
+print(rect.get_amount_inside(sq))
+```
+
+Esse código deve retornar:
+
+```bash
+50
+26
+Rectangle(width=10, height=3)
+**********
+**********
+**********
+
+81
+5.656854249492381
+Square(side=4)
+****
+****
+****
+****
+
+8
+```
+
+Os testes unitários para este projeto estão em `test_module.py`.
+
+## Desenvolvimento
+
+Escreva seu código em `shape_calculator.py`. Para o desenvolvimento, você pode usar `main.py` para testar sua função `shape_calculator()`. Clique no botão "Run" e `main.py` será executado.
+
+## Testes
+
+Importamos os testes de `test_module.py` em `main.py` para a sua conveniência. Os testes serão executados automaticamente sempre que você clicar no botão "Run".
+
+## Envio
+
+Copie o URL do seu projeto e envie-o para o freeCodeCamp.
# --hints--
diff --git a/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md b/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
index cefb7b43eb..cbe5ce952e 100644
--- a/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
+++ b/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/probability-calculator.md
@@ -8,20 +8,70 @@ dashedName: probability-calculator
# --description--
-Escreva um programa para determinar a probabilidade aproximada de retirar certas bolas aleatoriamente de um chapéu.
-
-Você pode acessar [a descrição completa do projeto e o código inicial no Replit](https://replit.com/github/freeCodeCamp/boilerplate-probability-calculator). Depois de ir para esse link, faça fork no projeto. Depois que você completar o projeto com base nas instruções do 'README.md', envie o link do seu projeto abaixo.
+Você [trabalhará neste projeto com nosso código inicial do Replit](https://replit.com/github/freeCodeCamp/boilerplate-probability-calculator).
Ainda estamos desenvolvendo a parte instrucional interativa do currículo Python. Por enquanto, aqui estão alguns vídeos no canal do freeCodeCamp.org do YouTube que ensinarão tudo o que você precisa saber para completar este projeto:
-
+- [Curso de Python em vídeo para todos](https://www.freecodecamp.org/news/python-for-everybody/) (14 horas)
+
+- [Curso Aprenda Python em vídeo](https://www.freecodecamp.org/news/learn-python-video-course/) (10 horas)
+
+# --instructions--
+
+Suponha que haja um chapéu contendo 5 bolas azuis, 4 bolas vermelhas e 2 bolas verdes. Qual é a probabilidade de um sorteio aleatório de 4 bolas conter pelo menos 1 bola vermelha e 2 bolas verdes? Embora seja possível calcular a probabilidade usando matemática avançada, uma maneira mais fácil é escrever um programa para realizar um grande número de experimentos para estimar uma probabilidade aproximada.
+
+Para este projeto, escreva um programa para determinar a probabilidade aproximada de retirar certas bolas aleatoriamente de um chapéu.
+
+Primeiro, crie uma classe `Hat` (Chapéu) em `prob_calculator.py`. A classe deve ter um número variável de argumentos que especificam o número de bolas de cada cor que estão no chapéu. Por exemplo, um objeto da classe poderia ser criado de qualquer uma dessas maneiras:
+
+```py
+hat1 = Hat(yellow=3, blue=2, green=6)
+hat2 = Hat(red=5, orange=4)
+hat3 = Hat(red=5, orange=4, black=1, blue=0, pink=2, striped=9)
+```
+
+Um chapéu será sempre criado com pelo menos uma bola. Os argumentos passados para o objeto de chapéu após a criação devem ser convertidos em uma variável de instância `contents`. `contents` deve ser uma lista de strings contendo um item para cada bola no chapéu. Cada item da lista deve ser um nome de cor que representa uma única bola dessa cor. Por exemplo, se sua instância de Hat for `{"red": 2, "blue": 1}`, `contents` deve ser `["red", "red", "blue"]`.
+
+A classe `Hat` deve ter um método `draw` que aceita um argumento indicando o número de bolas a serem retiradas do chapéu. Este método deve remover bolas aleatoriamente de `contents` e retornar essas bolas como uma lista de strings. As bolas não devem voltar ao chapéu durante a retirada, à semelhança de uma experiência sem substituição. Se o número de bolas a serem retiradas exceder a quantidade disponível, retorne todas as bolas.
+
+Em seguida, crie uma função`experiment`em `prob_calculator.py` (não dentro da classe `Hat`). Esta função deve aceitar os seguintes argumentos:
+
+- `hat`: Um objeto de chapéu contendo bolas que devem ser copiadas dentro da função.
+- `expected_balls`: Um objeto indicando o grupo exato de bolas que se tentará retirar do chapéu para o experimento. Por exemplo, para determinar a probabilidade de retirar 2 bolas azuis e 1 bola vermelha do chapéu, defina `expected_balls` como `{"blue":2, "red":1}`.
+- `num_balls_drawn`: O número de bolas a serem retiradas do chapéu em cada experimento.
+- `num_experiments`: O número de experimentos a serem realizados. Quanto mais experimentos realizados, mais precisa será a probabilidade aproximada.
+
+A função `experiment` deve retornar uma probabilidade.
+
+Por exemplo, digamos que você quer determinar a probabilidade de obter pelo menos 2 bolas vermelhas e 1 bola verde ao retirar 5 bolas de um chapéu contendo 6 bolas pretas, 4 vermelhas, e 3 verdes. Para fazer isso, realizamos `N` experimentos, contamos quantas vezes `M` nós obtivemos pelo menos 2 bolas vermelhas e 1 bola verde, e estimamos a probabilidade como `M/N`. Cada experimento consiste em começar com um chapéu contendo as bolas especificadas, retirar várias bolas e verificar se retiramos as bolas que estávamos tentando retirar.
+
+Veja como você chamaria a função `experiment` com base no exemplo acima de 2.000 experimentos:
+
+```py
+hat = Hat(black=6, red=4, green=3)
+probability = experiment(hat=hat,
+ expected_balls={"red":2,"green":1},
+ num_balls_drawn=5,
+ num_experiments=2000)
+```
+
+Como isto é baseado em sorteios aleatórios, a probabilidade será ligeiramente diferente cada vez que o código for executado.
+
+*Dica: Considere usar os módulos que já estão importados na parte superior de `prob_calculator.py`. Não inicialize uma seed aleatória dentro de `prob_calculator.py`.*
+
+## Desenvolvimento
+
+Escreva seu código em `prob_calculator.py`. Para o desenvolvimento, você pode usar `main.py` para testar seu código. Clique no botão "Run" e `main.py` será executado.
+
+O boilerplate inclui declarações de `import` para os módulos `copy` e `random`. Considere usá-los no seu projeto.
+
+## Testes
+
+Os testes unitários para este projeto estão em `test_module.py`. Importamos os testes de `test_module.py` em `main.py` para a sua conveniência. Os testes serão executados automaticamente sempre que você clicar no botão "Run".
+
+## Envio
+
+Copie o URL do seu projeto e envie-o para o freeCodeCamp.
# --hints--
diff --git a/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md b/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
index 1fbc694414..5d52a1b6c3 100644
--- a/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
+++ b/curriculum/challenges/portuguese/07-scientific-computing-with-python/scientific-computing-with-python-projects/time-calculator.md
@@ -8,20 +8,63 @@ dashedName: time-calculator
# --description--
-Escreva uma função chamada "add_time", que pode adicionar um tempo de início e retornar o resultado.
-
-Você pode acessar [a descrição completa do projeto e o código inicial no Replit](https://replit.com/github/freeCodeCamp/boilerplate-time-calculator). Depois de ir para esse link, faça fork no projeto. Depois que você completar o projeto com base nas instruções do 'README.md', envie o link do seu projeto abaixo.
+Você [trabalhará neste projeto com nosso código inicial do Replit](https://replit.com/github/freeCodeCamp/boilerplate-time-calculator).
Ainda estamos desenvolvendo a parte instrucional interativa do currículo Python. Por enquanto, aqui estão alguns vídeos no canal do freeCodeCamp.org do YouTube que ensinarão tudo o que você precisa saber para completar este projeto:
-
+- [Curso de Python em vídeo para todos](https://www.freecodecamp.org/news/python-for-everybody/) (14 horas)
+
+- [Curso Aprenda Python em vídeo](https://www.freecodecamp.org/news/learn-python-video-course/) (10 horas)
+
+# --instructions--
+
+Escreva uma função chamada `add_time`, que recebe dois parâmetros necessários e um parâmetro opcional:
+
+- uma hora de início no formato de relógio de 12 horas (terminando em AM ou PM)
+- um tempo de duração que indica o número de horas e minutos
+- (opcional) um dia de início na semana, sem distinção de maiúsculas ou minúsculas
+
+A função deve adicionar o tempo de duração ao horário inicial e retornar o resultado.
+
+Se o resultado for no dia seguinte, ele deve mostrar `(next day)` (dia seguinte) após o tempo. Se o resultado for mais de um dia depois, ele deve mostrar `(n days later)` (n dias depois) após o tempo, onde "n" é o número de dias depois.
+
+Se a função receber o parâmetro opcional do dia de início na semana, então o resultado deve exibir o dia da semana do resultado. O dia da semana no resultado deve aparecer após o tempo e antes do número de dias depois.
+
+Abaixo vemos alguns exemplos dos diferentes casos que a função deve tratar. Preste muita atenção ao espaçamento e à pontuação dos resultados.
+
+```py
+add_time("3:00 PM", "3:10")
+# Returns: 6:10 PM
+
+add_time("11:30 AM", "2:32", "Monday")
+# Returns: 2:02 PM, Monday
+
+add_time("11:43 AM", "00:20")
+# Returns: 12:03 PM
+
+add_time("10:10 PM", "3:30")
+# Returns: 1:40 AM (next day)
+
+add_time("11:43 PM", "24:20", "tueSday")
+# Returns: 12:03 AM, Thursday (2 days later)
+
+add_time("6:30 PM", "205:12")
+# Returns: 7:42 AM (9 days later)
+```
+
+Não importe nenhuma biblioteca do Python. Suponha que os horários de início são tempos válidos. Os minutos no tempo de duração serão um número inteiro menor que 60, mas a hora pode ser qualquer número inteiro.
+
+## Desenvolvimento
+
+Escreva seu código em `time_calculator.py`. Para o desenvolvimento, você pode usar `main.py` para testar sua função `time_calculator()`. Clique no botão "Run" e `main.py` será executado.
+
+## Testes
+
+Os testes unitários para este projeto estão em `test_module.py`. Importamos os testes de `test_module.py` em `main.py` para a sua conveniência. Os testes serão executados automaticamente sempre que você clicar no botão "Run".
+
+## Envio
+
+Copie o URL do seu projeto e envie-o para o freeCodeCamp.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-193-squarefree-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-193-squarefree-numbers.md
index 2a032d5fe3..241c48c828 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-193-squarefree-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-193-squarefree-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f42f1000cf542c50ff41
-title: 'Problema 193: Números livres de raízes quadradas'
+title: 'Problema 193: Números livres de quadrados'
challengeType: 5
forumTopicId: 301831
dashedName: problem-193-squarefree-numbers
@@ -8,9 +8,9 @@ dashedName: problem-193-squarefree-numbers
# --description--
-Um número inteiro positivo $n$ é chamado de livre de raiz quadrada, se nenhum quadrado de um número primo dividir $n$. Assim, 1, 2, 3, 5, 6, 7, 10, 11 são livres de raiz quadrada, mas 4, 8, 9, 12 não são.
+Um número inteiro positivo $n$ é chamado de livre de quadrados, se nenhum quadrado de um número primo dividir $n$. Assim, 1, 2, 3, 5, 6, 7, 10, 11 são livres de quadrados, mas 4, 8, 9, 12 não são.
-Quantos números livres de raiz quadrada existem abaixo de $2^{50}$?
+Quantos números livres de quadrados existem abaixo de $2^{50}$?
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-201-subsets-with-a-unique-sum.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-201-subsets-with-a-unique-sum.md
index 045fd9b2b8..c54e71586d 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-201-subsets-with-a-unique-sum.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-201-subsets-with-a-unique-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f4361000cf542c50ff48
-title: 'Problem 201: Subsets with a unique sum'
+title: 'Problema 201: Subconjuntos com uma soma única'
challengeType: 5
forumTopicId: 301841
dashedName: problem-201-subsets-with-a-unique-sum
@@ -8,24 +8,24 @@ dashedName: problem-201-subsets-with-a-unique-sum
# --description--
-For any set A of numbers, let sum(A) be the sum of the elements of A.
+Para qualquer conjunto $A$ de números, considere $sum(A)$ a soma dos elementos de $A$.
-Consider the set B = {1,3,6,8,10,11}. There are 20 subsets of B containing three elements, and their sums are:
+Considere o conjunto $B = \\{1,3,6,8,10,11\\}$. Há 20 subconjuntos de $B$ contendo três elementos, e suas somas são:
-sum({1,3,6}) = 10, sum({1,3,8}) = 12, sum({1,3,10}) = 14, sum({1,3,11}) = 15, sum({1,6,8}) = 15, sum({1,6,10}) = 17, sum({1,6,11}) = 18, sum({1,8,10}) = 19, sum({1,8,11}) = 20, sum({1,10,11}) = 22, sum({3,6,8}) = 17, sum({3,6,10}) = 19, sum({3,6,11}) = 20, sum({3,8,10}) = 21, sum({3,8,11}) = 22, sum({3,10,11}) = 24, sum({6,8,10}) = 24, sum({6,8,11}) = 25, sum({6,10,11}) = 27, sum({8,10,11}) = 29.
+$$\begin{align} & sum(\\{1,3,6\\}) = 10 \\\\ & sum(\\{1,3,8\\}) = 12 \\\\ & sum(\\{1,3,10\\}) = 14 \\\\ & sum(\\{1,3,11\\}) = 15 \\\\ & sum(\\{1,6,8\\}) = 15 \\\\ & sum(\\{1,6,10\\}) = 17 \\\\ & sum(\\{1,6,11\\}) = 18 \\\\ & sum(\\{1,8,10\\}) = 19 \\\\ & sum(\\{1,8,11\\}) = 20 \\\\ & sum(\\{1,10,11\\}) = 22 \\\\ & sum(\\{3,6,8\\}) = 17 \\\\ & sum(\\{3,6,10\\}) = 19 \\\\ & sum(\\{3,6,11\\}) = 20 \\\\ & sum(\\{3,8,10\\}) = 21 \\\\ & sum(\\{3,8,11\\}) = 22 \\\\ & sum(\\{3,10,11\\}) = 24 \\\\ & sum(\\{6,8,10\\}) = 24 \\\\ & sum(\\{6,8,11\\}) = 25 \\\\ & sum(\\{6,10,11\\}) = 27 \\\\ & sum(\\{8,10,11\\}) = 29 \\end{align}$$
-Some of these sums occur more than once, others are unique. For a set A, let U(A,k) be the set of unique sums of k-element subsets of A, in our example we find U(B,3) = {10,12,14,18,21,25,27,29} and sum(U(B,3)) = 156.
+Algumas destas somas ocorrem mais de uma vez, outras são únicas. Para um conjunto de $A$, considere $U(A,k)$ como sendo o conjunto de somas únicas de subconjuntos de $k$ elementos de $A$, No nosso exemplo, encontramos $U(B,3) = \\{10,12,14,18,21,25,27,29\\}$ e $sum(U(B,3)) = 156$.
-Now consider the 100-element set S = {12, 22, ... , 1002}. S has 100891344545564193334812497256 50-element subsets.
+Agora, considere o $100$º conjunto de elementos $S = \\{1^2, 2^2, \ldots , {100}^2\\}$. $S$ tem $100.891.344.545.564.193.334.812.497.256\\;$ subconjuntos de $50$ elementos.
-Determine the sum of all integers which are the sum of exactly one of the 50-element subsets of S, i.e. find sum(U(S,50)).
+Determine a soma de todos os números inteiros que são a soma de exatamente um dos subconjuntos de $50$ elementos de $S$, ou seja, encontre $sum(U(S,50))$.
# --hints--
-`euler201()` should return 115039000.
+`uniqueSubsetsSum()` deve retornar `115039000`.
```js
-assert.strictEqual(euler201(), 115039000);
+assert.strictEqual(uniqueSubsetsSum(), 115039000);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler201(), 115039000);
## --seed-contents--
```js
-function euler201() {
+function uniqueSubsetsSum() {
return true;
}
-euler201();
+uniqueSubsetsSum();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-202-laserbeam.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-202-laserbeam.md
index c42f68e414..d5036bcb25 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-202-laserbeam.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-202-laserbeam.md
@@ -1,6 +1,6 @@
---
id: 5900f4371000cf542c50ff49
-title: 'Problem 202: Laserbeam'
+title: 'Problema 202: Raio laser'
challengeType: 5
forumTopicId: 301843
dashedName: problem-202-laserbeam
@@ -8,20 +8,22 @@ dashedName: problem-202-laserbeam
# --description--
-Three mirrors are arranged in the shape of an equilateral triangle, with their reflective surfaces pointing inwards. There is an infinitesimal gap at each vertex of the triangle through which a laser beam may pass.
+Três espelhos são organizados na forma de um triângulo equilátero, com suas superfícies reflexivas apontando para dentro. Há uma lacuna infinitesimal em cada vértice do triângulo através da qual um raio laser pode passar.
-Label the vertices A, B and C. There are 2 ways in which a laser beam may enter vertex C, bounce off 11 surfaces, then exit through the same vertex: one way is shown below; the other is the reverse of that.
+Rotule os vértices $A$, $B$ e $C$. Existem 2 maneiras pelas quais um raio laser pode entrar no vértice $C$, ricochetear 11 vezes nas superfícies e depois sair pelo mesmo vértice: uma maneira é mostrada abaixo; a outra é fazendo o caminho inverso.
-There are 80840 ways in which a laser beam may enter vertex C, bounce off 1000001 surfaces, then exit through the same vertex.
+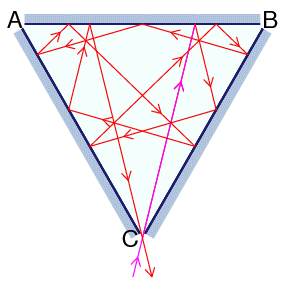 -In how many ways can a laser beam enter at vertex C, bounce off 12017639147 surfaces, then exit through the same vertex?
+Há 80.840 maneiras pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 1.000.001 vezes nas superfícies e depois sair pelo mesmo vértice.
+
+Quantas maneiras existem pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 12.017.639.147 vezes nas superfícies e depois sair pelo mesmo vértice?
# --hints--
-`euler202()` should return 1209002624.
+`laserbeam()` deve retornar `1209002624`.
```js
-assert.strictEqual(euler202(), 1209002624);
+assert.strictEqual(laserbeam(), 1209002624);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler202(), 1209002624);
## --seed-contents--
```js
-function euler202() {
+function laserbeam() {
return true;
}
-euler202();
+laserbeam();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
index 4ecf609e4b..1de4647282 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4a
-title: 'Problem 203: Squarefree Binomial Coefficients'
+title: 'Problema 203: Coeficientes binomiais livres de quadrados'
challengeType: 5
forumTopicId: 301844
dashedName: problem-203-squarefree-binomial-coefficients
@@ -8,22 +8,22 @@ dashedName: problem-203-squarefree-binomial-coefficients
# --description--
-The binomial coefficients nCk can be arranged in triangular form, Pascal's triangle, like this:
+Os coeficientes binomiais $\displaystyle\binom{n}{k}$ podem ser organizados em forma triangular, no triângulo de Pascal, assim:
-111121133114641151010511615201561172135352171 .........
+$$\begin{array}{ccccccccccccccc} & & & & & & & 1 & & & & & & & \\\\ & & & & & & 1 & & 1 & & & & & & \\\\ & & & & & 1 & & 2 & & 1 & & & & & \\\\ & & & & 1 & & 3 & & 3 & & 1 & & & & \\\\ & & & 1 & & 4 & & 6 & & 4 & & 1 & & & \\\\ & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 & & \\\\ & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1 & \\\\ 1 & & 7 & & 21 & & 35 & & 35 & & 21 & & 7 & & 1 \\\\ & & & & & & & \ldots \end{array}$$
-It can be seen that the first eight rows of Pascal's triangle contain twelve distinct numbers: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 and 35.
+Podemos ver que as primeiras oito linhas do triângulo de Pascal contêm doze números distintos: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 e 35.
-A positive integer n is called squarefree if no square of a prime divides n. Of the twelve distinct numbers in the first eight rows of Pascal's triangle, all except 4 and 20 are squarefree. The sum of the distinct squarefree numbers in the first eight rows is 105.
+Um número inteiro positivo n é chamado de livre de quadrados se nenhum quadrado de um número primo dividir n. Dos doze números distintos nas primeiras oito linhas do triângulo de Pascal, todos os números exceto 4 e 20 são livres de quadrados. A soma dos números distintos livres de quadrados nas primeiras oito linhas é 105.
-Find the sum of the distinct squarefree numbers in the first 51 rows of Pascal's triangle.
+Encontre a soma dos números distintos livres de quadrados nas primeiras 51 linhas do triângulo de Pascal.
# --hints--
-`euler203()` should return 34029210557338.
+`squarefreeBinomialCoefficients()` deve retornar `34029210557338`.
```js
-assert.strictEqual(euler203(), 34029210557338);
+assert.strictEqual(squarefreeBinomialCoefficients(), 34029210557338);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler203(), 34029210557338);
## --seed-contents--
```js
-function euler203() {
+function squarefreeBinomialCoefficients() {
return true;
}
-euler203();
+squarefreeBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
index 4d81e08eea..918620d1c3 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4b
-title: 'Problem 204: Generalised Hamming Numbers'
+title: 'Problema 204: Números de Hamming generalizados'
challengeType: 5
forumTopicId: 301845
dashedName: problem-204-generalised-hamming-numbers
@@ -8,22 +8,22 @@ dashedName: problem-204-generalised-hamming-numbers
# --description--
-A Hamming number is a positive number which has no prime factor larger than 5.
+Um número de Hamming é um número positivo que não tem fator primo maior que 5.
-So the first few Hamming numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
+Assim, os primeiros números de Hamming são 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 e 15.
-There are 1105 Hamming numbers not exceeding 108.
+Há 1105 números de Hamming que não excedem ${10}^8$.
-We will call a positive number a generalised Hamming number of type n, if it has no prime factor larger than n. Hence the Hamming numbers are the generalised Hamming numbers of type 5.
+Chamaremos um número positivo de número generalizado de Hamming do tipo $n$, se ele não tiver fator primo maior que $n$. Assim, os números de Hamming são os números generalizados de Hamming do tipo 5.
-How many generalised Hamming numbers of type 100 are there which don't exceed 109?
+Quantos números de Hamming generalizados do tipo 100 existem que não excedem ${10}^9$?
# --hints--
-`euler204()` should return 2944730.
+`generalisedHammingNumbers()` deve retornar `2944730`.
```js
-assert.strictEqual(euler204(), 2944730);
+assert.strictEqual(generalisedHammingNumbers(), 2944730);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler204(), 2944730);
## --seed-contents--
```js
-function euler204() {
+function generalisedHammingNumbers() {
return true;
}
-euler204();
+generalisedHammingNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
index 41bf903b6d..fc2f40557e 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4391000cf542c50ff4c
-title: 'Problem 205: Dice Game'
+title: 'Problema 205: Jogo de dados'
challengeType: 5
forumTopicId: 301846
dashedName: problem-205-dice-game
@@ -8,20 +8,20 @@ dashedName: problem-205-dice-game
# --description--
-Peter has nine four-sided (pyramidal) dice, each with faces numbered 1, 2, 3, 4.
+Pedro tem nove dados de quatro lados (piramidais), e cada uma das faces recebe um número 1, 2, 3 e 4.
-Colin has six six-sided (cubic) dice, each with faces numbered 1, 2, 3, 4, 5, 6.
+Colin tem seis dados de seis lados (cúbicos), e cada uma das fazes recebe um número 1, 2, 3, 4, 5 e 6.
-Peter and Colin roll their dice and compare totals: the highest total wins. The result is a draw if the totals are equal.
+Pedro e Colin rolam seus dados e comparam os totais: o maior total ganha. O resultado é um empate se os totais forem iguais.
-What is the probability that Pyramidal Pete beats Cubic Colin? Give your answer rounded to seven decimal places in the form 0.abcdefg
+Qual é a probabilidade que o Pedro Piramidal vencer Colin Cúbico? Arredonde sua resposta para até sete casas decimais usando o formato 0.abcdefg
# --hints--
-`euler205()` should return 0.5731441.
+`diceGame()` deve retornar `0.5731441`.
```js
-assert.strictEqual(euler205(), 0.5731441);
+assert.strictEqual(diceGame(), 0.5731441);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler205(), 0.5731441);
## --seed-contents--
```js
-function euler205() {
+function diceGame() {
return true;
}
-euler205();
+diceGame();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
index eaedced890..46e24b7b08 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
@@ -1,6 +1,6 @@
---
id: 5900f43a1000cf542c50ff4d
-title: 'Problem 206: Concealed Square'
+title: 'Problema 206: Quadrado escondido'
challengeType: 5
forumTopicId: 301847
dashedName: problem-206-concealed-square
@@ -8,14 +8,14 @@ dashedName: problem-206-concealed-square
# --description--
-Find the unique positive integer whose square has the form 1_2_3_4_5_6_7_8_9_0, where each “\_” is a single digit.
+Encontre o número inteiro positivo cujo quadrado tem o formato 1_2_3_4_5_6_7_8_9_0, onde cada "_" é um único algarismo.
# --hints--
-`euler206()` should return 1389019170.
+`concealedSquare()` deve retornar `1389019170`.
```js
-assert.strictEqual(euler206(), 1389019170);
+assert.strictEqual(concealedSquare(), 1389019170);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler206(), 1389019170);
## --seed-contents--
```js
-function euler206() {
+function concealedSquare() {
return true;
}
-euler206();
+concealedSquare();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
index 19f1d12c8d..440218de4f 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
@@ -1,6 +1,6 @@
---
id: 5900f43c1000cf542c50ff4e
-title: 'Problem 207: Integer partition equations'
+title: 'Problema 207: Equações de partições inteiras'
challengeType: 5
forumTopicId: 301848
dashedName: problem-207-integer-partition-equations
@@ -8,24 +8,28 @@ dashedName: problem-207-integer-partition-equations
# --description--
-For some positive integers k, there exists an integer partition of the form 4t = 2t + k,
+Para alguns números inteiros positivos $k$, existe uma partição inteira de forma $4^t = 2^t + k$,
-where 4t, 2t, and k are all positive integers and t is a real number.
+onde $4^t$, $2^t$ e $k$ são todos números inteiros positivos e $t$ é um número real.
-The first two such partitions are 41 = 21 + 2 and 41.5849625... = 21.5849625... + 6.
+As duas primeiras partições desse tipo são $4^1 = 2^1 + 2$ e $4^{1.584\\,962\\,5\ldots} = 2^{1.584\\,962\\,5\ldots} + 6$.
-Partitions where t is also an integer are called perfect. For any m ≥ 1 let P(m) be the proportion of such partitions that are perfect with k ≤ m. Thus P(6) = 1/2.
+As partições onde $t$ é também um número inteiro são chamadas de perfeitas. Para qualquer $m ≥ 1$, considere $P(m)$ como sendo a proporção de tais partições que são perfeitas com $k ≤ m$.
-In the following table are listed some values of P(m) P(5) = 1/1 P(10) = 1/2 P(15) = 2/3 P(20) = 1/2 P(25) = 1/2 P(30) = 2/5 ... P(180) = 1/4 P(185) = 3/13
+Assim, $P(6) = \frac{1}{2}$.
-Find the smallest m for which P(m) < 1/12345
+Na tabela a seguir estão listados alguns valores de $P(m)$
+
+$$\begin{align} & P(5) = \frac{1}{1} \\\\ & P(10) = \frac{1}{2} \\\\ & P(15) = \frac{2}{3} \\\\ & P(20) = \frac{1}{2} \\\\ & P(25) = \frac{1}{2} \\\\ & P(30) = \frac{2}{5} \\\\ & \ldots \\\\ & P(180) = \frac{1}{4} \\\\ & P(185) = \frac{3}{13} \end{align}$$
+
+Encontre o menor $m$ para o qual $P(m) < \frac{1}{12.345}$
# --hints--
-`euler207()` should return 44043947822.
+`integerPartitionEquations()` deve retornar `44043947822`.
```js
-assert.strictEqual(euler207(), 44043947822);
+assert.strictEqual(integerPartitionEquations(), 44043947822);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler207(), 44043947822);
## --seed-contents--
```js
-function euler207() {
+function integerPartitionEquations() {
return true;
}
-euler207();
+integerPartitionEquations();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
index 36d5a8fff5..6d59d5c4ff 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff51
-title: 'Problem 208: Robot Walks'
+title: 'Problema 208: Caminhadas robóticas'
challengeType: 5
forumTopicId: 301849
dashedName: problem-208-robot-walks
@@ -8,18 +8,22 @@ dashedName: problem-208-robot-walks
# --description--
-A robot moves in a series of one-fifth circular arcs (72°), with a free choice of a clockwise or an anticlockwise arc for each step, but no turning on the spot.
+Um robô se move em uma série arco circular de um quinto de volta (72°), com uma escolha livre de sentido horário ou anti-horário para cada etapa, mas sem virar no local.
-One of 70932 possible closed paths of 25 arcs starting northward is
+Um dos 70932 caminhos fechados possíveis de 25 arcos iniciando para o norte é
-Given that the robot starts facing North, how many journeys of 70 arcs in length can it take that return it, after the final arc, to its starting position? (Any arc may be traversed multiple times.)
+
-In how many ways can a laser beam enter at vertex C, bounce off 12017639147 surfaces, then exit through the same vertex?
+Há 80.840 maneiras pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 1.000.001 vezes nas superfícies e depois sair pelo mesmo vértice.
+
+Quantas maneiras existem pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 12.017.639.147 vezes nas superfícies e depois sair pelo mesmo vértice?
# --hints--
-`euler202()` should return 1209002624.
+`laserbeam()` deve retornar `1209002624`.
```js
-assert.strictEqual(euler202(), 1209002624);
+assert.strictEqual(laserbeam(), 1209002624);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler202(), 1209002624);
## --seed-contents--
```js
-function euler202() {
+function laserbeam() {
return true;
}
-euler202();
+laserbeam();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
index 4ecf609e4b..1de4647282 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4a
-title: 'Problem 203: Squarefree Binomial Coefficients'
+title: 'Problema 203: Coeficientes binomiais livres de quadrados'
challengeType: 5
forumTopicId: 301844
dashedName: problem-203-squarefree-binomial-coefficients
@@ -8,22 +8,22 @@ dashedName: problem-203-squarefree-binomial-coefficients
# --description--
-The binomial coefficients nCk can be arranged in triangular form, Pascal's triangle, like this:
+Os coeficientes binomiais $\displaystyle\binom{n}{k}$ podem ser organizados em forma triangular, no triângulo de Pascal, assim:
-111121133114641151010511615201561172135352171 .........
+$$\begin{array}{ccccccccccccccc} & & & & & & & 1 & & & & & & & \\\\ & & & & & & 1 & & 1 & & & & & & \\\\ & & & & & 1 & & 2 & & 1 & & & & & \\\\ & & & & 1 & & 3 & & 3 & & 1 & & & & \\\\ & & & 1 & & 4 & & 6 & & 4 & & 1 & & & \\\\ & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 & & \\\\ & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1 & \\\\ 1 & & 7 & & 21 & & 35 & & 35 & & 21 & & 7 & & 1 \\\\ & & & & & & & \ldots \end{array}$$
-It can be seen that the first eight rows of Pascal's triangle contain twelve distinct numbers: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 and 35.
+Podemos ver que as primeiras oito linhas do triângulo de Pascal contêm doze números distintos: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 e 35.
-A positive integer n is called squarefree if no square of a prime divides n. Of the twelve distinct numbers in the first eight rows of Pascal's triangle, all except 4 and 20 are squarefree. The sum of the distinct squarefree numbers in the first eight rows is 105.
+Um número inteiro positivo n é chamado de livre de quadrados se nenhum quadrado de um número primo dividir n. Dos doze números distintos nas primeiras oito linhas do triângulo de Pascal, todos os números exceto 4 e 20 são livres de quadrados. A soma dos números distintos livres de quadrados nas primeiras oito linhas é 105.
-Find the sum of the distinct squarefree numbers in the first 51 rows of Pascal's triangle.
+Encontre a soma dos números distintos livres de quadrados nas primeiras 51 linhas do triângulo de Pascal.
# --hints--
-`euler203()` should return 34029210557338.
+`squarefreeBinomialCoefficients()` deve retornar `34029210557338`.
```js
-assert.strictEqual(euler203(), 34029210557338);
+assert.strictEqual(squarefreeBinomialCoefficients(), 34029210557338);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler203(), 34029210557338);
## --seed-contents--
```js
-function euler203() {
+function squarefreeBinomialCoefficients() {
return true;
}
-euler203();
+squarefreeBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
index 4d81e08eea..918620d1c3 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4b
-title: 'Problem 204: Generalised Hamming Numbers'
+title: 'Problema 204: Números de Hamming generalizados'
challengeType: 5
forumTopicId: 301845
dashedName: problem-204-generalised-hamming-numbers
@@ -8,22 +8,22 @@ dashedName: problem-204-generalised-hamming-numbers
# --description--
-A Hamming number is a positive number which has no prime factor larger than 5.
+Um número de Hamming é um número positivo que não tem fator primo maior que 5.
-So the first few Hamming numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
+Assim, os primeiros números de Hamming são 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 e 15.
-There are 1105 Hamming numbers not exceeding 108.
+Há 1105 números de Hamming que não excedem ${10}^8$.
-We will call a positive number a generalised Hamming number of type n, if it has no prime factor larger than n. Hence the Hamming numbers are the generalised Hamming numbers of type 5.
+Chamaremos um número positivo de número generalizado de Hamming do tipo $n$, se ele não tiver fator primo maior que $n$. Assim, os números de Hamming são os números generalizados de Hamming do tipo 5.
-How many generalised Hamming numbers of type 100 are there which don't exceed 109?
+Quantos números de Hamming generalizados do tipo 100 existem que não excedem ${10}^9$?
# --hints--
-`euler204()` should return 2944730.
+`generalisedHammingNumbers()` deve retornar `2944730`.
```js
-assert.strictEqual(euler204(), 2944730);
+assert.strictEqual(generalisedHammingNumbers(), 2944730);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler204(), 2944730);
## --seed-contents--
```js
-function euler204() {
+function generalisedHammingNumbers() {
return true;
}
-euler204();
+generalisedHammingNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
index 41bf903b6d..fc2f40557e 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4391000cf542c50ff4c
-title: 'Problem 205: Dice Game'
+title: 'Problema 205: Jogo de dados'
challengeType: 5
forumTopicId: 301846
dashedName: problem-205-dice-game
@@ -8,20 +8,20 @@ dashedName: problem-205-dice-game
# --description--
-Peter has nine four-sided (pyramidal) dice, each with faces numbered 1, 2, 3, 4.
+Pedro tem nove dados de quatro lados (piramidais), e cada uma das faces recebe um número 1, 2, 3 e 4.
-Colin has six six-sided (cubic) dice, each with faces numbered 1, 2, 3, 4, 5, 6.
+Colin tem seis dados de seis lados (cúbicos), e cada uma das fazes recebe um número 1, 2, 3, 4, 5 e 6.
-Peter and Colin roll their dice and compare totals: the highest total wins. The result is a draw if the totals are equal.
+Pedro e Colin rolam seus dados e comparam os totais: o maior total ganha. O resultado é um empate se os totais forem iguais.
-What is the probability that Pyramidal Pete beats Cubic Colin? Give your answer rounded to seven decimal places in the form 0.abcdefg
+Qual é a probabilidade que o Pedro Piramidal vencer Colin Cúbico? Arredonde sua resposta para até sete casas decimais usando o formato 0.abcdefg
# --hints--
-`euler205()` should return 0.5731441.
+`diceGame()` deve retornar `0.5731441`.
```js
-assert.strictEqual(euler205(), 0.5731441);
+assert.strictEqual(diceGame(), 0.5731441);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler205(), 0.5731441);
## --seed-contents--
```js
-function euler205() {
+function diceGame() {
return true;
}
-euler205();
+diceGame();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
index eaedced890..46e24b7b08 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
@@ -1,6 +1,6 @@
---
id: 5900f43a1000cf542c50ff4d
-title: 'Problem 206: Concealed Square'
+title: 'Problema 206: Quadrado escondido'
challengeType: 5
forumTopicId: 301847
dashedName: problem-206-concealed-square
@@ -8,14 +8,14 @@ dashedName: problem-206-concealed-square
# --description--
-Find the unique positive integer whose square has the form 1_2_3_4_5_6_7_8_9_0, where each “\_” is a single digit.
+Encontre o número inteiro positivo cujo quadrado tem o formato 1_2_3_4_5_6_7_8_9_0, onde cada "_" é um único algarismo.
# --hints--
-`euler206()` should return 1389019170.
+`concealedSquare()` deve retornar `1389019170`.
```js
-assert.strictEqual(euler206(), 1389019170);
+assert.strictEqual(concealedSquare(), 1389019170);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler206(), 1389019170);
## --seed-contents--
```js
-function euler206() {
+function concealedSquare() {
return true;
}
-euler206();
+concealedSquare();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
index 19f1d12c8d..440218de4f 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
@@ -1,6 +1,6 @@
---
id: 5900f43c1000cf542c50ff4e
-title: 'Problem 207: Integer partition equations'
+title: 'Problema 207: Equações de partições inteiras'
challengeType: 5
forumTopicId: 301848
dashedName: problem-207-integer-partition-equations
@@ -8,24 +8,28 @@ dashedName: problem-207-integer-partition-equations
# --description--
-For some positive integers k, there exists an integer partition of the form 4t = 2t + k,
+Para alguns números inteiros positivos $k$, existe uma partição inteira de forma $4^t = 2^t + k$,
-where 4t, 2t, and k are all positive integers and t is a real number.
+onde $4^t$, $2^t$ e $k$ são todos números inteiros positivos e $t$ é um número real.
-The first two such partitions are 41 = 21 + 2 and 41.5849625... = 21.5849625... + 6.
+As duas primeiras partições desse tipo são $4^1 = 2^1 + 2$ e $4^{1.584\\,962\\,5\ldots} = 2^{1.584\\,962\\,5\ldots} + 6$.
-Partitions where t is also an integer are called perfect. For any m ≥ 1 let P(m) be the proportion of such partitions that are perfect with k ≤ m. Thus P(6) = 1/2.
+As partições onde $t$ é também um número inteiro são chamadas de perfeitas. Para qualquer $m ≥ 1$, considere $P(m)$ como sendo a proporção de tais partições que são perfeitas com $k ≤ m$.
-In the following table are listed some values of P(m) P(5) = 1/1 P(10) = 1/2 P(15) = 2/3 P(20) = 1/2 P(25) = 1/2 P(30) = 2/5 ... P(180) = 1/4 P(185) = 3/13
+Assim, $P(6) = \frac{1}{2}$.
-Find the smallest m for which P(m) < 1/12345
+Na tabela a seguir estão listados alguns valores de $P(m)$
+
+$$\begin{align} & P(5) = \frac{1}{1} \\\\ & P(10) = \frac{1}{2} \\\\ & P(15) = \frac{2}{3} \\\\ & P(20) = \frac{1}{2} \\\\ & P(25) = \frac{1}{2} \\\\ & P(30) = \frac{2}{5} \\\\ & \ldots \\\\ & P(180) = \frac{1}{4} \\\\ & P(185) = \frac{3}{13} \end{align}$$
+
+Encontre o menor $m$ para o qual $P(m) < \frac{1}{12.345}$
# --hints--
-`euler207()` should return 44043947822.
+`integerPartitionEquations()` deve retornar `44043947822`.
```js
-assert.strictEqual(euler207(), 44043947822);
+assert.strictEqual(integerPartitionEquations(), 44043947822);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler207(), 44043947822);
## --seed-contents--
```js
-function euler207() {
+function integerPartitionEquations() {
return true;
}
-euler207();
+integerPartitionEquations();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
index 36d5a8fff5..6d59d5c4ff 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff51
-title: 'Problem 208: Robot Walks'
+title: 'Problema 208: Caminhadas robóticas'
challengeType: 5
forumTopicId: 301849
dashedName: problem-208-robot-walks
@@ -8,18 +8,22 @@ dashedName: problem-208-robot-walks
# --description--
-A robot moves in a series of one-fifth circular arcs (72°), with a free choice of a clockwise or an anticlockwise arc for each step, but no turning on the spot.
+Um robô se move em uma série arco circular de um quinto de volta (72°), com uma escolha livre de sentido horário ou anti-horário para cada etapa, mas sem virar no local.
-One of 70932 possible closed paths of 25 arcs starting northward is
+Um dos 70932 caminhos fechados possíveis de 25 arcos iniciando para o norte é
-Given that the robot starts facing North, how many journeys of 70 arcs in length can it take that return it, after the final arc, to its starting position? (Any arc may be traversed multiple times.)
+ +
+Dado que o robô começa virado para o norte, quantas jornadas de 70 arcos de comprimento ele pode fazer que o retornem, após o arco final, para sua posição inicial?
+
+**Observação:** qualquer arco pode ser atravessado várias vezes.
# --hints--
-`euler208()` should return 331951449665644800.
+`robotWalks()` deve retornar `331951449665644800`.
```js
-assert.strictEqual(euler208(), 331951449665644800);
+assert.strictEqual(robotWalks(), 331951449665644800);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler208(), 331951449665644800);
## --seed-contents--
```js
-function euler208() {
+function robotWalks() {
return true;
}
-euler208();
+robotWalks();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
index f743744736..77d259dced 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff4f
-title: 'Problem 209: Circular Logic'
+title: 'Problema 209: Lógica circular'
challengeType: 5
forumTopicId: 301850
dashedName: problem-209-circular-logic
@@ -8,20 +8,34 @@ dashedName: problem-209-circular-logic
# --description--
-A k-input binary truth table is a map from k input bits
+Uma tabela verdade binária de $k$ entradas é um mapa de $k$ bits de entrada (dígitos binários, 0 [false] ou 1 [true]) para 1 bit de saída. Por exemplo, as tabelas verdade binárias de $2$ entradas para as funções lógicas de $AND$ e $XOR$ são:
-(binary digits, 0 \[false] or 1 \[true]) to 1 output bit. For example, the 2-input binary truth tables for the logical AND and XOR functions are:
+| x | y | x AND y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 0 |
+| 1 | 0 | 0 |
+| 1 | 1 | 1 |
-x y x AND y000010100111x y x XOR y000011101110How many 6-input binary truth tables, τ, satisfy the formula
+| x | y | x XOR y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 1 |
+| 1 | 0 | 1 |
+| 1 | 1 | 0 |
-τ(a, b, c, d, e, f) AND τ(b, c, d, e, f, a XOR (b AND c)) = 0 for all 6-bit inputs (a, b, c, d, e, f)?
+Quantas tabelas verdade binárias de $6$ entradas, $τ$, satisfazem a fórmula
+
+$$τ(a, b, c, d, e, f) \\; AND \\; τ(b, c, d, e, f, a \\; XOR \\; (b \\; AND \\; c)) = 0$$
+
+para todas as entradas de $6$ bits ($a$, $b$, $c$, $d$, $e$, $f$)?
# --hints--
-`euler209()` should return 15964587728784.
+`circularLogic()` deve retornar `15964587728784`.
```js
-assert.strictEqual(euler209(), 15964587728784);
+assert.strictEqual(circularLogic(), 15964587728784);
```
# --seed--
@@ -29,12 +43,12 @@ assert.strictEqual(euler209(), 15964587728784);
## --seed-contents--
```js
-function euler209() {
+function circularLogic() {
return true;
}
-euler209();
+circularLogic();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
index 1fc7d98033..e5dc0ee273 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff50
-title: 'Problem 210: Obtuse Angled Triangles'
+title: 'Problema 210: Triângulos de ângulos obtusos'
challengeType: 5
forumTopicId: 301852
dashedName: problem-210-obtuse-angled-triangles
@@ -8,22 +8,22 @@ dashedName: problem-210-obtuse-angled-triangles
# --description--
-Consider the set S(r) of points (x,y) with integer coordinates satisfying |x| + |y| ≤ r.
+Considere o conjunto $S(r)$ de pontos ($x$,$y$) com coordenadas inteiras que satisfaçam $|x| + |y| ≤ r$.
-Let O be the point (0,0) and C the point (r/4,r/4).
+Considere $O$ como sendo o ponto (0,0) e $C$ o ponto($\frac{r}{4}$,$\frac{r}{4}$).
-Let N(r) be the number of points B in S(r), so that the triangle OBC has an obtuse angle, i.e. the largest angle α satisfies 90°<α<180°.
+Considere $N(r)$ como sendo o número de pontos $B$ em $S(r)$, para que o triângulo $OBC$ tenha um ângulo obtuso, ou seja, o maior ângulo $α$ satisfaz $90°<α<180°$.
-So, for example, N(4)=24 and N(8)=100.
+Assim, por exemplo, $N(4)=24$ e $N(8)=100$.
-What is N(1,000,000,000)?
+Qual é $N(1.000.000.000)$?
# --hints--
-`euler210()` should return 1598174770174689500.
+`obtuseAngledTriangles()` deve retornar `1598174770174689500`.
```js
-assert.strictEqual(euler210(), 1598174770174689500);
+assert.strictEqual(obtuseAngledTriangles(), 1598174770174689500);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler210(), 1598174770174689500);
## --seed-contents--
```js
-function euler210() {
+function obtuseAngledTriangles() {
return true;
}
-euler210();
+obtuseAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
index bde41e4a79..8f0529eb0c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff52
-title: 'Problem 211: Divisor Square Sum'
+title: 'Problema 211: Soma dos quadrados dos divisores'
challengeType: 5
forumTopicId: 301853
dashedName: problem-211-divisor-square-sum
@@ -8,18 +8,18 @@ dashedName: problem-211-divisor-square-sum
# --description--
-For a positive integer n, let σ2(n) be the sum of the squares of its divisors. For example,
+Para um número inteiro positivo $n$, considere $σ_2(n)$ como sendo a soma dos quadrados de seus divisores. Por exemplo:
-σ2(10) = 1 + 4 + 25 + 100 = 130.
+$$σ_2(10) = 1 + 4 + 25 + 100 = 130$$
-Find the sum of all n, 0 < n < 64,000,000 such that σ2(n) is a perfect square.
+Encontre a soma de todos os $n$, $0 < n < 64.000.000$, de tal forma que $σ_2(n)$ seja um quadrado perfeito.
# --hints--
-`euler211()` should return 1922364685.
+`divisorSquareSum()` deve retornar `1922364685`.
```js
-assert.strictEqual(euler211(), 1922364685);
+assert.strictEqual(divisorSquareSum(), 1922364685);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler211(), 1922364685);
## --seed-contents--
```js
-function euler211() {
+function divisorSquareSum() {
return true;
}
-euler211();
+divisorSquareSum();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
index 901bbbc3d1..0a48b57aaf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff53
-title: 'Problem 212: Combined Volume of Cuboids'
+title: 'Problema 212: Volume combinado de cuboides'
challengeType: 5
forumTopicId: 301854
dashedName: problem-212-combined-volume-of-cuboids
@@ -8,28 +8,30 @@ dashedName: problem-212-combined-volume-of-cuboids
# --description--
-An axis-aligned cuboid, specified by parameters { (x0,y0,z0), (dx,dy,dz) }, consists of all points (X,Y,Z) such that x0 ≤ X ≤ x0+dx, y0 ≤ Y ≤ y0+dy and z0 ≤ Z ≤ z0+dz. The volume of the cuboid is the product, dx × dy × dz. The combined volume of a collection of cuboids is the volume of their union and will be less than the sum of the individual volumes if any cuboids overlap.
+Um cuboide alinhado em seus eixos, especificado pelos parâmetros $\{ (x_0,y_0,z_0), (dx,dy,dz) \}$, consiste em todos os pontos ($X$,$Y$,$Z$), de modo que $x_0 ≤ X ≤ x_0 + dx$, $y_0 ≤ Y ≤ y_0 + dy$ e $z_0 ≤ Z ≤ z_0 + dz$. O volume do cuboide é o produto, $dx × dy × dz$. O volume combinado de uma coleção de cuboides é o volume da sua união e será inferior à soma dos volumes individuais se houver sobreposição de qualquer um dos cuboides.
-Let C1,...,C50000 be a collection of 50000 axis-aligned cuboids such that Cn has parameters
+Considere $C_1, \ldots, C_{50000}$ como sendo uma coleção de 50.000 cuboides alinhados em seus eixos, de modo que $C_n$ tenha parâmetros
-x0 = S6n-5 modulo 10000y0 = S6n-4 modulo 10000z0 = S6n-3 modulo 10000dx = 1 + (S6n-2 modulo 399)dy = 1 + (S6n-1 modulo 399)dz = 1 + (S6n modulo 399)
+$$\begin{align} & x_0 = S_{6n - 5} \\; \text{modulo} \\; 10000 \\\\ & y_0 = S_{6n - 4} \\; \text{modulo} \\; 10000 \\\\ & z_0 = S_{6n - 3} \\; \text{modulo} \\; 10000 \\\\ & dx = 1 + (S_{6n - 2} \\; \text{modulo} \\; 399) \\\\ & dy = 1 + (S_{6n - 1} \\; \text{modulo} \\; 399) \\\\ & dz = 1 + (S_{6n} \\; \text{modulo} \\; 399) \\\\ \end{align}$$
-where S1,...,S300000 come from the "Lagged Fibonacci Generator":
+onde $S_1, \ldots, S_{300000}$ vem do "Gerador Fibonacci com atraso":
-For 1 ≤ k ≤ 55, Sk = \[100003 - 200003k + 300007k3] (modulo 1000000)For 56 ≤ k, Sk = \[Sk-24 + Sk-55] (modulo 1000000)
+Para $1 ≤ k ≤ 55$, $S_k = [100003 - 200003k + 300007k^3] \\; (modulo \\; 1000000)$
-Thus, C1 has parameters {(7,53,183),(94,369,56)}, C2 has parameters {(2383,3563,5079),(42,212,344)}, and so on.
+Para $56 ≤ k$, $S_k = [S_{k - 24} + S_{k - 55}] \\; (modulo \\; 1000000)$
-The combined volume of the first 100 cuboids, C1,...,C100, is 723581599.
+Assim, $C_1$ tem parâmetros $\{(7,53,183), (94,369,56)\}$, $C_2$ tem parâmetros $\{(2383,3563,5079), (42,212,344)\}$ e assim por diante.
-What is the combined volume of all 50000 cuboids, C1,...,C50000 ?
+O volume combinado dos primeiros 100 cuboides, $C_1, \ldots, C_{100}$, é 723581599.
+
+Qual é o volume combinado de todos os 50000 cuboides, $C_1, \ldots, C_{50000}$?
# --hints--
-`euler212()` should return 328968937309.
+`combinedValueOfCuboids()` deve retornar `328968937309`.
```js
-assert.strictEqual(euler212(), 328968937309);
+assert.strictEqual(combinedValueOfCuboids(), 328968937309);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler212(), 328968937309);
## --seed-contents--
```js
-function euler212() {
+function combinedValueOfCuboids() {
return true;
}
-euler212();
+combinedValueOfCuboids();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
index 2fbc23393c..92200998a2 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff54
-title: 'Problem 213: Flea Circus'
+title: 'Problema 213: Circo de pulgas'
challengeType: 5
forumTopicId: 301855
dashedName: problem-213-flea-circus
@@ -8,18 +8,18 @@ dashedName: problem-213-flea-circus
# --description--
-A 30×30 grid of squares contains 900 fleas, initially one flea per square.
+Uma grade de 30×30 quadrados contém 900 pulgas, inicialmente uma pulga por quadrado.
-When a bell is rung, each flea jumps to an adjacent square at random (usually 4 possibilities, except for fleas on the edge of the grid or at the corners).
+Quando uma campainha é tocada, cada pulga salta para um quadrado adjacente aleatoriamente (geralmente 4 possibilidades, exceto para as pulgas nas bordas da grade ou nos cantos).
-What is the expected number of unoccupied squares after 50 rings of the bell? Give your answer rounded to six decimal places.
+Qual é o número esperado de quadrados desocupados após 50 toques da campainha? Dê sua resposta arredondada para seis casas decimais.
# --hints--
-`euler213()` should return 330.721154.
+`fleaCircus()` deve retornar `330.721154`.
```js
-assert.strictEqual(euler213(), 330.721154);
+assert.strictEqual(fleaCircus(), 330.721154);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler213(), 330.721154);
## --seed-contents--
```js
-function euler213() {
+function fleaCircus() {
return true;
}
-euler213();
+fleaCircus();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
index 754596cef6..9675f70327 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
@@ -1,6 +1,6 @@
---
id: 5900f4421000cf542c50ff55
-title: 'Problem 214: Totient Chains'
+title: 'Problema 214: Cadeias de totientes'
challengeType: 5
forumTopicId: 301856
dashedName: problem-214-totient-chains
@@ -8,24 +8,22 @@ dashedName: problem-214-totient-chains
# --description--
-Let φ be Euler's totient function, i.e. for a natural number n,
+Considere $φ$ como sendo a função totiente de Euler, ou seja, para um número natural $n$, $φ(n)$ é o número de $k$, $1 ≤ k ≤ n$, para os quais o máximo divisor comum é $gcd(k,n) = 1$.
-φ(n) is the number of k, 1 ≤ k ≤ n, for which gcd(k,n) = 1.
+Ao iterar por $φ$, cada número inteiro positivo gera uma cadeia decrescente de números terminando em 1. Ex: se começarmos com 5 a sequência 5,4,2,1 é gerada. Aqui está uma lista de todas as cadeias com comprimento 4:
-By iterating φ, each positive integer generates a decreasing chain of numbers ending in 1. E.g. if we start with 5 the sequence 5,4,2,1 is generated. Here is a listing of all chains with length 4:
+$$\begin{align} 5,4,2,1 & \\\\ 7,6,2,1 & \\\\ 8,4,2,1 & \\\\ 9,6,2,1 & \\\\ 10,4,2,1 & \\\\ 12,4,2,1 & \\\\ 14,6,2,1 & \\\\ 18,6,2,1 & \end{align}$$
-5,4,2,1 7,6,2,1 8,4,2,1 9,6,2,1 10,4,2,1 12,4,2,1 14,6,2,1 18,6,2,1
+Apenas duas dessas cadeias começam com um número primo e sua soma é 12.
-Only two of these chains start with a prime, their sum is 12.
-
-What is the sum of all primes less than 40000000 which generate a chain of length 25?
+Qual é a soma de todos os números primos menores do que $40.000.000$ que gera uma cadeia de comprimento 25?
# --hints--
-`euler214()` should return 1677366278943.
+`totientChains()` deve retornar `1677366278943`.
```js
-assert.strictEqual(euler214(), 1677366278943);
+assert.strictEqual(totientChains(), 1677366278943);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler214(), 1677366278943);
## --seed-contents--
```js
-function euler214() {
+function totientChains() {
return true;
}
-euler214();
+totientChains();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
index 45f7f563e7..99a6eb9baf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
@@ -1,6 +1,6 @@
---
id: 5900f4431000cf542c50ff56
-title: 'Problem 215: Crack-free Walls'
+title: 'Problema 215: Paredes sem rachaduras'
challengeType: 5
forumTopicId: 301857
dashedName: problem-215-crack-free-walls
@@ -8,20 +8,22 @@ dashedName: problem-215-crack-free-walls
# --description--
-Consider the problem of building a wall out of 2×1 and 3×1 bricks (horizontal×vertical dimensions) such that, for extra strength, the gaps between horizontally-adjacent bricks never line up in consecutive layers, i.e. never form a "running crack".
+Considere o problema da construção de uma parede de 2×1 e 3×1 tijolos (dimensões verticais × horizontais), de modo que, para ter uma força extra, as lacunas entre os blocos adjacentes horizontalmente nunca se alinham em camadas consecutivas, ou seja, nunca formam uma "rachadura".
-For example, the following 9×3 wall is not acceptable due to the running crack shown in red:
+Por exemplo, a parede 9×3 a seguir não é aceitável devido à rachadura da execução mostrada em vermelho:
-There are eight ways of forming a crack-free 9×3 wall, written W(9,3) = 8.
+
+
+Dado que o robô começa virado para o norte, quantas jornadas de 70 arcos de comprimento ele pode fazer que o retornem, após o arco final, para sua posição inicial?
+
+**Observação:** qualquer arco pode ser atravessado várias vezes.
# --hints--
-`euler208()` should return 331951449665644800.
+`robotWalks()` deve retornar `331951449665644800`.
```js
-assert.strictEqual(euler208(), 331951449665644800);
+assert.strictEqual(robotWalks(), 331951449665644800);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler208(), 331951449665644800);
## --seed-contents--
```js
-function euler208() {
+function robotWalks() {
return true;
}
-euler208();
+robotWalks();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
index f743744736..77d259dced 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff4f
-title: 'Problem 209: Circular Logic'
+title: 'Problema 209: Lógica circular'
challengeType: 5
forumTopicId: 301850
dashedName: problem-209-circular-logic
@@ -8,20 +8,34 @@ dashedName: problem-209-circular-logic
# --description--
-A k-input binary truth table is a map from k input bits
+Uma tabela verdade binária de $k$ entradas é um mapa de $k$ bits de entrada (dígitos binários, 0 [false] ou 1 [true]) para 1 bit de saída. Por exemplo, as tabelas verdade binárias de $2$ entradas para as funções lógicas de $AND$ e $XOR$ são:
-(binary digits, 0 \[false] or 1 \[true]) to 1 output bit. For example, the 2-input binary truth tables for the logical AND and XOR functions are:
+| x | y | x AND y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 0 |
+| 1 | 0 | 0 |
+| 1 | 1 | 1 |
-x y x AND y000010100111x y x XOR y000011101110How many 6-input binary truth tables, τ, satisfy the formula
+| x | y | x XOR y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 1 |
+| 1 | 0 | 1 |
+| 1 | 1 | 0 |
-τ(a, b, c, d, e, f) AND τ(b, c, d, e, f, a XOR (b AND c)) = 0 for all 6-bit inputs (a, b, c, d, e, f)?
+Quantas tabelas verdade binárias de $6$ entradas, $τ$, satisfazem a fórmula
+
+$$τ(a, b, c, d, e, f) \\; AND \\; τ(b, c, d, e, f, a \\; XOR \\; (b \\; AND \\; c)) = 0$$
+
+para todas as entradas de $6$ bits ($a$, $b$, $c$, $d$, $e$, $f$)?
# --hints--
-`euler209()` should return 15964587728784.
+`circularLogic()` deve retornar `15964587728784`.
```js
-assert.strictEqual(euler209(), 15964587728784);
+assert.strictEqual(circularLogic(), 15964587728784);
```
# --seed--
@@ -29,12 +43,12 @@ assert.strictEqual(euler209(), 15964587728784);
## --seed-contents--
```js
-function euler209() {
+function circularLogic() {
return true;
}
-euler209();
+circularLogic();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
index 1fc7d98033..e5dc0ee273 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff50
-title: 'Problem 210: Obtuse Angled Triangles'
+title: 'Problema 210: Triângulos de ângulos obtusos'
challengeType: 5
forumTopicId: 301852
dashedName: problem-210-obtuse-angled-triangles
@@ -8,22 +8,22 @@ dashedName: problem-210-obtuse-angled-triangles
# --description--
-Consider the set S(r) of points (x,y) with integer coordinates satisfying |x| + |y| ≤ r.
+Considere o conjunto $S(r)$ de pontos ($x$,$y$) com coordenadas inteiras que satisfaçam $|x| + |y| ≤ r$.
-Let O be the point (0,0) and C the point (r/4,r/4).
+Considere $O$ como sendo o ponto (0,0) e $C$ o ponto($\frac{r}{4}$,$\frac{r}{4}$).
-Let N(r) be the number of points B in S(r), so that the triangle OBC has an obtuse angle, i.e. the largest angle α satisfies 90°<α<180°.
+Considere $N(r)$ como sendo o número de pontos $B$ em $S(r)$, para que o triângulo $OBC$ tenha um ângulo obtuso, ou seja, o maior ângulo $α$ satisfaz $90°<α<180°$.
-So, for example, N(4)=24 and N(8)=100.
+Assim, por exemplo, $N(4)=24$ e $N(8)=100$.
-What is N(1,000,000,000)?
+Qual é $N(1.000.000.000)$?
# --hints--
-`euler210()` should return 1598174770174689500.
+`obtuseAngledTriangles()` deve retornar `1598174770174689500`.
```js
-assert.strictEqual(euler210(), 1598174770174689500);
+assert.strictEqual(obtuseAngledTriangles(), 1598174770174689500);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler210(), 1598174770174689500);
## --seed-contents--
```js
-function euler210() {
+function obtuseAngledTriangles() {
return true;
}
-euler210();
+obtuseAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
index bde41e4a79..8f0529eb0c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff52
-title: 'Problem 211: Divisor Square Sum'
+title: 'Problema 211: Soma dos quadrados dos divisores'
challengeType: 5
forumTopicId: 301853
dashedName: problem-211-divisor-square-sum
@@ -8,18 +8,18 @@ dashedName: problem-211-divisor-square-sum
# --description--
-For a positive integer n, let σ2(n) be the sum of the squares of its divisors. For example,
+Para um número inteiro positivo $n$, considere $σ_2(n)$ como sendo a soma dos quadrados de seus divisores. Por exemplo:
-σ2(10) = 1 + 4 + 25 + 100 = 130.
+$$σ_2(10) = 1 + 4 + 25 + 100 = 130$$
-Find the sum of all n, 0 < n < 64,000,000 such that σ2(n) is a perfect square.
+Encontre a soma de todos os $n$, $0 < n < 64.000.000$, de tal forma que $σ_2(n)$ seja um quadrado perfeito.
# --hints--
-`euler211()` should return 1922364685.
+`divisorSquareSum()` deve retornar `1922364685`.
```js
-assert.strictEqual(euler211(), 1922364685);
+assert.strictEqual(divisorSquareSum(), 1922364685);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler211(), 1922364685);
## --seed-contents--
```js
-function euler211() {
+function divisorSquareSum() {
return true;
}
-euler211();
+divisorSquareSum();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
index 901bbbc3d1..0a48b57aaf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff53
-title: 'Problem 212: Combined Volume of Cuboids'
+title: 'Problema 212: Volume combinado de cuboides'
challengeType: 5
forumTopicId: 301854
dashedName: problem-212-combined-volume-of-cuboids
@@ -8,28 +8,30 @@ dashedName: problem-212-combined-volume-of-cuboids
# --description--
-An axis-aligned cuboid, specified by parameters { (x0,y0,z0), (dx,dy,dz) }, consists of all points (X,Y,Z) such that x0 ≤ X ≤ x0+dx, y0 ≤ Y ≤ y0+dy and z0 ≤ Z ≤ z0+dz. The volume of the cuboid is the product, dx × dy × dz. The combined volume of a collection of cuboids is the volume of their union and will be less than the sum of the individual volumes if any cuboids overlap.
+Um cuboide alinhado em seus eixos, especificado pelos parâmetros $\{ (x_0,y_0,z_0), (dx,dy,dz) \}$, consiste em todos os pontos ($X$,$Y$,$Z$), de modo que $x_0 ≤ X ≤ x_0 + dx$, $y_0 ≤ Y ≤ y_0 + dy$ e $z_0 ≤ Z ≤ z_0 + dz$. O volume do cuboide é o produto, $dx × dy × dz$. O volume combinado de uma coleção de cuboides é o volume da sua união e será inferior à soma dos volumes individuais se houver sobreposição de qualquer um dos cuboides.
-Let C1,...,C50000 be a collection of 50000 axis-aligned cuboids such that Cn has parameters
+Considere $C_1, \ldots, C_{50000}$ como sendo uma coleção de 50.000 cuboides alinhados em seus eixos, de modo que $C_n$ tenha parâmetros
-x0 = S6n-5 modulo 10000y0 = S6n-4 modulo 10000z0 = S6n-3 modulo 10000dx = 1 + (S6n-2 modulo 399)dy = 1 + (S6n-1 modulo 399)dz = 1 + (S6n modulo 399)
+$$\begin{align} & x_0 = S_{6n - 5} \\; \text{modulo} \\; 10000 \\\\ & y_0 = S_{6n - 4} \\; \text{modulo} \\; 10000 \\\\ & z_0 = S_{6n - 3} \\; \text{modulo} \\; 10000 \\\\ & dx = 1 + (S_{6n - 2} \\; \text{modulo} \\; 399) \\\\ & dy = 1 + (S_{6n - 1} \\; \text{modulo} \\; 399) \\\\ & dz = 1 + (S_{6n} \\; \text{modulo} \\; 399) \\\\ \end{align}$$
-where S1,...,S300000 come from the "Lagged Fibonacci Generator":
+onde $S_1, \ldots, S_{300000}$ vem do "Gerador Fibonacci com atraso":
-For 1 ≤ k ≤ 55, Sk = \[100003 - 200003k + 300007k3] (modulo 1000000)For 56 ≤ k, Sk = \[Sk-24 + Sk-55] (modulo 1000000)
+Para $1 ≤ k ≤ 55$, $S_k = [100003 - 200003k + 300007k^3] \\; (modulo \\; 1000000)$
-Thus, C1 has parameters {(7,53,183),(94,369,56)}, C2 has parameters {(2383,3563,5079),(42,212,344)}, and so on.
+Para $56 ≤ k$, $S_k = [S_{k - 24} + S_{k - 55}] \\; (modulo \\; 1000000)$
-The combined volume of the first 100 cuboids, C1,...,C100, is 723581599.
+Assim, $C_1$ tem parâmetros $\{(7,53,183), (94,369,56)\}$, $C_2$ tem parâmetros $\{(2383,3563,5079), (42,212,344)\}$ e assim por diante.
-What is the combined volume of all 50000 cuboids, C1,...,C50000 ?
+O volume combinado dos primeiros 100 cuboides, $C_1, \ldots, C_{100}$, é 723581599.
+
+Qual é o volume combinado de todos os 50000 cuboides, $C_1, \ldots, C_{50000}$?
# --hints--
-`euler212()` should return 328968937309.
+`combinedValueOfCuboids()` deve retornar `328968937309`.
```js
-assert.strictEqual(euler212(), 328968937309);
+assert.strictEqual(combinedValueOfCuboids(), 328968937309);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler212(), 328968937309);
## --seed-contents--
```js
-function euler212() {
+function combinedValueOfCuboids() {
return true;
}
-euler212();
+combinedValueOfCuboids();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
index 2fbc23393c..92200998a2 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff54
-title: 'Problem 213: Flea Circus'
+title: 'Problema 213: Circo de pulgas'
challengeType: 5
forumTopicId: 301855
dashedName: problem-213-flea-circus
@@ -8,18 +8,18 @@ dashedName: problem-213-flea-circus
# --description--
-A 30×30 grid of squares contains 900 fleas, initially one flea per square.
+Uma grade de 30×30 quadrados contém 900 pulgas, inicialmente uma pulga por quadrado.
-When a bell is rung, each flea jumps to an adjacent square at random (usually 4 possibilities, except for fleas on the edge of the grid or at the corners).
+Quando uma campainha é tocada, cada pulga salta para um quadrado adjacente aleatoriamente (geralmente 4 possibilidades, exceto para as pulgas nas bordas da grade ou nos cantos).
-What is the expected number of unoccupied squares after 50 rings of the bell? Give your answer rounded to six decimal places.
+Qual é o número esperado de quadrados desocupados após 50 toques da campainha? Dê sua resposta arredondada para seis casas decimais.
# --hints--
-`euler213()` should return 330.721154.
+`fleaCircus()` deve retornar `330.721154`.
```js
-assert.strictEqual(euler213(), 330.721154);
+assert.strictEqual(fleaCircus(), 330.721154);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler213(), 330.721154);
## --seed-contents--
```js
-function euler213() {
+function fleaCircus() {
return true;
}
-euler213();
+fleaCircus();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
index 754596cef6..9675f70327 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
@@ -1,6 +1,6 @@
---
id: 5900f4421000cf542c50ff55
-title: 'Problem 214: Totient Chains'
+title: 'Problema 214: Cadeias de totientes'
challengeType: 5
forumTopicId: 301856
dashedName: problem-214-totient-chains
@@ -8,24 +8,22 @@ dashedName: problem-214-totient-chains
# --description--
-Let φ be Euler's totient function, i.e. for a natural number n,
+Considere $φ$ como sendo a função totiente de Euler, ou seja, para um número natural $n$, $φ(n)$ é o número de $k$, $1 ≤ k ≤ n$, para os quais o máximo divisor comum é $gcd(k,n) = 1$.
-φ(n) is the number of k, 1 ≤ k ≤ n, for which gcd(k,n) = 1.
+Ao iterar por $φ$, cada número inteiro positivo gera uma cadeia decrescente de números terminando em 1. Ex: se começarmos com 5 a sequência 5,4,2,1 é gerada. Aqui está uma lista de todas as cadeias com comprimento 4:
-By iterating φ, each positive integer generates a decreasing chain of numbers ending in 1. E.g. if we start with 5 the sequence 5,4,2,1 is generated. Here is a listing of all chains with length 4:
+$$\begin{align} 5,4,2,1 & \\\\ 7,6,2,1 & \\\\ 8,4,2,1 & \\\\ 9,6,2,1 & \\\\ 10,4,2,1 & \\\\ 12,4,2,1 & \\\\ 14,6,2,1 & \\\\ 18,6,2,1 & \end{align}$$
-5,4,2,1 7,6,2,1 8,4,2,1 9,6,2,1 10,4,2,1 12,4,2,1 14,6,2,1 18,6,2,1
+Apenas duas dessas cadeias começam com um número primo e sua soma é 12.
-Only two of these chains start with a prime, their sum is 12.
-
-What is the sum of all primes less than 40000000 which generate a chain of length 25?
+Qual é a soma de todos os números primos menores do que $40.000.000$ que gera uma cadeia de comprimento 25?
# --hints--
-`euler214()` should return 1677366278943.
+`totientChains()` deve retornar `1677366278943`.
```js
-assert.strictEqual(euler214(), 1677366278943);
+assert.strictEqual(totientChains(), 1677366278943);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler214(), 1677366278943);
## --seed-contents--
```js
-function euler214() {
+function totientChains() {
return true;
}
-euler214();
+totientChains();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
index 45f7f563e7..99a6eb9baf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
@@ -1,6 +1,6 @@
---
id: 5900f4431000cf542c50ff56
-title: 'Problem 215: Crack-free Walls'
+title: 'Problema 215: Paredes sem rachaduras'
challengeType: 5
forumTopicId: 301857
dashedName: problem-215-crack-free-walls
@@ -8,20 +8,22 @@ dashedName: problem-215-crack-free-walls
# --description--
-Consider the problem of building a wall out of 2×1 and 3×1 bricks (horizontal×vertical dimensions) such that, for extra strength, the gaps between horizontally-adjacent bricks never line up in consecutive layers, i.e. never form a "running crack".
+Considere o problema da construção de uma parede de 2×1 e 3×1 tijolos (dimensões verticais × horizontais), de modo que, para ter uma força extra, as lacunas entre os blocos adjacentes horizontalmente nunca se alinham em camadas consecutivas, ou seja, nunca formam uma "rachadura".
-For example, the following 9×3 wall is not acceptable due to the running crack shown in red:
+Por exemplo, a parede 9×3 a seguir não é aceitável devido à rachadura da execução mostrada em vermelho:
-There are eight ways of forming a crack-free 9×3 wall, written W(9,3) = 8.
+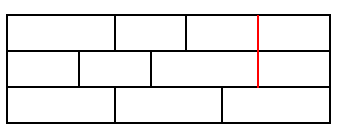 -Calculate W(32,10).
+Existem oito maneiras de formar uma parede 9×3 sem rachaduras, as quais descrevemos como $W(9,3) = 8$.
+
+Calcule $W(32,10)$.
# --hints--
-`euler215()` should return 806844323190414.
+`crackFreeWalls()` deve retornar `806844323190414`.
```js
-assert.strictEqual(euler215(), 806844323190414);
+assert.strictEqual(crackFreeWalls(), 806844323190414);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler215(), 806844323190414);
## --seed-contents--
```js
-function euler215() {
+function crackFreeWalls() {
return true;
}
-euler215();
+crackFreeWalls();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
index e7591cd46f..3a71653636 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
@@ -1,6 +1,6 @@
---
id: 5900f4451000cf542c50ff57
-title: 'Problem 216: Investigating the primality of numbers of the form 2n2-1'
+title: 'Problema 216: Investigação da primalidade dos números da forma 2n2-1'
challengeType: 5
forumTopicId: 301858
dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
@@ -8,22 +8,22 @@ dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
# --description--
-Consider numbers t(n) of the form t(n) = 2n2-1 with n > 1.
+Considere os números $t(n)$ da forma $t(n) = 2n^2 - 1$, sendo $n > 1$.
-The first such numbers are 7, 17, 31, 49, 71, 97, 127 and 161.
+Os primeiros desses números são 7, 17, 31, 49, 71, 97, 127 e 161.
-It turns out that only 49 = 7\*7 and 161 = 7\*23 are not prime.
+Ocorre que apenas $49 = 7 \times 7$ e $161 = 7 \times 23$ dentre esses não são números primos.
-For n ≤ 10000 there are 2202 numbers t(n) that are prime.
+Para $n ≤ 10000$, há 2202 números $t(n)$ que são primos.
-How many numbers t(n) are prime for n ≤ 50,000,000 ?
+Quantos números $t(n)$ são primos para $n ≤ 50.000.000$?
# --hints--
-`euler216()` should return 5437849.
+`primalityOfNumbers()` deve retornar `5437849`.
```js
-assert.strictEqual(euler216(), 5437849);
+assert.strictEqual(primalityOfNumbers(), 5437849);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler216(), 5437849);
## --seed-contents--
```js
-function euler216() {
+function primalityOfNumbers() {
return true;
}
-euler216();
+primalityOfNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
index 625b4a6c6d..44b7af79d1 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff58
-title: 'Problem 217: Balanced Numbers'
+title: 'Problema 217: Números balanceados'
challengeType: 5
forumTopicId: 301859
dashedName: problem-217-balanced-numbers
@@ -8,22 +8,22 @@ dashedName: problem-217-balanced-numbers
# --description--
-A positive integer with k (decimal) digits is called balanced if its first ⌈k/2⌉ digits sum to the same value as its last ⌈k/2⌉ digits, where ⌈x⌉, pronounced ceiling of x, is the smallest integer ≥ x, thus ⌈π⌉ = 4 and ⌈5⌉ = 5.
+Um número inteiro positivo com $k$ casas (decimais) é chamado de balanceado se os seus primeiros $⌈\frac{k}{2}⌉$ algarismos têm a soma igual aos seus últimos $⌈\frac{k}{2}⌉$ algarismos, onde $⌈x⌉$, o teto pronunciado de $x$, é o menor inteiro, sendo $≥ x$, portanto $⌈π⌉ = 4$ e $⌈5⌉ = 5$.
-So, for example, all palindromes are balanced, as is 13722.
+Então, por exemplo, todos os palíndromos são balanceados, assim como 13722.
-Let T(n) be the sum of all balanced numbers less than 10n.
+Considere $T(n)$ como sendo a soma de todos os números balanceados menores que $10^n$.
-Thus: T(1) = 45, T(2) = 540 and T(5) = 334795890.
+Assim: $T(1) = 45$, $T(2) = 540$ e $T(5) = 334.795.890$.
-Find T(47) mod 315
+Encontre $T(47)\\,mod\\,3^{15}$
# --hints--
-`euler217()` should return 6273134.
+`balancedNumbers()` deve retornar `6273134`.
```js
-assert.strictEqual(euler217(), 6273134);
+assert.strictEqual(balancedNumbers(), 6273134);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler217(), 6273134);
## --seed-contents--
```js
-function euler217() {
+function balancedNumbers() {
return true;
}
-euler217();
+balancedNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
index db91d74874..2e1df0ab68 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff59
-title: 'Problem 218: Perfect right-angled triangles'
+title: 'Problema 218: Triângulos retos perfeitos'
challengeType: 5
forumTopicId: 301860
dashedName: problem-218-perfect-right-angled-triangles
@@ -8,26 +8,32 @@ dashedName: problem-218-perfect-right-angled-triangles
# --description--
-Consider the right angled triangle with sides a=7, b=24 and c=25.
+Considere o triângulo reto com lados $a=7$, $b=24$ e $c=25$.
-The area of this triangle is 84, which is divisible by the perfect numbers 6 and 28.
+A área deste triângulo é 84, que é divisível pelos números perfeitos 6 e 28.
-Moreover it is a primitive right angled triangle as gcd(a,b)=1 and gcd(b,c)=1.
+Além disso, ele é um triângulo reto primitivo, já que tem os maiores divisores comuns $gcd(a,b) = 1$ e $gcd(b,c) = 1$.
-Also c is a perfect square.
+Por fim, $c$ é um quadrado perfeito.
-We will call a right angled triangle perfect if -it is a primitive right angled triangle -its hypotenuse is a perfect square
+Chamaremos um triângulo de triângulo reto perfeito se:
-We will call a right angled triangle super-perfect if -it is a perfect right angled triangle and -its area is a multiple of the perfect numbers 6 and 28.
+- for um triângulo reto primitivo
+- sua hipotenusa for um quadrado perfeito
-How many perfect right-angled triangles with c≤1016 exist that are not super-perfect?
+Chamaremos um triângulo de triângulo reto superperfeito se:
+
+- for um triângulo reto perfeito
+- sua área for um múltiplo dos números perfeitos 6 e 28.
+
+Quantos triângulos retos perfeitos com $c ≤ {10}^{16}$ existem que não são superperfeitos?
# --hints--
-`euler218()` should return 0.
+`perfectRightAngledTriangles()` deve retornar `0`.
```js
-assert.strictEqual(euler218(), 0);
+assert.strictEqual(perfectRightAngledTriangles(), 0);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler218(), 0);
## --seed-contents--
```js
-function euler218() {
+function perfectRightAngledTriangles() {
return true;
}
-euler218();
+perfectRightAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
index 38d16eba87..92b02718d5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5a
-title: 'Problem 219: Skew-cost coding'
+title: 'Problema 219: Codificação de custo modificado'
challengeType: 5
forumTopicId: 301861
dashedName: problem-219-skew-cost-coding
@@ -8,26 +8,26 @@ dashedName: problem-219-skew-cost-coding
# --description--
-Let A and B be bit strings (sequences of 0's and 1's).
+Considere $A$ e $B$ como sendo strings de bits (sequências de 0s e 1s).
-If A is equal to the leftmost length(A) bits of B, then A is said to be a prefix of B.
+Se $A$ for igual ao bits comprimento ($A$) mais à esquerda de $B$, então $A$ é pode ser considerado um prefixo de $B$.
-For example, 00110 is a prefix of 001101001, but not of 00111 or 100110.
+Por exemplo, 00110 é um prefixo de 001101001, mas não de 00111 ou 100110.
-A prefix-free code of size n is a collection of n distinct bit strings such that no string is a prefix of any other. For example, this is a prefix-free code of size 6:
+Um código de tamanho $n$ sem prefixo é uma coleção de $n$ strings de bits distintos, de modo que nenhuma string é um prefixo de outra. Por exemplo, este é um código de tamanho 6 sem prefixos:
-0000, 0001, 001, 01, 10, 11
+$$0000, 0001, 001, 01, 10, 11$$
-Now suppose that it costs one penny to transmit a '0' bit, but four pence to transmit a '1'. Then the total cost of the prefix-free code shown above is 35 pence, which happens to be the cheapest possible for the skewed pricing scheme in question. In short, we write Cost(6) = 35.
+Suponhamos agora que custa um centavo transmitir um bit "0", mas quatro centavos transmitir um bit "1". Então, o custo total do código sem o prefixo mostrado acima é de 35 centavos, que é o mais barato possível para o regime de preços modificados em questão. Em resumo, escrevemos $Cost(6) = 35$.
-What is Cost(109) ?
+Qual é o $Cost(10^9)$?
# --hints--
-`euler219()` should return 64564225042.
+`skewCostCoding()` deve retornar `64564225042`.
```js
-assert.strictEqual(euler219(), 64564225042);
+assert.strictEqual(skewCostCoding(), 64564225042);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler219(), 64564225042);
## --seed-contents--
```js
-function euler219() {
+function skewCostCoding() {
return true;
}
-euler219();
+skewCostCoding();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
index 1fccaef107..1f7114f3bd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5b
-title: 'Problem 220: Heighway Dragon'
+title: 'Problema 220: Dragão de Heighway'
challengeType: 5
forumTopicId: 301863
dashedName: problem-220-heighway-dragon
@@ -8,24 +8,33 @@ dashedName: problem-220-heighway-dragon
# --description--
-Let D0 be the two-letter string "Fa". For n≥1, derive Dn from Dn-1 by the string-rewriting rules:
+Considere $D_0$ como sendo a string de duas letras "Fa". Para $n ≥ 1$, derive $D_n$ de $D_{n - 1}$ pelas regras de reescrita da string:
-"a" → "aRbFR" "b" → "LFaLb"
+- "a" → "aRbFR"
+- "b" → "LFaLb"
-Thus, D0 = "Fa", D1 = "FaRbFR", D2 = "FaRbFRRLFaLbFR", and so on.
+Assim, $D_0$ = "Fa", $D_1$ = "FaRbFR", $D_2$ = "FaRbFRRLFaLbFR" e assim por diante.
-These strings can be interpreted as instructions to a computer graphics program, with "F" meaning "draw forward one unit", "L" meaning "turn left 90 degrees", "R" meaning "turn right 90 degrees", and "a" and "b" being ignored. The initial position of the computer cursor is (0,0), pointing up towards (0,1).
+Essas strings podem ser interpretadas como instruções para um programa gráfico do computador, com "F" significando "desenhar uma unidade", "L" significando "virar 90 graus à esquerda", "R" significando "virar 90 graus à direita " e "a" e "b" sendo ignorados. A posição inicial do cursor do computador é (0,0), apontando na direção de (0,1).
-Then Dn is an exotic drawing known as the Heighway Dragon of order n. For example, D10 is shown below; counting each "F" as one step, the highlighted spot at (18,16) is the position reached after 500 steps.
+Então $D_n$ é um desenho exótico conhecido como Dragão de Heighway da ordem $n$. Por exemplo, $D_{10}$ é mostrado abaixo. Contando cada "F" como uma etapa, o local destacado em (18,16) é a posição alcançada após 500 etapas.
-What is the position of the cursor after 1012 steps in D50 ? Give your answer in the form x,y with no spaces.
+
-Calculate W(32,10).
+Existem oito maneiras de formar uma parede 9×3 sem rachaduras, as quais descrevemos como $W(9,3) = 8$.
+
+Calcule $W(32,10)$.
# --hints--
-`euler215()` should return 806844323190414.
+`crackFreeWalls()` deve retornar `806844323190414`.
```js
-assert.strictEqual(euler215(), 806844323190414);
+assert.strictEqual(crackFreeWalls(), 806844323190414);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler215(), 806844323190414);
## --seed-contents--
```js
-function euler215() {
+function crackFreeWalls() {
return true;
}
-euler215();
+crackFreeWalls();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
index e7591cd46f..3a71653636 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
@@ -1,6 +1,6 @@
---
id: 5900f4451000cf542c50ff57
-title: 'Problem 216: Investigating the primality of numbers of the form 2n2-1'
+title: 'Problema 216: Investigação da primalidade dos números da forma 2n2-1'
challengeType: 5
forumTopicId: 301858
dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
@@ -8,22 +8,22 @@ dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
# --description--
-Consider numbers t(n) of the form t(n) = 2n2-1 with n > 1.
+Considere os números $t(n)$ da forma $t(n) = 2n^2 - 1$, sendo $n > 1$.
-The first such numbers are 7, 17, 31, 49, 71, 97, 127 and 161.
+Os primeiros desses números são 7, 17, 31, 49, 71, 97, 127 e 161.
-It turns out that only 49 = 7\*7 and 161 = 7\*23 are not prime.
+Ocorre que apenas $49 = 7 \times 7$ e $161 = 7 \times 23$ dentre esses não são números primos.
-For n ≤ 10000 there are 2202 numbers t(n) that are prime.
+Para $n ≤ 10000$, há 2202 números $t(n)$ que são primos.
-How many numbers t(n) are prime for n ≤ 50,000,000 ?
+Quantos números $t(n)$ são primos para $n ≤ 50.000.000$?
# --hints--
-`euler216()` should return 5437849.
+`primalityOfNumbers()` deve retornar `5437849`.
```js
-assert.strictEqual(euler216(), 5437849);
+assert.strictEqual(primalityOfNumbers(), 5437849);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler216(), 5437849);
## --seed-contents--
```js
-function euler216() {
+function primalityOfNumbers() {
return true;
}
-euler216();
+primalityOfNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
index 625b4a6c6d..44b7af79d1 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff58
-title: 'Problem 217: Balanced Numbers'
+title: 'Problema 217: Números balanceados'
challengeType: 5
forumTopicId: 301859
dashedName: problem-217-balanced-numbers
@@ -8,22 +8,22 @@ dashedName: problem-217-balanced-numbers
# --description--
-A positive integer with k (decimal) digits is called balanced if its first ⌈k/2⌉ digits sum to the same value as its last ⌈k/2⌉ digits, where ⌈x⌉, pronounced ceiling of x, is the smallest integer ≥ x, thus ⌈π⌉ = 4 and ⌈5⌉ = 5.
+Um número inteiro positivo com $k$ casas (decimais) é chamado de balanceado se os seus primeiros $⌈\frac{k}{2}⌉$ algarismos têm a soma igual aos seus últimos $⌈\frac{k}{2}⌉$ algarismos, onde $⌈x⌉$, o teto pronunciado de $x$, é o menor inteiro, sendo $≥ x$, portanto $⌈π⌉ = 4$ e $⌈5⌉ = 5$.
-So, for example, all palindromes are balanced, as is 13722.
+Então, por exemplo, todos os palíndromos são balanceados, assim como 13722.
-Let T(n) be the sum of all balanced numbers less than 10n.
+Considere $T(n)$ como sendo a soma de todos os números balanceados menores que $10^n$.
-Thus: T(1) = 45, T(2) = 540 and T(5) = 334795890.
+Assim: $T(1) = 45$, $T(2) = 540$ e $T(5) = 334.795.890$.
-Find T(47) mod 315
+Encontre $T(47)\\,mod\\,3^{15}$
# --hints--
-`euler217()` should return 6273134.
+`balancedNumbers()` deve retornar `6273134`.
```js
-assert.strictEqual(euler217(), 6273134);
+assert.strictEqual(balancedNumbers(), 6273134);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler217(), 6273134);
## --seed-contents--
```js
-function euler217() {
+function balancedNumbers() {
return true;
}
-euler217();
+balancedNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
index db91d74874..2e1df0ab68 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff59
-title: 'Problem 218: Perfect right-angled triangles'
+title: 'Problema 218: Triângulos retos perfeitos'
challengeType: 5
forumTopicId: 301860
dashedName: problem-218-perfect-right-angled-triangles
@@ -8,26 +8,32 @@ dashedName: problem-218-perfect-right-angled-triangles
# --description--
-Consider the right angled triangle with sides a=7, b=24 and c=25.
+Considere o triângulo reto com lados $a=7$, $b=24$ e $c=25$.
-The area of this triangle is 84, which is divisible by the perfect numbers 6 and 28.
+A área deste triângulo é 84, que é divisível pelos números perfeitos 6 e 28.
-Moreover it is a primitive right angled triangle as gcd(a,b)=1 and gcd(b,c)=1.
+Além disso, ele é um triângulo reto primitivo, já que tem os maiores divisores comuns $gcd(a,b) = 1$ e $gcd(b,c) = 1$.
-Also c is a perfect square.
+Por fim, $c$ é um quadrado perfeito.
-We will call a right angled triangle perfect if -it is a primitive right angled triangle -its hypotenuse is a perfect square
+Chamaremos um triângulo de triângulo reto perfeito se:
-We will call a right angled triangle super-perfect if -it is a perfect right angled triangle and -its area is a multiple of the perfect numbers 6 and 28.
+- for um triângulo reto primitivo
+- sua hipotenusa for um quadrado perfeito
-How many perfect right-angled triangles with c≤1016 exist that are not super-perfect?
+Chamaremos um triângulo de triângulo reto superperfeito se:
+
+- for um triângulo reto perfeito
+- sua área for um múltiplo dos números perfeitos 6 e 28.
+
+Quantos triângulos retos perfeitos com $c ≤ {10}^{16}$ existem que não são superperfeitos?
# --hints--
-`euler218()` should return 0.
+`perfectRightAngledTriangles()` deve retornar `0`.
```js
-assert.strictEqual(euler218(), 0);
+assert.strictEqual(perfectRightAngledTriangles(), 0);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler218(), 0);
## --seed-contents--
```js
-function euler218() {
+function perfectRightAngledTriangles() {
return true;
}
-euler218();
+perfectRightAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
index 38d16eba87..92b02718d5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5a
-title: 'Problem 219: Skew-cost coding'
+title: 'Problema 219: Codificação de custo modificado'
challengeType: 5
forumTopicId: 301861
dashedName: problem-219-skew-cost-coding
@@ -8,26 +8,26 @@ dashedName: problem-219-skew-cost-coding
# --description--
-Let A and B be bit strings (sequences of 0's and 1's).
+Considere $A$ e $B$ como sendo strings de bits (sequências de 0s e 1s).
-If A is equal to the leftmost length(A) bits of B, then A is said to be a prefix of B.
+Se $A$ for igual ao bits comprimento ($A$) mais à esquerda de $B$, então $A$ é pode ser considerado um prefixo de $B$.
-For example, 00110 is a prefix of 001101001, but not of 00111 or 100110.
+Por exemplo, 00110 é um prefixo de 001101001, mas não de 00111 ou 100110.
-A prefix-free code of size n is a collection of n distinct bit strings such that no string is a prefix of any other. For example, this is a prefix-free code of size 6:
+Um código de tamanho $n$ sem prefixo é uma coleção de $n$ strings de bits distintos, de modo que nenhuma string é um prefixo de outra. Por exemplo, este é um código de tamanho 6 sem prefixos:
-0000, 0001, 001, 01, 10, 11
+$$0000, 0001, 001, 01, 10, 11$$
-Now suppose that it costs one penny to transmit a '0' bit, but four pence to transmit a '1'. Then the total cost of the prefix-free code shown above is 35 pence, which happens to be the cheapest possible for the skewed pricing scheme in question. In short, we write Cost(6) = 35.
+Suponhamos agora que custa um centavo transmitir um bit "0", mas quatro centavos transmitir um bit "1". Então, o custo total do código sem o prefixo mostrado acima é de 35 centavos, que é o mais barato possível para o regime de preços modificados em questão. Em resumo, escrevemos $Cost(6) = 35$.
-What is Cost(109) ?
+Qual é o $Cost(10^9)$?
# --hints--
-`euler219()` should return 64564225042.
+`skewCostCoding()` deve retornar `64564225042`.
```js
-assert.strictEqual(euler219(), 64564225042);
+assert.strictEqual(skewCostCoding(), 64564225042);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler219(), 64564225042);
## --seed-contents--
```js
-function euler219() {
+function skewCostCoding() {
return true;
}
-euler219();
+skewCostCoding();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
index 1fccaef107..1f7114f3bd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5b
-title: 'Problem 220: Heighway Dragon'
+title: 'Problema 220: Dragão de Heighway'
challengeType: 5
forumTopicId: 301863
dashedName: problem-220-heighway-dragon
@@ -8,24 +8,33 @@ dashedName: problem-220-heighway-dragon
# --description--
-Let D0 be the two-letter string "Fa". For n≥1, derive Dn from Dn-1 by the string-rewriting rules:
+Considere $D_0$ como sendo a string de duas letras "Fa". Para $n ≥ 1$, derive $D_n$ de $D_{n - 1}$ pelas regras de reescrita da string:
-"a" → "aRbFR" "b" → "LFaLb"
+- "a" → "aRbFR"
+- "b" → "LFaLb"
-Thus, D0 = "Fa", D1 = "FaRbFR", D2 = "FaRbFRRLFaLbFR", and so on.
+Assim, $D_0$ = "Fa", $D_1$ = "FaRbFR", $D_2$ = "FaRbFRRLFaLbFR" e assim por diante.
-These strings can be interpreted as instructions to a computer graphics program, with "F" meaning "draw forward one unit", "L" meaning "turn left 90 degrees", "R" meaning "turn right 90 degrees", and "a" and "b" being ignored. The initial position of the computer cursor is (0,0), pointing up towards (0,1).
+Essas strings podem ser interpretadas como instruções para um programa gráfico do computador, com "F" significando "desenhar uma unidade", "L" significando "virar 90 graus à esquerda", "R" significando "virar 90 graus à direita " e "a" e "b" sendo ignorados. A posição inicial do cursor do computador é (0,0), apontando na direção de (0,1).
-Then Dn is an exotic drawing known as the Heighway Dragon of order n. For example, D10 is shown below; counting each "F" as one step, the highlighted spot at (18,16) is the position reached after 500 steps.
+Então $D_n$ é um desenho exótico conhecido como Dragão de Heighway da ordem $n$. Por exemplo, $D_{10}$ é mostrado abaixo. Contando cada "F" como uma etapa, o local destacado em (18,16) é a posição alcançada após 500 etapas.
-What is the position of the cursor after 1012 steps in D50 ? Give your answer in the form x,y with no spaces.
+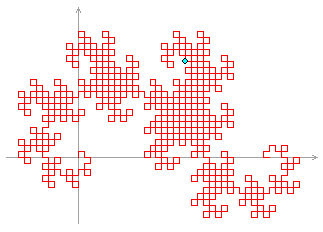 +
+Qual é a posição do cursor depois de ${10}^{12}$ etapas em $D_{50}$? Dê sua resposta como uma string na forma `x,y` sem espaços.
# --hints--
-`euler220()` should return 139776, 963904.
+`heighwayDragon()` deve retornar uma string.
```js
-assert.strictEqual(euler220(), 139776, 963904);
+assert(typeof heighwayDragon() === 'string');
+```
+
+`heighwayDragon()` deve retornar a string `139776,963904`.
+
+```js
+assert.strictEqual(heighwayDragon(), '139776,963904');
```
# --seed--
@@ -33,12 +42,12 @@ assert.strictEqual(euler220(), 139776, 963904);
## --seed-contents--
```js
-function euler220() {
+function heighwayDragon() {
return true;
}
-euler220();
+heighwayDragon();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
index 260f8c73a0..27e78a6ac5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
@@ -12,7 +12,7 @@ Considere os triângulos com os lados inteiros $a$, $b$ e $c$ com $a ≤ b ≤ c
Um triângulo que tem seus lados sendo números inteiros $(a,b,c)$ é chamado primitivo se $gcd(a,b,c) = 1$.
-Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10\\,000\\,000$?
+Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10.000.000$?
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
index b1538fd20d..f01a6615b9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
@@ -8,7 +8,7 @@ dashedName: problem-34-digit-factorials
# --description--
-145 é um número curioso, pois 1! + 4! + 5! = 1 + 24 + 120 = 145.
+145 é um número curioso, já que 1! + 4! + 5! = 1 + 24 + 120 = 145.
Calcule os números e a soma dos números que são iguais à soma do fatorial de seus dígitos.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
index cf4cbb03f0..c8c70165cd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
@@ -12,7 +12,7 @@ Na parábola $y = \frac{x^2}{k}$, três pontos $A(a, \frac{a^2}{k})$, $B(b, \fra
Considere que $F(K, X)$ é o número de quadras de inteiros $(k, a, b, c)$, de tal forma que pelo menos um ângulo do triângulo $ABC$ é 45°, com $1 ≤ k ≤ K$ e $-X ≤ a < b < c ≤ X$.
-Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12\\,492$.
+Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12.492$.
Encontre $F({10}^6, {10}^9)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
index ab71c30048..99daff2390 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
@@ -14,7 +14,7 @@ Um exemplo de um conjunto titânico é $S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (
Por outro lado, o conjunto {(0, 0), (1, 1), (2, 2), (4, 4)} não é um conjunto titânico, já que a linha que passa por dois pontos quaisquer no conjunto também passa pelos outros dois.
-Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$ e $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$.
+Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33.554.178$, $T(111)\bmod {10}^8 = 13.500.401$ e $T({10}^5)\bmod {10}^8 = 63.259.062$.
Encontre $T({10}^{11})\bmod {10}^8$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
index a3475fd12d..f6675060dd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
@@ -12,7 +12,7 @@ Uma fileira de $n$ quadrados contém um sapo no quadrado mais à esquerda. Em su
Considere que $F(m, n)$ é o número de maneiras pelas quais o sapo pode viajar, sendo que, no máximo, um quadrado pode permanecer sem ser visitado.
-Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$.
+Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429.619.151$.
Encontre os últimos 9 dígitos de $F(10, {10}^{12})$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
index 636f277786..aa2fcd535b 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
@@ -16,9 +16,9 @@ A expressão $0.1(6)$ significa $0.16666666\dots$, e tem um ciclo recorrente de
Frações unitárias cujo denominador não tem outros fatores primos além de 2 e/ou 5 não são consideradas como tendo um ciclo recorrente. Definimos 0 como o comprimento do ciclo recorrente dessas frações unitárias.
-Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1\\,000\\,000$ é igual a $55\\,535\\,191\\,115$.
+Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1.000.000$ é igual a $55.535.191.115$.
-Calcule $\sum L(n)$ por $3 ≤ n ≤ 100\\,000\\,000$.
+Calcule $\sum L(n)$ por $3 ≤ n ≤ 100.000.000$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
index c6502c485f..db2a31a52c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
@@ -15,7 +15,7 @@ Considere $n$ um inteiro positivo. Um trio de números inteiros ($a$, $b$, $c$)
Defina $f(n)$ como $a + b + c$ para o trio da fatoração ($a$, $b$, $c$) de $n$ que minimiza $\frac{c}{a}$. Podemos mostrar que esse trio é único.
-Por exemplo, $f(165) = 19$, $f(100\\,100) = 142$ e $f(20!) = 4\\,034\\,872$.
+Por exemplo, $f(165) = 19$, $f(100.100) = 142$ e $f(20!) = 4.034.872$.
Encontre $f(43!)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
index 4adbf773f9..f71d42c2d9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
@@ -26,7 +26,7 @@ Ajuda ler os dígitos em voz alta:
...
-Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31\\,254$, $B(40) = 20\\,259$ e $C(40) = 11\\,625$.
+Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31.254$, $B(40) = 20.259$ e $C(40) = 11.625$.
Calcule $A(n)$, $B(n)$ e $C(n)$ para $n = {10}^{12}$. Dê o modulo $2^{30}$ de sua respostas como uma string e separe seus valores para $A$, $B$ e $C$ por uma vírgula. Ex: para $n = 40$, a resposta seria `31254,20259,11625`.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
index 1af6f12cbf..36638c3847 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
@@ -18,9 +18,9 @@ Considere $C(n)$ o número de triângulos cujos vértices estão em $P_n$ e que
Exemplos:
-$$\start{align} & C(8) = 20 \\\\ & C(600) = 8\\,950\\,634 \\\\ & C(40\\,000) = 2\\,66610\\,948\\,988 \end{align}$$
+$$\start{align} & C(8) = 20 \\\\ & C(600) = 8.950.634 \\\\ & C(40.000) = 266.610.948.988 \end{align}$$
-Encontre $C(2\\,000\\,000)$.
+Encontre $C(2.000.000)$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
index a895ff2632..5f50265cae 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
@@ -1,6 +1,6 @@
---
id: 5900f3b21000cf542c50fec5
-title: 'Problema 70: Permutações Totiente'
+title: 'Problema 70: Permutações de totientes'
challengeType: 5
forumTopicId: 302183
dashedName: problem-70-totient-permutation
@@ -8,7 +8,7 @@ dashedName: problem-70-totient-permutation
# --description--
-A função Totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
+A função totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
Curiosamente, ${\phi}(87109) = 79180$, e pode ser visto que 87109 é uma permutação de 79180.
+
+Qual é a posição do cursor depois de ${10}^{12}$ etapas em $D_{50}$? Dê sua resposta como uma string na forma `x,y` sem espaços.
# --hints--
-`euler220()` should return 139776, 963904.
+`heighwayDragon()` deve retornar uma string.
```js
-assert.strictEqual(euler220(), 139776, 963904);
+assert(typeof heighwayDragon() === 'string');
+```
+
+`heighwayDragon()` deve retornar a string `139776,963904`.
+
+```js
+assert.strictEqual(heighwayDragon(), '139776,963904');
```
# --seed--
@@ -33,12 +42,12 @@ assert.strictEqual(euler220(), 139776, 963904);
## --seed-contents--
```js
-function euler220() {
+function heighwayDragon() {
return true;
}
-euler220();
+heighwayDragon();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
index 260f8c73a0..27e78a6ac5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
@@ -12,7 +12,7 @@ Considere os triângulos com os lados inteiros $a$, $b$ e $c$ com $a ≤ b ≤ c
Um triângulo que tem seus lados sendo números inteiros $(a,b,c)$ é chamado primitivo se $gcd(a,b,c) = 1$.
-Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10\\,000\\,000$?
+Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10.000.000$?
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
index b1538fd20d..f01a6615b9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
@@ -8,7 +8,7 @@ dashedName: problem-34-digit-factorials
# --description--
-145 é um número curioso, pois 1! + 4! + 5! = 1 + 24 + 120 = 145.
+145 é um número curioso, já que 1! + 4! + 5! = 1 + 24 + 120 = 145.
Calcule os números e a soma dos números que são iguais à soma do fatorial de seus dígitos.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
index cf4cbb03f0..c8c70165cd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
@@ -12,7 +12,7 @@ Na parábola $y = \frac{x^2}{k}$, três pontos $A(a, \frac{a^2}{k})$, $B(b, \fra
Considere que $F(K, X)$ é o número de quadras de inteiros $(k, a, b, c)$, de tal forma que pelo menos um ângulo do triângulo $ABC$ é 45°, com $1 ≤ k ≤ K$ e $-X ≤ a < b < c ≤ X$.
-Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12\\,492$.
+Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12.492$.
Encontre $F({10}^6, {10}^9)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
index ab71c30048..99daff2390 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
@@ -14,7 +14,7 @@ Um exemplo de um conjunto titânico é $S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (
Por outro lado, o conjunto {(0, 0), (1, 1), (2, 2), (4, 4)} não é um conjunto titânico, já que a linha que passa por dois pontos quaisquer no conjunto também passa pelos outros dois.
-Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$ e $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$.
+Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33.554.178$, $T(111)\bmod {10}^8 = 13.500.401$ e $T({10}^5)\bmod {10}^8 = 63.259.062$.
Encontre $T({10}^{11})\bmod {10}^8$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
index a3475fd12d..f6675060dd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
@@ -12,7 +12,7 @@ Uma fileira de $n$ quadrados contém um sapo no quadrado mais à esquerda. Em su
Considere que $F(m, n)$ é o número de maneiras pelas quais o sapo pode viajar, sendo que, no máximo, um quadrado pode permanecer sem ser visitado.
-Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$.
+Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429.619.151$.
Encontre os últimos 9 dígitos de $F(10, {10}^{12})$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
index 636f277786..aa2fcd535b 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
@@ -16,9 +16,9 @@ A expressão $0.1(6)$ significa $0.16666666\dots$, e tem um ciclo recorrente de
Frações unitárias cujo denominador não tem outros fatores primos além de 2 e/ou 5 não são consideradas como tendo um ciclo recorrente. Definimos 0 como o comprimento do ciclo recorrente dessas frações unitárias.
-Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1\\,000\\,000$ é igual a $55\\,535\\,191\\,115$.
+Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1.000.000$ é igual a $55.535.191.115$.
-Calcule $\sum L(n)$ por $3 ≤ n ≤ 100\\,000\\,000$.
+Calcule $\sum L(n)$ por $3 ≤ n ≤ 100.000.000$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
index c6502c485f..db2a31a52c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
@@ -15,7 +15,7 @@ Considere $n$ um inteiro positivo. Um trio de números inteiros ($a$, $b$, $c$)
Defina $f(n)$ como $a + b + c$ para o trio da fatoração ($a$, $b$, $c$) de $n$ que minimiza $\frac{c}{a}$. Podemos mostrar que esse trio é único.
-Por exemplo, $f(165) = 19$, $f(100\\,100) = 142$ e $f(20!) = 4\\,034\\,872$.
+Por exemplo, $f(165) = 19$, $f(100.100) = 142$ e $f(20!) = 4.034.872$.
Encontre $f(43!)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
index 4adbf773f9..f71d42c2d9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
@@ -26,7 +26,7 @@ Ajuda ler os dígitos em voz alta:
...
-Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31\\,254$, $B(40) = 20\\,259$ e $C(40) = 11\\,625$.
+Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31.254$, $B(40) = 20.259$ e $C(40) = 11.625$.
Calcule $A(n)$, $B(n)$ e $C(n)$ para $n = {10}^{12}$. Dê o modulo $2^{30}$ de sua respostas como uma string e separe seus valores para $A$, $B$ e $C$ por uma vírgula. Ex: para $n = 40$, a resposta seria `31254,20259,11625`.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
index 1af6f12cbf..36638c3847 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
@@ -18,9 +18,9 @@ Considere $C(n)$ o número de triângulos cujos vértices estão em $P_n$ e que
Exemplos:
-$$\start{align} & C(8) = 20 \\\\ & C(600) = 8\\,950\\,634 \\\\ & C(40\\,000) = 2\\,66610\\,948\\,988 \end{align}$$
+$$\start{align} & C(8) = 20 \\\\ & C(600) = 8.950.634 \\\\ & C(40.000) = 266.610.948.988 \end{align}$$
-Encontre $C(2\\,000\\,000)$.
+Encontre $C(2.000.000)$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
index a895ff2632..5f50265cae 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
@@ -1,6 +1,6 @@
---
id: 5900f3b21000cf542c50fec5
-title: 'Problema 70: Permutações Totiente'
+title: 'Problema 70: Permutações de totientes'
challengeType: 5
forumTopicId: 302183
dashedName: problem-70-totient-permutation
@@ -8,7 +8,7 @@ dashedName: problem-70-totient-permutation
# --description--
-A função Totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
+A função totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
Curiosamente, ${\phi}(87109) = 79180$, e pode ser visto que 87109 é uma permutação de 79180.
 -In how many ways can a laser beam enter at vertex C, bounce off 12017639147 surfaces, then exit through the same vertex?
+Há 80.840 maneiras pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 1.000.001 vezes nas superfícies e depois sair pelo mesmo vértice.
+
+Quantas maneiras existem pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 12.017.639.147 vezes nas superfícies e depois sair pelo mesmo vértice?
# --hints--
-`euler202()` should return 1209002624.
+`laserbeam()` deve retornar `1209002624`.
```js
-assert.strictEqual(euler202(), 1209002624);
+assert.strictEqual(laserbeam(), 1209002624);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler202(), 1209002624);
## --seed-contents--
```js
-function euler202() {
+function laserbeam() {
return true;
}
-euler202();
+laserbeam();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
index 4ecf609e4b..1de4647282 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4a
-title: 'Problem 203: Squarefree Binomial Coefficients'
+title: 'Problema 203: Coeficientes binomiais livres de quadrados'
challengeType: 5
forumTopicId: 301844
dashedName: problem-203-squarefree-binomial-coefficients
@@ -8,22 +8,22 @@ dashedName: problem-203-squarefree-binomial-coefficients
# --description--
-The binomial coefficients nCk can be arranged in triangular form, Pascal's triangle, like this:
+Os coeficientes binomiais $\displaystyle\binom{n}{k}$ podem ser organizados em forma triangular, no triângulo de Pascal, assim:
-111121133114641151010511615201561172135352171 .........
+$$\begin{array}{ccccccccccccccc} & & & & & & & 1 & & & & & & & \\\\ & & & & & & 1 & & 1 & & & & & & \\\\ & & & & & 1 & & 2 & & 1 & & & & & \\\\ & & & & 1 & & 3 & & 3 & & 1 & & & & \\\\ & & & 1 & & 4 & & 6 & & 4 & & 1 & & & \\\\ & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 & & \\\\ & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1 & \\\\ 1 & & 7 & & 21 & & 35 & & 35 & & 21 & & 7 & & 1 \\\\ & & & & & & & \ldots \end{array}$$
-It can be seen that the first eight rows of Pascal's triangle contain twelve distinct numbers: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 and 35.
+Podemos ver que as primeiras oito linhas do triângulo de Pascal contêm doze números distintos: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 e 35.
-A positive integer n is called squarefree if no square of a prime divides n. Of the twelve distinct numbers in the first eight rows of Pascal's triangle, all except 4 and 20 are squarefree. The sum of the distinct squarefree numbers in the first eight rows is 105.
+Um número inteiro positivo n é chamado de livre de quadrados se nenhum quadrado de um número primo dividir n. Dos doze números distintos nas primeiras oito linhas do triângulo de Pascal, todos os números exceto 4 e 20 são livres de quadrados. A soma dos números distintos livres de quadrados nas primeiras oito linhas é 105.
-Find the sum of the distinct squarefree numbers in the first 51 rows of Pascal's triangle.
+Encontre a soma dos números distintos livres de quadrados nas primeiras 51 linhas do triângulo de Pascal.
# --hints--
-`euler203()` should return 34029210557338.
+`squarefreeBinomialCoefficients()` deve retornar `34029210557338`.
```js
-assert.strictEqual(euler203(), 34029210557338);
+assert.strictEqual(squarefreeBinomialCoefficients(), 34029210557338);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler203(), 34029210557338);
## --seed-contents--
```js
-function euler203() {
+function squarefreeBinomialCoefficients() {
return true;
}
-euler203();
+squarefreeBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
index 4d81e08eea..918620d1c3 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4b
-title: 'Problem 204: Generalised Hamming Numbers'
+title: 'Problema 204: Números de Hamming generalizados'
challengeType: 5
forumTopicId: 301845
dashedName: problem-204-generalised-hamming-numbers
@@ -8,22 +8,22 @@ dashedName: problem-204-generalised-hamming-numbers
# --description--
-A Hamming number is a positive number which has no prime factor larger than 5.
+Um número de Hamming é um número positivo que não tem fator primo maior que 5.
-So the first few Hamming numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
+Assim, os primeiros números de Hamming são 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 e 15.
-There are 1105 Hamming numbers not exceeding 108.
+Há 1105 números de Hamming que não excedem ${10}^8$.
-We will call a positive number a generalised Hamming number of type n, if it has no prime factor larger than n. Hence the Hamming numbers are the generalised Hamming numbers of type 5.
+Chamaremos um número positivo de número generalizado de Hamming do tipo $n$, se ele não tiver fator primo maior que $n$. Assim, os números de Hamming são os números generalizados de Hamming do tipo 5.
-How many generalised Hamming numbers of type 100 are there which don't exceed 109?
+Quantos números de Hamming generalizados do tipo 100 existem que não excedem ${10}^9$?
# --hints--
-`euler204()` should return 2944730.
+`generalisedHammingNumbers()` deve retornar `2944730`.
```js
-assert.strictEqual(euler204(), 2944730);
+assert.strictEqual(generalisedHammingNumbers(), 2944730);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler204(), 2944730);
## --seed-contents--
```js
-function euler204() {
+function generalisedHammingNumbers() {
return true;
}
-euler204();
+generalisedHammingNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
index 41bf903b6d..fc2f40557e 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4391000cf542c50ff4c
-title: 'Problem 205: Dice Game'
+title: 'Problema 205: Jogo de dados'
challengeType: 5
forumTopicId: 301846
dashedName: problem-205-dice-game
@@ -8,20 +8,20 @@ dashedName: problem-205-dice-game
# --description--
-Peter has nine four-sided (pyramidal) dice, each with faces numbered 1, 2, 3, 4.
+Pedro tem nove dados de quatro lados (piramidais), e cada uma das faces recebe um número 1, 2, 3 e 4.
-Colin has six six-sided (cubic) dice, each with faces numbered 1, 2, 3, 4, 5, 6.
+Colin tem seis dados de seis lados (cúbicos), e cada uma das fazes recebe um número 1, 2, 3, 4, 5 e 6.
-Peter and Colin roll their dice and compare totals: the highest total wins. The result is a draw if the totals are equal.
+Pedro e Colin rolam seus dados e comparam os totais: o maior total ganha. O resultado é um empate se os totais forem iguais.
-What is the probability that Pyramidal Pete beats Cubic Colin? Give your answer rounded to seven decimal places in the form 0.abcdefg
+Qual é a probabilidade que o Pedro Piramidal vencer Colin Cúbico? Arredonde sua resposta para até sete casas decimais usando o formato 0.abcdefg
# --hints--
-`euler205()` should return 0.5731441.
+`diceGame()` deve retornar `0.5731441`.
```js
-assert.strictEqual(euler205(), 0.5731441);
+assert.strictEqual(diceGame(), 0.5731441);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler205(), 0.5731441);
## --seed-contents--
```js
-function euler205() {
+function diceGame() {
return true;
}
-euler205();
+diceGame();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
index eaedced890..46e24b7b08 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
@@ -1,6 +1,6 @@
---
id: 5900f43a1000cf542c50ff4d
-title: 'Problem 206: Concealed Square'
+title: 'Problema 206: Quadrado escondido'
challengeType: 5
forumTopicId: 301847
dashedName: problem-206-concealed-square
@@ -8,14 +8,14 @@ dashedName: problem-206-concealed-square
# --description--
-Find the unique positive integer whose square has the form 1_2_3_4_5_6_7_8_9_0, where each “\_” is a single digit.
+Encontre o número inteiro positivo cujo quadrado tem o formato 1_2_3_4_5_6_7_8_9_0, onde cada "_" é um único algarismo.
# --hints--
-`euler206()` should return 1389019170.
+`concealedSquare()` deve retornar `1389019170`.
```js
-assert.strictEqual(euler206(), 1389019170);
+assert.strictEqual(concealedSquare(), 1389019170);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler206(), 1389019170);
## --seed-contents--
```js
-function euler206() {
+function concealedSquare() {
return true;
}
-euler206();
+concealedSquare();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
index 19f1d12c8d..440218de4f 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
@@ -1,6 +1,6 @@
---
id: 5900f43c1000cf542c50ff4e
-title: 'Problem 207: Integer partition equations'
+title: 'Problema 207: Equações de partições inteiras'
challengeType: 5
forumTopicId: 301848
dashedName: problem-207-integer-partition-equations
@@ -8,24 +8,28 @@ dashedName: problem-207-integer-partition-equations
# --description--
-For some positive integers k, there exists an integer partition of the form 4t = 2t + k,
+Para alguns números inteiros positivos $k$, existe uma partição inteira de forma $4^t = 2^t + k$,
-where 4t, 2t, and k are all positive integers and t is a real number.
+onde $4^t$, $2^t$ e $k$ são todos números inteiros positivos e $t$ é um número real.
-The first two such partitions are 41 = 21 + 2 and 41.5849625... = 21.5849625... + 6.
+As duas primeiras partições desse tipo são $4^1 = 2^1 + 2$ e $4^{1.584\\,962\\,5\ldots} = 2^{1.584\\,962\\,5\ldots} + 6$.
-Partitions where t is also an integer are called perfect. For any m ≥ 1 let P(m) be the proportion of such partitions that are perfect with k ≤ m. Thus P(6) = 1/2.
+As partições onde $t$ é também um número inteiro são chamadas de perfeitas. Para qualquer $m ≥ 1$, considere $P(m)$ como sendo a proporção de tais partições que são perfeitas com $k ≤ m$.
-In the following table are listed some values of P(m) P(5) = 1/1 P(10) = 1/2 P(15) = 2/3 P(20) = 1/2 P(25) = 1/2 P(30) = 2/5 ... P(180) = 1/4 P(185) = 3/13
+Assim, $P(6) = \frac{1}{2}$.
-Find the smallest m for which P(m) < 1/12345
+Na tabela a seguir estão listados alguns valores de $P(m)$
+
+$$\begin{align} & P(5) = \frac{1}{1} \\\\ & P(10) = \frac{1}{2} \\\\ & P(15) = \frac{2}{3} \\\\ & P(20) = \frac{1}{2} \\\\ & P(25) = \frac{1}{2} \\\\ & P(30) = \frac{2}{5} \\\\ & \ldots \\\\ & P(180) = \frac{1}{4} \\\\ & P(185) = \frac{3}{13} \end{align}$$
+
+Encontre o menor $m$ para o qual $P(m) < \frac{1}{12.345}$
# --hints--
-`euler207()` should return 44043947822.
+`integerPartitionEquations()` deve retornar `44043947822`.
```js
-assert.strictEqual(euler207(), 44043947822);
+assert.strictEqual(integerPartitionEquations(), 44043947822);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler207(), 44043947822);
## --seed-contents--
```js
-function euler207() {
+function integerPartitionEquations() {
return true;
}
-euler207();
+integerPartitionEquations();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
index 36d5a8fff5..6d59d5c4ff 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff51
-title: 'Problem 208: Robot Walks'
+title: 'Problema 208: Caminhadas robóticas'
challengeType: 5
forumTopicId: 301849
dashedName: problem-208-robot-walks
@@ -8,18 +8,22 @@ dashedName: problem-208-robot-walks
# --description--
-A robot moves in a series of one-fifth circular arcs (72°), with a free choice of a clockwise or an anticlockwise arc for each step, but no turning on the spot.
+Um robô se move em uma série arco circular de um quinto de volta (72°), com uma escolha livre de sentido horário ou anti-horário para cada etapa, mas sem virar no local.
-One of 70932 possible closed paths of 25 arcs starting northward is
+Um dos 70932 caminhos fechados possíveis de 25 arcos iniciando para o norte é
-Given that the robot starts facing North, how many journeys of 70 arcs in length can it take that return it, after the final arc, to its starting position? (Any arc may be traversed multiple times.)
+
-In how many ways can a laser beam enter at vertex C, bounce off 12017639147 surfaces, then exit through the same vertex?
+Há 80.840 maneiras pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 1.000.001 vezes nas superfícies e depois sair pelo mesmo vértice.
+
+Quantas maneiras existem pelas quais um raio laser pode entrar em um vértice $C$, ricochetear 12.017.639.147 vezes nas superfícies e depois sair pelo mesmo vértice?
# --hints--
-`euler202()` should return 1209002624.
+`laserbeam()` deve retornar `1209002624`.
```js
-assert.strictEqual(euler202(), 1209002624);
+assert.strictEqual(laserbeam(), 1209002624);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler202(), 1209002624);
## --seed-contents--
```js
-function euler202() {
+function laserbeam() {
return true;
}
-euler202();
+laserbeam();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
index 4ecf609e4b..1de4647282 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-203-squarefree-binomial-coefficients.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4a
-title: 'Problem 203: Squarefree Binomial Coefficients'
+title: 'Problema 203: Coeficientes binomiais livres de quadrados'
challengeType: 5
forumTopicId: 301844
dashedName: problem-203-squarefree-binomial-coefficients
@@ -8,22 +8,22 @@ dashedName: problem-203-squarefree-binomial-coefficients
# --description--
-The binomial coefficients nCk can be arranged in triangular form, Pascal's triangle, like this:
+Os coeficientes binomiais $\displaystyle\binom{n}{k}$ podem ser organizados em forma triangular, no triângulo de Pascal, assim:
-111121133114641151010511615201561172135352171 .........
+$$\begin{array}{ccccccccccccccc} & & & & & & & 1 & & & & & & & \\\\ & & & & & & 1 & & 1 & & & & & & \\\\ & & & & & 1 & & 2 & & 1 & & & & & \\\\ & & & & 1 & & 3 & & 3 & & 1 & & & & \\\\ & & & 1 & & 4 & & 6 & & 4 & & 1 & & & \\\\ & & 1 & & 5 & & 10 & & 10 & & 5 & & 1 & & \\\\ & 1 & & 6 & & 15 & & 20 & & 15 & & 6 & & 1 & \\\\ 1 & & 7 & & 21 & & 35 & & 35 & & 21 & & 7 & & 1 \\\\ & & & & & & & \ldots \end{array}$$
-It can be seen that the first eight rows of Pascal's triangle contain twelve distinct numbers: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 and 35.
+Podemos ver que as primeiras oito linhas do triângulo de Pascal contêm doze números distintos: 1, 2, 3, 4, 5, 6, 7, 10, 15, 20, 21 e 35.
-A positive integer n is called squarefree if no square of a prime divides n. Of the twelve distinct numbers in the first eight rows of Pascal's triangle, all except 4 and 20 are squarefree. The sum of the distinct squarefree numbers in the first eight rows is 105.
+Um número inteiro positivo n é chamado de livre de quadrados se nenhum quadrado de um número primo dividir n. Dos doze números distintos nas primeiras oito linhas do triângulo de Pascal, todos os números exceto 4 e 20 são livres de quadrados. A soma dos números distintos livres de quadrados nas primeiras oito linhas é 105.
-Find the sum of the distinct squarefree numbers in the first 51 rows of Pascal's triangle.
+Encontre a soma dos números distintos livres de quadrados nas primeiras 51 linhas do triângulo de Pascal.
# --hints--
-`euler203()` should return 34029210557338.
+`squarefreeBinomialCoefficients()` deve retornar `34029210557338`.
```js
-assert.strictEqual(euler203(), 34029210557338);
+assert.strictEqual(squarefreeBinomialCoefficients(), 34029210557338);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler203(), 34029210557338);
## --seed-contents--
```js
-function euler203() {
+function squarefreeBinomialCoefficients() {
return true;
}
-euler203();
+squarefreeBinomialCoefficients();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
index 4d81e08eea..918620d1c3 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-204-generalised-hamming-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4381000cf542c50ff4b
-title: 'Problem 204: Generalised Hamming Numbers'
+title: 'Problema 204: Números de Hamming generalizados'
challengeType: 5
forumTopicId: 301845
dashedName: problem-204-generalised-hamming-numbers
@@ -8,22 +8,22 @@ dashedName: problem-204-generalised-hamming-numbers
# --description--
-A Hamming number is a positive number which has no prime factor larger than 5.
+Um número de Hamming é um número positivo que não tem fator primo maior que 5.
-So the first few Hamming numbers are 1, 2, 3, 4, 5, 6, 8, 9, 10, 12, 15.
+Assim, os primeiros números de Hamming são 1, 2, 3, 4, 5, 6, 8, 9, 10, 12 e 15.
-There are 1105 Hamming numbers not exceeding 108.
+Há 1105 números de Hamming que não excedem ${10}^8$.
-We will call a positive number a generalised Hamming number of type n, if it has no prime factor larger than n. Hence the Hamming numbers are the generalised Hamming numbers of type 5.
+Chamaremos um número positivo de número generalizado de Hamming do tipo $n$, se ele não tiver fator primo maior que $n$. Assim, os números de Hamming são os números generalizados de Hamming do tipo 5.
-How many generalised Hamming numbers of type 100 are there which don't exceed 109?
+Quantos números de Hamming generalizados do tipo 100 existem que não excedem ${10}^9$?
# --hints--
-`euler204()` should return 2944730.
+`generalisedHammingNumbers()` deve retornar `2944730`.
```js
-assert.strictEqual(euler204(), 2944730);
+assert.strictEqual(generalisedHammingNumbers(), 2944730);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler204(), 2944730);
## --seed-contents--
```js
-function euler204() {
+function generalisedHammingNumbers() {
return true;
}
-euler204();
+generalisedHammingNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
index 41bf903b6d..fc2f40557e 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-205-dice-game.md
@@ -1,6 +1,6 @@
---
id: 5900f4391000cf542c50ff4c
-title: 'Problem 205: Dice Game'
+title: 'Problema 205: Jogo de dados'
challengeType: 5
forumTopicId: 301846
dashedName: problem-205-dice-game
@@ -8,20 +8,20 @@ dashedName: problem-205-dice-game
# --description--
-Peter has nine four-sided (pyramidal) dice, each with faces numbered 1, 2, 3, 4.
+Pedro tem nove dados de quatro lados (piramidais), e cada uma das faces recebe um número 1, 2, 3 e 4.
-Colin has six six-sided (cubic) dice, each with faces numbered 1, 2, 3, 4, 5, 6.
+Colin tem seis dados de seis lados (cúbicos), e cada uma das fazes recebe um número 1, 2, 3, 4, 5 e 6.
-Peter and Colin roll their dice and compare totals: the highest total wins. The result is a draw if the totals are equal.
+Pedro e Colin rolam seus dados e comparam os totais: o maior total ganha. O resultado é um empate se os totais forem iguais.
-What is the probability that Pyramidal Pete beats Cubic Colin? Give your answer rounded to seven decimal places in the form 0.abcdefg
+Qual é a probabilidade que o Pedro Piramidal vencer Colin Cúbico? Arredonde sua resposta para até sete casas decimais usando o formato 0.abcdefg
# --hints--
-`euler205()` should return 0.5731441.
+`diceGame()` deve retornar `0.5731441`.
```js
-assert.strictEqual(euler205(), 0.5731441);
+assert.strictEqual(diceGame(), 0.5731441);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler205(), 0.5731441);
## --seed-contents--
```js
-function euler205() {
+function diceGame() {
return true;
}
-euler205();
+diceGame();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
index eaedced890..46e24b7b08 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-206-concealed-square.md
@@ -1,6 +1,6 @@
---
id: 5900f43a1000cf542c50ff4d
-title: 'Problem 206: Concealed Square'
+title: 'Problema 206: Quadrado escondido'
challengeType: 5
forumTopicId: 301847
dashedName: problem-206-concealed-square
@@ -8,14 +8,14 @@ dashedName: problem-206-concealed-square
# --description--
-Find the unique positive integer whose square has the form 1_2_3_4_5_6_7_8_9_0, where each “\_” is a single digit.
+Encontre o número inteiro positivo cujo quadrado tem o formato 1_2_3_4_5_6_7_8_9_0, onde cada "_" é um único algarismo.
# --hints--
-`euler206()` should return 1389019170.
+`concealedSquare()` deve retornar `1389019170`.
```js
-assert.strictEqual(euler206(), 1389019170);
+assert.strictEqual(concealedSquare(), 1389019170);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler206(), 1389019170);
## --seed-contents--
```js
-function euler206() {
+function concealedSquare() {
return true;
}
-euler206();
+concealedSquare();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
index 19f1d12c8d..440218de4f 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-207-integer-partition-equations.md
@@ -1,6 +1,6 @@
---
id: 5900f43c1000cf542c50ff4e
-title: 'Problem 207: Integer partition equations'
+title: 'Problema 207: Equações de partições inteiras'
challengeType: 5
forumTopicId: 301848
dashedName: problem-207-integer-partition-equations
@@ -8,24 +8,28 @@ dashedName: problem-207-integer-partition-equations
# --description--
-For some positive integers k, there exists an integer partition of the form 4t = 2t + k,
+Para alguns números inteiros positivos $k$, existe uma partição inteira de forma $4^t = 2^t + k$,
-where 4t, 2t, and k are all positive integers and t is a real number.
+onde $4^t$, $2^t$ e $k$ são todos números inteiros positivos e $t$ é um número real.
-The first two such partitions are 41 = 21 + 2 and 41.5849625... = 21.5849625... + 6.
+As duas primeiras partições desse tipo são $4^1 = 2^1 + 2$ e $4^{1.584\\,962\\,5\ldots} = 2^{1.584\\,962\\,5\ldots} + 6$.
-Partitions where t is also an integer are called perfect. For any m ≥ 1 let P(m) be the proportion of such partitions that are perfect with k ≤ m. Thus P(6) = 1/2.
+As partições onde $t$ é também um número inteiro são chamadas de perfeitas. Para qualquer $m ≥ 1$, considere $P(m)$ como sendo a proporção de tais partições que são perfeitas com $k ≤ m$.
-In the following table are listed some values of P(m) P(5) = 1/1 P(10) = 1/2 P(15) = 2/3 P(20) = 1/2 P(25) = 1/2 P(30) = 2/5 ... P(180) = 1/4 P(185) = 3/13
+Assim, $P(6) = \frac{1}{2}$.
-Find the smallest m for which P(m) < 1/12345
+Na tabela a seguir estão listados alguns valores de $P(m)$
+
+$$\begin{align} & P(5) = \frac{1}{1} \\\\ & P(10) = \frac{1}{2} \\\\ & P(15) = \frac{2}{3} \\\\ & P(20) = \frac{1}{2} \\\\ & P(25) = \frac{1}{2} \\\\ & P(30) = \frac{2}{5} \\\\ & \ldots \\\\ & P(180) = \frac{1}{4} \\\\ & P(185) = \frac{3}{13} \end{align}$$
+
+Encontre o menor $m$ para o qual $P(m) < \frac{1}{12.345}$
# --hints--
-`euler207()` should return 44043947822.
+`integerPartitionEquations()` deve retornar `44043947822`.
```js
-assert.strictEqual(euler207(), 44043947822);
+assert.strictEqual(integerPartitionEquations(), 44043947822);
```
# --seed--
@@ -33,12 +37,12 @@ assert.strictEqual(euler207(), 44043947822);
## --seed-contents--
```js
-function euler207() {
+function integerPartitionEquations() {
return true;
}
-euler207();
+integerPartitionEquations();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
index 36d5a8fff5..6d59d5c4ff 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-208-robot-walks.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff51
-title: 'Problem 208: Robot Walks'
+title: 'Problema 208: Caminhadas robóticas'
challengeType: 5
forumTopicId: 301849
dashedName: problem-208-robot-walks
@@ -8,18 +8,22 @@ dashedName: problem-208-robot-walks
# --description--
-A robot moves in a series of one-fifth circular arcs (72°), with a free choice of a clockwise or an anticlockwise arc for each step, but no turning on the spot.
+Um robô se move em uma série arco circular de um quinto de volta (72°), com uma escolha livre de sentido horário ou anti-horário para cada etapa, mas sem virar no local.
-One of 70932 possible closed paths of 25 arcs starting northward is
+Um dos 70932 caminhos fechados possíveis de 25 arcos iniciando para o norte é
-Given that the robot starts facing North, how many journeys of 70 arcs in length can it take that return it, after the final arc, to its starting position? (Any arc may be traversed multiple times.)
+ +
+Dado que o robô começa virado para o norte, quantas jornadas de 70 arcos de comprimento ele pode fazer que o retornem, após o arco final, para sua posição inicial?
+
+**Observação:** qualquer arco pode ser atravessado várias vezes.
# --hints--
-`euler208()` should return 331951449665644800.
+`robotWalks()` deve retornar `331951449665644800`.
```js
-assert.strictEqual(euler208(), 331951449665644800);
+assert.strictEqual(robotWalks(), 331951449665644800);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler208(), 331951449665644800);
## --seed-contents--
```js
-function euler208() {
+function robotWalks() {
return true;
}
-euler208();
+robotWalks();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
index f743744736..77d259dced 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff4f
-title: 'Problem 209: Circular Logic'
+title: 'Problema 209: Lógica circular'
challengeType: 5
forumTopicId: 301850
dashedName: problem-209-circular-logic
@@ -8,20 +8,34 @@ dashedName: problem-209-circular-logic
# --description--
-A k-input binary truth table is a map from k input bits
+Uma tabela verdade binária de $k$ entradas é um mapa de $k$ bits de entrada (dígitos binários, 0 [false] ou 1 [true]) para 1 bit de saída. Por exemplo, as tabelas verdade binárias de $2$ entradas para as funções lógicas de $AND$ e $XOR$ são:
-(binary digits, 0 \[false] or 1 \[true]) to 1 output bit. For example, the 2-input binary truth tables for the logical AND and XOR functions are:
+| x | y | x AND y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 0 |
+| 1 | 0 | 0 |
+| 1 | 1 | 1 |
-x y x AND y000010100111x y x XOR y000011101110How many 6-input binary truth tables, τ, satisfy the formula
+| x | y | x XOR y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 1 |
+| 1 | 0 | 1 |
+| 1 | 1 | 0 |
-τ(a, b, c, d, e, f) AND τ(b, c, d, e, f, a XOR (b AND c)) = 0 for all 6-bit inputs (a, b, c, d, e, f)?
+Quantas tabelas verdade binárias de $6$ entradas, $τ$, satisfazem a fórmula
+
+$$τ(a, b, c, d, e, f) \\; AND \\; τ(b, c, d, e, f, a \\; XOR \\; (b \\; AND \\; c)) = 0$$
+
+para todas as entradas de $6$ bits ($a$, $b$, $c$, $d$, $e$, $f$)?
# --hints--
-`euler209()` should return 15964587728784.
+`circularLogic()` deve retornar `15964587728784`.
```js
-assert.strictEqual(euler209(), 15964587728784);
+assert.strictEqual(circularLogic(), 15964587728784);
```
# --seed--
@@ -29,12 +43,12 @@ assert.strictEqual(euler209(), 15964587728784);
## --seed-contents--
```js
-function euler209() {
+function circularLogic() {
return true;
}
-euler209();
+circularLogic();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
index 1fc7d98033..e5dc0ee273 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff50
-title: 'Problem 210: Obtuse Angled Triangles'
+title: 'Problema 210: Triângulos de ângulos obtusos'
challengeType: 5
forumTopicId: 301852
dashedName: problem-210-obtuse-angled-triangles
@@ -8,22 +8,22 @@ dashedName: problem-210-obtuse-angled-triangles
# --description--
-Consider the set S(r) of points (x,y) with integer coordinates satisfying |x| + |y| ≤ r.
+Considere o conjunto $S(r)$ de pontos ($x$,$y$) com coordenadas inteiras que satisfaçam $|x| + |y| ≤ r$.
-Let O be the point (0,0) and C the point (r/4,r/4).
+Considere $O$ como sendo o ponto (0,0) e $C$ o ponto($\frac{r}{4}$,$\frac{r}{4}$).
-Let N(r) be the number of points B in S(r), so that the triangle OBC has an obtuse angle, i.e. the largest angle α satisfies 90°<α<180°.
+Considere $N(r)$ como sendo o número de pontos $B$ em $S(r)$, para que o triângulo $OBC$ tenha um ângulo obtuso, ou seja, o maior ângulo $α$ satisfaz $90°<α<180°$.
-So, for example, N(4)=24 and N(8)=100.
+Assim, por exemplo, $N(4)=24$ e $N(8)=100$.
-What is N(1,000,000,000)?
+Qual é $N(1.000.000.000)$?
# --hints--
-`euler210()` should return 1598174770174689500.
+`obtuseAngledTriangles()` deve retornar `1598174770174689500`.
```js
-assert.strictEqual(euler210(), 1598174770174689500);
+assert.strictEqual(obtuseAngledTriangles(), 1598174770174689500);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler210(), 1598174770174689500);
## --seed-contents--
```js
-function euler210() {
+function obtuseAngledTriangles() {
return true;
}
-euler210();
+obtuseAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
index bde41e4a79..8f0529eb0c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff52
-title: 'Problem 211: Divisor Square Sum'
+title: 'Problema 211: Soma dos quadrados dos divisores'
challengeType: 5
forumTopicId: 301853
dashedName: problem-211-divisor-square-sum
@@ -8,18 +8,18 @@ dashedName: problem-211-divisor-square-sum
# --description--
-For a positive integer n, let σ2(n) be the sum of the squares of its divisors. For example,
+Para um número inteiro positivo $n$, considere $σ_2(n)$ como sendo a soma dos quadrados de seus divisores. Por exemplo:
-σ2(10) = 1 + 4 + 25 + 100 = 130.
+$$σ_2(10) = 1 + 4 + 25 + 100 = 130$$
-Find the sum of all n, 0 < n < 64,000,000 such that σ2(n) is a perfect square.
+Encontre a soma de todos os $n$, $0 < n < 64.000.000$, de tal forma que $σ_2(n)$ seja um quadrado perfeito.
# --hints--
-`euler211()` should return 1922364685.
+`divisorSquareSum()` deve retornar `1922364685`.
```js
-assert.strictEqual(euler211(), 1922364685);
+assert.strictEqual(divisorSquareSum(), 1922364685);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler211(), 1922364685);
## --seed-contents--
```js
-function euler211() {
+function divisorSquareSum() {
return true;
}
-euler211();
+divisorSquareSum();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
index 901bbbc3d1..0a48b57aaf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff53
-title: 'Problem 212: Combined Volume of Cuboids'
+title: 'Problema 212: Volume combinado de cuboides'
challengeType: 5
forumTopicId: 301854
dashedName: problem-212-combined-volume-of-cuboids
@@ -8,28 +8,30 @@ dashedName: problem-212-combined-volume-of-cuboids
# --description--
-An axis-aligned cuboid, specified by parameters { (x0,y0,z0), (dx,dy,dz) }, consists of all points (X,Y,Z) such that x0 ≤ X ≤ x0+dx, y0 ≤ Y ≤ y0+dy and z0 ≤ Z ≤ z0+dz. The volume of the cuboid is the product, dx × dy × dz. The combined volume of a collection of cuboids is the volume of their union and will be less than the sum of the individual volumes if any cuboids overlap.
+Um cuboide alinhado em seus eixos, especificado pelos parâmetros $\{ (x_0,y_0,z_0), (dx,dy,dz) \}$, consiste em todos os pontos ($X$,$Y$,$Z$), de modo que $x_0 ≤ X ≤ x_0 + dx$, $y_0 ≤ Y ≤ y_0 + dy$ e $z_0 ≤ Z ≤ z_0 + dz$. O volume do cuboide é o produto, $dx × dy × dz$. O volume combinado de uma coleção de cuboides é o volume da sua união e será inferior à soma dos volumes individuais se houver sobreposição de qualquer um dos cuboides.
-Let C1,...,C50000 be a collection of 50000 axis-aligned cuboids such that Cn has parameters
+Considere $C_1, \ldots, C_{50000}$ como sendo uma coleção de 50.000 cuboides alinhados em seus eixos, de modo que $C_n$ tenha parâmetros
-x0 = S6n-5 modulo 10000y0 = S6n-4 modulo 10000z0 = S6n-3 modulo 10000dx = 1 + (S6n-2 modulo 399)dy = 1 + (S6n-1 modulo 399)dz = 1 + (S6n modulo 399)
+$$\begin{align} & x_0 = S_{6n - 5} \\; \text{modulo} \\; 10000 \\\\ & y_0 = S_{6n - 4} \\; \text{modulo} \\; 10000 \\\\ & z_0 = S_{6n - 3} \\; \text{modulo} \\; 10000 \\\\ & dx = 1 + (S_{6n - 2} \\; \text{modulo} \\; 399) \\\\ & dy = 1 + (S_{6n - 1} \\; \text{modulo} \\; 399) \\\\ & dz = 1 + (S_{6n} \\; \text{modulo} \\; 399) \\\\ \end{align}$$
-where S1,...,S300000 come from the "Lagged Fibonacci Generator":
+onde $S_1, \ldots, S_{300000}$ vem do "Gerador Fibonacci com atraso":
-For 1 ≤ k ≤ 55, Sk = \[100003 - 200003k + 300007k3] (modulo 1000000)For 56 ≤ k, Sk = \[Sk-24 + Sk-55] (modulo 1000000)
+Para $1 ≤ k ≤ 55$, $S_k = [100003 - 200003k + 300007k^3] \\; (modulo \\; 1000000)$
-Thus, C1 has parameters {(7,53,183),(94,369,56)}, C2 has parameters {(2383,3563,5079),(42,212,344)}, and so on.
+Para $56 ≤ k$, $S_k = [S_{k - 24} + S_{k - 55}] \\; (modulo \\; 1000000)$
-The combined volume of the first 100 cuboids, C1,...,C100, is 723581599.
+Assim, $C_1$ tem parâmetros $\{(7,53,183), (94,369,56)\}$, $C_2$ tem parâmetros $\{(2383,3563,5079), (42,212,344)\}$ e assim por diante.
-What is the combined volume of all 50000 cuboids, C1,...,C50000 ?
+O volume combinado dos primeiros 100 cuboides, $C_1, \ldots, C_{100}$, é 723581599.
+
+Qual é o volume combinado de todos os 50000 cuboides, $C_1, \ldots, C_{50000}$?
# --hints--
-`euler212()` should return 328968937309.
+`combinedValueOfCuboids()` deve retornar `328968937309`.
```js
-assert.strictEqual(euler212(), 328968937309);
+assert.strictEqual(combinedValueOfCuboids(), 328968937309);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler212(), 328968937309);
## --seed-contents--
```js
-function euler212() {
+function combinedValueOfCuboids() {
return true;
}
-euler212();
+combinedValueOfCuboids();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
index 2fbc23393c..92200998a2 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff54
-title: 'Problem 213: Flea Circus'
+title: 'Problema 213: Circo de pulgas'
challengeType: 5
forumTopicId: 301855
dashedName: problem-213-flea-circus
@@ -8,18 +8,18 @@ dashedName: problem-213-flea-circus
# --description--
-A 30×30 grid of squares contains 900 fleas, initially one flea per square.
+Uma grade de 30×30 quadrados contém 900 pulgas, inicialmente uma pulga por quadrado.
-When a bell is rung, each flea jumps to an adjacent square at random (usually 4 possibilities, except for fleas on the edge of the grid or at the corners).
+Quando uma campainha é tocada, cada pulga salta para um quadrado adjacente aleatoriamente (geralmente 4 possibilidades, exceto para as pulgas nas bordas da grade ou nos cantos).
-What is the expected number of unoccupied squares after 50 rings of the bell? Give your answer rounded to six decimal places.
+Qual é o número esperado de quadrados desocupados após 50 toques da campainha? Dê sua resposta arredondada para seis casas decimais.
# --hints--
-`euler213()` should return 330.721154.
+`fleaCircus()` deve retornar `330.721154`.
```js
-assert.strictEqual(euler213(), 330.721154);
+assert.strictEqual(fleaCircus(), 330.721154);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler213(), 330.721154);
## --seed-contents--
```js
-function euler213() {
+function fleaCircus() {
return true;
}
-euler213();
+fleaCircus();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
index 754596cef6..9675f70327 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
@@ -1,6 +1,6 @@
---
id: 5900f4421000cf542c50ff55
-title: 'Problem 214: Totient Chains'
+title: 'Problema 214: Cadeias de totientes'
challengeType: 5
forumTopicId: 301856
dashedName: problem-214-totient-chains
@@ -8,24 +8,22 @@ dashedName: problem-214-totient-chains
# --description--
-Let φ be Euler's totient function, i.e. for a natural number n,
+Considere $φ$ como sendo a função totiente de Euler, ou seja, para um número natural $n$, $φ(n)$ é o número de $k$, $1 ≤ k ≤ n$, para os quais o máximo divisor comum é $gcd(k,n) = 1$.
-φ(n) is the number of k, 1 ≤ k ≤ n, for which gcd(k,n) = 1.
+Ao iterar por $φ$, cada número inteiro positivo gera uma cadeia decrescente de números terminando em 1. Ex: se começarmos com 5 a sequência 5,4,2,1 é gerada. Aqui está uma lista de todas as cadeias com comprimento 4:
-By iterating φ, each positive integer generates a decreasing chain of numbers ending in 1. E.g. if we start with 5 the sequence 5,4,2,1 is generated. Here is a listing of all chains with length 4:
+$$\begin{align} 5,4,2,1 & \\\\ 7,6,2,1 & \\\\ 8,4,2,1 & \\\\ 9,6,2,1 & \\\\ 10,4,2,1 & \\\\ 12,4,2,1 & \\\\ 14,6,2,1 & \\\\ 18,6,2,1 & \end{align}$$
-5,4,2,1 7,6,2,1 8,4,2,1 9,6,2,1 10,4,2,1 12,4,2,1 14,6,2,1 18,6,2,1
+Apenas duas dessas cadeias começam com um número primo e sua soma é 12.
-Only two of these chains start with a prime, their sum is 12.
-
-What is the sum of all primes less than 40000000 which generate a chain of length 25?
+Qual é a soma de todos os números primos menores do que $40.000.000$ que gera uma cadeia de comprimento 25?
# --hints--
-`euler214()` should return 1677366278943.
+`totientChains()` deve retornar `1677366278943`.
```js
-assert.strictEqual(euler214(), 1677366278943);
+assert.strictEqual(totientChains(), 1677366278943);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler214(), 1677366278943);
## --seed-contents--
```js
-function euler214() {
+function totientChains() {
return true;
}
-euler214();
+totientChains();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
index 45f7f563e7..99a6eb9baf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
@@ -1,6 +1,6 @@
---
id: 5900f4431000cf542c50ff56
-title: 'Problem 215: Crack-free Walls'
+title: 'Problema 215: Paredes sem rachaduras'
challengeType: 5
forumTopicId: 301857
dashedName: problem-215-crack-free-walls
@@ -8,20 +8,22 @@ dashedName: problem-215-crack-free-walls
# --description--
-Consider the problem of building a wall out of 2×1 and 3×1 bricks (horizontal×vertical dimensions) such that, for extra strength, the gaps between horizontally-adjacent bricks never line up in consecutive layers, i.e. never form a "running crack".
+Considere o problema da construção de uma parede de 2×1 e 3×1 tijolos (dimensões verticais × horizontais), de modo que, para ter uma força extra, as lacunas entre os blocos adjacentes horizontalmente nunca se alinham em camadas consecutivas, ou seja, nunca formam uma "rachadura".
-For example, the following 9×3 wall is not acceptable due to the running crack shown in red:
+Por exemplo, a parede 9×3 a seguir não é aceitável devido à rachadura da execução mostrada em vermelho:
-There are eight ways of forming a crack-free 9×3 wall, written W(9,3) = 8.
+
+
+Dado que o robô começa virado para o norte, quantas jornadas de 70 arcos de comprimento ele pode fazer que o retornem, após o arco final, para sua posição inicial?
+
+**Observação:** qualquer arco pode ser atravessado várias vezes.
# --hints--
-`euler208()` should return 331951449665644800.
+`robotWalks()` deve retornar `331951449665644800`.
```js
-assert.strictEqual(euler208(), 331951449665644800);
+assert.strictEqual(robotWalks(), 331951449665644800);
```
# --seed--
@@ -27,12 +31,12 @@ assert.strictEqual(euler208(), 331951449665644800);
## --seed-contents--
```js
-function euler208() {
+function robotWalks() {
return true;
}
-euler208();
+robotWalks();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
index f743744736..77d259dced 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-209-circular-logic.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff4f
-title: 'Problem 209: Circular Logic'
+title: 'Problema 209: Lógica circular'
challengeType: 5
forumTopicId: 301850
dashedName: problem-209-circular-logic
@@ -8,20 +8,34 @@ dashedName: problem-209-circular-logic
# --description--
-A k-input binary truth table is a map from k input bits
+Uma tabela verdade binária de $k$ entradas é um mapa de $k$ bits de entrada (dígitos binários, 0 [false] ou 1 [true]) para 1 bit de saída. Por exemplo, as tabelas verdade binárias de $2$ entradas para as funções lógicas de $AND$ e $XOR$ são:
-(binary digits, 0 \[false] or 1 \[true]) to 1 output bit. For example, the 2-input binary truth tables for the logical AND and XOR functions are:
+| x | y | x AND y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 0 |
+| 1 | 0 | 0 |
+| 1 | 1 | 1 |
-x y x AND y000010100111x y x XOR y000011101110How many 6-input binary truth tables, τ, satisfy the formula
+| x | y | x XOR y |
+| - | - | ------- |
+| 0 | 0 | 0 |
+| 0 | 1 | 1 |
+| 1 | 0 | 1 |
+| 1 | 1 | 0 |
-τ(a, b, c, d, e, f) AND τ(b, c, d, e, f, a XOR (b AND c)) = 0 for all 6-bit inputs (a, b, c, d, e, f)?
+Quantas tabelas verdade binárias de $6$ entradas, $τ$, satisfazem a fórmula
+
+$$τ(a, b, c, d, e, f) \\; AND \\; τ(b, c, d, e, f, a \\; XOR \\; (b \\; AND \\; c)) = 0$$
+
+para todas as entradas de $6$ bits ($a$, $b$, $c$, $d$, $e$, $f$)?
# --hints--
-`euler209()` should return 15964587728784.
+`circularLogic()` deve retornar `15964587728784`.
```js
-assert.strictEqual(euler209(), 15964587728784);
+assert.strictEqual(circularLogic(), 15964587728784);
```
# --seed--
@@ -29,12 +43,12 @@ assert.strictEqual(euler209(), 15964587728784);
## --seed-contents--
```js
-function euler209() {
+function circularLogic() {
return true;
}
-euler209();
+circularLogic();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
index 1fc7d98033..e5dc0ee273 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-210-obtuse-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f43e1000cf542c50ff50
-title: 'Problem 210: Obtuse Angled Triangles'
+title: 'Problema 210: Triângulos de ângulos obtusos'
challengeType: 5
forumTopicId: 301852
dashedName: problem-210-obtuse-angled-triangles
@@ -8,22 +8,22 @@ dashedName: problem-210-obtuse-angled-triangles
# --description--
-Consider the set S(r) of points (x,y) with integer coordinates satisfying |x| + |y| ≤ r.
+Considere o conjunto $S(r)$ de pontos ($x$,$y$) com coordenadas inteiras que satisfaçam $|x| + |y| ≤ r$.
-Let O be the point (0,0) and C the point (r/4,r/4).
+Considere $O$ como sendo o ponto (0,0) e $C$ o ponto($\frac{r}{4}$,$\frac{r}{4}$).
-Let N(r) be the number of points B in S(r), so that the triangle OBC has an obtuse angle, i.e. the largest angle α satisfies 90°<α<180°.
+Considere $N(r)$ como sendo o número de pontos $B$ em $S(r)$, para que o triângulo $OBC$ tenha um ângulo obtuso, ou seja, o maior ângulo $α$ satisfaz $90°<α<180°$.
-So, for example, N(4)=24 and N(8)=100.
+Assim, por exemplo, $N(4)=24$ e $N(8)=100$.
-What is N(1,000,000,000)?
+Qual é $N(1.000.000.000)$?
# --hints--
-`euler210()` should return 1598174770174689500.
+`obtuseAngledTriangles()` deve retornar `1598174770174689500`.
```js
-assert.strictEqual(euler210(), 1598174770174689500);
+assert.strictEqual(obtuseAngledTriangles(), 1598174770174689500);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler210(), 1598174770174689500);
## --seed-contents--
```js
-function euler210() {
+function obtuseAngledTriangles() {
return true;
}
-euler210();
+obtuseAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
index bde41e4a79..8f0529eb0c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-211-divisor-square-sum.md
@@ -1,6 +1,6 @@
---
id: 5900f43f1000cf542c50ff52
-title: 'Problem 211: Divisor Square Sum'
+title: 'Problema 211: Soma dos quadrados dos divisores'
challengeType: 5
forumTopicId: 301853
dashedName: problem-211-divisor-square-sum
@@ -8,18 +8,18 @@ dashedName: problem-211-divisor-square-sum
# --description--
-For a positive integer n, let σ2(n) be the sum of the squares of its divisors. For example,
+Para um número inteiro positivo $n$, considere $σ_2(n)$ como sendo a soma dos quadrados de seus divisores. Por exemplo:
-σ2(10) = 1 + 4 + 25 + 100 = 130.
+$$σ_2(10) = 1 + 4 + 25 + 100 = 130$$
-Find the sum of all n, 0 < n < 64,000,000 such that σ2(n) is a perfect square.
+Encontre a soma de todos os $n$, $0 < n < 64.000.000$, de tal forma que $σ_2(n)$ seja um quadrado perfeito.
# --hints--
-`euler211()` should return 1922364685.
+`divisorSquareSum()` deve retornar `1922364685`.
```js
-assert.strictEqual(euler211(), 1922364685);
+assert.strictEqual(divisorSquareSum(), 1922364685);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler211(), 1922364685);
## --seed-contents--
```js
-function euler211() {
+function divisorSquareSum() {
return true;
}
-euler211();
+divisorSquareSum();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
index 901bbbc3d1..0a48b57aaf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-212-combined-volume-of-cuboids.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff53
-title: 'Problem 212: Combined Volume of Cuboids'
+title: 'Problema 212: Volume combinado de cuboides'
challengeType: 5
forumTopicId: 301854
dashedName: problem-212-combined-volume-of-cuboids
@@ -8,28 +8,30 @@ dashedName: problem-212-combined-volume-of-cuboids
# --description--
-An axis-aligned cuboid, specified by parameters { (x0,y0,z0), (dx,dy,dz) }, consists of all points (X,Y,Z) such that x0 ≤ X ≤ x0+dx, y0 ≤ Y ≤ y0+dy and z0 ≤ Z ≤ z0+dz. The volume of the cuboid is the product, dx × dy × dz. The combined volume of a collection of cuboids is the volume of their union and will be less than the sum of the individual volumes if any cuboids overlap.
+Um cuboide alinhado em seus eixos, especificado pelos parâmetros $\{ (x_0,y_0,z_0), (dx,dy,dz) \}$, consiste em todos os pontos ($X$,$Y$,$Z$), de modo que $x_0 ≤ X ≤ x_0 + dx$, $y_0 ≤ Y ≤ y_0 + dy$ e $z_0 ≤ Z ≤ z_0 + dz$. O volume do cuboide é o produto, $dx × dy × dz$. O volume combinado de uma coleção de cuboides é o volume da sua união e será inferior à soma dos volumes individuais se houver sobreposição de qualquer um dos cuboides.
-Let C1,...,C50000 be a collection of 50000 axis-aligned cuboids such that Cn has parameters
+Considere $C_1, \ldots, C_{50000}$ como sendo uma coleção de 50.000 cuboides alinhados em seus eixos, de modo que $C_n$ tenha parâmetros
-x0 = S6n-5 modulo 10000y0 = S6n-4 modulo 10000z0 = S6n-3 modulo 10000dx = 1 + (S6n-2 modulo 399)dy = 1 + (S6n-1 modulo 399)dz = 1 + (S6n modulo 399)
+$$\begin{align} & x_0 = S_{6n - 5} \\; \text{modulo} \\; 10000 \\\\ & y_0 = S_{6n - 4} \\; \text{modulo} \\; 10000 \\\\ & z_0 = S_{6n - 3} \\; \text{modulo} \\; 10000 \\\\ & dx = 1 + (S_{6n - 2} \\; \text{modulo} \\; 399) \\\\ & dy = 1 + (S_{6n - 1} \\; \text{modulo} \\; 399) \\\\ & dz = 1 + (S_{6n} \\; \text{modulo} \\; 399) \\\\ \end{align}$$
-where S1,...,S300000 come from the "Lagged Fibonacci Generator":
+onde $S_1, \ldots, S_{300000}$ vem do "Gerador Fibonacci com atraso":
-For 1 ≤ k ≤ 55, Sk = \[100003 - 200003k + 300007k3] (modulo 1000000)For 56 ≤ k, Sk = \[Sk-24 + Sk-55] (modulo 1000000)
+Para $1 ≤ k ≤ 55$, $S_k = [100003 - 200003k + 300007k^3] \\; (modulo \\; 1000000)$
-Thus, C1 has parameters {(7,53,183),(94,369,56)}, C2 has parameters {(2383,3563,5079),(42,212,344)}, and so on.
+Para $56 ≤ k$, $S_k = [S_{k - 24} + S_{k - 55}] \\; (modulo \\; 1000000)$
-The combined volume of the first 100 cuboids, C1,...,C100, is 723581599.
+Assim, $C_1$ tem parâmetros $\{(7,53,183), (94,369,56)\}$, $C_2$ tem parâmetros $\{(2383,3563,5079), (42,212,344)\}$ e assim por diante.
-What is the combined volume of all 50000 cuboids, C1,...,C50000 ?
+O volume combinado dos primeiros 100 cuboides, $C_1, \ldots, C_{100}$, é 723581599.
+
+Qual é o volume combinado de todos os 50000 cuboides, $C_1, \ldots, C_{50000}$?
# --hints--
-`euler212()` should return 328968937309.
+`combinedValueOfCuboids()` deve retornar `328968937309`.
```js
-assert.strictEqual(euler212(), 328968937309);
+assert.strictEqual(combinedValueOfCuboids(), 328968937309);
```
# --seed--
@@ -37,12 +39,12 @@ assert.strictEqual(euler212(), 328968937309);
## --seed-contents--
```js
-function euler212() {
+function combinedValueOfCuboids() {
return true;
}
-euler212();
+combinedValueOfCuboids();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
index 2fbc23393c..92200998a2 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-213-flea-circus.md
@@ -1,6 +1,6 @@
---
id: 5900f4411000cf542c50ff54
-title: 'Problem 213: Flea Circus'
+title: 'Problema 213: Circo de pulgas'
challengeType: 5
forumTopicId: 301855
dashedName: problem-213-flea-circus
@@ -8,18 +8,18 @@ dashedName: problem-213-flea-circus
# --description--
-A 30×30 grid of squares contains 900 fleas, initially one flea per square.
+Uma grade de 30×30 quadrados contém 900 pulgas, inicialmente uma pulga por quadrado.
-When a bell is rung, each flea jumps to an adjacent square at random (usually 4 possibilities, except for fleas on the edge of the grid or at the corners).
+Quando uma campainha é tocada, cada pulga salta para um quadrado adjacente aleatoriamente (geralmente 4 possibilidades, exceto para as pulgas nas bordas da grade ou nos cantos).
-What is the expected number of unoccupied squares after 50 rings of the bell? Give your answer rounded to six decimal places.
+Qual é o número esperado de quadrados desocupados após 50 toques da campainha? Dê sua resposta arredondada para seis casas decimais.
# --hints--
-`euler213()` should return 330.721154.
+`fleaCircus()` deve retornar `330.721154`.
```js
-assert.strictEqual(euler213(), 330.721154);
+assert.strictEqual(fleaCircus(), 330.721154);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler213(), 330.721154);
## --seed-contents--
```js
-function euler213() {
+function fleaCircus() {
return true;
}
-euler213();
+fleaCircus();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
index 754596cef6..9675f70327 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-214-totient-chains.md
@@ -1,6 +1,6 @@
---
id: 5900f4421000cf542c50ff55
-title: 'Problem 214: Totient Chains'
+title: 'Problema 214: Cadeias de totientes'
challengeType: 5
forumTopicId: 301856
dashedName: problem-214-totient-chains
@@ -8,24 +8,22 @@ dashedName: problem-214-totient-chains
# --description--
-Let φ be Euler's totient function, i.e. for a natural number n,
+Considere $φ$ como sendo a função totiente de Euler, ou seja, para um número natural $n$, $φ(n)$ é o número de $k$, $1 ≤ k ≤ n$, para os quais o máximo divisor comum é $gcd(k,n) = 1$.
-φ(n) is the number of k, 1 ≤ k ≤ n, for which gcd(k,n) = 1.
+Ao iterar por $φ$, cada número inteiro positivo gera uma cadeia decrescente de números terminando em 1. Ex: se começarmos com 5 a sequência 5,4,2,1 é gerada. Aqui está uma lista de todas as cadeias com comprimento 4:
-By iterating φ, each positive integer generates a decreasing chain of numbers ending in 1. E.g. if we start with 5 the sequence 5,4,2,1 is generated. Here is a listing of all chains with length 4:
+$$\begin{align} 5,4,2,1 & \\\\ 7,6,2,1 & \\\\ 8,4,2,1 & \\\\ 9,6,2,1 & \\\\ 10,4,2,1 & \\\\ 12,4,2,1 & \\\\ 14,6,2,1 & \\\\ 18,6,2,1 & \end{align}$$
-5,4,2,1 7,6,2,1 8,4,2,1 9,6,2,1 10,4,2,1 12,4,2,1 14,6,2,1 18,6,2,1
+Apenas duas dessas cadeias começam com um número primo e sua soma é 12.
-Only two of these chains start with a prime, their sum is 12.
-
-What is the sum of all primes less than 40000000 which generate a chain of length 25?
+Qual é a soma de todos os números primos menores do que $40.000.000$ que gera uma cadeia de comprimento 25?
# --hints--
-`euler214()` should return 1677366278943.
+`totientChains()` deve retornar `1677366278943`.
```js
-assert.strictEqual(euler214(), 1677366278943);
+assert.strictEqual(totientChains(), 1677366278943);
```
# --seed--
@@ -33,12 +31,12 @@ assert.strictEqual(euler214(), 1677366278943);
## --seed-contents--
```js
-function euler214() {
+function totientChains() {
return true;
}
-euler214();
+totientChains();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
index 45f7f563e7..99a6eb9baf 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-215-crack-free-walls.md
@@ -1,6 +1,6 @@
---
id: 5900f4431000cf542c50ff56
-title: 'Problem 215: Crack-free Walls'
+title: 'Problema 215: Paredes sem rachaduras'
challengeType: 5
forumTopicId: 301857
dashedName: problem-215-crack-free-walls
@@ -8,20 +8,22 @@ dashedName: problem-215-crack-free-walls
# --description--
-Consider the problem of building a wall out of 2×1 and 3×1 bricks (horizontal×vertical dimensions) such that, for extra strength, the gaps between horizontally-adjacent bricks never line up in consecutive layers, i.e. never form a "running crack".
+Considere o problema da construção de uma parede de 2×1 e 3×1 tijolos (dimensões verticais × horizontais), de modo que, para ter uma força extra, as lacunas entre os blocos adjacentes horizontalmente nunca se alinham em camadas consecutivas, ou seja, nunca formam uma "rachadura".
-For example, the following 9×3 wall is not acceptable due to the running crack shown in red:
+Por exemplo, a parede 9×3 a seguir não é aceitável devido à rachadura da execução mostrada em vermelho:
-There are eight ways of forming a crack-free 9×3 wall, written W(9,3) = 8.
+ -Calculate W(32,10).
+Existem oito maneiras de formar uma parede 9×3 sem rachaduras, as quais descrevemos como $W(9,3) = 8$.
+
+Calcule $W(32,10)$.
# --hints--
-`euler215()` should return 806844323190414.
+`crackFreeWalls()` deve retornar `806844323190414`.
```js
-assert.strictEqual(euler215(), 806844323190414);
+assert.strictEqual(crackFreeWalls(), 806844323190414);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler215(), 806844323190414);
## --seed-contents--
```js
-function euler215() {
+function crackFreeWalls() {
return true;
}
-euler215();
+crackFreeWalls();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
index e7591cd46f..3a71653636 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
@@ -1,6 +1,6 @@
---
id: 5900f4451000cf542c50ff57
-title: 'Problem 216: Investigating the primality of numbers of the form 2n2-1'
+title: 'Problema 216: Investigação da primalidade dos números da forma 2n2-1'
challengeType: 5
forumTopicId: 301858
dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
@@ -8,22 +8,22 @@ dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
# --description--
-Consider numbers t(n) of the form t(n) = 2n2-1 with n > 1.
+Considere os números $t(n)$ da forma $t(n) = 2n^2 - 1$, sendo $n > 1$.
-The first such numbers are 7, 17, 31, 49, 71, 97, 127 and 161.
+Os primeiros desses números são 7, 17, 31, 49, 71, 97, 127 e 161.
-It turns out that only 49 = 7\*7 and 161 = 7\*23 are not prime.
+Ocorre que apenas $49 = 7 \times 7$ e $161 = 7 \times 23$ dentre esses não são números primos.
-For n ≤ 10000 there are 2202 numbers t(n) that are prime.
+Para $n ≤ 10000$, há 2202 números $t(n)$ que são primos.
-How many numbers t(n) are prime for n ≤ 50,000,000 ?
+Quantos números $t(n)$ são primos para $n ≤ 50.000.000$?
# --hints--
-`euler216()` should return 5437849.
+`primalityOfNumbers()` deve retornar `5437849`.
```js
-assert.strictEqual(euler216(), 5437849);
+assert.strictEqual(primalityOfNumbers(), 5437849);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler216(), 5437849);
## --seed-contents--
```js
-function euler216() {
+function primalityOfNumbers() {
return true;
}
-euler216();
+primalityOfNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
index 625b4a6c6d..44b7af79d1 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff58
-title: 'Problem 217: Balanced Numbers'
+title: 'Problema 217: Números balanceados'
challengeType: 5
forumTopicId: 301859
dashedName: problem-217-balanced-numbers
@@ -8,22 +8,22 @@ dashedName: problem-217-balanced-numbers
# --description--
-A positive integer with k (decimal) digits is called balanced if its first ⌈k/2⌉ digits sum to the same value as its last ⌈k/2⌉ digits, where ⌈x⌉, pronounced ceiling of x, is the smallest integer ≥ x, thus ⌈π⌉ = 4 and ⌈5⌉ = 5.
+Um número inteiro positivo com $k$ casas (decimais) é chamado de balanceado se os seus primeiros $⌈\frac{k}{2}⌉$ algarismos têm a soma igual aos seus últimos $⌈\frac{k}{2}⌉$ algarismos, onde $⌈x⌉$, o teto pronunciado de $x$, é o menor inteiro, sendo $≥ x$, portanto $⌈π⌉ = 4$ e $⌈5⌉ = 5$.
-So, for example, all palindromes are balanced, as is 13722.
+Então, por exemplo, todos os palíndromos são balanceados, assim como 13722.
-Let T(n) be the sum of all balanced numbers less than 10n.
+Considere $T(n)$ como sendo a soma de todos os números balanceados menores que $10^n$.
-Thus: T(1) = 45, T(2) = 540 and T(5) = 334795890.
+Assim: $T(1) = 45$, $T(2) = 540$ e $T(5) = 334.795.890$.
-Find T(47) mod 315
+Encontre $T(47)\\,mod\\,3^{15}$
# --hints--
-`euler217()` should return 6273134.
+`balancedNumbers()` deve retornar `6273134`.
```js
-assert.strictEqual(euler217(), 6273134);
+assert.strictEqual(balancedNumbers(), 6273134);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler217(), 6273134);
## --seed-contents--
```js
-function euler217() {
+function balancedNumbers() {
return true;
}
-euler217();
+balancedNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
index db91d74874..2e1df0ab68 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff59
-title: 'Problem 218: Perfect right-angled triangles'
+title: 'Problema 218: Triângulos retos perfeitos'
challengeType: 5
forumTopicId: 301860
dashedName: problem-218-perfect-right-angled-triangles
@@ -8,26 +8,32 @@ dashedName: problem-218-perfect-right-angled-triangles
# --description--
-Consider the right angled triangle with sides a=7, b=24 and c=25.
+Considere o triângulo reto com lados $a=7$, $b=24$ e $c=25$.
-The area of this triangle is 84, which is divisible by the perfect numbers 6 and 28.
+A área deste triângulo é 84, que é divisível pelos números perfeitos 6 e 28.
-Moreover it is a primitive right angled triangle as gcd(a,b)=1 and gcd(b,c)=1.
+Além disso, ele é um triângulo reto primitivo, já que tem os maiores divisores comuns $gcd(a,b) = 1$ e $gcd(b,c) = 1$.
-Also c is a perfect square.
+Por fim, $c$ é um quadrado perfeito.
-We will call a right angled triangle perfect if -it is a primitive right angled triangle -its hypotenuse is a perfect square
+Chamaremos um triângulo de triângulo reto perfeito se:
-We will call a right angled triangle super-perfect if -it is a perfect right angled triangle and -its area is a multiple of the perfect numbers 6 and 28.
+- for um triângulo reto primitivo
+- sua hipotenusa for um quadrado perfeito
-How many perfect right-angled triangles with c≤1016 exist that are not super-perfect?
+Chamaremos um triângulo de triângulo reto superperfeito se:
+
+- for um triângulo reto perfeito
+- sua área for um múltiplo dos números perfeitos 6 e 28.
+
+Quantos triângulos retos perfeitos com $c ≤ {10}^{16}$ existem que não são superperfeitos?
# --hints--
-`euler218()` should return 0.
+`perfectRightAngledTriangles()` deve retornar `0`.
```js
-assert.strictEqual(euler218(), 0);
+assert.strictEqual(perfectRightAngledTriangles(), 0);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler218(), 0);
## --seed-contents--
```js
-function euler218() {
+function perfectRightAngledTriangles() {
return true;
}
-euler218();
+perfectRightAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
index 38d16eba87..92b02718d5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5a
-title: 'Problem 219: Skew-cost coding'
+title: 'Problema 219: Codificação de custo modificado'
challengeType: 5
forumTopicId: 301861
dashedName: problem-219-skew-cost-coding
@@ -8,26 +8,26 @@ dashedName: problem-219-skew-cost-coding
# --description--
-Let A and B be bit strings (sequences of 0's and 1's).
+Considere $A$ e $B$ como sendo strings de bits (sequências de 0s e 1s).
-If A is equal to the leftmost length(A) bits of B, then A is said to be a prefix of B.
+Se $A$ for igual ao bits comprimento ($A$) mais à esquerda de $B$, então $A$ é pode ser considerado um prefixo de $B$.
-For example, 00110 is a prefix of 001101001, but not of 00111 or 100110.
+Por exemplo, 00110 é um prefixo de 001101001, mas não de 00111 ou 100110.
-A prefix-free code of size n is a collection of n distinct bit strings such that no string is a prefix of any other. For example, this is a prefix-free code of size 6:
+Um código de tamanho $n$ sem prefixo é uma coleção de $n$ strings de bits distintos, de modo que nenhuma string é um prefixo de outra. Por exemplo, este é um código de tamanho 6 sem prefixos:
-0000, 0001, 001, 01, 10, 11
+$$0000, 0001, 001, 01, 10, 11$$
-Now suppose that it costs one penny to transmit a '0' bit, but four pence to transmit a '1'. Then the total cost of the prefix-free code shown above is 35 pence, which happens to be the cheapest possible for the skewed pricing scheme in question. In short, we write Cost(6) = 35.
+Suponhamos agora que custa um centavo transmitir um bit "0", mas quatro centavos transmitir um bit "1". Então, o custo total do código sem o prefixo mostrado acima é de 35 centavos, que é o mais barato possível para o regime de preços modificados em questão. Em resumo, escrevemos $Cost(6) = 35$.
-What is Cost(109) ?
+Qual é o $Cost(10^9)$?
# --hints--
-`euler219()` should return 64564225042.
+`skewCostCoding()` deve retornar `64564225042`.
```js
-assert.strictEqual(euler219(), 64564225042);
+assert.strictEqual(skewCostCoding(), 64564225042);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler219(), 64564225042);
## --seed-contents--
```js
-function euler219() {
+function skewCostCoding() {
return true;
}
-euler219();
+skewCostCoding();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
index 1fccaef107..1f7114f3bd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5b
-title: 'Problem 220: Heighway Dragon'
+title: 'Problema 220: Dragão de Heighway'
challengeType: 5
forumTopicId: 301863
dashedName: problem-220-heighway-dragon
@@ -8,24 +8,33 @@ dashedName: problem-220-heighway-dragon
# --description--
-Let D0 be the two-letter string "Fa". For n≥1, derive Dn from Dn-1 by the string-rewriting rules:
+Considere $D_0$ como sendo a string de duas letras "Fa". Para $n ≥ 1$, derive $D_n$ de $D_{n - 1}$ pelas regras de reescrita da string:
-"a" → "aRbFR" "b" → "LFaLb"
+- "a" → "aRbFR"
+- "b" → "LFaLb"
-Thus, D0 = "Fa", D1 = "FaRbFR", D2 = "FaRbFRRLFaLbFR", and so on.
+Assim, $D_0$ = "Fa", $D_1$ = "FaRbFR", $D_2$ = "FaRbFRRLFaLbFR" e assim por diante.
-These strings can be interpreted as instructions to a computer graphics program, with "F" meaning "draw forward one unit", "L" meaning "turn left 90 degrees", "R" meaning "turn right 90 degrees", and "a" and "b" being ignored. The initial position of the computer cursor is (0,0), pointing up towards (0,1).
+Essas strings podem ser interpretadas como instruções para um programa gráfico do computador, com "F" significando "desenhar uma unidade", "L" significando "virar 90 graus à esquerda", "R" significando "virar 90 graus à direita " e "a" e "b" sendo ignorados. A posição inicial do cursor do computador é (0,0), apontando na direção de (0,1).
-Then Dn is an exotic drawing known as the Heighway Dragon of order n. For example, D10 is shown below; counting each "F" as one step, the highlighted spot at (18,16) is the position reached after 500 steps.
+Então $D_n$ é um desenho exótico conhecido como Dragão de Heighway da ordem $n$. Por exemplo, $D_{10}$ é mostrado abaixo. Contando cada "F" como uma etapa, o local destacado em (18,16) é a posição alcançada após 500 etapas.
-What is the position of the cursor after 1012 steps in D50 ? Give your answer in the form x,y with no spaces.
+
-Calculate W(32,10).
+Existem oito maneiras de formar uma parede 9×3 sem rachaduras, as quais descrevemos como $W(9,3) = 8$.
+
+Calcule $W(32,10)$.
# --hints--
-`euler215()` should return 806844323190414.
+`crackFreeWalls()` deve retornar `806844323190414`.
```js
-assert.strictEqual(euler215(), 806844323190414);
+assert.strictEqual(crackFreeWalls(), 806844323190414);
```
# --seed--
@@ -29,12 +31,12 @@ assert.strictEqual(euler215(), 806844323190414);
## --seed-contents--
```js
-function euler215() {
+function crackFreeWalls() {
return true;
}
-euler215();
+crackFreeWalls();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
index e7591cd46f..3a71653636 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1.md
@@ -1,6 +1,6 @@
---
id: 5900f4451000cf542c50ff57
-title: 'Problem 216: Investigating the primality of numbers of the form 2n2-1'
+title: 'Problema 216: Investigação da primalidade dos números da forma 2n2-1'
challengeType: 5
forumTopicId: 301858
dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
@@ -8,22 +8,22 @@ dashedName: problem-216-investigating-the-primality-of-numbers-of-the-form-2n2-1
# --description--
-Consider numbers t(n) of the form t(n) = 2n2-1 with n > 1.
+Considere os números $t(n)$ da forma $t(n) = 2n^2 - 1$, sendo $n > 1$.
-The first such numbers are 7, 17, 31, 49, 71, 97, 127 and 161.
+Os primeiros desses números são 7, 17, 31, 49, 71, 97, 127 e 161.
-It turns out that only 49 = 7\*7 and 161 = 7\*23 are not prime.
+Ocorre que apenas $49 = 7 \times 7$ e $161 = 7 \times 23$ dentre esses não são números primos.
-For n ≤ 10000 there are 2202 numbers t(n) that are prime.
+Para $n ≤ 10000$, há 2202 números $t(n)$ que são primos.
-How many numbers t(n) are prime for n ≤ 50,000,000 ?
+Quantos números $t(n)$ são primos para $n ≤ 50.000.000$?
# --hints--
-`euler216()` should return 5437849.
+`primalityOfNumbers()` deve retornar `5437849`.
```js
-assert.strictEqual(euler216(), 5437849);
+assert.strictEqual(primalityOfNumbers(), 5437849);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler216(), 5437849);
## --seed-contents--
```js
-function euler216() {
+function primalityOfNumbers() {
return true;
}
-euler216();
+primalityOfNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
index 625b4a6c6d..44b7af79d1 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-217-balanced-numbers.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff58
-title: 'Problem 217: Balanced Numbers'
+title: 'Problema 217: Números balanceados'
challengeType: 5
forumTopicId: 301859
dashedName: problem-217-balanced-numbers
@@ -8,22 +8,22 @@ dashedName: problem-217-balanced-numbers
# --description--
-A positive integer with k (decimal) digits is called balanced if its first ⌈k/2⌉ digits sum to the same value as its last ⌈k/2⌉ digits, where ⌈x⌉, pronounced ceiling of x, is the smallest integer ≥ x, thus ⌈π⌉ = 4 and ⌈5⌉ = 5.
+Um número inteiro positivo com $k$ casas (decimais) é chamado de balanceado se os seus primeiros $⌈\frac{k}{2}⌉$ algarismos têm a soma igual aos seus últimos $⌈\frac{k}{2}⌉$ algarismos, onde $⌈x⌉$, o teto pronunciado de $x$, é o menor inteiro, sendo $≥ x$, portanto $⌈π⌉ = 4$ e $⌈5⌉ = 5$.
-So, for example, all palindromes are balanced, as is 13722.
+Então, por exemplo, todos os palíndromos são balanceados, assim como 13722.
-Let T(n) be the sum of all balanced numbers less than 10n.
+Considere $T(n)$ como sendo a soma de todos os números balanceados menores que $10^n$.
-Thus: T(1) = 45, T(2) = 540 and T(5) = 334795890.
+Assim: $T(1) = 45$, $T(2) = 540$ e $T(5) = 334.795.890$.
-Find T(47) mod 315
+Encontre $T(47)\\,mod\\,3^{15}$
# --hints--
-`euler217()` should return 6273134.
+`balancedNumbers()` deve retornar `6273134`.
```js
-assert.strictEqual(euler217(), 6273134);
+assert.strictEqual(balancedNumbers(), 6273134);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler217(), 6273134);
## --seed-contents--
```js
-function euler217() {
+function balancedNumbers() {
return true;
}
-euler217();
+balancedNumbers();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
index db91d74874..2e1df0ab68 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-218-perfect-right-angled-triangles.md
@@ -1,6 +1,6 @@
---
id: 5900f4461000cf542c50ff59
-title: 'Problem 218: Perfect right-angled triangles'
+title: 'Problema 218: Triângulos retos perfeitos'
challengeType: 5
forumTopicId: 301860
dashedName: problem-218-perfect-right-angled-triangles
@@ -8,26 +8,32 @@ dashedName: problem-218-perfect-right-angled-triangles
# --description--
-Consider the right angled triangle with sides a=7, b=24 and c=25.
+Considere o triângulo reto com lados $a=7$, $b=24$ e $c=25$.
-The area of this triangle is 84, which is divisible by the perfect numbers 6 and 28.
+A área deste triângulo é 84, que é divisível pelos números perfeitos 6 e 28.
-Moreover it is a primitive right angled triangle as gcd(a,b)=1 and gcd(b,c)=1.
+Além disso, ele é um triângulo reto primitivo, já que tem os maiores divisores comuns $gcd(a,b) = 1$ e $gcd(b,c) = 1$.
-Also c is a perfect square.
+Por fim, $c$ é um quadrado perfeito.
-We will call a right angled triangle perfect if -it is a primitive right angled triangle -its hypotenuse is a perfect square
+Chamaremos um triângulo de triângulo reto perfeito se:
-We will call a right angled triangle super-perfect if -it is a perfect right angled triangle and -its area is a multiple of the perfect numbers 6 and 28.
+- for um triângulo reto primitivo
+- sua hipotenusa for um quadrado perfeito
-How many perfect right-angled triangles with c≤1016 exist that are not super-perfect?
+Chamaremos um triângulo de triângulo reto superperfeito se:
+
+- for um triângulo reto perfeito
+- sua área for um múltiplo dos números perfeitos 6 e 28.
+
+Quantos triângulos retos perfeitos com $c ≤ {10}^{16}$ existem que não são superperfeitos?
# --hints--
-`euler218()` should return 0.
+`perfectRightAngledTriangles()` deve retornar `0`.
```js
-assert.strictEqual(euler218(), 0);
+assert.strictEqual(perfectRightAngledTriangles(), 0);
```
# --seed--
@@ -35,12 +41,12 @@ assert.strictEqual(euler218(), 0);
## --seed-contents--
```js
-function euler218() {
+function perfectRightAngledTriangles() {
return true;
}
-euler218();
+perfectRightAngledTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
index 38d16eba87..92b02718d5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-219-skew-cost-coding.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5a
-title: 'Problem 219: Skew-cost coding'
+title: 'Problema 219: Codificação de custo modificado'
challengeType: 5
forumTopicId: 301861
dashedName: problem-219-skew-cost-coding
@@ -8,26 +8,26 @@ dashedName: problem-219-skew-cost-coding
# --description--
-Let A and B be bit strings (sequences of 0's and 1's).
+Considere $A$ e $B$ como sendo strings de bits (sequências de 0s e 1s).
-If A is equal to the leftmost length(A) bits of B, then A is said to be a prefix of B.
+Se $A$ for igual ao bits comprimento ($A$) mais à esquerda de $B$, então $A$ é pode ser considerado um prefixo de $B$.
-For example, 00110 is a prefix of 001101001, but not of 00111 or 100110.
+Por exemplo, 00110 é um prefixo de 001101001, mas não de 00111 ou 100110.
-A prefix-free code of size n is a collection of n distinct bit strings such that no string is a prefix of any other. For example, this is a prefix-free code of size 6:
+Um código de tamanho $n$ sem prefixo é uma coleção de $n$ strings de bits distintos, de modo que nenhuma string é um prefixo de outra. Por exemplo, este é um código de tamanho 6 sem prefixos:
-0000, 0001, 001, 01, 10, 11
+$$0000, 0001, 001, 01, 10, 11$$
-Now suppose that it costs one penny to transmit a '0' bit, but four pence to transmit a '1'. Then the total cost of the prefix-free code shown above is 35 pence, which happens to be the cheapest possible for the skewed pricing scheme in question. In short, we write Cost(6) = 35.
+Suponhamos agora que custa um centavo transmitir um bit "0", mas quatro centavos transmitir um bit "1". Então, o custo total do código sem o prefixo mostrado acima é de 35 centavos, que é o mais barato possível para o regime de preços modificados em questão. Em resumo, escrevemos $Cost(6) = 35$.
-What is Cost(109) ?
+Qual é o $Cost(10^9)$?
# --hints--
-`euler219()` should return 64564225042.
+`skewCostCoding()` deve retornar `64564225042`.
```js
-assert.strictEqual(euler219(), 64564225042);
+assert.strictEqual(skewCostCoding(), 64564225042);
```
# --seed--
@@ -35,12 +35,12 @@ assert.strictEqual(euler219(), 64564225042);
## --seed-contents--
```js
-function euler219() {
+function skewCostCoding() {
return true;
}
-euler219();
+skewCostCoding();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
index 1fccaef107..1f7114f3bd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-220-heighway-dragon.md
@@ -1,6 +1,6 @@
---
id: 5900f4481000cf542c50ff5b
-title: 'Problem 220: Heighway Dragon'
+title: 'Problema 220: Dragão de Heighway'
challengeType: 5
forumTopicId: 301863
dashedName: problem-220-heighway-dragon
@@ -8,24 +8,33 @@ dashedName: problem-220-heighway-dragon
# --description--
-Let D0 be the two-letter string "Fa". For n≥1, derive Dn from Dn-1 by the string-rewriting rules:
+Considere $D_0$ como sendo a string de duas letras "Fa". Para $n ≥ 1$, derive $D_n$ de $D_{n - 1}$ pelas regras de reescrita da string:
-"a" → "aRbFR" "b" → "LFaLb"
+- "a" → "aRbFR"
+- "b" → "LFaLb"
-Thus, D0 = "Fa", D1 = "FaRbFR", D2 = "FaRbFRRLFaLbFR", and so on.
+Assim, $D_0$ = "Fa", $D_1$ = "FaRbFR", $D_2$ = "FaRbFRRLFaLbFR" e assim por diante.
-These strings can be interpreted as instructions to a computer graphics program, with "F" meaning "draw forward one unit", "L" meaning "turn left 90 degrees", "R" meaning "turn right 90 degrees", and "a" and "b" being ignored. The initial position of the computer cursor is (0,0), pointing up towards (0,1).
+Essas strings podem ser interpretadas como instruções para um programa gráfico do computador, com "F" significando "desenhar uma unidade", "L" significando "virar 90 graus à esquerda", "R" significando "virar 90 graus à direita " e "a" e "b" sendo ignorados. A posição inicial do cursor do computador é (0,0), apontando na direção de (0,1).
-Then Dn is an exotic drawing known as the Heighway Dragon of order n. For example, D10 is shown below; counting each "F" as one step, the highlighted spot at (18,16) is the position reached after 500 steps.
+Então $D_n$ é um desenho exótico conhecido como Dragão de Heighway da ordem $n$. Por exemplo, $D_{10}$ é mostrado abaixo. Contando cada "F" como uma etapa, o local destacado em (18,16) é a posição alcançada após 500 etapas.
-What is the position of the cursor after 1012 steps in D50 ? Give your answer in the form x,y with no spaces.
+ +
+Qual é a posição do cursor depois de ${10}^{12}$ etapas em $D_{50}$? Dê sua resposta como uma string na forma `x,y` sem espaços.
# --hints--
-`euler220()` should return 139776, 963904.
+`heighwayDragon()` deve retornar uma string.
```js
-assert.strictEqual(euler220(), 139776, 963904);
+assert(typeof heighwayDragon() === 'string');
+```
+
+`heighwayDragon()` deve retornar a string `139776,963904`.
+
+```js
+assert.strictEqual(heighwayDragon(), '139776,963904');
```
# --seed--
@@ -33,12 +42,12 @@ assert.strictEqual(euler220(), 139776, 963904);
## --seed-contents--
```js
-function euler220() {
+function heighwayDragon() {
return true;
}
-euler220();
+heighwayDragon();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
index 260f8c73a0..27e78a6ac5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
@@ -12,7 +12,7 @@ Considere os triângulos com os lados inteiros $a$, $b$ e $c$ com $a ≤ b ≤ c
Um triângulo que tem seus lados sendo números inteiros $(a,b,c)$ é chamado primitivo se $gcd(a,b,c) = 1$.
-Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10\\,000\\,000$?
+Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10.000.000$?
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
index b1538fd20d..f01a6615b9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
@@ -8,7 +8,7 @@ dashedName: problem-34-digit-factorials
# --description--
-145 é um número curioso, pois 1! + 4! + 5! = 1 + 24 + 120 = 145.
+145 é um número curioso, já que 1! + 4! + 5! = 1 + 24 + 120 = 145.
Calcule os números e a soma dos números que são iguais à soma do fatorial de seus dígitos.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
index cf4cbb03f0..c8c70165cd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
@@ -12,7 +12,7 @@ Na parábola $y = \frac{x^2}{k}$, três pontos $A(a, \frac{a^2}{k})$, $B(b, \fra
Considere que $F(K, X)$ é o número de quadras de inteiros $(k, a, b, c)$, de tal forma que pelo menos um ângulo do triângulo $ABC$ é 45°, com $1 ≤ k ≤ K$ e $-X ≤ a < b < c ≤ X$.
-Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12\\,492$.
+Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12.492$.
Encontre $F({10}^6, {10}^9)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
index ab71c30048..99daff2390 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
@@ -14,7 +14,7 @@ Um exemplo de um conjunto titânico é $S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (
Por outro lado, o conjunto {(0, 0), (1, 1), (2, 2), (4, 4)} não é um conjunto titânico, já que a linha que passa por dois pontos quaisquer no conjunto também passa pelos outros dois.
-Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$ e $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$.
+Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33.554.178$, $T(111)\bmod {10}^8 = 13.500.401$ e $T({10}^5)\bmod {10}^8 = 63.259.062$.
Encontre $T({10}^{11})\bmod {10}^8$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
index a3475fd12d..f6675060dd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
@@ -12,7 +12,7 @@ Uma fileira de $n$ quadrados contém um sapo no quadrado mais à esquerda. Em su
Considere que $F(m, n)$ é o número de maneiras pelas quais o sapo pode viajar, sendo que, no máximo, um quadrado pode permanecer sem ser visitado.
-Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$.
+Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429.619.151$.
Encontre os últimos 9 dígitos de $F(10, {10}^{12})$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
index 636f277786..aa2fcd535b 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
@@ -16,9 +16,9 @@ A expressão $0.1(6)$ significa $0.16666666\dots$, e tem um ciclo recorrente de
Frações unitárias cujo denominador não tem outros fatores primos além de 2 e/ou 5 não são consideradas como tendo um ciclo recorrente. Definimos 0 como o comprimento do ciclo recorrente dessas frações unitárias.
-Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1\\,000\\,000$ é igual a $55\\,535\\,191\\,115$.
+Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1.000.000$ é igual a $55.535.191.115$.
-Calcule $\sum L(n)$ por $3 ≤ n ≤ 100\\,000\\,000$.
+Calcule $\sum L(n)$ por $3 ≤ n ≤ 100.000.000$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
index c6502c485f..db2a31a52c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
@@ -15,7 +15,7 @@ Considere $n$ um inteiro positivo. Um trio de números inteiros ($a$, $b$, $c$)
Defina $f(n)$ como $a + b + c$ para o trio da fatoração ($a$, $b$, $c$) de $n$ que minimiza $\frac{c}{a}$. Podemos mostrar que esse trio é único.
-Por exemplo, $f(165) = 19$, $f(100\\,100) = 142$ e $f(20!) = 4\\,034\\,872$.
+Por exemplo, $f(165) = 19$, $f(100.100) = 142$ e $f(20!) = 4.034.872$.
Encontre $f(43!)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
index 4adbf773f9..f71d42c2d9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
@@ -26,7 +26,7 @@ Ajuda ler os dígitos em voz alta:
...
-Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31\\,254$, $B(40) = 20\\,259$ e $C(40) = 11\\,625$.
+Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31.254$, $B(40) = 20.259$ e $C(40) = 11.625$.
Calcule $A(n)$, $B(n)$ e $C(n)$ para $n = {10}^{12}$. Dê o modulo $2^{30}$ de sua respostas como uma string e separe seus valores para $A$, $B$ e $C$ por uma vírgula. Ex: para $n = 40$, a resposta seria `31254,20259,11625`.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
index 1af6f12cbf..36638c3847 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
@@ -18,9 +18,9 @@ Considere $C(n)$ o número de triângulos cujos vértices estão em $P_n$ e que
Exemplos:
-$$\start{align} & C(8) = 20 \\\\ & C(600) = 8\\,950\\,634 \\\\ & C(40\\,000) = 2\\,66610\\,948\\,988 \end{align}$$
+$$\start{align} & C(8) = 20 \\\\ & C(600) = 8.950.634 \\\\ & C(40.000) = 266.610.948.988 \end{align}$$
-Encontre $C(2\\,000\\,000)$.
+Encontre $C(2.000.000)$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
index a895ff2632..5f50265cae 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
@@ -1,6 +1,6 @@
---
id: 5900f3b21000cf542c50fec5
-title: 'Problema 70: Permutações Totiente'
+title: 'Problema 70: Permutações de totientes'
challengeType: 5
forumTopicId: 302183
dashedName: problem-70-totient-permutation
@@ -8,7 +8,7 @@ dashedName: problem-70-totient-permutation
# --description--
-A função Totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
+A função totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
Curiosamente, ${\phi}(87109) = 79180$, e pode ser visto que 87109 é uma permutação de 79180.
+
+Qual é a posição do cursor depois de ${10}^{12}$ etapas em $D_{50}$? Dê sua resposta como uma string na forma `x,y` sem espaços.
# --hints--
-`euler220()` should return 139776, 963904.
+`heighwayDragon()` deve retornar uma string.
```js
-assert.strictEqual(euler220(), 139776, 963904);
+assert(typeof heighwayDragon() === 'string');
+```
+
+`heighwayDragon()` deve retornar a string `139776,963904`.
+
+```js
+assert.strictEqual(heighwayDragon(), '139776,963904');
```
# --seed--
@@ -33,12 +42,12 @@ assert.strictEqual(euler220(), 139776, 963904);
## --seed-contents--
```js
-function euler220() {
+function heighwayDragon() {
return true;
}
-euler220();
+heighwayDragon();
```
# --solutions--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
index 260f8c73a0..27e78a6ac5 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
@@ -12,7 +12,7 @@ Considere os triângulos com os lados inteiros $a$, $b$ e $c$ com $a ≤ b ≤ c
Um triângulo que tem seus lados sendo números inteiros $(a,b,c)$ é chamado primitivo se $gcd(a,b,c) = 1$.
-Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10\\,000\\,000$?
+Quantos triângulos primitivos (com os lados sendo números inteiros) existem com um perímetro que não excede $10.000.000$?
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
index b1538fd20d..f01a6615b9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-34-digit-factorials.md
@@ -8,7 +8,7 @@ dashedName: problem-34-digit-factorials
# --description--
-145 é um número curioso, pois 1! + 4! + 5! = 1 + 24 + 120 = 145.
+145 é um número curioso, já que 1! + 4! + 5! = 1 + 24 + 120 = 145.
Calcule os números e a soma dos números que são iguais à soma do fatorial de seus dígitos.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
index cf4cbb03f0..c8c70165cd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-397-triangle-on-parabola.md
@@ -12,7 +12,7 @@ Na parábola $y = \frac{x^2}{k}$, três pontos $A(a, \frac{a^2}{k})$, $B(b, \fra
Considere que $F(K, X)$ é o número de quadras de inteiros $(k, a, b, c)$, de tal forma que pelo menos um ângulo do triângulo $ABC$ é 45°, com $1 ≤ k ≤ K$ e $-X ≤ a < b < c ≤ X$.
-Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12\\,492$.
+Por exemplo, $F(1, 10) = 41$ e $F(10, 100) = 12.492$.
Encontre $F({10}^6, {10}^9)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
index ab71c30048..99daff2390 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-415-titanic-sets.md
@@ -14,7 +14,7 @@ Um exemplo de um conjunto titânico é $S = \\{(0, 0), (0, 1), (0, 2), (1, 1), (
Por outro lado, o conjunto {(0, 0), (1, 1), (2, 2), (4, 4)} não é um conjunto titânico, já que a linha que passa por dois pontos quaisquer no conjunto também passa pelos outros dois.
-Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33\\,554\\,178$, $T(111)\bmod {10}^8 = 13\\,500\\,401$ e $T({10}^5)\bmod {10}^8 = 63\\,259\\,062$.
+Para qualquer inteiro positivo $N$, consideremos que $T(N)$ é o número de conjuntos titânicos $S$ em que cada ponto ($x$, $y$) satisfaz $0 ≤ x$, $y ≤ N$. Pode-se verificar que $T(1) = 11$, $T(2) = 494$, $T(4) = 33.554.178$, $T(111)\bmod {10}^8 = 13.500.401$ e $T({10}^5)\bmod {10}^8 = 63.259.062$.
Encontre $T({10}^{11})\bmod {10}^8$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
index a3475fd12d..f6675060dd 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-416-a-frogs-trip.md
@@ -12,7 +12,7 @@ Uma fileira de $n$ quadrados contém um sapo no quadrado mais à esquerda. Em su
Considere que $F(m, n)$ é o número de maneiras pelas quais o sapo pode viajar, sendo que, no máximo, um quadrado pode permanecer sem ser visitado.
-Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429\\,619\\,151$.
+Por exemplo, $F(1, 3) = 4$, $F(1, 4) = 15$, $F(1, 5) = 46$, $F(2, 3) = 16$ e $F(2, 100)\bmod {10}^9 = 429.619.151$.
Encontre os últimos 9 dígitos de $F(10, {10}^{12})$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
index 636f277786..aa2fcd535b 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-417-reciprocal-cycles-ii.md
@@ -16,9 +16,9 @@ A expressão $0.1(6)$ significa $0.16666666\dots$, e tem um ciclo recorrente de
Frações unitárias cujo denominador não tem outros fatores primos além de 2 e/ou 5 não são consideradas como tendo um ciclo recorrente. Definimos 0 como o comprimento do ciclo recorrente dessas frações unitárias.
-Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1\\,000\\,000$ é igual a $55\\,535\\,191\\,115$.
+Considere que $L(n)$ denota o comprimento do ciclo recorrente de $\frac{1}{n}$. Você recebe a informação de que $\sum L(n)$ por $3 ≤ n ≤ 1.000.000$ é igual a $55.535.191.115$.
-Calcule $\sum L(n)$ por $3 ≤ n ≤ 100\\,000\\,000$.
+Calcule $\sum L(n)$ por $3 ≤ n ≤ 100.000.000$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
index c6502c485f..db2a31a52c 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-418-factorisation-triples.md
@@ -15,7 +15,7 @@ Considere $n$ um inteiro positivo. Um trio de números inteiros ($a$, $b$, $c$)
Defina $f(n)$ como $a + b + c$ para o trio da fatoração ($a$, $b$, $c$) de $n$ que minimiza $\frac{c}{a}$. Podemos mostrar que esse trio é único.
-Por exemplo, $f(165) = 19$, $f(100\\,100) = 142$ e $f(20!) = 4\\,034\\,872$.
+Por exemplo, $f(165) = 19$, $f(100.100) = 142$ e $f(20!) = 4.034.872$.
Encontre $f(43!)$.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
index 4adbf773f9..f71d42c2d9 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-419-look-and-say-sequence.md
@@ -26,7 +26,7 @@ Ajuda ler os dígitos em voz alta:
...
-Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31\\,254$, $B(40) = 20\\,259$ e $C(40) = 11\\,625$.
+Defina $A(n)$, $B(n)$ e $C(n)$ como o número de uns, dois e três no $n$'ésimo elemento da sequência, respectivamente. Podemos verificar se $A(40) = 31.254$, $B(40) = 20.259$ e $C(40) = 11.625$.
Calcule $A(n)$, $B(n)$ e $C(n)$ para $n = {10}^{12}$. Dê o modulo $2^{30}$ de sua respostas como uma string e separe seus valores para $A$, $B$ e $C$ por uma vírgula. Ex: para $n = 40$, a resposta seria `31254,20259,11625`.
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
index 1af6f12cbf..36638c3847 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-456-triangles-containing-the-origin-ii.md
@@ -18,9 +18,9 @@ Considere $C(n)$ o número de triângulos cujos vértices estão em $P_n$ e que
Exemplos:
-$$\start{align} & C(8) = 20 \\\\ & C(600) = 8\\,950\\,634 \\\\ & C(40\\,000) = 2\\,66610\\,948\\,988 \end{align}$$
+$$\start{align} & C(8) = 20 \\\\ & C(600) = 8.950.634 \\\\ & C(40.000) = 266.610.948.988 \end{align}$$
-Encontre $C(2\\,000\\,000)$.
+Encontre $C(2.000.000)$.
# --hints--
diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
index a895ff2632..5f50265cae 100644
--- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
+++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-70-totient-permutation.md
@@ -1,6 +1,6 @@
---
id: 5900f3b21000cf542c50fec5
-title: 'Problema 70: Permutações Totiente'
+title: 'Problema 70: Permutações de totientes'
challengeType: 5
forumTopicId: 302183
dashedName: problem-70-totient-permutation
@@ -8,7 +8,7 @@ dashedName: problem-70-totient-permutation
# --description--
-A função Totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
+A função totiente de Euler, ${\phi}(n)$ (às vezes chamada de função phi), é usada para determinar a quantidade de números menores que `n`, que são primos próximos de `n`. Por exemplo, 1, 2, 4, 5, 7 e 8 são todos inferiores a nove e primos relativos de nove, ${\phi}(9) = 6$. O número 1 é considerado um primo relativo para todos os números positivos, portanto ${\phi}(1) = 1$.
Curiosamente, ${\phi}(87109) = 79180$, e pode ser visto que 87109 é uma permutação de 79180.