diff --git a/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-strategies.md b/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-strategies.md index 0d29b5c99a..b0389c7b98 100644 --- a/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-strategies.md +++ b/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-strategies.md @@ -1,6 +1,6 @@ --- id: 5895f70df9fc0f352b528e68 -title: Authentication Strategies +title: Estrategias de autenticación challengeType: 2 forumTopicId: 301547 dashedName: authentication-strategies @@ -8,11 +8,11 @@ dashedName: authentication-strategies # --description-- -A strategy is a way of authenticating a user. You can use a strategy for allowing users to authenticate based on locally saved information (if you have them register first) or from a variety of providers such as Google or GitHub. For this project, we will set up a local strategy. To see a list of the hundreds of strategies, visit Passport's site [here](http://passportjs.org/). +Una estrategia es una manera de autenticar a un usuario. Puedes utilizar una estrategia para permitir que los usuarios se autentiquen basándose en la información guardada localmente (si les haces registrarse primero) o desde una variedad de proveedores como Google o GitHub. Para este proyecto, estableceremos una estrategia local. Para ver una lista de los cientos de estrategias, visita el sitio de Passport [aquí](http://passportjs.org/). -Add `passport-local@~1.0.0` as a dependency and add it to your server as follows: `const LocalStrategy = require('passport-local');` +Agrega `passport-local@~1.0.0` como dependencia y agrégalo a tu servidor de la siguiente manera: `const LocalStrategy = require('passport-local');` -Now you will have to tell passport to **use** an instantiated LocalStrategy object with a few settings defined. Make sure this (as well as everything from this point on) is encapsulated in the database connection since it relies on it! +Ahora tendrás que decirle a passport que **use** un objeto LocalStrategy instanciado con algunas configuraciones definidas. ¡Asegúrate que esto (al igual que todo lo que se haga a partir de ahora) esté encapsulado en la conexión a la base de datos, ya que depende de ella! ```js passport.use(new LocalStrategy( @@ -28,17 +28,17 @@ passport.use(new LocalStrategy( )); ``` -This is defining the process to use when we try to authenticate someone locally. First, it tries to find a user in our database with the username entered, then it checks for the password to match, then finally, if no errors have popped up that we checked for, like an incorrect password, the `user`'s object is returned and they are authenticated. +Esto es definir el proceso a utilizar cuando intentamos autenticar a alguien localmente. Primero, intenta encontrar un usuario en nuestra base de datos con el nombre de usuario introducido, luego comprueba que la contraseña coincida, y finalmente, si no han aparecido los errores que hemos comprobado, como una contraseña incorrecta, se devuelve el objeto del `user` y se autentifica. -Many strategies are set up using different settings, but generally it is easy to set it up based on the README in that strategy's repository. A good example of this is the GitHub strategy where we don't need to worry about a username or password because the user will be sent to GitHub's auth page to authenticate. As long as they are logged in and agree then GitHub returns their profile for us to use. +Muchas estrategias se configuran con diferentes ajustes, pero generalmente es fácil configurarlo basándose en el README del repositorio de esa estrategia. Un buen ejemplo de esto es la estrategia de GitHub, donde no necesitamos preocuparnos por un nombre de usuario o una contraseña porque el usuario será enviado a la página de autenticación de GitHub para autenticarse. Siempre que hayan iniciado sesión y estén de acuerdo, GitHub nos devuelve su perfil para que lo utilicemos. -In the next step, we will set up how to actually call the authentication strategy to validate a user based on form data! +En el siguiente paso, ¡configuraremos cómo llamar a la estrategia de autenticación para validar un usuario basado en los datos del formulario! -Submit your page when you think you've got it right. If you're running into errors, you can check out the project completed up to this point [here](https://gist.github.com/camperbot/53b495c02b92adeee0aa1bd3f3be8a4b). +Envía tu página cuando creas que lo has hecho bien. Si te encuentras con errores, puedes revisar el proyecto completado hasta este punto [aquí](https://gist.github.com/camperbot/53b495c02b92adeee0aa1bd3f3be8a4b). # --hints-- -Passport-local should be a dependency. +Passport-local debe ser una dependencia. ```js (getUserInput) => @@ -57,7 +57,7 @@ Passport-local should be a dependency. ); ``` -Passport-local should be correctly required and setup. +Passport-local debe ser correctamente requerido y configurado. ```js (getUserInput) => diff --git a/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-with-socket.io.md b/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-with-socket.io.md index 3020f56e31..6fb5b11740 100644 --- a/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-with-socket.io.md +++ b/curriculum/challenges/espanol/06-quality-assurance/advanced-node-and-express/authentication-with-socket.io.md @@ -1,6 +1,6 @@ --- id: 589fc831f9fc0f352b528e77 -title: Authentication with Socket.IO +title: Autenticación con Socket.IO challengeType: 2 forumTopicId: 301548 dashedName: authentication-with-socket-io @@ -8,9 +8,9 @@ dashedName: authentication-with-socket-io # --description-- -Currently, you cannot determine who is connected to your web socket. While `req.user` contains the user object, that's only when your user interacts with the web server, and with web sockets you have no `req` (request) and therefore no user data. One way to solve the problem of knowing who is connected to your web socket is by parsing and decoding the cookie that contains the passport session then deserializing it to obtain the user object. Luckily, there is a package on NPM just for this that turns a once complex task into something simple! +Actualmente, no puedes determinar quién está conectado a tu web socket. Mientras que `req.user` contiene el objeto user, eso es sólo cuando tu usuario interactúa con el servidor web, y con los web sockets no tienes la `req` (petición) y por lo tanto no hay datos del usuario. Una forma de resolver el problema de saber quién está conectado a tu socket web es analizando (parsing) y decodificando la cookie que contiene la sesión del pasaporte y luego deserializándola para obtener el objeto user. Por suerte, ¡hay un paquete en NPM sólo para esto que convierte una tarea antes compleja en algo sencillo! -Add `passport.socketio@~3.7.0`, `connect-mongo@~3.2.0`, and `cookie-parser@~1.4.5` as dependencies and require them as `passportSocketIo`, `MongoStore`, and `cookieParser` respectively. Also, we need to initialize a new memory store, from `express-session` which we previously required. It should look like this: +Agrega `passport.socketio@~3.7.0`, `connect-mongo@~3.2.0`y `cookie-parser@~1.4.5` como dependencias y requiérelas como `passportSocketIo`, `MongoStore`y `cookieParser` respectivamente. Además, necesitamos inicializar un nuevo almacén de memoria, a partir de `express-session` que requerimos previamente. Debe verse así: ```js const MongoStore = require('connect-mongo')(session); @@ -18,7 +18,7 @@ const URI = process.env.MONGO_URI; const store = new MongoStore({ url: URI }); ``` -Now we just have to tell Socket.IO to use it and set the options. Be sure this is added before the existing socket code and not in the existing connection listener. For your server, it should look like this: +Ahora sólo tenemos que decirle a Socket.IO que lo utilice y establezca las opciones. Asegúrate de que esto se agrega antes del código de socket existente y no en el oyente de conexión existente. Para tu servidor, debe verse así: ```js io.use( @@ -33,11 +33,15 @@ io.use( ); ``` -Be sure to add the `key` and `store` to the `session` middleware mounted on the app. This is necessary to tell *SocketIO* which session to relate to. +Ten en cuenta que configurar la autenticación de Passport para Socket.IO es muy similar a la forma en que configuramos el middleware de `session` para la API. Esto se debe a que deben usar el mismo método de autenticación: obtener el session id de una cookie y validarlo. + +Anteriormente, cuando configuramos el middleware de `session`, no establecíamos explícitamente el nombre de la cookie para la sesión (`key`). Esto se debe a que el paquete `session` estaba usando el valor predeterminado. Ahora que hemos añadido otro paquete que necesita acceso al mismo valor desde las cookies, necesitamos establecer explícitamente el valor `key` en ambos objetos de configuración. + +Asegúrate de añadir la `key` con el nombre de la cookie al middleware `session` que coincida con la clave Socket.IO. Además, añade la referencia `store` a las opciones, cerca de donde establecemos `saveUninitialized: true`. Esto es necesario para decirle a Socket.IO con qué sesión relacionarse.
-Now, define the `success`, and `fail` callback functions: +Ahora, define las funciones callback de `success` y `fail`: ```js function onAuthorizeSuccess(data, accept) { @@ -53,19 +57,19 @@ function onAuthorizeFail(data, message, error, accept) { } ``` -The user object is now accessible on your socket object as `socket.request.user`. For example, now you can add the following: +El objeto user ahora es accesible en su objeto socket como `socket.request.user`. Por ejemplo, ahora puedes añadir lo siguiente: ```js console.log('user ' + socket.request.user.name + ' connected'); ``` -It will log to the server console who has connected! +¡Se registrará en la consola del servidor quién se ha conectado! -Submit your page when you think you've got it right. If you're running into errors, you can check out the project up to this point [here](https://gist.github.com/camperbot/1414cc9433044e306dd7fd0caa1c6254). +Envía tu página cuando creas que lo has hecho bien. Si te encuentras con errores, puedes revisar el proyecto completado hasta este punto [aquí](https://gist.github.com/camperbot/1414cc9433044e306dd7fd0caa1c6254). # --hints-- -`passport.socketio` should be a dependency. +`passport.socketio` debe ser una dependencia. ```js (getUserInput) => @@ -84,7 +88,7 @@ Submit your page when you think you've got it right. If you're running into erro ); ``` -`cookie-parser` should be a dependency. +`cookie-parser` debe ser una dependencia. ```js (getUserInput) => @@ -103,7 +107,7 @@ Submit your page when you think you've got it right. If you're running into erro ); ``` -passportSocketIo should be properly required. +passportSocketIo debe ser requerido correctamente. ```js (getUserInput) => @@ -121,7 +125,7 @@ passportSocketIo should be properly required. ); ``` -passportSocketIo should be properly setup. +passportSocketIo debe estar configurado correctamente. ```js (getUserInput) => diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-221-alexandrian-integers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-221-alexandrian-integers.md index 010d2bd57c..4fab3b0159 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-221-alexandrian-integers.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-221-alexandrian-integers.md @@ -1,6 +1,6 @@ --- id: 5900f4491000cf542c50ff5c -title: 'Problem 221: Alexandrian Integers' +title: 'Problema 221: Inteiros alexandrinos' challengeType: 5 forumTopicId: 301864 dashedName: problem-221-alexandrian-integers @@ -8,20 +8,25 @@ dashedName: problem-221-alexandrian-integers # --description-- -We shall call a positive integer A an "Alexandrian integer", if there exist integers p, q, r such that: A = p · q · r and 1/A = 1/p + 1/q + 1/r +Chamaremos um número inteiro positivo $A$ de "inteiro alexandrino" se existirem inteiros $p$, $q$, $r$, como: - +$$A = p \times q \times r$$ -For example, 630 is an Alexandrian integer (p = 5, q = −7, r = −18). In fact, 630 is the 6th Alexandrian integer, the first 6 Alexandrian integers being: 6, 42, 120, 156, 420 and 630. +e -Find the 150000th Alexandrian integer. +$$\frac{1}{A} = \frac{1}{p} + \frac{1}{q} + \frac{1}{r}$$ + + +Por exemplo, 630 é um inteiro alexandrino ($p = 5$, $q = − 7$, $r = − 18$). Na verdade, 630 é o 6° inteiro alexandrino, sendo os 6 primeiros números inteiros alexandrinos 6, 42, 120, 156, 420 e 630. + +Encontre o número 150.000º inteiro alexandrino. # --hints-- -`euler221()` should return 1884161251122450. +`alexandrianIntegers()` deve retornar `1884161251122450`. ```js -assert.strictEqual(euler221(), 1884161251122450); +assert.strictEqual(alexandrianIntegers(), 1884161251122450); ``` # --seed-- @@ -29,12 +34,12 @@ assert.strictEqual(euler221(), 1884161251122450); ## --seed-contents-- ```js -function euler221() { +function alexandrianIntegers() { return true; } -euler221(); +alexandrianIntegers(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-222-sphere-packing.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-222-sphere-packing.md index 423ce7ff8e..2ae536a594 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-222-sphere-packing.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-222-sphere-packing.md @@ -1,6 +1,6 @@ --- id: 5900f44b1000cf542c50ff5d -title: 'Problem 222: Sphere Packing' +title: 'Problema 222: Embalagem de esferas' challengeType: 5 forumTopicId: 301865 dashedName: problem-222-sphere-packing @@ -8,16 +8,16 @@ dashedName: problem-222-sphere-packing # --description-- -What is the length of the shortest pipe, of internal radius 50mm, that can fully contain 21 balls of radii 30mm, 31mm, ..., 50mm? +Qual é o comprimento do tubo mais curto, de um raio interno de 50 mm, que pode conter totalmente 21 bolas de raios de 30 mm, 31 mm, ..., 50 mm? -Give your answer in micrometres (10-6 m) rounded to the nearest integer. +Dê sua resposta em micrômetros (${10}^{-6}$ m), arredondada para o mais próximo número inteiro. # --hints-- -`euler222()` should return 1590933. +`spherePacking()` deve retornar `1590933`. ```js -assert.strictEqual(euler222(), 1590933); +assert.strictEqual(spherePacking(), 1590933); ``` # --seed-- @@ -25,12 +25,12 @@ assert.strictEqual(euler222(), 1590933); ## --seed-contents-- ```js -function euler222() { +function spherePacking() { return true; } -euler222(); +spherePacking(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-223-almost-right-angled-triangles-i.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-223-almost-right-angled-triangles-i.md index 28f8d8f214..8608316afb 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-223-almost-right-angled-triangles-i.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-223-almost-right-angled-triangles-i.md @@ -1,6 +1,6 @@ --- id: 5900f44b1000cf542c50ff5e -title: 'Problem 223: Almost right-angled triangles I' +title: 'Problema 223: Triângulos quase retos I' challengeType: 5 forumTopicId: 301866 dashedName: problem-223-almost-right-angled-triangles-i @@ -8,16 +8,16 @@ dashedName: problem-223-almost-right-angled-triangles-i # --description-- -Let us call an integer sided triangle with sides a ≤ b ≤ c barely acute if the sides satisfy a2 + b2 = c2 + 1. +Chamaremos um triângulo de comprimento dos lados expresso em números inteiros, com os lados $a ≤ b ≤ c$, de quase agudos se os lados satisfizerem $a^2 + b^2 = c^2 + 1$. -How many barely acute triangles are there with perimeter ≤ 25,000,000? +Quantos triângulos quase agudos existem com o perímetro $≤ 25.000.000$? # --hints-- -`euler223()` should return 61614848. +`almostRightAngledTrianglesOne()` deve retornar `61614848`. ```js -assert.strictEqual(euler223(), 61614848); +assert.strictEqual(almostRightAngledTrianglesOne(), 61614848); ``` # --seed-- @@ -25,12 +25,12 @@ assert.strictEqual(euler223(), 61614848); ## --seed-contents-- ```js -function euler223() { +function almostRightAngledTrianglesOne() { return true; } -euler223(); +almostRightAngledTrianglesOne(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-224-almost-right-angled-triangles-ii.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-224-almost-right-angled-triangles-ii.md index d9f557fd4a..cbe30409b0 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-224-almost-right-angled-triangles-ii.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-224-almost-right-angled-triangles-ii.md @@ -1,6 +1,6 @@ --- id: 5900f44e1000cf542c50ff5f -title: 'Problem 224: Almost right-angled triangles II' +title: 'Problema 224: Triângulos quase retos II' challengeType: 5 forumTopicId: 301867 dashedName: problem-224-almost-right-angled-triangles-ii @@ -8,16 +8,16 @@ dashedName: problem-224-almost-right-angled-triangles-ii # --description-- -Let us call an integer sided triangle with sides a ≤ b ≤ c barely obtuse if the sides satisfy a2 + b2 = c2 - 1. +Chamaremos um triângulo de comprimento dos lados expresso em números inteiros, com os lados $a ≤ b ≤ c$, de quase obtusos se os lados satisfizerem $a^2 + b^2 = c^2 - 1$. -How many barely obtuse triangles are there with perimeter ≤ 75,000,000? +Quantos triângulos quase obtusos existem com o perímetro $≤ 75.000.000$? # --hints-- -`euler224()` should return 4137330. +`almostRightAngledTrianglesTwo()` deve retornar `4137330`. ```js -assert.strictEqual(euler224(), 4137330); +assert.strictEqual(almostRightAngledTrianglesTwo(), 4137330); ``` # --seed-- @@ -25,12 +25,12 @@ assert.strictEqual(euler224(), 4137330); ## --seed-contents-- ```js -function euler224() { +function almostRightAngledTrianglesTwo() { return true; } -euler224(); +almostRightAngledTrianglesTwo(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-225-tribonacci-non-divisors.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-225-tribonacci-non-divisors.md index ff5fb05c1a..0bca2ab719 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-225-tribonacci-non-divisors.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-225-tribonacci-non-divisors.md @@ -1,6 +1,6 @@ --- id: 5900f44e1000cf542c50ff60 -title: 'Problem 225: Tribonacci non-divisors' +title: 'Problema 225: Não divisores Tribonacci' challengeType: 5 forumTopicId: 301868 dashedName: problem-225-tribonacci-non-divisors @@ -8,20 +8,20 @@ dashedName: problem-225-tribonacci-non-divisors # --description-- -The sequence 1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, 653, 1201 ... +A sequência 1, 1, 1, 3, 5, 9, 17, 31, 57, 105, 193, 355, 653, 1201... -is defined by T1 = T2 = T3 = 1 and Tn = Tn-1 + Tn-2 + Tn-3. +é definida por $T_1 = T_2 = T_3 = 1$ e $T_n = T_{n - 1} + T_{n - 2} + T_{n - 3}$. -It can be shown that 27 does not divide any terms of this sequence.In fact, 27 is the first odd number with this property. +Pode-se mostrar que 27 não divide nenhum termo desta sequência. De fato, 27 é o primeiro número ímpar com esta propriedade. -Find the 124th odd number that does not divide any terms of the above sequence. +Encontre o ${124}^{\text{o}}$ número ímpar que não divide nenhum dos termos da sequência acima. # --hints-- -`euler225()` should return 2009. +`tribonacciNonDivisors()` deve retornar `2009`. ```js -assert.strictEqual(euler225(), 2009); +assert.strictEqual(tribonacciNonDivisors(), 2009); ``` # --seed-- @@ -29,12 +29,12 @@ assert.strictEqual(euler225(), 2009); ## --seed-contents-- ```js -function euler225() { +function tribonacciNonDivisors() { return true; } -euler225(); +tribonacciNonDivisors(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-226-a-scoop-of-blancmange.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-226-a-scoop-of-blancmange.md index 3aadacc50b..cc4fceb398 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-226-a-scoop-of-blancmange.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-226-a-scoop-of-blancmange.md @@ -1,6 +1,6 @@ --- id: 5900f4511000cf542c50ff62 -title: 'Problem 226: A Scoop of Blancmange' +title: 'Problema 226: Uma colherada de manjar branco' challengeType: 5 forumTopicId: 301869 dashedName: problem-226-a-scoop-of-blancmange @@ -8,20 +8,22 @@ dashedName: problem-226-a-scoop-of-blancmange # --description-- -The blancmange curve is the set of points (x,y) such that 0 ≤ x ≤ 1 and ,where s(x) = the distance from x to the nearest integer. +A curva de manjar branco é um conjunto de pontos ($x$,$y$), tal que $0 ≤ x ≤ 1$ e $\displaystyle y = \sum_{n = 0}^{\infty} \frac{s(2^nx)}{2^n}$, onde $s(x)$ é a distância de $x$ até o próximo número inteiro. 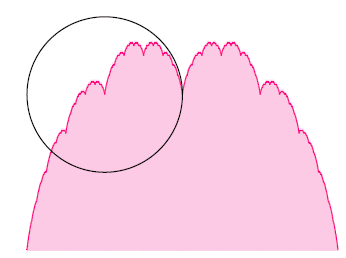-The area under the blancmange curve is equal to ½, shown in pink in the diagram below. +A área abaixo da curva de manjar branco é igual a$\frac{1}{2}$, que aparece em rosa no diagrama abaixo. -Let C be the circle with centre (¼,½) and radius ¼, shown in black in the diagram. +diagrama da curva de manjar branco, com o círculo C mostrado no diagrama -What area under the blancmange curve is enclosed by C?Give your answer rounded to eight decimal places in the form 0.abcdefgh +Considere $C$ como sendo o círculo com o centro ($\frac{1}{4}$,$\frac{1}{2}$) e raio $\frac{1}{4}$, que aparece em preto no diagrama. + +Qual área sob a curva de manjar branco está delimitada por $C$? Arredonde sua resposta para até oito casas decimais usando o formato 0.abcdefgh # --hints-- -`euler226()` should return 0.11316017. +`scoopOfBlancmange()` deve retornar `0.11316017`. ```js -assert.strictEqual(euler226(), 0.11316017); +assert.strictEqual(scoopOfBlancmange(), 0.11316017); ``` # --seed-- @@ -29,12 +31,12 @@ assert.strictEqual(euler226(), 0.11316017); ## --seed-contents-- ```js -function euler226() { +function scoopOfBlancmange() { return true; } -euler226(); +scoopOfBlancmange(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-227-the-chase.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-227-the-chase.md index aff8e9b934..b15665560d 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-227-the-chase.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-227-the-chase.md @@ -1,6 +1,6 @@ --- id: 5900f44f1000cf542c50ff61 -title: 'Problem 227: The Chase' +title: 'Problema 227: A caçada' challengeType: 5 forumTopicId: 301870 dashedName: problem-227-the-chase @@ -8,18 +8,26 @@ dashedName: problem-227-the-chase # --description-- -"The Chase" is a game played with two dice and an even number of players. +"A caçada" é um jogo que consiste em dois dados e um número par de jogadores. -The players sit around a table; the game begins with two opposite players having one die each. On each turn, the two players with a die roll it. If a player rolls a 1, he passes the die to his neighbour on the left; if he rolls a 6, he passes the die to his neighbour on the right; otherwise, he keeps the die for the next turn. The game ends when one player has both dice after they have been rolled and passed; that player has then lost. +Os jogadores sentam-se ao redor de uma mesa. O jogo começa com dois jogadores opostos tendo um dado cada. A cada turno, os dois jogadores que têm o dado o rolam. -In a game with 100 players, what is the expected number of turns the game lasts? Give your answer rounded to ten significant digits. +Se o jogador rolar um 1, ele passa o dado ao vizinho à esquerda. + +Se o jogador rolar um 6, ele passa o dado ao vizinho à direita. + +Caso contrário, ele mantém o dado no próximo turno. + +O jogo termina quando um jogador tem os dois dados depois que eles forem rolados e passados. Aquele jogador perdeu. + +Em um jogo com 100 jogadores, qual é o número esperado de turnos que dure o jogo? Dê sua resposta arredondada para dez algarismos significativos (total de casas somando antes e depois da vírgula). # --hints-- -`euler227()` should return 3780.618622. +`theChase()` deve retornar `3780.618622`. ```js -assert.strictEqual(euler227(), 3780.618622); +assert.strictEqual(theChase(), 0.618622); ``` # --seed-- @@ -27,12 +35,12 @@ assert.strictEqual(euler227(), 3780.618622); ## --seed-contents-- ```js -function euler227() { +function theChase() { return true; } -euler227(); +theChase(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-228-minkowski-sums.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-228-minkowski-sums.md index 3ee325d2be..324c0d1673 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-228-minkowski-sums.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-228-minkowski-sums.md @@ -1,6 +1,6 @@ --- id: 5900f4511000cf542c50ff63 -title: 'Problem 228: Minkowski Sums' +title: 'Problem 228: Somas de Minkowski' challengeType: 5 forumTopicId: 301871 dashedName: problem-228-minkowski-sums @@ -8,34 +8,26 @@ dashedName: problem-228-minkowski-sums # --description-- - +Considere $S_n$ como o polígono – ou forma – regular de $n$ lados, cujos vértices $v_k (k = 1, 2, \ldots, n)$ têm as coordenadas: -Let Sn be the regular n-sided polygon – or shape – whose vertices +$$\begin{align} & x_k = cos(\frac{2k - 1}{n} × 180°) \\\\ & y_k = sin(\frac{2k - 1}{n} × 180°) \end{align}$$ -vk (k = 1,2,…,n) have coordinates: +Cada $S_n$ deve ser interpretado como uma forma preenchida que consiste em todos os pontos no perímetro e no interior. -xk = cos( 2k-1/n ×180° ) +A soma de Minkowski, $S + T$, de duas formas $S$ e $T$ é o resultado de adicionar cada ponto em $S$ a cada ponto em $T$, onde a adição dos pontos é realizada através das coordenadas: $(u, v) + (x, y) = (u + x, v + y)$. -yk = sin( 2k-1/n ×180° ) +Por exemplo, a soma de $S_3$ e $S_4$ é a forma de seis lados mostrada em rosa abaixo: -Each Sn is to be interpreted as a filled shape consisting of all points on the perimeter and in the interior. +imagem mostrando S_3, S_4 e S_3 + S_4 -The Minkowski sum, S+T, of two shapes S and T is the result of - -adding every point in S to every point in T, where point addition is performed coordinate-wise: - -(u, v) + (x, y) = (u+x, v+y). - -For example, the sum of S3 and S4 is the six-sided shape shown in pink below: - -How many sides does S1864 + S1865 + … + S1909 have? +Quantos lados tem $S_{1864} + S_{1865} + \ldots + S_{1909}$? # --hints-- -`euler228()` should return 86226. +`minkowskiSums()` deve retornar `86226`. ```js -assert.strictEqual(euler228(), 86226); +assert.strictEqual(minkowskiSums(), 86226); ``` # --seed-- @@ -43,12 +35,12 @@ assert.strictEqual(euler228(), 86226); ## --seed-contents-- ```js -function euler228() { +function minkowskiSums() { return true; } -euler228(); +minkowskiSums(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-229-four-representations-using-squares.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-229-four-representations-using-squares.md index 0431ab815b..c0dcee7b6d 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-229-four-representations-using-squares.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-229-four-representations-using-squares.md @@ -1,6 +1,6 @@ --- id: 5900f4521000cf542c50ff64 -title: 'Problem 229: Four Representations using Squares' +title: 'Problema 229: Quatro representações usando quadrados' challengeType: 5 forumTopicId: 301872 dashedName: problem-229-four-representations-using-squares @@ -8,28 +8,28 @@ dashedName: problem-229-four-representations-using-squares # --description-- -Consider the number 3600. It is very special, because +Considere o número 3600. Ele é muito especial, porque -3600 = 482 + 362 3600 = 202 + 2×402 3600 = 302 + 3×302 3600 = 452 + 7×152 +$$\begin{align} & 3600 = {48}^2 + {36}^2 \\\\ & 3600 = {20}^2 + {2×40}^2 \\\\ & 3600 = {30}^2 + {3×30}^2 \\\\ & 3600 = {45}^2 + {7×15}^2 \\\\ \end{align}$$ -Similarly, we find that 88201 = 992 + 2802 = 2872 + 2×542 = 2832 + 3×522 = 1972 + 7×842. +Da mesma forma, descobrimos que $88201 = {99}^2 + {280}^2 = {287}^2 + 2 × {54}^2 = {283}^2 + 3 × {52}^2 = {197}^2 + 7 × {84}^2$. -In 1747, Euler proved which numbers are representable as a sum of two squares. We are interested in the numbers n which admit representations of all of the following four types: +Em 1747, Euler provou quais números são representáveis como uma soma de dois quadrados. Estamos interessados nos números $n$ que admitem representações de todos os quatro tipos a seguir: -n = a12 + b12n = a22 + 2 b22n = a32 + 3 b32n = a72 + 7 b72, +$$\begin{align} & n = {a_1}^2 + {b_1}^2 \\\\ & n = {a_2}^2 + 2{b_2}^2 \\\\ & n = {a_3}^2 + 3{b_3}^2 \\\\ & n = {a_7}^2 + 7{b_7}^2 \\\\ \end{align}$$ -where the ak and bk are positive integers. +onde $a_k$ e $b_k$ são números inteiros positivos. -There are 75373 such numbers that do not exceed 107. +Há 75373 números que não excedem ${10}^7$. -How many such numbers are there that do not exceed 2×109? +Quantos desses números existem e que não excedam $2 × {10}^9$? # --hints-- -`euler229()` should return 11325263. +`representationsUsingSquares()` deve retornar `11325263`. ```js -assert.strictEqual(euler229(), 11325263); +assert.strictEqual(representationsUsingSquares(), 11325263); ``` # --seed-- @@ -37,12 +37,12 @@ assert.strictEqual(euler229(), 11325263); ## --seed-contents-- ```js -function euler229() { +function representationsUsingSquares() { return true; } -euler229(); +representationsUsingSquares(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-230-fibonacci-words.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-230-fibonacci-words.md index 16ea313199..c529532c4b 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-230-fibonacci-words.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-230-fibonacci-words.md @@ -1,6 +1,6 @@ --- id: 5900f4531000cf542c50ff65 -title: 'Problem 230: Fibonacci Words' +title: 'Problema 230: Palavras de Fibonacci' challengeType: 5 forumTopicId: 301874 dashedName: problem-230-fibonacci-words @@ -8,32 +8,36 @@ dashedName: problem-230-fibonacci-words # --description-- -For any two strings of digits, A and B, we define FA,B to be the sequence (A,B,AB,BAB,ABBAB,...) in which each term is the concatenation of the previous two. +Para duas strings de algarismos quaisquer, $A$ e $B$, definimos $F_{A,B}$ como a sequência ($A, B, AB, BAB, ABBAB, \ldots$) na qual cada termo é a concatenação dos dois anteriores. -Further, we define DA,B(n) to be the nth digit in the first term of FA,B that contains at least n digits. +Além disso, definimos $D_{A,B}(n)$ como o $n^{\text{o}}$ algarismo do primeiro termo de $F_{A,B}$ que contém, pelo menos, $n$ algarismos. -Example: +Exemplo: -Let A=1415926535, B=8979323846. We wish to find DA,B(35), say. +Considere $A = 1.415.926.535$, $B = 8.979.323.846$. Queremos encontrar, digamos, $D_{A,B}(35)$. -The first few terms of FA,B are: 1415926535 8979323846 14159265358979323846 897932384614159265358979323846 14159265358979323846897932384614159265358979323846 +Os primeiros termos de $F_{A,B}$ são: -Then DA,B(35) is the 35th digit in the fifth term, which is 9. +$$\begin{align} & 1.415.926\\,535 \\\\ & 8.979.323.846 \\\\ & 14.159.265.358.979.323.846 \\\\ & 897.932.384.614.159.265.358.979.323.846 \\\\ & 14.159.265.358.979.323.846.897.932.384.614.15\color{red}{9}.265.358.979.323.846 \end{align}$$ -Now we use for A the first 100 digits of π behind the decimal point: 14159265358979323846264338327950288419716939937510 58209749445923078164062862089986280348253421170679 +Então, $D_{A,B}(35)$ é o ${35}^{\text{o}}$ algarismo no quinto termo, que é 9. -and for B the next hundred digits: +Agora, usamos para $A$ os primeiros 100 algarismos de $π$ antes do ponto decimal: -82148086513282306647093844609550582231725359408128 48111745028410270193852110555964462294895493038196 . +$$\begin{align} & 14.159.265.358.979.323.846.264.338.327.950.288.419.716.939.937.510 \\\\ & 58.209.749.445.923.078.164.062.862.089.986.280.348.253.421.170.679 \end{align}$$ -Find ∑n = 0,1,...,17 10n× DA,B((127+19n)×7n) . +e para $B$ os próximos cem algarismos: + +$$\begin{align} & 82.148.086.513.282.306.647.093.844.609.550.582.231.725.359.408.128 \\\\ & 48.111.745.028.410.270.193.852.110.555.964.462.294.895.493.038.196 \end{align}$$ + +Encontre $\sum_{n = 0, 1, \ldots, 17} {10}^n × D_{A,B}((127 + 19n) × 7^n)$. # --hints-- -`euler230()` should return 850481152593119200. +`fibonacciWords()` deve retornar `850481152593119200`. ```js -assert.strictEqual(euler230(), 850481152593119200); +assert.strictEqual(fibonacciWords(), 850481152593119200); ``` # --seed-- @@ -41,12 +45,12 @@ assert.strictEqual(euler230(), 850481152593119200); ## --seed-contents-- ```js -function euler230() { +function fibonacciWords() { return true; } -euler230(); +fibonacciWords(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-231-the-prime-factorisation-of-binomial-coefficients.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-231-the-prime-factorisation-of-binomial-coefficients.md index c313225c72..25a974bdc3 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-231-the-prime-factorisation-of-binomial-coefficients.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-231-the-prime-factorisation-of-binomial-coefficients.md @@ -1,6 +1,6 @@ --- id: 5900f4531000cf542c50ff66 -title: 'Problem 231: The prime factorisation of binomial coefficients' +title: 'Problema 231: Fatoração de números primos de coeficientes binomiais' challengeType: 5 forumTopicId: 301875 dashedName: problem-231-the-prime-factorisation-of-binomial-coefficients @@ -8,20 +8,20 @@ dashedName: problem-231-the-prime-factorisation-of-binomial-coefficients # --description-- -The binomial coefficient 10C3 = 120. +O coeficiente binomial $\displaystyle\binom{10}{3} = 120$. -120 = 23 × 3 × 5 = 2 × 2 × 2 × 3 × 5, and 2 + 2 + 2 + 3 + 5 = 14. +$120 = 2^3 × 3 × 5 = 2 × 2 × 2 × 3 × 5$, and $2 + 2 + 2 + 3 + 5 = 14$. -So the sum of the terms in the prime factorisation of 10C3 is 14. +Portanto, a soma dos termos na fatoração de números primos de $\displaystyle\binom{10}{3}$ é $14$. -Find the sum of the terms in the prime factorisation of 20000000C15000000. +Encontre a soma dos termos na fatoração de números primos de $\binom{20.000.000}{15.000.000}$. # --hints-- -`euler231()` should return 7526965179680. +`primeFactorisation()` deve retornar `7526965179680`. ```js -assert.strictEqual(euler231(), 7526965179680); +assert.strictEqual(primeFactorisation(), 7526965179680); ``` # --seed-- @@ -29,12 +29,12 @@ assert.strictEqual(euler231(), 7526965179680); ## --seed-contents-- ```js -function euler231() { +function primeFactorisation() { return true; } -euler231(); +primeFactorisation(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-232-the-race.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-232-the-race.md index c109669bd8..ece0f8ea43 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-232-the-race.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-232-the-race.md @@ -1,6 +1,6 @@ --- id: 5900f4551000cf542c50ff67 -title: 'Problem 232: The Race' +title: 'Problema 232: A corrida' challengeType: 5 forumTopicId: 301876 dashedName: problem-232-the-race @@ -8,20 +8,26 @@ dashedName: problem-232-the-race # --description-- -Two players share an unbiased coin and take it in turns to play "The Race". On Player 1's turn, he tosses the coin once: if it comes up Heads, he scores one point; if it comes up Tails, he scores nothing. On Player 2's turn, she chooses a positive integer T and tosses the coin T times: if it comes up all Heads, she scores 2T-1 points; otherwise, she scores nothing. Player 1 goes first. The winner is the first to 100 or more points. +Dois jogadores compartilham uma moeda não viesada e a usam, cada um na sua vez, para jogar "A Corrida". -On each turn Player 2 selects the number, T, of coin tosses that maximises the probability of her winning. +No turno do Jogador 1, ele joga uma vez a moeda: se der Cara, ele marca um ponto; se der Coroa, ele não marca nada. -What is the probability that Player 2 wins? +Na vez do Jogador 2, ela escolhe um número inteiro positivo $T$ e joga a moeda $T$ vezes: se der Cara sempre, ele faz $2^{T - 1}$ pontos. Caso contrário, ele não pontua. -Give your answer rounded to eight decimal places in the form 0.abcdefgh . +O jogador 1 joga primeiro. O vencedor é o primeiro a chegar a 100 pontos ou mais. + +Em cada turno, o Jogador 2 seleciona o número, $T$, de lançamentos da moeda que maximizam a probabilidade de sua vitória. + +Qual é a probabilidade de o Jogador 2 vencer? + +Arredonde sua resposta para até oito casas decimais usando o formato 0.abcdefgh. # --hints-- -`euler232()` should return 0.83648556. +`theRace()` deve retornar `0.83648556`. ```js -assert.strictEqual(euler232(), 0.83648556); +assert.strictEqual(theRace(), 0.83648556); ``` # --seed-- @@ -29,12 +35,12 @@ assert.strictEqual(euler232(), 0.83648556); ## --seed-contents-- ```js -function euler232() { +function theRace() { return true; } -euler232(); +theRace(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-233-lattice-points-on-a-circle.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-233-lattice-points-on-a-circle.md index 5903d7e8c9..f43b600527 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-233-lattice-points-on-a-circle.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-233-lattice-points-on-a-circle.md @@ -1,6 +1,6 @@ --- id: 5900f4551000cf542c50ff68 -title: 'Problem 233: Lattice points on a circle' +title: 'Problema 233: Pontos de rede em um círculo' challengeType: 5 forumTopicId: 301877 dashedName: problem-233-lattice-points-on-a-circle @@ -8,18 +8,18 @@ dashedName: problem-233-lattice-points-on-a-circle # --description-- -Let f(N) be the number of points with integer coordinates that are on a circle passing through (0,0), (N,0),(0,N), and (N,N). +Considere $f(N)$ como sendo o número de pontos com coordenadas compostas de números inteiros em um círculo que passa por $(0,0)$, $(N,0)$,$(0,N)$ e $(N,N)$. -It can be shown that f(10000) = 36. +Podemos mostrar que $f(10000) = 36$. -What is the sum of all positive integers N ≤ 1011 such that f(N) = 420 ? +Qual é a soma de todos os números inteiros positivos $N ≤ {10}^{11}$ tal que $f(N) = 420$? # --hints-- -`euler233()` should return 271204031455541300. +`latticePointsOnACircle()` deve retornar `271204031455541300`. ```js -assert.strictEqual(euler233(), 271204031455541300); +assert.strictEqual(latticePointsOnACircle(), 271204031455541300); ``` # --seed-- @@ -27,12 +27,12 @@ assert.strictEqual(euler233(), 271204031455541300); ## --seed-contents-- ```js -function euler233() { +function latticePointsOnACircle() { return true; } -euler233(); +latticePointsOnACircle(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-234-semidivisible-numbers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-234-semidivisible-numbers.md index edf39ca239..e7d8af1c51 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-234-semidivisible-numbers.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-234-semidivisible-numbers.md @@ -1,6 +1,6 @@ --- id: 5900f4571000cf542c50ff69 -title: 'Problem 234: Semidivisible numbers' +title: 'Problema 234: Números semidivisíveis' challengeType: 5 forumTopicId: 301878 dashedName: problem-234-semidivisible-numbers @@ -8,22 +8,22 @@ dashedName: problem-234-semidivisible-numbers # --description-- -For an integer n ≥ 4, we define the lower prime square root of n, denoted by lps(n), as the largest prime ≤ √n and the upper prime square root of n, ups(n), as the smallest prime ≥ √n. +Para um número inteiro $n ≥ 4$, definiremos a menor raiz quadrada de número primo de $n$, denotada por $lps(n)$, como $\text{maior primo} ≤ \sqrt{n}$ e a maior raiz quadrada de número primo de $n$, $ups(n)$, como $\text{menor primo} ≥ \sqrt{n}$. -So, for example, lps(4) = 2 = ups(4), lps(1000) = 31, ups(1000) = 37. +Por exemplo, $lps(4) = 2 = ups(4)$, $lps(1000) = 31$, $ups(1000) = 37$. -Let us call an integer n ≥ 4 semidivisible, if one of lps(n) and ups(n) divides n, but not both. +Chamaremos um número inteiro $n ≥ 4$ de semidivisível se $lps(n)$ ou $ups(n)$ dividir $n$, mas não os dois. -The sum of the semidivisible numbers not exceeding 15 is 30, the numbers are 8, 10 and 12. 15 is not semidivisible because it is a multiple of both lps(15) = 3 and ups(15) = 5. As a further example, the sum of the 92 semidivisible numbers up to 1000 is 34825. +A soma dos números semidivisíveis não excedendo 15 é 30, e os números são 8, 10 e 12. 15 não é semidivisível, pois ele é um múltiplo de $lps(15) = 3$ e de $ups(15) = 5$. Como outro exemplo, a soma dos 92 números semidivisíveis até 1000 é 34825. -What is the sum of all semidivisible numbers not exceeding 999966663333 ? +Qual é a soma de todos os números semidivisíveis que não excedem 999966663333? # --hints-- -`euler234()` should return 1259187438574927000. +`semidivisibleNumbers()` deve retornar `1259187438574927000`. ```js -assert.strictEqual(euler234(), 1259187438574927000); +assert.strictEqual(semidivisibleNumbers(), 1259187438574927000); ``` # --seed-- @@ -31,12 +31,12 @@ assert.strictEqual(euler234(), 1259187438574927000); ## --seed-contents-- ```js -function euler234() { +function semidivisibleNumbers() { return true; } -euler234(); +semidivisibleNumbers(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md index 549fc0275d..ca403ef871 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-235-an-arithmetic-geometric-sequence.md @@ -1,6 +1,6 @@ --- id: 5900f4571000cf542c50ff6a -title: 'Problem 235: An Arithmetic Geometric sequence' +title: 'Problema 235: Uma sequência geométrica aritmética' challengeType: 5 forumTopicId: 301879 dashedName: problem-235-an-arithmetic-geometric-sequence @@ -8,20 +8,20 @@ dashedName: problem-235-an-arithmetic-geometric-sequence # --description-- -Given is the arithmetic-geometric sequence u(k) = (900-3k)rk-1. +Você é informado de que a sequência aritmética geométrica $u(k) = (900 - 3k)r^{k - 1}$. -Let s(n) = Σk=1...nu(k). +Considere $s(n) = \sum_{k=1 \ldots n} u(k)$. -Find the value of r for which s(5000) = -600,000,000,000. +Encontre o valor de $r$ para o qual $s(5000) = -600.000.000.000$. -Give your answer rounded to 12 places behind the decimal point. +Dê sua resposta arredondada para 12 casas antes da vírgula. # --hints-- -`euler235()` should return 1.002322108633. +`arithmeticGeometricSequence()` deve retornar `1.002322108633`. ```js -assert.strictEqual(euler235(), 1.002322108633); +assert.strictEqual(arithmeticGeometricSequence(), 1.002322108633); ``` # --seed-- @@ -29,12 +29,12 @@ assert.strictEqual(euler235(), 1.002322108633); ## --seed-contents-- ```js -function euler235() { +function arithmeticGeometricSequence() { return true; } -euler235(); +arithmeticGeometricSequence(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-236-luxury-hampers.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-236-luxury-hampers.md index 01c7effbc3..580a94ee21 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-236-luxury-hampers.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-236-luxury-hampers.md @@ -1,6 +1,6 @@ --- id: 5900f4591000cf542c50ff6b -title: 'Problem 236: Luxury Hampers' +title: 'Problema 236: Cestos de luxo' challengeType: 5 forumTopicId: 301881 dashedName: problem-236-luxury-hampers @@ -8,24 +8,41 @@ dashedName: problem-236-luxury-hampers # --description-- -Suppliers 'A' and 'B' provided the following numbers of products for the luxury hamper market: +Os fornecedores "A" e "B" forneceram os seguintes números de produtos para o mercado de cestos de luxo: -Product'A''B'Beluga Caviar5248640Christmas Cake13121888Gammon Joint26243776Vintage Port57603776Champagne Truffles39365664 +| Produto | 'A' | 'B' | +| ------------------- | ---- | ---- | +| Caviar Beluga | 5248 | 640 | +| Bolo de Natal | 1312 | 1888 | +| Carne de cervo | 2624 | 3776 | +| Vinho do Porto | 5760 | 3776 | +| Trufas no champanhe | 3936 | 5664 | -Although the suppliers try very hard to ship their goods in perfect condition, there is inevitably some spoilage - i.e. products gone bad. +Embora os fornecedores se esforcem muito por transportar seus produtos em condições perfeitas, há inevitavelmente alguns estragos, ou seja, os produtos que se perdem. -The suppliers compare their performance using two types of statistic:The five per-product spoilage rates for each supplier are equal to the number of products gone bad divided by the number of products supplied, for each of the five products in turn. The overall spoilage rate for each supplier is equal to the total number of products gone bad divided by the total number of products provided by that supplier.To their surprise, the suppliers found that each of the five per-product spoilage rates was worse (higher) for 'B' than for 'A' by the same factor (ratio of spoilage rates), m>1; and yet, paradoxically, the overall spoilage rate was worse for 'A' than for 'B', also by a factor of m. +Os fornecedores comparam seu desempenho usando dois tipos de estatística: -There are thirty-five m>1 for which this surprising result could have occurred, the smallest of which is 1476/1475. +- As cinco taxas de desperdício por produto para cada fornecedor são iguais ao número de produtos que se perderam dividido pelo número de produtos fornecidos para cada um dos cinco produtos separadamente. +- A taxa de perda geral para cada fornecedor é igual ao número total de produtos que se perdeu dividido pelo número total de produtos fornecidos por esse fornecedor. -What's the largest possible value of m? Give your answer as a fraction reduced to its lowest terms, in the form u/v. +Para a surpresa deles, os fornecedores descobriram que cada uma das taxas de desperdício por produto era pior (superior) para 'B' do que para 'A' pelo mesmo fator (proporção de taxas de desperdício), $m > 1$; e, no entanto, paradoxalmente, a taxa geral de desperdício foi pior para o "A" do que para o "B", também por um fator de $m$. + +Há trinta e cinco $m > 1$ para os quais esse resultado surpreendente poderia ter ocorrido, sendo o menor deles $\frac{1476}{1475}$. + +Qual é o maior valor possível de $m$? Dê sua resposta como uma string com uma fração reduzida aos termos mais baixos, na forma `u/v`. # --hints-- -`euler236()` should return 123 / 59. +`luxuryHampers()` deve retornar uma string. ```js -assert.strictEqual(euler236(), 123 / 59); +assert(typeof luxuryHampers() === 'string'); +``` + +`luxuryHampers()` deve retornar a string `123/59`. + +```js +assert.strictEqual(luxuryHampers(), '123/59'); ``` # --seed-- @@ -33,12 +50,12 @@ assert.strictEqual(euler236(), 123 / 59); ## --seed-contents-- ```js -function euler236() { +function luxuryHampers() { return true; } -euler236(); +luxuryHampers(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-237-tours-on-a-4-x-n-playing-board.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-237-tours-on-a-4-x-n-playing-board.md index eec1076ec1..08905c90be 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-237-tours-on-a-4-x-n-playing-board.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-237-tours-on-a-4-x-n-playing-board.md @@ -1,6 +1,6 @@ --- id: 5900f4591000cf542c50ff6c -title: 'Problem 237: Tours on a 4 x n playing board' +title: 'Problema 237: Passeios por um tabuleiro de 4 x n' challengeType: 5 forumTopicId: 301882 dashedName: problem-237-tours-on-a-4-x-n-playing-board @@ -8,26 +8,25 @@ dashedName: problem-237-tours-on-a-4-x-n-playing-board # --description-- -Let T(n) be the number of tours over a 4 × n playing board such that: +Considere $T(n)$ como o número de passeios sobre um tabuleiro de 4 × $n$, tal que: -The tour starts in the top left corner. +- O passeio começa no canto superior esquerdo. +- O passeio consiste em movimentos para cima, para baixo, para esquerda ou para direita de um quadrado. +- O passeio visita cada quadrado exatamente uma vez. +- O passeio termina no canto inferior esquerdo. -The tour consists of moves that are up, down, left, or right one square. +O diagrama mostra um passeio sobre um tabuleiro de 4 × 10: -The tour visits each square exactly once. 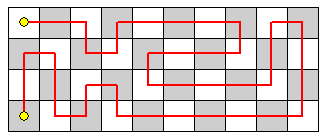+um passeio sobre o tabuleiro de 4 x 10 -The tour ends in the bottom left corner. - -The diagram shows one tour over a 4 × 10 board: - -T(10) is 2329. What is T(1012) modulo 108? +$T(10)$ é 2329. Qual é $T({10}^{12})$ modulo ${10}^8$? # --hints-- -`euler237()` should return 15836928. +`toursOnPlayingBoard()` deve retornar `15836928`. ```js -assert.strictEqual(euler237(), 15836928); +assert.strictEqual(toursOnPlayingBoard(), 15836928); ``` # --seed-- @@ -35,12 +34,12 @@ assert.strictEqual(euler237(), 15836928); ## --seed-contents-- ```js -function euler237() { +function toursOnPlayingBoard() { return true; } -euler237(); +toursOnPlayingBoard(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-238-infinite-string-tour.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-238-infinite-string-tour.md index 4bb7527686..7fc0e5912c 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-238-infinite-string-tour.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-238-infinite-string-tour.md @@ -1,6 +1,6 @@ --- id: 5900f45b1000cf542c50ff6d -title: 'Problem 238: Infinite string tour' +title: 'Problema 238: Passeio por uma string infinita' challengeType: 5 forumTopicId: 301883 dashedName: problem-238-infinite-string-tour @@ -8,34 +8,34 @@ dashedName: problem-238-infinite-string-tour # --description-- -Create a sequence of numbers using the "Blum Blum Shub" pseudo-random number generator: +Crie uma sequência de números usando o gerador de números pseudoaleatório "Blum Blum Shub": -s0 = 14025256 sn+1 = sn2 mod 20300713 +$$ s_0 = 14025256 \\\\ s_{n + 1} = {s_n}^2 \\; mod \\; 20.300.713 $$ -Concatenate these numbers s0s1s2… to create a string w of infinite length. Then, w = 14025256741014958470038053646… +Concatene esses números $s_0s_1s_2\ldots$ para criar uma string $w$ de comprimento infinito. Assim, $w = 14025256741014958470038053646\ldots$ -For a positive integer k, if no substring of w exists with a sum of digits equal to k, p(k) is defined to be zero. If at least one substring of w exists with a sum of digits equal to k, we define p(k) = z, where z is the starting position of the earliest such substring. +Para um número inteiro positivo $k$, se não existir nenhuma substring de $w$ com uma soma dos algarismos igual a $k$, $p(k)$ é definido como zero. Se pelo menos uma substring de $w$ existir com a soma dos algarismos igual a $k$, nós definimos $p(k) = z$, onde $z$ é a posição de início da primeira substring desse tipo. -For instance: +Por exemplo: -The substrings 1, 14, 1402, … with respective sums of digits equal to 1, 5, 7, … start at position 1, hence p(1) = p(5) = p(7) = … = 1. +As substrings 1, 14, 1402, … com as respectivas somas de algarismos iguais a 1, 5, 7, … começam na posição 1, e daí $p(1) = p(5) = p(7) = \ldots = 1$. -The substrings 4, 402, 4025, … with respective sums of digits equal to 4, 6, 11, … start at position 2, hence p(4) = p(6) = p(11) = … = 2. +As substrings 4, 402, 4025, … com as respectivas somas de algarismos iguais a 4, 6, 11, … começam na posição 2, e daí $p(4) = p(6) = p(11) = \ldots = 2$. -The substrings 02, 0252, … with respective sums of digits equal to 2, 9, … start at position 3, hence p(2) = p(9) = … = 3. +As substrings 02, 0252, … com as respectivas somas de algarismos iguais a 2, 9, … começam na posição 3, e daí $p(2) = p(9) = \ldots = 3$. -Note that substring 025 starting at position 3, has a sum of digits equal to 7, but there was an earlier substring (starting at position 1) with a sum of digits equal to 7, so p(7) = 1, not 3. +Observe que a substring 025, começando na posição 3, tem uma soma de algarismos igual a 7, mas havia uma substring anterior (começando na posição 1) com uma soma de algarismos igual a 7, então $p(7) = 1$, não 3. -We can verify that, for 0 < k ≤ 103, ∑ p(k) = 4742. +Podemos verificar que, para $0 < k ≤ {10}^3$, $\sum p(k) = 4742$. -Find ∑ p(k), for 0 < k ≤ 2·1015. +Encontre $\sum p(k)$, por $0 < k ≤ 2 \times {10}^{15}$. # --hints-- -`euler238()` should return 9922545104535660. +`infiniteStringTour()` deve retornar `9922545104535660`. ```js -assert.strictEqual(euler238(), 9922545104535660); +assert.strictEqual(infiniteStringTour(), 9922545104535660); ``` # --seed-- @@ -43,12 +43,12 @@ assert.strictEqual(euler238(), 9922545104535660); ## --seed-contents-- ```js -function euler238() { +function infiniteStringTour() { return true; } -euler238(); +infiniteStringTour(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-239-twenty-two-foolish-primes.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-239-twenty-two-foolish-primes.md index b68783fecf..8b7ed41fb6 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-239-twenty-two-foolish-primes.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-239-twenty-two-foolish-primes.md @@ -1,6 +1,6 @@ --- id: 5900f45c1000cf542c50ff6e -title: 'Problem 239: Twenty-two Foolish Primes' +title: 'Problema 239: Vinte e dois primos tolos' challengeType: 5 forumTopicId: 301884 dashedName: problem-239-twenty-two-foolish-primes @@ -8,18 +8,18 @@ dashedName: problem-239-twenty-two-foolish-primes # --description-- -A set of disks numbered 1 through 100 are placed in a line in random order. +Um conjunto de discos numerados de 1 a 100 é colocado em uma linha em ordem aleatória. -What is the probability that we have a partial derangement such that exactly 22 prime number discs are found away from their natural positions? (Any number of non-prime disks may also be found in or out of their natural positions.) +Qual é a probabilidade de termos um desvio parcial de tal forma que exatamente 22 discos de números primos sejam retirados de suas posições naturais? Qualquer número de discos não primos também pode ser encontrado em suas posições naturais ou fora dela. -Give your answer rounded to 12 places behind the decimal point in the form 0.abcdefghijkl. +Arredonde sua resposta para até doze casas decimais usando o formato 0.abcdefghijkl. # --hints-- -`euler239()` should return 0.001887854841. +`twentyTwoFoolishPrimes()` deve retornar `0.001887854841`. ```js -assert.strictEqual(euler239(), 0.001887854841); +assert.strictEqual(twentyTwoFoolishPrimes(), 0.001887854841); ``` # --seed-- @@ -27,12 +27,12 @@ assert.strictEqual(euler239(), 0.001887854841); ## --seed-contents-- ```js -function euler239() { +function twentyTwoFoolishPrimes() { return true; } -euler239(); +twentyTwoFoolishPrimes(); ``` # --solutions-- diff --git a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-240-top-dice.md b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-240-top-dice.md index 392edfa3dd..e8646c24ac 100644 --- a/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-240-top-dice.md +++ b/curriculum/challenges/portuguese/10-coding-interview-prep/project-euler/problem-240-top-dice.md @@ -1,6 +1,6 @@ --- id: 5900f45d1000cf542c50ff6f -title: 'Problem 240: Top Dice' +title: 'Problema 240: Dados superiores' challengeType: 5 forumTopicId: 301887 dashedName: problem-240-top-dice @@ -8,24 +8,18 @@ dashedName: problem-240-top-dice # --description-- -There are 1111 ways in which five 6-sided dice (sides numbered 1 to 6) can be rolled so that the top three sum to 15. Some examples are: +Há 1111 maneiras pelas quais cinco dados de 6 lados (lados numerados de 1 a 6) podem ser rolados de modo que os três maiores somem 15. Alguns exemplos: -D1,D2,D3,D4,D5 = 4,3,6,3,5 +$$\begin{align} & D_1,D_2,D_3,D_4,D_5 = 4,3,6,3,5 \\\\ & D_1,D_2,D_3,D_4,D_5 = 4,3,3,5,6 \\\\ & D_1,D_2,D_3,D_4,D_5 = 3,3,3,6,6 \\\\ & D_1,D_2,D_3,D_4,D_5 = 6,6,3,3,3 \end{align}$$ -D1,D2,D3,D4,D5 = 4,3,3,5,6 - -D1,D2,D3,D4,D5 = 3,3,3,6,6 - -D1,D2,D3,D4,D5 = 6,6,3,3,3 - -In how many ways can twenty 12-sided dice (sides numbered 1 to 12) be rolled so that the top ten sum to 70? +De quantas maneiras vinte dados de doze lados (lados numerados de 1 a 12) podem ser rolados de modo que a soma dos dez maiores seja 70? # --hints-- -`euler240()` should return 7448717393364182000. +`topDice()` deve retornar `7448717393364182000`. ```js -assert.strictEqual(euler240(), 7448717393364182000); +assert.strictEqual(topDice(), 7448717393364182000); ``` # --seed-- @@ -33,12 +27,12 @@ assert.strictEqual(euler240(), 7448717393364182000); ## --seed-contents-- ```js -function euler240() { +function topDice() { return true; } -euler240(); +topDice(); ``` # --solutions--