gaspersic/freeCodeCamp
1
0
Fork 0
Code Issues Pull Requests Projects Releases Wiki Activity

Correções (#23546)

Browse Source
This commit is contained in:
RF!
2019-08-14 12:17:26 -03:00
committed by Randell Dawson
parent 2d5480685d
commit ea44d04ac5
1 changed files with 4 additions and 4 deletions
Download Patch File Download Diff File Expand all files Collapse all files

8
guide/portuguese/logic/logical-operators/index.md
View File

@ -15,7 +15,7 @@ A || B retorna True se A ou B (ou ambos, A e B) forem verdadeiros. Apenas retorn
| A | B | OR (A, B) | | --- | --- | --- | | f | t | t | | f | f | f | | t | t | t | | t | f | t |
**NÃO (!)**
Retorna o valor oposto. Ex. se A é verdadeiro, então! A é falso, e se A é falso, então! A é verdadeiro. Este é o único operador lógico que trabalha em apenas uma entrada, o que torna um operador unário.
Retorna o valor oposto. Ex. se A é verdadeiro, então !A é falso, e se A é falso, então !A é verdadeiro. Este é o único operador lógico que trabalha em apenas uma entrada, o que torna um operador unário.
| A | B | NÃO (A) | NÃO SER) | --- | --- | --- | --- | | f | t | t | f | | f | f | t | t | | t | t | f | f | | t | f | f | t |
@ -25,7 +25,7 @@ Retorna o valor oposto. Ex. se A é verdadeiro, então! A é falso, e se A é fa
| A | B | XOR (A, B) | | --- | --- | --- | | f | t | t | | f | f | f | | t | t | f | | t | f | t |
**Implicação (A -> B)**
Leia como "se A, depois B" ou "A implica B". Apenas retorna False quando A é True e B é False. Caso contrário, a implicação é verdadeira.
Leia como "se A, então B" ou "A implica B". Apenas retorna False quando A é True e B é False. Caso contrário, a implicação é verdadeira.
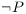
![](http://sites.millersville.edu/bikenaga/math-proof/truth-tables/truth-tables13.png)
Nota: Implicações são frequentemente usadas para provas matemáticas diretas. A representa a hipótese, enquanto B é a conclusão.
@ -35,7 +35,7 @@ A única vez que a condicional é falsa é quando um valor verdadeiro leva a um
| A | B | IF (A, B) | | --- | --- | --- | | f | t | t | | f | f | t | | t | t | t | | t | f | f |
**Equivalência lógica (iff: if and only if)**
"P se e somente se Q" é o mesmo que "P implica Q e Q implica P". Em outras palavras, as tabelas de verdade para P e Q são idênticas para todos os valores de verdade. Isso é conhecido como o biconditional. É o equivalente de A -> B **AND** B -> A. Isso significa que ambas as condicionais devem ser satisfeitas para que a bicondicional seja verdadeira.
"P se e somente se Q" é o mesmo que "P implica Q e Q implica P". Em outras palavras, as tabelas verdade para P e Q são idênticas para todos os valores de verdade. Isso é conhecido como o bicondicional. É o equivalente de A -> B **AND** B -> A. Isso significa que ambas as condicionais devem ser satisfeitas para que a bicondicional seja verdadeira.
Você pode ver facilmente que a saída do operador IFF na tabela verdade é a mesma que a AND das colunas 3 e 4.
@ -43,4 +43,4 @@ Você pode ver facilmente que a saída do operador IFF na tabela verdade é a me
#### Mais Informações:
\+ \* [Operadores lógicos em Javascript](https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Logical_Operators) + \* [Operadores lógicos em PHP](http://php.net/manual/en/language.operators.logical.php) + \* [Operadores lógicos em C ++](http://en.cppreference.com/w/cpp/language/operator_logical)
\+ \* [Operadores lógicos em Javascript](https://developer.mozilla.org/en-US/docs/Web/JavaScript/Reference/Operators/Logical_Operators) + \* [Operadores lógicos em PHP](http://php.net/manual/en/language.operators.logical.php) + \* [Operadores lógicos em C ++](http://en.cppreference.com/w/cpp/language/operator_logical)