Update index.md (#20404)

Some brief explainations of function used   and definations of notation used .

guide/english/machine-learning/logistic-regression/index.md

@@ -3,30 +3,39 @@ title: Logistic Regression
 ---
 ## Logistic Regression
 ![Logistic Function](https://qph.fs.quoracdn.net/main-qimg-7c9b7670c90b286160a88cb599d1b733)<br>
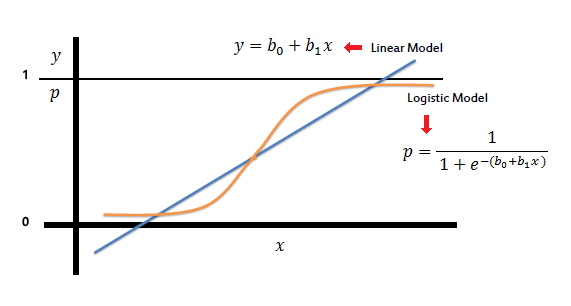
-Logistic regression is very similar to linear regression in that it attempts to predict a response variable Y given a set of X input variables. It's a form of supervised learning, which tries to predict the responses of unlabeled, unseen data by first training with labeled data, a set of observations of both independent (X) and dependent (Y) variables. But while <a href='https://guide.freecodecamp.org/machine-learning/linear-regression' target='_blank'>Linear Regression</a> assumes that the response variable (Y) is quantitative or continuous, Logistic Regression is used specifically when the response variable is qualititative,or discrete.<br>
+Logistic regression is very similar to linear regression As in both algorithms ,models are  trained to find a regression line to define function for futher prediction.Therefore, It's a form of supervised learning, which tries to predict the responses of unlabeled, unseen data by first training with labeled data,on a set of observations which consists of both independent (X) and dependent (Y) variables. But while <a href='https://guide.freecodecamp.org/machine-learning/linear-regression' target='_blank'>Linear Regression</a> assumes that the response variable (Y) is quantitative or continuous, Logistic Regression is used specifically when the response variable is qualititative,or discrete.<br>
 ![Linear vs Logistic](http://www.saedsayad.com/images/LogReg_1.png)
 
 #### How it Works 
 Logistic regression models the probability that Y, the response variable, belongs to a certain category. In many cases, the response variable will be a binary one, so logistic regression will want to model a function y = f(x) that outputs a normalized value that ranges  from, say, 0 to 1 for all values of X, corresponding to the two possible values of Y. It does this by using the logistic function: 
-Logistic regression is the appropriate regression analysis to conduct when the dependent variable is dichotomous (binary).  Like all regression analyses, the logistic regression is a predictive analysis.  Logistic regression is used to describe data and to explain the relationship between one dependent binary variable and one or more nominal, ordinal, interval or ratio-level independent variables.
+Logistic regression is the appropriate regression analysis to conduct when the dependent variable is dichotomous (binary) But it has  another form such as : mutivalued logistic regression which is used to classify for more than two classes.  Like all regression analyses, the logistic regression is a predictive analysis.  Logistic regression is used to describe data and to explain the relationship between one dependent binary variable and one or more nominal, ordinal, interval or ratio-level independent variables.
 
 ![Cost Function](https://cdn-images-1.medium.com/max/800/1*wHtYmENzug_W6fIE9xY8aw.jpeg)
 <br>
 Logistic regression is used to solve classification problems, where the output is of the form y∈{0,1}. Here, 0 is a negative class and 1 is a positive class. Let's say we have a hypothesis hθ(x), where x is our dataset(a matrix) of length m. θ is the parameteric matrix. We have : 0 < hθ(x) < 1
 
 In Logistic regression, hθ(x) is a sigmoid function, thus hθ(x) = g(θ'x).
+A Sigmoid function is an appropriate function developed by statician to classify which always result between 0 or 1 depending on its 
+input attributes and weights(which is theta **θ** here)
 g(θ'x) = 1/ 1 + e^(-θ'x) 
 
 Note: θ' is θ transpose.
-            
-#### Cost function
+**Transpose is used to multiply here it with attribute array It will be easily understoodable once you get in a bit depth with Linear algebra.**      
 
+#### Cost function
+Cost Function is a measure of How much our, Hypothetic function is farther to the observed one .
 The cost function used for Logistic regression is :
 
 J(θ)=(1/m)∑Cost(hθ(x(i)),y(i)) , where summation is from i=1 to m.
 
+Where hθ(x) is = hypothetic value calculated in accordance with attributes and wieghts which are calculated and balanced via algorithm such as gradient decent . 
+ y = is the corresponding value from observation data set 
+
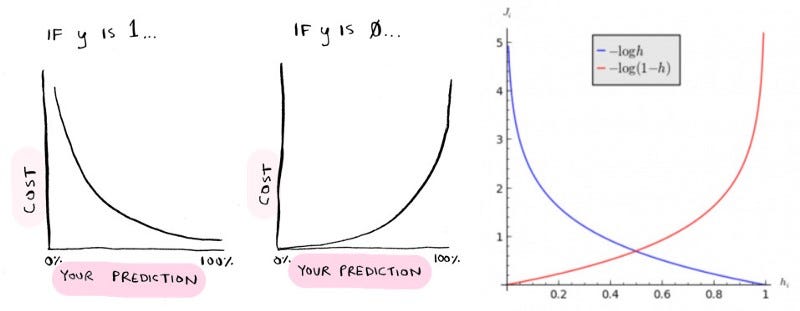
+Here cost function is not a proper sigmoid function in use but in place ,two log functions which performs with greater efficieny without 
+penalizing the learning algorithms are used.
 Cost(hθ(x),y)=−log(hθ(x))           if y = 1
 Cost(hθ(x),y)=−log(1−hθ(x))         if y = 0
+
 #### Predictions using logistic regression:
 Logistic regression models the probability of the default class(i.e. the first class).
 You can classify results given by : 
@@ -46,7 +55,8 @@ Here multiple(N*N(N-1)/2 where N=no. of classes) binary classifiers are made and
 
 #### Applications of logistic regression:
 1) To classify mail as spam or not spam.<br>
-2) To determine presence or absence of certain disease like cancer based on symptoms and other medical data.<br>
+2) To determine presence or absence of certain disease like cancer based on symptoms and other medical data
+Like- benign or  malignant.<br>
 3) Classify images based on pixel data.
 
 #### Logistic Regression Assumptions