+A(4, 3), B(5, 0), C(-4, -3)
+A(-3, 4), B(5, 0), C(3, -4)
+
+A(3, 4), B(5, 0), C(-3, -4)
+A(0, 5), B(5, 0), C(0, -5)
+A(1, 8), B(8, -1), C(-4, -7)
+
+A(8, 1), B(1, -8), C(-4, 7)
+A(2, 9), B(9, -2), C(-6, -7)
+A(9, 2), B(2, -9), C(-6, 7)
+
|
+A(-4, 3), B(5, 0), C(4, -3) +A(4, 3), B(5, 0), C(-4, -3) +A(-3, 4), B(5, 0), C(3, -4) + +A(3, 4), B(5, 0), C(-3, -4) +A(0, 5), B(5, 0), C(0, -5) +A(1, 8), B(8, -1), C(-4, -7) + +A(8, 1), B(1, -8), C(-4, 7) +A(2, 9), B(9, -2), C(-6, -7) +A(9, 2), B(2, -9), C(-6, 7) + |
+ |
+
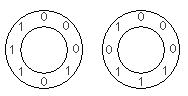For the first arrangement, the 3-digit subsequences, in clockwise order, are: 000, 001, 010, 101, 011, 111, 110 and 100.
-Each circular arrangement can be encoded as a number by concatenating the binary digits starting with the subsequence of all zeros as the most significant bits and proceeding clockwise. The two arrangements for N=3 are thus represented as 23 and 29: 00010111 2 = 23 00011101 2 = 29
+Each circular arrangement can be encoded as a number by concatenating the binary digits starting with the subsequence of all zeros as the most significant bits and proceeding clockwise. The two arrangements for $N = 3$ are thus represented as 23 and 29:
-Calling S(N) the sum of the unique numeric representations, we can see that S(3) = 23 + 29 = 52.
+$${00010111}_2 = 23\\\\
+{00011101}_2 = 29$$
-Find S(5).
+Calling $S(N)$ the sum of the unique numeric representations, we can see that $S(3) = 23 + 29 = 52$.
+
+Find $S(5)$.
# --hints--
-`euler265()` should return 209110240768.
+`binaryCircles()` should return `209110240768`.
```js
-assert.strictEqual(euler265(), 209110240768);
+assert.strictEqual(binaryCircles(), 209110240768);
```
# --seed--
@@ -33,12 +38,12 @@ assert.strictEqual(euler265(), 209110240768);
## --seed-contents--
```js
-function euler265() {
+function binaryCircles() {
return true;
}
-euler265();
+binaryCircles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
index 18569d5b8e..8b188974a5 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-266-pseudo-square-root.md
@@ -12,18 +12,18 @@ The divisors of 12 are: 1,2,3,4,6 and 12.
The largest divisor of 12 that does not exceed the square root of 12 is 3.
-We shall call the largest divisor of an integer n that does not exceed the square root of n the pseudo square root (PSR) of n.
+We shall call the largest divisor of an integer $n$ that does not exceed the square root of $n$ the pseudo square root ($PSR$) of $n$.
-It can be seen that PSR(3102)=47.
+It can be seen that $PSR(3102) = 47$.
-Let p be the product of the primes below 190. Find PSR(p) mod 1016.
+Let $p$ be the product of the primes below 190. Find $PSR(p)\bmod {10}^{16}$.
# --hints--
-`euler266()` should return 1096883702440585.
+`pseudoSquareRoot()` should return `1096883702440585`.
```js
-assert.strictEqual(euler266(), 1096883702440585);
+assert.strictEqual(pseudoSquareRoot(), 1096883702440585);
```
# --seed--
@@ -31,12 +31,12 @@ assert.strictEqual(euler266(), 1096883702440585);
## --seed-contents--
```js
-function euler266() {
+function pseudoSquareRoot() {
return true;
}
-euler266();
+pseudoSquareRoot();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-267-billionaire.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-267-billionaire.md
index 0c308ff3ec..2330fc805b 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-267-billionaire.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-267-billionaire.md
@@ -10,22 +10,22 @@ dashedName: problem-267-billionaire
You are given a unique investment opportunity.
-Starting with £1 of capital, you can choose a fixed proportion, f, of your capital to bet on a fair coin toss repeatedly for 1000 tosses.
+Starting with £1 of capital, you can choose a fixed proportion, $f$, of your capital to bet on a fair coin toss repeatedly for 1000 tosses.
Your return is double your bet for heads and you lose your bet for tails.
-For example, if f = 1/4, for the first toss you bet £0.25, and if heads comes up you win £0.5 and so then have £1.5. You then bet £0.375 and if the second toss is tails, you have £1.125.
+For example, if $f = \frac{1}{4}$, for the first toss you bet £0.25, and if heads comes up you win £0.5 and so then have £1.5. You then bet £0.375 and if the second toss is tails, you have £1.125.
-Choosing f to maximize your chances of having at least £1,000,000,000 after 1,000 flips, what is the chance that you become a billionaire?
+Choosing $f$ to maximize your chances of having at least £1,000,000,000 after 1,000 flips, what is the chance that you become a billionaire?
All computations are assumed to be exact (no rounding), but give your answer rounded to 12 digits behind the decimal point in the form 0.abcdefghijkl.
# --hints--
-`euler267()` should return 0.999992836187.
+`billionaire()` should return `0.999992836187`.
```js
-assert.strictEqual(euler267(), 0.999992836187);
+assert.strictEqual(billionaire(), 0.999992836187);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler267(), 0.999992836187);
## --seed-contents--
```js
-function euler267() {
+function billionaire() {
return true;
}
-euler267();
+billionaire();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
index c703c2b10f..21f4fa59ec 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-268-counting-numbers-with-at-least-four-distinct-prime-factors-less-than-100.md
@@ -13,14 +13,14 @@ dashedName: >-
It can be verified that there are 23 positive integers less than 1000 that are divisible by at least four distinct primes less than 100.
-Find how many positive integers less than 1016 are divisible by at least four distinct primes less than 100.
+Find how many positive integers less than ${10}^{16}$ are divisible by at least four distinct primes less than 100.
# --hints--
-`euler268()` should return 785478606870985.
+`fourDistinctPrimeFactors()` should return `785478606870985`.
```js
-assert.strictEqual(euler268(), 785478606870985);
+assert.strictEqual(fourDistinctPrimeFactors(), 785478606870985);
```
# --seed--
@@ -28,12 +28,12 @@ assert.strictEqual(euler268(), 785478606870985);
## --seed-contents--
```js
-function euler268() {
+function fourDistinctPrimeFactors() {
return true;
}
-euler268();
+fourDistinctPrimeFactors();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
index b4b2692610..da8ed3eaf3 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-269-polynomials-with-at-least-one-integer-root.md
@@ -8,24 +8,30 @@ dashedName: problem-269-polynomials-with-at-least-one-integer-root
# --description--
-A root or zero of a polynomial P(x) is a solution to the equation P(x) = 0.
+A root or zero of a polynomial $P(x)$ is a solution to the equation $P(x) = 0$.
-Define Pn as the polynomial whose coefficients are the digits of n.
+Define $P_n$ as the polynomial whose coefficients are the digits of $n$.
-For example, P5703(x) = 5x3 + 7x2 + 3.
+For example, $P_{5703}(x) = 5x^3 + 7x^2 + 3$.
-We can see that:Pn(0) is the last digit of n, Pn(1) is the sum of the digits of n, Pn(10) is n itself.Define Z(k) as the number of positive integers, n, not exceeding k for which the polynomial Pn has at least one integer root.
+We can see that:
-It can be verified that Z(100 000) is 14696.
+- $P_n(0)$ is the last digit of $n$,
+- $P_n(1)$ is the sum of the digits of $n$,
+- $Pn(10)$ is $n$ itself.
-What is Z(1016)?
+Define $Z(k)$ as the number of positive integers, $n$, not exceeding $k$ for which the polynomial $P_n$ has at least one integer root.
+
+It can be verified that $Z(100\\,000)$ is 14696.
+
+What is $Z({10}^{16})$?
# --hints--
-`euler269()` should return 1311109198529286.
+`polynomialsWithOneIntegerRoot()` should return `1311109198529286`.
```js
-assert.strictEqual(euler269(), 1311109198529286);
+assert.strictEqual(polynomialsWithOneIntegerRoot(), 1311109198529286);
```
# --seed--
@@ -33,12 +39,12 @@ assert.strictEqual(euler269(), 1311109198529286);
## --seed-contents--
```js
-function euler269() {
+function polynomialsWithOneIntegerRoot() {
return true;
}
-euler269();
+polynomialsWithOneIntegerRoot();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
index 5d490e3b17..e98082a6a2 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-270-cutting-squares.md
@@ -8,24 +8,24 @@ dashedName: problem-270-cutting-squares
# --description--
-A square piece of paper with integer dimensions N×N is placed with a corner at the origin and two of its sides along the x- and y-axes. Then, we cut it up respecting the following rules:
+A square piece of paper with integer dimensions $N×N$ is placed with a corner at the origin and two of its sides along the $x$- and $y$-axes. Then, we cut it up respecting the following rules:
-We only make straight cuts between two points lying on different sides of the square, and having integer coordinates.
+- We only make straight cuts between two points lying on different sides of the square, and having integer coordinates.
+- Two cuts cannot cross, but several cuts can meet at the same border point.
+- Proceed until no more legal cuts can be made.
-Two cuts cannot cross, but several cuts can meet at the same border point.
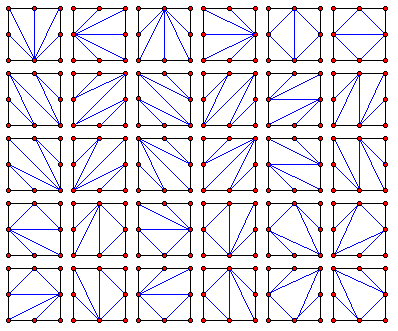
+Counting any reflections or rotations as distinct, we call $C(N)$ the number of ways to cut an $N×N$ square. For example, $C(1) = 2$ and $C(2) = 30$ (shown below).
-Proceed until no more legal cuts can be made.
+
-Counting any reflections or rotations as distinct, we call C(N) the number of ways to cut an N×N square. For example, C(1) = 2 and C(2) = 30 (shown below).
-
-What is C(30) mod 108 ?
+What is $C(30)\bmod {10}^8$ ?
# --hints--
-`euler270()` should return 82282080.
+`cuttingSquares()` should return `82282080`.
```js
-assert.strictEqual(euler270(), 82282080);
+assert.strictEqual(cuttingSquares(), 82282080);
```
# --seed--
@@ -33,12 +33,12 @@ assert.strictEqual(euler270(), 82282080);
## --seed-contents--
```js
-function euler270() {
+function cuttingSquares() {
return true;
}
-euler270();
+cuttingSquares();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
index e9f9bb785c..1566254c63 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-271-modular-cubes-part-1.md
@@ -8,18 +8,18 @@ dashedName: problem-271-modular-cubes-part-1
# --description--
-For a positive number n, define S(n) as the sum of the integers x, for which 1
+For a positive number $n$, define $S(n)$ as the sum of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
-When n=91, there are 8 possible values for x, namely : 9, 16, 22, 29, 53, 74, 79, 81. Thus, S(91)=9+16+22+29+53+74+79+81=363.
+When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $S(91) = 9 + 16 + 22 + 29 + 53 + 74 + 79 + 81 = 363$.
-Find S(13082761331670030).
+Find $S(13\\,082\\,761\\,331\\,670\\,030)$.
# --hints--
-`euler271()` should return 4617456485273130000.
+`modularCubesOne()` should return `4617456485273130000`.
```js
-assert.strictEqual(euler271(), 4617456485273130000);
+assert.strictEqual(modularCubesOne(), 4617456485273130000);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler271(), 4617456485273130000);
## --seed-contents--
```js
-function euler271() {
+function modularCubesOne() {
return true;
}
-euler271();
+modularCubesOne();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
index 3cfb07b5b3..136646718c 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-272-modular-cubes-part-2.md
@@ -8,18 +8,18 @@ dashedName: problem-272-modular-cubes-part-2
# --description--
-For a positive number n, define C(n) as the number of the integers x, for which 1
+For a positive number $n$, define $C(n)$ as the number of the integers $x$, for which $1 < x < n$ and $x^3 \equiv 1\bmod n$.
-When n=91, there are 8 possible values for x, namely : 9, 16, 22, 29, 53, 74, 79, 81. Thus, C(91)=8.
+When $n = 91$, there are 8 possible values for $x$, namely: 9, 16, 22, 29, 53, 74, 79, 81. Thus, $C(91) = 8$.
-Find the sum of the positive numbers n≤1011 for which C(n)=242.
+Find the sum of the positive numbers $n ≤ {10}^{11}$ for which $C(n)=242$.
# --hints--
-`euler272()` should return 8495585919506151000.
+`modularCubesTwo()` should return `8495585919506151000`.
```js
-assert.strictEqual(euler272(), 8495585919506151000);
+assert.strictEqual(modularCubesTwo(), 8495585919506151000);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler272(), 8495585919506151000);
## --seed-contents--
```js
-function euler272() {
+function modularCubesTwo() {
return true;
}
-euler272();
+modularCubesTwo();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
index 508c463ddd..f53c8f36ee 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-273-sum-of-squares.md
@@ -8,16 +8,24 @@ dashedName: problem-273-sum-of-squares
# --description--
-Consider equations of the form: a2 + b2 = N, 0 ≤ a ≤ b, a, b and N integer.
+Consider equations of the form: $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
-For N=65 there are two solutions: a=1, b=8 and a=4, b=7. We call S(N) the sum of the values of a of all solutions of a2 + b2 = N, 0 ≤ a ≤ b, a, b and N integer. Thus S(65) = 1 + 4 = 5. Find ∑S(N), for all squarefree N only divisible by primes of the form 4k+1 with 4k+1 < 150.
+For $N = 65$ there are two solutions:
+
+$a = 1, b = 8$ and $a = 4, b = 7$.
+
+We call $S(N)$ the sum of the values of $a$ of all solutions of $a^2 + b^2 = N$, $0 ≤ a ≤ b$, $a$, $b$ and $N$ integer.
+
+Thus $S(65) = 1 + 4 = 5$.
+
+Find $\sum S(N)$, for all squarefree $N$ only divisible by primes of the form $4k + 1$ with $4k + 1 < 150$.
# --hints--
-`euler273()` should return 2032447591196869000.
+`sumOfSquares()` should return `2032447591196869000`.
```js
-assert.strictEqual(euler273(), 2032447591196869000);
+assert.strictEqual(sumOfSquares(), 2032447591196869000);
```
# --seed--
@@ -25,12 +33,12 @@ assert.strictEqual(euler273(), 2032447591196869000);
## --seed-contents--
```js
-function euler273() {
+function sumOfSquares() {
return true;
}
-euler273();
+sumOfSquares();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
index 7841b6ed8f..8534028bc1 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-274-divisibility-multipliers.md
@@ -8,26 +8,28 @@ dashedName: problem-274-divisibility-multipliers
# --description--
-For each integer p > 1 coprime to 10 there is a positive divisibility multiplier m < p which preserves divisibility by p for the following function on any positive integer, n:
+For each integer $p > 1$ coprime to 10 there is a positive divisibility multiplier $m < p$ which preserves divisibility by $p$ for the following function on any positive integer, $n$:
-f(n) = (all but the last digit of n) + (the last digit of n) \* m
+$f(n) = (\text{all but the last digit of} \\; n) + (\text{the last digit of} \\; n) \times m$
-That is, if m is the divisibility multiplier for p, then f(n) is divisible by p if and only if n is divisible by p.
+That is, if $m$ is the divisibility multiplier for $p$, then $f(n)$ is divisible by $p$ if and only if $n$ is divisible by $p$.
-(When n is much larger than p, f(n) will be less than n and repeated application of f provides a multiplicative divisibility test for p.)
+(When $n$ is much larger than $p$, $f(n)$ will be less than $n$ and repeated application of $f$ provides a multiplicative divisibility test for $p$.)
For example, the divisibility multiplier for 113 is 34.
-f(76275) = 7627 + 5 *34 = 7797 : 76275 and 7797 are both divisible by 113f(12345) = 1234 + 5* 34 = 1404 : 12345 and 1404 are both not divisible by 113
+$f(76275) = 7627 + 5 \times 34 = 7797$: 76275 and 7797 are both divisible by 113
-The sum of the divisibility multipliers for the primes that are coprime to 10 and less than 1000 is 39517. What is the sum of the divisibility multipliers for the primes that are coprime to 10 and less than 107?
+$f(12345) = 1234 + 5 \times 34 = 1404$: 12345 and 1404 are both not divisible by 113
+
+The sum of the divisibility multipliers for the primes that are coprime to 10 and less than 1000 is 39517. What is the sum of the divisibility multipliers for the primes that are coprime to 10 and less than ${10}^7$?
# --hints--
-`euler274()` should return 1601912348822.
+`divisibilityMultipliers()` should return `1601912348822`.
```js
-assert.strictEqual(euler274(), 1601912348822);
+assert.strictEqual(divisibilityMultipliers(), 1601912348822);
```
# --seed--
@@ -35,12 +37,12 @@ assert.strictEqual(euler274(), 1601912348822);
## --seed-contents--
```js
-function euler274() {
+function divisibilityMultipliers() {
return true;
}
-euler274();
+divisibilityMultipliers();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
index a65dc0151c..52508d8381 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-275-balanced-sculptures.md
@@ -8,26 +8,27 @@ dashedName: problem-275-balanced-sculptures
# --description--
-Let us define a balanced sculpture of order n as follows:
+Let us define a balanced sculpture of order $n$ as follows:
-A polyomino made up of n+1 tiles known as the blocks (n tiles) and the plinth (remaining tile);
+- A polyomino made up of $n + 1$ tiles known as the blocks ($n$ tiles) and the plinth (remaining tile);
+- the plinth has its centre at position ($x = 0$, $y = 0$);
+- the blocks have $y$-coordinates greater than zero (so the plinth is the unique lowest tile);
+- the centre of mass of all the blocks, combined, has $x$-coordinate equal to zero.
-the plinth has its centre at position (x = 0, y = 0);
+When counting the sculptures, any arrangements which are simply reflections about the $y$-axis, are not counted as distinct. For example, the 18 balanced sculptures of order 6 are shown below; note that each pair of mirror images (about the $y$-axis) is counted as one sculpture:
-the blocks have y-coordinates greater than zero (so the plinth is the unique lowest tile);
+
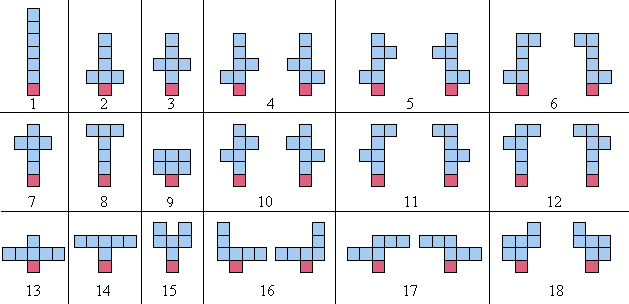-the centre of mass of all the blocks, combined, has x-coordinate equal to zero.
+There are 964 balanced sculptures of order 10 and 360505 of order 15.
-When counting the sculptures, any arrangements which are simply reflections about the y-axis, are not counted as distinct. For example, the 18 balanced sculptures of order 6 are shown below; note that each pair of mirror images (about the y-axis) is counted as one sculpture:
-
-There are 964 balanced sculptures of order 10 and 360505 of order 15.How many balanced sculptures are there of order 18?
+How many balanced sculptures are there of order 18?
# --hints--
-`euler275()` should return 15030564.
+`balancedSculptures()` should return `15030564`.
```js
-assert.strictEqual(euler275(), 15030564);
+assert.strictEqual(balancedSculptures(), 15030564);
```
# --seed--
@@ -35,12 +36,12 @@ assert.strictEqual(euler275(), 15030564);
## --seed-contents--
```js
-function euler275() {
+function balancedSculptures() {
return true;
}
-euler275();
+balancedSculptures();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
index 0e8392e57b..b5e187731b 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-276-primitive-triangles.md
@@ -8,18 +8,18 @@ dashedName: problem-276-primitive-triangles
# --description--
-Consider the triangles with integer sides a, b and c with a ≤ b ≤ c.
+Consider the triangles with integer sides $a$, $b$ and $c$ with $a ≤ b ≤ c$.
-An integer sided triangle (a,b,c) is called primitive if gcd(a,b,c)=1.
+An integer sided triangle $(a,b,c)$ is called primitive if $gcd(a,b,c) = 1$.
-How many primitive integer sided triangles exist with a perimeter not exceeding 10 000 000?
+How many primitive integer sided triangles exist with a perimeter not exceeding $10\\,000\\,000$?
# --hints--
-`euler276()` should return 5777137137739633000.
+`primitiveTriangles()` should return `5777137137739633000`.
```js
-assert.strictEqual(euler276(), 5777137137739633000);
+assert.strictEqual(primitiveTriangles(), 5777137137739633000);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler276(), 5777137137739633000);
## --seed-contents--
```js
-function euler276() {
+function primitiveTriangles() {
return true;
}
-euler276();
+primitiveTriangles();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
index 1f081396c2..108215479e 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-277-a-modified-collatz-sequence.md
@@ -8,28 +8,32 @@ dashedName: problem-277-a-modified-collatz-sequence
# --description--
-A modified Collatz sequence of integers is obtained from a starting value a1 in the following way:
+A modified Collatz sequence of integers is obtained from a starting value $a_1$ in the following way:
-an+1 = an/3 if an is divisible by 3. We shall denote this as a large downward step, "D".
+$a_{n + 1} = \frac{a_n}{3}$ if $a_n$ is divisible by 3. We shall denote this as a large downward step, "D".
-an+1 = (4an + 2)/3 if an divided by 3 gives a remainder of 1. We shall denote this as an upward step, "U".
+$a_{n + 1} = \frac{4a_n + 2}{3}$ if $a_n$ divided by 3 gives a remainder of 1. We shall denote this as an upward step, "U".
-an+1 = (2an - 1)/3 if an divided by 3 gives a remainder of 2. We shall denote this as a small downward step, "d".
+$a_{n + 1} = \frac{2a_n - 1}{3}$ if $a_n$ divided by 3 gives a remainder of 2. We shall denote this as a small downward step, "d".
-The sequence terminates when some an = 1.
+The sequence terminates when some $a_n = 1$.
-Given any integer, we can list out the sequence of steps. For instance if a1=231, then the sequence {an}={231,77,51,17,11,7,10,14,9,3,1} corresponds to the steps "DdDddUUdDD".
+Given any integer, we can list out the sequence of steps. For instance if $a_1 = 231$, then the sequence $\\{a_n\\} = \\{231, 77, 51, 17, 11, 7, 10, 14, 9, 3, 1\\}$ corresponds to the steps "DdDddUUdDD".
-Of course, there are other sequences that begin with that same sequence "DdDddUUdDD....". For instance, if a1=1004064, then the sequence is DdDddUUdDDDdUDUUUdDdUUDDDUdDD. In fact, 1004064 is the smallest possible a1 > 106 that begins with the sequence DdDddUUdDD.
+Of course, there are other sequences that begin with that same sequence "DdDddUUdDD....".
-What is the smallest a1 > 1015 that begins with the sequence "UDDDUdddDDUDDddDdDddDDUDDdUUDd"?
+For instance, if $a_1 = 1004064$, then the sequence is DdDddUUdDDDdUDUUUdDdUUDDDUdDD.
+
+In fact, 1004064 is the smallest possible $a_1 > {10}^6$ that begins with the sequence DdDddUUdDD.
+
+What is the smallest $a_1 > {10}^{15}$ that begins with the sequence "UDDDUdddDDUDDddDdDddDDUDDdUUDd"?
# --hints--
-`euler277()` should return 1125977393124310.
+`modifiedCollatzSequence()` should return `1125977393124310`.
```js
-assert.strictEqual(euler277(), 1125977393124310);
+assert.strictEqual(modifiedCollatzSequence(), 1125977393124310);
```
# --seed--
@@ -37,12 +41,12 @@ assert.strictEqual(euler277(), 1125977393124310);
## --seed-contents--
```js
-function euler277() {
+function modifiedCollatzSequence() {
return true;
}
-euler277();
+modifiedCollatzSequence();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
index 6e26a6a316..19e3042fdb 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-278-linear-combinations-of-semiprimes.md
@@ -8,20 +8,20 @@ dashedName: problem-278-linear-combinations-of-semiprimes
# --description--
-Given the values of integers 1 < a1 < a2 <... < an, consider the linear combination q1a1 + q2a2 + ... + qnan = b, using only integer values qk ≥ 0.
+Given the values of integers $1 < a_1 < a_2 < \ldots < a_n$, consider the linear combination $q_1a_1 + q_2a_2 + \ldots + q_na_n = b$, using only integer values $q_k ≥ 0$.
-Note that for a given set of ak, it may be that not all values of b are possible. For instance, if a1 = 5 and a2 = 7, there are no q1 ≥ 0 and q2 ≥ 0 such that b could be 1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18 or 23.
+Note that for a given set of $a_k$, it may be that not all values of $b$ are possible. For instance, if $a_1 = 5$ and $a_2 = 7$, there are no $q_1 ≥ 0$ and $q_2 ≥ 0$ such that $b$ could be 1, 2, 3, 4, 6, 8, 9, 11, 13, 16, 18 or 23.
-In fact, 23 is the largest impossible value of b for a1 = 5 and a2 = 7. We therefore call f(5, 7) = 23. Similarly, it can be shown that f(6, 10, 15)=29 and f(14, 22, 77) = 195.
+In fact, 23 is the largest impossible value of $b$ for $a_1 = 5$ and $a_2 = 7$. We therefore call $f(5, 7) = 23$. Similarly, it can be shown that $f(6, 10, 15)=29$ and $f(14, 22, 77) = 195$.
-Find ∑ f(p*q,p*r,q\*r), where p, q and r are prime numbers and p < q < r < 5000.
+Find $\sum f(pq,pr,qr)$, where $p$, $q$ and $r$ are prime numbers and $p < q < r < 5000$.
# --hints--
-`euler278()` should return 1228215747273908500.
+`linearCombinationOfSemiprimes()` should return `1228215747273908500`.
```js
-assert.strictEqual(euler278(), 1228215747273908500);
+assert.strictEqual(linearCombinationOfSemiprimes(), 1228215747273908500);
```
# --seed--
@@ -29,12 +29,12 @@ assert.strictEqual(euler278(), 1228215747273908500);
## --seed-contents--
```js
-function euler278() {
+function linearCombinationOfSemiprimes() {
return true;
}
-euler278();
+linearCombinationOfSemiprimes();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
index 9fc673b5ea..c83c6736f4 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-279-triangles-with-integral-sides-and-an-integral-angle.md
@@ -8,14 +8,14 @@ dashedName: problem-279-triangles-with-integral-sides-and-an-integral-angle
# --description--
-How many triangles are there with integral sides, at least one integral angle (measured in degrees), and a perimeter that does not exceed 108?
+How many triangles are there with integral sides, at least one integral angle (measured in degrees), and a perimeter that does not exceed ${10}^8$?
# --hints--
-`euler279()` should return 416577688.
+`trianglesWithIntegralSidesAndAngle()` should return `416577688`.
```js
-assert.strictEqual(euler279(), 416577688);
+assert.strictEqual(trianglesWithIntegralSidesAndAngle(), 416577688);
```
# --seed--
@@ -23,12 +23,12 @@ assert.strictEqual(euler279(), 416577688);
## --seed-contents--
```js
-function euler279() {
+function trianglesWithIntegralSidesAndAngle() {
return true;
}
-euler279();
+trianglesWithIntegralSidesAndAngle();
```
# --solutions--
diff --git a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
index 642a7d802f..7aec32e7cc 100644
--- a/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
+++ b/curriculum/challenges/english/10-coding-interview-prep/project-euler/problem-280-ant-and-seeds.md
@@ -16,10 +16,10 @@ What's the expected number of steps until all seeds have been dropped in the top
# --hints--
-`euler280()` should return 430.088247.
+`antAndSeeds()` should return `430.088247`.
```js
-assert.strictEqual(euler280(), 430.088247);
+assert.strictEqual(antAndSeeds(), 430.088247);
```
# --seed--
@@ -27,12 +27,12 @@ assert.strictEqual(euler280(), 430.088247);
## --seed-contents--
```js
-function euler280() {
+function antAndSeeds() {
return true;
}
-euler280();
+antAndSeeds();
```
# --solutions--