---
id: 5900f42f1000cf542c50ff40
title: '問題 194: 色付きの構成'
challengeType: 5
forumTopicId: 301832
dashedName: problem-194-coloured-configurations
---
# --description--
ユニット A とユニット B からなる下図について考えます。
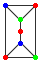
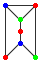 次の図のように、これらのユニットを縦の辺でつなげます。
次の図のように、これらのユニットを縦の辺でつなげます。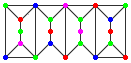 $(a,b,c)$ 型の構成は、$a$ 個のユニット A と $b$ 個のユニット B からなり、図の頂点は、隣接する 2 つの頂点が同色にならない形で最大 $c$ 種類の色が付けられています。 上図の連結ユニットは (2,2,6) 型の構成の例です。実は、これはすべての $c ≥ 4 に対する (2,2,c) 型の構成です。
$(a,b,c)$ 型の構成の数を $N(a,b,c)$ とします。 例えば、$N(1,0,3) = 24$, $N(0,2,4) = 92928$, $N(2,2,3) = 20736$ です。
$N(25,75,1984)$ の下位 8 桁を求めなさい。
# --hints--
`coloredConfigurations()` は `61190912` を返す必要があります。
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```
$(a,b,c)$ 型の構成は、$a$ 個のユニット A と $b$ 個のユニット B からなり、図の頂点は、隣接する 2 つの頂点が同色にならない形で最大 $c$ 種類の色が付けられています。 上図の連結ユニットは (2,2,6) 型の構成の例です。実は、これはすべての $c ≥ 4 に対する (2,2,c) 型の構成です。
$(a,b,c)$ 型の構成の数を $N(a,b,c)$ とします。 例えば、$N(1,0,3) = 24$, $N(0,2,4) = 92928$, $N(2,2,3) = 20736$ です。
$N(25,75,1984)$ の下位 8 桁を求めなさい。
# --hints--
`coloredConfigurations()` は `61190912` を返す必要があります。
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```

 次の図のように、これらのユニットを縦の辺でつなげます。
次の図のように、これらのユニットを縦の辺でつなげます。 $(a,b,c)$ 型の構成は、$a$ 個のユニット A と $b$ 個のユニット B からなり、図の頂点は、隣接する 2 つの頂点が同色にならない形で最大 $c$ 種類の色が付けられています。 上図の連結ユニットは (2,2,6) 型の構成の例です。実は、これはすべての $c ≥ 4 に対する (2,2,c) 型の構成です。
$(a,b,c)$ 型の構成の数を $N(a,b,c)$ とします。 例えば、$N(1,0,3) = 24$, $N(0,2,4) = 92928$, $N(2,2,3) = 20736$ です。
$N(25,75,1984)$ の下位 8 桁を求めなさい。
# --hints--
`coloredConfigurations()` は `61190912` を返す必要があります。
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```
$(a,b,c)$ 型の構成は、$a$ 個のユニット A と $b$ 個のユニット B からなり、図の頂点は、隣接する 2 つの頂点が同色にならない形で最大 $c$ 種類の色が付けられています。 上図の連結ユニットは (2,2,6) 型の構成の例です。実は、これはすべての $c ≥ 4 に対する (2,2,c) 型の構成です。
$(a,b,c)$ 型の構成の数を $N(a,b,c)$ とします。 例えば、$N(1,0,3) = 24$, $N(0,2,4) = 92928$, $N(2,2,3) = 20736$ です。
$N(25,75,1984)$ の下位 8 桁を求めなさい。
# --hints--
`coloredConfigurations()` は `61190912` を返す必要があります。
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```