---
id: 5900f4801000cf542c50ff92
title: '問題 275: 平衡な彫像'
challengeType: 5
forumTopicId: 301925
dashedName: problem-275-balanced-sculptures
---
# --description--
位数 $n$ の平衡な彫像を次のように定義します。
- ブロック ($n$ 枚のタイル) と台座 (残りのタイル) として知られる $n + 1$ 枚のタイルで構成されたポリオミノである。
- 台座の中心は ($x = 0$, $y = 0$) に位置する。
- ブロックの $y$ 座標は 0 より大きい (したがって台座は唯一の一番下のタイル)。
- すべてのブロックを合わせたときの重心の $x$ 座標は 0 に等しい。
彫像を数えるとき、単に $y$ 軸で反転させた配置は区別されません。 例えば、位数 6 の平衡な彫像 18 個を下に示します。($y$ 軸で反転して) 鏡像となる各ペアが 1 つの彫像としてカウントされることに注意してください。
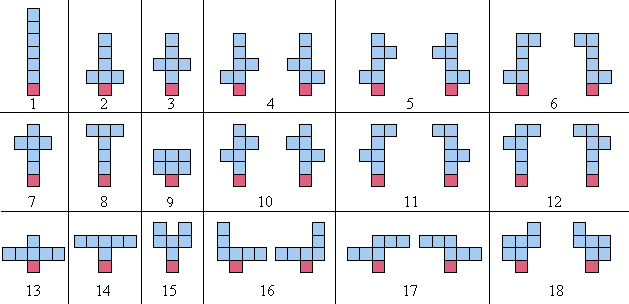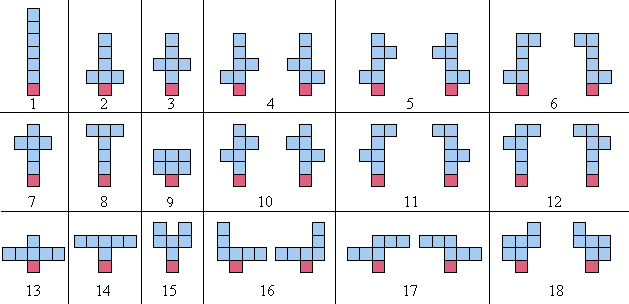位数 10 の平衡な彫像は 964 個、位数 15 の平衡な彫像は 360505 個あります。
位数 18 の平衡な彫像はいくつありますか。
# --hints--
`balancedSculptures()` は `15030564` を返す必要があります。
```js
assert.strictEqual(balancedSculptures(), 15030564);
```
# --seed--
## --seed-contents--
```js
function balancedSculptures() {
return true;
}
balancedSculptures();
```
# --solutions--
```js
// solution required
```