---
id: 5900f5021000cf542c510014
title: '問題 405: 長方形の敷き詰め'
challengeType: 5
forumTopicId: 302073
dashedName: problem-405-a-rectangular-tiling
---
# --description--
縦の長さが横の長さの 2 倍である長方形タイルを敷き詰めます。
1 枚の長方形タイルで敷き詰めたものを $T(0)$ とします。
$n > 0$ のとき、$T(n-1)$ のすべてのタイルを下図のように置き換えることで $T(n)$ を得ます。
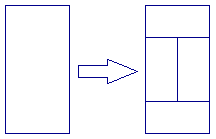 次のアニメーションは、$n$ が 0 から 5 のときのタイルの敷き詰め方 $T(n)$ を示しています。
次のアニメーションは、$n$ が 0 から 5 のときのタイルの敷き詰め方 $T(n)$ を示しています。
 $T(n)$ で 4 枚のタイルが集まる点の個数を $f(n)$ とします。 例えば、$f(1) = 0$, $f(4) = 82$, $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$ です。
$k = {10}^{18}$ のとき、$f({10}^k)$ mod ${17}^7$ を求めなさい。
# --hints--
`rectangularTiling()` は `237696125` を返す必要があります。
```js
assert.strictEqual(rectangularTiling(), 237696125);
```
# --seed--
## --seed-contents--
```js
function rectangularTiling() {
return true;
}
rectangularTiling();
```
# --solutions--
```js
// solution required
```
$T(n)$ で 4 枚のタイルが集まる点の個数を $f(n)$ とします。 例えば、$f(1) = 0$, $f(4) = 82$, $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$ です。
$k = {10}^{18}$ のとき、$f({10}^k)$ mod ${17}^7$ を求めなさい。
# --hints--
`rectangularTiling()` は `237696125` を返す必要があります。
```js
assert.strictEqual(rectangularTiling(), 237696125);
```
# --seed--
## --seed-contents--
```js
function rectangularTiling() {
return true;
}
rectangularTiling();
```
# --solutions--
```js
// solution required
```
 次のアニメーションは、$n$ が 0 から 5 のときのタイルの敷き詰め方 $T(n)$ を示しています。
次のアニメーションは、$n$ が 0 から 5 のときのタイルの敷き詰め方 $T(n)$ を示しています。
 $T(n)$ で 4 枚のタイルが集まる点の個数を $f(n)$ とします。 例えば、$f(1) = 0$, $f(4) = 82$, $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$ です。
$k = {10}^{18}$ のとき、$f({10}^k)$ mod ${17}^7$ を求めなさい。
# --hints--
`rectangularTiling()` は `237696125` を返す必要があります。
```js
assert.strictEqual(rectangularTiling(), 237696125);
```
# --seed--
## --seed-contents--
```js
function rectangularTiling() {
return true;
}
rectangularTiling();
```
# --solutions--
```js
// solution required
```
$T(n)$ で 4 枚のタイルが集まる点の個数を $f(n)$ とします。 例えば、$f(1) = 0$, $f(4) = 82$, $f({10}^9)\bmod {17}^7 = 126\\,897\\,180$ です。
$k = {10}^{18}$ のとき、$f({10}^k)$ mod ${17}^7$ を求めなさい。
# --hints--
`rectangularTiling()` は `237696125` を返す必要があります。
```js
assert.strictEqual(rectangularTiling(), 237696125);
```
# --seed--
## --seed-contents--
```js
function rectangularTiling() {
return true;
}
rectangularTiling();
```
# --solutions--
```js
// solution required
```