---
id: 5900f51f1000cf542c510031
title: '問題 434: 剛なグラフ'
challengeType: 5
forumTopicId: 302105
dashedName: problem-434-rigid-graphs
---
# --description--
まず、次のことを思い出してください。グラフとは、頂点と、頂点間を結ぶ辺との集まりであり、辺によって結ばれた 2 つの頂点は「隣接している」と表現されます。
グラフは、各頂点をユークリッド空間上の点と関連付けることでユークリッド空間に埋め込むことができます。
柔軟なグラフとは、隣接する 2 頂点の対のそれぞれで 2 頂点間の距離が一定に保たれたまま、 少なくとも 2 つの隣接していない頂点間の距離が変化するような方法で、1 つ以上の頂点を連続的に動すことができるグラフの埋め込みのことです。
剛なグラフとは、柔軟でないグラフの埋め込みのことでです。
平たく言えば、頂点を 360 度回転する蝶番とに置き換え、辺を弾力のない固い棒に置き換えたときに、グラフの残りの部分から独立して動かすことのできる部分がないグラフは剛なグラフです。
ユークリッド平面に埋め込まれた格子グラフは、下のアニメーションが示すように剛なグラフではありません。
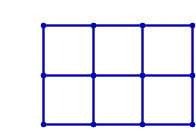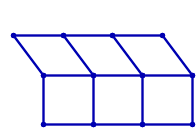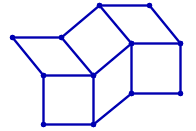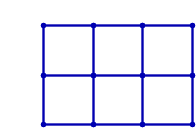ただし、マスに対角線の辺を追加すれば剛なグラフになります。 例えば、2x3 の格子グラフの場合、剛なグラフにする方法は次のように 19 通りあります。
なお、この問題の目的上、格子グラフに剛性を持たせる別の方法として、対角線の向きを変えたり 1 つのセルに対角線を 2 本追加したりすることは考えないものとします。
$m × n$ の格子グラフを剛なグラフにする方法の数を $R(m, n)$ とします。
例: $R(2, 3) = 19$, $R(5, 5) = 23\\,679\\,901$
$1 ≤ i$, $j ≤ N のとき、$\sum R(i, j) を $S(N)$ とします。
例: $S(5) = 25\\,021\\,721$
$S(100)$ を求め、mod $1\\,000\\,000\\,033$ で答えなさい。
# --hints--
`rigidGraphs()` は `863253606` を返す必要があります。
```js
assert.strictEqual(rigidGraphs(), 863253606);
```
# --seed--
## --seed-contents--
```js
function rigidGraphs() {
return true;
}
rigidGraphs();
```
# --solutions--
```js
// solution required
```