---
id: 5900f4801000cf542c50ff92
title: 'Problem 275: Balanced Sculptures'
challengeType: 5
forumTopicId: 301925
dashedName: problem-275-balanced-sculptures
---

# --description--

Let us define a balanced sculpture of order $n$ as follows:

- A polyomino made up of $n + 1$ tiles known as the blocks ($n$ tiles) and the plinth (remaining tile);
- the plinth has its centre at position ($x = 0$, $y = 0$);
- the blocks have $y$-coordinates greater than zero (so the plinth is the unique lowest tile);
- the centre of mass of all the blocks, combined, has $x$-coordinate equal to zero.

When counting the sculptures, any arrangements which are simply reflections about the $y$-axis, are <u>not</u> counted as distinct. For example, the 18 balanced sculptures of order 6 are shown below; note that each pair of mirror images (about the $y$-axis) is counted as one sculpture:

<img class="img-responsive center-block" alt="18 balanced sculptures of order 6" src="https://cdn.freecodecamp.org/curriculum/project-euler/balanced-sculptures.gif" style="background-color: white; padding: 10px;">

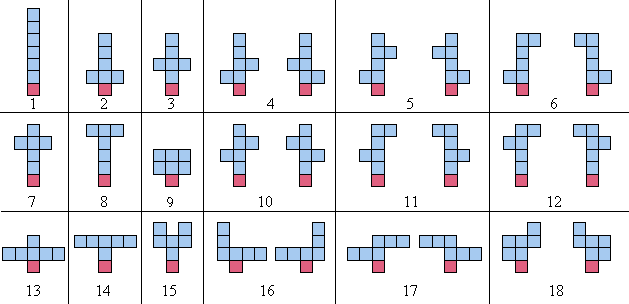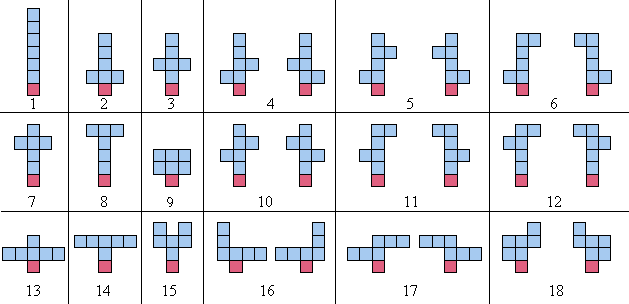There are 964 balanced sculptures of order 10 and 360505 of order 15.

How many balanced sculptures are there of order 18?

# --hints--

`balancedSculptures()` should return `15030564`.

```js
assert.strictEqual(balancedSculptures(), 15030564);
```

# --seed--

## --seed-contents--

```js
function balancedSculptures() {

  return true;
}

balancedSculptures();
```

# --solutions--

```js
// solution required
```