---
id: 5900f48b1000cf542c50ff9e
title: 'Problem 287: Quadtree encoding (a simple compression algorithm)'
challengeType: 5
forumTopicId: 301938
dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
---
# --description--
The quadtree encoding allows us to describe a $2^N×2^N$ black and white image as a sequence of bits (0 and 1). Those sequences are to be read from left to right like this:
- the first bit deals with the complete $2^N×2^N$ region;
- "0" denotes a split:
- the current $2^n×2^n$ region is divided into 4 sub-regions of dimension $2^{n - 1}×2^{n - 1}$,
- the next bits contains the description of the top left, top right, bottom left and bottom right sub-regions - in that order;
- "10" indicates that the current region contains only black pixels;
- "11" indicates that the current region contains only white pixels.
Consider the following 4×4 image (colored marks denote places where a split can occur):
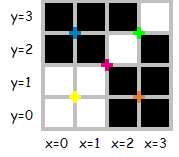 This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
- otherwise the pixel is white.
What is the length of the minimal sequence describing $D_{24}$?
# --hints--
`quadtreeEncoding()` should return `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
- otherwise the pixel is white.
What is the length of the minimal sequence describing $D_{24}$?
# --hints--
`quadtreeEncoding()` should return `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
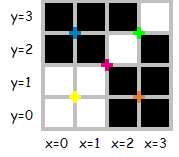 This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
- otherwise the pixel is white.
What is the length of the minimal sequence describing $D_{24}$?
# --hints--
`quadtreeEncoding()` should return `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
This image can be described by several sequences, for example : "001010101001011111011010101010", of length 30, or "0100101111101110", of length 16, which is the minimal sequence for this image.
For a positive integer $N$, define $D_N$ as the $2^N×2^N$ image with the following coloring scheme:
- the pixel with coordinates $x = 0$, $y = 0$ corresponds to the bottom left pixel,
- if ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ then the pixel is black,
- otherwise the pixel is white.
What is the length of the minimal sequence describing $D_{24}$?
# --hints--
`quadtreeEncoding()` should return `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```