---
id: 5900f4b91000cf542c50ffcb
title: 'Problem 332: Spherical triangles'
challengeType: 5
forumTopicId: 301990
dashedName: problem-332-spherical-triangles
---

# --description--

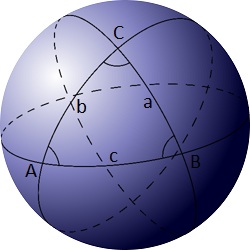
A spherical triangle is a figure formed on the surface of a sphere by three great circular arcs intersecting pairwise in three vertices.

<img class="img-responsive center-block" alt="spherical triangle formed on the surface of a sphere" src="https://cdn.freecodecamp.org/curriculum/project-euler/spherical-triangles.jpg" style="background-color: white; padding: 10px;">

Let $C(r)$ be the sphere with the centre (0,0,0) and radius $r$.

Let $Z(r)$ be the set of points on the surface of $C(r)$ with integer coordinates.

Let $T(r)$ be the set of spherical triangles with vertices in $Z(r)$. Degenerate spherical triangles, formed by three points on the same great arc, are <u>not</u> included in $T(r)$.

Let $A(r)$ be the area of the smallest spherical triangle in $T(r)$.

For example $A(14)$ is 3.294040 rounded to six decimal places.

Find $\displaystyle \sum_{r = 1}^{50} A(r)$. Give your answer rounded to six decimal places.

# --hints--

`sphericalTriangles()` should return `2717.751525`.

```js
assert.strictEqual(sphericalTriangles(), 2717.751525);
```

# --seed--

## --seed-contents--

```js
function sphericalTriangles() {

  return true;
}

sphericalTriangles();
```

# --solutions--

```js
// solution required
```