---
id: 5900f5241000cf542c510037
title: 'Problem 440: GCD and Tiling'
challengeType: 5
forumTopicId: 302112
dashedName: problem-440-gcd-and-tiling
---
# --description--
We want to tile a board of length $n$ and height 1 completely, with either 1 × 2 blocks or 1 × 1 blocks with a single decimal digit on top:
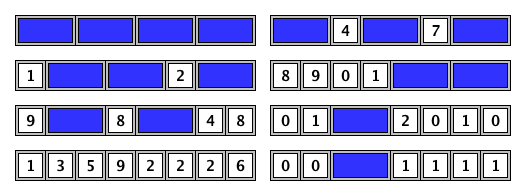
 For example, here are some of the ways to tile a board of length $n = 8$:
For example, here are some of the ways to tile a board of length $n = 8$:
 Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
For example, $T(1) = 10$ and $T(2) = 101$.
Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
For example:
$$\begin{align}
& S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
& S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
\end{align}$$
Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` should return `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```
Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
For example, $T(1) = 10$ and $T(2) = 101$.
Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
For example:
$$\begin{align}
& S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
& S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
\end{align}$$
Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` should return `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```
 For example, here are some of the ways to tile a board of length $n = 8$:
For example, here are some of the ways to tile a board of length $n = 8$:
 Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
For example, $T(1) = 10$ and $T(2) = 101$.
Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
For example:
$$\begin{align}
& S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
& S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
\end{align}$$
Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` should return `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```
Let $T(n)$ be the number of ways to tile a board of length $n$ as described above.
For example, $T(1) = 10$ and $T(2) = 101$.
Let $S(L)$ be the triple sum $\sum_{a, b, c} gcd(T(c^a), T(c^b))$ for $1 ≤ a, b, c ≤ L$.
For example:
$$\begin{align}
& S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\
& S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280.
\end{align}$$
Find $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` should return `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```