---
id: 5900f5431000cf542c510056
title: 'Problem 471: Triangle inscribed in ellipse'
challengeType: 5
forumTopicId: 302148
dashedName: problem-471-triangle-inscribed-in-ellipse
---
# --description--
The triangle $ΔABC$ is inscribed in an ellipse with equation $\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1$, $0 < 2b < a$, $a$ and $b$ integers.
Let $r(a, b)$ be the radius of the incircle of $ΔABC$ when the incircle has center $(2b, 0)$ and $A$ has coordinates $\left(\frac{a}{2}, \frac{\sqrt{3}}{2}b\right)$.
For example, $r(3, 1) = \frac{1}{2}, r(6, 2) = 1, r(12, 3) = 2$.
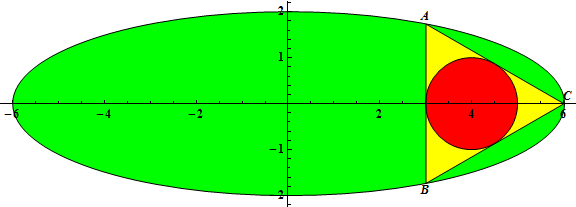
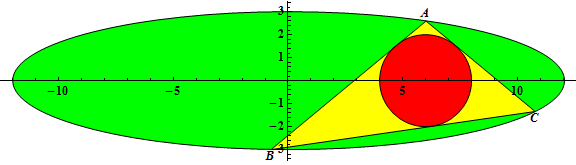 Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` should return a string.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```
Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` should return a string.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```

 Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` should return a string.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```
Let $G(n) = \sum_{a = 3}^n \sum_{b = 1}^{\left\lfloor\frac{a - 1}{2} \right\rfloor} r(a, b)$
You are given $G(10) = 20.59722222$, $G(100) = 19223.60980$ (rounded to 10 significant digits).
Find $G({10}^{11})$. Give your answer as a string in scientific notation rounded to 10 significant digits. Use a lowercase `e` to separate mantissa and exponent.
For $G(10)$ the answer would have been `2.059722222e1`
# --hints--
`triangleInscribedInEllipse()` should return a string.
```js
assert(typeof triangleInscribedInEllipse() === 'string');
```
`triangleInscribedInEllipse()` should return the string `1.895093981e31`.
```js
assert.strictEqual(triangleInscribedInEllipse(), '1.895093981e31');
```
# --seed--
## --seed-contents--
```js
function triangleInscribedInEllipse() {
return true;
}
triangleInscribedInEllipse();
```
# --solutions--
```js
// solution required
```