---
id: 5900f48b1000cf542c50ff9e
title: 'Problema 287: Codifica Quadtree (un semplice algoritmo di compressione)'
challengeType: 5
forumTopicId: 301938
dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
---
# --description--
La codifica Quadtree ci permette di descrivere un'immagine $2^N×2^N$ in bianco e nero come sequenza di bit (0 e 1). Queste sequenze devono essere lette da sinistra a destra in questo modo:
- il primo bit si occupa dell'intera regione $2^N×2^N$;
- "0" indica una suddivisione:
- la regione attuale $2^n×2^n$ è divisa in 4 sottoregioni di dimensione $2^{n - 1}×2^{n - 1}$,
- i bit successivi contengono la descrizione delle sottoregioni in alto a sinistra, in alto a destra, in basso a sinistra e in basso a destra - in quell'ordine;
- "10" indica che la regione corrente contiene solo pixel neri;
- "11" indica che la regione corrente contiene solo pixel bianchi.
Considera la seguente immagine 4×4 (i segni colorati indicano i luoghi in cui può verificarsi una divisione):
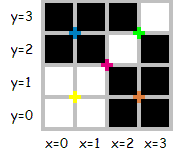 Questa immagine può essere descritta da diverse sequenze, ad esempio: "001010101001011111011010101010", di lunghezza 30, o "0100101111101110", di lunghezza 16, che è la sequenza minima per questa immagine.
Per un numero intero positivo $N$, definisci $D_N$ come l'immagine $2^N×2^N$ con il seguente schema di colorazione:
- il pixel con le coordinate $x = 0$, $y = 0$ corrisponde al pixel in basso a sinistra,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ allora il pixel è nero,
- altrimenti il pixel è bianco.
Qual è la lunghezza della sequenza minima che descrive $D_{24}$?
# --hints--
`quadtreeEncoding()` dovrebbe restituire `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
Questa immagine può essere descritta da diverse sequenze, ad esempio: "001010101001011111011010101010", di lunghezza 30, o "0100101111101110", di lunghezza 16, che è la sequenza minima per questa immagine.
Per un numero intero positivo $N$, definisci $D_N$ come l'immagine $2^N×2^N$ con il seguente schema di colorazione:
- il pixel con le coordinate $x = 0$, $y = 0$ corrisponde al pixel in basso a sinistra,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ allora il pixel è nero,
- altrimenti il pixel è bianco.
Qual è la lunghezza della sequenza minima che descrive $D_{24}$?
# --hints--
`quadtreeEncoding()` dovrebbe restituire `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
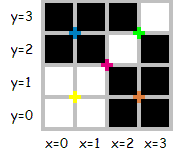 Questa immagine può essere descritta da diverse sequenze, ad esempio: "001010101001011111011010101010", di lunghezza 30, o "0100101111101110", di lunghezza 16, che è la sequenza minima per questa immagine.
Per un numero intero positivo $N$, definisci $D_N$ come l'immagine $2^N×2^N$ con il seguente schema di colorazione:
- il pixel con le coordinate $x = 0$, $y = 0$ corrisponde al pixel in basso a sinistra,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ allora il pixel è nero,
- altrimenti il pixel è bianco.
Qual è la lunghezza della sequenza minima che descrive $D_{24}$?
# --hints--
`quadtreeEncoding()` dovrebbe restituire `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
Questa immagine può essere descritta da diverse sequenze, ad esempio: "001010101001011111011010101010", di lunghezza 30, o "0100101111101110", di lunghezza 16, che è la sequenza minima per questa immagine.
Per un numero intero positivo $N$, definisci $D_N$ come l'immagine $2^N×2^N$ con il seguente schema di colorazione:
- il pixel con le coordinate $x = 0$, $y = 0$ corrisponde al pixel in basso a sinistra,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$ allora il pixel è nero,
- altrimenti il pixel è bianco.
Qual è la lunghezza della sequenza minima che descrive $D_{24}$?
# --hints--
`quadtreeEncoding()` dovrebbe restituire `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```