---
id: 5900f4ee1000cf542c510000
title: 'Problema 385: Ellissi dentro triangoli'
challengeType: 5
forumTopicId: 302049
dashedName: problem-385-ellipses-inside-triangles
---
# --description--
Per qualsiasi triangolo $T$ nel piano, si può dimostrare che esiste un'unica ellisse con l'area più grande che è completamente all'interno di $T$.
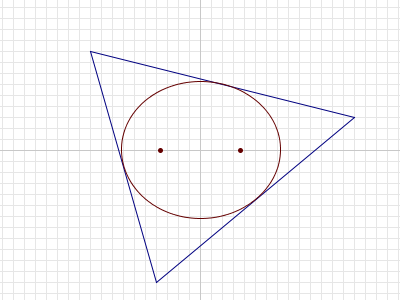 Per un dato $n$, considera i triangoli $T$ in modo che:
- i vertici di $T$ hanno coordinate intere con valore assoluto $≤ n$, e
- i fuochi1 della più grande ellisse dentro $T$ sono $(\sqrt{13}, 0)$ e $(-\sqrt{13}, 0)$.
Sia $A(n)$ la somma delle aree di tutti questi triangoli.
Ad esempio, se $n = 8$, ci sono due triangoli. I loro vertici sono (-4,-3), (-4,3), (8,0) e (4,3), (4,-3), (-8,0), e l'area di ciascun triangolo è 36. Quindi $A(8) = 36 + 36 = 72$.
Si può verificare che $A(10) = 252$, $A(100) = 34\\,632$ e che $A(1000) = 3\\,529\\,008$.
Trova $A(1\\,000\\,000\\,000)$.
1 I fuochi di una ellisse sono due punti $A$ e $B$ tali che per ogni punto $P$ del limite dell'ellisse, $AP + PB$ è costante.
# --hints--
`ellipsesInsideTriangles()` dovrebbe restituire `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```
Per un dato $n$, considera i triangoli $T$ in modo che:
- i vertici di $T$ hanno coordinate intere con valore assoluto $≤ n$, e
- i fuochi1 della più grande ellisse dentro $T$ sono $(\sqrt{13}, 0)$ e $(-\sqrt{13}, 0)$.
Sia $A(n)$ la somma delle aree di tutti questi triangoli.
Ad esempio, se $n = 8$, ci sono due triangoli. I loro vertici sono (-4,-3), (-4,3), (8,0) e (4,3), (4,-3), (-8,0), e l'area di ciascun triangolo è 36. Quindi $A(8) = 36 + 36 = 72$.
Si può verificare che $A(10) = 252$, $A(100) = 34\\,632$ e che $A(1000) = 3\\,529\\,008$.
Trova $A(1\\,000\\,000\\,000)$.
1 I fuochi di una ellisse sono due punti $A$ e $B$ tali che per ogni punto $P$ del limite dell'ellisse, $AP + PB$ è costante.
# --hints--
`ellipsesInsideTriangles()` dovrebbe restituire `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```
 Per un dato $n$, considera i triangoli $T$ in modo che:
- i vertici di $T$ hanno coordinate intere con valore assoluto $≤ n$, e
- i fuochi1 della più grande ellisse dentro $T$ sono $(\sqrt{13}, 0)$ e $(-\sqrt{13}, 0)$.
Sia $A(n)$ la somma delle aree di tutti questi triangoli.
Ad esempio, se $n = 8$, ci sono due triangoli. I loro vertici sono (-4,-3), (-4,3), (8,0) e (4,3), (4,-3), (-8,0), e l'area di ciascun triangolo è 36. Quindi $A(8) = 36 + 36 = 72$.
Si può verificare che $A(10) = 252$, $A(100) = 34\\,632$ e che $A(1000) = 3\\,529\\,008$.
Trova $A(1\\,000\\,000\\,000)$.
1 I fuochi di una ellisse sono due punti $A$ e $B$ tali che per ogni punto $P$ del limite dell'ellisse, $AP + PB$ è costante.
# --hints--
`ellipsesInsideTriangles()` dovrebbe restituire `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```
Per un dato $n$, considera i triangoli $T$ in modo che:
- i vertici di $T$ hanno coordinate intere con valore assoluto $≤ n$, e
- i fuochi1 della più grande ellisse dentro $T$ sono $(\sqrt{13}, 0)$ e $(-\sqrt{13}, 0)$.
Sia $A(n)$ la somma delle aree di tutti questi triangoli.
Ad esempio, se $n = 8$, ci sono due triangoli. I loro vertici sono (-4,-3), (-4,3), (8,0) e (4,3), (4,-3), (-8,0), e l'area di ciascun triangolo è 36. Quindi $A(8) = 36 + 36 = 72$.
Si può verificare che $A(10) = 252$, $A(100) = 34\\,632$ e che $A(1000) = 3\\,529\\,008$.
Trova $A(1\\,000\\,000\\,000)$.
1 I fuochi di una ellisse sono due punti $A$ e $B$ tali che per ogni punto $P$ del limite dell'ellisse, $AP + PB$ è costante.
# --hints--
`ellipsesInsideTriangles()` dovrebbe restituire `3776957309612154000`.
```js
assert.strictEqual(ellipsesInsideTriangles(), 3776957309612154000);
```
# --seed--
## --seed-contents--
```js
function ellipsesInsideTriangles() {
return true;
}
ellipsesInsideTriangles();
```
# --solutions--
```js
// solution required
```