---
id: 5900f5081000cf542c51001a
title: 'Problema 412: numerazione di Gnomon'
challengeType: 5
forumTopicId: 302081
dashedName: problem-412-gnomon-numbering
---
# --description--
Per i numeri interi, $m$, $n$ ($0 ≤ n < m$), sia $L(m, n)$ una griglia $m×m$ con la griglia $n×n$ in alto a destra rimossa.
Per esempio, $L(5, 3)$ è così:
Vogliamo numerare ogni cella di $L(m, n)$ con i numeri consecutivi 1, 2, 3, ... cosiccé il numero in ogni cella è più piccolo del numero sotto di esso e del numero alla sua sinistra.
Per esempio, ecco due modi validi di numerare $L(5, 3)$:
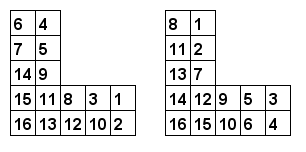Sia $LC(m, n$) il numero di modi validi di numerare $L(m, n)$. Si può verficare che $LC(3, 0) = 42$, $LC(5, 3) = 250\\,250$, $LC(6, 3) = 406\\,029\\,023\\,400$ e che $LC(10, 5)\bmod 76\\,543\\,217 = 61\\,251\\,715$.
Trova $LC(10\\,000, 5\\,000)\bmod 76\\,543\\,217$.
# --hints--
`gnomonNumbering()` dovrebbe restituire `38788800`.
```js
assert.strictEqual(gnomonNumbering(), 38788800);
```
# --seed--
## --seed-contents--
```js
function gnomonNumbering() {
return true;
}
gnomonNumbering();
```
# --solutions--
```js
// solution required
```