---
id: 5900f5241000cf542c510037
title: 'Problema 440: GCD e Tiling'
challengeType: 5
forumTopicId: 302112
dashedName: problem-440-gcd-and-tiling
---
# --description--
Vogliamo ricoprire completamente una tavola di lunghezza $n$ e altezza 1, con blocchi 1 × 2 o 1 × 1 con una singola cifra decimale in alto:
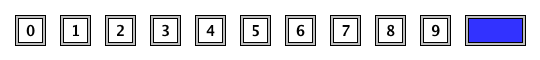 Per esempio, ecco alcuni dei modi per piastrellare una tavola di lunghezza $n = 8$:
Per esempio, ecco alcuni dei modi per piastrellare una tavola di lunghezza $n = 8$:
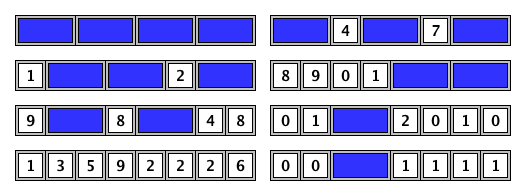 Sia $T(n)$ il numero di modi per piastrellare una tavola di lunghezza $n$ come descritto sopra.
Per esempio, $T(1) = 10$ e $T(2) = 101$.
Sia $S(L)$ la tripla somma $\sum_{a, b, c} gcd(T(c^a), T(c^b)$ per $1 ≤ a, b, c ≤ L$.
Per esempio:
$$\begin{align} & S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}$$
Trova $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` dovrebbe restituire `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```
Sia $T(n)$ il numero di modi per piastrellare una tavola di lunghezza $n$ come descritto sopra.
Per esempio, $T(1) = 10$ e $T(2) = 101$.
Sia $S(L)$ la tripla somma $\sum_{a, b, c} gcd(T(c^a), T(c^b)$ per $1 ≤ a, b, c ≤ L$.
Per esempio:
$$\begin{align} & S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}$$
Trova $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` dovrebbe restituire `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```
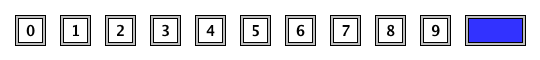 Per esempio, ecco alcuni dei modi per piastrellare una tavola di lunghezza $n = 8$:
Per esempio, ecco alcuni dei modi per piastrellare una tavola di lunghezza $n = 8$:
 Sia $T(n)$ il numero di modi per piastrellare una tavola di lunghezza $n$ come descritto sopra.
Per esempio, $T(1) = 10$ e $T(2) = 101$.
Sia $S(L)$ la tripla somma $\sum_{a, b, c} gcd(T(c^a), T(c^b)$ per $1 ≤ a, b, c ≤ L$.
Per esempio:
$$\begin{align} & S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}$$
Trova $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` dovrebbe restituire `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```
Sia $T(n)$ il numero di modi per piastrellare una tavola di lunghezza $n$ come descritto sopra.
Per esempio, $T(1) = 10$ e $T(2) = 101$.
Sia $S(L)$ la tripla somma $\sum_{a, b, c} gcd(T(c^a), T(c^b)$ per $1 ≤ a, b, c ≤ L$.
Per esempio:
$$\begin{align} & S(2) = 10\\,444 \\\\
& S(3) = 1\\,292\\,115\\,238\\,446\\,807\\,016\\,106\\,539\\,989 \\\\ & S(4)\bmod 987\\,898\\,789 = 670\\,616\\,280. \end{align}$$
Trova $S(2000)\bmod 987\\,898\\,789$.
# --hints--
`gcdAndTiling()` dovrebbe restituire `970746056`.
```js
assert.strictEqual(gcdAndTiling(), 970746056);
```
# --seed--
## --seed-contents--
```js
function gcdAndTiling() {
return true;
}
gcdAndTiling();
```
# --solutions--
```js
// solution required
```