---
id: 5900f42f1000cf542c50ff40
title: 'Problema 194: Configurações colorizadas'
challengeType: 5
forumTopicId: 301832
dashedName: problem-194-coloured-configurations
---
# --description--
Considere gráficos construídos com as unidades A:
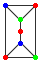 e B:
e B: 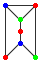 , onde as unidades são grudadas ao longo das arestas verticais, como no desenho
, onde as unidades são grudadas ao longo das arestas verticais, como no desenho 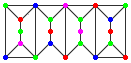 .
Uma configuração do tipo $(a,b,c)$ é um gráfico que faz parte de $a$ unidades A e $b$ unidades B, onde os vértices do gráfico são colorizados usando até $c$ cores, de modo que nenhum dois vértices adjacentes tenham a mesma cor. O gráfico composto acima é um exemplo de configuração do tipo $(2,2,6)$. De fato, é do tipo $(2,2,c)$ para todos os $c ≥ 4$
Considere $N(a,b,c)$ o número de configurações do tipo $(a,b,c)$. Por exemplo, $N(1,0,3) = 24$, $N(0,2,4) = 92928$ e $N(2,2,3) = 20736$.
Encontre os últimos 8 algarismos de $N(25,75,1984)$.
# --hints--
`coloredConfigurations()` deve retornar `61190912`.
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```
.
Uma configuração do tipo $(a,b,c)$ é um gráfico que faz parte de $a$ unidades A e $b$ unidades B, onde os vértices do gráfico são colorizados usando até $c$ cores, de modo que nenhum dois vértices adjacentes tenham a mesma cor. O gráfico composto acima é um exemplo de configuração do tipo $(2,2,6)$. De fato, é do tipo $(2,2,c)$ para todos os $c ≥ 4$
Considere $N(a,b,c)$ o número de configurações do tipo $(a,b,c)$. Por exemplo, $N(1,0,3) = 24$, $N(0,2,4) = 92928$ e $N(2,2,3) = 20736$.
Encontre os últimos 8 algarismos de $N(25,75,1984)$.
# --hints--
`coloredConfigurations()` deve retornar `61190912`.
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```
 e B:
e B:  , onde as unidades são grudadas ao longo das arestas verticais, como no desenho
, onde as unidades são grudadas ao longo das arestas verticais, como no desenho  .
Uma configuração do tipo $(a,b,c)$ é um gráfico que faz parte de $a$ unidades A e $b$ unidades B, onde os vértices do gráfico são colorizados usando até $c$ cores, de modo que nenhum dois vértices adjacentes tenham a mesma cor. O gráfico composto acima é um exemplo de configuração do tipo $(2,2,6)$. De fato, é do tipo $(2,2,c)$ para todos os $c ≥ 4$
Considere $N(a,b,c)$ o número de configurações do tipo $(a,b,c)$. Por exemplo, $N(1,0,3) = 24$, $N(0,2,4) = 92928$ e $N(2,2,3) = 20736$.
Encontre os últimos 8 algarismos de $N(25,75,1984)$.
# --hints--
`coloredConfigurations()` deve retornar `61190912`.
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```
.
Uma configuração do tipo $(a,b,c)$ é um gráfico que faz parte de $a$ unidades A e $b$ unidades B, onde os vértices do gráfico são colorizados usando até $c$ cores, de modo que nenhum dois vértices adjacentes tenham a mesma cor. O gráfico composto acima é um exemplo de configuração do tipo $(2,2,6)$. De fato, é do tipo $(2,2,c)$ para todos os $c ≥ 4$
Considere $N(a,b,c)$ o número de configurações do tipo $(a,b,c)$. Por exemplo, $N(1,0,3) = 24$, $N(0,2,4) = 92928$ e $N(2,2,3) = 20736$.
Encontre os últimos 8 algarismos de $N(25,75,1984)$.
# --hints--
`coloredConfigurations()` deve retornar `61190912`.
```js
assert.strictEqual(coloredConfigurations(), 61190912);
```
# --seed--
## --seed-contents--
```js
function coloredConfigurations() {
return true;
}
coloredConfigurations();
```
# --solutions--
```js
// solution required
```