---
id: 5900f4801000cf542c50ff92
title: 'Problema 275: Esculturas balanceadas'
challengeType: 5
forumTopicId: 301925
dashedName: problem-275-balanced-sculptures
---
# --description--
Vamos definir uma escultura balanceada de ordem $n$ da seguinte forma:
- Um poliminó composto por $n + 1$ blocos, sendo que $n$ são os "blocos" e o bloco restante (+1) é o "pedestal";
- o pedestal tem seu centro na posição ($x = 0$, $y = 0$);
- os blocos têm coordenadas $y$ maiores que zero (portanto o pedestal é o único bloco inferior);
- o centro de massa de todos os blocos, combinados, tem a coordenada $x$ igual a zero.
Ao contar as esculturas, todos os arranjos que são simplesmente reflexões sobre o eixo $y$, não são contados como distintos. Por exemplo, as 18 esculturas equilibradas de ordem 6 são mostradas abaixo. Observe que cada par de imagens espelhadas (sobre o eixo $y$) é contado como uma escultura:
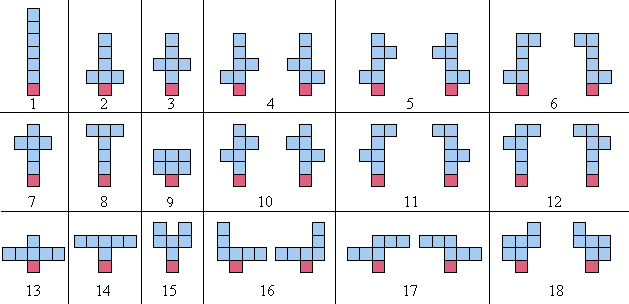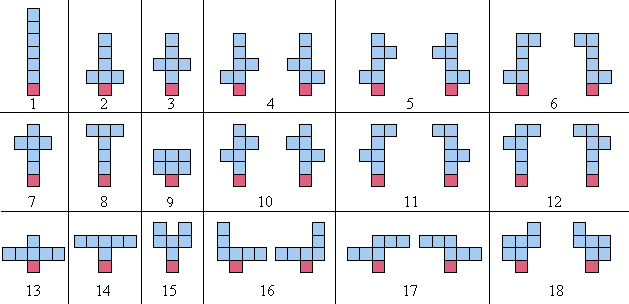Existem 964 esculturas equilibradas da ordem de 10 e 360505 da ordem de 15.
Quantas esculturas equilibradas existem na ordem de 18?
# --hints--
`balancedSculptures()` deve retornar `15030564`.
```js
assert.strictEqual(balancedSculptures(), 15030564);
```
# --seed--
## --seed-contents--
```js
function balancedSculptures() {
return true;
}
balancedSculptures();
```
# --solutions--
```js
// solution required
```