---
id: 5900f48b1000cf542c50ff9e
title: 'Problema 287: Codificação quadtree (um algoritmo simples de compressão)'
challengeType: 5
forumTopicId: 301938
dashedName: problem-287-quadtree-encoding-a-simple-compression-algorithm
---
# --description--
A codificação quadtree nos permite descrever uma imagem $2^N×2^N$ preta e branca como uma sequência de bits (0 e 1). Essas sequências devem ser lidas da esquerda para a direita assim:
- o primeiro bit tem a ver com a região completa do $2^N×2^N$;
- "0" indica uma divisão:
- a região atual $2^n×2^n$ é dividida em 4 sub-regiões de dimensão $2^{n - 1}×2^{n - 1}$,
- os próximos bits contêm a descrição das sub-regiões superior esquerda, superior direita, inferior esquerda e inferior direita - nessa ordem;
- "10" indica que a região atual contém apenas pixels pretos;
- "11" indica que a região atual contém apenas pixels brancos.
Considere a seguinte imagem 4×4 (pontos coloridos denotam lugares onde uma divisão pode ocorrer):
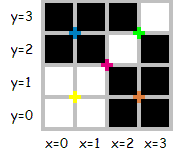 Essa imagem pode ser descrita por várias sequências, por exemplo: "001010101001011111011010101010", de comprimento 30, ou "0100101111101110", de comprimento 16, que é a sequência mínima para essa imagem.
Para um número inteiro positivo $N$, defina $D_N$ como a imagem $2^N×2^N$ com o seguinte esquema de cores:
- o pixel com coordenadas $x = 0$, $y = 0$ corresponde ao pixel inferior esquerdo,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, o pixel é preto,
- caso contrário, o pixel é branco.
Qual é o comprimento da sequência mínima que descreve $D_{24}$?
# --hints--
`quadtreeEncoding()` deve retornar `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
Essa imagem pode ser descrita por várias sequências, por exemplo: "001010101001011111011010101010", de comprimento 30, ou "0100101111101110", de comprimento 16, que é a sequência mínima para essa imagem.
Para um número inteiro positivo $N$, defina $D_N$ como a imagem $2^N×2^N$ com o seguinte esquema de cores:
- o pixel com coordenadas $x = 0$, $y = 0$ corresponde ao pixel inferior esquerdo,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, o pixel é preto,
- caso contrário, o pixel é branco.
Qual é o comprimento da sequência mínima que descreve $D_{24}$?
# --hints--
`quadtreeEncoding()` deve retornar `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
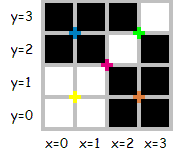 Essa imagem pode ser descrita por várias sequências, por exemplo: "001010101001011111011010101010", de comprimento 30, ou "0100101111101110", de comprimento 16, que é a sequência mínima para essa imagem.
Para um número inteiro positivo $N$, defina $D_N$ como a imagem $2^N×2^N$ com o seguinte esquema de cores:
- o pixel com coordenadas $x = 0$, $y = 0$ corresponde ao pixel inferior esquerdo,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, o pixel é preto,
- caso contrário, o pixel é branco.
Qual é o comprimento da sequência mínima que descreve $D_{24}$?
# --hints--
`quadtreeEncoding()` deve retornar `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```
Essa imagem pode ser descrita por várias sequências, por exemplo: "001010101001011111011010101010", de comprimento 30, ou "0100101111101110", de comprimento 16, que é a sequência mínima para essa imagem.
Para um número inteiro positivo $N$, defina $D_N$ como a imagem $2^N×2^N$ com o seguinte esquema de cores:
- o pixel com coordenadas $x = 0$, $y = 0$ corresponde ao pixel inferior esquerdo,
- se ${(x - 2^{N - 1})}^2 + {(y - 2^{N - 1})}^2 ≤ 2^{2N - 2}$, o pixel é preto,
- caso contrário, o pixel é branco.
Qual é o comprimento da sequência mínima que descreve $D_{24}$?
# --hints--
`quadtreeEncoding()` deve retornar `313135496`.
```js
assert.strictEqual(quadtreeEncoding(), 313135496);
```
# --seed--
## --seed-contents--
```js
function quadtreeEncoding() {
return true;
}
quadtreeEncoding();
```
# --solutions--
```js
// solution required
```